
CALCULUS I
Solutions to Practice Problems
Review
Paul Dawkins
Calculus I
© 2007 Paul Dawkins
i
http://tutorial.math.lamar.edu/terms.aspx
Table of Contents
Preface ............................................................................................................................................ 1
Review............................................................................................................................................. 1
Review : Functions ..................................................................................................................................... 1
Review : Inverse Functions .......................................................................................................................25
Review : Trig Functions ............................................................................................................................34
Review : Solving Trig Equations ..............................................................................................................51
Review : Solving Trig Equations with Calculators, Part I ........................................................................80
Review : Solving Trig Equations with Calculators, Part II .....................................................................102
Review : Exponential Functions .............................................................................................................118
Review : Logarithm Functions ................................................................................................................122
Review : Exponential and Logarithm Equations .....................................................................................130
Review : Common Graphs ......................................................................................................................148
Preface
Here are the solutions to the practice problems for my Calculus I notes. Some solutions will have
more or less detail than other solutions. The level of detail in each solution will depend up on
several issues. If the section is a review section, this mostly applies to problems in the first
chapter, there will probably not be as much detail to the solutions given that the problems really
should be review. As the difficulty level of the problems increases less detail will go into the
basics of the solution under the assumption that if you’ve reached the level of working the harder
problems then you will probably already understand the basics fairly well and won’t need all the
explanation.
This document was written with presentation on the web in mind. On the web most solutions are
broken down into steps and many of the steps have hints. Each hint on the web is given as a
popup however in this document they are listed prior to each step. Also, on the web each step can
be viewed individually by clicking on links while in this document they are all showing. Also,
there are liable to be some formatting parts in this document intended for help in generating the
web pages that haven’t been removed here. These issues may make the solutions a little difficult
to follow at times, but they should still be readable.
Review
Review : Functions
1. Perform the indicated function evaluations for
( )
2
3 5
2
f x
x
x
= −
−
.

Calculus I
© 2007 Paul Dawkins
2
http://tutorial.math.lamar.edu/terms.aspx
(a)
( )
4
f
(b)
( )
0
f
(c)
( )
3
f
−
(d)
(
)
6
f
t
−
(e)
(
)
7 4
f
x
−
(f)
(
)
f x h
+
(a)
( )
4
f
[Solution]
( )
( ) ( )
2
4
3 5 4
2 4
49
f
= −
−
= −
(b)
( )
0
f
[Solution]
( )
( ) ( )
2
0
3 5 0
2 0
3
f
= −
−
=
(c)
( )
3
f
−
[Solution]
( )
( ) ( )
2
3
3 5
3
2
3
0
f
− = − − − −
=
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(d)
(
)
6
f
t
−
[Solution]
(
)
(
) (
)
(
)
(
)
2
2
2
2
6
3 5 6
2 6
3 5 6
2 36 12
3 30 5
72 24
2
99 29
2
f
t
t
t
t
t
t
t
t
t
t
t
− = −
− −
−
= −
− −
−
+
= −
+ −
+
−
= − +
−
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(e)
(
)
7 4
f
x
−
[Solution]
(
)
(
) (
)
(
)
(
)
2
2
2
2
7 4
3 5 7 4
2 7 4
3 5 7 4
2 49 56
16
3 35 20
98 112
32
130 132
32
f
x
x
x
x
x
x
x
x
x
x
x
−
= −
−
−
−
= −
−
−
−
+
= −
+
−
+
−
= −
+
−
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
Also, don’t get excited about the fact that there is both an x and an h here. This works exactly the
same way as the first three it will just have a little more algebra involved.
(f)
(
)
f x h
+
[Solution]

Calculus I
© 2007 Paul Dawkins
3
http://tutorial.math.lamar.edu/terms.aspx
(
)
(
) (
)
(
)
(
)
2
2
2
2
2
3 5
2
3 5
2
2
3 5
5
2
4
2
f x
h
x
h
x
h
x
h
x
xh
h
x
h
x
xh
h
+
= −
+
−
+
= −
+
−
+
+
= −
−
−
−
−
2. Perform the indicated function evaluations for
( )
2
6
t
g t
t
=
+
.
(a)
( )
0
g
(b)
( )
3
g
−
(c)
( )
10
g
(d)
( )
2
g x
(e)
(
)
g t
h
+
(f)
(
)
2
3
1
g t
t
− +
(a)
( )
0
g
[Solution]
( )
( )
0
0
0
0
2 0
6
6
g
=
= =
+
(b)
( )
3
g
−
[Solution]
( )
( )
3
3
3
2
3
6
0
g
−
−
− =
=
− +
The minute we see the division by zero we know that
( )
3
g
−
does not exist.
(c)
( )
10
g
[Solution]
( )
( )
10
10
5
10
2 10
6
26
13
g
=
=
=
+
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(d)
( )
2
g x
[Solution]
( )
2
2
2
2
6
x
g x
x
=
+
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
Also, don’t get excited about the fact that there is both a t and an h here. This works exactly the
same way as the first three it will just have a little more algebra involved.
(e)
(
)
g t
h
+
[Solution]

Calculus I
© 2007 Paul Dawkins
4
http://tutorial.math.lamar.edu/terms.aspx
(
)
(
)
2
6
2
2
6
t
h
t
h
g t
h
t
h
t
h
+
+
+
=
=
+
+
+
+
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(f)
(
)
2
3
1
g t
t
− +
[Solution]
(
) (
)
2
2
2
2
2
3
1
3
1
3
1
2
6
8
2
3
1
6
t
t
t
t
g t
t
t
t
t
t
− +
− +
− + =
=
− +
− + +
3. Perform the indicated function evaluations for
( )
2
1
h z
z
=
−
.
(a)
( )
0
h
(b)
( )
1
2
h
−
(c)
( )
1
2
h
(d)
( )
9
h
z
(e)
(
)
2
2
h z
z
−
(f)
(
)
h z
k
+
(a)
( )
0
h
[Solution]
( )
2
0
1 0
1 1
h
=
−
=
=
(b)
( )
1
2
h
−
[Solution]
2
1
1
3
3
1
2
2
4
2
h
−
=
− −
=
=
(c)
( )
1
2
h
[Solution]
2
1
1
3
3
1
2
2
4
2
h
=
−
=
=
Hint : Don’t let the fact that there are new variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(d)
( )
9
h
z
[Solution]
( )
( )
2
2
9
1
9
1 81
h
z
z
z
=
−
=
−
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(e)
(
)
2
2
h z
z
−
[Solution]

Calculus I
© 2007 Paul Dawkins
5
http://tutorial.math.lamar.edu/terms.aspx
(
)
(
)
(
)
2
2
2
4
3
2
2
3
4
2
1
2
1
4
4
1 4
4
h z
z
z
z
z
z
z
z
z
z
−
=
−
−
=
−
−
+
=
−
+
−
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
Also, don’t get excited about the fact that there is both a z and a k here. This works exactly the
same way as the first three it will just have a little more algebra involved.
(f)
(
)
h z
k
+
[Solution]
(
)
(
)
(
)
2
2
2
2
2
1
1
2
1
2
h z
k
z
k
z
zk
k
z
zk
k
+
=
− +
=
−
+
+
=
−
−
−
4. Perform the indicated function evaluations for
( )
4
3
1
R x
x
x
=
+ −
+
.
(a)
( )
0
R
(b)
( )
6
R
(c)
( )
9
R
−
(d)
(
)
1
R x
+
(e)
(
)
4
3
R x
−
(f)
(
)
1
1
x
R
−
(a)
( )
0
R
[Solution]
( )
4
0
3 0
3
4
0 1
R
=
+ −
=
−
+
(b)
( )
6
R
[Solution]
( )
4
4
4
17
6
3 6
9
3
6 1
7
7
7
R
=
+ −
=
− = − =
+
(c)
( )
9
R
−
[Solution]
( )
( )
4
4
9
3
9
6
9 1
8
R
− =
+ − −
= − −
− +
−
In this class we only deal with functions that give real values as answers. Therefore, because we
have the square root of a negative number in the first term this function is not defined.
Note that the fact that the second term is perfectly acceptable has no bearing on the fact that the
function will not be defined here. If any portion of the function is not defined upon evaluation
then the whole function is not defined at that point. Also note that if we allow complex numbers
this function will be defined.
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(d)
(
)
1
R x
+
[Solution]

Calculus I
© 2007 Paul Dawkins
6
http://tutorial.math.lamar.edu/terms.aspx
(
)
(
) ( )
4
4
1
3
1
4
1
1
2
R x
x
x
x
x
+ =
+
+ −
=
+ −
+ +
+
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(e)
(
)
4
3
R x
−
[Solution]
(
)
(
) ( )
4
4
4
2
4
4
4
4
4
4
3
3
3
2
2
3
1
R x
x
x
x
x
x
x
− =
+
−
−
=
−
=
−
−
−
− +
Hint : Don’t let the fact that there are now variables here instead of numbers get you confused.
This works exactly the same way as the first three it will just have a little more algebra involved.
(f)
(
)
1
1
x
R
−
[Solution]
(
)
1
1
1
1
4
1
4
1
1
3
1
2
2
4
1
1
x
x
R
x
x
x
x
x
− =
+
− −
=
+ − =
+ −
− +
5. The difference quotient of a function
( )
f x
is defined to be,
(
)
( )
f x
h
f x
h
+
−
compute the difference quotient for
( )
4
9
f x
x
=
−
.
Hint : Compute
(
)
f x h
+
, then compute the numerator and finally compute the difference
quotient.
Step 1
(
) (
)
4
9
4
4
9
f x
h
x
h
x
h
+
=
+ − =
+
−
Step 2
(
)
( )
(
)
4
4
9
4
9
4
f x
h
f x
x
h
x
h
+ −
=
+
− −
− =
Step 3
(
)
( )
4
4
f x
h
f x
h
h
h
+
−
=
=

Calculus I
© 2007 Paul Dawkins
7
http://tutorial.math.lamar.edu/terms.aspx
6. The difference quotient of a function
( )
f x
is defined to be,
(
)
( )
f x
h
f x
h
+
−
compute the difference quotient for
( )
2
6
g x
x
= −
.
Hint : Don’t get excited about the fact that the function is now named
( )
g x
, the difference
quotient still works in the same manner it just has g’s instead of f’s now. So, compute
(
)
g x
h
+
,
then compute the numerator and finally compute the difference quotient.
Step 1
(
)
(
)
2
2
2
6
6
2
g x
h
x
h
x
xh
h
+
= −
+
= −
−
−
Step 2
(
)
( )
(
)
2
2
2
2
6
2
6
2
g x
h
g x
x
xh
h
x
xh
h
+
−
= −
−
−
− −
= −
−
Step 3
(
) ( )
2
2
2
g x
h
g x
xh h
x h
h
h
+
−
−
−
=
= − −
7. The difference quotient of a function
( )
f x
is defined to be,
(
)
( )
f x
h
f x
h
+
−
compute the difference quotient for
( )
2
2
3
9
f t
t
t
=
− +
.
Hint : Don’t get excited about the fact that the function is now
( )
f t
, the difference quotient still
works in the same manner it just has t’s instead of x’s now. So, compute
(
)
f t
h
+
, then compute
the numerator and finally compute the difference quotient.
Step 1
(
)
(
)
(
)
(
)
2
2
2
2
2
2
3
9
2
2
3
3
9
2
4
2
3
3
9
f t
h
t
h
t
h
t
th
h
t
h
t
th
h
t
h
+
=
+
−
+
+ =
+
+
− −
+
=
+
+
− −
+
Step 2
(
)
( )
(
)
2
2
2
2
2
4
2
3
3
9
2
3
9
4
2
3
f t
h
f t
t
th
h
t
h
t
t
th
h
h
+
−
=
+
+
− −
+ −
− +
=
+
−

Calculus I
© 2007 Paul Dawkins
8
http://tutorial.math.lamar.edu/terms.aspx
Step 3
(
)
( )
2
4
2
3
4
2
3
f t
h
f t
th
h
h
t
h
h
h
+
−
+
−
=
= +
−
8. The difference quotient of a function
( )
f x
is defined to be,
(
)
( )
f x
h
f x
h
+
−
compute the difference quotient for
( )
1
2
y z
z
=
+
.
Hint : Don’t get excited about the fact that the function is now named
( )
y z
, the difference
quotient still works in the same manner it just has y’s and z’s instead of f’s and x’s now. So,
compute
(
)
y z
h
+
, then compute the numerator and finally compute the difference quotient.
Step 1
(
)
1
2
y z
h
z
h
+
=
+ +
Step 2
(
) ( )
(
)
(
)(
) (
)(
)
2
2
1
1
2
2
2
2
2
2
z
z
h
h
y z
h
y z
z
h
z
z
h
z
z
h
z
+ − + +
−
+
−
=
−
=
=
+ +
+
+ +
+
+ +
+
Note that, when dealing with difference quotients, it will almost always be advisable to combine
rational expressions into a single term in preparation of the next step.
Step 3
(
) ( )
(
) ( )
(
)
(
)(
)
(
)(
)
1
1
1
2
2
2
2
y z
h
y z
h
h z
h
h z
h
h
h
z
h
z
z
h
z
+
−
−
−
=
+
−
=
=
+ +
+
+ +
+
In this step we rewrote the difference quotient a little to make the numerator a little easier to deal
with. All that we’re doing here is using the fact that,
( )
( )
1
1
a
a
a
b
b
b
=
=

Calculus I
© 2007 Paul Dawkins
9
http://tutorial.math.lamar.edu/terms.aspx
9. The difference quotient of a function
( )
f x
is defined to be,
(
)
( )
f x
h
f x
h
+
−
compute the difference quotient for
( )
2
3
t
A t
t
=
−
.
Hint : Don’t get excited about the fact that the function is now named
( )
A t
, the difference
quotient still works in the same manner it just has A’s and t’s instead of f’s and x’s now. So,
compute
(
)
A t
h
+
, then compute the numerator and finally compute the difference quotient.
Step 1
(
)
(
)
(
)
2
2
2
3
3
t
h
t
h
A t
h
t
h
t
h
+
+
+
=
=
− +
− −
Step 2
(
)
( )
(
)(
)
(
)
(
)(
)
(
)
(
)(
)
(
)(
)
2
2
2
2
3
2 3
2
2
2
3
3
3
3
6
2
6
2
6
2
2
6
3
3
3
3
t
h
t
t
t
h
t
h
t
A t
h
A t
t
h
t
t
h
t
t
t
h
ht
t
t
th
h
t
h
t
t
h
t
+
− −
− −
+
+
−
=
−
=
− −
−
− −
−
−
+
−
−
−
−
=
=
− −
−
− −
−
Note that, when dealing with difference quotients, it will almost always be advisable to combine
rational expressions into a single term in preparation of the next step. Also, when doing this
don’t forget to simplify the numerator as much as possible. With most difference quotients you’ll
see a lot of cancelation as we did here.
Step 3
(
)
( )
(
)
( )
(
)
(
)(
)
(
)(
)
1
1
6
6
3
3
3
3
A t
h
A t
h
A t
h
A t
h
h
h
t
h
t
t
h
t
+
−
=
+
−
=
=
− −
−
− −
−
In this step we rewrote the difference quotient a little to make the numerator a little easier to deal
with. All that we’re doing here is using the fact that,
( )
( )
1
1
a
a
a
b
b
b
=
=
10. Determine all the roots of
( )
5
4
3
4
32
f x
x
x
x
=
−
−
.

Calculus I
© 2007 Paul Dawkins
10
http://tutorial.math.lamar.edu/terms.aspx
[Solution]
Set the function equal to zero and factor the left side.
(
)
(
)(
)
5
4
3
3
2
3
4
32
4
32
8
4
0
x
x
x
x
x
x
x
x
x
−
−
=
−
−
=
−
+
=
After factoring we can see that the three roots of this function are,
4,
0,
8
x
x
x
= −
=
=
11. Determine all the roots of
( )
2
12
11
5
R y
y
y
=
+
−
.
[Solution]
Set the function equal to zero and factor the left side.
(
)(
)
2
12
11
5
4
5 3
1
0
y
y
y
y
+
− =
+
− =
After factoring we see that the two roots of this function are,
5
1
,
4
3
y
y
= −
=
12. Determine all the roots of
( )
2
18 3
2
h t
t
t
=
− −
.
[Solution]
Set the function equal to zero and because the left side will not factor we’ll need to use the
quadratic formula to find the roots of the function.
2
18 3
2
0
t
t
− −
=
( )
( )( )
( )
( )( )
(
)
2
3
3
4
2 18
3
9 17
3
153
3 3 17
3
1
17
2
2
4
4
4
4
t
±
−
− −
±
±
±
=
=
=
=
= −
±
−
−
−
−
So, the quadratic formula gives the following two roots of the function,
(
)
(
)
3
3
1
17
2.342329
1
17
3.842329
4
4
−
+
=
−
−
= −
Calculus I
© 2007 Paul Dawkins
11
http://tutorial.math.lamar.edu/terms.aspx
13. Determine all the roots of
( )
3
2
7
g x
x
x
x
=
+
−
.
[Solution]
Set the equation equal to zero and factor the left side as much as possible.
(
)
3
2
2
7
7
1
0
x
x
x
x x
x
+
− =
+
− =
So, we can see that one root is
0
x
=
and because the quadratic doesn’t factor we’ll need to use
the quadratic formula on that to get the remaining two roots.
( )
( )( )
( )
4
7
7
4 1
1
7
53
2 1
2
x
− ±
−
−
− ±
=
=
We then have the following three roots of the function,
7
53
7
53
0,
0.140055,
7.140055
2
2
x
− +
− −
=
=
= −
14. Determine all the roots of
( )
4
2
6
27
W x
x
x
=
+
−
.
[Solution]
Set the function equal to zero and factor the left side as much as possible.
(
)(
)
4
2
2
2
6
27
3
9
0
x
x
x
x
+
−
=
−
+
=
Don’t so locked into quadratic equations that the minute you see an equation that is not quadratic
you decide you can’t deal with it. While this function was not a quadratic it still factored in an
obvious manner.
Now, the second term will never be zero (for any real value of x anyway and in this class those
tend to be the only ones we are interested in) and so we can ignore that term. The first will be
zero if,
2
2
3
0
3
3
x
x
x
− =
⇒
=
⇒
= ±
So, we have two real roots of this function. Note that if we allowed complex roots (which again,
we aren’t really interested in for this course) there would also be two complex roots from the
second term as well.

Calculus I
© 2007 Paul Dawkins
12
http://tutorial.math.lamar.edu/terms.aspx
15. Determine all the roots of
( )
5
4
3
3
7
8
f t
t
t
t
= −
−
.
[Solution]
Set the function equal to zero and factor the left side as much as possible.
5
4
2
1
1
1
3
3
3
3
3
3
7
8
7
8
8
1
0
t
t
t
t t
t
t t
t
−
− =
−
−
=
−
+ =
Don’t so locked into quadratic equations that the minute you see an equation that is not quadratic
you decide you can’t deal with it. While this function was not a quadratic it still factored, it just
wasn’t as obvious that it did in this case. You could have clearly seen that if factored if it had
been,
(
)
2
7
8
t t
t
− −
but notice that the only real difference is that the exponents are fractions now, but it still has the
same basic form and so can be factored.
Okay, back to the problem. From the factored form we get,
( )
1
1
3
3
3
1
1
3
3
3
0
8
0
8
8
512
1
0
1
1
1
t
t
t
t
t
t
t
=
− =
⇒
=
⇒
=
=
+ =
⇒
= −
⇒
= −
= −
So, the function has three roots,
1,
0,
512
t
t
t
= −
=
=
16. Determine all the roots of
( )
4
5
8
z
h z
z
z
=
−
−
−
.
[Solution]
Set the function equal to zero and clear the denominator by multiplying by the least common
denominator,
(
)(
)
5
8
z
z
−
−
, and then solve the resulting equation.

Calculus I
© 2007 Paul Dawkins
13
http://tutorial.math.lamar.edu/terms.aspx
(
)(
)
(
) (
)
(
)(
)
2
4
5
8
0
5
8
8
4
5
0
12
20
0
10
2
0
z
z
z
z
z
z z
z
z
z
z
z
−
−
−
=
−
−
− −
−
=
−
+
=
−
−
=
So, it looks like the function has two roots,
2
z
=
and
10
z
=
however recall that because we
started off with a function that contained rational expressions we need to go back to the original
function and make sure that neither of these will create a division by zero problem in the original
function. In this case neither do and so the two roots are,
2
10
z
z
=
=
17. Determine all the roots of
( )
2
4
1
2
3
w
w
g w
w
w
−
=
+
+
−
.
[Solution]
Set the function equal to zero and clear the denominator by multiplying by the least common
denominator,
(
)(
)
1 2
3
w
w
+
−
, and then solve the resulting equation.
(
)(
)
(
) (
)(
)
2
2
4
1 2
3
0
1
2
3
2
2
3
4
1
0
5
9
4
0
w
w
w
w
w
w
w
w
w
w
w
w
−
+
−
+
=
+
−
− +
−
+ =
−
− =
This quadratic doesn’t factor so we’ll need to use the quadratic formula to get the solution.
( )
( )( )
( )
2
9
9
4 5
4
9
161
2 5
10
w
±
−
−
−
±
=
=
So, it looks like this function has the following two roots,
9
161
9
161
2.168858
0.368858
10
10
+
−
=
= −
Recall that because we started off with a function that contained rational expressions we need to
go back to the original function and make sure that neither of these will create a division by zero
problem in the original function. Neither of these do and so they are the two roots of this
function.

Calculus I
© 2007 Paul Dawkins
14
http://tutorial.math.lamar.edu/terms.aspx
18. Find the domain and range of
( )
2
3
2
1
Y t
t
t
=
− +
.
[Solution]
This is a polynomial (a 2
nd
degree polynomial in fact) and so we know that we can plug any value
of t into the function and so the domain is all real numbers or,
(
)
Domain :
or
,
t
− ∞ < < ∞
−∞ ∞
The graph of this 2
nd
degree polynomial (or quadratic) is a
parabola
that opens upwards (because
the coefficient of the
2
t
is positive) and so we know that the vertex will be the lowest point on
the graph. This also means that the function will take on all values greater than or equal to the y-
coordinate of the vertex which will in turn give us the range.
So, we need the vertex of the parabola. The t-coordinate is,
( )
2
1
2 3
3
t
−
= −
=
and the y coordinate is then,
1
2
3
3
Y
=
.
The range is then,
2
Range :
,
3
∞
19. Find the domain and range of
( )
2
4
7
g z
z
z
= − −
+
.
[Solution]
This is a polynomial (a 2
nd
degree polynomial in fact) and so we know that we can plug any value
of z into the function and so the domain is all real numbers or,
(
)
Domain :
or
,
z
− ∞ < < ∞
−∞ ∞
The graph of this 2
nd
degree polynomial (or quadratic) is a
parabola
that opens downwards
(because the coefficient of the
2
z
is negative) and so we know that the vertex will be the highest

Calculus I
© 2007 Paul Dawkins
15
http://tutorial.math.lamar.edu/terms.aspx
point on the graph. This also means that the function will take on all values less than or equal to
the y-coordinate of the vertex which will in turn give us the range.
So, we need the vertex of the parabola. The z-coordinate is,
( )
4
2
2
1
z
−
= −
= −
−
and the y coordinate is then,
( )
2
11
g
− =
.
The range is then,
(
]
Range :
,11
−∞
20. Find the domain and range of
( )
2
2
1
f z
z
= +
+
.
[Solution]
We know that when we have square roots that we can’t take the square root of a negative number.
However, because,
2
1 1
z
+ ≥
we will never be taking the square root of a negative number in this case and so the domain is all
real numbers or,
(
)
Domain :
or
,
z
− ∞ < < ∞
−∞ ∞
For the range we need to recall that square roots will only return values that are positive or zero
and in fact the only way we can get zero out of a square root will be if we take the square root of
zero. For our function, as we’ve already noted, the quantity that is under the root is always at
least 1 and so this root will never be zero. Also recall that we have the following fact about
square roots,
If
1 then
1
x
x
≥
≥
So, we now know that,
2
1 1
z
+ ≥
Finally, we are adding 2 onto the root and so we know that the function must always be greater
than or equal to 3 and so the range is,
[
)
Range : 3,
∞

Calculus I
© 2007 Paul Dawkins
16
http://tutorial.math.lamar.edu/terms.aspx
21. Find the domain and range of
( )
3 14 3
h y
y
= −
+
.
[Solution]
In this case we need to require that,
14
14 3
0
3
y
y
+
≥
⇒
≥ −
in order to make sure that we don’t take the square root of negative numbers. The domain is then,
14
14
Domain :
or
,
3
3
y
−
≤ < ∞
−
∞
For the range for this function we can notice that the quantity under the root can be zero (if
14
3
y
= −
). Also note that because the quantity under the root is a line it will take on all positive
values and so the square root will in turn take on all positive value and zero. The square root is
then multiplied by -3. This won’t change the fact that the root can be zero, but the minus sign
will change the sign of the non-zero values from positive to negative. The 3 will only affect the
general size of the square root but it won’t change the fact that the square root will still take on all
positive (or negative after we add in the minus sign) values.
The range is then,
(
]
Range :
, 0
−∞
22. Find the domain and range of
( )
5
8
M x
x
= − +
.
[Solution]
We’re dealing with an absolute value here and the quantity inside is a line, which we can plug all
values of x into, and so the domain is all real numbers or,
(
)
Domain :
or
,
x
− ∞ < < ∞
−∞ ∞
For the range let’s again note that the quantity inside the absolute value is a linear function that
will take on all real values. We also know that absolute value functions will never be negative
and will only be zero if we take the absolute value of zero. So we now know that,
8
0
x
+ ≥

Calculus I
© 2007 Paul Dawkins
17
http://tutorial.math.lamar.edu/terms.aspx
However, we are subtracting this from 5 and so we’ll be subtracting a positive or zero number
from 5 and so the range is,
(
]
Range :
, 5
−∞
23. Find the domain of
( )
3
3
1
12
7
w
w
f w
w
−
+
=
−
.
[Solution]
In this case we need to avoid division by zero issues and so we’ll need to determine where the
denominator is zero. To do this we will solve,
7
12
7
0
12
w
w
− =
⇒
=
We can plug all other values of w into the function without any problems and so the domain is,
7
Domain : All real numbers except
12
w
=
24. Find the domain of
( )
3
2
5
10
9
R z
z
z
z
=
+
+
.
[Solution]
In this case we need to avoid division by zero issues and so we’ll need to determine where the
denominator is zero. To do this we will solve,
(
)
(
)(
)
3
2
2
10
9
10
9
1
9
0
0,
1,
9
z
z
z
z z
z
z z
z
z
z
z
+
+
=
+
+
=
+
+
=
⇒
=
= −
= −
The three values above are the only values of z that we can’t plug into the function. All other
values of z can be plugged into the function and will return real values. The domain is then,
Domain : All real numbers except
0,
1,
9
z
z
z
=
= −
= −
25. Find the domain of
( )
3
2
6
7
4
t
t
g t
t
t
−
=
− −
.

Calculus I
© 2007 Paul Dawkins
18
http://tutorial.math.lamar.edu/terms.aspx
[Solution]
In this case we need to avoid division by zero issues and so we’ll need to determine where the
denominator is zero. To do this we will solve,
( )
( )( )
( )
(
)
2
2
1
1
4
4 7
1
7
4
0
1
113
2
4
8
t
t
t
±
−
− −
− −
=
⇒
=
= −
±
−
The two values above are the only values of t that we can’t plug into the function. All other
values of t can be plugged into the function and will return real values. The domain is then,
(
)
1
Domain : All real numbers except
1
113
8
t
= −
±
26. Find the domain of
( )
2
25
g x
x
=
−
.
[Solution]
In this case we need to avoid square roots of negative numbers and so we need to require,
2
25
0
x
−
≥
Note that once we have the original inequality written down we can do a little rewriting of things
as follows to make things a little easier to see.
2
25
5
5
x
x
≤
⇒
− ≤ ≤
At this point it should be pretty easy to find the values of x that will keep the quantity under the
radical positive or zero and so we won’t need to do a numberline or sign table to determine the
range.
The domain is then,
Domain : 5
5
x
− ≤ ≤
27. Find the domain of
( )
4
3
2
20
h x
x
x
x
=
− −
.
Calculus I
© 2007 Paul Dawkins
19
http://tutorial.math.lamar.edu/terms.aspx
Step 1 Hint : We need to avoid negative numbers under the square root and because the quantity
under the root is a polynomial we know that it can only change sign if it goes through zero and so
we first need to determine where it is zero.
[Show Step One]
In this case we need to avoid square roots of negative numbers and so we need to require,
(
)
(
)(
)
4
3
2
2
2
2
20
20
5
4
0
x
x
x
x
x
x
x
x
x
−
−
=
− −
=
−
+
≥
Once we have the polynomial in factored form we can see that the left side will be zero at
0
x
=
,
4
x
= −
and
5
x
=
. Because the quantity under the radical is a polynomial we know that it can
only change sign if it goes through zero and so these are the only points the only places where the
polynomial on the left can change sign.
Step 2 Hint : Because the polynomial can only change sign at these points we know that it will be
the same sign in each region defined by these points and so all we need to know is the value of
the polynomial as a single point in each region.
[Show Step Two]
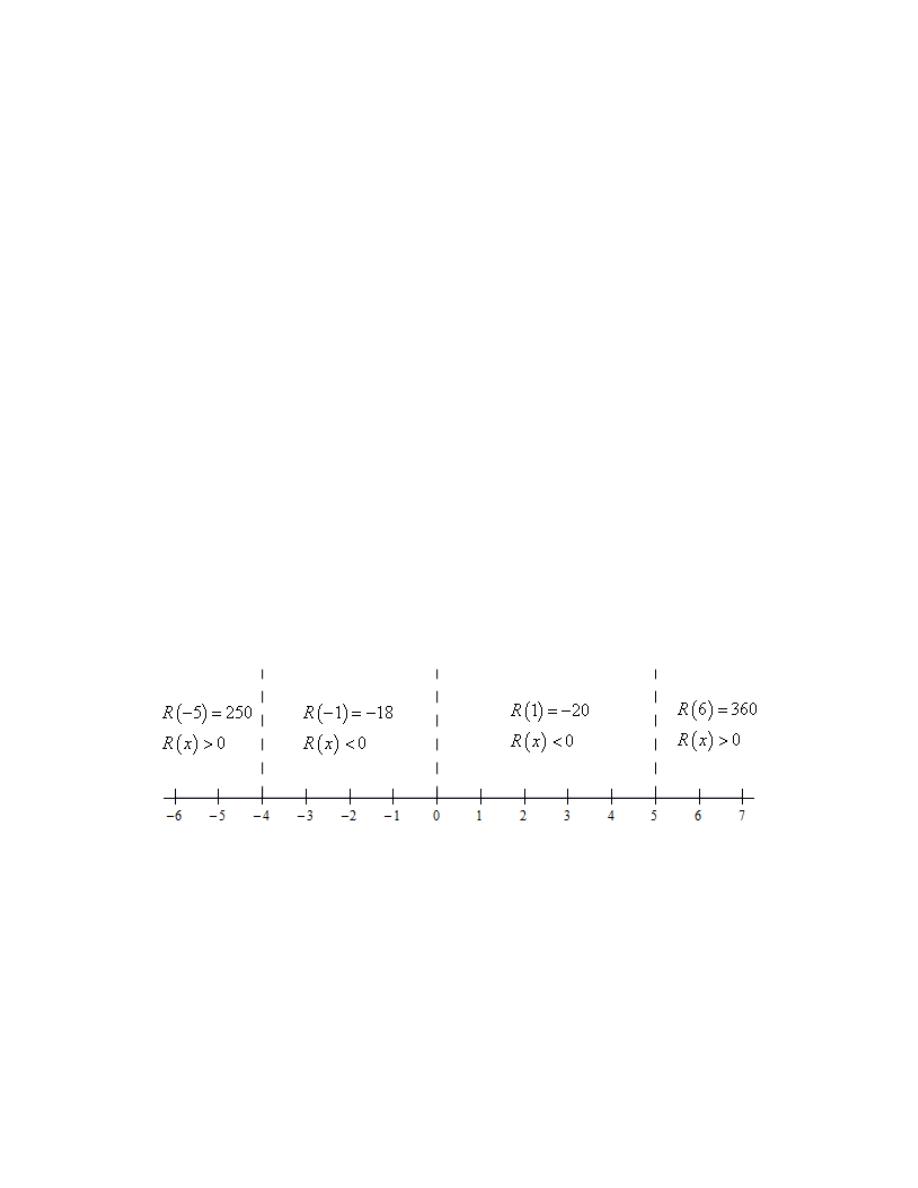
Here is a number line giving the value/sign of the polynomial at a test point in each of the region
defined by these three points. To make it a little easier to read the number line let’s define the
polynomial under the radical to be,
( )
(
)(
)
4
3
2
2
20
5
4
R x
x
x
x
x
x
x
=
− −
=
−
+
Now, here is the number line,
Step 3 Hint : Now all we need to do is write down the values of x where the polynomial under the
root will be positive or zero and we’ll have the domain. Be careful with the points where the
polynomial is zero.
[Show Step Three]
The domain will then be all the points where the polynomial under the root is positive or zero and
so the domain is,
Domain :
4,
0, 5
x
x
x
− ∞ < ≤ −
=
≤ < ∞

Calculus I
© 2007 Paul Dawkins
20
http://tutorial.math.lamar.edu/terms.aspx
In this case we need to be very careful and not miss
0
x
=
. This is the point separating two
regions which give negative values of the polynomial, but it will give zero and so it also part of
the domain. This point is often very is very easy to miss.
28. Find the domain of
( )
3
2
5
1
8
t
P t
t
t
t
+
=
− −
.
Step 1 Hint : We need to avoid negative numbers under the square root and because the quantity
under the root is a polynomial we know that it can only change sign if it goes through zero and so
we first need to determine where it is zero.
[Show Step One]
In this case we need to avoid square roots of negative numbers and because the square root is in
the denominator we’ll also need to avoid division by zero issues. We can satisfy both needs by
requiring,
(
)
3
2
2
8
8
0
t
t
t
t t
t
− − =
− −
>
Note that there is nothing wrong with the square root of zero, but we know that the square root of
zero is zero and so if we require that the polynomial under the root is strictly positive we’ll know
that we won’t have square roots of negative numbers and we’ll avoid division by zero.
Now, despite the fact that we need to avoid where the polynomial is zero we know that it will
only change signs if it goes through zero and so we’ll next need to determine where the
polynomial is zero.
Clearly one value is
0
t
=
and because the quadratic does not factor we can use the quadratic
formula on it to get the following two additional points.
( )
( )( )
2
1
1
4 1
8
1
33
1
33
3.372281
2
2
2
1
33
2.372281
2
t
t
t
±
−
−
−
±
+
=
=
=
=
−
=
= −
So, these three points (
0
t
=
,
2.372281
t
= −
and
3.372281
t
=
are the only places that the
polynomial under the root can change sign.
Step 2 Hint : Because the polynomial can only change sign at these points we know that it will be
the same sign in each region defined by these points and so all we need to know is the value of
the polynomial as a single point in each region.
Calculus I
© 2007 Paul Dawkins
21
http://tutorial.math.lamar.edu/terms.aspx
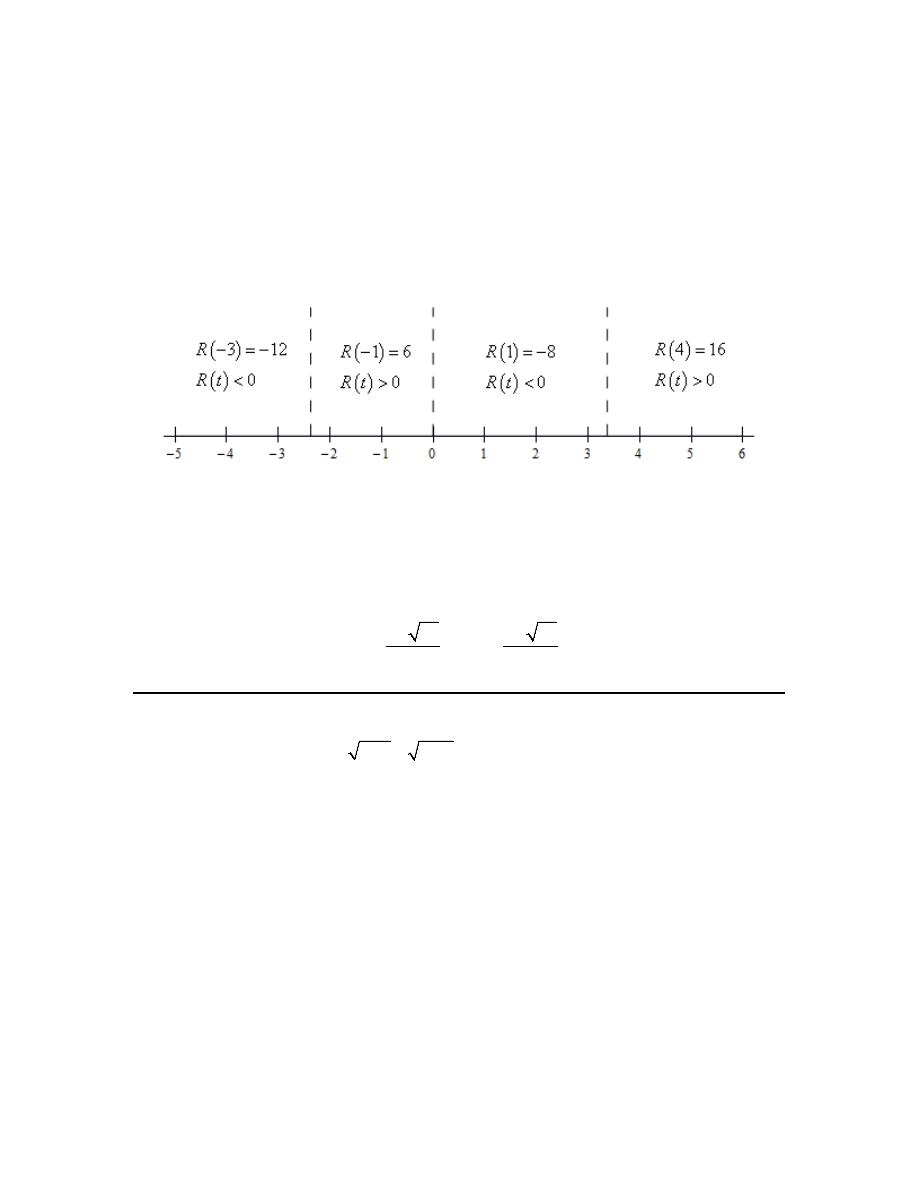
[Show Step Two]
Here is a number line giving the value/sign of the polynomial at a test point in each of the region
defined by these three points. To make it a little easier to read the number line let’s define the
polynomial under the radical to be,
( )
(
)
3
2
2
8
8
0
R t
t
t
t
t t
t
= − − =
− − >
Now, here is the number line,
Step 3 Hint : Now all we need to do is write down the values of x where the polynomial under the
root will be positive (recall we need to avoid division by zero) and we’ll have the domain.
[Show Step Three]
The domain will then be all the points where the polynomial under the root is positive, but not
zero as we also need to avoid division by zero, and so the domain is,
1
33
1
33
Domain :
0,
2
2
t
t
−
+
< <
< < ∞
29. Find the domain of
( )
1
6
f z
z
z
=
− +
+
.
Hint Step 1 : The domain of this function will be the set of all values of z that will work in both
terms of this function.
[Show Step 1]
The domain of this function will be the set of all z’s that we can plug into both terms in this
function and get a real number back as a value. This means that we first need to determine the
domain of each of the two terms.
For the first term we need to require,
1 0
1
z
z
− ≥
⇒
≥
For the second term we need to require,
6
0
6
z
z
+ ≥
⇒
≥ −

Calculus I
© 2007 Paul Dawkins
22
http://tutorial.math.lamar.edu/terms.aspx
Hint Step 2 : What values of z are in both of these?
[Show Step 2]
Now, we just need the set of z’s that are in both conditions above. In this case notice that all the z
that satisfy
1
z
≥
will also satisfy
6
z
≥ −
. The reverse is not true however. Any z that is in the
range
6
1
z
− ≤ <
will satisfy
6
z
≥
but will not satisfy
1
z
≥
.
So, in this case, the domain is in fact just the first condition above or,
Domain :
1
z
≥
30. Find the domain of
( )
1
2
9
2
h y
y
y
=
+ −
−
.
Hint Step 1 : The domain of this function will be the set of all values of y that will work in both
terms of this function.
[Show Step 1]
The domain of this function will be the set of all y’s that we can plug into both terms in this
function and get a real number back as a value. This means that we first need to determine the
domain of each of the two terms.
For the first term we need to require,
9
2
9
0
2
y
y
+ ≥
⇒
≥ −
For the second term we need to require,
2
0
2
y
y
− >
⇒
<
Note that we need the second condition to be strictly positive to avoid division by zero as well.
Hint Step 2 : What values of y are in both of these?
[Show Step 2]
Now, we just need the set of y’s that are in both conditions above. In this case we need all the y’s
that will be greater than or equal to
9
2
−
AND less than 2. The domain is then,
9
Domain :
2
2
y
− ≤ <

Calculus I
© 2007 Paul Dawkins
23
http://tutorial.math.lamar.edu/terms.aspx
31. Find the domain of
( )
2
4
36
9
A x
x
x
=
−
−
−
.
Hint Step 1 : The domain of this function will be the set of all values of x that will work in both
terms of this function.
[Show Step 1]
The domain of this function will be the set of all x’s that we can plug into both terms in this
function and get a real number back as a value. This means that we first need to determine the
domain of each of the two terms.
For the first term we need to require,
9
0
9
x
x
− ≠
⇒
≠
For the second term we need to require,
2
2
36
0
36
6 &
6
x
x
x
x
−
≥
→
≥
⇒
≤ −
≥
Hint Step 2 : What values of x are in both of these?
[Show Step 2]
Now, we just need the set of x’s that are in both conditions above. In this case the second
condition gives us most of the domain as it is the most restrictive. The first term is okay as long
as we avoid
9
x
=
and because this point will in fact satisfy the second condition we’ll need to
make sure and exclude it. The domain is then,
Domain :
6 &
6,
9
x
x
x
≤ −
≥
≠
32. Find the domain of
( )
2
3
1
1
Q y
y
y
=
+ −
−
.
[Solution]
The domain of this function will be the set of y’s that will work in both terms of this function.
So, we need the domain of each of the terms.
For the first term let’s note that,
2
1 1
y
+ ≥
and so will always be positive. The domain of the first term is then all real numbers.
For the second term we need to notice that we’re dealing with the cube root in this case and we
can plug all real numbers into a cube root and so the domain of this term is again all real
numbers.

Calculus I
© 2007 Paul Dawkins
24
http://tutorial.math.lamar.edu/terms.aspx
So, the domain of both terms is all real numbers and so the domain of the function as a whole
must also be all real numbers or,
Domain :
y
− ∞ < < ∞
33. Compute
(
)( )
f
g
x
and
(
)( )
g
f
x
for
( )
4
1
f x
x
=
−
,
( )
6 7
g x
x
=
+
.
[Solution]
Not much to do here other than to compute each of these.
(
)( )
( )
(
)( )
( )
[
]
(
)
6 7
4 6 7
1
4
1
6 7 4
1
28
1
f
g
x
f g x
f
x
x
g
f
x
g f x
g
x
x
x
=
=
+
=
+
−
=
=
− =
+
− =
−
34. Compute
(
)( )
f
g
x
and
(
)( )
g
f
x
for
( )
5
2
f x
x
=
+
,
( )
2
14
g x
x
x
=
−
.
[Solution]
Not much to do here other than to compute each of these.
(
)( )
( )
(
)
(
)( )
( )
[
]
(
)
(
)
2
2
2
2
2
14
5
14
2
5
70
2
5
2
5
2
14 5
2
25
50
24
f
g
x
f g x
f x
x
x
x
x
x
g
f
x
g f x
g
x
x
x
x
x
=
=
−
=
−
+ =
−
+
=
=
+
=
+
−
+
=
−
−
35. Compute
(
)( )
f
g
x
and
(
)( )
g
f
x
for
( )
2
2
1
f x
x
x
=
−
+
,
( )
2
8 3
g x
x
= −
.
[Solution]
Not much to do here other than to compute each of these.

Calculus I
© 2007 Paul Dawkins
25
http://tutorial.math.lamar.edu/terms.aspx
(
)( )
( )
(
) (
)
(
)( )
( )
(
)
2
2
2
2
4
2
2
2
2
4
3
2
8 3
8 3
2 8 3
1 9
42
49
2
1
8 3
2
1
3
12
18
12
5
f
g
x
f g x
f
x
x
x
x
x
g
f
x
g f x
g x
x
x
x
x
x
x
x
=
=
−
= −
−
−
+ =
−
+
=
=
−
+
= −
−
+
= −
+
−
+
+
36. Compute
(
)( )
f
g
x
and
(
)( )
g
f
x
for
( )
2
3
f x
x
=
+
,
( )
2
5
g x
x
=
+
.
[Solution]
Not much to do here other than to compute each of these.
(
)( )
( )
(
)
(
)( )
( )
(
)
2
2
2
2
2
2
2
4
2
5
5
3
8
3
5
3
6
14
f
g
x
f g x
f
x
x
x
g
f
x
g f x
g x
x
x
x
=
=
−
=
+
+ = +
=
=
+
=
+
+
=
+
+
Review : Inverse Functions
1. Find the inverse for
( )
6
15
f x
x
=
+
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
f x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
f
x
−
.
Step 1
6
15
y
x
=
+
Step 2
6
15
x
y
=
+
Step 3

Calculus I
© 2007 Paul Dawkins
26
http://tutorial.math.lamar.edu/terms.aspx
(
)
( )
(
)
1
15
6
1
1
15
15
6
6
x
y
y
x
f
x
x
−
−
=
=
−
→
=
−
Finally, compute either
(
)
( )
1
f
f
x
−
or
(
)
( )
1
f
f
x
−
to verify our work.
Step 4
Either composition can be done so let’s do
(
)
( )
1
f
f
x
−
in this case.
(
)
( )
( )
(
)
1
1
1
6
15
15
6
15 15
f
f
x
f
f
x
x
x
x
−
−
=
=
−
+
= − +
=
So, we got x out of the composition and so we know we’ve done our work correctly.
2. Find the inverse for
( )
3 29
h x
x
= −
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
h x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
h
x
−
.
Step 1
3 29
y
x
= −
Step 2
3 29
x
y
= −
Step 3
(
)
( )
(
)
1
3
29
1
1
3
3
29
29
x
y
y
x
h
x
x
−
− = −
= −
−
→
=
−
Notice that we multiplied the minus sign into the parenthesis. We did this in order to avoid
potentially losing the minus sign if it had stayed out in front. This does not need to be done in
order to get the inverse.

Calculus I
© 2007 Paul Dawkins
27
http://tutorial.math.lamar.edu/terms.aspx
Finally, compute either
(
)
( )
1
h h
x
−
or
(
)
( )
1
h
h
x
−
to verify our work.
Step 4
Either composition can be done so let’s do
(
)
( )
1
h h
x
−
in this case.
(
)
( )
( )
(
)
(
)
1
1
1
3 29
3
29
3
3
h h
x
h h
x
x
x
x
−
−
=
= −
−
= − −
=
So, we got x out of the composition and so we know we’ve done our work correctly.
3. Find the inverse for
( )
3
6
R x
x
=
+
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
R x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
R
x
−
.
Step 1
3
6
y
x
=
+
Step 2
3
6
x
y
=
+
Step 3
( )
3
1
3
3
6
6
6
x
y
y
x
R
x
x
−
− =
=
−
→
=
−
Finally, compute either
(
)
( )
1
R R
x
−
or
(
)
( )
1
R
R
x
−
to verify our work.
Step 4
Either composition can be done so let’s do
(
)
( )
1
R
R
x
−
in this case.
Calculus I
© 2007 Paul Dawkins
28
http://tutorial.math.lamar.edu/terms.aspx
(
)
( )
( )
(
)
1
1
3
3
3
3
6
6
R
R
x
R
R x
x
x
x
−
−
=
=
+ −
=
=
So, we got x out of the composition and so we know we’ve done our work correctly.
4. Find the inverse for
( )
(
)
5
4
3
21
g x
x
=
−
+
. Verify your inverse by computing one or both of
the composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
g x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
g
x
−
.
Step 1
(
)
5
4
3
21
y
x
=
−
+
Step 2
(
)
5
4
3
21
x
y
=
−
+
Step 3
(
)
(
) (
)
(
)
(
)
( )
(
)
5
5
5
1
5
5
21
4
3
1
21
3
4
1
21
3
4
1
1
3
21
3
21
4
4
x
y
x
y
x
y
y
x
g
x
x
−
−
=
−
−
=
−
−
= −
= +
−
→
= +
−
Finally, compute either
(
)
( )
1
g g
x
−
or
(
)
( )
1
g
g
x
−
to verify our work.
Step 4
Either composition can be done so let’s do
(
)
( )
1
g g
x
−
in this case.

Calculus I
© 2007 Paul Dawkins
29
http://tutorial.math.lamar.edu/terms.aspx
(
)
( )
( )
(
)
(
)
(
)
(
)
1
1
5
5
5
5
1
4
3
21
3
21
4
1
4
21
21
4
1
4
21
21
4
21
21
g g
x
g g
x
x
x
x
x
x
−
−
=
=
+
−
−
+
=
−
+
=
−
+
=
−
+
=
So, we got x out of the composition and so we know we’ve done our work correctly.
5. Find the inverse for
( )
5
9 11
W x
x
=
−
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
W x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
W
x
−
.
Step 1
5
9 11
y
x
=
−
Step 2
5
9 11
x
y
=
−
Step 3
(
)
( )
(
)
5
5
5
5
1
5
9 11
9 11
9
11
1
1
9
9
11
11
x
y
x
y
x
y
y
x
W
x
x
−
=
−
= −
− = −
= −
−
→
=
−
Notice that we multiplied the minus sign into the parenthesis. We did this in order to avoid
potentially losing the minus sign if it had stayed out in front. This does not need to be done in
order to get the inverse.
Finally, compute either
(
)
( )
1
W W
x
−
or
(
)
( )
1
W
W
x
−
to verify our work.
Calculus I
© 2007 Paul Dawkins
30
http://tutorial.math.lamar.edu/terms.aspx
Step 4
Either composition can be done so let’s do
(
)
( )
1
W
W
x
−
in this case.
(
)
( )
( )
(
)
[
]
(
)
( )
1
1
5
5
1
9
9 11
11
1
9
9 11
11
1
11
11
W
W
x
W
W x
x
x
x
x
−
−
=
=
−
−
=
− −
=
=
So, we got x out of the composition and so we know we’ve done our work correctly.
6. Find the inverse for
( )
7
5
8
f x
x
=
+
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
f x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
f
x
−
.
Step 1
7
5
8
y
x
=
+
Step 2
7
5
8
x
y
=
+
Step 3
(
)
( )
(
)
7
7
7
7
1
7
5
8
5
8
8
5
1
1
8
8
5
5
x
y
x
y
x
y
y
x
f
x
x
−
=
+
=
+
− =
=
−
→
=
−
Finally, compute either
(
)
( )
1
f
f
x
−
or
(
)
( )
1
f
f
x
−
to verify our work.
Step 4
Calculus I
© 2007 Paul Dawkins
31
http://tutorial.math.lamar.edu/terms.aspx
Either composition can be done so let’s do
(
)
( )
1
f
f
x
−
in this case.
(
)
( )
( )
(
)
1
1
7
7
7
7
7
7
1
5
8
8
5
8
8
f
f
x
f
f
x
x
x
x
x
−
−
=
=
−
+
=
− +
=
=
So, we got x out of the composition and so we know we’ve done our work correctly.
7. Find the inverse for
( )
1 9
4
x
h x
x
+
=
−
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
h x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
h
x
−
.
Step 1
1 9
4
x
y
x
+
=
−
Step 2
1 9
4
y
x
y
+
=
−
Step 3
(
)
(
)
( )
1
1 9
4
4
1 9
4
1 9
4
1 9
4
1
9
4
1
4
1
9
9
y
x
y
x
y
y
x
xy
y
x
y
xy
x
x y
x
x
y
h
x
x
x
−
+
=
−
−
= +
−
= +
− =
+
− =
+
−
−
=
→
=
+
+

Calculus I
© 2007 Paul Dawkins
32
http://tutorial.math.lamar.edu/terms.aspx
Note that the Algebra in these kinds of problems can often be fairly messy, but don’t let that
make you decide that you can’t do these problems. Messy Algebra will be a fairly common
occurrence in a Calculus class so you’ll need to get used to it!
Finally, compute either
(
)
( )
1
h h
x
−
or
(
)
( )
1
h
h
x
−
to verify our work.
Step 4
Either composition can be done so let’s do
(
)
( )
1
h
h
x
−
in this case. As with the previous step,
the Algebra here is going to be messy and in fact will probably be messier.
(
)
( )
( )
(
) (
)
(
)
1
1
1 9
4
1
4
4
1 9
4
9
4
4 1 9
4
9 4
1 9
4 36
4
36 9
1 9
37
37
h
h
x
h
h x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
−
−
=
+
−
−
−
=
+
−
+
−
+
− −
=
−
+ +
+
− +
=
−
+ +
=
=
In order to do the simplification we multiplied the numerator and denominator of the initial
fraction by
4
x
−
in order to clear out some of the denominators. This in turn allowed a fair
amount of simplification.
So, we got x out of the composition and so we know we’ve done our work correctly.
8. Find the inverse for
( )
6 10
8
7
x
f x
x
−
=
+
. Verify your inverse by computing one or both of the
composition as discussed in this section.
Hint : Remember the process described in this section. Replace the
( )
f x
, interchange the x’s
and y’s, solve for y and the finally replace the y with
( )
1
f
x
−
.
Step 1
6 10
8
7
x
y
x
−
=
+

Calculus I
© 2007 Paul Dawkins
33
http://tutorial.math.lamar.edu/terms.aspx
Step 2
6 10
8
7
y
x
y
−
=
+
Step 3
(
)
(
)
( )
1
6 10
8
7
8
7
6 10
8
7
6 10
8
10
6 7
8
10
6 7
6 7
6 7
8
10
8
10
y
x
y
x
y
y
xy
x
y
xy
y
x
x
y
x
x
x
y
f
x
x
x
−
−
=
+
+
= −
+
= −
+
= −
+
= −
−
−
=
→
=
+
+
Note that the Algebra in these kinds of problems can often be fairly messy, but don’t let that
make you decide that you can’t do these problems. Messy Algebra will be a fairly common
occurrence in a Calculus class so you’ll need to get used to it!
Finally, compute either
(
)
( )
1
f
f
x
−
or
(
)
( )
1
f
f
x
−
to verify our work.
Step 4
Either composition can be done so let’s do
(
)
( )
1
f
f
x
−
in this case. As with the previous step,
the Algebra here is going to be messy and in fact will probably be messier.
(
)
( )
( )
(
)
(
)
(
) (
)
1
1
6 7
6 10
8
10
8
10
6 7
8
10
8
7
8
10
6 8
10
10 6 7
8 6 7
7 8
10
48
60 60 70
48 56
56
70
118
118
f
f
x
f
f
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
−
−
=
−
−
+
+
=
−
+
+
+
+
−
−
=
−
+
+
+
−
+
=
−
+
+
=
=
So, we got x out of the composition and so we know we’ve done our work correctly.
Calculus I
© 2007 Paul Dawkins
34
http://tutorial.math.lamar.edu/terms.aspx
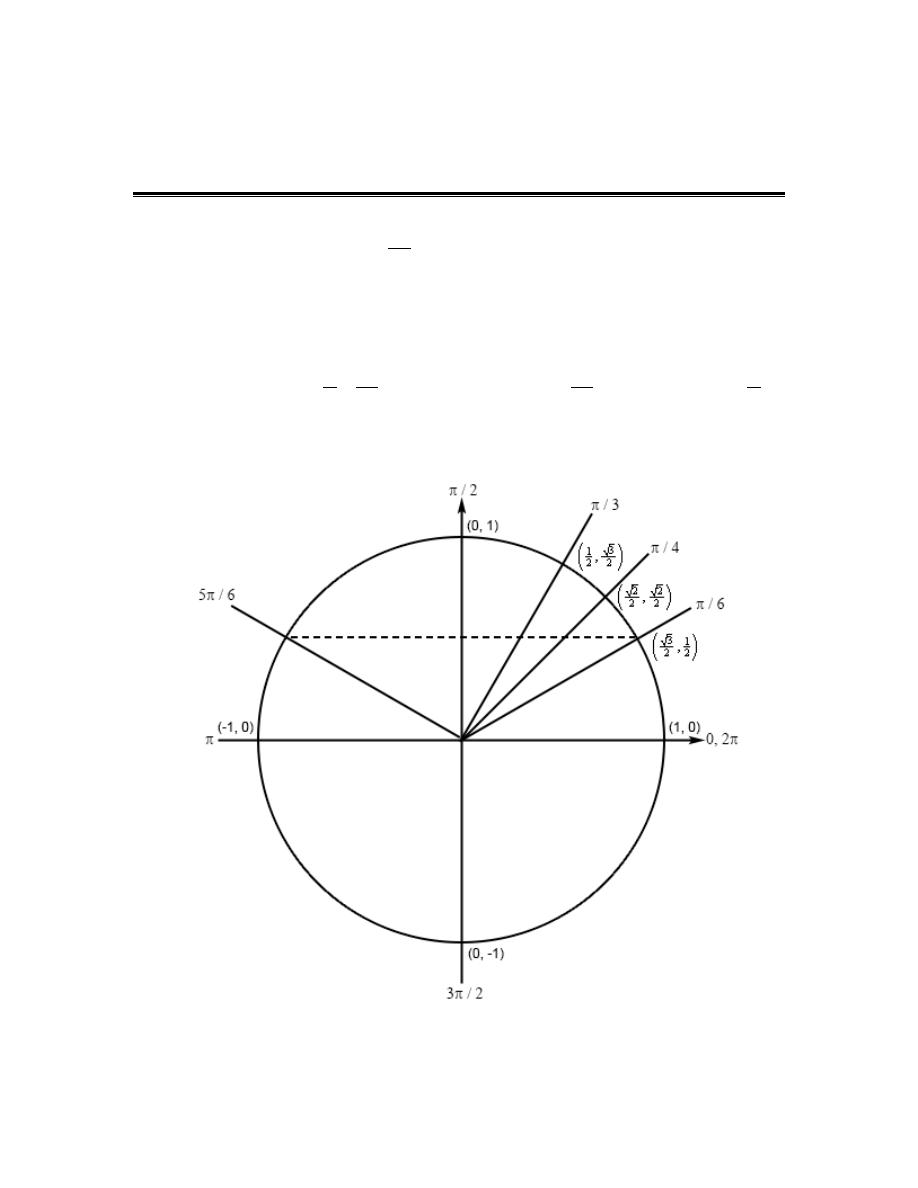
Review : Trig Functions
1. Determine the exact value of
5
cos
6
π
without using a calculator.
Hint 1 : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
Step 1
First we can notice that
5
6
6
π
π
π
− =
and so the terminal line for
5
6
π
will form an angle of
6
π
with the negative x-axis in the second quadrant and we’ll have the following unit circle for this
problem.

Calculus I
© 2007 Paul Dawkins
35
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
5
6
π
to the coordinates of the line representing
6
π
and use those to answer the
question.
Step 2
The coordinates of the line representing
5
6
π
will be the same as the coordinates of the line
representing
6
π
except that the x coordinate will now be negative. So, our new coordinates will
then be
3 1
,
2
2
−
and so the answer is,
5
3
cos
6
2
π
= −
2. Determine the exact value of
4
sin
3
π
−
without using a calculator.
Hint 1 : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
Step 1
First we can notice that
4
3
3
π
π
π
− − = −
and so (remembering that negative angles are rotated
clockwise) we can see that the terminal line for
4
3
π
−
will form an angle of
3
π
with the negative
x-axis in the second quadrant and we’ll have the following unit circle for this problem.
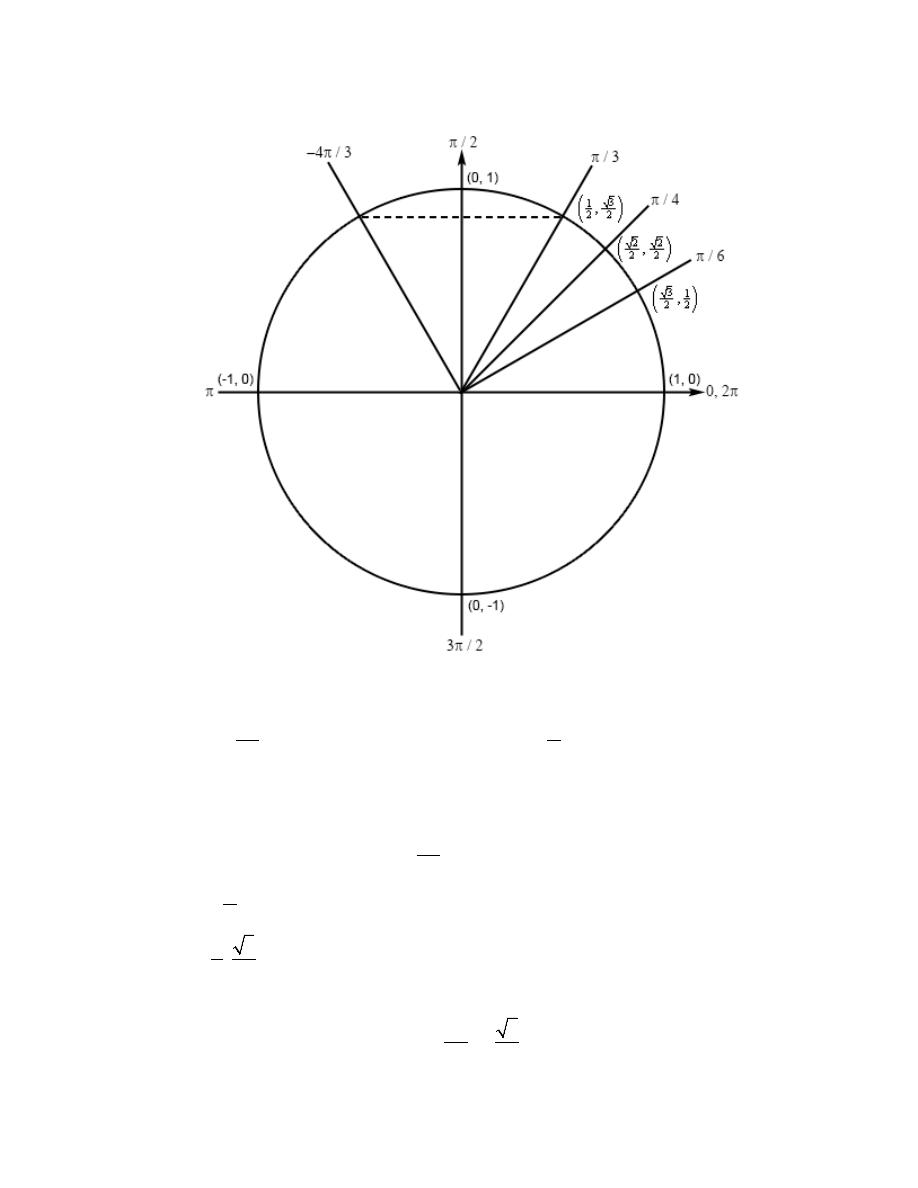
Calculus I
© 2007 Paul Dawkins
36
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
4
3
π
−
to the coordinates of the line representing
3
π
and use those to answer the
question.
Step 2
The coordinates of the line representing
4
3
π
−
will be the same as the coordinates of the line
representing
3
π
except that the x coordinate will now be negative. So, our new coordinates will
then be
1
3
,
2
2
−
and so the answer is,
4
3
sin
3
2
π
−
=
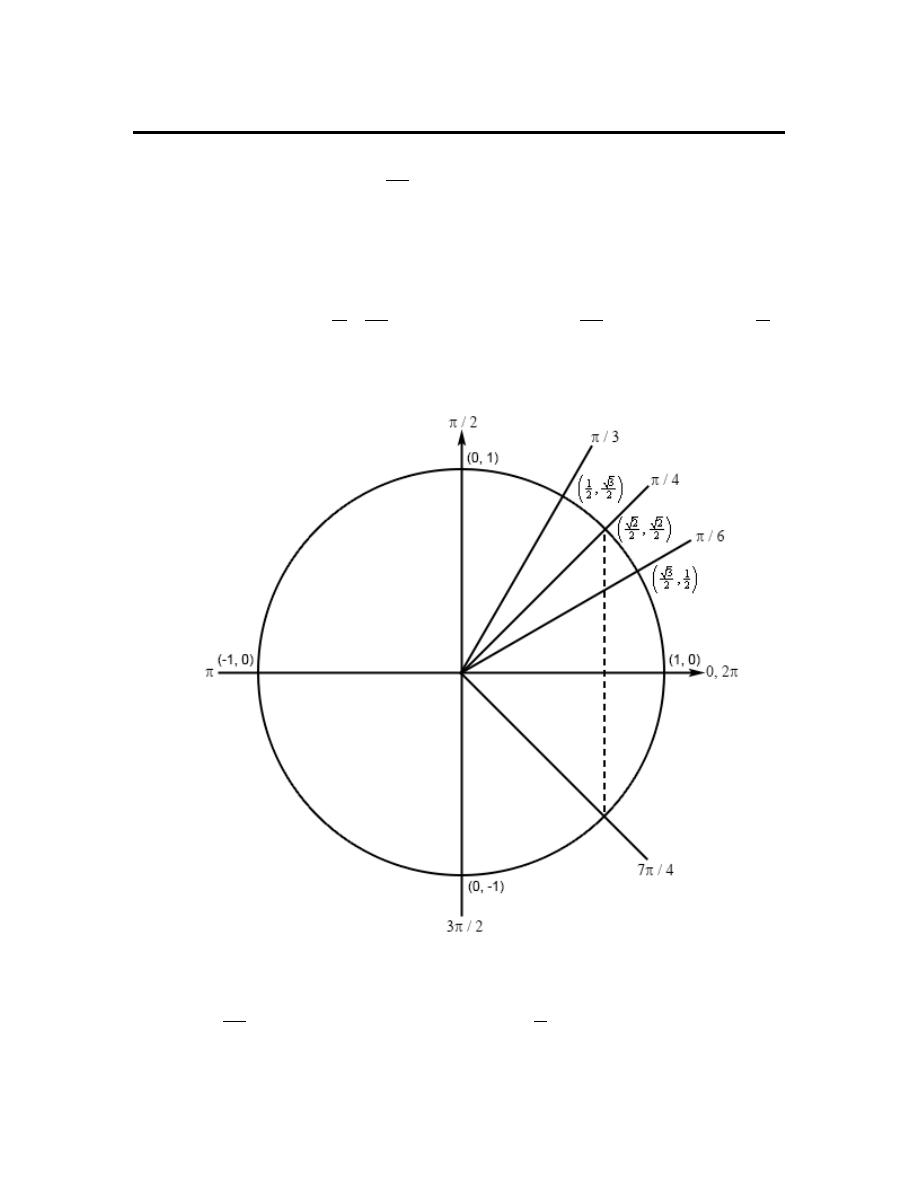
Calculus I
© 2007 Paul Dawkins
37
http://tutorial.math.lamar.edu/terms.aspx
3. Determine the exact value of
7
sin
4
π
without using a calculator.
Hint 1 : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
Step 1
First we can notice that
7
2
4
4
π
π
π
− =
and so the terminal line for
7
4
π
will form an angle of
4
π
with the positive x-axis in the fourth quadrant and we’ll have the following unit circle for this
problem.
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
7
4
π
to the coordinates of the line representing
4
π
and use those to answer the
question.

Calculus I
© 2007 Paul Dawkins
38
http://tutorial.math.lamar.edu/terms.aspx
Step 2
The coordinates of the line representing
7
4
π
will be the same as the coordinates of the line
representing
4
π
except that the y coordinate will now be negative. So, our new coordinates will
then be
2
2
,
2
2
−
and so the answer is,
7
2
sin
4
2
π
= −
4. Determine the exact value of
2
cos
3
π
−
without using a calculator.
Hint 1 : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
Step 1
First we can notice that
2
3
3
π
π
π
− + = −
so (recalling that negative angles rotate clockwise and
positive angles rotation counter clockwise) the terminal line for
2
3
π
−
will form an angle of
3
π
with the negative x-axis in the third quadrant and we’ll have the following unit circle for this
problem.
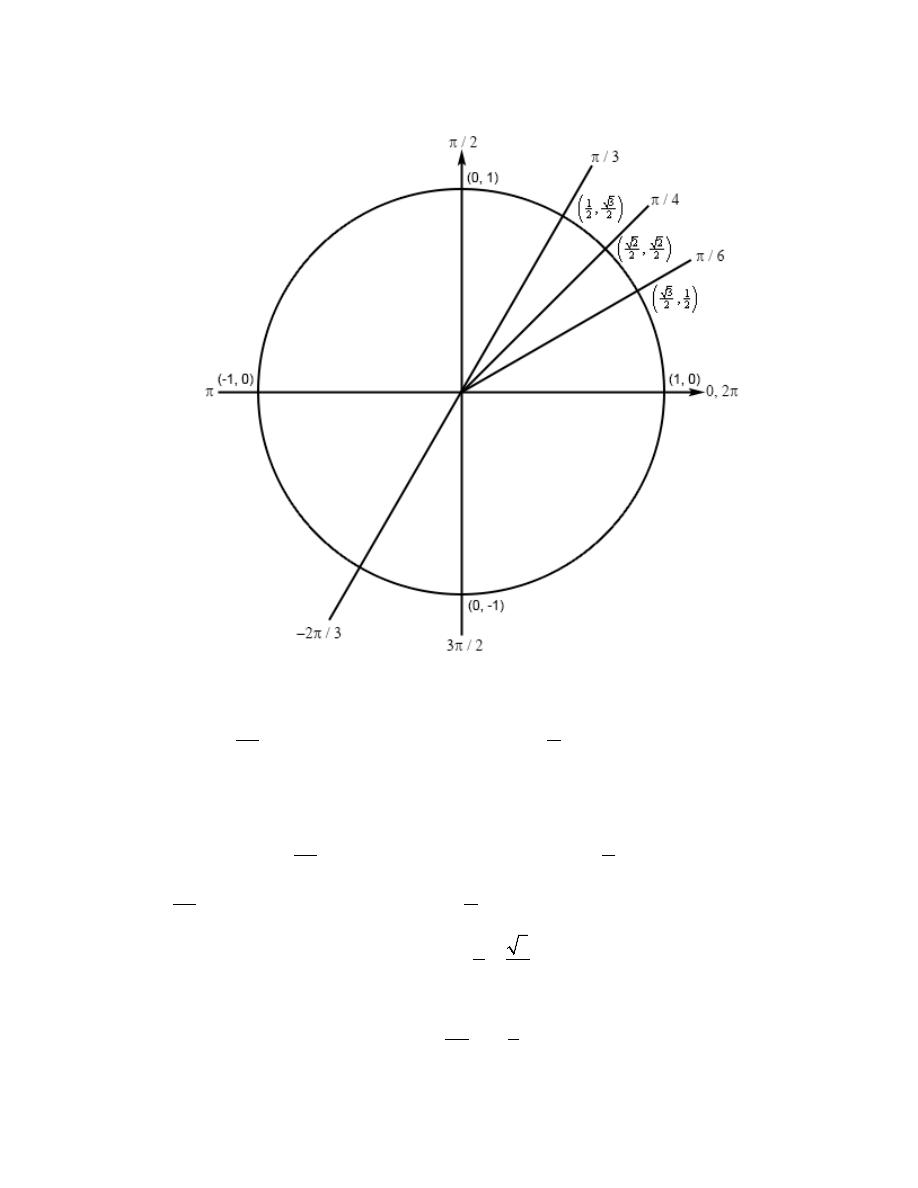
Calculus I
© 2007 Paul Dawkins
39
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
2
3
π
−
to the coordinates of the line representing
3
π
and use those to answer the
question.
Step 2
The line representing
2
3
π
−
is a mirror image of the line representing
3
π
and so the coordinates
for
2
3
π
−
will be the same as the coordinates for
3
π
except that both coordinates will now be
negative. So, our new coordinates will then be
1
3
,
2
2
−
−
and so the answer is,
2
1
cos
3
2
π
−
= −
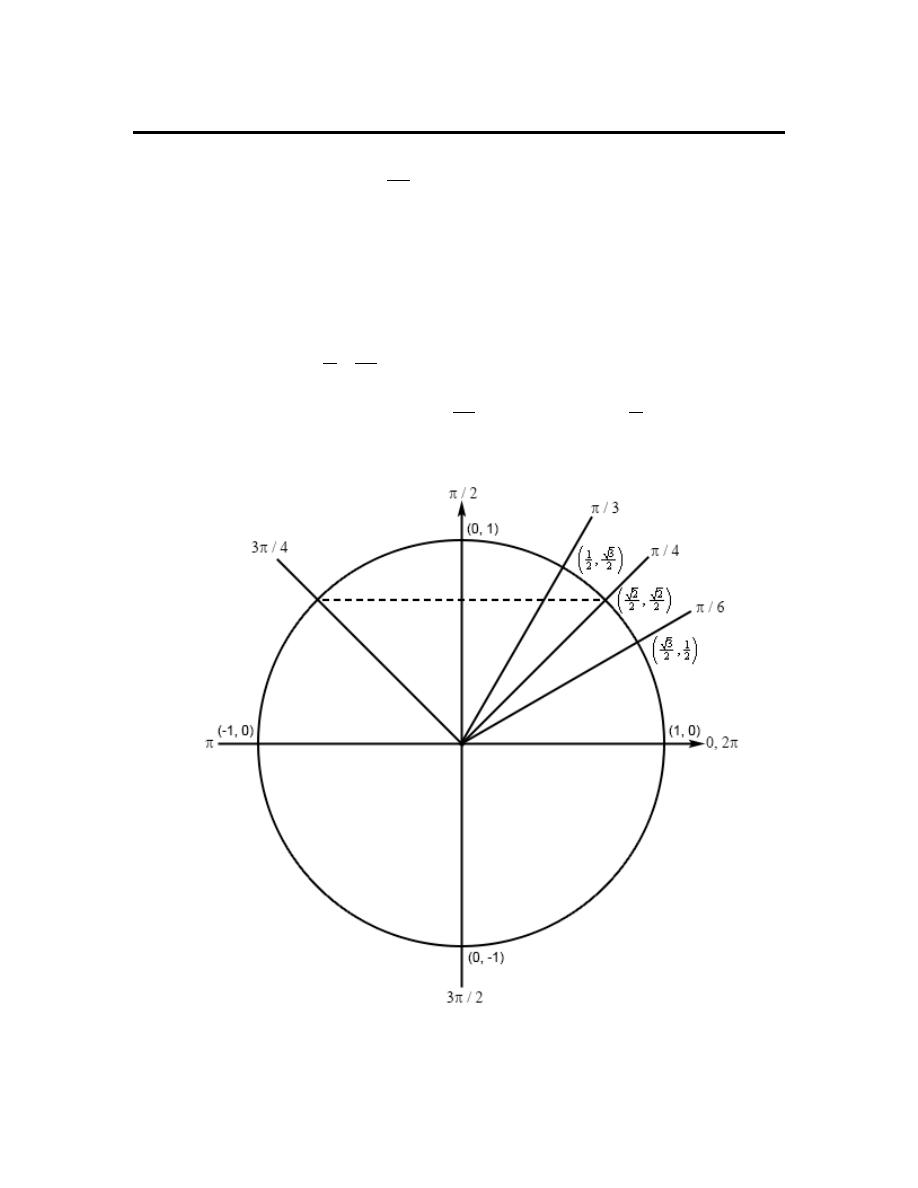
Calculus I
© 2007 Paul Dawkins
40
http://tutorial.math.lamar.edu/terms.aspx
5. Determine the exact value of
3
tan
4
π
without using a calculator.
Hint 1 : Even though a unit circle only tells us information about sine and cosine it is still useful
for tangents so sketch a unit circle and relate the angle to one of the standard angles in the first
quadrant.
Step 1
First we can notice that
3
4
4
π
π
π
− =
and so (remembering that negative angles are rotated
clockwise) we can see that the terminal line for
3
4
π
will form an angle of
4
π
with the negative x-
axis in the second quadrant and we’ll have the following unit circle for this problem.
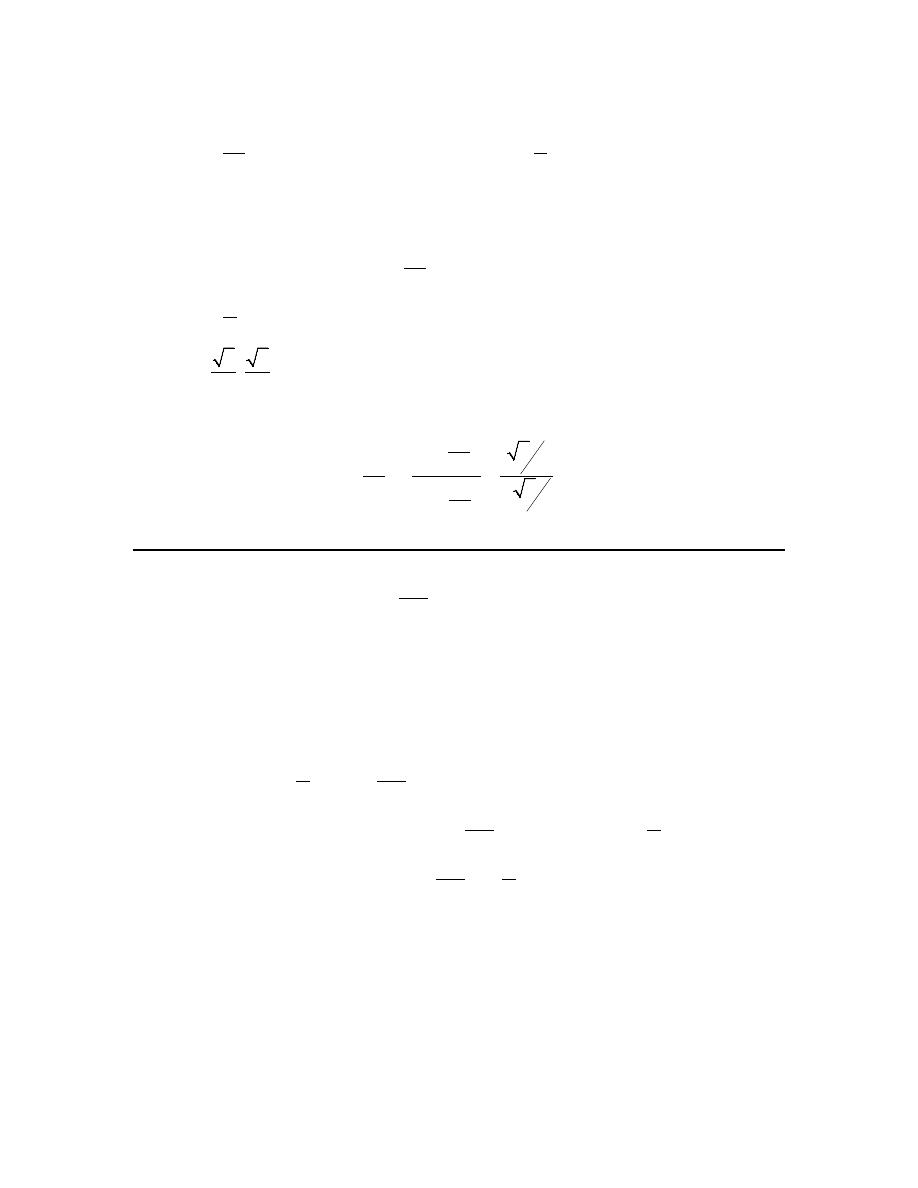
Calculus I
© 2007 Paul Dawkins
41
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
3
4
π
to the coordinates of the line representing
4
π
and and then recall how tangent is
defined in terms of sine and cosine to answer the question.
Step 2
The coordinates of the line representing
3
4
π
will be the same as the coordinates of the line
representing
4
π
except that the x coordinate will now be negative. So, our new coordinates will
then be
2
2
,
2
2
−
and so the answer is,
3
sin
2
3
4
2
tan
1
3
4
2
cos
2
4
π
π
π
=
=
= −
−
6. Determine the exact value of
11
sec
6
π
−
without using a calculator.
Hint 1 : Even though a unit circle only tells us information about sine and cosine it is still useful
for secant so sketch a unit circle and relate the angle to one of the standard angles in the first
quadrant.
Step 1
First we can notice that
11
2
6
6
π
π
π
−
= −
and so (remembering that negative angles are rotated
clockwise) we can see that the terminal line for
11
6
π
−
will form an angle of
6
π
with the positive
x-axis in the first quadrant. In other words
11
6
π
−
and
6
π
represent the same angle. So, we’ll
have the following unit circle for this problem.
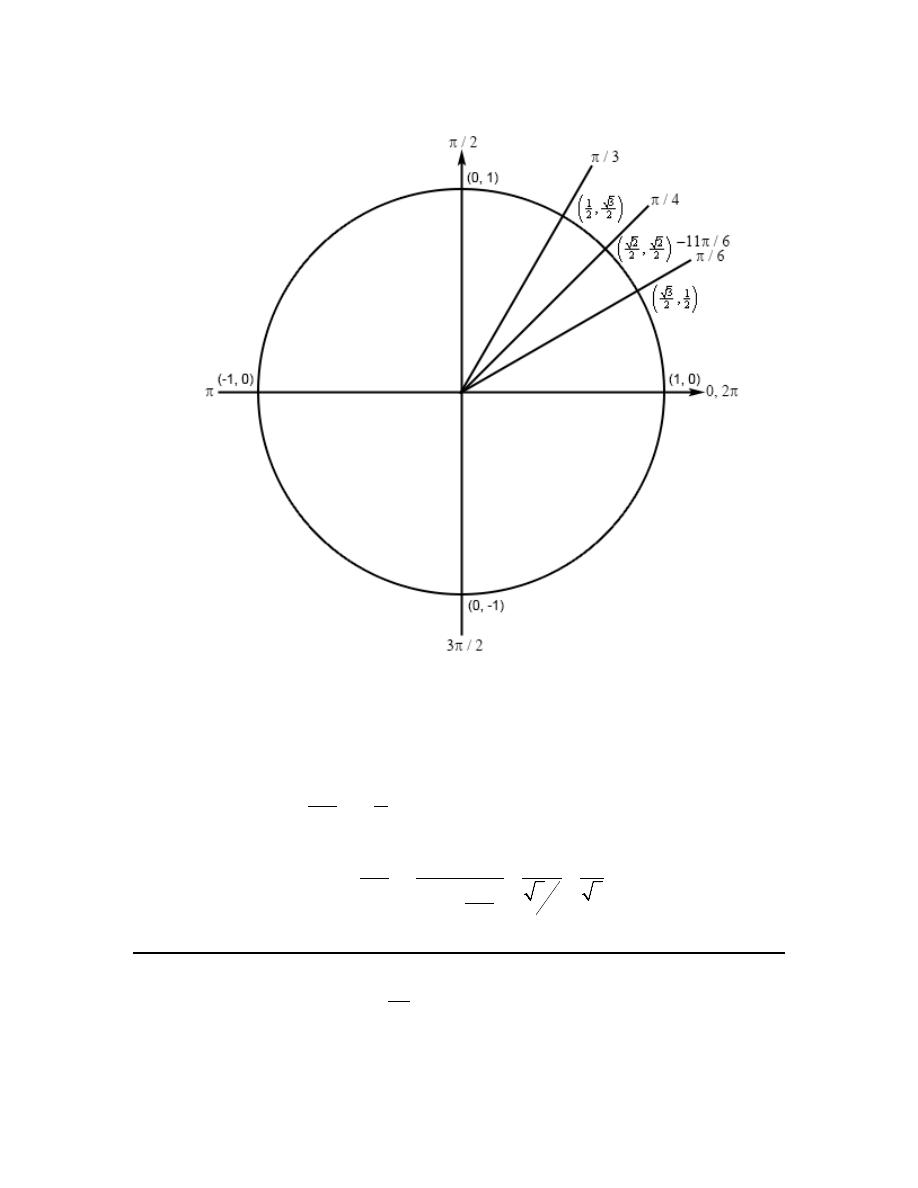
Calculus I
© 2007 Paul Dawkins
42
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry here use the definition of secant in terms of cosine to write
down the solution.
Step 2
Because the two angles
11
6
π
−
and
6
π
have the same coordinates the answer is,
11
1
1
2
sec
11
6
3
3
cos
2
6
π
π
−
=
=
=
−
7. Determine the exact value of
8
cos
3
π
without using a calculator.
Hint 1 : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
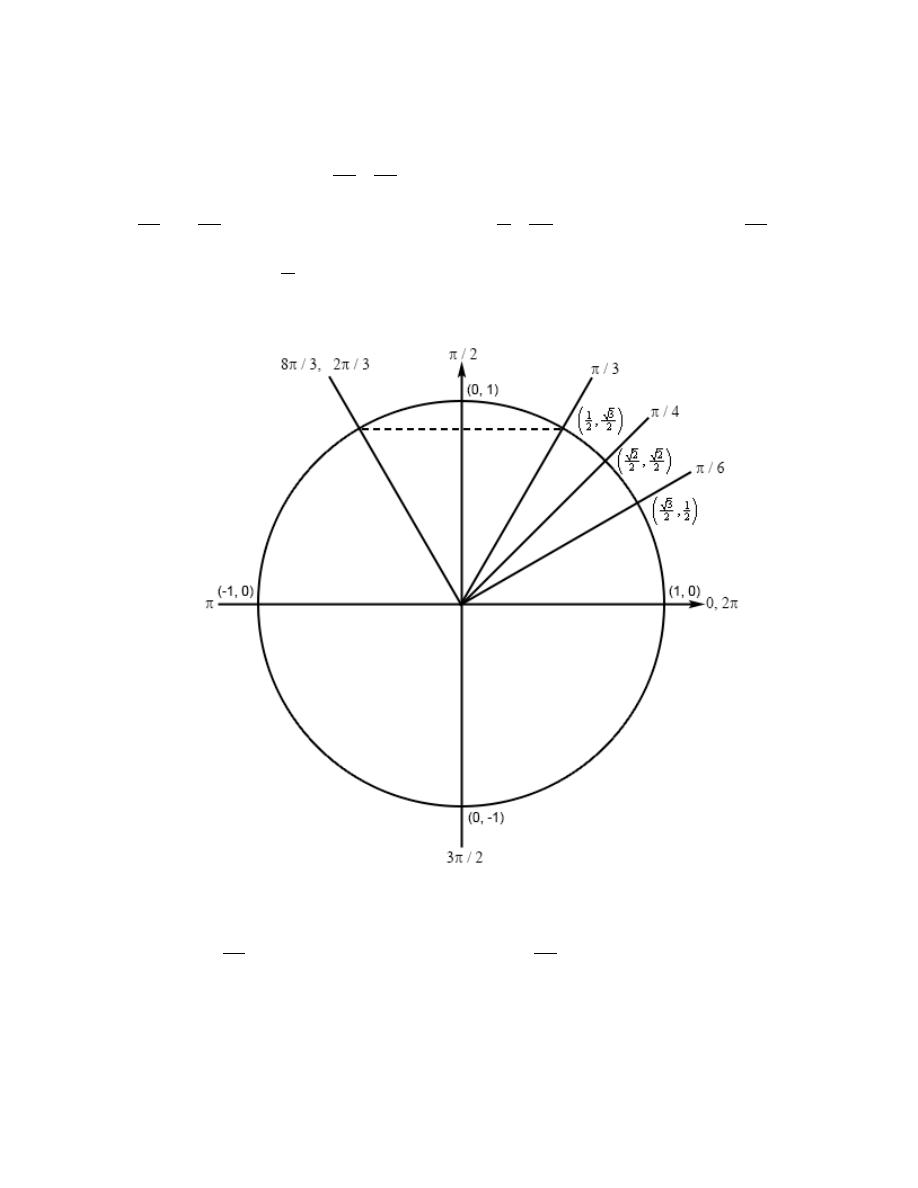
Calculus I
© 2007 Paul Dawkins
43
http://tutorial.math.lamar.edu/terms.aspx
Step 1
First we can notice that
2
8
2
3
3
π
π
π
+
=
and because
2
π
is one complete revolution the angles
8
3
π
and
2
3
π
are the same angle. Also, note that
2
3
3
π
π
π
− =
and so the terminal line for
8
3
π
will form an angle of
3
π
with the negative x-axis in the second quadrant and we’ll have the
following unit circle for this problem.
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
8
3
π
to the coordinates of the line representing
2
3
π
and use those to answer the
question.
Step 2

Calculus I
© 2007 Paul Dawkins
44
http://tutorial.math.lamar.edu/terms.aspx
The coordinates of the line representing
8
3
π
will be the same as the coordinates of the line
representing
3
π
except that the x coordinate will now be negative. So, our new coordinates will
then be
1
3
,
2
2
−
and so the answer is,
8
1
cos
3
2
π
= −
8. Determine the exact value of
tan
3
π
−
without using a calculator.
Hint 1 : Even though a unit circle only tells us information about sine and cosine it is still useful
for tangents so sketch a unit circle and relate the angle to one of the standard angles in the first
quadrant.
Step 1
To do this problem all we need to notice is that
3
π
−
will form an angle of
3
π
with the positive x-
axis in the fourth quadrant and we’ll have the following unit circle for this problem.
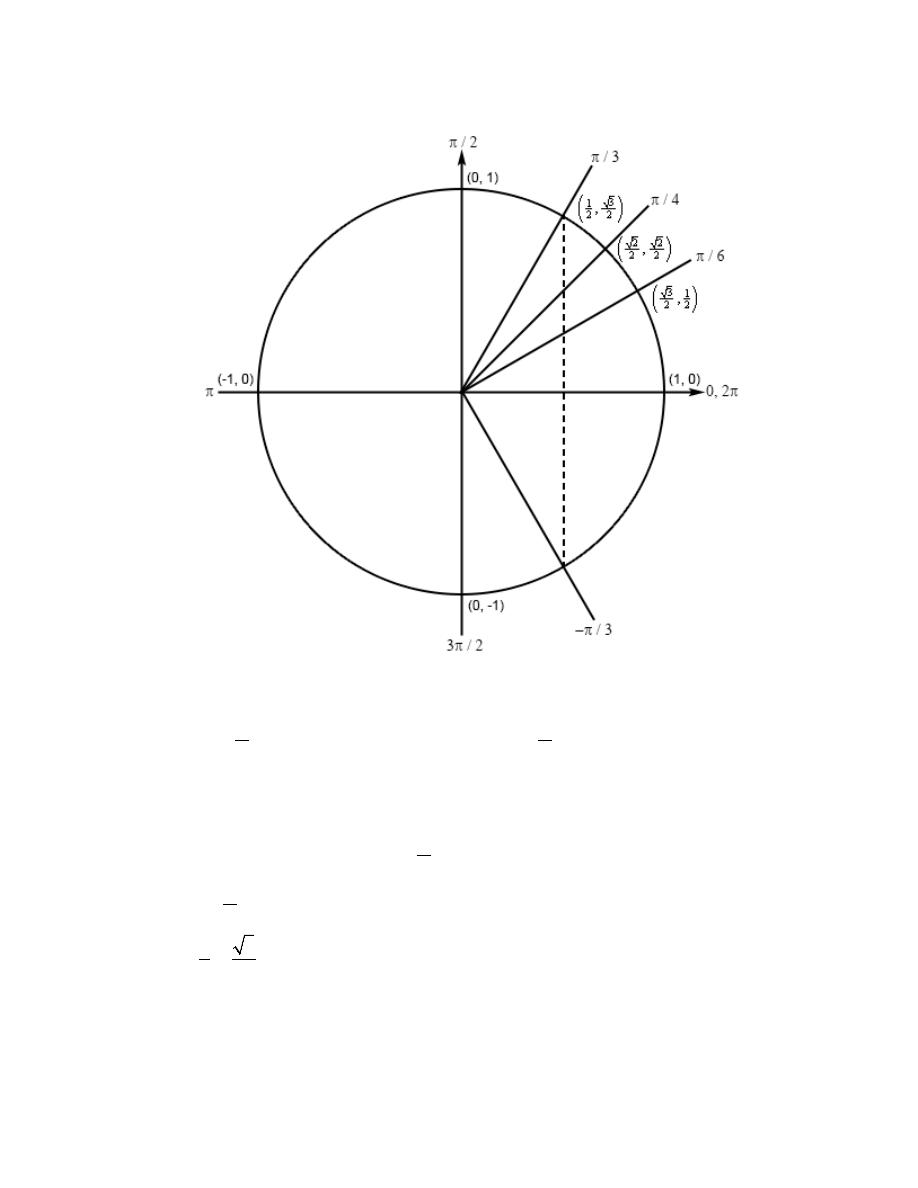
Calculus I
© 2007 Paul Dawkins
45
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
3
π
−
to the coordinates of the line representing
3
π
and use the definition of tangent
in terms of sine and cosine to answer the question.
Step 2
The coordinates of the line representing
3
π
−
will be the same as the coordinates of the line
representing
3
π
except that the y coordinate will now be negative. So, our new coordinates will
then be
1
3
,
2
2
−
and so the answer is,

Calculus I
© 2007 Paul Dawkins
46
http://tutorial.math.lamar.edu/terms.aspx
sin
3
3
2
tan
3
1
3
cos
2
3
π
π
π
−
−
−
=
=
= −
−
9. Determine the exact value of
15
tan
4
π
without using a calculator.
Hint 1 : Even though a unit circle only tells us information about sine and cosine it is still useful
for tangents so sketch a unit circle and relate the angle to one of the standard angles in the first
quadrant.
Step 1
First we can notice that
15
4
4
4
π
π
π
− =
and also note that
4
π
is two complete revolutions so the
terminal line for
15
4
π
and
4
π
−
represent the same angle. Also note that
4
π
−
will form an
angle of
4
π
with the positive x-axis in the fourth quadrant and we’ll have the following unit circle
for this problem.
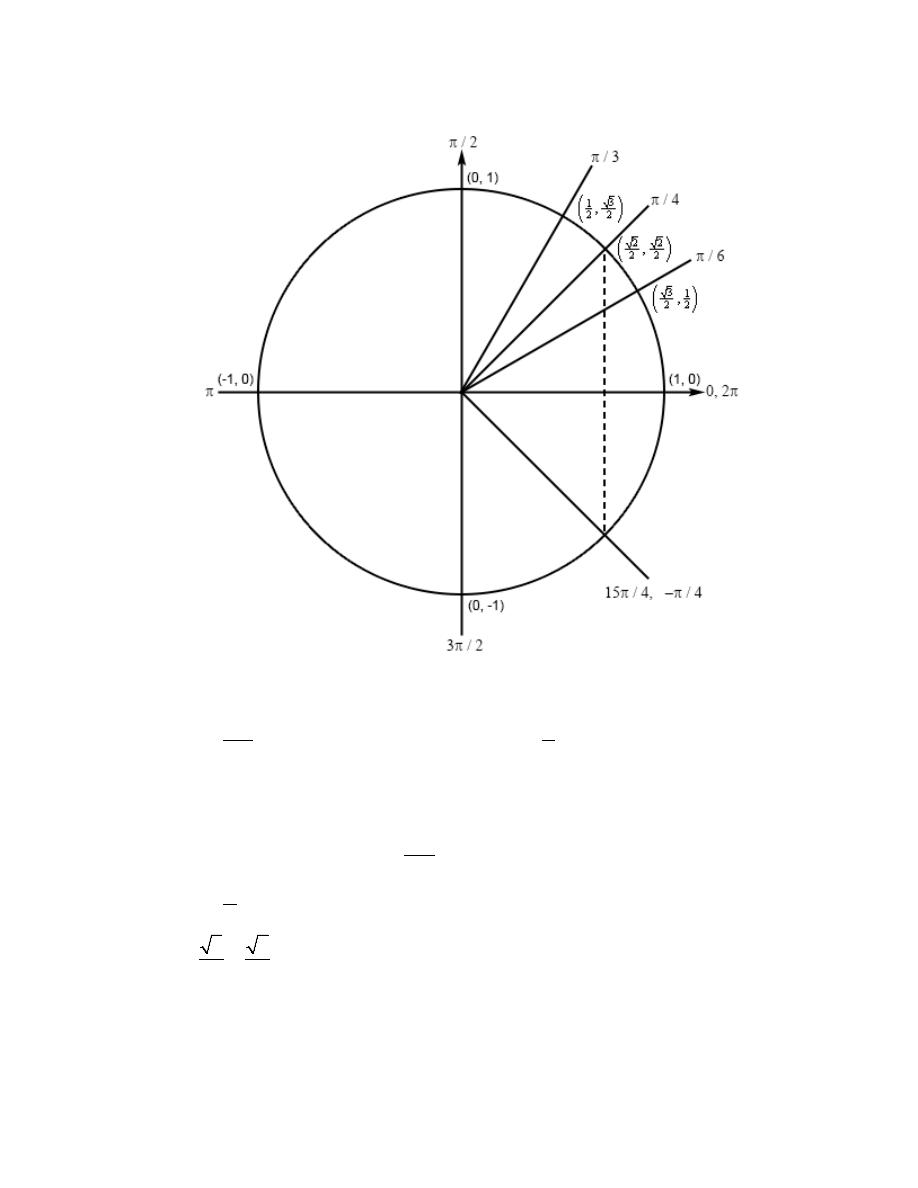
Calculus I
© 2007 Paul Dawkins
47
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
15
4
π
to the coordinates of the line representing
4
π
and the definition of tangent in
terms of sine and cosine to answer the question.
Step 2
The coordinates of the line representing
15
4
π
will be the same as the coordinates of the line
representing
4
π
except that the y coordinate will now be negative. So, our new coordinates will
then be
2
2
,
2
2
−
and so the answer is,
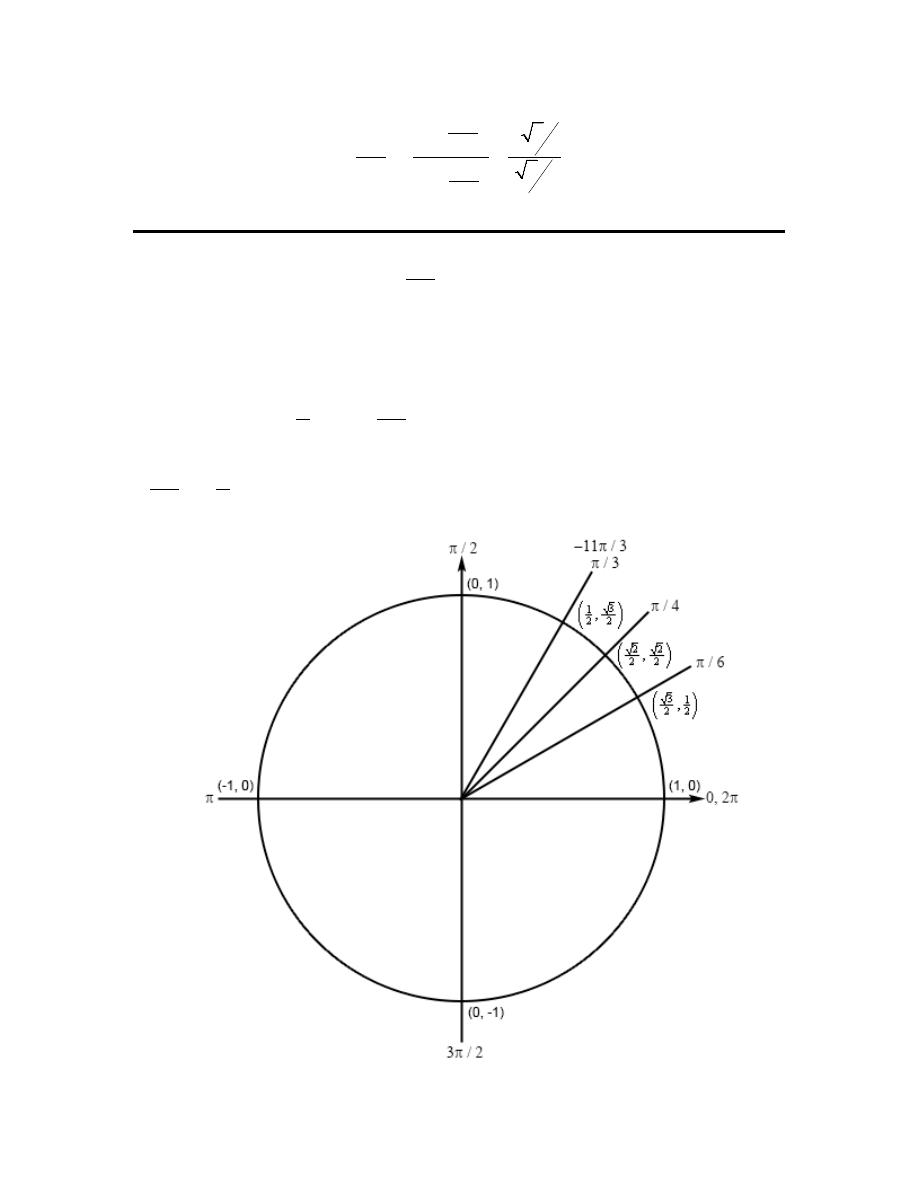
Calculus I
© 2007 Paul Dawkins
48
http://tutorial.math.lamar.edu/terms.aspx
15
sin
2
15
4
2
tan
1
15
4
2
cos
2
4
π
π
π
−
=
=
= −
10. Determine the exact value of
11
sin
3
π
−
without using a calculator.
Hint 1 : Sketch a unit circle and relate the angle to one of the standard angles in the first quadrant.
Step 1
First we can notice that
11
4
3
3
π
π
π
−
= −
and note that
4
π
is two complete revolutions (also,
remembering that negative angles are rotated clockwise) we can see that the terminal line for
11
3
π
−
and
3
π
are the same angle and so we’ll have the following unit circle for this problem.

Calculus I
© 2007 Paul Dawkins
49
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the very obvious symmetry here write down the answer to the question.
Step 2
Because
11
3
π
−
and
3
π
are the same angle the answer is,
11
3
sin
3
2
π
−
=
11. Determine the exact value of
29
sec
4
π
without using a calculator.
Hint 1 : Even though a unit circle only tells us information about sine and cosine it is still useful
for secant so sketch a unit circle and relate the angle to one of the standard angles in the first
quadrant.
Step 1
First we can notice that
5
25
6
4
4
π
π
π
+
=
and recalling that
6
π
is three complete revolutions we
can see that
25
4
π
and
5
4
π
represent the same angle. Next, note that
5
4
4
π
π
π
+ =
and so the
line representing
5
4
π
will form an angle of
4
π
with the negative x-axis in the third quadrant and
we’ll have the following unit circle for this problem.
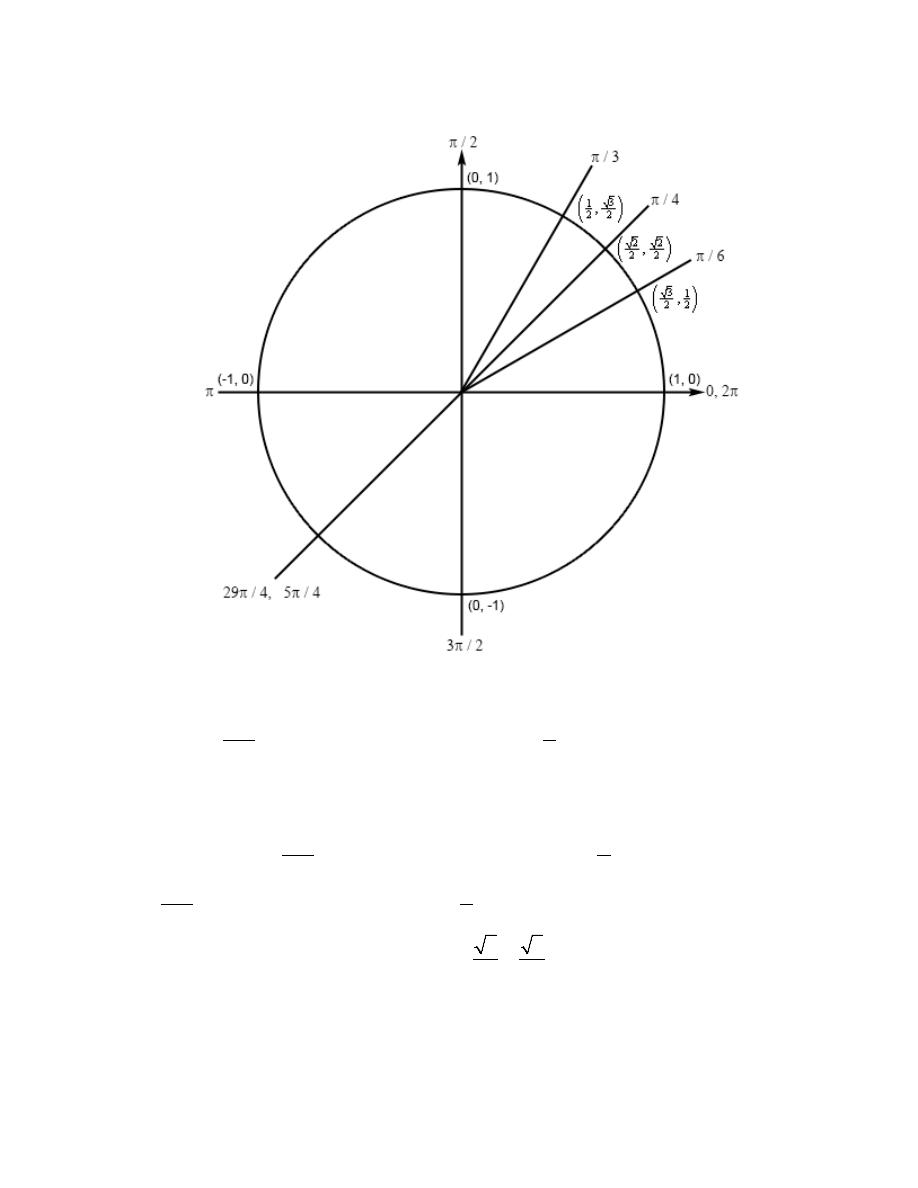
Calculus I
© 2007 Paul Dawkins
50
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Given the obvious symmetry in the unit circle relate the coordinates of the line
representing
25
4
π
to the coordinates of the line representing
4
π
and the recall how secant is
defined in terms of cosine to answer the question.
Step 2
The line representing
25
4
π
is a mirror image of the line representing
4
π
and so the coordinates
for
25
4
π
will be the same as the coordinates for
4
π
except that both coordinates will now be
negative. So, our new coordinates will then be
2
2
,
2
2
−
−
and so the answer is,

Calculus I
© 2007 Paul Dawkins
51
http://tutorial.math.lamar.edu/terms.aspx
29
1
1
2
sec
2
29
4
2
2
sec
2
4
π
π
=
=
= −
= −
−
Review : Solving Trig Equations
1. Without using a calculator find all the solutions to
( )
4 sin 3
2
t
=
.
Hint 1 : Isolate the sine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the sine (with a coefficient of one) on one side of the equation gives,
( )
1
sin 3
2
t
=
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which sine will have this value.
Step 2
Because we’re dealing with sine in this problem and we know that the y-axis represents sine on a
unit circle we’re looking for angles that will have a y coordinate of
1
2
. This means we’ll have an
angle in the first quadrant and an angle in the second quadrant (that we can use the angle in the
first quadrant to find). Here is a unit circle for this situation.
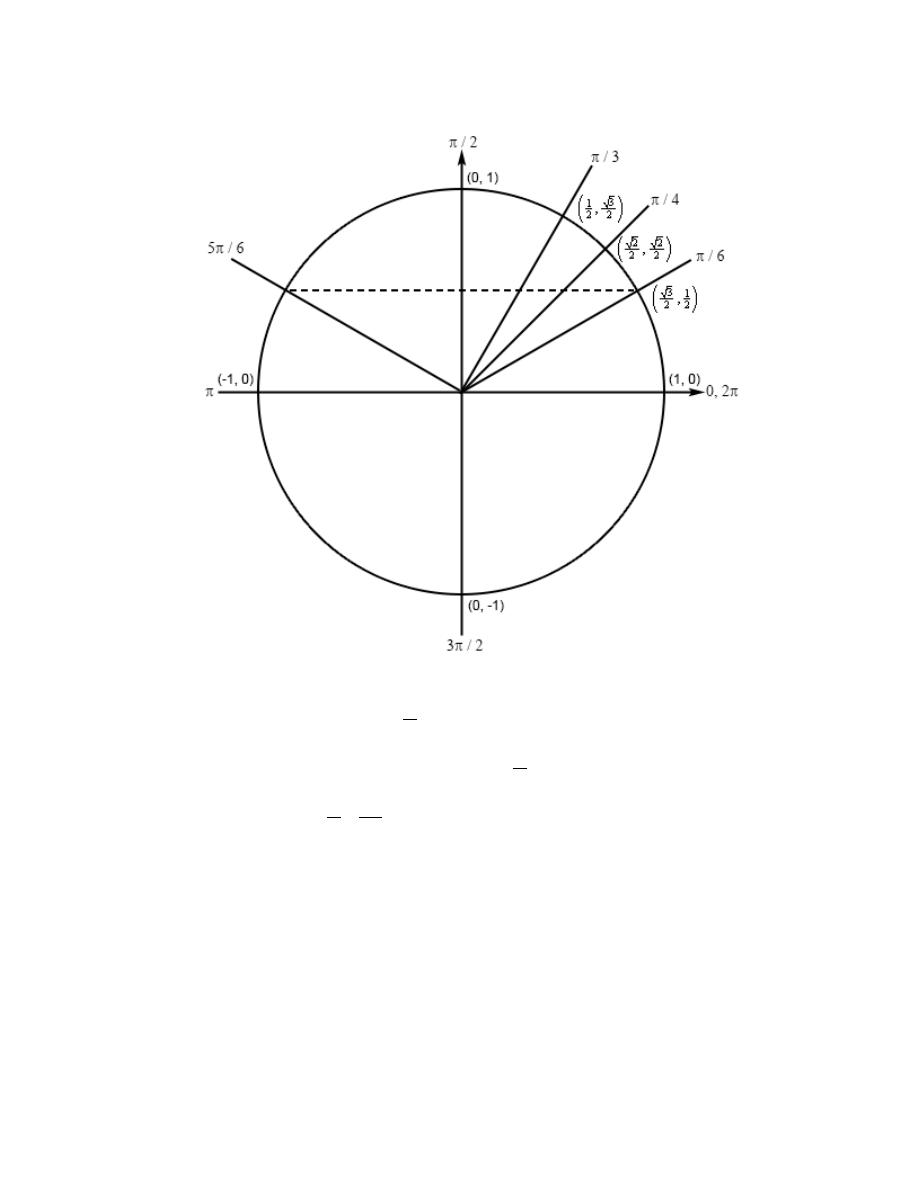
Calculus I
© 2007 Paul Dawkins
52
http://tutorial.math.lamar.edu/terms.aspx
Clearly the angle in the first quadrant is
6
π
and by some basic symmetry we can see that the
terminal line for the second angle must form an angle of
6
π
with the negative x-axis as shown
above and so it will be :
5
6
6
π
π
π
− =
.
Hint 3 : Using the two angles above write down all the angles for which sine will have this value
and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,

Calculus I
© 2007 Paul Dawkins
53
http://tutorial.math.lamar.edu/terms.aspx
5
3
2
OR 3
2
0, 1, 2,
6
6
t
n
t
n
n
π
π
π
π
= +
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 3.
2
5
2
OR
0, 1, 2,
18
3
18
3
n
n
t
t
n
π
π
π
π
=
+
=
+
= ± ±
2. Without using a calculator find the solution(s) to
( )
4 sin 3
2
t
=
that are in
4
0,
3
π
.
Hint 1 : First, find all the solutions to the equation without regard to the given interval.
Step 1
Because we found all the solutions to this equation in Problem 1 of this section we’ll just
list the result here. For full details on how these solutions were obtained please see the
solution to Problem 1.
All solutions to the equation are,
2
5
2
OR
0, 1, 2,
18
3
18
3
n
n
t
t
n
π
π
π
π
=
+
=
+
= ± ±
Hint 2 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in this interval.
Step 2
Note that because at least some of the solutions will have a denominator of 18 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 18. Doing
this will make it much easier to identify solutions that fall inside the interval so,
4
24
0,
0,
3
18
π
π
=
With the interval written in this form, if our potential solutions have a denominator of 18, all we
need to do is compare numerators. As long as the numerators are positive and less than
24
π
we’ll know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 18. So the solutions, written in this
form, are.

Calculus I
© 2007 Paul Dawkins
54
http://tutorial.math.lamar.edu/terms.aspx
12
5
12
OR
0, 1, 2,
18
18
18
18
n
n
t
t
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. So, let’s start at
0
n
=
and see what we get.
5
0 :
OR
18
18
13
17
1:
OR
18
18
25
2 :
18
n
t
t
n
t
t
n
t
π
π
π
π
π
=
=
=
=
=
=
=
=
24
29
OR
18
18
t
π
π
>
=
24
18
π
>
Note that we didn’t really need to plug in
2
n
=
above to see that they would not work. With
each increase in n we were really just adding another
12
18
π
onto the previous results and by a
quick inspection we could see that adding
12
π
to the numerator of either solution from the
1
n
=
step would result in a numerator that is larger than
24
π
and so would result in a solution that is
outside of the interval. This is not something that must be noticed in order to work the problem,
but noticing this would definitely help reduce the amount of actual work.
So, it looks like we have the four solutions to this equation in the given interval.
5
13
17
,
,
,
18 18
18
18
t
π
π
π
π
=
3. Without using a calculator find all the solutions to
2 cos
2
0
3
x
+ =
.
Hint 1 : Isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
2
cos
3
2
x
= −
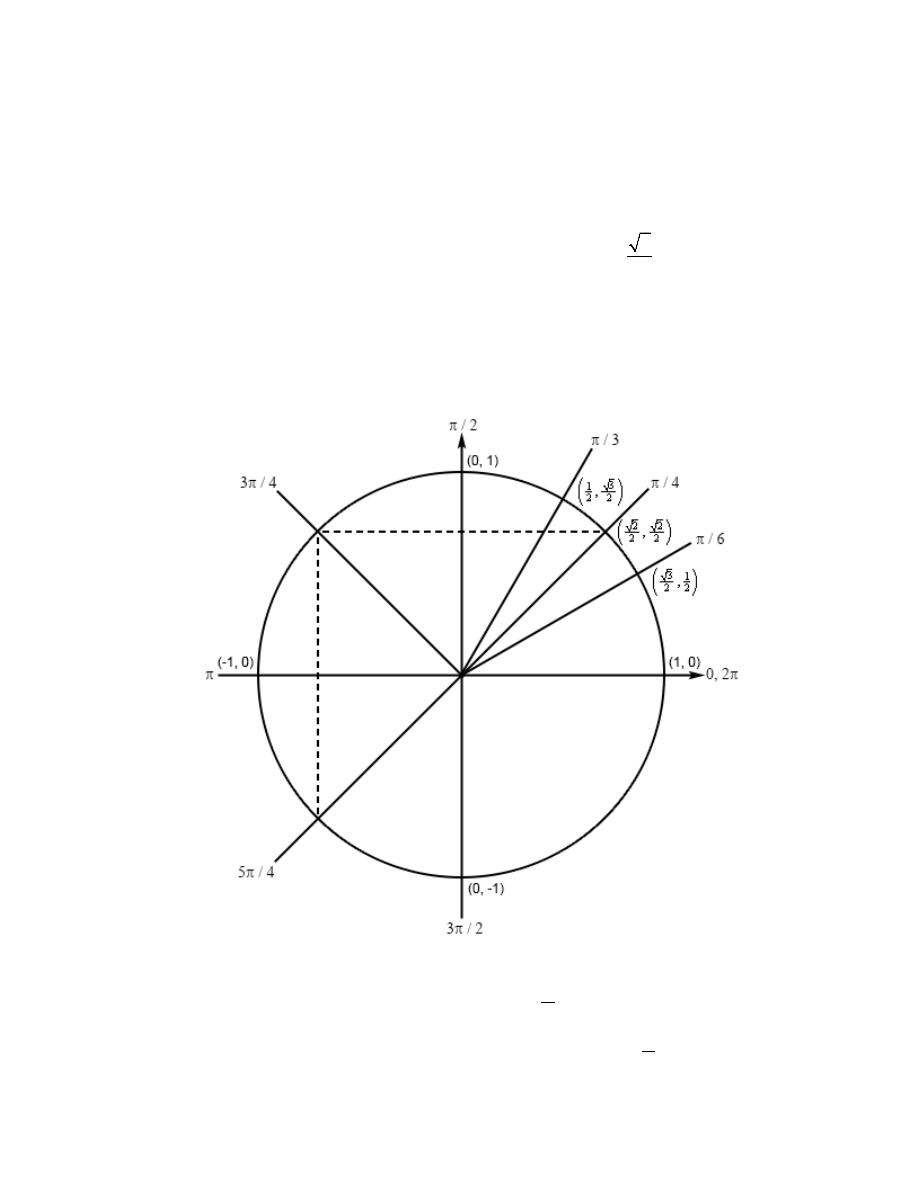
Calculus I
© 2007 Paul Dawkins
55
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which cosine will have this value.
Step 2
Because we’re dealing with cosine in this problem and we know that the x-axis represents cosine
on a unit circle we’re looking for angles that will have a x coordinate of
2
2
−
. This means that
we’ll have angles in the second and third quadrant.
Because of the negative value we can’t just find the corresponding angle in the first quadrant and
use that to find the second angle. However, we can still use the angles in the first quadrant to find
the two angles that we need. Here is a unit circle for this situation.
If we didn’t have the negative value then the angle would be
4
π
. Now, based on the symmetry in
the unit circle, the terminal line for both of the angles will form an angle of
4
π
with the negative

Calculus I
© 2007 Paul Dawkins
56
http://tutorial.math.lamar.edu/terms.aspx
x-axis. The angle in the second quadrant will then be
3
4
4
π
π
π
− =
and the angle in the third
quadrant will be
5
4
4
π
π
π
+ =
.
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
3
5
2
OR
2
0, 1, 2,
3
4
3
4
x
x
n
n
n
π
π
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 3.
9
15
6
OR
6
0, 1, 2,
4
4
x
n
x
n
n
π
π
π
π
=
+
=
+
= ± ±
4. Without using a calculator find the solution(s) to
2 cos
2
0
3
x
+ =
that are in
[
]
7 , 7
π π
−
.
Hint 1 : First, find all the solutions to the equation without regard to the given interval.
Step 1
Because we found all the solutions to this equation in Problem 3 of this section we’ll just
list the result here. For full details on how these solutions were obtained please see the
solution to Problem 3.
All solutions to the equation are,
9
15
6
OR
6
0, 1, 2,
4
4
x
n
x
n
n
π
π
π
π
=
+
=
+
= ± ±
Hint 2 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in this interval.
Step 2

Calculus I
© 2007 Paul Dawkins
57
http://tutorial.math.lamar.edu/terms.aspx
Note that because at least some of the solutions will have a denominator of 4 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 4. Doing
this will make it much easier to identify solutions that fall inside the interval so,
[
]
28
28
7 , 7
,
4
4
π
π
π π
−
= −
With the interval written in this form, if our potential solutions have a denominator of 4, all we
need to do is compare numerators. As long as the numerators are between
28
π
−
and
28
π
we’ll
know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 4. So the solutions, written in this
form, are.
9
24
15
24
OR
0, 1, 2,
4
4
4
4
n
n
x
x
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions.
39
2 :
4
n
x
π
= −
= −
28
33
OR
4
4
x
π
π
< −
= −
28
4
15
9
1:
OR
4
4
9
15
0 :
OR
4
4
33
1:
4
n
x
x
n
x
x
n
x
π
π
π
π
π
π
< −
= −
= −
= −
=
=
=
=
=
28
39
OR
4
4
x
π
π
>
=
28
4
π
>
Note that we didn’t really need to plug in
1
n
=
or
2
n
= −
above to see that they would not
work. With each increase in n we were really just adding (for positive n) or subtracting (for
negative n) another
24
4
π
from the previous results. By a quick inspection we could see that
adding
24
π
to the numerator of either solution from the
1
n
=
step would result in a numerator
that is larger than
28
π
and so would result in a solution that is outside of the interval. Likewise,
for the
2
n
= −
case, subtracting
24
π
from each of the numerators will result in numerators that
will be less than
28
π
−
and so will not be in the interval. This is not something that must be
noticed in order to work the problem, but noticing this would definitely help reduce the amount of
actual work.
So, it looks like we have the four solutions to this equation in the given interval.
15
9
9
15
,
,
,
4
4
4
4
x
π
π
π
π
= −
−

Calculus I
© 2007 Paul Dawkins
58
http://tutorial.math.lamar.edu/terms.aspx
5. Without using a calculator find the solution(s) to
( )
4 cos 6
12
z
=
that are in
0,
2
π
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
( )
12
2 3
3
cos 6
4
4
2
z
=
=
=
Notice that we needed to do a little simplification of the root to get the value into a more
recognizable form. This kind of simplification is usually a good thing to do.
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which cosine will have this value.
Step 2
Because we’re dealing with cosine in this problem and we know that the x-axis represents cosine
on a unit circle we’re looking for angles that will have a x coordinate of
3
2
. This means we’ll
have an angle in the first quadrant and an angle in the fourth quadrant (that we can use the angle
in the first quadrant to find). Here is a unit circle for this situation.
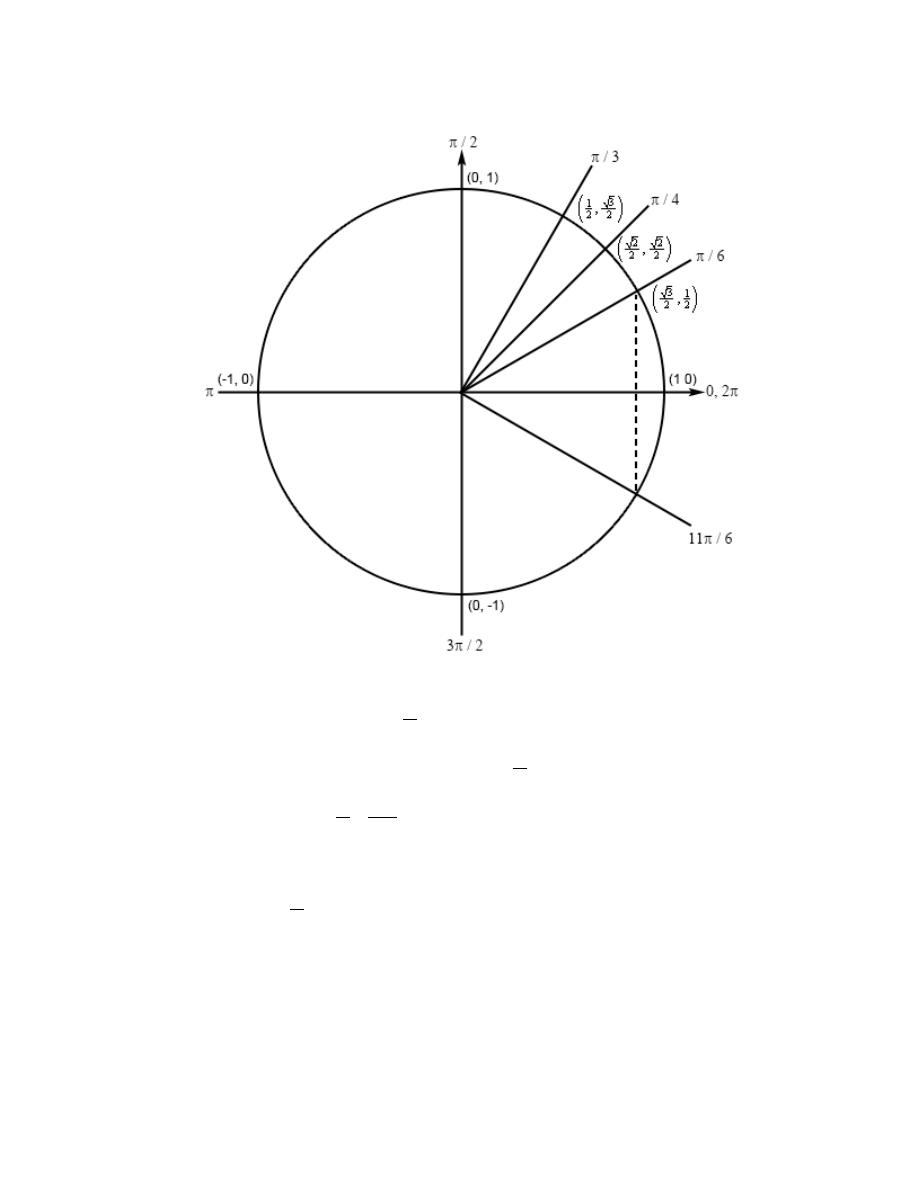
Calculus I
© 2007 Paul Dawkins
59
http://tutorial.math.lamar.edu/terms.aspx
Clearly the angle in the first quadrant is
6
π
and by some basic symmetry we can see that the
terminal line for the second angle must form an angle of
6
π
with the positive x-axis as shown
above and so it will be :
11
2
6
6
π
π
π
− =
.
Note that you don’t really need a positive angle for the second one. If you wanted to you could
just have easily used
6
π
−
for the second angle. There is nothing wrong with this and you’ll get
the same solutions in the end. The reason we chose to go with the positive angle is simply to
avoid inadvertently losing the minus sign on the second solution at some point in the future. That
kind of mistake is easy to make on occasion and by using positive angles here we will not need to
worry about making it.
Calculus I
© 2007 Paul Dawkins
60
http://tutorial.math.lamar.edu/terms.aspx
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
11
6
2
OR 6
2
0, 1, 2,
6
6
z
n
z
n
n
π
π
π
π
= +
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 6.
11
OR
0, 1, 2,
36
3
36
3
n
n
z
z
n
π
π
π π
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 36 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 36. Doing
this will make it much easier to identify solutions that fall inside the interval so,
18
0,
0,
2
36
π
π
=
With the interval written in this form, if our potential solutions have a denominator of 36, all we
need to do is compare numerators. As long as the numerators are positive and less than
18
π
we’ll know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 36. So the solutions, written in this
form, are.
12
11
12
OR
0, 1, 2,
36
36
36
36
n
n
z
z
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. So, let’s start at
0
n
=
and see what we get.
Calculus I
© 2007 Paul Dawkins
61
http://tutorial.math.lamar.edu/terms.aspx
11
0 :
OR
36
36
13
23
1:
OR
36
36
n
z
z
n
z
z
π
π
π
π
=
=
=
=
=
=
18
36
π
>
There are a couple of things we should note before proceeding. First, it is important to
understand both solutions from a given value of n will not necessarily be in the given interval. It
is completely possible, as this problem shows, that we will only get one or the other solution from
a given value of n to fall in the given interval.
Next notice that with each increase in n we were really just adding another
12
36
π
onto the
previous results and by a quick inspection we could see that adding
12
π
to the numerator of the
first solution from the
1
n
=
step would result in a numerator that is larger than
18
π
and so
would result in a solution that is outside of the interval. Therefore, there was no reason to plug in
2
n
=
into the first set of solutions. Of course, we also didn’t plug
2
n
=
into the second set
because once we’ve gotten out of the interval adding anything else on will remain out of the
interval.
So, it looks like we have the three solutions to this equation in the given interval.
11
13
,
,
36
36
36
z
π
π
π
=
6. Without using a calculator find the solution(s) to
3
2 sin
3
0
2
y
+ =
that are in
7
, 0
3
π
−
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the sine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the sine (with a coefficient of one) on one side of the equation gives,
3
3
sin
2
2
y
= −
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which cosine will have this value.
Step 2
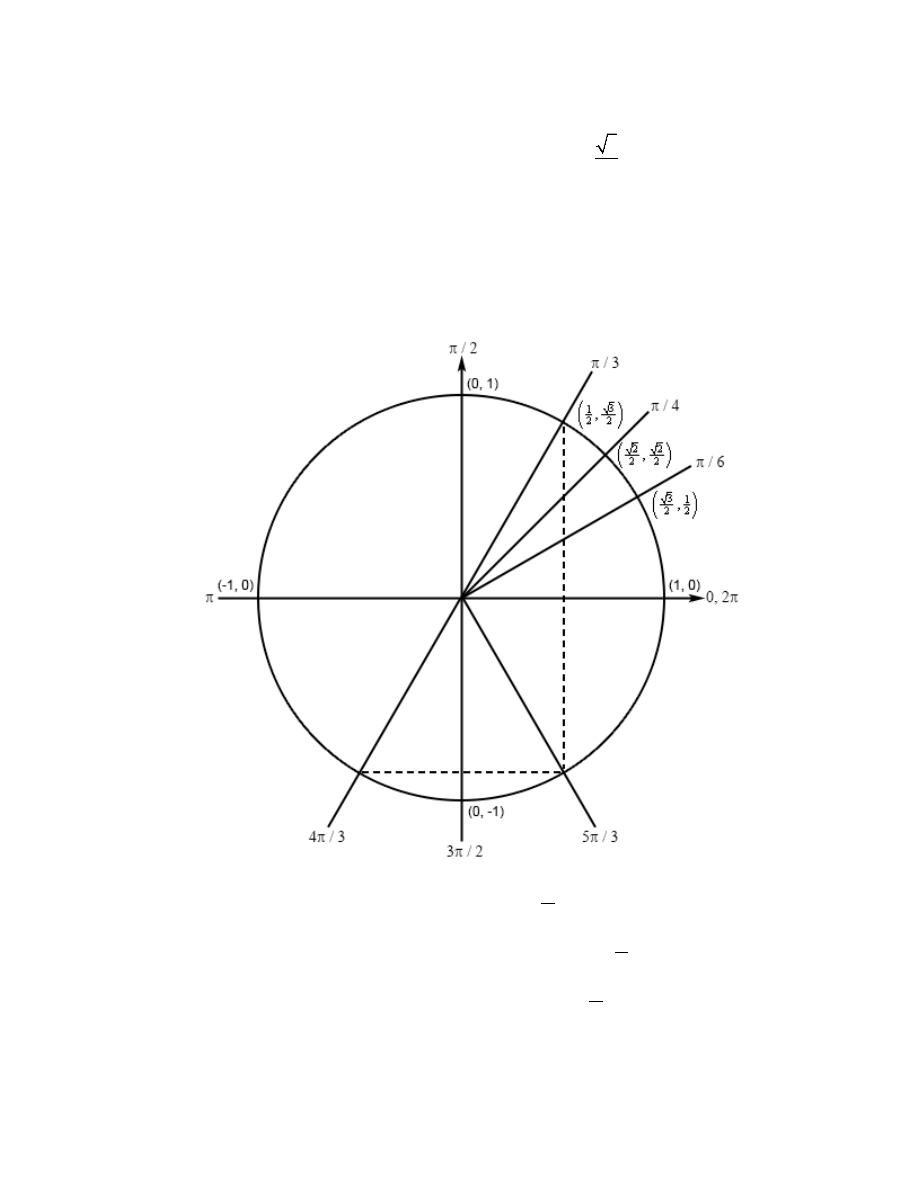
Calculus I
© 2007 Paul Dawkins
62
http://tutorial.math.lamar.edu/terms.aspx
Because we’re dealing with sine in this problem and we know that the y-axis represents sine on a
unit circle we’re looking for angles that will have a y coordinate of
3
2
−
. This means that we’ll
have angles in the third and fourth quadrant.
Because of the negative value we can’t just find the corresponding angle in the first quadrant and
use that to find the second angle. However, we can still use the angles in the first quadrant to find
the two angles that we need. Here is a unit circle for this situation.
If we didn’t have the negative value then the angle would be
3
π
. Now, based on the symmetry in
the unit circle, the terminal line for the first angle will form an angle of
3
π
with the negative x-
axis and the terminal line for the second angle will form an angle of
3
π
with the positive x-axis.

Calculus I
© 2007 Paul Dawkins
63
http://tutorial.math.lamar.edu/terms.aspx
The angle in the third quadrant will then be
4
3
3
π
π
π
+ =
and the angle in the fourth quadrant
will be
5
2
3
3
π
π
π
− =
.
Note that you don’t really need a positive angle for the second one. If you wanted to you could
just have easily used
3
π
−
for the second angle. There is nothing wrong with this and you’ll get
the same solutions in the end. The reason we chose to go with the positive angle is simply to
avoid inadvertently losing the minus sign on the second solution at some point in the future. That
kind of mistake is easy to make on occasion and by using positive angles here we will not need to
worry about making it.
Hint 3 : Using the two angles above write down all the angles for which sine will have this value
and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
3
4
3
5
2
OR
2
0, 1, 2,
2
3
2
3
y
y
n
n
n
π
π
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by
2
3
.
8
4
10
4
OR
0, 1, 2,
9
3
9
3
n
n
y
y
n
π
π
π
π
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 9 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 9. Doing
this will make it much easier to identify solutions that fall inside the interval so,
7
21
, 0
, 0
3
9
π
π
−
= −
With the interval written in this form, if our potential solutions have a denominator of 9, all we
need to do is compare numerators. As long as the numerators are negative and greater than
21
π
−
we’ll know that the solution is in the interval.
Calculus I
© 2007 Paul Dawkins
64
http://tutorial.math.lamar.edu/terms.aspx
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 9. So the solutions, written in this
form, are.
8
12
10
12
OR
0, 1, 2,
9
9
9
9
n
n
y
y
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions. First notice that, in this case, if we plug in positive values of n or
zero we will get positive solutions and these will not be in the interval and so there is no reason to
even try these. So, let’s start at
1
n
= −
and see what we get.
4
2
1:
OR
9
9
16
14
2 :
OR
9
9
n
y
y
n
y
y
π
π
π
π
= −
= −
= −
= −
= −
= −
Notice that with each increase (in the negative sense anyway) in n we were really just subtracting
another
12
9
π
from the previous results and by a quick inspection we could see that subtracting
12
π
from either of the numerators from the
2
n
= −
solutions the numerators will be less than
21
π
−
and so will be out of the interval. There is no reason to write down the
3
n
= −
solutions
since we know that they will not be in the given interval.
So, it looks like we have the four solutions to this equation in the given interval.
16
14
4
2
,
,
,
9
9
9
9
y
π
π
π
π
= −
−
−
−
7. Without using a calculator find the solution(s) to
( )
8 tan 2
5
3
x
− =
that are in
3
,
2
2
π π
−
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the tangent (with a coefficient of one) on one side of the equation.
Step 1
Isolating the tangent (with a coefficient of one) on one side of the equation gives,
( )
tan 2
1
x
=
Hint 2 : Determine all the angles in the range
[
]
0, 2
π
for which tangent will have this value.
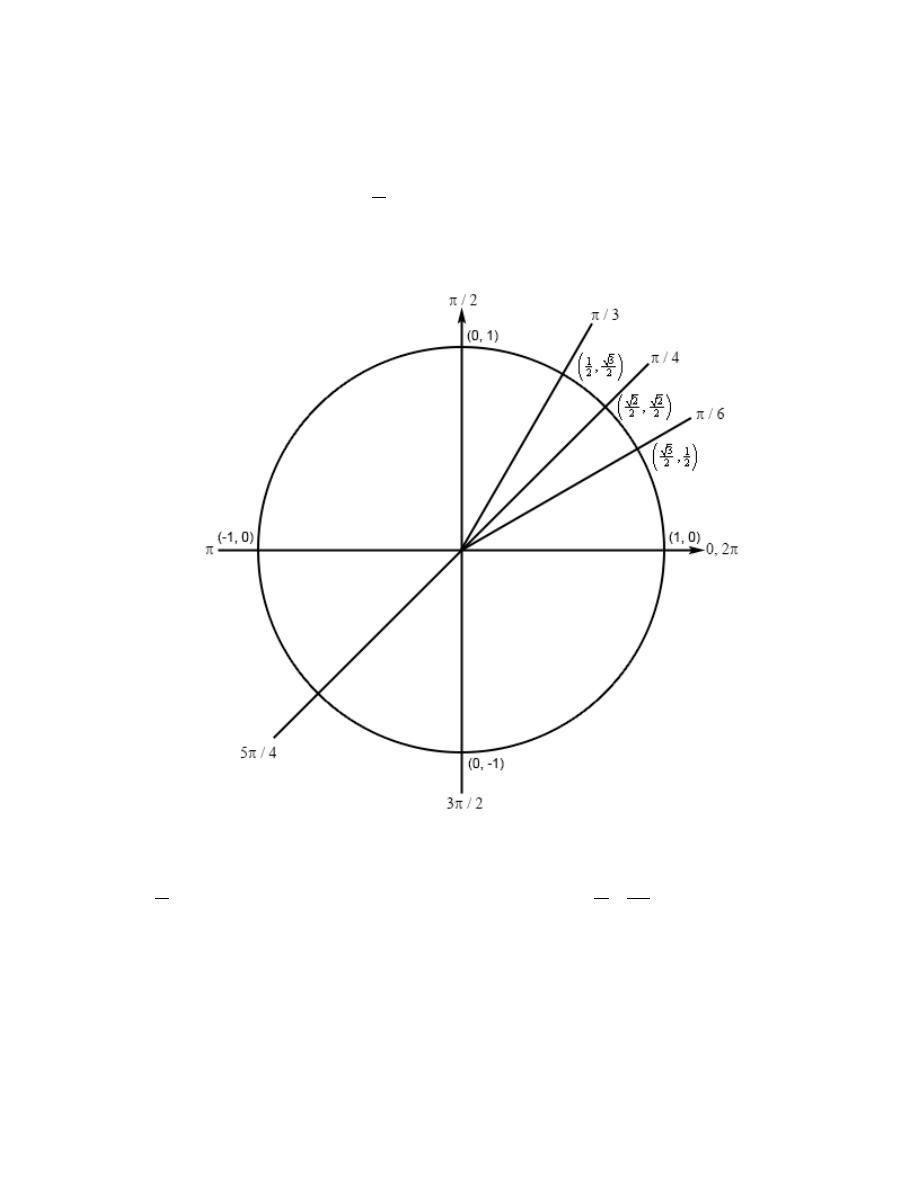
Calculus I
© 2007 Paul Dawkins
65
http://tutorial.math.lamar.edu/terms.aspx
Step 2
If tangent has a value of 1 then we know that sine and cosine must be the same. This means that,
in the first quadrant, the solution is
4
π
. We also know that sine and cosine will be the same in the
third quadrant and we can use the basic symmetry on our unit circle to determine this value. Here
is a unit circle for this situation.
By basic symmetry we can see that the line terminal line for the second angle must form an angle
of
4
π
with the negative x-axis as shown above and so it will be :
5
4
4
π
π
π
+ =
.
Hint 3 : Using the two angles above write down all the angles for which tangent will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.

Calculus I
© 2007 Paul Dawkins
66
http://tutorial.math.lamar.edu/terms.aspx
This then means that we must have,
5
2
2
OR 2
2
0, 1, 2,
4
4
x
n
x
n
n
π
π
π
π
= +
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 2.
5
OR
0, 1, 2,
8
8
x
n
x
n
n
π
π
π
π
= +
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 8 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 8. Doing
this will make it much easier to identify solutions that fall inside the interval so,
3
4
12
,
,
2
2
8
8
π π
π
π
−
= −
With the interval written in this form, if our potential solutions have a denominator of 8, all we
need to do is compare numerators. As long as the numerators are between
4
π
−
and
12
π
we’ll
know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 8. So the solutions, written in this
form, are.
8
5
8
OR
0, 1, 2,
8
8
8
8
n
n
x
x
n
π
π
π
π
= +
=
+
= ± ±
Now let’s find all the solutions.
7
1:
8
n
x
π
= −
= −
4
3
OR
8
8
5
0 :
OR
8
8
9
13
1:
OR
8
8
x
n
x
x
n
x
x
π
π
π
π
π
π
< −
= −
=
=
=
=
=
=
12
8
π
>
There are a couple of things we should note before proceeding. First, it is important to
understand both solutions from a given value of n will not necessarily be in the given interval. It
Calculus I
© 2007 Paul Dawkins
67
http://tutorial.math.lamar.edu/terms.aspx
is completely possible, as this problem shows, that we will only get one or the other solution from
a given value of n to fall in the given interval.
Next notice that with each increase in n we were really just adding/subtracting (depending upon
the sign of n) another
8
8
π
from the previous results and by a quick inspection we could see that
adding
8
π
to the numerator of the
1
n
=
solutions would result in numerators that are larger than
12
π
and so would result in solutions that are outside of the interval. Likewise, subtracting
8
π
from the
1
n
= −
solutions would result in numerators that are smaller than
4
π
−
and so would
result in solutions that are outside the interval. Therefore, there is no reason to even go past the
values of n listed here.
So, it looks like we have the four solutions to this equation in the given interval.
3
5
9
,
,
,
8
8
8
8
x
π π
π
π
= −
8. Without using a calculator find the solution(s) to
( )
16
9 sin 7
4
x
= −
−
that are in
9
2 ,
4
π
π
−
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the sine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the sine (with a coefficient of one) on one side of the equation gives,
( )
20
sin 7
1
9
x
= −
< −
Okay, at this point we can stop all work. We know that
1 sin
1
θ
− ≤
≤
for any argument and so
in this case there is no solution. This will happen on occasion and we shouldn’t get to excited
about it when it happens.
9. Without using a calculator find the solution(s) to
3 tan
5
4
4
t
+ =
that are in
[
]
0, 4
π
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the tangent (with a coefficient of one) on one side of the equation.

Calculus I
© 2007 Paul Dawkins
68
http://tutorial.math.lamar.edu/terms.aspx
Step 1
Isolating the tangent (with a coefficient of one) on one side of the equation gives,
1
tan
4
3
t
= −
Hint 2 : Determine all the angles in the range
[
]
0, 2
π
for which tangent will have this value.
Step 2
To get the first angle here let’s recall the definition of tangent in terms of sine and cosine.
( )
( )
4
4
sin
1
tan
4
cos
3
t
t
t
=
= −
Now, because of the section we’re in, we know that the angle must be one of the “standard”
angles and from a quick look at a unit circle (shown below) we know that for
6
π
we will have,
( )
( )
6
6
1
sin
1
2
cos
3
3
2
π
π
=
=
So, if we had a positive value on the tangent we’d have the first angle. We do have a negative
value however, but this work will allow us to get the two angles we’re after. Because the value is
negative this simply means that the sine and cosine must have the same values that they have for
6
π
except that one must be positive and the other must be negative. This means that the angles
that we’re after must be in the second and fourth quadrants. Here is a unit circle for this situation.
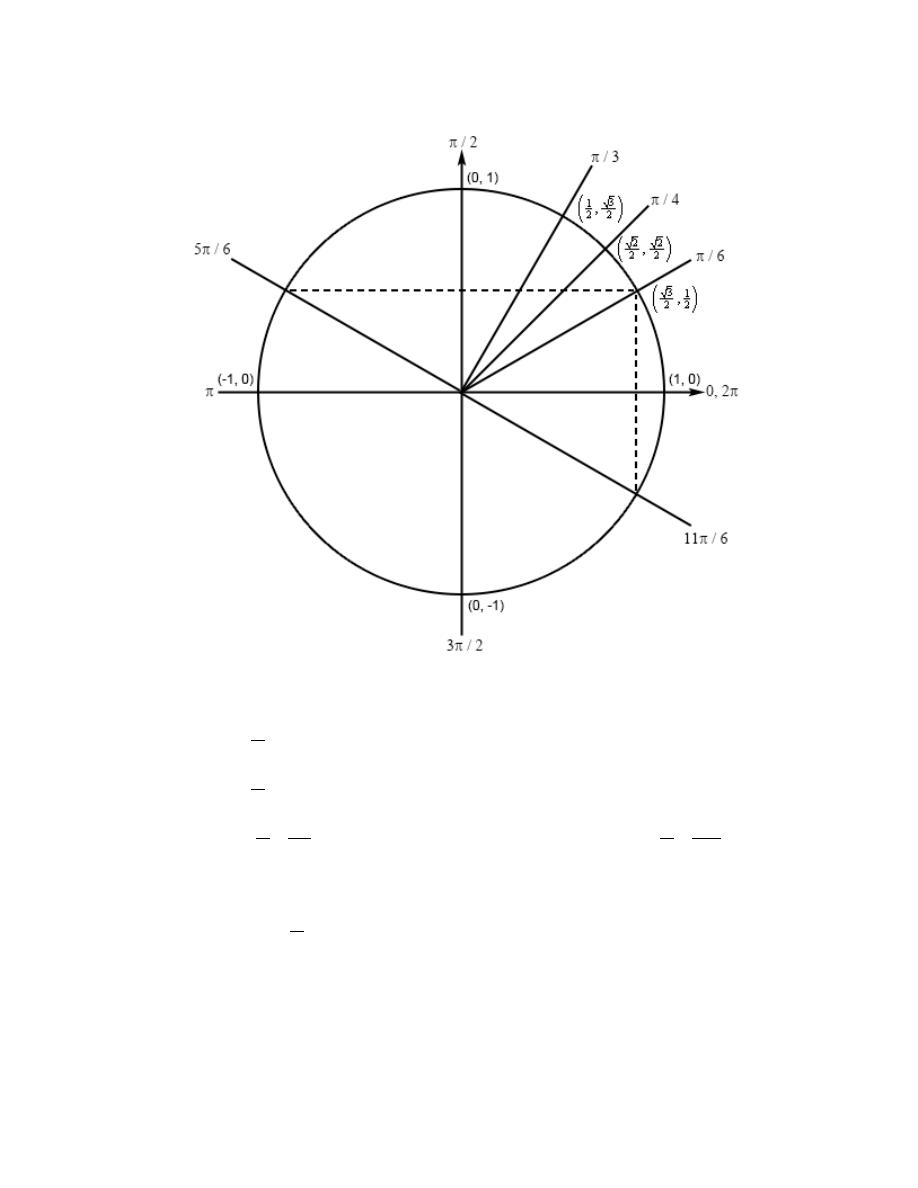
Calculus I
© 2007 Paul Dawkins
69
http://tutorial.math.lamar.edu/terms.aspx
By basic symmetry we can see that the terminal line for the angle in the second quadrant must
form an angle of
6
π
with the negative x-axis and the terminal line in the fourth quadrant must
form an angle of
6
π
with the positive x-axis as shown above. The angle in the second quadrant
will then be :
5
6
6
π
π
π
− =
while the angle in the fourth quadrant will be
11
2
6
6
π
π
π
− =
.
Note that you don’t really need a positive angle for the second one. If you wanted to you could
just have easily used
6
π
−
for the second angle. There is nothing wrong with this and you’ll get
the same solutions in the end. The reason we chose to go with the positive angle is simply to
avoid inadvertently losing the minus sign on the second solution at some point in the future. That
kind of mistake is easy to make on occasion and by using positive angles here we will not need to
worry about making it.

Calculus I
© 2007 Paul Dawkins
70
http://tutorial.math.lamar.edu/terms.aspx
Hint 3 : Using the two angles above write down all the angles for which tangent will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
5
11
2
OR
2
0, 1, 2,
4
6
4
6
t
t
n
n
n
π
π
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 4.
10
22
8
OR
8
0, 1, 2,
3
3
t
n
t
n
n
π
π
π
π
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 3 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 3. Doing
this will make it much easier to identify solutions that fall inside the interval so,
[
]
12
0, 4
0,
3
π
π
=
With the interval written in this form, if our potential solutions have a denominator of 3, all we
need to do is compare numerators. As long as the numerators are positive and less than
12
π
we’ll know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 3. So the solutions, written in this
form, are.
10
24
22
24
OR
0, 1, 2,
3
3
3
3
n
n
t
t
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. Next, notice that for any positive n we will be adding
24
3
π
onto a positive
quantity and so are guaranteed to be greater than
12
3
π
and so will out of the given interval. This

Calculus I
© 2007 Paul Dawkins
71
http://tutorial.math.lamar.edu/terms.aspx
leaves
0
n
=
and for this one we can notice that the only solution that will fall in the given
interval is then,
10
3
π
Before leaving this problem let’s note that on occasion we will only get a single solution out of all
the possible solutions that will fall in the given interval. So, don’t get excited about it if this
should happen.
10. Without using a calculator find the solution(s) to
( )
3 csc 9
7
5
z
− = −
that are in
4
,
3
9
π π
−
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosecant (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosecant (with a coefficient of one) on one side of the equation gives,
( )
2
csc 9
3
z
=
Hint 2 : We need to determine all the angles in the range
[
]
0, 2
π
for which cosecant will have
this value. The best way to do this is to rewrite this equation into one in terms of a different trig
function that we can more easily deal with.
Step 2
The best way to do this is to recall the definition of cosecant in terms of sine and rewrite the
equation in terms sine instead as that will be easier to deal with. Doing this gives,
( )
( )
( )
1
2
3
csc 9
sin 9
sin 9
2
3
z
z
z
=
=
⇒
=
The solution(s) to the equation with sine in it are the same as the solution(s) to the equation with
cosecant in it and so let’s work with that instead.
At this point we are now dealing with sine and we know that the y-axis represents sine on a unit
circle. So we’re looking for angles that will have a y coordinate of
3
2
. This means we’ll have
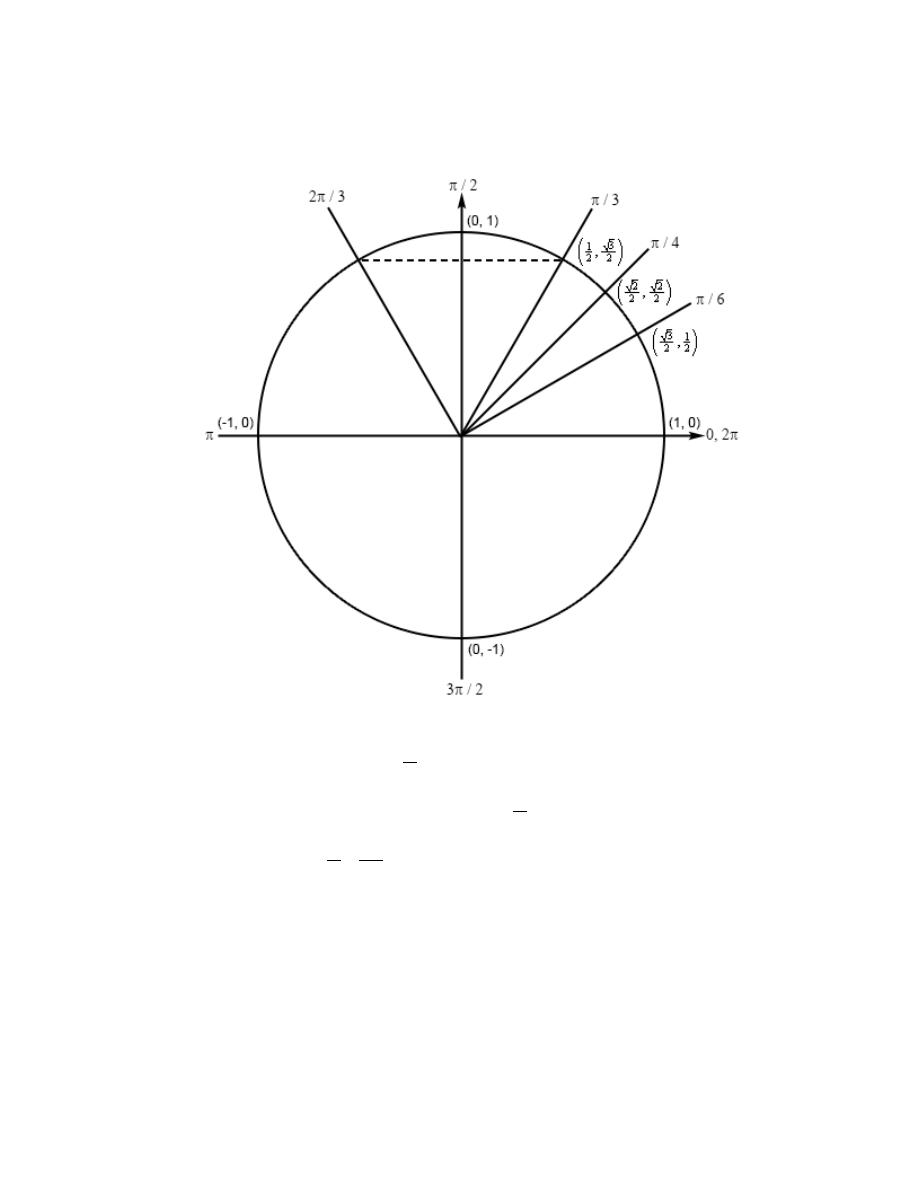
Calculus I
© 2007 Paul Dawkins
72
http://tutorial.math.lamar.edu/terms.aspx
an angle in the first quadrant and an angle in the second quadrant (that we can use the angle in the
first quadrant to find). Here is a unit circle for this situation
Clearly the angle in the first quadrant is
3
π
and by some basic symmetry we can see that the
terminal line for the second angle must form an angle of
3
π
with the negative x-axis as shown
above and so it will be :
2
3
3
π
π
π
− =
.
Hint 3 : Using the two angles above write down all the angles for which sine/cosecant will have
this value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.

Calculus I
© 2007 Paul Dawkins
73
http://tutorial.math.lamar.edu/terms.aspx
This then means that we must have,
2
9
2
OR 9
2
0, 1, 2,
3
3
z
n
z
n
n
π
π
π
π
= +
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 9.
2
2
2
OR
0, 1, 2,
27
9
27
9
n
n
z
z
n
π
π
π
π
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 27 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 27. Doing
this will make it much easier to identify solutions that fall inside the interval so,
4
9
12
,
,
3
9
27
27
π π
π
π
−
= −
With the interval written in this form, if our potential solutions have a denominator of 27, all we
need to do is compare numerators. As long as the numerators are between
9
π
−
and
12
π
we’ll
know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 27. So the solutions, written in this
form, are.
6
2
6
OR
0, 1, 2,
27
27
27
27
n
n
z
z
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions.
5
4
1:
OR
27
27
2
0 :
OR
27
27
7
8
1:
OR
27
27
n
z
z
n
z
z
n
z
z
π
π
π
π
π
π
= −
= −
= −
=
=
=
=
=
=
Notice that with each increase in n we were really just adding/subtracting (depending upon the
sign of n) another
6
27
π
from the previous results and by a quick inspection we could see that
adding
6
π
to the numerator of the
1
n
=
solutions would result in numerators that are larger than
12
π
and so would result in solutions that are outside of the interval. Likewise, subtracting
6
π
from the
1
n
= −
solutions would result in numerators that are smaller than
9
π
−
and so would

Calculus I
© 2007 Paul Dawkins
74
http://tutorial.math.lamar.edu/terms.aspx
result in solutions that are outside the interval. Therefore, there is no reason to even go past the
values of n listed here.
So, it looks like we have the six solutions to this equation in the given interval.
5
4
2
7
8
,
,
,
,
,
27
27
27
27
27
27
x
π
π π
π
π
π
= −
−
11. Without using a calculator find the solution(s) to
2
1 14 cos
6
5
x
−
= −
that are in
40
5 ,
3
π
π
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
2
1
cos
5
2
x
=
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which cosine will have this value.
Step 2
Because we’re dealing with cosine in this problem and we know that the x-axis represents cosine
on a unit circle we’re looking for angles that will have a x coordinate of
1
2
. This means we’ll
have an angle in the first quadrant and an angle in the fourth quadrant (that we can use the angle
in the first quadrant to find). Here is a unit circle for this situation.
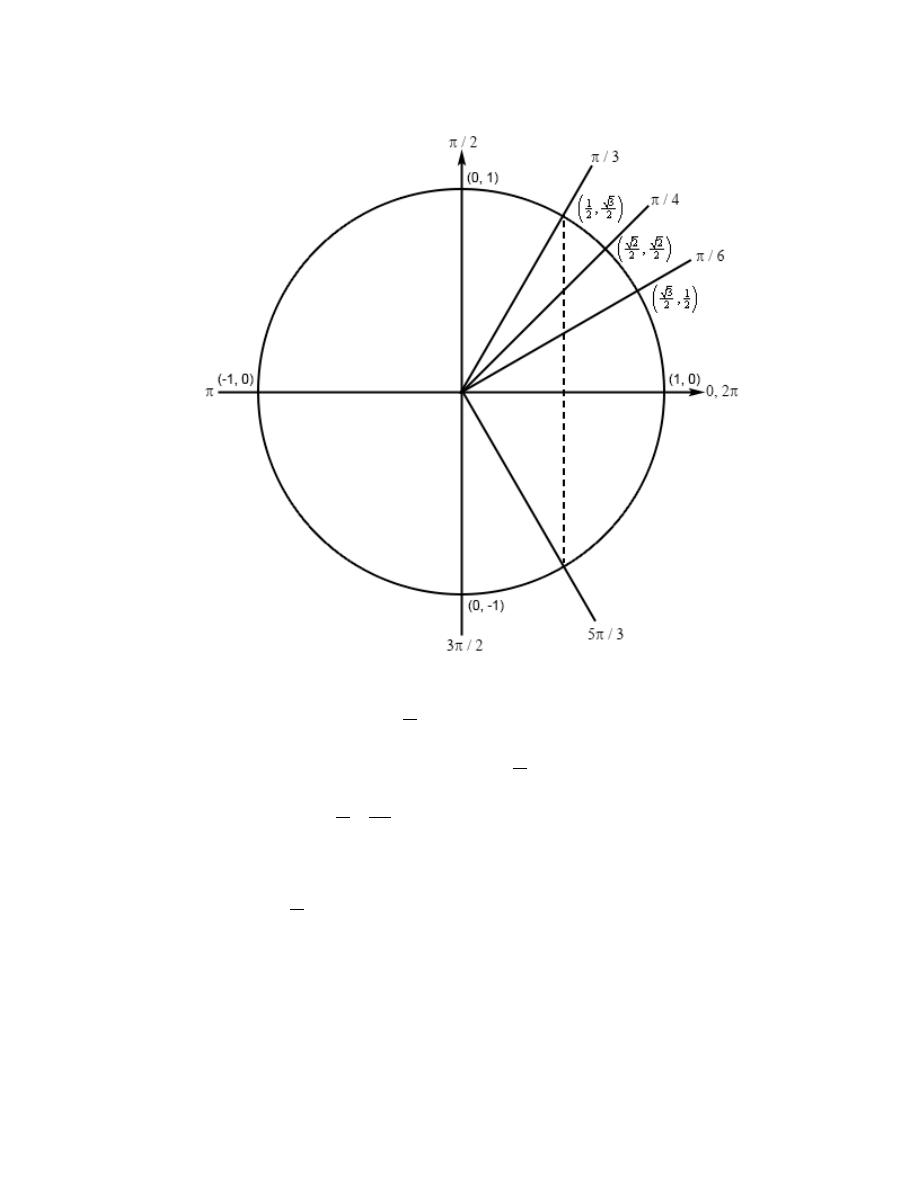
Calculus I
© 2007 Paul Dawkins
75
http://tutorial.math.lamar.edu/terms.aspx
Clearly the angle in the first quadrant is
3
π
and by some basic symmetry we can see that the
terminal line for the second angle must form an angle of
3
π
with the positive x-axis as shown
above and so it will be :
5
2
3
3
π
π
π
− =
.
Note that you don’t really need a positive angle for the second one. If you wanted to you could
just have easily used
3
π
−
for the second angle. There is nothing wrong with this and you’ll get
the same solutions in the end. The reason we chose to go with the positive angle is simply to
avoid inadvertently losing the minus sign on the second solution at some point in the future. That
kind of mistake is easy to make on occasion and by using positive angles here we will not need to
worry about making it.

Calculus I
© 2007 Paul Dawkins
76
http://tutorial.math.lamar.edu/terms.aspx
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
2
2
5
2
OR
2
0, 1, 2,
5
3
5
3
x
x
n
n
n
π
π
π
π
= +
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by
5
2
.
5
25
5
OR
5
0, 1, 2,
6
6
x
n
x
n
n
π
π
π
π
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 6 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 6. Doing
this will make it much easier to identify solutions that fall inside the interval so,
40
30
80
5 ,
,
3
6
6
π
π
π
π
=
With the interval written in this form, if our potential solutions have a denominator of 6, all we
need to do is compare numerators. As long as the numerators are between
30
π
and
80
π
we’ll
know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 6. So the solutions, written in this
form, are.
5
30
25
30
OR
0, 1, 2,
6
6
6
6
n
n
x
x
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. We can also see from a quick inspection that
0
n
=
will result in solutions that
are not in the interval and so let’s start at
1
n
=
and see what we get.

Calculus I
© 2007 Paul Dawkins
77
http://tutorial.math.lamar.edu/terms.aspx
35
55
1:
OR
6
6
65
85
2 :
OR
6
36
n
x
x
n
x
x
π
π
π
π
=
=
=
=
=
=
80
6
π
>
There are a couple of things we should note before proceeding. First, it is important to
understand both solutions from a given value of n will not necessarily be in the given interval. It
is completely possible, as this problem shows, that we will only get one or the other solution from
a given value of n to fall in the given interval.
Next notice that with each increase in n we were really just adding another
30
6
π
onto the
previous results and by a quick inspection we could see that adding
30
π
to the numerator of the
first solution from the
2
n
=
step would result in a numerator that is larger than
80
π
and so
would result in a solution that is outside of the interval. Therefore, there was no reason to plug in
3
n
=
into the first set of solutions. Of course, we also didn’t plug
3
n
=
into the second set
because once we’ve gotten out of the interval adding anything else on will remain out of the
interval.
Finally, unlike most of the problems in this section
0
n
=
did not produce any solutions that were
in the given interval. This will happen on occasion so don’t get excited about it when it happens.
So, it looks like we have the three solutions to this equation in the given interval.
35
55
65
,
,
6
6
6
z
π
π
π
=
12. Without using a calculator find the solution(s) to
15 17
4 cos
7
y
=
+
that are in
[
]
10 ,15
π
π
.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
1
cos
7
2
y
= −
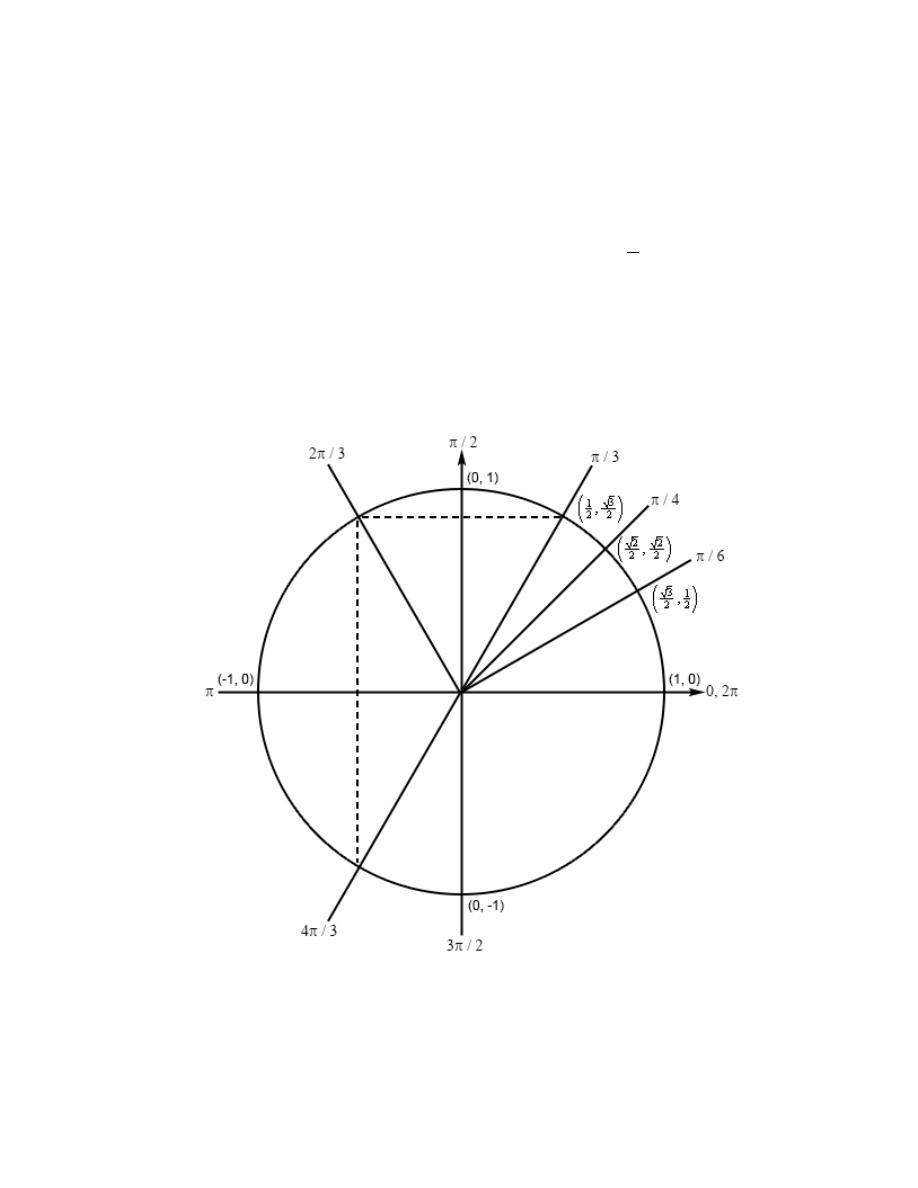
Calculus I
© 2007 Paul Dawkins
78
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which cosine will have this value.
Step 2
Because we’re dealing with cosine in this problem and we know that the x-axis represents cosine
on a unit circle we’re looking for angles that will have a x coordinate of
1
2
−
. This means that
we’ll have angles in the second and third quadrant.
Because of the negative value we can’t just find the corresponding angle in the first quadrant and
use that to find the second angle. However, we can still use the angles in the first quadrant to find
the two angles that we need. Here is a unit circle for this situation.

Calculus I
© 2007 Paul Dawkins
79
http://tutorial.math.lamar.edu/terms.aspx
If we didn’t have the negative value then the angle would be
3
π
. Now, based on the symmetry in
the unit circle, the terminal line for both of the angles will form an angle of
3
π
with the negative
x-axis. The angle in the second quadrant will then be
2
3
3
π
π
π
− =
and the angle in the third
quadrant will be
4
3
3
π
π
π
+ =
.
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
2
4
2
OR
2
0, 1, 2,
7
3
7
3
y
y
n
n
n
π
π
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 7.
14
28
14
OR
14
0, 1, 2,
3
3
y
n
y
n
n
π
π
π
π
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Note that because at least some of the solutions will have a denominator of 3 it will probably be
convenient to also have the interval written in terms of fractions with denominators of 3. Doing
this will make it much easier to identify solutions that fall inside the interval so,
30
45
,
3
3
π
π
With the interval written in this form, if our potential solutions have a denominator of 3, all we
need to do is compare numerators. As long as the numerators are between
30
π
and
45
π
we’ll
know that the solution is in the interval.
Also, in order to quickly determine the solution for particular values of n it will be much easier to
have both fractions in the solutions have denominators of 3. So the solutions, written in this
form, are.

Calculus I
© 2007 Paul Dawkins
80
http://tutorial.math.lamar.edu/terms.aspx
14
42
28
42
OR
0, 1, 2,
3
3
3
3
n
n
y
y
n
π
π
π
π
=
+
=
+
= ± ±
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. We can also see from a quick inspection that
0
n
=
will result in solutions that
are not in the interval and so let’s start at
1
n
=
and see what we get.
56
1:
3
n
x
π
=
=
45
70
OR
3
3
x
π
π
>
=
45
3
π
>
So, by plugging in
1
n
=
we get solutions that are already outside of the interval and increasing n
will simply mean adding another
42
3
π
onto these and so will remain outside of the given
interval. We also noticed earlier than all other value of n will result in solutions outside of the
given interval.
What all this means is that while there are solutions to the equation none fall inside the
given interval and so the official answer would then be no solutions in the given
interval.
Review : Solving Trig Equations with Calculators, Part I
1. Find all the solutions to
( )
7 cos 4
11 10
x
+ =
. Use at least 4 decimal places in your work.
Hint 1 : Isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
( )
1
cos 4
7
x
= −
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which cosine will have this value.
Step 2
First, using our calculator we can see that,
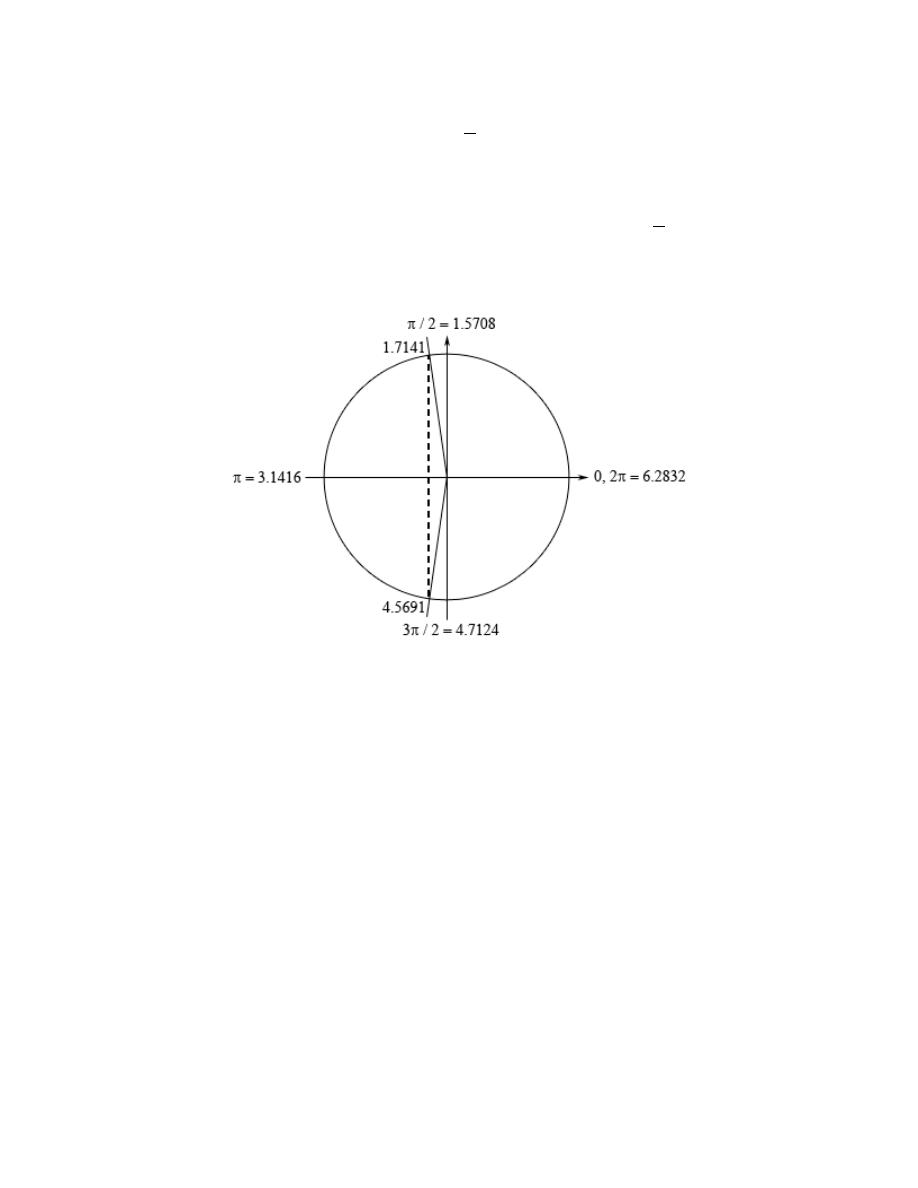
Calculus I
© 2007 Paul Dawkins
81
http://tutorial.math.lamar.edu/terms.aspx
1
1
4
cos
1.7141
7
x
−
=
−
=
Now we’re dealing with cosine in this problem and we know that the x-axis represents cosine on
a unit circle and so we’re looking for angles that will have a x coordinate of
1
7
−
. This means
that we’ll have angles in the second (this is the one our calculator gave us) and third quadrant.
Here is a unit circle for this situation.
From the symmetry of the unit circle we can see that we can either use –1.7141 or
2
1.7141
4.5691
π
−
=
for the second angle. Each will give the same set of solutions. However,
because it is easy to lose track of minus signs we will use the positive angle for our second
solution.
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
4
1.7141 2
OR 4
4.5691 2
0, 1, 2,
x
n
x
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 4.

Calculus I
© 2007 Paul Dawkins
82
http://tutorial.math.lamar.edu/terms.aspx
0.4285
OR
1.1423
0, 1, 2,
2
2
n
n
x
x
n
π
π
=
+
=
+
= ± ±
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
2. Find the solution(s) to
6 5 cos
10
3
x
+
=
that are in
[
]
0, 38
. Use at least 4 decimal places in
your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
4
cos
3
5
x
=
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which cosine will have this value.
Step 2
First, using our calculator we can see that,
1
4
cos
0.6435
3
5
x
−
=
=
Now we’re dealing with cosine in this problem and we know that the x-axis represents cosine on
a unit circle and so we’re looking for angles that will have a x coordinate of
4
5
. This means that
we’ll have angles in the first (this is the one our calculator gave us) and fourth quadrant. Here is
a unit circle for this situation.
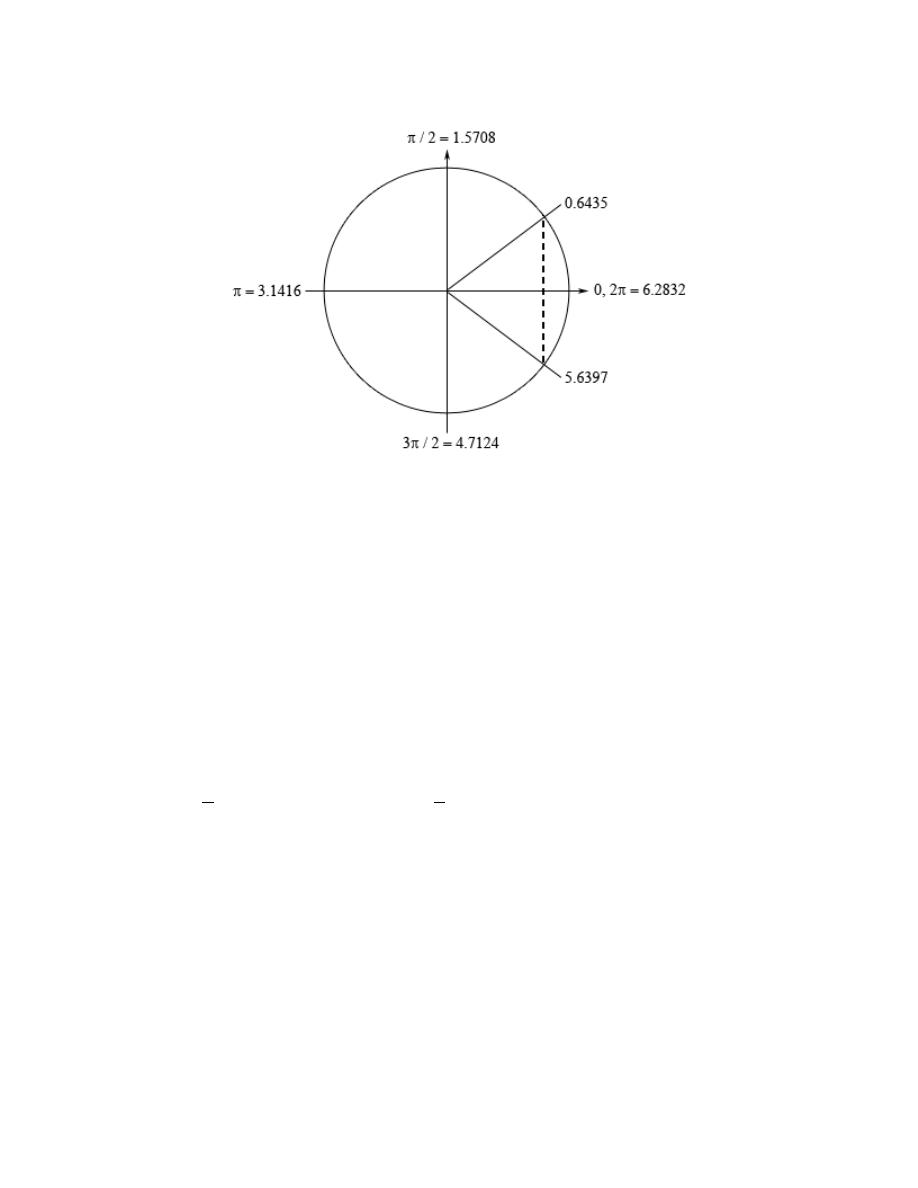
Calculus I
© 2007 Paul Dawkins
83
http://tutorial.math.lamar.edu/terms.aspx
From the symmetry of the unit circle we can see that we can either use –0.6435 or
2
0.6435
5.6397
π
−
=
for the second angle. Each will give the same set of solutions. However,
because it is easy to lose track of minus signs we will use the positive angle for our second
solution.
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
0.6435 2
OR
5.6397
2
0, 1, 2,
3
3
x
x
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 3 and
we’ll convert everything to decimals to help with the final step.
1.9305 6
OR
16.9191 6
0, 1, 2,
1.9305 18.8496
OR
16.9191 18.8496
0, 1, 2,
x
n
x
n
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4

Calculus I
© 2007 Paul Dawkins
84
http://tutorial.math.lamar.edu/terms.aspx
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. So, let’s start at
0
n
=
and see what we get.
0 :
1.9305
OR
16.9191
1:
20.7801
OR
35.7687
n
x
x
n
x
x
=
=
=
=
=
=
Notice that with each increase in n we were really just adding another 18.8496 onto the previous
results and by doing this to the results from the
1
n
=
step we will get solutions that are outside
of the interval and so there is no reason to even plug in
2
n
=
.
So, it looks like we have the four solutions to this equation in the given interval.
1.9305, 16.9191, 20.7801, 35.7687
x
=
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
3. Find all the solutions to
3
6 11sin
8
t
= −
. Use at least 4 decimal places in your work.
Hint 1 : Isolate the sine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the sine (with a coefficient of one) on one side of the equation gives,
3
sin
8
11
t
=
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which sine will have this value.
Step 2
First, using our calculator we can see that,
1
3
sin
0.2762
8
11
t
−
=
=
Now we’re dealing with sine in this problem and we know that the y-axis represents sine on a unit
circle and so we’re looking for angles that will have a y coordinate of
3
11
. This means that we’ll
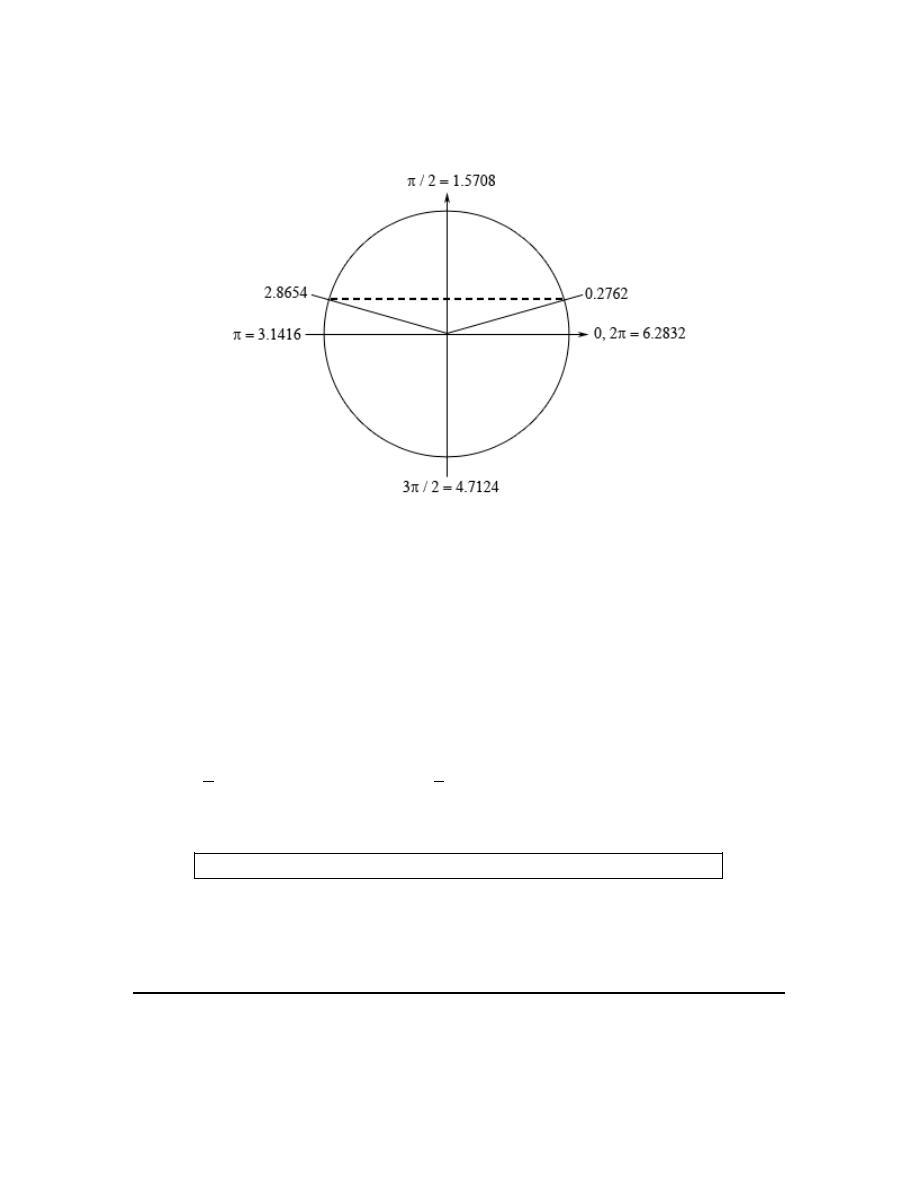
Calculus I
© 2007 Paul Dawkins
85
http://tutorial.math.lamar.edu/terms.aspx
have angles in the first (this is the one our calculator gave us) and second quadrant. Here is a unit
circle for this situation.
From the symmetry of the unit circle we can see that
0.2762
2.8654
π
−
=
is the second angle.
Hint 3 : Using the two angles above write down all the angles for which sine will have this value
and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
0.2762 2
OR
2.8654 2
0, 1, 2,
8
8
t
t
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 8.
2.2096 16
OR
22.9232 16
0, 1, 2,
t
n
t
n
n
π
π
=
+
=
+
= ± ±
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
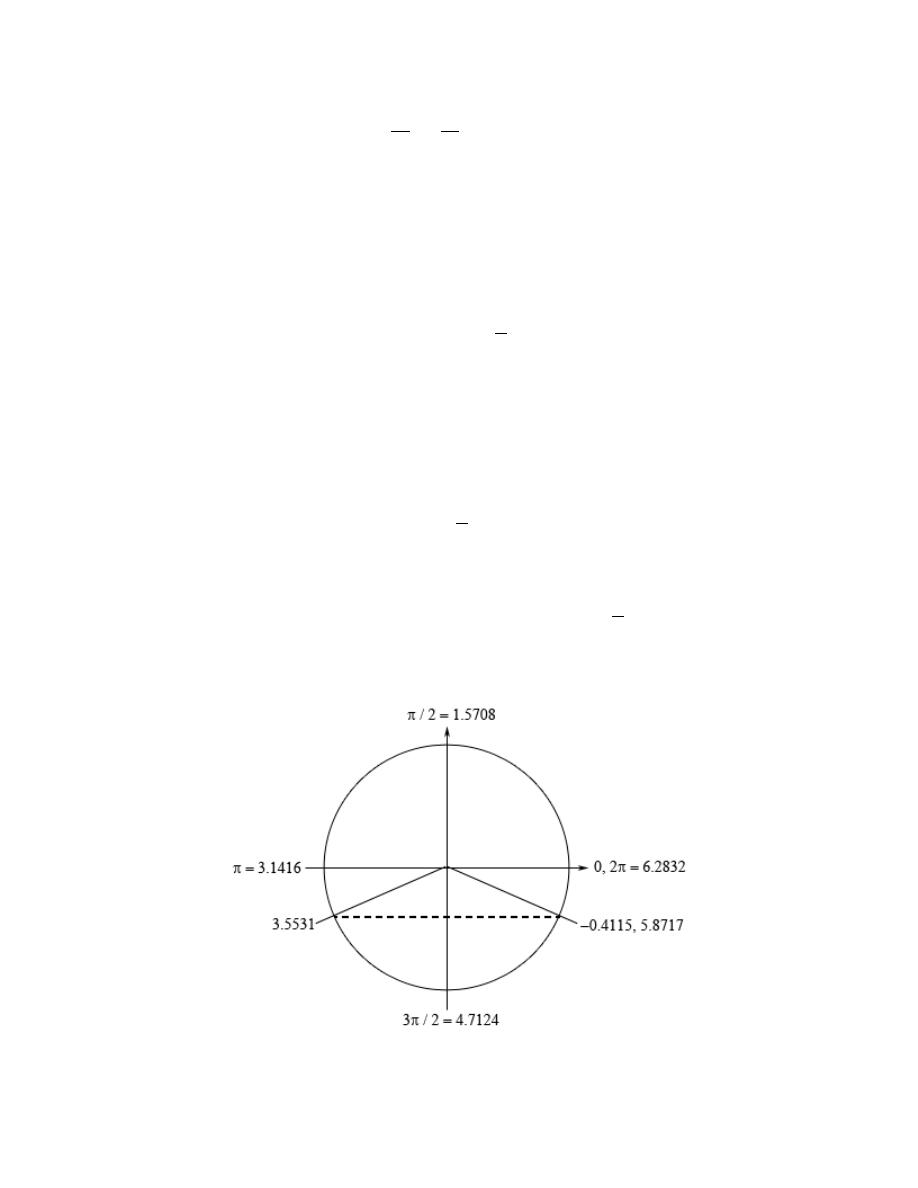
Calculus I
© 2007 Paul Dawkins
86
http://tutorial.math.lamar.edu/terms.aspx
4. Find the solution(s) to
( )
13
3
4 sin 6
10
10
z
+
= −
that are in
[ ]
0, 2
. Use at least 4 decimal places
in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the sine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the sine (with a coefficient of one) on one side of the equation gives,
( )
2
sin 6
5
z
= −
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which sine will have this value.
Step 2
First, using our calculator we can see that,
1
2
6
sin
0.4115
5
z
−
=
−
= −
Now we’re dealing with sine in this problem and we know that the y-axis represents sine on a unit
circle and so we’re looking for angles that will have a y coordinate of
2
5
−
. This means that we’ll
have angles in the fourth (this is the one our calculator gave us) and third quadrant. Here is a unit
circle for this situation.

Calculus I
© 2007 Paul Dawkins
87
http://tutorial.math.lamar.edu/terms.aspx
From the symmetry of the unit circle we can see that the second angle will make an angle of
0.4115 with the negative x-axis and so the second angle will be
0.4115
3.5531
π
+
=
. Also, as
noted on the unit circle above a positive angle that represents the first angle (i.e. the angle in the
fourth quadrant) is
2
0.4115
5.8717
π
−
=
. We can use either the positive or the negative angle
here and we’ll get the same solutions. However, because it is often easy to lose track of minus
signs we will be using the positive angle in the fourth quadrant for our work here.
Hint 3 : Using the two angles above write down all the angles for which sine will have this value
and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
6
3.5531 2
OR 6
5.8717
2
0, 1, 2,
z
n
z
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 6 and
we’ll convert everything to decimals to help with the final step.
0.5922
OR
0.9786
0, 1, 2,
3
3
0.5922 1.0472
OR
0.9786 1.0472
0, 1, 2,
n
n
z
z
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. So, let’s start at
0
n
=
and see what we get.
0 :
0.5922
OR
0.9786
1:
1.6394
OR
2.0258
n
z
z
n
z
z
=
=
=
=
=
=
2
>
Notice that with each increase in n we were really just adding another 1.0472 onto the previous
results and by doing this to the results from the
1
n
=
step we will get solutions that are outside
of the interval and so there is no reason to even plug in
2
n
=
. Also, as we’ve seen in this
problem it is completely possible for only one of the solutions from a given interval to be in the
given interval so don’t worry about that when it happens.
So, it looks like we have the three solutions to this equation in the given interval.

Calculus I
© 2007 Paul Dawkins
88
http://tutorial.math.lamar.edu/terms.aspx
0.5922, 0.9786, 1.6394
z
=
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
5. Find the solution(s) to
4
4
9 cos
21sin
0
9
9
z
z
+
=
that are in
[
]
10,10
−
. Use at least 4
decimal places in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to reduce the equation down to a single trig function (with a coefficient of one)
on one side of the equation.
Step 1
Because we’ve got both a sine and a cosine here it makes some sense to reduce this down to
tangent. So, reducing to a tangent (with a coefficient of one) on one side of the equation gives,
4
3
tan
9
7
z
= −
Hint 2 : Using a calculator and your knowledge of solving trig equations involving tangents to
determine all the angles in the range
[
]
0, 2
π
for which tangent will have this value.
Step 2
First, using our calculator we can see that,
1
4
3
tan
0.4049
9
7
z
−
=
−
= −
As we discussed in Example 5 of this section the second angle for equations involving tangent
will always be the
π
plus the first angle. Therefore,
(
)
0.4049
2.7367
π
+ −
=
will be the
second angle.
Also, because it is very easy to lose track of minus signs we’ll use the fact that we know that any
angle plus
2
π
will give another angle whose terminal line is identical to the original angle to
eliminate the minus sign on the first angle. So, another angle that will work for the first angle is
(
)
2
0.4049
5.8783
π
+ −
=
. Note that there is nothing wrong with using the negative angle and if
you chose to work with that you will get the same solutions. We are using the positive angle only
to make sure we don’t accidentally lose the minus sign on the angle we received from our
calculator.

Calculus I
© 2007 Paul Dawkins
89
http://tutorial.math.lamar.edu/terms.aspx
Hint 3 : Using the two angles above write down all the angles for which tangent will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
4
4
2.7367
2
OR
5.8783 2
0, 1, 2,
9
9
z
z
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by
9
4
and
we’ll convert everything to decimals to help with the final step.
9
9
6.1576
OR
13.2262
0, 1, 2,
2
2
6.1576 14.1372
OR
13.2262 14.1372
0, 1, 2,
n
n
z
z
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions.
1:
7.9796
OR
0.9110
0 :
6.1576
OR
13.2262
n
z
z
n
z
z
= −
= −
= −
=
=
=
10
>
Notice that with each increase in n we were really just adding/subtracting (depending on the sign
of n) another 14.1372 onto the previous results. A quick inspection of the results above will
quickly show us that we don’t need to go any farther and we won’t bother with any other values
of n. Also, as we’ve seen in this problem it is completely possible for only one of the solutions
from a given interval to be in the given interval so don’t worry about that when it happens.
So, it looks like we have the three solutions to this equation in the given interval.
7.9796,
0.9110, 6.1576
z
= −
−
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.

Calculus I
© 2007 Paul Dawkins
90
http://tutorial.math.lamar.edu/terms.aspx
6. Find the solution(s) to
3 tan
1 11 2 tan
4
4
w
w
− = −
that are in
[
]
50, 0
−
. Use at least 4
decimal places in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the tangent (with a coefficient of one) on one side of the equation.
Step 1
Isolating the tangent (with a coefficient of one) on one side of the equation gives,
12
tan
4
5
w
=
Hint 2 : Using a calculator and your knowledge of solving trig equations involving tangents to
determine all the angles in the range
[
]
0, 2
π
for which tangent will have this value.
Step 2
First, using our calculator we can see that,
1
12
tan
1.1760
4
5
w
−
=
=
As we discussed in Example 5 of this section the second angle for equations involving tangent
will always be the
π
plus the first angle. Therefore,
1.1760
4.3176
π
+
=
will be the second
angle.
Hint 3 : Using the two angles above write down all the angles for which tangent will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
1.1760 2
OR
4.3176 2
0, 1, 2,
4
4
w
w
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 4 and
we’ll convert everything to decimals to help with the final step.
4.7040 8
OR
17.2704 8
0, 1, 2,
4.7040 25.1327
OR
17.2704 25.1327
0, 1, 2,
w
n
w
n
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±

Calculus I
© 2007 Paul Dawkins
91
http://tutorial.math.lamar.edu/terms.aspx
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions. First, notice that if we plug in positive n or
0
n
=
we will have
positive solutions and these solutions will be out of the interval. Therefore, we’ll start with
1
n
= −
.
1:
20.4287
OR
7.8623
2 :
45.5614
OR
32.9950
n
w
w
n
w
w
= −
= −
= −
= −
= −
= −
Notice that with each increase in n we were really just subtracting another 25.1327 from the
previous results. A quick inspection of the results above will quickly show us that we don’t need
to go any farther and we won’t bother with any other values of n.
So, it looks like we have the four solutions to this equation in the given interval.
45.5614,
32.9950,
20.4287,
7.8623
w
= −
−
−
−
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
7. Find the solution(s) to
17 3sec
2
2
z
−
=
that are in
[
]
20, 45
. Use at least 4 decimal places
in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the secant (with a coefficient of one) on one side of the equation.
Step 1
Isolating the secant (with a coefficient of one) on one side of the equation gives,
sec
5
2
z
=
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which secant will have this value. The best way to do this is to rewrite the
equation into one in terms of a different trig function that we can more easily deal with.
Step 2
In order to get the solutions it will be much easier to recall the definition of secant in terms of
cosine and rewrite the equation into one involving cosine. Doing this gives,
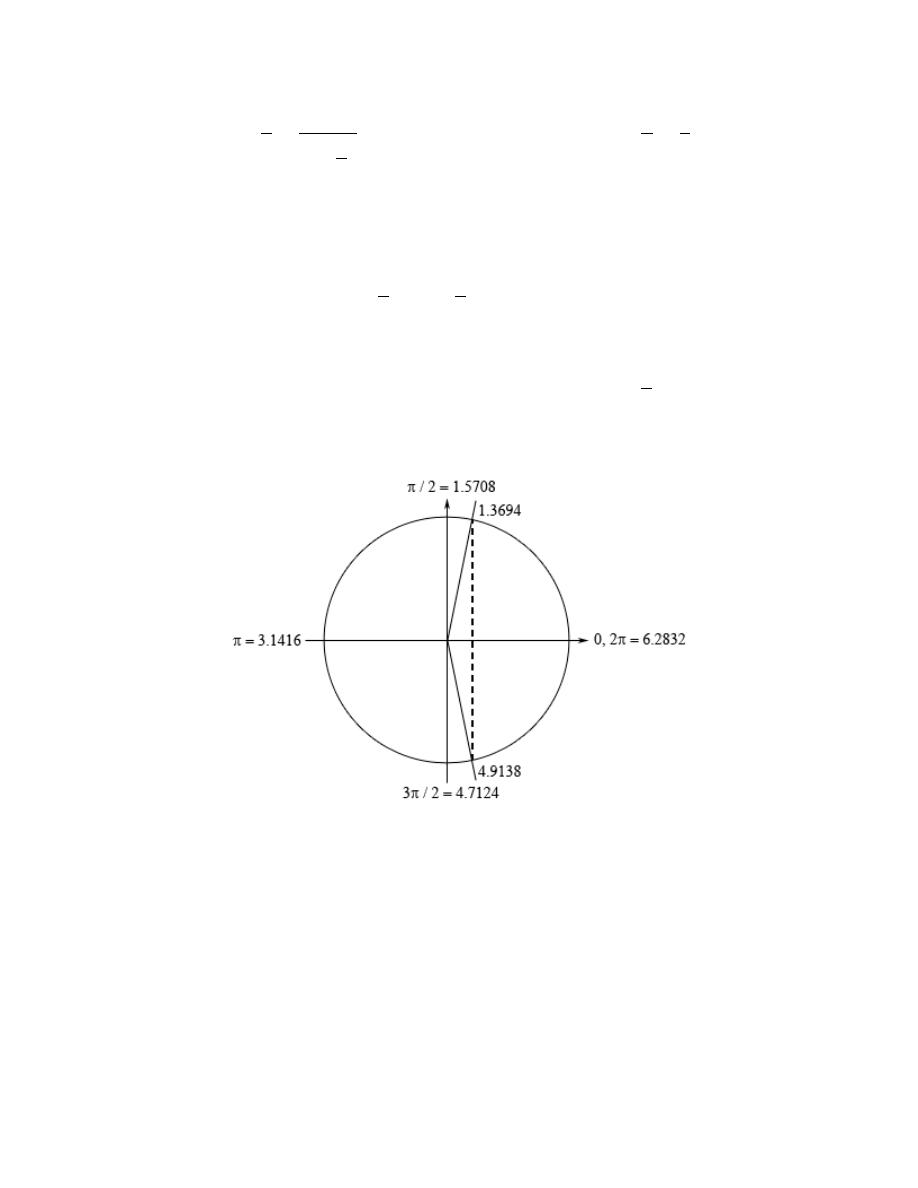
Calculus I
© 2007 Paul Dawkins
92
http://tutorial.math.lamar.edu/terms.aspx
1
1
sec
5
cos
2
2
5
cos
2
z
z
z
=
=
⇒
=
The solution(s) to the equation involving the cosine are the same as the solution(s) to the equation
involving the secant and so working with that will be easier. Using our calculator we can see
that,
1
1
cos
1.3694
2
5
z
−
=
=
Now we’re dealing with cosine in this problem and we know that the x-axis represents cosine on
a unit circle and so we’re looking for angles that will have a x coordinate of
1
5
. This means that
we’ll have angles in the first (this is the one our calculator gave us) and fourth quadrant. Here is
a unit circle for this situation.
From the symmetry of the unit circle we can see that we can either use –1.3694 or
2
1.3694
4.9138
π
−
=
for the second angle. Each will give the same set of solutions. However,
because it is easy to lose track of minus signs we will use the positive angle for our second
solution.
Hint 3 : Using the two angles above write down all the angles for which cosine/secant will have
this value and use these to write down all the solutions to the equation.
Step 3
Calculus I
© 2007 Paul Dawkins
93
http://tutorial.math.lamar.edu/terms.aspx
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
1.3694 2
OR
4.9138 2
0, 1, 2,
2
2
z
z
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 2 and
we’ll convert everything to decimals to help with the final step.
2.7388 4
OR
9.8276 4
0, 1, 2,
2.7388 12.5664
OR
9.8276 12.5664
0, 1, 2,
z
n
z
n
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. Also note that if we use
0
n
=
we will still not be in the interval and so let’s start
things off at
1
n
=
.
1:
15.3052
n
z
=
=
20
OR
22.3940
2 :
27.8716
OR
34.9604
3 :
40.4380
OR
47.5268
z
n
z
z
n
z
z
<
=
=
=
=
=
=
=
45
>
Notice that with each increase in n we were really just adding another 12.5664 onto the previous
results and by a quick inspection of the results above we can see that we don’t need to go any
farther. Also, as we’ve seen in this problem it is completely possible for only one of the solutions
from a given interval to be in the given interval so don’t worry about that when it happens.
So, it looks like we have the four solutions to this equation in the given interval.
22.3940, 27.8716, 34.9604, 40.4380
z
=
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
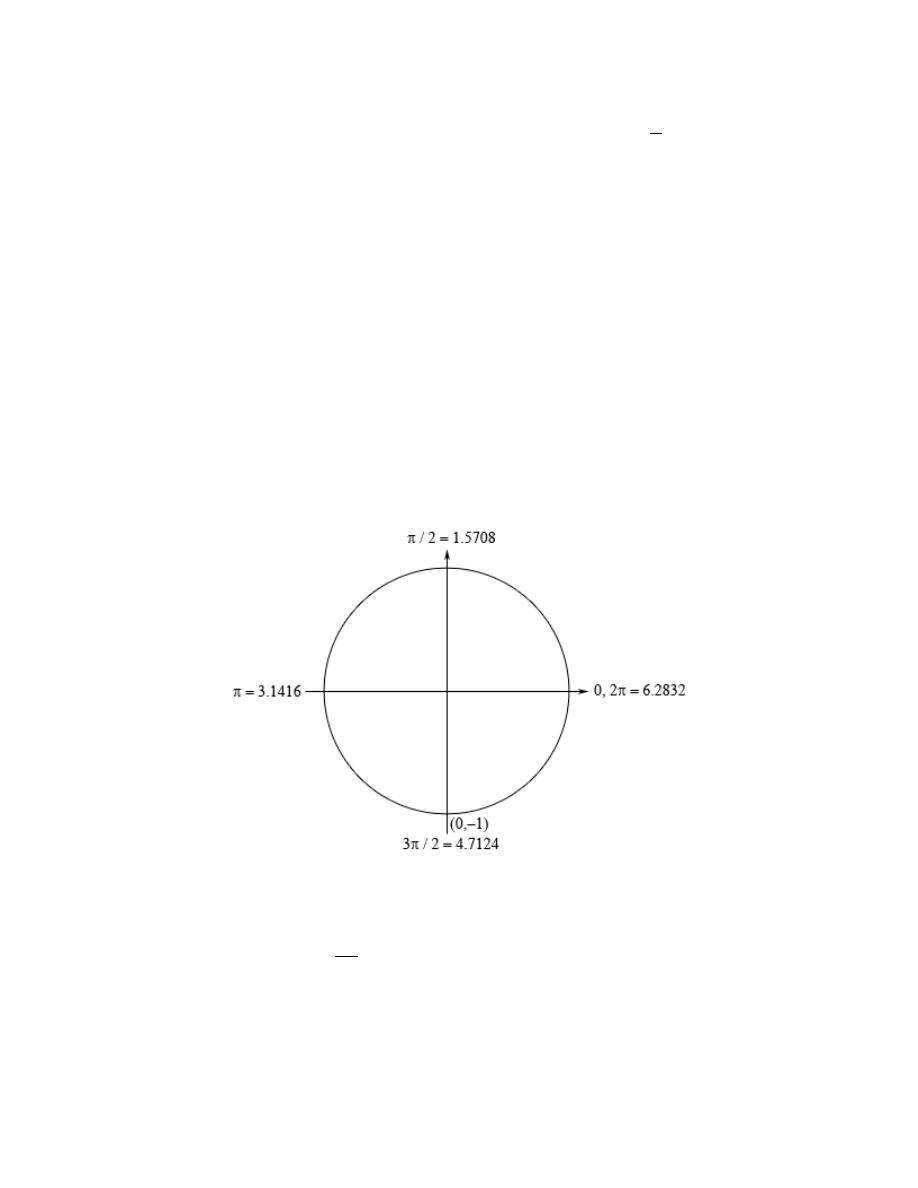
Calculus I
© 2007 Paul Dawkins
94
http://tutorial.math.lamar.edu/terms.aspx
8. Find the solution(s) to
( )
( )
12 sin 7
11 3 4 sin 7
y
y
+ = +
that are in
1
2,
2
− −
. Use at least 4
decimal places in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the sine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the sine (with a coefficient of one) on one side of the equation gives,
( )
sin 7
1
y
= −
Hint 2 : Use your knowledge of the unit circle to determine all the angles in the range
[
]
0, 2
π
for
which sine will have this value.
Step 2
If you need to use a calculator to get the solution for this that is fine, but this is also one of the
standard angles as we can see from the unit circle below.
Because we’re dealing with sine in this problem and we know that the y-axis represents sine on a
unit circle we’re looking for angle(s) that will have a y coordinate of –1. The only angle that will
have this y coordinate will be
3
4.7124
2
π
=
.
Note that unlike all the other problems that we’ve worked to this point this will be the only angle.
There is simply not another angle in the range
[
]
0, 2
π
for which sine will have this value. Don’t

Calculus I
© 2007 Paul Dawkins
95
http://tutorial.math.lamar.edu/terms.aspx
get so locked into the usual case where we get two possible angles in the
[
]
0, 2
π
that when these
single solution cases roll around you decide you must have done something wrong. They happen
on occasion and we need to be able to deal with them when they occur.
Hint 3 : Using the angle above write down all the angles for which sine will have this value and
use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have the angle above we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto the angle.
This then means that we must have,
7
4.7124
2
0, 1, 2,
y
n
n
π
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 7 and
we’ll convert everything to decimals to help with the final step.
2
0.6732
0, 1, 2,
7
0.6732 0.8976
0, 1, 2,
n
y
n
n
n
π
=
+
= ± ±
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions. First notice that, in this case, if we plug in positive values of n or
0
n
=
we will get positive solutions and these will not be in the interval and so there is no reason
to even try these. So, let’s start at
1
n
= −
and see what we get.
1:
0.2244
n
y
= −
= −
0.5
2 :
1.122
3 :
2.0196
n
y
n
y
> −
= −
= −
= −
= −
2
< −
So, it looks like we have only a single solution to this equation in the given interval.
1.122
y
= −
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.

Calculus I
© 2007 Paul Dawkins
96
http://tutorial.math.lamar.edu/terms.aspx
9. Find the solution(s) to
( )
5 14 tan 8
30
x
−
=
that are in
[
]
1,1
−
. Use at least 4 decimal places
in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the tangent (with a coefficient of one) on one side of the equation.
Step 1
Isolating the tangent (with a coefficient of one) on one side of the equation gives,
( )
25
tan 8
14
x
= −
Hint 2 : Using a calculator and your knowledge of solving trig equations involving tangents to
determine all the angles in the range
[
]
0, 2
π
for which tangent will have this value.
Step 2
First, using our calculator we can see that,
1
25
8
tan
1.0603
14
x
−
=
−
= −
As we discussed in Example 5 of this section the second angle for equations involving tangent
will always be the
π
plus the first angle. Therefore,
(
)
1.0603
2.0813
π
+ −
=
will be the
second angle.
Hint 3 : Using the two angles above write down all the angles for which tangent will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
8
1.0603 2
OR 8
2.0813 2
0, 1, 2,
x
n
x
n
n
π
π
= −
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is divide both sides by 8 and
we’ll convert everything to decimals to help with the final step.
0.1325
OR
0.2602
0, 1, 2,
4
4
0.1325 0.7854
OR
0.2602 0.7854
0, 1, 2,
n
n
x
x
n
n
n
n
π
π
= −
+
=
+
= ± ±
= −
+
=
+
= ± ±

Calculus I
© 2007 Paul Dawkins
97
http://tutorial.math.lamar.edu/terms.aspx
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions.
1:
0.9179
OR
0.5252
0 :
0.1325
OR
0.2602
1:
0.6529
OR
1.0456
n
x
x
n
x
x
n
x
x
= −
= −
= −
=
= −
=
=
=
=
1
>
Notice that with each increase in n we were really just adding/subtracting another 0.7854 from the
previous results. A quick inspection of the results above will quickly show us that we don’t need
to go any farther and we won’t bother with any other values of n. Also, as we’ve seen in this
problem it is completely possible for only one of the solutions from a given interval to be in the
given interval so don’t worry about that when it happens.
So, it looks like we have the five solutions to this equation in the given interval.
0.9179,
0.5252,
0.1325, 0.2602, 0.6529
x
= −
−
−
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
10. Find the solution(s) to
0
18 2 csc
3
t
=
+
that are in
[ ]
0, 5
. Use at least 4 decimal places in
your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosecant (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosecant (with a coefficient of one) on one side of the equation gives,
csc
9
3
t
= −
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which cosecant will have this value. The best way to do this is to rewrite the
equation into one in terms of a different trig function that we can more easily deal with.
Step 2
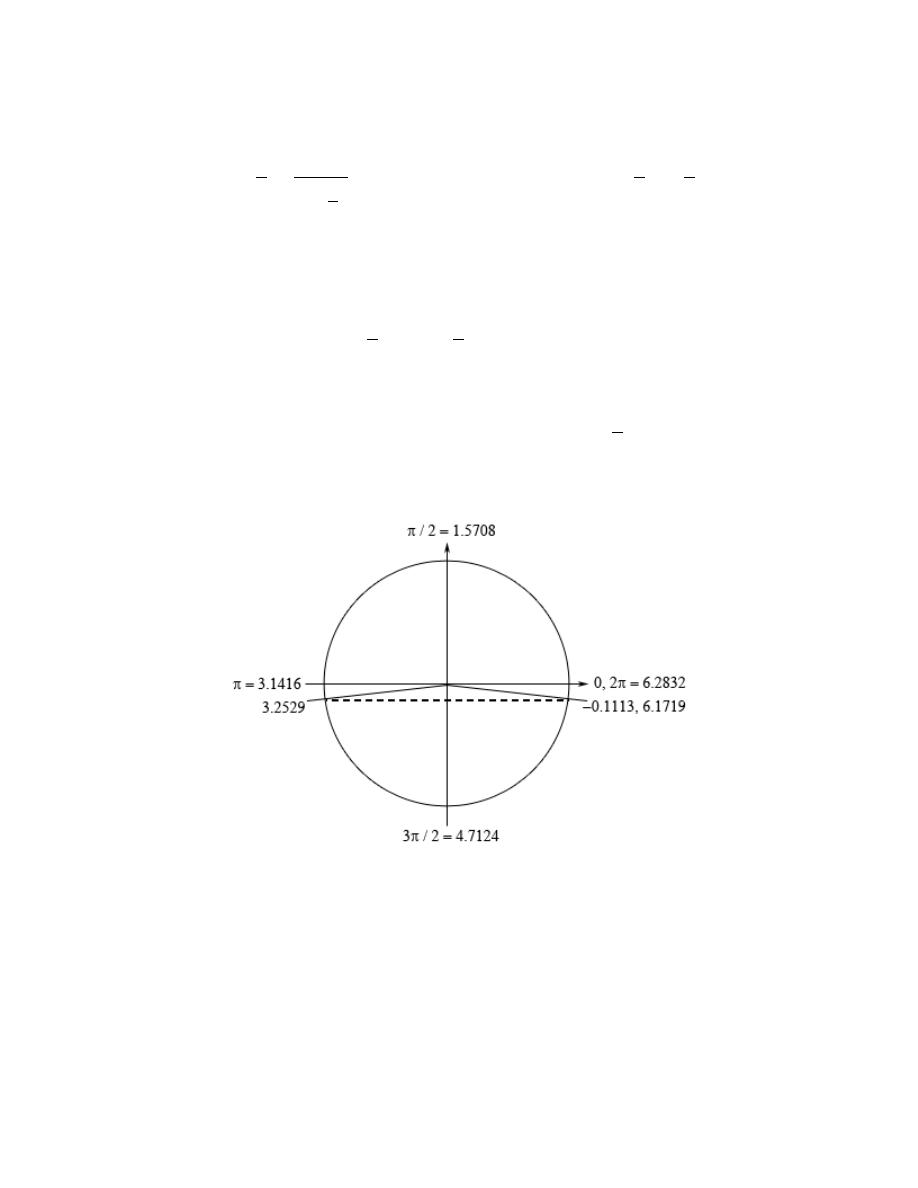
Calculus I
© 2007 Paul Dawkins
98
http://tutorial.math.lamar.edu/terms.aspx
In order to get the solutions it will be much easier to recall the definition of cosecant in terms of
sine and rewrite the equation into one involving sine. Doing this gives,
1
1
csc
9
sin
3
3
9
sin
3
t
t
t
=
= −
⇒
= −
The solution(s) to the equation involving the sine are the same as the solution(s) to the equation
involving the cosecant and so working with that will be easier. Using our calculator we can see
that,
1
1
sin
0.1113
3
9
t
−
=
−
= −
Now we’re dealing with sine in this problem and we know that the y-axis represents sine on a unit
circle and so we’re looking for angles that will have a y coordinate of
1
9
−
. This means that we’ll
have angles in the fourth (this is the one our calculator gave us) and third quadrant. Here is a unit
circle for this situation.
From the symmetry of the unit circle we can see that the second angle will make an angle of
0.1113 with the negative x-axis and so the second angle will be
0.1113
3.2529
π
+
=
. Also, as
noted on the unit circle above a positive angle that represents the first angle (i.e. the angle in the
fourth quadrant) is
2
0.1113
6.1719
π
−
=
. We can use either the positive or the negative angle
here and we’ll get the same solutions. However, because it is often easy to lose track of minus
signs we will be using the positive angle in the fourth quadrant for our work here.
Hint 3 : Using the two angles above write down all the angles for which sine/cosecant will have
this value and use these to write down all the solutions to the equation.

Calculus I
© 2007 Paul Dawkins
99
http://tutorial.math.lamar.edu/terms.aspx
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.
This then means that we must have,
3.2529 2
OR
6.1719 2
0, 1, 2,
3
3
t
t
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 3 and
we’ll convert everything to decimals to help with the final step.
9.7587 6
OR
18.5157 6
0, 1, 2,
9.7587 18.8496
OR
18.5157 18.8496
0, 1, 2,
t
n
t
n
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. Also note that even if we start off with
0
n
=
we will get solutions that are
already out of the given interval.
So, despite the fact that there are solutions to this equation none of them fall in the given interval
and so there are no solutions to this equation. Do not get excited about the answer here. This
kind of situation will happen on occasion and so we need to be aware of it and able to deal with it.
11 Find the solution(s) to
1
1
2
cos
2
8
4
3
x
+ =
that are in
[
]
0,100
. Use at least 4 decimal places
in your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the cosine (with a coefficient of one) on one side of the equation.
Step 1
Isolating the cosine (with a coefficient of one) on one side of the equation gives,
5
cos
8
6
x
=
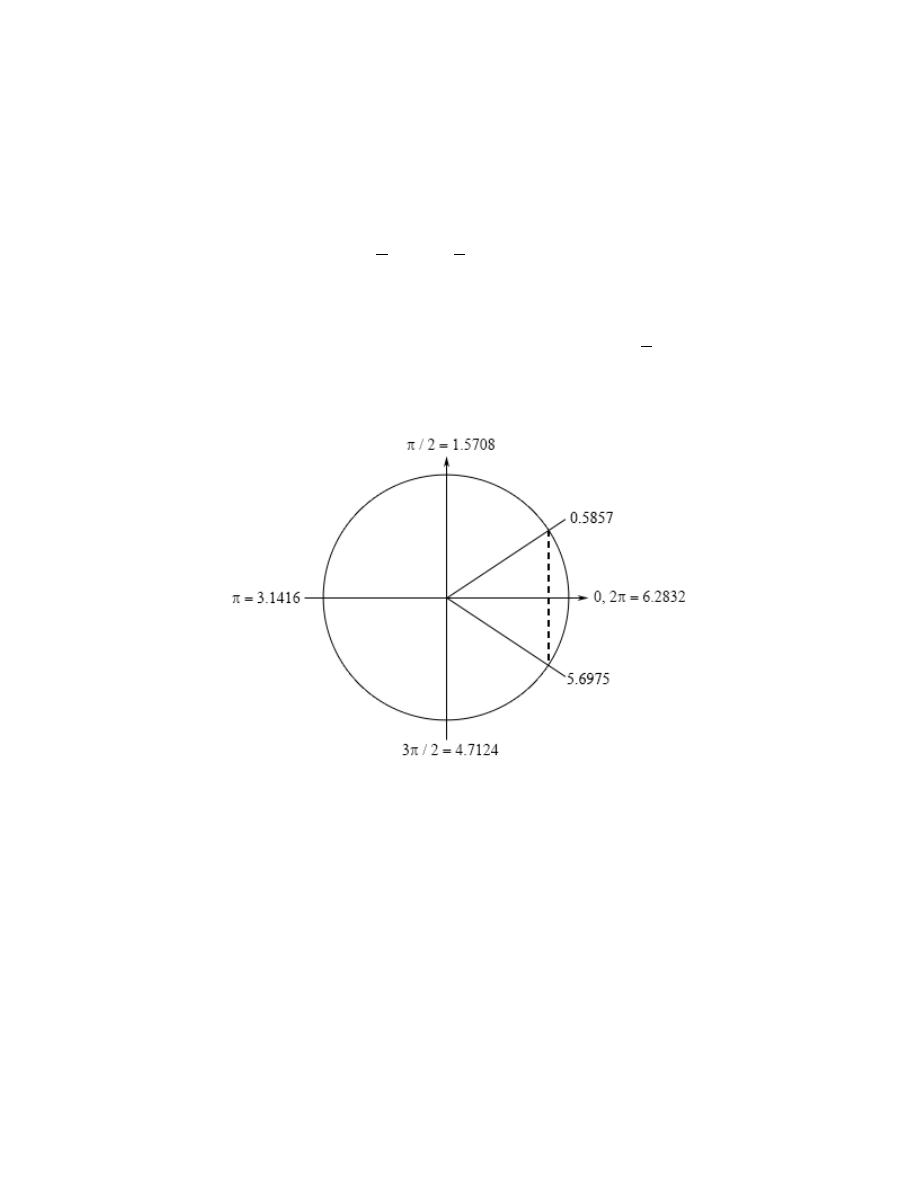
Calculus I
© 2007 Paul Dawkins
100
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Using a calculator and your knowledge of the unit circle to determine all the angles in the
range
[
]
0, 2
π
for which cosine will have this value.
Step 2
First, using our calculator we can see that,
1
5
cos
0.5857
8
6
x
−
=
=
Now we’re dealing with cosine in this problem and we know that the x-axis represents cosine on
a unit circle and so we’re looking for angles that will have a x coordinate of
5
6
. This means that
we’ll have angles in the first (this is the one our calculator gave us) and fourth quadrant. Here is
a unit circle for this situation.
From the symmetry of the unit circle we can see that we can either use –0.5857 or
2
0.5857
5.6975
π
−
=
for the second angle. Each will give the same set of solutions. However,
because it is easy to lose track of minus signs we will use the positive angle for our second
solution.
Hint 3 : Using the two angles above write down all the angles for which cosine will have this
value and use these to write down all the solutions to the equation.
Step 3
From the discussion in the notes for this section we know that once we have these two angles we
can get all possible angles by simply adding “
2 n
π
+
for
0, 1, 2,
n
= ± ±
” onto each of these.

Calculus I
© 2007 Paul Dawkins
101
http://tutorial.math.lamar.edu/terms.aspx
This then means that we must have,
0.5857
2
OR
5.6975 2
0, 1, 2,
8
8
x
x
n
n
n
π
π
=
+
=
+
= ± ±
Finally, to get all the solutions to the equation all we need to do is multiply both sides by 8 and
we’ll convert everything to decimals to help with the final step.
4.6856 16
OR
45.5800 16
0, 1, 2,
4.6856 50.2655
OR
45.58 50.2655
0, 1, 2,
x
n
x
n
n
n
n
n
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Hint 4 : Now all we need to do is plug in values of n to determine which solutions will actually
fall in the given interval.
Step 4
Now let’s find all the solutions. First notice that, in this case, if we plug in negative values of n
we will get negative solutions and these will not be in the interval and so there is no reason to
even try these. So, let’s start at
0
n
=
and see what we get.
0 :
4.6856
OR
45.58
1:
54.9511
OR
95.8455
n
x
x
n
x
x
=
=
=
=
=
=
Notice that with each increase in n we were really just adding another 50.2655 onto the previous
results and by doing this to the results from the
1
n
=
step we will get solutions that are outside
of the interval and so there is no reason to even plug in
2
n
=
.
So, it looks like we have the four solutions to this equation in the given interval.
4.6856, 45.58, 54.9511, 95.8455
x
=
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
12. Find the solution(s) to
( )
4
1 3sec 2
3
t
= +
that are in
[
]
4, 6
−
. Use at least 4 decimal places in
your work.
Hint 1 : Find all the solutions to the equation without regard to the given interval. The first step
in this process is to isolate the secant (with a coefficient of one) on one side of the equation.
Step 1
Isolating the secant (with a coefficient of one) on one side of the equation gives,

Calculus I
© 2007 Paul Dawkins
102
http://tutorial.math.lamar.edu/terms.aspx
( )
1
sec 2
9
t
=
At this point we can stop. We know that
sec
1
or
sec
1
θ
θ
≤ −
≤
This means that it is impossible for secant to ever be
1
9
and so there will be no solution to this
equation.
Note that if you didn’t recall the restrictions on secant the next step would have been to convert
this to cosine so let’s do that.
( )
( )
( )
1
1
sec 2
cos 2
9
cos 2
9
t
t
t
=
=
⇒
=
At this point we can note that
1 cos
1
θ
− ≤
≤
and so again there is no way for cosine to be 9 and
again we get that there will be no solution to this equation.
Review : Solving Trig Equations with Calculators, Part II
1. Find all the solutions to
(
)
3 14 sin 12
7
13
t
−
+
=
. Use at least 4 decimal places in your work.
Hint : With the exception of the argument, which is a little more complex, this is identical to the
equations that we solved in the previous section.
Solution
The argument of the sine is a little more complex in this equation than those we saw in the
previous section, but the solution process is identical. Therefore, we will be assuming that you
recall the process from the previous section and do not need all the hints or quite as many details
as we put into the solutions there. If you are unsure of the process you should go back to the
previous section and work some of the problems there before proceeding with the section.
First, isolating the sine on one side of the equation gives,
(
)
5
sin 12
7
7
t
+
= −
Using a calculator we get,

Calculus I
© 2007 Paul Dawkins
103
http://tutorial.math.lamar.edu/terms.aspx
1
5
12
7
sin
0.7956
7
t
−
+ =
−
= −
From our knowledge of the unit circle we can see that a positive angle that corresponds to this
angle is
2
0.7956
5.4876
π
−
=
. Either these angles can be used here but we’ll use the positive
angle to avoid the possibility of losing the minus sign. Also, from a quick look at a unit circle we
can see that a second angle in the range
[
]
0, 2
π
will be
0.7965
3.9372
π
+
=
.
Now, all possible angles for which sine will have this value are,
12
7
3.9372
2
OR 12
7
5.4876
2
0, 1, 2,
t
n
t
n
n
π
π
+ =
+
+ =
+
= ± ±
At this point all we need to do is solve each of these for t and we’ll have all the solutions to the
equation. Doing this gives,
0.2552
OR
0.1260
0, 1, 2,
6
6
n
n
t
t
n
π
π
= −
+
= −
+
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
2. Find all the solutions to
(
)
3sec 4 9
24
0
z
−
−
=
. Use at least 4 decimal places in your work.
Hint : With the exception of the argument, which is a little more complex, this is identical to the
equations that we solved in the previous section.
Solution
The argument of the secant is a little more complex in this equation than those we saw in the
previous section, but the solution process is identical. Therefore, we will be assuming that you
recall the process from the previous section and do not need all the hints or quite as many details
as we put into the solutions there. If you are unsure of the process you should go back to the
previous section and work some of the problems there before proceeding with the section.
First, isolating the secant on one side of the equation gives and converting the equation into one
involving cosine (to make the work a little easier) gives,
(
)
(
)
1
sec 4 9
8
cos 4 9
8
z
z
−
=
⇒
−
=

Calculus I
© 2007 Paul Dawkins
104
http://tutorial.math.lamar.edu/terms.aspx
Using a calculator we get,
1
1
4 9
cos
1.4455
8
z
−
−
=
=
From a quick look at a unit circle we can see that a second angle in the range
[
]
0, 2
π
will be
2
1.4455
4.8377
π
−
=
. Now, all possible angles for which secant will have this value are,
4 9
1.4455 2
OR 4 9
4.8377
2
0, 1, 2,
z
n
z
n
n
π
π
−
=
+
−
=
+
= ± ±
At this point all we need to do is solve each of these for z and we’ll have all the solutions to the
equation. Doing this gives,
2
2
0.2838
OR
0.09308
0, 1, 2,
9
9
n
n
z
z
n
π
π
=
−
= −
−
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
3. Find all the solutions to
(
)
(
) ( )
4 sin
2
15sin
2 tan 4
0
x
x
x
+ −
+
=
. Use at least 4 decimal
places in your work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques.
Step 1
Notice that each term has a sine in it and so we can factor this out of each term to get,
(
)
( )
(
)
sin
2 4 15 tan 4
0
x
x
+
−
=
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
(
)
( )
sin
2
0
OR
4 15 tan 4
0
x
x
+
=
−
=
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2

Calculus I
© 2007 Paul Dawkins
105
http://tutorial.math.lamar.edu/terms.aspx
Each of these equations are similar to equations solved in the previous section or in the earlier
problems of this section. Therefore, we will be assuming that you can recall the solution process
for each and we will not be putting in as many details. If you are unsure of the process you
should go back to the previous section and work some of the problems there before proceeding
with the solution to this problem.
We’ll start with,
(
)
sin
2
0
x
+
=
From a unit circle we can see that we must have,
2
0
2
OR
2
2
0, 1, 2,
x
n
x
n
n
π
π
π
+ = +
+ = +
= ± ±
Notice that we can further reduce this down to,
2
0, 1, 2,
x
n
n
π
+ =
= ± ±
Finally, the solutions from this equation are,
2
0, 1, 2,
x
n
n
π
=
−
= ± ±
The second equation will take a little more (but not much more) work. First, isolating the tangent
gives,
( )
4
tan 4
15
x
=
Using our calculator we get,
1
4
4
tan
0.2606
15
x
−
=
=
From our knowledge on solving equations involving tangents we know that the second angle in
the range
[
]
0, 2
π
will be
0.2606
3.4022
π
+
=
.
Finally, the solutions to this equation are,
4
0.2606 2
OR
4
3.4022 2
0, 1, 2,
0.06515
OR
0.8506
0, 1, 2,
2
2
x
n
x
n
n
n
n
x
x
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Putting all of this together gives the following set of solutions.
2,
0.06515
, OR
0.8506
0, 1, 2,
2
2
n
n
x
n
x
x
n
π
π
π
=
−
=
+
=
+
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.

Calculus I
© 2007 Paul Dawkins
106
http://tutorial.math.lamar.edu/terms.aspx
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
4. Find all the solutions to
3
3
3cos
sin
14 cos
0
7
2
7
y
y
y
+
=
. Use at least 4 decimal places
in your work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques.
Step 1
Notice that each term has a cosine in it and so we can factor this out of each term to get,
3
cos
3sin
14
0
7
2
y
y
+
=
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
3
cos
0
OR
3sin
14
0
7
2
y
y
=
+
=
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2
Each of these equations are similar to equations solved in the previous section. Therefore, we will
be assuming that you can recall the solution process for each and we will not be putting in as
many details. If you are unsure of the process you should go back to the previous section and
work some of the problems there before proceeding with the solution to this problem.
We’ll start with,
3
cos
0
7
y
=
From a unit circle we can see that we must have,
3
3
3
2
OR
2
0, 1, 2,
7
2
7
2
y
y
n
n
n
π
π
π
π
= +
=
+
= ± ±
Notice that we can further reduce this down to,

Calculus I
© 2007 Paul Dawkins
107
http://tutorial.math.lamar.edu/terms.aspx
3
0, 1, 2,
7
2
y
n
n
π π
= +
= ± ±
Finally, the solutions from this equation are,
7
7
0, 1, 2,
6
3
n
y
n
π
π
=
+
= ± ±
The second equation will take a little more (but not much more) work. First, isolating the sine
gives,
14
sin
1
2
3
y
= − < −
At this point recall that we know
1 sin
1
θ
− ≤
≤
and so this equation will have no solutions.
Therefore, the only solutions to this equation are,
7
7
0, 1, 2,
6
3
n
y
n
π
π
=
+
= ± ±
Do get too excited about the fact that we only got solutions from one of the two equations we got
after factoring. This will happen on occasion and so we need to be ready for these cases when
they happen.
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
5. Find all the solutions to
( )
( )
2
7 cos
3
cos 3
0
x
x
−
=
. Use at least 4 decimal places in your
work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques.
Step 1
Notice that we can factor a cosine out of each term to get,
( )
( )
(
)
cos 3
7 cos 3
1
0
x
x
− =

Calculus I
© 2007 Paul Dawkins
108
http://tutorial.math.lamar.edu/terms.aspx
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
( )
( )
cos 3
0
OR
7 cos 3
1 0
x
x
=
− =
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2
Each of these equations are similar to equations solved in the previous section. Therefore, we will
be assuming that you can recall the solution process for each and we will not be putting in as
many details. If you are unsure of the process you should go back to the previous section and
work some of the problems there before proceeding with the solution to this problem.
We’ll start with,
( )
cos 3
0
x
=
From a unit circle we can see that we must have,
3
3
2
OR
3
2
0, 1, 2,
2
2
x
n
x
n
n
π
π
π
π
= +
=
+
= ± ±
Notice that we can further reduce this down to,
3
0, 1, 2,
2
x
n
n
π π
= +
= ± ±
Finally, the solutions from this equation are,
0, 1, 2,
6
3
n
x
n
π π
= +
= ± ±
The second equation will take a little more (but not much more) work. First, isolating the cosine
gives,
( )
1
cos 3
7
x
=
Using our calculator we get,
1
1
3
cos
1.4274
7
x
−
=
=
From a quick look at a unit circle we know that the second angle in the range
[
]
0, 2
π
will be
2
1.4274
4.8558
π
−
=
.
Finally, the solutions to this equation are,

Calculus I
© 2007 Paul Dawkins
109
http://tutorial.math.lamar.edu/terms.aspx
3
1.4274 2
OR
3
4.8558 2
0, 1, 2,
2
2
0.4758
OR
1.6186
0, 1, 2,
3
3
x
n
x
n
n
n
n
x
x
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Putting all of this together gives the following set of solutions.
2
2
,
0.4758
, OR
1.6186
0, 1, 2,
6
3
3
3
n
n
n
x
x
x
n
π π
π
π
= +
=
+
=
+
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
6. Find all the solutions to
2
tan
tan
12
4
4
w
w
=
+
. Use at least 4 decimal places in your
work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques. If you’re not sure how to factor this think about how you
would factor
2
12
0
x
x
− −
=
.
Step 1
This equation may look very different from anything that we’ve ever been asked to factor,
however it is something that we can factor. First think about factoring the following,
(
)(
)
2
2
12
12
4
3
0
x
x
x
x
x
x
= +
→
− −
=
−
+ =
If we can factor this algebraic equation then we can factor the given equation in exactly the same
manner.
2
2
tan
tan
12
4
4
tan
tan
12
0
4
4
tan
4
tan
3
0
4
4
w
w
w
w
w
w
=
+
−
−
=
−
+
=

Calculus I
© 2007 Paul Dawkins
110
http://tutorial.math.lamar.edu/terms.aspx
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
tan
4
0
OR
tan
3
0
4
4
w
w
− =
+ =
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2
Each of these equations are similar to equations solved in the previous section. Therefore, we will
be assuming that you can recall the solution process for each and we will not be putting in as
many details. If you are unsure of the process you should go back to the previous section and
work some of the problems there before proceeding with the solution to this problem.
We’ll start with the first equation and isolate the tangent to get,
tan
4
4
w
=
Using our calculator we get,
( )
1
tan
4
1.3258
4
w
−
=
=
From our knowledge on solving equations involving tangents we know that the second angle in
the range
[
]
0, 2
π
will be
1.3258
4.4674
π
+
=
.
All the solutions to the first equation are then,
1.3258 2
OR
4.4674 2
0, 1, 2,
4
4
5.3032 8
OR
17.8696 8
0, 1, 2,
w
w
n
n
n
w
n
w
n
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Now, let’s solve the second equation.
( )
1
tan
3
tan
3
1.2490
4
4
w
w
−
= −
→
=
− = −
From our knowledge of the unit circle we can see that a positive angle that corresponds to this
angle is
2
1.2490
5.0342
π
−
=
. Either these angles can be used here but we’ll use the positive
angle to avoid the possibility of losing the minus sign. Also, the second angle in the range
[
]
0, 2
π
is
(
)
1.2490
1.8926
π
+ −
=
.
All the solutions to the second equation are then,

Calculus I
© 2007 Paul Dawkins
111
http://tutorial.math.lamar.edu/terms.aspx
1.8926 2
OR
5.0342 2
0, 1, 2,
4
4
7.5704 8
OR
20.1368 8
0, 1, 2,
w
w
n
n
n
w
n
w
n
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Putting all of this together gives the following set of solutions.
5.3032 8
,
7.5704 8
,
0, 1, 2,
17.8696 8
,
20.1368 8
w
n
w
n
n
w
n w
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
7. Find all the solutions to
(
)
(
)
2
4 csc 1
6
25 csc 1
t
t
− + =
−
. Use at least 4 decimal places in
your work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques. If you’re not sure how to factor this think about how you
would factor
2
4
25
6
0
x
x
−
+ =
.
Step 1
This equation may look very different from anything that we’ve ever been asked to factor,
however it is something that we can factor. First think about factoring the following,
(
)(
)
2
2
4
6
25
4
25
6
4
1
6
0
x
x
x
x
x
x
+ =
→
−
+ =
−
−
=
If we can factor this algebraic equation then we can factor the given equation in exactly the same
manner.
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
2
2
4 csc 1
6
25 csc 1
4 csc 1
25 csc 1
6
0
4 csc 1
1 csc 1
6
0
t
t
t
t
t
t
− + =
−
− −
− + =
− −
− −
=
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
(
)
(
)
4 csc 1
1 0
OR
csc 1
6
0
t
t
− − =
− − =

Calculus I
© 2007 Paul Dawkins
112
http://tutorial.math.lamar.edu/terms.aspx
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2
Each of these equations are similar to equations solved in the previous section and earlier in this
section. Therefore, we will be assuming that you can recall the solution process for each and we
will not be putting in as many details. If you are unsure of the process you should go back to the
previous section and work some of the problems there before proceeding with the solution to this
problem.
We’ll start with the first equation, isolate the cosecant and convert to an equation in terms of sine
for easier solving. Doing this gives,
(
)
(
)
1
csc 1
sin 1
4 1
4
t
t
− =
→
− = >
We now know that there are now solutions to the first equation because we know
1 sin
1
θ
− ≤
≤
.
Now, let’s solve the second equation.
(
)
(
)
1
csc 1
6
sin 1
6
t
t
− =
→
− =
Using our calculator we get,
1
1
1
sin
0.1674
6
t
−
− =
=
A quick glance at a unit circle shows us that the second angle in the range
[
]
0, 2
π
is
0.1674
2.9742
π
−
=
.
All the solutions to the second equation are then,
1
0.1674 2
OR
1
2.9742 2
0, 1, 2,
0.8326 2
OR
1.9742 2
0, 1, 2,
t
n
t
n
n
t
n
t
n
n
π
π
π
π
− =
+
− =
+
= ± ±
=
−
= −
−
= ± ±
Because we had not solutions to the first equation all the solutions to the original equation are
then,
0.8326 2
OR
1.9742 2
0, 1, 2,
t
n
t
n
n
π
π
=
−
= −
−
= ± ±
Do get too excited about the fact that we only got solutions from one of the two equations we got
after factoring. This will happen on occasion and so we need to be ready for these cases when
they happen.
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.

Calculus I
© 2007 Paul Dawkins
113
http://tutorial.math.lamar.edu/terms.aspx
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
8. Find all the solutions to
( )
4 sec 7
21
y
y
y
= −
. Use at least 4 decimal places in your work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques.
Step 1
Notice that if we move all the terms to one side we can then factor a y out of the equation. Doing
this gives,
( )
( )
(
)
4 sec 7
21
0
4 sec 7
21
0
y
y
y
y
y
+
=
+
=
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
( )
0
OR
4 sec 7
21 0
y
y
=
+
=
Be careful with this type of equation to not make the mistake of just canceling the y from both
sides in the initial step. Had you done that you would have missed the
0
y
=
solution.
When solving equations it is important to remember that you can’t cancel anything from both
sides unless you know for a fact that what you are canceling will never be zero.
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2
There really isn’t anything that we need to do with the first equation and so we can move right on
to the second equation. Note that this equation is similar to equations solved in the previous
section. Therefore, we will be assuming that you can recall the solution process for each and we
will not be putting in as many details. If you are unsure of the process you should go back to the
previous section and work some of the problems there before proceeding with the solution to this
problem.
First, isolating the secant and converting to cosines (to make the solving a little easier) gives,
( )
( )
21
4
sec 7
cos 7
4
21
y
y
= −
→
= −

Calculus I
© 2007 Paul Dawkins
114
http://tutorial.math.lamar.edu/terms.aspx
Using our calculator we get,
1
4
7
cos
1.7624
21
y
−
=
−
=
From a quick look at a unit circle we know that the second angle in the range
[
]
0, 2
π
will be
2
1.7624
4.5208
π
−
=
.
Finally, the solutions to this equation are,
7
1.7624 2
OR
7
4.5208 2
0, 1, 2,
2
2
0.2518
OR
0.6458
0, 1, 2,
7
7
y
n
y
n
n
n
n
y
y
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Putting all of this together gives the following set of solutions.
2
2
0,
0.2518
, OR
0.6458
0, 1, 2,
7
7
n
n
y
y
y
n
π
π
=
=
+
=
+
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
9. Find all the solutions to
(
)
(
)
2
10
sin 3
2
7 sin 3
2
x
x
x
x
+
=
+
. Use at least 4 decimal places in
your work.
Hint 1 : Factor the equation and using basic algebraic properties get some equations that can be
dealt with using known techniques.
Step 1
Notice that if we move all the terms to one side we can then factor an x and a sine out of the
equation. Doing this gives,
(
)
(
)
(
) (
)
2
10
sin 3
2
7 sin 3
2
0
10
7 sin 3
2
0
x
x
x
x
x
x
x
+
−
+
=
−
+
=
Now, we have a product of three factors that equals zero and so by basic algebraic properties we
know that we must have,

Calculus I
© 2007 Paul Dawkins
115
http://tutorial.math.lamar.edu/terms.aspx
(
)
0,
10
7
0,
OR
sin 3
2
0
x
x
x
=
− =
+
=
Be careful with this type of equation to not make the mistake of just canceling the x or the sine
from both sides in the initial step. Had you done that you would have missed the
0
x
=
solution
and the solutions we will get from solving
(
)
sin 3
2
0
x
+
=
.
When solving equations it is important to remember that you can’t cancel anything from both
sides unless you know for a fact that what you are canceling will never be zero.
Hint 2 : Solve each of these three equations to attain all the solutions to the original equation.
Step 2
There really isn’t anything that we need to do with the first equation and so we can move right on
to the second equation (which also doesn’t really present any problems). Solving the second
equation gives,
7
10
x
=
Now let’s take a look at the third equation. This equation is similar to equations solved earlier in
this section. Therefore, we will be assuming that you can recall the solution process for each and
we will not be putting in as many details. If you are unsure of the process you should go back to
the previous section and work some of the problems there before proceeding with the solution to
this problem.
From a unit circle we can see that we must have,
3
2
0
2
OR
3
2
2
0, 1, 2,
x
n
x
n
n
π
π
π
+ = +
+ = +
= ± ±
Notice that we can further reduce this down to,
3
2
0, 1, 2,
x
n
n
π
+ =
= ± ±
Finally, the solutions from this equation are,
2
0, 1, 2,
3
n
x
n
π
−
=
= ± ±
Putting all of this together gives the following set of solutions.
7
2
0,
, OR
0, 1, 2,
10
3
n
x
x
x
n
π
−
=
=
=
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.

Calculus I
© 2007 Paul Dawkins
116
http://tutorial.math.lamar.edu/terms.aspx
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.
10. Find all the solutions to
(
)
6
2
3 tan
15 10
11
t
t
t
−
=
−
. Use at least 4 decimal places in your
work.
Hint 1 : Factor the equation and using basic algebraic properties get two equations that can be
dealt with using known techniques.
Step 1
This one may be a little trickier to factor than the others in this section, but it can be factored.
First get everything on one side of the equation and then notice that we can factor out a
2
3
t
−
from the equation as follows,
(
)
(
)
(
)
(
)
6
2
3 tan
10
15
0
11
6
2
3 tan
5 2
3
0
11
6
2
3
tan
5
0
11
t
t
t
t
t
t
t
t
−
+
−
=
−
+
− =
−
+
=
Now, we have a product of two factors that equals zero and so by basic algebraic properties we
know that we must have,
6
2
3
0
OR
tan
5
0
11
t
t
− =
+ =
Be careful with this type of equation to not make the mistake of just canceling the
2
3
t
−
from
both sides. Had you done that you would have missed the solution from the first equation.
When solving equations it is important to remember that you can’t cancel anything from both
sides unless you know for a fact that what you are canceling will never be zero.
Hint 2 : Solve each of these two equations to attain all the solutions to the original equation.
Step 2
Solving the first equation gives,
3
2
t
=

Calculus I
© 2007 Paul Dawkins
117
http://tutorial.math.lamar.edu/terms.aspx
Now we can move onto the second equation and note that this equation is similar to equations
solved in the previous section. Therefore, we will be assuming that you can recall the solution
process for each and we will not be putting in as many details. If you are unsure of the process
you should go back to the previous section and work some of the problems there before
proceeding with the solution to this problem.
First, isolating the tangent gives,
6
tan
5
11
t
= −
Using our calculator we get,
( )
1
6
tan
5
1.3734
11
t
−
=
− = −
From our knowledge of the unit circle we can see that a positive angle that corresponds to this
angle is
2
1.3734
4.9098
π
−
=
. Either these angles can be used here but we’ll use the positive
angle to avoid the possibility of losing the minus sign. Also, the second angle in the range
[
]
0, 2
π
is
(
)
1.3734
1.7682
π
+ −
=
.
Finally, the solutions to this equation are,
6
6
1.7682 2
OR
4.9098 2
0, 1, 2,
11
11
11
11
3.2417
OR
9.0013
0, 1, 2,
3
3
t
t
n
n
n
n
n
t
t
n
π
π
π
π
=
+
=
+
= ± ±
=
+
=
+
= ± ±
Putting all of this together gives the following set of solutions.
3
11
11
,
3.2417
, OR
9.0013
0, 1, 2,
2
3
3
n
n
t
t
t
n
π
π
=
=
+
=
+
= ± ±
If an interval had been given we would next proceed with plugging in values of n to determine
which solutions fall in that interval. Since we were not given an interval this is as far as we can
go.
Note that depending upon the amount of decimals you used here your answers may vary slightly
from these due to round off error. Any differences should be slight and only appear around the
4
th
decimal place or so however.

Calculus I
© 2007 Paul Dawkins
118
http://tutorial.math.lamar.edu/terms.aspx
Review : Exponential Functions
1. Sketch the graph of
( )
1 2
3
x
f x
+
=
.
Solution
There are several methods that can be used for getting the graph of this function. One way would
be to use some of the various algebraic transformations. The point of the problems in this section
however are more to force you to do some evaluation of these kinds of functions to make sure
you can do them. So, while you could use transformations, we’ll be doing these the “old
fashioned” way of plotting points. If you’d like some practice of the transformations you can
check out the practice problems for the
Common Graphs
section of this chapter.
So, with that out of the way here is a table of values for this function.
x
-2
-1 0
1
2
( )
f x
1
27
1
3
3 27 243
A natural question at this point is “how did we know to use these values of x”? That is a good
question and not always an easy one to answer. For exponential functions the key is to recall that
when the exponent is positive the function will grow very quickly and when the exponent is
negative the function will quickly get close to zero. This means that often (but not always) we’ll
want to keep the exponent in the range of about
[
]
4, 4
−
and by exponent we mean the value of
1 2x
+
after we plug in the x.
Note that we often won’t need the whole range given above to see what the curve looks like. As
we plug in values of x we can look at our answers and if they aren’t changing much then we’ll
know that the exponent has gone far enough in the negative direction so that the exponential is
essentially zero. Likewise, once the value really starts changing fast we’ll know that the
exponent has gone far enough in the positive direction as well. The given above is just a way to
give us some starting values of x and nothing more.
Here is the sketch of the graph of this function.
Calculus I
© 2007 Paul Dawkins
119
http://tutorial.math.lamar.edu/terms.aspx
2. Sketch the graph of
( )
3
4
2
7
x
h x
−
=
−
.
Solution
There are several methods that can be used for getting the graph of this function. One way would
be to use some of the various algebraic transformations. The point of the problems in this section
however are more to force you to do some evaluation of these kinds of functions to make sure
you can do them. So, while you could use transformations, we’ll be doing these the “old
fashioned” way of plotting points. If you’d like some practice of the transformations you can
check out the practice problems for the
Common Graphs
section of this chapter.
So, with that out of the way here is a table of values for this function.
x
-10
-6
-2
0
2
6
10
( )
h x
38.2548 15.6274 4.3137 1 -1.3431 -4.1716 -5.5858
A natural question at this point is “how did we know to use these values of x”? That is a good
question and not always an easy one to answer. For exponential functions the key is to recall that
when the exponent is positive the function will grow very quickly and when the exponent is
negative the function will quickly get close to zero. This means that often (but not always) we’ll
want to keep the exponent in the range of about
[
]
4, 4
−
and by exponent we mean the value of
3
4
x
−
after we plug in the x.
Note that we often won’t need the whole range given above to see what the curve looks like. As
we plug in values of x we can look at our answers and if they aren’t changing much then we’ll
know that the exponent has gone far enough in the negative direction so that the exponential is
Calculus I
© 2007 Paul Dawkins
120
http://tutorial.math.lamar.edu/terms.aspx
essentially zero. Likewise, once the value really starts changing fast we’ll know that the
exponent has gone far enough in the positive direction as well. The given above is just a way to
give us some starting values of x and nothing more.
Here is the sketch of the graph of this function.
3. Sketch the graph of
( )
2
4
8 3
t
h t
−
= + e
.
Solution
There are several methods that can be used for getting the graph of this function. One way would
be to use some of the various algebraic transformations. The point of the problems in this section
however are more to force you to do some evaluation of these kinds of functions to make sure
you can do them. So, while you could use transformations, we’ll be doing these the “old
fashioned” way of plotting points. If you’d like some practice of the transformations you can
check out the practice problems for the
Common Graphs
section of this chapter.
So, with that out of the way here is a table of values for this function.
t
-1
0
1
2
3
( )
h t
8.0074 8.0549 8.4060 11 30.1672
A natural question at this point is “how did we know to use these values of t”? That is a good
question and not always an easy one to answer. For exponential functions the key is to recall that
when the exponent is positive the function will grow very quickly and when the exponent is
negative the function will quickly get close to zero. This means that often (but not always) we’ll
want to keep the exponent in the range of about
[
]
4, 4
−
and by exponent we mean the value of
2
4
t
−
after we plug in the t.
Calculus I
© 2007 Paul Dawkins
121
http://tutorial.math.lamar.edu/terms.aspx
Note that we often won’t need the whole range given above to see what the curve looks like. As
we plug in values of t we can look at our answers and if they aren’t changing much then we’ll
know that the exponent has gone far enough in the negative direction so that the exponential is
essentially zero. Likewise, once the value really starts changing fast we’ll know that the
exponent has gone far enough in the positive direction as well. The given above is just a way to
give us some starting values of t and nothing more.
Here is the sketch of the graph of this function.
4. Sketch the graph of
( )
2 3
1
10
4
z
g z
− −
=
− e
.
Solution
There are several methods that can be used for getting the graph of this function. One way would
be to use some of the various algebraic transformations. The point of the problems in this section
however are more to force you to do some evaluation of these kinds of functions to make sure
you can do them. So, while you could use transformations, we’ll be doing these the “old
fashioned” way of plotting points. If you’d like some practice of the transformations you can
check out the practice problems for the
Common Graphs
section of this chapter.
So, with that out of the way here is a table of values for this function.
z
-2
-1
0
1
2
( )
g z
-3.6495 9.3204 9.9662 9.9983 9.9999
A natural question at this point is “how did we know to use these values of z”? That is a good
question and not always an easy one to answer. For exponential functions the key is to recall that
when the exponent is positive the function will grow very quickly and when the exponent is
Calculus I
© 2007 Paul Dawkins
122
http://tutorial.math.lamar.edu/terms.aspx
negative the function will quickly get close to zero. This means that often (but not always) we’ll
want to keep the exponent in the range of about
[
]
4, 4
−
and by exponent we mean the value of
2 3z
− −
after we plug in the z.
Note that we often won’t need the whole range given above to see what the curve looks like. As
we plug in values of z we can look at our answers and if they aren’t changing much then we’ll
know that the exponent has gone far enough in the negative direction so that the exponential is
essentially zero. Likewise, once the value really starts changing fast we’ll know that the
exponent has gone far enough in the positive direction as well. The given above is just a way to
give us some starting values of z and nothing more.
Here is the sketch of the graph of this function.
Review : Logarithm Functions
1. Without using a calculator determine the exact value of
3
log 81
.
Hint : Recall that converting a logarithm to exponential form can often help to evaluate these
kinds of logarithms.
Solution
Converting the logarithm to exponential form gives,
?
3
log 81
?
3
81
=
⇒
=
From this we can quickly see that
4
3
81
=
and so we must have,

Calculus I
© 2007 Paul Dawkins
123
http://tutorial.math.lamar.edu/terms.aspx
3
log 81
4
=
2. Without using a calculator determine the exact value of
5
log 125
.
Hint : Recall that converting a logarithm to exponential form can often help to evaluate these
kinds of logarithms.
Solution
Converting the logarithm to exponential form gives,
?
5
log 125
?
5
125
=
⇒
=
From this we can quickly see that
3
5
125
=
and so we must have,
5
log 125
3
=
3. Without using a calculator determine the exact value of
2
1
log
8
.
Hint : Recall that converting a logarithm to exponential form can often help to evaluate these
kinds of logarithms.
Solution
Converting the logarithm to exponential form gives,
?
2
1
1
log
?
2
8
8
=
⇒
=
Now, we know that if we raise an integer to a negative exponent we’ll get a fraction and so we
must have a negative exponent and then we know that
3
2
8
=
. Therefore we can see that
3
1
2
8
−
=
and so we must have,
2
1
log
3
8
= −
4. Without using a calculator determine the exact value of
1
4
log 16
.
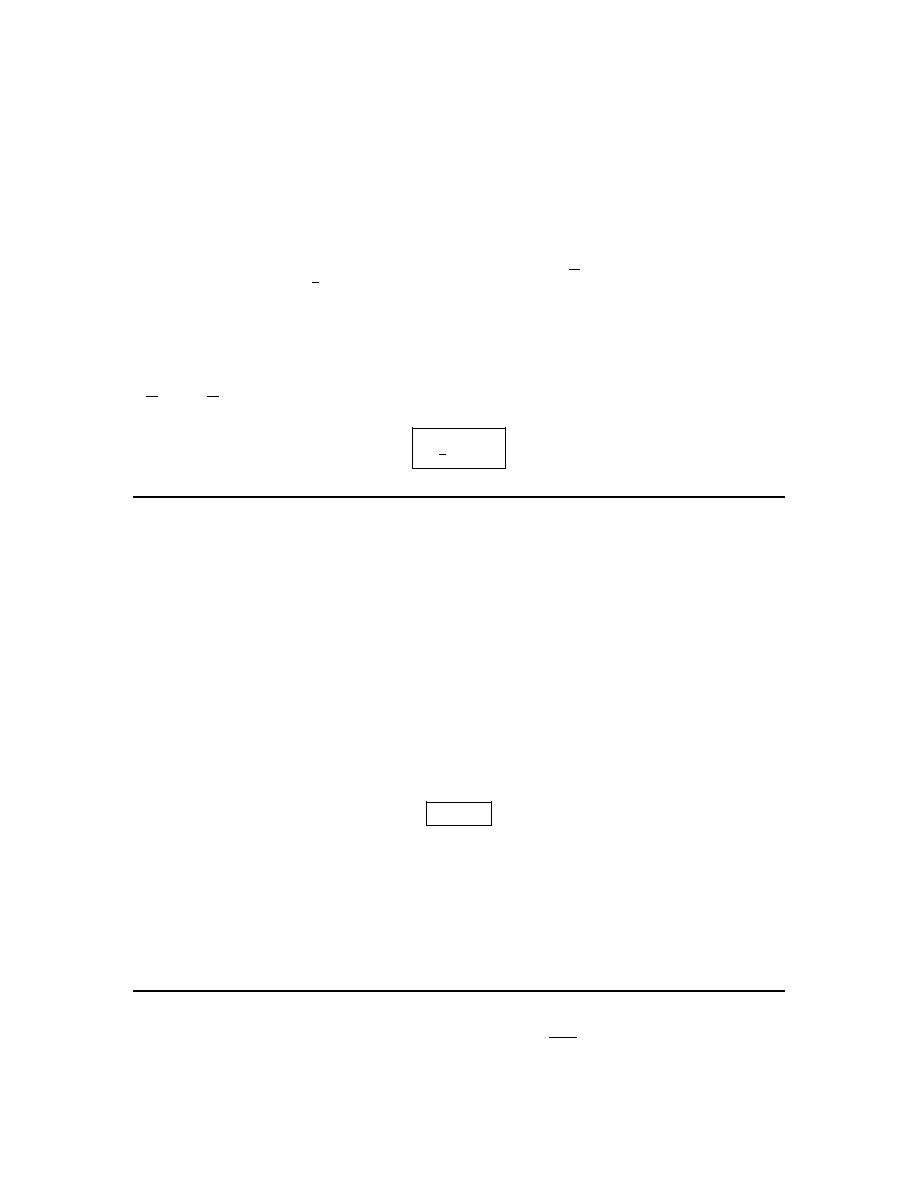
Calculus I
© 2007 Paul Dawkins
124
http://tutorial.math.lamar.edu/terms.aspx
Hint : Recall that converting a logarithm to exponential form can often help to evaluate these
kinds of logarithms.
Solution
Converting the logarithm to exponential form gives,
?
1
4
1
log 16
?
16
4
=
⇒
=
Now, we know that if we raise an fraction to a power and get an integer out we must have had a
negative exponent. Now, we also know that
2
4
16
=
. Therefore we can see that
2
2
1
4
16
4
1
−
=
=
and so we must have,
1
4
log 16
2
= −
5. Without using a calculator determine the exact value of
4
ln e
.
Hint : Recall that converting a logarithm to exponential form can often help to evaluate these
kinds of logarithms. Also recall what the base is for a natural logarithm.
Solution
Recalling that the base for a natural logarithm is e and converting the logarithm to exponential
form gives,
4
4
?
4
ln
log
?
=
=
⇒
=
e
e
e
e
e
From this we can quickly see that
4
4
=
e
e
and so we must have,
4
ln
4
=
e
Note that an easier method of determining the value of this logarithm would have been to recall
the properties of logarithm. In particular the property that states,
log
x
b
b
x
=
Using this we can also very quickly see what the value of the logarithm is.
6. Without using a calculator determine the exact value of
1
log
100
.
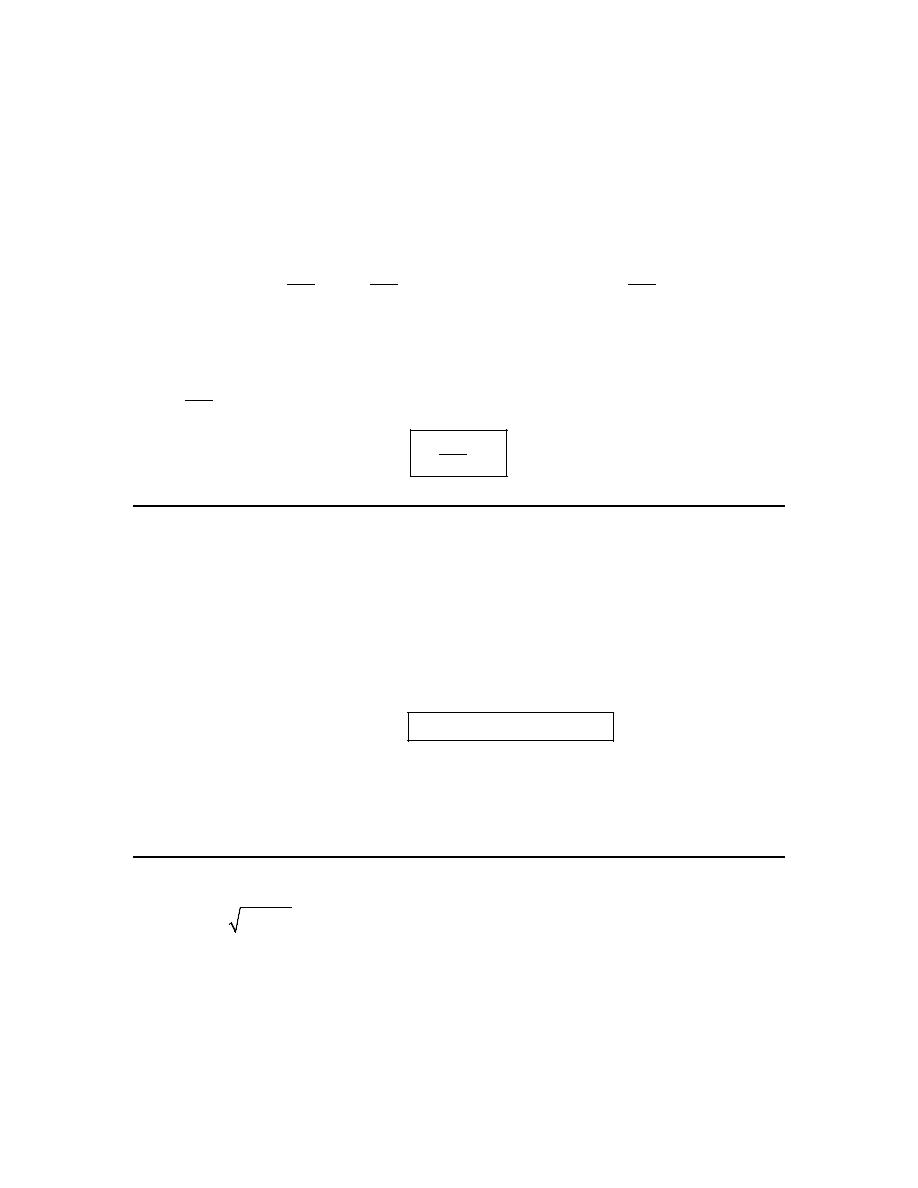
Calculus I
© 2007 Paul Dawkins
125
http://tutorial.math.lamar.edu/terms.aspx
Hint : Recall that converting a logarithm to exponential form can often help to evaluate these
kinds of logarithms. Also recall what the base is for a common logarithm.
Solution
Recalling that the base for a natural logarithm is 10 and converting the logarithm to exponential
form gives,
?
10
1
1
1
log
log
?
10
100
100
100
=
=
⇒
=
Now, we know that if we raise an integer to a negative exponent we’ll get a fraction and so we
must have a negative exponent and then we know that
2
10
100
=
. Therefore we can see that
2
1
10
100
−
=
and so we must have,
1
log
2
100
= −
7. Write
(
)
4
7
log 3x y
−
in terms of simpler logarithms.
Solution
So, we’re being asked here to use as many of the properties as we can to reduce this down into
simpler logarithms. So, here is the work for this problem.
(
)
( )
( )
( )
( )
( )
( )
4
7
4
7
log 3
log 3
log
log
log 3
4 log
7 log
x y
x
y
x
y
−
−
=
+
+
=
+
−
Remember that we can only bring an exponent out of a logarithm if is on the whole argument of
the logarithm. In other words, we couldn’t bring any of the exponents out of the logarithms until
we had dealt with the product.
8. Write
(
)
2
2
ln x y
z
+
in terms of simpler logarithms.
Solution
So, we’re being asked here to use as many of the properties as we can to reduce this down into
simpler logarithms. So, here is the work for this problem.
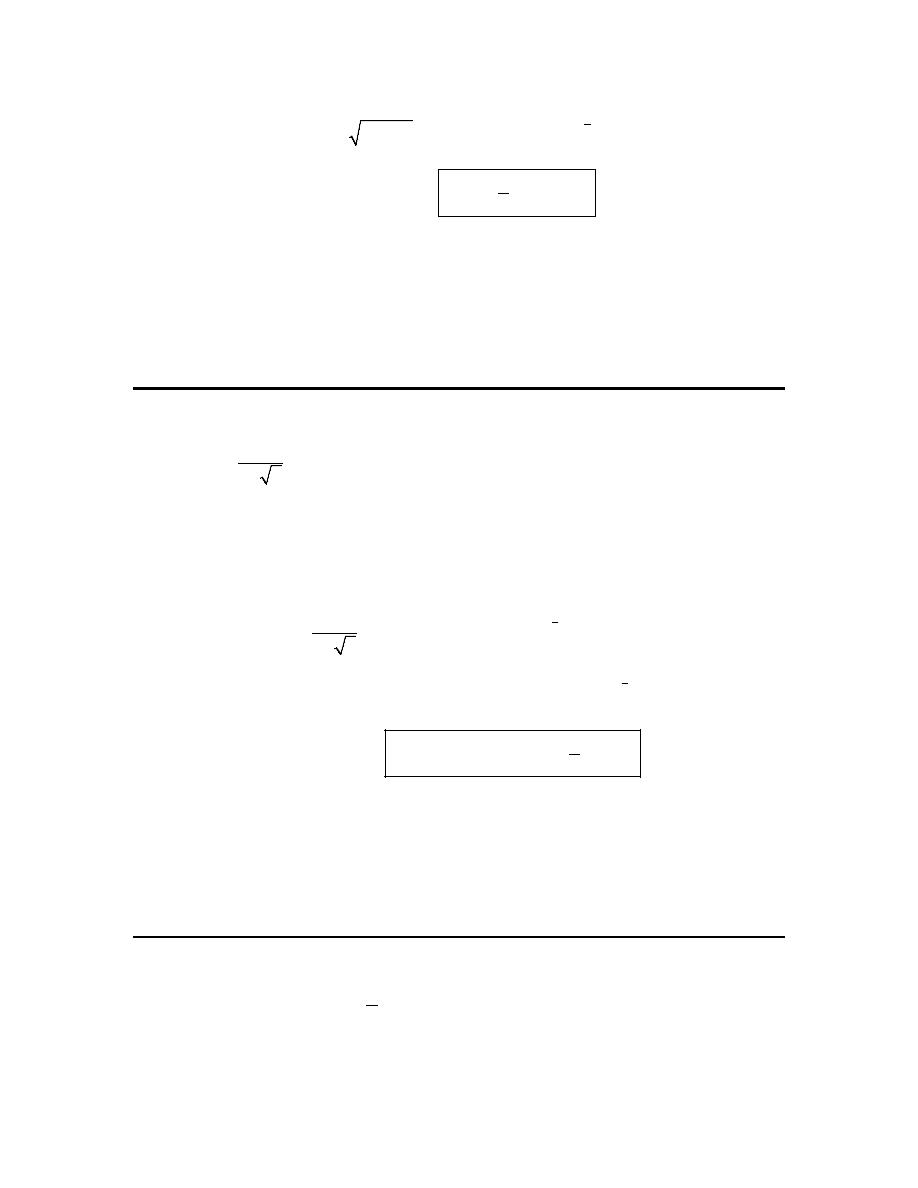
Calculus I
© 2007 Paul Dawkins
126
http://tutorial.math.lamar.edu/terms.aspx
(
)
( )
(
)
( )
(
)
1
2
2
2
2
2
2
2
ln
ln
ln
1
ln
ln
2
x y
z
x
y
z
x
y
z
+
=
+
+
=
+
+
Remember that we can only bring an exponent out of a logarithm if is on the whole argument of
the logarithm. In other words, we couldn’t bring any of the exponents out of the logarithms until
we had dealt with the product. Also, in the second logarithm while each term is squared the
whole argument is not squared, i.e. it’s not
(
)
2
x
y
+
and so we can’t bring those 2’s out of the
logarithm.
9. Write
4
2 5
4
log
x
y
z
−
in terms of simpler logarithms.
Solution
So, we’re being asked here to use as many of the properties as we can to reduce this down into
simpler logarithms. So, here is the work for this problem.
(
)
(
)
( )
(
)
( )
( )
1
2
5
4
4
4
2 5
1
2
5
4
4
4
4
4
4
4
log
log
4
log
log
4
log
log
1
log
4
2 log
log
5
x
x
y z
y
z
x
y
z
x
y
z
−
=
− −
=
− −
+
=
− −
−
Remember that we can only bring an exponent out of a logarithm if is on the whole argument of
the logarithm. In other words, we couldn’t bring any of the exponents out of the logarithms until
we had dealt with the quotient and product. Recall as well that we can’t split up an
sum/difference in a logarithm. Finally, make sure that you are careful in dealing with the minus
sign we get from breaking up the quotient when dealing with the product in the denominator.
10. Combine
4
4
4
1
2 log
5 log
log
2
x
y
z
+
−
into a single logarithm with a coefficient of one.
Hint :The properties that we use to break up logarithms can be used in reverse as well.

Calculus I
© 2007 Paul Dawkins
127
http://tutorial.math.lamar.edu/terms.aspx
Solution
To convert this into a single logarithm we’ll be using the properties that we used to break up
logarithms in reverse. The first step in this process is to use the property,
( )
log
log
r
b
b
x
r
x
=
to make sure that all the logarithms have coefficients of one. This needs to be done first because
all the properties that allow us to combine sums/differences of logarithms require coefficients of
one on individual logarithms. So, using this property gives,
( )
( )
1
2
5
2
4
4
4
log
log
log
x
y
z
+
−
Now, there are several ways to proceed from this point. We can use either of the two properties.
( )
log
log
log
log
log
log
b
b
b
b
b
b
x
xy
x
y
x
y
y
=
+
=
−
and in fact we’ll need to use both in the end. Which we use first does not matter as we’ll end up
with the same result in the end. Here is the rest of the work for this problem.
(
)
( )
2
5
4
4
4
4
4
2
5
4
1
2 log
5 log
log
log
log
2
log
x
y
z
x y
z
x y
z
+
−
=
−
=
Note that the only reason we converted the fractional exponent to a root was to make the final
answer a little nicer.
11. Combine
(
)
(
)
3ln
5
4 ln
2 ln
1
t
t
s
+ −
−
−
into a single logarithm with a coefficient of one.
Hint :The properties that we use to break up logarithms can be used in reverse as well.
Solution
To convert this into a single logarithm we’ll be using the properties that we used to break up
logarithms in reverse. The first step in this process is to use the property,
( )
log
log
r
b
b
x
r
x
=
to make sure that all the logarithms have coefficients of one. This needs to be done first because
all the properties that allow us to combine sums/differences of logarithms require coefficients of
one on individual logarithms. So, using this property gives,
(
)
( )
(
)
3
2
4
ln
5
ln
ln
1
t
t
s
+
−
−
−
Now, there are several ways to proceed from this point. We can use either of the two properties.

Calculus I
© 2007 Paul Dawkins
128
http://tutorial.math.lamar.edu/terms.aspx
( )
log
log
log
log
log
log
b
b
b
b
b
b
x
xy
x
y
x
y
y
=
+
=
−
and in fact we’ll need to use both in the end.
We should also be careful with the fact that there are two minus signs in here as that sometimes
adds confusion to the problem. They are easy to deal with however if we just factor a minus sign
out of the last two terms and then proceed from there as follows.
(
)
(
)
(
)
( )
(
)
(
)
(
)
(
)
(
)
(
)
(
)
3
2
4
3
3
2
4
2
4
3ln
5
4 ln
2 ln
1
ln
5
ln
ln
1
5
ln
5
ln
1
ln
1
t
t
s
t
t
s
t
t
t
s
t
s
+ −
−
− =
+
−
+
−
+
=
+
−
−
=
−
12. Combine
1
log
6 log
2
3
a
b
−
+
into a single logarithm with a coefficient of one.
Hint :The properties that we use to break up logarithms can be used in reverse as well. For the
constant see if you figure out a way to write that as a logarithm.
Solution
To convert this into a single logarithm we’ll be using the properties that we used to break up
logarithms in reverse. The first step in this process is to use the property,
( )
log
log
r
b
b
x
r
x
=
to make sure that all the logarithms have coefficients of one. This needs to be done first because
all the properties that allow us to combine sums/differences of logarithms require coefficients of
one on individual logarithms. So, using this property gives,
( )
1
6
3
log
log
2
a
b
−
+
Now, for the 2 let’s notice that we can write this in terms of a logarithm as,
2
2
log10
log100
=
=
Note that this is really just using the property,
log
x
b
b
x
=
So, we now have,
( )
1
6
3
log
log
log100
a
b
−
+
Calculus I
© 2007 Paul Dawkins
129
http://tutorial.math.lamar.edu/terms.aspx
Now, there are several ways to proceed from this point. We can use either of the two properties.
( )
log
log
log
log
log
log
b
b
b
b
b
b
x
xy
x
y
x
y
y
=
+
=
−
and in fact we’ll need to use both in the end. Which we use first does not matter as we’ll end up
with the same result in the end. Here is the rest of the work for this problem.
( )
(
)
( )
1
6
2
6
3
3
3
6
log
log
log10
log 100
log
100
log
a
b
a
b
a
b
−
+
=
−
=
Note that the only reason we converted the fractional exponent to a root was to make the final
answer a little nicer.
13. Use the change of base formula and a calculator to find the value of
12
log 35
.
Solution
We can use either the natural logarithm or the common logarithm to do this so we’ll do both.
12
ln 35
3.55534806
log 35
1.43077731
ln12
2.48490665
=
=
=
12
log 35
1.54406804
log 35
1.43077731
log12
1.07918125
=
=
=
So, as we noted at the start it doesn’t matter which logarithm we use we’ll get the same answer in
the end.
14. Use the change of base formula and a calculator to find the value of
2
3
log 53
.
Solution
We can use either the natural logarithm or the common logarithm to do this so we’ll do both.
2
3
ln 53
3.97029191
log 53
9.79194469
2
0.40546511
ln
3
=
=
= −
−

Calculus I
© 2007 Paul Dawkins
130
http://tutorial.math.lamar.edu/terms.aspx
2
3
log 53
1.72427587
log 53
9.79194469
2
0.17609126
log
3
=
=
= −
−
So, as we noted at the start it doesn’t matter which logarithm we use we’ll get the same answer in
the end.
Review : Exponential and Logarithm Equations
1. Find all the solutions to
7 3
12 4
7
x
+
−
=
e
. If there are no solutions clearly explain why.
Step 1
There isn’t all that much to do here for this equation. First we need to isolate the exponential on
one side by itself with a coefficient of one.
7 3
7 3
5
4
5
4
x
x
+
+
−
= −
⇒
=
e
e
Step 2
Now all we need to do is take the natural logarithm of both sides and then solve for x.
(
)
7 3
5
ln
ln
4
5
7 3
ln
4
1
5
ln
7
2.25895
3
4
x
x
x
+
=
+
=
=
−
= −
e
Depending upon your preferences either the exact or decimal solution can be used.
2. Find all the solutions to
2
2
1 10 3
z
z
−
=
− e
. If there are no solutions clearly explain why.
Step 1
There isn’t all that much to do here for this equation. First we need to isolate the exponential on
one side by itself with a coefficient of one.
2
2
2
2
9
3
3
z
z
z
z
−
−
− = −
⇒
=
e
e
Step 2
Now all we need to do is take the natural logarithm of both sides and then solve for z.

Calculus I
© 2007 Paul Dawkins
131
http://tutorial.math.lamar.edu/terms.aspx
(
)
( )
( )
( )
2
2
2
2
ln
ln 3
2
ln 3
2
ln 3
0
z
z
z
z
z
z
−
=
−
=
−
−
=
e
Now, before proceeding with the solution here let’s pause and make sure that we don’t get too
excited about the “strangeness” of the quadratic above. If we’d had the quadratic,
2
2
5
0
z
z
−
− =
for instance, we’d know that all we would need to do is use the quadratic formula to get the
solutions.
That’s all we need to as well for the quadratic that we have from our work. Of course we don’t
have a 5 we have a ln(3), but ln(3) is just a number and so we can use the quadratic formula to
find the solutions here as well. Here is the work for that.
( ) ( )
( )
( )
(
)
( )
( )
( )
(
)
( )
( )
2
2
2
4 1
ln 3
2
4 4 ln 3
2 1
2
2
4 1 ln 3
2 2 1 ln 3
1
1 ln 3
0.4487, 2.4487
2
2
z
− − ±
−
−
−
±
+
=
=
±
+
±
+
=
=
= ±
+
= −
Notice that we did a little simplification on the root. This doesn’t need to be done, but can make
the exact solution a little easier to deal with. Also, depending upon your preferences either the
exact or decimal solution can be used.
Before leaving this solution we should again make a point that not all quadratics will be the
“simple” type of quadratics that you may be used to solving from an Algebra class. They can,
and often will be, messier that those. That doesn’t mean that you can’t solve them. They are, for
all intents and purposes, identical to the types of problems you are used to working. The only real
difference is that they numbers are a little messier.
So, don’t get too excited about this kind of problem. They will happen on occasion and you are
capable of solving them!
3. Find all the solutions to
6
1
2
0
t
t
t
−
−
=
e
. If there are no solutions clearly explain why.
Hint : Be careful to not cancel terms that shouldn’t be canceled. Remember that you can’t cancel
something unless you know for a fact that it won’t ever be zero. Also, note that if you can cancel
something then it can be factored out of the equation.
Step 1
First notice that we can factor a t out of both terms to get,

Calculus I
© 2007 Paul Dawkins
132
http://tutorial.math.lamar.edu/terms.aspx
(
)
6
1
2
0
t
t
−
−
=
e
Be careful to not cancel the t from both terms. When solving equations you can only cancel
something if you know for a fact that it won’t be zero. If the term can be zero and you cancel it
you will miss solutions and that will the case here.
Step 2
We now have a product of terms that is equal to zero so we know,
6
1
0
OR
2
0
t
t
−
=
−
=
e
So, we have one solution already,
0
t
=
, and again note that if we had canceled the t at the
beginning we would have missed this solution. Now all we need to do is solve the equation
involving the exponential.
Step 3
We can now solve the exponential equation in the same manner as the first couple of problems in
this section.
( )
( )
( )
( )
(
)
6
1
6
1
2
ln
ln 2
6
1
ln 2
1
1 ln 2
0.2822
6
t
t
t
t
−
−
=
=
− =
=
+
=
e
e
Depending upon your preferences either the exact or decimal solution can be used.
4. Find all the solutions to
(
)
2
2
4
1
12
3
x
x
x
−
+ =
+ e
. If there are no solutions clearly explain why.
Hint : Be careful to not cancel terms that shouldn’t be canceled. Remember that you can’t cancel
something unless you know for a fact that it won’t ever be zero. Also, note that if you can cancel
something then it can be factored out of the equation.
Step 1
It may not be apparent at first glance, but with some work we can do a little factoring on this
equation. To do that first move everything to one side and then the factoring might become a
little more apparent.
Calculus I
© 2007 Paul Dawkins
133
http://tutorial.math.lamar.edu/terms.aspx
(
)
(
) (
)
(
)
(
)
2
2
2
2
2
2
4
1
12
3
0
4
1
3 4
1
0
4
1 1 3
0
x
x
x
x
x
x
x
x
−
−
−
+ −
+
=
+ −
+
=
+
−
=
e
e
e
Note that in the second step we put parenthesis around the first couple of terms solely to make the
factoring in the next step a little more apparent. It does not need to be done in practice.
Be careful to not cancel the
4
1
x
+
from both terms. When solving equations you can only
cancel something if you know for a fact that it won’t be zero. If the term can be zero and you
cancel it you will miss solutions, and that will be the case here.
Step 2
We now have a product of terms that is equal to zero so we know,
2
2
4
1
0
OR
1 3
0
x
x
−
+ =
−
=
e
From the first equation we can quickly arrive at one solution,
1
4
x
= −
, and again note that if we
had canceled the
4
1
x
+
at the beginning we would have missed this solution. Now all we need
to do is solve the equation involving the exponential.
Step 3
We can now solve the exponential equation in the same manner as the first couple of problems in
this section.
( )
2
2
2
2
2
2
1
3
1
ln
ln
3
1
2
ln
3
1
2 ln
3
1
2 ln
0.9494
3
x
x
x
x
x
−
−
=
=
− =
= +
= ±
+
= ±
e
e
Depending upon your preferences either the exact or decimal solution can be used.
5. Find all the solutions to
3
8
5 10
2
11
0
y
y
+
−
−
=
e
e
. If there are no solutions clearly explain why.
Calculus I
© 2007 Paul Dawkins
134
http://tutorial.math.lamar.edu/terms.aspx
Hint : The best way to proceed here is to reduce the equation down to a single exponential.
Step 1
With both exponentials in the equation this may be a little difficult to solve, so let’s do some
work to reduce this down to an equation with a single exponential.
3
8
5 10
3
8
5 10
13
3
2
11
11
2
11
2
y
y
y
y
y
+
−
+
−
+
=
=
=
e
e
e
e
e
Note that we could have divided by either exponential but by dividing by the one that we did we
avoid a negative exponent on the y, which is sometimes easy to lose track of.
Step 2
Now all we need to do is take the logarithm of both sides and solve for y.
(
)
13
3
11
ln
ln
2
11
13
3
ln
2
1
11
ln
3
0.09963
13
2
y
y
y
+
=
+ =
=
−
= −
e
Depending upon your preferences either the exact or decimal solution can be used.
6. Find all the solutions to
6
12
7
14
0
x
x
−
−
+
=
e
e
. If there are no solutions clearly explain why.
Hint : The best way to proceed here is to reduce the equation down to a single exponential.
Step 1
With both exponentials in the equation this may be a little difficult to solve, so let’s do some
work to reduce this down to an equation with a single exponential.
6
12
7
12
7
6
13
13
14
14
14
x
x
x
x
x
−
−
−
−
−
= −
= −
= −
e
e
e
e
e

Calculus I
© 2007 Paul Dawkins
135
http://tutorial.math.lamar.edu/terms.aspx
At this point we can stop. We know that exponential functions are always positive and there is no
way for this to be negative and therefore there is no solution to this equation.
Note that if we hadn’t caught the exponent being negative our next step would have been to take
the logarithm of both side and we also know that we can only take the logarithm of positive
numbers and so again we’d see that there is no solution to this equation.
7. Find all the solutions to
2
1
1 8 ln
14
7
x
−
−
=
. If there are no solutions clearly explain why.
Step 1
There isn’t all that much to do here for this equation. First we need to isolate the logarithm on
one side by itself with a coefficient of one.
2
1
2
1
13
1 8 ln
14
ln
7
7
8
x
x
−
−
−
=
⇒
= −
Step 2
Now all we need to do is exponentiate both sides using e (because we’re working with the natural
logarithm) and then solve for x.
2
1
13
ln
7
8
13
8
13
8
2
1
7
1
1 7
1.1892
2
x
x
x
−
−
−
−
=
−
=
=
+
=
e
e
e
e
Step 3
We’re dealing with logarithms and so we need to make sure that we won’t have any problems
with any of our potential solutions. In other words, we need to make sure that if we plug in the
potential solution into the original equation we won’t end up taking the logarithm of a negative
number or zero.
Plugging in we can see that we won’t be taking the logarithm of a negative number and so the
solution is,
13
8
1
1 7
1.1892
2
x
−
=
+
=
e
Depending upon your preferences either the exact or decimal solution can be used.

Calculus I
© 2007 Paul Dawkins
136
http://tutorial.math.lamar.edu/terms.aspx
8. Find all the solutions to
(
)
(
)
ln
1
1 ln 3
2
y
y
− = +
+
. If there are no solutions clearly explain
why.
Hint : Don’t forget about the basic logarithm properties and how they can be used to combine
multiple logarithms into a single logarithm.
Step 1
We need to reduce this down to an equation with a single logarithm and to do that we first should
rewrite it a little. Upon doing that we can use the basic logarithm properties to combine the two
logarithms into a single logarithm as follows,
(
)
(
)
ln
1
ln 3
2
1
1
ln
1
3
2
y
y
y
y
− −
+
=
−
=
+
Step 2
Now all we need to do is exponentiate both sides using e (because we’re working with the natural
logarithm) and then solve for y.
(
)
(
)
1
ln
3
2
1
1
3
2
1
3
2
3
2
1 3
1 2
1 2
0.8996
1 3
y
y
y
y
y
y
y
y
y
−
+
=
−
=
+
− =
+
=
+
−
= +
+
=
= −
−
e
e
e
e
e
e
e
e
e
e
Step 3
We’re dealing with logarithms and so we need to make sure that we won’t have any problems
with any of our potential solutions. In other words, we need to make sure that if we plug in the
potential solutions into the original equation we won’t end up taking the logarithm of a negative
number or zero.
Upon inspection we can quickly see that if we plug in our potential solution into the first
logarithm we’ll be taking the logarithm of a negative number. The same will be true for the
second logarithm and so
0.8996
y
= −
can’t be a solution.
Because this was our only potential solution we know now that there will be no solutions to this
equation.

Calculus I
© 2007 Paul Dawkins
137
http://tutorial.math.lamar.edu/terms.aspx
9. Find all the solutions to
( )
(
)
log
log
21
2
w
w
+
−
=
. If there are no solutions clearly explain
why.
Hint : Don’t forget about the basic logarithm properties and how they can be used to combine
multiple logarithms into a single logarithm.
Step 1
We need to reduce this down to an equation with a single logarithm and to do that we first should
rewrite it a little. Upon doing that we can use the basic logarithm properties to combine the two
logarithms into a single logarithm as follows,
(
)
(
)
(
)
2
log
21
2
log
21
2
w w
w
w
−
=
−
=
Step 2
Now all we need to do is exponentiate both sides using 10 (because we’re working with the
common logarithm) and then solve for y.
(
)
(
)
(
)(
)
2
2
log
21
2
2
2
log
21
2
10
10
21
100
21
100
0
25
4
0
4,
25
w
w
w
w
w
w
w
w
w
w
w
w
−
−
=
=
−
=
−
−
=
−
+
=
⇒
= −
=
Step 3
We’re dealing with logarithms and so we need to make sure that we won’t have any problems
with any of our potential solutions. In other words, we need to make sure that if we plug either of
the two potential solutions into the original equation we won’t end up taking the logarithm of a
negative number or zero.
Upon inspection we can quickly see that if we plug in
4
w
= −
we will be taking a logarithm of a
negative number (in both of the logarithms in this case) and so
4
w
= −
can’t be a solution. On
the other hand, if we plug in
25
w
=
we won’t be taking logarithms of negative numbers and so
25
w
=
is a solution.
In summary then, the only solution to the equation is :
25
w
=
.
10. Find all the solutions to
( )
(
)
2 log
log 7
1
0
z
z
−
− =
. If there are no solutions clearly explain
why.
Calculus I
© 2007 Paul Dawkins
138
http://tutorial.math.lamar.edu/terms.aspx
Hint : This problem can be worked in the same manner as the previous two or because each term
is a logarithm an easier solution would be to use the fact that,
If log
log
then
b
b
x
y
x
y
=
=
Step 1
While we could use the same method we used in the previous couple of examples to solve this
equation there is an easier method. Because each of the terms is a logarithm and it’s all equal to
zero we can use the fact that,
If log
log
then
b
b
x
y
x
y
=
=
So, a quick rewrite of the equation gives,
( )
(
)
( )
(
)
2
2 log
log 7
1
log
log 7
1
z
z
z
z
=
−
=
−
Note that in order to use the fact above we need both logarithms to have coefficients of one and
so we also had to make quick use of one of the logarithm properties to make sure we had a
coefficient of one.
Step 2
Now all we need to do use the fact and solve for z.
2
2
7
1
7
1
0
z
z
z
z
=
−
−
+ =
In this case we’ll need to use the quadratic formula to finish this out.
( ) ( )
( )( )
( )
2
7
7
4 1 1
7
45
0.1459, 6.8541
2 1
2
z
− − ±
−
−
±
=
=
=
Step 3
We’re dealing with logarithms and so we need to make sure that we won’t have any problems
with any of our potential solutions. In other words, we need to make sure that if we plug either of
the two potential solutions into the original equation we won’t end up taking the logarithm of a
negative number or zero.
In this case it is pretty easy to plug them in and see that neither of the two potential solutions will
result in taking logarithms of negative numbers and so both are solutions to the equation.
In summary then, the solutions to the equation ar,
7
45
0.1459, 6.8541
2
z
±
=
=

Calculus I
© 2007 Paul Dawkins
139
http://tutorial.math.lamar.edu/terms.aspx
Depending upon your preferences either the exact or decimal solution can be used.
Before leaving this solution we should again make a point that not all quadratics will be the
“simple” type of quadratics that you may be used to solving from an Algebra class. They can,
and often will be, messier that those. That doesn’t mean that you can’t solve them. They are, for
all intents and purposes, identical to the types of problems you are used to working. The only real
difference is that they numbers are a little messier.
So, don’t get too excited about this kind of problem. They will happen on occasion and you are
capable of solving them!
11. Find all the solutions to
2
16
17
11
t
−
=
+
. If there are no solutions clearly explain why.
Hint : These look a little different from the first few problems in this section, but they work in
essentially the same manner. The main difference is that we’re not dealing with
power
e
or
power
10
and so there is no obvious logarithm to use and so can use any logarithm.
Step 1
First we need to isolate the term with the exponent in it on one side by itself.
2
17
5
t
−
=
Step 2
At this point we need to take the logarithm of both sides so we can use logarithm properties to get
the t out of the exponent. It doesn’t matter which logarithm we use, but if we want a decimal
value for the answer it will need to be one that we can work with. For this solution we’ll use the
natural logarithm.
Upon taking the logarithm we then need to use logarithm properties to get the t’s out of the
exponent at which point we can solve for t. Here is the rest of the work for this problem,
(
)
( )
(
) ( )
( )
( )
( )
( )
( )
2
ln 17
ln 5
2 ln 17
ln 5
ln 5
2
ln 17
ln 5
2
2.5681
ln 17
t
t
t
x
−
=
−
=
− =
= +
=
Depending upon your preferences either the exact or decimal solution can be used. Also note that
if you had used, say the common logarithm, you would get exactly the same answer.

Calculus I
© 2007 Paul Dawkins
140
http://tutorial.math.lamar.edu/terms.aspx
12. Find all the solutions to
3 8
2
7
11
w
−
− =
. If there are no solutions clearly explain why.
Hint : These look a little different from the first few problems in this section, but they work in
essentially the same manner. The main difference is that we’re not dealing with
power
e
or
power
10
and so there is no obvious logarithm to use and so can use any logarithm.
Step 1
First we need to isolate the term with the exponent in it on one side by itself.
3 8
2
18
w
−
=
Step 2
At this point we need to take the logarithm of both sides so we can use logarithm properties to get
the w out of the exponent. It doesn’t matter which logarithm we use, but if we want a decimal
value for the answer it will need to be one that we can work with. For this solution we’ll use the
natural logarithm.
Upon taking the logarithm we then need to use logarithm properties to get the w’s out of the
exponent at which point we can solve for w. Here is the rest of the work for this problem,
(
)
( )
(
) ( )
( )
( )
( )
( )
( )
3 8
ln 2
ln 18
3 8
ln 2
ln 18
ln 18
3 8
ln 2
ln 18
1
3
0.1462
8
ln 2
w
w
w
w
−
=
−
=
−
=
=
−
= −
Depending upon your preferences either the exact or decimal solution can be used. Also note that
if you had used, say the common logarithm, you would get exactly the same answer.
Compound Interest. If we put P dollars into an account that earns interest at a rate of r (written
as a decimal as opposed to the standard percent) for t years then,
a. if interest is compounded m times per year we will have,
1
t m
r
A
P
m
=
+
dollars after t years.
b. if interest is compounded continuously we will have,
r t
A
P
= e
dollars after t years.
Calculus I
© 2007 Paul Dawkins
141
http://tutorial.math.lamar.edu/terms.aspx
13. We have $10,000 to invest for 44 months. How much money will we have if we put the
money into an account that has an annual interest rate of 5.5% and interest is compounded,
Hint : There really isn’t a whole lot to these other than to identify the quantities and then plug into
the appropriate equation and compute the amount. Also note that you’ll need to make sure that
you don’t do too much in the way of rounding with the numbers here. A little rounding can lead
to very large errors in these kinds of computations.
(a) quarterly [Solution]
From the problem statement we can see that,
5.5
44
11
10000
0.055
100
12
3
P
r
t
=
=
=
=
=
Remember that the value of r must be given as a decimal, i.e. the percentage divided by 100.
Also remember that t must be in years and so we’ll need to convert to years.
For this part we are compounding interest rate quarterly and that means it will compound 4 times
per year and so we also then know that,
4
m
=
At this point all that we need to do is plug into the equation and run the numbers through a
calculator to compute the amount of money that we’ll have.
( )
(
)
(
)
11
4
44
3
3
0.055
10000 1
10000 1.01375
10000 1.221760422
12217.60
4
A
=
+
=
=
=
So, we’ll have $12,217.60 in the account after 44 months.
(b) monthly [Solution]
From the problem statement we can see that,
5.5
44
11
10000
0.055
100
12
3
P
r
t
=
=
=
=
=
Remember that the value of r must be given as a decimal, i.e. the percentage divided by 100.
Also remember that t must be in years and so we’ll need to convert to years.
For this part we are compounding interest rate monthly and that means it will compound 12
times per year and so we also then know that,
12
m
=

Calculus I
© 2007 Paul Dawkins
142
http://tutorial.math.lamar.edu/terms.aspx
At this point all that we need to do is plug into the equation and run the numbers through a
calculator to compute the amount of money that we’ll have.
( )
(
)
(
)
11
12
3
44
0.055
10000 1
10000 1.00453333
10000 1.222876562
12228.77
12
A
=
+
=
=
=
So, we’ll have $12,228.77 in the account after 44 months.
(c) continuously [Solution]
From the problem statement we can see that,
5.5
44
11
10000
0.055
100
12
3
P
r
t
=
=
=
=
=
Remember that the value of r must be given as a decimal, i.e. the percentage divided by 100.
Also remember that t must be in years and so we’ll need to convert to years.
For this part we are compounding continuously and so we won’t have an m and will be
using the other equation and all we have all we need to do the computation so,
(
)
(
)
11
0.055
0.2016666667
3
10000
10000
10000 1.223440127
12234.40
A
=
=
=
=
e
e
So, we’ll have $12,234.40 in the account after 44 months.
Compound Interest. If we put P dollars into an account that earns interest at a rate of r (written
as a decimal as opposed to the standard percent) for t years then,
c. if interest is compounded m times per year we will have,
1
t m
r
A
P
m
=
+
dollars after t years.
d. if interest is compounded continuously we will have,
r t
A
P
= e
dollars after t years.
14. We are starting with $5000 and we’re going to put it into an account that earns an annual
interest rate of 12%. How long should we leave the money in the account in order to double our
money if interest is compounded,
Hint : Identify the given quantities, plug into the appropriate equation and use the techniques
from earlier problem to solve for t.

Calculus I
© 2007 Paul Dawkins
143
http://tutorial.math.lamar.edu/terms.aspx
(a) quarterly [Solution]
From the problem statement we can see that,
12
10000
5000
0.12
100
A
P
r
=
=
=
=
Remember that the value of r must be given as a decimal, i.e. the percentage divided by 100.
Also, for this part we are compounding interest rate quarterly and that means it will compound 4
times per year and so we also then know that,
4
m
=
Plugging into the equation gives us,
(
)
4
4
0.12
10000
5000 1
5000 1.03
4
t
t
=
+
=
Using the techniques from this section we can solve for t.
( )
(
)
( )
(
)
( )
(
)
4
4
2 1.03
ln 2
ln 1.03
ln 2
4 ln 1.03
ln 2
5.8624
4 ln 1.03
t
t
t
t
=
=
=
=
=
So, we’ll double our money in approximately 5.8624 years.
(b) monthly [Solution]
From the problem statement we can see that,
12
10000
5000
0.12
100
A
P
r
=
=
=
=
Remember that the value of r must be given as a decimal, i.e. the percentage divided by 100.
Also, for this part we are compounding interest rate monthly and that means it will compound 12
times per year and so we also then know that,
12
m
=
Plugging into the equation gives us,
(
)
12
12
0.12
10000
5000 1
5000 1.01
12
t
t
=
+
=
Using the techniques from this section we can solve for t.

Calculus I
© 2007 Paul Dawkins
144
http://tutorial.math.lamar.edu/terms.aspx
( )
(
)
( )
(
)
( )
(
)
12
12
2 1.01
ln 2
ln 1.01
ln 2
12 ln 1.01
ln 2
5.8051
12 ln 1.01
t
t
t
t
=
=
=
=
=
So, we’ll double our money in approximately 5.8051 years.
(c) continuously [Solution]
From the problem statement we can see that,
12
10000
5000
0.12
100
A
P
r
=
=
=
=
Remember that the value of r must be given as a decimal, i.e. the percentage divided by 100. For
this part we are compounding continuously and so we won’t have an m and will be using the
other equation.
Plugging into the continuously compounding interest equation gives,
0.12
10000
5000
t
=
e
Now, solving this gives,
( )
( )
( )
( )
0.12
0.12
2
ln 2
ln
ln 2
0.12
ln 2
5.7762
0.12
t
t
t
t
=
=
=
=
=
e
e
So, we’ll double our money in approximately 5.7762 years.
Exponential Growth/Decay. Many quantities in the world can be modeled (at least for a short
time) by the exponential growth/decay equation.
0
k t
Q
Q
= e
If k is positive then we will get exponential growth and if k is negative we will get exponential
decay.
15. A population of bacteria initially has 250 present and in 5 days there will be 1600 bacteria
present.

Calculus I
© 2007 Paul Dawkins
145
http://tutorial.math.lamar.edu/terms.aspx
(a) Determine the exponential growth equation for this population.
Hint : We have an equation with two unknowns and two values of the population at two times so
use these values to find the two unknowns.
[Solution]
We can start off here by acknowledging that we know,
( )
( )
0
250
and
5
1600
Q
Q
=
=
If we use the first condition in the equation we get,
( )
( )
0
0
0
0
250
0
250
k
Q
Q
Q
Q
=
=
=
→
=
e
We now know the first unknown in the equation. Plugging this as well as the second condition
into the equation gives us,
( )
5
1600
5
250
k
Q
=
=
e
We can use techniques from earlier problems in this section to determine the value of k.
5
5
1600
250
1600
250
32
ln
5
5
1
32
ln
0.3712596
5
5
k
k
k
k
=
=
=
=
=
e
e
Depending upon your preferences we can use either the exact value or the decimal value. Note
however that because k is in the exponent of an exponential function we’ll need to use quite a few
decimal places to avoid potentially large differences in the value that we’d get if we rounded off
too much.
Putting all of this together the exponential growth equation for this population is,
1
32
ln
5
5
250
t
Q
=
e
(b) How long will it take for the population to grow from its initial population of 250 to
a population of 2000? [Solution]
What we’re really being asked to do here is to solve the equation,
( )
1
32
ln
5
5
2000
250
t
Q t
=
=
e

Calculus I
© 2007 Paul Dawkins
146
http://tutorial.math.lamar.edu/terms.aspx
and we know from earlier problems in this section how to do that. Here is the solution work for
this part.
( )
( )
( )
1
32
ln
5
5
32
5
2000
250
1
32
ln 8
ln
5
5
5 ln 8
5.6010
ln
t
t
t
=
=
=
=
e
It will take 5.601 days for the population to reach 2000.
Exponential Growth/Decay. Many quantities in the world can be modeled (at least for a short
time) by the exponential growth/decay equation.
0
k t
Q
Q
= e
If k is positive then we will get exponential growth and if k is negative we will get exponential
decay.
16. We initially have 100 grams of a radioactive element and in 1250 years there will be 80 grams
left.
(a) Determine the exponential decay equation for this element.
Hint : We have an equation with two unknowns and two values of the amount of the element left
at two times so use these values to find the two unknowns.
[Solution]
We can start off here by acknowledging that we know,
( )
(
)
0
100
and
1250
80
Q
Q
=
=
If we use the first condition in the equation we get,
( )
( )
0
0
0
0
100
0
100
k
Q
Q
Q
Q
=
=
=
→
=
e
We now know the first unknown in the equation. Plugging this as well as the second condition
into the equation gives us,
(
)
1250
80
1250
100
k
Q
=
=
e
We can use techniques from earlier problems in this section to determine the value of k.

Calculus I
© 2007 Paul Dawkins
147
http://tutorial.math.lamar.edu/terms.aspx
1250
1250
80 100
80
100
4
ln
1250
5
1
4
ln
0.000178515
1250
5
k
k
k
k
=
=
=
=
= −
e
e
Depending upon your preferences we can use either the exact value or the decimal value. Note
however that because k is in the exponent of an exponential function we’ll need to use quite a few
decimal places to avoid potentially large differences in the value that we’d get if we rounded off
too much.
Putting all of this together the exponential decay equation for this population is,
1
4
ln
1250
5
100
t
Q
=
e
(b) How long will it take for half of the element to decay? [Solution]
What we’re really being asked to do here is to solve the equation,
( )
1
4
ln
1250
5
50
100
t
Q t
=
=
e
and we know from earlier problems in this section how to do that. Here is the solution work for
this part.
( )
( )
1
4
ln
1250
5
1
2
4
5
50
100
1
1
4
ln
ln
2
1250
5
1250 ln
3882.8546
ln
t
t
t
=
=
=
=
e
It will take 3882.8546 years for half of the element to decay. On a side note this time is called the
half-life of the element.
(c) How long will it take until there is only 1 gram of the element left? [Solution]
In this part we’re being asked to solve the equation,
( )
1
4
ln
1250
5
1
100
t
Q t
=
=
e
and we know from earlier problems in this section how to do that. Here is the solution work for
this part.
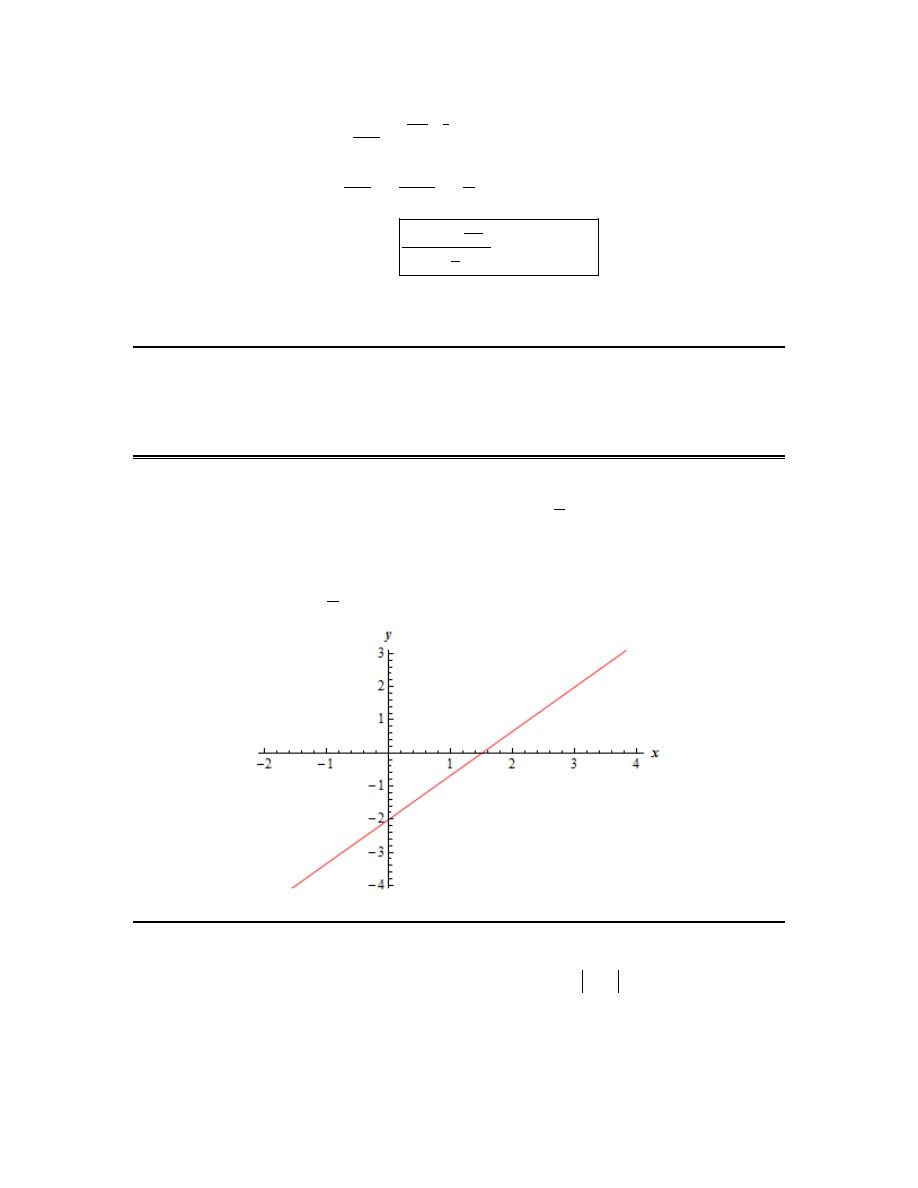
Calculus I
© 2007 Paul Dawkins
148
http://tutorial.math.lamar.edu/terms.aspx
( )
( )
1
4
ln
1250
5
1
100
4
5
1
100
1
1
4
ln
ln
100
1250
5
1250 ln
25797.1279
ln
t
t
t
=
=
=
=
e
There will only be 1 gram of the element left after 25,797.1279 years.
Review : Common Graphs
1. Without using a graphing calculator sketch the graph of
4
2
3
y
x
=
−
.
Solution
This is just a line with slope
4
3
and y-intercept
(
)
0, 2
−
so here is the graph.
2. Without using a graphing calculator sketch the graph of
( )
3
f x
x
= −
.
Hint : Recall that the graph of
(
)
g x c
+
is simply the graph of
( )
g x
shifted right by c units if
0
c
<
or shifted left by c units if
0
c
>
.
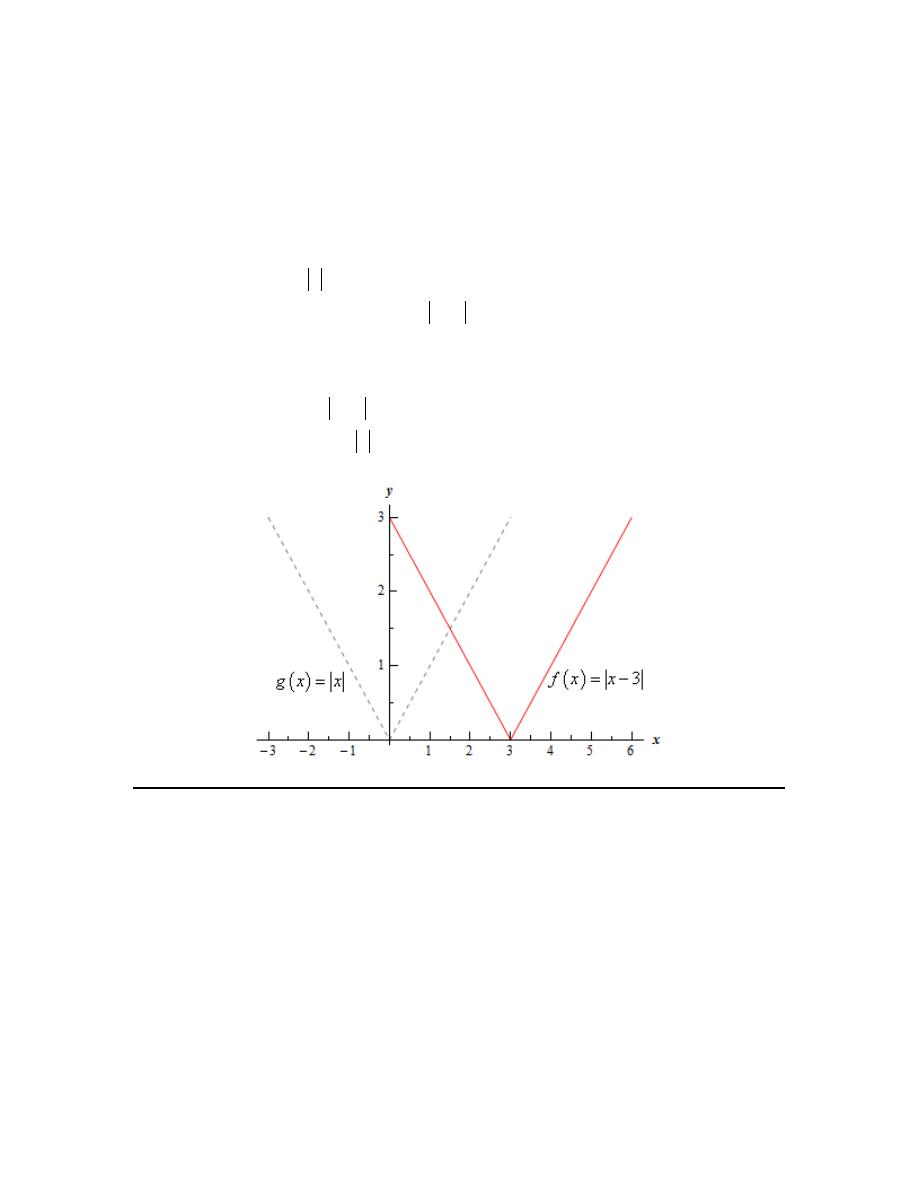
Calculus I
© 2007 Paul Dawkins
149
http://tutorial.math.lamar.edu/terms.aspx
Solution
Recall the basic Algebraic transformations. If we know the graph of
( )
g x
then the graph of
(
)
g x c
+
is simply the graph of
( )
g x
shifted right by c units if
0
c
<
or shifted left by c units if
0
c
>
.
So, in our case if
( )
g x
x
=
we can see that,
( )
(
)
3
3
f x
x
g x
= − =
−
and so the graph we’re being asked to sketch is the graph of the absolute value function shifted
right by 3 units.
Here is the graph of
( )
3
f x
x
= −
and note that to help see the transformation we have also
sketched in the graph of
( )
g x
x
=
.
3. Without using a graphing calculator sketch the graph of
( )
( )
sin
6
g x
x
=
+
.
Hint : Recall that the graph of
( )
f x
c
+
is simply the graph of
( )
f x
shifted down by c units if
0
c
<
or shifted up by c units if
0
c
>
.
Solution
Recall the basic Algebraic transformations. If we know the graph of
( )
f x
then the graph of
( )
f x
c
+
is simply the graph of
( )
f x
shifted down by c units if
0
c
<
or shifted up by c units
if
0
c
>
.
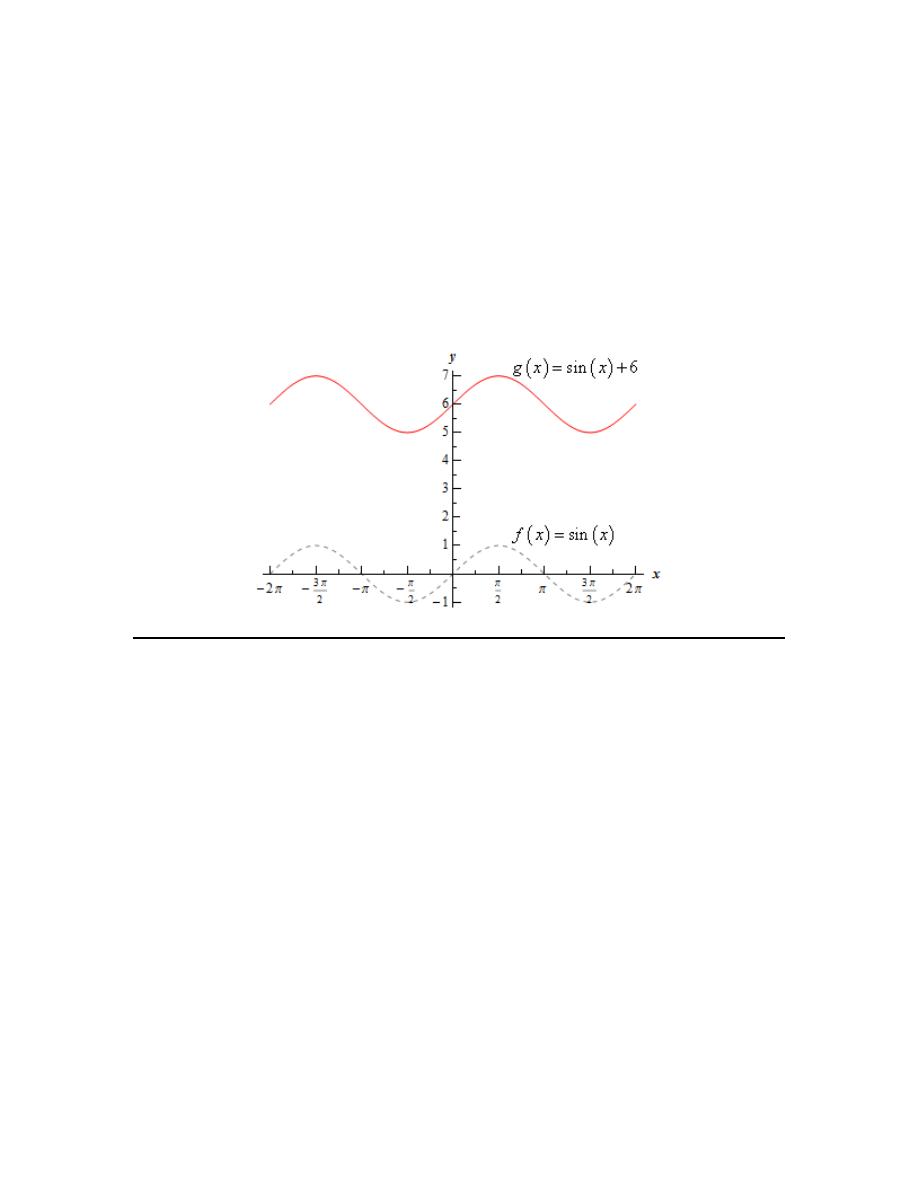
Calculus I
© 2007 Paul Dawkins
150
http://tutorial.math.lamar.edu/terms.aspx
So, in our case if
( )
( )
sin
f x
x
=
we can see that,
( )
( )
( )
sin
6
6
g x
x
f x
=
+ =
+
and so the graph we’re being asked to sketch is the graph of the sine function shifted up by 6
units.
Here is the graph of
( )
( )
sin
6
g x
x
=
+
and note that to help see the transformation we have also
sketched in the graph of
( )
( )
sin
f x
x
=
.
4. Without using a graphing calculator sketch the graph of
( )
( )
ln
5
f x
x
=
−
.
Hint : Recall that the graph of
( )
g x
c
+
is simply the graph of
( )
g x
shifted down by c units if
0
c
<
or shifted up by c units if
0
c
>
.
Solution
Recall the basic Algebraic transformations. If we know the graph of
( )
g x
then the graph of
( )
g x
c
+
is simply the graph of
( )
g x
shifted down by c units if
0
c
<
or shifted up by c units if
0
c
>
.
So, in our case if
( )
( )
ln
g x
x
=
we can see that,
( )
( )
( )
ln
5
5
f x
x
g x
=
− =
−
and so the graph we’re being asked to sketch is the graph of the natural logarithm function shifted
down by 5 units.
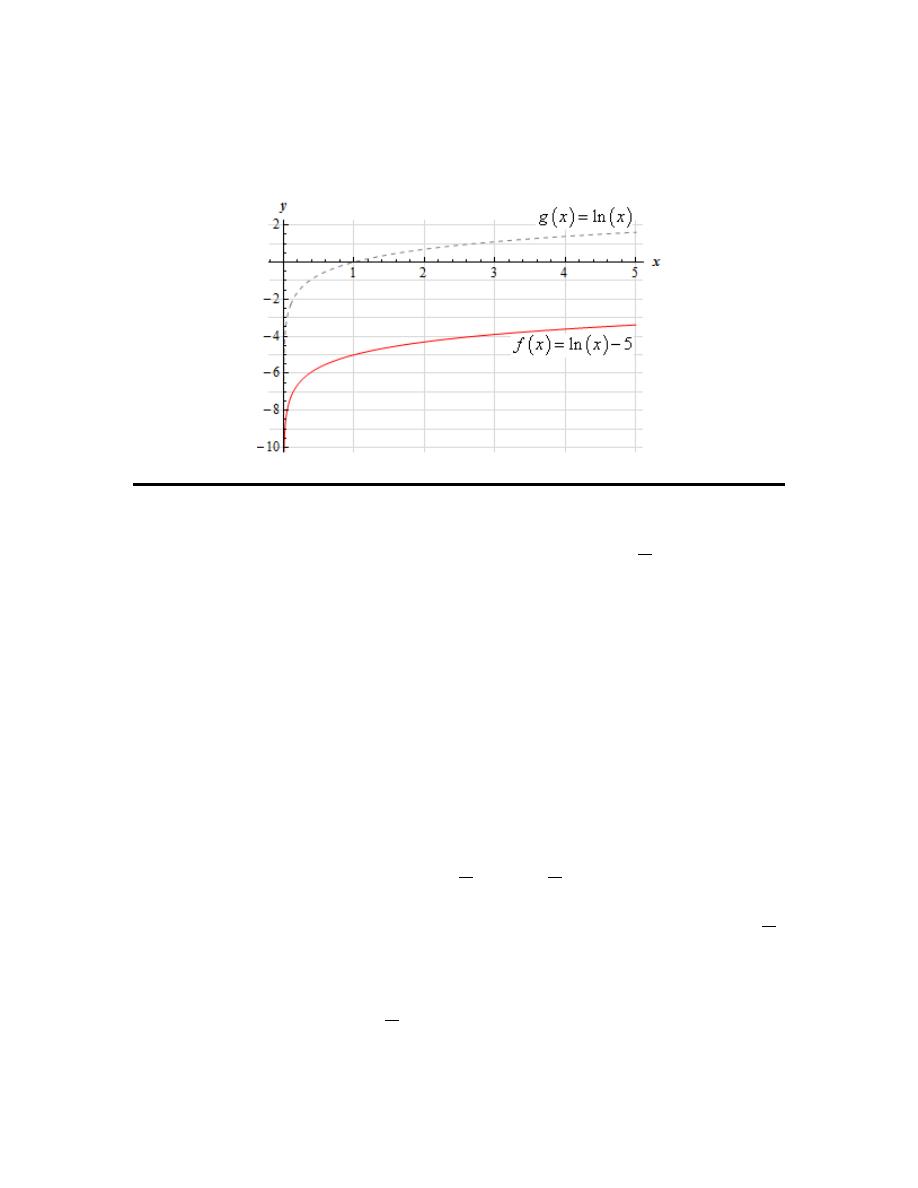
Calculus I
© 2007 Paul Dawkins
151
http://tutorial.math.lamar.edu/terms.aspx
Here is the graph of
( )
( )
ln
5
f x
x
=
−
and note that to help see the transformation we have also
sketched in the graph of
( )
( )
ln
g x
x
=
.
5. Without using a graphing calculator sketch the graph of
( )
cos
2
h x
x
π
=
+
.
Hint : Recall that the graph of
(
)
g x c
+
is simply the graph of
( )
g x
shifted right by c units if
0
c
<
or shifted left by c units if
0
c
>
.
Solution
Recall the basic Algebraic transformations. If we know the graph of
( )
g x
then the graph of
(
)
g x c
+
is simply the graph of
( )
g x
shifted right by c units if
0
c
<
or shifted left by c units if
0
c
>
.
So, in our case if
( )
( )
cos
g x
x
=
we can see that,
( )
cos
2
2
h x
x
g x
π
π
=
+
=
+
and so the graph we’re being asked to sketch is the graph of the cosine function shifted left by
2
π
units.
Here is the graph of
( )
cos
2
h x
x
π
=
+
and note that to help see the transformation we have
also sketched in the graph of
( )
( )
cos
g x
x
=
.
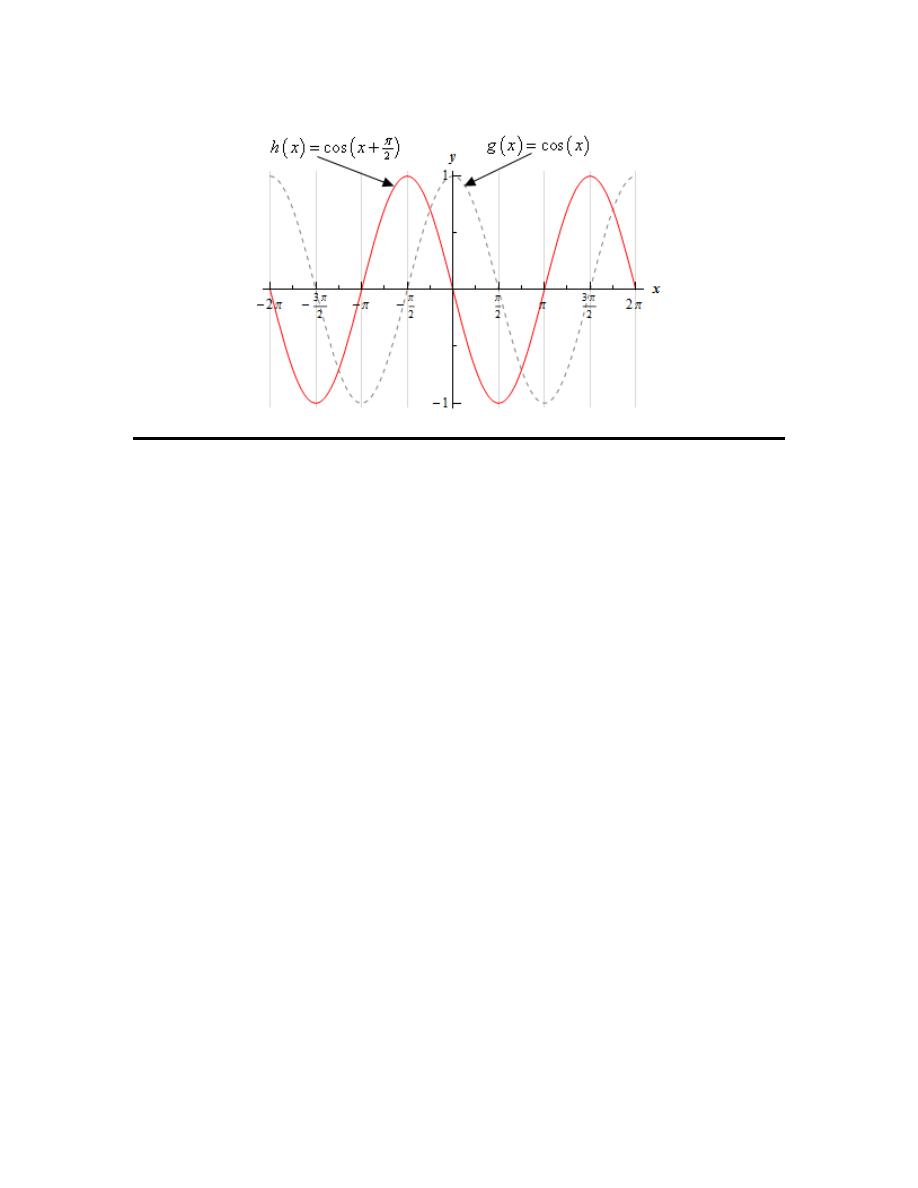
Calculus I
© 2007 Paul Dawkins
152
http://tutorial.math.lamar.edu/terms.aspx
6. Without using a graphing calculator sketch the graph of
( ) (
)
2
3
4
h x
x
=
−
+
.
Hint : The Algebraic transformations that we used to help us graph the first few graphs in this
section can be used together to shift the graph of a function both up/down and right/left at the
same time.
Solution
The Algebraic transformations we were using in the first few problems of this section can be
combined to shift a graph up/down and right/left at the same time. If we know the graph of
( )
g x
then the graph of
(
)
g x c
k
+ +
is simply the graph of
( )
g x
shifted right by c units if
0
c
<
or shifted left by c units if
0
c
>
and shifted up by k units if
0
k
>
or shifted down by k
units if
0
k
<
.
So, in our case if
( )
2
g x
x
=
we can see that,
( ) (
)
(
)
2
3
4
3
4
h x
x
g x
=
−
+ =
− +
and so the graph we’re being asked to sketch is the graph of
( )
2
g x
x
=
shifted right by 3 units
and up by 4 units.
Here is the graph of
( ) (
)
2
3
4
h x
x
=
−
+
and note that to help see the transformation we have
also sketched in the graph of
( )
2
g x
x
=
.
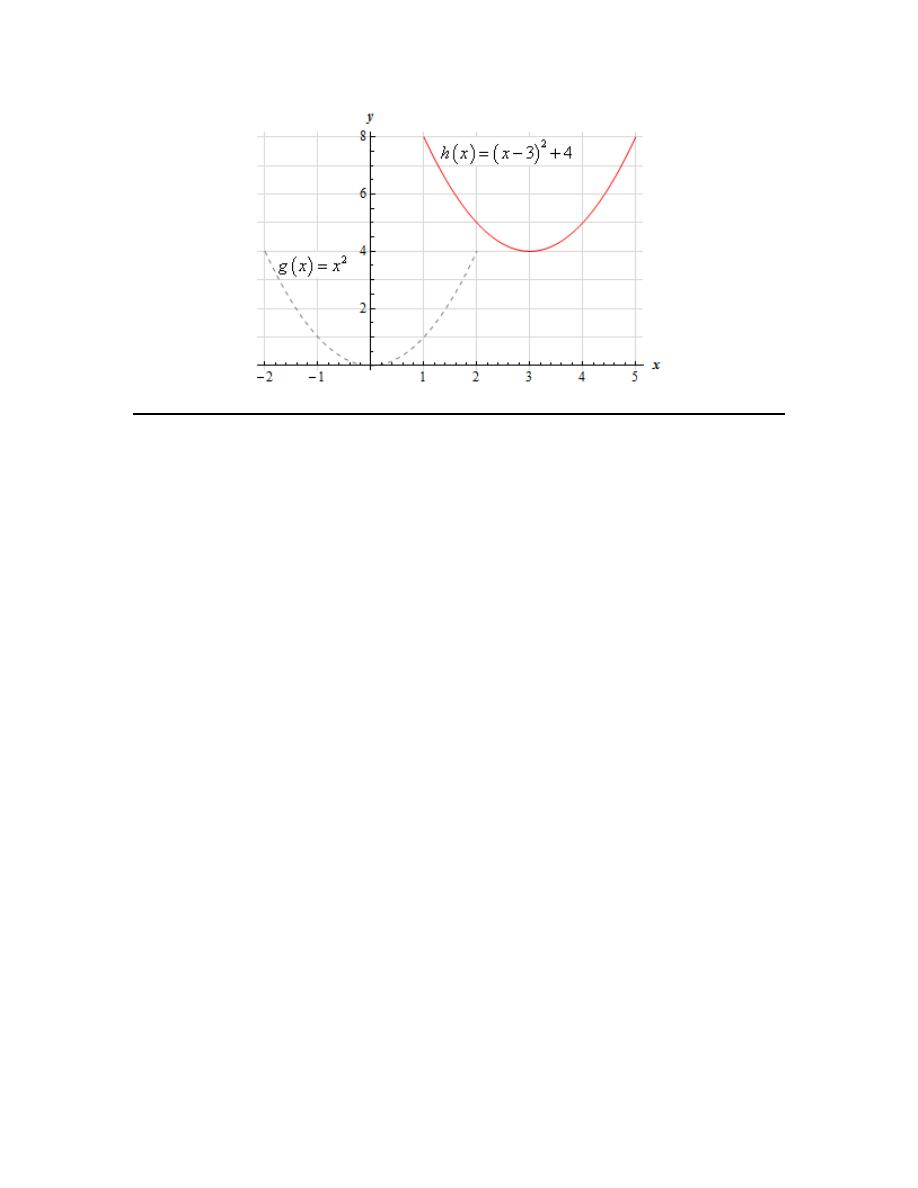
Calculus I
© 2007 Paul Dawkins
153
http://tutorial.math.lamar.edu/terms.aspx
7. Without using a graphing calculator sketch the graph of
( )
2
3
x
W x
+
=
−
e
.
Hint : The Algebraic transformations that we used to help us graph the first few graphs in this
section can be used together to shift the graph of a function both up/down and right/left at the
same time.
Solution
The Algebraic transformations we were using in the first few problems of this section can be
combined to shift a graph up/down and right/left at the same time. If we know the graph of
( )
g x
then the graph of
(
)
g x c
k
+ +
is simply the graph of
( )
g x
shifted right by c units if
0
c
<
or shifted left by c units if
0
c
>
and shifted up by k units if
0
k
>
or shifted down by k
units if
0
k
<
.
So, in our case if
( )
x
g x
= e
we can see that,
( )
(
)
2
3
2
3
x
W x
g x
+
=
− =
+ −
e
and so the graph we’re being asked to sketch is the graph of
( )
x
g x
= e
shifted left by 2 units and
down by 3 units.
Here is the graph of
( )
2
3
x
W x
+
=
−
e
and note that to help see the transformation we have also
sketched in the graph of
( )
x
g x
= e
.
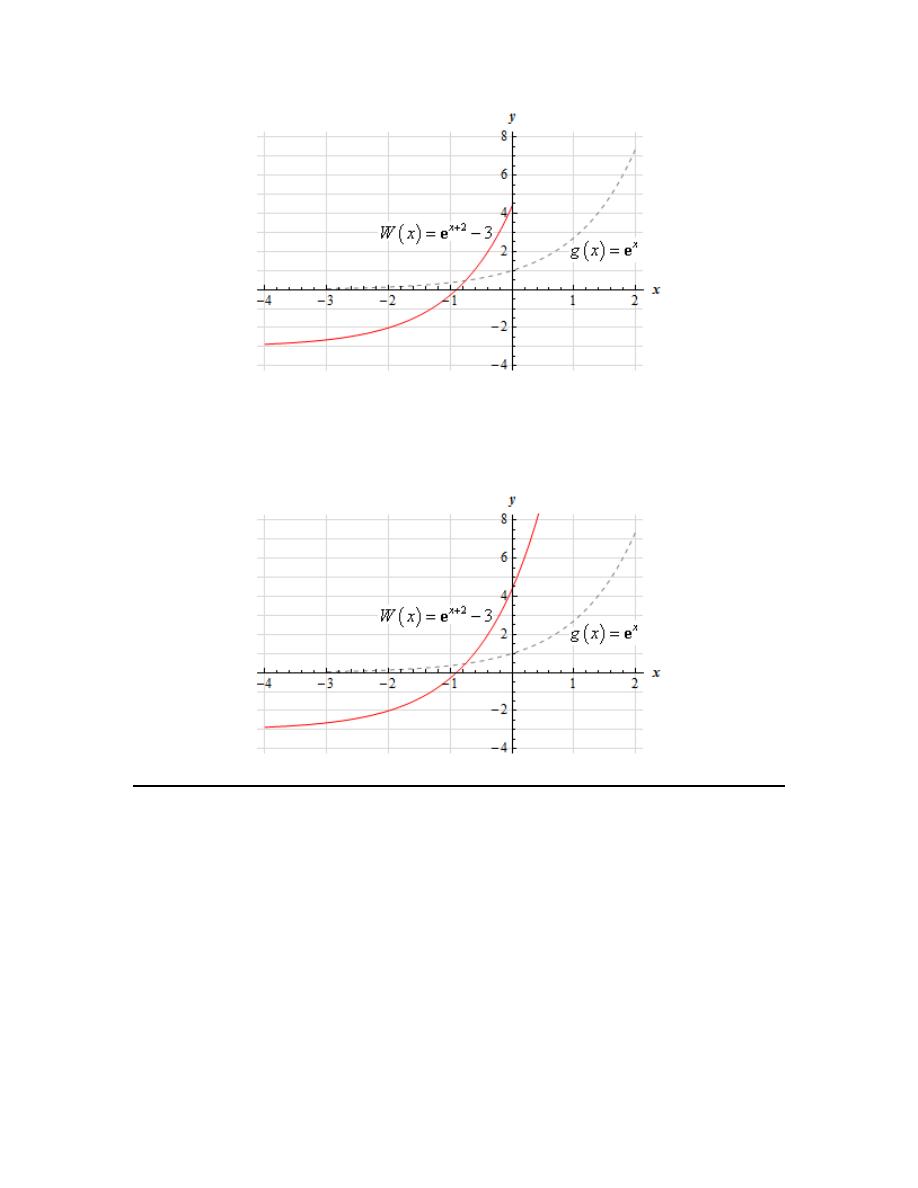
Calculus I
© 2007 Paul Dawkins
154
http://tutorial.math.lamar.edu/terms.aspx
In this case the resulting sketch of
( )
W x
that we get by shifting the graph of
( )
g x
is not really
the best, as it pretty much cuts off at
0
x
=
so in this case we should probably extend the graph of
( )
W x
a little. Here is a better sketch of the graph.
8. Without using a graphing calculator sketch the graph of
( ) (
)
2
1
2
f y
y
=
−
+
.
Hint : The Algebraic transformations can also be used to help us sketch graphs of functions in the
form
( )
x
f y
=
, but we do need to remember that we’re now working with functions in which
the variables have been interchanged.
Solution
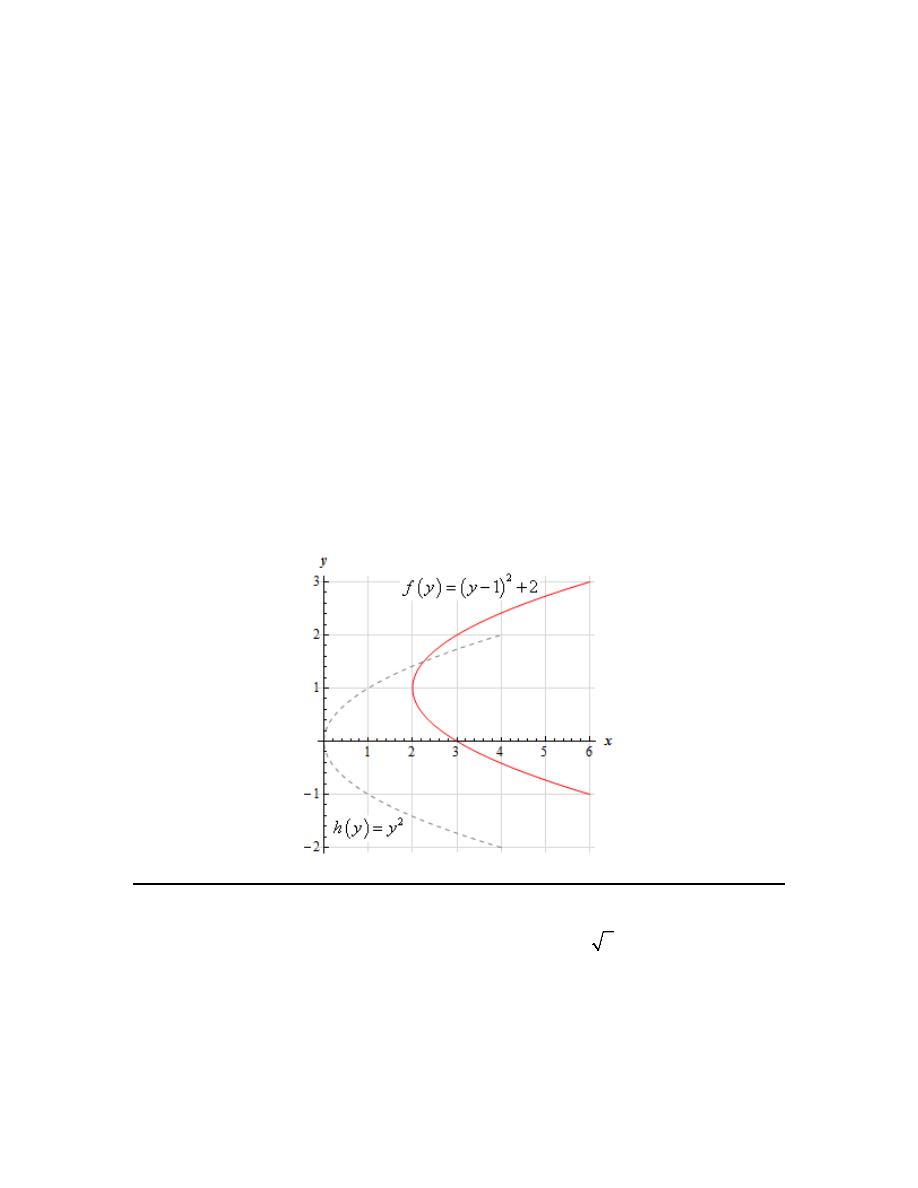
Calculus I
© 2007 Paul Dawkins
155
http://tutorial.math.lamar.edu/terms.aspx
Even though our function is in the form
( )
x
f y
=
we can still use the Algebraic transformations
to help us sketch this graph. We do need to be careful however and remember that we’re working
with interchanged variables and so the transformations will also switch.
In this case if we know the graph of
( )
h y
then the graph of
(
)
h y c
k
+ +
is simply the graph of
( )
h x
shifted up by c units if
0
c
<
or shifted down by c units if
0
c
>
and shifted right by k
units if
0
k
>
or shifted left by k units if
0
k
<
.
So, in our case if
( )
2
h y
y
=
we can see that,
( ) (
)
(
)
2
1
2
1
2
f y
y
h y
=
−
+ =
− +
and so the graph we’re being asked to sketch is the graph of
( )
2
h y
y
=
shifted up by 1 units and
right by 2 units.
Here is the graph of
( ) (
)
2
1
2
f y
y
=
−
+
and note that to help see the transformation we have
also sketched in the graph of
( )
2
h y
y
=
.
9. Without using a graphing calculator sketch the graph of
( )
R x
x
= −
.
Hint : Recall that the graph of
( )
f x
−
is the graph of
( )
f x
reflected about the x-axis.
Solution
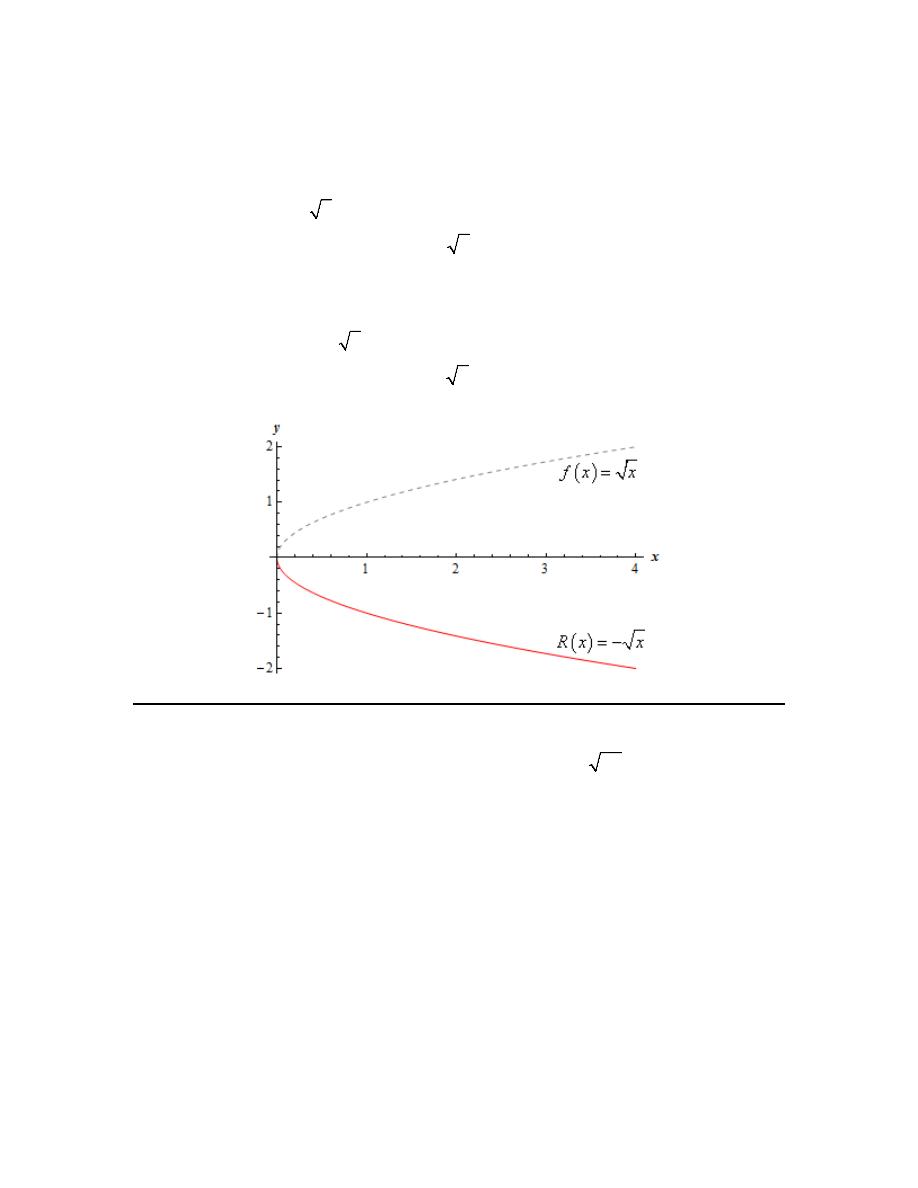
Calculus I
© 2007 Paul Dawkins
156
http://tutorial.math.lamar.edu/terms.aspx
Recall the basic Algebraic transformations. If we know the graph of
( )
f x
then the graph of
( )
f x
−
is simply the graph of
( )
f x
reflected about the x-axis.
So, in our case if
( )
f x
x
=
we can see that,
( )
( )
R x
x
f x
= −
= −
and so the graph we’re being asked to sketch is the graph of the square root function reflected
about the x-axis.
Here is the graph of
( )
R x
x
= −
(the solid curve) and note that to help see the transformation
we have also sketched in the graph of
( )
f x
x
=
(the dashed curve).
10. Without using a graphing calculator sketch the graph of
( )
g x
x
= −
.
Hint : Recall that the graph of
( )
f
x
−
is the graph of
( )
f x
reflected about the y-axis.
Solution
First, do not get excited about the minus sign under the root. We all know that we won’t get real
numbers if we take the square root of a negative number, but that minus sign doesn’t necessarily
mean that we’ll be taking the square root of negative numbers. If we plug in positive value of x
then clearly we will be taking the square root of negative numbers, but if we plug in negative
values of x we will now be taking the square root of positive numbers and so there really is
nothing wrong with the function as written. We’ll just be using a different set of x’s than what we
may be used to working with when dealing with square roots.
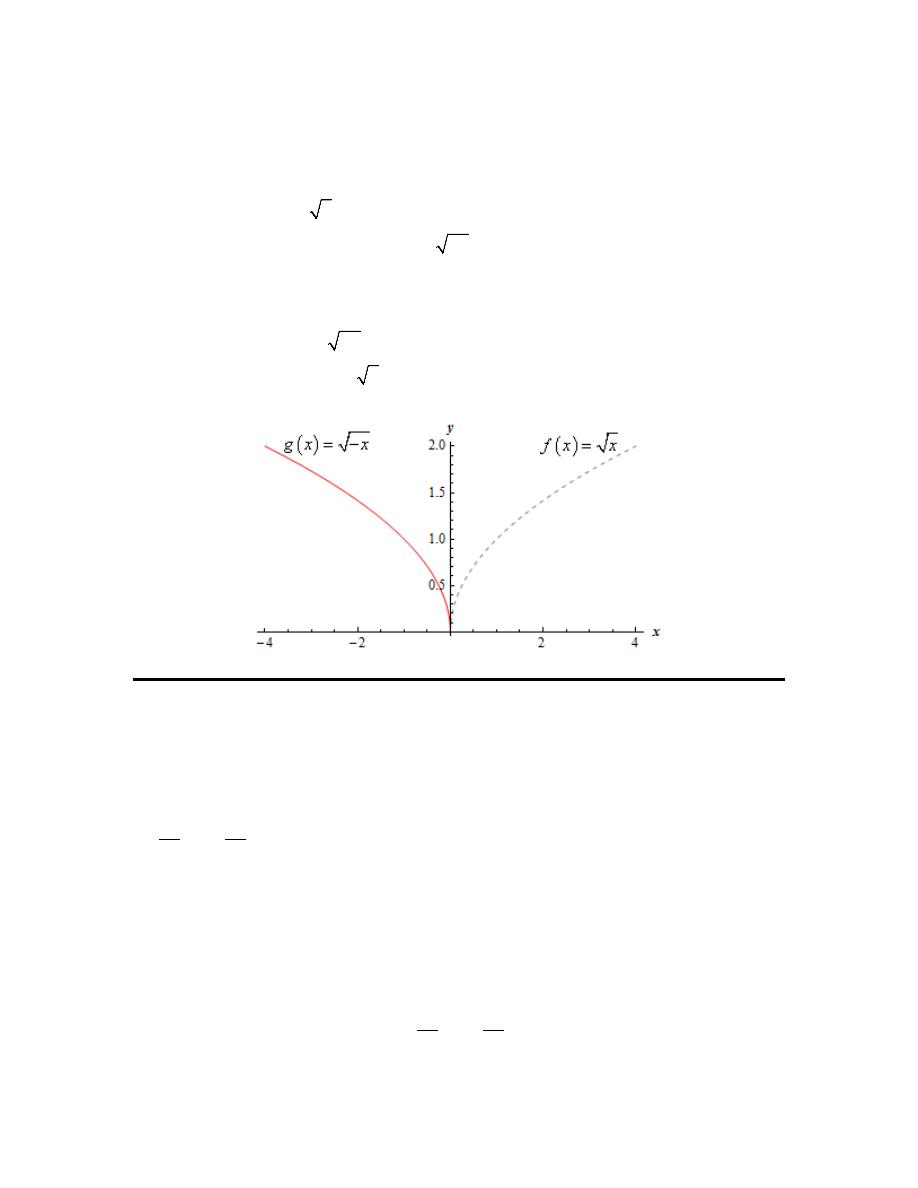
Calculus I
© 2007 Paul Dawkins
157
http://tutorial.math.lamar.edu/terms.aspx
Now, recall the basic Algebraic transformations. If we know the graph of
( )
f x
then the graph
of
( )
f
x
−
is simply the graph of
( )
f x
reflected about the y-axis.
So, in our case if
( )
f x
x
=
we can see that,
( )
( )
g x
x
f
x
= − =
−
and so the graph we’re being asked to sketch is the graph of the square root function reflected
about the y-axis.
Here is the graph of
( )
g x
x
= −
and note that to help see the transformation we have also
sketched in the graph of
( )
f x
x
=
.
11. Without using a graphing calculator sketch the graph of
( )
2
2
3
4
h x
x
x
=
−
+
.
Hint : Recall that the graph of
( )
2
f x
ax
bx c
=
+
+
is the graph of a parabola with vertex
,
2
2
b
b
f
a
a
−
−
that opens upwards if
0
a
>
and downwards if
0
a
<
and y-intercept at
( )
0, c
.
Solution
We know that the graph of
( )
2
f x
ax
bx c
=
+
+
will be a parabola that opens upwards if
0
a
>
and opens downwards if
0
a
<
. We also know that its vertex is at,
,
2
2
b
b
f
a
a
−
−
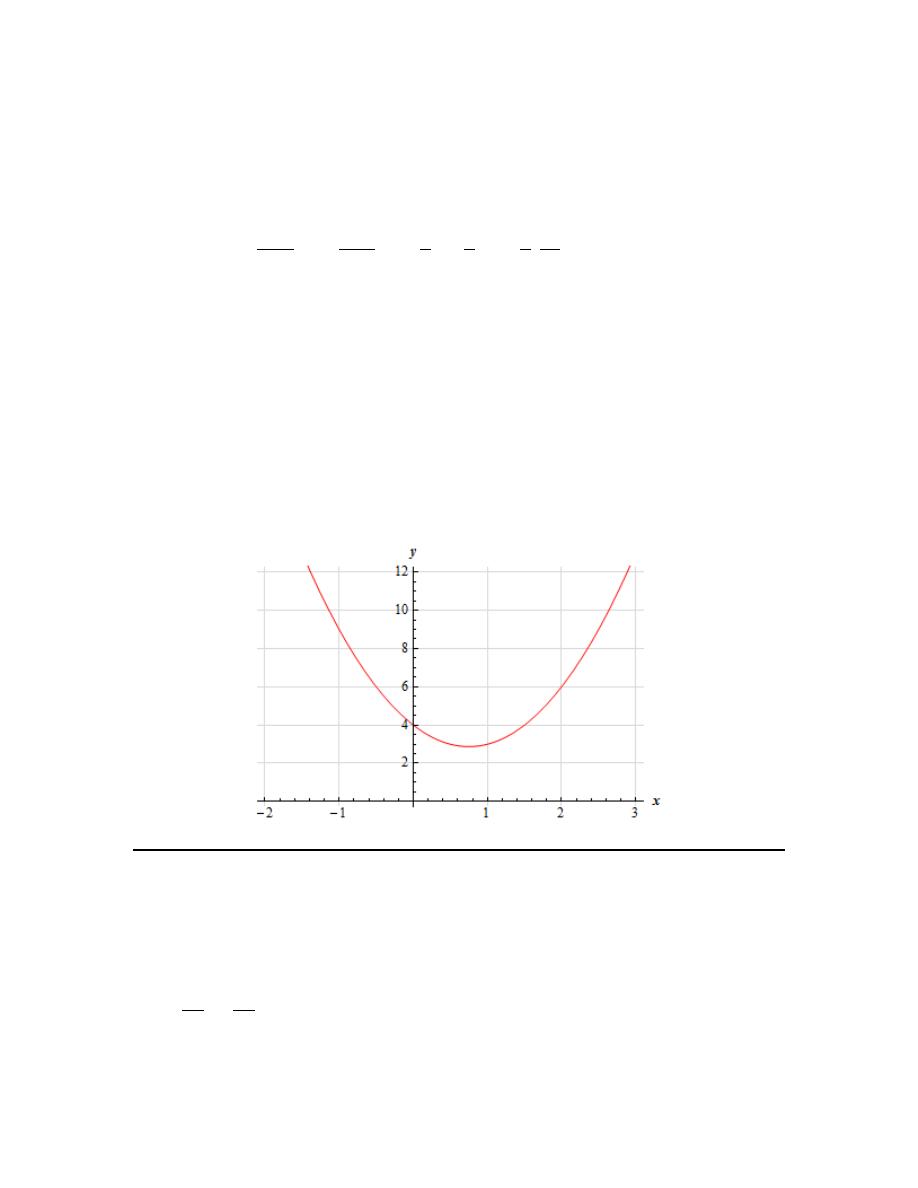
Calculus I
© 2007 Paul Dawkins
158
http://tutorial.math.lamar.edu/terms.aspx
The y-intercept of the parabola is the point
( )
(
)
( )
0,
0
0,
f
c
=
and the x-intercepts (if any) are
found by solving
( )
0
f x
=
So, or our case we know we have a parabola that opens upwards and that its vertex is at,
( )
( )
(
)
3
3
3
3
3 23
,
,
,
0.75, 2.875
2 2
2 2
4
4
4 8
f
f
−
−
−
−
=
=
=
We can also see that the y-intercept is
( )
0, 4
. Because the vertex is above the x-axis and the
parabola opens upwards we can see that there will be no x-intercepts.
It is usually best to have at least one point on either side of the vertex and we know that parabolas
are symmetric about the vertical line running through the vertex. Therefore, because we know
that the y-intercept is 0.75 units to the left of the vertex that we must also have a point that is 0.75
to the right of the vertex with the same y-value and this point is :
(
)
1.5, 4
.
Here is a sketch of this parabola.
12. Without using a graphing calculator sketch the graph of
( )
2
4
8
3
f y
y
y
= −
+
+
.
Hint : Recall that the graph of
( )
2
f y
ay
by
c
=
+
+
is the graph of a parabola with vertex
,
2
2
b
b
f
a
a
−
−
that opens towards the right if
0
a
>
and towards the left if
0
a
<
and x-
intercept at
( )
, 0
c
.
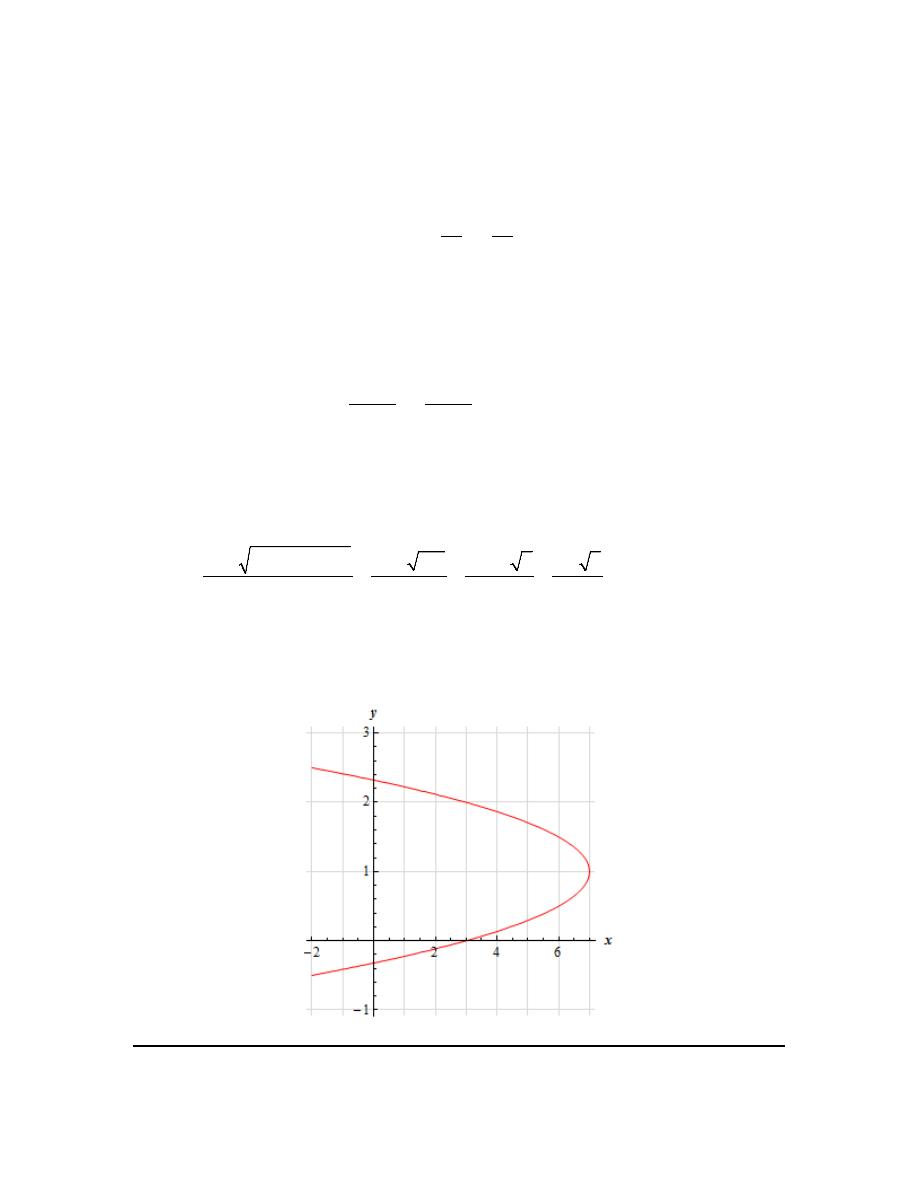
Calculus I
© 2007 Paul Dawkins
159
http://tutorial.math.lamar.edu/terms.aspx
Solution
We know that the graph of
( )
2
f y
ay
by c
=
+
+
will be a parabola that opens towards the right
if
0
a
>
and opens towards the left if
0
a
<
. We also know that its vertex is at,
,
2
2
b
b
f
a
a
−
−
The x-intercept of the parabola is the point
( )
(
)
( )
0 , 0
, 0
f
c
=
and the x-intercepts (if any) are
found by solving
( )
0
f y
=
So, or our case we know we have a parabola that opens towards the left and that its vertex is at,
( )
( )
( )
(
)
( )
8
8
,
1 ,1
7,1
2
4
2
4
f
f
−
−
=
=
−
−
We can also see that the y-intercept is
( )
3, 0
.
To find the y-intercepts all we need to do is solve :
2
4
8
3
0
y
y
−
+
+ =
.
( )( )
( )
2
8
8
4
4 3
8
112
8 4 7
2
7
0.3229, 2.3229
2
4
8
8
2
y
− ±
− −
− ±
− ±
±
=
=
=
=
= −
−
−
−
So, the two y-intercepts are :
(
)
0, 0.3229
−
and
(
)
0, 2.3229
.
Here is a sketch of this parabola.
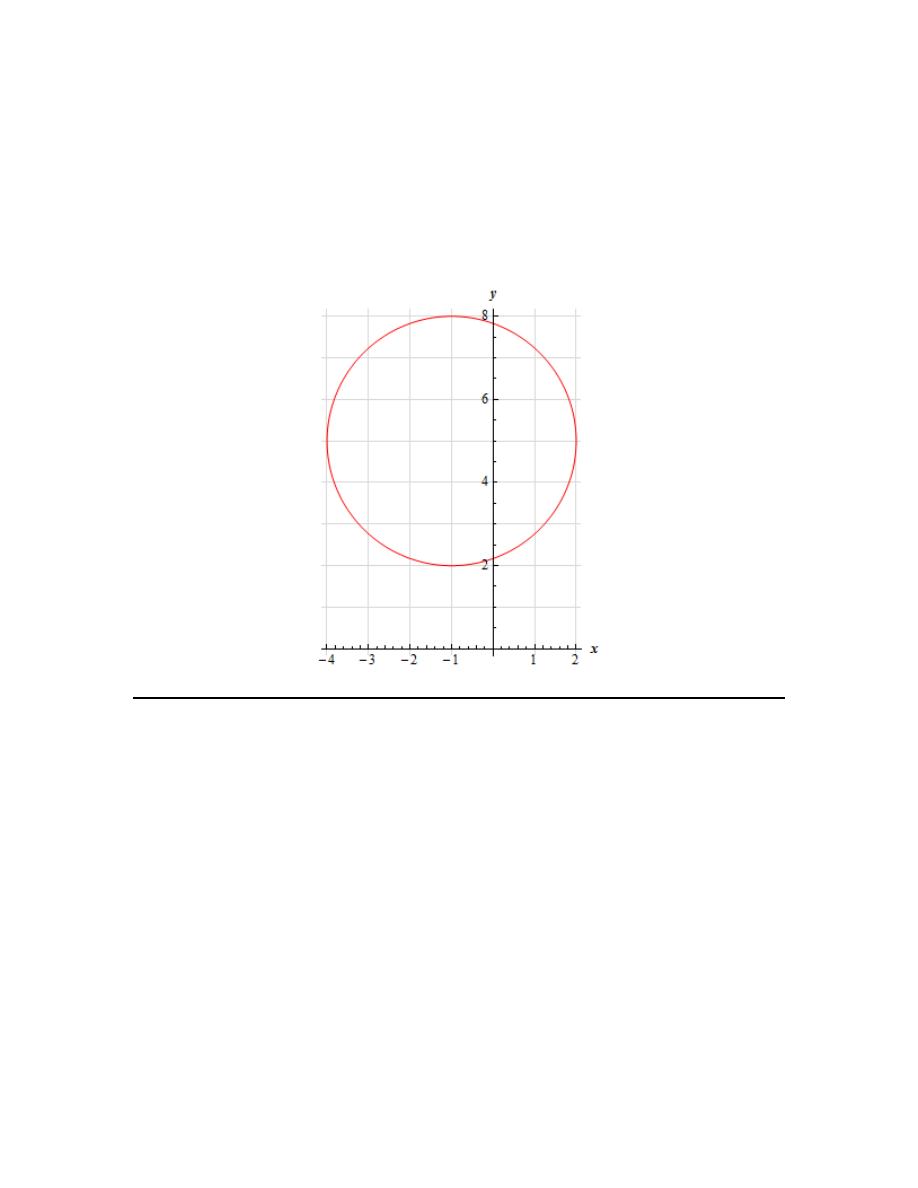
Calculus I
© 2007 Paul Dawkins
160
http://tutorial.math.lamar.edu/terms.aspx
13. Without using a graphing calculator sketch the graph of
(
) (
)
2
2
1
5
9
x
y
+
+
−
=
.
Solution
This is just a circle in standard form and so we can see that it has a center of
(
)
1, 5
−
and a radius
of 3. Here is a quick sketch of the circle.
14. Without using a graphing calculator sketch the graph of
2
2
4
6
87
0
x
x
y
y
−
+
−
−
=
.
Hint : Complete the square a couple of times to put this into standard from. This will allow you
to identify the type of graph this will be .
Solution
The first thing that we should do is complete the square on the x’s and the y’s to see what we’ve
got here. This could be a circle, ellipse, or hyperbola and completing the square a couple of times
will put it into standard form and we’ll be able to identify the graph at that point.
Here is the completing the square work.

Calculus I
© 2007 Paul Dawkins
161
http://tutorial.math.lamar.edu/terms.aspx
(
)
(
)
(
) (
)
(
) (
)
2
2
2
2
2
2
4
4 4
6
9 9
87
0
2
3
100
0
2
3
100
x
x
y
y
x
y
x
y
−
+ − +
−
+ − −
=
−
+
−
−
=
−
+
−
=
So, we’ve got a circle with center
( )
2, 3
and radius 10. Here is a sketch of the circle.
15. Without using a graphing calculator sketch the graph of
(
)
2
2
25
2
1
16
y
x
+
+
=
.
Solution
This is just an ellipse that is almost in standard form. With a little rewrite we can put it into
standard form as follows,
(
)
2
2
2
1
1
4
25
x
y
+
+
=
We can now see that the ellipse has a center of
(
)
2, 0
−
while the left/right most points will be
1
0.2
5
=
units away from the center and the top/bottom most points will be 2 units away from the
center. Here is a quick sketch of the ellipse.
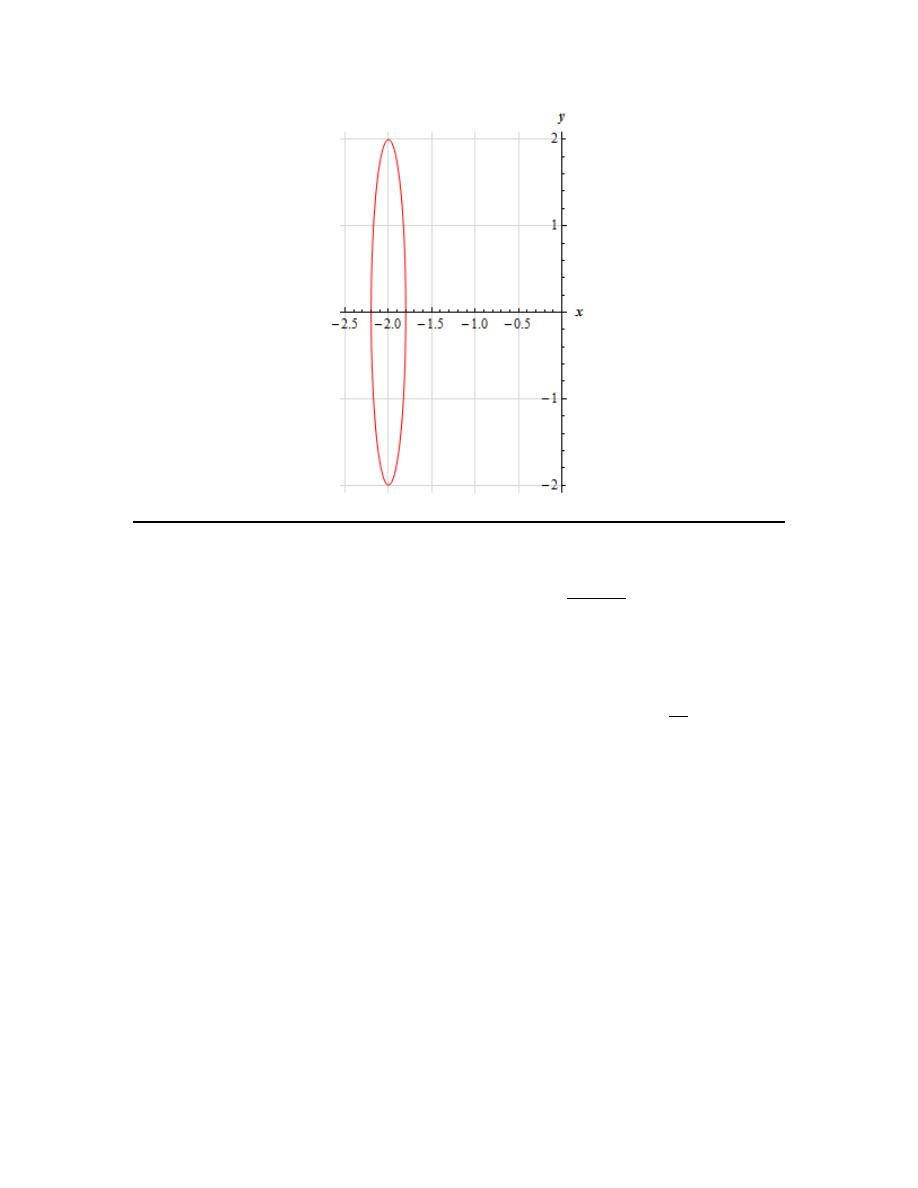
Calculus I
© 2007 Paul Dawkins
162
http://tutorial.math.lamar.edu/terms.aspx
16. Without using a graphing calculator sketch the graph of
(
)
2
2
6
1
9
y
x
−
+
=
.
Solution
This is just an ellipse that is in standard form (if it helps rewrite the first term as
2
1
x
) and so we
can see that it has a center of
( )
0, 6
while the left/right most points will be 1 unit away from the
center and the top/bottom most points will be 3 units away from the center.
Here is a quick sketch of the ellipse.
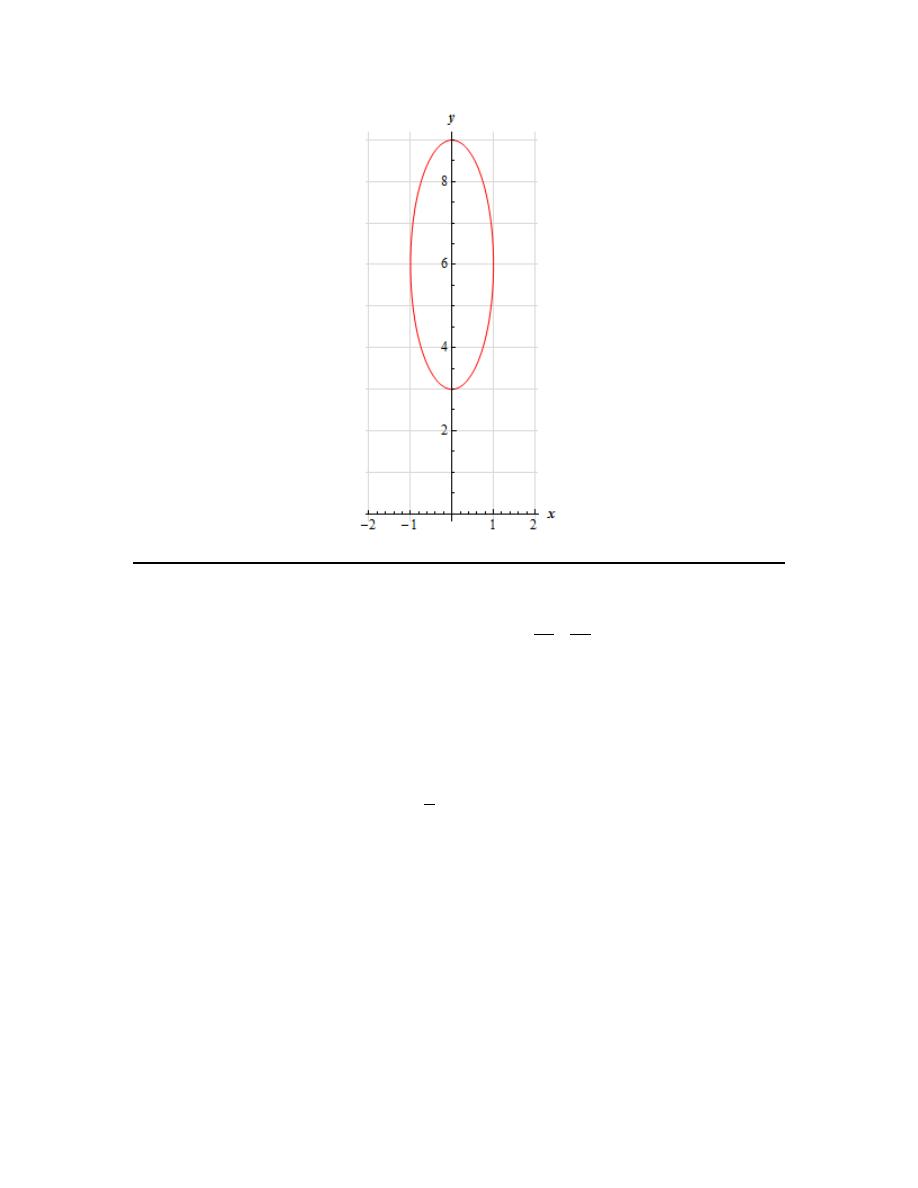
Calculus I
© 2007 Paul Dawkins
163
http://tutorial.math.lamar.edu/terms.aspx
17. Without using a graphing calculator sketch the graph of
2
2
1
36
49
x
y
−
=
.
Solution
This is a hyperbola in standard form with the minus sign in front of the y term and so will open
right and left. The center of the hyperbola is at
( )
0, 0
, the two vertices are at
(
)
6, 0
−
and
( )
6, 0
, and the slope of the two asymptotes are
7
6
±
.
Here is a quick sketch of the hyperbola.
Calculus I
© 2007 Paul Dawkins
164
http://tutorial.math.lamar.edu/terms.aspx
18. Without using a graphing calculator sketch the graph of
(
) (
)
2
2
4
2
1
16
x
y
+
+
−
=
.
Solution
This is a hyperbola in standard form with the minus sign in front of the x term and so will open up
and down. The center of the hyperbola is at
(
)
4, 2
− −
, the two vertices are at
(
)
1, 1
− −
and
(
)
1, 3
− −
, and the slope of the two asymptotes are
1
4
±
.
Here is a quick sketch of the hyperbola.

Calculus I
© 2007 Paul Dawkins
165
http://tutorial.math.lamar.edu/terms.aspx
