diagnosis pres

Statistics in Screening/Diagnosis

Annie Herbert
Research & Development Department
Salford Royal Hospitals NHS Foundation Trust
annie.herbert@manchester.ac.uk
0161 2064567

Outline

Intro: Design, recording results

Sensitivity

Specificity

Continuous variables: ROC curves

Predictive values


Likelihood ratio

Bias

Introduction: diagnostic test

Introduction: assessing a diagnostic test

All participants

Index test

Reference test

2 x 2 Table of results

+
-
+
-
90
10
60
240
2 x 2 Table of results


Reference test
Index test

Introduction: 2x2 table of results

• ‘TRUTH’
• (by Reference test
• – Gold standard)

• Total

• +
• -

• TEST RESULT

• (by Index test)
• +
• True
• Positive
• False
• Positive
• Total said to have disease


• -
• False Negative
• True Negative
• Total said not to have disease
• Total

• Total with disease

• Total without disease

Hypothetical example – Breast cancer screening study

Gold standard:
Mammography

Cheaper/more convenient option:

GP examination

Breast cancer screening results

• ‘TRUTH’
• (by mammography)


• Total

• +

• -

• TEST RESULT (by GP Exam)

• +
• 95
• 45
• 140

• -

• 5
• 855
• 860
• Total

• 100

• 900
• 1000


Sensitivity - Definition
What proportion of people who have the condition are identified as positive by the test?

If a test has a high sensitivity, most people with the condition are picked up by the test.

+ve test

Have condition

Sensitivity - Calculation

• ‘TRUTH’
• (by gold standard)

• +

• -
• TEST RESULT
• +
• a
• b

• -

• c
• d
• Total


• a+c
• b+d

Sensitivity = a/(a+c)

Sensitivity - Example

• Mammography

• +
• -
• GP Exam
• +
• 95
• 45

• -

• 5
• 855
• Total


• 100
• 900

Sensitivity = 95/100 = 0.95

I.e. 95% of patients diagnosed as having breast cancer by the mammogram are picked up by GP examination.

Specificity - Definition

What proportion of people who don’t have the condition are identified as negative by the test?

If a test has a high specificity, most people without the condition are ruled out by the test.

-ve test

Don’t have condition

Specificity - Calculation

• ‘TRUTH’
• (by gold standard)

• +

• -
• TEST RESULT
• +
• a
• b


• -
• c
• d
• Total

• a+c

• b+d

Specificity = d/(b+d)

Specificity - Example

• Mammography

• +
• -
• GP Exam
• +
• 95
• 45


• -
• 5
• 855
• Total

• 100

• 900

Specificity = 855/900 = 0.95

I.e. 95% of patients diagnosed as not having breast cancer by the mammogram are ruled out by GP examination.

Sensitivity & Specificity - Notes

It is essential to have a confirmed ‘true’ diagnosis (+ve or -ve). The accuracies of sensitivity and specificity are only as good as that of the gold standard.

Sensitivity and specificity are estimated from a sample, and so should be accompanied by confidence intervals to convey amount of uncertainty.
(StatsDirect: Analysis -> Proportions -> Single)

Tests based on continuous variables (1)

One or more continuous variables can be a marker for a condition, where a very low/high level indicates a low/high likelihood of having the condition.

A cut-off level can be determined where having higher/lower than that cut-off indicates a positive test result.


Different cut-off points will give different sensitivity/specificity values.

Tests based on continuous variables (2)

E.g. Creatinekinase in patients with unstable angina or acute myocardial infarction
Data of Frances Boa, from ‘An introduction to Medical Statistics’ by Martin Bland

Tests based on continuous variables (3)

Sensitivity
= 27/27
= 1.0

• Truth

• +
• -
• Test
• +
• 27
• 54


• -
• 0
• 39
• Total

• 27

• 93

Specificity

= 39/93
= 0.42

Cut-off level at 80

Tests based on continuous variables (4)

Sensitivity

= 26/27
= 0.96

• Truth

• +
• -
• Test
• +
• 26
• 35

• -

• 1
• 58
• Total

• 27

• 93

Specificity

= 58/93
= 0.62

Cut-off level at 100

The trade-off
Plot sensitivity against (1-specificity) to get the ROC (‘receiver operating characteristic’) curve.

Ideally want high sensitivity and high specificity (but increase in one is at expense of the other).

Also requires some clinical judgement,

e.g. Likely considered better to send women without breast cancer to have a mammogram than give those with breast cancer the all clear.

Check sensitivity and specificity values in a new sample.

ROC curve

ROC plot for MI data

0.00

0.25

0.50

0.75

1.00

0.00

0.25

0.50

0.75

1.00

Sensitivity
1-Specificity

The diagonal line represents

sensitivity = specificity,
i.e. taking the test is as good as flipping a coin.

Sensitivity = 1.0

Specificity = 1.0


Sensitivity = 0.0
Specificity = 0.0

Optimum cut-off

MI data:

‘Optimum’ cut-off point selected = 302

Sensitivity (95% CI) = 0.93 (0.76 to 0.99)

Specificity (95% CI) = 0.97 (0.91 to 0.99)

Note: ‘optimum’ assumes sensitivity and specificity
of equal concern.

Area under the ROC curve

Area under the ROC curve can be between 0 (sensitivity and specificity always 0.0) and 1 (sensitivity and specificity always 1.0).

Can be useful for comparing two tests.

MI data: Area under curve is an estimate of ‘probability that creatinekinase of random person with MI will be higher than for random person with angina’.


The difference between sensitivity & specificity and predictive values…
Sensitivity & Specificity: How good is the test at making the right diagnosis?

Predictive Values: Once diagnosis has been made, how reliable is it?

Positive Predictive Value - Definition
Proportion of those with a positive test result that actually have the condition.

If a test has a high positive predictive value, if someone tests positive for the condition, there is a high probability that they have it.

Have condition

Test positive

Positive Predictive Value - Calculation

PPV
= a/(a+b)

• ‘TRUTH’

• Total

• +

• -

• TEST RESULT

• +
• a
• b
• a+b

• -

• c
• d
• c+d

Positive Predictive Value - Example

PPV
= 95/140
= 0.68

• ‘TRUTH’

• (by mammogram)

• Total

• +
• -

• TEST RESULT (by GP Exam)

• +
• 95
• 45
• 140

• -

• 5
• 855
• 860
I.e. 68% of patients who test positive for breast cancer by GP examination could be expected to test positive by mammogram.


Negative Predictive Value - Definition
Proportion of those with a negative test result that really don’t have the condition.

If a test has a high negative predictive value, if someone tests negative for the condition, there is a high probability that they don’t have it.

Don’t have condition

Test negative

Negative Predictive Value - Calculation

NPV
= d/(c+d)

• ‘TRUTH’

• Total

• +

• -


• TEST RESULT
• +
• a
• b
• a+b

• -

• c
• d
• c+d

Negative Predictive Value - Example

NPV
= 855/860
= 0.99

• ‘TRUTH’

• (by mammogram)


• Total

• +

• -

• TEST RESULT (by GP Exam)

• +
• 95
• 45
• 140

• -

• 5
• 855
• 860
I.e. 99% of patients who test negative for breast cancer by GP examination would be expected to test negative by mammogram.

Prevalence

What proportion of people in a cohort have the disease? E.g. “The prevalence of breast cancer in females over 40 years of age is approximately 1.5%”.

‘Prevalence’ is not the same as ‘incidence’.

Sensitivity & specificity values are unaffected by prevalence, though predictive values are.

E.g. Test with 95% sensitivity and 95% specificity:

MeReC Briefing: supplement to issue 30



Example: Self administered cognitive screening test (TYM) for detection of Alzheimer’s disease: cross sectional study, Brown et al, June 2009
“A score of 42/50 had a sensitivity of 93% and specificity of 86% in the diagnosis of Alzheimer’s disease. The TYM was more sensitive in detection of Alzheimer’s disease than the mini-mental examination, detecting 93% of patients compared with 52% for the mini-mental state examination. The negative and positive predictive values of the TYM with the cut off of 42 were 99% and 42% with a prevalence of Alzheimer’s disease of 10%.”

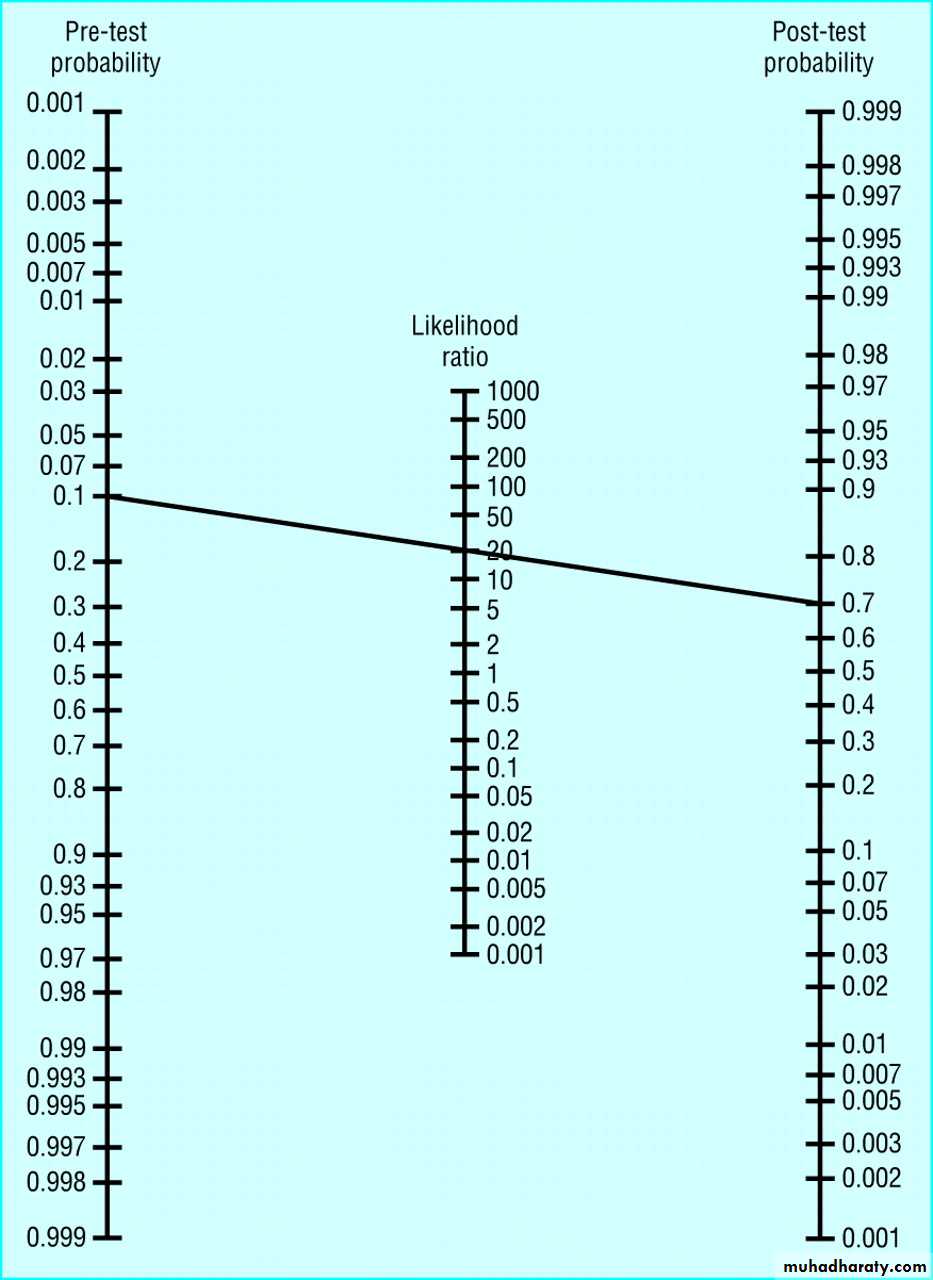
Likelihood Ratio - Definition

How many times more (or less) a patient with the condition is likely to have that particular result than a patient without the disease.

Can be used to calculate the probability of individual patient having condition based on test results.

Copyright ©2004 BMJ Publishing Group Ltd.

Deeks, J. J et al. BMJ 2004;329:168-169
Use of Fagan's nomogram for calculating post-test probabilities:


Bias in studies:
Is the reference appropriate?

Was the same reference used for all patients (verification bias)?

Were assessors blind to case details?

Was it a ‘diagnostic case-control study’?

Which population was the test tested in?

Summary

All patients must have both new test & reference test (gold standard).

Report 2x2 table and give sensitivity, specificity with precision.

A good screening test is not necessarily a good diagnostic test.

Test cut-offs in an independent sample.

Predictive values vary according to prevalence.


Consider all potential sources of bias.

Recommended Texts

BMJ Statistics Notes:
1) Sensitivity & Specificity
2) Predictive Values
3) ROC Curves
4) Likelihood Ratios

Assessing bias

How to read a paper: Papers that report diagnostic or screening tests by Trisha Greenhalgh; BMJ 1997 315 pg. 540.