U
NIVERSITY OF
T
ECHNOLOGY
Electromechanical Department
2009‐2010
Fourier series
Dr.Eng Muhammad.A.R.Yass
Sultan
M O H D
_
Y A S S
9 7 @
Y A H O O
.
C O M
Engineering and
Numerical Analysis
3
rd
Class
Special Function
Dr.Eng
Muhammad.A.R.Yass
Sultan
Hind
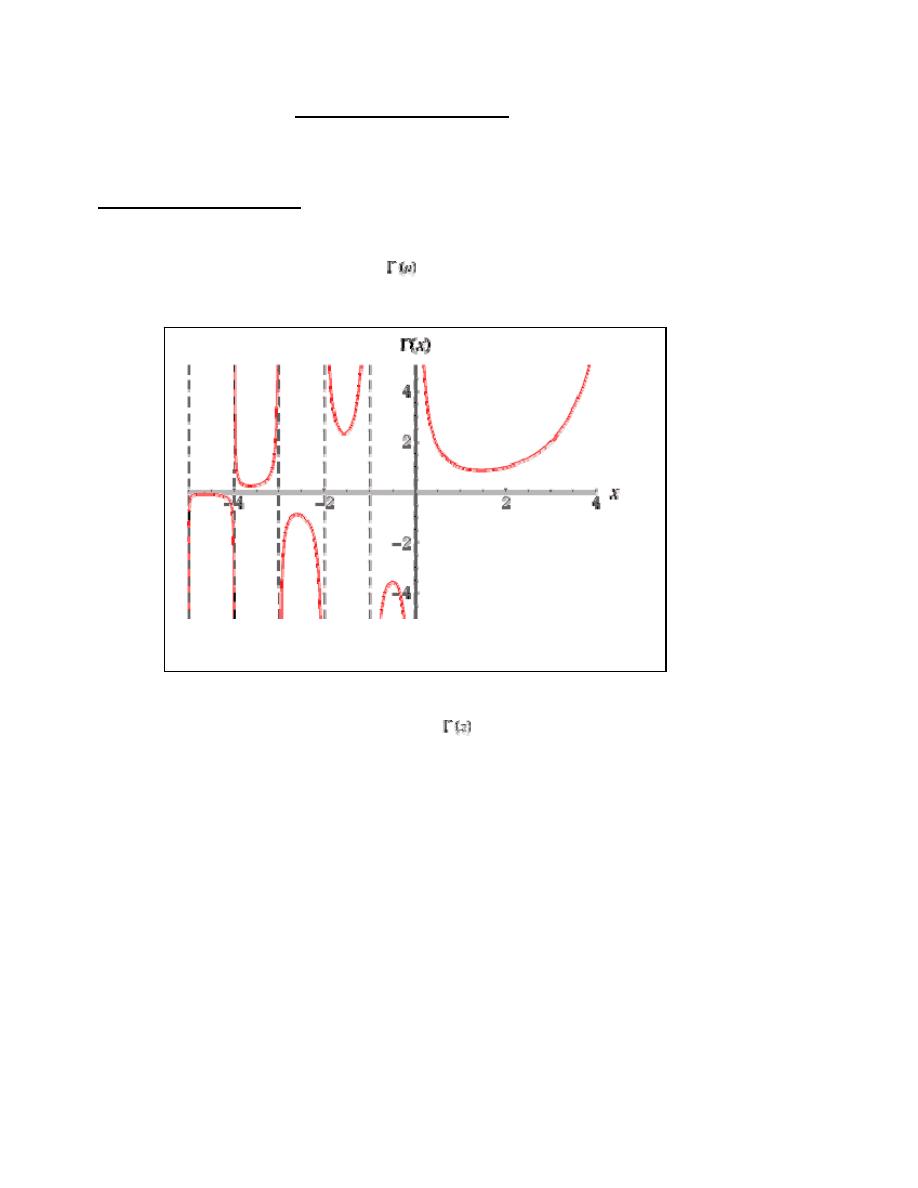
The (complete) gamma function
is defined to be an extension of the factorial
to complex and real number arguments. It is related to the factorial by
Plots of the real and imaginary parts of
in the complex plane are illustrated
above.
Integrating equation (3) by parts for a real argument, it can be seen that
Gamma Function
Γ
1
1
Γ
1 Γ
1
Special Function

Some special values of G(x)
If is an integer
, 2, 3, ..., then
(10)
(11)
(12)
(13)
where
is a double factorial. The first few values for
, 3, 5, ... are therefore
n=odd=1,3,5,7

Example(1):- Find
Γ 1
Solution:-
Γ
Γ 1
|
1
Γ 1
1
Example(2):- Prove that
Γ 1 2
√
Solution:-
Γ
Γ 1 2
… … …
… . .
2
Γ 1 2
2
2
Γ 1 2
2
2
4
Changing to spherical coordinate(
,
where
cos
, ,
sin
Γ 1 2
4
4
1
2
Γ 1 2
√
Example(2):- Evaluate
a:-
∞
b:-
3
c:-
√
Solution:-
a:-
∞
∞
∞
Γ 1 2
∞
Γ 1 2
√
……………………………………………………………….
b:-
3
4 3
4 3 2
4√ 3
Γ 1 2
∞
4√ 3
1
4√ 3
Γ 1 2

………………………………………………………………..
c:-
√
…
… …
1
√
√
We have
Γ 1 2
∞
√ then
√
Hint
… … … . .
∞ … … .
0
Example:- Evaluate a:-
Γ
b:-
Γ
Solution:-
a:-
Γ
we have
Γ
let
Γ
2√
b:-
Γ
let
Γ
√
Example:- Evaluate
x e
dx where m,n,a positive constant
Solution:- Let
x e
dx
y
a
e dx
1
a
y
e dy
1
a
Γ
m
1
n

Beta function
We define Beta function as
,
1
… … … … … … … … … 1
or
,
… … … … … … … . 2
or
,
Γ
Γ
Γ
… … … … … … … … … … … … … … … . . 3
,
1
Γ p Γ 1
p
π
sin pπ
… … 4 0
1
Examples:- Evaluate
4
0 0
1 1
√
√
1
1
1
1
Z

1
4
1
1
4
Γ
1
4 Γ
1
2
Γ
1
4
1
2
1
4
Γ
1
4 Γ
1
2
Γ
3
4
Example:- Evaluate
√
Solution:-
√
dx let t
… … x
2t … … . dx
2dt … . x
4t
√ √
√
Compare with eq(1)
1
2 … . .
3
1
… . .
√
√
Example:- Evaluate
Solution:-
y
a
y dy
y a 1
dy let t
… . y
t a
y
t a … . . y
at … … . dy
a t dt
Compare with eq(1)
1
… . .
;
1
… . .
x
2
0
0
2
1

2
Γ
5
2 Γ
3
2
Γ 4
3
2
1
2 √
1
2
3!
32
Example:- Evaluate
Solution:-
sin θ dθ
sin θ cos θ dθ compare with 2
2m-1=6 m=7/2………………2n-1=0 m=1/2
sin θ dθ
Example:- prove that
Solution:-
2
1
…
; 2
1
0 … . .
Γ
1
2 p
1 Γ
1
2
2Γ
1
2 p
2
2
Γ r
1
2 Γ
1
2
2Γ r
1
1
2
3
2 … .
1
2 Γ
1
2 . Γ
1
2
2
1 … … 1
2
1 2
3 … .1
2 2
2 … 2
2
1.3.5 … … . . 2
1
2.4.6 … . .2
2
2
1
Γ r
1 Γ
1
2
2Γ r
3
2
1 … .1. √
2
1
2
1
2 …
1
2 √
2.4.6 … 2
1.3.5. . 2
1
In both cases

Bessel Function
1
2
!
1
Solution
1) Prove that when
0 ,
1
.
. .
…
Bessel polynomial
0
1
2
!
1
1
2
0! μ 0
1
1
2
1! μ 1
1
1
2
2! μ 2
1
1
2
1
2
1
μ 2
2 . 2! μ 3
2 . 3! μ 4
…
μ
1
! μ
1
!
1
2
2 . 2! .2!
2 . 3! 3!
…
1
4
64
2 . 3! 3!
…
1
1
2
!
2
1
2
!
1 !
μ
2
1 !

2
1
2.4
2.4 . 6
… … …
2
2 4
2 . 4 . 6
… …
3
2
. sin
1
2
!
1
2
1
1
2
!
1.5
√
√2
1
2
0! μ 1.5
1
2
1! μ 2.5
1
2
2! μ 3.5
√
√2
1
μ
1.5
2.1 ! μ 2.5
2! μ 3.5
… …
μ 1.5
0.5 μ 0.5
1
2
√
μ 2.5
1.5 μ 1.5
3
2
1
2
√
μ 3.5
2.5 μ 2.5
5
2
μ 2.5
5
2
3
2
1
2
√
μ 4.5
3.5 μ 3.5
7
2
5
2
3
2
1
2
√

√
√2
1
1
2 √
2 . 1!
3
2
1
2 √
2 . 2! .
5
2
3
2
1
2 √
… …
√
√2
1
2 √
1
3 2 !
5 4 3 2!
… …
2√
√2√
1
3!
5!
… …
√
2
√
1
3!
5!
… …
√ √2
√
3!
5!
… …
2
3!
5!
… …
Note
sin
3!
5!
7!
… …
cos
1
2!
4!
… …
2
sin sin
1
2
1 !
cos
1
2 !
7 prove that

2
cos
4
1
2
1
2
! μ
1
1
1
2
! μ
1
1
2
2
2
! μ
1
Note
μ
1
!
1 2
2
!
!
1 2
2
!
!
Note
1
μ
1
. μ
2
μ
1
!
3
μ
1 μ
1
1 !
4
!
1 !

L.H.S
1
2
!
1 !
L.H.S
1
2
!
1 !
… … …
1
2
. ! μ
1
1
μ
1
1
1
!
1 !
اﻟﻄﺮف
اﻻﻳﻤﻦ
1
2
!
1 !
… … …
اﻻﻳﻤﻦ اﻟﻄﺮف
اﻟﻄﺮف
اﻻﻳﺴﺮ
1
2
! μ
1
1
2
! μ
1
1
1
2
. ! μ
1
1

5
اﻟﻄﺮف اﻻﻳﺴﺮ
1
2
! μ
1
1
2
! μ
1
1 2
2
! μ
1
1
2
! μ
1
Note k! k k‐1 !
1
2
1 ! μ
1
1
2
1 ! μ
1
… 8 اﻻﻳﺴﺮ اﻟﻄﺮف
اﻟﻄﺮف اﻻﻳﻤﻦ
.
1
2
! μ
1
1
1
2
! μ
2

1
2
! μ
2
1
2
! μ
2
Putting in a bore eq. K K ‐1
1
2
1 ! μ
1
2
1
2
1 ! μ
1
… … …
اﻟﻄﺮف اﻻﻳﻤﻦ
=
اﻟﻄﺮف اﻻﻳﺴﺮ
6 prove that
2
Sol. We have from 4
̀
.
̀
.
̀
̀
–
… … …

5
̀
.
̀
̀
/
̀
… … …
Subtract eq. ** from eq. ** we obtain
0
2
و
.
ـه
.
م
8 show that ̀
We have ̀
Putting n 0 then
̀
0
̀
9 show that ̀
/
sin
We have from 6
Putting n ½

2
1
2
1
2
sin
1
2
sin
2
cos
2 sin
cos
2
sin
cos
10 prove that ̀
We have from 6 eq. * and ** added
2 ̀
̀
1
2
11 use Bessel polynomial to show that
̀̀
1
̀
Sol. We have from 6 eq. * ̀
̀̀
̀
̀
Put n 1

̀̀
̀
̀
. 8 ̀
̀̀
̀
̀
̀̀
̀
̀̀
̀
̀̀
1
̀
و
.
ـه
.
م
7 prove that
2
cos
Putting un Bessel polynomial n ‐ ½
1 2
! μ
1
2
1
2
1 2
! μ
1
2
1
2
1
2 0! μ 0.5
1
2.1
! μ 1.5
1
2
. 2! μ 2.5
… …
2
1
μ 0.5
2!
4 3 2!
… … …

√2
√
1
√
1
2!
4 3 2!
… … …
2
1
2!
4!
… … …
cos
1
2!
4!
… … …
2
cos
و
.
ـه
.
م
12 write J
4 x
in terms of J
0 x
and J
1 x
Sol.
2
6
Putting n 1 4 n 3
2 3
6
6
4
2
2 1
6
4
2
2
48
24
6
2

48
8
1
24
و
.
ـه
.
م
13 Evaluate
.
.
.
Here m 3 , n 1
.
2
8
.
.
0
0
M 1
N 1
.
2
8
.
8
2

Home work
1.
.
2.
.
3.
.
4.
.
5.
√
6.
7.
