
א
א
אאא
ã¹]<gè…‚jÖ]æ<ËÖ]<Üé×Ãj×Ö<íÚ^ÃÖ]<퉉ö¹]
אאא
א
٧٤١
٧٤١
א
א

א
٧٤١
א
א
א
،،אא،א
W
אאאאאאאאאא
א א א א א
א א ،א
אאאאאא
،אאאאאא
א
אא
K
אאאאאאא
א،אאא
א،
אאאאאא
א،אאאא
אאאאאאאאאאאאא
א א ،א
אא،אא
K
אא
?
א
?
?
?
א
אאאאאא
K
אאאאאאא
،א،אאאא
אאאאא
K
،אאאא
א
K
אאאא

٧٤١
א
א
א
אאאא
KKK
،
א،אאאאאא
אאא
K
אאאאא
א
א،אא،אאאא
אאאאאאאא
אאא
K
א
אאאא
،אאאאא،אאא
،אאא
אאא
אאאא
אאאא
K
אאאאא
אאא
א
אאאא
K
א
אאאא،אא
אא،א،אא
K
אאאא،
،
א
אא
א،א
אא
K
،א
KKKKKK

אא
אא
א
א
אאא
ã¹]<gè…‚jÖ]æ<ËÖ]<Üé×Ãj×Ö<íÚ^ÃÖ]<퉉ö¹]
אאאא
א
א
١

אאא
אא
W
•
אא
א
K
•
אא
K
•
אאאאאאא
K
•
אאאאא
K
•
אאאאא
K

١
J
١
Introduction
א
א
K
אאאאא
)
Binary Number System
(
אאאאאאא
)
Digital Electronic Circuits
(
K
אא،אאאא
)
Decimal Number System
(
א
K
אאא
אאאאאא
)
Octal Number System
(
אאא
)
Hexadecimal Numbering System
(
K
אאאאאאא
אאאאאאא
K
א
א
א
אאאאאאא
K
אאאאא
W
١K
א
K
٢K
אאא
K
٣K
אאאאאא
K
٤
K
א
אאא
K
٥
K
אאאאא
K
אאאא
)
Digit
(
א
)
Number
(
،
)
Symbol
(
אאאאא
،א
)
٠{١{٢{٣{٤, ... , ٨{٩
(
אאא
אאאאאאאא،אא
אאא،א
)
٤١
(
אאא
)
٣٢١
(
،א
אאא
א
)
٤١
(
)
١،٤
(
אאא
א
)
٣٢١
(
)
١،٢،٣
(
)
٦
(
א
א
K

١
J
٢
אאא
Decimal Numbering System
אאאאאאא
א
אאאא
K
אאאא
)
٠١
(
א
٠١
)
٠١
(
٠{١{٢{٣{٤{٥{٦{٧{٨{٩
K
אא
)
Positional Weight
(
אא
)
٨٢١
(
א
א
)
٨
(
אא
F
א
E
،א
אאא
١
)
٨× ١ = ٨
(
אא،
)
٢
(
אא
F
אא
E
אאא
٠١
)
٢× ١٠ = ٢٠
(
،
אא
F
١
E
אא
F
א
E
אאא
٠٠١
)
١× ١٠٠ = ١٠٠
(
K
א
،אאאאא
W
(
١× ١٠٠) + (٢ × ١٠) + (٨ × ١) = ١٠٠ + ٢٠ + ٨ = ١٢٨
אאא
F
٠١
E
אא
אאאא
٠١
٠١
٠
=
١
W
........
٠١
٥
٠١
٤
٠١
٣
٠١
٢
٠١
١
٠١
٠
א
٨٢١
W
١
٢
٨
אאאא
٠١
٢
٠١
١
٠١
٠
١× ١٠
٢
+
٢× ١٠
١
+
٨× ١٠
٠
()٨٢١
٠١
=
٠٠١+ ٢٠ + ٨
אא
)
٨٢١
(
אא
٠١
א
א
)
Subscript
(
אאאא
K

אאאאאא
א
٠١
١
W
٠١
٢
٠١
١
٠١
٠
• ٠١
١
٠١
٢
٠١
٣
........
١
J
٣
אאא
Binary Numbering System
אאאא
א
)
٢
(
)
٢
(
א
)
١،٠
(
.
אאאאאאא
)
٢
(
W
.....
٢
٤
٢
٣
٢
٢
٢
١
٢
٠
אאאא
W
.....
١ ٢ ٤ ٨ ٦١
אא
)
١٠٠١١
(
W
٢
٤
٢
٣
٢
٢
٢
١
٢
٠
١ ٠ ٠ ١ ١
= (
١× ٢
٤
) + ( ١× ٢
٣
) + ( ٠× ٢
٢
) + ( ٠× ٢
١
) + ( ١× ٢
٠
)
= ٦١+ ٨ + ٠ + ٠ + ١ = (٢٥)
٠١
אא،אאאאא
אאאאאא
(
)٢
אא
אא
(
)١٠٠١١
٢
K
אאאאא
W
■
אא
)
Bit
(
W
אא
(Bit)
א
)
Binary Digit
(
אא
אאא
K
אאא
F
א
E
א
א،אא
(
)١٠٠١
٢
)
٤-bits
(
א
(
)١٠١١٠١١
٢
)
٧-bits
(
א
K
אא
(Decimal Point)

■
אא
)
Number of Binary Combinations
(
W
אא
א
אאא
)
bits
(
K
אאא
W
N =
n
2
W
N
=
אאא
n
=
א
)
bits
(
אא
()٢
אא
W
N = ٢
٢
= ٤
אא
()٣
אא
W
N = ٢
٣
= ٨
אא
()٤
אא
W
N
=
٢
٤
= ٦١
אאאאא
K
■
אא
)
Bit
(
W
אאא
א
אאא
٢
٠
)
١
(
()١
א
אאא
٢
١
()٢
א
٢
٢
()٤
א
K
אאאאא
אא
אאא،אאא،אא
)
it
B
ignificant
S
east
L
(
א
א
)
LSB
(
אאא
אאאא
)
it
B
ignificant
S
ost
M
(
אא
)
MSB
(
K
■
א
)
Byte
EW
אא
)
Bit
(
אאא
אאאאא،אאאא
)
٠
(
אא
)
١
(
א
א
F
E
אאא
אאא
K
א
א
א
א
K
א
)
Byte
(
אאאא
K
אא
א
W
١byte = ٨ bits
١
J
٤
אאאאא
Decimal-to-Binary Conversion

אאאא،אאא
)
Sum of Weights Method
(
אא
אא
)
٢
(
)
Repeated Division–by– ٢Method
(
אאא
אאא
K
١
J
٤
J
١
אאאאאא
אא
٠١
)
٤١
(
،א
א
٤١
٢
א،
א
٢
א
)
٠
.(
אאאאאא
K
אאא
)
LSB
(
אאאא
)
MSB
(
אא،
W
٤١÷ ٢ = ٧
٠
٧÷ ٢ = ٣
١
٣÷ ٢ = ١
١
١÷ ٢ = ٠
١
٠ ١ ١ ١
(MSB) (LSB)
W
()٤١
٠١
= ()٠١١١
٢
F
١
J
١
WE
אא
()٥٢
٠١
א
K
א
W
א

א
א
٥٢÷ ٢ = ١٢
( ١LSB)
٢١÷ ٢ = ٦
٠
٦÷ ٢ = ٣
٠
٣÷ ٢ = ١
١
١÷ ٢ = ٠
( ١MSB)
א
W
()٤١
٠١
= ()٠١١١
٢
F
١
J
٢
WE
אא
()٧٨
٠١
א
K
א
W
٧٨÷ ٢ = ٤٣
( ١LSB)
٣٤÷ ٢ = ٢١
١
١٢÷ ٢ = ١٠
١
٠١÷ ٢ = ٥
٠
٥÷ ٢ = ٢
١
٢÷ ٢ = ١
٠
١÷ ٢ = ٠
( ١MSB)
א
W
()٧٨
٠١
= ()١١١٠١٠١
٢
١
J
٤
J
٢
אאאאא
אאאאאא
אא
()٢
K
אאא
)
Decimal Fractions
(
אא
אא
()٢
K
אא
)
٥٢١٣٫٠
(
אא
אא
٥٢١٣٫٠
()٢
אאא،
()٢
אאא
()٠
אאאא
K
אא
)
Carried Digits
(
אאאא
אאאא
א
K
אאא
)
MSB
(
אאא
)
LSB
(
K
א
W
٥٢١٣٫٠
× ٢= ٠٫٦٢٥
٠
א

א
٥٢٦٫٠
× ٢= ١٫٢٥
١
٥٢٫٠
× ٢= ٠٫٥
٠
٥٫٠
× ٢= ١٫٠٠
١
(LSB)
( ٠ ١ ٠ ١MSB)
F
١
J
٣
WE
אא
()٥٢٫٩٣
٠١
א
K
א
W
אאאאא
()٢
W
٩٣÷ ٢ = ١٩
( ١LSB)
٩١÷ ٢ = ٩
١
٩÷ ٢ = ٤
١
٤÷ ٢ = ٢
٠
٢÷ ٢ = ١
٠
١÷ ٢ = ٠
( ١MSB)
א
W
()٩٣
٠١
= ()١١١٠٠١
אאאא
()٢
W
٥٢٫٠
× ٢= ٠٫٥
٠
٥٫٠
× ٢= ١٫٠٠
١
W
()٥٢٫٠
٠١
= ()١٠٫٠
٢
אאא
W
()٥٢٫٩٣
٠١
= ()١٠٫١١١٠٠١
٢
١
J
٥
אאאאא
Binary-to-Decimal Conversion
אא
אאאאא
()٢
אאאא
٦١, ٨, ٤, ٢, ١
א
K
אאא
א

אא
)
Bit
(
אא
()١
אאאאאא
K
אאא
W
F
١
J
٤
WE
אא
١٠٠١٠١١
א
K
א
W
()١
אא
אא
W
٢
٦
٢
٥
٢
٤
٢
٣
٢
٢
٢
١
٢
٠
:
א
١ ٠ ٠ ١ ٠ ١ ١:
אא
=
١× ٢
٦
+ ١× ٢
٥
+ ٠× ٢
٤
+ ١× ٢
٣
+ ٠× ٢
٢
+ ٠× ٢
١
+ ١× ٢
٠
= ٤٦+ ٣٢ + ٨ + ١ = (١٠٥)
٠١
אאאאאא
ﺧﺎﻧ ﺎت
)
Bits
(
אא
)
Binary Point
(
אאאאא
אא
)
Decimal Point
(
אא
אאאא
W
……٢
٤
٢
٣
٢
٢
٢
١
٢
٠
• ٢
-١
٢
-٢
٢
-٣
٢
-٤
…….
אא
F
١
J
٥
WE
אאא
()١١٠١٫٠
٢
א
K
א
W
• ٢
-١
٢
-٢
٢
-٣
٢
-٤
٠
• ١ ١ ٠ ١
∴()١١٠١٫٠
٢
=
١
× ٢
-١
+ ١× ٢
-٣
+ ١× ٢
-٤
= ٥٫٠+ ٠٫١٢٥ + ٠٫٠٦٢٥ = (٠٫٦٨٧٥)
٠١

١
J
٦
אאאא
Binary Arithmetic
אאאאאא
אא
K
אאאאא
K
١
J
٦
J
١
אא
Binary Addition
אאא،אאאא
)
Binary Digits
(
W
٠+ ٠ = ٠
٠+ ١ = ١
١ + ٠ = ١
١ + ١ = ٠carry
F
א
E
١
⇒ = ٠١
אאא
אאא،אא
١+ ١= ١٠
()٢
אא،
()١
אאאאא
אאא
K
אאאא
W
F
١
J
٦
WE
אא
١١٠, ١١٠
K
א
W
אאאא
W
١
١
٦
١
١
٠
+
٣+ ٠
١
١
F
E
٩
١
٠
٠
١
F
١
J
٧
WE
אאא
١١٠, ١٠٠
K
א
W
٤
١
٠
٠
+
٠ ٣
١
١
F
E
٧
١
١
١
١
J
٦
J
٢
אא
Binary Subtraction
אא
W
١
J
אא
א
K
٢
J
אא
K
אא،אא
K
א
אא
F
א
E
אאאאאא
אאאאא
א
W
٠– ٠= ٠

١
١– ٠ = ١
١– ١= ٠
٠ – ١= ١ (
)١
א
(
)١
א
אאא
W
•
אא
K
•
א
אאא
אאאאא
W
()٠
()٠
()١
()١
א
()٠
K
()٠
()١
א
()١
K
()١
()٠
א
()١
()٠
אא
F
א
E
()١
()١
()٠
K
אאאאא
K
F
١
J
٨
WE
אאא
()١٠١
אא
()١١٠
K
א
W
٠
א
١
٠
١
א
١
١
٠
–
٠
١
٠
١
J
٧
אאאאא
One's and Two's Complements of Binary Numbers
אאאאאאא
K
א
אאאאאאאא
K
אא
)
١
(
)
٠
(
)
٠
(
)
١
(
א
א
W
א
(
١)
אא
א
(
٠١)
(
١)
א
(
١)
א
(
١)
א
(
٠)
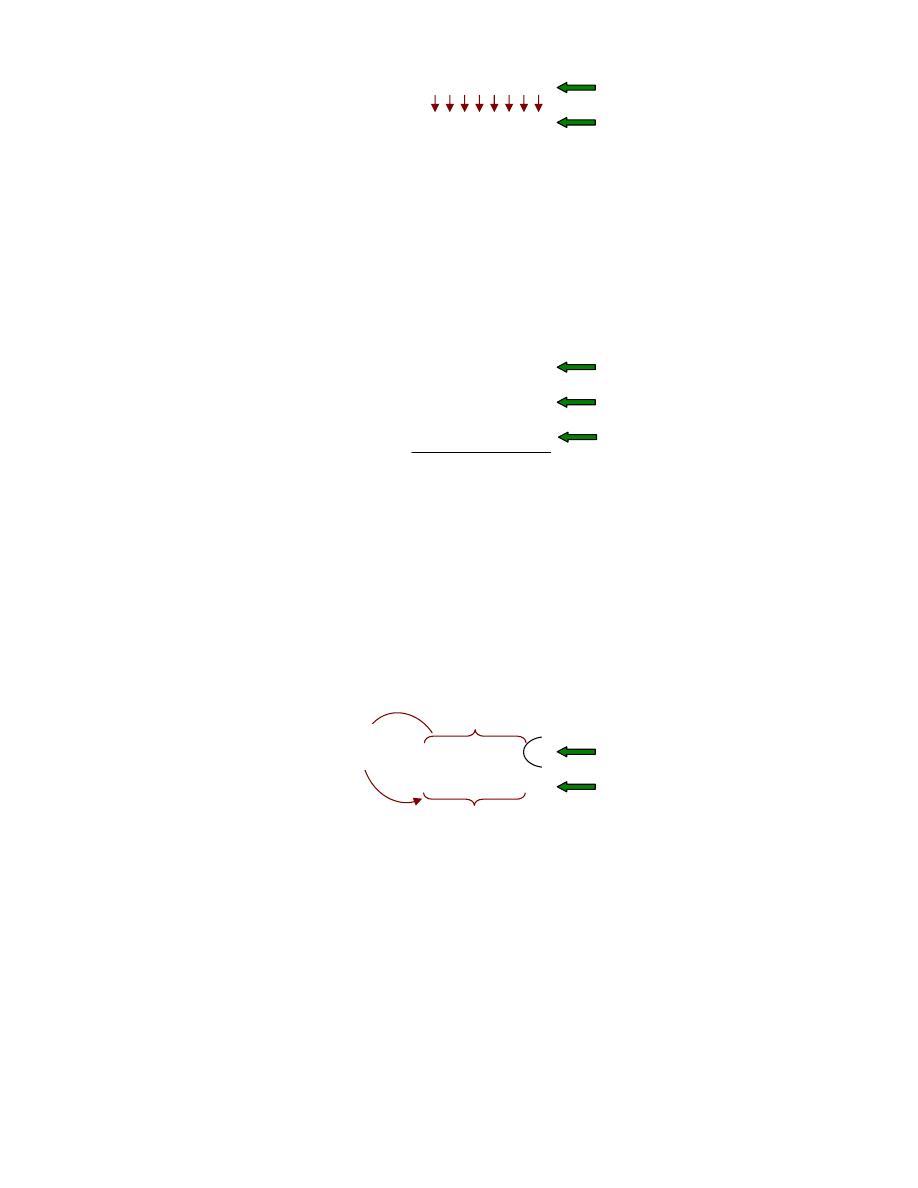
אא
١ ١ ٠ ٠ ١ ١ ٠ ١
אא
٠ ٠ ١ ١ ٠ ٠ ١ ٠
אאא
א
W
אא
W
אא
K
א
()١
א
אאאא
W
אא
Z
אא
+
١
אא
אא
١١٠٠١١٠١
K
אאא
()١
אא
K
אא
١ ١ ٠ ٠ ١ ١ ٠ ١
אא
٠ ٠ ١ ١ ٠ ٠ ١ ٠
()١
١
+
אא
٠ ١ ١ ١ ٠ ٠ ١ ٠
אא
W
אאאא
)
LSB
(
אא
)
٠
(
אא
אאאאא
א
אאאא
א
F
אאאאאא
אאאא
אא
E
،
אא
()١٠١١٠١٠١
٢
אא
W
אא
١ ٠ ١ ١ ٠ ١ ٠ ١
אא
١ ١ ٠ ٠ ١ ٠ ١ ٠
١
J
٨
אאא
א
Representation of Signed Numbers
א
אאאאאאא
אאא
אאאאאא
אא
א،א
()٠
،א
()١
א
K
אאא
אאאא
אאאא
)
Sign Bit
(
א
א
)
Magnitude
.(
אא

אאאאאא
W
אא
)
Sign-Magnitude
(
אא
)
١'s Complement
(
אא
)
٢'s Complement
.(
١
J
٨
J
١
אא
)
Sign-Magnitude System
(
אא
،אא
אא
)
Bit
(
אאא
אאאאאא
K
א
אאאאא
א
אאא
אא
K
אא
(+)٣٢
אא
א
W
١ ١ ١ ٠ ١ ٠ ٠ ٠
אא
(-)٣٢
ﻓﺈﻧﻨﺎ
W
١
١
١
٠
٠
١
٠
٠
١
אאא
(+)٣٢
،
(–)٣٢
א
K
١
J
٨
J
٢
אא
)
١'s Complement System
(
אאאאאאאאאא
אא
K
אאא
אאא
א
K
אא
(–)٣٢
אאא
W
א
)
+٣٢
(
١
١
١
٠
١
٠
٠
٠
א
)
٣٢
–
(
٠
٠
٠
١
٠
١
١
١
אאאאאאאא
א
K
١
J
٨
J
٣
אא
)
٢'s Complement
(
אא
אאאאא
א
אא
K
אאאאאא
K
אא
(-)٣٢
אאא
(+)٣٢
W
א
(Sign Bit)
אא
(Magnitude Bits)

א
(Discard carry)
א
)
+٣٢
(
١
١
١
٠
١
٠
٠
٠
א
)
٣٢
-
(
١
٠
٠
١
٠
١
١
١
אאאאאאא
K
١
J
٩
אאאאאא
Arithmetic Operations with Signed
Numbers
אאאא
،
אאאאאאאא
،
אא
F
١
J
٦
KE
א
א
אאאאאא
אא
אאא
K
אאאאאאא
א
W
F
١
J
٩
WE
א
אא
٠١١١٠٠٠٠
אא
٠١٠١١١١١
אאאא
K
א
W
א
W
٤١– (– ٦) = ٤١+ ٦ = ٢٠
א
W
٠ ١ ١ ١ ٠ ٠ ٠ ٠
א
(
H )٤١
+ ٠ ١ ١ ٠ ٠ ٠ ٠ ٠
א
א
(
H )٦
٠ ٠ ١ ٠ ١ ٠ ٠ ٠
א
(
H )٠٢
F
١
J
٠١
WE
אאאאאא
W
()٠٠٠١٠٠٠٠
٢
– ()٠٠١٠٠٠٠٠
٢
א
W
א
W
٨– ٤ = ٨+ (-٤) = ٤
W
٠ ٠ ٠ ١ ٠ ٠ ٠ ٠
א
(
H )٨
+ ٠ ٠ ١ ١ ١ ١ ١ ١
אא
(
)٤
٠ ٠ ١ ٠ ٠ ٠ ٠ ٠ ١
א
(
H )٤
F
١
J
١١
WE
אאאאאא
K
()١١١٠٠١١١
٢
– ()١٠٠١٠٠٠٠
٢
א
W
א
W

א
(Discard carry)
–
٥٢– (+٩) = – ٥٢– ٩ = -٣٤
W
١ ١ ١ ٠ ٠ ١ ١ ١
א
(
)٥٢
+ ١ ١ ١ ٠ ١ ١ ١ ١
אא
(
)٩
٠ ١ ١ ١ ١ ٠ ١ ١ ١
א
(
)٤٣
١
J
٠١
אאא
The Octal Numbering System
אאאא
()٨
()٨
(٠،١،٢،٣،٤،٥،٦،٧)
אאאאאא
אאאאאא،אאא
אאאאאאאא
K
١
J
٠١
J
١
אאאא
Octal-to-Decimal Conversion
אאאא
אאא
()٨
(……٨
٣
٨
٢
٨
١
٨
٠
)
،א
אאאא
)
…... ١ ٨ ٤٦ ٢١٥
(
،א
K
אא
אאא
אאא
K
אאא
()٥٧٢٢
٨
אא
W
אא
: ٨
٣
٨
٢
٨
١
٨
٠
אא
: ٥ ٧ ٢ ٢
∴ ()٥٧٢٢
٨
= ( ٢
× ٨
٣
) + ( ٢
× ٨
٢
) + ( ٧
× ٨
١
) + ( ٥
× ٨
٠
)
= ( ٢
× )٢١٥+ (٢ × ٦٤) + (٧ × ٨) + (٥ × ١)
= ٤٢٠١+ ١٢٨ + ٥٦ + ٥ = (١٢١٣)
٠١
١
J
٠١
J
٢
אאאא
Decimal–to–Octal Conversion
אאא
א
אא
א
()٨
אאאאאאא،
()٨
()٢
K
١
J
٠١
J
٢
J
١
אאאאאא
אא
٠١
)
٠٥١
(
אא
א
٠٥١
()٨
אא
()٨
א
()٠
.
אאאאא
א
K
אא
אא
אאא

א
א
اﻟﺤﺎﻣﻞ
)
LSD
(
igit}
D
ignificant
S
east
L
{
אאאא
igit}
D
ignificant
S
ost
M
{
)
MSD
(
אא
W
٠٥١÷ ٨ = ١٨
( ٦LSD)
٨١÷ ٨ = ٢
٢
٢÷ ٨ = ٠
( ٢MSD)
א
W
()٠٥١
٠١
= ()٦٢٢
٨
F
١
J
٢١
WE
אא
٠١
)
٤٢٦
(
אא
K
א
W
٤٢٦÷ ٨ = ٧٨
( ٠LSD)
٨٧÷ ٨ = ٩
٦
٩÷ ٨ = ١
١
١÷ ٨ = ٠
( ١MSD)
א
W
()٤٢٦
٠١
= ()١١٦
٨
١
J
٠١
J
٢
J
٢
אאאאא
אאא
אאאאא
אא
()٨
K
אא
)
٥٦٢٫٠
(
אא
אא
٥٦٢٫٠
(
)٨
،
אאא
()٨
אאא
()٠
אאא
א
K
א
א
)
Carried Digits
(
אאאאא
K
אאא
)
LSD
(
אא
)
MSD
(
א
W
٥٦٢٫٠
× ٨= ٢٫١٢
( ٢MSD)
٢١٫٠
× ٨= ٠٫٩٦
٠
٦٩٫٠
× ٨= ٧٫٦ ٨
٧
٨٦٫٠
× ٨= ٥٫٤٤
٥
٤٤٫٠
× ٨= ٣٫٥٢
٣
٢٥٫٠
× ٨= ٤٫١٦
٤
(LSD)
אאאאאא
()٦
אא
W
()٥٢٦٫٠
٠١
= ()٤٣٥٧٠٢٫٠
٨

א
اﻟﺤﺎﻣﻞ
F
١
J
٣١
WE
אא
٠١
)
٥٢٦٥٫٤٤
(
אא
K
א
W
אאאאא
()٨
K
٤٤÷ ٨ = ٥
( ٤LSD)
٥÷ ٨ = ٠
( ٥MSD)
א
W
()٤٤
٠١
= ()٤٥
٨
אאאא
()٨
W
٥٢٦٥٫٠
× ٨= ٤٫٥
٤
٥٫٠
× ٨= ٤٫٠٠
٤
W
()٥٢٦٥٫٠
٠١
= ()٤٤٫٠
٨
אאא
W
()٥٢٦٥٫٤٤
٠١
= ()٤٤٫٤٥
٨

١
J
٠١
J
٣
אאאאא
Octal-to-Decimal Conversion
אאאאאא
א
()٨
אאאא
٦٩٠٤, ٥١٢, ٦٤, ٨, ١
א
K
אא
אאא
)
Digit
(
א
אאא
א
K
אא
K
F
١
J
٤١
WE
אא
()٤٢٣
٨
אא
K
א
W
אא
: ٨
٢
٨
١
٨
٠
אא
: ٤ ٢ ٣
∴ ()٤٢٣
٨
= ( ٣
× ٨
٢
) + ( ٢
× ٨
١
) + ( ٤
× ٨
٠
)
= ( ٣
× )٤٦+ (٢ × ٨) + (٤ × ١)
= ٢٩١+ ١٦ + ٤ = (٢١٢)
٠١
אאאאאאאאא
אאא
)
Octal Point
(
אא
אאאא
W
……٨
٤
٨
٣
٨
٢
٨
١
٨
٠
• ٨
-١
٨
-٢
٨
-٣
٨
-٤
…….
אא
F
١
J
٥١
WE
אא
()٤١٫٧٦٥
٨
אא
K
א
W
אא
: ٨
٢
٨
١
٨
٠
• ٨
-١
٨
-٢
אא
: ٧ ٦ ٥
• ٤ ١
∴ ()٤١٫٧٦٥
٨
= ( ٥
× ٨
٢
) + ( ٦
× ٨
١
) + ( ٧
× ٨
٠
) + ( ١
× ٨
-١
) + ( ٤
× ٨
-٢
)
= ( ٥
× )٤٦+ (٦ × ٨) + (٧ × ١) + (١ × ٠٫١٢٥) + (٤ × ٠٫٠١٥٦٢٥)
= ٠٢٣+ ٤٨٠ + ٧ + ٠٫١٢٥ + ٠٫٠٦٢٥ = (٣٧٥٫١٨٧٥)
٠١
١
J
٠١
J
٤
אאא
אא
Octal-to-Binary Conversion
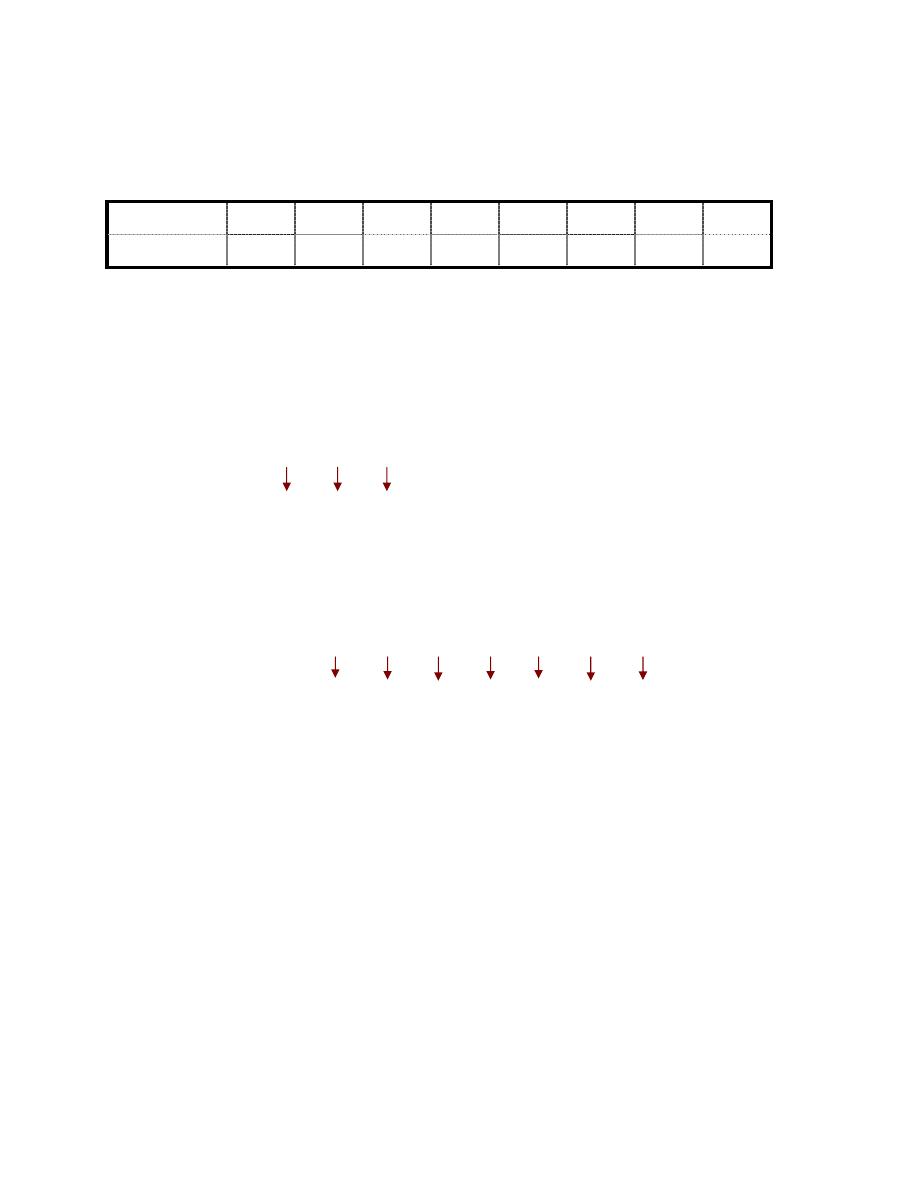
)
Digit
(
אא
)
٣-bits
(
،
אאאאא
K
א
א
F
١
J
١
KE
٧
٦
٥
٤
٣
٢
١
٠
אא
١١١
٠١١
١٠١
٠٠١
١١٠
٠١٠
١٠٠
٠٠٠
אא
F
١
J
١
E
אאא
K
אאא
א
K
F
١
J
٦١
WE
אא
()٧٥٣
٨
אא
K
א
W
()٧٥٣
٨
=
٣
٥
٧
١١١ ١٠١ ١١٠
= ()١١١١٠١١١٠
٢
F
١
J
٧١
WE
אא
()٣٤٥٫٦٧٢١
٨
א
K
א
W
()٣٤٥٫٦٧٢١
٨
=
١
٢
٧
٦
• ٥
٤
٣
٠١١ ١١١ ٠١٠ ١٠٠
• ١١٠ ٠٠١ ١٠١
= ()١١٠٠٠١١٠١٫٠١١١١١٠١٠١
٢
אאא
K
١
J
٠١
J
٥
אאאאא
Binary-to-Octal Conversion
אאאאאאאא
א
K
אא
–
J
אאא
א
אאא
אאאא
א
א
אאאא
K
F
١
J
٨١
WE
אא
()١٠١٠٠٫٠٠١١١٠١٠٠١١٠١
٢
אא
K
א
W

٠٠١ ١١٠ ١٠٠ ١١٠ ١٠٠
• ٠١٠ ١٠٠
١
٣
١
٣
٤
• ٢ ١
אאאאאא
W
()١٠١٠٠٫٠٠١١١٠١٠٠١١٠١
٢
= ()٢١٫٤٣١٣١
٨
١
J
٠١
J
٦
אאאא
Arithmetic Operations in Octal System
אאאא
K
١
J
٠١
J
٦
J
١
א
א
Octal Addition
אא
אאא
–
א
)
٠،٩
(
א
()٩
אאא،
()٩
א
()٠١
א
אאאאא
K
אא
א
אאאא
)
٠،١
(
אא
()٠١
אא
אאאא
K
א
אאאאאאאא
אאא
()٧
אאא
–
אאאא
()٧
א
()٠١
אאאאאא،א
)
١١, ١٢, ١٣, ١٤, ١٥, ١٦, ١٧
(
אאא
)
٠٢،٢١, ٢٢, ...... , ٢٧
(
אאא
)
٠٣, ٣١, ..... , ٣٧
(
א
K
א
F
١
J
٢
E
אאאאא
אאאאאאאא
אאא
אא
K
אא
א
W
•
אאאאאאא
()٧
K
•
אאא
()٧
אא
()٢
אא،א
()٧
אא
()٨
א
()٧
א
אא
()٠١
א
()٢
אא
אאא
F
אאאא
אאא
KE

+
٠
١
٢
٣
٤
٥
٦
٧
٠
٠
١
٢
٣
٤
٥
٦
٧
١
١
٢
٣
٤
٥
٦
٧
٠١
٢
٢
٣
٤
٥
٦
٧
٠١
١١
٣
٣
٤
٥
٦
٧
٠١
١١
٢١
٤
٤
٥
٦
٧
٠١
١١
٢١
٣١
٥
٥
٦
٧
٠١
١١
٢١
٣١
٤١
٦
٦
٧
٠١
١١
٢١
٣١
٤١
٥١
٧
٧
٠١
١١
٢١
٣١
٤١
٥١
٦١
F
١
J
٢
E
אאא
K
F
١
J
٩١
WE
אאא
()٨٣
٨
،
()٢٤
٨
K
א
W
אא
W
٤٣
+ ٢٤
٦٧
∴()٤٣
٨
+ ()٢٤
٨
= ()٦٧
٨
אא
(٤،٢)
(٣،٤)
()٧
א
K

F
١
J
٠٢
WE
אאא
()٦٥
٨
،
()٣٦
٨
K
א
W
٦ ٥
+ ٣ ٦
١ ٤ ١
אאא
()٧
()٢
א
א
)
Carry
(
אא
K
١
J
٠١
J
٦
J
٢
אאא
Subtraction in Octal System
אאא
W
•
אא
אאא
K
•
אאא
()١
אא
–
אאא
()٨
אאאאאאא
אא
K
F
١
J
١٢
WE
אא
W
()٧٥٦
٨
– ()٦٤٣
٨
א
W
א
W
٧ ٥ ٦
א
– ٦ ٤ ٣
א
١ ١ ٣
∴()٧٥٦
٨
– ()٦٤٣
٨
= ()١١٣
٨
אאא
אא
K
F
١
J
٢٢
WE
אא
W
()٢٣٧
٨
– ()٤٣٦
٨
א
W
٢ ٣ ٧
א
– ٤ ٣ ٦
א
٦ ٧ ٠
∴()٢٣٧
٨
– ()٤٣٦
٨
= ()٦٧
٨
אא
()٤
()٢
אא
א
()١
א،אאאאאא
אא
א
()٣
()٢
אא
K
٦
١ ٢

א
١
J
١١
אאאא
Hexadecimal Numbering System
אאא
א
א
()٦١
)
٦١
(
א
)
٠،١،٢،٣،٤،٥،٦،٧،٨،٩,A,B,C,D,E,F
(
א
)
A,B,C,D,E,F
(
אא
(٠١, ١١, ١٢, ١٣, ١٤, ١٥)
א
K
١
J
١١
J
١
אאאא
Hexadecimal–to–Decimal Conversion
אאאאאאא
א
٦١
(……٦١
٣
٦١
٢
٦١
١
٦١
٠
)
א
אאא
)
... ٦١ ٦٥٢ ٦٩٠٤
١
(
א
אא
٦١
)
٩٣٫٢٢٥
(
W
אא
: ٦١
٢
٦١
١
٦١
٠
• ٦١
-١
٦١
-٢
אא
: ٢ ٢ ٥
• ٩ ٣
∴ ()٩٣٫٢٢٥
٦١
= ( ٥
× ٦١
٢
) + ( ٢
× ٦١
١
) + ( ٢
× ٦١
٠
) + ( ٣
× ٦١
-١
) + ( ٩
× ٦١
-٢
)
= ( ٥
× )٦٥٢+ (٢ × ١٦) + (٢ × ١) + (٣ × ٠٫٠٦٢٥) + (٩ × ٠٫٠٠٣٩٠٦٢)
= ٠٨٢١+ ٣٢ + ٢ + ٠٫١٨٧٥ + ٠٫٠٣٥١٥٥٨ = (١٣١٤٫٢٢٢٦٥٥)
٠١
אא
אאאא
K
א
אאא
()٦١
אא
K
١
J
١١
J
٢
אאאא
Decimal-to-Hexadecimal
Conversion
אאאא
אאאא
()٦١
אאאאאאאאאא
אא
()٦١
()٨
()٢
.
١
J
١١
J
٢
J
١
אאאאאאא
אא
٠١
)
٧٩
(
אא
א
٧٩
()٦١
אא
()٦١
א
()٠
K
אאאאא
אא
K
،אאא
אאא
)
LSD
(
אא
)
MSD
(
אא
W
٧٩÷ ١٦ = ٦
( ١LSD)
٦÷ ١٦ = ٠
( ٦MSD)
א
W

א
اﻟﺤﺎﻣﻞ
()٧٩
٠١
= ()١٦
٦١
F
١
J
٣٢
WE
אא
()٤١٣
٠١
אאא
K
א
W
٤١٣÷ ١٦ = ١٩ A (LSD)
٩١÷ ١٦ = ١
٣
١÷ ١٦ = ٠
( ١MSD)
א
W
()٤١٣
٠١
= (٣١A)
٦١
١
J
١١
J
٢
J
٢
אאאאאא
אאאאאאא
אא
א
()٦١
K
אא
()٥٢١٨٧٫٠
٠١
אאא
אא
()٦١
אא
א
()٦١
אאאאא
()٠
אאא
א
K
אאאאאא
אא
K
אאא
(LSD)
אאא
(MSD)
א
W
٥٢١٨٧٫٠
× ٦١= ١٢٫٥
C
٥٫٠
× ٦١= ٨٫٠٠
٨
W
∴()٥٢١٨٧٫٠
٠١
= (.٠C٨)
٦١

א
א
F
١
J
٤٢
WE
אא
()٢٥٫٩٢٣
٠١
אא
K
א
W
אאאאא
٦١
W
٩٢٣÷ ١٦ = ٢٠
( ٩LSD)
٠٢÷ ١٦ = ١
٤
١÷ ١٦ = ٠
( ١MSD)
א
W
∴()٩٢٣
٠١
= ()٩٤١
٦١
אא
()٦١
אא
W
٢٥٫٠
× ٦١= ٨٫٣٢ ٨ (MSD)
٢٣٫٠
× ٦١= ٥٫١٢ ٥
٢١٫٠
× ٦١= ١٫٩٢ ١
٢٩٫٠
× ٦١= ١٤٫٧٢ E
٢٧٫٠
× ٦١= ١١٫٥٢ B
٢٥٫٠
× ٦١= ٨٫٣٢ ٨ (LSD)
אאאאא
()٦
א
W
()٢٥٫٠
٠١
= (١٥٨٫٠EB٨)
٦١
אאא
W
()٢٥٫٩٢٣
٠١
= (١٥٨٫٩٤١EB٨)
٦١
١
J
١١
J
٣
אאאא
Hexadecimal-to-Decimal Conversion
אאאאאאא
א
()٦١
K
אאאאא
אא
K
אא
W
F
١
J
٥٢
WE
אאא
(F٩B)
٦١
אא
K
א
W
אא
: ٦١
٢
٦١
١
٦١
٠
אא
: F ٩B
∴ (F٩B)
٦١
= (F
× ٦١
٢
) + ( ٩
× ٦١
١
) + (B
× ٦١
٠
)
= ( ٥١
× )٦٥٢+ (٩ × ١٦) + (١١ × ١)
= ٠٤٨٣+ ١٤٤ + ١١ = (٣٩٩٥)
٠١
אאאאאאאאאאא
אאאאא
W
……٦١
٣
٦١
٢
٦١
١
٦١
٠
• ٦١
-١
٦١
-٢
٦١
-٣
…….
אא
F
١
J
٦٢
WE
אאא
(A.٥١C٣)
٦١
א
K
א
W
אא
: ٦١
٢
٦١
١
٦١
٠
• ٦١
-١
٦١
-٢
א
א
: A ٥ ١
• C ٣
∴ (A.٥١C٣)
٦١
= (A
× ٦١
٢
) + ( ١
× ٦١
١
) + ( ٥
× ٦١
٠
) + (C
× ٦١
-١
) + ( ٣
× ٦١
-٢
)
= ( ٠١
× )٦٥٢+ (١ × ١٦) + (٥ × ١) + (١٢ × ٠٫٠٦٢٥) + (٣ × ٠٫٠٠٣٩٠٦٢)
= ٠٦٥٢+ ١٦ + ٥ + ٠٫٧٥ + ٠٫٠١١٧١٨٦ = (٢٥٨١٫٧٦١٧)
٠١
١
J
١١
J
٤
אאאאא
Hexadecimal-to-Binary Conversion
אאאא
(٠،١،٢,……,٩,A,B,C,D,E,F)
אאא
(A,B,C,D,E,F)
אאאא
(٠١،١١،١٢،١٣،١٤،١٥)
K
אאאאא
אאא،אא
(٤-bits)
אא
F
١
J
٣
WE
F
١
J
٧٢
WE
א
(٣A٥)
٦١
א
K
א
W
(٣A٥)
٦١
=
٣A ٥
١٠١٠ ٠١٠١ ١١٠٠
= ()١٠١٠٠١٠١١١٠٠
٢
אא
אא
אאא
٠
٠٠٠٠
٠
١
١٠٠٠
١
٢
٠١٠٠
٢
٣
١١٠٠
٣
٤
٠٠١٠
٤
٥
١٠١٠
٥
٦
٠١١٠
٦
٧
١١١٠
٧
٨
٠٠٠١
٨
٩
١٠٠١
٩
٠١
٠١٠١
A
١١
١١٠١
B
٢١
٠٠١١
C
٣١
١٠١١
D
٤١
٠١١١
E
٥١
١١١١
F
F
١
J
٣
E
אאא
K
F
١
J
٨٢
WE
א
(B.٥٣D١)
٦١
אא
K
א
W
(B.٥٣D١)
٦١
= B
٥ ٣
• D ١
١٠١٠ ١١٠٠ ١١٠١
• ١٠٠٠ ١٠١١
= ()١٠٠٠١٠١١٫١٠١٠١١٠٠١١٠١
٢
١
J
١١
J
٥
אאאאא
Binary-to-Hexadecimal Conversion
אא
אאאא
אאאאאאא
אאאא
K
אאאאאא
אא
א
אאאא
K
F
١
J
٩٢
WE
אא
()١٠٠١٠١٫١٠١١١١٠١١
٢
אא
K
א
W
١٠١١ ١١٠١ ١٠٠٠
• ٠٠١٠ ٠١٠١
١
B
D
• A
٤
אאא
K
∴()١٠٠١٠١٫١٠١١١١٠١١
٢
= (١BD.A٤)
٦١
F
١
J
٠٣
WE
אא
()١٠٠١١٠٫١١٠٠١٠٠١٠١١
٢
אאא
K

א
W
١١٠١ ٠١٠١ ١٠٠٠
• ٠٠٠١ ٠١١٠
١
A B
• ٦
٨
∴()١٠٠١١٠٫١١٠٠١٠٠١٠١١
٢
= (١AB.٦٨)
٦١
١
J
١١
J
٦
אאאאא
Hexadecimal-to-Octal Conversion
אאאאאאאאא
אאאאאאא
אאא
W
F
١
J
١٣
WE
א
(AB٣E.٨٧D)
٦١
אא
K
א
W
אאא
א
W
(AB٣E.٨٧D)
٦١
= ()١٠١١١١١٠٠٠٠١٫٠١١١١١٠٠١١٠١٠١٠١
٢
אאאאא
W
٠١١ ١١١ ١٠٠ ١٠١ ٠١٠ ١٠٠
• ١٠١ ١١١ ١٠٠ ٠٠١
١
٢
٦ ٧ ٤ ٥
• ٥ ٧ ١ ٤
אא
K
∴(AB٣E.٨٧D)
٦١
= ()٥٧١٤٫٦٧٤٥٢١
٨
١
J
١١
J
٧
אאאאא
Octal-to-Hexadecimal Conversion
אאאא
،
א
،אאאא
אאאא
W
F
١
J
٢٣
WE
אא
()٢٤٣٫٥٢
٨
אאא
K
א
W
אא
W
∴()٢٤٣٫٥٢
٨
= ()٠١٠٠٠١١١٠٫١٠١٠١٠
٢
אאאאא
W
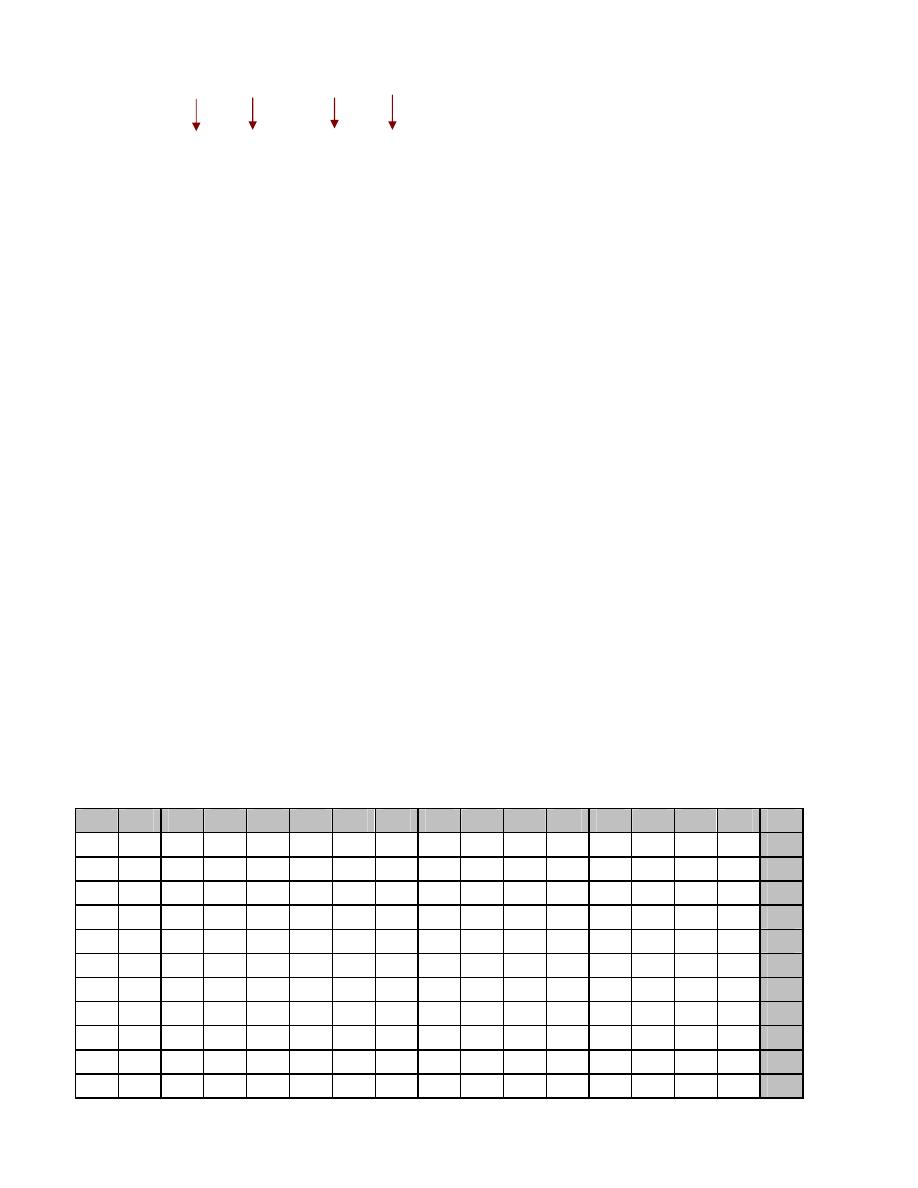
١٠١٠ ١٠٠٠
• ١٠٠٠ ١١١٠
١
٢
• ٧
١
אא
אאאא
K
∴()٢٤٣٫٥٢
٨
= ()١٧٫٢١
٦١
١
J
١١
J
٨
אאאאא
Arithmetic Operations in Hexadecimal System
אאאא
K
١
J
١١
J
٨
J
١
אא
אא
Hexadecimal Addition
אאאא
(٠,F)
אאאא
(F)
()٠١
אא،
()٠١
אאאאאאא
אאא
אאאא
K
א
אאאאאאא
אא
()٩
٦١
א
(A)
٦١
אא
()٩
٦١
(B)
٦١
א
(F)
٦١
K
אא
(F)
٦١
א
()٠١
٦١
אא
אאאאא
(F)
٦١
א
()١١
٦١
אאא
אאאאא
K
א
F
١
J
٤
E
א
،אאא
אאאאאאאאאא
אאאאא
K
+
٠
١
٢
٣
٤
٥
٦
٧
٨
٩
A
B
C
D
E
F
٠
٠
١
٢
٣
٤
٥
٦
٧
٨
٩
A
B
C
D
E
F
١
١
٢
٣
٤
٥
٦
٧
٨
٩
A
B
C
D
E
F
٠١
٢
٢
٣
٤
٥
٦
٧
٨
٩
A
B
C
D
E
F
٠١
١١
٣
٣
٤
٥
٦
٧
٨
٩
A
B
C
D
E
F
٠١
١١
٢١
٤
٤
٥
٦
٧
٨
٩
A
B
C
D
E
F
٠١
١١
٢١
٣١
٥
٥
٦
٧
٨
٩
A
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٦
٦
٧
٨
٩
A
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٧
٧
٨
٩
A
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٨
٨
٩
A
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٩
٩
A
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
A
A
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
٩١
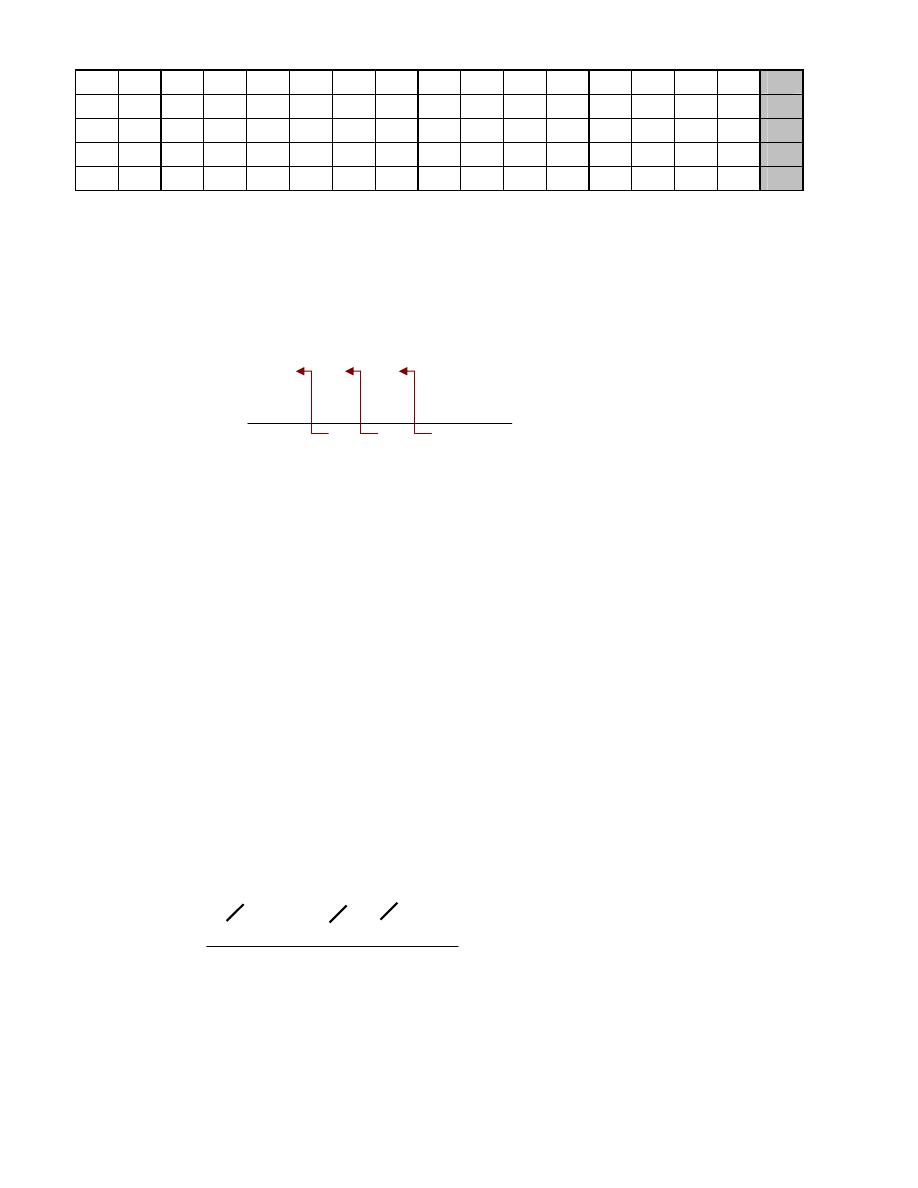
١
١
١
B
B
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
٩١
١A
C
C
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
٩١
١A
١B
D
D
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
٩١
١A
١B
١C
E
E
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
٩١
١A
١B
١C
١D
F
F
٠١
١١
٢١
٣١
٤١
٥١
٦١
٧١
٨١
٩١
١A
١B
١C
١D
١E
F
١
J
٤
E
אאאא
K
F
١
J
٣٣
WE
אא
W
(٥٣AB٢)
٦١
+ (١A٦٧٥)
٦١
א
W
אאאאאא
K
٣
٥A B ٢
+ ١A ٦
٧
٥
٥
٠
١
٢
٧
∴(٥٣AB٢)
٦١
+ (١A٦٧٥)
٦١
= ()٧٢١٠٥
٦١
١
J
١١
J
٨
J
٢
אאאא
Hexadecimal Subtraction
אאאאא
W
•
אאאאאאא
אאאאא
K
•
אא
א
()١
אאאאא
אאאאאאאא
אא
W
F
١
J
٤٣
WE
אא
W
(F٢ABD)
٦١
– (EF٤CE)
٦١
א
W
F
٢A B D
– E
F
٤C E
٣
٥E D
אאא
K
١
١
A
٩
١
E


١
E
אאאאאא
W
a)
٤٦b) ١١٢ c) ٢٥٧ d) ٢٧{٢٦
e)
٧٧{٠٦٢٥ f) ٤٧{٨٧٥ g) ٣٣{١٢٥
٢
E
אאאאאא
W
a)
١١٠١١b) ١١١٠١٠١ c) ١١١١١١ d) ١١١٠{١١
e)
١٠١٠١{١١٠١ f) ١١٠٠٠٠١{١١٠١١
٣
E
אאאא
W
a)
٠٠١+ ١١١
b)
٠١١١{١١ + ١١{١٠
c)
١١١١+ ١١٠١
d)
١٠٠١{١٠١ + ١١٠١{١١
٤
E
אאאאא
W
a)
١٠١١– ٠١٠٠
b)
١٠٠١– ٠١١١
c)
٠١٠١١– ١٠١١١
d)
٠٠١١– ١٠٠١
٥
E
אאאאאא
W
a)
١٠١٠١١٠٠
b)
٠٠١٠٠١١١
c)
١٠١٠١٠٠٠
٦
E
אאאאאא
W
a)
٠١١٠١١١١
b)
١٠١١١٠١٠
c)
١١٠٠١١٠٠
٧
E
א
אאא
אאאאאאא
אא
(
٨-bits)
W
a)
H ٨٢
b) –
٣٨c)
H ٩٩
d) –
٠٢١
٨
E
א
אאאאאאאאא
אא
(
٨-bits)
W
a)
H ٤١
b) –
٣٦c)
H ٧٠١d)
–
٢٢١

٩
E
אא
F
٨
E
אאאא
K
٠١
E
אאאאאאאאא
אא
W
a)
١٠٠٠١١١٠١
b)
٠٠١٠٠١١٠
c)
١١٠٠١١٠١
١١
E
אאאאאאאאאאא
W
a)
١٠١١١٠٠١
b)
٠١١٠٠١١٠
c)
١٠١١٠١٠١
٢١
E
אאאאאאאאאאא
W
a)
١١٠١٠١٠١
b)
١٠١١١١٠٠٠
c)
١١٠١١١٠١
٤١
E
אאאאא
W
a)
٠١١٠١٠٠٠– ٠٠١١٠٠١١
b)
٠٠٠٠١١١٠– ١٠١٠١١١١
c)
٠٠١١٠٠٠١– ٠٠١١١٠٠١
d)
١٠٠١١٠١١– ١١١٠٠١١١
٥١
E
אאאאאאא
W
a)
٠٥
b)
٠٠١
c)
١٩٣٦
d)
٧٧{٣٧٥
e)
٠٢١{٥١٥٦٢٥ f) ١٤٤{٥٦٢٥ g) ٩١٥{١٤١
٦١
E
אאאאאאא
W
a)
٢٤
b)
٤٥٢
c)
٧٥٠١
d)
٧٣{٥
e)
٦٩{١١
f)
٥١١{٣
g)
٧٦٣٤١{١٢
٧١
E
א
אאאאאא
W
a)
٢٧
b)
٣١١
c)
٦١{٣ d)
٧٣{٦
e)
٢٢١{٧٧٥
f)
٧١٤{٦٣٢
g)
٦٧٢{٦٢١
٨١
E
אאאאאאא
W
a)
١٠١٠١١{١١٠١ b)
٠٠١٠١١١١{١١٠١٠١
c)
١١١٠١١٠١١{١٠١٠١
d)
١١٠١٠٠١٠٠٠١{١٠٠١ e)
١١١٠١٠١{١١١٠١
٩١
E
אאאא
W
a) (
)٥١
٨
+ (
)٧١
٨
b) (
)٤٤
٨
+ (
)٦٦
٨
c) (
)٣٢١
٨
+ (
)١٢٣
٨
d) (
)٢٧٢
٨
+ (
)٦٥٤
٨

٠٢
E
אאאא
W
a) (
)٢٣
٨
– (
)٥٢
٨
b) (
)٧٤١
٨
– (
)٤٧
٨
c) (
)٥١٣
٨
– (
)٢٢٢
٨
d) (
)٧٣٤
٨
– (
)٠٤٣
٨
١٢
E
אאאאאאאא
W
a)
٤١
b)
٠٨
c)
٠٦٥
d)
٠٠٠٣
e)
٠٠٥٢٦f)
٤٠٢{١٢٥ g) ٢٥٥{٨٧٥ h)
١٣٦{٢٥
٢٢
E
אאאאאא
א
W
a)
٩F
b) D
٢٥
c)
٧٦F
d) ABCD
e) F.
٤
f) B
.٣E
g)
١١١١{١ h)
٨٨٨{٨
٣٢
E
אאאאאאאאא
W
a)
٨
b)
١C
c) A
٤٦d) ١F.C e)
٩٣٢{٤
٤٢
E
אאאאא
אאא
W
a)
١٠٠١{١١١١
b)
٠٠٠٠١{١
c)
١٠١٠١١{١١٠٠١
d)
١١١٠٠١٠١{١١١٠١١ e) ١٠٠٠٠٠٠{٠٠٠١١١
f)
٠٠١١١١١{١٠٠٠٠١١
٥٢
E
אאאאאא
W
a)
٣١A
b)
٥٢E٦
c)
٦١٠٣
d) B
.٤C
e)
.٨٧D٣
f)
.٩٥٦٢F٤١
٦٢
E
אאאאאא
W
a)
٧٣
b)
٥٢٧c) ٢٤٧٦{٢
d)
٧١١١{١٦
e)
٠٠٦١{٥٢٤
f)
٠٠٠٣{٦١٢٥
٧٢
E
אאאא
W
a) (
)١٤
٦١
+ (
)٦٣
٦١
b) (C
)٨
٦١
+ (
٣A)
٦١
c) (
٩B)
٦١
+ (
)٥٦
٦١
d) (
١١D)
٦١
+ (
٢E١)
٦١
f) (
٧٧CB٥)
٦١
+ (A
٥F٧٢)
٦١
g) (
٣١EFD)
٦١
+ (
١٢BB٣)
٦١

-
١
-
אאאא
אאאא
א
א
אאא
ã¹]<gè…‚jÖ]æ<ËÖ]<Üé×Ãj×Ö<íÚ^ÃÖ]<퉉ö¹]
אאאא
אא
אא
٢

אא
٧٤١
א
א
אאאא
א
-
٥٣
-
אאא
אא
W
•
אאאאא
K
•
אאאאא
K
•
אאאא
K
•
אאאאא
K
•
אאאאא
K
•
אאאא
K
•
אאאאא
K
•
אאאאאאא
K
אא
٧٤١
א
א
אאאא
א
-
٦٣
-
٢
J
١
Introduction
א
אא
J
א
J
א
J
א
J
،אא
אאאא
א
אאאא،אאאא
אאאאאא،אא
אאא
K
،אאאאא
?
אא
?
א
אאאאא
אא
K
א
אאאאאאא
אא
AND
א،
OR
א،
NOT
א
(INVERTER)
K
א
،אאאאאאאאא
א
אאא
K
٢
J
٢
אא
Logic Signal Levels
אאאאאא
אא،אא
K
אאאא
א
،،
،א
אאא
אא،א
אאא
J
א
א
(HIGH)
א
(
)١
א،א
(LOW)
א
(
)٠
אא،א
(
)١
א
א
(TRUE)
،
אא
(
)٠
אאא
(FALSE)
K
א،א
(Positive Logic)
،
א
א
(Negative Logic)
K
אאאאא
(
)١
א
אא
(
)٠
אא،אא،א
(
)٠
א
אא
(
)١
אאא
K
אא
٧٤١
א
א
אאאא
א
-
٧٣
-
٢
J
٣
א
AND
AND Gate
אא
AND
אאאאא
אאא
(Logic Functions)
K
אא
AND
אא،א
א
(Logical Multiplication)
،
אאאא
אאא
א
F
٢
J
١
E
،
א
A
,
B
א
אאא
(Two Binary Variables)
(
)٠
א
א
(Open)
(
)١
אא
(Closed)
K
F
٢
J
١
E
אא
AND
אא
K
א
"
L
"
אאא
(
)١
א
(ON)
(
)٠
א
(OFF)
K
אא
،
،א
F
٢
J
١
E
אא
א
(L)
א
K
אא
(L)
אאאא،א
(Truth Table)
K
L
B
A
F
٢
J
١
E
אא
F
٢
J
١
KE
Voltage Source
(A)
(L)
(B)
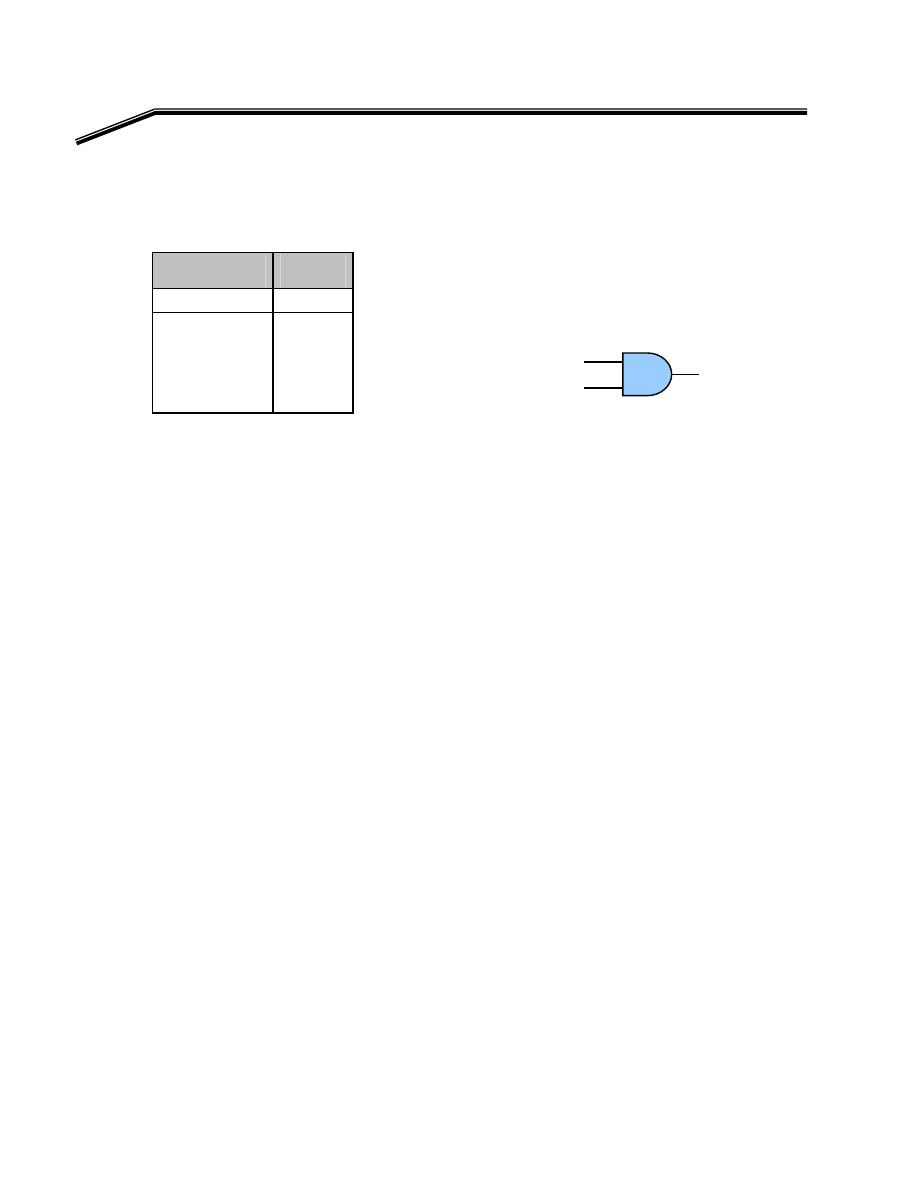
אא
٧٤١
א
א
אאאא
א
-
٨٣
-
א
F
٢
J
٢
E
אאא
(Standard)
א
AND
א،
A
,
B
א
Y
אא،
AND
K
א
F
٢
J
٢
E
אא
AND
K
א
א
Y
B
A
٠
٠
٠
٠
١
٠
٠
٠
١
١
١
١
F
٢
J
٢
E
אא
AND
K
F
٢
J
٢
E
אא
AND
K
א
(bits)
،
א
(
)١
א
א
A
,
B
(
)١
،א
א
AND
،אא
א
(
)١
א
(
)١
K
אא
J
אאא
א
W
n
2
N
=
W
N
אא
n
אא
K
W
אא
4
2
N
2
=
=
אא
8
2
N
3
=
=
אא
16
2
N
4
=
=
F
٢
J
١
EW
•
אאא
AND
K
•
אא
AND
؟
א
W
א
AND
،אא
F
٢
J
٣
E
א
אא
K
Y
B
A
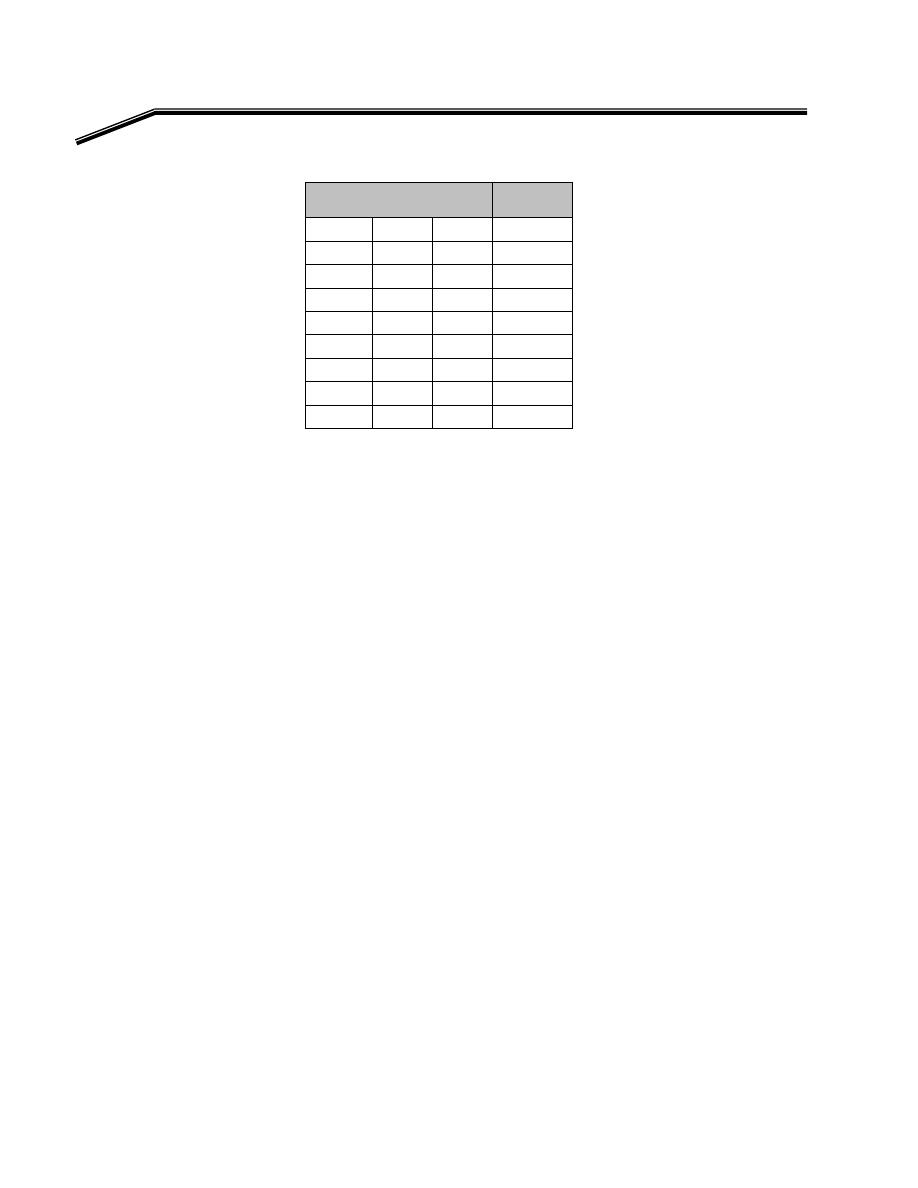
אא
٧٤١
א
א
אאאא
א
-
٩٣
-
א
א
Y
C
B
A
٠
٠
٠
٠
٠
١
٠
٠
٠
٠
١
٠
٠
١
١
٠
٠
٠
٠
١
٠
١
٠
١
٠
٠
١
١
١
١
١
١
F
٢
J
٣
E
אא
AND
K
•
אאא
W
32
2
2
N
5
n
=
=
=
אא
(Boolean Algebra)
אאאא
אא،א
(Boolean Expression)
אא
K
אאא
AND
א
W
B
A
Y
•
=
א
W
א
Y
A AND B
F
•
AND
E
א،
אא
W
Y = AB
א
Y
A AND B
K
אאא
(Pulses)
א
א
(HIGH)
א
(LOW)
K
א
א
AND
אא،אא
א
K
،
F
٢
J
٣
E
א
A
,
B
(
)١
א
א
t
١
אא
Y
א
(
)١
،
אא
t
٢
א،
A
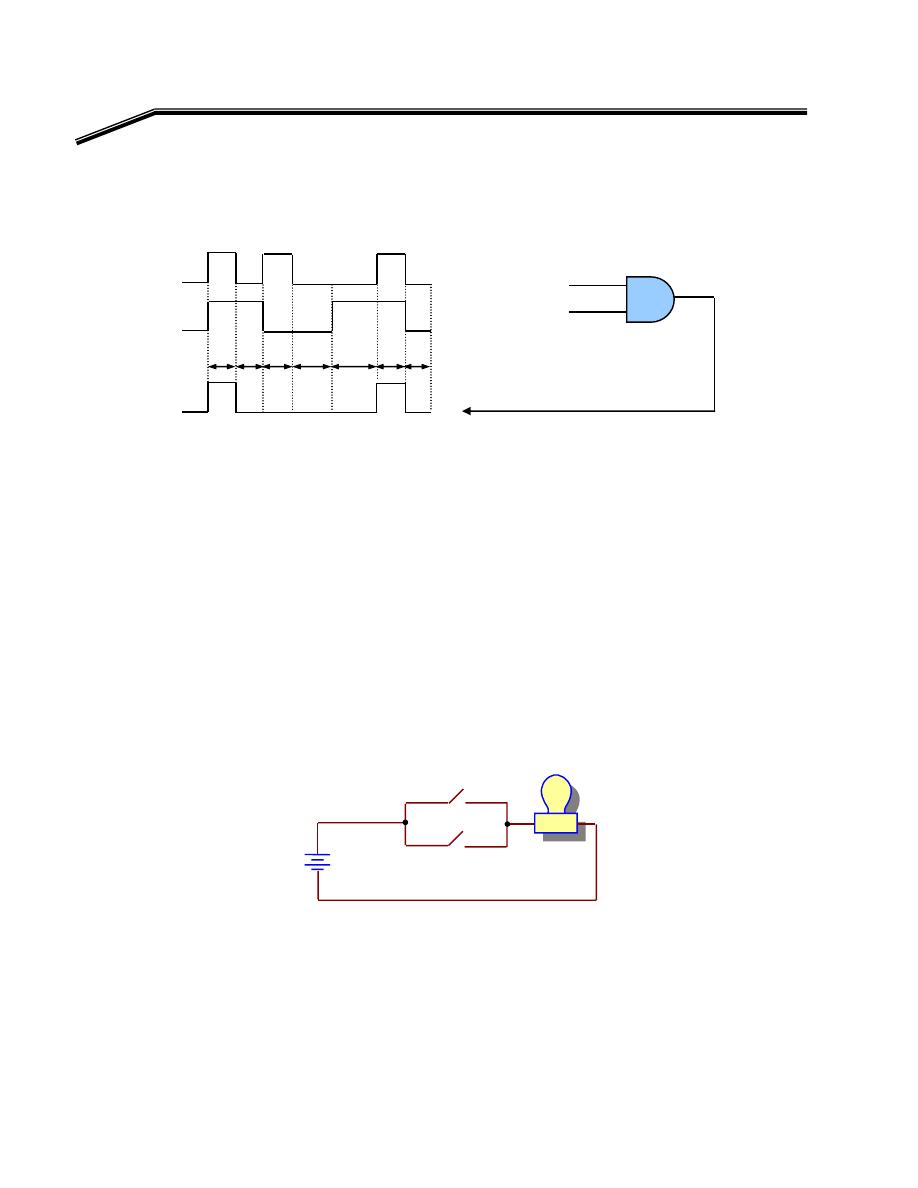
אא
٧٤١
א
א
אאאא
א
-
٠٤
-
(
)٠
א
B
א
Y
(
)٠
،
אאא
אא
K
אאא
אאא
(Timing Diagram)
K
F
٢
J
٣
E
אאא
AND
K
٢
J
٤
א
OR
OR Gate
אא
OR
אאאאאאאא
K
אא
OR
،א
אאא
(Logical Addition)
אאאאאאא،
F
٢
J
٤
E
K
אא
AND
א
A
,
B
(
)٠
א
(Open)
(
)١
א
(Closed)
K
F
٢
J
٤
E
אא
OR
אא
K
F
٢
J
٤
E
אא،אאא
אא
(L)
א
K
Voltage Source
(B)
(A)
Y
B
A
t
٧
t
٦
t
٥
t
٤
t
٣
t
٢
t
١
Y
A
B
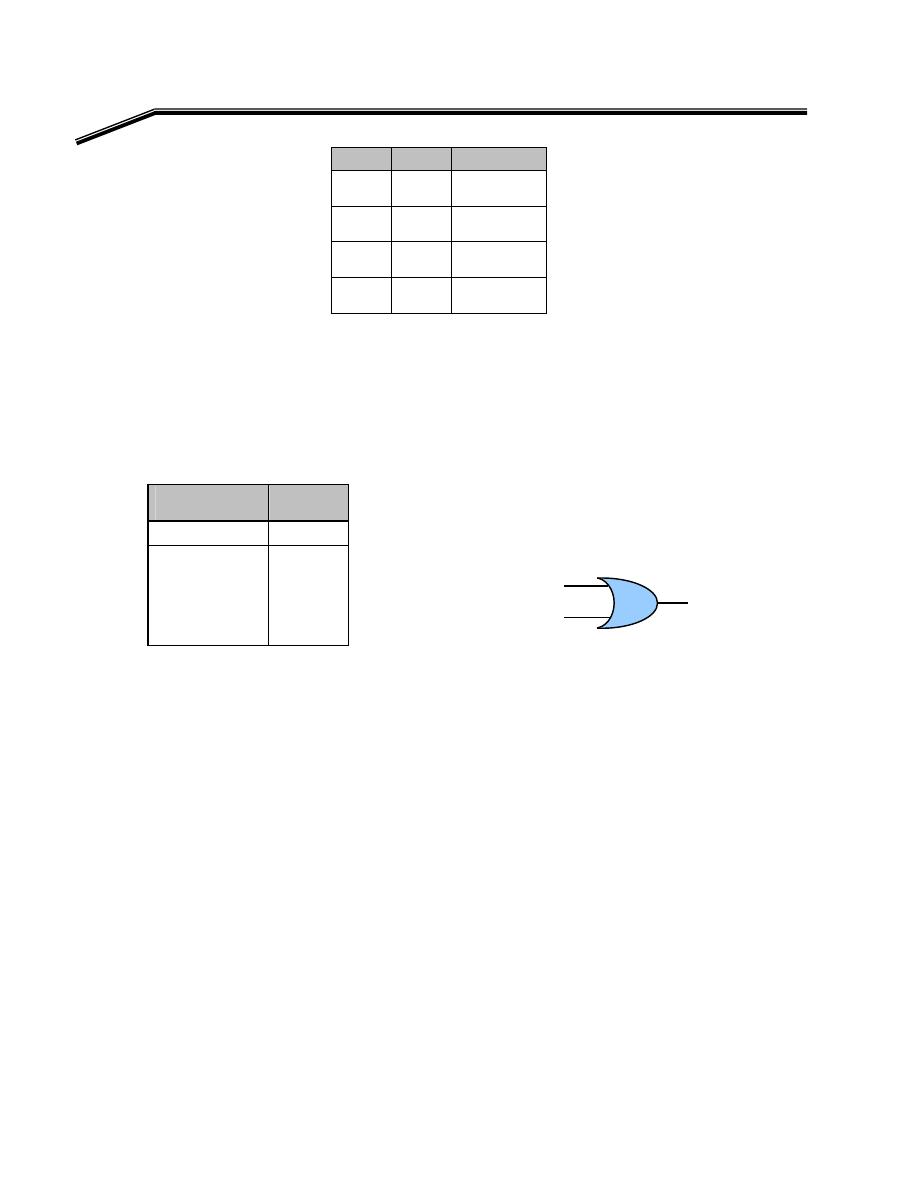
אא
٧٤١
א
א
אאאא
א
-
١٤
-
L
B
A
F
٢
J
٤
E
אא
F
٢
J
٤
KE
א
F
٢
J
٥
E
אאאא
OR
א،
A
,
B
א
Y
K
א
F
٢
J
٥
E
אא
OR
K
א
א
Y
B
A
٠
٠
٠
١
١
٠
١
٠
١
١
١
١
F
٢
J
٥
E
אא
OR
K
F
٢
J
٥
E
אא
OR
K
א
F
٢
J
٥
E
א
(
)١
א
א
(
)١
،
א
(
)٠
א
(
)٠
א
K
אאא
OR
א
W
Y = A + B
א
W
א
Y
A OR B
+)
OR
(
K
א
א
OR
،אא
א
AND
אאא
א
K
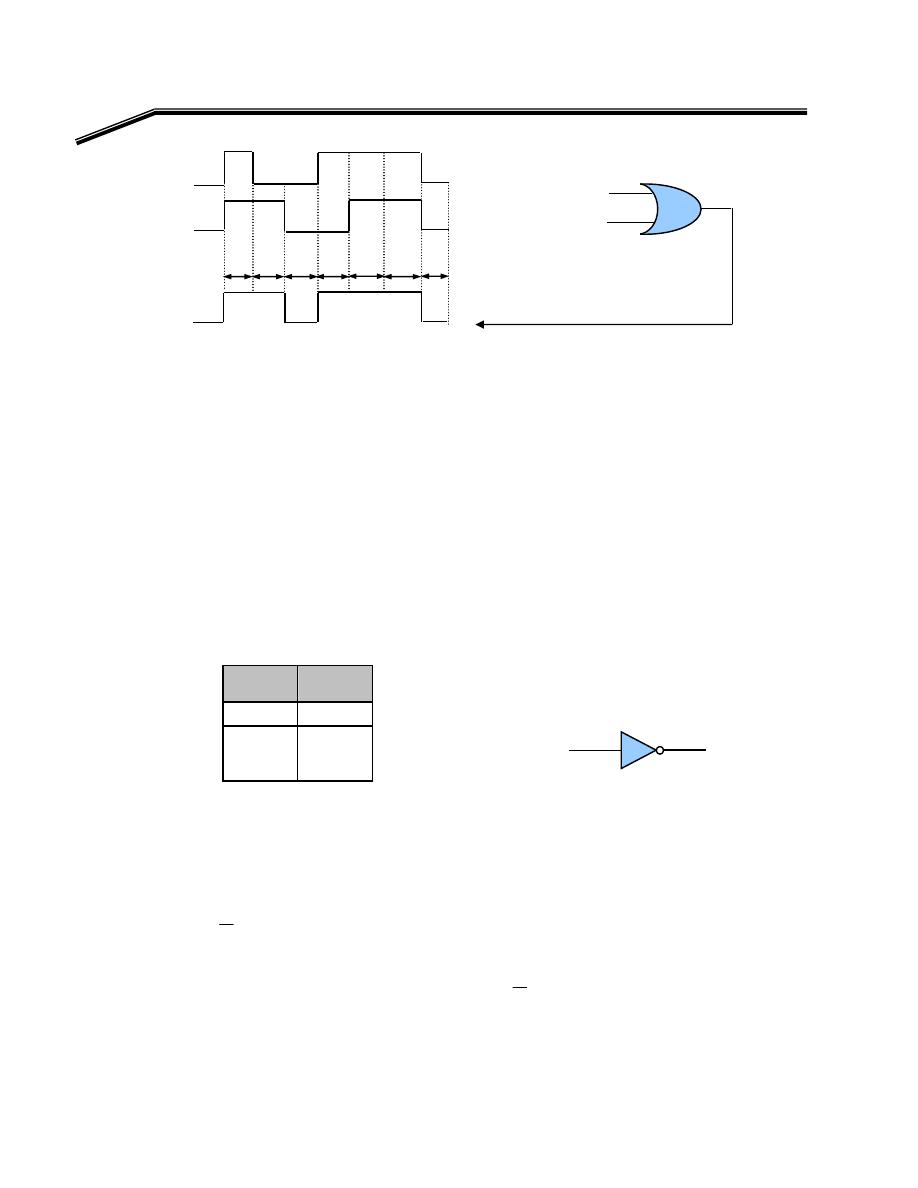
F
٢
J
٦
E
א
A
,
B
(
)١
אא
t
١
א
א
Y
א
(
)١
،
אא
t
٢
א،
A
(
)٠
א
B
א
Y
(
)١
،
אאאאא
K
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٢٤
-
F
٢
J
٦
E
אאא
OR
K
٢
J
٥
א
NOT
F
א
E
NOT Gate (INVERTER)
אא
NOT
א
(Inversion)
א
(Complementation)
K
א،אאא
(
)١
א
(
)٠
،
א
(
)٠
(
)١
K
אא
NOT
אאא
K
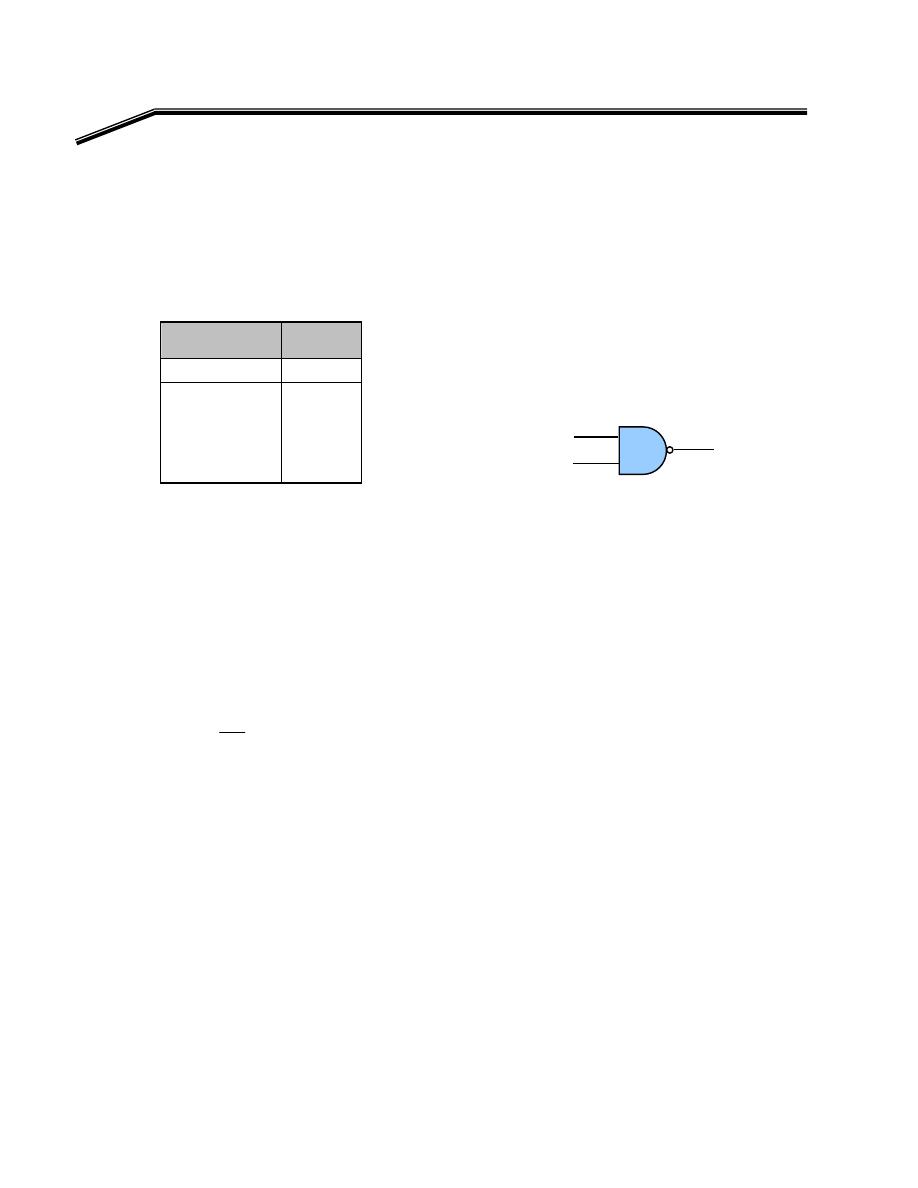
F
٢
J
٧
E
א،אאאאא
F
٢
J
٦
E
אאא
K
א
א
Y
A
١
٠
٠
١
F
٢
J
٧
E
אא
NOT
K
F
٢
J
٦
E
אא
NOT
א
K
א،אאא
אא
W
Y =
A
אא
W
א
Y
not A
א
A
bar
א
،א
א
Y
A bar
F
A
E
K
٢
J
٦
א
NAND
NAND Gate
Y
A
B
Y
t
٧
t
٦
t
٥
t
٤
t
٣
t
٢
t
١
A
B
Y
A
אא
٧٤١
א
א
אאאא
א
-
٣٤
-
(NAND)
א
(NOT AND)
AND
אא،
אאאאא
AND
F
٢
J
٨
E
،
אאא
אא
א
AND
א
אאאא
K
F
٢
J
٧
E
אא
NAND
K
א
א
Y
B
A
١
٠
٠
١
١
٠
١
٠
١
٠
١
١
F
٢
J
٨
E
אא
NAND
K
F
٢
J
٧
E
אא
NAND
K
אא
(
)٠
אאא
(
)١
א،א
(
)١
אאא
(
)٠
،א
אאא
AND
K
אא
NAND
،אאאאאאא
אאאא
NOT,
OR, AND
،
אא،אא
NAND
א
W
Y =
AB
אא
NAND
،אא
אא
NAND
(
)٠
א
(
)١
K
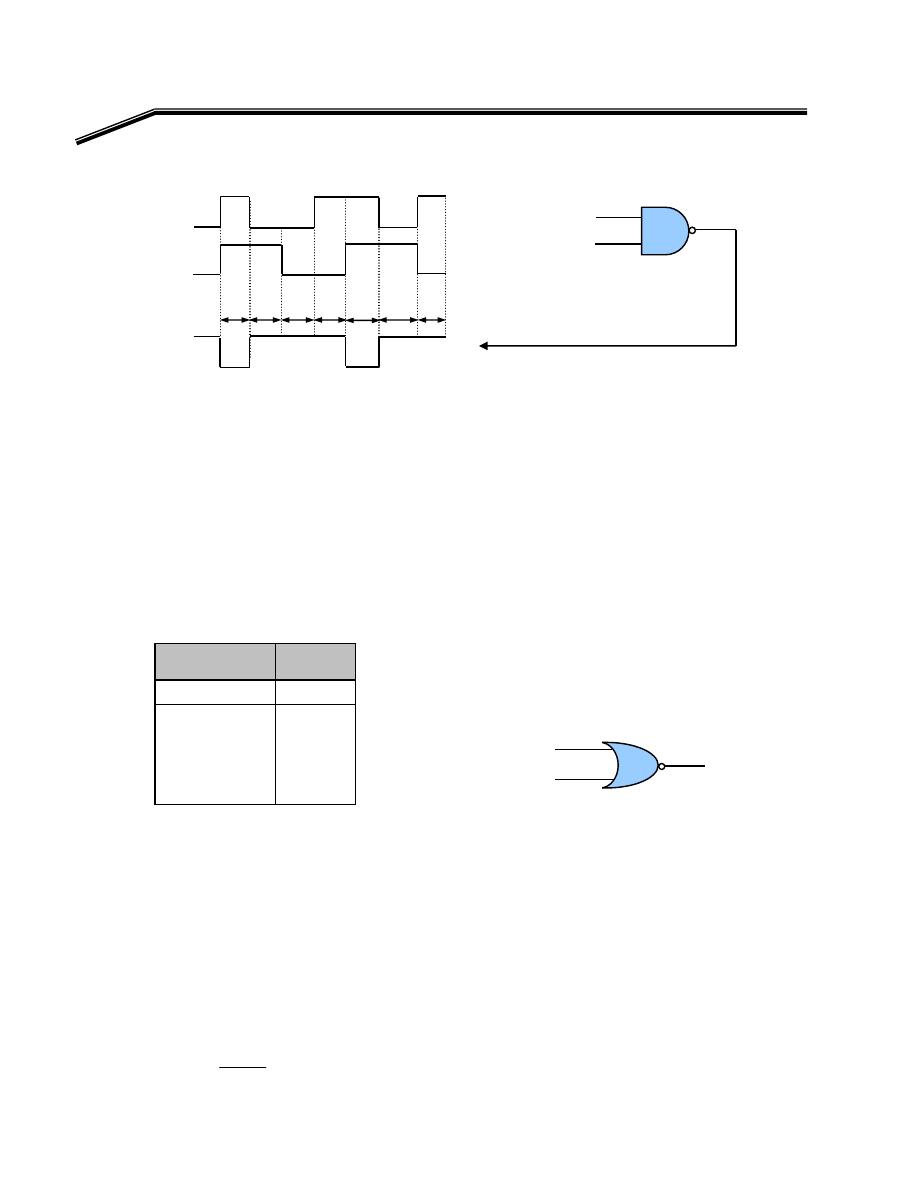
F
٢
J
٩
E
א
A
,
B
(
)١
אא
t
١
א
א
Y
א
(
)٠
،
אא
t
٢
א،
A
(
)٠
א
B
(
)١
א
Y
(
)١
،
אאא
אא
K
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٤٤
-
Y
B
A
F
٢
J
٩
E
אאא
NAND
K
٢
J
٧
א
NOR
NOR Gate
(NOR)
א
(NOT OR)
OR
אא،
אאא
(NOT gate)
אא
OR
F
٢
J
٠١
E
،
אאאא
NOR
K
אא
NOR
F
٢
J
٨
KE
א
א
Y
B
A
١
٠
٠
٠
١
٠
٠
٠
١
٠
١
١
F
٢
J
٠١
E
אא
NOR
K
F
٢
J
٨
E
אא
NOR
K
אא
(Y)
(
)٠
אא
א
(
)١
א
א،
(
)١
אא
(
)٠
א
K
אא
NOR
אאא
NAND
אאאאאא
א،א
NOT, OR, AND
،
K
א
אא
NOR
W
Y =
B
A
+
Y
t
٧
t
٦
t
٥
t
٤
t
٣
t
٢
t
١
A
B
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٥٤
-
Y
A
B
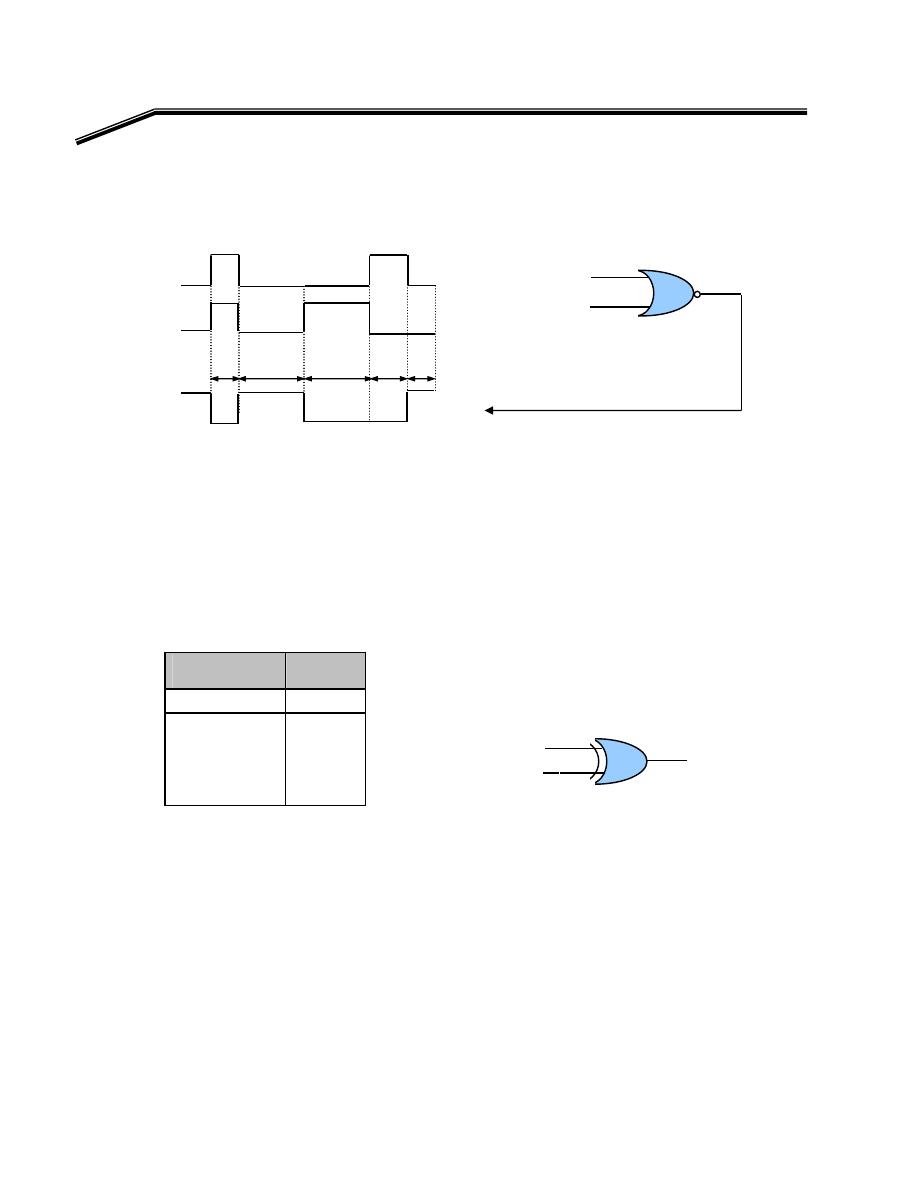
F
٢
J
١١
E
א
NOR
א
A
,
B
א
،א
אא
NOR
אא
(Y)
א
K
F
٢
J
١١
E
אאא
NOR
K
٢
J
٨
א
OR
א
F
א
E
Exclusive-OR Gate
אא
OR
אא
?
?
XOR-gate
،
F
٢
J
٢١
E
אאא
K
אא
XOR
אאא
א
K
א
א
Y
B
A
٠
٠
٠
١
١
٠
١
٠
١
٠
١
١
F
٢
J
٢١
E
אא
XOR
K
F
٢
J
٩
E
אא
XOR
K
אא
XOR
(
)٢ ٩
،
אא
(Y)
(
)١
אא
A
,
B
،
(
)١
א
(
)٠
،א
(
)٠
א
K
אא
XOR
אא
OR
אאא
A = B =
١
אא،
XOR
(
)١
א
(
)١
(
)١
،אא
א
אאאאא
K
Y
t
٥
t
٤
t
٣
t
٢
t
١
A
B
Y
B
A
אא
٧٤١
א
א
אאאא
א
-
٦٤
-
אאאאאא
W
Y =
B
A
B
A
+
א
א
אא
W
Y = A
⊕ B
א
⊕
A
B
K
אאאא
XOR
אאאא
AND, OR, NOT
אא،
F
٢
J
٣١
E
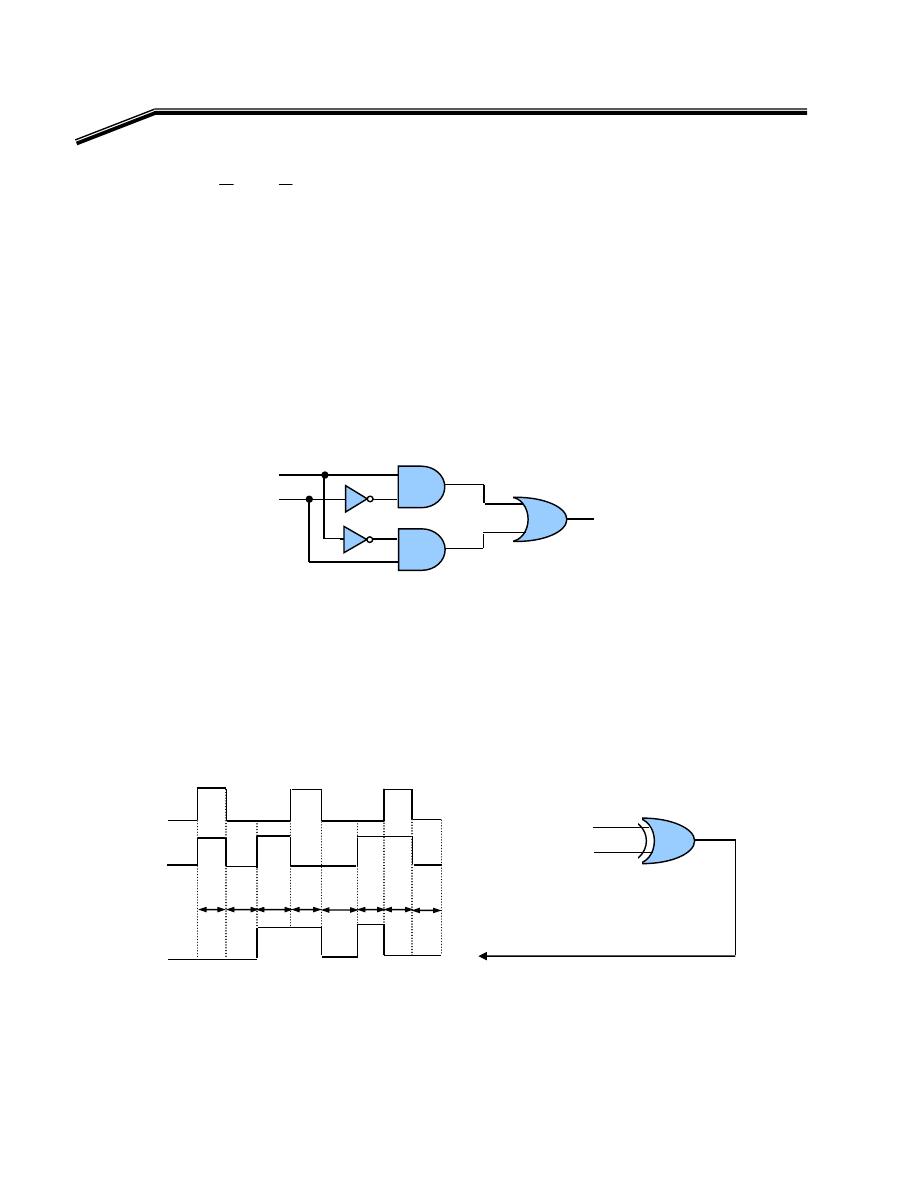
אא
א
אא
XOR
א
K
F
٢
J
٣١
E
אא
XOR
א
AND, OR, NOT
K
F
٢
J
٤١
E
אא
XOR
א
אאא،א
א
K
F
٢
J
٤١
E
אאא
XOR
K
t
٨
t
٧
t
٦
t
٥
t
٤
t
٣
t
٢
t
١
A
B
Y
Y
A
B
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٧٤
-
Y
A
B
٢
J
٩
א
NOR
א
F
א
E
Exclusive-NOR Gate
אא
NOR
א
XNOR-gate
א،
א
אאא
XOR
،
F
٢
J
٥١
E
אאא
K
אא
XNOR
F
٢
J
٠١
E
אא،
(Y)
(
)١
אא
A, B
A = B =
٠
A = B =
١
(
)٠
א
(
)١
א
(
)٠
،א
(
)١
א،אא
א
אאאא
K
א
א
Y
B
A
١
٠
٠
٠
١
٠
٠
٠
١
١
١
١
F
٢
J
٥١
E
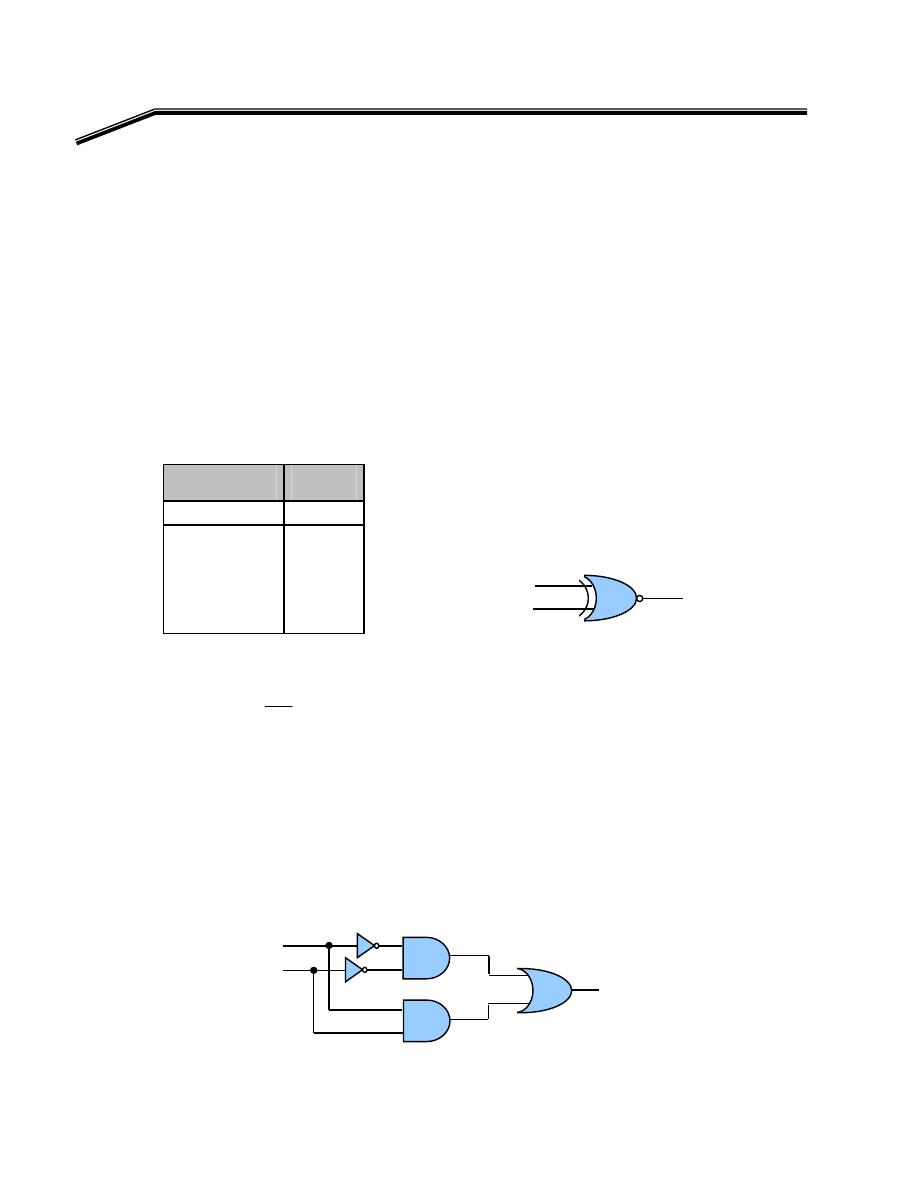
אא
XNOR
K
F
٢
J
٠١
E
אא
XNOR
K
אאאאאא
W
Y =
B
A
AB
+
אאא
W
Y = A ~ B
א
~
א
K
אאאא
XNOR
אא
אא
AND, OR, NOT
אא،
F
٢
J
٦١
E
אאא
אא
XNOR
א
K
F
٢
J
٦١
E
אא
XNOR
א
AND, OR, NOT
K
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٨٤
-
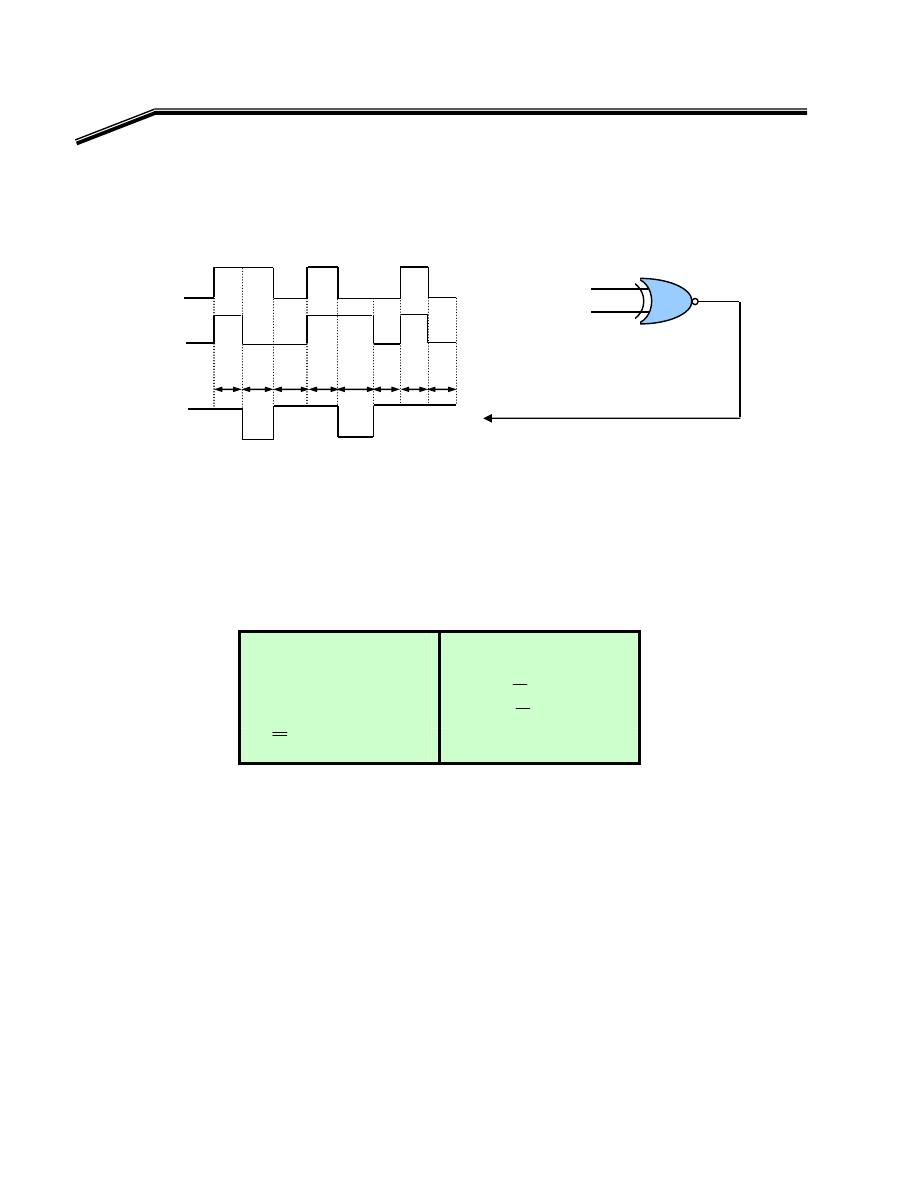
F
٢
J
٧١
E
א
XNOR
א
A
,
B
،א
אא
XNOR
אא
(Y)
K
F
٢
J
٧١
E
אאא
XNOR
K
٢
J
٠١
אאא
Rules of Boolean Algebra
F
٢
J
١١
E
אאאא
אאא
א
K
.٢A + ١ = ١
.١A + ٠ = A
.٤A • ١ = A
.٣A • ٠ = ٠
.٦A + A = ١
.٥A + A = A
.٨A • A = ٠
.٧A • A = A
.٠١A + AB = A
.٩A = A
F
٢
J
١١
E
אאאא
K
אאאאאאא
א
K
א
(
١)
:
A +
٠ = A
אאא
א
OR
א
(
)٠
،אא
A
א،
(
)١
(
)٠
K
א
A=
١
א
(
)١
א
A
K
א
A=
٠
א
(
)٠
A
K
א
OR
(
)٠
א
אא
(A +
٠= A)
K
א
(
٢)
:
A +
١ = ١
אאאא
OR
א
(
)١
א
،א
A
א،
(
)١
א
(
)٠
K
(
)١
אא
OR
א
Y
t
٨
t
٧
t
٦
t
٥
t
٤
t
٣
t
٢
t
١
A
B
Y
A
B

אא
٧٤١
א
א
אאאא
א
-
٩٤
-
(
)١
אאא
אא
K
א
OR
(
)١
אא
(
)١
(A +
١= ١)
K
א
(
٣)
:
A
• ٠ = ٠
אאאא
AND
א
(
)٠
،אא
A
،
אא
(
)٠
א
אאאא
K
א
AND
(
)٠
אא
(
)٠
(A
• ٠= ٠)
K
א
(
٤)
:
A
• ١ = A
אאאא
AND
א
(
)١
א
،א
A
،
אא
(A)
،
אא
A=
٠
אא
AND
(
)٠
،
אא
A=
١
אא
AND
(
)١
אא
(
)١
K
א
AND
(
)١
א
אא
(A
• ١= A)
K
א
(
٥)
:
A + A = A
אא
אא
OR
א
A
،
אאא
K
אא
A =
٠
٠+ ٠= ٠
אא،
A =
١
א
١+ ١= ١
K
א
(
٦)
:
1
A
A
=
+
א
W
א
A
א
OR
א
A
אאאא
אא
(
)١
K
א
A=
٠
1
1
0
0
0
=
+
=
+
K
א
A =
١
1
0
1
1
1
=
+
=
+
K
א
(
٧)
:
A
• A = A
אא
A
אא
AND
אא
א
K
אא
A =
٠
٠• ٠= ٠
אא،
A =
١
א
١• ١= ١
،
א
אא
AND
א
A
K
א
(
٨)
:
0
A
A
=
•
א
A
א
AND
א
A
אא
אא
אא
(
)٠
،
אאא
A
A
(
)٠
،א
(
)٠
א
AND
אא
(
)٠
K
א
(
٩)
:
A
A
=
אאאא
K
אא
A =
٠
(
)١
،
א
(
)١
(
)٠
אא
K
אא
٧٤١
א
א
אאאא
א
-
٠٥
-
א
(
٠١)
:
אאא
(
)٢
א
(
)٤
W
A + AB = A (
١+ B)
= A (
)١
= A
٢
J
١١
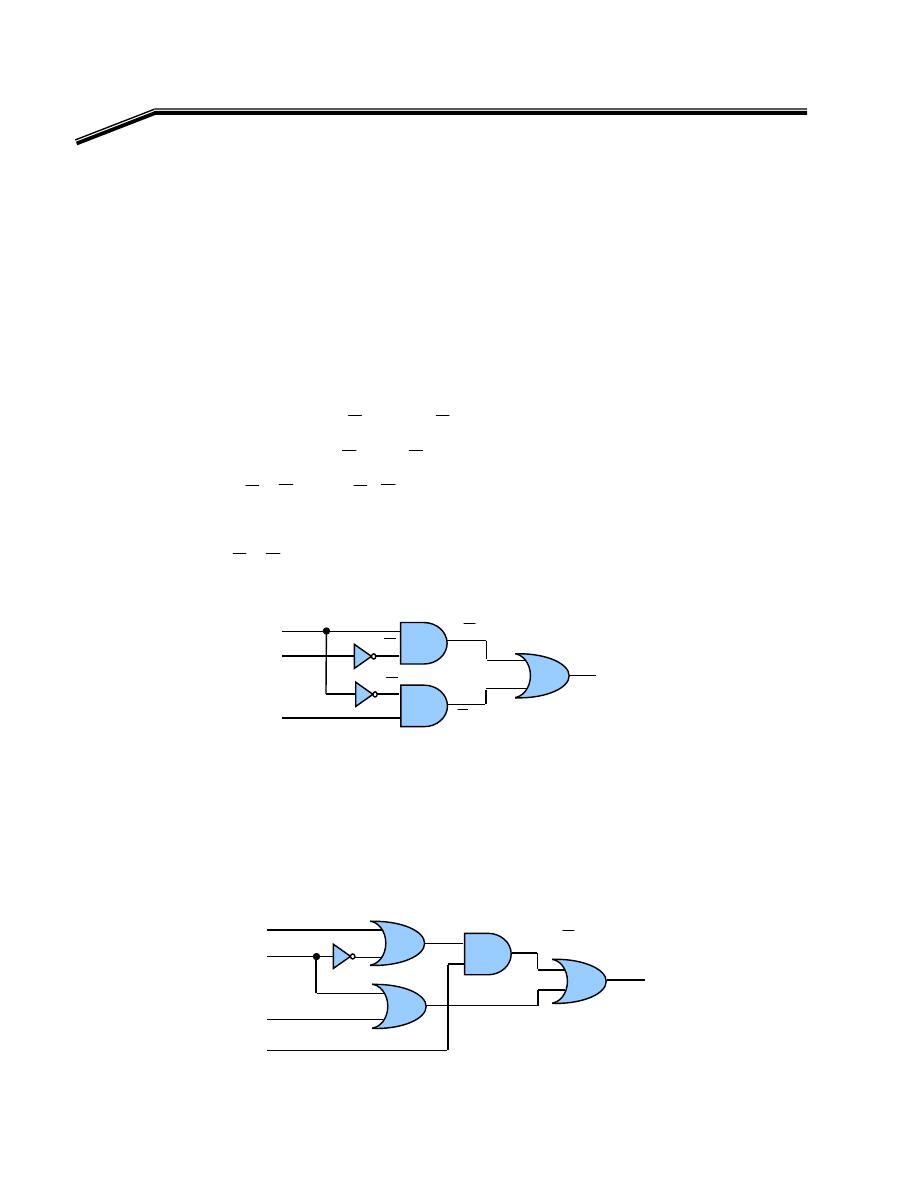
אאא
The Boolean Expression for a Logic Circuit
،אאא
אא
אא
אאא
K
אאא،
א
F
٢
J
٨١
E
K
אא
אאא
W
١
K
אאא
AND
אא
B
A,
B
A
K
٢
K
אאא
AND
אא
,C
A
C
A
K
٣
K
אאא
OR
אא
C
A
,
B
A
C
A
B
A
+
K
אאא
W
C
A
B
A
Y
+
=
F
٢
J
٨١
E
אאאא
K
F
٢
J
٢
EW
א
אאאאא
F
٢
J
٩١
E
K
א
W
)
B
A
(
D
+
C
B
+
C
B
+
D
C
Y
A
B
B
A
A
B
C
A
Y
A
B
C

אא
٧٤١
א
א
אאאא
א
-
١٥
-
F
٢
J
٩١
E
אאא
F
٢
J
٢
E
אאא
K
אאאאא
W
)
C
B
(
)
B
A
(
D
Y
+
+
+
=
٢
J
٢١
א
אאא
Implementation of a Logic Circuit Using a Boolean Expression
אאאא
אא
K
אאאא
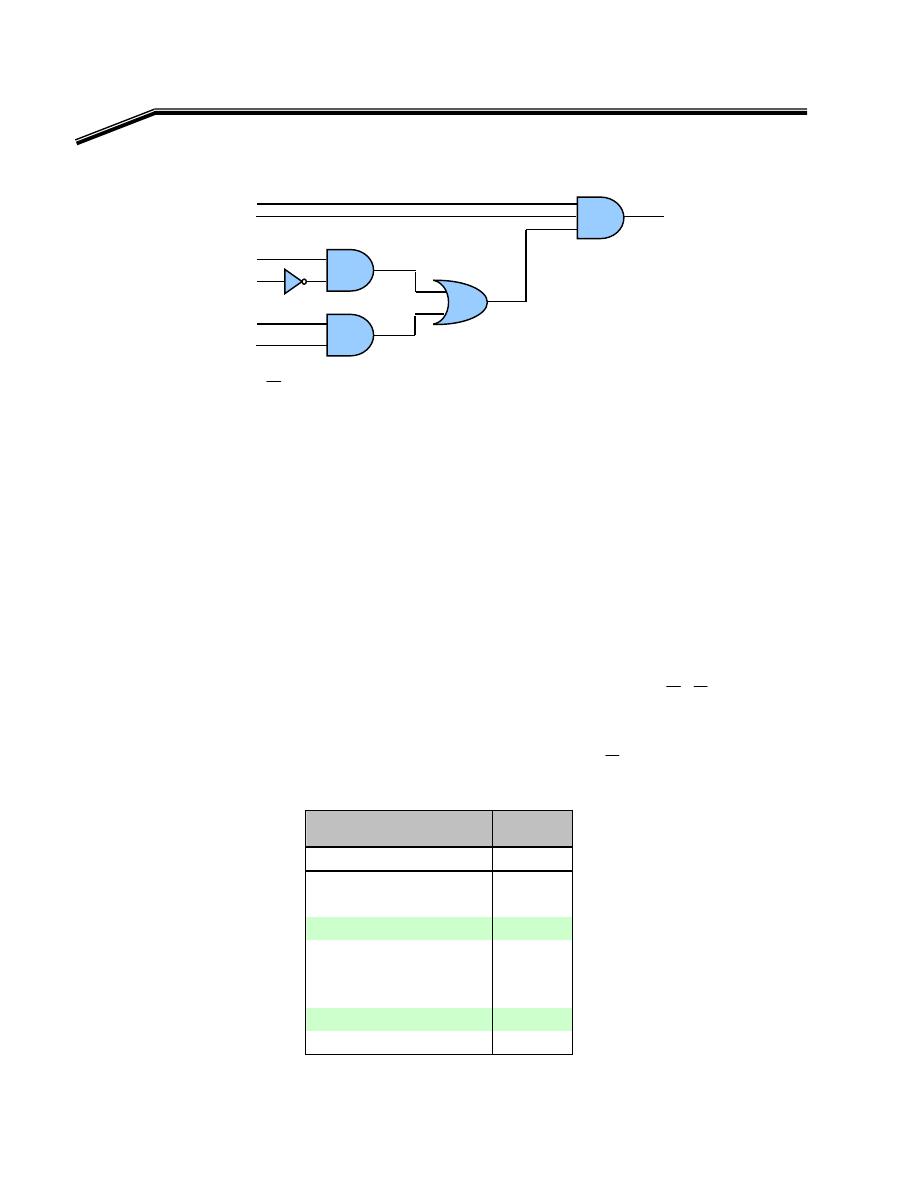
W
)
EF
D
C
(
AB
Y
+
=
אאאאא
A
,
B
)
EF
D
C
(
+
א
AND
א،
)
EF
D
C
(
+
D
,
C
א
AND
،
E,F
א
AND
אא،
AND
א
OR
K
אא
W
)
EF
D
C
(
B
A
Y
+
=
אאאאא
)
EF
D
C
(
+
؛
א
אאאא
EF
,
D
C
אא؛
D
אאא،
K
אאאאאא
)
EF
D
C
(
AB
+
W
١
K
א
NOT
א
D
K
٢
K
א
AND
א
EF
,
D
C
K
٣
K
א
OR
אא
)
EF
D
C
(
+
K
٤
K
א
AND
אא
Y
K
AND
AND
OR
NOT
אא
٧٤١
א
א
אאאא
א
-
٢٥
-
אאאאאאא
F
٢
J
٠٢
KE
F
٢
J
٠٢
E
אאאא
EF)
D
AB(C
+
K
٢
J
٣١
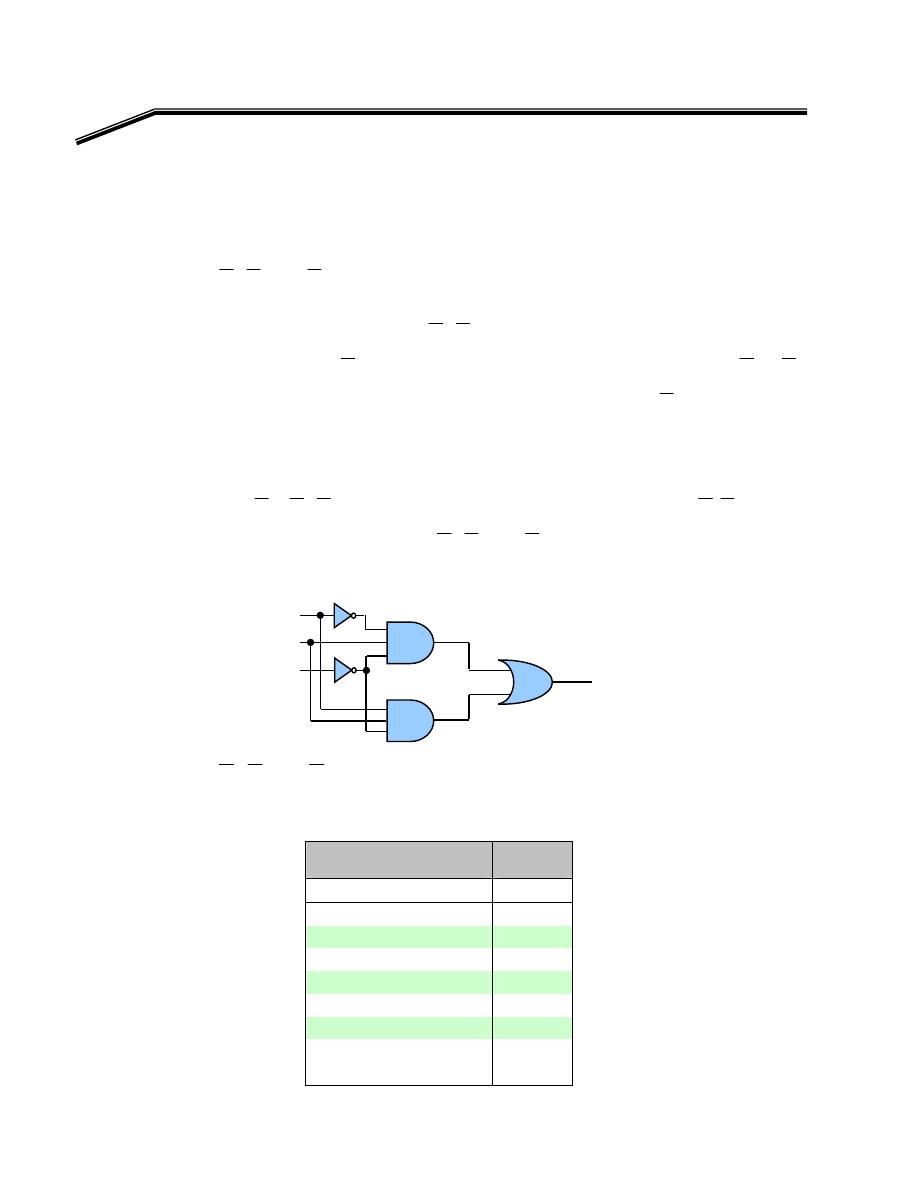
אא
Implementation of a Logic Circuit via a Truth Table
אאאאא
אאאאא،אא
א
K
F
٢
J
٢١
E
אא،אא
אאא
אא
K
אאאא
W
١K
אאאא
Y =
١
אאא،
א
Y =
١
א
A
=
٠, B = ١, C = ٠
،
א
א
C
B
A
אא
(
)١
א،
(
)٠
،
א
(
)١
אאאא
אא
C
AB
K
א
א
Y
C
B
A
٠
٠
٠
٠
٠
١
٠
٠
١
٠
١
٠
٠
١
١
٠
٠
٠
٠
١
٠
١
٠
١
١
٠
١
١
٠
١
١
١
F
٢
J
٢١
E
אאא
K
A
B
D
C
E
F
Y
אא
٧٤١
א
א
אאאא
א
-
٣٥
-
٢K
אאאאא
Y =
١
א
OR
W
C
AB
C
B
A
Y
+
=
אא
אאא
C
B
A
אאא
C
,
B
,
A
א
AND
אאאא،
C
AB
אאא
C
,
B
,
A
א
AND
אאאא،
OR
אאא
Y
K
אאאאאאא
W
א
NOT
א
C
,
A
א؛
AND
א
א
C
B
A
،
C
AB
א،
OR
אאא
C
AB
C
B
A
+
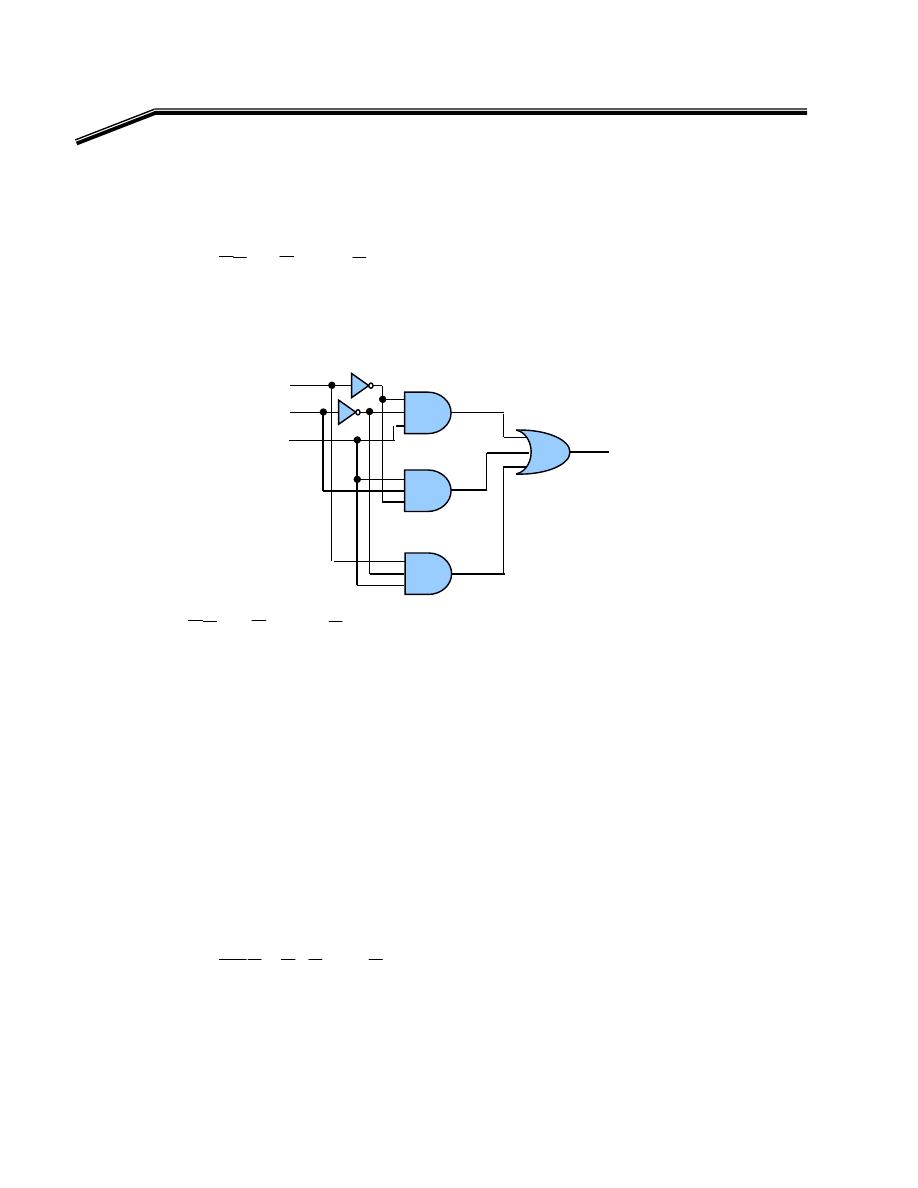
אאאאאאא،
F
٢
J
١٢
E
K
F
٢
J
١٢
E
אאא
א
C
AB
C
B
A
+
K
F
٢
J
٣
EW
אאאאאאא
F
٢
J
٣١
KE
א
א
Y
C
B
A
٠
٠
٠
٠
١
١
٠
٠
٠
٠
١
٠
١
١
١
٠
٠
٠
٠
١
١
١
٠
١
٠
٠
١
١
٠
١
١
١
C
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٤٥
-
F
٢
J
٣١
E
אאא
אא
K
א
W
אאאאאאא
Y =
١
F
אא
E
א
OR
W
C
B
A
BC
A
C
B
A
Y
+
+
=
אאא
F
٢
J
٢٢
E
K
F
٢
J
٢٢
E
אאאא
C
B
A
BC
A
C
B
A
+
+
K
٢
J
٤١
אאא
Converting a Boolean Expression to a Truth Table
אאאאא
א
(
١or ٠)
K
،אא
(
٢
٢
=
)٤
،
،אא
(
٢
٣
=
)٨
،
א
K
אאא،אא
א
אא
(
)١
א
(Y)
،אא
(
)٠
אא،אא
K
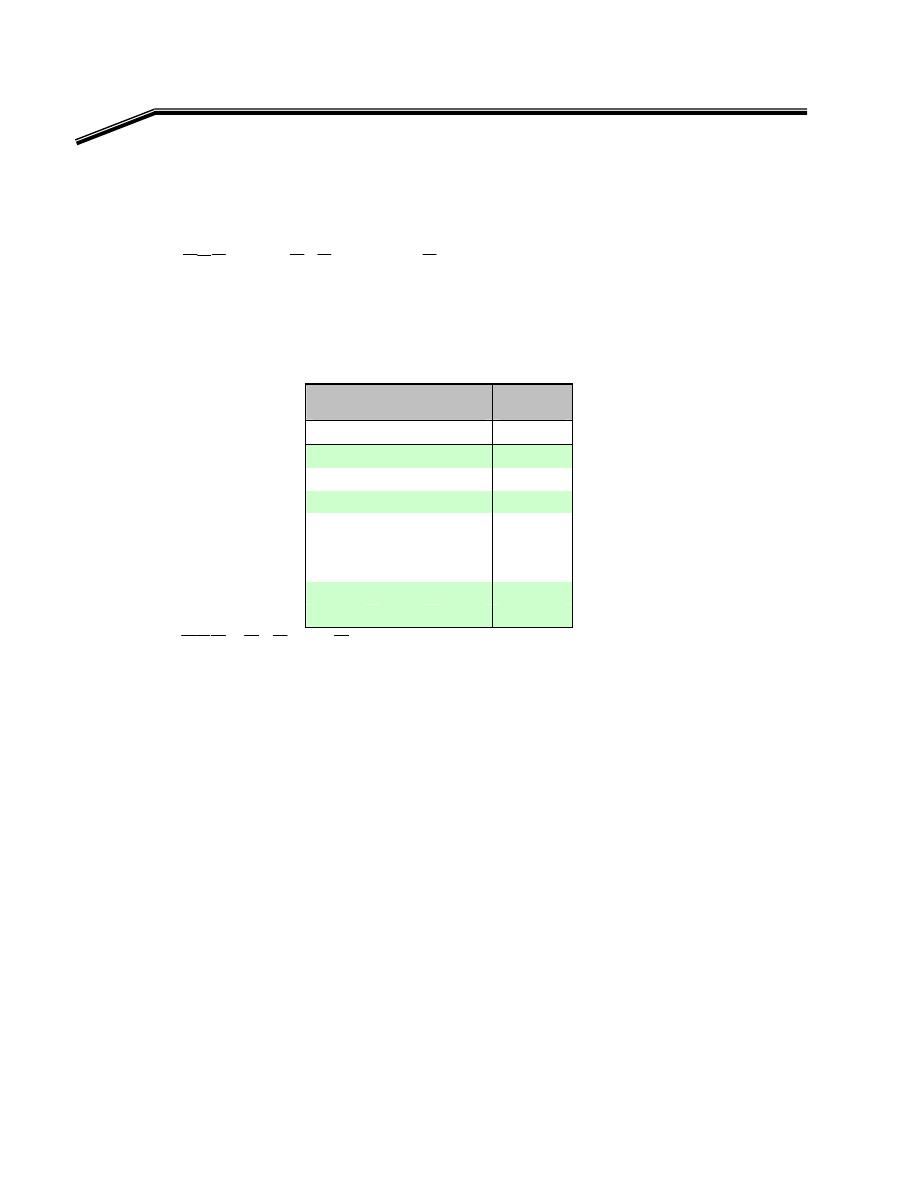
F
٢
J
٤
WE
אאא
W
ABC
C
AB
C
B
A
C
B
A
Y
+
+
+
=
B
A
C
Y
אא
٧٤١
א
א
אאאא
א
-
٥٥
-
א
W
א
(A, B, C)
א،אאא
אאאאא
F
٢
J
٤١
E
K
אאאאאא
W
111
ABC
,
110
C
AB
,
010
C
B
A
,
000
C
B
A
=
=
=
=
אא
(
)١
א
(Y)
،
אאא
(
)٠
א
(Y)
K
א
א
Y
C
B
A
١
٠
٠
٠
٠
١
٠
٠
١
٠
١
٠
٠
١
١
٠
٠
٠
٠
١
٠
١
٠
١
١
٠
١
١
١
١
١
١
F
٢
J
٤١
E
אא
ABC
C
AB
C
B
A
C
B
A
Y
+
+
+
=
K
٢
J
٥١
אאאאאא
Simplification of Boolean Expressions Using Boolean algebra
אאאאאאא
F
אאא
E
،א،אאא
א،א،אאא
אאא
K
F
٢
J
٥
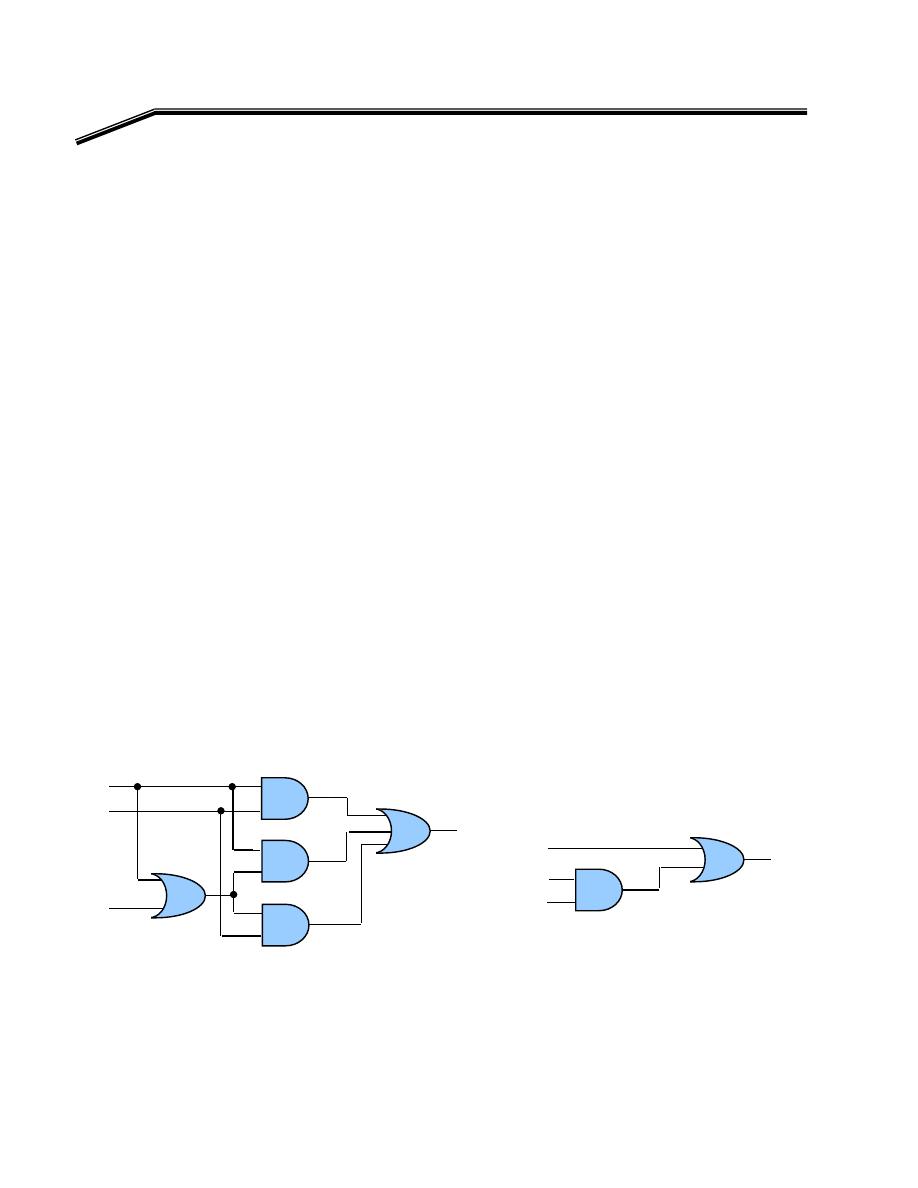
WE
א
אאאאאאא
W
)
C
A
(
B
)
C
A
(
A
AB
Y
+
+
+
+
=
א
W
אאאאאאא
W
BC
AB
AC
AA
AB
Y
+
+
+
+
=
אא
٧٤١
א
א
אאאא
א
-
٦٥
-
א
AA
A
F
אא
٧
אאא
E
אא
W
BC
AB
AC
A
AB
Y
+
+
+
+
=
א
٥
A + A = A
،
AB + AB = AB
אא،
W
BC
AC
A
AB
Y
+
+
+
=
א
A
אאאא
W
BC
)
C
1
B
(
A
Y
+
+
+
=
א
٢
A +
١= ١
،
W
Y = A
• ١+ BC
אא
٤
A
• ١= A
،
W
Y = A + BC
א
אא
K
אאאאאא
אא
אאאאאאאא،א
אא
K
F
٢
J
٣٢
E
אא
אא
אא
F
א
F
E
E
אאא،
אא
F
א
F
E
KE
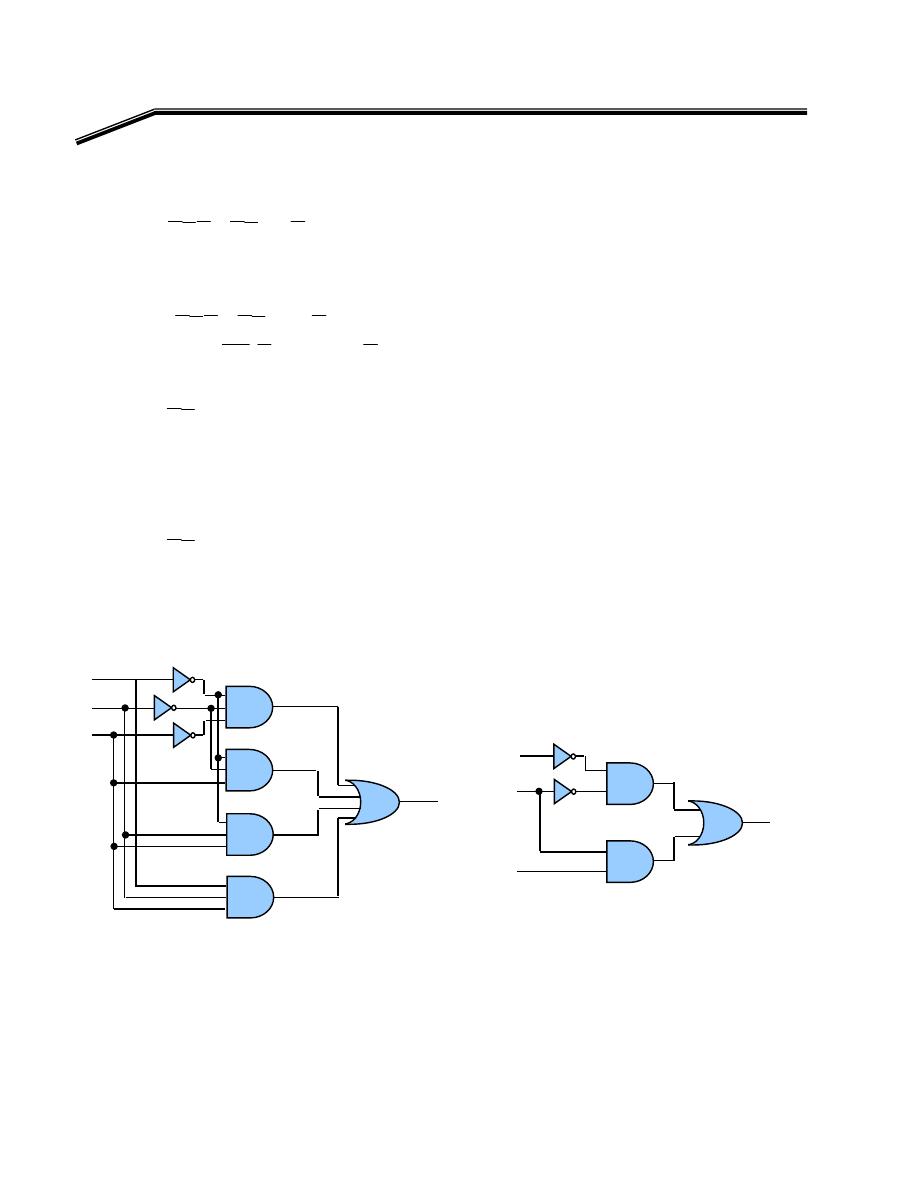
F
٢
J
٣٢
E
אאא
F
٢
J
٥
E
K
אא
אא
א،
A
,
B, C
،
אאא
K
A
B
C
F
E
Y
Y
A
B
F
E
C
אא
٧٤١
א
א
אאאא
א
-
٧٥
-
F
٢
J
٦
WE
אאאאאאא
א
K
ABC
BC
A
C
B
A
C
B
A
Y
+
+
+
=
א
W
،אאאא،אאא
W
)
ABC
BC
A
(
)
C
B
A
C
B
A
(
Y
+
+
+
=
)
A
A
(
BC
)
C
C
(
B
A
+
+
+
=
א
٦
W
1
BC
1
B
A
Y
•
+
•
=
א
٤
אאא
W
BC
B
A
Y
+
=
F
٢
J
٤٢
E
אא
אא
K
F
٢
J
٤٢
E
אאא
F
٢
J
٦
E
K
B
A
C
Y
C
Y
A
B
F
E
F
E

אא
٧٤١
א
א
אאאא
א
-
٨٥
-
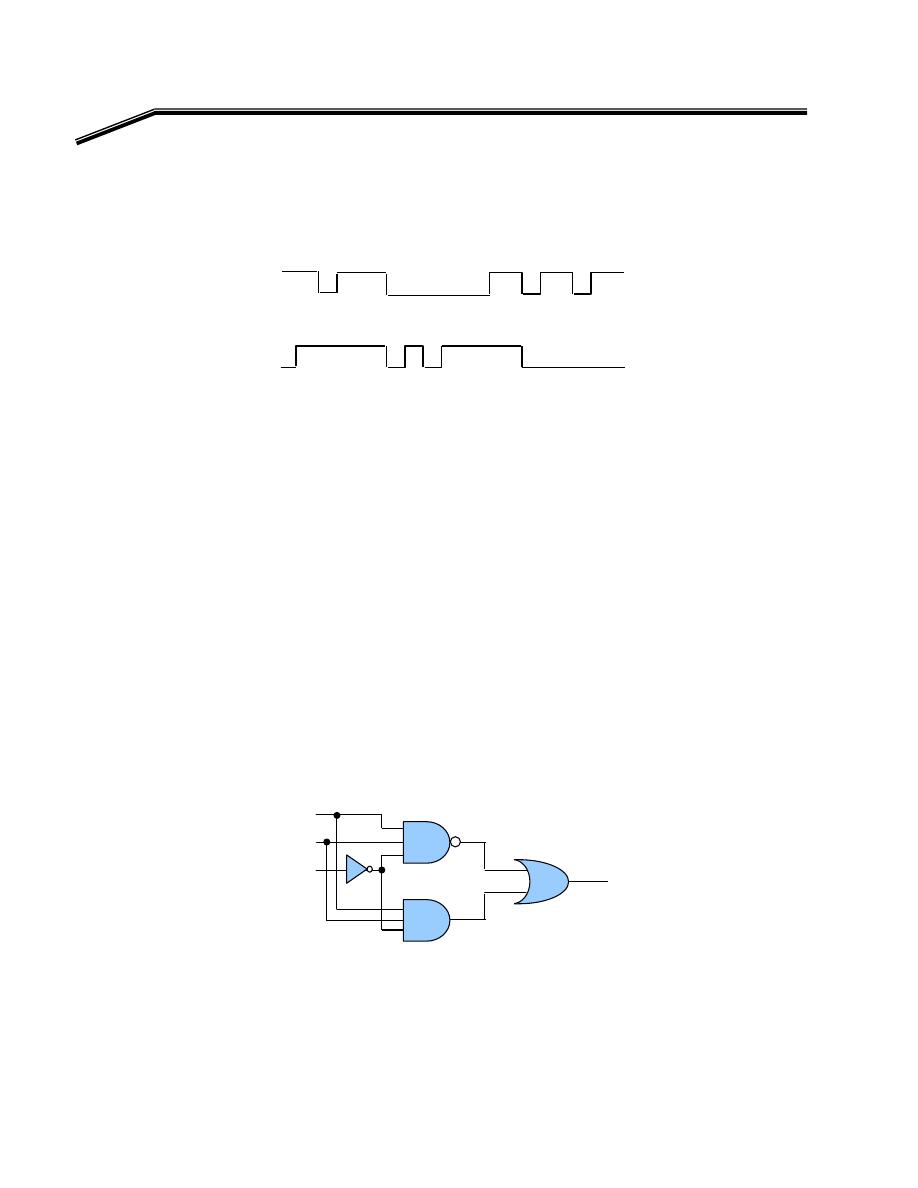
١
E
אאא
X
א
AND
אא
A,B
،
א
אא
J
١
K
J
١
٢
E
אאא
X
א
OR
אא
A,B
،
א
אא
J
١
K
٣
E
אאא
X
א
NAND
אא
A,B
،
א
אא
J
٢
K
J
٢
X
A
B
A
B
X
אא
٧٤١
א
א
אאאא
א
-
٩٥
-
٤
E
אאא
X
א
NOR
אא
A,B
אא،
אא
J
٣
K
J
٣
٥
E
אאא
X
א
XOR
אא
A,B
אא،
אא
J
٣
K
٦
E
אאא
X
א
XNOR
אא
A,B
אא،
אא
J
٣
K
٧
E
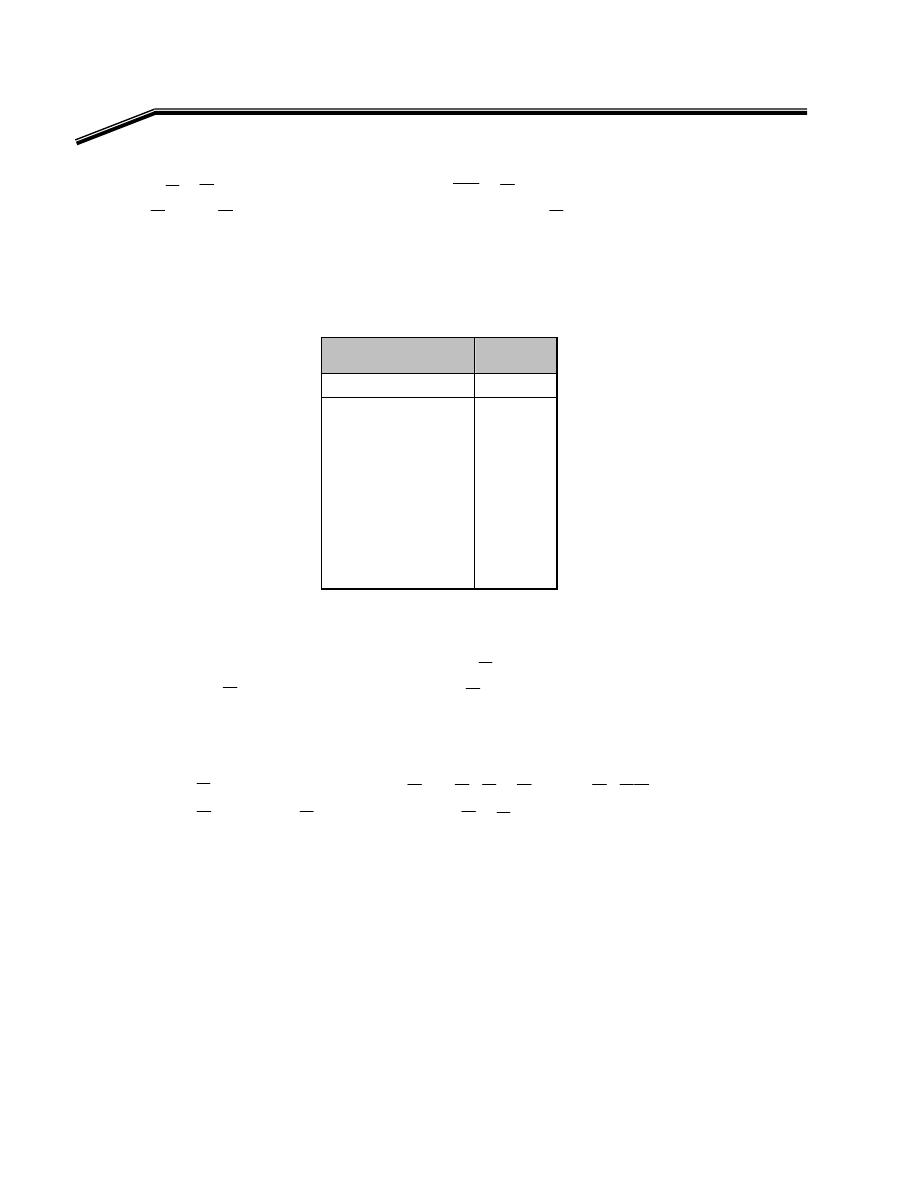
אאאאא
J
٤K
J
٤
A
B
X
C
Y
A
B
אא
٧٤١
א
א
אאאא
א
-
٠٦
-
٨
E
אאאא
אאאא
W
a)
B
A
B
A
+
b)
c)
d)
٩
E
אאאאאא
K
א
א
Y
C
B
A
٠
٠
٠
٠
١
١
٠
٠
٠
٠
١
٠
١
١
١
٠
٠
٠
٠
١
١
١
٠
١
٠
٠
١
١
١
١
١
١
٠١
E
אאאאא
W
a)
b)
c)
d)
١١
E
אאאאאאא
W
a)
b)
b)
d)
BC
A
AB
AB
+
+
)
D
C
(
B
A
+
)]
C
B
(
D
C
[
B
A
+
+
+
C
)
B
A
(
+
)
C
B
)(
B
A
(
+
+
)
B
A
AC
(
A
+
)
B
A
A
(
A
+
)
C
A
)(
B
A
(
+
+
E
D
C
B
A
BCD
A
C
B
A
B
A
+
+
+
)
C
AB
AB
)(
A
A
(
+
+
AB
C
)
B
A
(
AB
+
+
+

אאאאא
אאאאא
א
א
אאא
ã¹]<gè…‚jÖ]æ<ËÖ]<Üé×Ãj×Ö<íÚ^ÃÖ]<퉉ö¹]
אאאא
אא
א
אא
٣
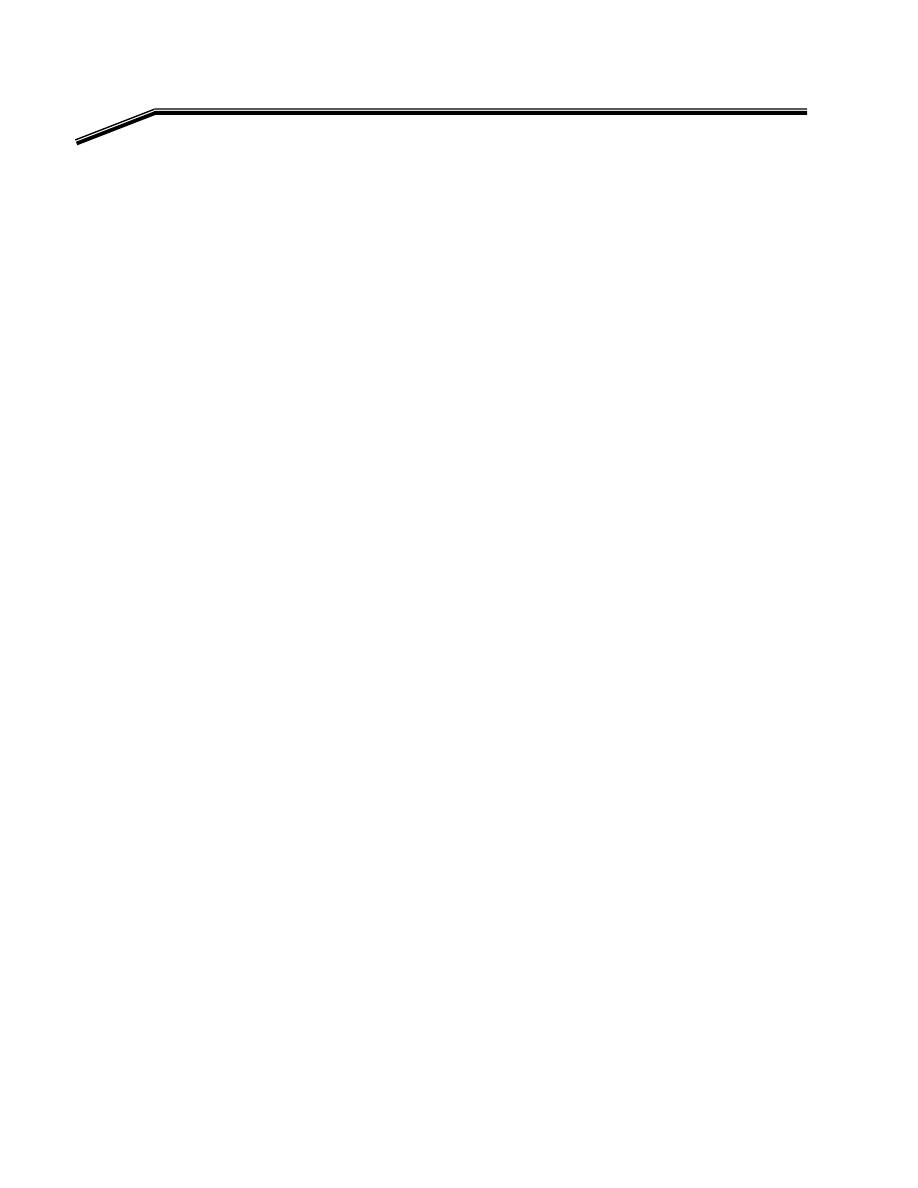
אא
٧٤١
א
א
אאאאא
א
-
١٦
-
אאא
אא
W
•
K
•
אאאא
NAND
אא
NOR
K
•
אאאאא
אא
NAND
NOR
K
•
אאאאא
K
•
אאאא
K

אא
٧٤١
א
א
אאאאא
א
-
٢٦
-
٣
J
١
Introduction
א،אאאאאא
אאאא
אאא
K
אאאא
،،אאא
אאאאא
K
،אאאאא
א
)
٠
١
(
אאא
K
אאאאאאאאאא
NAND
אא
NOR
אאאאאא
K
אאאא
)
Karnaugh-Map
(
א
א
–
K
)
K–map
(
K
אאאאאאאא
אא
א
K
٢
J
٣
Demorgan's Theorems
אאא،אא
א
AND
א
OR
K
אא
)
bars
(
אא
אא،א
W
א
W
א
W
B
A
B
A
+
=
•
אא
OR
א
AND
F
٣
J
١
E
אא
NOR
אאאא
AND
אאאאאאאא
K
אאא
F
٣
J
١
E
K
אאאאאאא
AND
א
)
negative AND
(
K
B
A
B
A
•
=
+
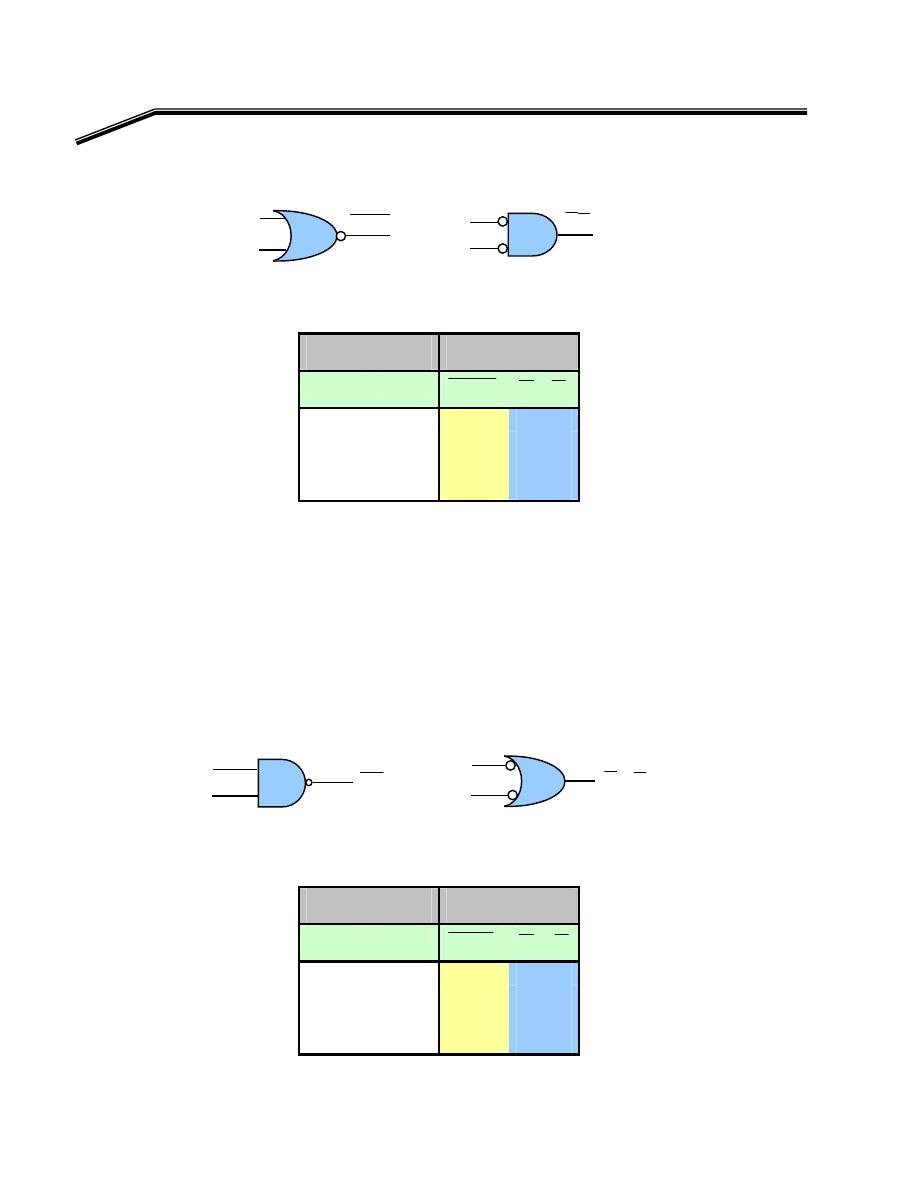
אא
٧٤١
א
א
אאאאא
א
-
٣٦
-
F
٣
J
١
E
א
OR
AND
K
א
א
B
A
١
١
٠
٠
٠
٠
١
٠
٠
٠
٠
١
٠
٠
١
١
F
٣
J
١
E
אא
K
אא
AND
א
OR
F
٣
J
٢
E
אא
NAND
אאאא
OR
א
א
F
אאאאאא
E
א،
אאא
F
٣
J
٢
KE
אאאא
א
א
OR
א
)
negative OR
(
K
F
٣
J
٢
E
א
AND
OR
K
א
א
B
A
١
١
٠
٠
٠
٠
١
٠
٠
٠
٠
١
٠
٠
١
١
F
٣
J
٢
E
אא
K
B
A
+
B
A
•
B
A
+
B
A
B
A
B
A
AB
A
B
B
A
+
A
B
≡
B
A
•
B
A
+

אא
٧٤١
א
א
אאאאא
א
-
٤٦
-
אאאא
K
אא
א
א
K
F
٣
J
١
WE
אאא
W
)
C
B
A
(
)
C
B
(A
Y
+
+
•
+
+
=
א
W
C
B
A
B C
A
C
B
A
C
B
A
)
C
B
A
(
)
C
B
A
(
)
C
B
A
(
)
C
B
(A
Y
+
=
+
=
+
+
+
+
+
=
+
+
•
+
+
=
F
٣
J
٢
WE
א
אא
W
א
W
)
D
C
(
B
A
)
D
C
)(
B
.
A
(
CD
).
B
A
(
CD
)
B
A
(
Y
+
=
+
=
+
=
+
+
=
٣
J
٣
אאאא
NOR
,
NAND
The Universal Property of NAND and NOR Gates
אאאאאאאא
AND
א،
OR
אא،
K
א
אא
NAND
א
NOR
א
)
Universal Gates
(
K
אאא
א
NAND
אאא
AND
،
NOR
K
א
NOR
א
אא
NOR
אא
AND
،
OR
NAND
K
CD
)
B
A
(
Y
+
+
=
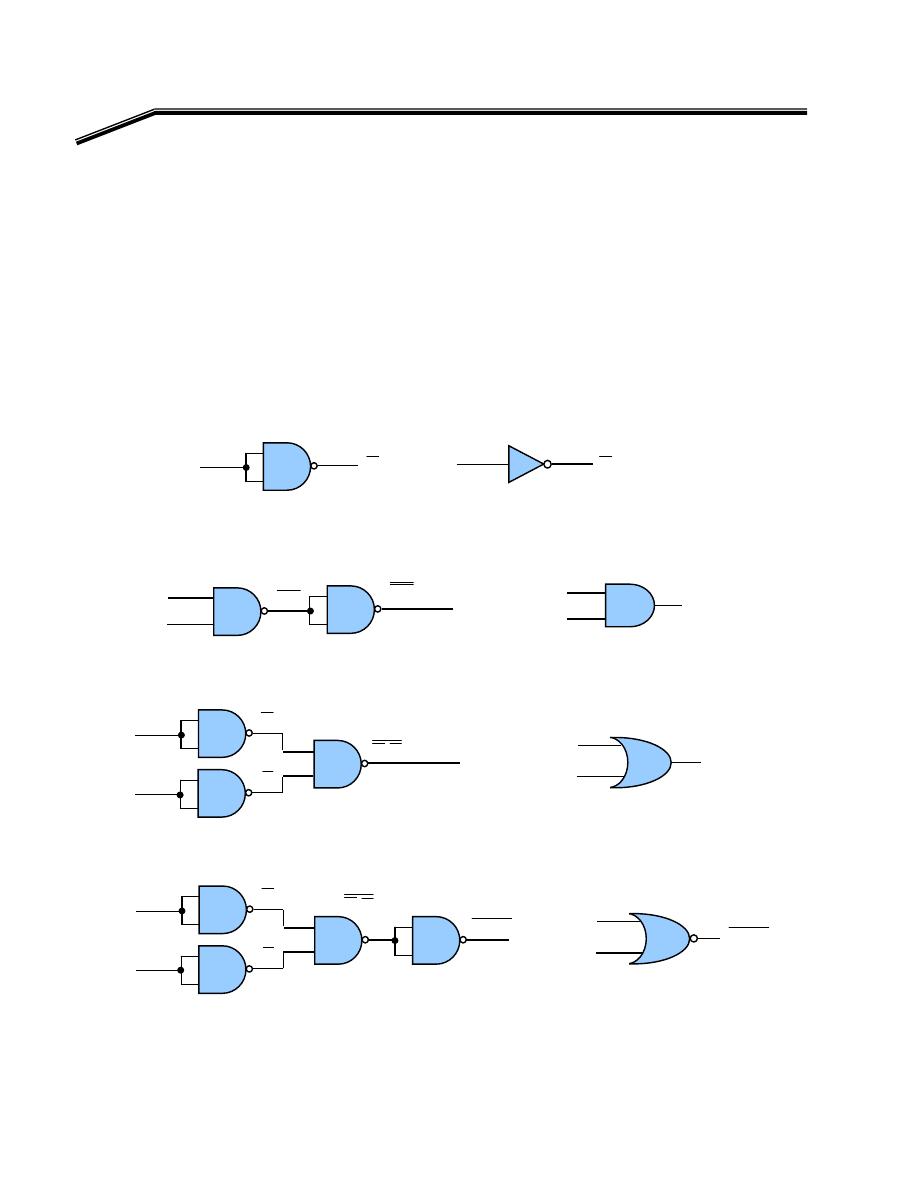
אא
٧٤١
א
א
אאאאא
א
-
٥٦
-
٣
J
٣
J
١
אא
NAND
NAND gate as a Universal Logic Element
אא
NAND
א
א
،אא
AND
،
OR
،
NOR
K
אאא
NAND
אאא
٣
J
٣
F
E
א
NAND
א
K
AND
אא
NAND
٣
J
٣
F
KE
אא
OR
א
א
NAND
٣
J
٣
F
KE
אאא
NOR
٣
J
٣
F
KE
F
٣
J
٣
E
אאא
NAND
K
A
A
A
A
≡
F
E
AB
B
A
AB
AB
=
AB
A
B
≡
F
E
A
A
≡
B
B
B
A
B
.
A
+
=
A + B
A
B
F
E
B
A
+
A
A
≡
B
B
B
A
B
.
A
+
=
B
A
+
A
B
F
E
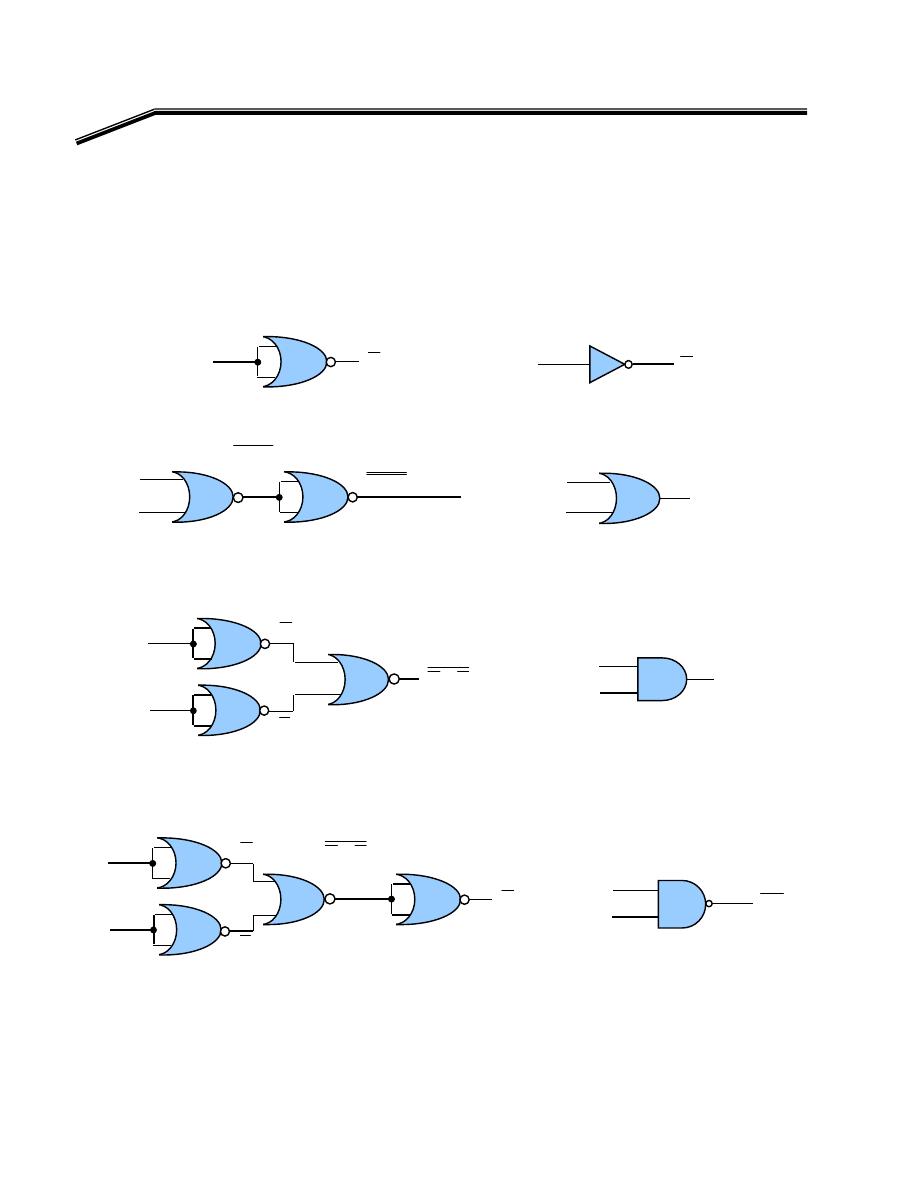
אא
٧٤١
א
א
אאאאא
א
-
٦٦
-
٣
J
٣
J
٢
אא
NOR
NOR Gate as a Universal Logic Element
א
NAND
،
אא
NOR
א
אא
،
AND
،
OR
،
א
NAND
K
F
٣
J
٤
E
אא
NOR
א
NOT
א
OR
אא
NAND
K
F
٣
J
٤
E
אאא
NOR
K
A
A
≡
A
A
B
.
A
B
A
=
+
A
A
B
B
≡
AB
B
A
B
.
A
B
A
=
+
A
A
A
B
B
≡
AB
A
B
≡
A + B
A
B
B
A
B
A
+
=
+
A
B
B
A
+
F
E
F
E
F
E
F
E
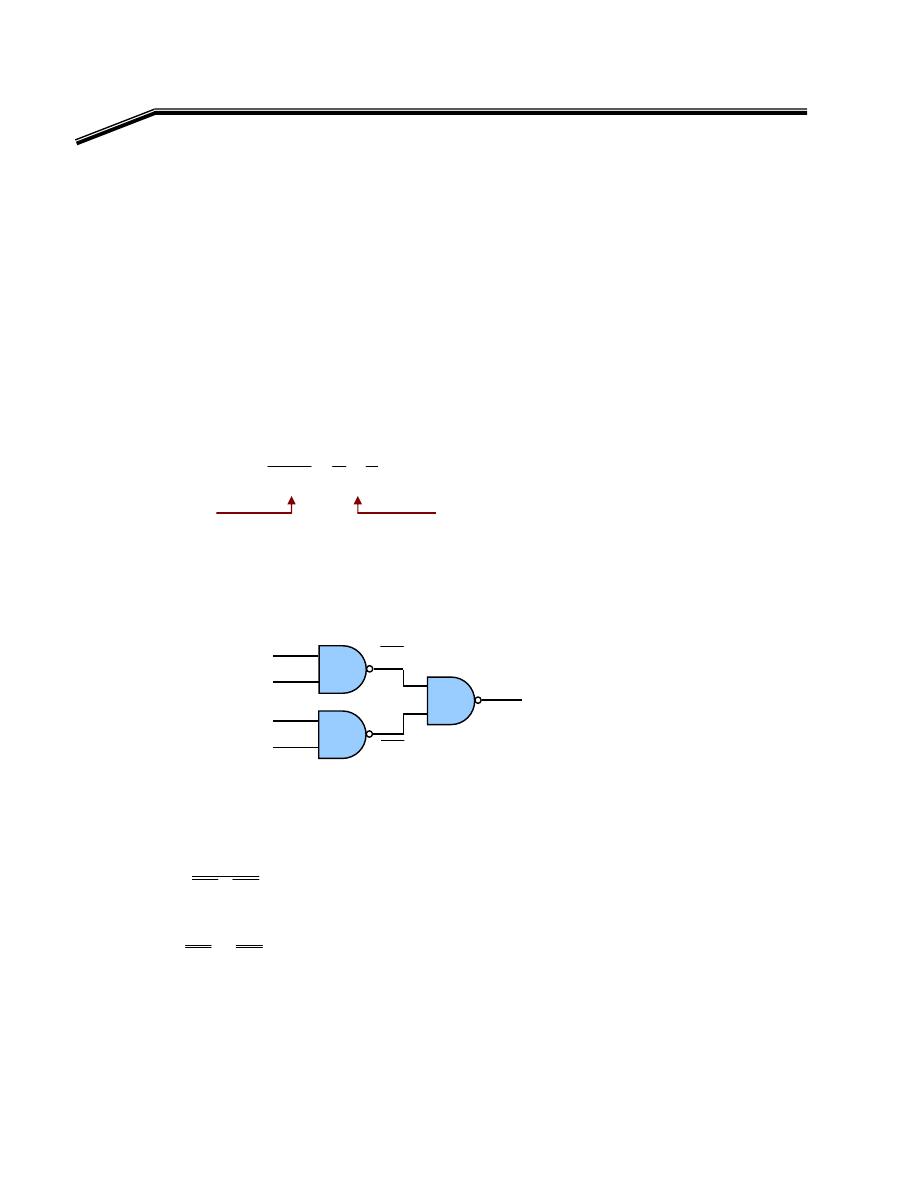
אא
٧٤١
א
א
אאאאא
א
-
٧٦
-
٣
J
٤
אאאאא
אא
NAND
،
NOR
Design of Combinational Logic Circuits using NAND and NOR Gates
א
אא
NAND
א،
NOR
אא
אאא
אא
NAND
אא
OR
א
)
Negative-OR
(
،
אא
NOR
אא
AND
א
)
Negative - AND
(
K
א
א
OR
،
AND
אאאא
)
Logic diagram
(
א
K
٣
J
٤
J
١
אאא
NAND
NAND Logic
א،
NAND
א
NAND
א
OR
א،א
א
W
B
A
B
A
+
=
•
אאאאא
F
٣
J
٥
KE
F
٣
J
٥
E
אאא
NAND
K
אא
)
Y
(
אא
א
אאא
W
)
CD
)(
AB
(
Y
=
א
W
CD
AB
Y
+
=
אאא
)
bars
(
W
CD
AB
Y
+
=
א
)
Y
(
،
AB+CD
א،
AND
א
.OR
אאא
)
Y
(
אא
NAND
א
NAND
Negative-OR
Y = AB + CD
AB
A
B
CD
C
D
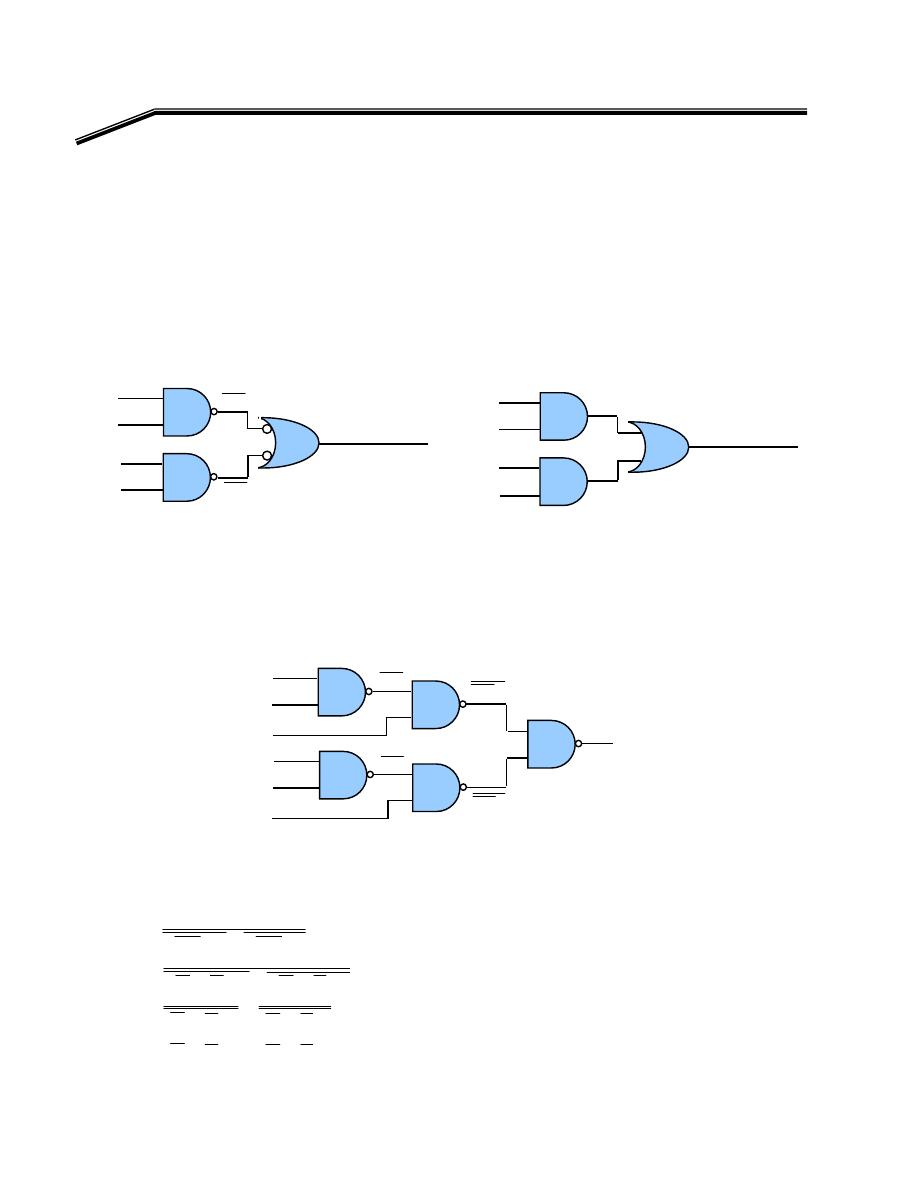
אא
٧٤١
א
א
אאאאא
א
-
٨٦
-
F
٣
J
٥
E
א
AND
א
NAND
א
א
OR
K
אא
)
Y
(
א
٣
J
٦
F
E
א
אאא
NAND
אא
OR
א
K
אא
א
٣
J
٦
F
E
،
אא
F
٣
-
٥
E
אא
٣
J
٦
F
E
،
W
(AND-AND-OR)
(NAND-NAND-NAND)
F
٣
J
٧
E
אא
NAND
א
אא
אאא
OR
J
א
K
א
(Y)
א
F
٣
J
٧
WE
F
)
E
D
(
C
)
B
A
(
F
)
E
D
(
C
)
B
A
(
]
F
)
E
D
[(
]
C
)
B
A
[(
]
F
)
DE
[(
]
C
)
AB
[(
F
+
+
+
=
+
+
+
=
+
•
+
=
•
=
Y
F
DE
C
AB
AB
A
B
C
DE
D
E
F
F
٣
J
٧
E
אאאאאא
OR
J
א
K
Y = AB + CD
AB
A
B
CD
C
D
F
E
≡
Y = AB + CD
A
B
C
D
F
E
F
٣
J
٦
E
AND-AND-OR
אא
F
٣
J
٥
KE
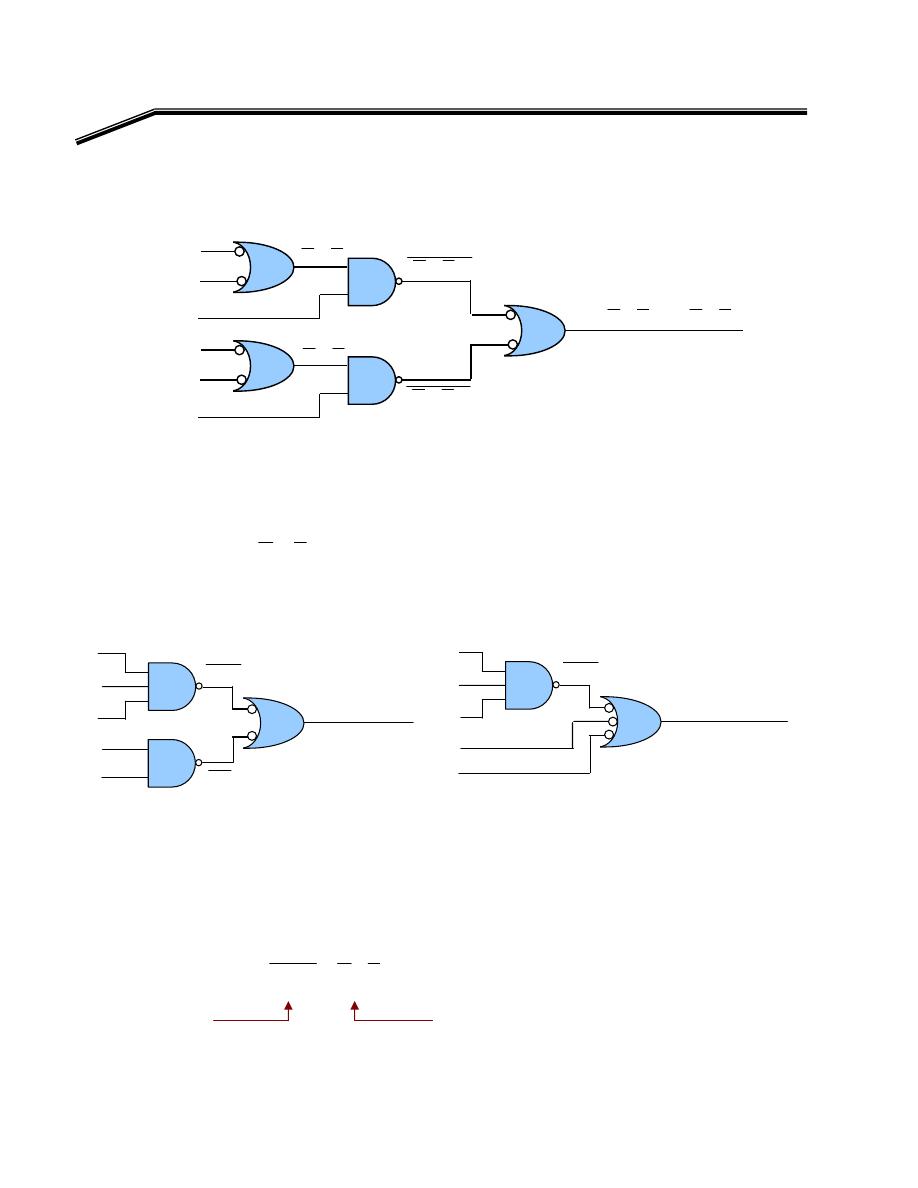
אא
٧٤١
א
א
אאאאא
א
-
٩٦
-
אא
OR
J
אאא
NAND
אאא
F
٣
J
٨
E
א،
(Y)
אאא
K
F
٣
J
٣
WE
א
א
א
א
NAND
W
א
W
אא
F
٣
J
٩
KE
٣
J
٤
J
٢
אאא
NOR
NOR Logic
אא
NOR
א
NOR
א
AND
J
אא
א
W
B
A
B
A
•
=
+
אאאא
F
٣
J
٠١
KE
NOR
Negative-AND
E
D
ABC
Y
)
b
(
DE
ABC
Y
)
a
(
+
+
=
+
=
F
٣
J
٩
E
אאא
א
F
٣
J
٣
KE
E
ABC
DE
Y = ABC + DE
A
B
C
D
F
E
E
ABC
Y = ABC + D + E
A
B
C
D
F
E
F
)
E
D
(
C
)
B
A
(
Y
+
+
+
=
B
A
+
A
B
C
)
B
A
(
+
C
E
D
+
D
E
F
)
E
D
(
+
F
F
٣
J
٨
E
אאא
F
٣
J
٧
E
אא
OR
J
א
K
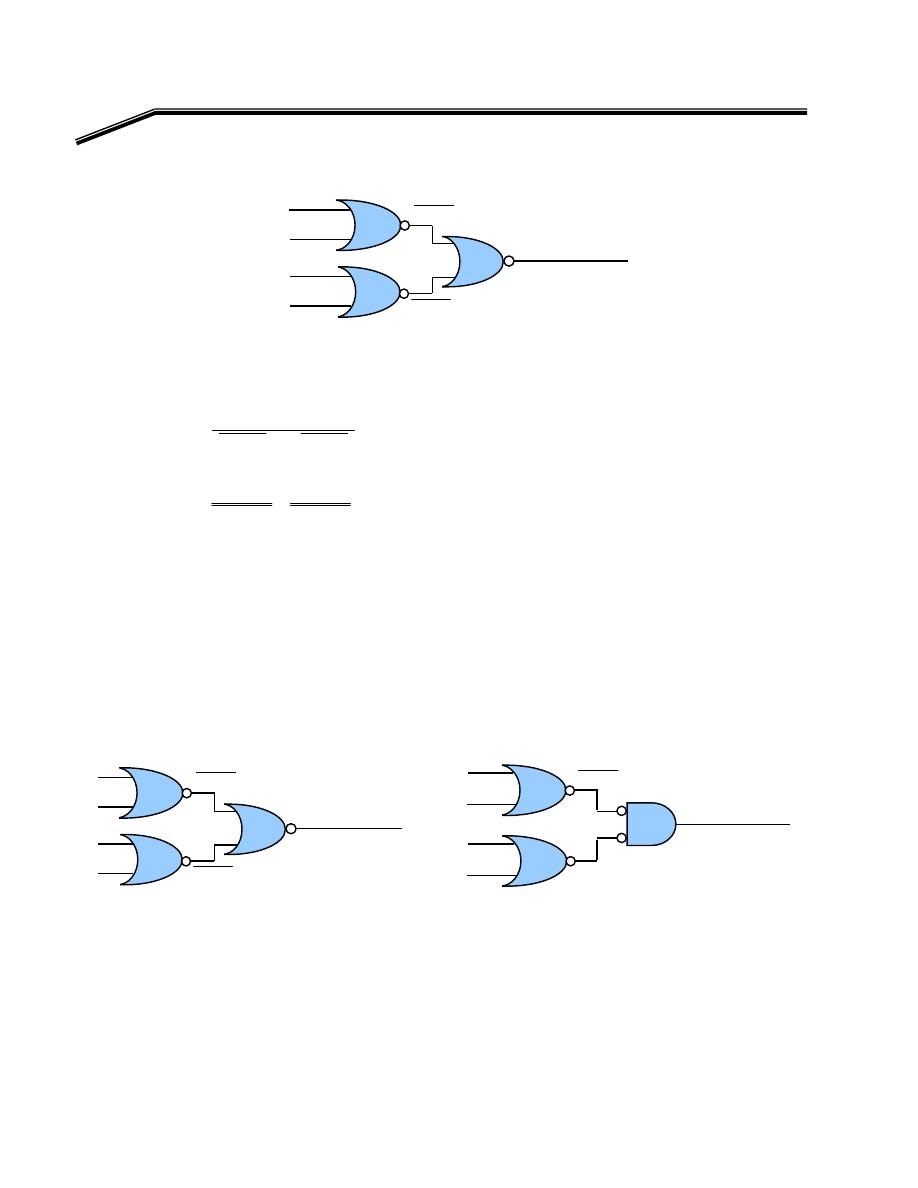
אא
٧٤١
א
א
אאאאא
א
-
٠٧
-
אאאאא
W
א
W
אאא
W
א
(A + B)(C + D)
א
OR
א
AND
א،
אאא
א
OR
אאאא
AND
٣
J
١١
F
KE
אאא
٣
J
١١
F
E
אא
AND
J
א
K
F
٣
J
١١
E
אאא
F
٣
J
٠١
E
אא
AND
J
א
K
F
٣
J
٢١
E
אא
NOR
אאא،
אא
AND
J
א
K
א
(Y)
א
W
)
D
C
(
)
B
A
(
Y
+
+
+
=
)
D
C
(
)
B
A
(
Y
+
•
+
=
)
D
C
(
)
B
A
(
Y
+
•
+
=
≡
(A + B) (C + D)
B
A
+
A
B
C
D
(A + B) (C + D)
B
A
+
A
D
C
+
B
C
D
F
E
F
E
(A + B) (C + D)
D
C
B
A
+
A
D
C
+
B
F
٣
J
٠١
E
אאא
NOR
K
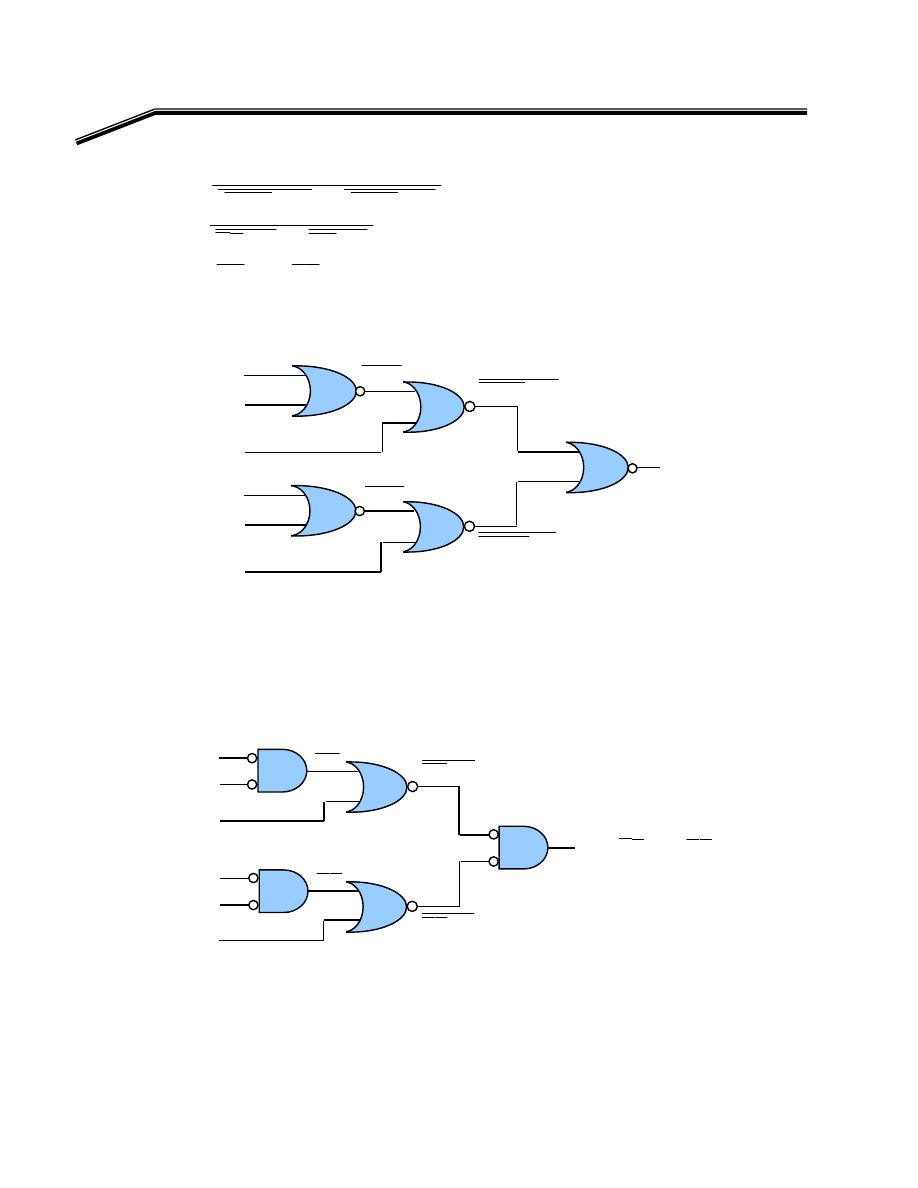
אא
٧٤١
א
א
אאאאא
א
-
١٧
-
אא
AND
J
אאא
NOR
אא
F
٣
J
٣١
KE
F
٣
J
٣١
E
אאאא
F
٣
J
٢١
KE
)
F
E
D
)(
C
B
A
(
]
F
E
D
[
]
C
B
A
[
]
F
)
E
D
(
[
]
C
)
B
A
(
[
Y
+
+
=
+
+
+
=
+
+
+
+
+
=
Y
F
)
E
D
(
+
+
C
)
B
A
(
+
+
C
A
B
B
A
+
F
D
E
E
D
+
F
٣
J
٢١
E
א
א
NOR
K
F
E
D
+
C
B
A
+
C
F
D
E
B
A
B
A
E
D
F)
E
D
(
)
C
B
A
(
Y
+
+
=
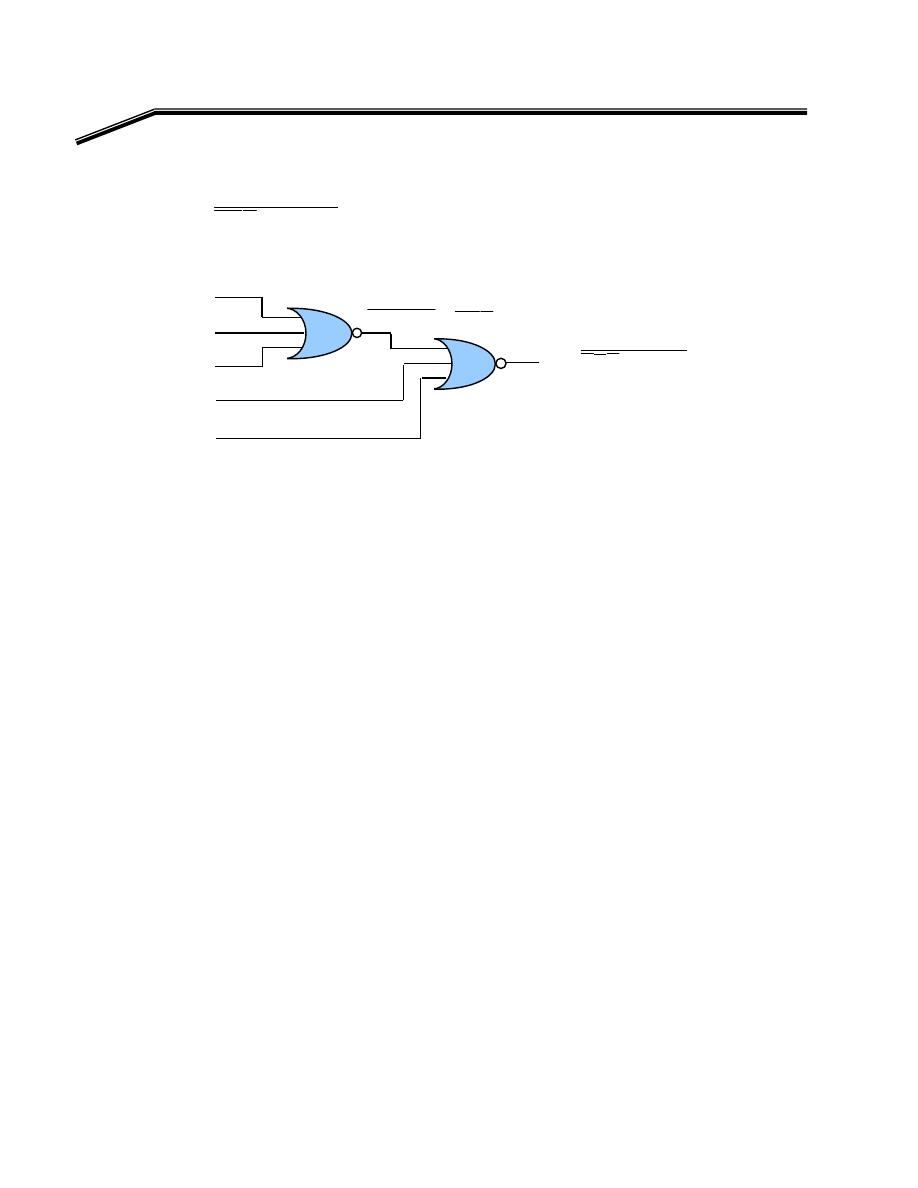
אא
٧٤١
א
א
אאאאא
א
-
٢٧
-
F
٣
J
٤
WE
אאאאא
NOR
W
א
W
אא
F
٣
J
٤١
KE
F
٣
J
٤١
E
אאאאא
NOR
K
٣
J
٥
Karnaugh Map
K-
אא،אאא
אא
K
א
א
א
אאאאאא
،אאא
אאא
אאא
K
K
אאא
א
K
،א
)
array
(
א
)
cells
(
،
אא
א
K
אאאא
א
K
،،،אאאא
،א
אא
K
אאא
אאאא
אאאא
א
)
Quine - McClusky
(
אאאאא
א
K
אאא
)
E
D
(
C
B
A
Y
+
+
=
E
C
B
A
C
B
A
=
+
+
D
C
A
B
)
E
D
(
C
B
A
Y
+
+
=
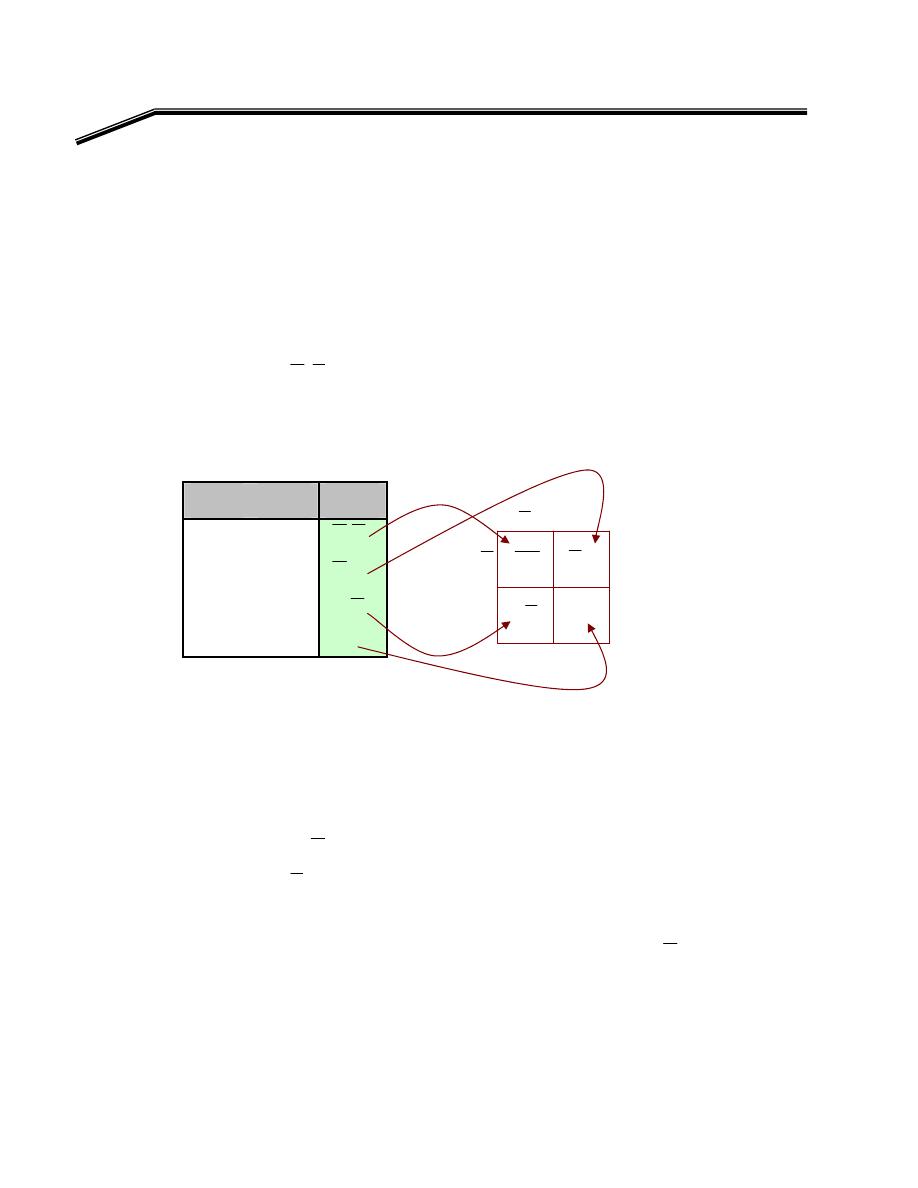
אא
٧٤١
א
א
אאאאא
א
-
٣٧
-
אא،
K
אא
8
2
3
=
אא
16
2
4
=
K
٣
J
٦
אאא
Simplification using Karnaugh-map
אאא
F
א
KE
F
٣
J
٥١
E
،
א
)
B
،
A
(
א
)
B
,
A
(
F
א
E
(
٠٠{٠١{١٠{١١)
K
Y
B
A
٠
٠
١
٠
٠
١
A B
١
١
F
٣
J
٥١
E
א
K
אאאא
K
א
)
Input Labels
(
א
F
٣
J
٦١
E
אא
K
אא،
א
A
،אא
א
A
אא
K
אא
B
אא
א،א
B
אאא
K
،
אאאא
א
B
A
K
AB
B
A
B
B
A
A
B
A
B
A
B
A
B
A
B
A
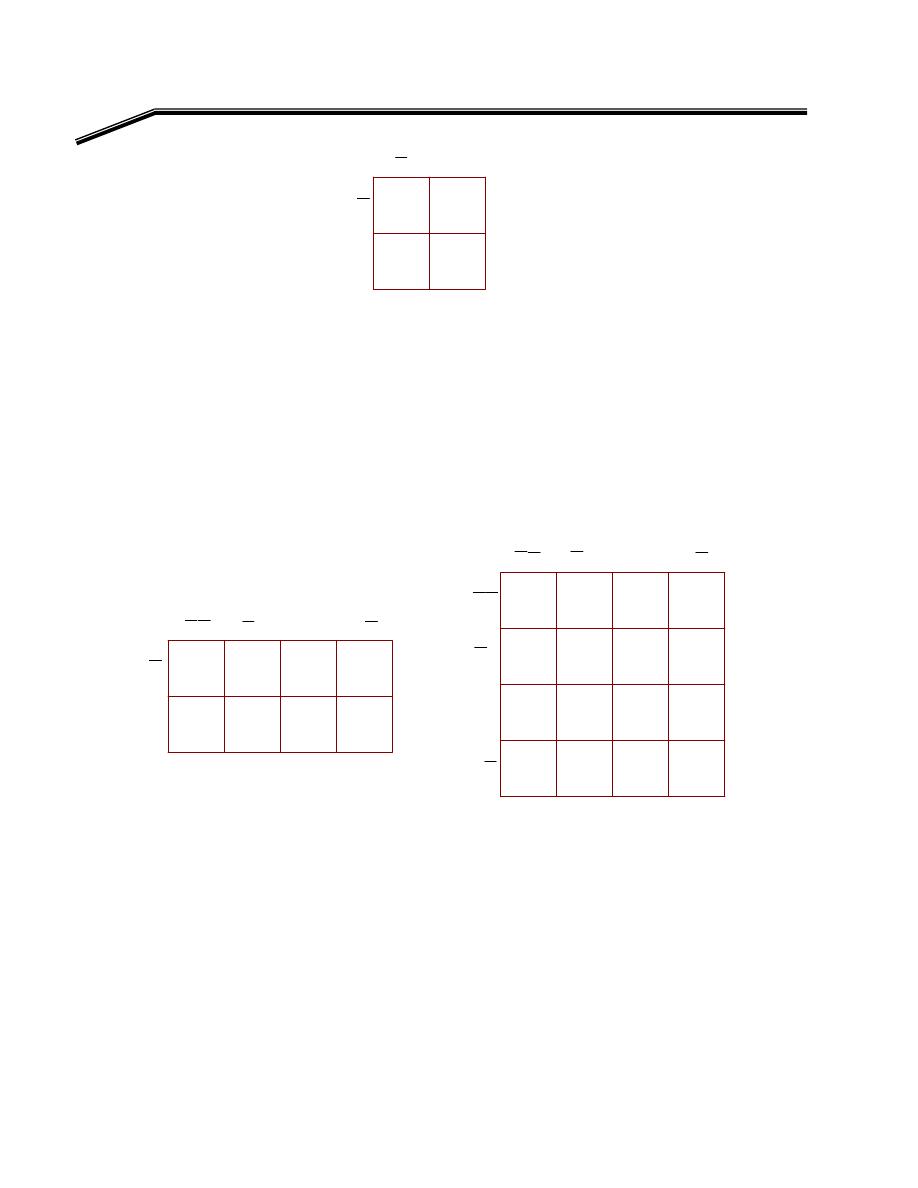
אא
٧٤١
א
א
אאאאא
א
-
٤٧
-
F
٣
J
٦١
E
F
٢
٢
=
٤
KE
٣
J
٧١
F
E
،
٣
J
٧١
F
E
א
F
E
،
א
F
KE
F
٣
J
٧١
E
אא
K
א
،
אאא
K
אא،
א
٣
J
٨١
F
KE
B
B
A
A
C
B
BC
C
B
C
B
A
A
D
C
CD
D
C
D
C
B
A
B
A
AB
B
A
F
E
F
E
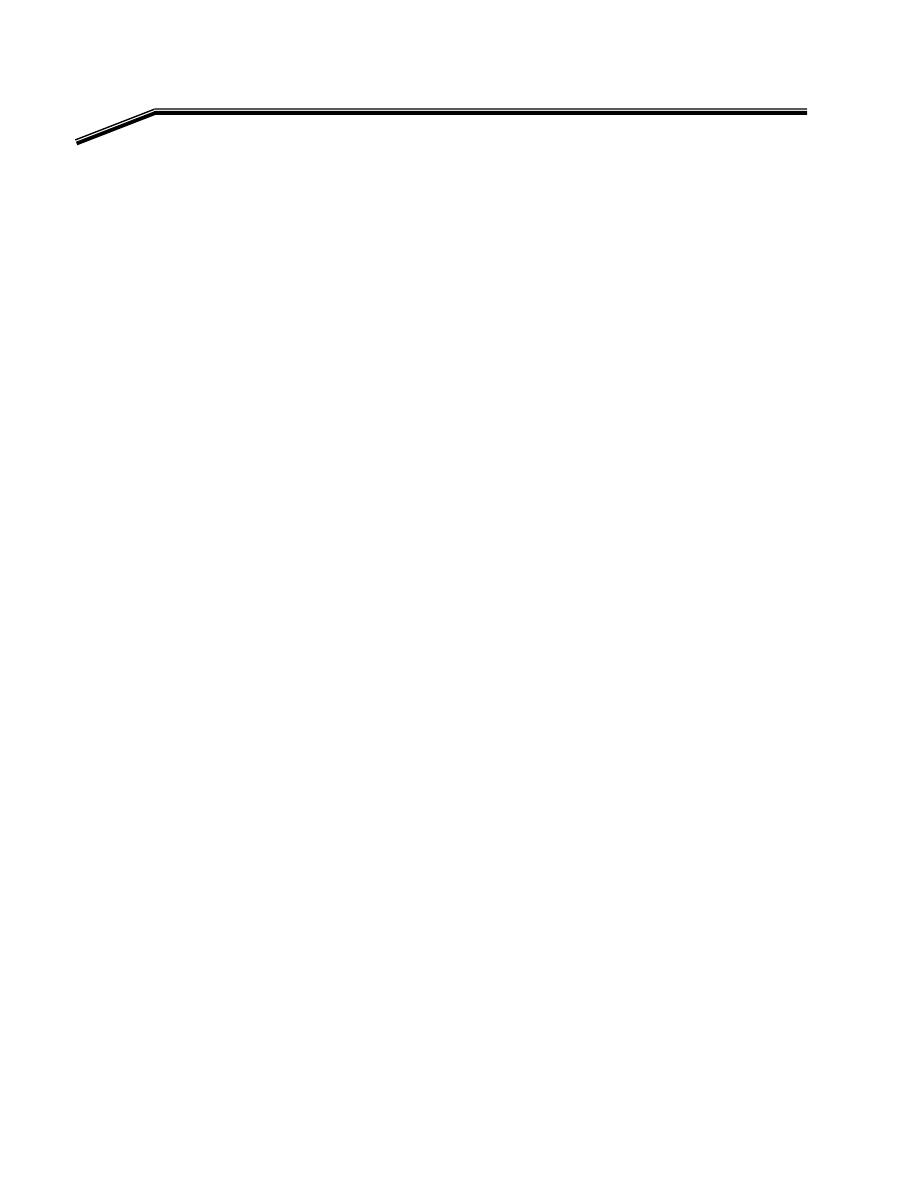
אא
٧٤١
א
א
אאאאא
א
-
٥٧
-
،אאאאאא
אא
()١
אאאא
OR
٣
J
٨١
F
KE
אאאאא
٣
J
٨١
F
KE
אא
אאא
٣
J
٨١
F
KE
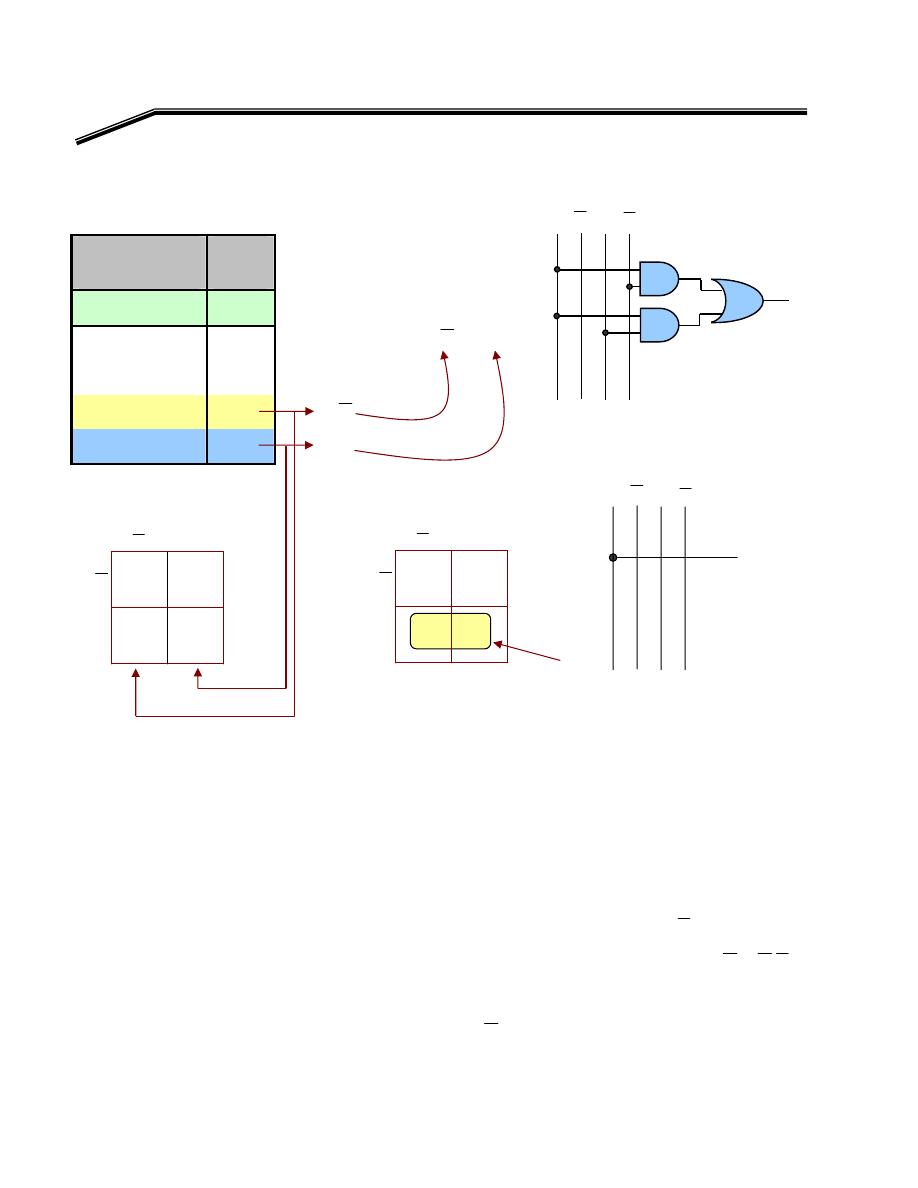
אא
٧٤١
א
א
אאאאא
א
-
٦٧
-
א
א
Y
B
A
٠
٠
٠
٠
١
٠
١
٠
١
١
١
١
F
FE
E
F
E
F
٣
J
٨١
E
אאא
K
אא
אאאא
K
א
()١
א
()١
א،אא
()٠
א
()٠
אא
K
()١
אא
א
F
B
A
E
אאא،
F
AB
KE
אא
)
B
A
,
B
A
(
()٠
،א
()٠
אא
K
אאאא
Complements)
E
א،
1
A
A
=
+
K
אאא
٣
J
٨١
F
E
א،
אאאא
K
A
A
Y
F
E
B
A
B
A
١
0
B
B
0
1
B
A
B
A
Y
+
=
١
0
B
B
A
A
0
1
A
Y
B
A
A
B
F
E
B
A
A
B
F
E

אא
٧٤١
א
א
אאאאא
א
-
٧٧
-
א
٣
J
٨١
F
E
אא
)
adjacent cells
(
א
K
אא
א
א،
K
אאא
)
١
(
א
٣
J
٨١
F
E
אאא
א
K
אאא
B
A
AB,
B
،
B
،א
،א
A
W
AB
B
A
Y
+
=
F
אאא
E
A
1
A
)
B
B
(
A
Y
=
•
=
+
=
אא
א
אאאא
٣
J
٨١
F
E
א
א
)
Y
(
א
)
A
(
K
אאא
٣
J
٨١
F
KE
F
٣
J
٥
WE
אאא
٣
J
٩١
F
E
א
K
א
W
אא،א
،א
٣
J
٩١
F
KE
אאאא
)
١
(
א
٣
J
٩١
F
E
אאא
٣
J
٩١
F
KE
)
٠
(
אא،אאא
٣
J
٩١
F
E
אאאאאא،
F
אא
E
א
K
אאא
A
A,
א
C
B
אאא،
C
C,
א
B
A
K
אאאאאאאאא
،א
٣
J
٩١
F
KE
אאאא
א
AND
א
א
OR
א
אאא
٦١
אאא،
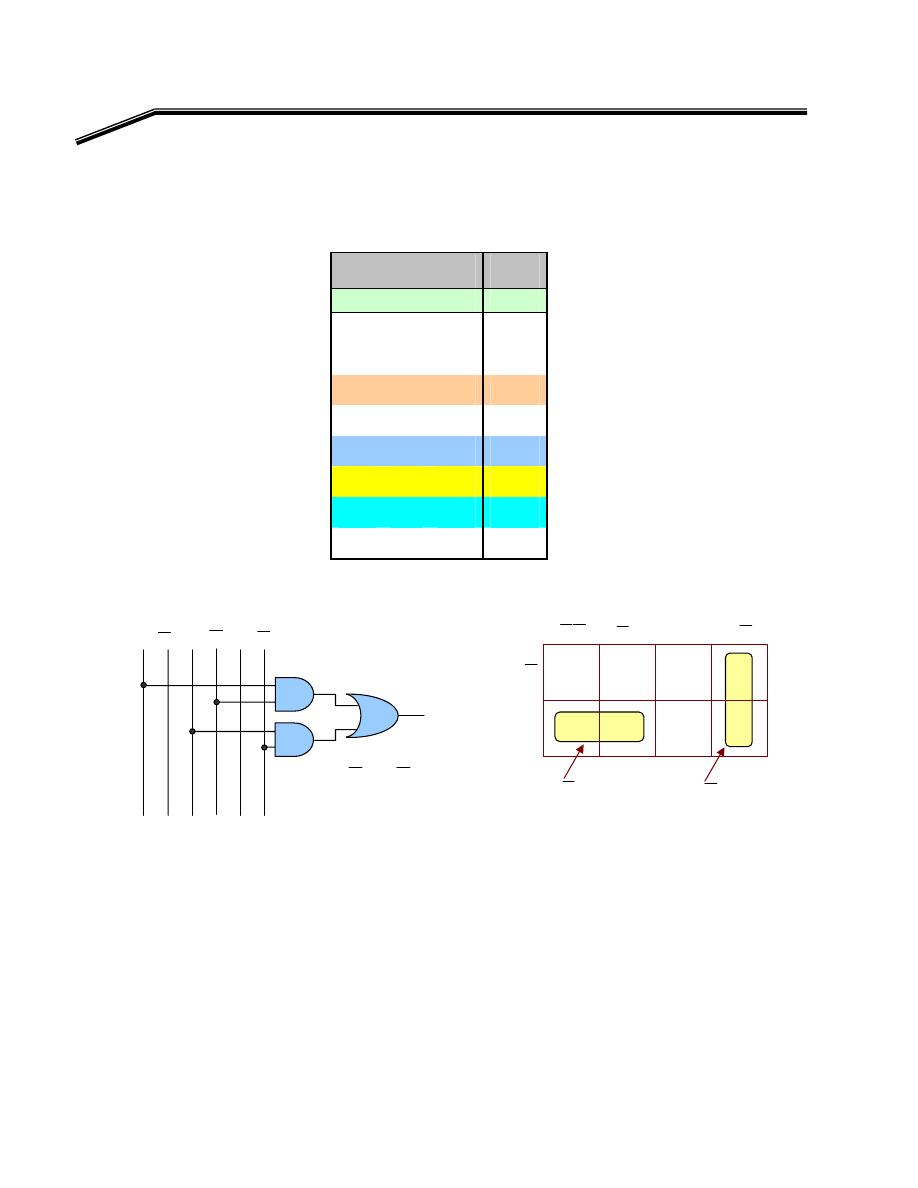
אא
٧٤١
א
א
אאאאא
א
-
٨٧
-
א
AND
א
OR
אאא،
אא
٦
א
٣
J
٩١
F
KE
א
א
Y
C
B
A
٠
٠
٠
٠
٠
١
٠
٠
١
٠
١
٠
٠
١
١
٠
١
٠
٠
١
١
١
٠
١
١
٠
١
١
٠
١
١
١
F
E
F
٣
J
٩١
E
אא
K
א
)
١'s
(
א
F
א
E
אא،،
٢
K
F
٣
J
٠٢
E
،א
אאאא
K
אא
אא
F
١'s
E
אאא
א
K
אאאא
،א
אא
F
אא
F
E
C
B
B
A
C
B
BC
C
B
C
B
A
A
١
١
١
١
Y
F
E
C
B
B
A
Y
+
=
B
A B
C
C
A
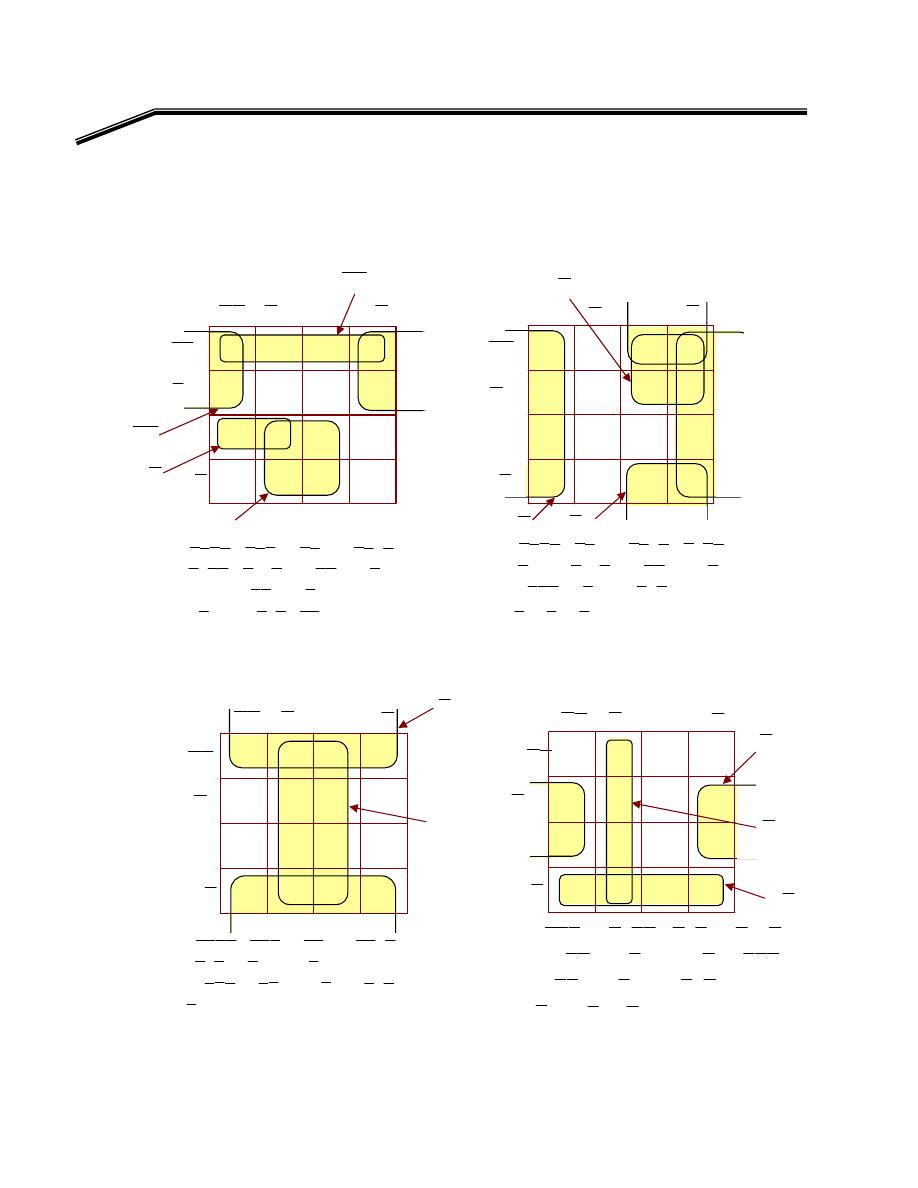
אא
٧٤١
א
א
אאאאא
א
-
٩٧
-
،
א،אא
אאא
KE
F
E
F
E
D
B
B
A
D
C
CD
D
C
D
C
AB
B
A
١
١
١
١
١
١
٠
١
١
٠
١
١
١
١
B
A
D
B
Y
D
C
B
A
D
C
AB
D
C
B
A
D
C
B
A
ABCD
CD
B
A
BCD
A
D
C
B
A
D
C
B
A
CD
B
A
D
C
B
A
D
C
B
A
Y
+
=
+
+
+
+
+
+
+
+
+
+
+
=
F
א
E
F
א
E
D
B
B
A
D
C
Y
D
C
B
A
CD
B
A
D
C
B
A
D
C
B
A
D
ABC
D
C
AB
D
C
AB
D
BC
A
D
C
B
A
D
C
B
A
D
C
B
A
Y
+
+
=
+
+
+
+
+
+
+
+
+
+
=
F
א
E
D
B
B
A
B
A
D
C
CD
D
C
D
C
B
A
٠
١
٠
٠
١
١
٠
١
١
١
٠
١
١
١
١
١
B
A
AB
D
C
F
٣
J
٠٢
E
אא
K
F
א
E
F
א
E
C
AB
D
A
B
A
AD
D
C
CD
D
C
D
C
B
A
١
١
١
١
١
٠
٠
١
١
١
١
٠
٠
١
١
٠
F
א
E
CD
B
A
D
C
B
A
ABCD
D
C
AB
D
C
AB
D
BC
A
D
C
B
A
D
C
B
A
CD
B
A
D
C
B
A
D
C
B
A
Y
+
+
+
+
+
+
+
+
+
+
=
B
A
D
B
A
AD
C
AB
Y
+
+
+
=
F
E
B
A
B
A
C
B
D
D
C
B
A
CD
B
A
D
C
B
A
D
ABC
D
C
AB
D
BC
A
BCD
A
D
C
B
A
D
C
B
A
CD
B
A
D
C
B
A
Y
+
+
+
+
+
+
+
+
+
+
=
F
א
E
D
C
B
C
A
Y
+
+
=
F
א
E
F
E
٠
٠
٠
٠
١
C
A
١
١
١
١
١
١
١
١
١
D
C
CD
D
C
B
A
B
A
AB
B
A
١

אא
٧٤١
א
א
אאאאא
א
-
٠٨
-
٣
J
٦W
א
אאאאא
٣
J
١٢
F
E
א
K
א
א
Y
D
C
B
A
٠
٠
٠
٠
٠
١
١
٠
٠
٠
٠
٠
١
٠
٠
١
١
١
٠
٠
٠
٠
٠
١
٠
١
١
٠
١
٠
٠
٠
١
١
٠
١
١
١
١
٠
٠
٠
٠
٠
١
٠
١
٠
٠
١
٠
٠
١
٠
١
١
١
١
٠
١
٠
٠
٠
١
١
٠
١
٠
١
١
٠
٠
١
١
١
١
١
١
١
١
٣
J
١٢
F
E
אאאא
K
אאאאאאא
)
Y
(
אא
()١
،
٣
J
١٢
F
KE
א
אאא
W
ABCD
CD
B
A
BCD
A
D
C
B
A
CD
B
A
D
C
B
A
Y
+
+
+
+
+
=
אאא
٣
J
١٢
F
E
،
אאא
)
Y
(
אאא
K
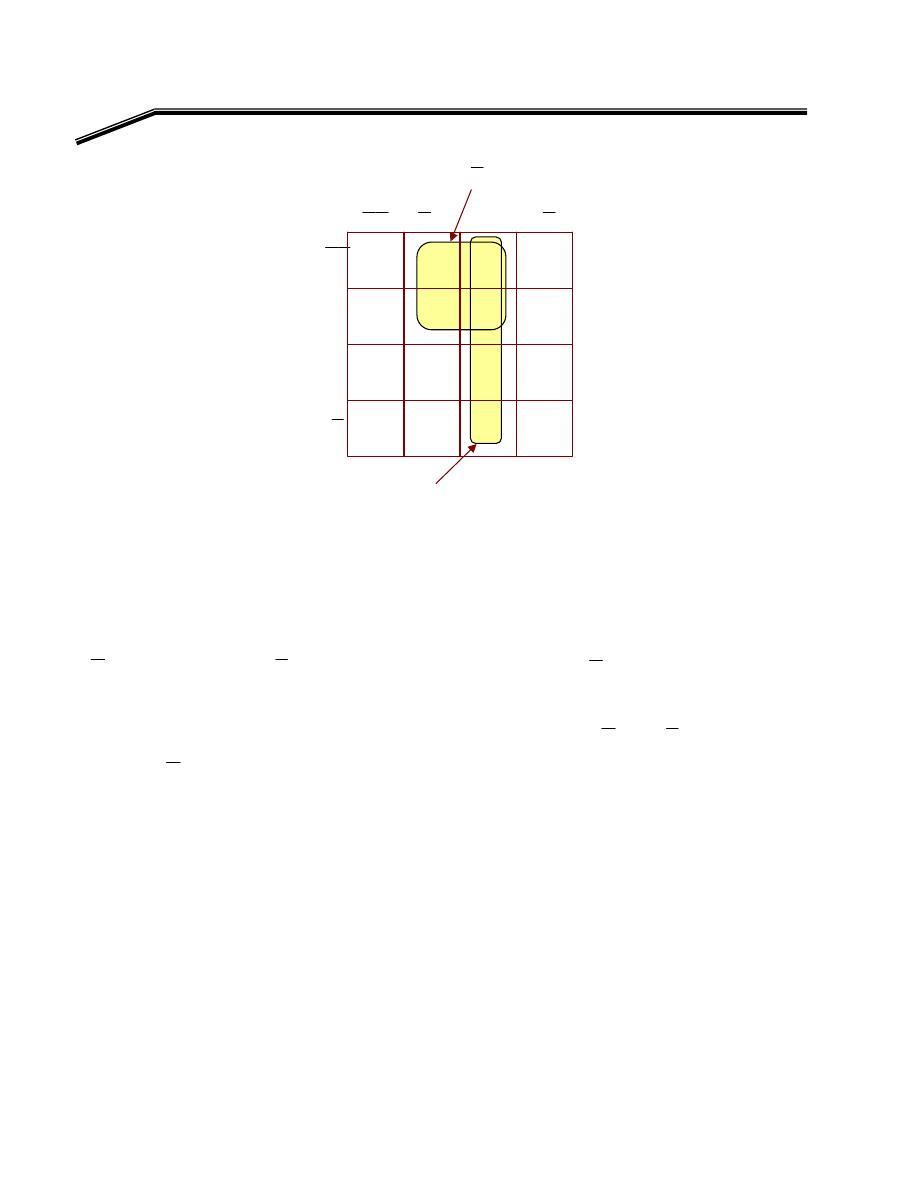
אא
٧٤١
א
א
אאאאא
א
-
١٨
-
٣
J
١٢
F
E
א
٣
J
٦K
٣
J
١٢
F
E
א
א
)
١'s
(
K
אאאא
א
B
א
B
א
C
א،
C
א
D
A
K
אאא
אא
B
،
B
،
A
،
A
א
CD
K
אאא
W
CD
D
A
Y
+
=
٣
J
٧
אאאא
Binary Adders and Subtractors
אאאאאאאאא
אאאאאאא،א
K
אא
אאאאאאא
אאאאאאאאא
K
٣
J
٧
J
١
אאא
The Half-Adder Circuit
א،אאאא
F
٣
J
٣
E
אאא
א
B
A,
אא
[Sum(S)]
אאא
]
)
C
(
[Carry
.
D
A
CD
B
A
D
C
CD
D
C
D
C
AB
B
A
٠
١
١
٠
٠
١
١
٠
٠
٠
١
٠
٠
٠
١
٠
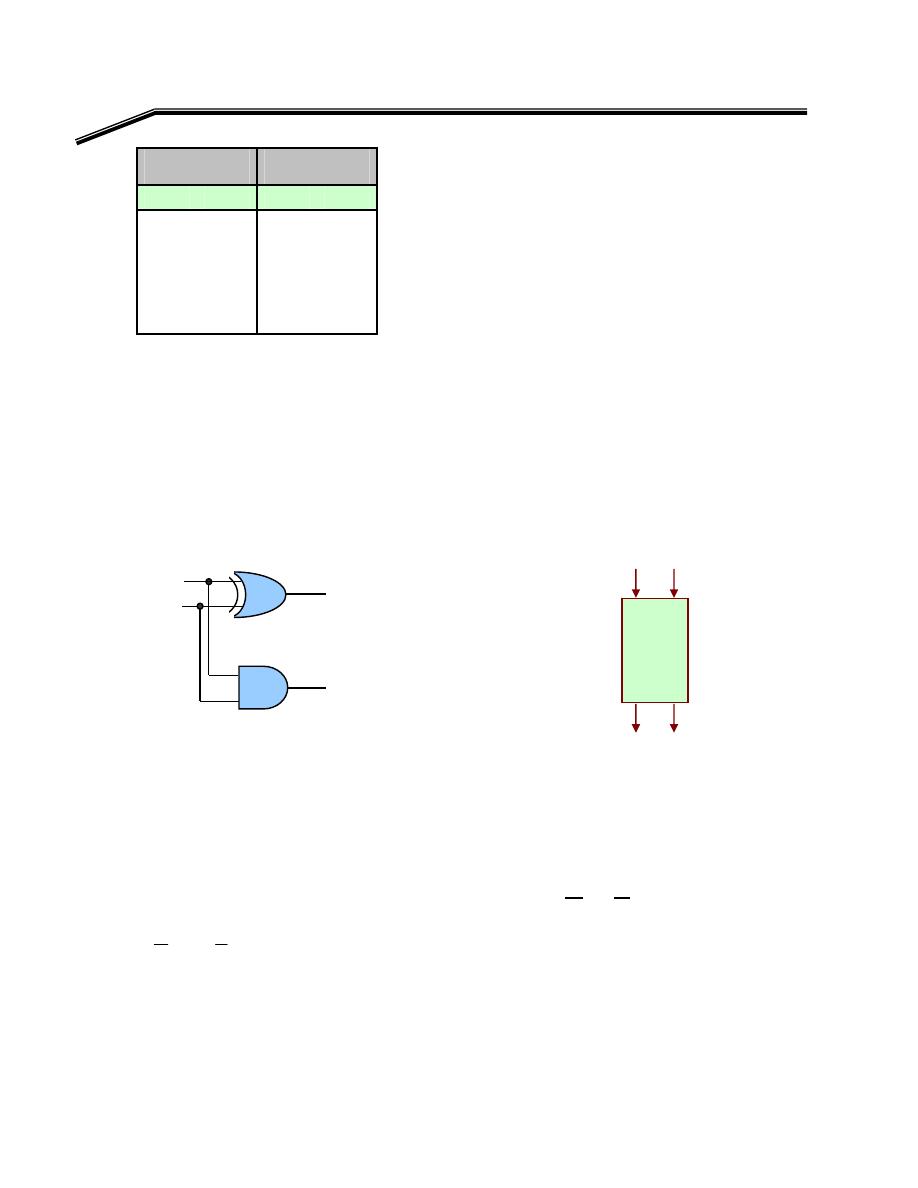
אא
٧٤١
א
א
אאאאא
א
-
٢٨
-
א
א
C
S
B
A
٠+ ٠= ٠
٠
٠
٠
٠
٠+ ١ = ١
٠
١
١
٠
١+ ٠ = ١
٠
١
٠
١
١+ ١= ١٠
٢
or ٢
٠١
١ ٠ א
١
٠
١
١
F
٣
J
٣
E
אאאא
K
אא
)
S
(
אאא
)
XOR
(
K
א
א
א
)
c
(
אא
AND
K
٣
J
٢٢
F
E
אאא
B
,
A
אא
S
,
C
אאאא
K
אאאא
K
F
E
F
E
F
٣
J
٢٢
E
אאאא
K
אאאאא
٣
J
٢٢
F
E
א
HA
F
dder
A
alf
H
E
אא
K
אאא
א
S,C
א،אא
W
AB
C
B
A
B
A
S
=
+
=
٣
J
٧
J
٢
אאא
The Full-Adder Circuit
אאאא
)
٢-bits
(
אאאא
)
carry
(
،אאא
C
S
B
A
HA
≡
C(carry)
S(sum)
A
א
א
B
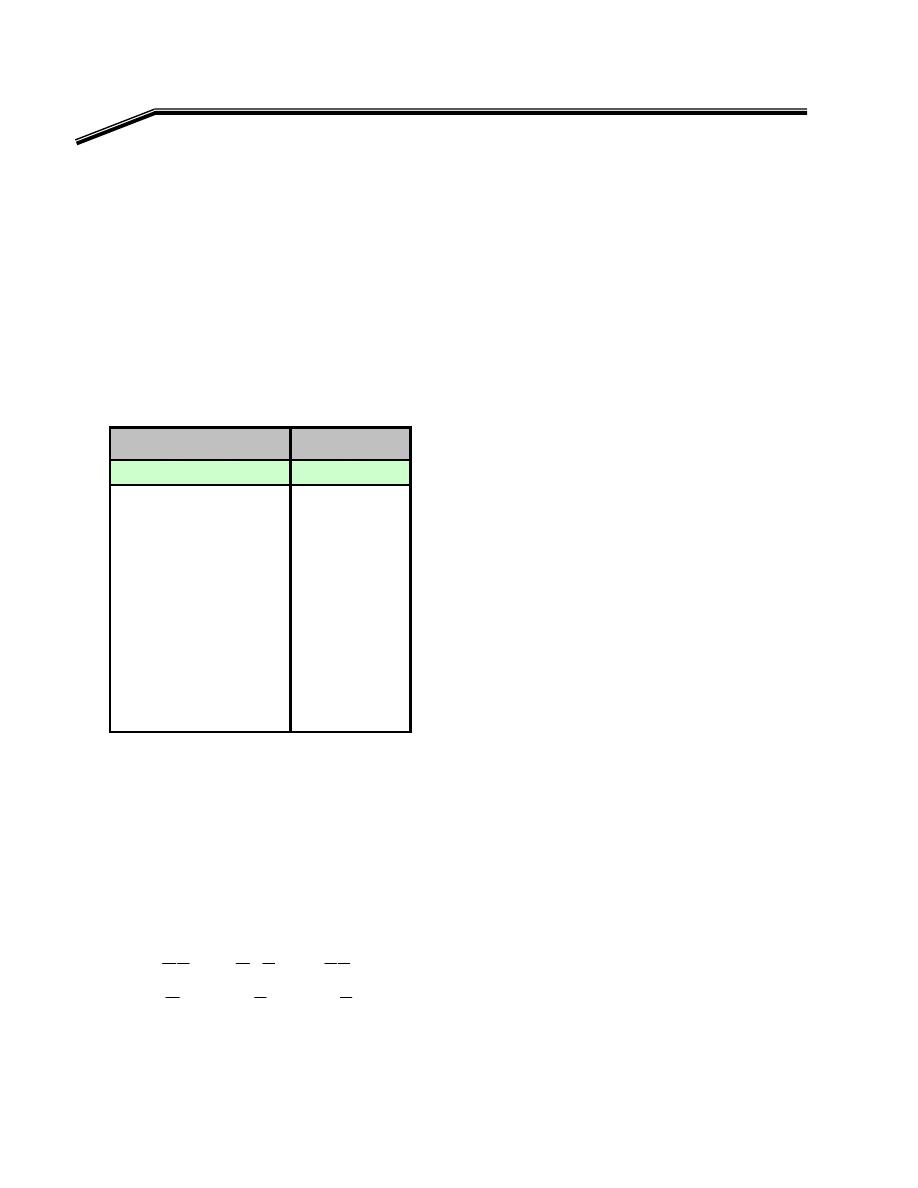
אא
٧٤١
א
א
אאאאא
א
-
٣٨
-
א
אא
)
bits
(
،אאאא
א
אאאאא،א
K
אאאאא
)
bits
(
،א
אא،
A,B
אאאאא
C
in
F
Input carry
E
אאאאא
K
א
)
Carry
(
،
א
)
Sum
ٍ
.(
אאאא
F
٣
J
٤
KE
א
א
C
S
C
in
B
A
٠+ ٠+ ٠= ٠
٠
٠
٠
٠
٠
٠+ ٠+ ١ = ١
٠
١
١
٠
٠
٠+ ١ + ٠= ١
٠
١
٠
١
٠
٠+ ١ + ١ = ١٠
٢
or ٢
٠١
١ ٠א
١
٠
١
١
٠
١+ ٠ + ٠ = ١
٠
١
٠
٠
١
١+ ٠ + ١= ١٠
٢
or ٢
٠١
١
٠א
١
٠
١
٠
١
١+ ١+ ٠ = ١٠
٢
or ٢
٠١
١ ٠ א
١
٠
٠
١
١
١+ ١+ ١= ١١
٢
or ٣
٠١
١ ١א
١
١
١
١
١
F
٣
J
٤
E
אאאא
K
אאאאאא
C
,
B
,
A
א
א
F
8
2
3
=
E
א
K
אא
S
,
C
א
אאאאא
K
אאאא
C
S,
א
W
in
in
in
in
in
in
in
in
ABC
C
AB
C
B
A
BC
A
C
ABC
C
B
A
C
B
A
C
B
A
S
+
+
+
=
+
+
+
=

אא
٧٤١
א
א
אאאאא
א
-
٤٨
-
אא،אאאאאא
אאאא
S
W
in
in
in
in
in
in
C
)
AB
B
A
(
C
)
B
A
B
A
(
ABC
C
B
A
C
B
A
C
B
A
S
+
+
+
=
+
+
+
=
אא
B
A
B
A
+
XOR
אא،
AB
B
A
+
XNOR
אאאא
W
in
in
C
)
B
A
(
C
)
B
A
(
S
⊕
+
⊕
=
א
XOR
)
B
A
(
⊕
א
in
C
אא
S
W
in
in
C
B
A
C
)
B
A
(
S
⊕
⊕
=
⊕
⊕
=
S
אא
XOR
א،
B
,
A
א
א
in
C
K
א
C
אא
W
)
1
C
C
(
AB
C
)
B
A
(
)
C
C
(
AB
C
)
B
A
B
A
(
ABC
C
AB
C
B
A
BC
A
C
in
in
in
in
in
in
in
in
in
in
=
+
⇐
+
⊕
=
+
+
+
=
+
+
+
=
S
C
א
٣
J
٣٢
F
KE
אאא
אא
٣
J
٣٢
F
E
א
FA
א
)
dder
A
ull
F
(
אא
K
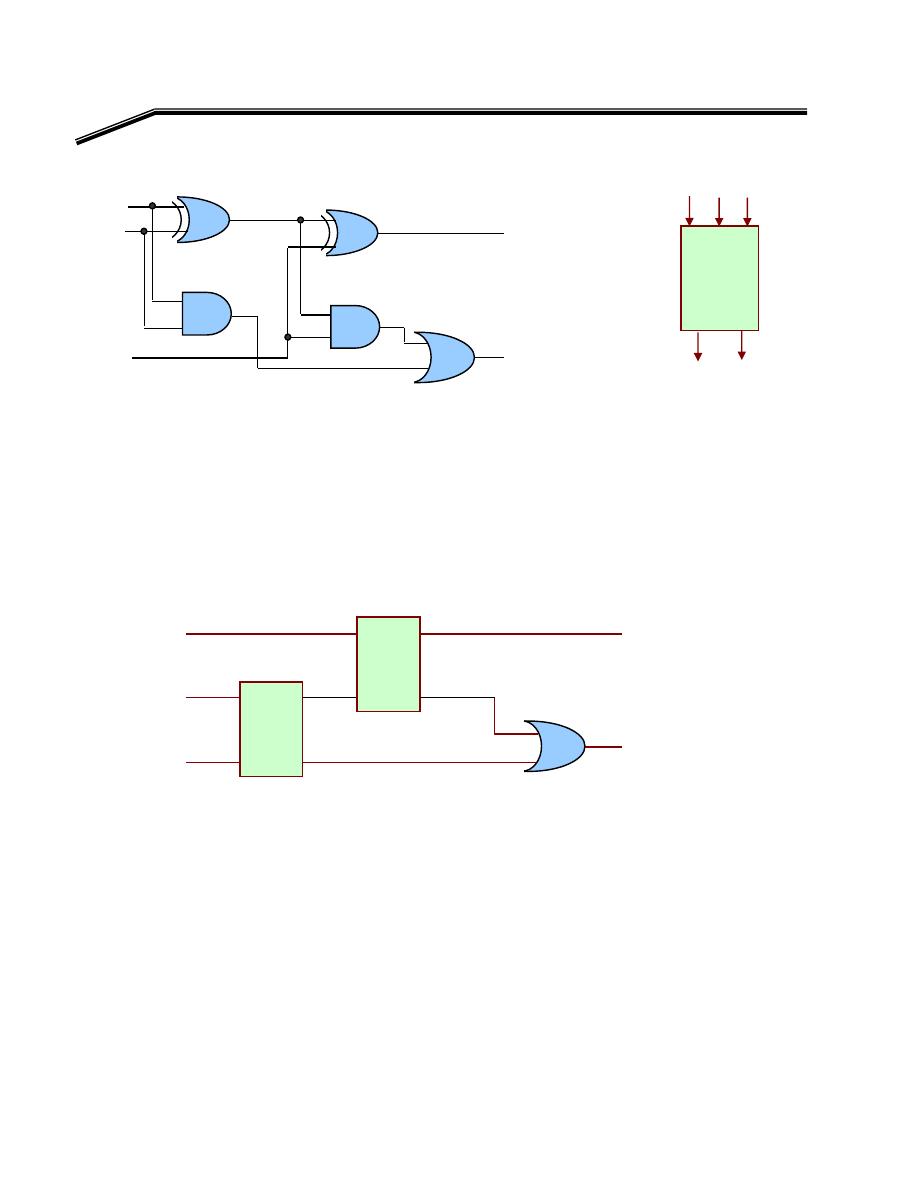
אא
٧٤١
א
א
אאאאא
א
-
٥٨
-
F
٣
J
٣٢
E
אאאא
K
אא
٣
J
٣٢
F
E
אאא
אא
OR
אאאא
٢
א
OR
א
F
٣
J
٤٢
KE
٣
J
٧
J
٣
אאא
Half Subtractor Circuit
אא
א
K
אאאא
K
א،אאאאאא
K
،א
)
bit
(
אאא
א
)
bit
(
אא
)
difference
(
K
،אאא
C
in
C(carry)
S(sum)
A
B
C
S
B
A
FA
≡
C
in
F
E
F
E
C
S
C
S
B
A
B
A
C
in
C
S
HA
HA
F
٣
J
٤٢
E
אאא
K
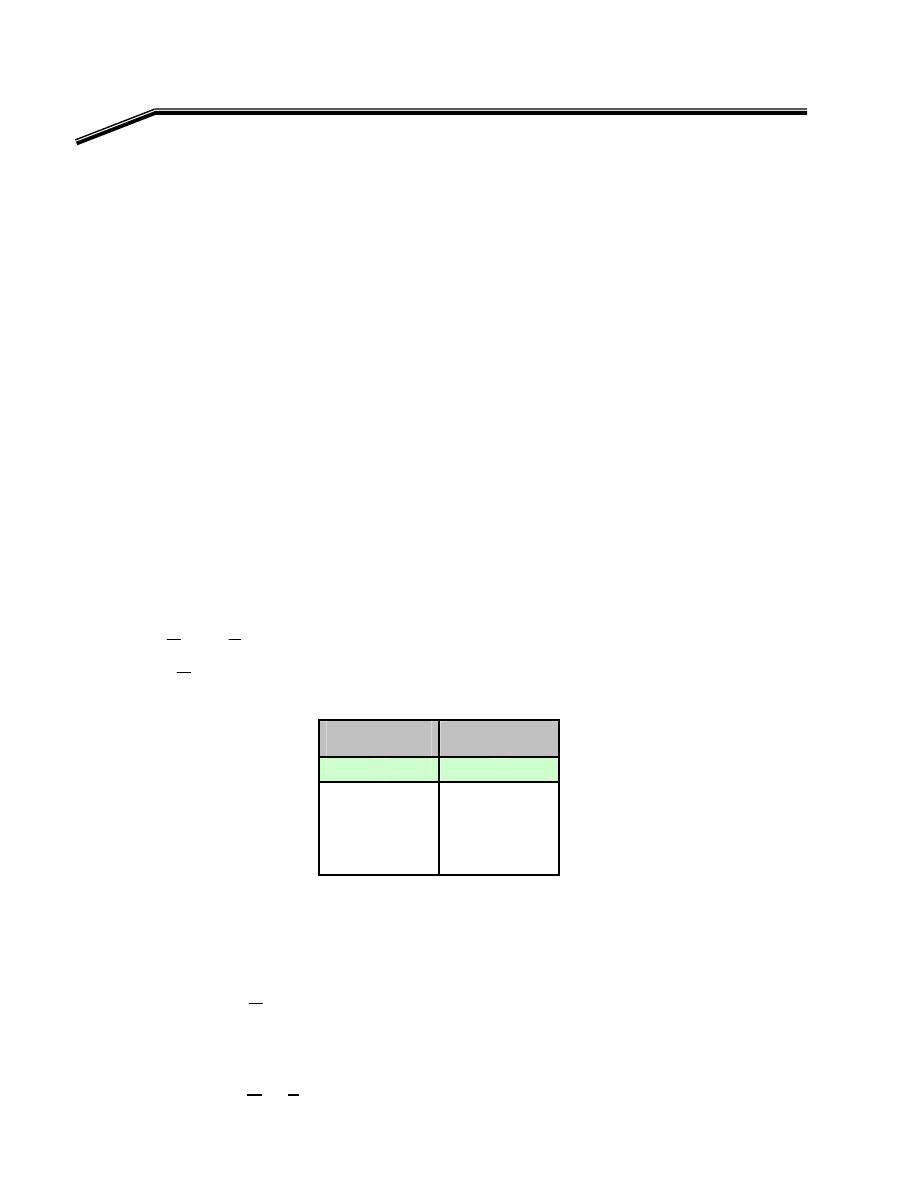
אא
٧٤١
א
א
אאאאא
א
-
٦٨
-
א
)
١
(
)
Borrowed
(
אא
K
،
K
אאאא
)
٢-bits
(
א
)
١
(
א
א
K
A
א
B
K
)
A – B
(
א
B, A
K
B
A
≥
،
א
W
٠– ٠= ٠, ١ – ٠= ١, ١ – ١ = ٠
אא
)
Difference bit
.(
א
A<B
٠– ١
א،
א
א
)
١
(
אא
K
אאא
٢
،א
א،אא
)
٠١
(
א
K
א
)
٢
(
،
א
٢– ١ = ١
K
א،אא
)
D
(
אא
א
א
)
B
٠
(
K
אאאאאא
F
٣
J
٥
KE
אא
)
D
(
א،
)
0
B
(
א
א
א
W
B
A
B
B
A
B
A
D
0
=
+
=
א
א
B
٠
D
B
A
٠
٠
٠
٠
١
١
١
٠
٠
١
٠
١
٠
٠
١
١
F
٣
J
٥
E
אאאא
K
א
)
D
(
א
(S)
א
א
XOR
א،
)
0
B
(
א
)
C
(
אאא
A
א
)
0
B
(
א
AND
א
A
،
B
K
٣
J
٥٢
F
E
،אא
٣
J
٥٢
F
E
א
א،א
HS
א
)
ubtractor
S
alf
H
(
K
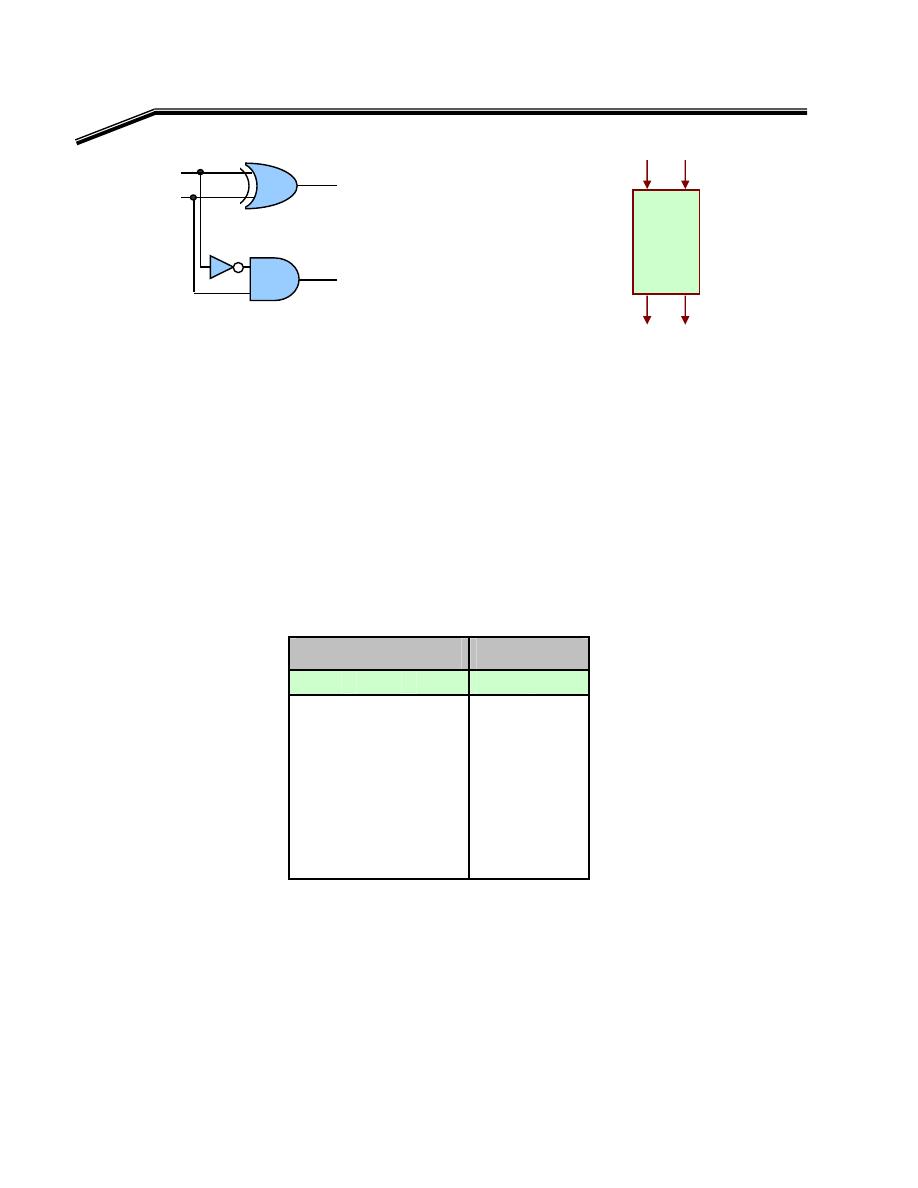
אא
٧٤١
א
א
אאאאא
א
-
٧٨
-
٣
J
٧
J
٤
אאא
The Full-Subtractor Circuit
אאאאא
)
٢-bits
(
א
א
)
١
(
אא
K
אא
K
אא
in
B
,
B
,
A
א
)
A
(
א
)
B
(
א
א
)
n
i
B
(
א
K
א
0
B
,
D
אאא
K
אאאא
F
٣
J
٦
KE
א
א
B
٠
D
B
in
B
A
٠
٠
٠
٠
٠
١
١
١
٠
٠
١
١
٠
١
٠
١
٠
١
١
٠
٠
١
٠
٠
١
٠
٠
١
٠
١
٠
٠
٠
١
١
١
١
١
١
١
F
٣
J
٦
E
אאאא
K
אאאאא
0's,1's
א
אא
K
0's,1's
אא
א
in
B
B
A
−
−
K
אא
0
B
in
=
א
א
אא
K
1
B
0,
B
0,
A
in
=
=
=
)
١
(
אאא
1
B
0
=
)
٢
(
A
،
٢– ٠ – ١ = ١
،
1
D
=
K
B٠
B
٠
(borrow)
D(difference)
A
א
D
B
A
B
HS
≡
א
F
٣
J
٥٢
E
אאאא
K

אא
٧٤١
א
א
אאאאא
א
-
٨٨
-
1
B
,
1
B
0,
A
in
=
=
=
)
١
(
אאא
1
B
0
=
،
A =
٢
،
٢– ١ – ١ = ٠
،
0
D
=
K
1
B
0,
B
,
1
A
in
=
=
=
،
A – B – B
in
=
٠
א
0
B
0
=
،
0
D
=
K
א
1
B
,
1
B
,
1
A
in
=
=
=
)
١
(
אאא
1
B
0
=
،
A=
٣
،
٣– ١ – ١ = ١
،
1
D
=
K
אאאא
א
W
(S)
،אא
אא
א
W
א
(B
٠
)
אא،
W
א
(B
٠
), (D)
٣
J
٦٢
F
E
א،
אאא
א
٣
J
٦٢
F
E
א،
FS
א
)
ubtractor
S
ull
F
(
אא
K
אאא
٣
J
٦٢
F
E
אאא
אא
OR
אא،
אא
٢
א
OR
א
F
٣
J
٧٢
KE
in
in
in
in
ABB
B
B
A
B
B
A
B
B
A
D
+
+
+
=
in
B
B
A
in
B
B)
(A
D
⊕
⊕
=
⊕
⊕
=
)
1
B
B
(
B
A
)
B
A
(
B
B
)
B
B
(
B
A
)
AB
B
A
(
B
ABB
BB
A
B
B
A
B
B
A
B
in
in
in
0
in
in
in
in
in
in
in
0
=
+
⇐
+
⊕
=
+
+
+
=
+
+
+
=
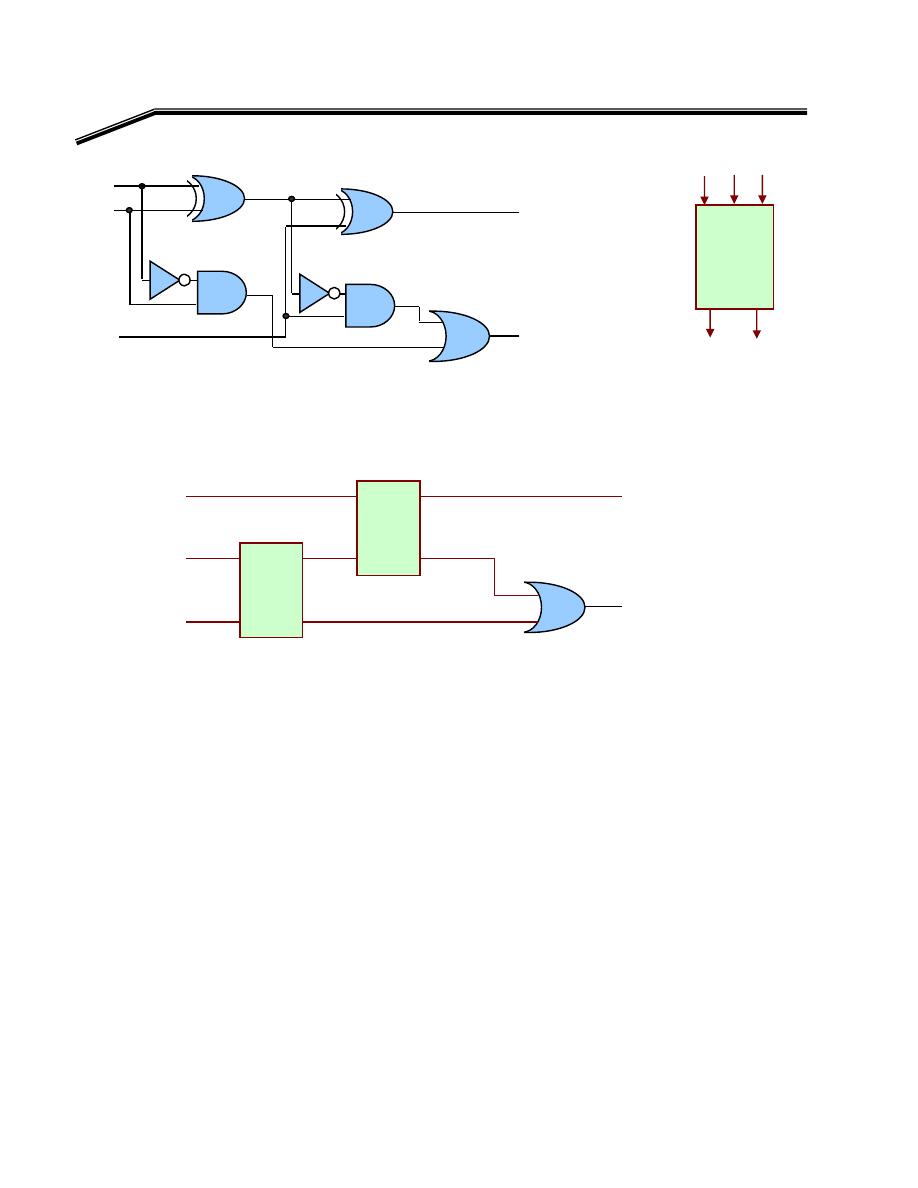
אא
٧٤١
א
א
אאאאא
א
-
٩٨
-
B
in
B
٠
D
A
B
D
B
A
FS
≡
B
in
F
E
F
E
B
٠
F
٣
J
٦٢
E
אאאא
K
B
٠
D
B
٠
D
B
A
B
A
B
in
B
٠
D
HS
HS
F
٣
J
٧٢
E
אאא
K
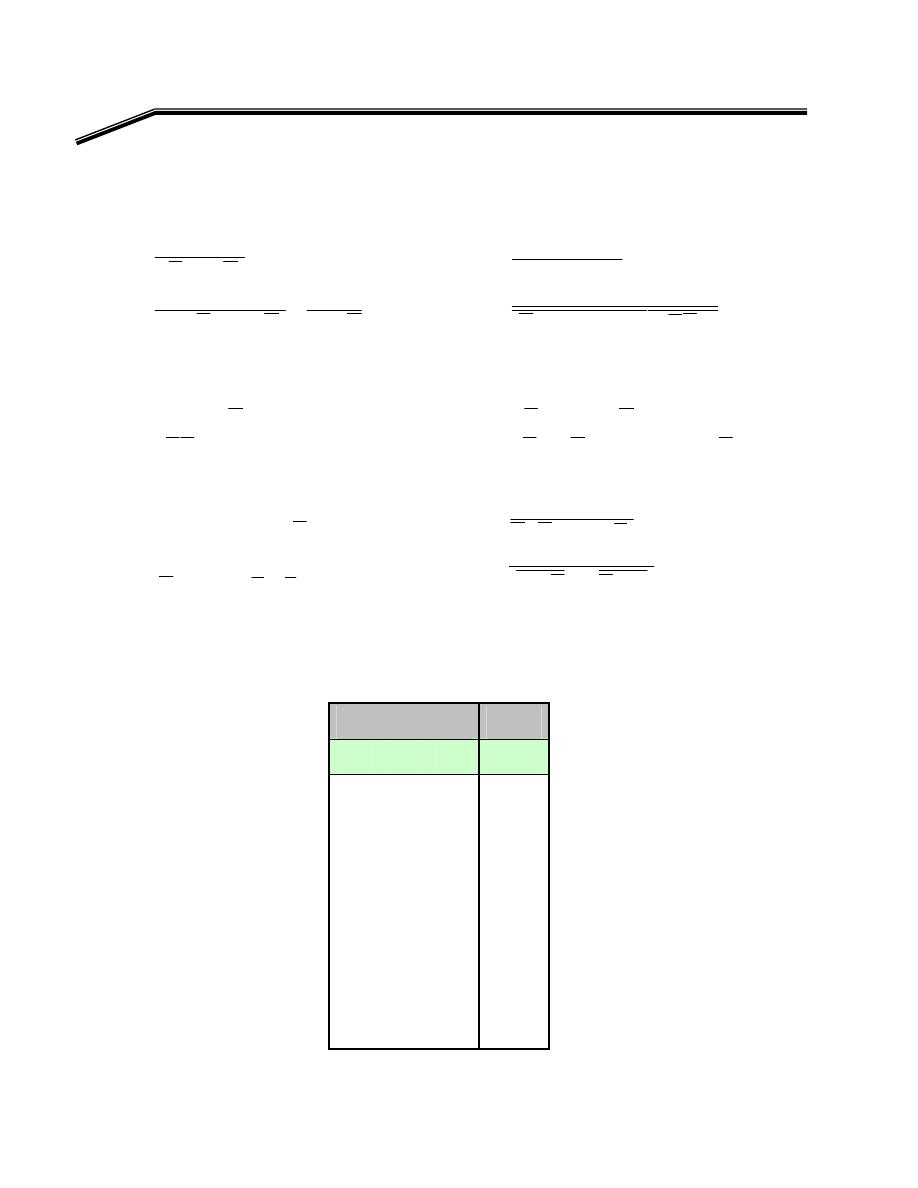
אא
٧٤١
א
א
אאאאא
א
-
٠٩
-
١
E
אאא
W
a)
b)
c)
d)
٢
E
אאאא
א
NAND
W
a)
b)
c)
d)
٣
E
אאאא
א
NOR
W
a)
b)
c)
d)
٤
E
אאא
אא
W
א
א
Y
C
B
A
١
٠
٠
٠
١
١
٠
٠
٠
٠
١
٠
٠
١
١
٠
١
٠
٠
١
٠
١
٠
١
١
٠
١
١
١
١
١
١
)
D
C
(
B
A
+
)
EF
CD
(
AB
+
D
ABC
)
D
C
B
A
(
+
+
+
+
)
D
C
B
A
(
)
D
C
B
A
(
+
+
+
E
D
ABCD
+
D
AB
C
B
A
+
+
E
D
C
B
A
+
+
C
AB
ABC
BC
A
C
B
A
+
+
+
)
B
A
(
)
C
B
A
(
+
+
+
)
E
D
(
C
B
A
+
+
)
F
E
D
(
)
C
B
A
(
+
+
)
D
C
(
)
B
A
(
+
+
+

אא
٧٤١
א
א
אאאאא
א
-
١٩
-
٥
E
אא
אאאא
W
a)
b)
c)
d)
٦
E
אאאא
F
٣
J
٣٢
E
אא،
(
١or ٠)
אא
W
a)
A
=
١, B = ١, C
in
=
١b)
A
=
٠, B = ١, C
in
=
١
c)
A
=
٠, B = ١, C
in
=
٠d)
A
=
١, B = ١, C
in
=
٠
٧
E
אאאאאאאאאא
W
a) S = ٠, C
out
= ٠
b) S = ١, C
out
= ٠
c) S = ١, C
out
= ١
d) S = ٠, C
out
= ١
٨
E
אאאא
F
٣
J
٦٢
E
אא،
(
١or ٠)
אא
W
a) A =
١, B = ١, B
in
=
١b)
A
=
١, B = ٠, B
in
=
١
c) A =
١, B = ١, B
in
=
٠d)
A
=
٠, B = ١, B
in
=
١
D
BC
A
D
C
AB
D
C
B
A
D
ABC
D
C
B
A
D
C
B
A
F
1
+
+
+
+
+
=
D
C
B
A
D
ABC
D
BC
A
D
C
AB
D
C
B
A
D
C
B
A
D
ABC
F
2
+
+
+
+
+
+
=
D
C
B
A
D
C
AB
D
C
AB
D
C
B
A
D
C
B
A
F
3
+
+
+
+
=
CD
B
A
D
C
B
A
D
BC
A
BCD
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
F
4
+
+
+
+
+
+
+
+
=

אאאא
אאאא
א
א
אאא
ã¹]<gè…‚jÖ]æ<ËÖ]<Üé×Ãj×Ö<íÚ^ÃÖ]<퉉ö¹]
אאאא
אאאא
٤
אאא
٧٤١
א
א
אאאא
א
-
٢٩
-
אאא
אא
W
•
אאאאאא
K
•
אאאאאא
K
•
אאאא
J
אאא
K
•
אאאא
K
•
אא
٥٥٥
א
K
•
אאאאא
K
•
אאאאאא
א
אאאא
K
•
אאאאא
א
אאא
K
אאא
٧٤١
א
א
אאאא
א
-
٣٩
-
אא
٤
J
١
Introduction
אאאאאא،אאא
)
Combinational Logic Circuits
(
אאא
א
א،אאאאאאאאאא،א
אאאא
)
Sequential Logic Circuits
(
אאאא
א
)
Memory
(
אא
אאאא
א
K
אא،אאאאאאאאאא
אאאאא
)
Flip-Flop Circuit
(
،
אא
אאא
)
٠
(
א
)
١
(
K
אאאא
)
١
(
א
)
١
(
א،
אא
)
٠
(
א
)
٠
(
K
אאא
א
אאא
אאאאאא
א
אאאא
)
Bistable Multivibrator
.(
אא
NAND
א
NOR
אא
)
Digital Integrated Circuits
(
K
אאאאא
)
Timers
(
،
אאא
)
Counters
(
،
אא
)
Shift Registers
(
אאא
א
K
٤
J
٢
א
Latches
אאאא
אא
אא
K
אאא
אא
א
א
אאאאאא
אא
K
אאאאאא
א
א
K
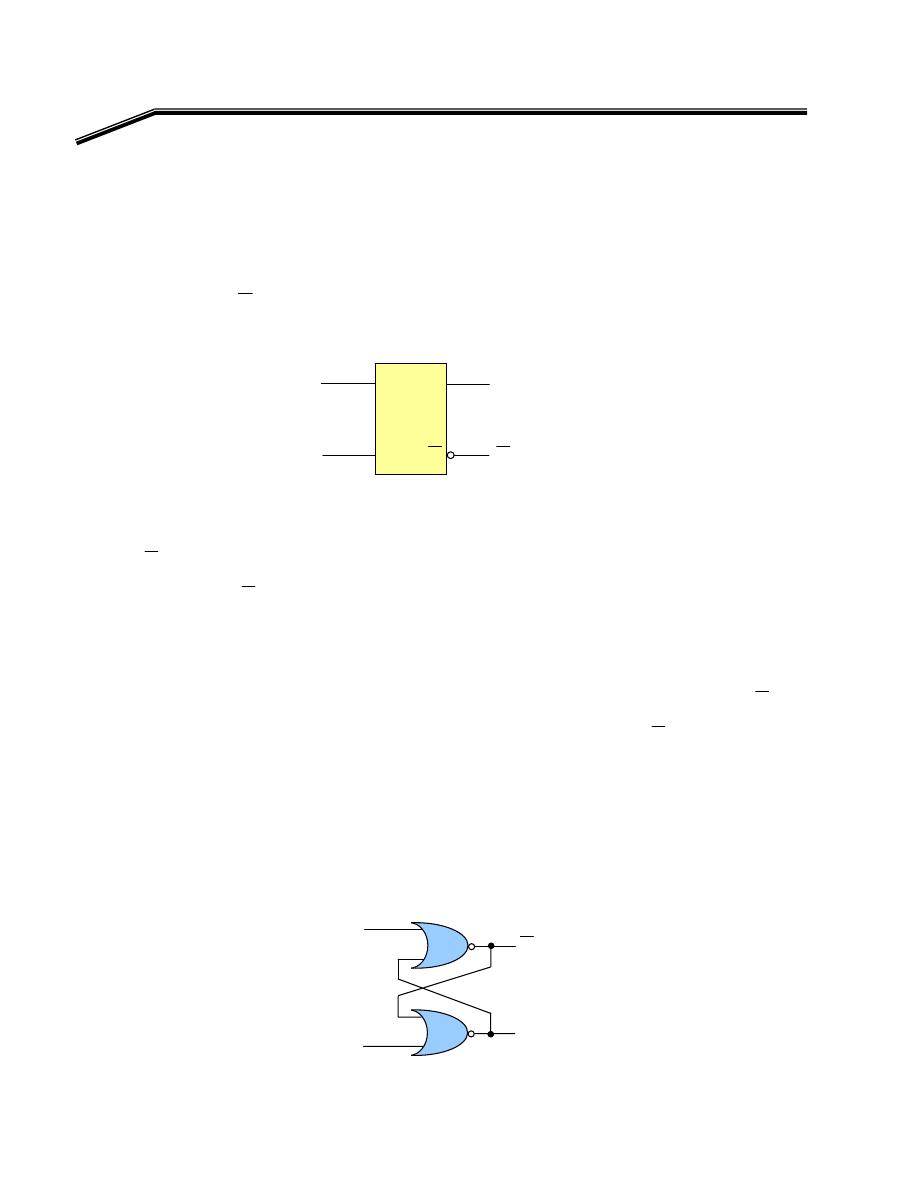
אאא
٧٤١
א
א
אאאא
א
-
٤٩
-
א
)
Latch
(
אאאא
א
)
Bistable Multivibrator
(
K
F
٤
J
١
E
אאאאא
S-R
S
אאא
"
١
"
)
Set Input
(
R
אאא
"
٠
"
)
Reset Input
(
Q
א
Q
א
K
F
٤
J
١
E
אא
אאא
S-R
K
אא
)
Set Condition
(
٠
=
Q
Q =
١
,
)
Reset Condition
(
١
=
Q
٠,
.
Q =
א
א
א
S
א
)
١
(
אא
Q =
١
F
אא
E
א
Q
אאא،א
٠
=
Q
K
אא
R
א
Q =
٠
F
א
א
E
א
א
١
=
Q
א،
S,R
אא
)
١
(
אא
)
unpredictable
(
،
אא
א
K
אא
S-R
א
NOR
אאאא
אאאאא
F
٤
J
٢
KE
F
٤
J
٢
E
אא
S-R
אאא
K
R
Q
Q
S
output
Q
Q output
RESET
INPUT
SET
INPUT
R
S
Q
Q
אאא
٧٤١
א
א
אאאא
א
-
٥٩
-
אאאאא
NOR
)
١
(
F
אא
א
E
א،
אאאאאא
F
٤
J
١
E
אאאאא،
א
אאא
)
Active High Inputs
(
K
א
א
א
(Mode of Operation)
Q
R
S
א
F
א
E
No Change
Q
٠
٠
٠
אא
Latch RESETS
٠
١
٠
אא
Latch SETS
١
٠
١
א
Invalid condition
?
١
١
F
٤
J
١
E
אאא
S-R
א
אא
K
אאא
W
١
-
אא
)
٠
(
א
S,R
אא
א
)
Q
(
F
אא
א
E
אאא
א
K
٢
-
אאא
R
)
٠
(
)
١
(
אא
Q
)
٠
(
Q =
٠
F
אא
E
אא،אאא
Q =
٠
K
٣
-
אאא
S
)
٠
(
)
١
(
אאא
Q
)
٠
(
)
١
(
Q =
١
F
אא
E
א،אאא
א
Q =
١
K
٤
-
אא
)
١
(
א
S,R
אאא
אא
NOR
אאאא،
א
K
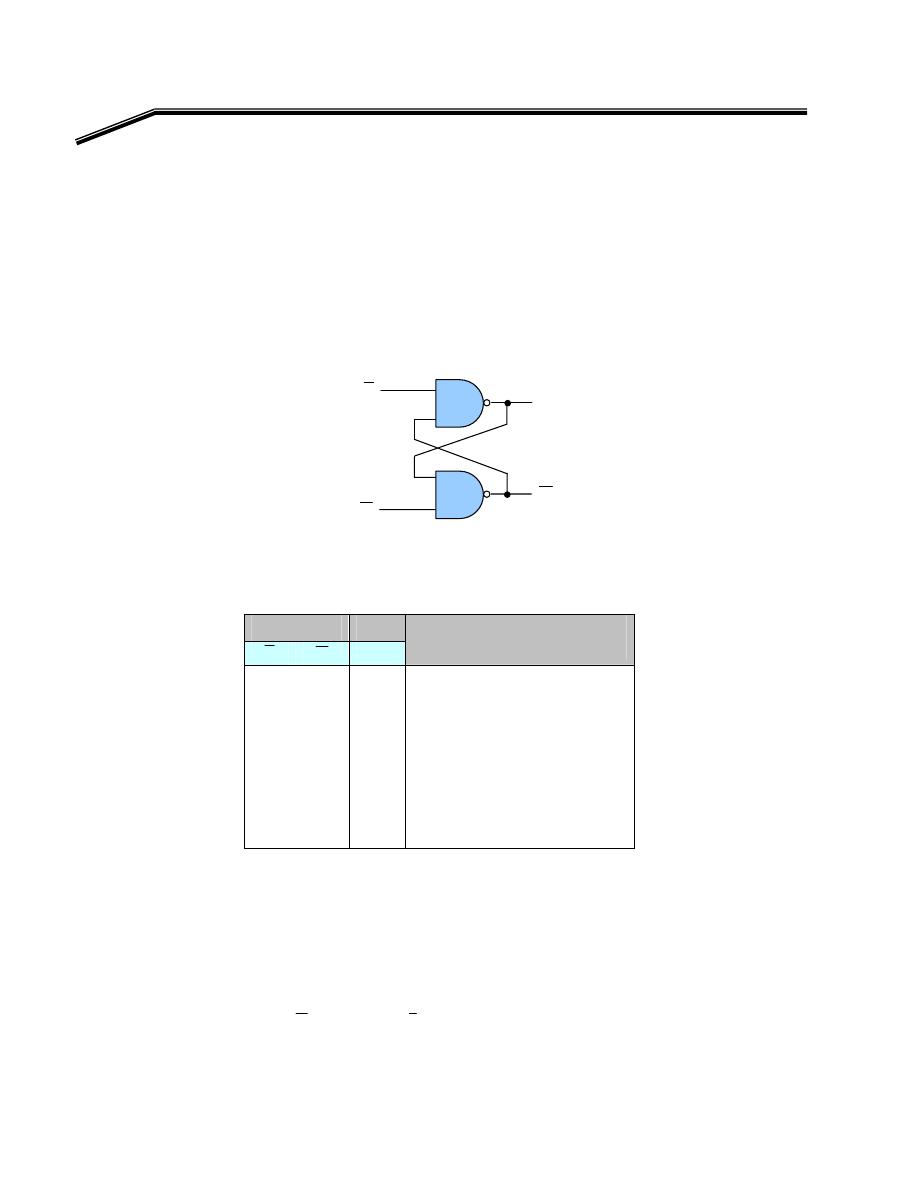
אאא
٧٤١
א
א
אאאא
א
-
٦٩
-
٥
-
אאאאא
،אאאאא،אא
א
K
אאא
NAND
F
٤
J
٣
E
אאא
א
NAND
)
٠
(
א
א
אאא
F
٤
J
٢
E
אאאאא
א
אאא
)
Active Low Inputs
(
K
F
٤
J
٣
E
אא
S-R
אאא
K
א
א
א
(Mode of Operation)
Q
R
S
א
Invalid condition
?
٠
٠
אא
Latch SETS
١
١
٠
א
א
Latch RESETS
٠
٠
١
א
F
א
E
No Change
Q
٠
١
١
F
٤
J
٢
E
אאא
S-R
א
אא
K
אאא
W
١
-
אא
)
١
(
אאאאא
Q
F
אא
KE
٢
-
אאא
٠
=
S
א،
١
=
R
אא
)
١
(
אא،אאא
Q =
١
K
R
Q
Q
S
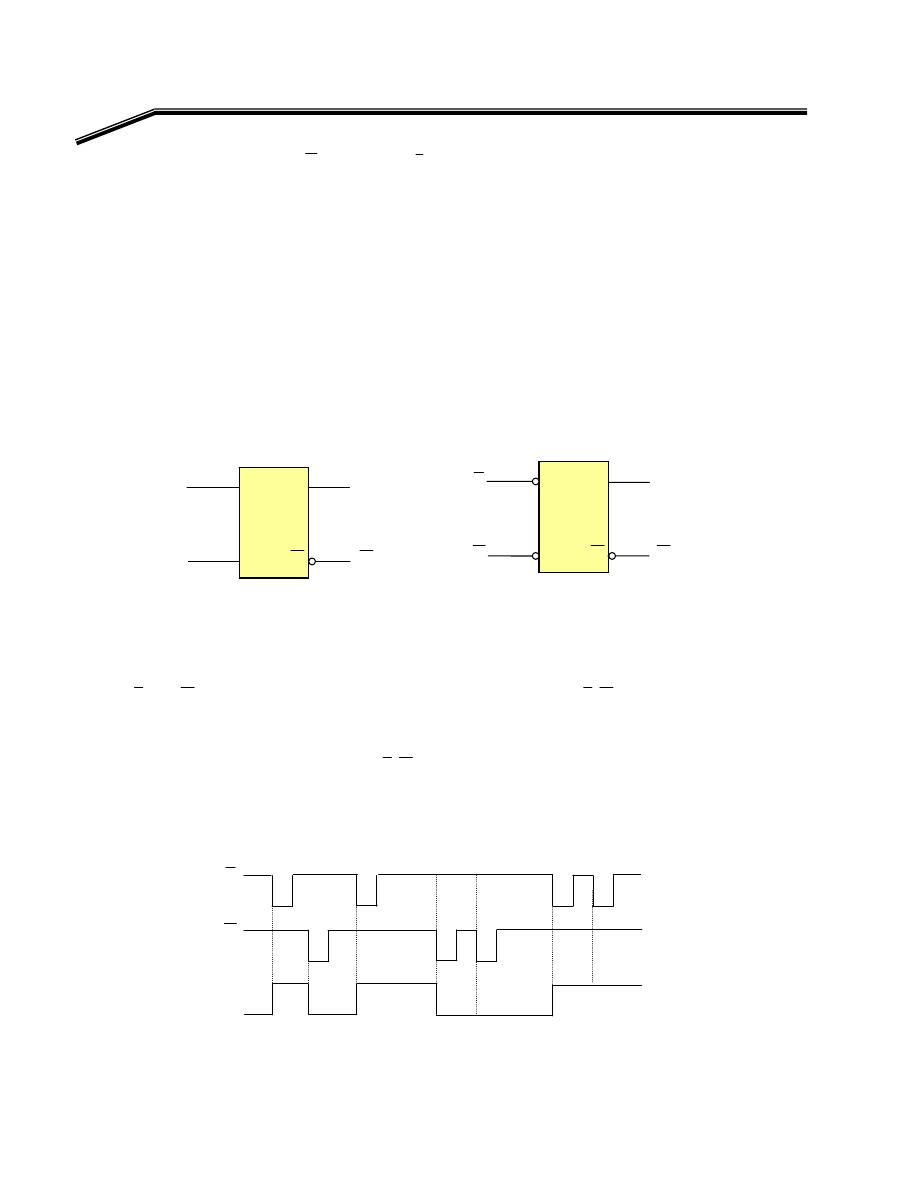
אאא
٧٤١
א
א
אאאא
א
-
٧٩
-
٣
-
אאא
١
=
S
א،
٠
=
R
אא
)
٠
(
אא،אאאא،
Q =
٠
K
٤
-
א
)
٠
(
אאאאאא
NAND
א
K
א
F
٤
J
٤
E
אא
)
Logic Symbol
(
אא
א
אא
אאאאאא
K
F
FE
E
F
٤
J
٤
E
אאאא
א
אאאא
K
אאאא
א
אאא
R
,
S
א
)
Q
(
K
0
R
0,
S
=
=
،
אא
K
٤
J
١W
אא
R
,
S
F
٤
J
٥
KE
א
א
)
Q
(
אאא
Q
א
Q =
٠
K
א
W
F
٤
J
٥
E
אאאא
K
Q
S
R
Q
Q
R
S
Q
Q
S
R
Q
Q
S
Q
R
Q
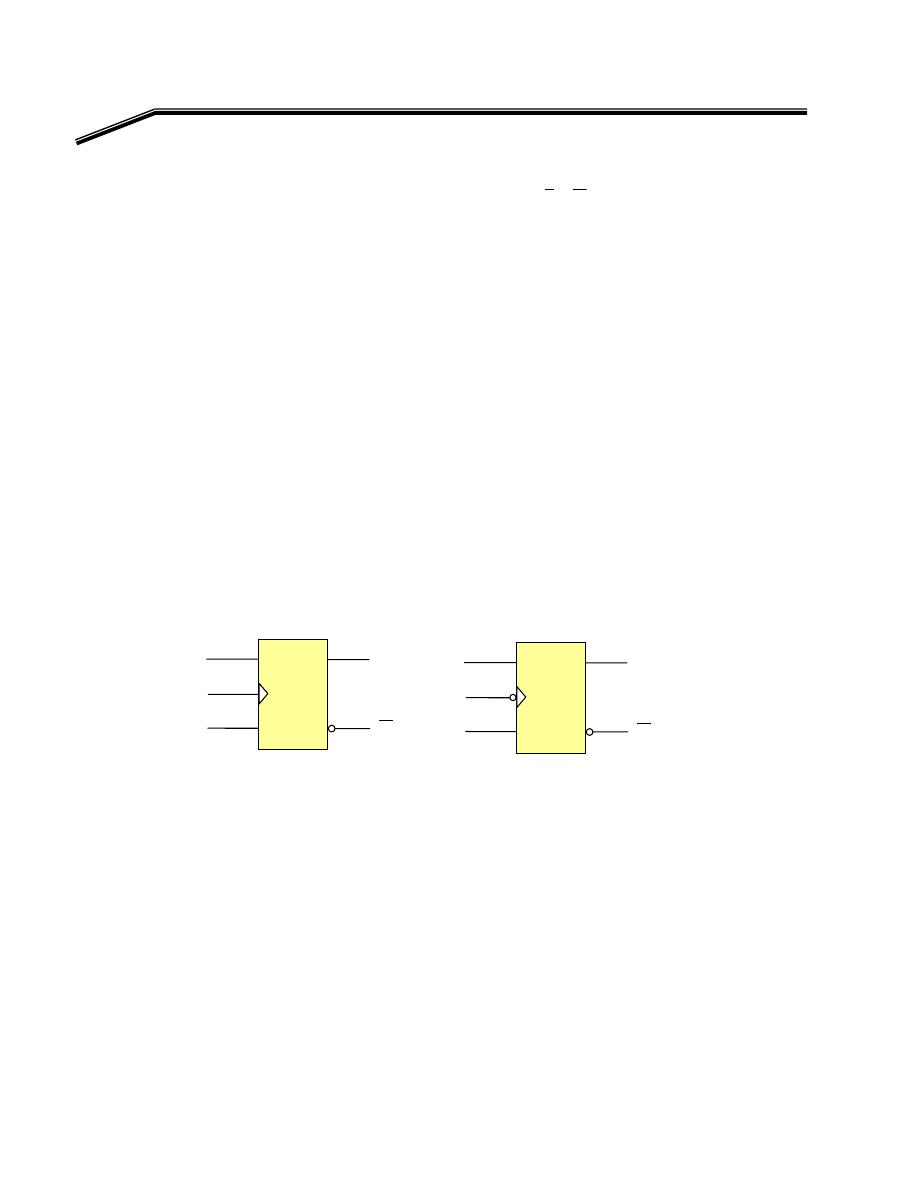
אאא
٧٤١
א
א
אאאא
א
-
٨٩
-
٤
J
٣
א
S-R
אא
Clocked S-R Flip–Flop
א
S-R
R
S
−
אאאאאא
אא
)
Q
(
א
אאא
،אאאאא
אאאאאאאא
K
אאאאא
F
א
E
אא
א
אאא
א،אא
א
S-R
אאא
א
K
אאא
אא
א
)
Clock Pulse
(
א
א
)
CK
(
،
אאאאא
K
F
٤
J
٦
E
אא
S-R
אא
אאא
)
CK
(
K
F
FE
E
F
٤
J
٦
E
אא
S-R
אא
K
א
٤
J
٦
F
E
אאא
א
S-R
אא
)
Positive Edge Trigger
(
א
א
)
٠
(
)
١
(
א،
٤
J
٦
F
E
אאאאא
אאא
)
Negative Edge Trigger
(
א
א
)
١
(
)
٠
(
K
F
٤
J
٧
E
אא
S-R
אאאא
NAND
א،
NAND
אאאא
K
אא
Q
Q
Q
Q
S
R
CK
S
R
CK
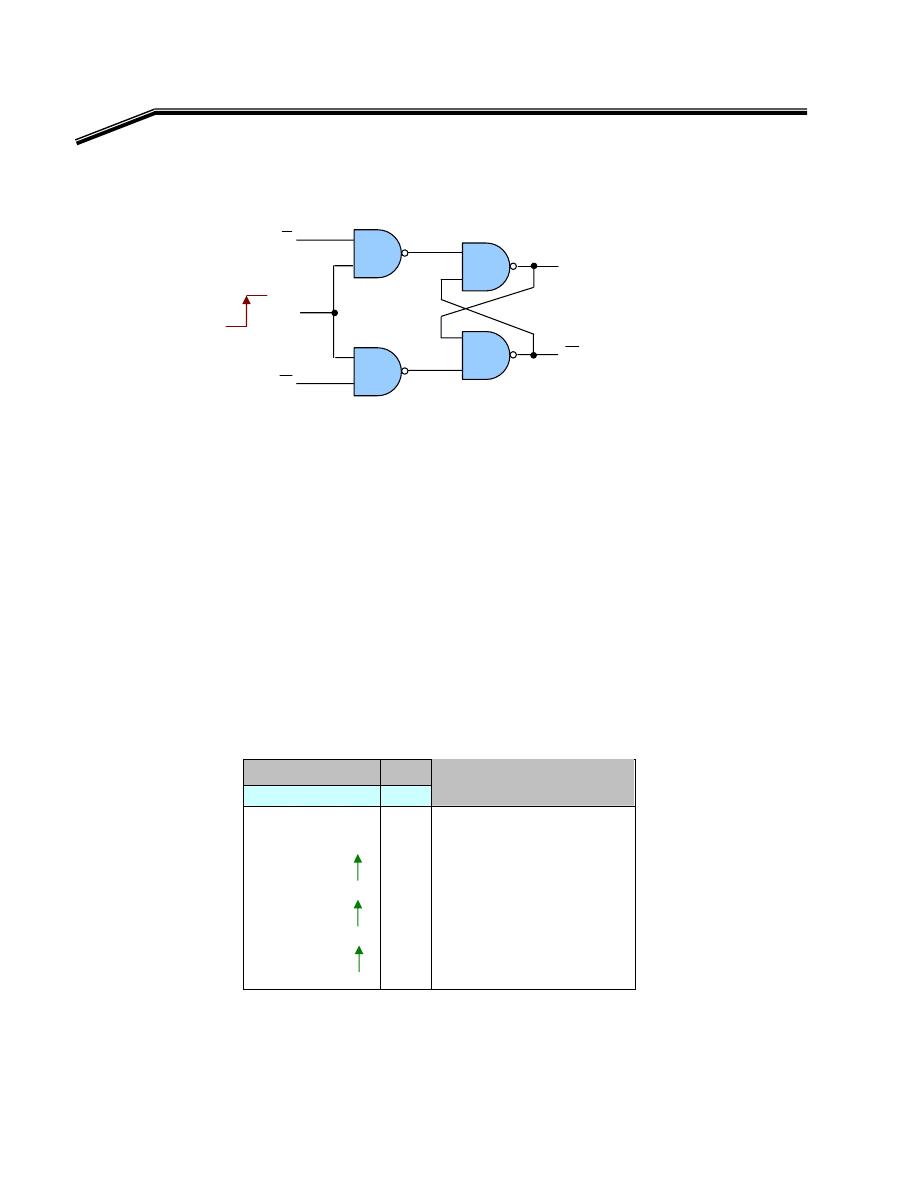
אאא
٧٤١
א
א
אאאא
א
-
٩٩
-
א
S,R
א
)
Q
(
אאאא
אאא
K
F
٤
J
٧
E
אא
S-R
אא
K
א
F
٤
J
٣
E
א
S-R
אאאא
W
١
J
אא
CK
אא،א
S,R
אא
)
٠
(
א
אאאא
K
٢
J
אא
R
א
)
S = ٠,R = ١
(
אא
)
٠
(
)
١
(
א
)
٠
(
אא
א
)
Reset
.(
٣
J
אא
S
אא
)
S = ١,R = ٠
(
אא
)
٠
(
)
١
(
א
Q =
١
אאא
)
Set
.(
אא
S =
١, R =
١
א
א
K
א
א
א
(Mode of Operation)
Q
CK
R
S
א
F
א
E
No Change
Q
٠
X
٠
٠
א
א
Latch RESETS
٠
١
٠
אא
Latch SETS
١
٠
١
א
Invalid condition
?
١
١
א
(
)٠
א
(
)١
Z
↑
Z
X
אאא
Z
Q
٠
F
٤
J
٣
E
אאא
S-R
אא
K
CK
R
Q
Q
S
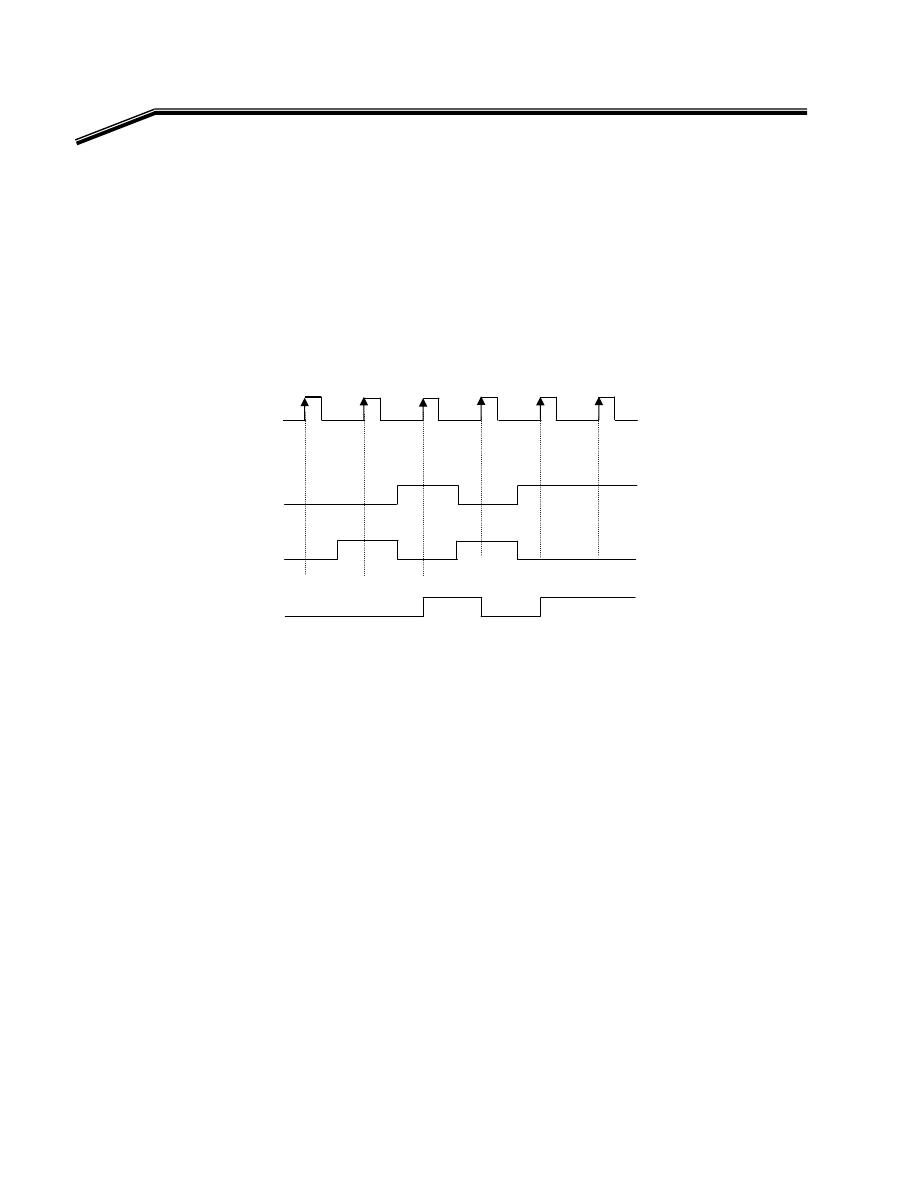
אאא
٧٤١
א
א
אאאא
א
-
٠٠١
-
אא
S-R
אאא
]
א
)
١
(
)
٠
(
[
אא
א
אאא
אא
)
١
(
)
٠
(
K
٤
J
٢W
אא
)
Q
(
אא
S-R
א
F
٤
J
٦
E
א،
א
S,R,CK
F
٤
J
٧
KE
אאא
Q =
٠
אא
K
F
٤
J
٧
E
אאאא
S-R
אא
K
א
W
١
-
אאא
S =
٠, R = ٠
א،
)
Q
(
Q =
٠
K
٢
-
אאא
S =
٠, R = ١
א،
Q = ٠
)
Reset
(
K
٣
-
אאא
S =
١, R = ٠
א،
Q
)
١
(
Q =
١
)
Set
(
K
٤
-
אאאא
S =
٠, R = ١
א،
Q = ٠
)
Reset
.(
٥
-
אאא
S =
١, R = ٠
א،
=١
Q
)
Set
(
K
٦
-
אאא
S =
١, R = ٠
א،
)
١
(
Q =
١
K
٦
٥
٤
٣
٢
١
CK
S
R
Q
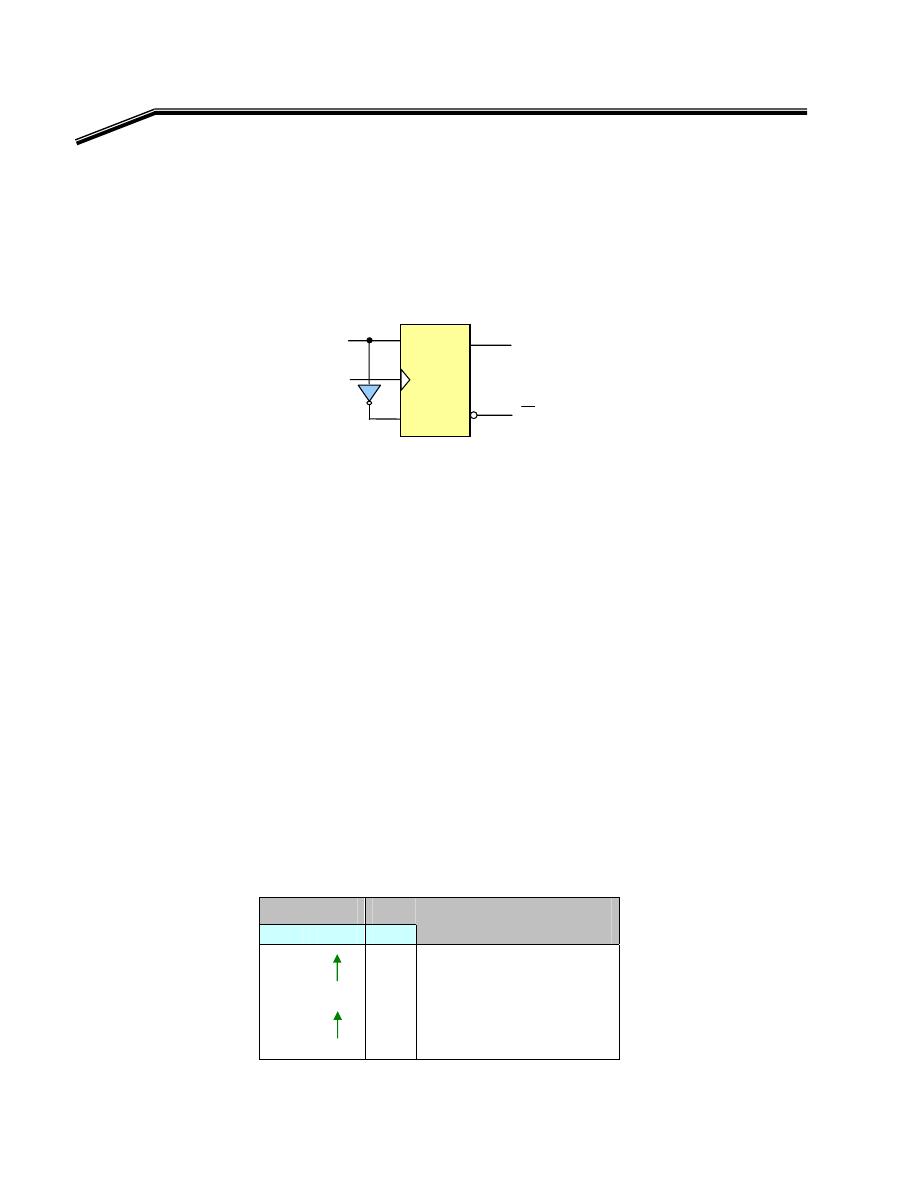
אאא
٧٤١
א
א
אאאא
א
-
١٠١
-
٤
J
٤
אאא
D
D-Type Flip-Flop
אאאא
D
א
אא
)
Single Bit
(
א
)
٠
١
(
K
אאא
S-R
אאאא
D
F
٤
J
٨
KE
F
٤
J
٨
E
א
אא
D
K
אאא
D
אא
D
אא
CK
K
א
D
אא
)
١
(
אאא
CK
،
א
אאא
)
١
(
[
Set
]
א،
א
S =
١
א،
R =
٠
אאא
S-R
אא
F
٤
J
٣
E
א
Q =
١
K
א
D
אא
)
٠
(
אאא
CK
،
אא
אא
)
٠
(
[
Reset
]
،
אא
S =
٠
א،
R =
١
F
٤
J
٣
E
א
Q =
٠
K
אא
)
Set
(
)
١
(
א
א،א
א
)
٠
(
)
٠
(
אא
K
אאאא
א
D
אאאא
אא
)
Positive Edge Trigger
(
א
F
٤
J
٤
KE
א
א
א
(Mode of Operation)
Q
CK
D
אא
(SET)
(stores a
)١
١
١
אא
(RESET)
(stores a
)٠
٠
٠
א
(
)٠
א
(
)١
Z
↑
D
Q
Q
CK
R
S
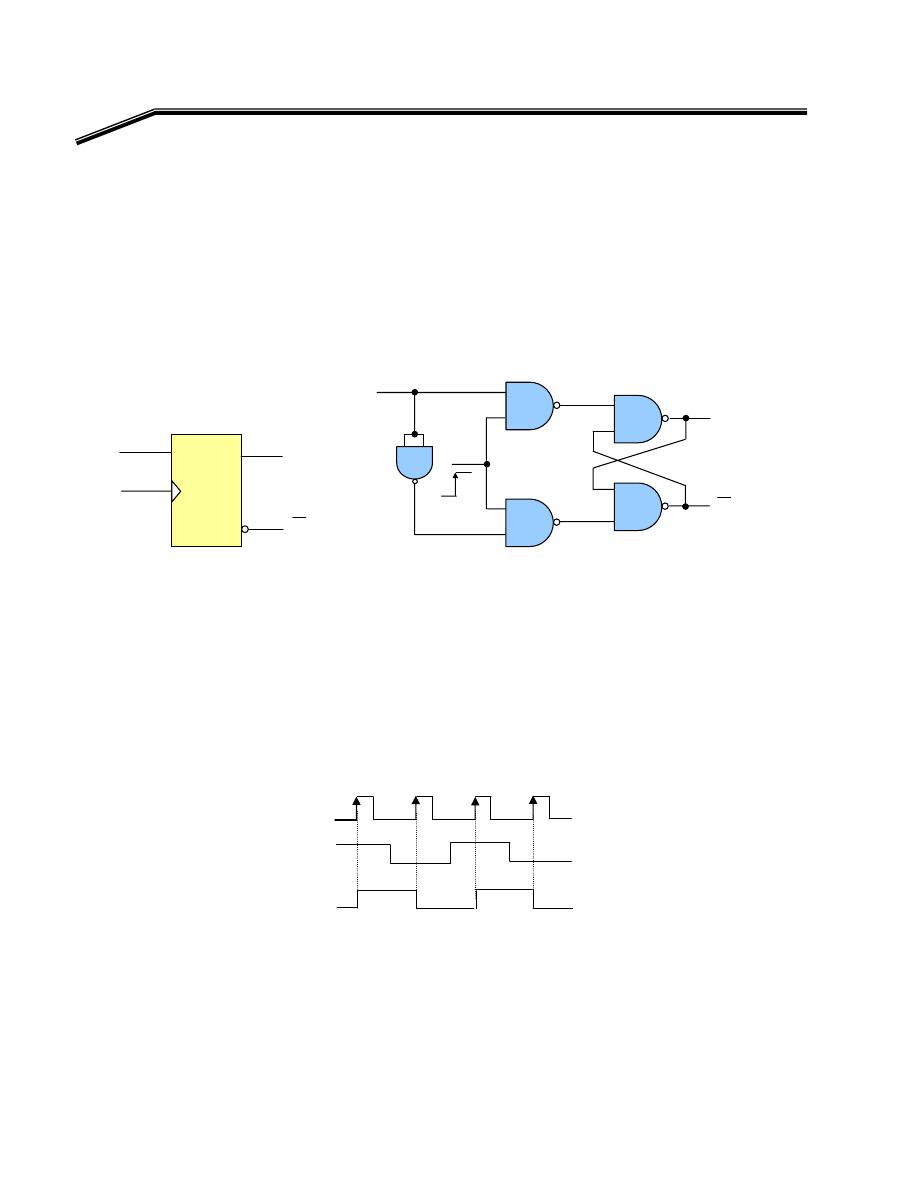
אאא
٧٤١
א
א
אאאא
א
-
٢٠١
-
F
٤
J
٣
E
אאא
D
אא
K
אא
)
Q
(
א
)
D
(
אא
K
א
F
٤
J
٩
E
אא
D
אאא
)
D
(
אא
)
CK
(
אאא
K
א
F
٤
J
٠١
E
אא
D
א
NAND
K
F
٤
J
٠١
E
אא
D
א
NAND
K
F
٤
J
٩
E
אא
D
K
٤
J
٣W
אא
F
Q
E
אאא
D
א
F
٤
J
٩
E
א
א
F
D
E
F
٤
J
١١
KE
אאא
Q =
٠
א
K
א
W
F
٤
J
١١
E
אאאאא
D
K
א
)
Q
(
א
)
D
(
אאאא
)
٠
(
)
١
(
א
א
K
Q
Q
D
CK
R
Q
Q
S
CK
D
CK
D
Q
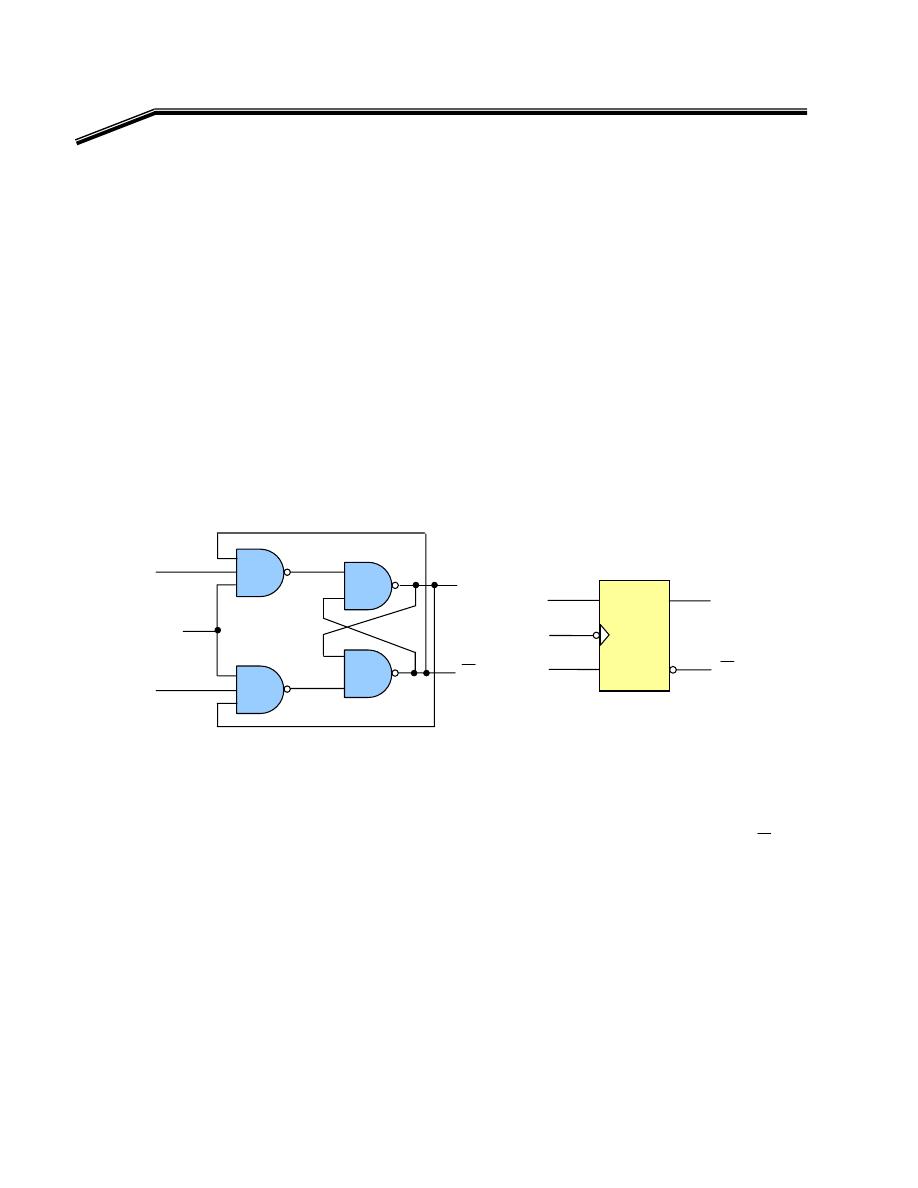
אאא
٧٤١
א
א
אאאא
א
-
٣٠١
-
٤
J
٥
א
J-K
אא
J-K Flip Flop
אא
J-K
אאאא
K
א
א
J,K
אא
،א
א
אא
S-R
א
א
K
א
J-K
א
S-R
אאא
אאאא
)
Set
(
א
א
)
Reset
.(
אא
J-K
אא
S-R
K
א
F
٤
J
٢١
E
אא
J-K
אאאא
K
אאא
S-R
אא
א
אאא
J,K
אא
)
١
(
אא
K
F
٤
J
٢١
E
אא
J-K
אאאא
K
F
٤
J
٢١
E
אאאאא
SR
א
Q
،
Q
א
K
א
F
٤
J
٥
E
א
J-K
אאא
א
J,K
)
٠
(
אאאא،
א
)
Reset
(
א
)
٠
(
אא
J =
٠, K = ١
א،אא
אאאא
)
Set
(
J-K
אא
J =
١, K = ٠
אא
K
אאאא
J-K
א
)
Toggle
(
،
א
J,K
אא
)
١
(
א
Q
אא
אאא
CK
K
K
J
CK
Q
Q
Q
Q
CK
J
K
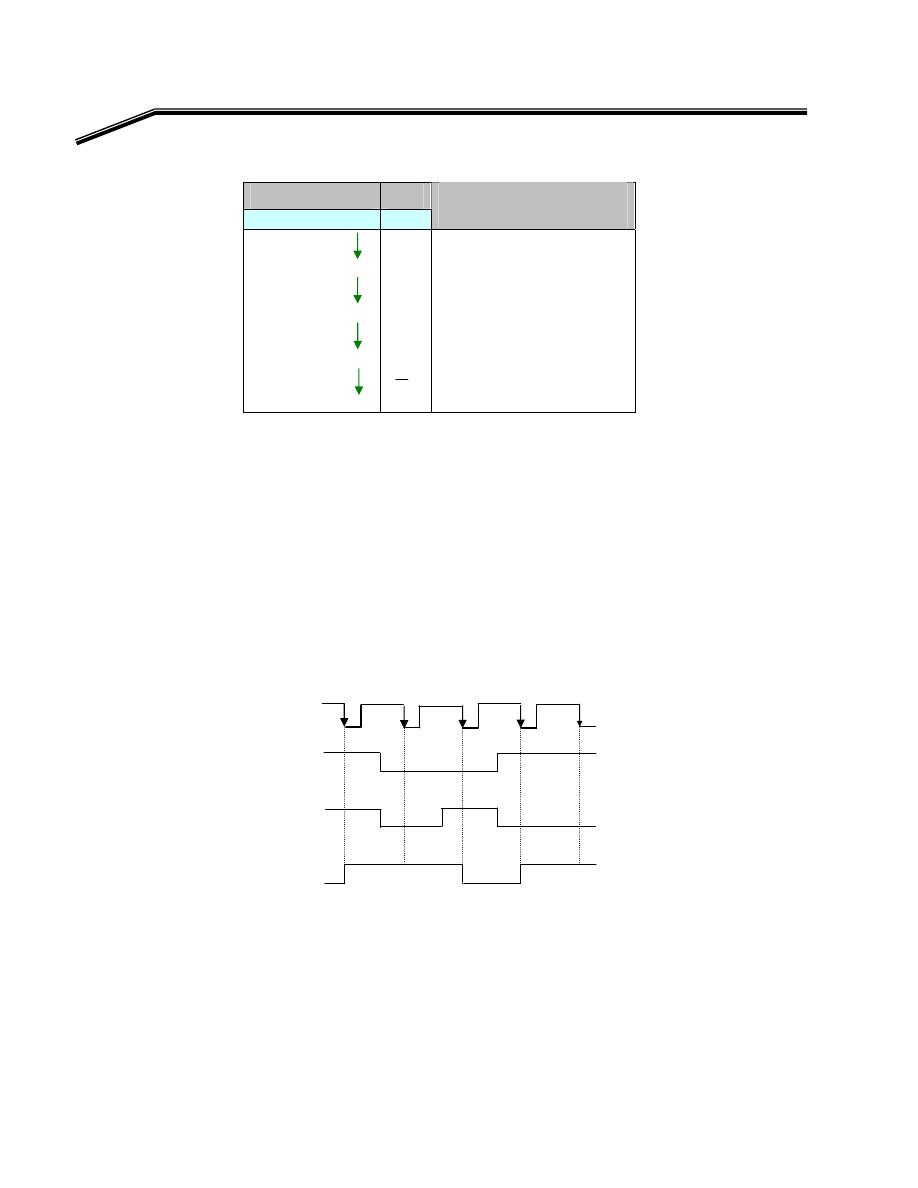
אאא
٧٤١
א
א
אאאא
א
-
٤٠١
-
א
א
א
(Mode of Operation)
Q
CK
K
J
א
F
א
E
No Change
Q
٠
٠
٠
א
א
(RESET)
٠
١
٠
אא
(SET)
١
٠
١
א
Toggle
0
Q
١
١
א
(
)١
א
(
)٠
Z
↓
אאא
Z
Q
٠
F
٤
J
٥
E
א
J-K
אא
K
٤
J
٤W
אא
)
Q
(
א
א
J-K
א
F
٤
J
٢١
E
א
א
J-K
CK
F
٤
J
٣١
KE
אא
Q =
٠
א
K
א
W
F
٤
J
٣١
E
אאאא
J-K
אא
K
١
-
،אאא
J,K
)
١
(
אא
א
Q
א
)
١
(
K
٢
-
אאאאאאא
J = K =
٠
K
٣
-
،אא
J =
٠, K = ١
)
Reset
(
Q =
٠
K
٥
٤
٣
٢
١
CK
J
K
Q
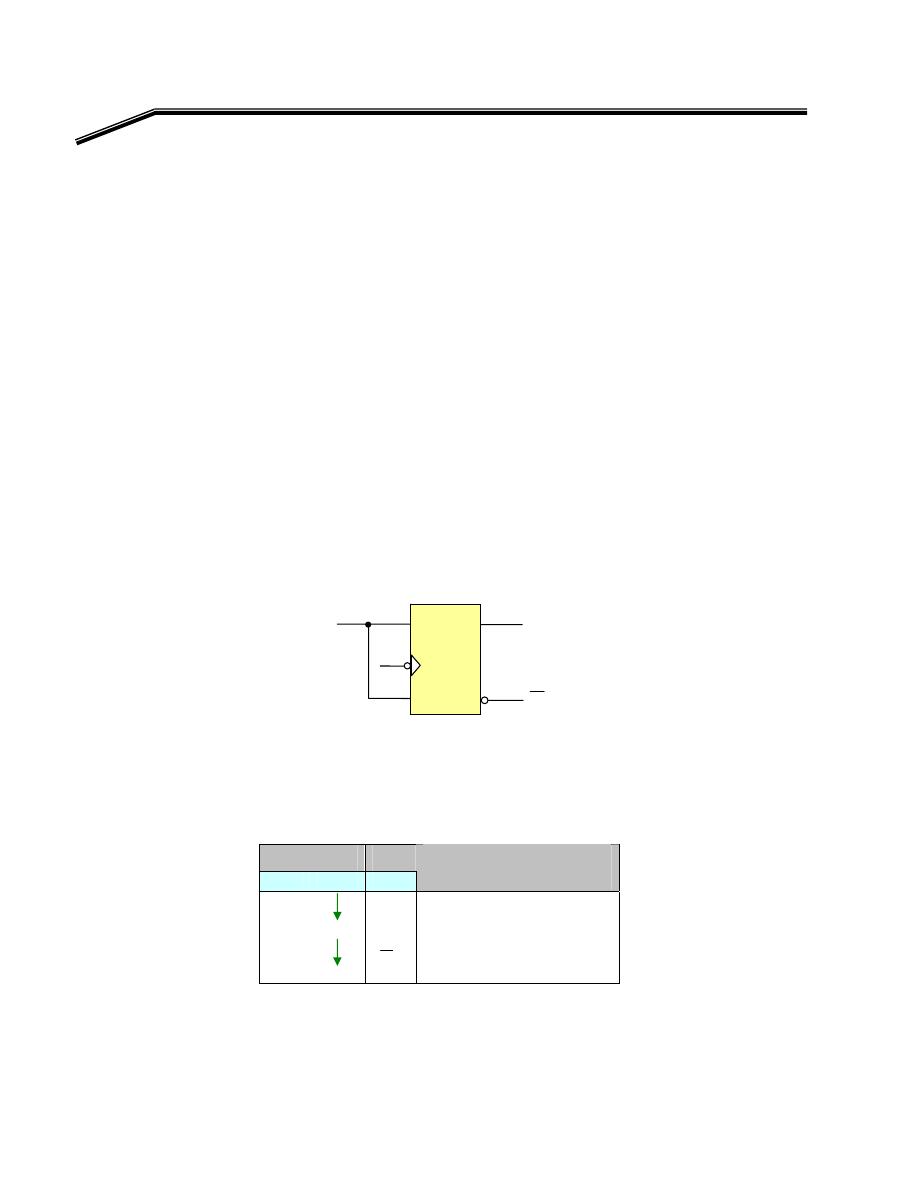
אאא
٧٤١
א
א
אאאא
א
-
٥٠١
-
٤
-
،אאא
J =
١, K = ٠
)
Set
(
Q =
١
K
٥
-
א
)
Set
(
אאא
J,K
א
Q
א
)
١
(
K
٤
J
٦
אאא
T
T-Type Flip-Flop
אא
א
T
אא
J-K
אא
א
J,K
א
F
٤
J
٤١
E
אא،
T
אא
T
אא
K
א
T
א
)
Toggle
(
א
א
K
א
)
T
(
א
)
١
(
א
CK
،אא
אאאאא
CK
אאאא
אאאאאא
א
CK
F
٤
J
٤١
KE
F
٤
J
٤١
E
אאאאא
T
K
אאאא
T
F
٤
J
٦
KE
א
א
א
(Mode of Operation)
Q
CK
T
א
F
א
E
No Change
Q
٠
٠
א
Toggle
0
Q
١
א
(
)١
א
(
)٠
Z
↓
אאא
Z
Q
٠
F
٤
J
٥
E
א
א
T
K
T
Q
Q
J
CK
K
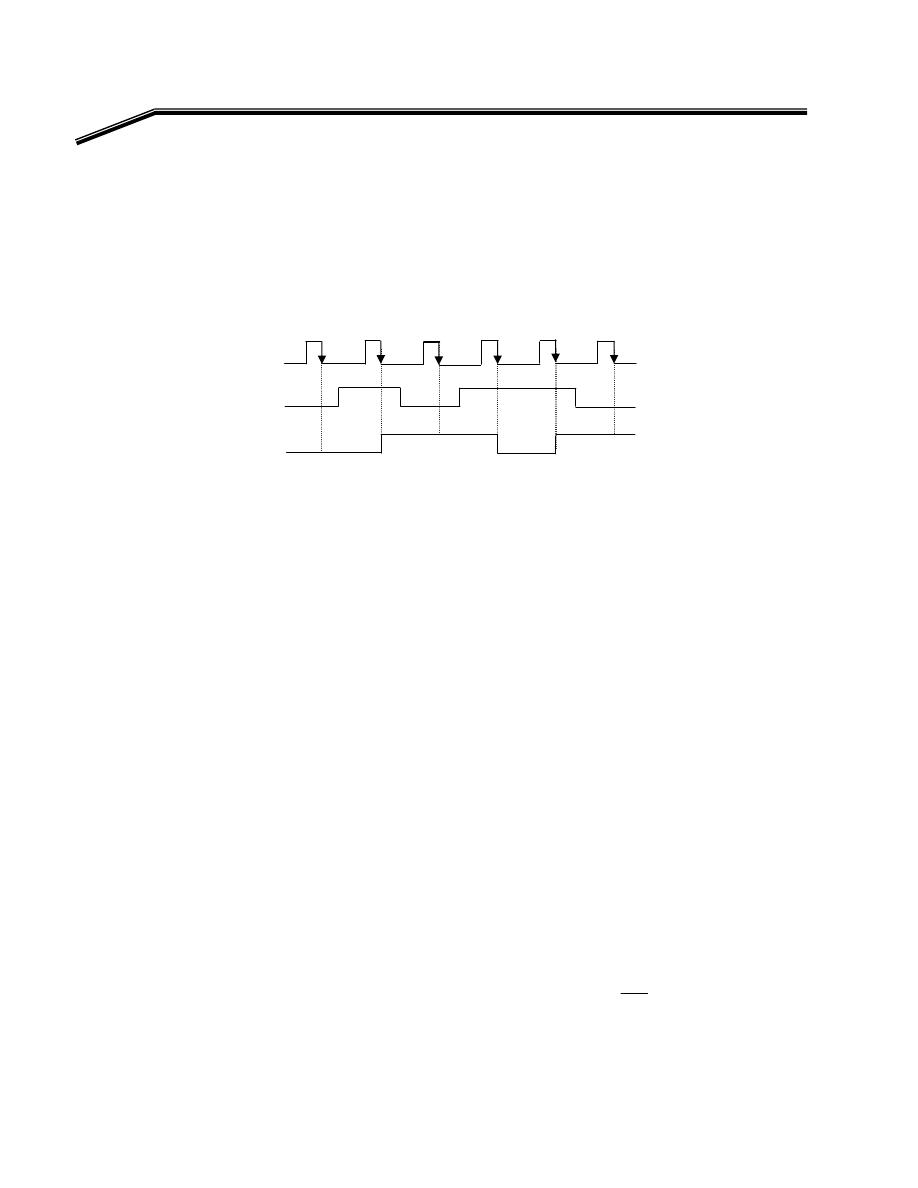
אאא
٧٤١
א
א
אאאא
א
-
٦٠١
-
٤
J
٥W
אא
Q
אאא
)
T
(
א
F
٤
J
٤١
E
א
א
T
א
CK
F
٤
J
٥١
E
אא
Q =
٠
א
K
א
W
F
٤
J
٥١
E
אאאא
א
T
K
אא
Q
א
T =
١
،אאא
אאא
T =
٠
Q
Q =
٠
אא،
T =
١
א
Q
)
٠
(
)
١
(
א
K
٤
J
٧
א
–
א
Master-Slave Flip-Flop
אאאאאא
אאאאא
)
Edge Triggered
(
K
אאאא
א
)
Pulse Triggered
(
אא
–
א
)
Master-Slave
(
،
אא
אאא
)
Complete Clock Pulse
(
א
אא
K
٤
J
٦١
F
E
א
S-R
אא
J
א،א
S-R
אאא
)
Master
(
א
)
Slave
(
אא،
)
Master
(
אאאא
)
CK
(
אא،
)
Slave
(
אא
)
CK
(
K
CK
T
Q
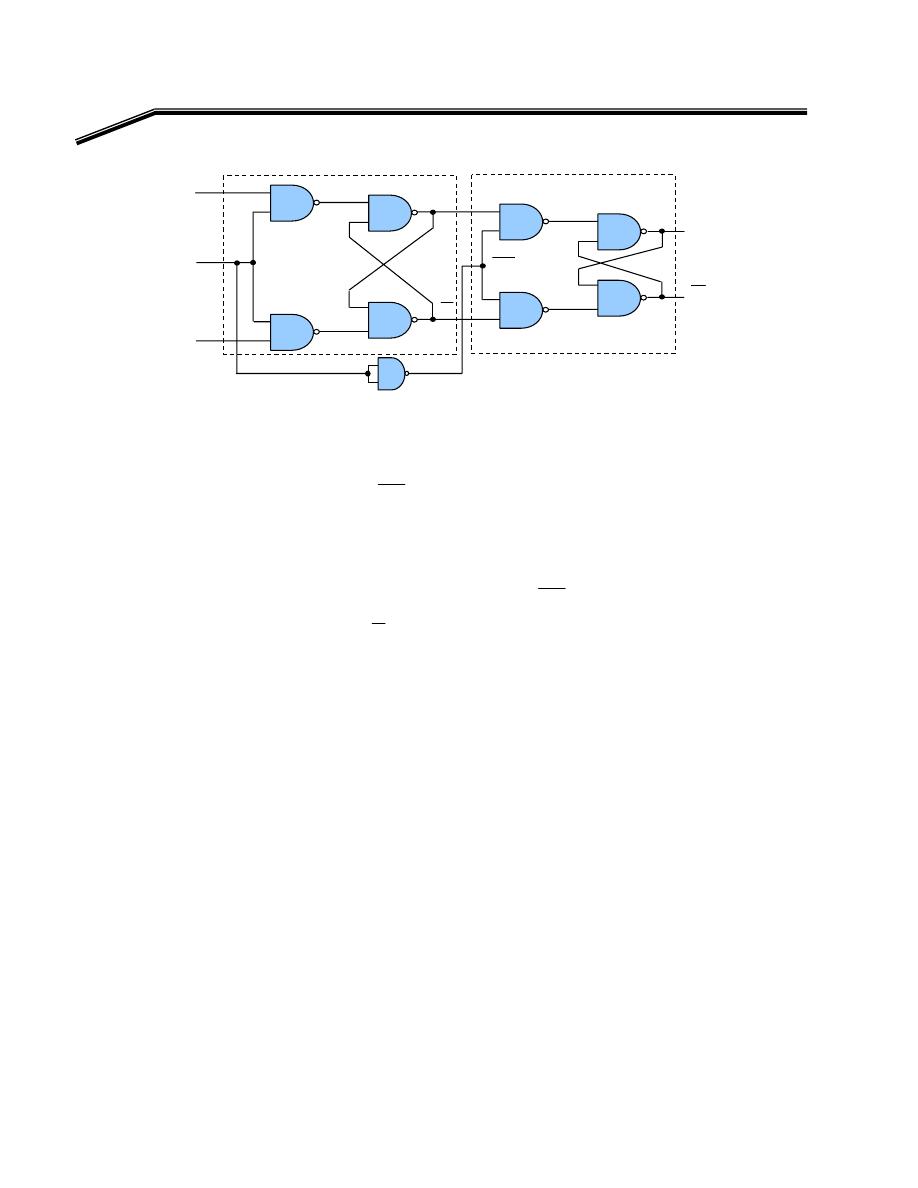
אאא
٧٤١
א
א
אאאא
א
-
٧٠١
-
٤
J
٦١
F
E
אא
S-R
א
J
א
K
אא
CK
،
CK
٤
J
٦١
F
E
،
אא
)
Master
(
אאאא
)
CK
(
אא،
)
Slave
(
אאאאא
אאא
)
CK
(
K
Q
،
Q
א
S,R
W
א
א
W
אא
)
High
(
)
CK
(
אא
)
Master
(
א
)
Enabled
(
אאא
)
Set
(
א
א
)
Reset
(
אא
S,R
K
אא
W
א
א
)
Low
(
)
CK
(
אא
)
slave
(
א
)
Enabled
(
א
Q
אאאא
Y
K
אא
٤
J
٦١
F
E
אאא
S-R
א
J
א
K
א
אאא
S-R
אא
K
א
)
CK
(
אא
אאא
)
High
(
א
)
Low
(
אא
K
٤
J
٦١
F
E
אאא
S-R
א
J
،א
אא
)
CK
(
א
t
٠
t
٥
אאא
S,R
K
Slave
Master
CK
Y
Y
R
CK
S
Q
Q
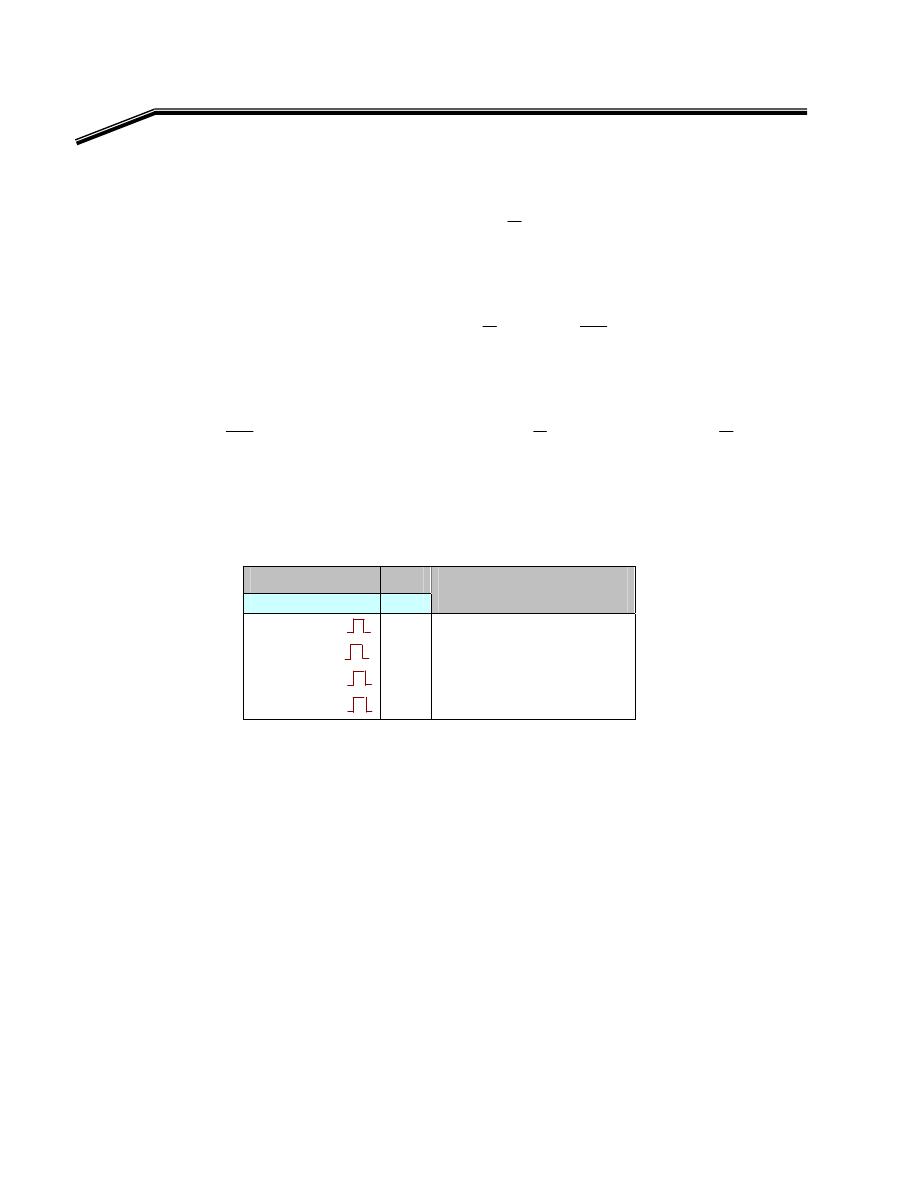
אאא
٧٤١
א
א
אאאא
א
-
٨٠١
-
•
א
t
٠
אא،
)
Master
(
א
)
Enabled
(
אא
)
High
(
אא
)
CK
(
א
S =
١, R = ٠
אא
)
Set
(
א
א،א
Y =
١
)
0
Y
=
(
K
•
א
t
١
אא،
)
Disabled
(
אא
)
Low
(
CK
אא،
)
Slave
(
א
)
Enabled
(
א
א
)
High
(
CK
K
Y
,
Y
،אאא
א
Q
אא
)
Set
(
Q =
١
K
אאאא
אאא
F
0
Y
,
1
Y
=
=
א
0
Q
,
1
Q
=
=
אא
1
CK
=
KE
אאאאאאא
K
א
א
א
(Mode of Operation)
Q
CK
R
S
א
F
א
E
Q
٠
٠
٠
אא (RESET)
٠
١
٠
אא(SET)
١
٠
١
א
؟
١
١
٤
J
٦١
F
E
אאא
S-R
א
J
א
K
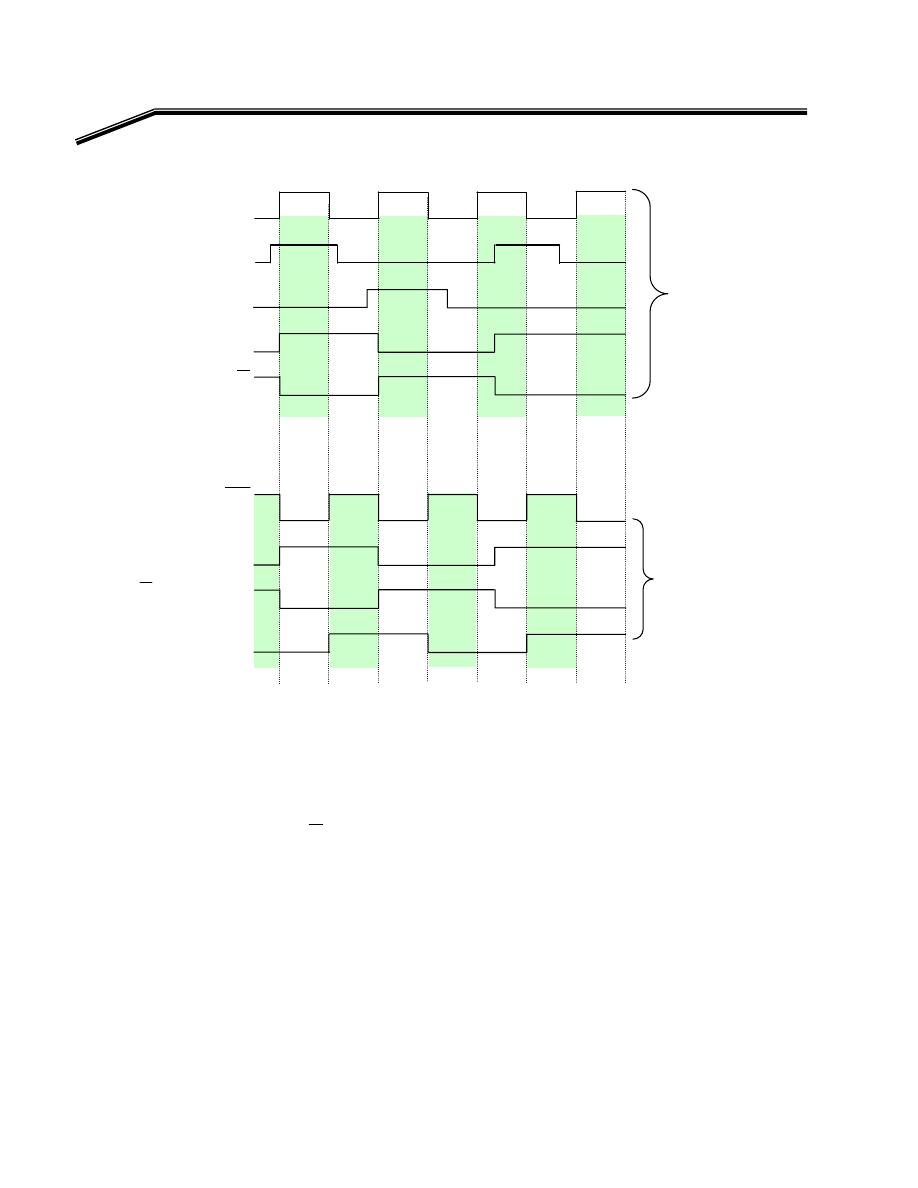
אאא
٧٤١
א
א
אאאא
א
-
٩٠١
-
٤
J
٦١
F
E
אאאא
S-R
אא
K
•
א
t
٢
אא،אאא،
)
High
(
CK
א
S =
٠, R = ١
א
1
Y
,
0
Y
=
=
אא
)
Reset
.(
•
א
t
٣
אאאא،
)
Low
(
CK
،
אאא
K
אאא
א
)
Reset
(
א
Q =
٠
K
•
א
t
٤
א،
S,R
א
)
Low
(
א
Y
אא،
א
)
Y = ٠
(
K
אא
t
٤
،
א
S
א
)
High
(
אא
Y =
١
K
Master
Enable
t
٥
t
٣
t
٤
t
١
t
٢
t
٠
Master
Enable
Q
)
set
Re
Slave
(
Y
Y (Slave Set)
CK
Slave
Enable
Slave
Enable
Slave
Enabl
Master
Enable
Master
Enable
Y
Y
R (RESET)
S (SET)
CK
ﻜﺎل
أﺷ
ﻧﺒﻀﺎت اﻟﺘﺎﺑﻊ
(Master)
أﺷﻜﺎت ﻧﺒﻀﺎت
اﻟﻤﺘﺒﻮع
(Slave)
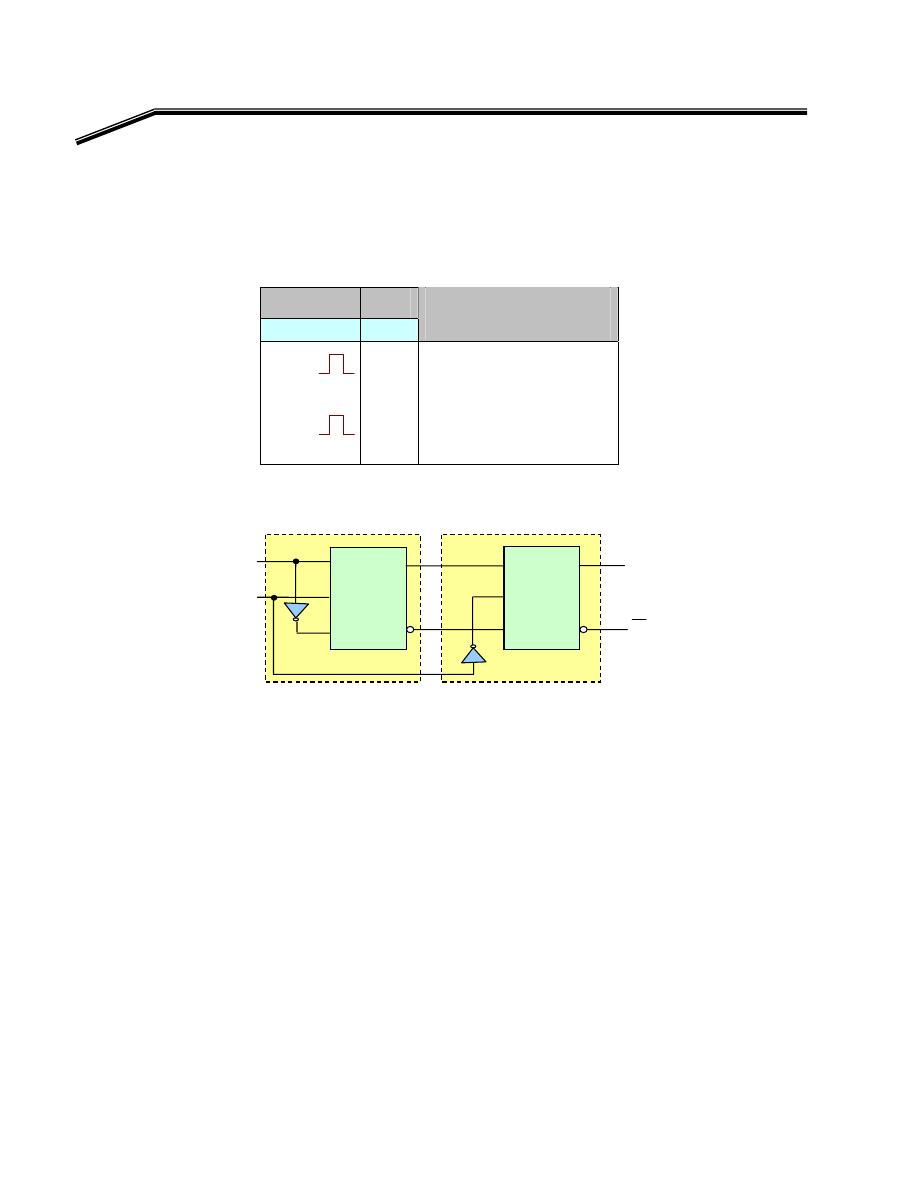
אאא
٧٤١
א
א
אאאא
א
-
٠١١
-
•
א
t
٥
،אאאאא،
א
Y =
١
א
Q
Q =
١
K
א
א
א
(Mode of Operation)
Q
CK
D
אא
(SET)
(stores a
)١
١
١
א
א
(RESET)
(stores a
)٠
٠
٠
F
٤
J
٧١
E
אא
א
D
א
J
אאא
K
٤
J
٧١
F
E
אא
D
א
–
،א
٤
J
٧١
F
E
אא
K
אא
S-R
א
–
،א
אא
D
א
–
א
א
א
CK
א
Q
K
٤
J
٨١
F
E
אא
J-K
א
–
א،א
٤
J
٨١
F
E
אאאא
K
א
٤
J
٨١
F
E
אאא
J-K
א
–
אא
א
)
Q
(
אאא
אא
S-R
א
–
א
K
F
E
Clock in
D
CK
Q
Q
F
E
S
CK
R
S
CK
R
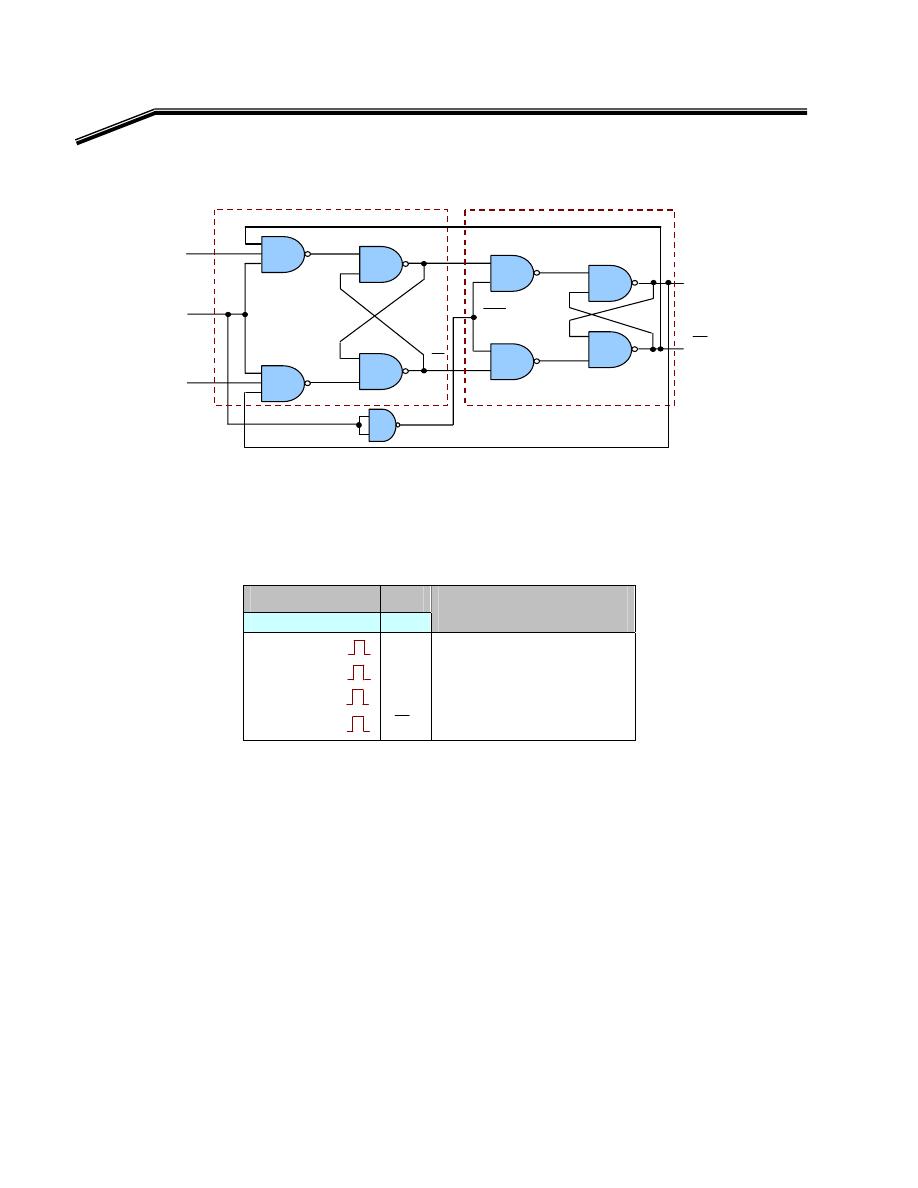
אאא
٧٤١
א
א
אאאא
א
-
١١١
-
٤
J
٨١
F
E
אא
J-K
א
J
א
K
א
א
א
(Mode of Operation)
Q
CK
K
J
א
F
א
E
Q
٠
٠
٠
א
א
(RESET)
٠
١
٠
אא(SET)
١
٠
١
א(Toggle)
0
Q
١
١
٤
J
٨١
F
E
אאא
J-K
א
J
א
K
Slave
Master
CK
Y
Y
K
CK
J
Q
Q
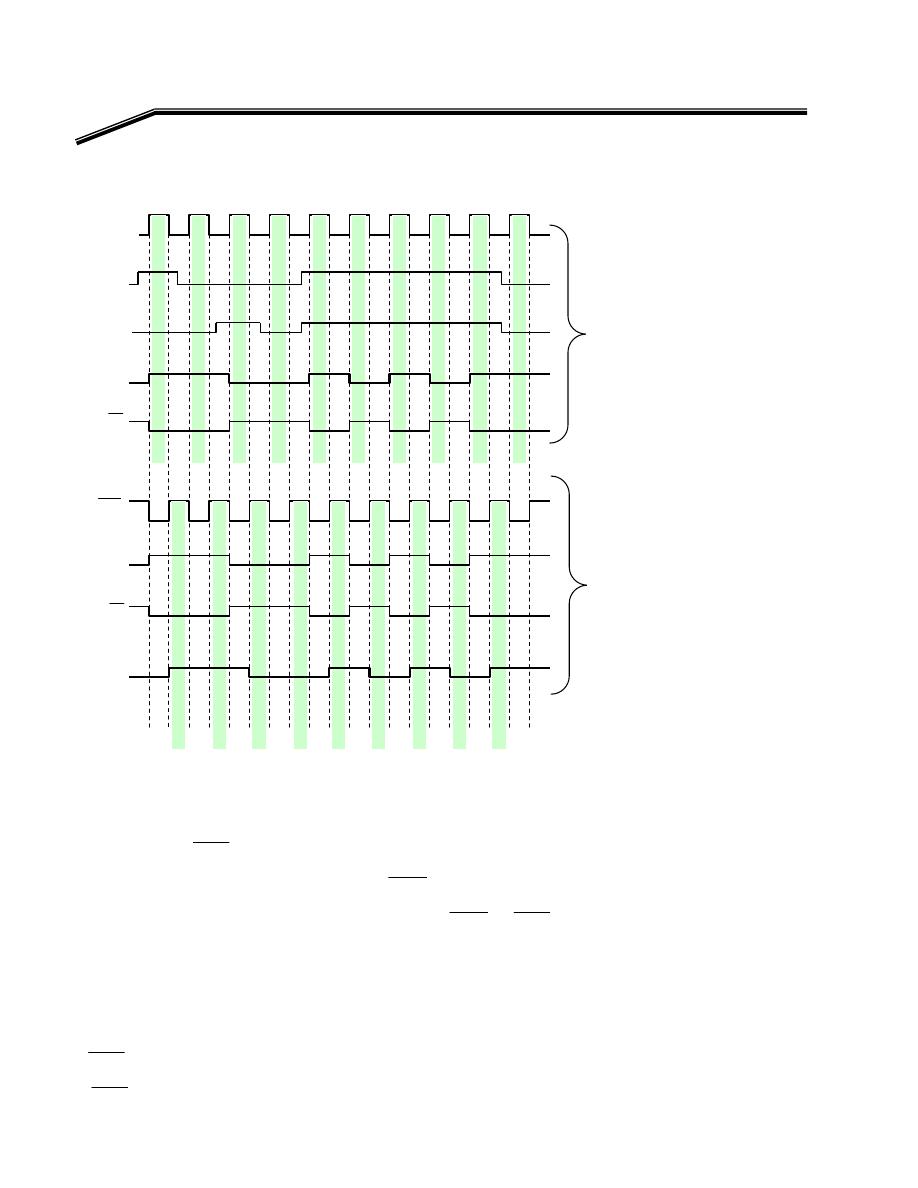
אאא
٧٤١
א
א
אאאא
א
-
٢١١
-
٤
J
٨١
F
E
אאא
J-K
א
J
א
K
אאאא
אא
K
א
א
א
)
PRESET
(
)
PRE
(
א
א
א
)
CLEAR
(
)
CLR
(
א
F
٤
J
٩١
E
אא
א
S-R
PRE
،
CLR
K
אא
،אאא
אאא
)
SET
(
Q =
١
،
אא
)
RESET
(
Q =
٠
א،
א
Q
א
K
אא
א
)
RESET
(
א
)
CLEAR
(
אאאא
K
א
)
PRE
(
א،א
Q
א
)
١
(
0
PRE
=
،
Q
Y
Y
CK
Y
Y
J
ME ME ME ME ME ME ME ME ME ME
SE SE SE SE SE SE SE SE SE
CK
K
ME = Master Enabled
أﺷﻜﺎل ﻧﺒﻀﺎت اﻟﺘﺎﺑﻊ
(Master)
SE = Slave Enabled
أﺷﻜﺎل ﻧﺒﻀﺎت اﻟﻤﺘﺒﻮع
(Slave)
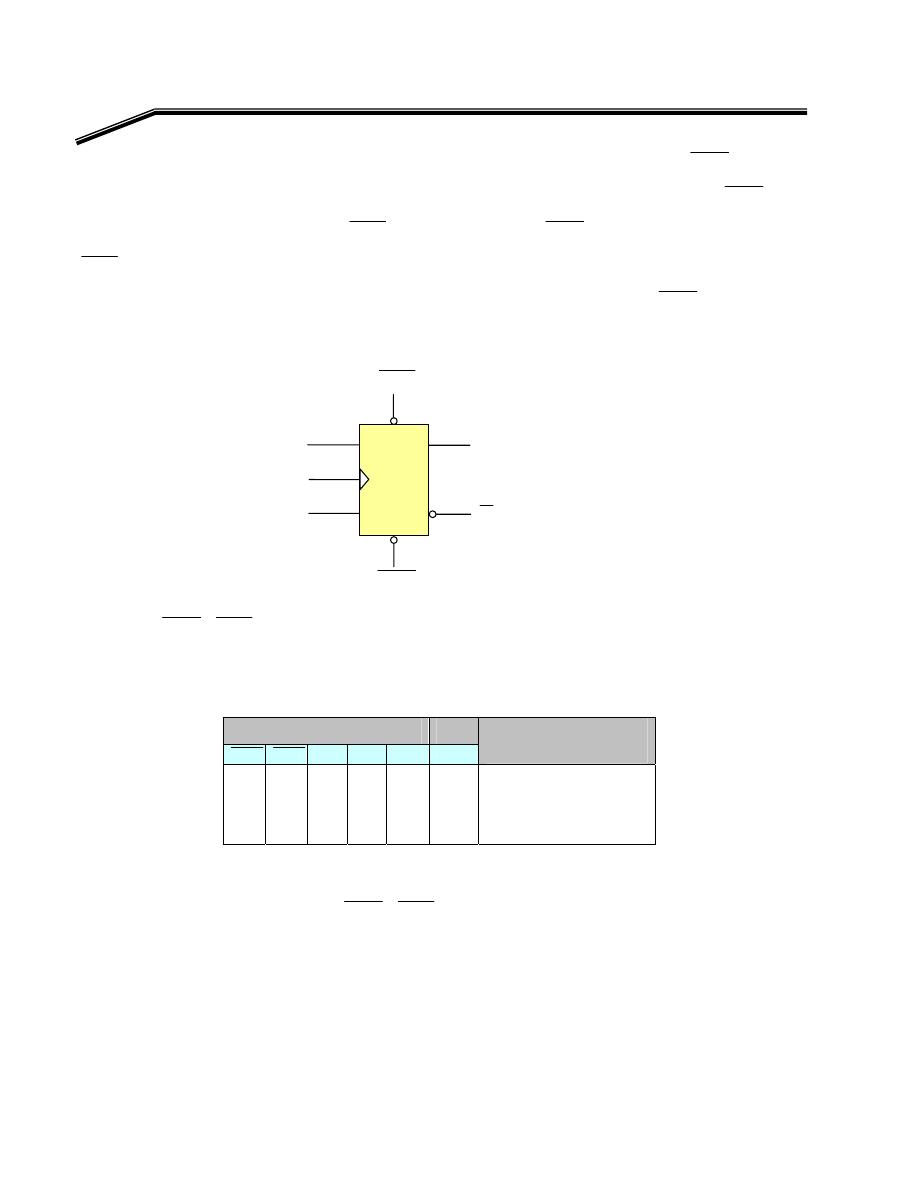
אאא
٧٤١
א
א
אאאא
א
-
٣١١
-
א
)
CLR
(
א
Q
א
)
٠
(
0
CLR
=
K
F
٤
J
٧
E
א
א
אא
S-R
א
1
CLR
=
א
0
PRE
=
F
E
א
Q
)
١
(
אא،
R
S,
CK,
K
אא
א
1
PRE
=
0
CLR
=
F
E
אא
Q
)
٠
(
א
א
R
S,
CK,
K
F
٤
J
٩١
E
אאאא
S-R
PRE
،
CLR
K
א
א
א
(Mode of Operation)
Q
R
S
CK
אא(SET)
١
X
X
X
١
٠
א
א
(RESET)
٠
X
X
X
٠
١
א
?
X
X
X
٠
٠
F
٤
J
٧
E
א
PRE
،
CLR
אא
S-R
K
PRE
CLR
CLR
PRE
Q
Q
R
CK
S
אאא
٧٤١
א
א
אאאא
א
-
٤١١
-
אא
٤
J
٨
אא
Timer Circuits
א
،אאא،אאא
א
)
Clock Signal
(
אאאא
K
א
K
אא
)
Sharp
(
אא
)
Positive Edge
(
אאא
)
Negative Edge
(
אאאא
K
א
S-R,D-Type
J-K,
אא
אא
א
א
)
Bistable Multivibrator
(
،
)
bi
(
)
Set and Reset States
.(
א،א
אא
)
Astable Multivibrator
(
א
אאא،
אאא
א
)
Monostable Multivibrator
(
אאאא
)
Mono
(
)
Triggered
(
)
Rectangular Pulse
(
)
Fixed Duration
(
K
٤
J
٨
J
١
אאאאא
Astable Multivibrator Circuit
אאאאאאאא
)
Free running
(
אא
F
٤
J
٠٢
E
א
א
)
Inverter
(
)
Schmitt-trigger
(
K
F
٤
J
٠٢
E
אאאאא
K
∫ ∫
٠(١
)١( ٠
C
R
Discharge
F
א
E
Charge
F
א
E
+٥V
+
אאא
٧٤١
א
א
אאאא
א
-
٥١١
-
،אאא
אא
)
٠
(
אא،
)
Low
(
אא
)
Not
(
)
High
.(
א
)
C
(
אא
)
R
(
אאא،
אא
C
R,
אאאא،
)
High
(
א
K
אאא
(Low)
،
א
K
א
אא
)
Low
(
،
אא
(High)
א
K
٤
J
٨
J
٢
אאאאאא
Monostable Multivibrator Circuit
٤
J
١٢
F
E
אאאאאא
K
א
)
Trigger
(
א
)
Low
(
אא،
Q
)
Low
(
،
אאא
NOR
(High)
אאא
(Low)
אאא
א
K
א
(High)
א،
א
NOR
א
)
Low
(
K
א
א
(High)
)
Low
(
אא
NOR
،אאא،
א
(High)
א
Q
אא
٤
J
١٢
F
KE
אא
Q
אאא
NOR
אא
א
)
Low
(
אא
K
F
٤
J
١٢
E
אאאאאאא
K
Output
Pulse (Q)
Input
Trigger (T)
C
R
+٥V
+
F
E
Output
Pulse (Q)
Input
Trigger (T)
F
E
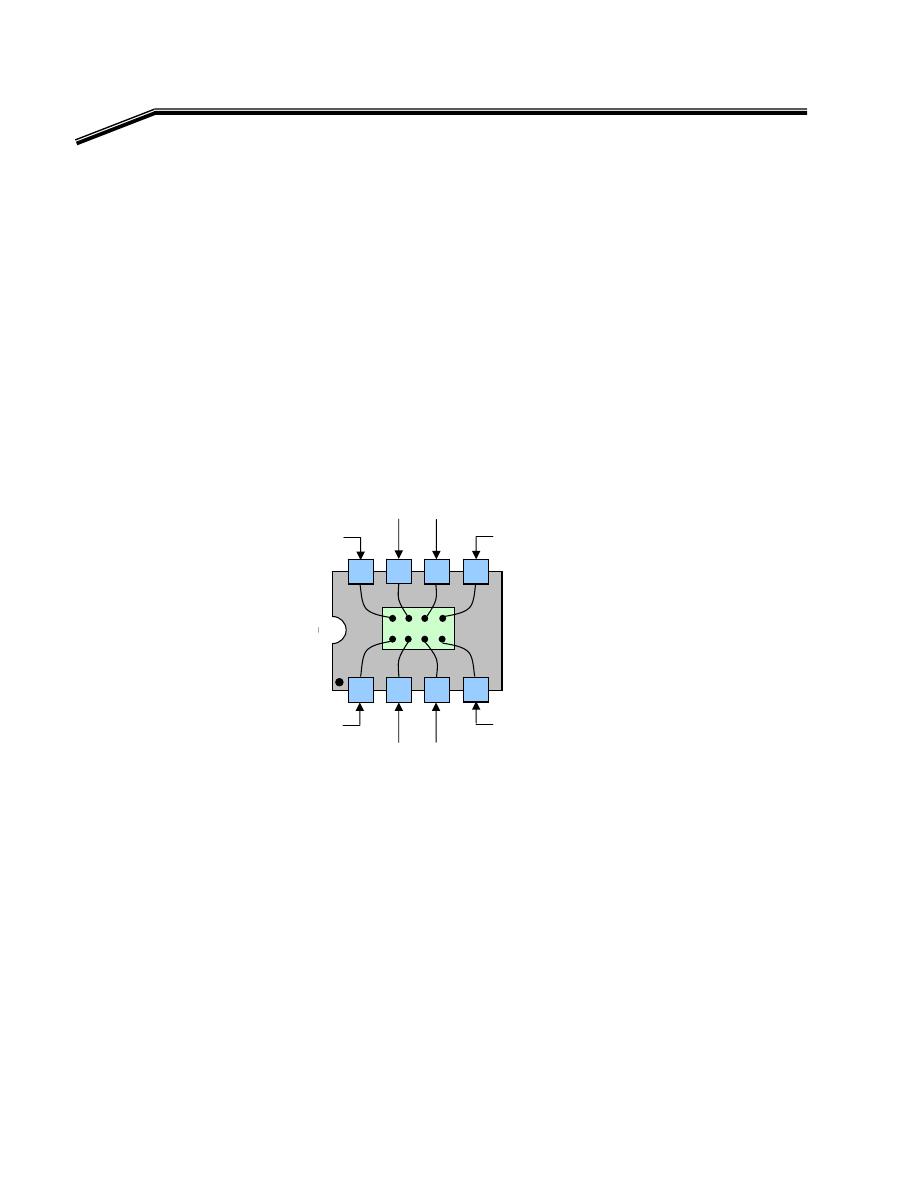
אאא
٧٤١
א
א
אאאא
א
-
٦١١
-
אא
NOR
אא
)
resistor–capacitor network
(
،
אא
K
אא
C
א
R
،
אא
אא
(High)
א
)
Low
(
א
Q
K
٤
J
٨
J
٣
אא
٥٥٥
The
٥٥٥Timer Circuit
אא
٥٥٥
،אאאא
)
IC
(
אא
F
٤
J
٢٢
E
א،
٥٥٥
א،אאאאא
Ω
K
5
K
F
٤
J
٢٢
E
אא
٥٥٥
K
א،
א
)
Astable mode
(
אאאאא
)
Monostable mode
(
א
א
)
Frequency Divider
(
)
Modulator
(
א
אא
א
K
٤
J
٨
J
٣
J
١
א
٥٥٥
אאאא
٥٥٥Timer as an Astable
Multivibrator
Ground
F
א
E
Trigger
F
א
E
Output
F
א
E
Reset
F
אא
E
Control Voltage
F
א
E
Threshold
F
א
E
Discharge
F
א
E
+V
CC
F
א
E
٥
٦
٧
٨
١
٢
٣
٤
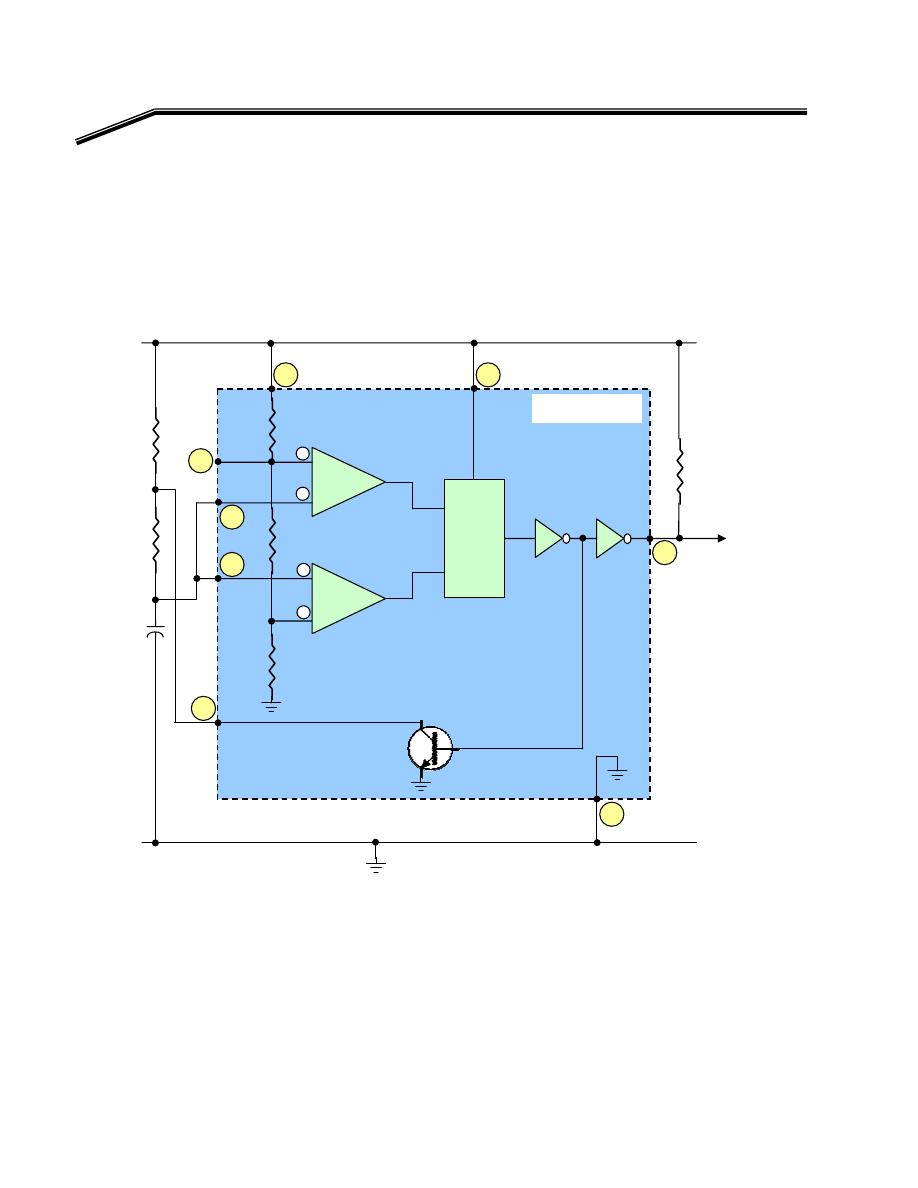
אאא
٧٤١
א
א
אאאא
א
-
٧١١
-
٤
J
٣٢
F
E
א
٥٥٥
אא
)
Astable
(
א
)
Free running
(
K
אא
٤
J
٣٢
F
E
אא
C
،א
אא
+Vcc
F
א
E
)
٠
(
K
٤
J
٣٢
F
E
א
٥٥٥
אא
K
Output
F
א
E
R
L
+٥V
+
٥٥٥Timer
Inverter
F
E
Inverting
Buffer/Driver
Q
S-R
Flip-Flop
R
S
Discharge Transistor
F
א
א
E
٥K
Ω
٣/١V
CC
٥K
Ω
٣/٢V
CC
٥K
Ω
Comparator
(B)
Comparator
(A)
R
A
R
B
C
١
٢
٣
٤
٥
٦
٧
٨
-
+
-
+
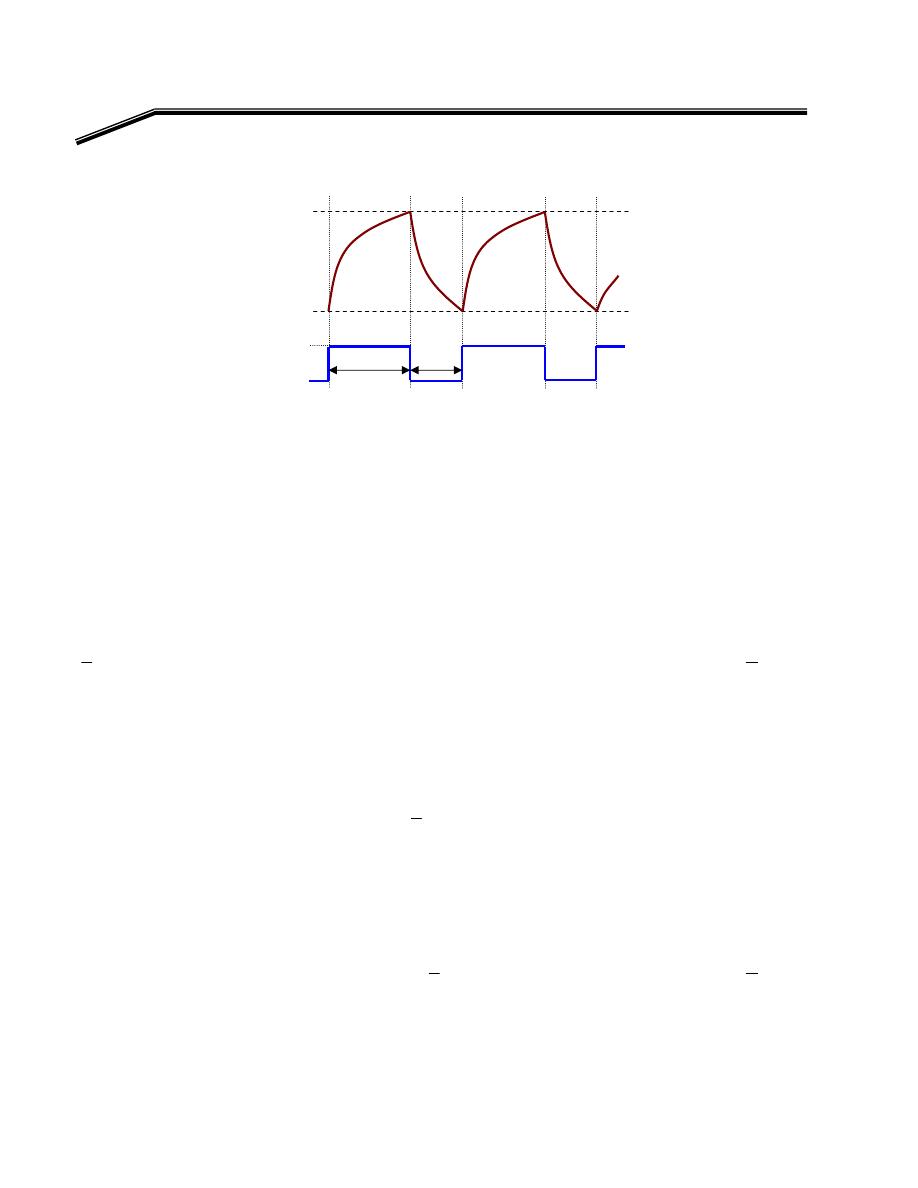
אאא
٧٤١
א
א
אאאא
א
-
٨١١
-
٤
J
٣٢
F
E
א
C
א
K
אאאאא
S-R
א
)
High
(
]
א
T
١
א
[
K
אאאא
א
(Low)
א
אאא
)
Discharge Transistor
(
א
OFF
K
אאאא
OFF
،
אא
)
C
(
אא
+Vcc
א
R
A
R
B
,
K
א
T
٢
،
אא
א
CC
V
3
2
،
אא
A
(High)
אא
CC
V
3
1
אאא
(RESET)
Q =
٠
K
אא
)
٣
(
٥٥٥
א
(Low)
،
אא
(High)
א،
ON
K
אאאא
ON
،
א
C
K
א
T
٣
אא،
CC
V
3
1
،
א
B
א
(High)
אא
S-R
א
(SET)
Q =
١
אא،
K
אאא
OFF
،
C
א
K
א
٤
J
٣٢
F
E
א،
C
א
R
A
R
B
,
א
CC
V
3
2
א،
R
B
א
CC
V
3
1
K
א
t
p
)
Positive time
(
א
W
C
)
R
R
(
7
.
0
t
B
A
p
+
=
t
p
t
n
T
١
T
٢
T
٣
T
٤
T
٥
٣/٢V
CC
Voltage
Across "C"
٣/١V
CC
(+V
CC
)
()٠
Output

אאא
٧٤١
א
א
אאאא
א
-
٩١١
-
א
t
n
)
Negative time
(
א
W
C
R
7
.
0
t
B
n
=
א
T
F
אא
E
א
t
p
א،
t
n
W
T = t
p
+ t
n
C
)
R
2
R
(
7
.
0
B
A
+
=
א
٥٥٥
אא
W
C
)
R
2
R
(
7
.
0
1
T
1
f
B
A
+
=
=
אאא
W
C
)
R
2
R
(
43
.
1
f
B
A
+
=
٤
J
٨
J
٣
J
٢
א
אאאאא
٥٥٥Timer as a Monostable Multivibrator
٤
J
٤٢
F
E
א
٥٥٥
אאאאא
)
one-shot
.(
אא
٤
J
٤٢
F
E
א
א
)
Input - trigger
(
אא،א،
٥٥٥
K
א
)
P
w
(
אא
C
R
A
,
K
א
T
١
٤
J
٤٢
F
E
אא،
S-R
)
RESET
(
)
Low
(
Q =
٠
K
אא
(Low)
א
א
S-R
א
،א
)
inverted and buffered
(
א،אא
٥٥٥
א
)
٣
(
٠V
(Low)
K
א
(Low)
אא
S-R
(High)
א
א،א
ON
אאאא،
K
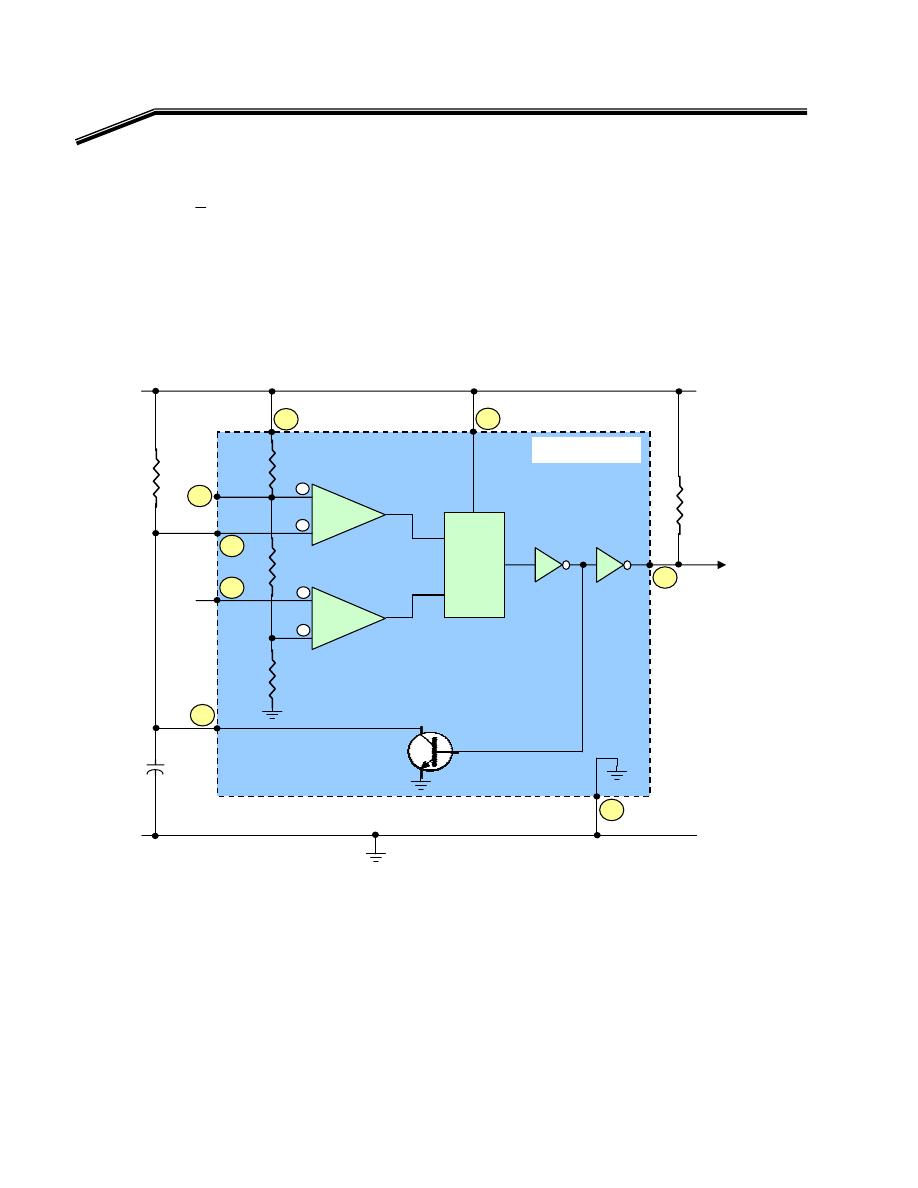
אאא
٧٤١
א
א
אאאא
א
-
٠٢١
-
א
T
٢
א،
)
Trigger
(
א
()٢
אא
٥٥٥
אא
K
אאאא
B
CC
V
3
1
،
א
B
(High)
אא،
S-R
א
)
SET
(
א
Q =
١
K
א
א
(High)
אא
S-R
אאא
)
٣
(
٥٥٥
א
(High)
אאא
OFF
K
٤
J
٤٢
F
E
א
٥٥٥
א
אא
K
Output
R
L
+٥V
٥٥٥Timer
Inverter
Inverting
Buffer/Driver
Q
S-R
Flip-Flop
R
S
Discharge Transistor
٥K
Ω
٣/١V
CC
٥K
Ω
٣/٢V
CC
٥K
Ω
Comparator
(B)
Comparator
(A)
R
A
C
١
٢
٣
٤
٥
٦
٧
٨
-
+
-
+
+
Trigger
Input
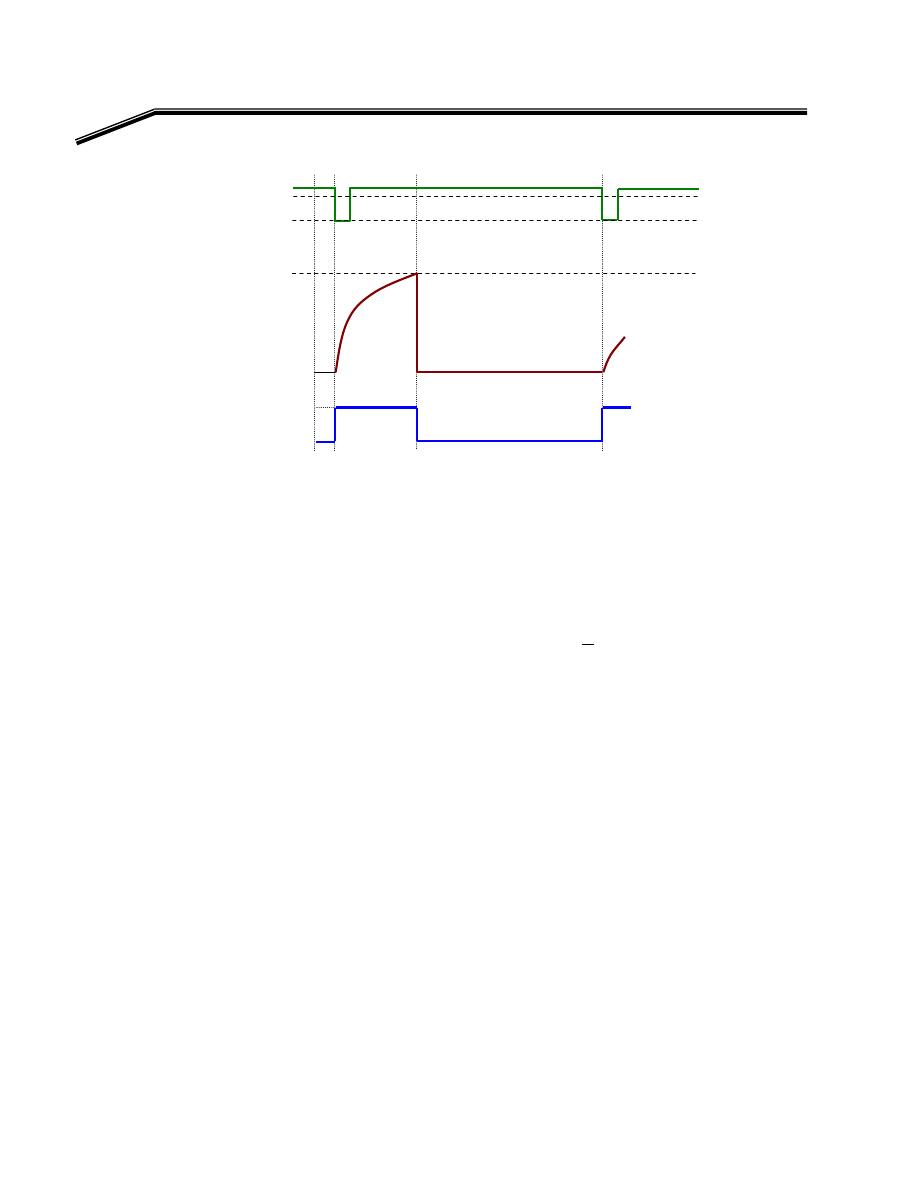
אאא
٧٤١
א
א
אאאא
א
-
١٢١
-
٤
J
٤٢
F
E
אא
C
אא
K
אא
C
אא
R
A
+V
CC
א
٤
J
٤٢
F
KE
א
٥٥٥
א
(High)
א
א
CC
V
3
2
K
א
)
T
٣
(
،
א
A
(High)
،
אא
S-R
א
)
RESET
(
אא،
)
٣
(
א
(Low)
אאא،
ON
א
C
K
אאאאאאאא
K
אא
)
Leading edge
(
،אא
א
א
)
Trailing edge
(
אא
C
א
R
A
א
א
K
אאא
W
C
R
1
.
1
P
A
w
=
T
١
T
٢
٣/٢V
CC
Voltage
Across "C"
٣/١V
CC
Output
٠V
Trigger
Input
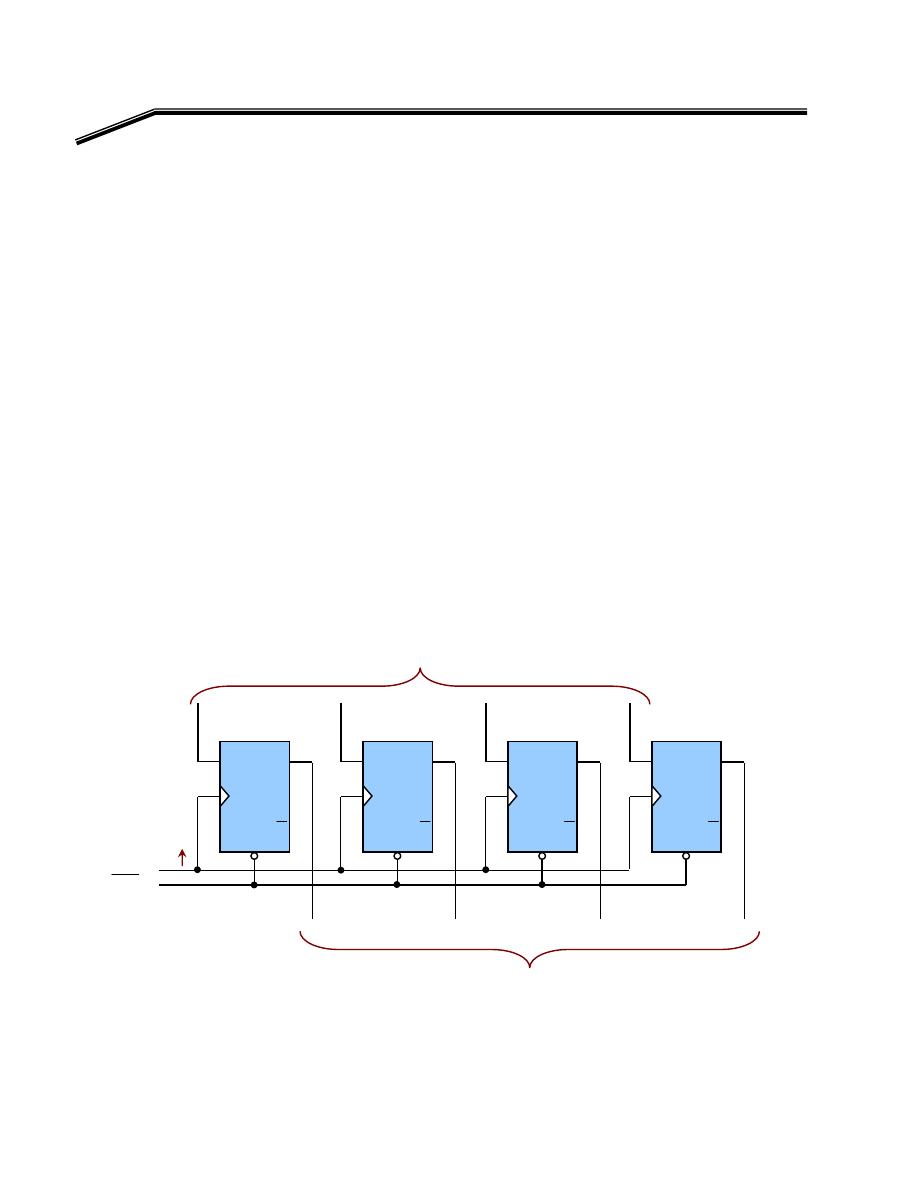
אאא
٧٤١
א
א
אאאא
א
-
٢٢١
-
٤
J
٩
אא
Shift Registers
،אא،אאאאאא
אאאא
)
bit
(
אא
אאא،
א،
אאא
אא
)
Buffer Register
(
אאא
)
Shift Left
(
א
)
Shift
Right
(
אאא
)
Serial Data
(
א
)
Parallel Data
(
א
אא
)
Shift Registers
(
K
٤
J
٩
J
١
א
Buffer Registers
א
)
Digital word
(
אא
)
bits
(
K
٤
J
٥٢
F
E
א
)
٤-stages
(
אאאא
D
אאאאא
)
Positive edge-triggered
(
K
٤
J
٥٢
F
E
אאאאאא
D
K
CLR
CK
D
١
D
٢
D
٣
D
٤
Q
١
Q
٢
Q
٣
Q
٤
אאאא
(
٤-bit word to be stored)
אאא
(parallel data outputs)
F
E
Q
Q
D
CLR
D
Q
Q
CLR
Q
Q
CLR
D
Q
Q
CLR
D
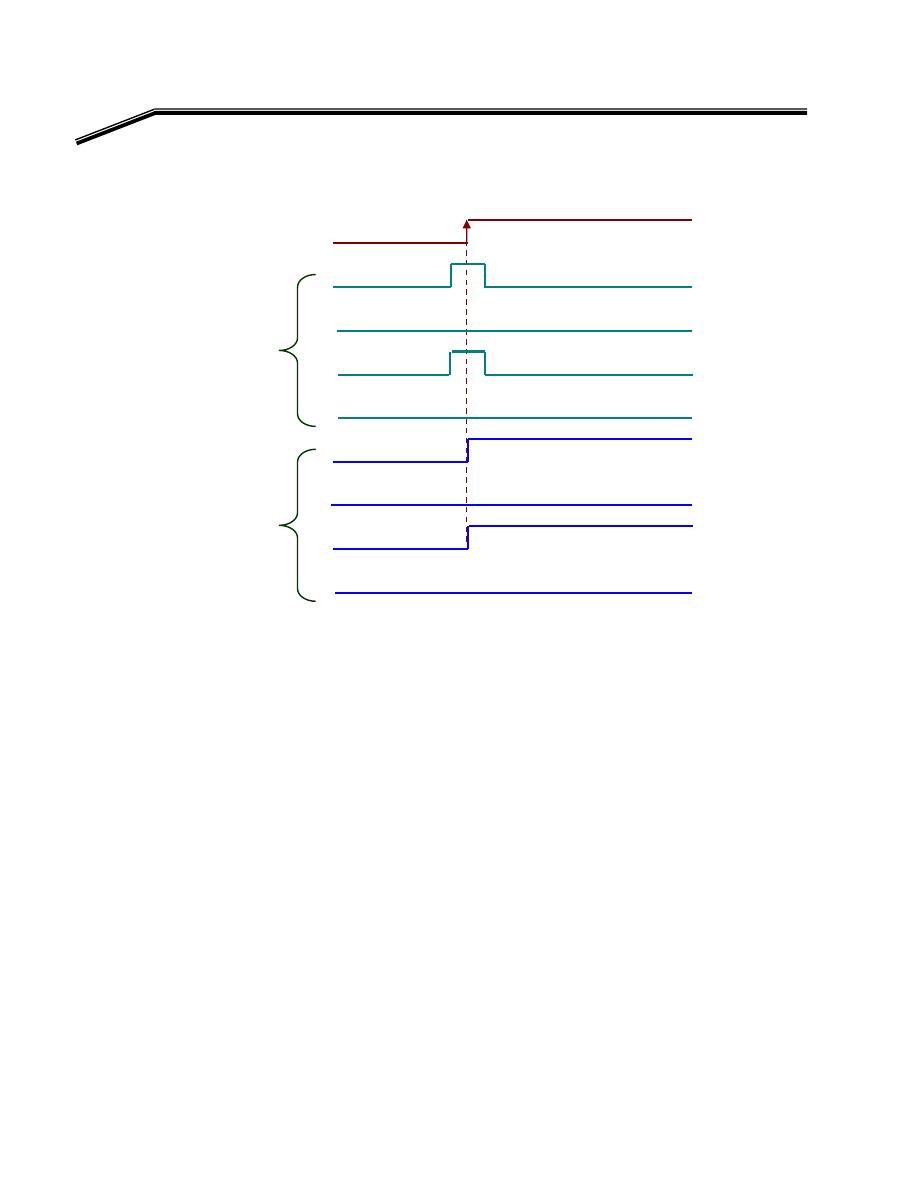
אאא
٧٤١
א
א
אאאא
א
-
٣٢١
-
٤
J
٥٢
F
E
אאא
٤
J
٥٢
F
KE
אאא
)
٤-bits
(
אא
D
٤
D
٣
,
D
٢
,
D
١
,
א
Q
٤
Q
٣
, Q
٢
,
Q
١
,
א
אא
)
CK
(
K
אאא
٤
J
٥٢
F
E
אאאא
א
Q
٤
Q
٣
, Q
٢
,
Q
١
,
אא
אאא
K
אא
K
א،אאא
،אא
אאא
J
אא
)
Parallel-in, Parallel-out Registers
(
K
א
)
Clear-input
(
א
אא
)
active-low
(
אא
F
א
KE
Clock
D
١
D
٢
D
٣
D
٤
Q
١
Q
٢
Q
٣
Q
٤
א
Input data
א
Output data
١
٠
١
٠
F
E
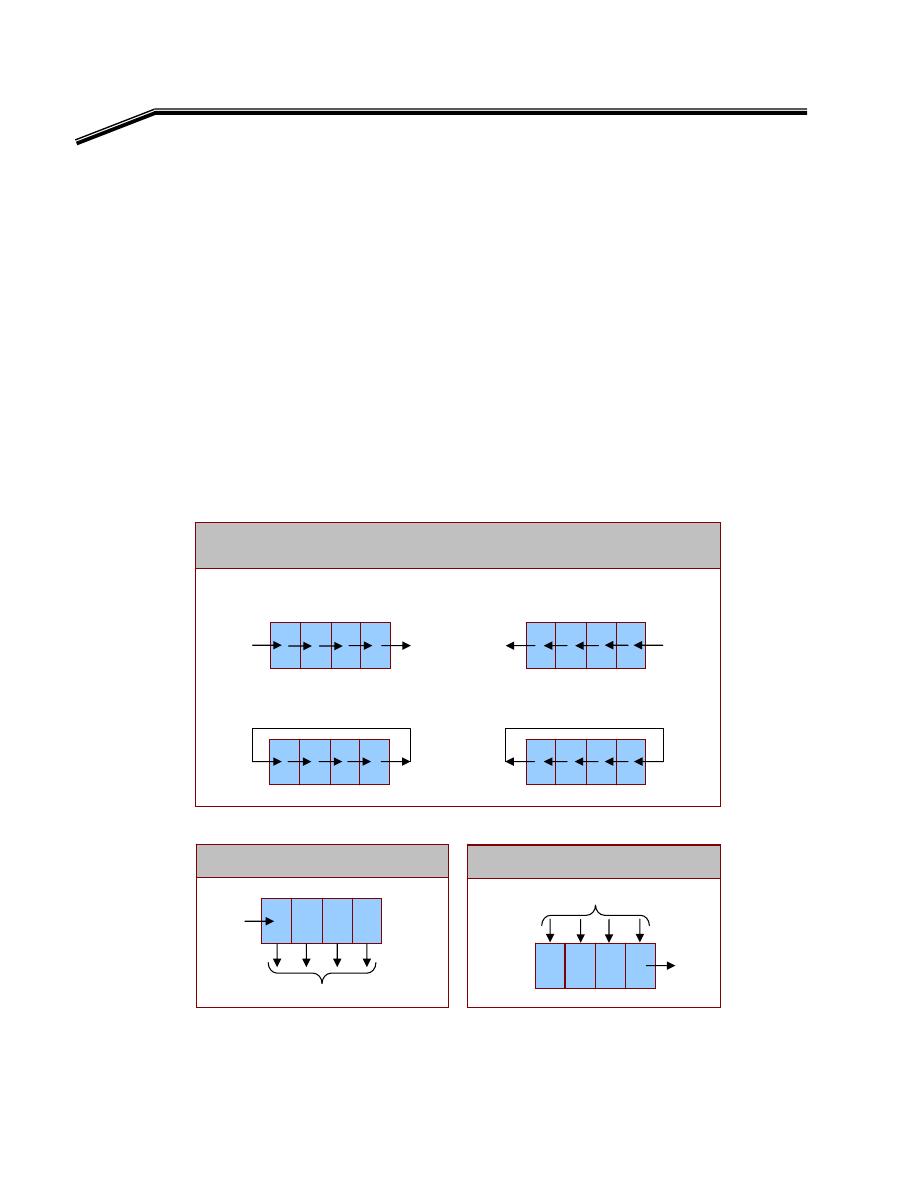
אאא
٧٤١
א
א
אאאא
א
-
٤٢١
-
٤
J
٩
J
٢
אא
Shift Registers
אאאא
)
move
(
א
)
Shift
(
א
K
אאאא
אא
F
٤
J
٦٢
KE
W
١
-
אאא
–
אא
)
(Serial-in, Serial-out Shift Registers
אא
(SISO)
K
٢
-
אאא
–
אא
)
Serial-in, Parallel-out Shift Registers
(
אא
(SIPO)
.
٣
J
אאא
–
אא
)
Parallel-in, Serial-out Shift Registers
(
אא
(PISO)
K
٤
J
٦٢
F
E
אא
K
Serial-in, serial-out (SISO) Shift Registers
Shift Right
Shift Left
Rotate Right
Rotate Left
Serial-In
Serial-Out
Serial-In
F
E
Serial-in, parallel-out (SIPO) Shift Registers
Parallel-in,
Serial-out Shift (PISO) Registers
Parallel Data In
Parallel Data Out
Serial-In
Serial-Out
F
E
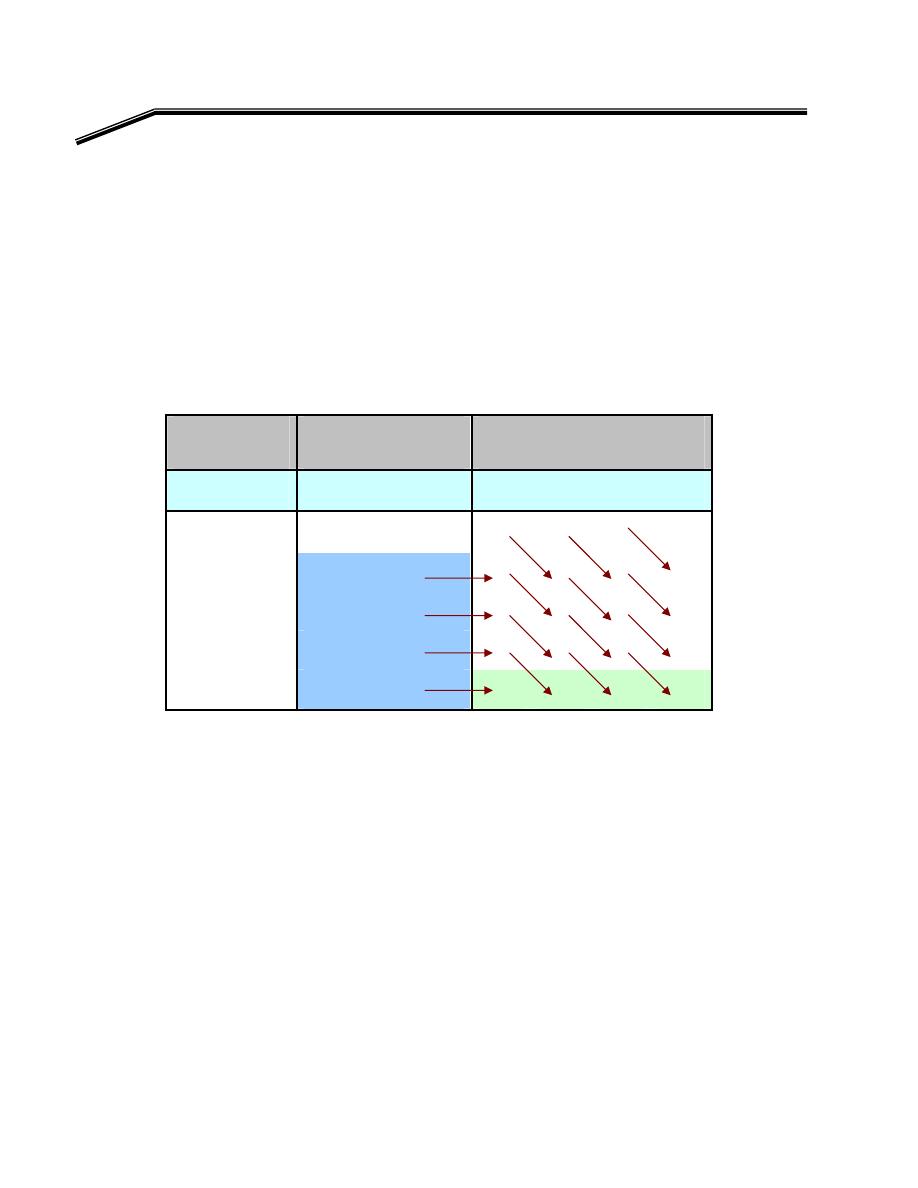
אאא
٧٤١
א
א
אאאא
א
-
٥٢١
-
אאאא
א
W
٤
J
٩
J
٢
J
١
אאאא
–
אא
Serial-in, Serial-out (SISO) Shift registers
F
٤
J
٨
E
אאא،
K
אא
אא
٠١١٠
F
אא
E
אאאא
١٠٠١
אאאא
K
א
אאא
אא
Q
٣
Q
٢
Q
١
Q
٠
Input
Clock
٠
١
١
٠
—
—
١
١
٠
١
١
١
st
١
٠
١
٠
٠
٢
nd
٠
١
٠
٠
٠
٣
rd
١
٠
٠
١
١
٤
th
F
٤
J
٨
E
אא
K
אאא
)
١
st
Clock pulse
(
אאא
אאאא
אאאאאא
אאאאא
K
אאא
)
٢
nd
Clock pulse
(
،
אא
)
٠١١٠
(
אאא
אאא
)
١٠٠١
(
K
אאא،אאא
K
،אאאא
אאא
(
)٠١١٠
א
אאא،א
)
١٠٠١
(
אאאא
K
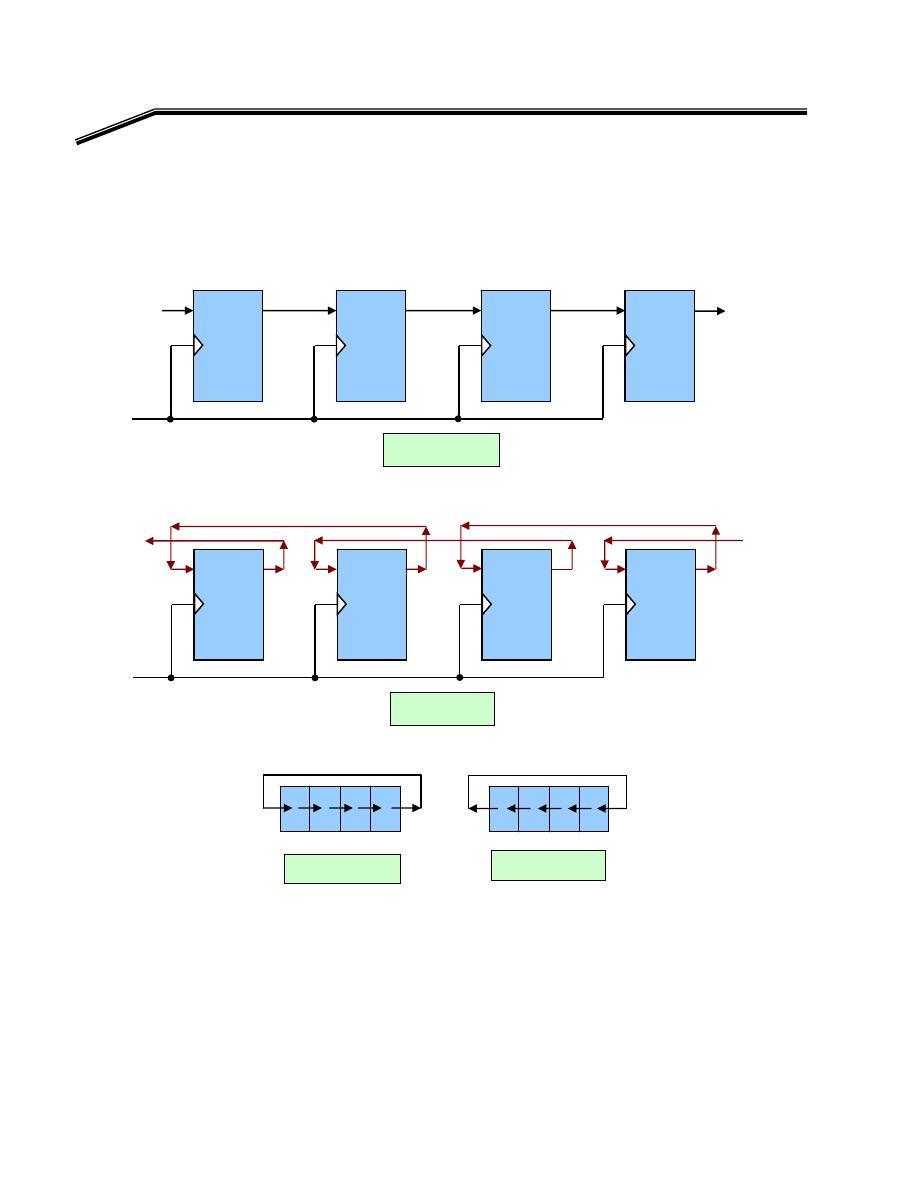
אאא
٧٤١
א
א
אאאא
א
-
٦٢١
-
אא،אאאאא
אאאא
א
K
F
٤
J
٧٢
E
אאאאא
K
٤
J
٧٢
F
E
אא
)
٤-bits
(
אא
אא
D
K
אאאא
D
אאא
)
FF٠
(
א،
אא
)
Q
٠
(
א
D
אאא
)
FF١
(
אאא،
)
Q
١
(
Serial
Data Out
FF٠
FF١
FF٢
FF٣
Serial
Data
Input
Clock
Input
F
E
SISO Shift Right
D
2
Q
D
1
Q
D
CK
0
Q
D
FF٠
FF١
FF٢
FF٣
Serial
Data
Input
Clock
Input
Serial
Data Out
F
E
SISO Shift Left
SISO Rotate Right
SISO Rotate Left
F
E
D
0
Q
CK
1
Q
D
CK
2
Q
D
CK
3
Q
אאא
٧٤١
א
א
אאאא
א
-
٧٢١
-
אאאא
)
FF٢
(
אאא،
)
Q
٢
(
אא
אאא
)
FF٣
(
،
אאאאאאאאאאא
א
K
אא
)
Clock input
(
،אא
)
Positive edge
(
אאא
)
١-bit
(
אא
،
אאאא
–
אאאאא
،אא
אאאא
א
K
،
אא
א
٤
J
٧٢
F
E
אא
D
אאאאא
–
אא
)
SISO Shift-Right Shift Register
.(
אאא
٤
J
٧٢
F
E
אא
אא
D
אא
–
א
א
)
SISO Shift- Left Shift Register
(
K
אאא،א
٤
J
٧٢
F
E
،
٤
J
٧٢
F
E
אאא
א،
א
אאא
–
אאא
)
SISO Rotate-Right
(
אא
–
א
אא
)
SISO Rotate-Left
(
٤
J
٧٢
F
KE
٤
J
٩
J
٢
J
٢
אא
א
–
אא
Serial-in, parallel out (SIPO) Shift registers
א
F
٤
J
٨٢
E
אאאאאאאא
א
–
אא
K
אאאא،אאא
)
٤-bits
(
אאא
)
Serial data input
(
אאאאא
F
א
אא
KE
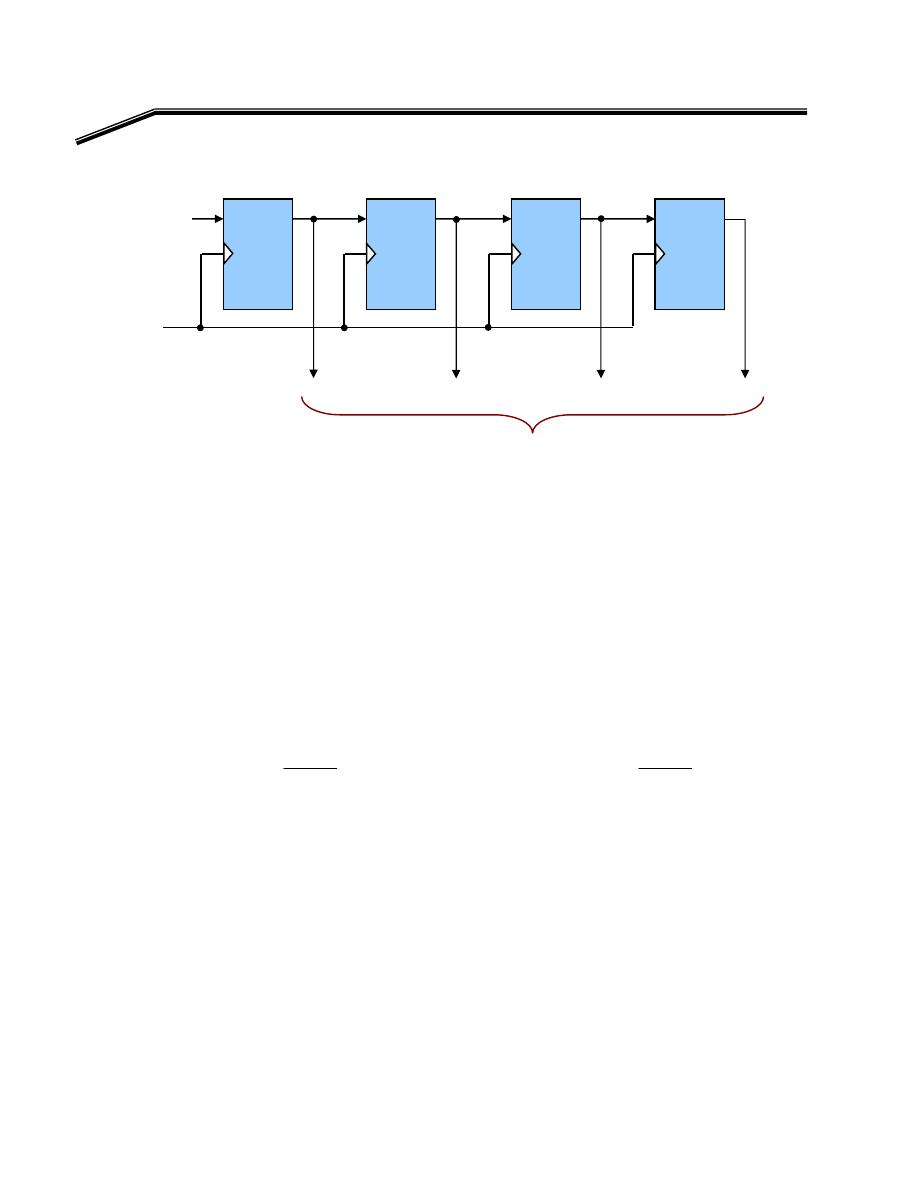
אאא
٧٤١
א
א
אאאא
א
-
٨٢١
-
F
٤
J
٨٢
E
אאאא
J
אא
K
)
٤-bits
(
אאאאא
א
K
אאאאאאא
Q
٣
,Q
٢
,Q
١
,Q
٠
)
(
)
٤-bits
(
אא
K
٤
J
٩
J
٢
J
٣
אאא
–
אא
Parallel-in, Serial-out (PISO) Shift registers
F
٤
J
٩٢
E
אאאא
–
אאאאאא
D
K
אאא
א
LOAD
/
SHIFT
K
א
LOAD
/
SHIFT
א
)
Low
(
،
אא
AND
אא
)
Enabled
(
א
א
Inverter
א
K
אאאא
א
)
D
٣
,D
٢
,D
١
,D
٠
(
א
אאא
K
אא
)
Clock pulse
(
،
אאאא
)
Q
٣
,Q
٢
,Q
١
,Q
٠
.(
0
Q
1
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
Serial
Data
Input
Clock
Input
0
Q
1
Q
2
Q
3
Q
Parallel data outputs
D
2
Q
D
CK
D
D
CK
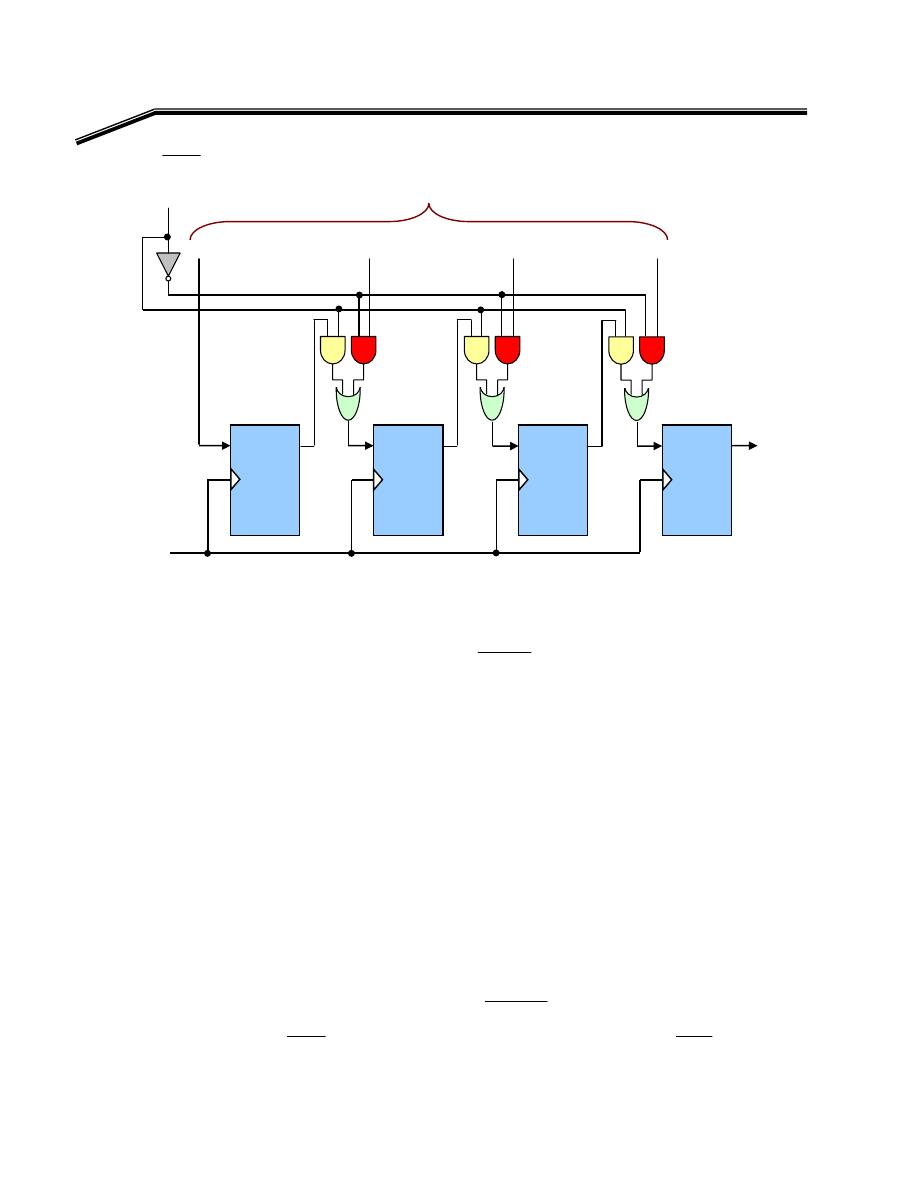
אאא
٧٤١
א
א
אאאא
א
-
٩٢١
-
F
٤
J
٩٢
E
אאא
J
אא
K
א
LOAD
/
SHIFT
א
)
High
(
،
אא
AND
אא
)
Enabled
(
K
אאאא
Q
٠
א
D
אאא
)
FF١
(
א،
Q
١
אאאא
)
FF٢
(
،
א
Q
٢
אאאא
)
FF٣
(
K
،אא
אא
אאאאאאא
)
١-bit
(
אאאא
F
clock input
.(
٤
J
٩
J
٢
J
٤
אאא
F
א
E
Shift Register Sequencer (Ring
Counter)
٤
J
٠٣
F
E
אאא
אאא
)
FF٣
(
אאא
FF
٠
F
א
Q
٣
D
٠
KE
אאאאאא
אאאא
K
א
SRART
א
Low
א
Q
٠
א
High
)
0
PRE
=
(
א،
Q
١
,Q
٢
,Q
٣
א
Low
F
0
CLR
=
E
א
٤
J
٠٣
F
KE
Parallel data inputs
Clock
Input
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
CK
0
D
1
D
2
D
3
D
)
load
for
0
,
shift
for
1
(
control
)
LOAD
/
SHIFT
(
Serial
Out
D
D
D
D
CK
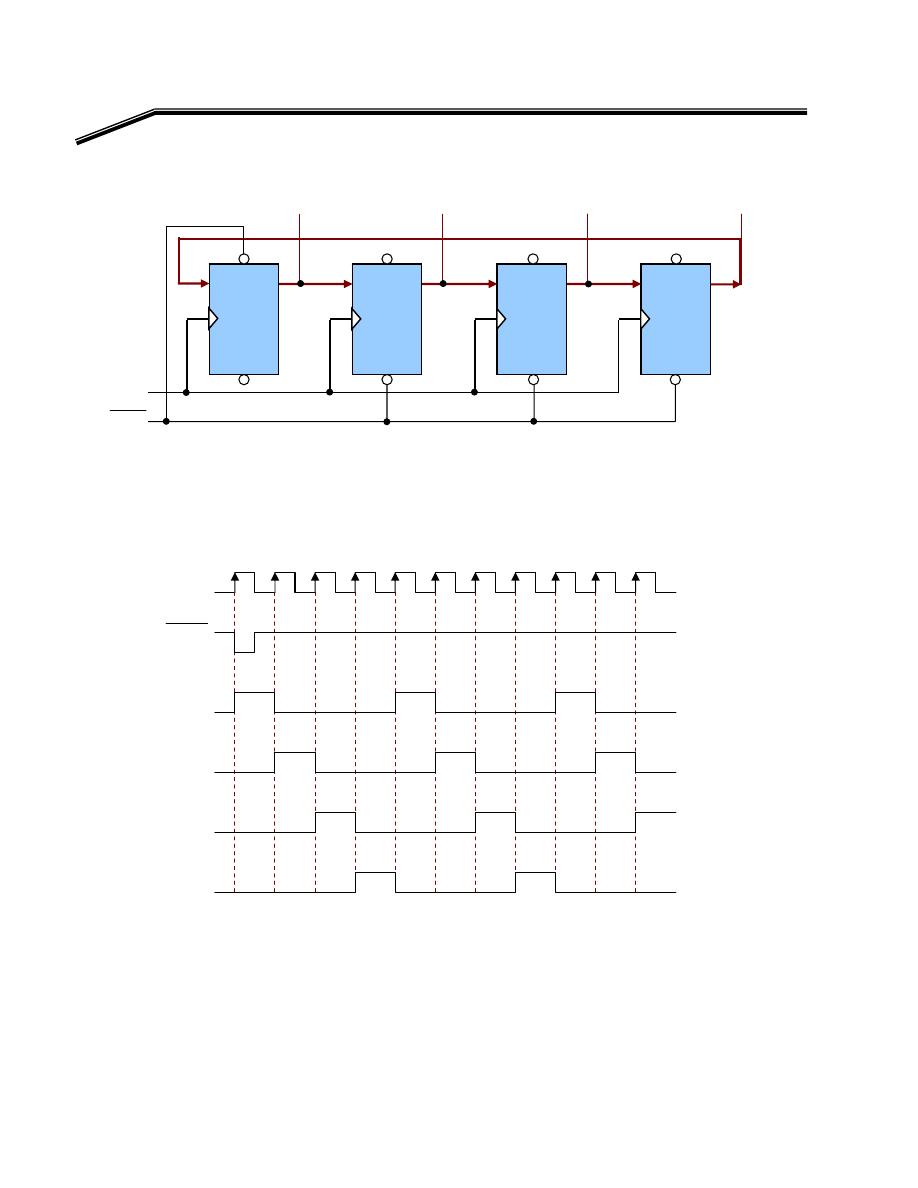
אאא
٧٤١
א
א
אאאא
א
-
٠٣١
-
CK
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
CK
Clock
F
E
0
D
1
D
2
D
3
D
PRE
PRE
PRE
PRE
CLR
CLR
CLR
CLR
START
0
Q
1
Q
2
Q
3
Q
٤
J
٠٣
F
E
אאא
K
٠
١
٢
٣
٠
١
٢
٣
٠
١
٢
Clock
START
0
Q
1
Q
2
Q
3
Q
٠ ٠ ٠ ١
٠ ٠ ١ ٠
٠
٠
١
٠
١ ٠ ٠ ٠
F
E
٤
J
٠٣
F
E
אאא
K
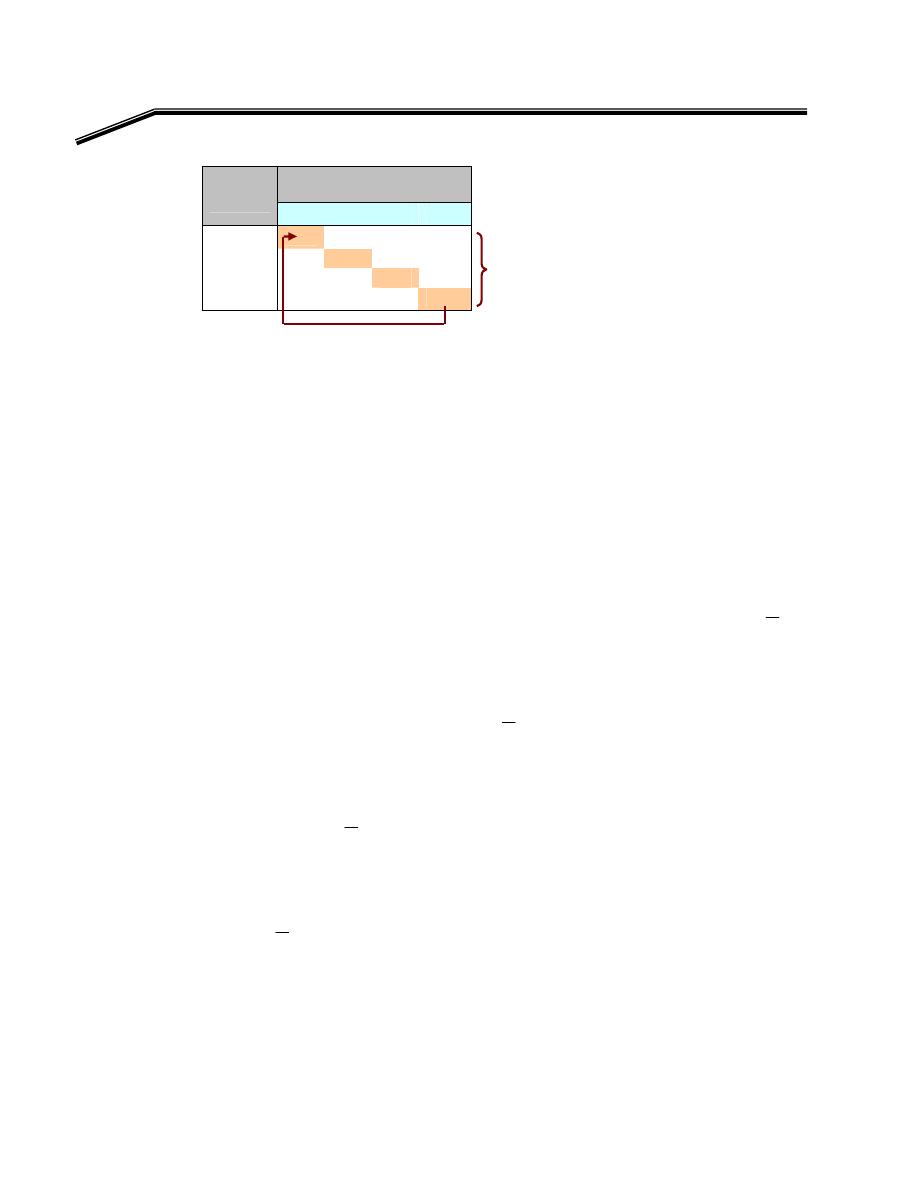
אאא
٧٤١
א
א
אאאא
א
-
١٣١
-
אא
Clock
Pulses
Q
٠
Q
١
Q
٢
Q
٣
٠
١
٠
٠
٠
١
٠
١
٠
٠
Four flip-flops will have
٢
٠
٠
١
٠
Four output states.
٣
٠
٠
٠
١
F
٤
J
٩
E
אאא
K
א
אא
(
)٠٠٠١
א،אאא
)
١
(
אאאאאאאא
F
٤
J
٩
KE
٤
J
٩
J
٢
J
٥
א
Johnson Counter
٤
J
١٣
F
E
א
א،אא
אאאאאאא
F
3
Q
E
אאאא
)
D
٠
(
K
،אאא
א
אא
אא
א
٤
J
١٣
F
E
אא
F
٤
J
٠١
E
،
٠٠٠١
،
Q
٣
א
(Low)
،אא
3
Q
א
(High)
אא
א
D
٠
،
אאאא
)
High inputs
(
א
אאאאאא
)
High
(
K
Q
٣
א
(High)
F
אאא
E
،
3
Q
א
(Low)
،
D
٠
(Low)
K
אאאאא
א
)
Low inputs
(
אאאא
)
Low
(
K
Q
٣
א
)
Low
(
F
אאא
E
،
3
Q
א
(High)
D
٠
(High)
אאאא
K
Repeat Sequence
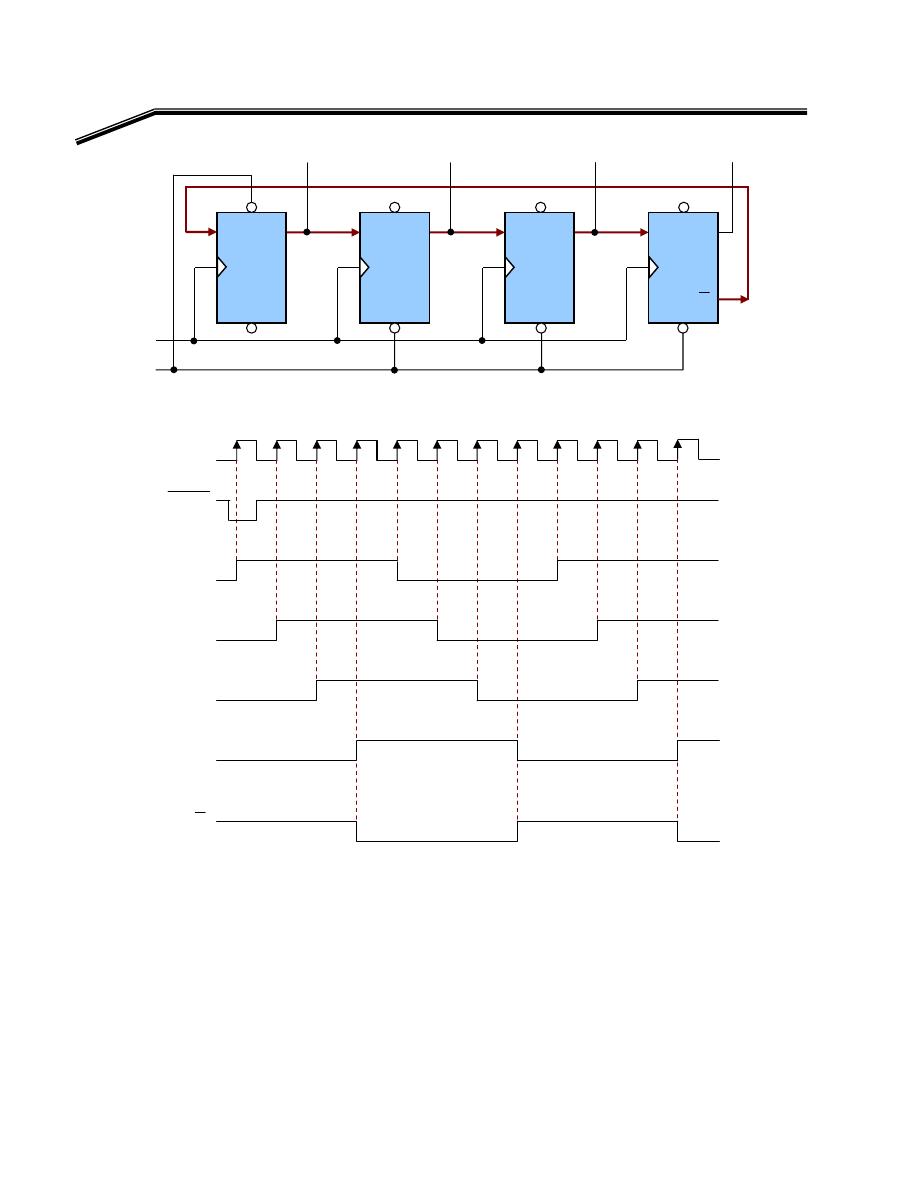
אאא
٧٤١
א
א
אאאא
א
-
٢٣١
-
F
٤
J
١٣
E
אאאאא
K
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
CK
Clock
F
E
0
D
1
D
2
D
3
D
PRE
PRE
PRE
PRE
CLR
CLR
CLR
CLR
0
Q
1
Q
2
Q
3
Q
٠
١
٢
٣
٤
٥
٦
٧
٠
١
٢
Clock
START
0
Q
1
Q
2
Q
3
Q
F
E
3
Q
3
Q
٣
CK
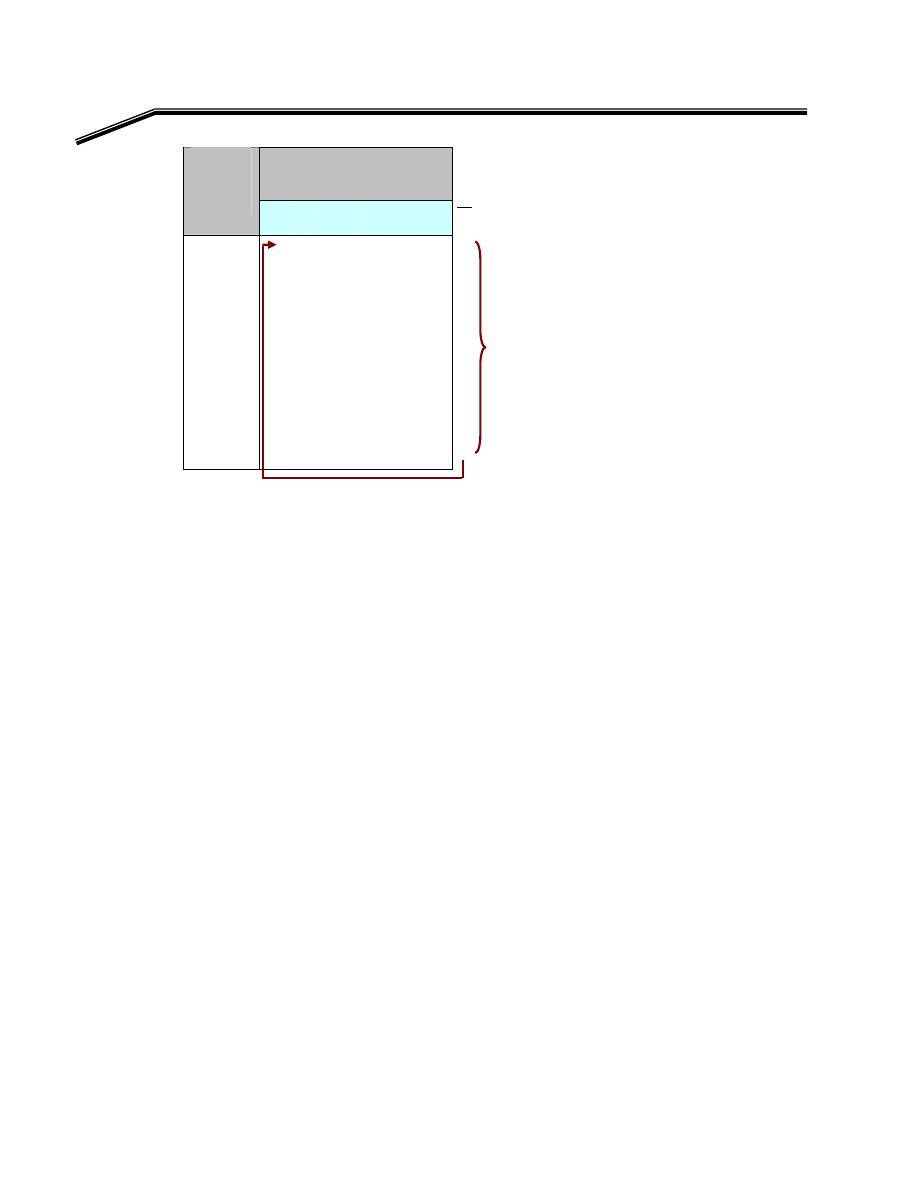
אאא
٧٤١
א
א
אאאא
א
-
٣٣١
-
אא
Clock
Pulses
Q
٠
Q
١
Q
٢
Q
٣
٠
١
٠
٠
٠
١
١
١
١
٠
٠
١
٢
١
١
١
٠
١
٣
١
١
١
١
٠Four flip-flops will have
٤
٠
١
١
١
٠eight output states.
٥
٠
٠
١
١
٠
٦
٠
٠
٠
١
٠
٧
٠
٠
٠
٠
١
F
٤
J
٠١
E
אא
K
א
،אאאאאאאא
אאאאא
F
F
٤
J
٩
KEE
אאאאאא
אאא،א
٤
J
١٣
F
E
)
٢
× ٤flip-flops = ٨
(
F
٤
J
٠١
KE
3
Q
Repeat Sequence

אאא
J
אא
٧٤١
א
א
אאאא
א
אא
-
٣٣١
-
٤
J
٠١
אאא
Counters
אאאא
אאאא
אא
א
K
אאא
)
binary bits
(
،
אאאאאאאא
אא
)
clock input
(
K
אאאאא
אא
אאאאאאאא
אא
K
אאאאאא
א
א
)
Asynchronous Counters
(
אא
אאאא
)
Synchronous Counters
(
K
אאאאאאאאאאאא
אא
K
אאאאאאאא
،א
אאאאאאא
)
Master Clock
(
K
،אאאאאאאאאא
אאאאאאא
K
٤
J
٠١
J
١
אאאא
אאא
Asynchronous Binary-Up Counters
٤
J
٢٣
F
E
אאא
K
J-K
אא
K
אאאאאא
א
אאאא
K
א
J,K
א
)
High
(
،
אא
)
Toggle
(
)
Negative edge
(
אא
K
א
אאאאאא
)
Q
(
א
٤
J
٢٣
F
KE
א
Q
٣
,Q
٢
,Q
١
,Q
٠
אא
)
٤-bit word
(
א
אא
٠٠٠٠
אאא
אאאא
F
٤
J
١١
KE
אא
FF
٠
)
Q
٠
(
)
LSB
(
אא
FF
٣
)
Q
٣
(
א
)
MSB
(
K
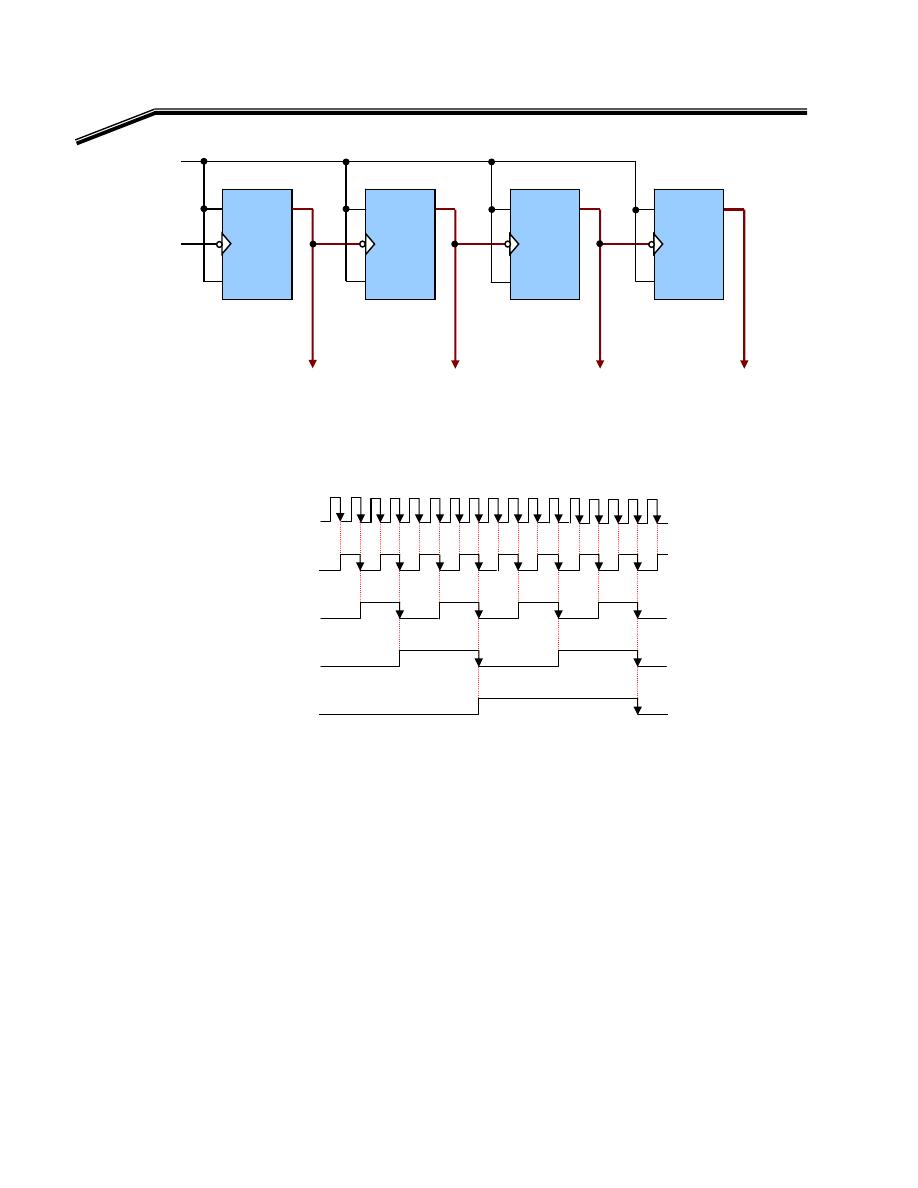
אאא
٧٤١
א
א
אאאא
א
-
٤٣١
-
F
٤
J
٢٣
E
אאאא
K
אא
)
FF٠
(
אאא
)
Clock input
(
،
א
Q
٠
)
Toggle
(
،אאא
א
Q
٠
٤
J
٢٣
F
KE
אאאא
אא
Q
٠
"
٠
"
"
١
"
אאא
"
١
"
"
٠
"
א
K
א
א
Q
٠
אאא
FF
١
،
Q
٠
א
Q
١
)
Toggle
(
K
Q
١
א
Q
٢
،
Q
٢
א
Q
٣
K
Q
٠
Q
١
Q
٢
Q
٣
٠
٠
٠
٠
٧١ ٦١ ٥١ ٤١ ٣١ ٢١ ١١ ٠١ ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١
F
E
CK
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
CK
CK
CK
Clock
Input
0
Q
1
Q
2
Q
3
Q
K K K K
J
J
J
J
F
E
FF٢
FF٣
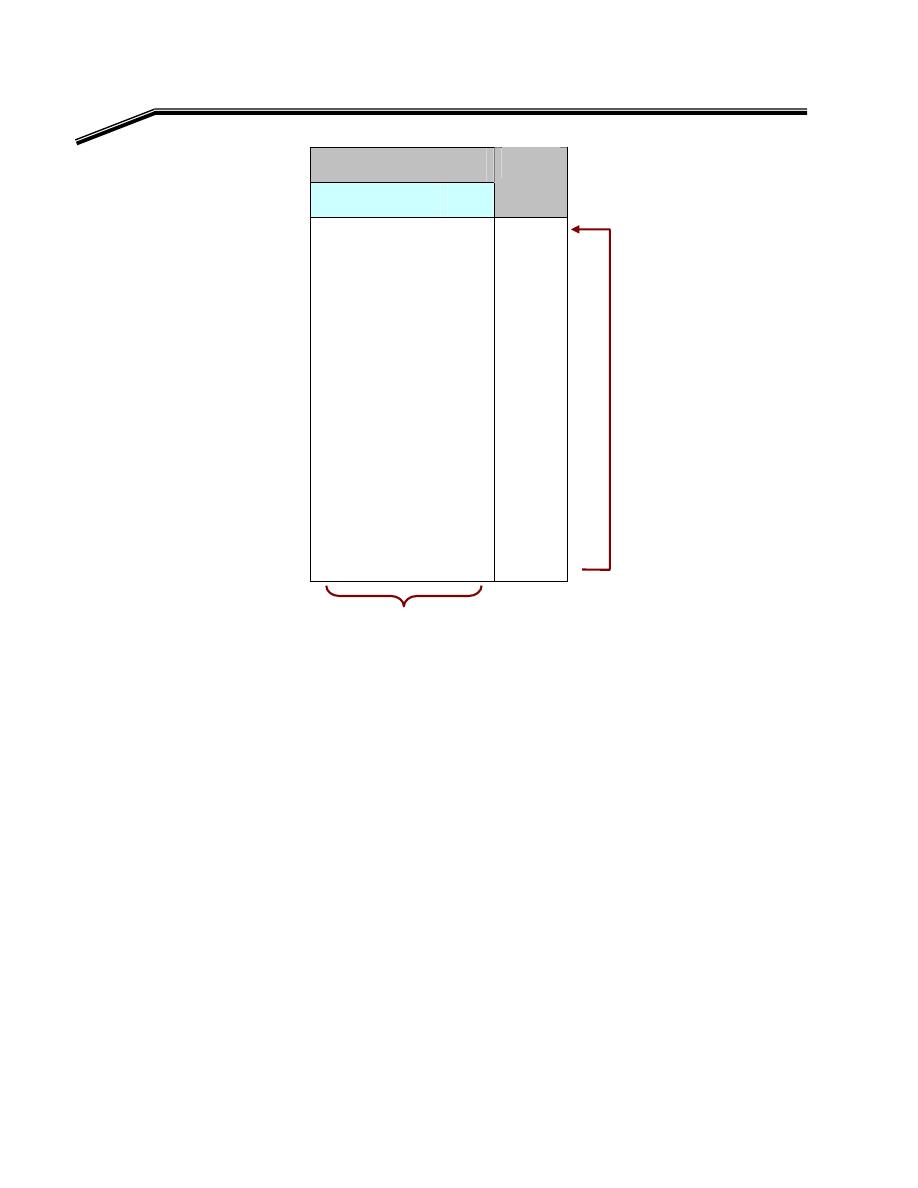
אאא
٧٤١
א
א
אאאא
א
-
٥٣١
-
אא
א
Q
٠
Q
١
Q
٢
Q
٣
٠
٠
٠
٠
٠
١
١
٠
٠
٠
٢
٠
١
٠
٠
٣
١
١
٠
٠
٤
٠
٠
١
٠
٥
١
٠
١
٠
٦
٠
١
١
٠
٧
١
١
١
٠
٨
٠
٠
٠
١
٩
١
٠
٠
١
٠١
٠
١
٠
١
١١
١
١
٠
١
٢١
٠
٠
١
١
٣١
١
٠
١
١
٤١
٠
١
١
١
٥١
١
١
١
١
F
٤
J
١١
E
אאאאא
K
•
א
The Maximum Count (N) of a Counter
אאא
F
٤
J
١١
E
אאא،
א
אא
١٠٠٠
]
א
)
١
(
אא
[
אאאא،
א
٠١٠٠
]
א
)
٢
(
אא
[
אאאאא،
١١٠٠
]
)
٣
(
אא
[
א،
K
אאאא
אאאא،אאאא
W
1
2
N
n
−
=
W
= N
אאא
(N = maximum count before cycle repeats)
= n
אא
אאא
(
n = number of flip-flops in the counter circuit)
Cycle Repeats
Binary Count
אאא
٧٤١
א
א
אאאא
א
-
٦٣١
-
אאאא
٤
J
٢٣
F
E
א
W
)
1111
(
15
1
16
1
2
1
2
N
2
10
4
n
=
−
=
−
=
−
=
•
אאא
The Modulus (MOD) of a counter
אאא
)
Modulus of a counter
(
)
MOD
(
א
אאא
K
אאא
٤
J
٢٣
F
E
MOD
()٦١
אא
()٦١
٠٠٠٠
١١١١
א
F
٤
J
١١
KE
MOD
א
אא
W
MOD
=
٢
n
MOD = modulus of the counter
n = number of flip-flops in the counter circuit
אאאא
٤
J
٢٣
F
E
אאאאא
W
16
2
2
MOD
4
n
=
=
=
•
אא
The Frequency Division of a counter
אאאאא
٤
J
٢٣
F
E
אא
)
frequency divider
(
א
אאאאאא
٢
،
אא
אא
٢
K
א
٢
،א
א
٢
א
٢
،א
אאאא
אא
٤
٤
J
٢٣
F
E
אאאא

אאא
٧٤١
א
א
אאאא
א
-
٧٣١
-
א
Q
١
K
،
אאאאא
٢
،
א
אאא
٤
א،
٨
א،
٦١
א
K
אאאאאא
W
Division Factor =
٢
n
F
א
E
N = number of flip-flops in the counter circuit
•
א
א
The Propagation Delay Time (t
p
) of a counter
אא
א
אאא
)
Ripple counter
(
אא،
אא،א
אאא
K
،אאאאאא
אא
אאאא
K
،
אאא
F
אאא
E
א
אאא
١١١٠
٠٠٠١
K
אא
א
)
t
p
(
ns
10
ns
40
)
٤Flip-Flops
× ٠١ns
(
אא
١١١٠
٠٠٠١
K
א
)
counting speed
(
אא
אאאאאאא
K
אא
אאא
W
p
9
t
n
10
1
f
×
×
=
W
f = upper clock pulse frequency limit
n = number of flip-flops in the counter circuit
t
p
= propagation delay time of each flip-flop in nanoseconds
٤
J
٠١
J
٢
אאאאאאא
Asynchronous Binary Down Counters
אאאאאאאא
א
"
١
"
K
אאאאאאאאא
א
"
١
"
א
K
א
٤
J
٣٣
F
E
א
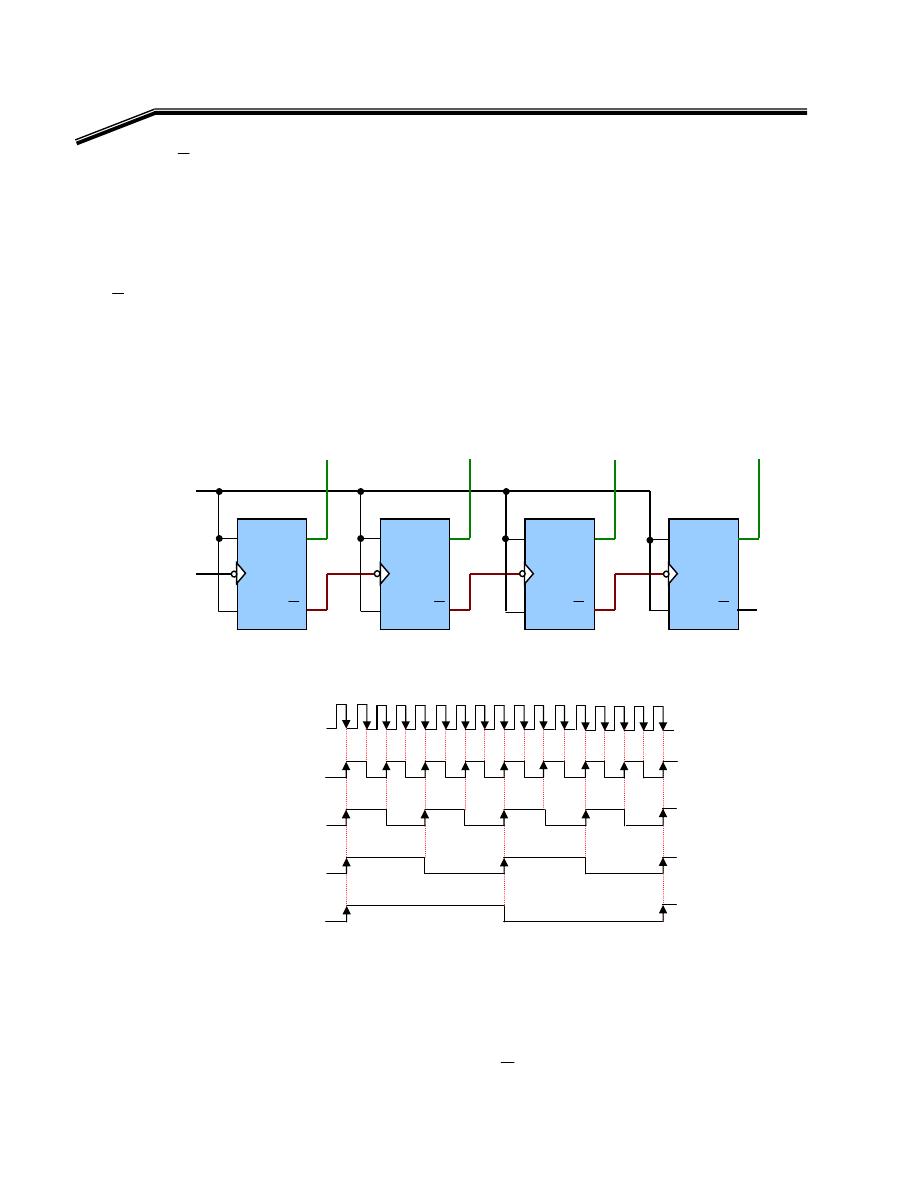
אאא
٧٤١
א
א
אאאא
א
-
٨٣١
-
אאאא
J-K
K
א
Q
אא
Q
אאא
K
אאא
Q
אאא
٤
J
٣٣
F
KE
א
אאאא
(RESET)
Q
٣
,Q
٢
,Q
١
,Q
٠
٠٠٠٠
K
אאאא
Q
Low
א
Q
١١١١
K
אאאאאא
FF
٣,FF٢,FF١
High
K
אא
J,K
א
אא
High
א
)
Toggle
(
אאא
K
F
٤
J
٣٣
E
אאאא
K
אאאאא
א
FF
٠
،
א
Q
٠
"
٠
"
"
١
"
אא،
0
Q
"
١
"
"
٠
"
אא
CK
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
CK
Clock
Input
0
Q
1
Q
2
Q
3
Q
K K K K
HIGH
F
E
Clock
Input
Q
٠
Q
١
Q
٢
Q
٣
٠
٠
٠
٠
٦١ ٥١ ٤١ ٣١ ٢١ ١١ ٠١ ٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١
١٧
F
E
0
Q
1
Q
2
Q
3
Q
J
J
J
J
אאא
٧٤١
א
א
אאאא
א
-
٩٣١
-
אא
FF
١
א،
Q
١
"
١
"
"
٠
"
א
1
Q
"
١
"
"
٠
"
K
אא
1
Q
"
١
"
"
٠
"
א
FF
٢
א،
K
אא
א
Q
٠
Q
١
Q
٢
Q
٣
٥١
١
١
١
١
٤١
٠
١
١
١
٣١
١
٠
١
١
٢١
٠
٠
١
١
١١
١
١
٠
١
٠١
٠
١
٠
١
٩
١
٠
٠
١
٨
٠
٠
٠
١
٧
١
١
١
٠
٦
٠
١
١
٠
٥
١
٠
١
٠
٤
٠
٠
١
٠
٣
١
١
٠
٠
٢
٠
١
٠
٠
١
١
٠
٠
٠
٠
٠
٠
٠
٠
F
٤
J
٢١
E
אאאאא
K
אאאאאא
Q
٣
,Q
٢
,Q
١
,Q
٠
(
)٥١
٠١
=
١١١١
אא
א
F
٤
J
٢١
KE
אאאא
אאאאא
K
א
א
٤
J
٣٣
F
E
אא،
FF
٠
،אא
א
Q
٠
א،א
Q
٣
,Q
٢
,Q
١
אאאאאא
K
Cycle Repeats
Binary Count
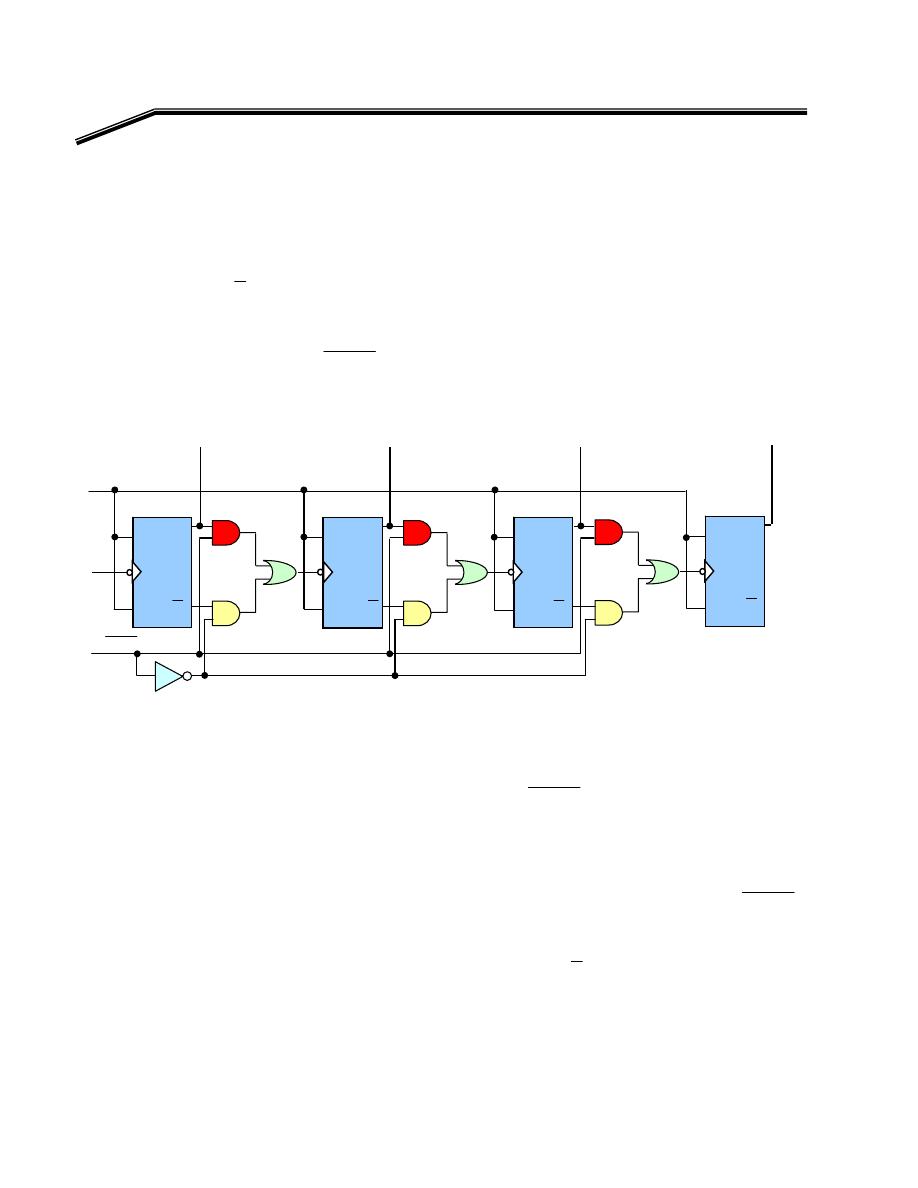
אאא
٧٤١
א
א
אאאא
א
-
٠٤١
-
٤
J
٠١
J
٣
אאאאא
L
אאא
Asynchronous Binary Up/Down Counters
אאאא،אאאאאאא
אאאאאאאאא
Q
אאאאאאא
אא
Q
K
F
٤
J
٤٣
E
א
L
AND-OR
אא
DOWN
UP /
K
F
٤
J
٤٣
E
אאאא
K
אא
DOWN
UP /
א
High
،
אא
AND
א
א
)
Enabled
(
،
Q
אאאא
אא،אאא،א
DOWN
UP /
א
Low
،
אאאאא
א
)
Disabled
(
אאאאאא
)
Enabled
(
Q
אאאא
אא،א
א
K
Clock
Input
0
Q
HIGH
CK
0
Q
FF٠
0
Q
1
Q
FF١
CK
1
Q
1
Q
2
Q
FF٢
CK
2
Q
2
Q
3
Q
FF٣
CK
3
Q
3
Q
K
K
K
K
UP/DOWN control
J
J
J
J
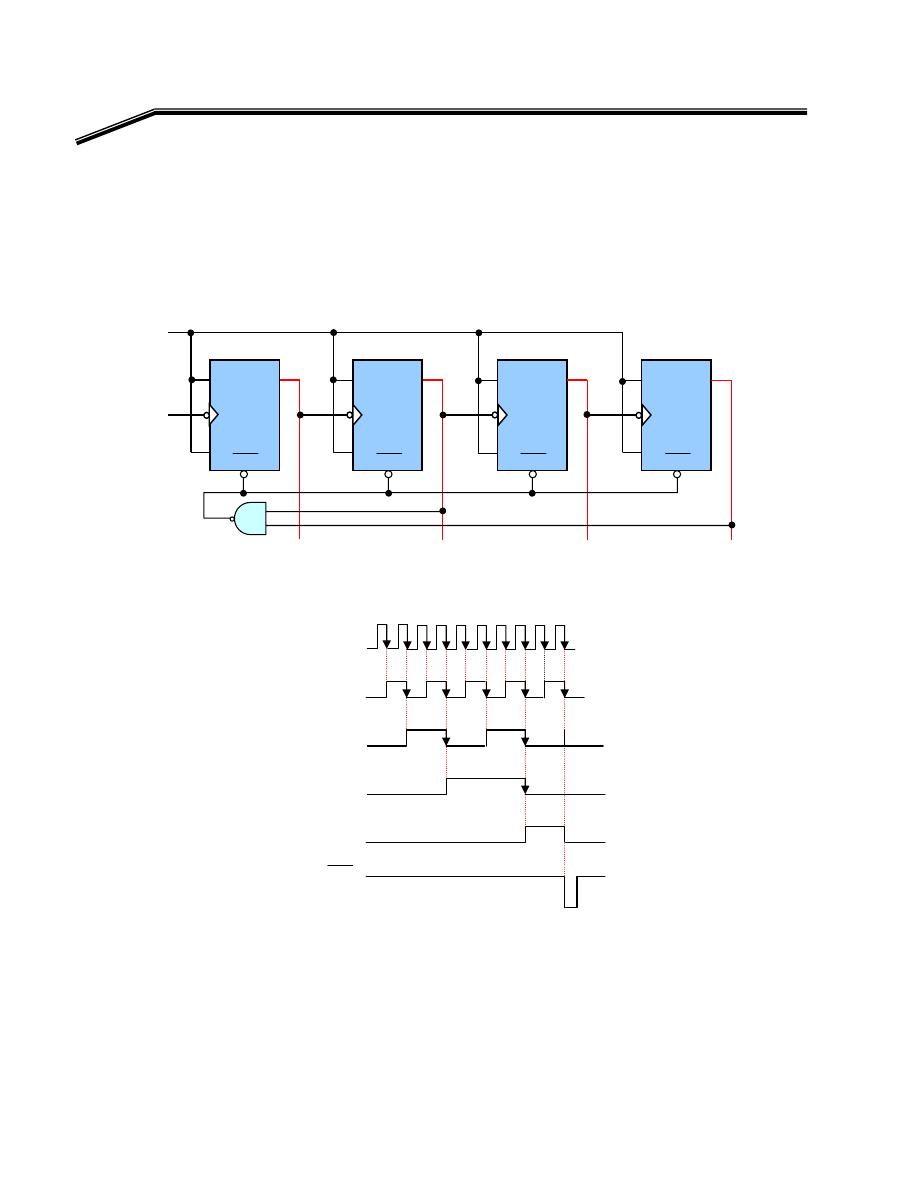
אאא
٧٤١
א
א
אאאא
א
-
١٤١
-
٤
J
٠١
J
٤
אאאאאא
Asynchronous Decade (MOD
)٠١Counters
٤
J
٥٣
F
E
אאאאאאא
אא
)
MOD-٠١
(
K
F
٤
J
٥٣
E
אא
אא
K
HIGH
CK
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
CK
Clock
Input
0
Q
1
Q
2
Q
3
Q
K K K K
F
E
Clock
Input
Q
٠
Q
١
Q
٢
Q
٣
٠
٠
٠
٠
٩ ٨ ٧ ٦ ٥ ٤ ٣ ٢ ١
١٠
F
E
CLR
CLR
CLR
CLR
CLR
J
J
J
J
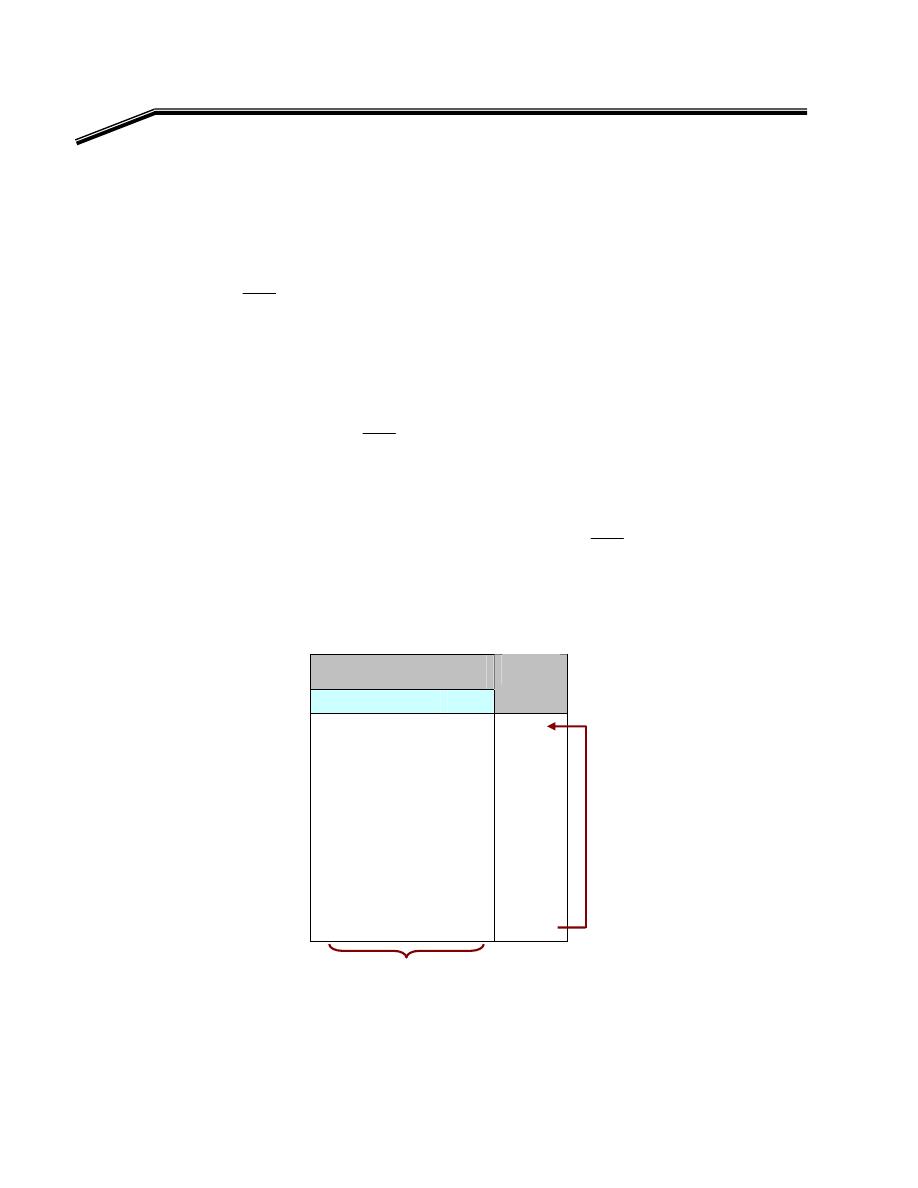
אאא
٧٤١
א
א
אאאא
א
-
٢٤١
-
אאא
٠٠٠٠
F
٠
E
١٠٠١
F
٩
E
א
אא
٤
J
٥٣
F
E
אא
F
٤
J
٣١
KE
א
אאאא
٠١٠١
١١١١
F
٠١
אא
٥١
E
א
NAND
אאאא
F
CLR
E
אא
א
K
אאא
Q
١
אא
Q
٣
K
אא
א
٠١٠١
F
٠١
אא
E
Q
٣
,Q
١
א
High
،
א
NAND
Low
)
CLEAR
(
א
K
א
א
٤
J
٥٣
F
E
א
CLR
)
inactive
(
א
٠٠٠٠
١٠٠١
K
אאאא
Q
٣
,Q
١
א
High
K
א
א
Q
١
،
Q
٣
،
)
CLEAR
(
אאאא
אא
CLR
K
אאאאא
F
٤
J
٣١
E
אא،אא
٠
א
٩
א
K
אא
א
Q
٠
Q
١
Q
٢
Q
٣
٠
٠
٠
٠
٠
١
١
٠
٠
٠
٢
٠
١
٠
٠
٣
١
١
٠
٠
٤
٠
٠
١
٠
٥
١
٠
١
٠
٦
٠
١
١
٠
٧
١
١
١
٠
٨
٠
٠
٠
١
٩
١
٠
٠
١
F
٤
J
٣١
E
אאאאא
K
Cycle Repeats
Binary Count
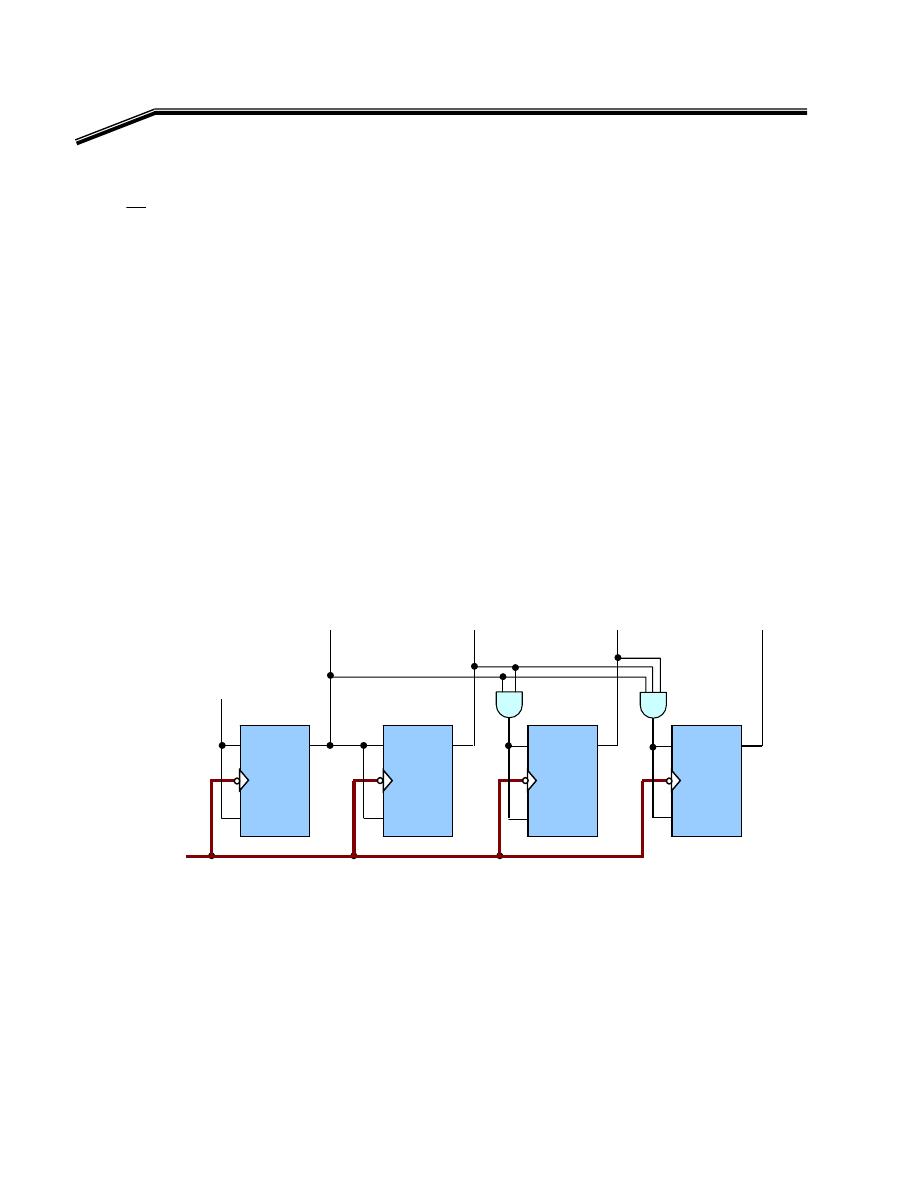
אאא
٧٤١
א
א
אאאא
א
-
٣٤١
-
אאאא
٠
٩
)
MOD-٠١
(
א،אאא
Q
٣
)
10
1
(
אאא
)
Clock input
.(
אאאאאא
אאא
)
Digital clocks
(
،
אא
)
Digital Voltmeter
(
אא
א
)
Frequency Counter
(
K
٤
J
٠١
J
٥
אאאאאאא
Synchronous Binary Counters
٤
J
٦٣
F
E
אא
J-K
א
AND
אאאא
)
٤-bit
(
)
MOD-٦١
(
אא
אא
F
E
אאאאאאא
)
Triggered
(
אאא
K
אאאא
،אאא
אא
אא
K
F
٤
J
٦٣
E
אאא
K
אאאאא
J,K
אא
FF
٠
א
High
،
א
)
Toggle
(
א
א،אאאאאאאא
Low
High
High
Low
א
K
0
Q
1
Q
2
Q
3
Q
FF٠
FF١
FF٢
FF٣
CK
CK
CK
Clock
Input
0
Q
1
Q
2
Q
3
Q
K K K K
HIGH
A
B
J
J
J
J
CK
אאא
٧٤١
א
א
אאאא
א
-
٤٤١
-
א
J,K
אא
FF
١
אאא
٢
אא
FF
٠
K
אא
Q
٠
א
Low
،
א
Q
١
אא
FF
١
)
No change
(
א
Q
٠
א
High
،
א
Q
١
)
Toggle
(
K
א
J,K
אא
FF
٢
אא
AND(A)
Q
٠
,Q
١
K
א
Q
٠
= Q
١
= High
א
AND(A)
High
،
אא
)
Enable
(
אא
FF
٢
אא
K
א
J,K
אא
FF
٣
אא
AND(B)
א
Q
٢
,Q
١
,Q
٠
K
א
Q
٢
,Q
١
,Q
٠
א
High
א
AND(B)
High
אאאא
FF
٣
א
K
٤
J
٠١
J
٦
אאאאאא
Synchronous Counters Advantages
אאאאאאאאא
)
Ripple counters
(
אאאאאא،אא
٤
J
٢٣
F
E
אאאאאא
٤
J
٣٣
F
KE
אאאאאאא
א
א
K
،אאא
אאא
אאא
K
אא
)
Propagation-delay time
(
אאא
א
אאאאאא
K
אאאא
،אאא
אאא
F
אא
E
K
אאאאאאאא
א
אא
אאא،
אאא،אאא
،א
אאא
אא
K
אאא
٧٤١
א
א
אאאא
א
-
٥٤١
-
אא
אא
אא
אאאא
K
א
א
אאא
אאאאא
W
t
p
= Single (flip-flop) t
p
+ Single (AND-gate) t
p
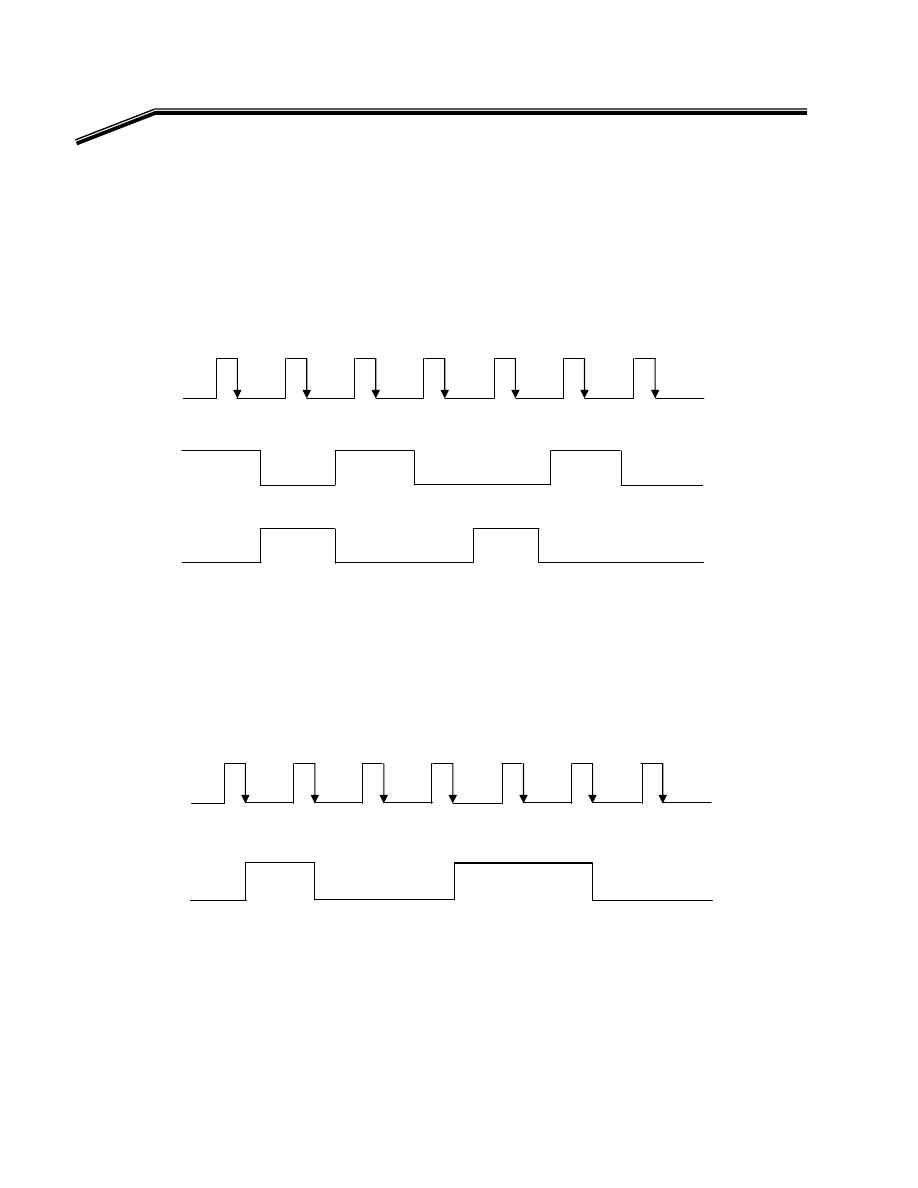
אאא
٧٤١
א
א
אאאא
א
-
٦٤١
-
١
E
אא
(Q)
אא
S-R
אאא
א
אא
(negative edge trigger)
אאא
K
אאא
Q=
٠
אא
K
٢
E
אא
(Q)
אאא
D
אא
אא
אא
(positive edge trigger)
אאא
K
אאא
Q=
٠
אא
K
٣
E
אא
(Q)
אא
JK
אא
אא
אא
(negative edge trigger)
אאא
K
א
אא
Q=
٠
אא
K
CK
S
R
CK
D
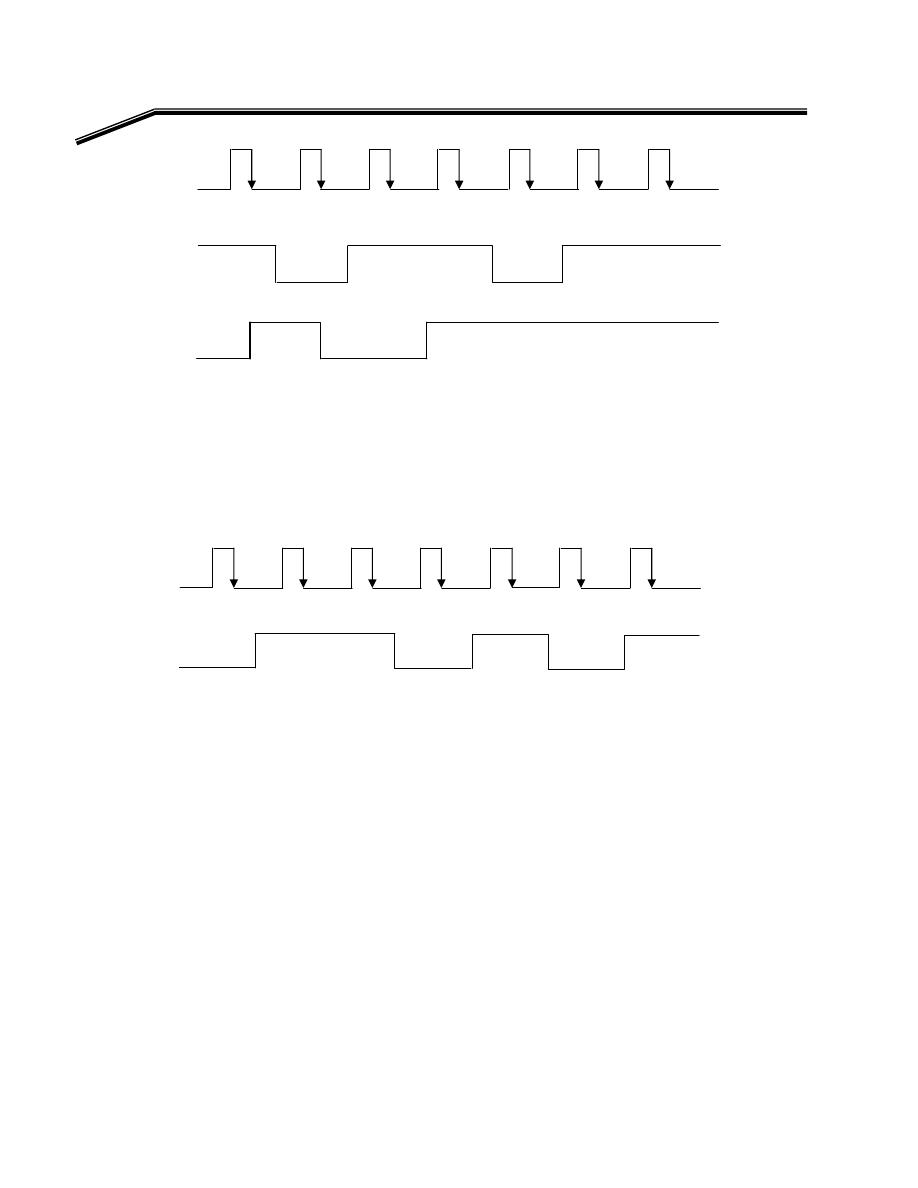
אאא
٧٤١
א
א
אאאא
א
-
٧٤١
-
٤
E
אא
(Q)
אאא
T
אא
אא
אא
(negative edge trigger)
אאא
K
אאא
Q=
٠
אא
K
٥
E
אא
(f)
אא
٥٥٥
אאאא
אאא،
R
A
=
٠١kΩ
א
R
B
=
٣kΩ
א،
C =
٠{١µf
K
٦
E
אא
٥٥٥
אאא
אא،אא
א
R
A
=
٢١kΩ
Ω
א،
C =
٠{٠١µf
K
CK
J
K
CK
T

-
٣٣١
-
אא
אא
א
א
אאא
ã¹]<gè…‚jÖ]æ<ËÖ]<Üé×Ãj×Ö<íÚ^ÃÖ]<퉉ö¹]
א
אאא
אא
٥
אא
٧٤١
א
א
אא
א
-
٨٤١
-
אאא
אא
W
•
אאא
K
•
אאאא
K
•
אאא
K
•
אאא
K
•
אאא
K

אא
٧٤١
א
א
אא
א
-
٩٤١
-
)
AB
and
B
A
,
B
A
,
B
A
(
٥
J
١
Introduction
،אאאאא
K
א
אאא
(fuse–programmable)
א
א
(Customer)
א
אא
K
א
(fusible links)
א،אאאאאא
אאאא،א
א
K
אא
W
•
אאא
))
PLA
(
rray
A
ogic
L
rogrammable
P
The
(
•
אא
))
PAL
(
ogic
L
rray
A
rogrammable
P
The
(
•
אא
א
))
PLS
(
equencer
S
ogic
L
rogrammable
P
The
(
•
אאא
(Erasable Programmable Logic Device (EPLD))
(F)
א
אאא
(FPLA, FPAL, ….)
(Field Programmable Logic Devices)
K
٥
J
٢
אאא
Basic Programmable Logic Devices
א
F
٥
J
١
E
אאאא
J
PLD
)
٢-input/٤-output
(
K
א،אאאא
אאאא
)
noninverting Buffer
(
א
)
Inverting Buffer
(
K
א
AND
High
אאאאא
A,B
א
F
٥
J
١
E
אא،
AND
אא
)
Product Lines
(
،
א
،
א
א
K
א
אא
OR
)
fusible link
(
F
٥
J
١
E
אא،
)
×
(
אא
J
.PLD
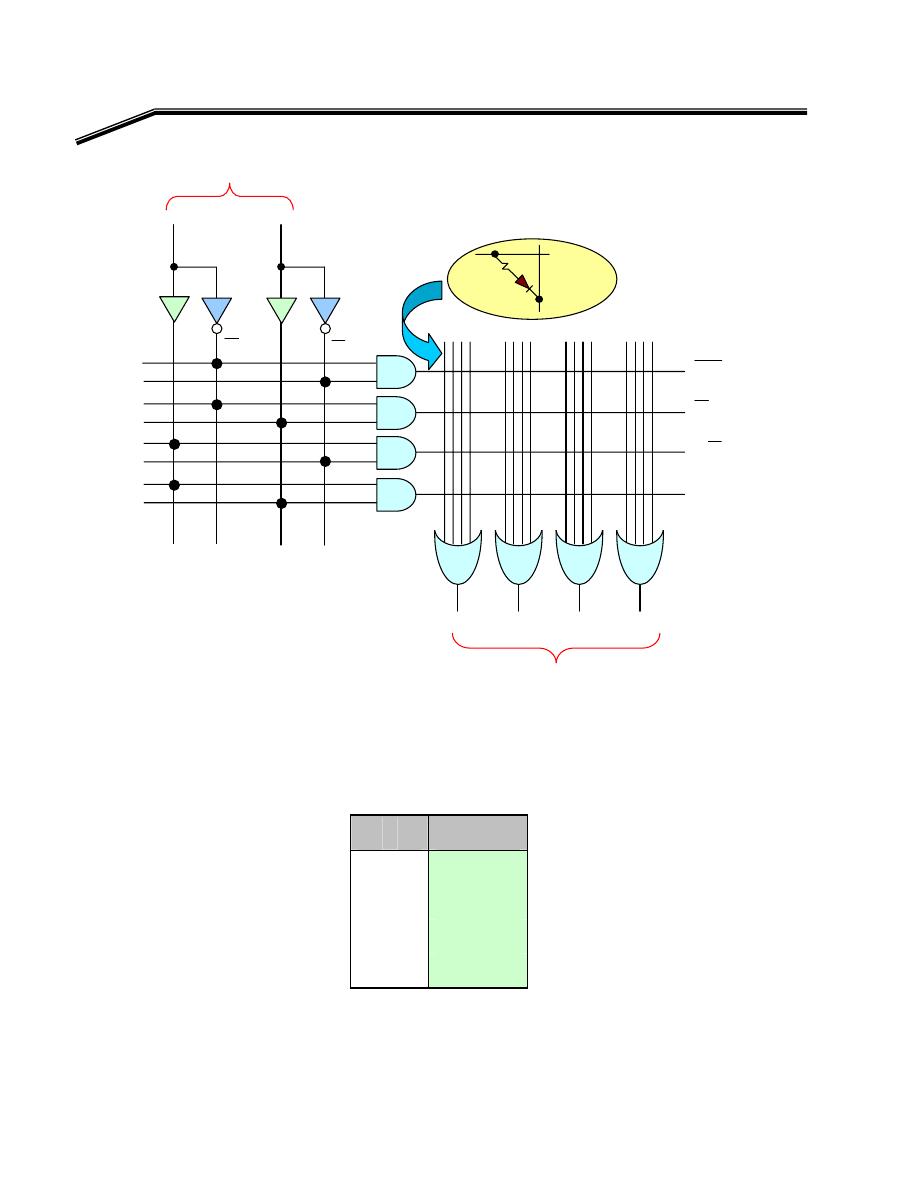
אא
٧٤١
א
א
אא
א
-
٠٥١
-
F
٥
J
١
E
אאא
PLD
K
High Out
B
A
AND ٠
٠
٠
AND ١
١
٠
AND ٢
٠
١
AND ٣
١
١
F
٥
J
١
E
אא
AND
א
F
٥
J
١
KE
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
Fusible
Link
B
A
B
A
B
A
AB
0
1
2
3
Q
Q
Q
Q
A
B
A
A
B
B
٠
١
٢
٣
Inputs
Outputs
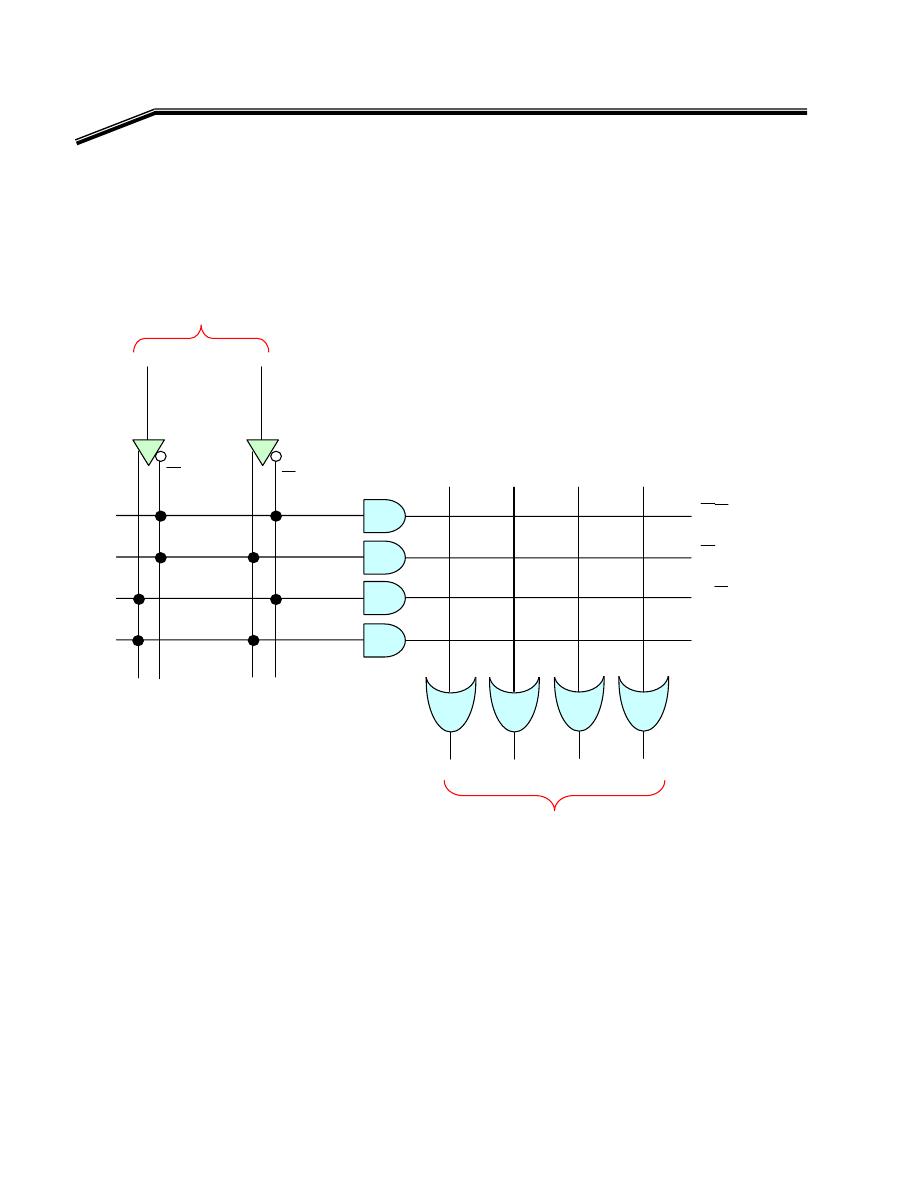
אא
٧٤١
א
א
אא
א
-
١٥١
-
אא
F
٥
J
١
E
אאא،
א
K
א
J
PLDs
אאאא
אאא
K
F
٥
J
٢
E
אא
F
٥
J
١
E
אא
א
K
אאאאאאא،אאא
א
אאאאא،
K
א
א
AND
א،אאא
אא
K
אאא
OR
אא
)
×’s
(
א
)
fusible link
(
K
F
٥
J
٢
E
אא
PLD
K
×
×
×
×
×
×
×
×
×
×
×
×
×
×
B
A
B
A
B
A
AB
0
1
2
3
Q
Q
Q
Q
A
B
A
A
B
B
٠
١
٢
٣
Inputs
Outputs
I
٣
×
×
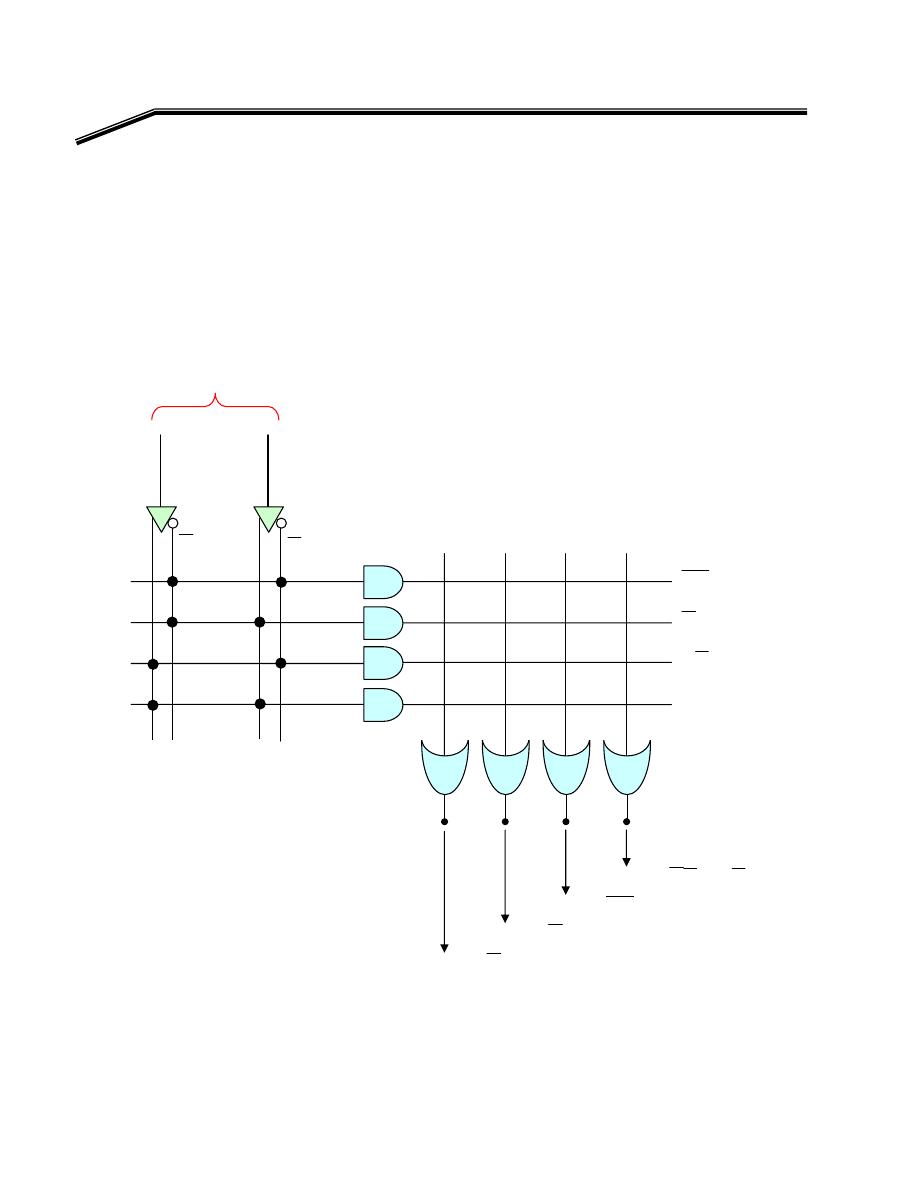
אא
٧٤١
א
א
אא
א
-
٢٥١
-
אא
OR, AND
אאא،
×’s
א
K
אאאא
PLD
א
א
K
F
٥
J
٣
E
א
B
A,
)
Q
٠
,Q
١
,Q
٢
,Q
٣
(
א
PLD
א،
F
٥
J
٢
KE
×
×
×
×
×
×
B
A
B
A
B
A
AB
A
B
A
A
B
B
٠
١
٢
٣
Inputs
F
٥
J
٣
E
אא
PLD
K
١
٠
٢
٣
B
A
B
A
Q
0
+
=
B
A
Q
1
=
AB
B
A
Q
2
+
=
B
A
Q
3
=
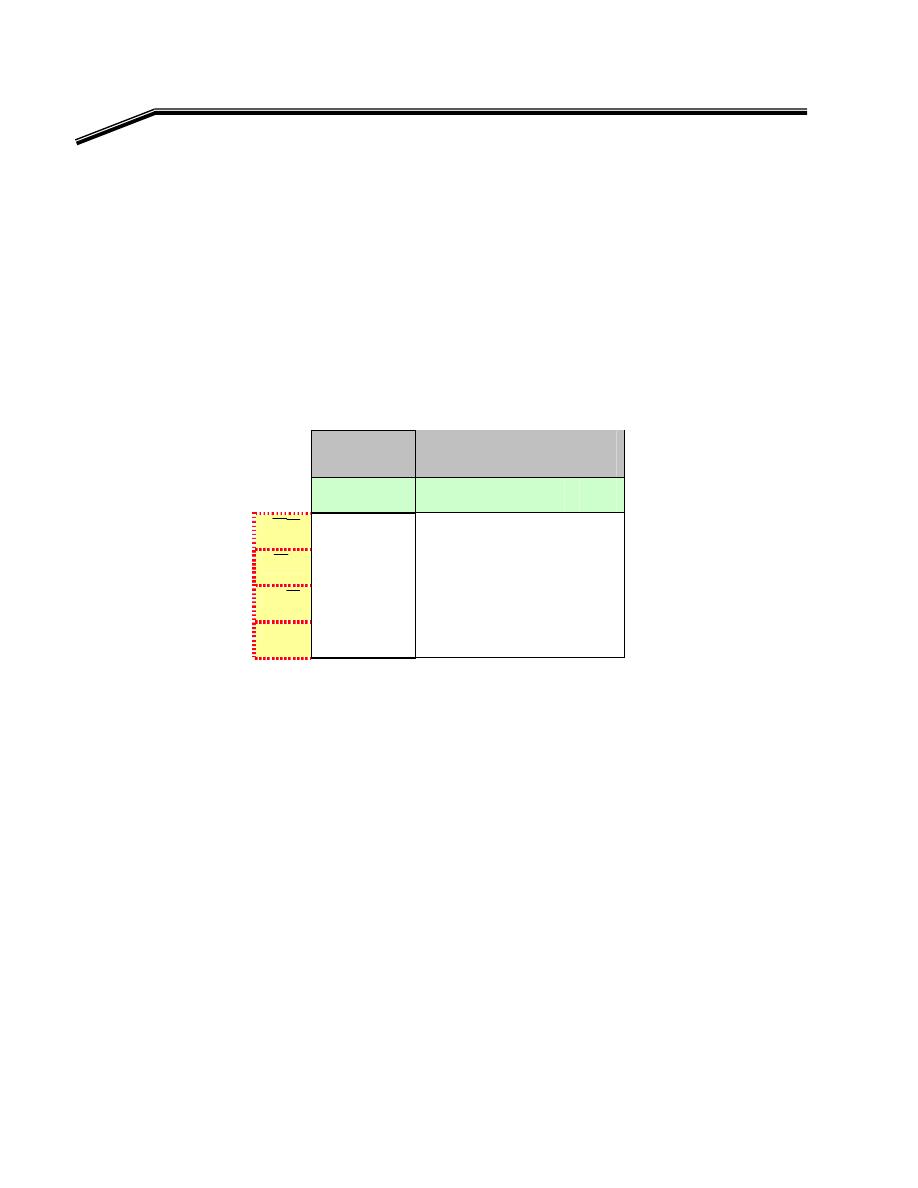
אא
٧٤١
א
א
אא
א
-
٣٥١
-
אא
)
blowing fuses
(
١،٣،٤
א
OR
٣
،
א
Q
٣
High
AB =
١٠
K
אא
١،٣
א
OR
٢
،
א
Q
٢
High
AB =
١٠
AB =
١١
K
אא
٢،٣،٤
א
OR
١
،
א
Q
١
High
AB =
٠٠
K
א
אא
٢،٤
א
٠
،
א
Q
٠
High
AB =
٠٠
AB =
٠١
K
א
א
Q
٠
Q
١
Q
٢
Q
٣
B
A
١
١
٠
٠
٠
٠
B
A
٠
٠
١
١
١
٠
B
A
١
٠
٠
٠
٠
١
B
A
٠
٠
١
٠
١
١
AB
F
٥
J
٢
E
אאא
F
٥
J
٣
KE
א
PLD
אאא
)
Programmable Output Polarity fuse
(
א
XOR
F
٥
J
٤
E
אאאא،
א
)
Intact
(
)
blown
(
K
،אא
אאא
XOR
Low
א
אא
K
،אא
אאא
XOR
High
אאא
K
אא
F
٥
J
٣
KE
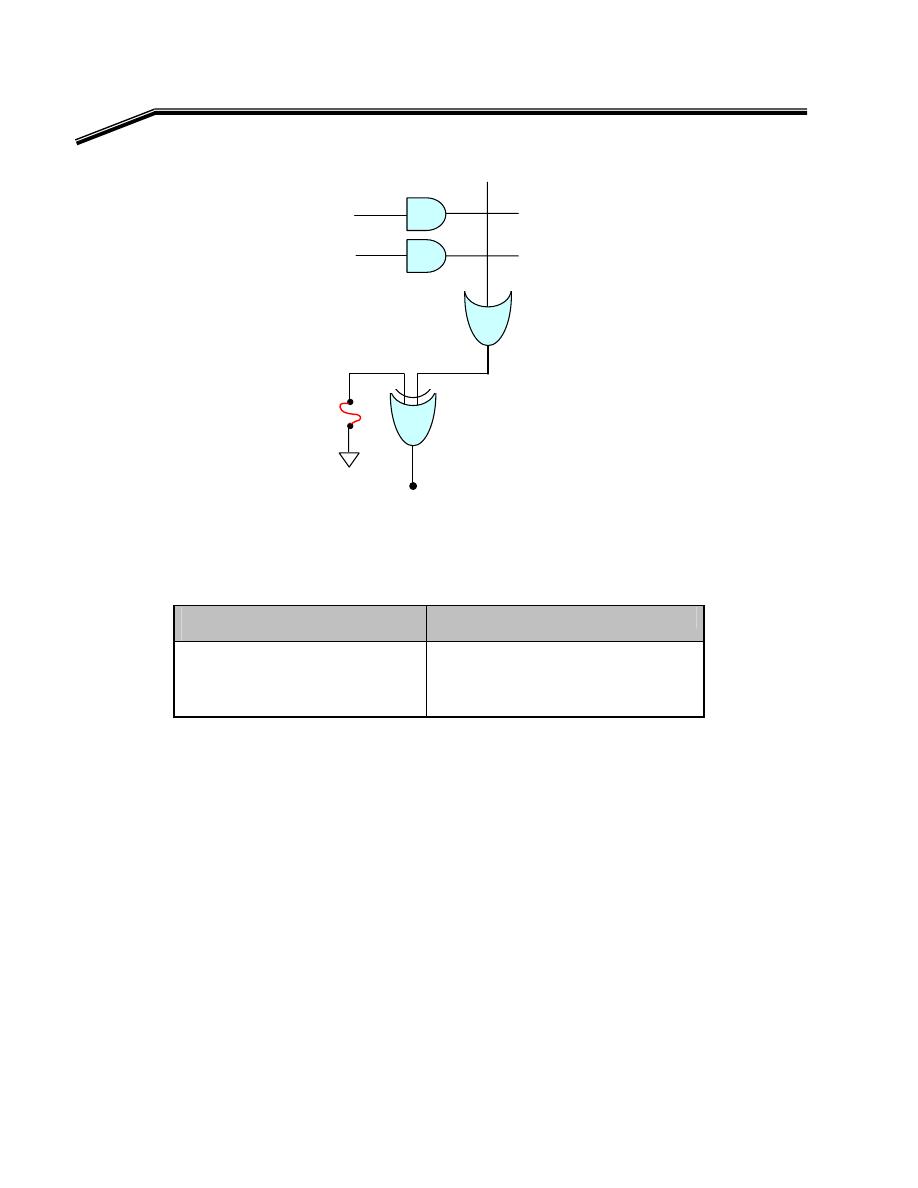
אא
٧٤١
א
א
אא
א
-
٤٥١
-
XOR's Operation
Polarity Fuse
F
א
E
Will not invert
F
א
E
Intact
F
א
E
Will invert
F
א
E
Blown
F
א
E
F
٥
J
٣
E
אאא
K
٥
J
٣
אאא
The Programmable Logic Array (PLA)
א
،אאא
PLD
)
٨-bit inputs
(
)
٢-bit outputs
(
)
٢١
(
אא
(
)٦٥٢
K
א،א
א
)
PLA
(
K
אאא
PLA
א
F
٥
J
٥
E
אא
PLA
AND
OR
אאאאאא
K
×
×
F
٥
J
٤
E
אא
PLD
K
Output
Polarity
Fuse
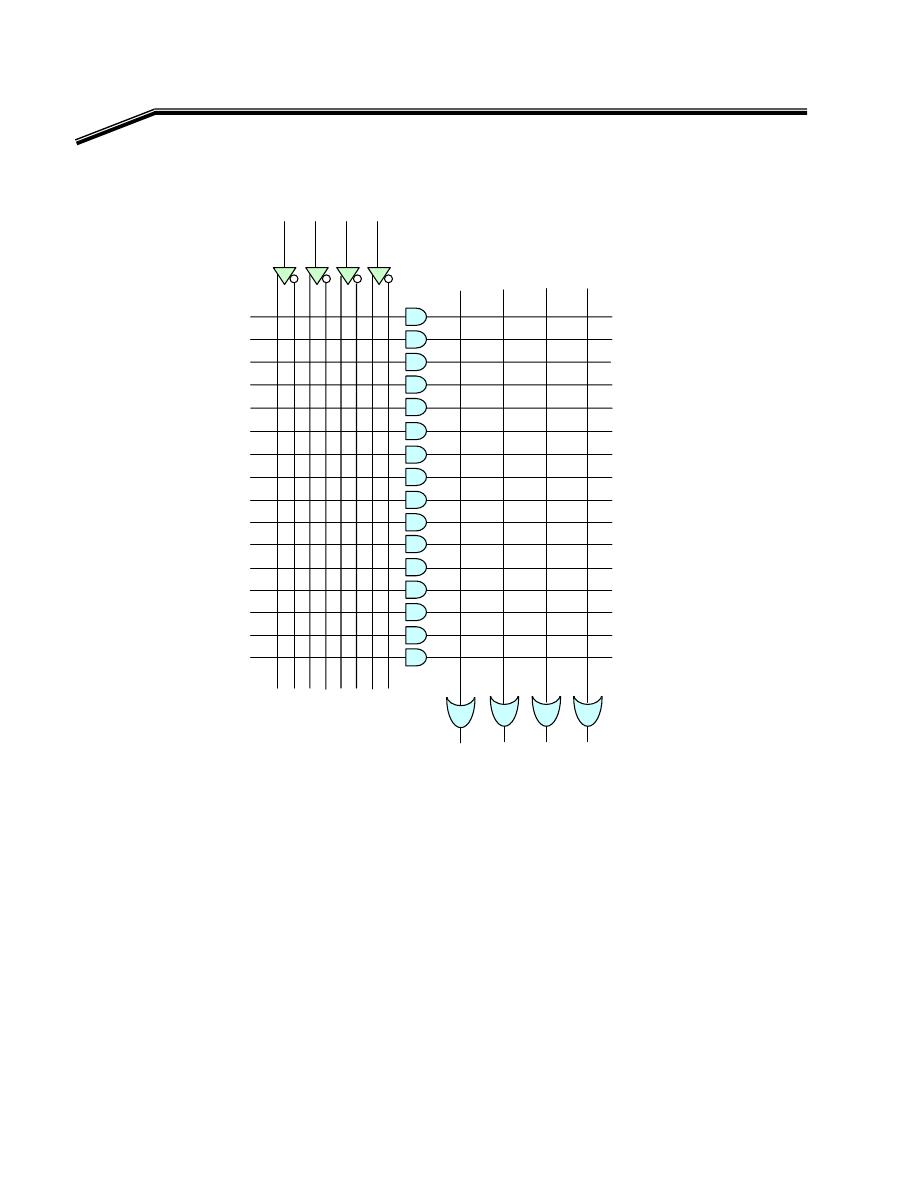
אא
٧٤١
א
א
אא
א
-
٥٥١
-
٥
J
٤
אא
The Programmable Array Logic (PAL)
אאא
F
PLA
E
AND
OR
אא
K
אא
PLA
אא،،אאאא
K
אאאאאאא
K
א
PAL
،
AND
OR
F
א
E
F
٥
J
٦
KE
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
F
٥
J
٥
E
אאא
PLA
K
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
I
٣
I
٢
I
١
I
٠
O
٣
O
٢
O
١
O
٠
×
×
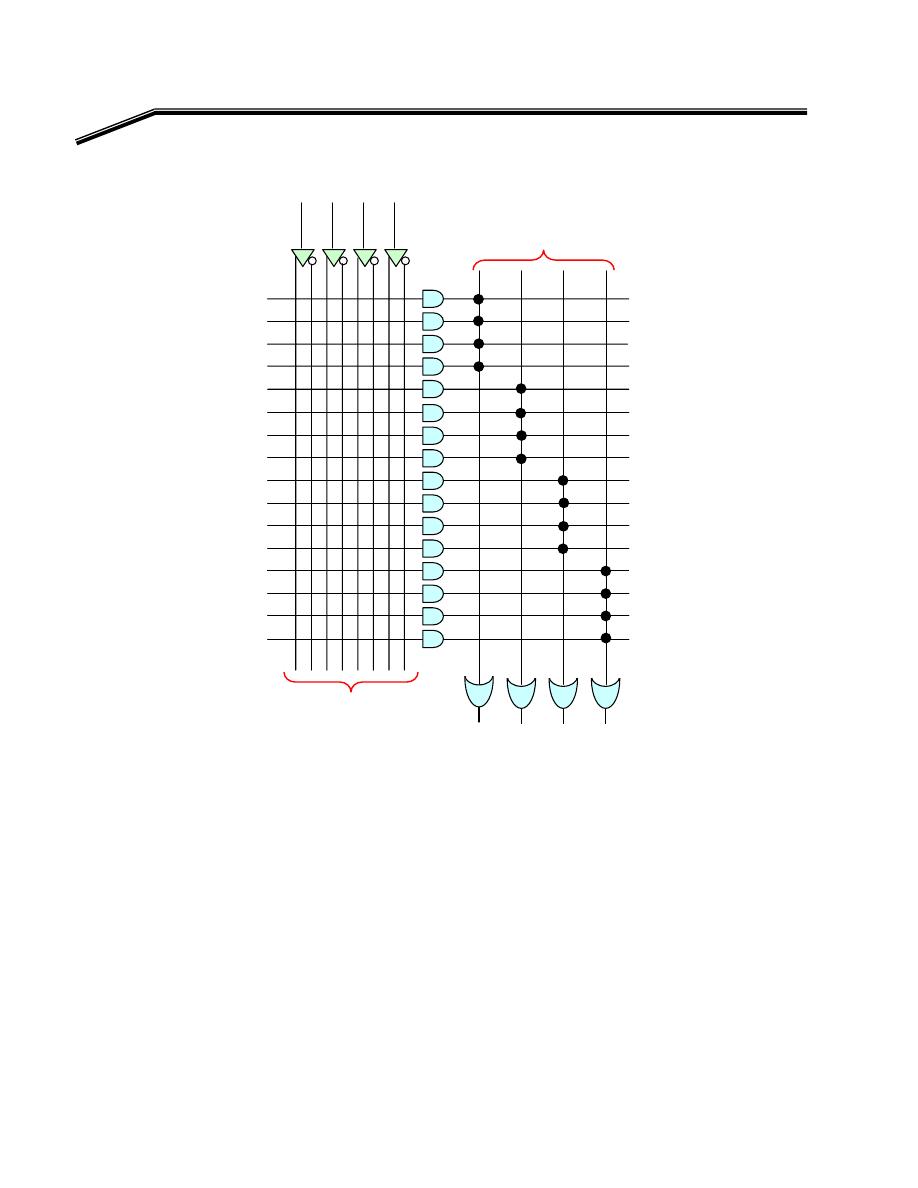
אא
٧٤١
א
א
אא
א
-
٦٥١
-
א
PLA
א
א
אאאא
،א
K
F
٥
J
٦
E
אאא
PAL
K
OR
AND
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
O
٣
O
٢
O
١
O
٠
I
٣
I
٢
I
١
I
٠
אא
٧٤١
א
א
אא
א
-
٧٥١
-
٥
J
٥
אאא
The Programmable Logic Sequencer (PLS)
אאא
)
PLS
(
אאא
א
K
א،אא
)
Input and output registers
(
אאאאא،
K
٥
J
٦
אאא
Erasable Programmable Logic Device (EPLD)
אאא
)
PLDs
(
א
אאאא
)
blowing their internal fuses
(
K
،א
،א
א
א
PLD
אא
אא
K
א
אאאאאאא
K
א
)
erase
(
אאאאא
א
،אא
K
×

אא
٧٤١
א
א
אא
א
-
٨٥١
-
١
E
אא
PLD
א
A, B
Q
٠
,Q
١
,Q
٢
,Q
٣
א
K
א
א
Q
٠
Q
١
Q
٢
Q
٣
B
A
١
١
١
٠
٠
٠
٠
٠
١
١
١
٠
١
٠
١
٠
٠
١
٠
٠
٠
١
١
١
٢
E
אאאאא
Q
٠
,Q
٣
אא
א
K
٣
E
אאאאאאא
PLA
K
א
٧٤١
א
א
א
א
א
א
אא
W
אא
אאא
١
J
١
٢
١
J
٢
אאא
٣
١
J
٣
אאא
٤
١
J
٤
אאאאא
٦
١
J
٤
J
١
אאאאאא
٦
١
J
٤
J
٢
א
אאאא
٧
١
J
٥
אאאאא
٩
١
J
٦
אאאא
٠١
١
J
٦
J
١
אא
٠١
١
J
٦
J
٢
אא
٠١
١
J
٧
אאאאא
١١
١
J
٨
אא
אא
٢١
١
J
٨
J
١
אא
٣١
١
J
٨
J
٢
אא
٣١
١
J
٨
J
٣
אא
٤١
١
J
٩
אאאאאא
٤١
١
J
٠١
אאא
٥١
١
J
٠١
J
١
אאאא
٥١
١
J
٠١
J
٢
אאאא
٦١
١
J
٠١
J
٢
J
١
אאאאאא
٦١
א
٧٤١
א
א
א
١
J
٠١
J
٢
J
٢
אאאאא
٦١
١
J
٠١
J
٣
אאאאא
٨١
١
J
٠١
J
٤
אאא
אא
٩١
١
J
٠١
J
٥
אאאאא
٩١
١
J
٠١
J
٦
אאאא
٠٢
١
J
٠١
J
٦
J
١
א
א
٠٢
١
J
٠١
J
٦
J
٢
אאא
٢٢
١
J
١١
אאאא
٣٢
١
J
١١
J
١
א
אאא
٣٢
١
J
١١
J
٢
אאאא
٣٢
١
J
١١
J
٢
J
١
אאאאא
אא
٣٢
١
J
١١
J
٢
J
٢
אאאאאא
٤٢
١
J
١١
J
٣
אאאא
٥٢
١
J
١١
J
٤
אאאאא
٦٢
١
J
١١
J
٥
אאאאא
٧٢
١
J
١١
J
٦
אאאאא
٨٢
١
J
١١
J
٧
אאאאא
٩٢
١
J
١١
J
٨
א
אאאא
٩٢
١
J
١١
J
٨
J
١
אאאא
٩٢
١
J
١١
J
٨
J
٢
אאאא
٠٣
א
٧٤١
א
א
א
١٣
אא
W
אאאא
אאא
٥٣
٢
J
١
٦٣
٢
J
٢
א
א
٦٣
٢
J
٣
א
AND
٧٣
٢
J
٤
א
OR
٠٤
٢
J
٥
א
NOT
F
א
E
٢٤
٢
J
٦
א
NAND
٢٤
٢
J
٧
א
NOR
٤٤
٢
J
٨
א
OR
א
F
א
E
٥٤
٢
J
٩
א
NOR
א
F
א
E
٧٤
٢
J
٠١
אאא
٨٤
٢
J
١١
אאא
٠٥
٢
J
٢١
אאאא
١٥
٢
J
٣١
אא
٢٥
٢
J
٤١
אאא
٤٥
٢
J
٥١
אאא
אאא
٥٥
٨٥
אא
W
אאאאא
אאא
١٦
٣
J
١
٢٦
٢
J
٣
٢٦
٣
J
٣
אאאא
NOR , NAND
٤٦
٣
J
٣
J
١
אא
NAND
٥٦
א
٧٤١
א
א
א
٣
J
٣
J
٢
א
א
NOR
٦٦
٣
J
٤
אאאאא
אא
NAND
،
NOR
٧٦
٣
J
٤
J
١
אאא
NAND
٧٦
٣
J
٤
J
٢
אאא
NOR
٩٦
٣
J
٥
٢٧
٣
J
٦
אאא
٣٧
٣
J
٧
אאאא
١٨
٣
J
٧
J
١
אאא
١٨
٣
J
٧
J
٢
אאא
٢٨
٣
J
٧
J
٣
אאא
٥٨
٣
J
٧
J
٤
אאא
٧٨
٠٩
אאא
W
אאאא
אאא
٢٩
٤
J
١
٣٩
٤
J
٢
א
٣٩
٤
J
٣
א
S-R
אא
٨٩
٤
J
٤
אאא
D
١٠١
٤
J
٥
א
J-K
אא
٣٠١
٤
J
٦
אאא
T
٥٠١
٤
J
٧
א
–
א
٦٠١
٤
J
٨
א
א
٤١١
٤
J
٨
J
١
אא
אאא
٤١١
٤
J
٨
J
٢
אאאאאא
٥١١
א
٧٤١
א
א
א
٤
J
٨
J
٣
אא
٥٥٥
٦١١
٤
J
٨
J
٣
J
١
א
٥٥٥
אאאא
٦١١
٤
J
٨
J
٣
J
٢
אאאאא
א
٩١١
٤
J
٩
אא
١٢١
٤
J
٩
J
١
א
٢٢١
٤
J
٩
J
٢
אא
٤٢١
٤
J
٩
J
٢
J
١
אאאא
–
אא
٥٢١
٤
J
٩
J
٢
J
٢
אאא
–
אא
٧٢١
٤
J
٩
J
٢
J
٣
אאא
–
אא
٨٢١
٤
J
٩
J
٢
J
٤
אאא
F
א
E
٩٢١
٤
J
٩
J
٢
J
٥
א
١٣١
٤
J
٠١
אאא
٣٣١
٤
J
٠١
J
١
אאאאאאא
٣٣١
٤
J
٠١
J
٢
אאאאאאא
٧٣١
٤
J
٠١
J
٣
אא
אאא
L
אאא
٠٤١
٤
J
٠١
J
٤
אאאאאא
١٤١
٤
J
٠١
J
٥
אאאאאאא
٣٤١
٤
J
٠١
J
٦
אאאאאא
٤٤١
٦٤١
אא
W
אא
א
אא
٨٤١
٥
J
١
٩٤١
٥
J
٢
אאא
٩٤١
٥
J
٣
אאא
٤٥١
٥
J
٤
אא
٥٥١
א
٧٤١
א
א
א
٥
J
٥
אאא
٧٥١
٥
J
٦
אא
א
٧٥١
٨٥١

אאאאאא
אא
F
א
E
א
GOTEVOT appreciates the financial support provided by BAE SYSTEMS
