
ENGINEERING
ELECTROMAGNETICS
ENGINEERING
ELECTROMAGNETICS
Dr. Kaydar M. Quboa
Asst. Prof.
Dept. of Electrical Engineering
College of Engineering
University of Mosul
2015-2016
Dr. Kaydar M. Quboa
Asst. Prof.
Dept. of Electrical Engineering
College of Engineering
University of Mosul
2015-2016
1

Text book
Text book
2

1-VECTOR ANALYSIS
1.1 Scalars And Vectors
1-VECTOR ANALYSIS
1.1 Scalars And Vectors
•
The term scalar refers to a quantity whose value may
be represented by a single (positive or negative) real
number. The x, y, and z we use in basic algebra are
scalars. Other scalar quantities are mass, density,
pressure and others.
•
A vector quantity has both a magnitude and a
direction in space. Force, velocity, acceleration, and a
straight line from the positive to the negative
terminal of a storage battery are examples of
vectors.
3
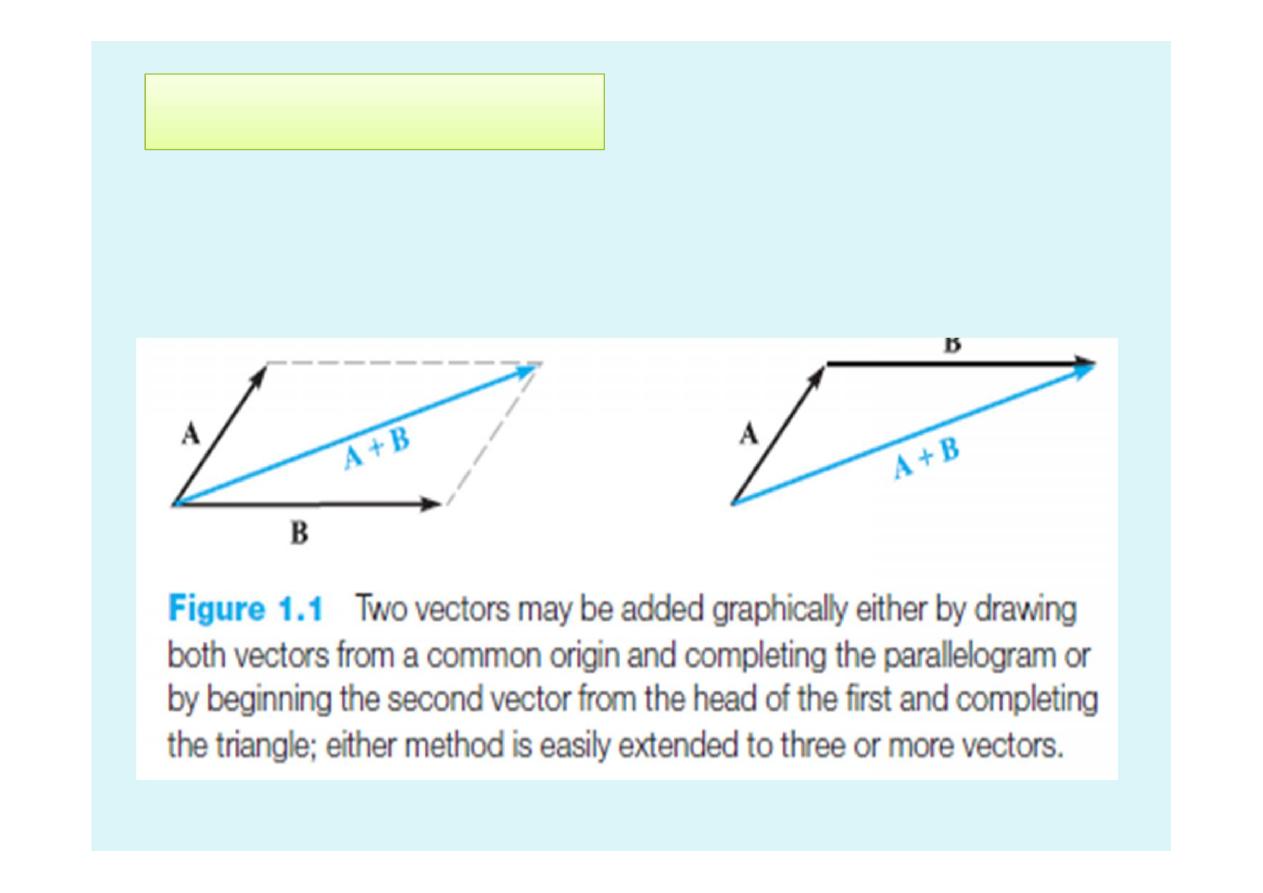
1.2 Vector Algebra
1.2 Vector Algebra
•
The addition of vectors follows the
parallelogram law shown in Figure 1.1 for the
sum of two vectors, A and B.
4
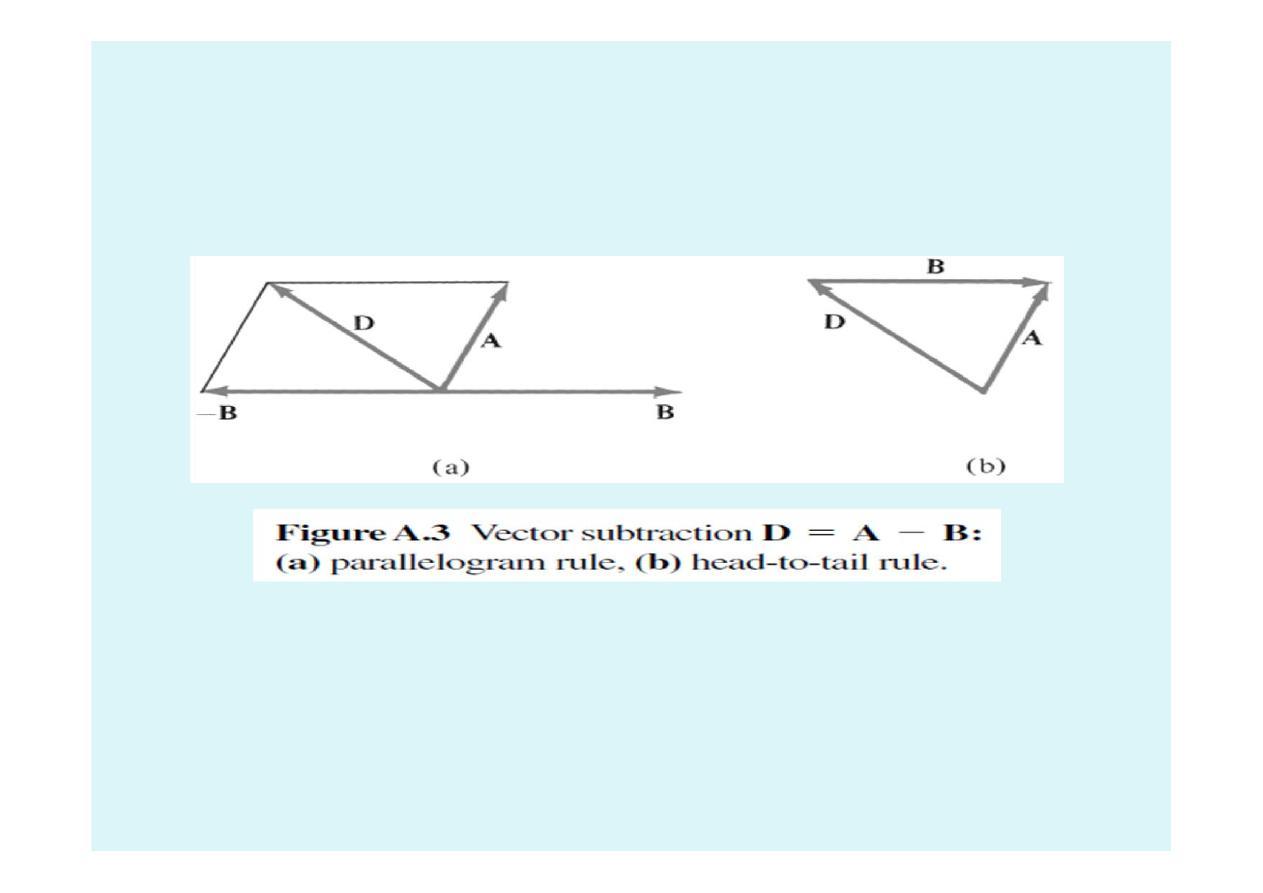
•
The rule for the subtraction of vectors follows from that
for addition, for we may always express A−B as A+(−B);
the sign, or direction, of the second vector is reversed,
and this vector is then added to the first by the rule for
vector addition.
•
Vectors may be multiplied by scalars. The magnitude of
the vector changes, but its direction does not when the
scalar is positive, although it reverses direction when
multiplied by a negative scalar.
•
Division of a vector by a scalar is a multiplication by the
reciprocal ( )ﻣﻘﻠوبof that scalar.
•
The multiplication of a vector by a vector is discussed
in Sections 1.6 and 1.7.
5
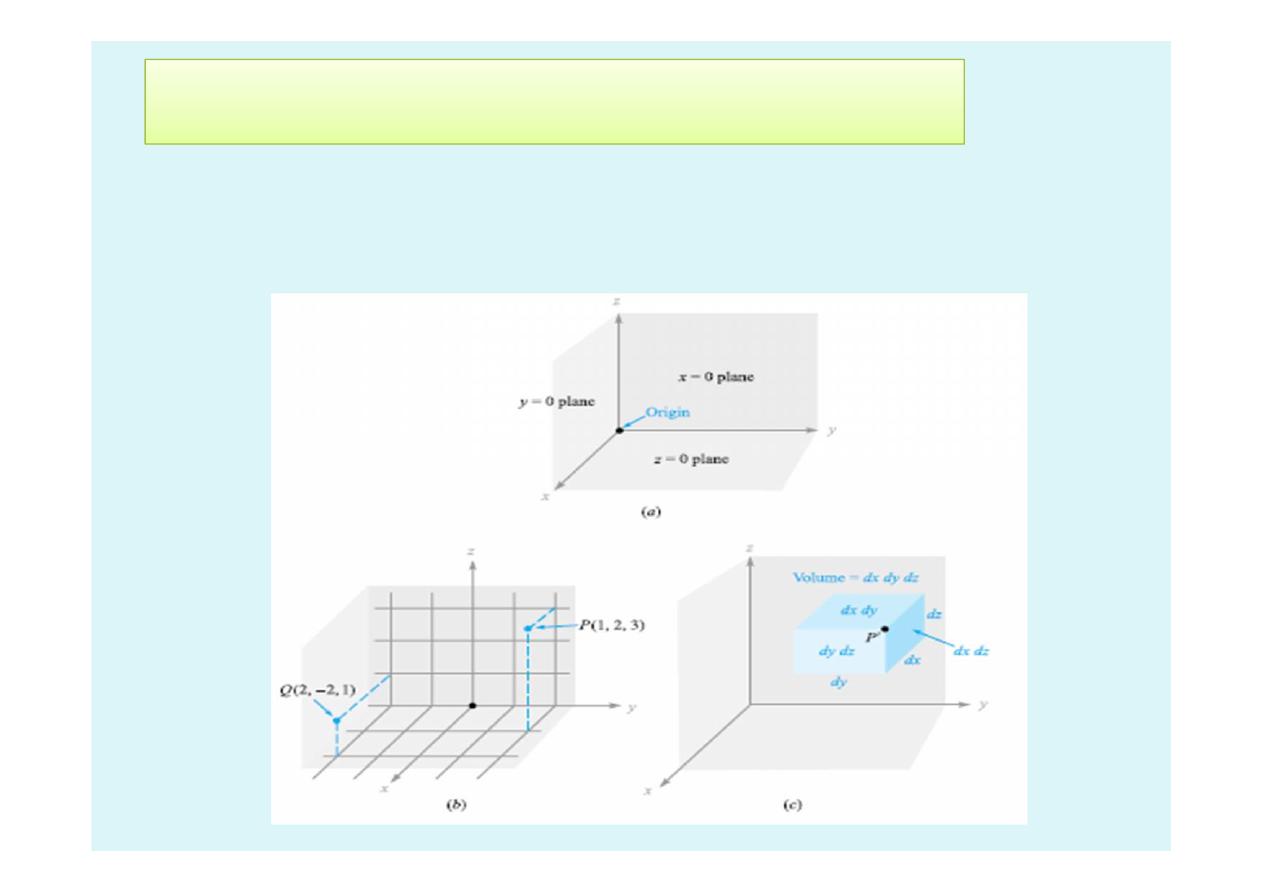
1.3 The Rectangular Coordinate System
1.3 The Rectangular Coordinate System
•
In the rectangular coordinate system we set up three
coordinate axes mutually at right angles to each other
and call them the x, y, and z axes as shown in Figure 1.2.
6
Figure 1.2
1.4 Vector Components And Unit Vectors
1.4 Vector Components And Unit Vectors
•
To describe a vector in the rectangular coordinate
system, let us first consider a vector r extending
outward from the origin. A logical way to identify this
vector is by giving the three component vectors, lying
along the three coordinate axes, whose vector sum must
be the given vector. If the component vectors of the
vector r are x, y, and z, then r = x+y+z. The component
vectors are shown in Figure 1.3a.
7
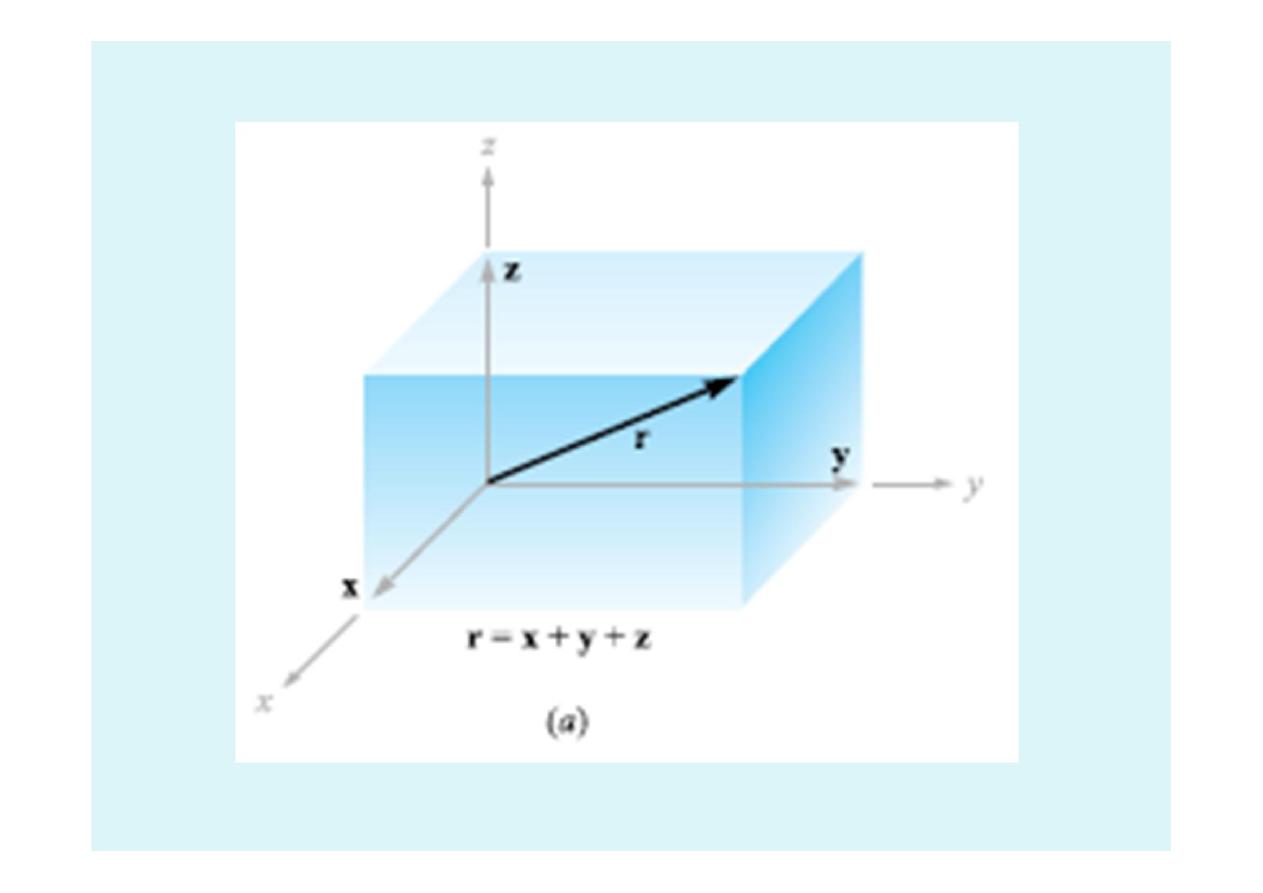
Figure 1.3a
8
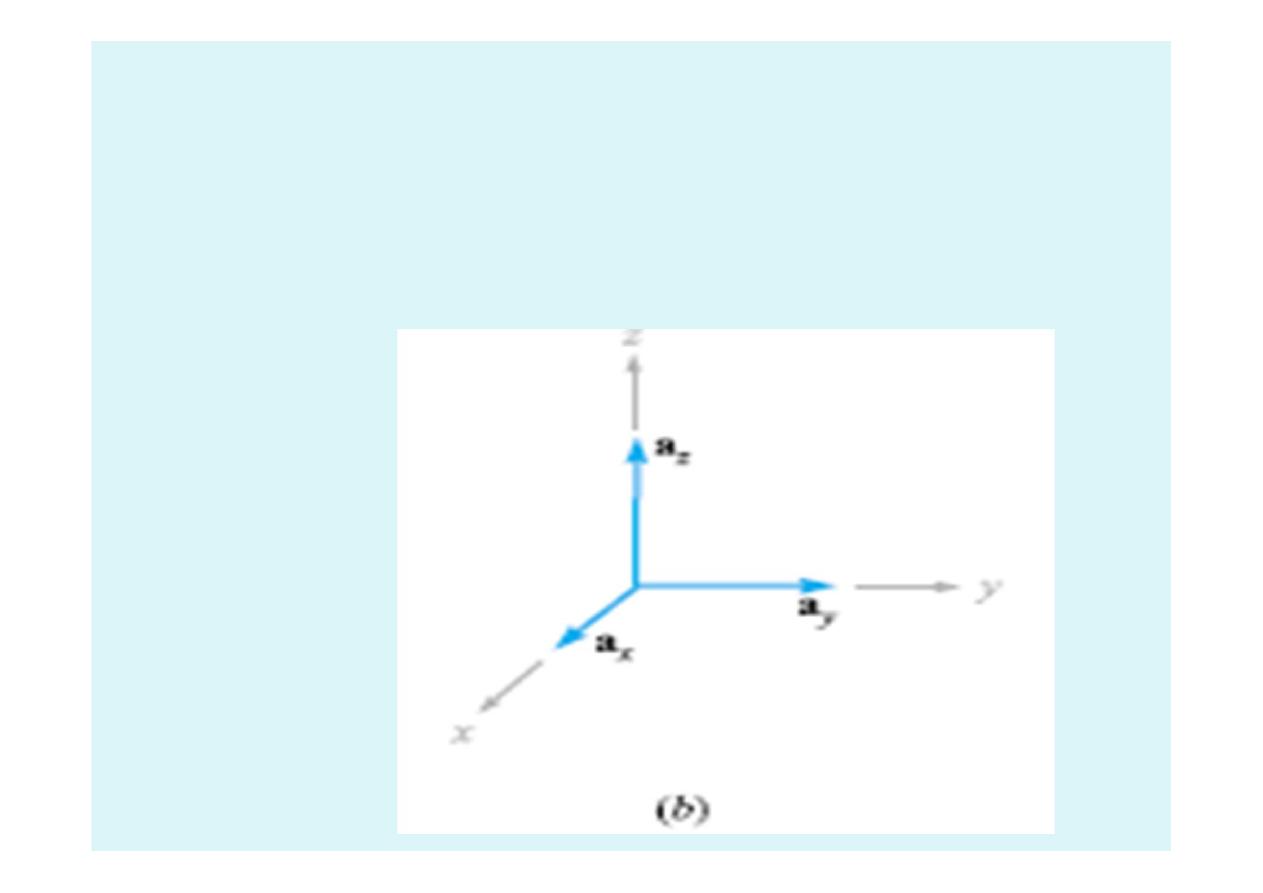
We use the symbol a for a unit vector and identify its
direction by an appropriate subscript. Thus ax , ay ,and az
are the unit vectors in the rectangular coordinate
system.They are directed along the x, y, and z axes,
respectively, as shown in Figure 1.3b.
9
Figure 1.3b
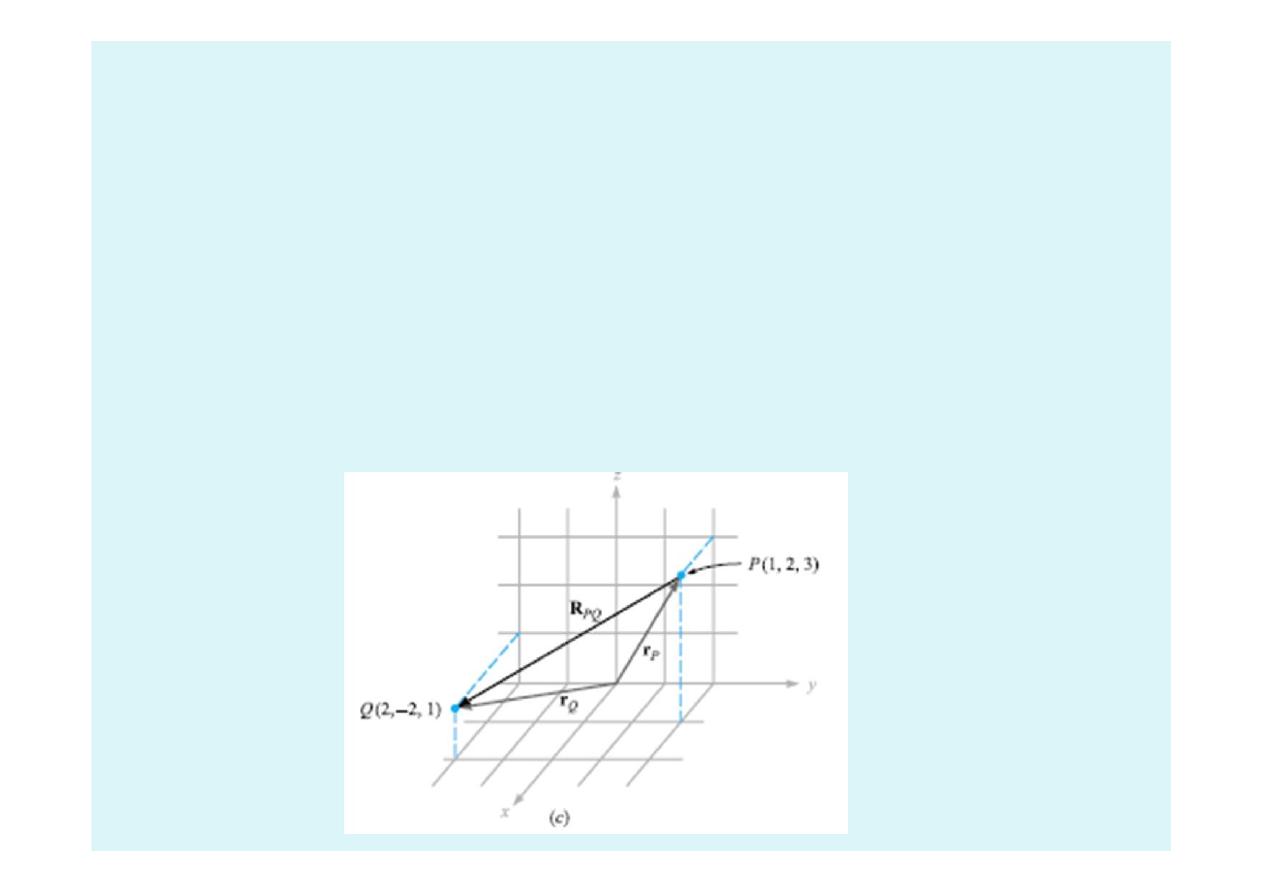
•
A vector rp pointing from the origin to point P(1, 2, 3) is written r
P
=
a
x
+ 2a
y
+ 3a
z
.
•
The vector from P to Q may be obtained by applying the rule of
vector addition. This rule shows that the vector from the origin to P
plus the vector from P to Q is equal to the vector from the origin to
Q. The desired vector from P(1, 2, 3) to Q(2,−2, 1) is:
•
R
PQ
= r
Q
− r
P
= (2 − 1)a
x
+ (−2 − 2)a
y
+ (1 − 3)a
z
= a
x
− 4a
y
− 2a
z
•
The vectors r
P
, r
Q
, and R
PQ
are shown in Figure 1.3c.
10
Figure 1.3c

•
Any vector B then may be described by:
•
B = Bx a
x
+ By a
y
+ Bz a
z
.
•
The magnitude of B written |B| or simply B, is
given by:
•
A unit vector in a given direction is a vector in
that direction divided by its magnitude.
11
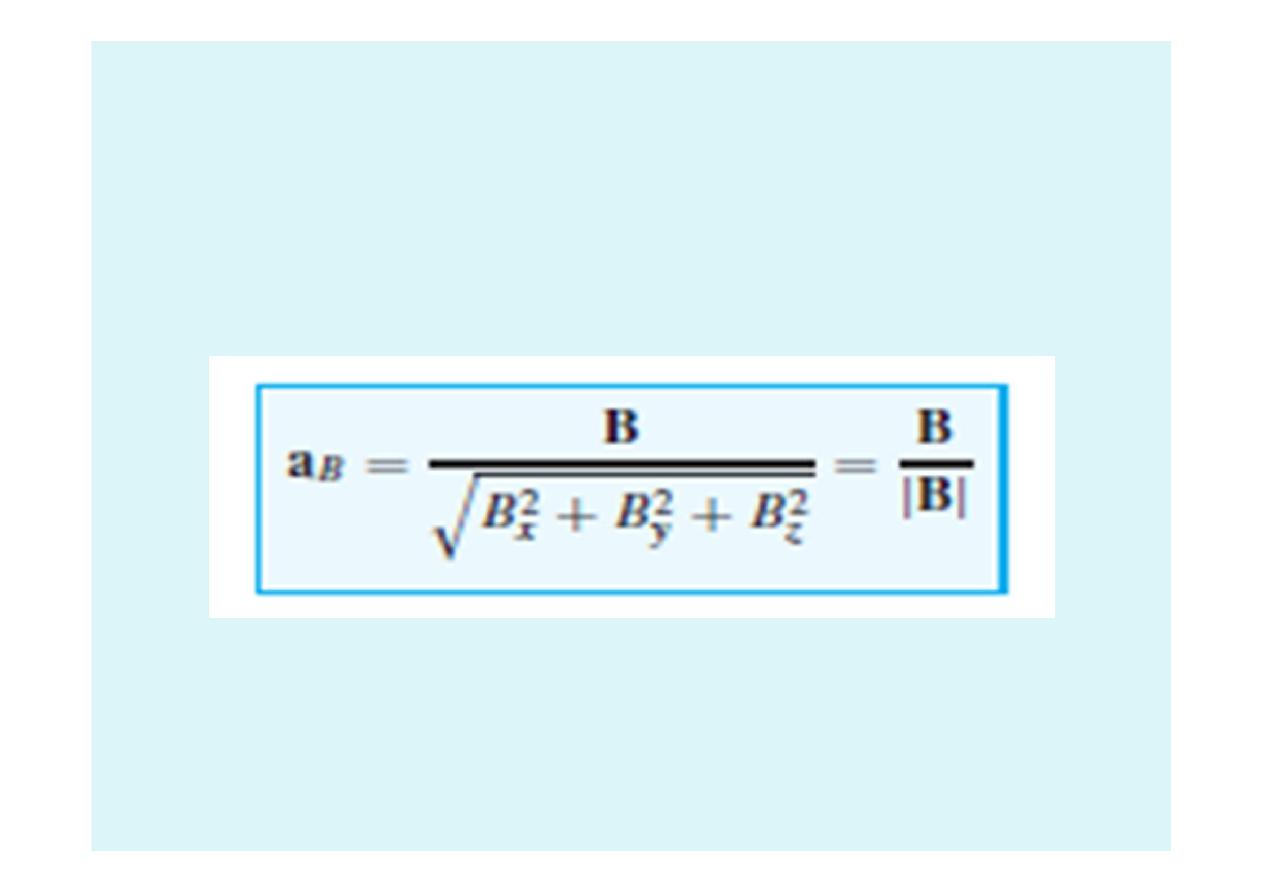
•
A unit vector in the direction of the vector B is:
12

EXAMPLE: Specify the unit vector extending from the
origin toward the point G(2,−2,−1).
13

1.5 Vector Addition And Subtraction
14
1.5 Vector Addition and Subtraction
1.5 Vector Addition and Subtraction

15
16

17
1.6 VECTOR MULTIPLICATION
1.6 VECTOR MULTIPLICATION
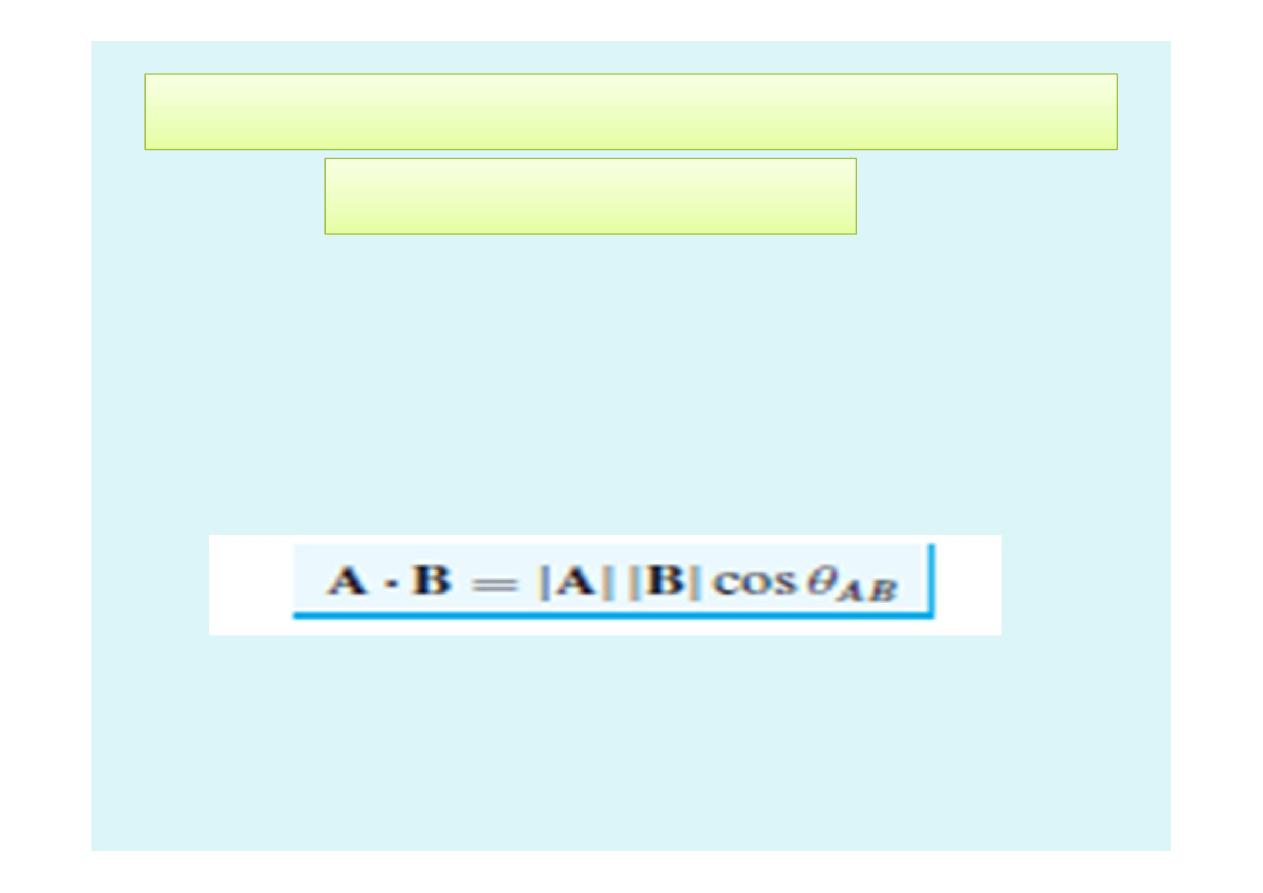
•
Given two vectors A and B, the dot product, or
scalar product, is defined as:
18
The Dot Product
The Dot Product
•
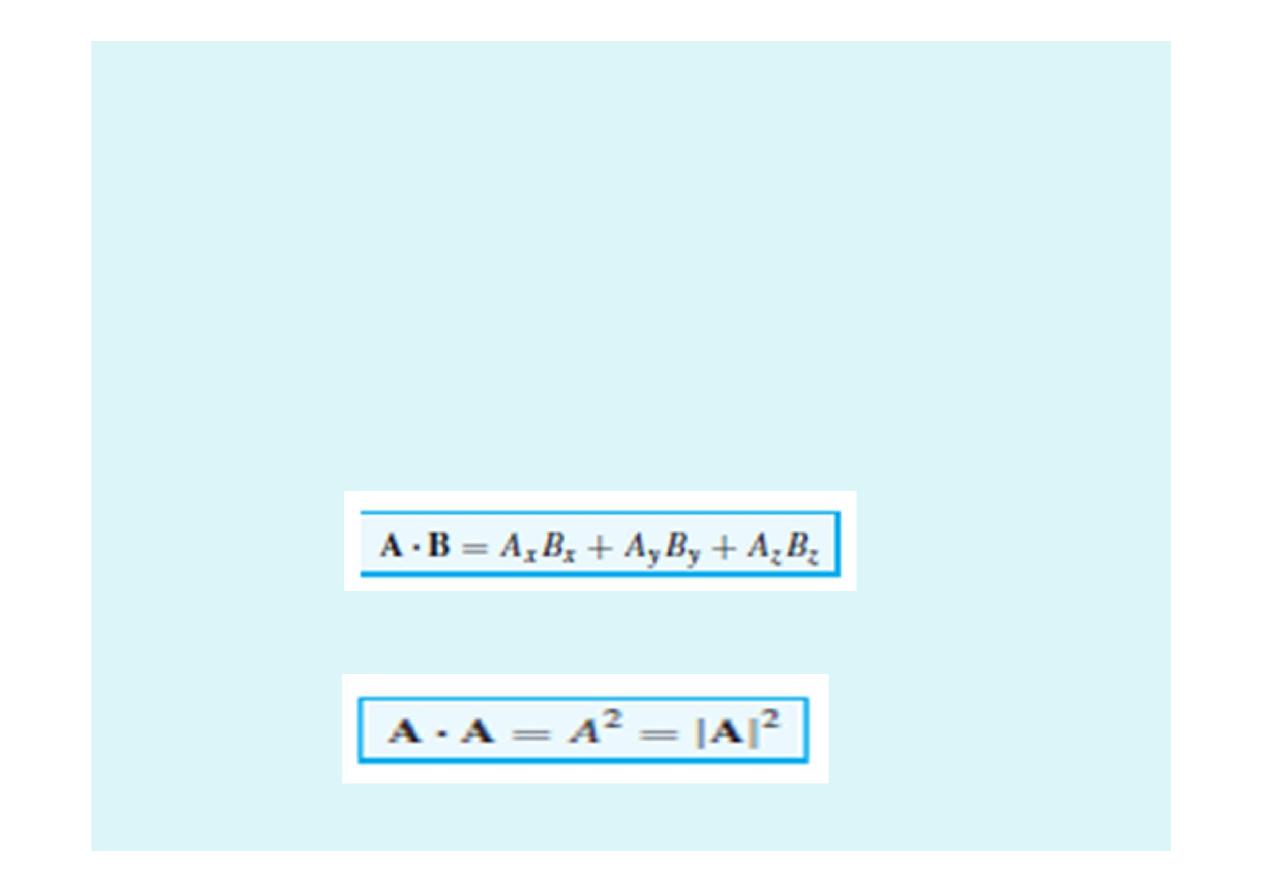
Let A = Axax + Ayay + Azaz and B = Bxax + Byay + Bzaz.
Because the angle between two different unit vectors of the
rectangular coordinate system is 90◦, we then have
ax · ay = ay · ax = ax · az = az · ax = ay · az = az · ay = 0
The remaining three terms involve the dot product of a unit
vector with itself, which is unity, giving finally:
A vector dotted with itself yields the magnitude squared, or
19

The Cross Product
The Cross Product
•
The cross product A × B is a vector.
•
The magnitude of A × B is equal to the product
of the magnitudes of A, B, and the sine of the
smaller angle between A and B;
•
The direction of A×B is perpendicular to the
plane containing A and B and is along one of the
two possible perpendiculars which is in the
direction of advance of a right-handed screw as
A is turned into B. This direction is illustrated in
Figure 1.5.
20
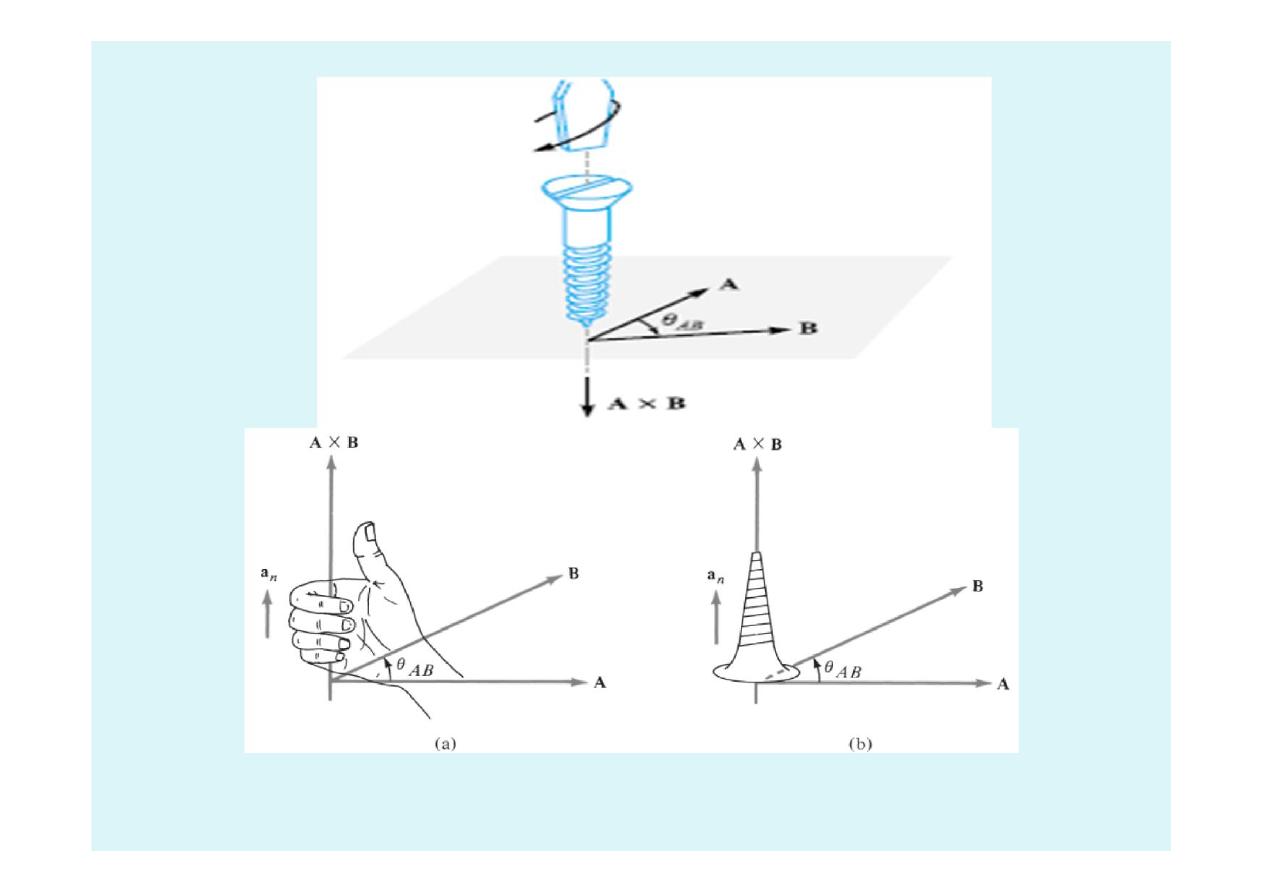
Figure 1.5
21
•
As an equation we can write:
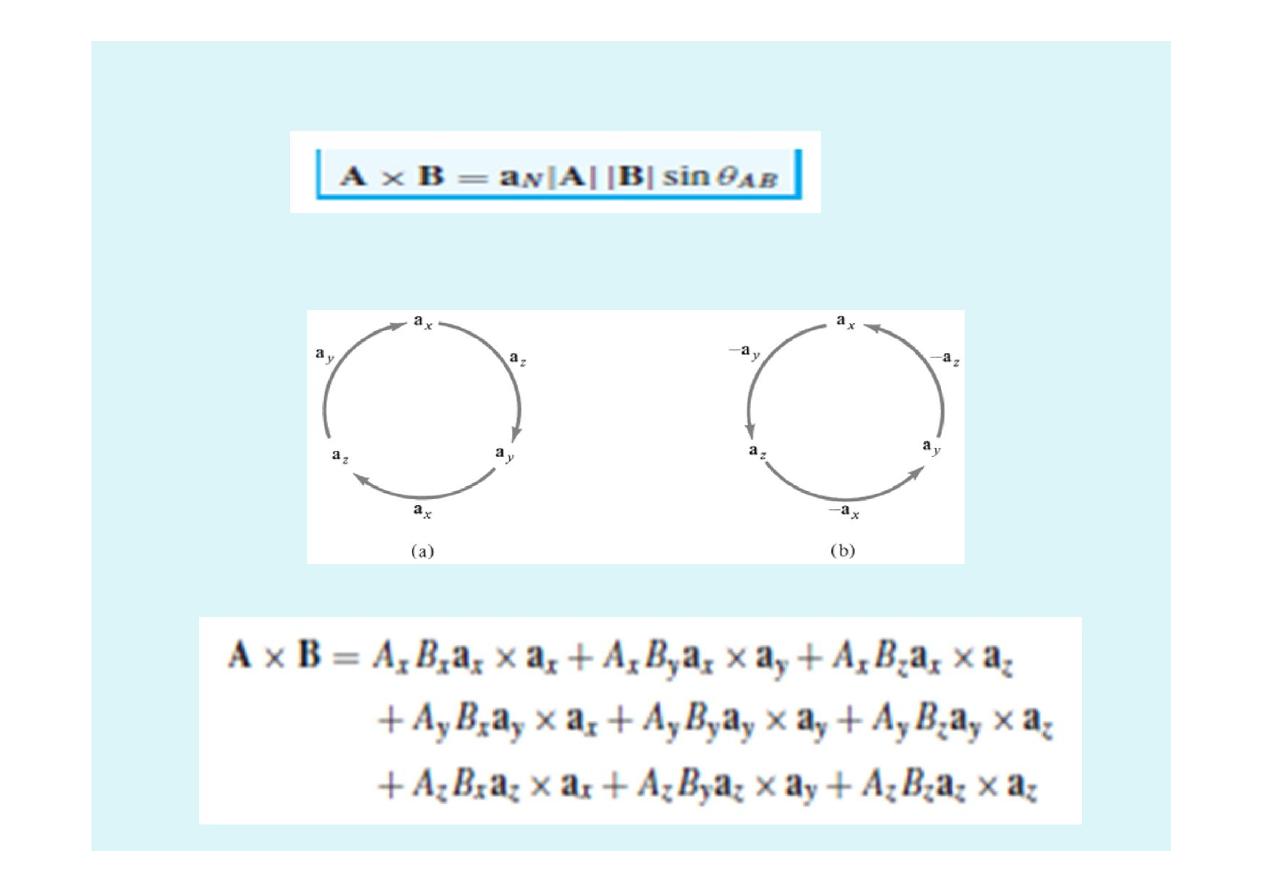
Note: ax×ay=az; ay×az=ax and az×ax=ay
then:
22

•
then,
•
or written as:
23

•
Example: if A = 2ax − 3ay + az and B = −4ax −
2ay + 5az, find A X B.
Solution:
24
25
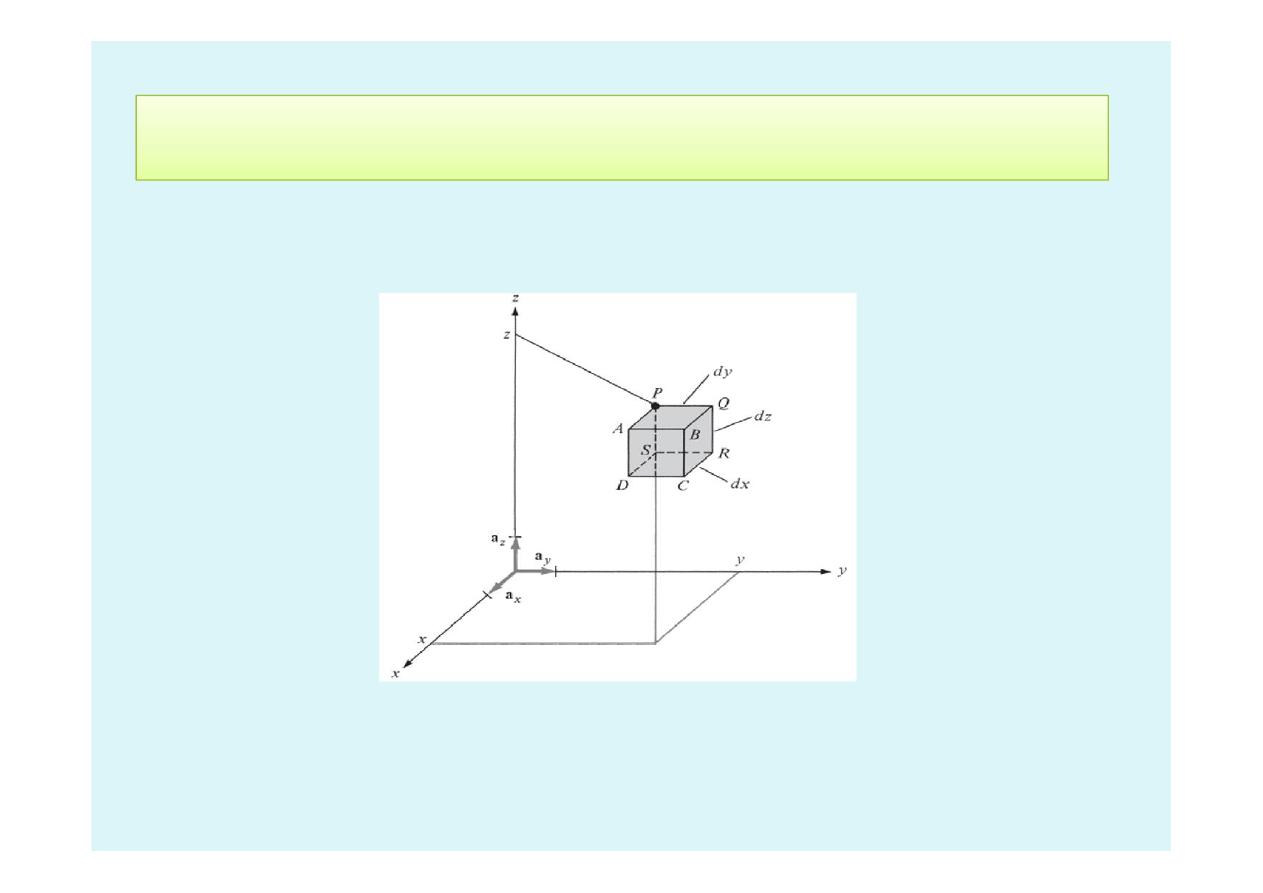
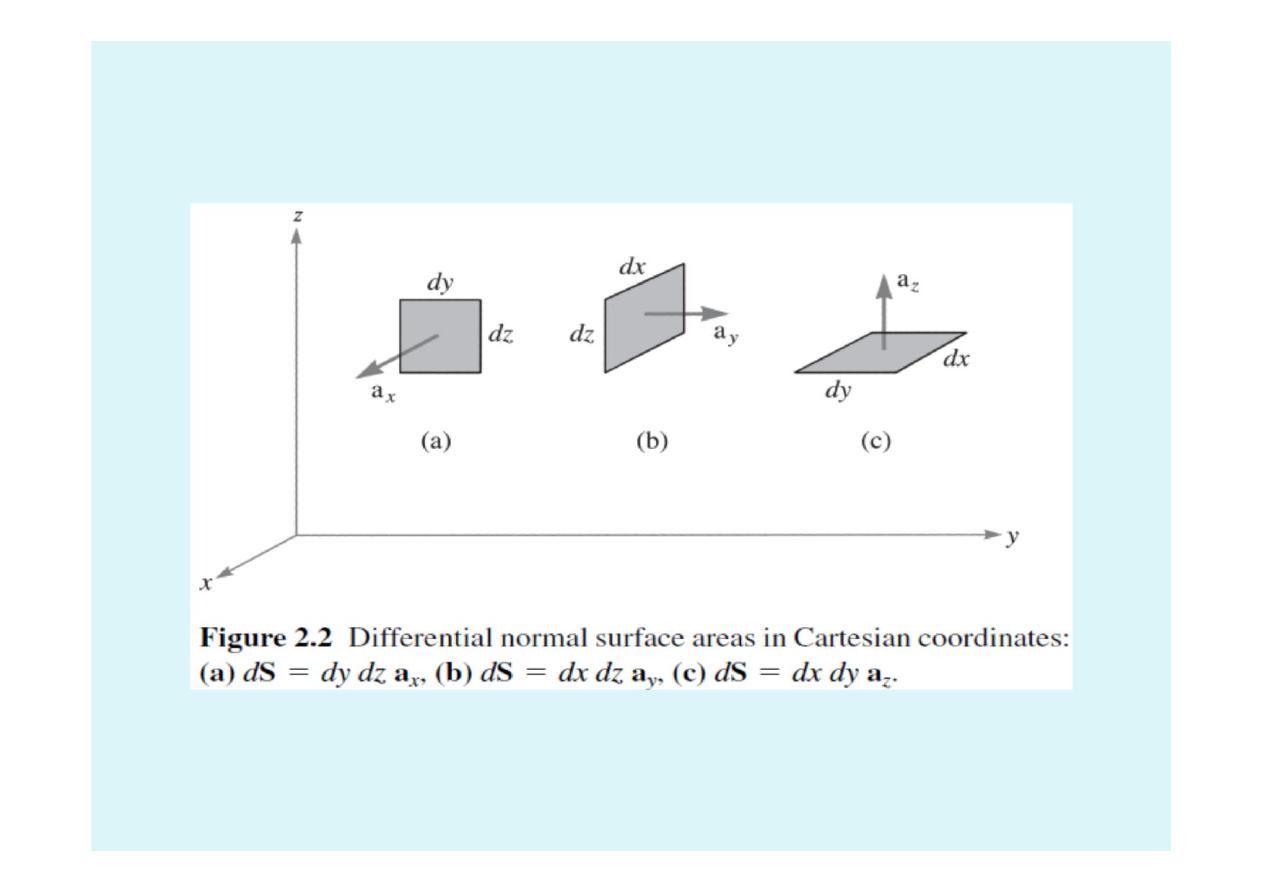
1.7 Review of Rectangular Coordinate System
1.7 Review of Rectangular Coordinate System
26
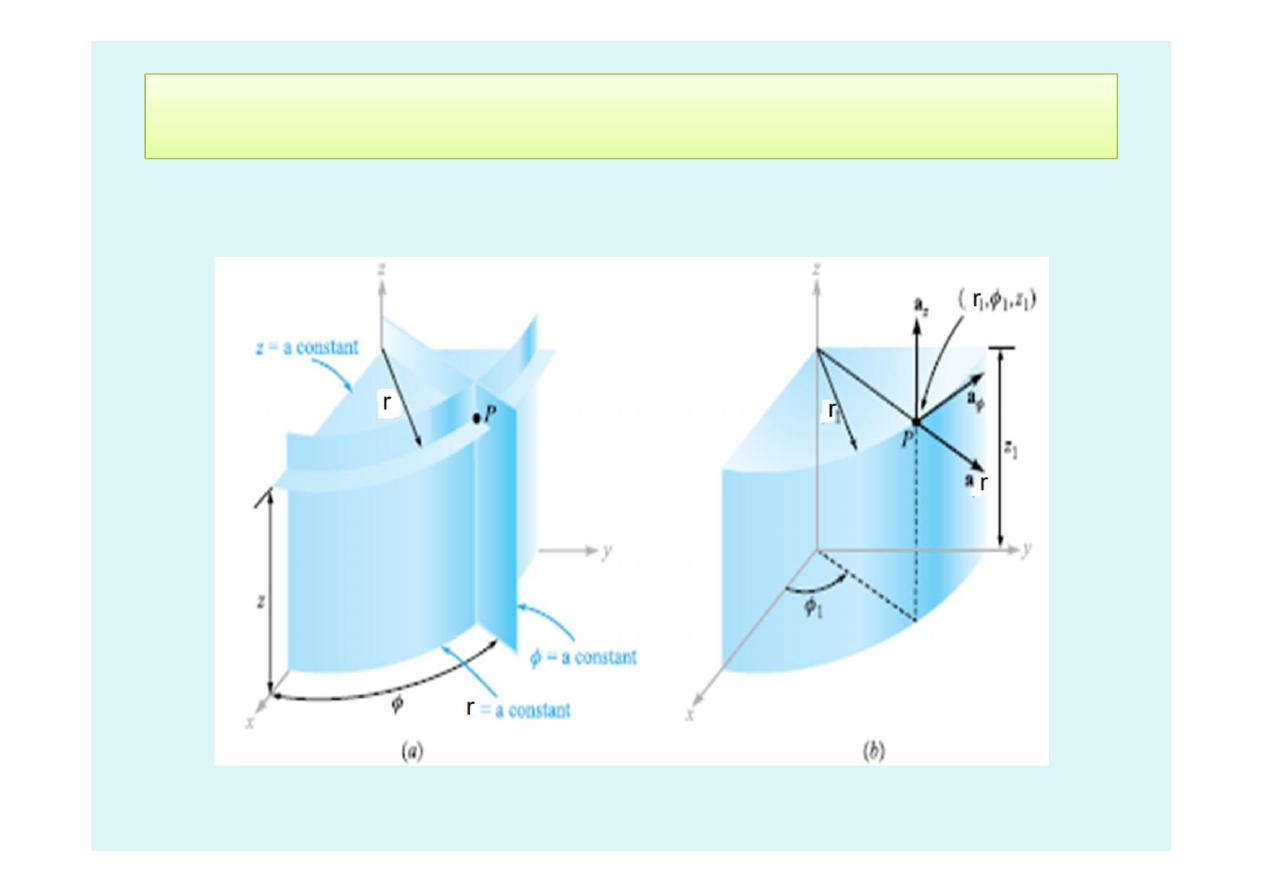
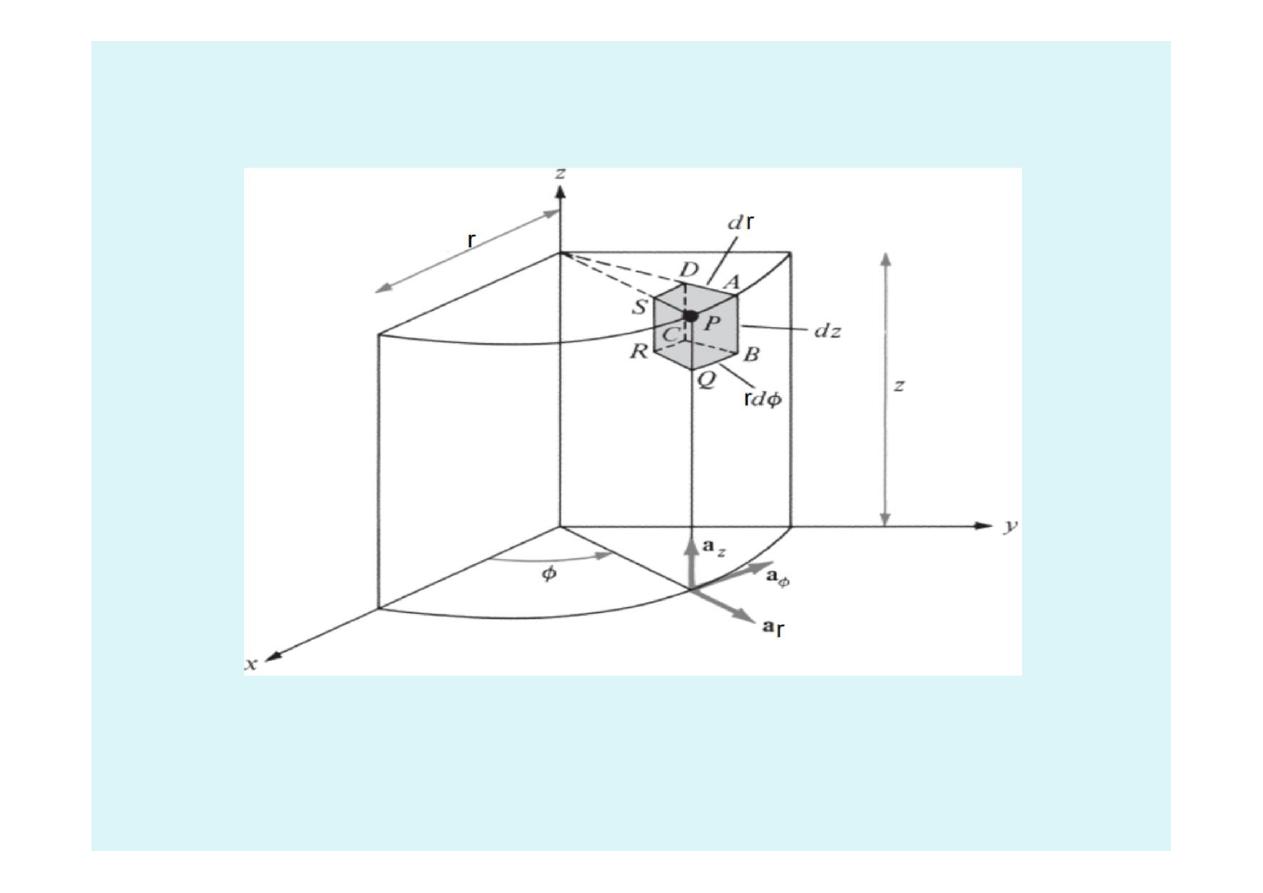
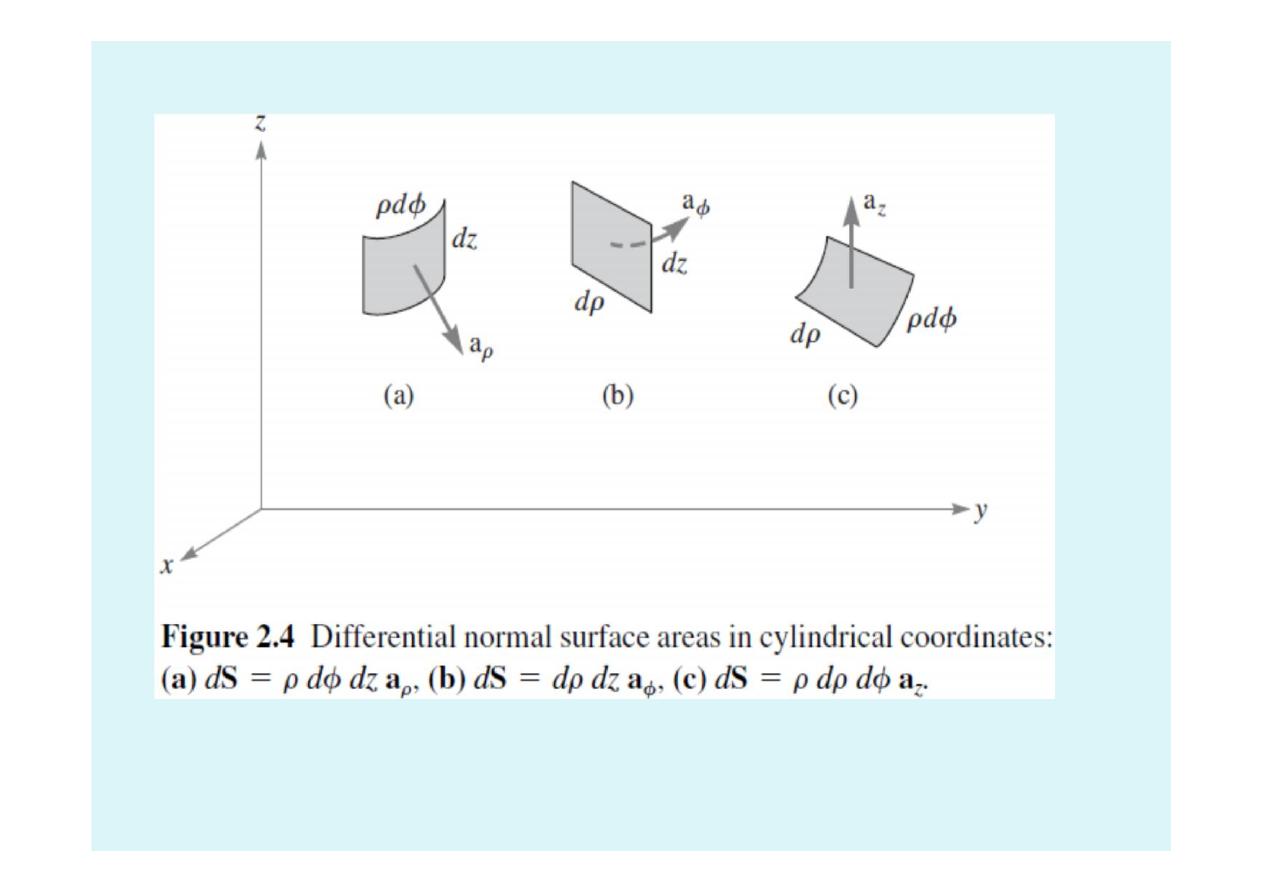
1.8 Cylindrical Coordinate System
1.8 Cylindrical Coordinate System
27
28
29
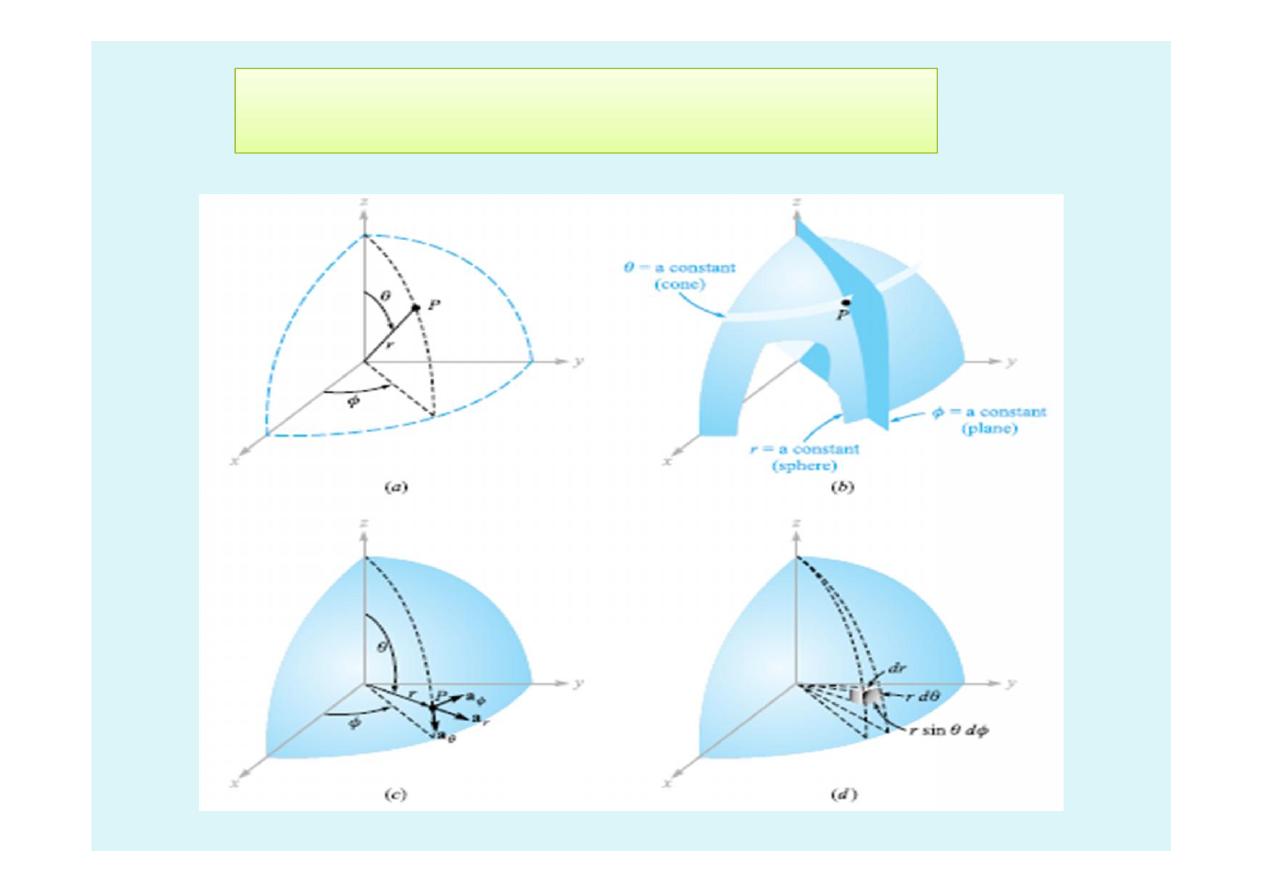
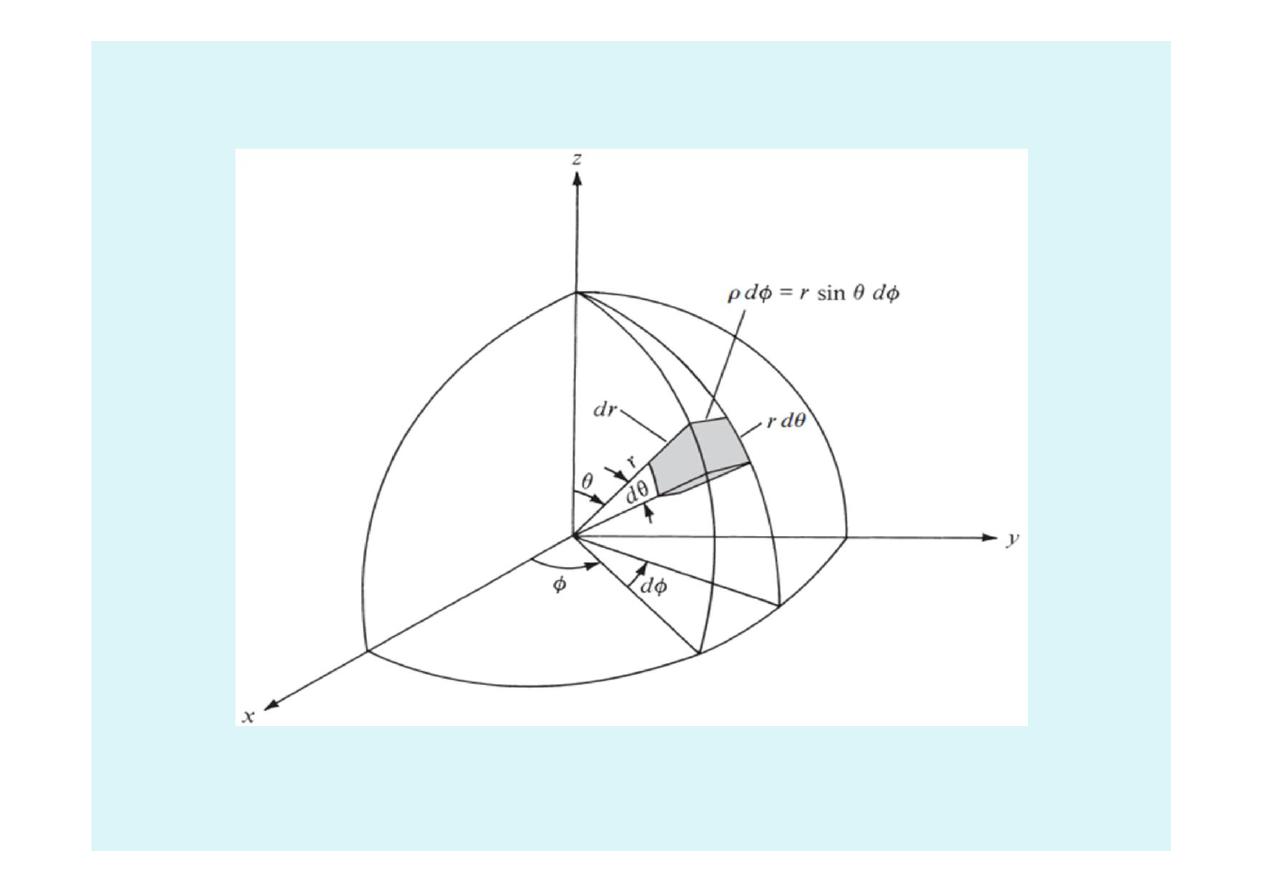
1.9 The Spherical Coordinate System
1.9 The Spherical Coordinate System
30
31
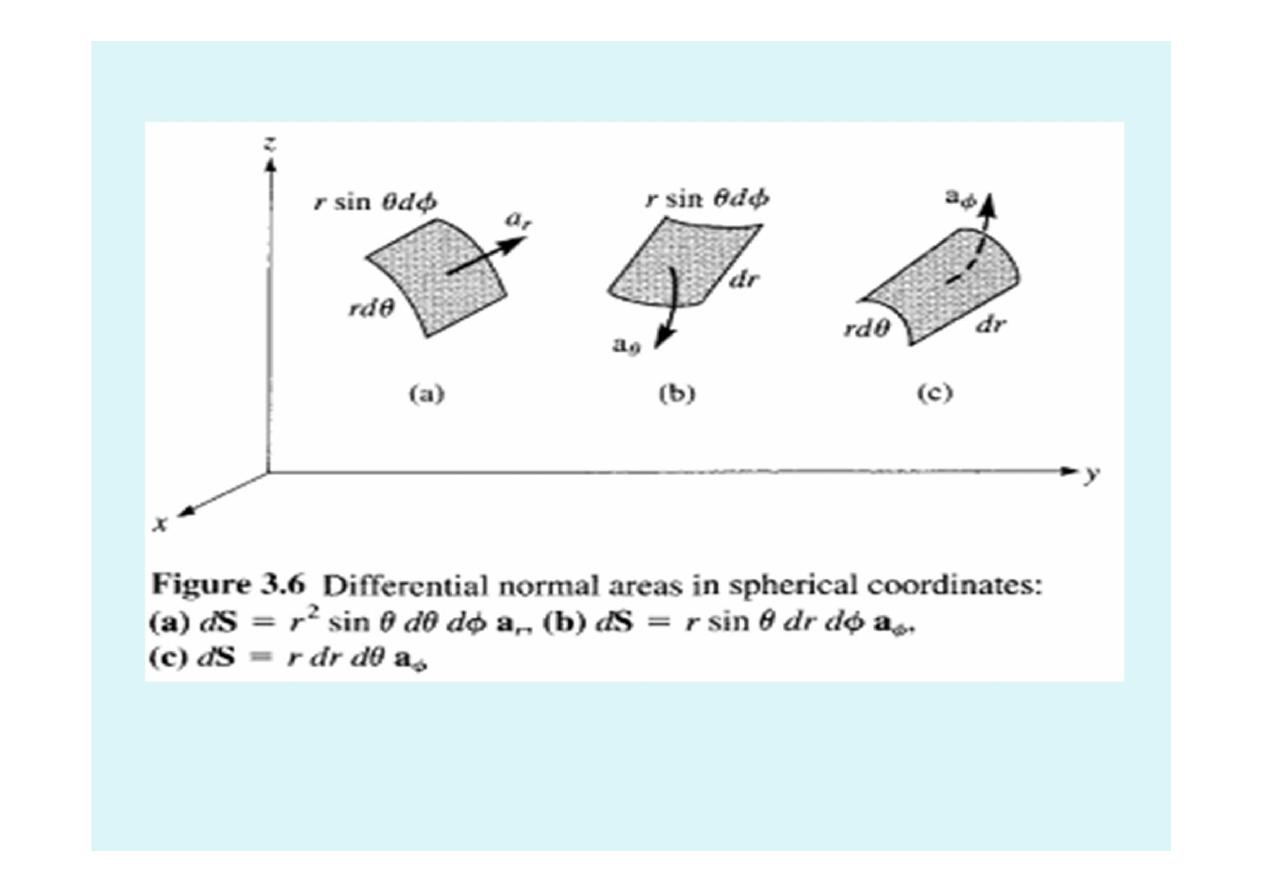
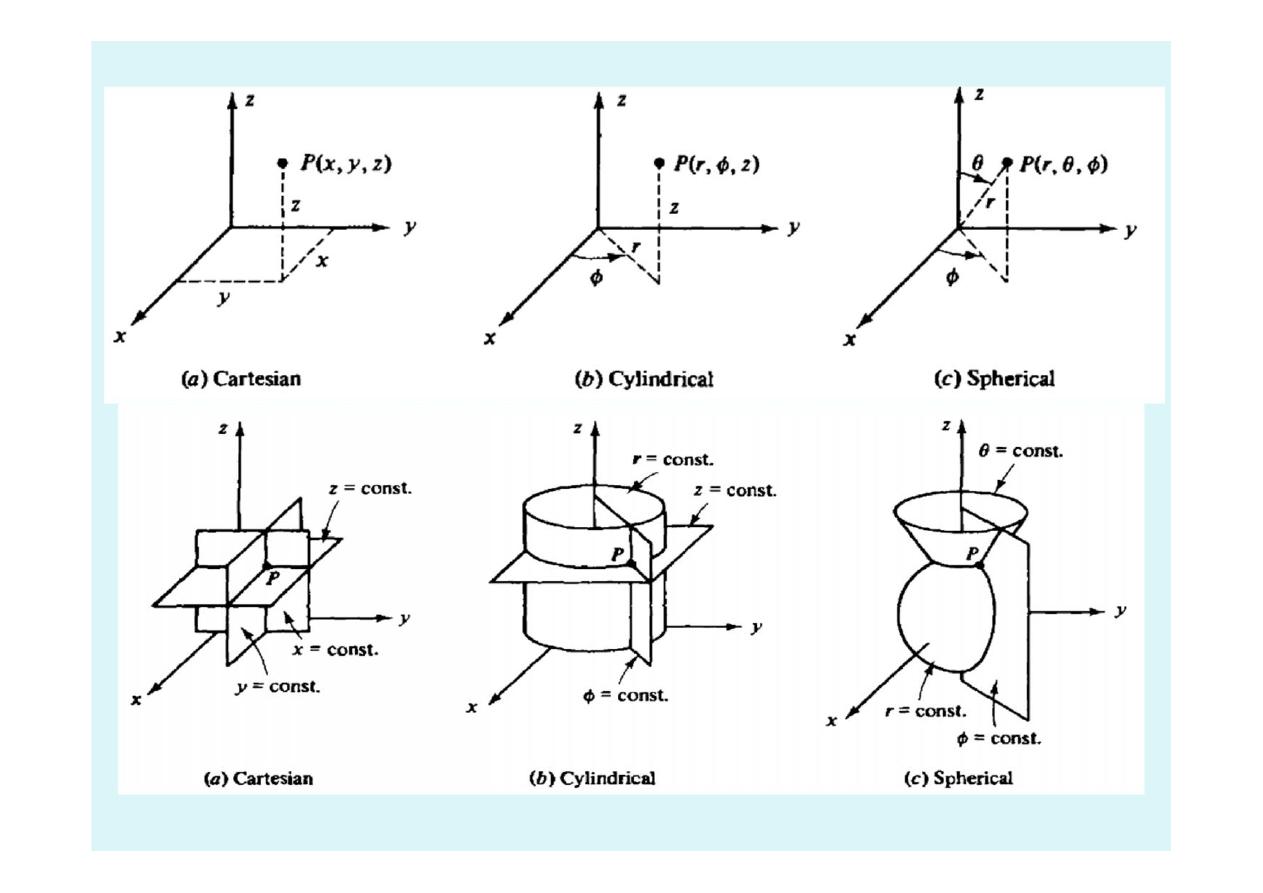
33
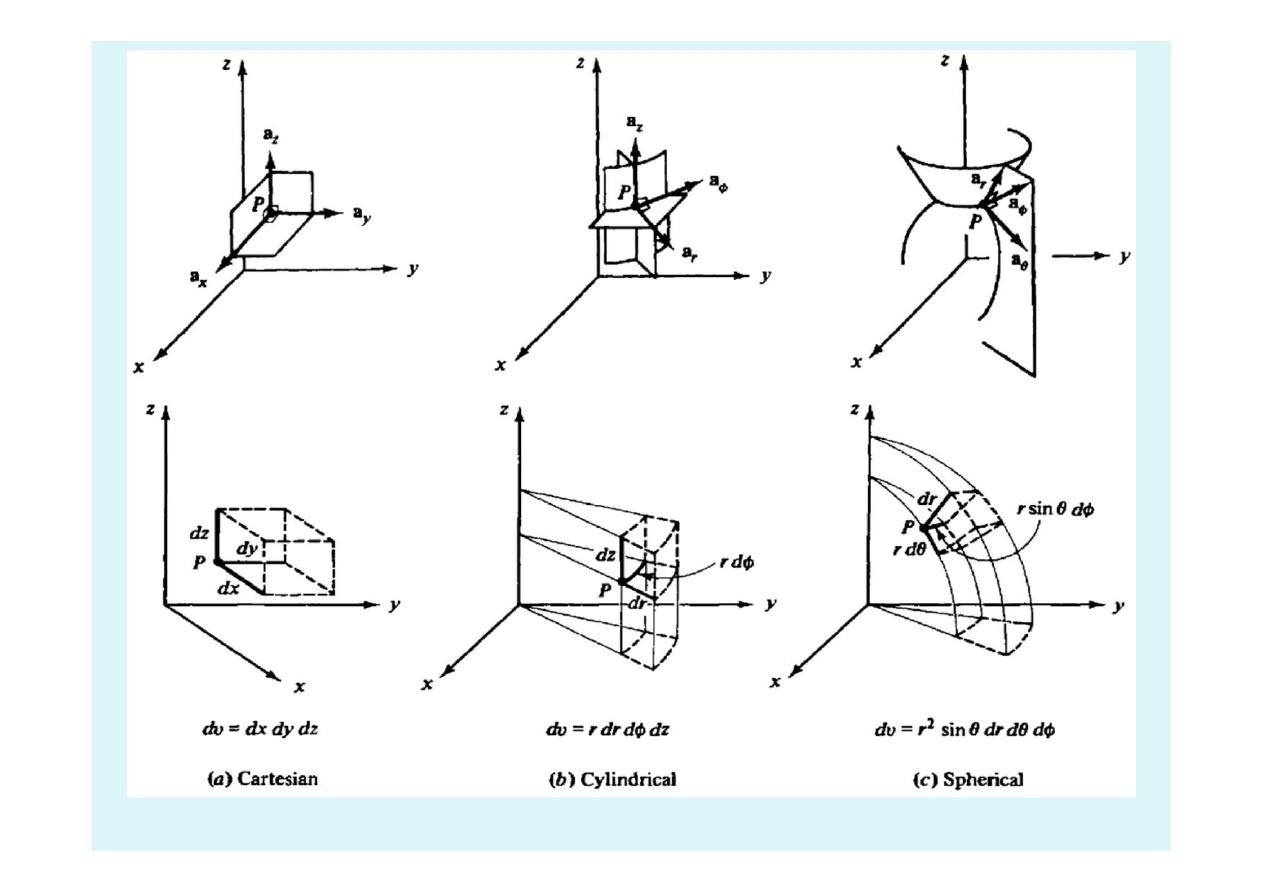
34
Differential Volume
Differential Volume
Differential Volume
