
3- ELECTRIC FLUX DENSITY AND
GAUSS’S LAW
1

3- ELECTRIC FLUX DENSITY AND GAUSS’S LAW
3.1 Electric Flux Density
3- ELECTRIC FLUX DENSITY AND GAUSS’S LAW
3.1 Electric Flux Density
•
The electric field is dependent on the medium in which
the charge is placed.
•
A new vector called the Electric flux density D measured
in ( C/m2 ) which is independent of the medium and
defined for free space by:
and for any material as:
where
2
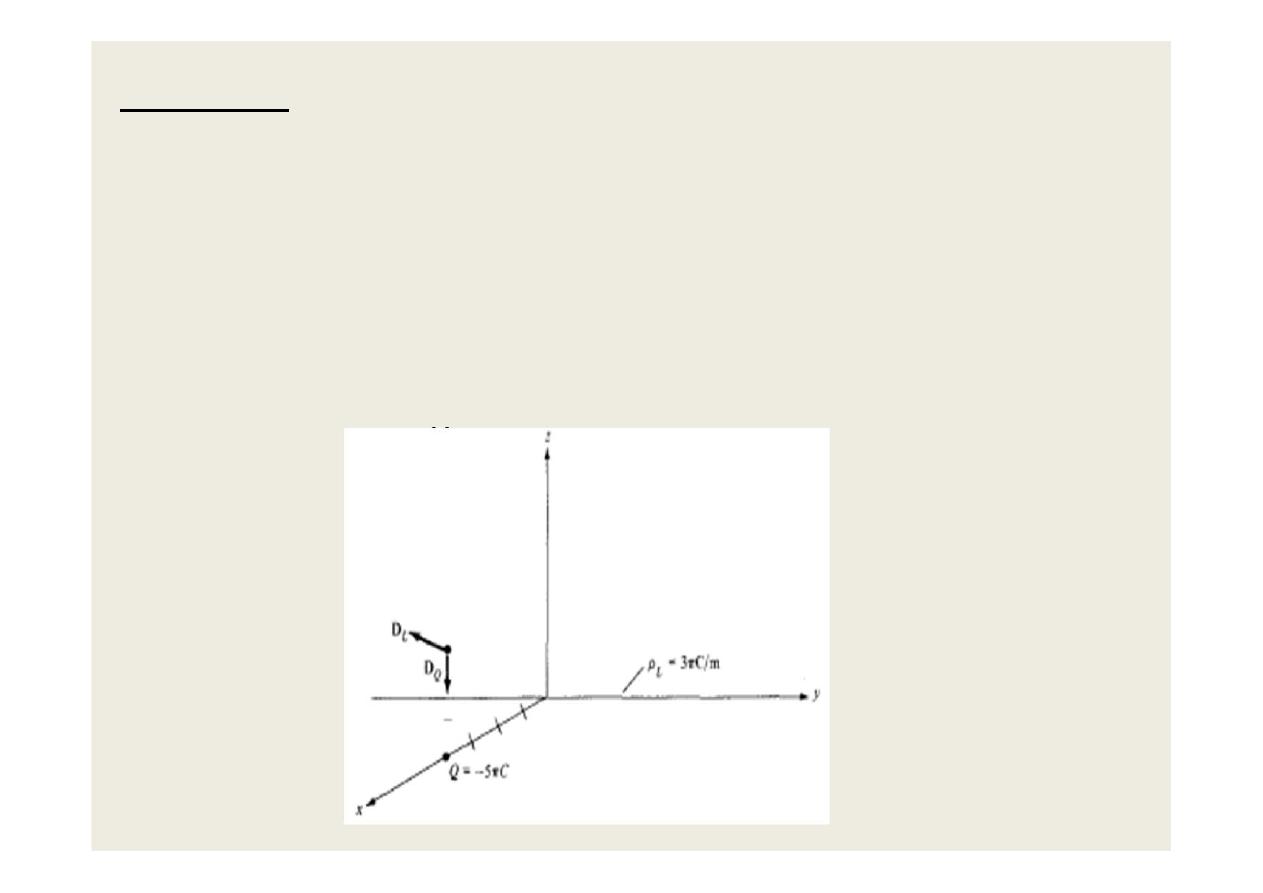
Example: Determine D at (4, 0, 3) if there is a point charge
—5π mC at (4, 0, 0) and a line charge 3π mC/m along the y-
axis.
Solution:
Let D = DQ + DL where DQ and DL are flux densities due
to the point charge and line charge, respectively, as
shown in the figure
3

4

3.2- Gauss's Law
3.2- Gauss's Law
•
Gauss’s law states that:
The electric flux density (D) passing through any closed
surface is equal to the total charge enclosed ( Qenc ) by
that surface.
•
The closed surface (known as Gaussian surface) is
chosen such that:
D is normal or tangential to the Gaussian surface and
ІDІ is constant on that surface.
•
When D is normal to the surface, D • dS = D dS because
D is constant on the surface.
•
When D is tangential to the surface, D • dS = 0.
5

•
The dS is defined as the differential surface (or
area) defined as
dS = dSa
n
•
where dS is the area of the surface element
and a
n
is a unit vector normal to the surface
dS and directed away from the volume.
6
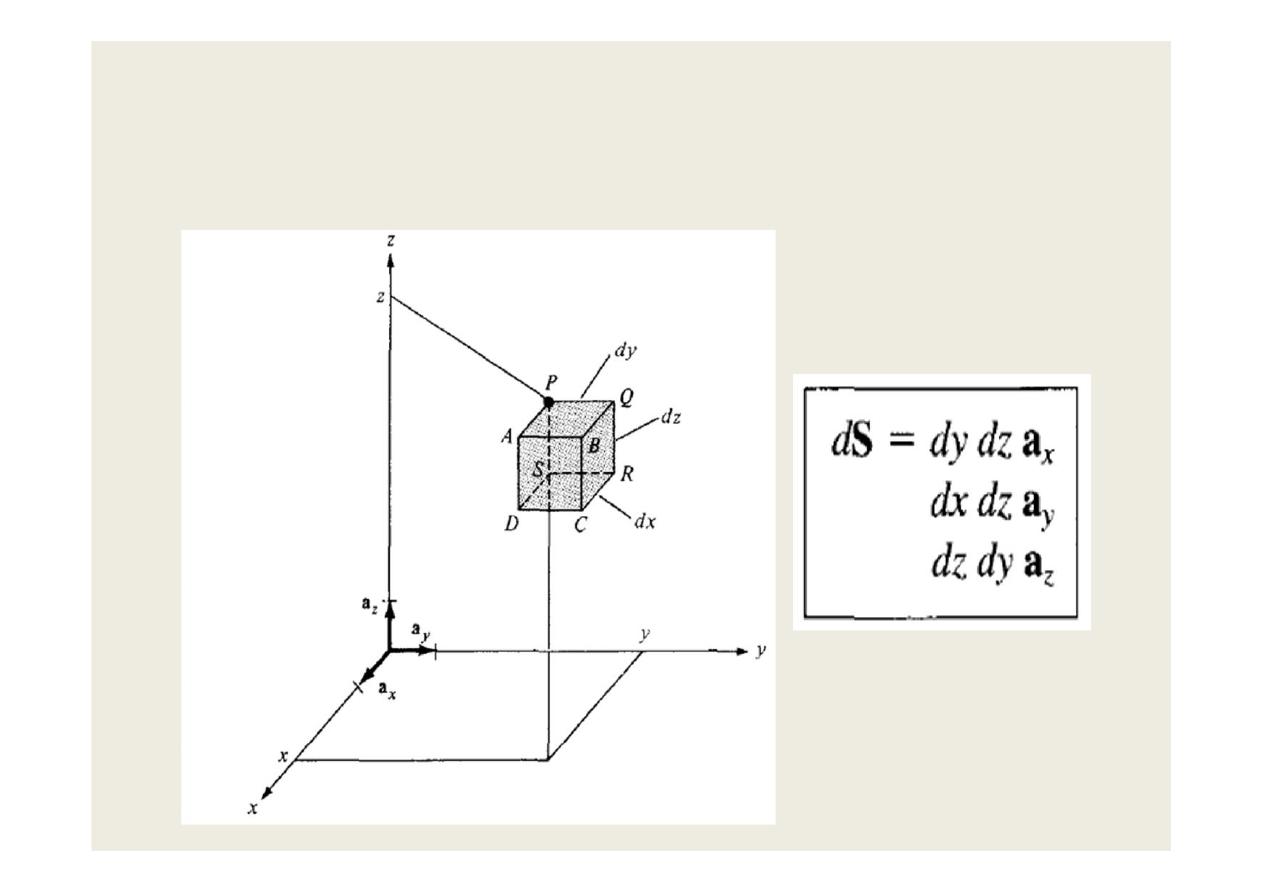
The differential normal area dS in:
A- Cartesian Coordinates is shown in the figures.
7
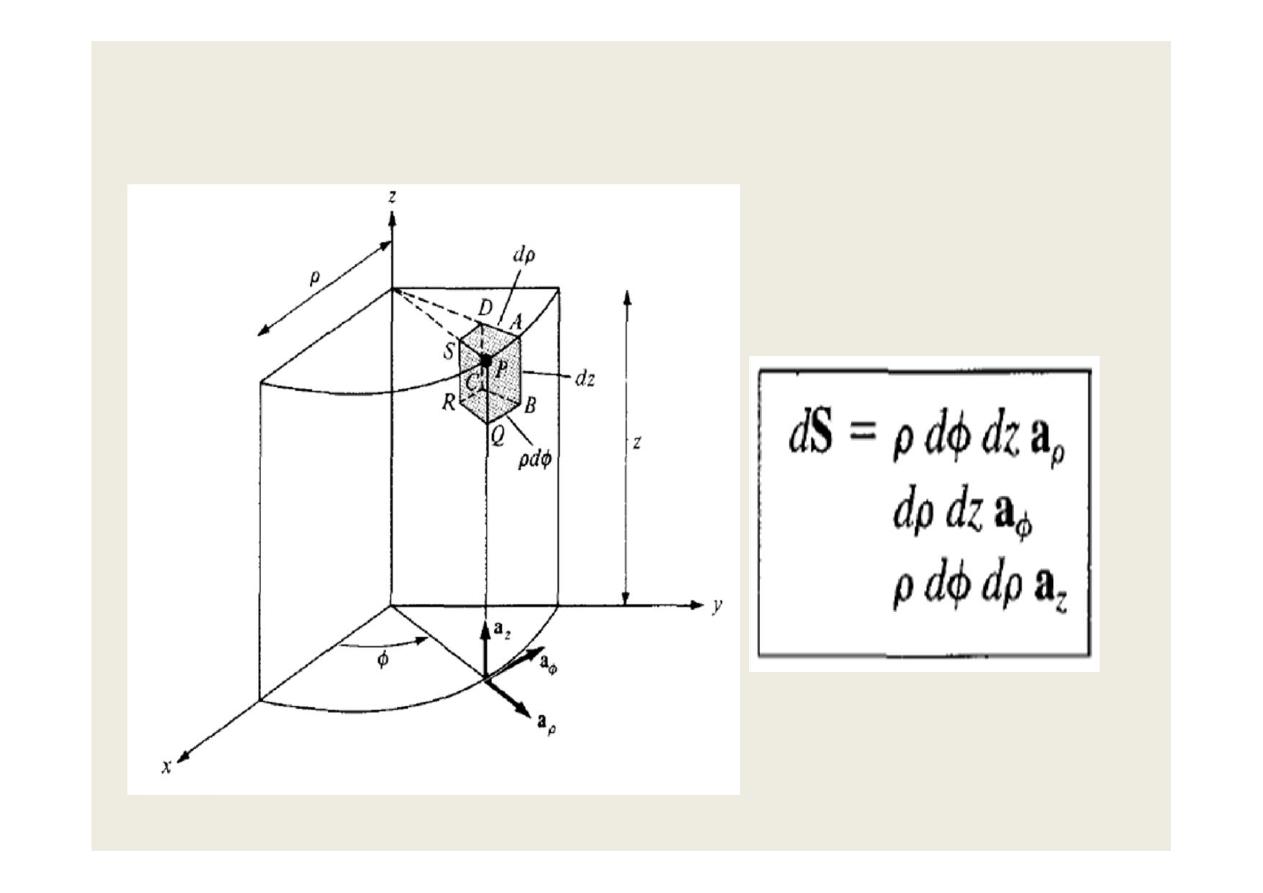
B- Cylindrical Coordinates is shown in the figures.
8
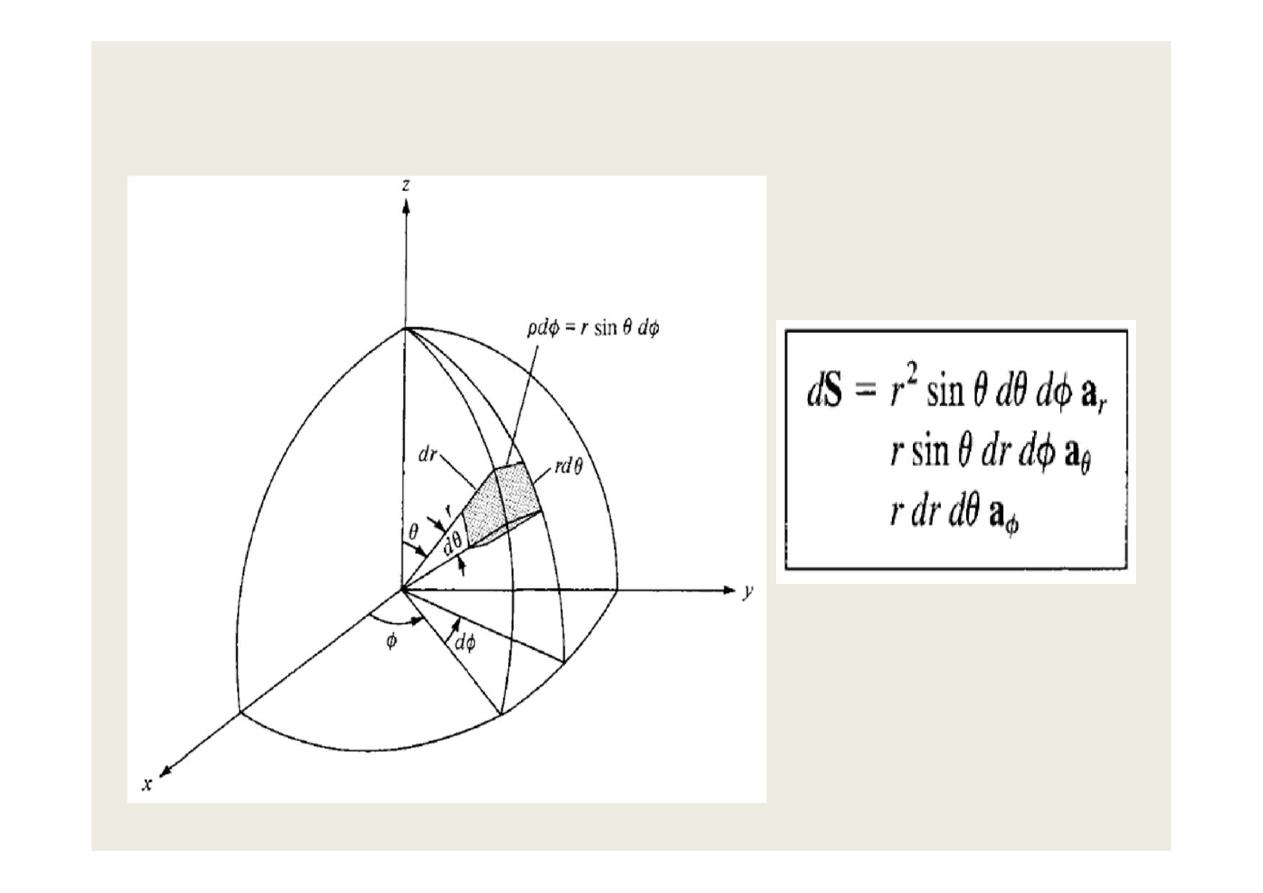
•
C- Spherical Coordinates is shown in the figures.
9
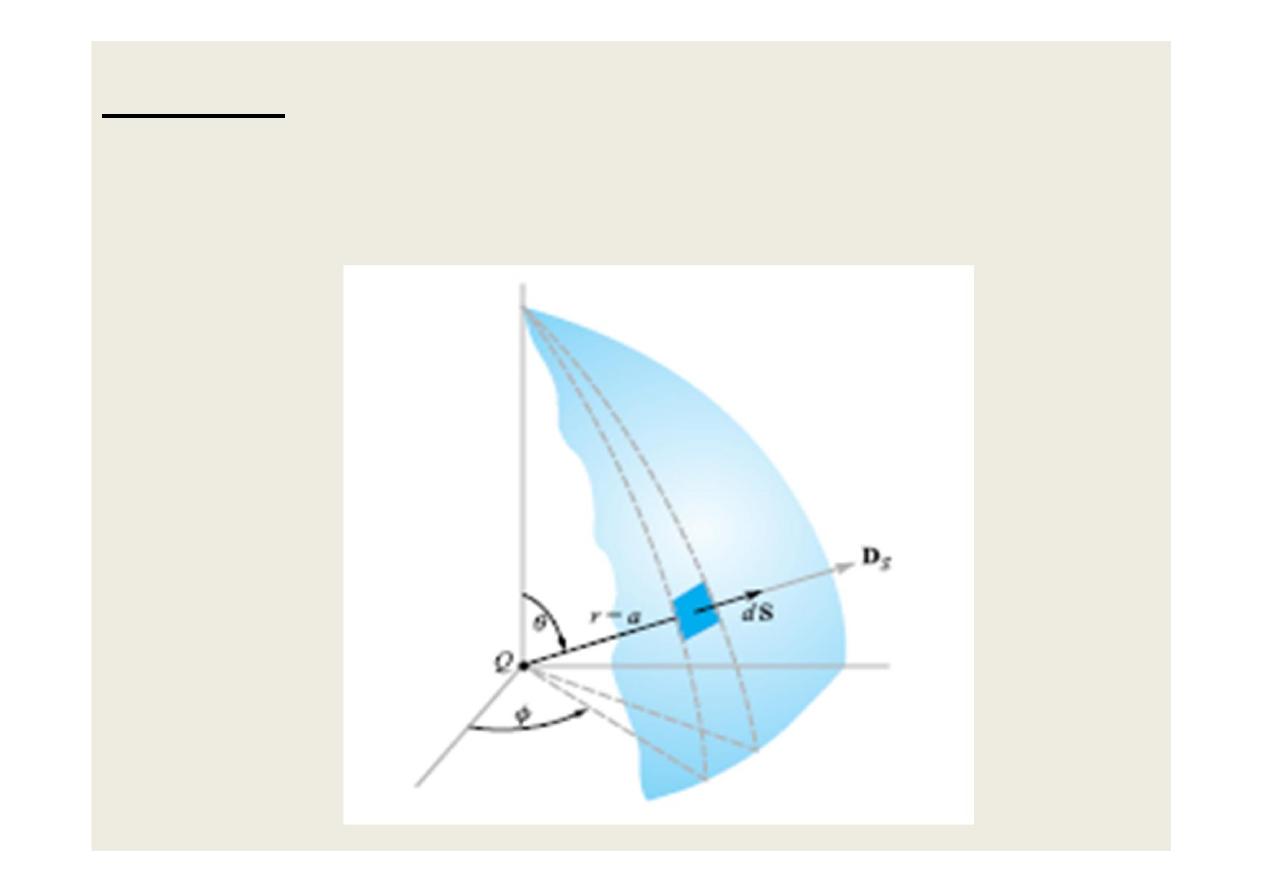
Example: Point Charge
•
A point charge Q is located at the origin. Determine
D at a point P
10

•
Since D is everywhere normal to the Gaussian
surface, that is, D = Dr ar . Applying Gauss's
law ( Qenclosed = Q ) gives:
where
is the area of the Gaussian surface. Thus
11
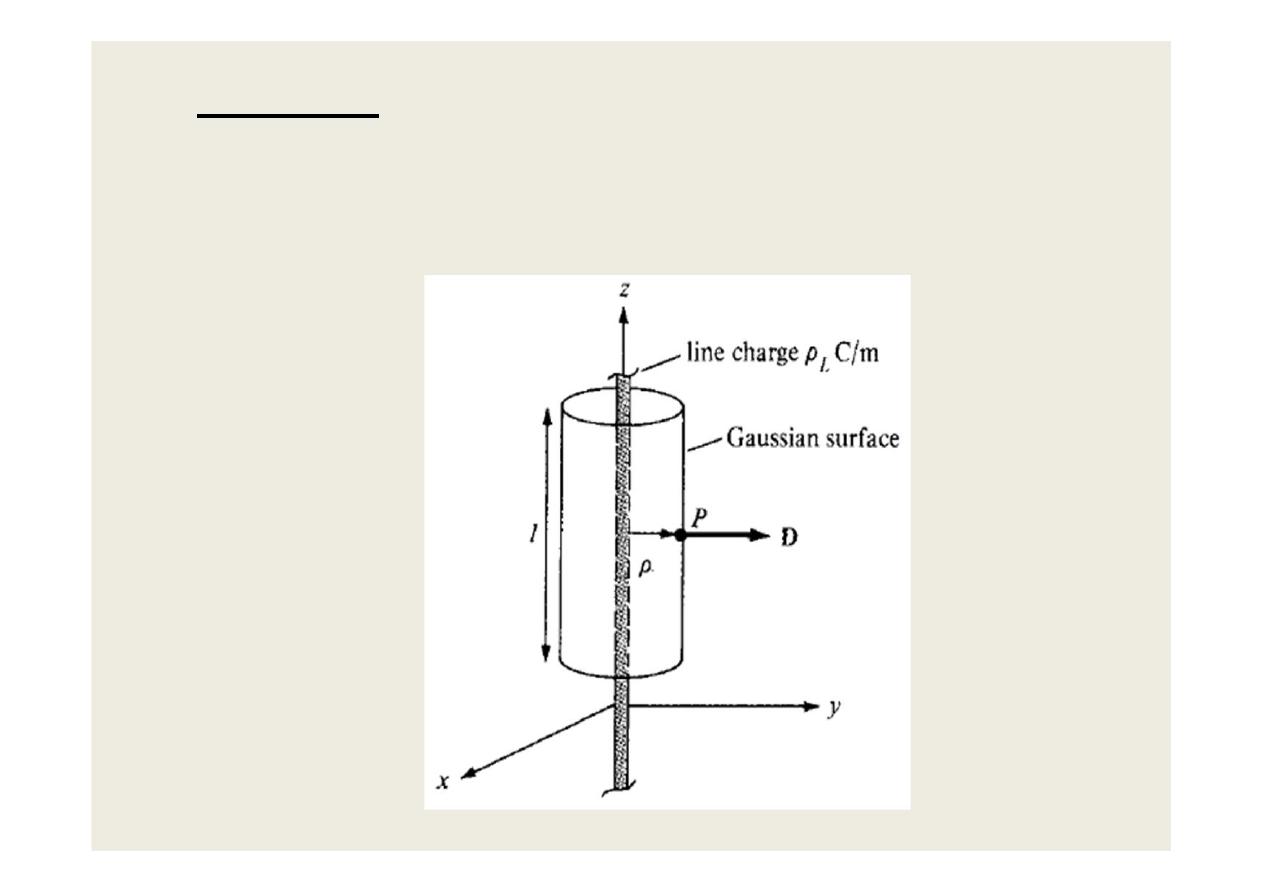
•
Example: Infinite Line Charge
•
An infinite line of uniform charge pL C/m lies
along the z-axis. Determine D at a point P.
12

•
we choose a cylindrical surface containing P to
satisfy symmetry condition as shown in Figure. D is
constant on and normal to the cylindrical Gaussian
surface; that is, D = Dp ap. If we apply Gauss's law
to an arbitrary length l of the line:
where is the surface area of the
Gaussian surface. Note that
evaluated on the
top and bottom surfaces of the cylinder is zero since D has
no z-component; that means that D is tangential to those
surfaces. Thus
13
•
Example: Uniformly Charged Sphere
A sphere of radius a with a uniform volume charge
density pv C/m3. Determine D everywhere.
Solution:
•
We construct Gaussian surfaces for r < a and r > a
separately.
•
Since the charge has spherical symmetry, it is
obvious that a spherical surface is an appropriate
Gaussian surface.
14

•
For r < a: The total charge enclosed by the spherical
surface of radius r, as shown in figure (a), is
and
Hence, or
15

For r > a, the Gaussian surface is shown in
figure (b).
and then or
16
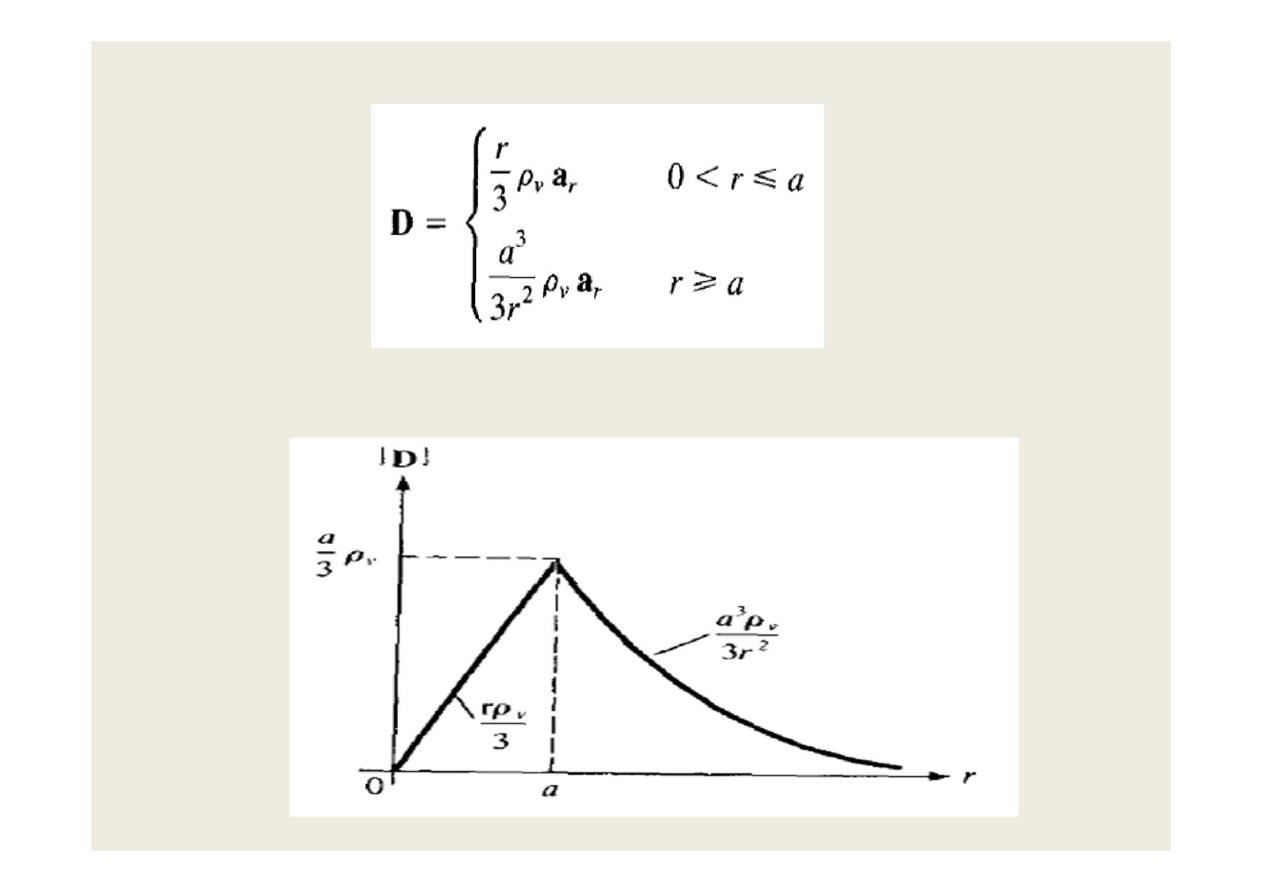
•
Thus,
•
and |D| is as sketched in the figure
17
•
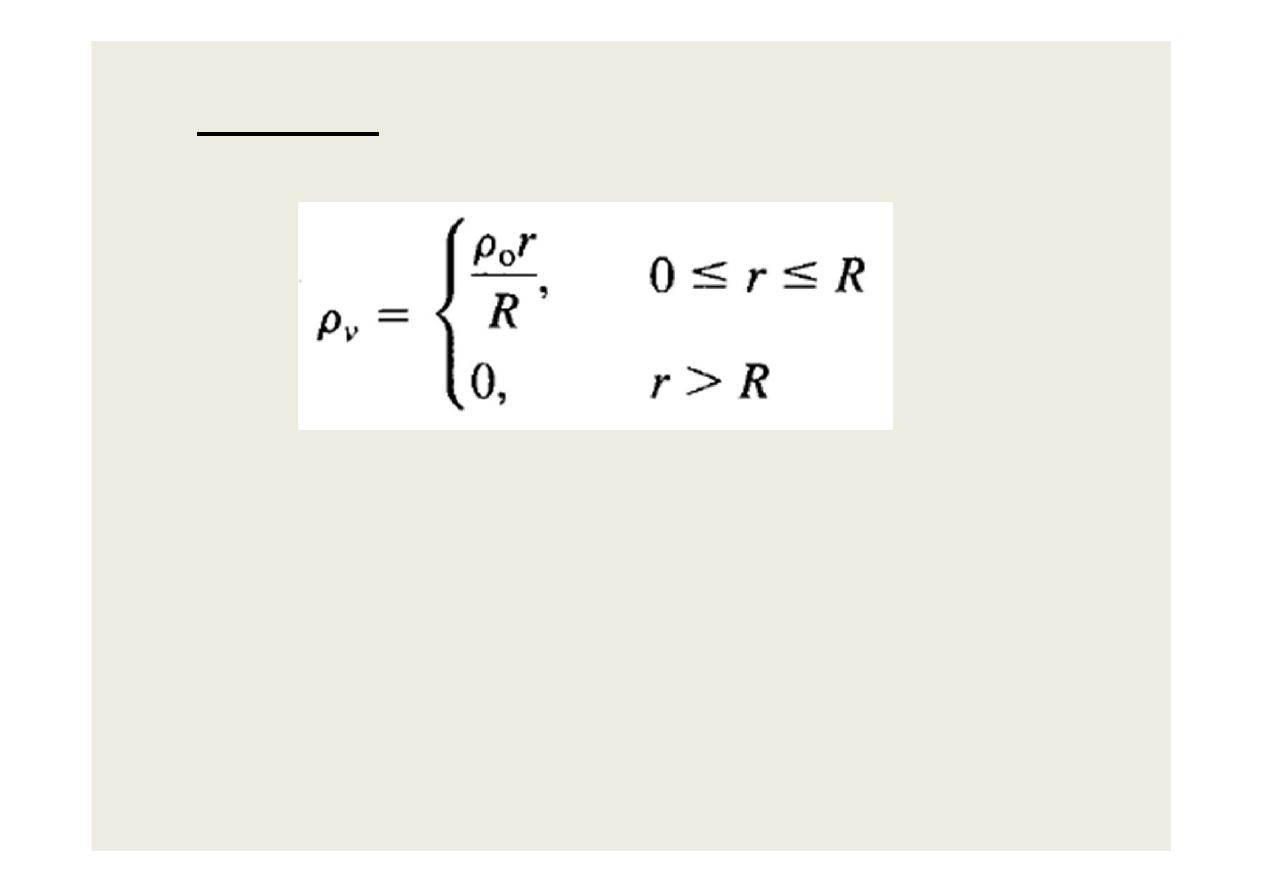
Example: A charge distribution with spherical
symmetry has density
Determine E everywhere.
18
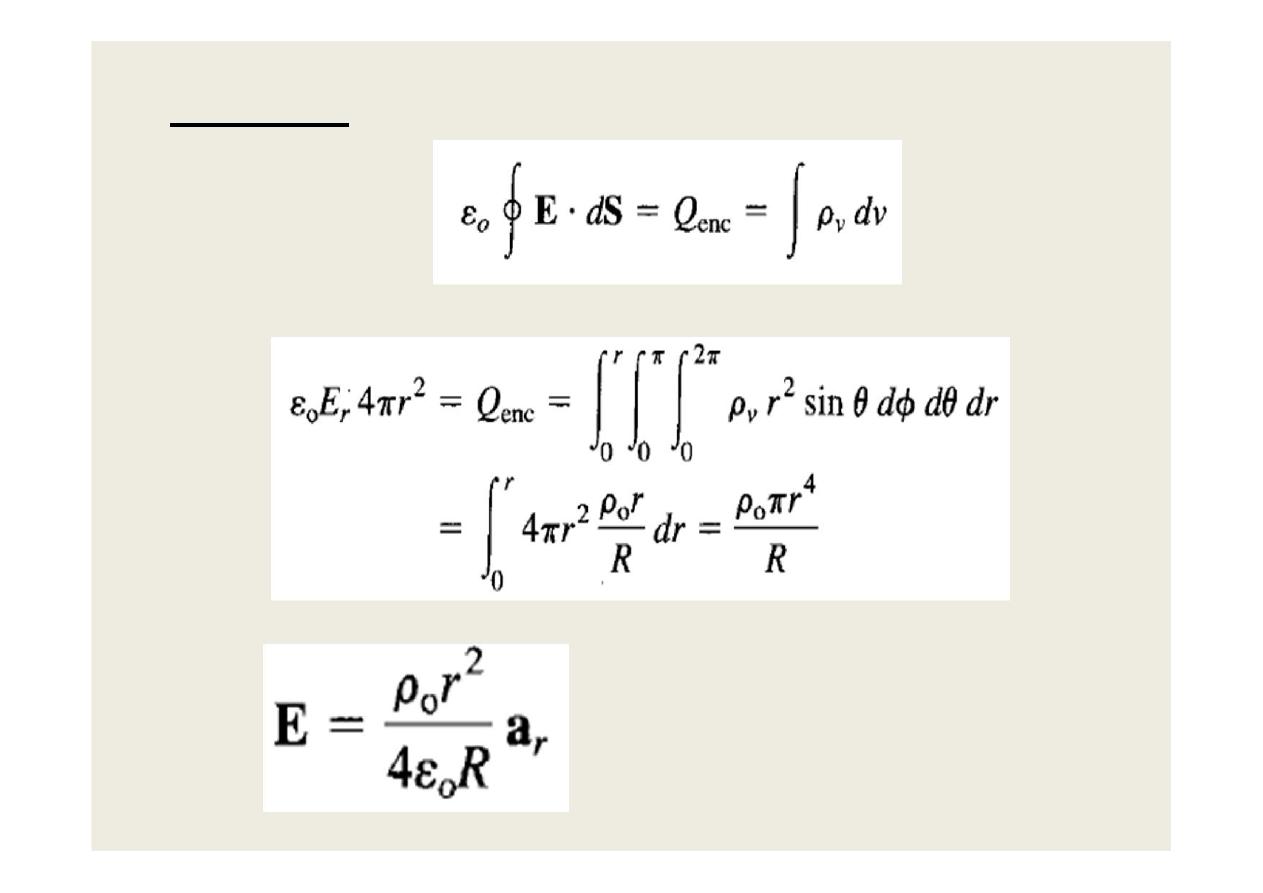
Solution:
•
For r < R:
or
19
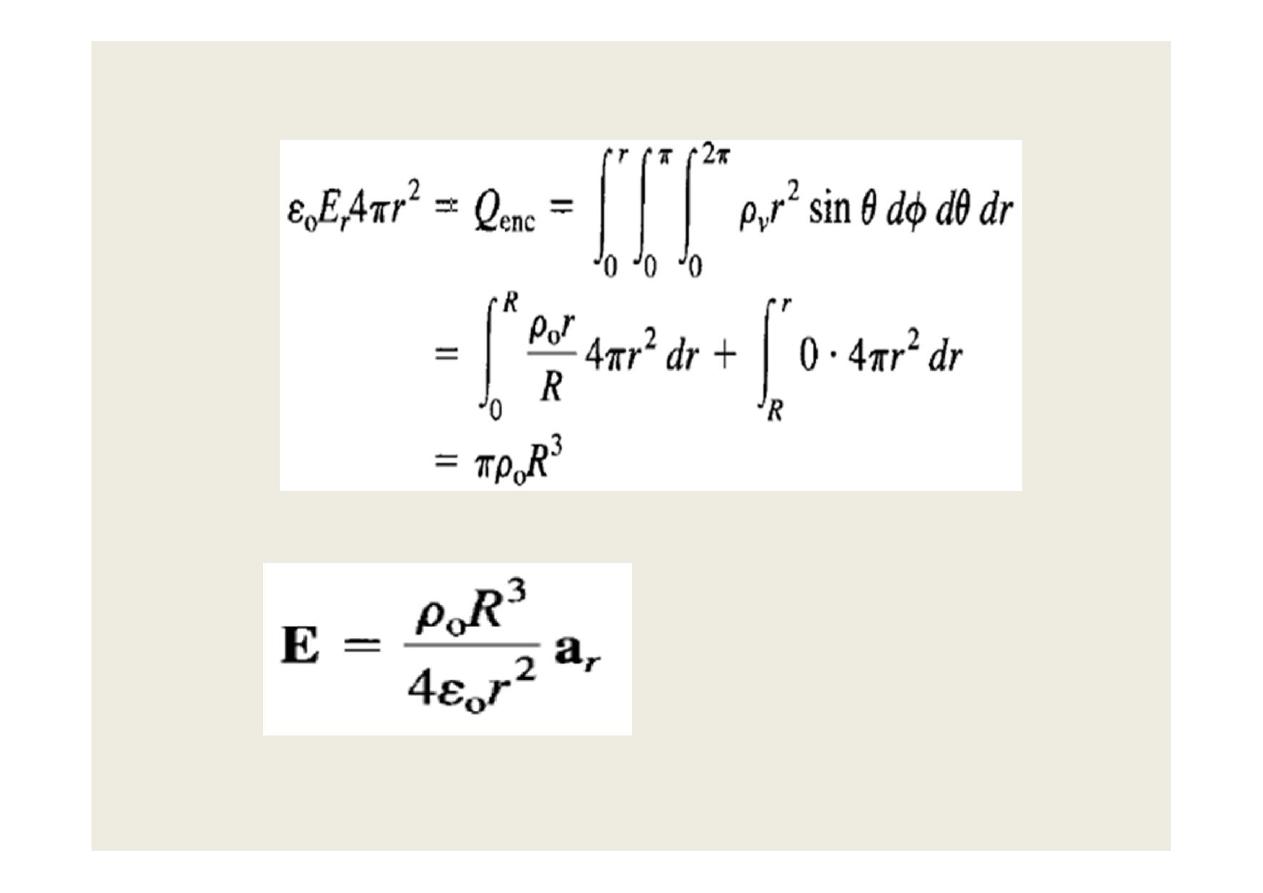
•
For r > R:
or
20
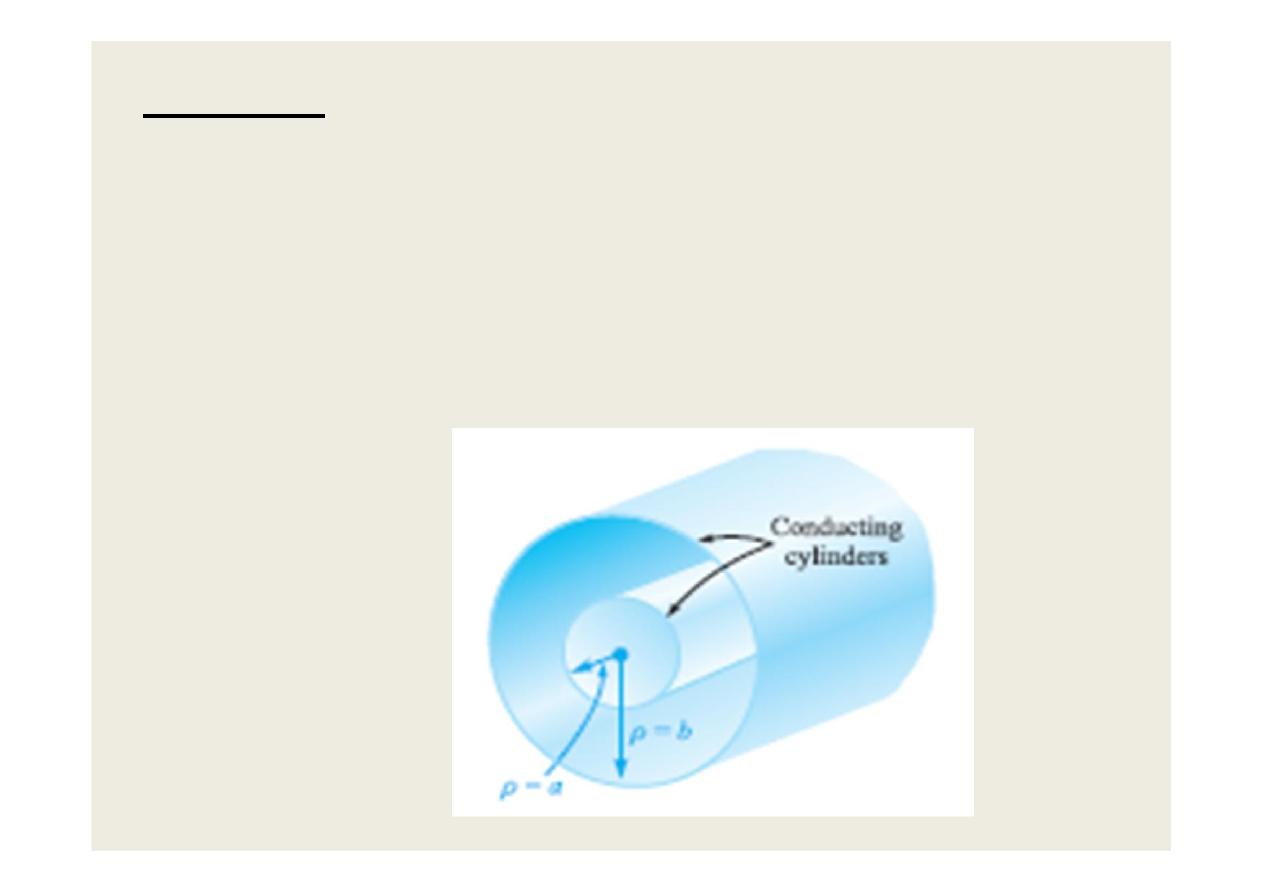
•
Example: A coaxial cable
Two coaxial cylindrical conductors of inner radius a
and outer radius b are infinite in extent . Assume a
total charge +Q is placed on the outer surface of the
inner cylinder and –Q on the inner surface of the
outer cylinder, find D everywhere.
21
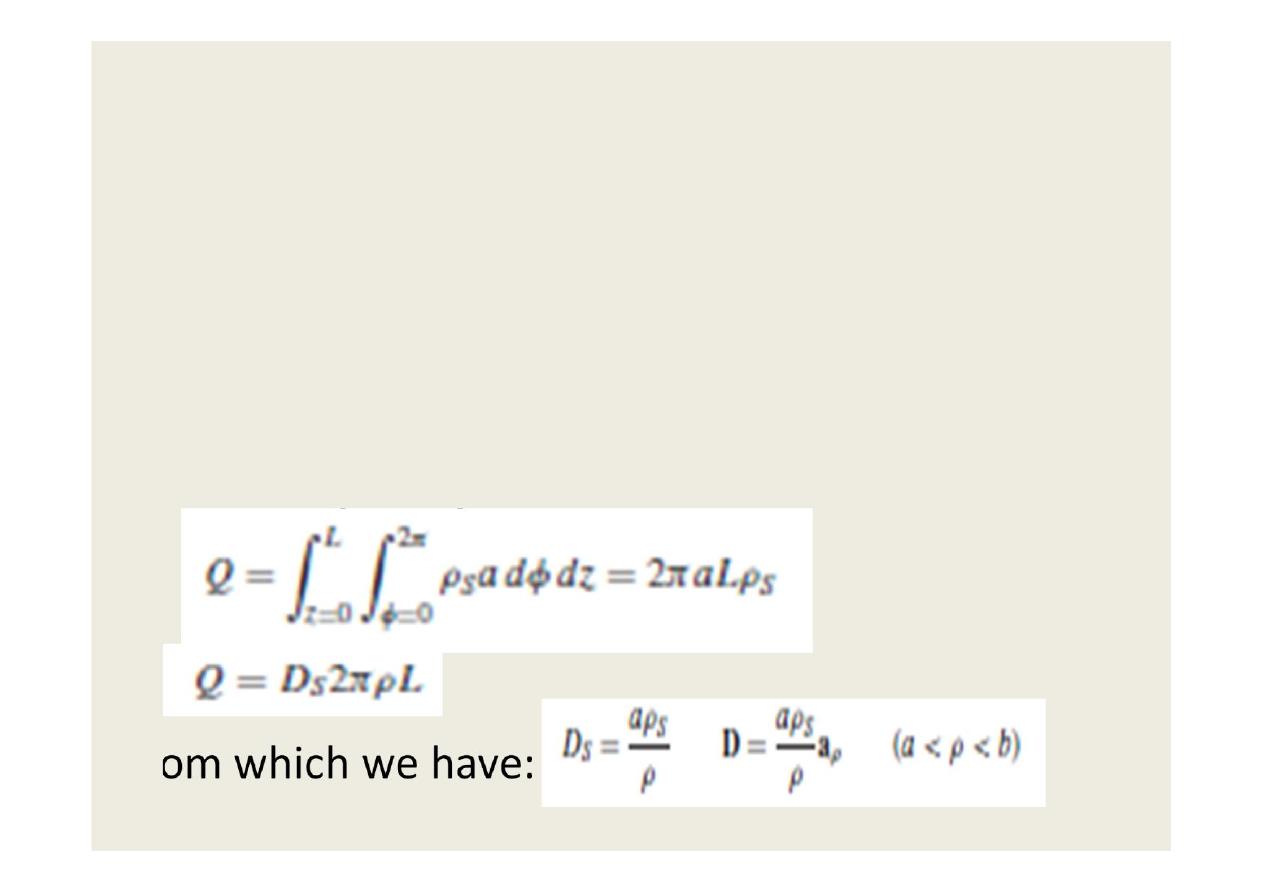
•
We choose Gaussian surface as a circular
cylinder of length L and radius ρ
•
For Gaussian surface of ρ < a:
Qenc = 0 , then: D = 0 for ρ < a.
•
For Gaussian surface a < ρ < b:
We will assume a charge distribution of ρS on the
outer surface of the inner conductor
from which we have:
22
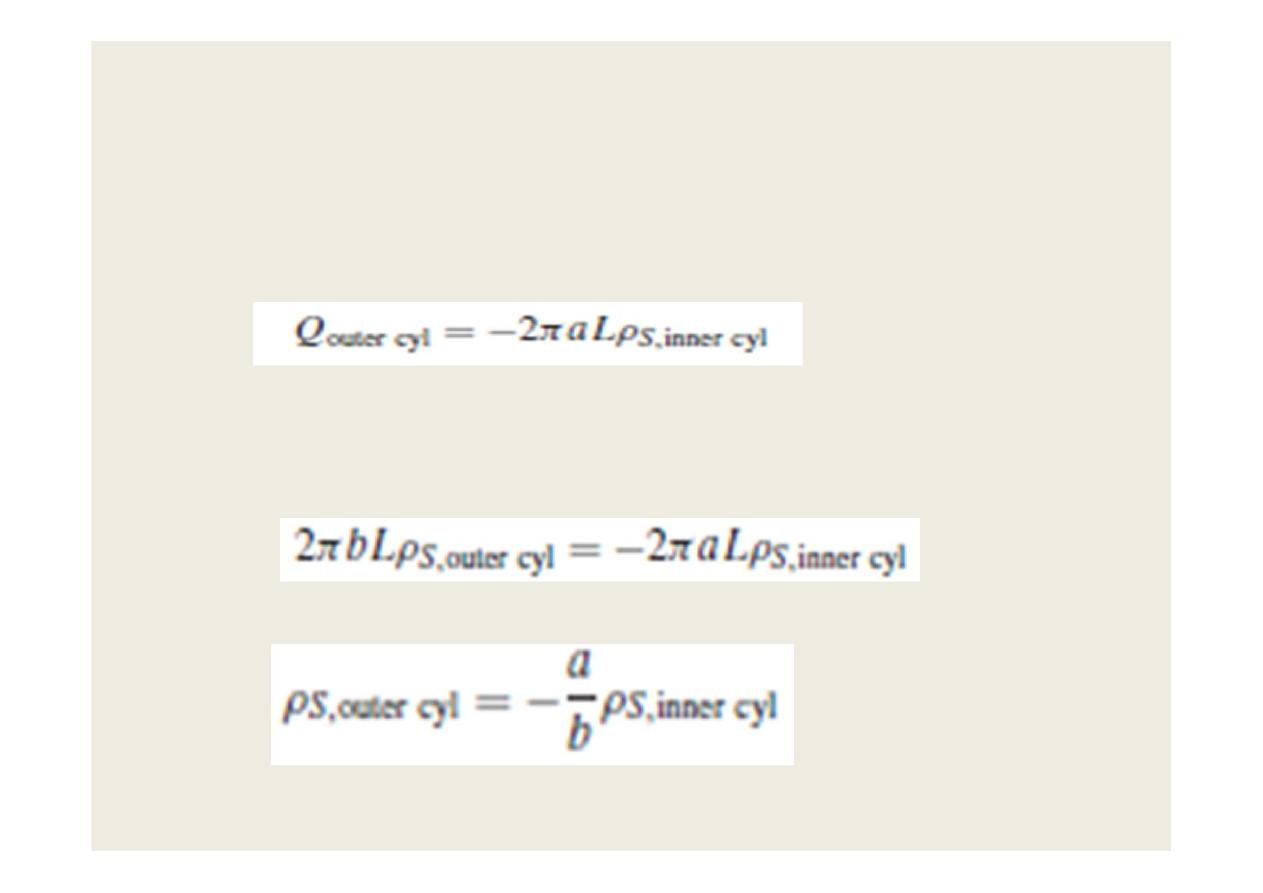
Because the charge on the inner cylinder must
terminate on a negative charge on the inner surface
of the outer cylinder, the total charge on that
surface must be
and the surface charge on the outer cylinder is
found as
or
23

•
For Gaussian surface of ρ > b:
The total charge enclosed would then be zero,
for there are equal and opposite charges on
each conducting cylinder. Hence
24

•
Example:
A 50-cm length of coaxial cable having an inner
radius of 1 mm and an outer radius of 4 mm. The
space between conductors is assumed to be filled
with air. The total charge on the inner conductor is
30 nC. Find the charge density on each conductor,
and the E and D fields.
25

26
