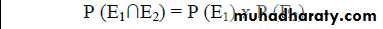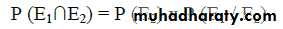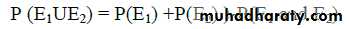ThiQar college of MedicineFamily & Community medicine dept.
Biostatistics L- propability Third stage by: Dr. Muslim N. SaeedDecember 29th,2016كل عام وأنتم بخير
أطيب الأماني بمناسبة السنة الجديدةObjectives
1- Define the probability.2- Explain the applications of probability in
medical sciences.
3- Describe types of probability.
Introduction
Why should we understand probability?Is probability essential for physician?
-Example 1: Genetic Counseling: A couple has a baby
with a genetic defect. They are considering having
another baby. What is the likelihood that the second child
will have a genetic defect also?
-Example 2: Prognosis; A physician is considering several
therapies for the treatment of a patient. Which therapy
should be used? Each therapy produces a result that is
somewhere between success and failure. The final choice
is “weighed the probability” against the others.
Example 3: Is a food additive carcinogenic? An
investigator explores this in an experiment that compares
two groups. Some of the treated individuals develop
cancer and only few of the controls develop cancer.. Is the
excess number of cancers meaningful (higher probability
than control)?
Example 4: Smoking and Cancer: Lung cancer occurs
commonly in smoker but only sometimes in non smokers.
Probability of other factors related to a variable outcome.
Probabilities are a tool in decision making, and the key
to understand inferential statistics
-Example 5: The data below shows the finding of a
survey. Is living near electricity transmission equipment associated with occurrence of cancer?Cancer Not
Near 200 1646 11%
Not 50 7289 1%
Among those living near electricity equipment, 11% have cancer. Among those living elsewhere, only 1% have cancer. Is this a meaningful difference?
- The difference (if significant) in this example is
reflected for population and called inference-Probability is the bridge between Descriptive Statistics and Inferential Statistics.
Probability Definition:
It is the likelihood of occurrence of a certain
event compared to the total events.
no. of times E occur
P(E)= -----------------------------------------
no. of times E can occur
*P(E) probability of occurrence of event E
The concept of probability is frequently encountered in every day communication of health workers, we may here the physician say that a patient has 50-50 chance of surviving, or a patient 95% has the disease.
-The value of probability = 0 – 1
-No negative value in probability.
-Probability (E) = 0 means event is impossible
-Probability (E) = 1 means event is sure
sometimes proportion and probability are used
interchangeably.Example: the probability of serum cholesterol level between 180 and 210(mg/100 ml) is the
proportion of people in a certain target population having their cholesterol levels falling between 180 and 210 (mg/100 ml).
Element of probability
1) Total probability value must be between 1 & zero (0 ≤ P≤1), no negative value.P = 0 → Not occur. P = 1→ should occur.
P = 0.5→ 50% will occur & 50% will not occur.
2) The sum of the probabilities of mutually exclusive (can't occur simultaneously) outcome is equal to one.(black or white, male or female, blood group A or B or AB or O)
In other word :
The sum of the probabilities (or relative
frequencies) of all event that can occur in the
sample must be 1 (or 100%).
Ex. In a sample of 50 people, 21 had blood group O, 22
had blood group A, 5 had type B, and 2 had blood
group AB
p(O)= 0.42
p(A)= 0.44
p(B)= 0.1
p(AB)= 0.04
p(neither A nor O)= 0.14
p(not AB)= 1 - 0.04= 0.96
There are 3 types of probability:
1) Classical Probability:Assume that all outcomes in the sample space are equally
likely to occur. One does not actually have to perform the
experiment to determine the probability.
Ex: When a single die is rolled, each outcome has the
same probability of occurring Since there are 6 outcomes,
each outcome has a probability of 1/6.
2) Empirical Probability (Relative frequency):
Depend on actual experience to determine the likelihood of outcomes
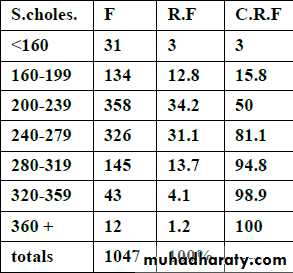
Ex: In a study, we have the following table for serum cholesterol of 1047 male patients aged 40-59 year.
-The probability to get individuals with serum cholesterol of 820-319 is 145 / 1047 = 13.7%
Probability to get those below 200 is (31 +134)/ 1047 = 15.8 %
So we can express probability in terms of relative frequency or cumulative relative frequency.
3) Subjective (personalistic) Probability:
Based on person’s experience and evaluation of the situation But does not rely on the repeatability of any process. A physician might say that on the basis of his diagnosis,
there is a 30% chance that the patient will need an operation.
If a doctor says “you have a 50% chance of recovery,”
the doctor believes that half of similar cases will recover in the long run.
Presumably, this is based on knowledge, and not on a
whim. The benefit of stating subjective probabilities is that they can be tested and modified according to
experience.
Joint probability:
It is the probability that the events (2 or more, E1, E2 ..etc) can occur simultaneously. We have the following 2 rules:1) Multiplication rule (And, ∩, both).
a) Independent events (E1 not affected by E2).
-Two events are statistically independent if the chances, or likelihood, of one event is in no way related to the likelihood of the other event. Individual is male with red hair.
EX: Event A = “a woman is hypertensive”
Event B = “her husband (not relative) is hypertensive”.The assumption of independence seems reasonable since
the two persons are not genetically related. If the
probability of being hypertensive is 0.07 for woman and
0.09 for man, then the probability that BOTH the woman
and her husband are hypertensive is:
P(A and B) = P(A) x P(B) = 0.07 x 0.09 = 0.0063
Ex: The probability that an individual belonging to blood group A is 0.42, and the individual being a football player is 0.50. What is the probability of the individual both belonging to blood group A & being football player?
Since the events are independent → P (E1∩E2) = P (E1) x P (E2) = 0.42 x 0.50 = 0.21
b) Dependent events (E1 affected by E2).
EX: Probability of being male 1s 0.5, and that that male being bold is 0,05. What is the probability of both being male and bold?Since the events are dependent→ P (E1∩E2) =
P(E2) x P(E1 / E2) =0.5 x 0.05/0.5= 0.005
EX: the chance that person has Huntington ’s chorea is
0.0002 (if the parent does not have Huntington’s Chorea).An offspring of a person with Huntington’s Chorea has a
50% chance of contracting Huntington’s Chorea
(offspring with chorea giving that his father had chorea).
Probability 2 persons have Huntington’s Chorea =
P(A and B) = 0.0002 X 0.0002= 0.00000008
Probability both parent and child have Huntington’s
Chorea = P(A) P(B|A) = 0.0002 x 0.5 = 0.0001
Conditional probability: Probability of an event
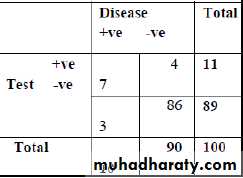
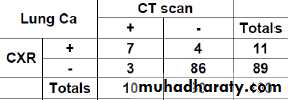
occurring (E1) giving that the other event (E2) has already occur.Ex: Using the information of table below:
Calculate:1- The probability of selection person dis. +ve & test +ve.
2- The probability of selection person dis. -ve & test -ve.
As the variables are dependent, so P (E1∩E2) = P (E2)x P(E1 / E2)
1- P (dis. +ve & test +ve.) = 11/100 x 7/11 = 7/100
2- P (dis. -ve & test -ve.) = 90/100 x 86/90 = 86/100
2) Additional rule. (Or, U, either)
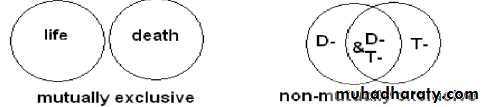
a) Mutually exclusive events (can't occur together).Two events are mutually exclusive if they cannot occur at the same time.
EX: if a baby has a 0·04% chance of being homozygous for the sickle cell gene and a 3·92% chance of being a heterozygote, then the probability that it carries the gene either as a homozygote or as a heterozygote is 0·04 + 3·92 = 3·96%.
Ex: The probability that an individual belonging to blood group A is 0.4 and the individual belonging to blood group B is 0.3. What is the probability of the individual belonging to blood group A or B?
As the variables are mutually exclusive events (can't occur together), so:
P (E1UE2) = P (E1) +P (E2) = 0.4 +0.3 = 0.7
b) Not mutually exclusive events (can occur together).
Ex: Using the information of table above, calculate theprobability of selection person dis. -ve or test -ve.
As the variables are not mutually exclusive events (can occur together), so:
P (E1UE2) = P (E1) +P (E2)-P (E1 and E2) = {90\100+89\100 } – 86\100 = 0.93
EX: From table, what is the probability to have a person that is CT scan –ve or CXR negative?
= 0.90+0.89-0.86 =0.93=93%