
Gases
Chapter 5
Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
Elements
that exist as
gases
at 25
0
C and 1 atmosphere
5.1

5.1

•
Gases assume the volume and shape of their containers.
•
Gases are the most compressible state of matter.
•
Gases will mix evenly and completely when confined to
the same container.
•
Gases have much lower densities than liquids and solids.
5.1
Physical Characteristics of Gases
Units of Pressure
1 pascal (Pa) = 1 N/m
2
1 atm = 760 mmHg = 760 torr
1 atm = 101,325 Pa
5.2
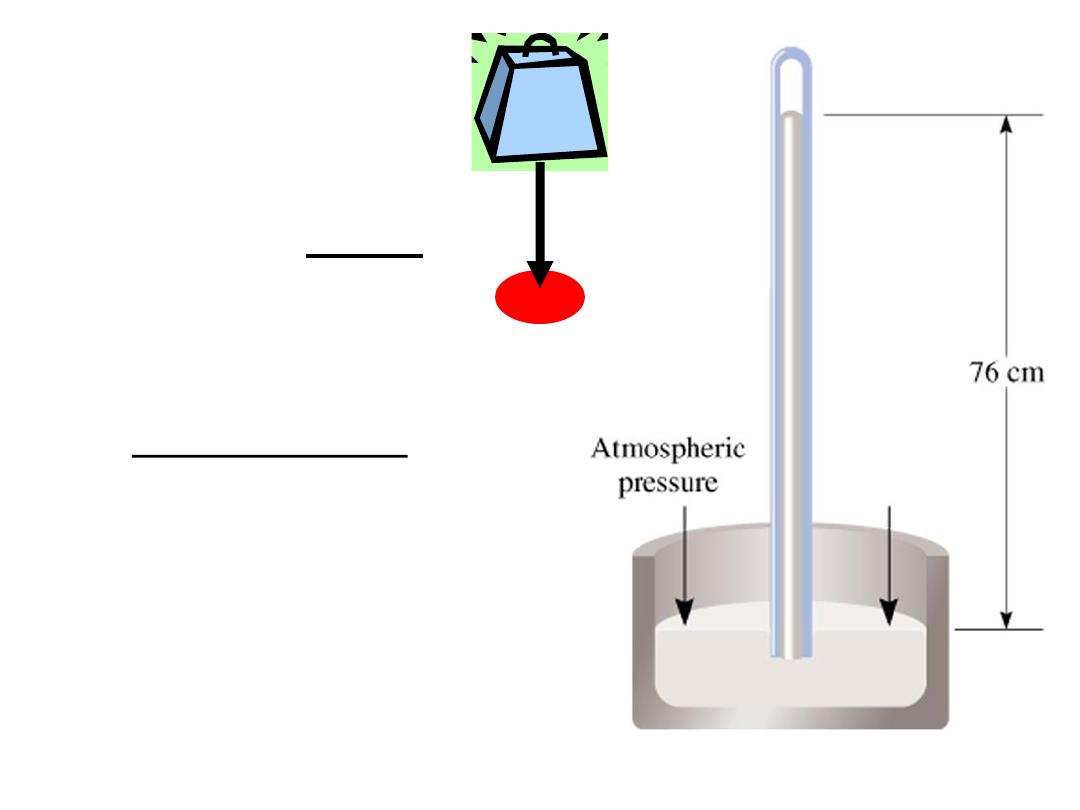
Barometer
Pressure =
Force
Area
(
force
= mass x acceleration)
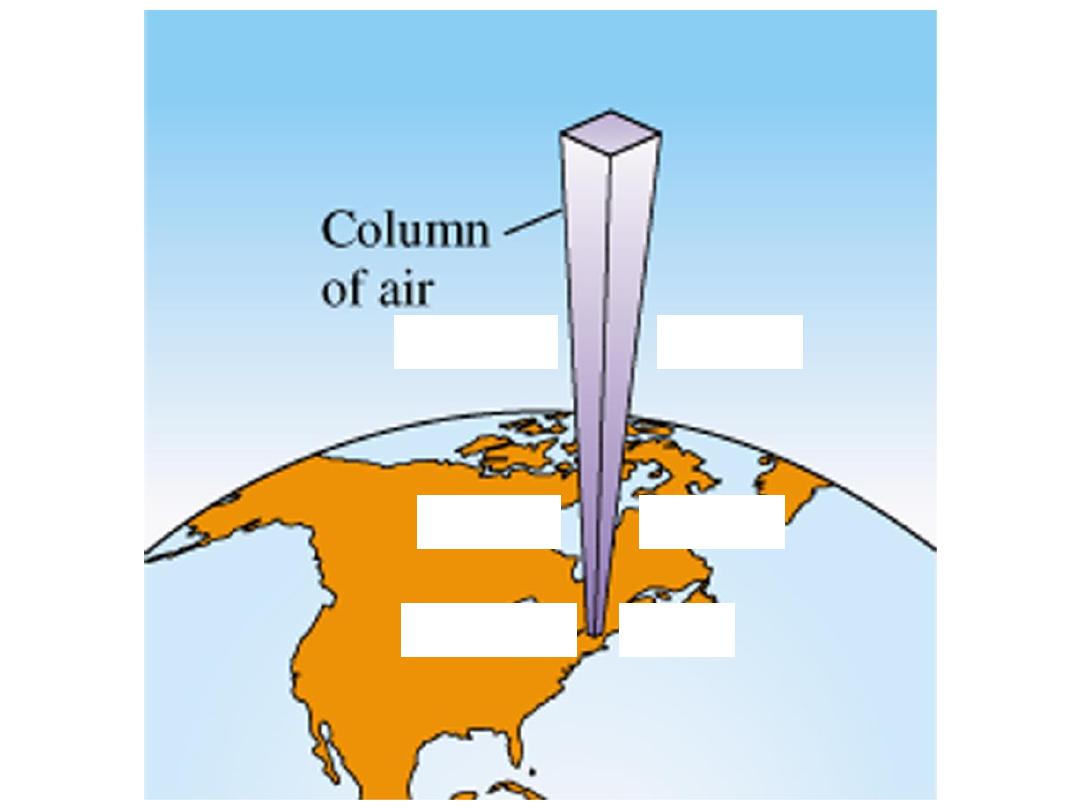
Sea level
1 atm
4 miles
0.5 atm
10 miles
0.2 atm
5.2
5.2
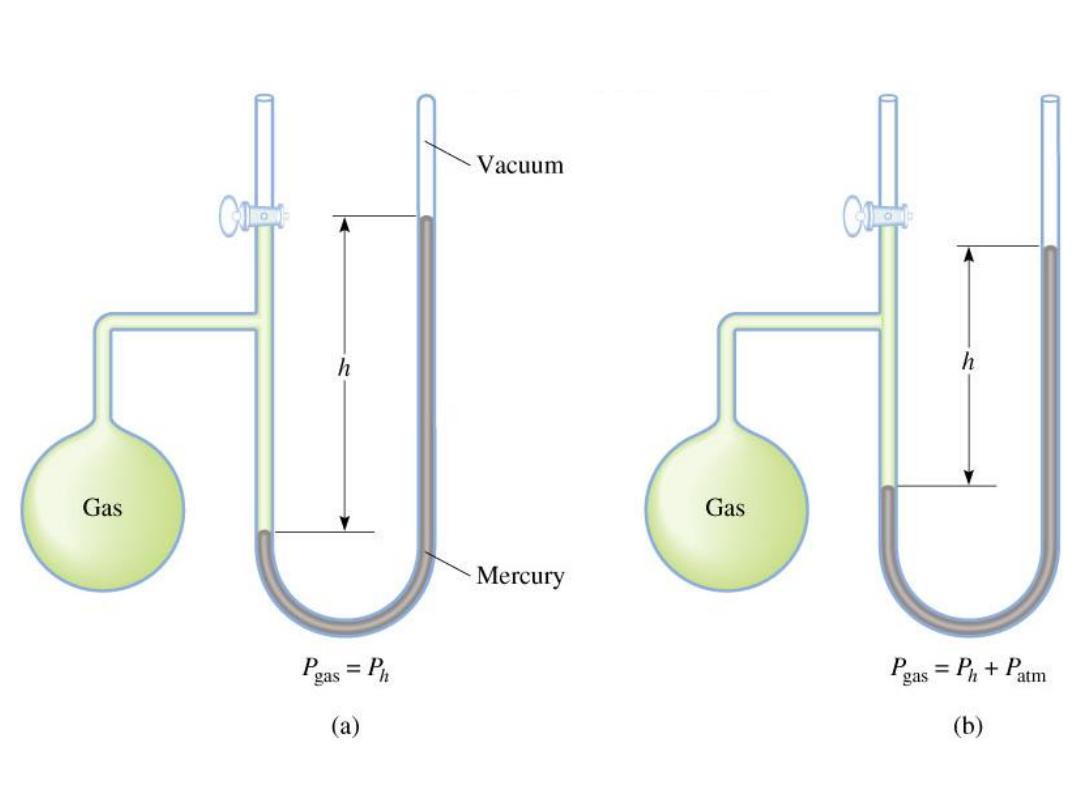
Manometers Used to Measure Gas Pressures
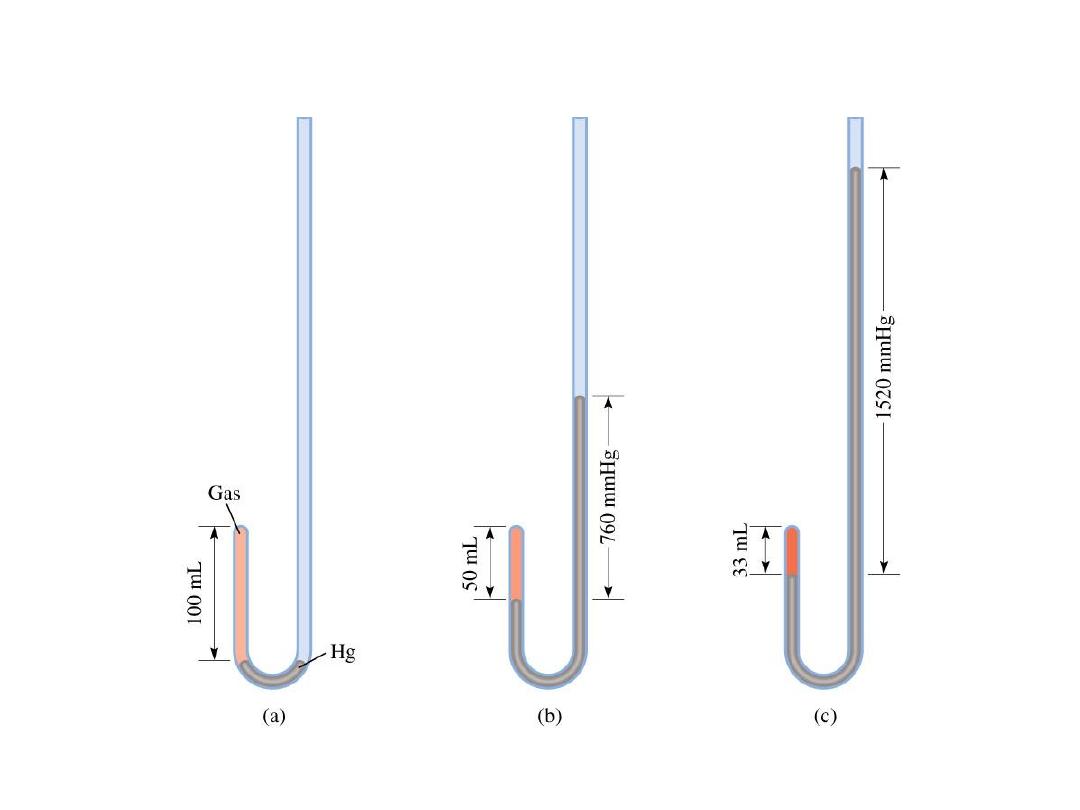
5.3
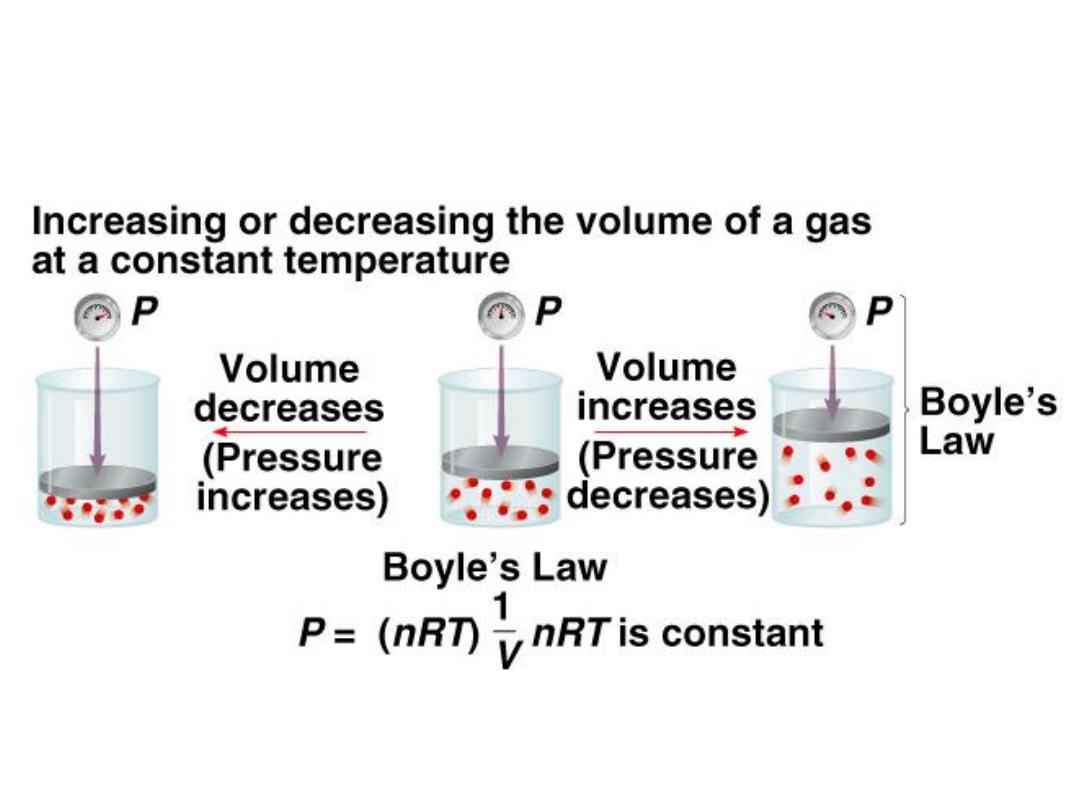
As P (h) increases
V decreases
Apparatus for Studying the Relationship Between
Pressure and Volume of a Gas
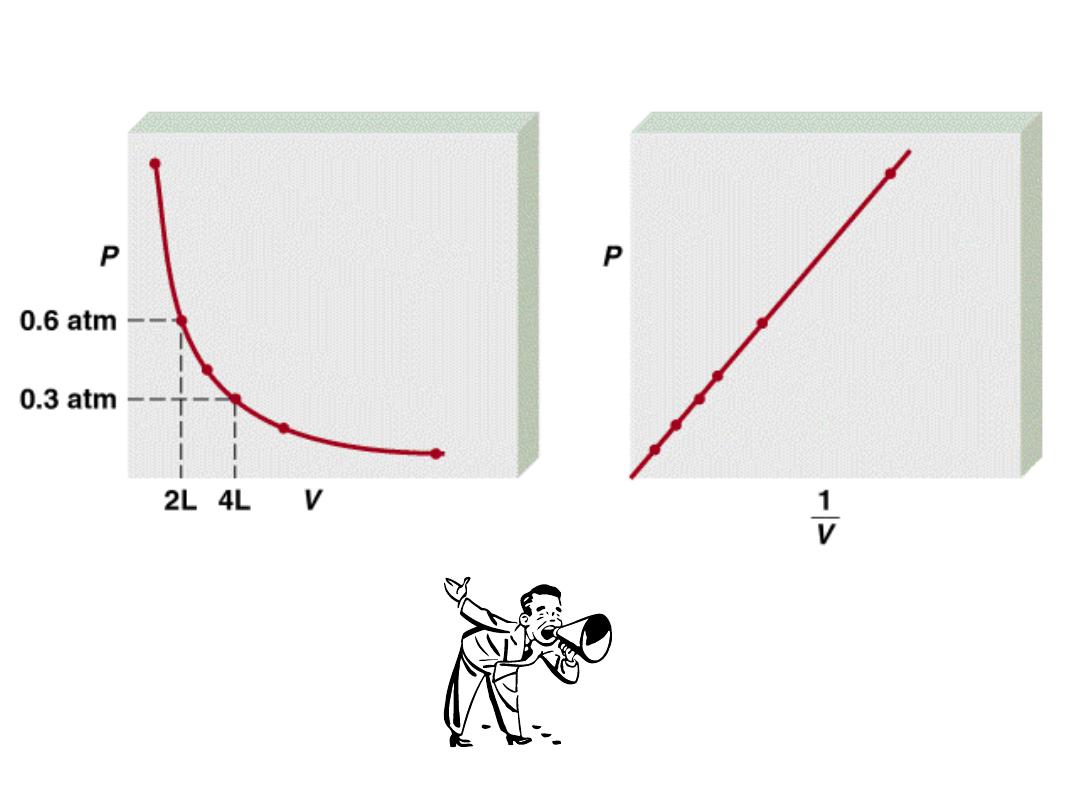
P
a 1/V
P x V = constant
P
1
x V
1
= P
2
x V
2
5.3
Boyle’s Law
Constant temperature
Constant amount of gas

A sample of chlorine gas occupies a volume of 946 mL
at a pressure of 726 mmHg. What is the pressure of
the gas (in mmHg) if the volume is reduced at constant
temperature to 154 mL?
P
1
x V
1
= P
2
x V
2
P
1
= 726 mmHg
V
1
= 946 mL
P
2
= ?
V
2
= 154 mL
P
2
=
P
1
x V
1
V
2
726 mmHg x 946 mL
154 mL
=
= 4460 mmHg
5.3
P x V = constant
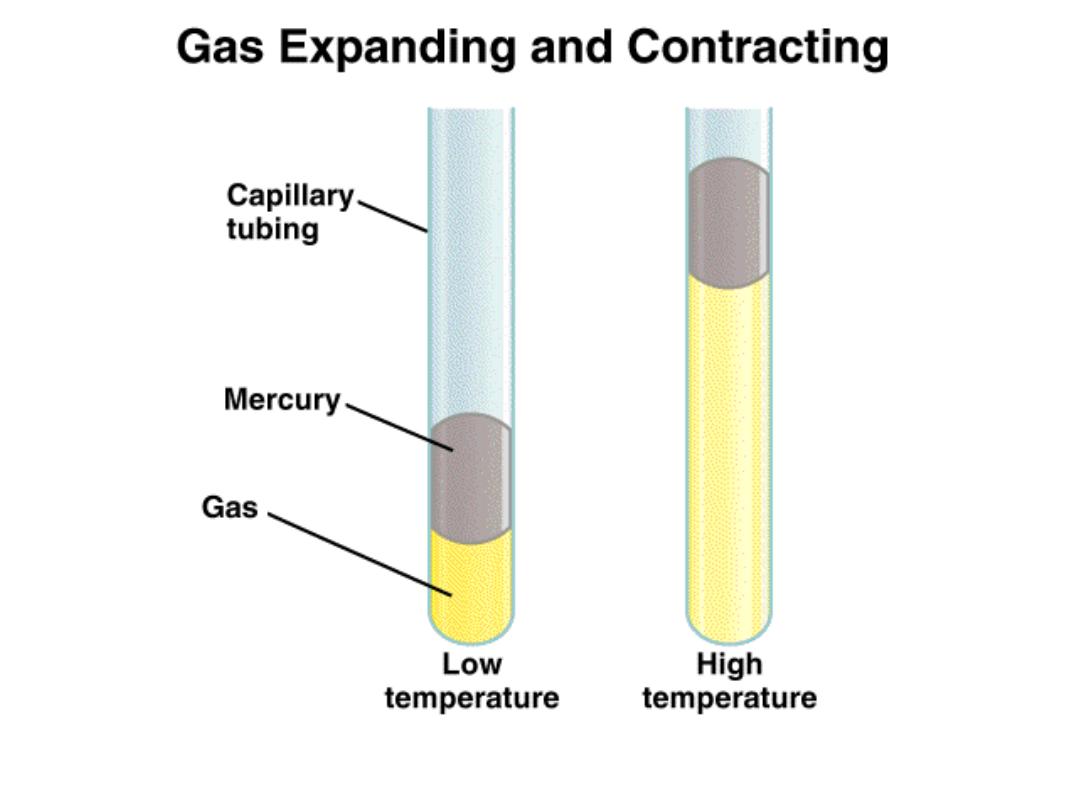
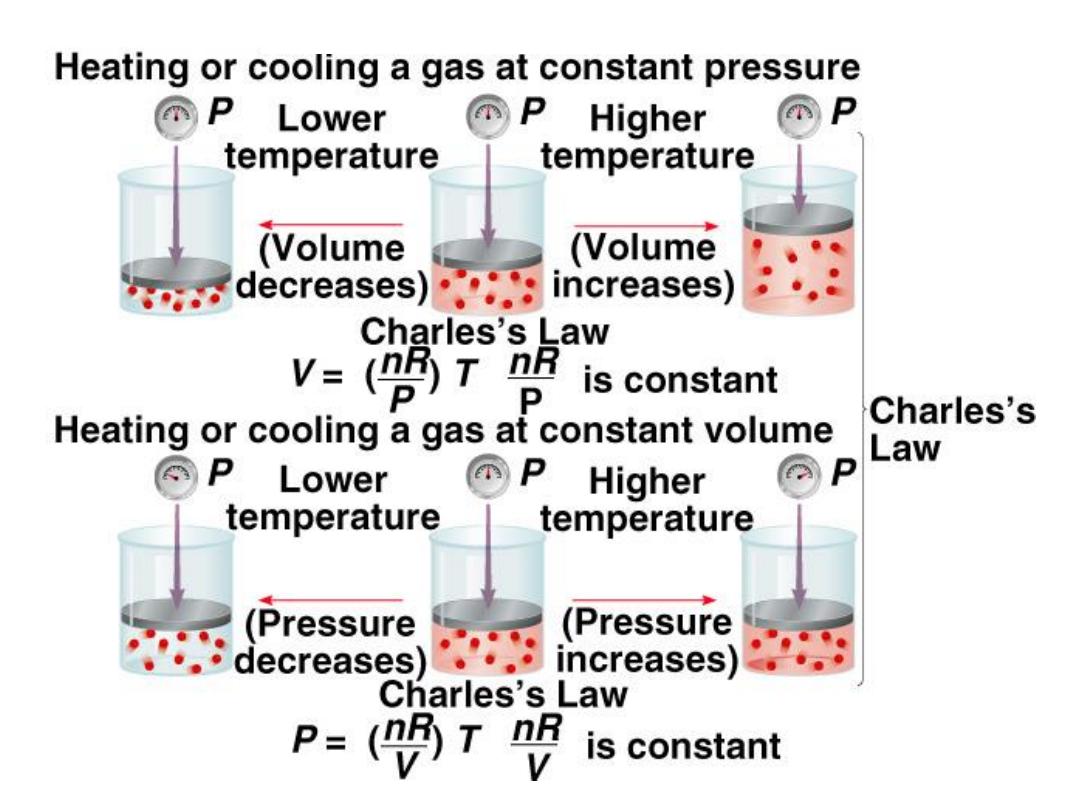
As T increases
V increases
5.3
Variation of gas volume with temperature
at constant pressure.
5.3
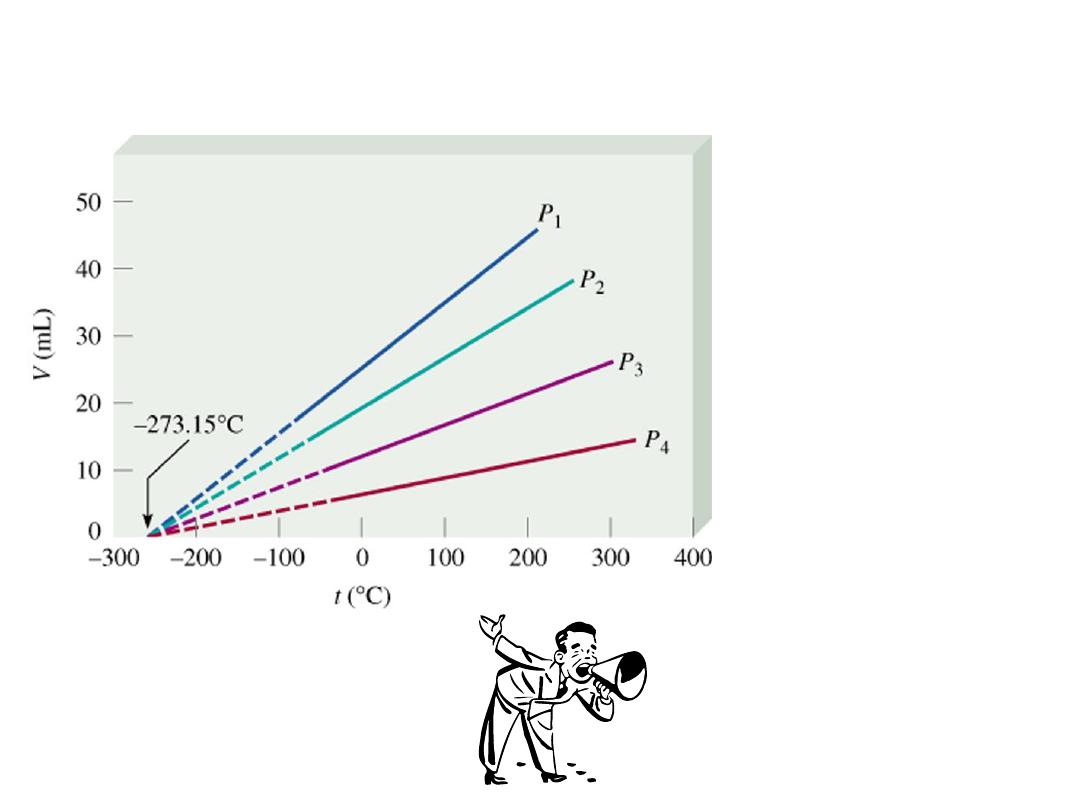
V
a T
V = constant x T
V
1
/T
1
= V
2
/T
2
T (K) = t (
0
C) + 273.15
Charles’ &
Gay-
Lussac’s
Law
Temperature must be
in Kelvin
A sample of carbon monoxide gas occupies 3.20 L at
125
0
C. At what temperature will the gas occupy a
volume of 1.54 L if the pressure remains constant?
V
1
= 3.20 L
T
1
= 398.15 K
V
2
= 1.54 L
T
2
= ?
T
2
=
V
2
x T
1
V
1
1.54 L x 398.15 K
3.20 L
=
= 192 K
5.3
V
1
/T
1
= V
2
/T
2
T
1
= 125 (
0
C) + 273.15 (K) = 398.15 K
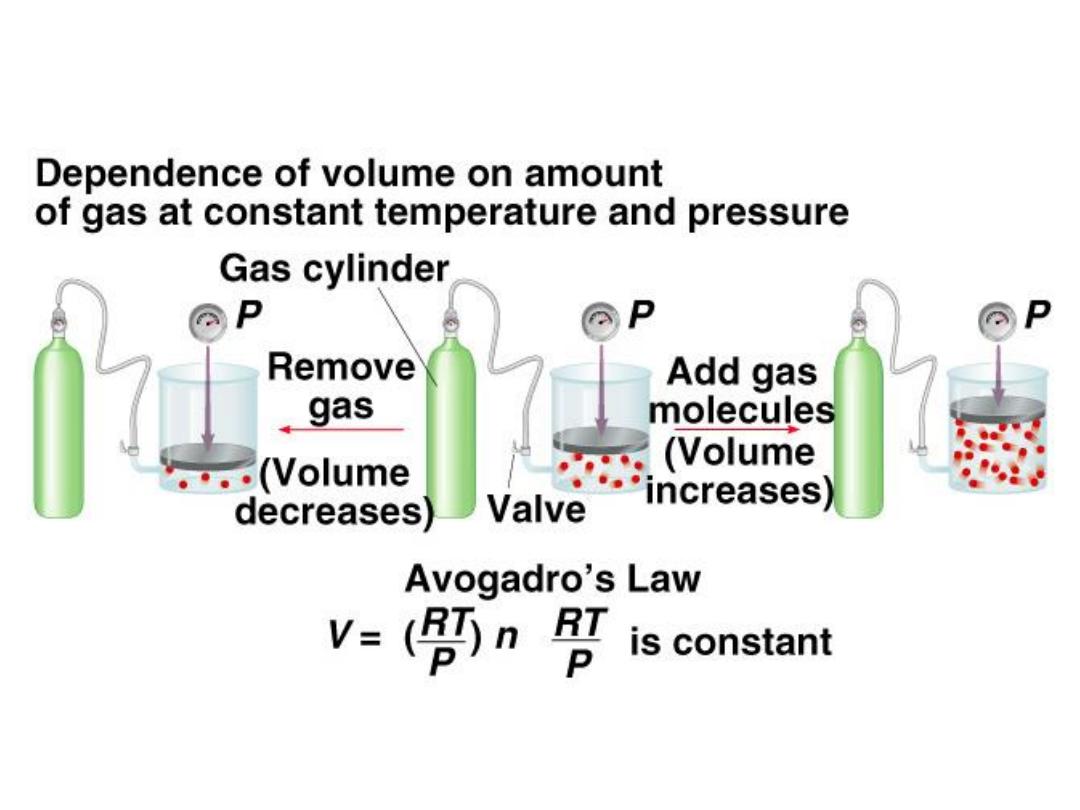
Avogadro’s Law
V
a number of moles (n)
V = constant x n
V
1
/ n
1
= V
2
/ n
2
5.3
Constant temperature
Constant pressure

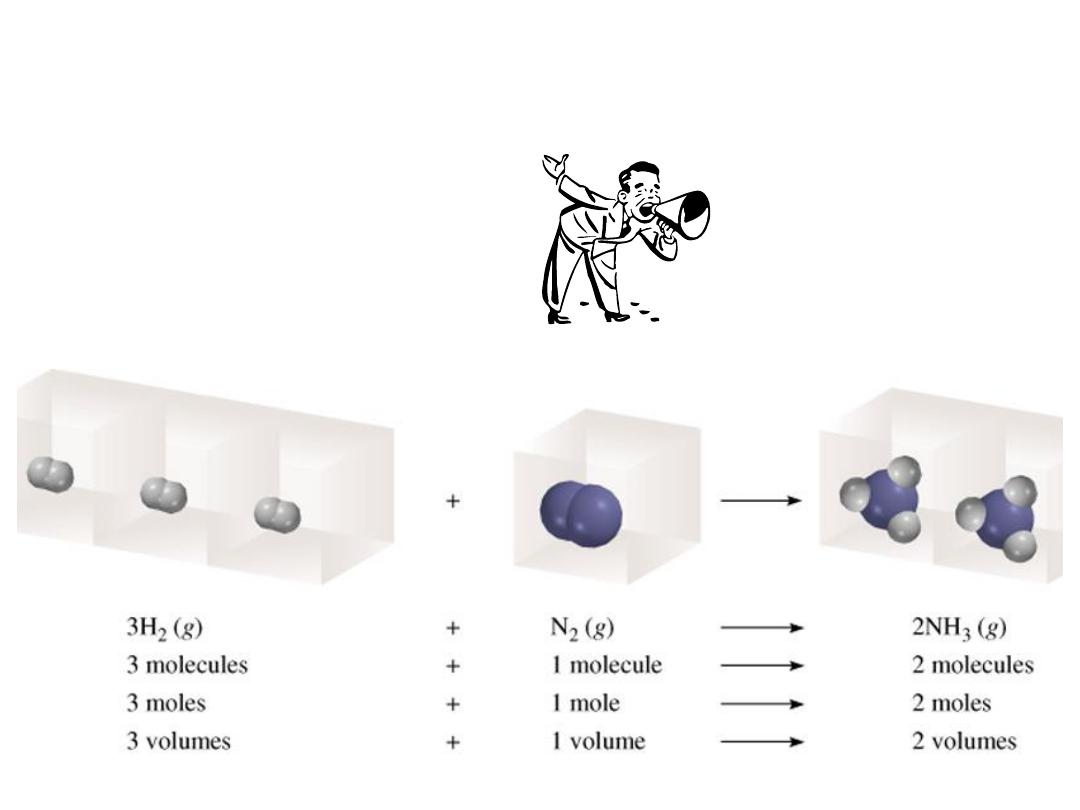
Ammonia burns in oxygen to form nitric oxide (NO)
and water vapor. How many volumes of NO are
obtained from one volume of ammonia at the same
temperature and pressure?
4NH
3
+ 5O
2
4NO + 6H
2
O
1 mole NH
3
1 mole NO
At constant T and P
1 volume NH
3
1 volume NO
5.3
5.3
5.3
5.3
Ideal Gas Equation
5.4
Charles’ law: V
a T (at constant n and P)
Avogadro’s law: V
a n (at constant P and T)
Boyle’s law: V
a (at constant n and T)
1
P
V
a
nT
P
V = constant x = R
nT
P
nT
P
R is the gas constant
PV = nRT

The conditions 0
0
C and 1 atm are called standard
temperature and pressure (STP).
PV = nRT
R =
PV
nT
=
(1 atm)(22.414L)
(1 mol)(273.15 K)
R = 0.082057 L
• atm / (mol • K)
5.4
Experiments show that at STP, 1 mole of an ideal
gas occupies 22.414 L.
What is the volume (in liters) occupied by 49.8 g of HCl
at STP?
PV = nRT
V =
nRT
P
T = 0
0
C = 273.15 K
P = 1 atm
n = 49.8 g x
1 mol HCl
36.45 g HCl
= 1.37 mol
V =
1 atm
1.37 mol x 0.0821 x 273.15 K
L
•atm
mol
•K
V = 30.6 L
5.4

Argon is an inert gas used in lightbulbs to retard the
vaporization of the filament. A certain lightbulb
containing argon at 1.20 atm and 18
0
C is heated to
85
0
C at constant volume. What is the final pressure of
argon in the lightbulb (in atm)?
PV = nRT
n, V and R are constant
nR
V
=
P
T
= constant
P
1
T
1
P
2
T
2
=
P
1
= 1.20 atm
T
1
= 291 K
P
2
= ?
T
2
= 358 K
P
2
= P
1
x
T
2
T
1
= 1.20 atm x 358 K
291 K
= 1.48 atm
5.4
Density (d) Calculations
d =
m
V
=
P
M
RT
m is the mass of the gas in g
M
is the molar mass of the gas
Molar Mass (
M
) of a Gaseous Substance
dRT
P
M
=
d is the density of the gas in g/L
5.4
A 2.10-L vessel contains 4.65 g of a gas at 1.00 atm
and 27.0
0
C. What is the molar mass of the gas?
5.4
dRT
P
M
=
d =
m
V
4.65 g
2.10 L
=
=
2.21
g
L
M
=
2.21
g
L
1 atm
x 0.0821 x 300.15 K
L
•atm
mol
•K
M
=
54.6 g/mol
Gas Stoichiometry
What is the volume of CO
2
produced at 37
0
C and 1.00
atm when 5.60 g of glucose are used up in the reaction:
C
6
H
12
O
6
(s) + 6O
2
(g) 6CO
2
(g) + 6H
2
O (l)
g C
6
H
12
O
6
mol C
6
H
12
O
6
mol CO
2
V CO
2
5.60 g C
6
H
12
O
6
1 mol C
6
H
12
O
6
180 g C
6
H
12
O
6
x
6 mol CO
2
1 mol C
6
H
12
O
6
x
= 0.187 mol CO
2
V =
nRT
P
0.187 mol x 0.0821 x 310.15 K
L
•atm
mol
•K
1.00 atm
=
= 4.76 L
5.5
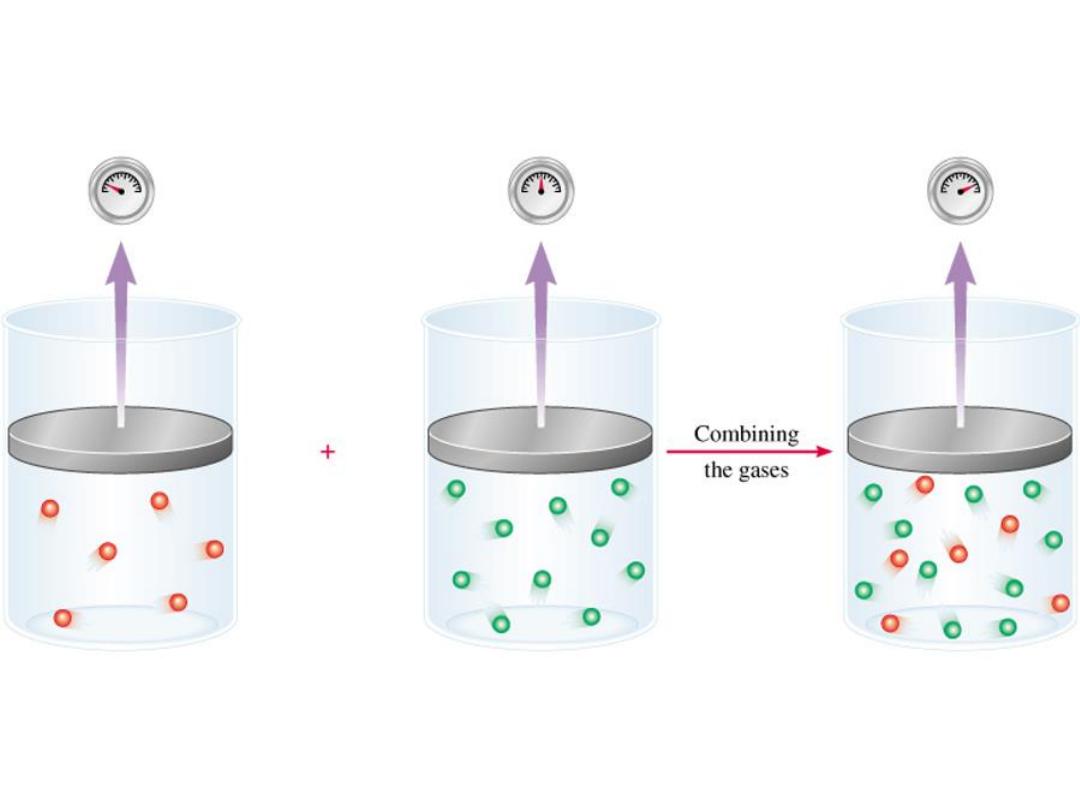
Dalton’s Law of Partial Pressures
V and T
are
constant
P
1
P
2
P
total
=
P
1
+
P
2
5.6
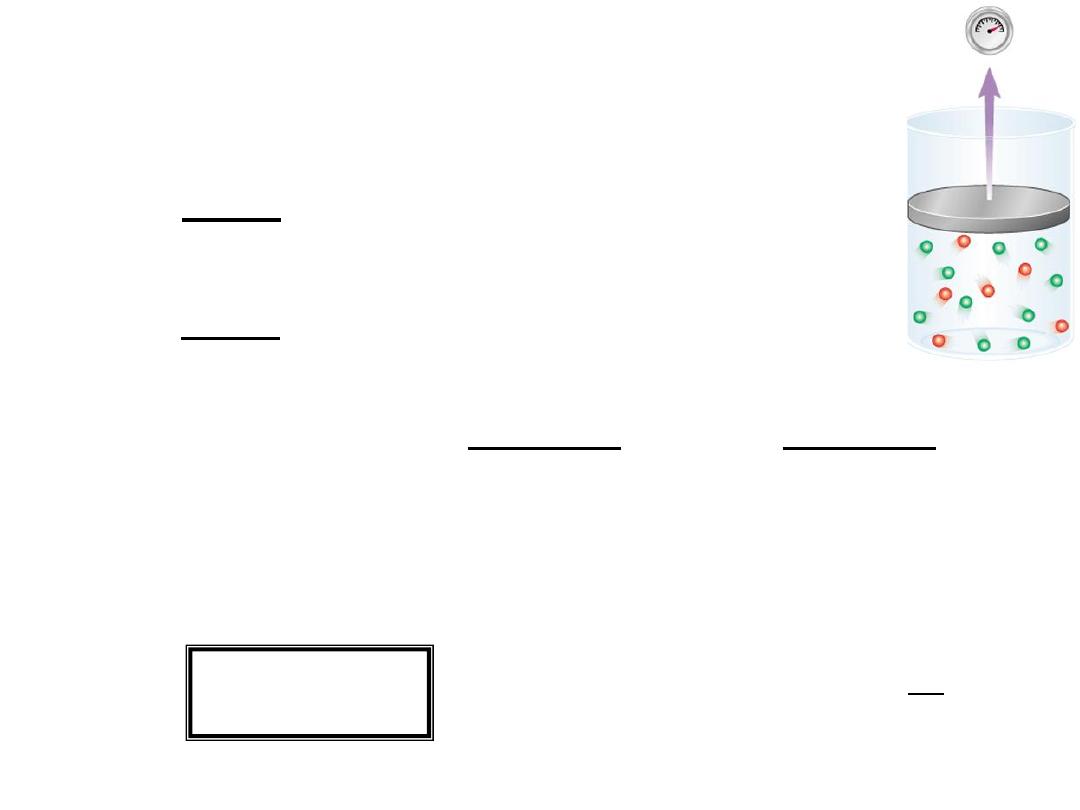
Consider a case in which two gases,
A
and
B
, are in a
container of volume V.
P
A
=
n
A
RT
V
P
B
=
n
B
RT
V
n
A
is the number of moles of
A
n
B
is the number of moles of
B
P
T
=
P
A
+
P
B
X
A
=
n
A
n
A
+
n
B
X
B
=
n
B
n
A
+
n
B
P
A
=
X
A
P
T
P
B
=
X
B
P
T
P
i
= X
i
P
T
5.6
mole fraction (X
i
) =
n
i
n
T

A sample of natural gas contains 8.24 moles of CH
4
,
0.421 moles of C
2
H
6
, and 0.116 moles of C
3
H
8
. If the
total pressure of the gases is 1.37 atm, what is the
partial pressure of propane (C
3
H
8
)?
P
i
= X
i
P
T
X
propane
=
0.116
8.24 + 0.421 + 0.116
P
T
= 1.37 atm
= 0.0132
P
propane
= 0.0132 x 1.37 atm = 0.0181 atm
5.6
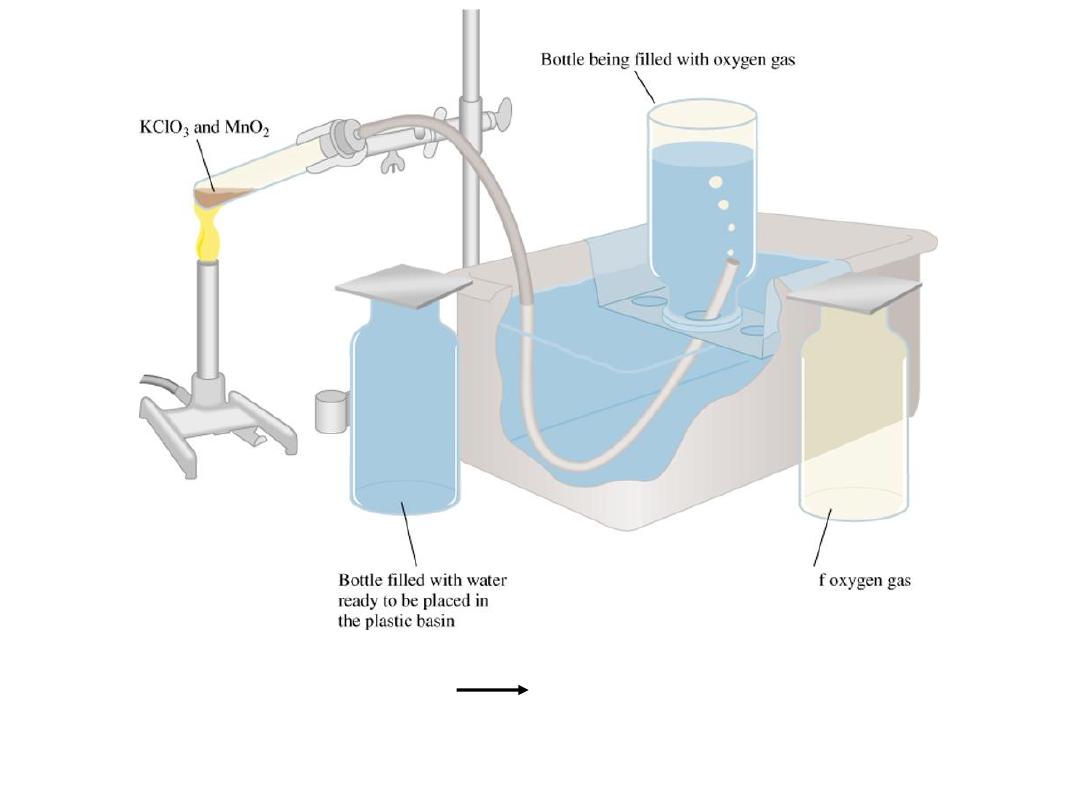
2KClO
3
(s) 2KCl (s) + 3O
2
(g)
Bottle full of oxygen
gas and water vapor
P
T
= P
O
+ P
H O
2
2
5.6
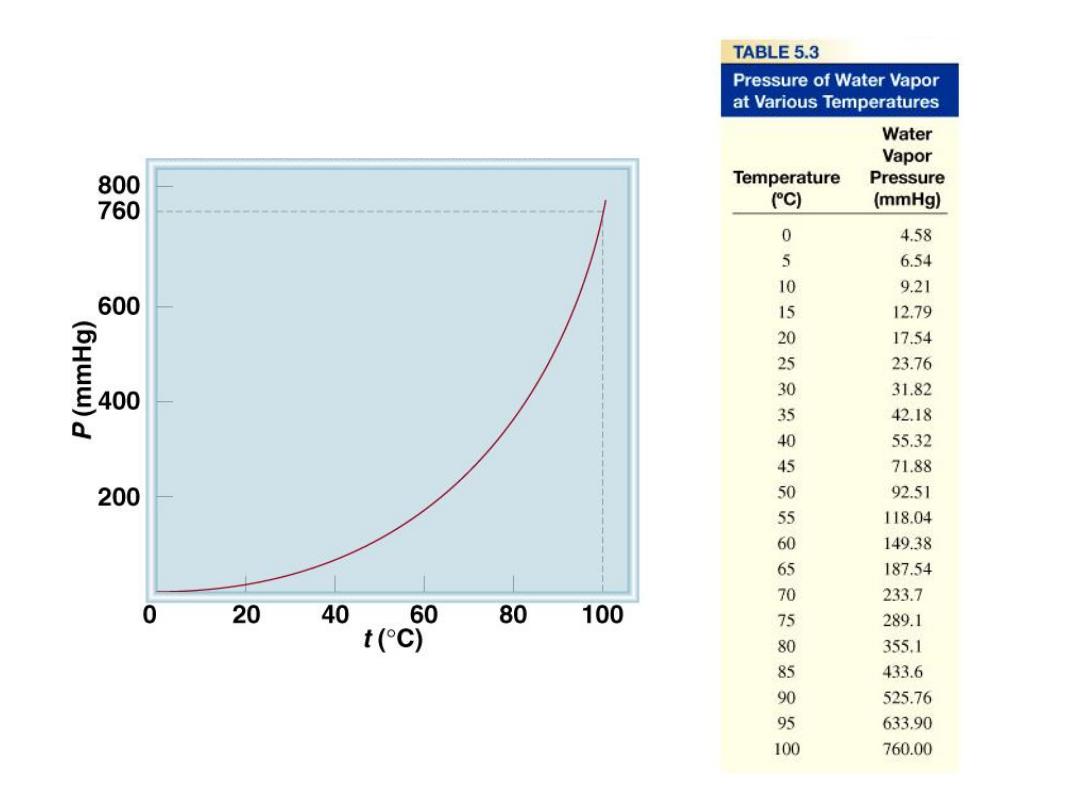
5.6
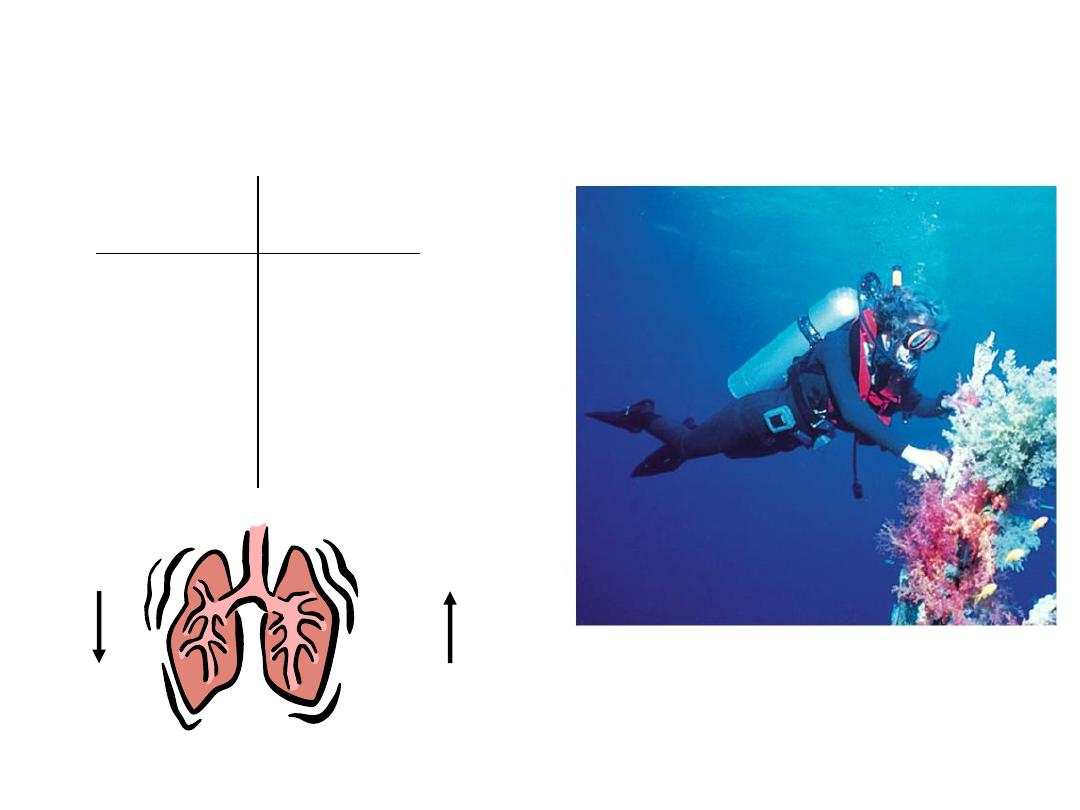
Chemistry in Action:
Scuba Diving and the Gas Laws
P
V
Depth (ft)
Pressure
(atm)
0
1
33
2
66
3
5.6

Kinetic Molecular Theory of Gases
1. A gas is composed of molecules that are separated from
each other by distances far greater than their own
dimensions. The molecules can be considered to be points;
that is, they possess mass but have negligible volume.
2. Gas molecules are in constant motion in random directions,
and they frequently collide with one another. Collisions
among molecules are perfectly elastic.
3. Gas molecules exert neither attractive nor repulsive forces
on one another.
4. The average kinetic energy of the molecules is proportional
to the temperature of the gas in kelvins. Any two gases at
the same temperature will have the same average kinetic
energy
5.7
KE = ½ mu
2

Kinetic theory of gases and …
• Compressibility of Gases
• Boyle’s Law
P
a collision rate with wall
Collision rate
a number density
Number density
a 1/V
P
a 1/V
• Charles’ Law
P
a collision rate with wall
Collision rate
a average kinetic energy of gas molecules
Average kinetic energy
a T
P
a T
5.7

Kinetic theory of gases and …
• Avogadro’s Law
P
a collision rate with wall
Collision rate
a number density
Number density
a n
P
a n
• Dalton’s Law of Partial Pressures
Molecules do not attract or repel one another
P exerted by one type of molecule is unaffected by the
presence of another gas
P
total
=
SP
i
5.7
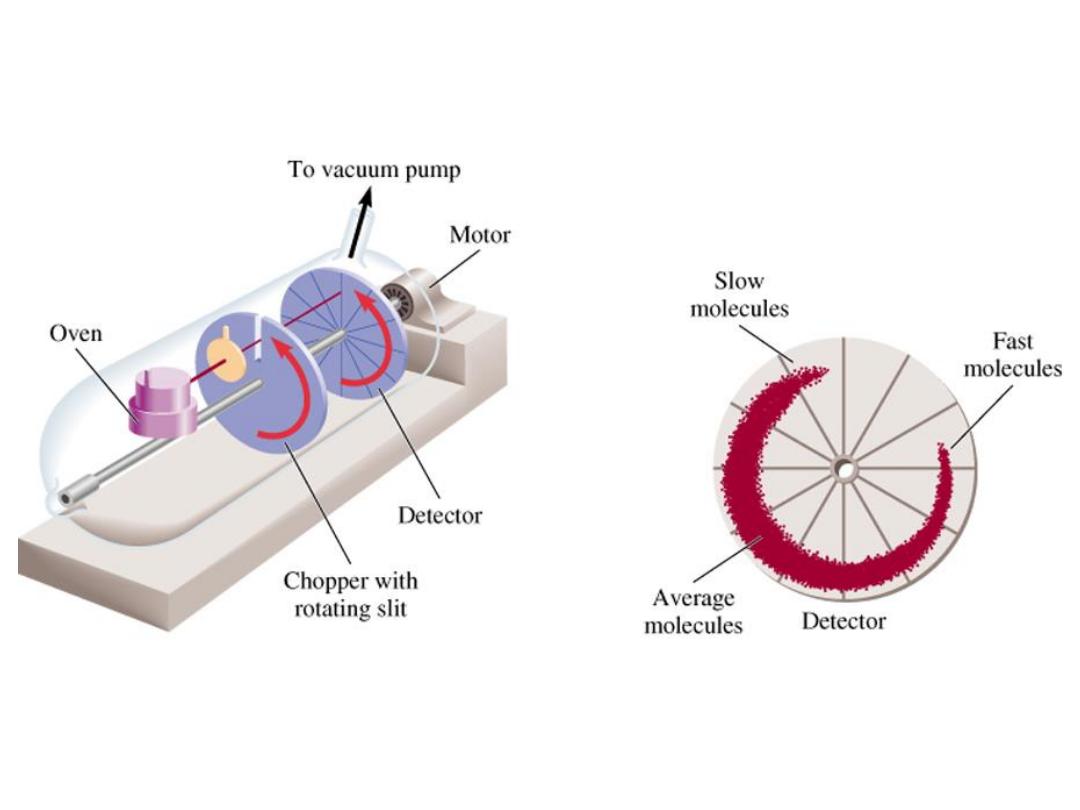
Apparatus for studying molecular speed distribution
5.7
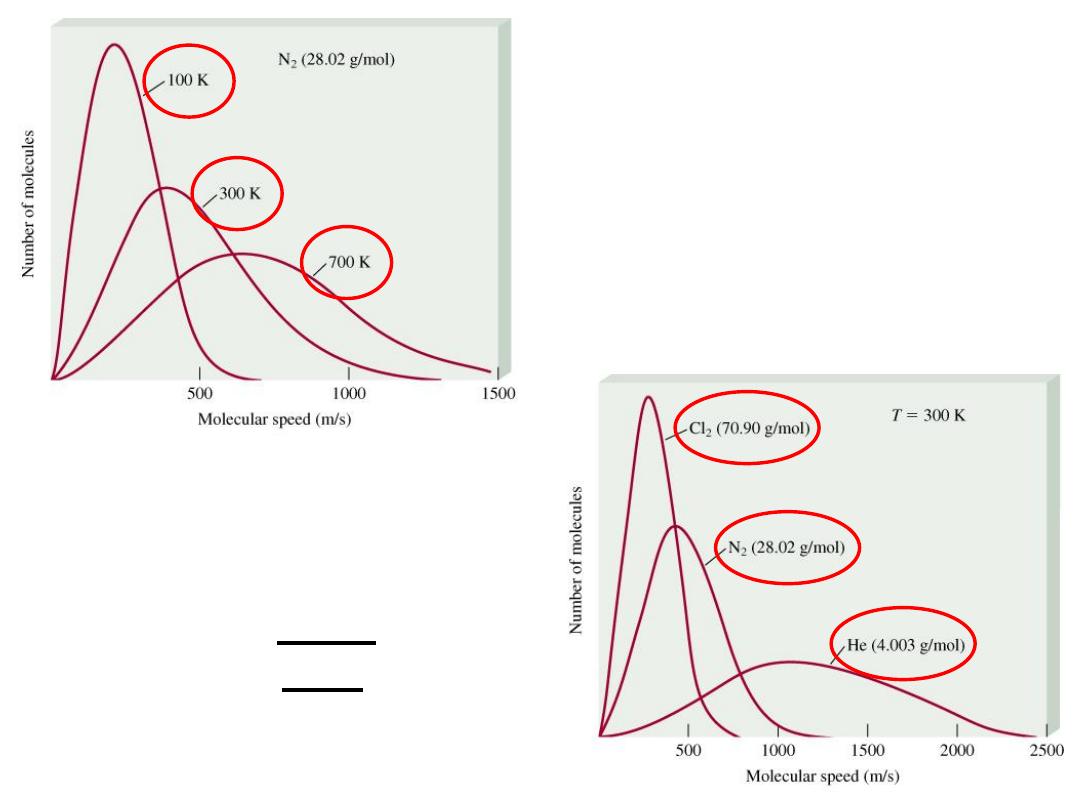
The distribution of speeds
for nitrogen gas molecules
at three different temperatures
The distribution of speeds
of three different gases
at the same temperature
5.7
u
rms
=
3RT
M
Chemistry in Action: Super Cold Atoms
Gaseous Rb Atoms
1.7 x 10
-7
K
Bose-Einstein Condensate

Gas diffusion is the gradual mixing of molecules of one gas
with molecules of another by virtue of their kinetic properties.
5.7
NH
3
17 g/mol
HCl
36 g/mol
NH
4
Cl
r
1
r
2
M
2
M
1
=
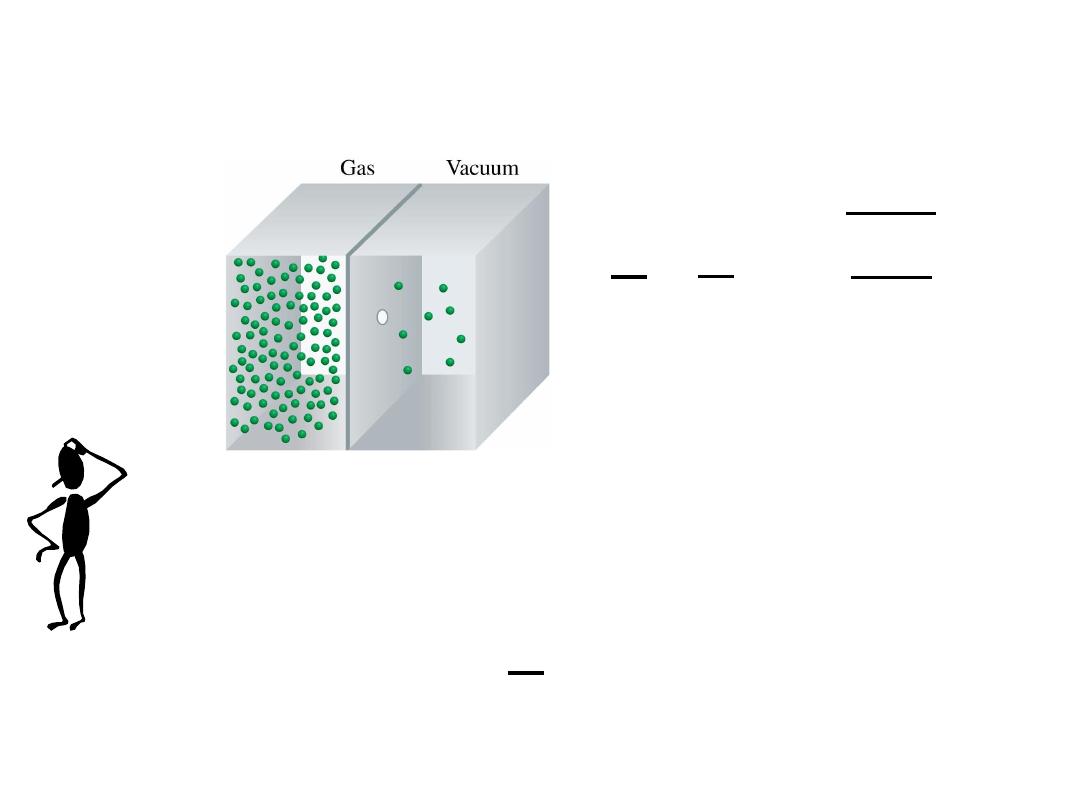
Gas effusion is the is the process by which gas under
pressure escapes from one compartment of a container to
another by passing through a small opening.
5.7
r
1
r
2
t
2
t
1
M
2
M
1
=
=
Nickel forms a gaseous compound of the formula
Ni(CO)
x
What is the value of x given that under the same
conditions methane (CH
4
) effuses 3.3 times faster than
the compound?
r
1
= 3.3 x r
2
M
1
= 16 g/mol
M
2
=
r
1
r
2
( )
2
x
M
1
= (3.3)
2
x 16 = 174.2
58.7 + x
• 28 = 174.2
x = 4.1 ~ 4
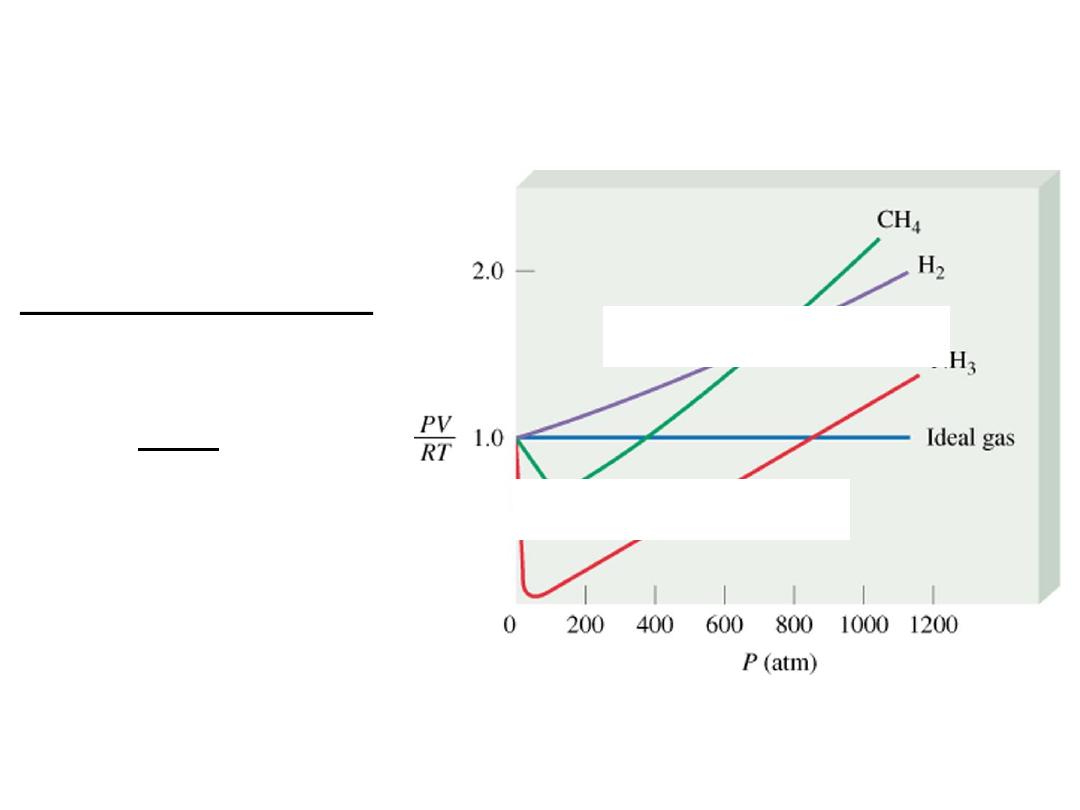
Deviations from Ideal Behavior
1 mole of ideal gas
PV = nRT
n =
PV
RT
= 1.0
5.8
Repulsive Forces
Attractive Forces
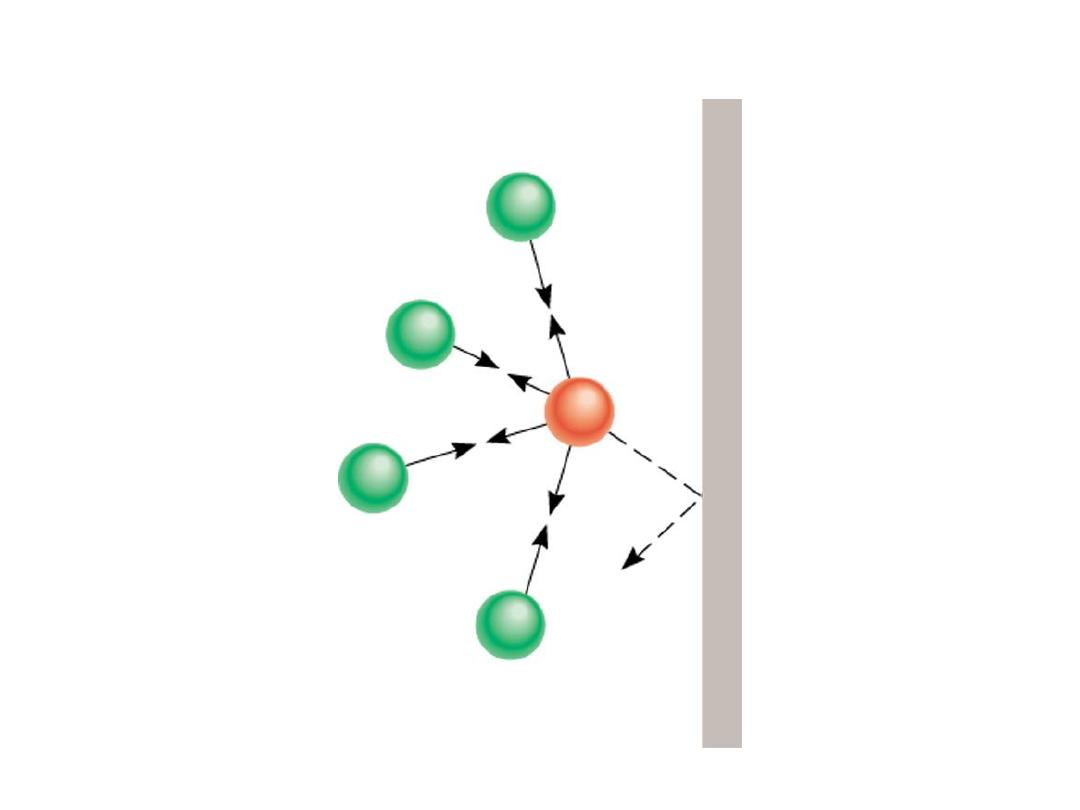
Effect of intermolecular forces on the pressure exerted by a gas.
5.8
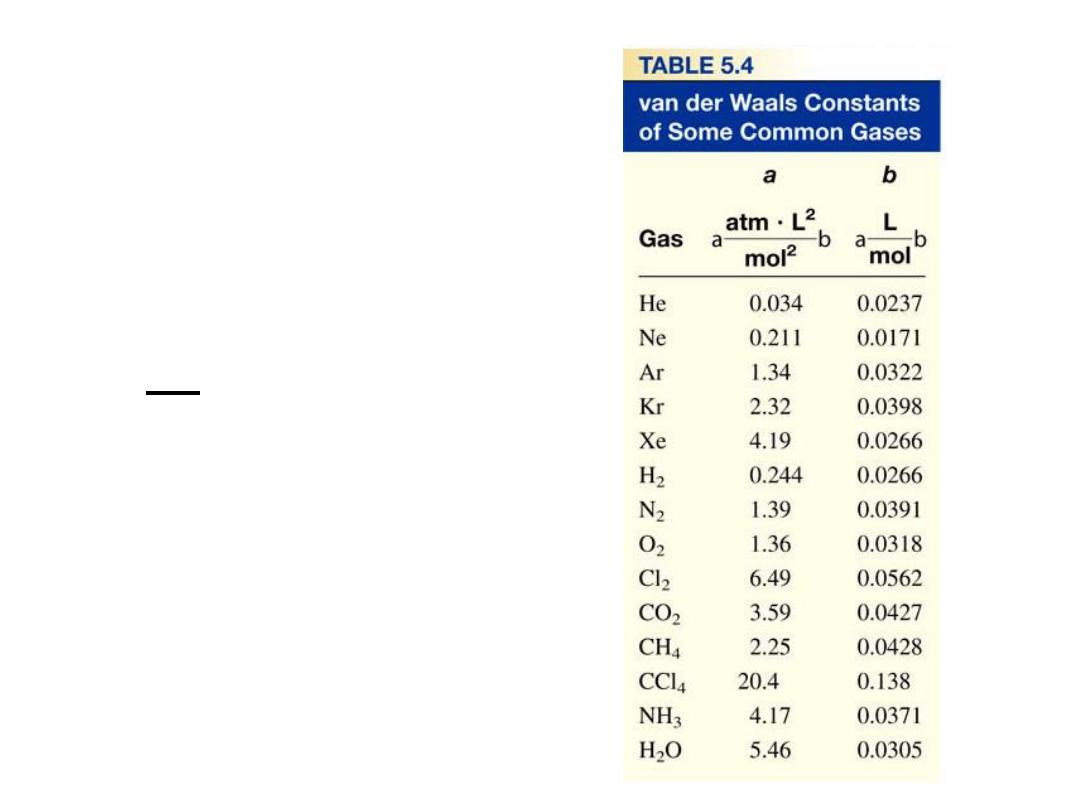
5.8
Van der Waals equation
nonideal gas
P + (V
– nb) = nRT
an
2
V
2
(
)
}
corrected
pressure
}
corrected
volume
