Chemical Kinetics
Chapter 13
Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
Chemical Kinetics
Thermodynamics
– does a reaction take place?
Kinetics
– how fast does a reaction proceed?
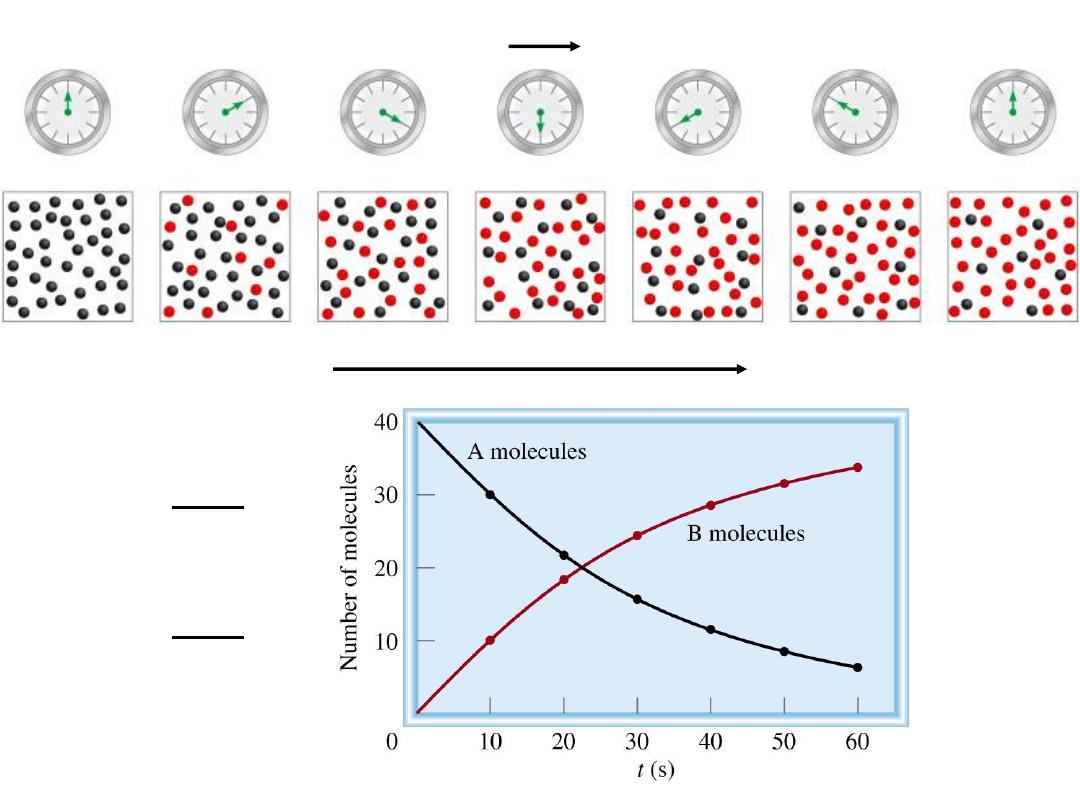
Reaction rate is the change in the concentration of a
reactant or a product with time (M/s).
A B
rate = -
D[A]
Dt
rate =
D[B]
Dt
D[A] = change in concentration of A over
time period
Dt
D[B] = change in concentration of B over
time period
Dt
Because [A] decreases with time,
D[A] is negative
.
13.1
A
B
13.1
rate = -
D[A]
Dt
rate =
D[
B
]
Dt
time
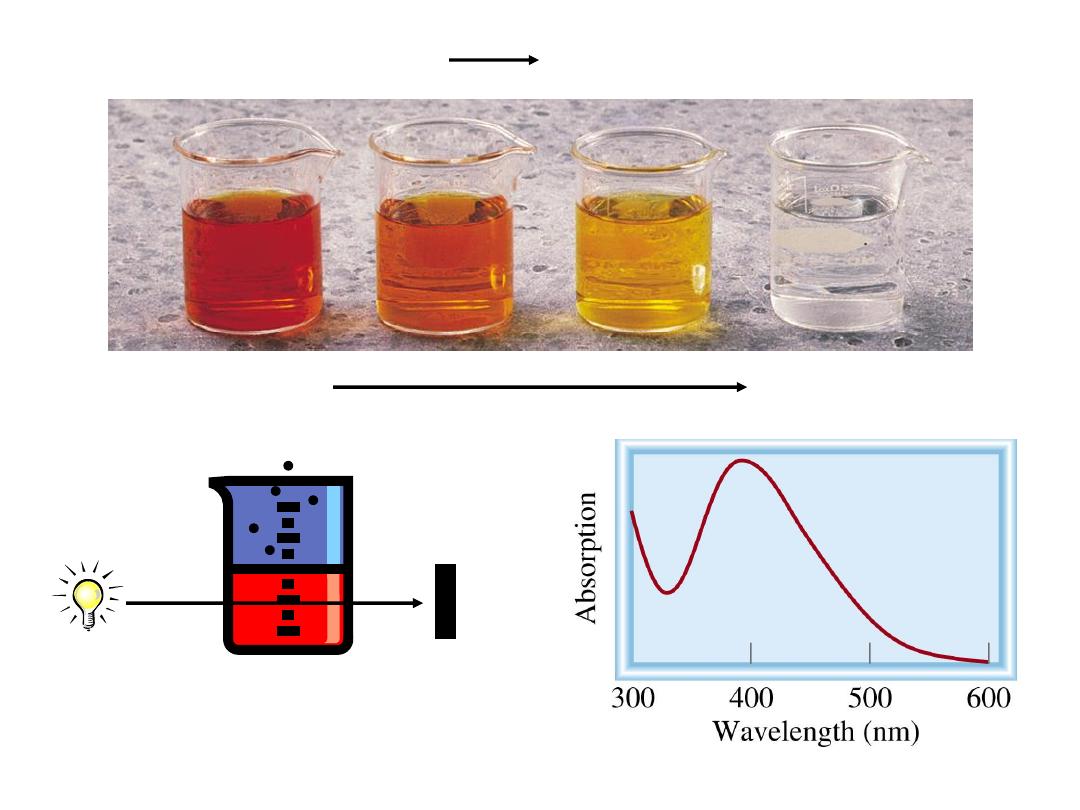
Br
2
(aq)
+ HCOOH
(aq)
2Br
-
(aq)
+ 2H
+
(aq)
+ CO
2
(g)
time
393 nm
light
Detector
D[Br
2
]
a DAbsorption
13.1
Br
2
(aq)
+ HCOOH
(aq)
2Br
-
(aq)
+ 2H
+
(aq)
+ CO
2
(g)
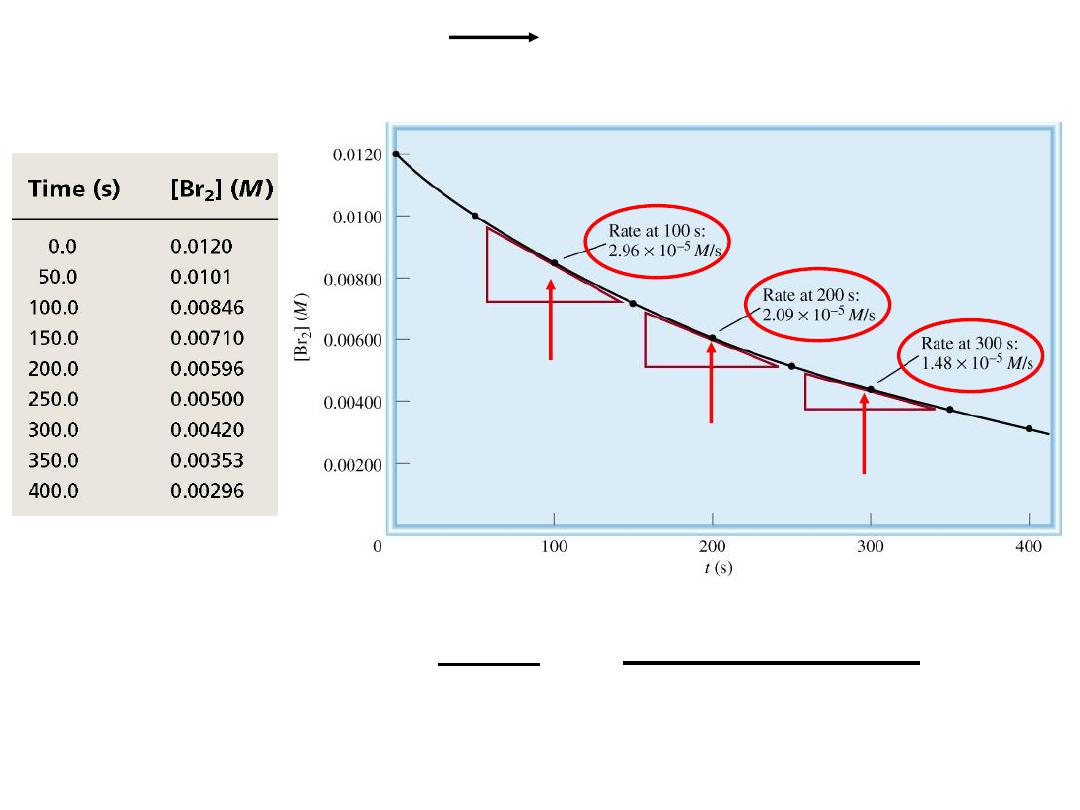
average rate = -
D[Br
2
]
Dt
= -
[Br
2
]
final
– [Br
2
]
initial
t
final
- t
initial
slope of
tangent
slope of
tangent
slope of
tangent
instantaneous rate = rate for specific instance in time
13.1
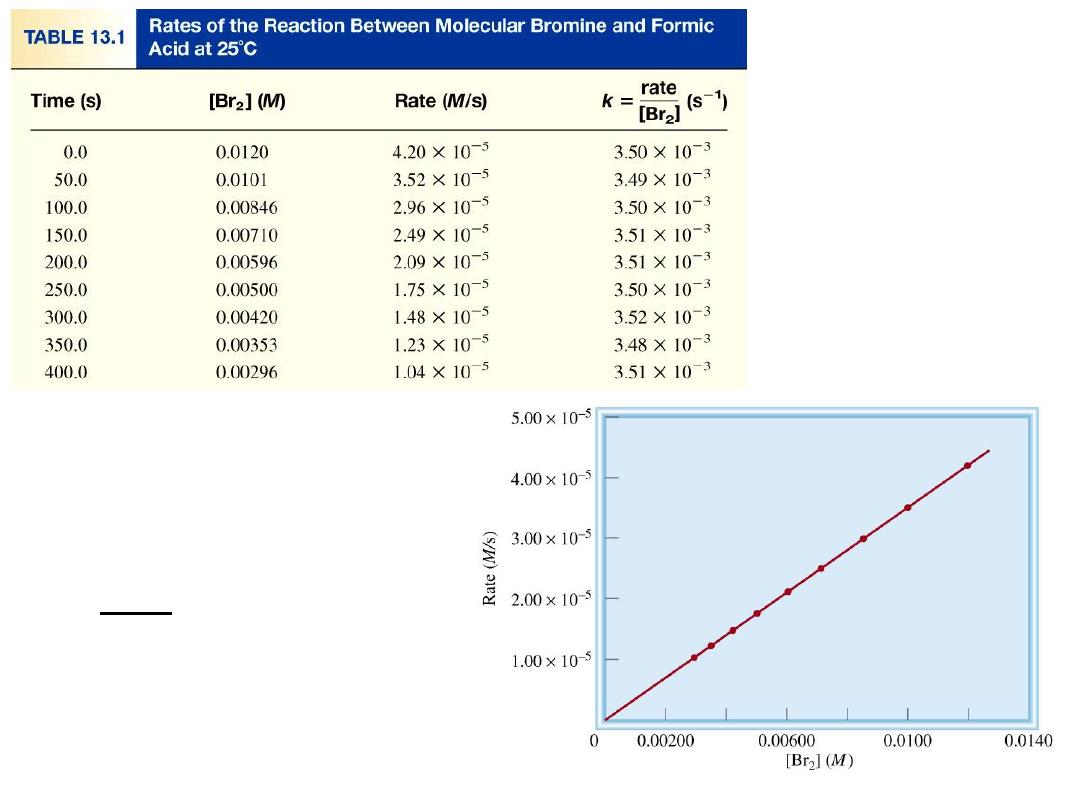
rate
a [Br
2
]
rate = k [Br
2
]
k =
rate
[Br
2
]
13.1
= rate constant
= 3.50 x 10
-3
s
-1

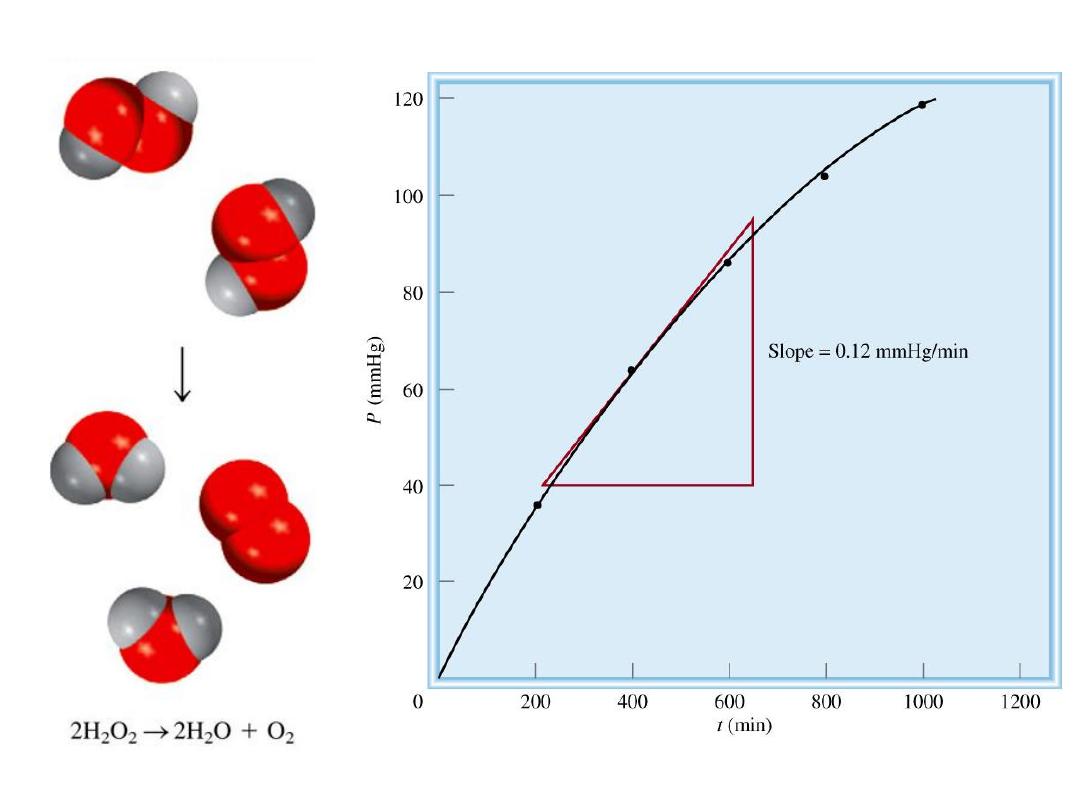
2H
2
O
2
(aq) 2H
2
O (l) + O
2
(g)
PV = nRT
P = RT = [O
2
]RT
n
V
[O
2
] = P
RT
1
rate =
D[O
2
]
Dt
RT
1
DP
Dt
=
measure
DP over time
13.1
13.1
Reaction Rates and Stoichiometry
13.1
2A B
Two moles of A disappear for each mole of B that is formed.
rate =
D[B]
Dt
rate = -
D[A]
Dt
1
2
aA + bB cC + dD
rate = -
D[A]
Dt
1
a
= -
D[B]
Dt
1
b
=
D[C]
Dt
1
c
=
D[D]
Dt
1
d
Write the rate expression for the following reaction:
CH
4
(g)
+ 2O
2
(g)
CO
2
(g)
+ 2H
2
O
(g)
rate = -
D[CH
4
]
Dt
= -
D[O
2
]
Dt
1
2
=
D[H
2
O]
Dt
1
2
=
D[CO
2
]
Dt
13.1
The Rate Law
13.2
The rate law expresses the relationship of the rate of a reaction
to the rate constant and the concentrations of the reactants
raised to some powers.
aA + bB cC + dD
Rate = k [A]
x
[B]
y
reaction is xth order in A
reaction is yth order in B
reaction is (x +y)th order overall
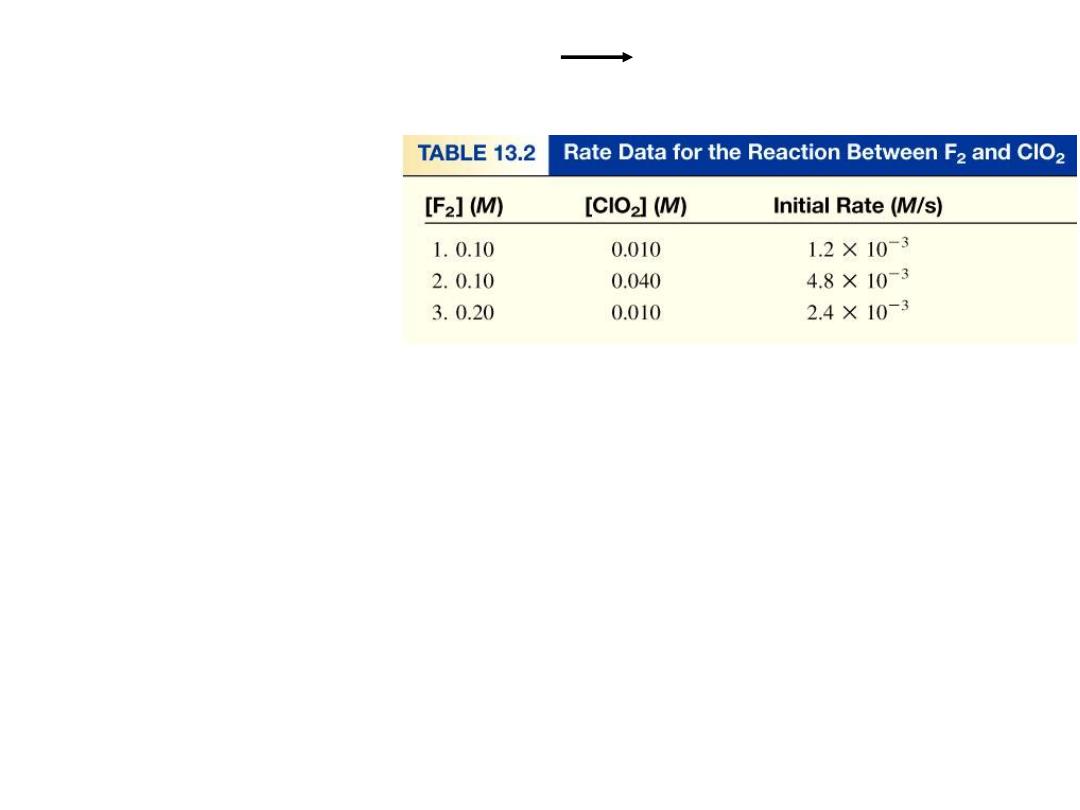
F
2
(g)
+ 2ClO
2
(g)
2FClO
2
(g)
rate = k [F
2
]
x
[ClO
2
]
y
Double [F
2
] with [ClO
2
] constant
Rate doubles
x = 1
Quadruple [ClO
2
] with [F
2
] constant
Rate quadruples
y = 1
rate = k [F
2
][ClO
2
]
13.2
F
2
(g)
+ 2ClO
2
(g)
2FClO
2
(g)
rate = k [F
2
][ClO
2
]
Rate Laws
•
Rate laws are always determined experimentally.
•
Reaction order is always defined in terms of reactant
(not product) concentrations.
•
The order of a reactant is not related to the
stoichiometric coefficient of the reactant in the balanced
chemical equation.
1
13.2
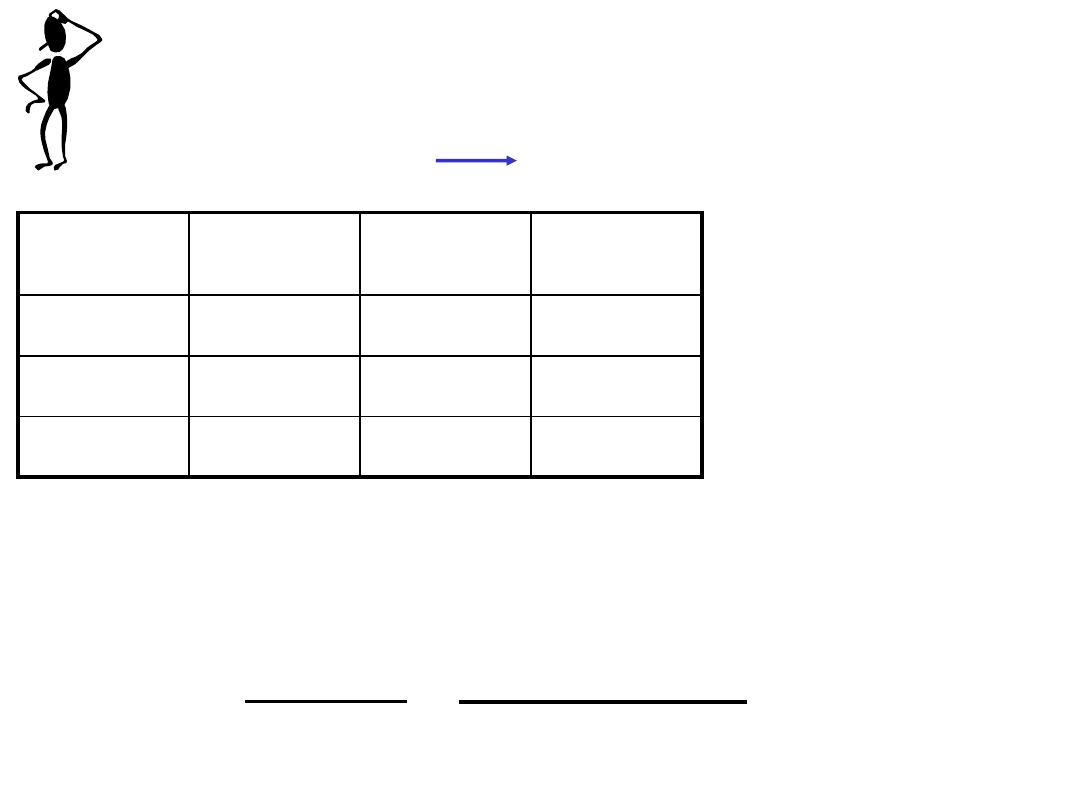
Determine the rate law and calculate the rate constant for
the following reaction from the following data:
S
2
O
8
2-
(aq)
+ 3I
-
(aq)
2SO
4
2-
(aq)
+ I
3
-
(aq)
Experiment
[S
2
O
8
2-
]
[I
-
]
Initial Rate
(M/s)
1
0.08
0.034
2.2 x 10
-4
2
0.08
0.017
1.1 x 10
-4
3
0.16
0.017
2.2 x 10
-4
rate = k [S
2
O
8
2-
]
x
[I
-
]
y
Double [I
-
], rate doubles (experiment 1 & 2)
y = 1
Double [S
2
O
8
2-
], rate doubles (experiment 2 & 3)
x = 1
k =
rate
[S
2
O
8
2-
][I
-
]
=
2.2 x 10
-4
M/s
(0.08 M)(0.034 M)
= 0.08/M
•
s
13.2
rate = k [S
2
O
8
2-
][I
-
]
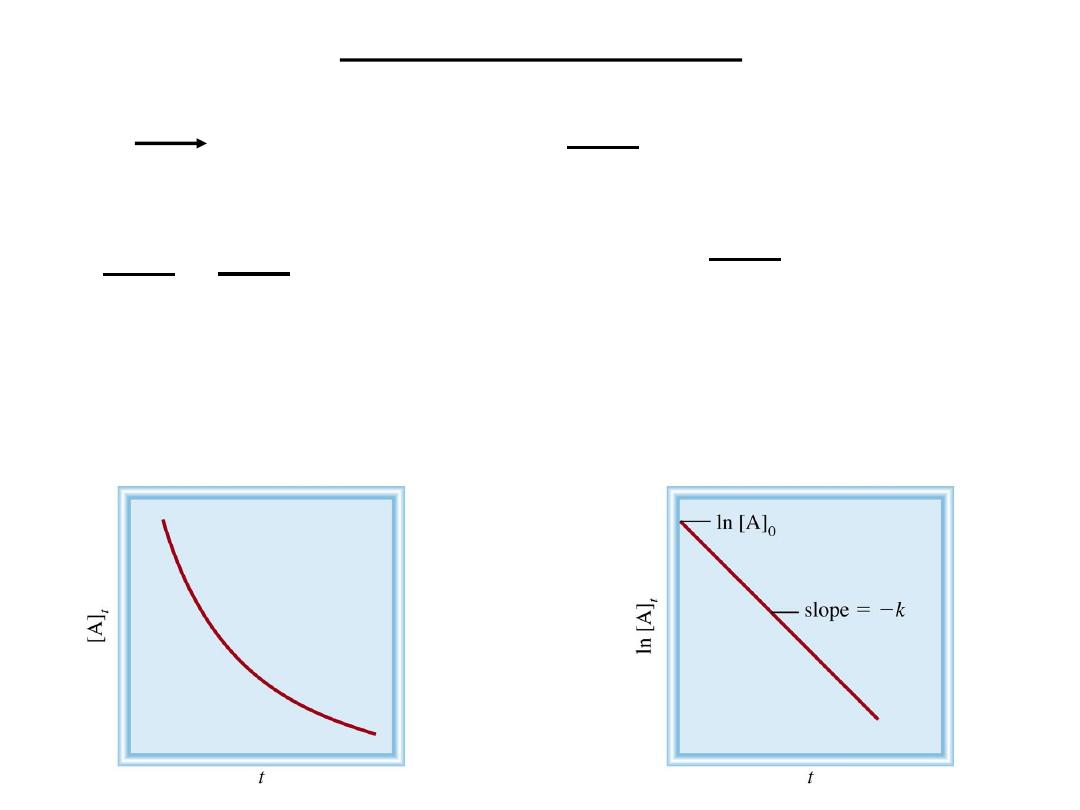
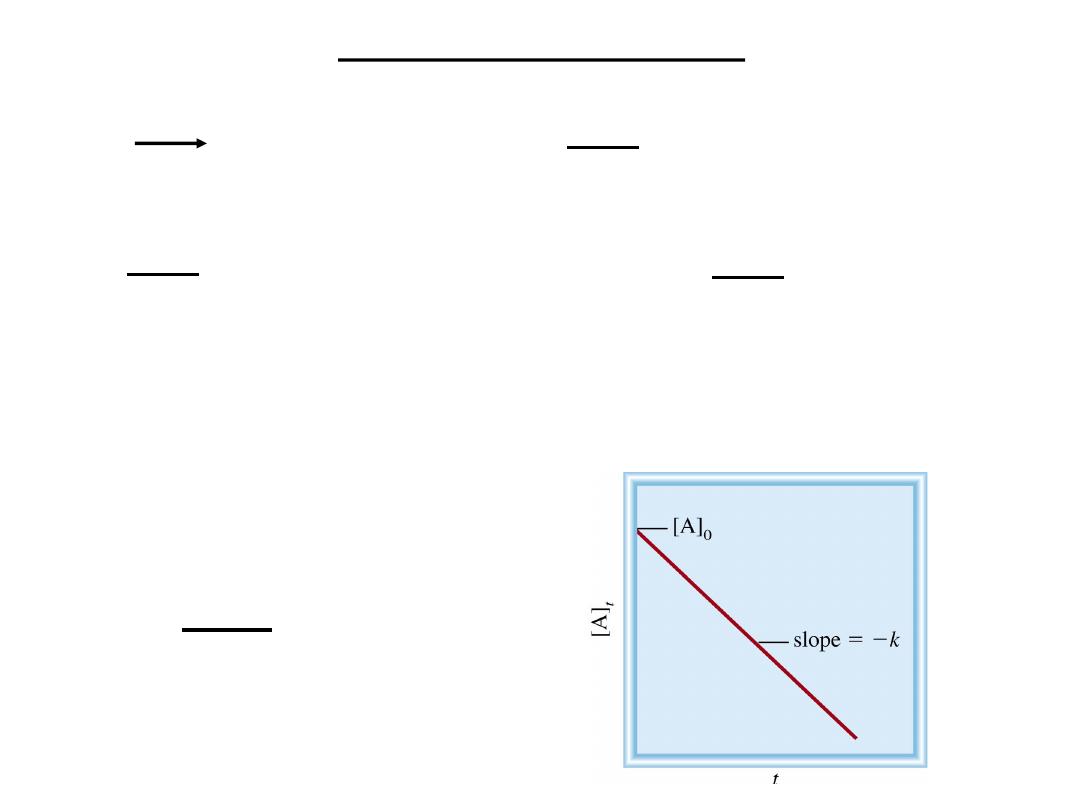
First-Order Reactions
13.3
A product
rate = -
D[A]
Dt
rate = k [A]
k =
rate
[A]
= 1/s or s
-1
M/s
M
=
D[A]
Dt
= k [A]
-
[A] is the concentration of A at any time t
[A]
0
is the concentration of A at time t=0
[A] = [A]
0
exp(-kt)
ln[A] = ln[A]
0
- kt
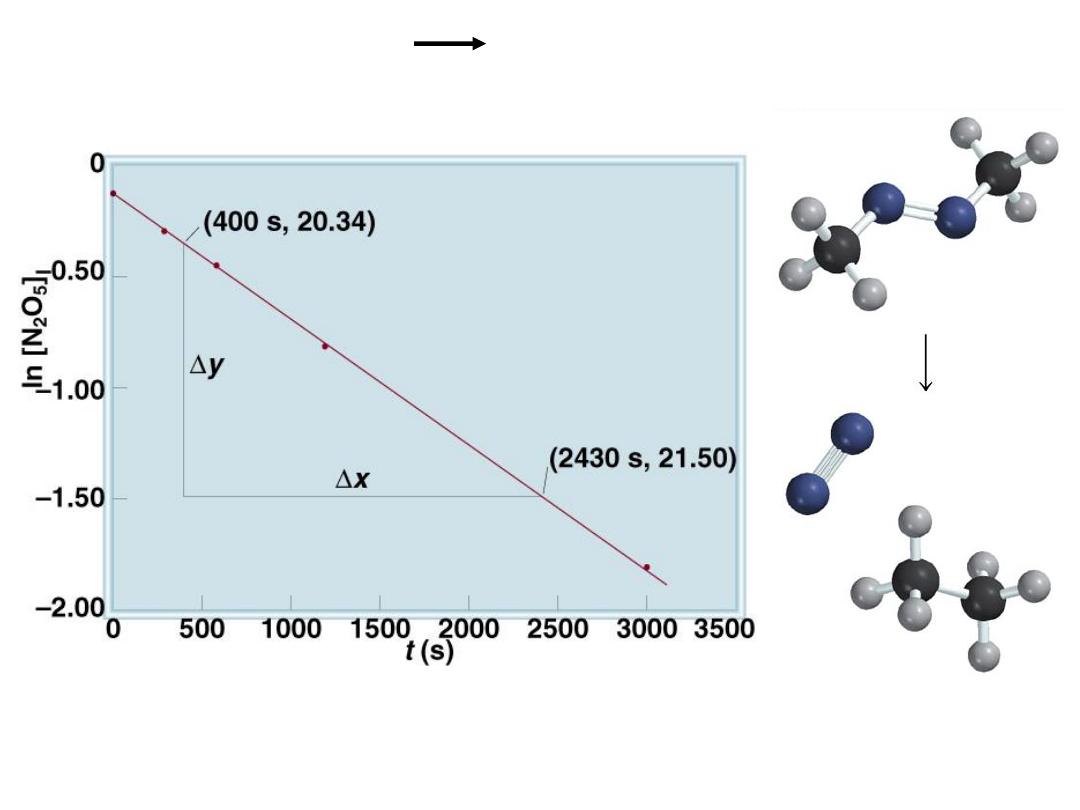
13.3
2N
2
O
5
4NO
2
(g) + O
2
(g)
The reaction 2A B is first order in A with a rate
constant of 2.8 x 10
-2
s
-1
at 80
0
C. How long will it take for A
to decrease from 0.88 M to 0.14 M ?
ln[A] = ln[A]
0
- kt
kt = ln[A]
0
– ln[A]
t =
ln[A]
0
– ln[A]
k
= 66 s
[A]
0
= 0.88 M
[A] = 0.14 M
ln
[A]
0
[A]
k
=
ln
0.88 M
0.14 M
2.8 x 10
-2
s
-1
=
13.3
First-Order Reactions
13.3
The half-life, t
½
, is the time required for the concentration of a
reactant to decrease to half of its initial concentration.
t
½
= t when [A] = [A]
0
/2
ln
[A]
0
[A]
0
/2
k
=
t
½
ln2
k
=
0.693
k
=
What is the half-life of N
2
O
5
if it decomposes with a rate
constant of 5.7 x 10
-4
s
-1
?
t
½
ln2
k
=
0.693
5.7 x 10
-4
s
-1
=
= 1200 s = 20 minutes
How do you know decomposition is first order?
units of k (s
-1
)
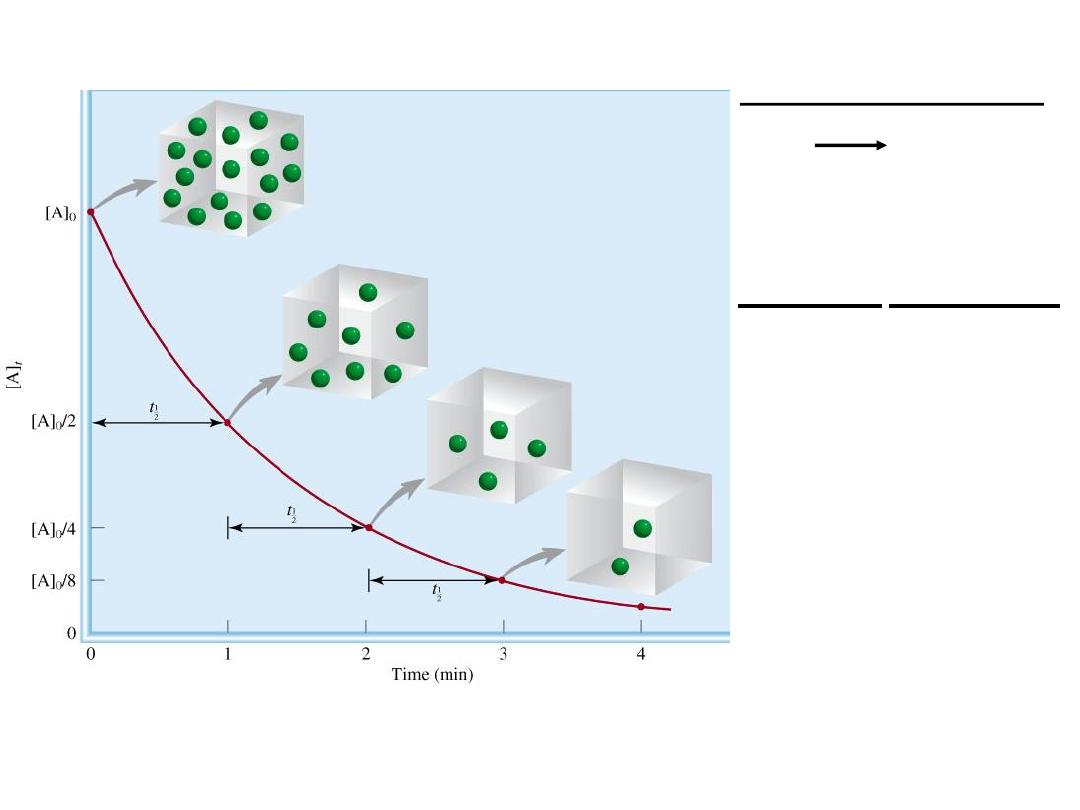
A product
First-order reaction
# of
half-lives [A] = [A]
0
/n
1
2
3
4
2
4
8
16
13.3
Second-Order Reactions
13.3
A product
rate = -
D[A]
Dt
rate = k [A]
2
k =
rate
[A]
2
= 1/M
•
s
M/s
M
2
=
D[A]
Dt
= k [A]
2
-
[A] is the concentration of A at any time t
[A]
0
is the concentration of A at time t=0
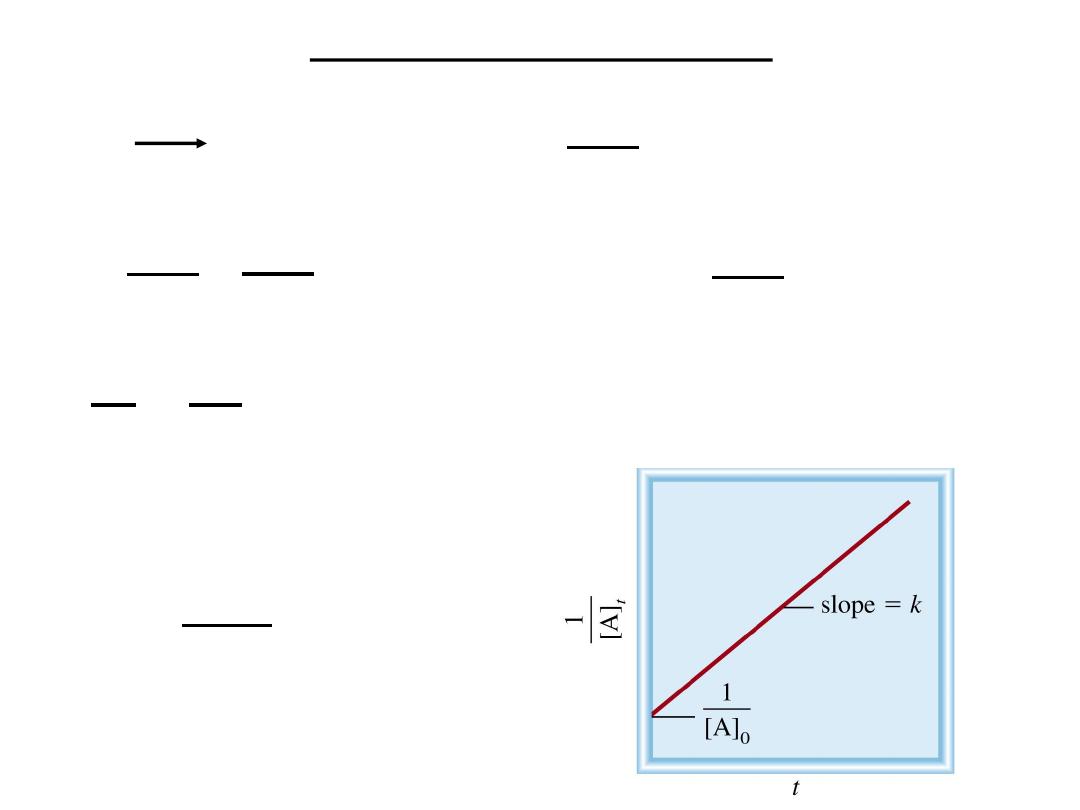
1
[A]
=
1
[A]
0
+ kt
t
½
= t when [A] = [A]
0
/2
t
½
=
1
k[A]
0
Zero-Order Reactions
13.3
A product
rate = -
D[A]
Dt
rate = k [A]
0
= k
k =
rate
[A]
0
= M/s
D[A]
Dt
= k
-
[A] is the concentration of A at any time t
[A]
0
is the concentration of A at time t=0
t
½
= t when [A] = [A]
0
/2
t
½
=
[A]
0
2k
[A] = [A]
0
- kt
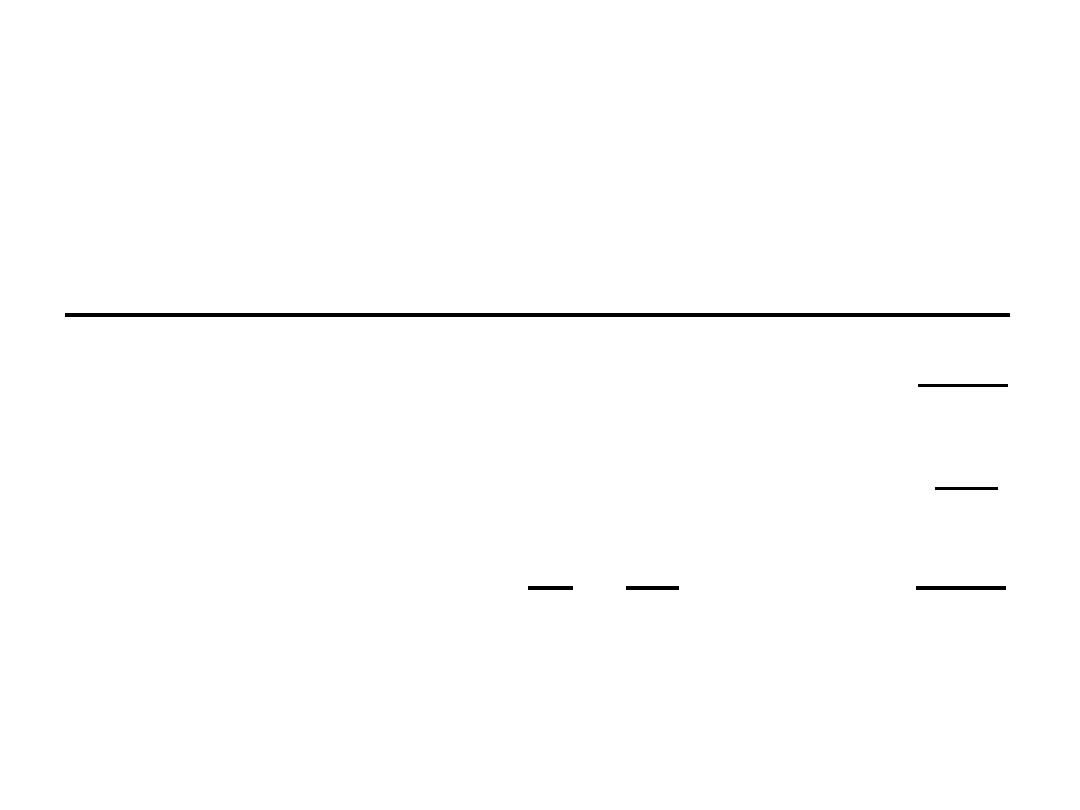
Summary of the Kinetics of Zero-Order, First-Order
and Second-Order Reactions
Order
Rate Law
Concentration-Time
Equation
Half-Life
0
1
2
rate = k
rate = k [A]
rate = k [A]
2
ln[A] = ln[A]
0
- kt
1
[A]
=
1
[A]
0
+ kt
[A] = [A]
0
- kt
t
½
ln2
k
=
t
½
=
[A]
0
2k
t
½
=
1
k[A]
0
13.3
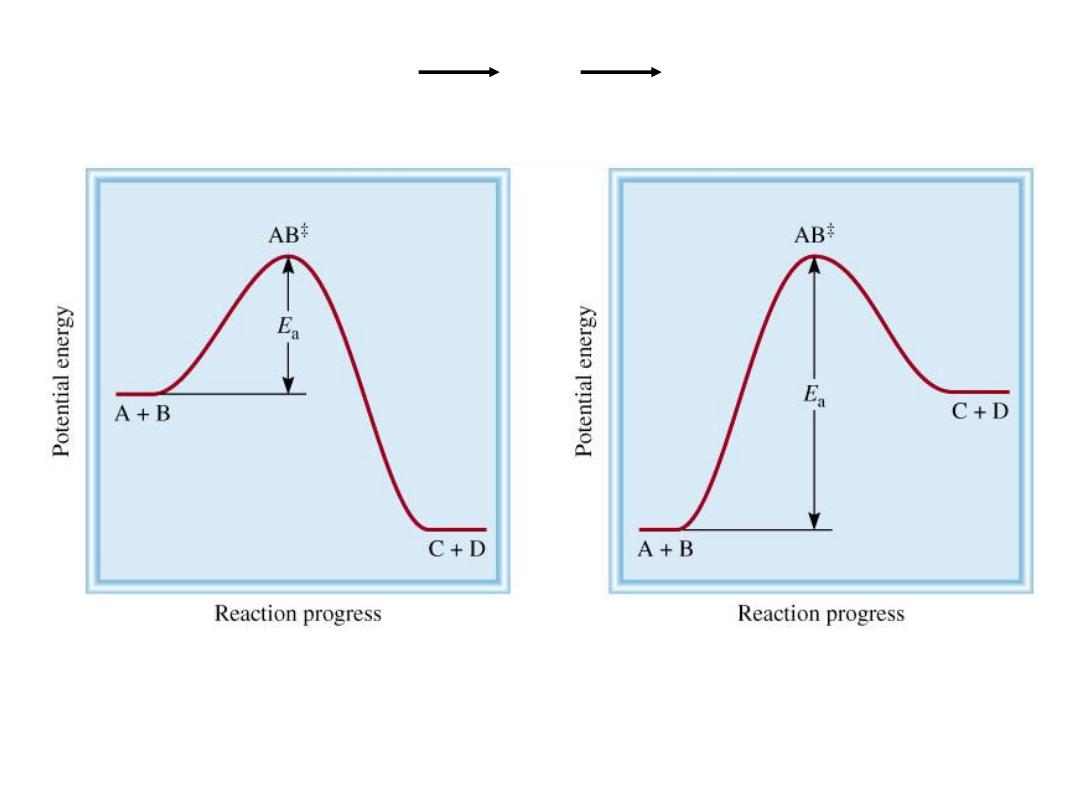
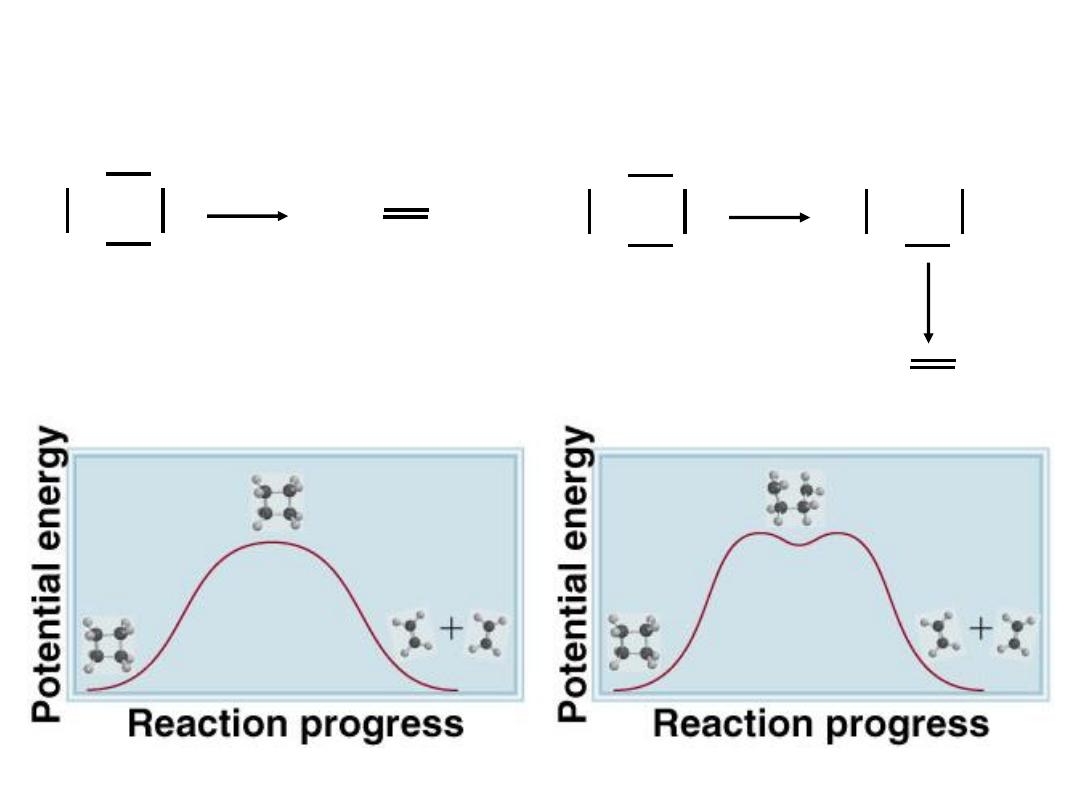
Exothermic Reaction
Endothermic Reaction
The activation energy (E
a
) is the minimum amount of
energy required to initiate a chemical reaction.
13.4
A + B AB C + D
+
+
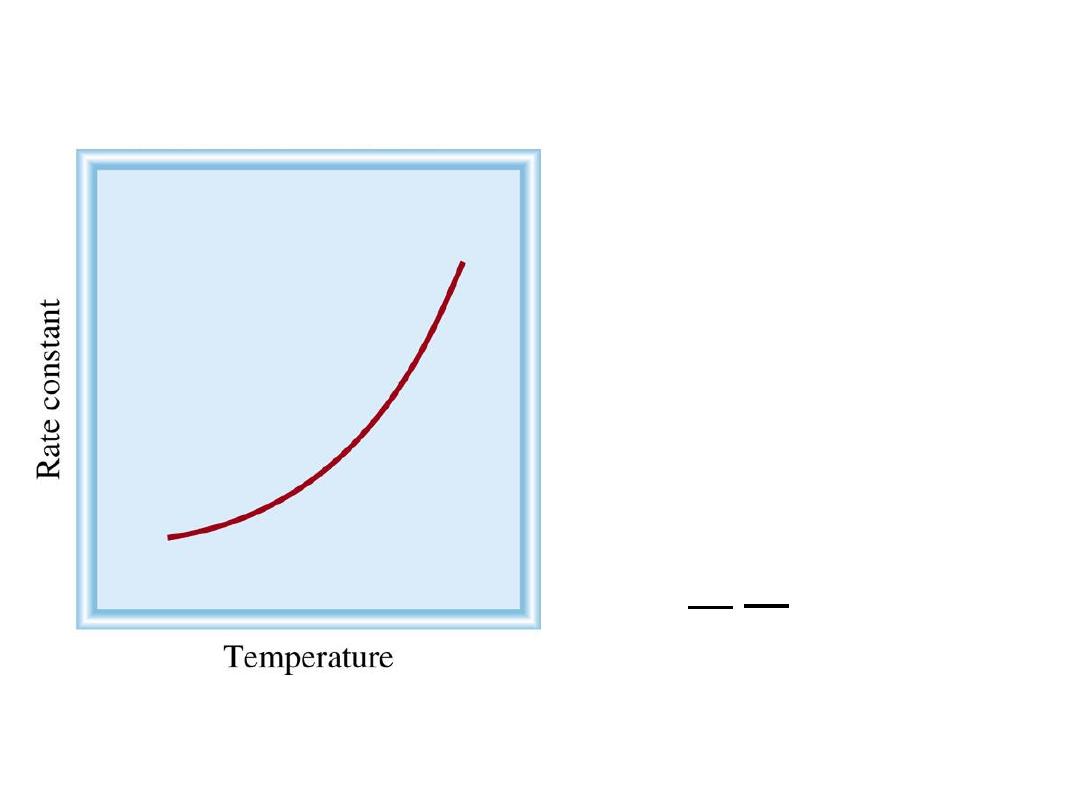
Temperature Dependence of the Rate Constant
k = A
•
exp( -E
a
/ RT )
E
a
is the activation energy (J/mol)
R is the gas constant (8.314 J/K
•mol)
T is the absolute temperature
A is the frequency factor
lnk = -
E
a
R
1
T
+ lnA
(Arrhenius equation)
13.4
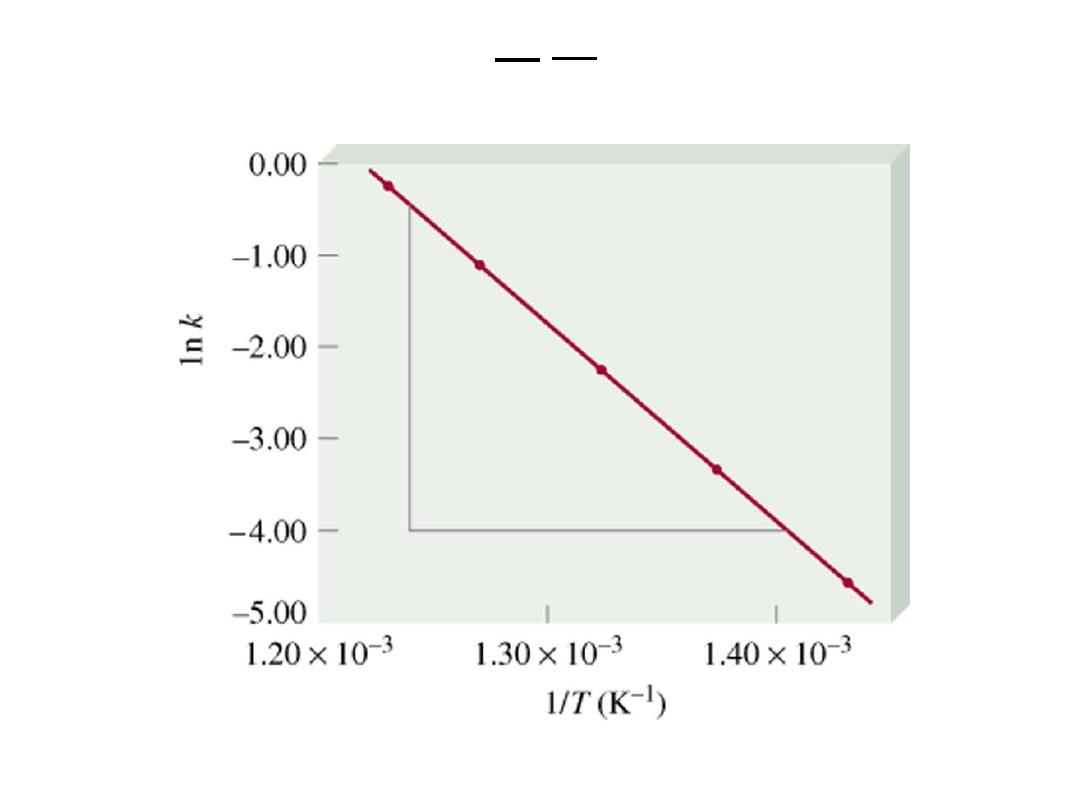
13.4
lnk = -
E
a
R
1
T
+ lnA
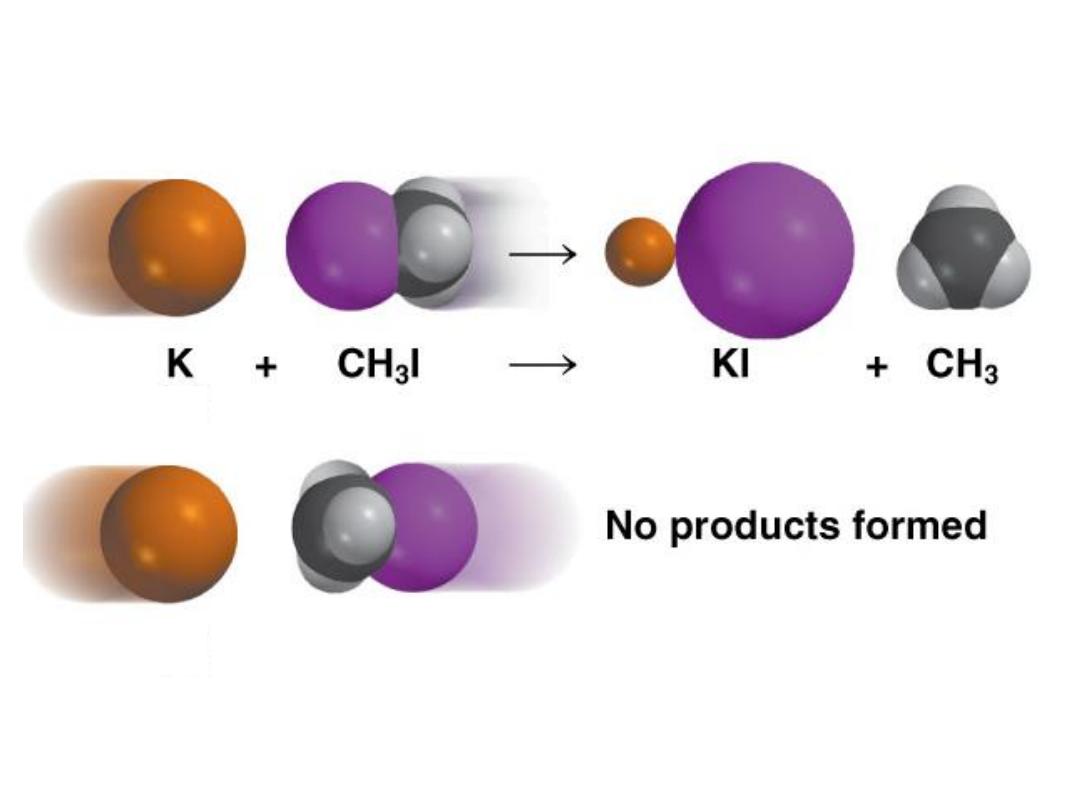
13.4
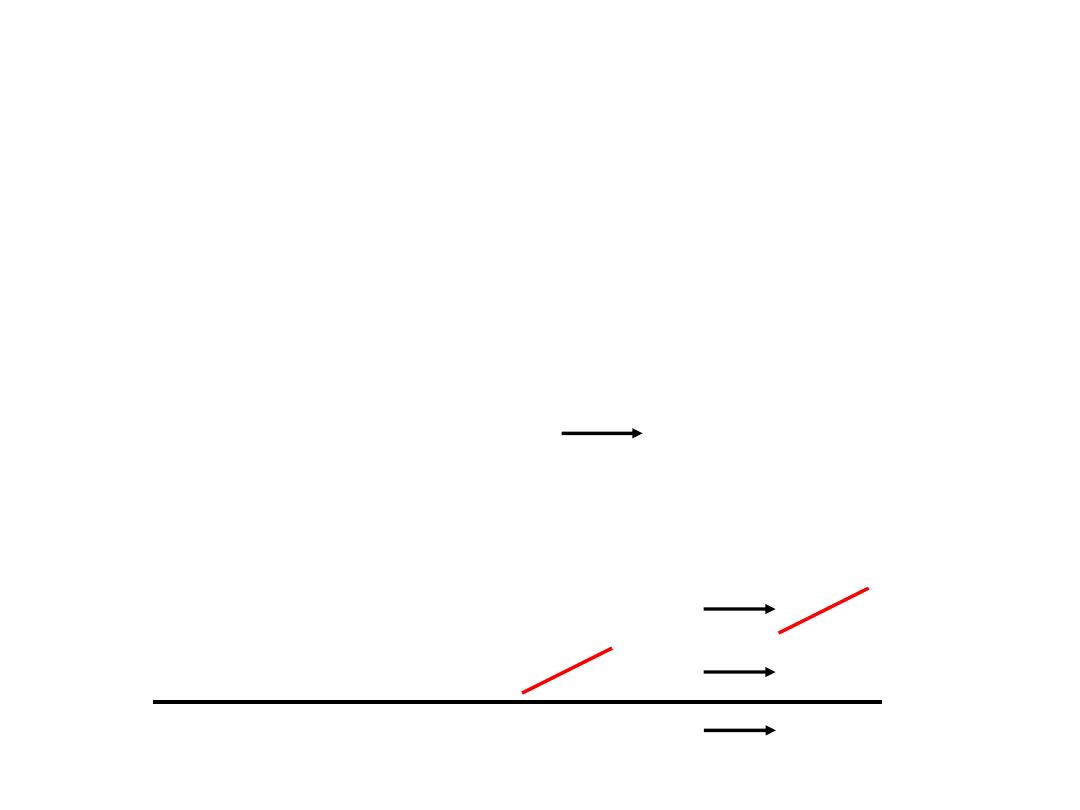
13.5
Reaction Mechanisms
The overall progress of a chemical reaction can be represented
at the molecular level by a series of simple elementary steps
or elementary reactions.
The sequence of elementary steps that leads to product
formation is the reaction mechanism.
2NO (g) + O
2
(g) 2NO
2
(g)
N
2
O
2
is detected during the reaction!
Elementary step:
NO + NO N
2
O
2
Elementary step:
N
2
O
2
+ O
2
2NO
2
Overall reaction:
2NO + O
2
2NO
2
+
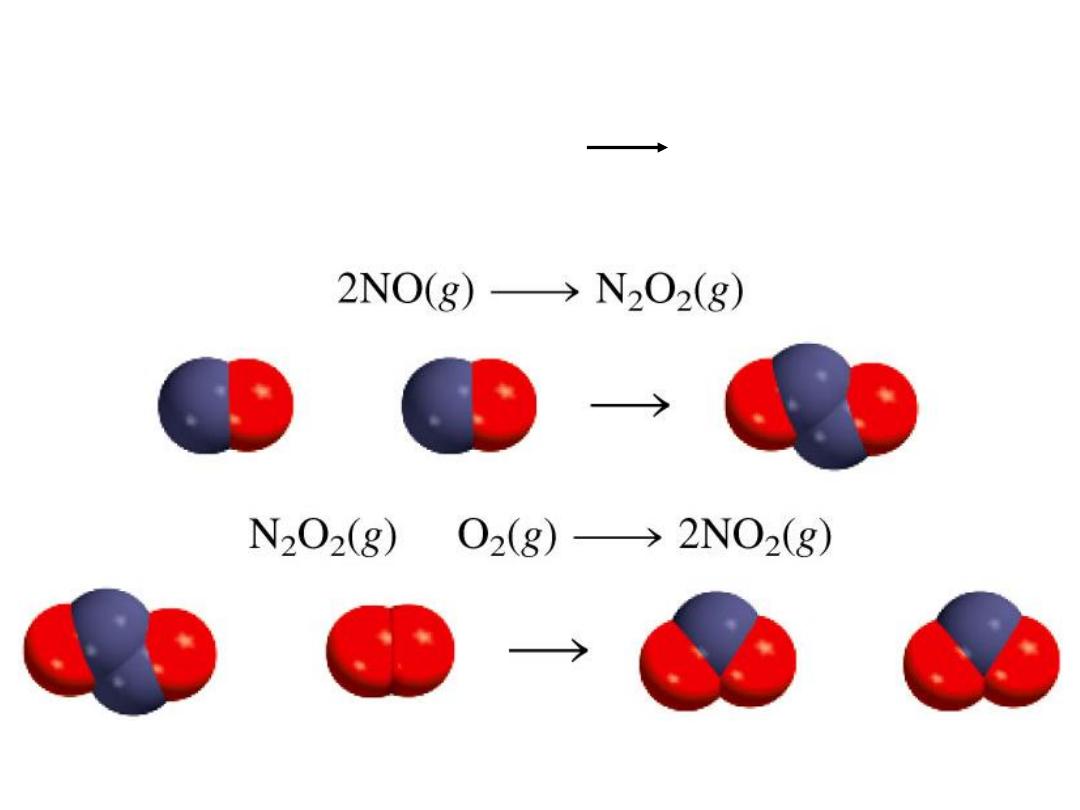
2NO (g) + O
2
(g) 2NO
2
(g)
13.5
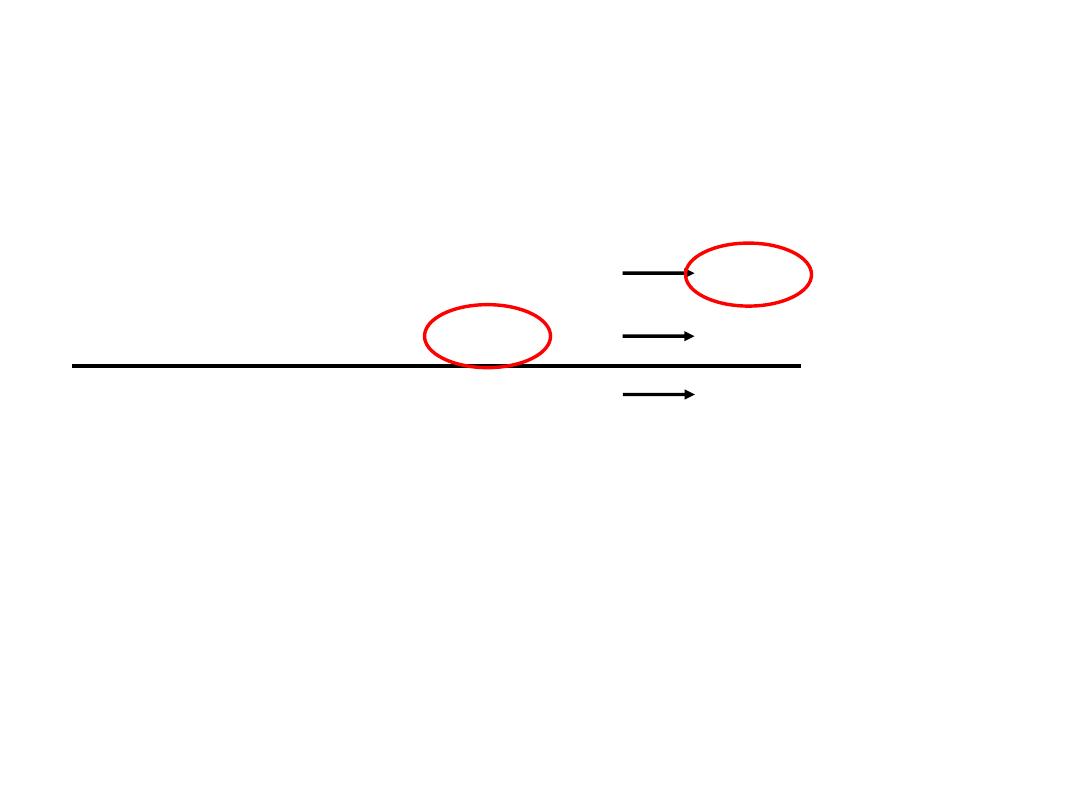
13.5
Elementary step:
NO + NO N
2
O
2
Elementary step:
N
2
O
2
+ O
2
2NO
2
Overall reaction:
2NO + O
2
2NO
2
+
Intermediates are species that appear in a reaction
mechanism but not in the overall balanced equation.
An intermediate is always formed in an early elementary step
and consumed in a later elementary step.
The molecularity of a reaction is the number of molecules
reacting in an elementary step.
•
Unimolecular reaction
– elementary step with 1 molecule
•
Bimolecular reaction
– elementary step with 2 molecules
•
Termolecular reaction
– elementary step with 3 molecules
Unimolecular reaction
A products
rate = k [A]
Bimolecular reaction
A + B products
rate = k [A][B]
Bimolecular reaction
A + A products
rate = k [A]
2
Rate Laws and Elementary Steps
13.5
Writing plausible reaction mechanisms:
•
The sum of the elementary steps must give the overall
balanced equation for the reaction.
•
The rate-determining step should predict the same rate
law that is determined experimentally.
The rate-determining step is the slowest step in the
sequence of steps leading to product formation.
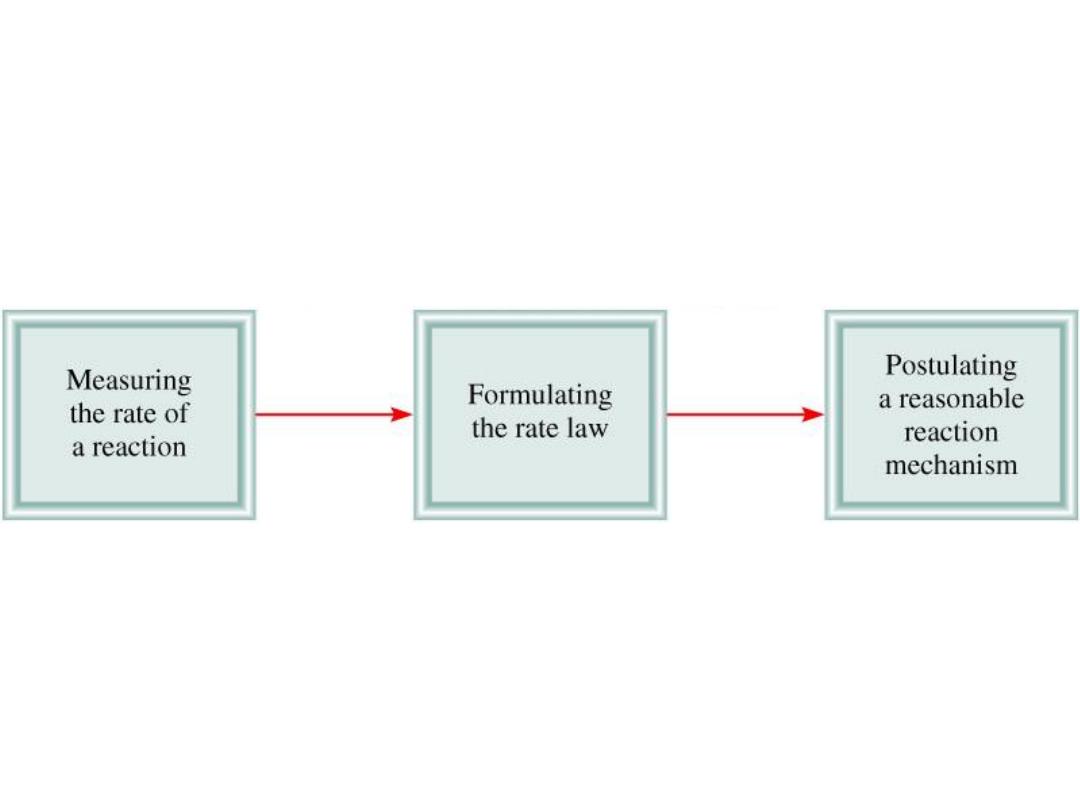
13.5
Sequence of Steps in Studying a Reaction Mechanism
The experimental rate law for the reaction between NO
2
and CO to produce NO and CO
2
is rate = k[NO
2
]
2
. The
reaction is believed to occur via two steps:
Step 1:
NO
2
+ NO
2
NO + NO
3
Step 2:
NO
3
+ CO NO
2
+ CO
2
What is the equation for the overall reaction?
NO
2
+ CO NO + CO
2
What is the intermediate?
NO
3
What can you say about the relative rates of steps 1 and 2?
rate = k[NO
2
]
2
is the rate law for step 1 so
step 1 must be slower than step 2
13.5
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
CH
2
•
•
CH
2
CH
2
2
Chemistry In Action: Femtochemistry
13.5
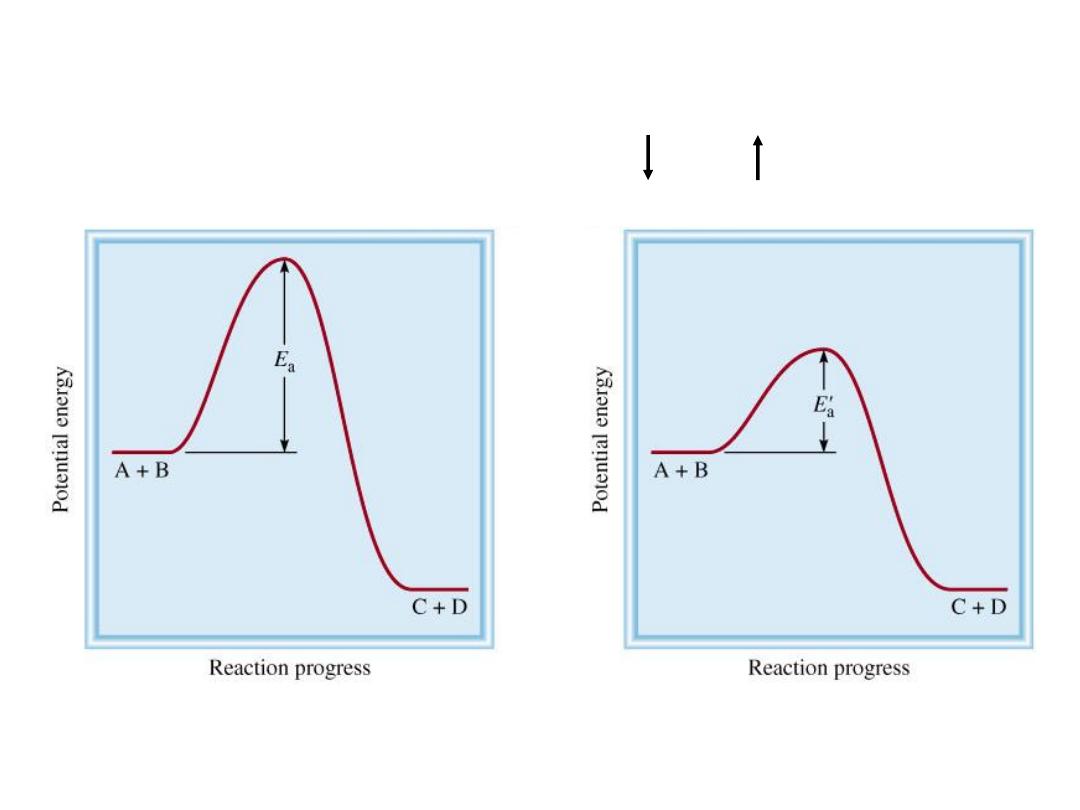
A catalyst is a substance that increases the rate of a
chemical reaction without itself being consumed.
k = A
•
exp( -E
a
/ RT )
E
a
k
rate
catalyzed
> rate
uncatalyzed
E
a
< E
a
‘
13.6
Uncatalyzed
Catalyzed

In heterogeneous catalysis, the reactants and the catalysts
are in different phases.
In homogeneous catalysis, the reactants and the catalysts
are dispersed in a single phase, usually liquid.
•
Haber synthesis of ammonia
•
Ostwald process for the production of nitric acid
•
Catalytic converters
•
Acid catalysis
•
Base catalysis
13.6
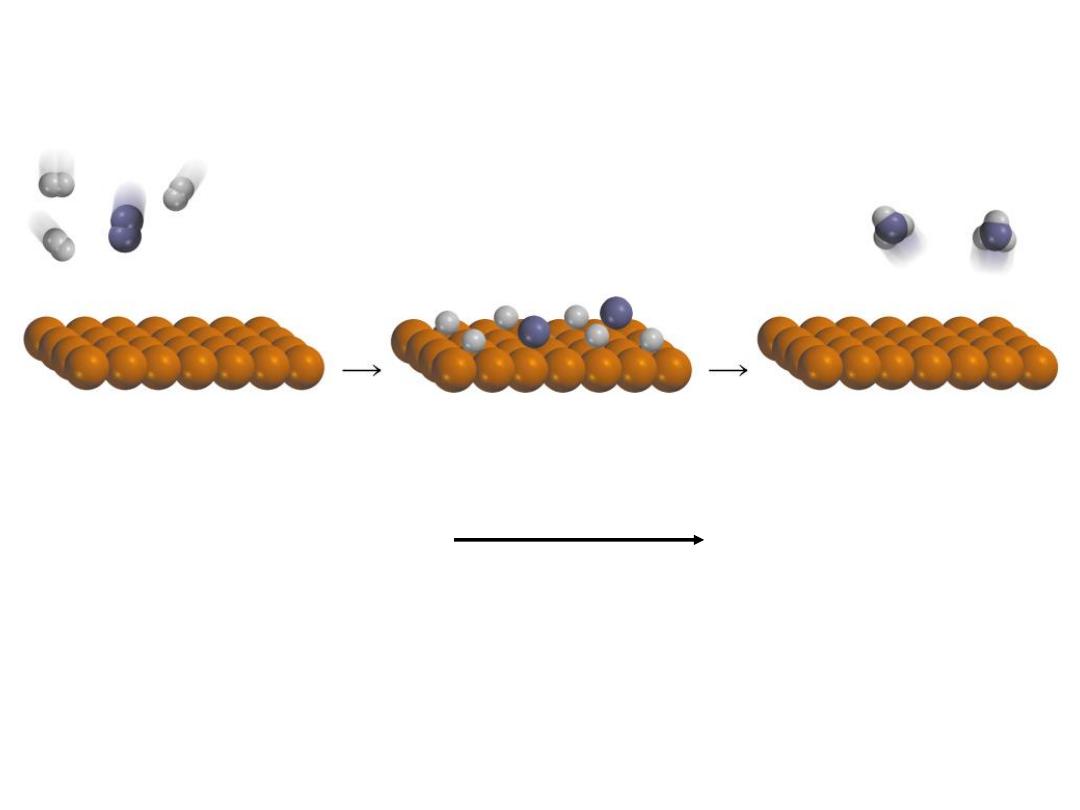
N
2
(g) + 3H
2
(g) 2NH
3
(g)
Fe/Al
2
O
3
/K
2
O
catalyst
Haber Process
13.6

Ostwald Process
Hot Pt wire
over NH
3
solution
Pt-Rh catalysts used
in Ostwald process
4NH
3
(g)
+ 5O
2
(g)
4NO
(g)
+ 6H
2
O
(g)
Pt catalyst
2NO
(g)
+ O
2
(g)
2NO
2
(g)
2NO
2
(g)
+ H
2
O
(l)
HNO
2
(aq)
+ HNO
3
(aq)
13.6
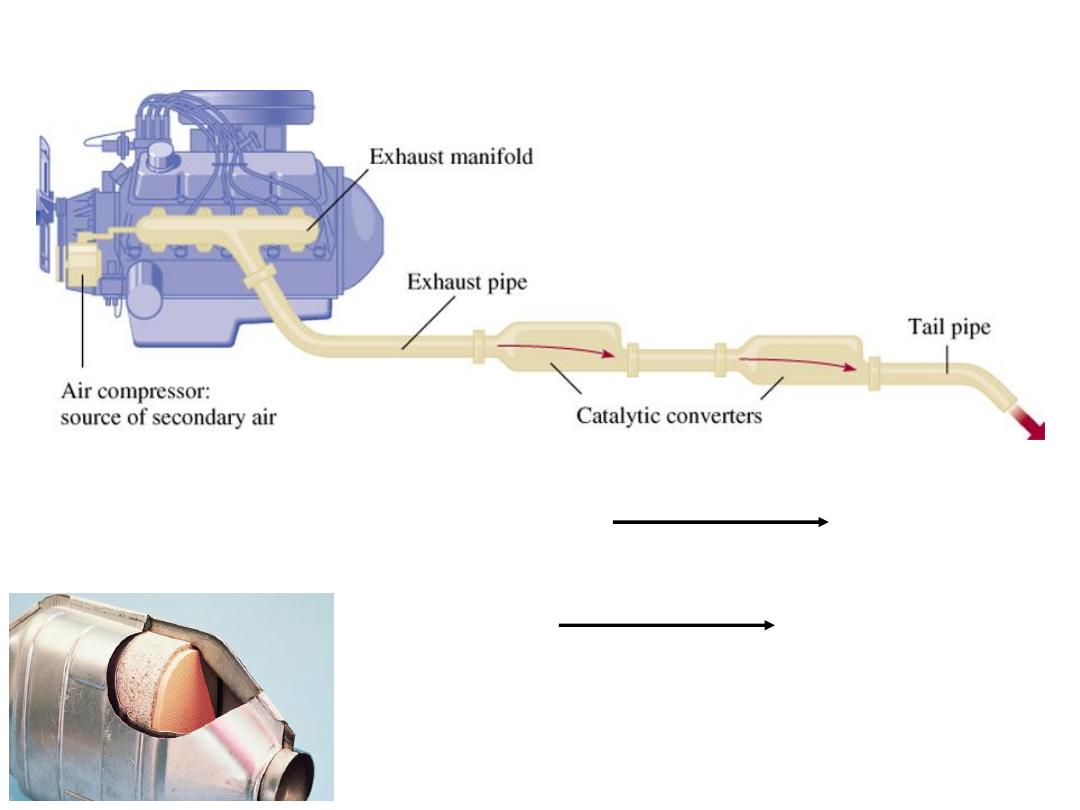
Catalytic Converters
13.6
CO + Unburned Hydrocarbons + O
2
CO
2
+ H
2
O
catalytic
converter
2NO + 2NO
2
2N
2
+ 3O
2
catalytic
converter
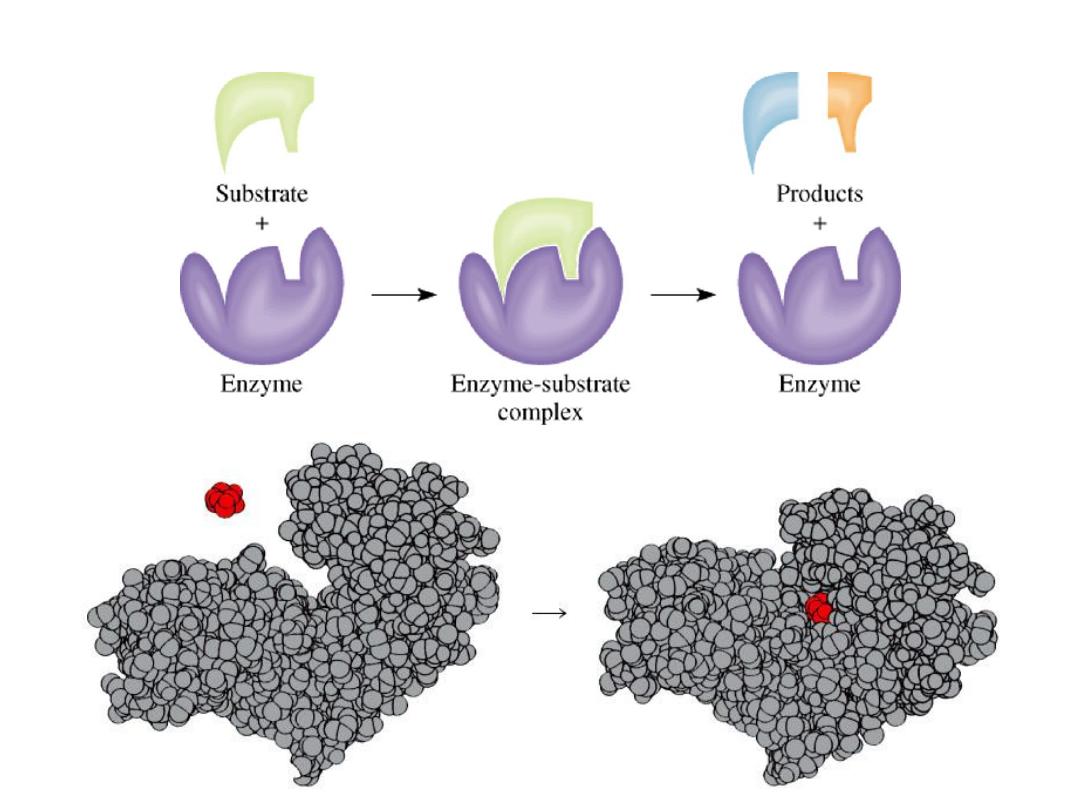
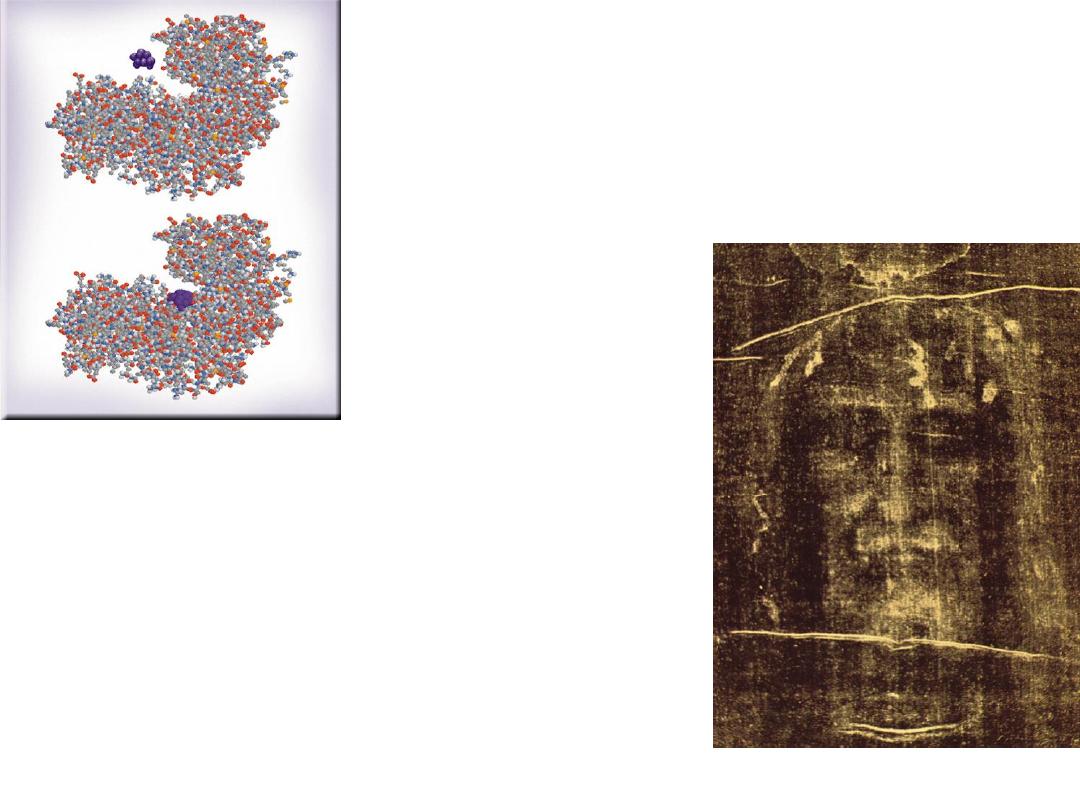
Enzyme Catalysis
13.6
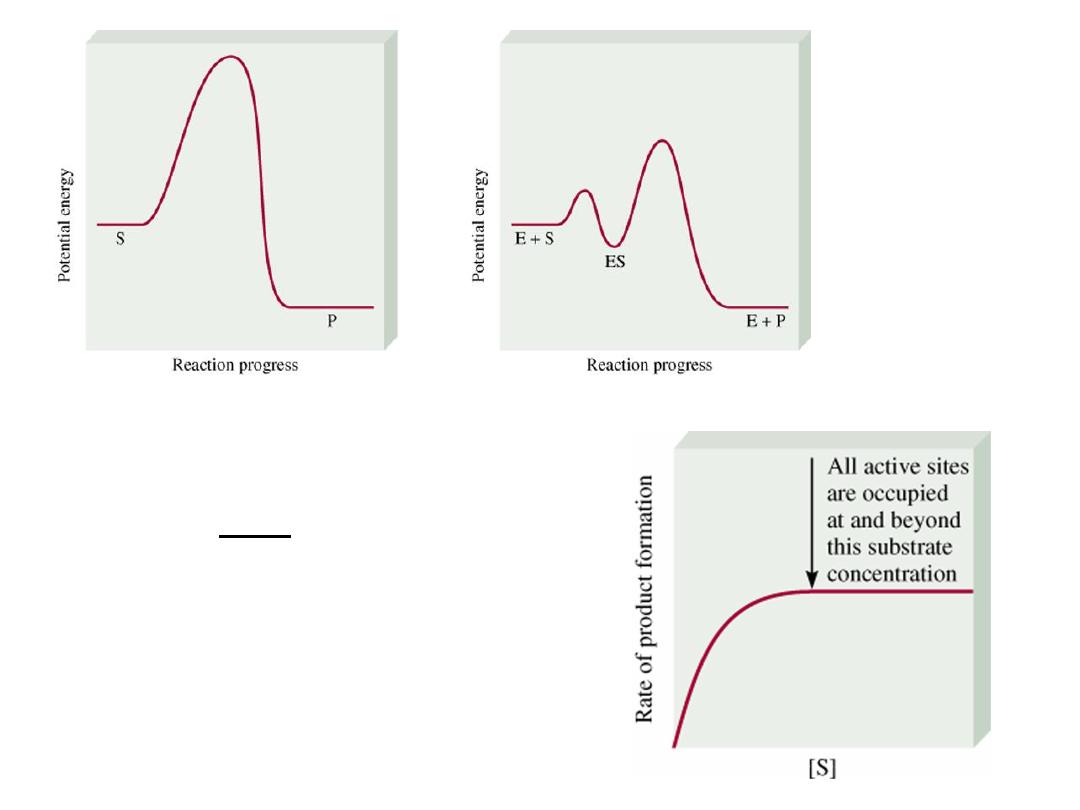
uncatalyzed
enzyme
catalyzed
13.6
rate =
D[P]
Dt
rate = k [ES]
