Probability pdf - Biostatistics

Probability

Probability: is a numerical measure of the likelihood that an event will occur

An experiment: is any process that generates well-defined outcomes

Sample space (S): is the set of all possible outcomes of an experiment

An event (A): is an outcome or set of outcomes that are of interest to the experiment. An
event (A) is a subset of the sample space (S)

The probability of an event A {P (A)}: is a measure of the likelihood that an event A will
occur

Example: Tossing a coin

Experiment: Toss a coin and observe the up face

S { } S= {H, T}

H (head) T (tail)

Example: Tossing a coin twice

Experiment: flip a coin twice and observe the sequence (keeping track of order) of up
faces.

S= {HH, HT, TH, TT}

A= {Tossing at least one head}

A = {HH, HT, TH}

Example = Tossing by a dice

Experiment: Tossing a six-sided dice and

S= {1, 2, 3, 4, 5, 6}

A= {roll an even number}

A = {2, 4, 6}

Methods of assigning probability

Classical probability: Each outcome is equally likely

It is applicable to games of chance

In the cases, if there are N outcomes in S, then the probability of any one outcome is 1/N

If A is any event and nA is the number of outcomes in A, then:

P (A) =

Example: Tossing a dice:

S= {1, 2, 3, 4, 5, 6}

P (1) = P(2)= P(3)=P (4)=P(5)=P(6)=

A= {roll an even number}= {2, 4, 6}

P (A) = 3/6 = 0.5

Empirical probability is simply the relative frequency that some event is observed to
happen (or fail).

Number of times an event occurred divided by the number of trials:

P (A) =

Where:

N= total number of trails

nA Number of outcomes producing A

Relative frequency example

Children No.

Frequency

Relative frequency

40/215 = 0.19

80/215 = 0.37

50/215 = 0.23

30/215 = 0.14

10/215 = 0.05

5/215 = 0.02

Sum

215

215/215 = 1.00

Basic concepts of probability:

  Probability values are always assigned on a scale from 0 to 1
  A probability near 0 indicates an event is unlikely to occur
  A probability near 1 indicates an event is almost certain to occur
  A probability near of 0.5 indicates event is just as likely as it is unlikely
  The sum of the probabilities of all outcomes must be 1

Definitions

Mutually exclusive events: occurrence of one event precludes the occurrence of the other
event

Independent event: occurrence of one event does not affect the occurrence or non-
occurrence of the other event

Complementary events: all elementary events that are not in the event A are in its
complementary event.

P (Sample space)

P (A') = 1-P (A)

Laws of Probability

The addition rule: The probability of one event or another

P (A or B) = P (A) + P (B) – P (A and B)

If A and B are mutually exclusive events (A and B can not occur at the same time), then

P (A or B) = P (A) + P (B)

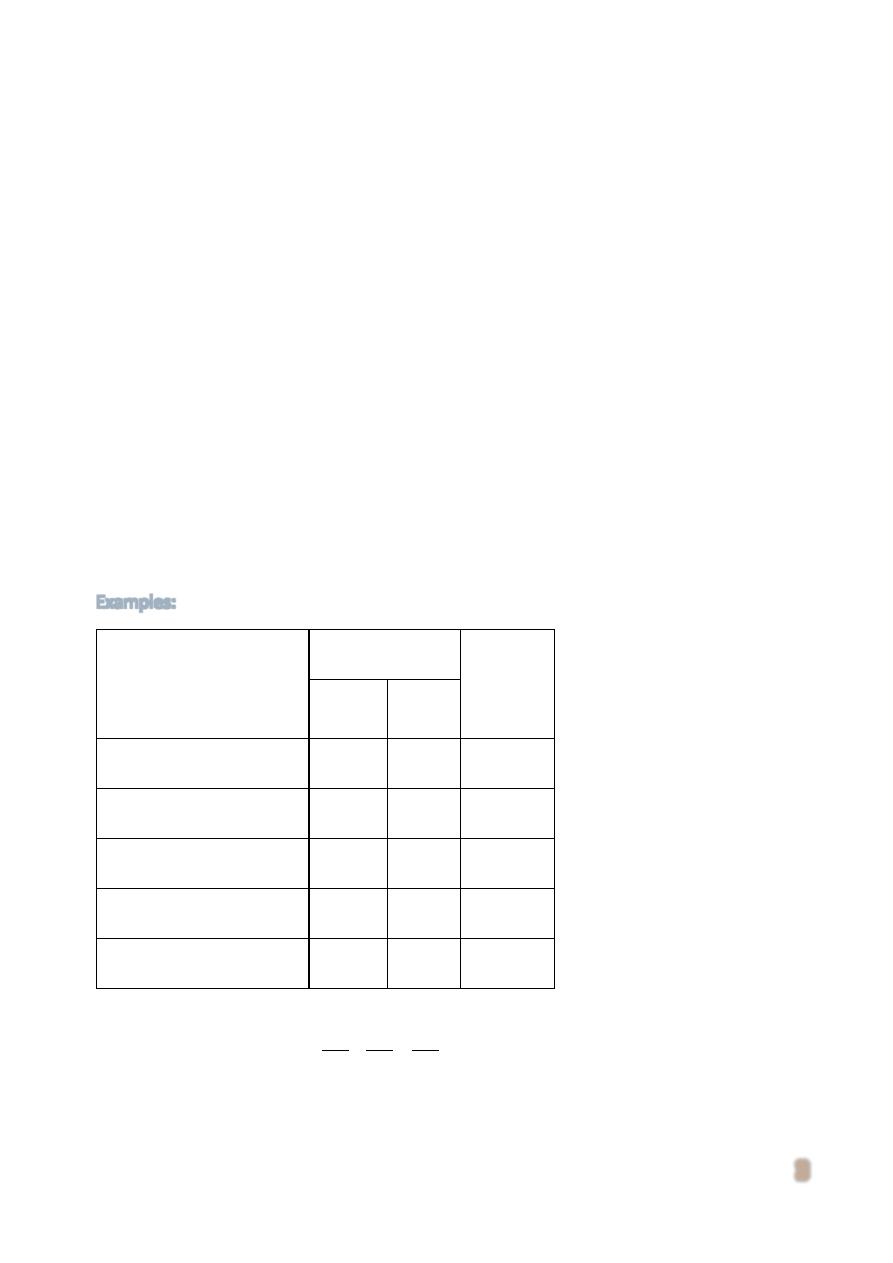
Examples:

Type of position

Gender

Total

Managerial

Professional

Technical

Clerical

2.7

Total

100

155

P (T C) = P (T) + P (C):

645

155

100

155





Law of multiplication: The probability of both the A and B occur together

P (A and B) = P(A) × P(B/A)

If A and B are independent (the occurrence of one does not affect the occurrence of the
other):

P (B/A)= P(B), and then

P (A and B) = P(A) × P(B)

Probability of at least one = 1- Probability of non

Probability Distribution

Defined: It is the distribution of all possible outcomes of a particular event. Examples of
probability distribution are:

The binomial distribution (only 2 statistically independent outcomes are possible on each
attempt) (Example coin flip)

The normal distribution

Other underlying distributions exist (such as the Poisson, t, f, chi-square, ect.) that are
used to make statistical inferences.

The normal probability distribution

The normal curve is bell-shaped that has a single peak at the exact centre of the
distribution.

The arithmetic mean, median, and mode of the distribution are equal and located at the
peak

The normal probability distribution is symmetrical about its mean (of the observations
are above the mean and are below).

It is determined by 2 quantities: the mean and the SD.

The random variable has an infinite theoretical range (Tails do not touch X – axis).

The total area under the curve is = 1

Figure

  68% of the area under the carve is between  1 SD
  95% of the area under the carve is between  1.96 SD
  99% of the area under the carve is between  2.58 SD

Why the normal distribution is important?

A/ Because many types of data that are of interest have a normal distribution

Central Limit theorem

Sampling distribution of means becomes normal as N increases, regardless of shape of
original distribution

Binominal distribution becomes normal as N increases

N.B:

 Normal distribution is a continuous one
 Binomial distribution is a quantitative discrete

Standard normal distribution (curve)

A normal distribution with a

of zero and SD of 1 is called standard normal

distribution

Any normal distribution can be converted to the standard normal distribution using the Z-
statistics (value)

Z-value (SND): is the distance between the selected value, designated X, and the
population mean (M), divided by the population SD (



)

Z =







The standard normal distribution curve is bell-shaped curve centered around zero with a
SD=1

Z- score

Z-score is often called the standardized value or Standard Normal Deviate (SND). It

denotes the number of SD.s a data value X is distant from the



and in which.

A data value less than sample mean will have a z-score less then zero;

A data value greater than the sample

will have a z-score greater than zero; and

A data value = the will have a z-score of zero

Normal curve table

The normal curve table gives the precise percentage of scores (values) between the (z-
score of zero) and any other z-score. It can be used to determine:

Proportion of scores above or below a particular z-score

Proportion of scores between the and a particular z–score

Proportion of scores between two z–scores

By converting raw scores to z-scores, can be used in the same way for raw sources.

Can also used in the opposite way:

Determine a z-score for a particular proportion of scores under the normal curve.

Table lists positive z-scores

Can work for negatives too

Why? Because curve is symmetrical

Steps for figuring percentage above or below a z-score:

Convert raw score to z-score, if necessary

Draw a normal curve:

indicate where z-score falls

Shade area you are trying to find

Find the exact percentage with normal curve table

Figure

Steps for figuring a z-score or raw score from a percentage:

Draw normal curve, shedding an approximate area for the percentage concerned

Find the exact z-score using normal curve table

Convert z–score to raw score, if desired

Figure

Example:

For = 2200, M = 2000, = 200, Z = (2200-2000)/200=1

For = 1700, M = 2000, = 200, Z = (1700 – 2000)/200= -1.5

A z-value of 1 indicates that the value of 2200 is 1 SD above the of 2000, while a z-
value of -1.5 indicates that the value of 1700 is 1.5 SD below the of 2000.

Example:

For M= 500, = 365, determine the position of 722 in SD units

Figure



X 

365

500

722 

365

222

= 0.61

We can also determine how much of the area under the normal curve is found
between any point on the curve and the

Once you have a z-score, you can use the table to find the area of the z-score

0.61 (from table A) = 0 .2291 = 0.23

Therefore, 22.9% or 23%

Q/ How much of the population lies between 500 and 722?

A/ 0.5 – 0.23 = 0.27

Q/ How much of the population is to the left?

A/ 0.5 + 0.23 = 0.73

Example:

The daily water usage per person in an area, is normally distributed with a of 20
gallons and a SD of 5 gallons

Q1/ About 68% of the daily water usage per person in this area lies between what 2
values?

A/ About 68% of the daily water usage will lie between 15 and 25 gallons

Q2/ What is the probability that a person from this area, selected at random, will use less
then 20 gallons par day?

A/ P (X < 20) = 0.5

Q3/ What percent uses between 20 and 24 gallons?

The z-value associated with X=24:

z = (24 -20)/ 5 = 0.8

From the table, the probability of z= 0.8 is 0.2119.

Thus, P (20 < × < 24) = 0.5 – 0.2119 = 0.2881 = 28.81%

Figure

What percent of the population uses between 18 and 26 gallous?

A/ The z-value associated with X = 18:

z = (18-20)/5= -0.4

and for X=26:

z= (26-20)/5 = 1.2

Thus P (18 <× < 26) = P (-0.4 < Z < 1.2) =0.6554 – 0.1151 =0.5403

Example: Height of young women:

The distribution of heights of women, aged 20-29 years, is approximately normal with
=64 inch and SD= 2.7 inch

Q/ Approximately, 68% of women have height between ……………. and ………….

Q/ ~ 2.5% of women are shorter than ……..

Q/ Approximately, what proportion of women are taller then 72.1=?

Mubark A. Wilkins