
م
إ إ ي ط د أ
م.ةاممح
2015
لمحقول
J j S
>i (j
f
فيق^طظموم

ات ن. ك
ال ذا س ب ة
و حا ص ل
ضز
ب
ا ل ذ ا ل ه ة
Solubility Equilibria and the Solubility Products
ه
قد
تذو ب
بعحض
المركبات
بشكل
كامل
ف ي
الماء
(
soluble
)
وبع ضها
ق د
يذو ب
بكميا ت
ش حي حة
(
slightly soluble
،)
ونست طيع
االستدالل
ع ل ى
الذائبية
من
حا صل
ض ر ب
الذائبية
.
Solubility product constant (Ksp
)
)
(
وه
)
A +(aq)
+ B
ؤ
—
(
AB(aq
؛-►
(
A B (S
ون ست طي ع
ا
خ ضا ر
ها
كالتال ي
؛
(
ا ل ن ا ئ ي ة
)
solubility
=
لربم
")
ء م
=
([
AB(aq)] =
[A +(aq
]
ه
كلما
زاد ت
(
KSp
)
زاد ت
الذائبية
.
solubility
T
=<
آ
KSp
:
Example
Cl
( a q
)
+
(
و ه
)
Ag
ج
(
AgCl(s
( ل
K Sp = [ A g +] [ C H
20H ”(aa
)
+
م)صم
رب
ت
؛
(
2
)
Ca(O H)2(s
2
-[
p
= [Ca ] [OH
؛؛
K

- 4
Example
:
"?
16
~
Calculate the solubility o f A gl
MK Sp
= 1 .5 x l0
Solution
:
(
٩١٤
)
1
+
(
A g+(aq
ج
(
Agl(s
[
٢
]
[
+
Ksp
= [Ag
A g+] = [I ] = X
]
=<
س
ب
(
>=
KsP= ( X ) (X
نأ خ زإل ج ذ ر\
الطرص
\
1.5x10'I6 = X2
8
“
1.22
X
10
=
ما
~
X = Vl .5
X
10
ب م<
ty
؛
l
؛
lq)] = s©lub
)؛
A gl
]
=
[
٢
]
=
[
+
X = [Ag
ت
Example
:
~^
Copper (I) bromide has a measured solubility o f 2.0 x l 0
.
mol/L at 2 5 ° c . Calculate its
K Sp
value
قيس ت
الذائبية
لب ر وميد
النحا س
وو جد ت
ت س ا و ي
(
2 . 0 x l 0 4 m ol/L
)
ع ن د
درجة
حرارة
2 5
°
c
،
احسب
قيمة
K Sp
•
Solution
:
Br(~q
)
+
،(ا
أ ل ه'
؛ ؛
CuBr
(
x)
(x
)
4
'
x) = 2 x l 0 ) = In so lu b ility = [CuBr(aq)] = [Cu+1] =
٦ ٢ ۴
-؟
KSp
= (2x1 O'4) (2x1 O'4) = 4x10
=<
Example
:
p
value for bismuth sulfide (B i2S3), which
؛؛
Calculate the K
.
mol/L at 2 5 ° c
؟
’
~
has a solubility o f 1 .0 x l0

Solution:
B ، 2 S 3 ( s ) ^ 2 B i ^ ) + 3 S ^
Solubility = [Bi2S3(aq)] =
X
= l x i o 15
=>
K Sp
= [Bi+3]2 [S-2]3
k
[
p
= [ 2 ( 1
x
1 0 ‘5) ] 2 [ 3 ( 1
x
1 0 "15) ] 3 = 1 .0 8 X 10"53
Example:
The KSp value for copper (II) iodate, C u (I0 3)2, is 1 .4 x l0 '7 at
2 5 ° c . Calculate its solubility at 2 5 ° c .
Solution:
C u ( I 0 3)2(s) (
ا،
ه
)
و
2 1 0
+
ل ه، ا ر
ئ
أثها
]
مء=اسل
1.4xlCT7
= ( x ) ( 2
x
) 2
1.4x10 = 4 x
ء ء ا
ء
و
ظ
م ا
-
ل
m o l / L

Example
:
How many grams of B a (I0 3)2 (487 g/mol) can be dissolved
?
in
500
mL of water at
25°c
كم
عدد
الغرامات
من
2
(
Mw=487 g/mol) B a (I0 3
)
ت ست طيع
الذوبان
ف ي
(
500
ml
)
م ن
الماء
د
درجة
حرارة
25
°
c
؟
؟(
1 0
Ksp=1.57
X
)
ع زيز ي
الطالب
ف ي
أي
سؤال
يت ضمن
و جود
ثاب ت
يج ب
ذكر
در جة
الحرارة
ف ي
هذا
السؤال
ألن
مع ظم
الثواب ت
ئتأثر
بتغي ر
در جة
الحرارة
،
وذكر
د ر ج ة
الحرارة
ال
يدخل
ف ي
عملية
الحساب
.
Solution
مالحظةت
2+
4 - 2 1 0
Ba(IO )
2X
X
Ksp = [Ba2+] [ I 0 3f
1 . 5 7
x
10"9 = 4 X 3
=> Solubility =
x =
الذائممة
M = ^
n
= M x V
v = 500 ml = 0.5L
=> n = 7.32X10'4 X 0.5 = 3.66X10“4 mol
^ r a = n x Mw
= 3 .6 6xl0'4x487 = 0.178 g

تأثبز
األيو
ن
ال م شت ر ك
Common Ion Effect
5 A ; q) + B w
؛
(
A B (s
ه
األيون
المشترك
هو
أي
مركب
قد
ي ع ط ي
عند
تفككه
أحد
ا أل ي و ن ا ت
ر
A
أو
■
ة
.)
ه
لذلك
كلما
زاد ت
كمية
األيون
المشترك
فإن
التفاعل
س و ف
ينزا ح
ل ل ي س ا ر
مما
يؤد ي
إلى
تقليل
الذاثبية
للمرك ب
.
ل
solubility
=<
آ
common ion
Example
:
in a
(
ا
؛
Calculate the solubility of solid CaF^ (Ksp = 4.0x10
0.025
M NaF solution
.
:
Solution
CaF2(s)^ C a ^ ) + 2FM
،
.
,
ئ
ت
. .
(
0.025
M)
(0.025 M
)
م
0.025
M

= ءKSp = [Ca+2] [ F f
4 x l0 ‘" = ( x ) (0.025)
=> x = 6.4x10 M
ا ا
يتكون
راس ب
فق ط
ف ي
حال
كان ت
؛
A+] [ B - ] > K
]
2
)
أما
إذا
كان
(
B ] < Kjp
]
٦ ٨٢
)
ف ال
يو جد
را س ب
(
precipitate
.)
Example
:
A solution is prepared by adding 750.0 ml o f 4 .0 0 x 1 0 M
3
(
o f 2.00X10'2 M KIOj. Will C e (I0 3
١٦٦١
Ce(NO.,)s to 300.0
?
p
= 1.9x10’ ) precipitate from ^ is solution
؛؛
K
)
ط و ل
ش ز
بإ ضافة
750
ml
بتركيز
رس
4x10
)
من
2
(
C e (N 0 3
م ع
300
ml
بتركيز
( مء
؛
2 x 1 0
)
م ن
©,
K1
،
ه ل
س ي ن ز س ب
.(
C c(IO
■'°(
1.9x10
ء ء م=
ف ي
هذا
المطول
؟

Solution:
C e (N 0 3)3 ->
Ce
+
3 N 0 3'
4x10 M
4 x 1 0 M
“
K+ + I 0 3
ج
KIOj
)
2x10 M
2x1
(
5 C e ( I 0 3)3(s
' ؛
Ce
+ 3 I 0 3
'
سو ف
نقوم
ب ح سا ب
نزاكيز
األيونا ت
(
I 0 3
الجديدة
ب ال م ح ل و ل
الجديد
الذي
بمظك
ح جم
ي ساو ي
(
750
+
300
=
1050
m l
.)
(
1050
)
4 x l0 ’3) x(750) = (M2)
x
)
M 2 = 2.86x10 M
يت
٦٨٩٨٨
*
زت
1
)^
=
(
300
)
(
2 x l0 '2)x
M2 = 5.71xlO '3 M
°
’
‘
2 .8 6 x l0 '3] [5 .7 x l0 '3]3 = 5 .2 9 x l0
]
=
ئل
'
ئ ه
1
]
[
3
+
Ce
]
ت
°(
’
'
5.29x10' > KSp (1 .9 x l0
ع
(سو ف
يترسب
)
C e (I0 3)3 will precipitate
=<
Example
:
A solution is prepared by mixing 150.0 ml of l.OOxlO"2 M
M NaF. Calculate the
'؛
M g (N 0 3)2 and 250.0 ml of 1.00x10
concentrations of M g+2 and F at equilibrium with solid
(.
p
= 6.4x10
؛
M gF2 (K

محلول
ح صر
ب خل ط
150
ml
بتركيز
1 x 1 0 2
)
من
2
(
M g (N 0 3
م ع
250
ml
بتركيز
(
M
'؛
1x10
)
من
NaF
.
ا ص ب
ت ر ك ي ز
**(
M g
)
و ز م
عند
االتزان
مع
الراسب
(»
KSp — 6.4x10 ) M gF
2
:
Solution
٢٩
يج ب
تحديد
عدد
م و ال ت
كل
من
((
+
M g
)
و
(
F
))
لمعرفة
من
هو
العامل
المحدد
(
limiting reactant
)
ومن
هي
المادة
الزائدة
(
ex cess
)
•
N
0
,i,, = M x V = ( lx l0 ^ )(0 .1 5 ) = 1 .5 x l0 ‘3 mol
؛)
n M
(ا
n M g ( N
0 .,)2
=
n
Mg =
5 •
أ
x10
أ
mol
2 ) n N>F= M x V = ( l x l 0 _')(0.25) = 2 . 5 x l 0 _2mol
=> n NaF = n p_ = 2 .5 x l0 ~ 2 mol
M g ^ + 2 F Uq)^ M g F 2
n = 1 .5 x 1 0 3 mol
n = 2 .5 x l0 ‘2 mol
1. 5x10
-
2 .5 x 1 0
٠
—-
- 1 . 5 x 1 0
-1 .2 5 x 1 0 "
٦
2

R eactant with M g+2 j
٢
(
total
؟
(
Ffexcess
الن ي
ن ائ ط ت
م ع
2
+
M g
ا ص
ك'ز لا
آل
-
مل
<>
1.5
<>
2
- )
ق
'
وة< > لم
=
!excess)
= 2 . 2 x l 0 ‘2 mol
5.5xlO~2M
V
tou
,
(0.15 + 0.25)
٧
Total
=>[!■] = 5.5
x
10'2 M
ه
أما
أيونات
+
M g
فه ي
التي
نتجت
عن
تفكك
الراس ب
(
M gF2
)
فق ط
.
Example
:
Calculate the molar solubility of B a (I0 3)2 in a solution that
2
(
is 0.0200 M in B a (N 0 3
احسب
الذائبية
المو ال رية
ل
2
(
B a (I0 3
م ا' و ر
Ksp=1.57 X
)
ف ي
م حل و ل
ي حت و ي
(
B a (N 0 3)2 ،> (0.0200 M
؟
+ 2F"
(x)
(2x + 5.5x1 O'
4—
—>
M gF2(s)
K Sp
= [Mg+2] [F
6 . 4 x 1 0 ‘9 = ( x ) ( 5 . 5 x 1 0
x
=
2 . 1 x 1 0
M
=> [Mg+2] = 2.1X10' هM
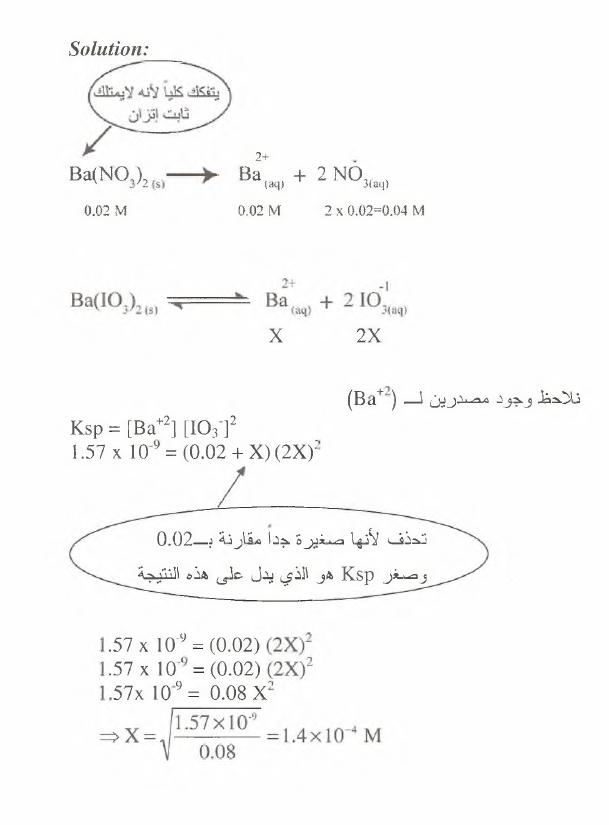
Solution:
2
+
س
ه* م م
م ء, م
0.02 M
2
X
0.02=0.04 M
Ba(lSIO,)2
0.02 M
2X
X
نالحظ
وجود
م ص د ري ن
ل
ر
+
لءج
)
K s p = [B a +2] [IO
3-]2
1.57 x 10 = (0 .0 2 + X )(2 X ):
0.02—
تحذف
ألنها
ص غي رة
جدا
مقارنة
ب
هو
الذي
يدل
عل ى
هذه
النتيجة
Ksp
و صغر
.5 7 x 1 0 '9 = (0.02)
.57 % 10 = (0.02)
؛
O.O^X
؟ =
5 7 x l 0

Example
:
Calculate the solubility of B a (I0
3) 2
in a solution prepared by
mixing 200 mL of 0.0100 M B a (N 0
3) 2
with 100 mL of
0.100
M N a I 0
3
احسب
ذائبية
2
(
B a (I0 3
(
و
1 0
Ksp==1.57 X
)
ف ي
محلول
ي ح ض ر
ب وا س ط ة
خلط
(
200
m l
)
من
2
(
B a (N 0 3
بت ركي ز
(
M
م ه ل م
.
م
)
مع
(
100
m l
)
صن
N a I0 3
بت ر كي ز
(
0.100
M
؟)
:
Solution
عند
خل ط
هاتين
ال م ا د ت ي ن
(
2
(
N a I0 3 + B a (N 0 3
)
س ي ن ت ج
ر ا س ب
م ن
2
(
B a (I0 3
و س و ف
تبق ى
إ حد ى
المادتي ن
المتفا علتي ن
بشكل
ز ا ئ د
(
excess
)
لذلك
يج ب
معرفة
هذه
الكمية
الزائدة
لي صب ح
حل
هذا
السؤال
كما
م ر
م ع ن ا
سابقأ
ف ي
تأثي ر
ا أليو ن
الم شت ر ك
.
اا
،'
آ؛
آأ
:
4" 2 Naio,.,
r ^ z = = ^
2
ب
ر
ق
(
و مأ ) ه و
NaNCX
v = 1 0 0
ml
M = 0 . 1 M
n = M x V
= 0.1
X
0.1
= l x l 0 ’2 mol
v = 2 0 0 m l
M = 0 . 0 1 M
n = M x V
= 2 x 10‘3 mol
L .R
ا أل صغ ر
ت
هو
العام ل
الم حدد
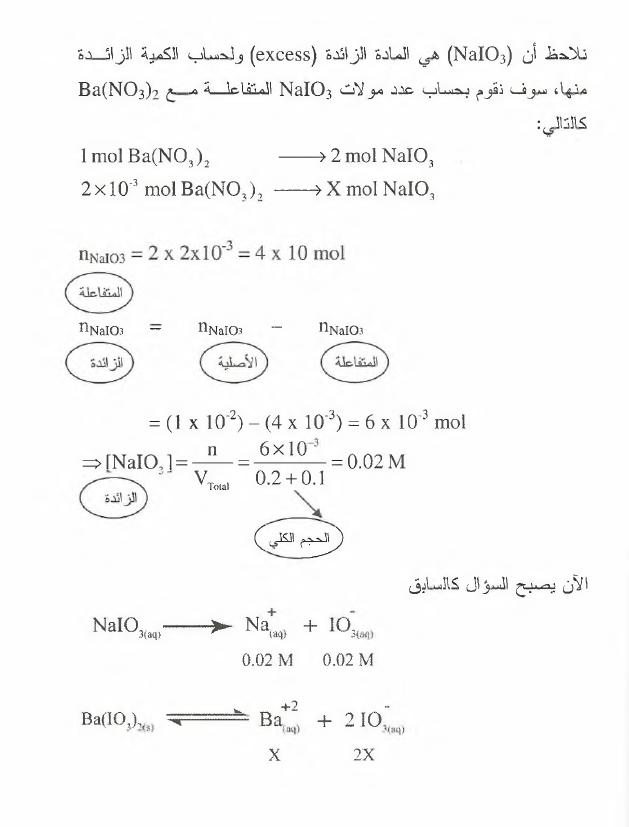
نالحظ
أن
(
N a I 0 3
)
ه ي
المادة
الزائدة
(
cxccss
)
ول ح سا ب
الكمية
ا ل ز ا ئ د ة
منها
،
س و ف
نق وم
ب ح سا ب
عدد
مو ال ت
N a I 0 3
ال م ت ف ا عل ة
م ع
(?
B a (N 0 3
كالتال ي
:
2
mol N a I 0 3
ؤ
—
—
2
(
lm o lB a ( N 0 3
2 x l 0 '3 m o lB a (N O J , — —> X m ol N a I 0 3
HNaI03
-
nNaI03
“
103ال ل
= ( ١ X
10‘2) - (4 X 10‘3) = 6 x 10'3 mol
^ r N a I 0 ,1 = - n- = 6 x l °
= 0.02M
٠ ٧
0.2 + 0.1
)
م
( ت ي
اآلن
يب سب ح
المؤ
ال
كالسابق
N a I 0 3(—
حN a ^ + 1 0 مب
0.02 M
0.02 M
.
.
.
•
2
_
+
W
.
. . .
.
2 1 0
ب
ج
ج
“
٩
'
Ba(IO,),f
X
2X
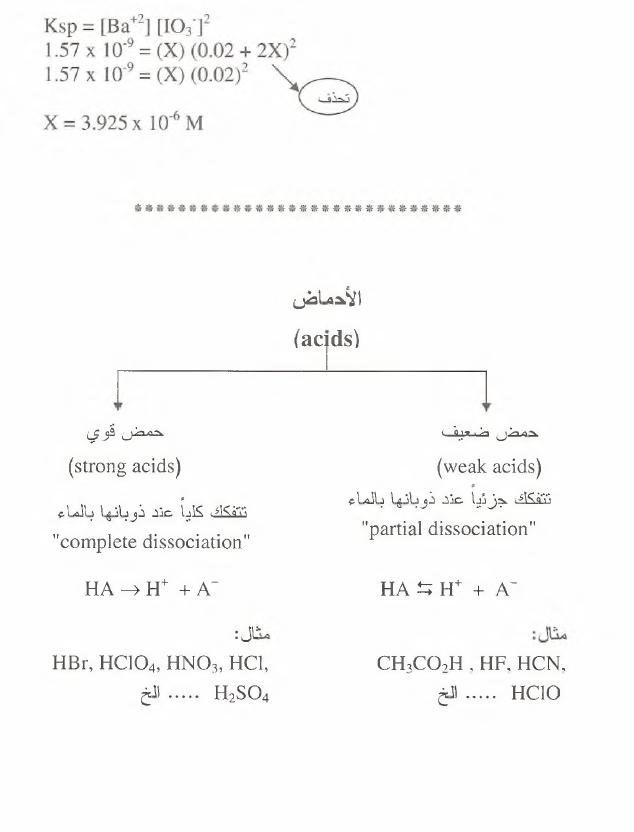
ا أل ح ما ض
(acjds)
حم خ ل
ضمعيف
(weak acids)
نتفكك
ج زئيأ
عند
ذ وبانها
بال ما ء
"partial dissociation"
H A ^ H + + A~
C H .C O .H ,H F , HCN,
..... الخHCIO
حم ض
قوي
(strong acids)
نتفكك
كليأ
عند
ذوبانها
ب ال ما ء
"complete dissociation"
H A ^ H + +A~
HBr, HC104, ,
ا ئ
س
وه<
..... الخH2S 0 4
