
الثرموداينمك
المرحلة الثانية
Thermodynamic

2
•
الفصل األول
-
الخواص العامة للغازات
:
•

3
•
درجة الحرارة
C) Temperature
•
نمك و التوازن الحراريٌادومرثلل يرفصلا نوناقلا
\
•
ن الغازاتٌناوق
:
•
ًن الغاز المثالٌناوق
:
4
•
سنتطرق خاللها بدراسة عالقة
T
•
مع
P , V ,
ثم اشتقاق القانون
:
5
•
ةٌقٌقحلا تازاغلا
6
•
معادلة فاندرفالز
:
•
ًالفصل الثان
-
نمكٌادومرثلل لولأا نوناقلا
:
7
•
الفصل الثالث
-
ةٌرارحلا ءاٌمٌكلا
•
ةٌرارحلا ءاٌمٌكلا
8
•
الشغل او توسع الشغل
•
د و تحول الطاقة من ضغطٌربتلا ءادبم
•
،الى شغل
.....
•
9
•
ةٌرارحلا تلاوحتلا

10
•
الفصل الرابع
-
نمكٌادومرثلل ثلاثلاو ًناثلا نوناقلا
:
11
•
الفصل الخامس
-
ًائٌمٌكلا نازتلااو ةرحلا ةقاطلا نٌب ةقلاعلا ًف ةمدقم
•
الفصل السادس
-
ًائٌمٌكلا نازتلأا
12
•
من االتزانات االخرى
:

13
•

14
•
رات الطورٌغت
:
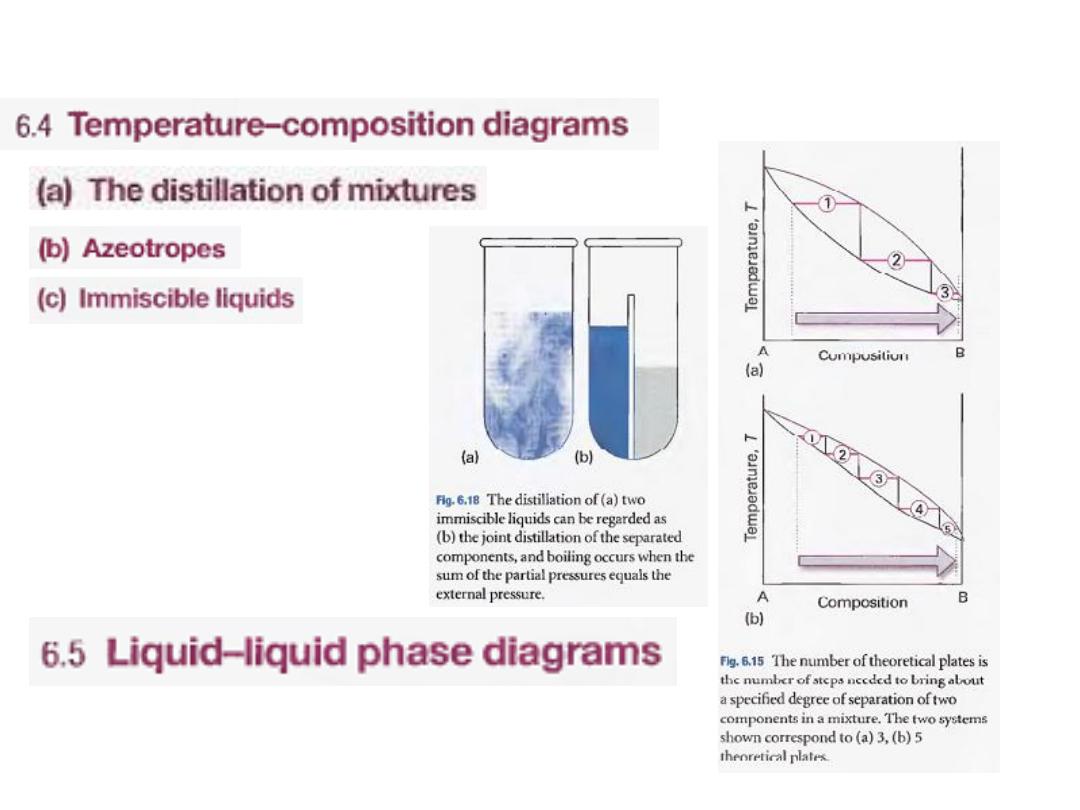
15
•
مخططات حرارة
-
مكونات
:

Thermodynamics
Lecture 2

2
•
خصائص الغازات
•
الغاز المثالي
The perfect gas
•
We shall find it helpful to picture a gas as a
collection of molecules (or atoms) in
continuous
random motion
, with
average speeds that
increase as the temperature is raised.
•
A gas differs from a liquid in that,
except during
collisions,
the molecules of a gas are widely
separated from one another and move in paths
that are largely unaffected by intermolecular
forces.

3
1.1 The states of gases
The physical state of a sample
of a substance,
its physical condition, is defined by its physical properties. Two samples of a
substance that have the same physical properties are in the same state.
V,
for example, is specified by giving its volume,
,
The state of a pure gas
amount of substance (number of moles), n, pressure, p,
and
temperature
,
T
However,
it has been established experimentally that it is sufficient to specify
only three of these variables, for then the fourth variable is fixed.
That is, it
is an experimental fact that each substance is described by an equation of
state, an equation that
interrelates these four variables. The general form of an equation of state is
•
معادلة الحالة
:
تلك المعادلة التي تربط المتغيرات االربعة
لوصف الحالة لتلك المادة
.
p =f(T,v,n)
(1.1)

4
فالمعادلة تلك تخبرنا
:
This equation tells us that
, if we
know the values
of T, V, and n for a particular
substance, then the pressure has a fixed value.
is described by its own equation
Each substance
of state, but we know the explicit form of the
equation in only a few special cases.
One very important example
is the equation of
state of
a 'perfect gas',
which has the form:
p = nRT/V
•
where R is a constant.
Much of the rest of this chapter will examine the
origin of this equation of state and its
applications.
5
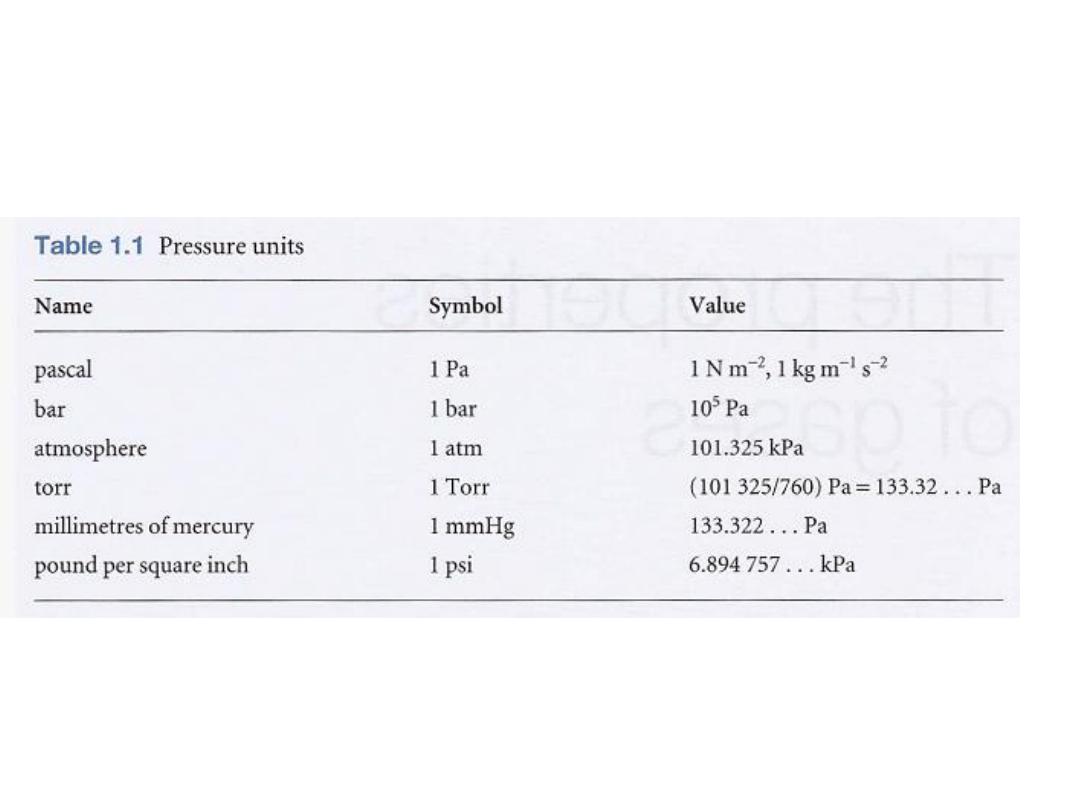
•
وحدات الضغط
:

7
•
الضغط و وحداته
:
a) Pressure
(
[1,2a] In terms of base units,
•
Pressure is defined as force divided by the area to
which the force is applied. The greater the force acting
on a given area, the greater the pressure. The origin of
the force exerted by a gas is the incessant battering of
the molecules on the walls of its container. The
collisions are so numerous that they exert an
effectively steady force, which is experienced as a
steady pressure.
•
1
defined as
is
(Pa),
pascal
, the
The SI unit of pressure
newton per metre-squared
: 1 Pa= 1 Nm
-2

8
•
وهناك عدد اخر من الوحدات مازال يستخدم كما في الجدول
السابق
Several other units are still widely used (Table 1.1); of these
units, the most commonly
used are atmosphere (1 atm = 1.013 25 x 105 Pa exactly) and bar
(1 bar = 105 Pal. A pressure of 1 bar is
the standard pressure
for reporting data; we denote it
pᶱ.

8
قياس الضغط
:
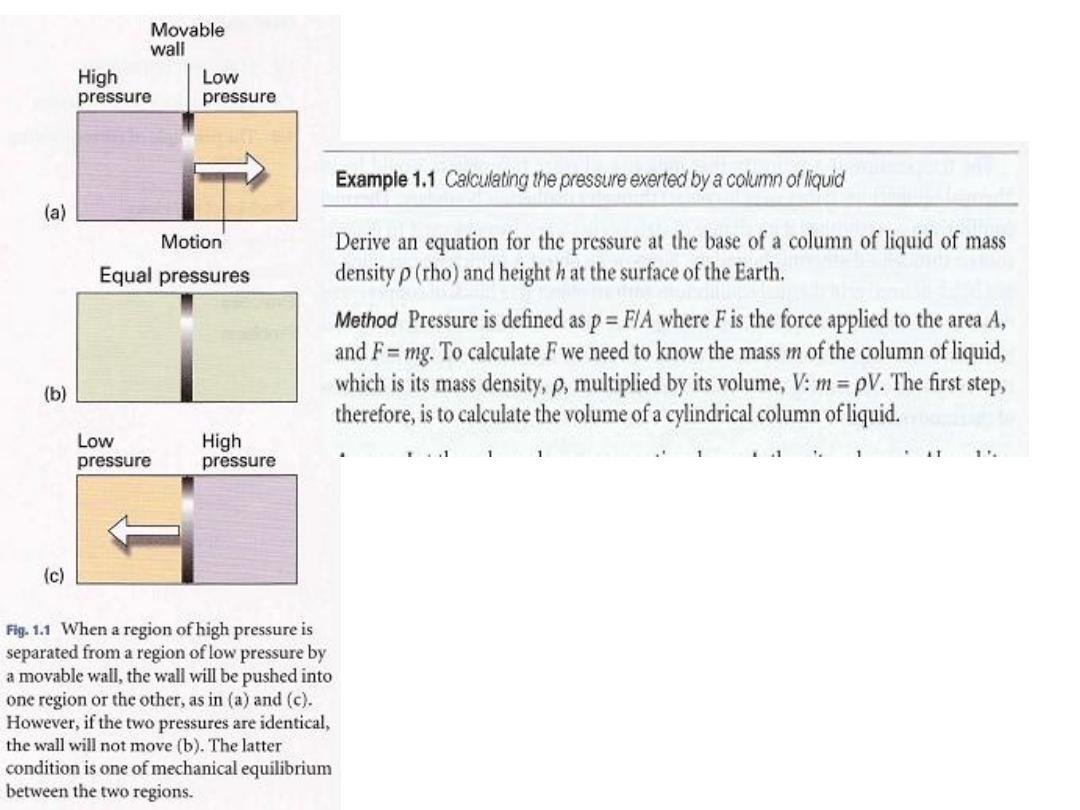
(b) The measurement of pressure
The pressure exerted by the atmosphere is
measured with
a barometer
. The original version
of a barometer (which was
invented by Torricelli,
a student of Galileo
) was an inverted tube of
mercury sealed at the upper end. When the
column of mercury is in mechanical equilibrium
with the atmosphere, the pressure at its base is
equal to that exerted by the atmosphere. It
follows that the height of the mercury column is
proportional to the external pressure.
9
•
قياس الضغط
:

10
•
الجواب
:
•
وإذا كان السطح مائال او محدبا او مقعرا فيحسب كمايلي
:
Derive an expression for the pressure at the base of a column of
liquid of length I held at an angle
e
(theta) to the vertical (1).
p = ρ gℓ cos
ϴ

11
•
انواع مقاييس الضغط
:
The pressure of a sample of gas inside a container is
measured by using a pressure gauge, which
is a device
with electrical properties that depend on the pressure
.
For instance,
a Bayard-Alpert pressure gauge
is
based
on the ionization of the molecules present in the gas
and the resulting current of ions is interpreted in terms
of the pressure.
In a capacitance manometer
, the deflection of a
diaphragm relative to a fixed electrode is monitored
through its effect on the capacitance of the
arrangement.
Certain semiconductors
also respond to pressure and are
used as transducers in solid-state pressure gauges.

12
•
درجة الحرارة
:
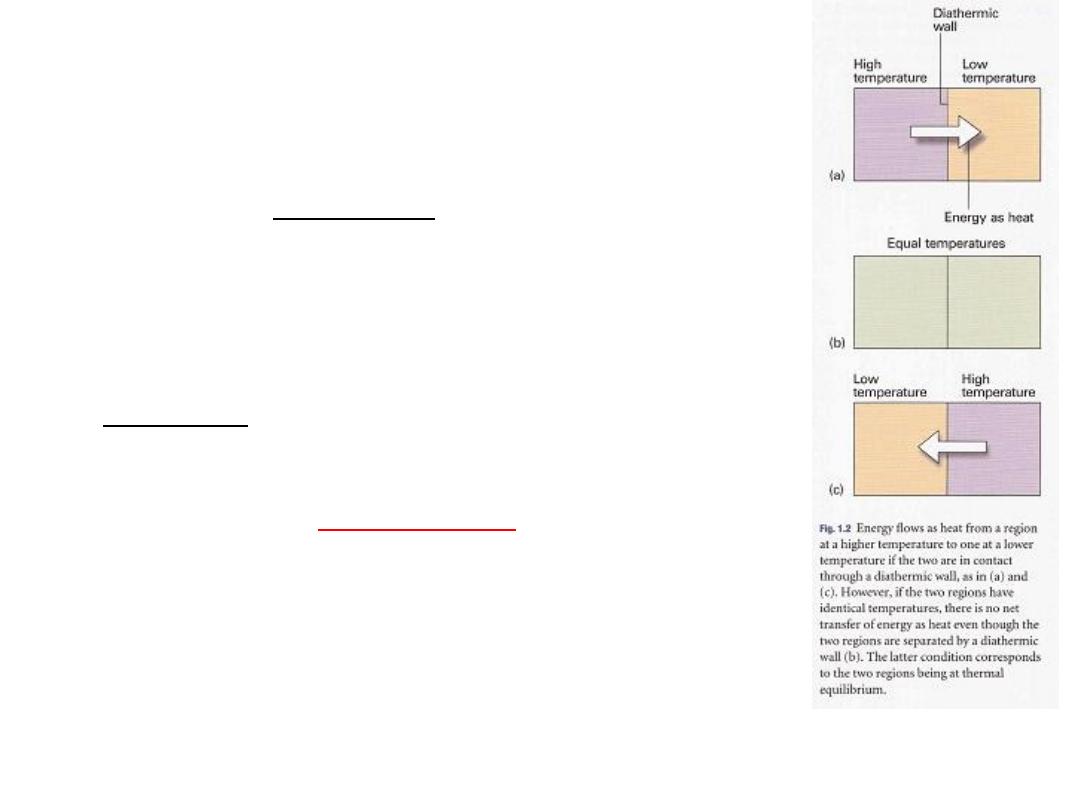
(c) Temperature
The concept of temperature springs from the observation
that a change in physical state (for example, a change
of volume) can occur when two objects are in contact
with one another, as when a red-hot metal is plunged
into water. Later (Section 2.1) we shall see that the
change in state can be interpreted as arising from a
flow of energy as heat from one object to another
. The
is the property that indicates the
T,
temperature,
direction of the flow of energy through a thermally
conducting, rigid wall
. If energy flows from A to B when
they are in contact, then we say that A has a higher
temperature than B (Fig. 1.2).
13
It will prove u
seful to distinguish between two
types of boundary that can separate the objects.
thermally conducting)
(
diathermic
A boundary is
if a change of state is observed when two objects
at different temperatures are brought into contact.
A metal container has
diathermic
walls. A boundary
if no change
thermally insulating)
(
adiabatic
is
occurs even though the two objects have different
is an approximation to an adiabatic
vacuum flask
temperatures. A
container
.

14
The temperature
is a property that indicates whether two objects would be in
.
boundary
diathermic
if they were in contact through a
'
thermal equilibrium
Thermal equilibrium
is established if no change of state occurs when two objects
A to B are in contact through a diathermic boundary
. Suppose an object
A
(which we can think of as a block of iron)
is in thermal equilibrium with
•
uppose an object A (which we can think of as a block of iron) is in
thermal equilibrium with an
object B (a block of copper),
and
•
that B is also in thermal equilibrium with another
object C (a flask
of water).
Then it has been found experimentally that A and C will
also be in thermal equilibrium when they are put in contact (Fig.
1.3).
•
This observation is summarized by the Zeroth Law of
thermodynamics:
•
If A is in thermal equilibrium with B, and B is in thermal equilibrium
with C, then C is also in thermal equilibrium with A

15
This observation is summarized by the:
:
Law of thermodynamics
Zeroth
•
If A is in thermal equilibrium with B, and B is in thermal equilibrium with C,
then C is also in thermal equilibrium with A

16
•
In the early days of thermometry
(and still in laboratory practice today),
temperatures were related to the length of a column of liquid, and the
difference in lengths shown when the thermometer was
first in contact
with melting
ice
and then
with boiling water
was divided into 100 steps
called' degrees', the lower point being labelled 0.This procedure led to the
Celsius scale
of temperature. In this text, temperatures ϴ.
•
hermodynamic and Celsius temperatures are related by the exact
expression
(
(1. 4
..........
T/K= ϴ/ ⁰ C + 273.1
This relation,
in the form ϴ/ ⁰ C = T/K - 273.15,
is the current definition of the
Celsius scale in terms of the more fundamental Kelvin scale. It implies that
a difference in temperature of 1°C is equivalent to a difference of 1 K.

17
•
A note on good practice We write
T = 0, not T = 0 K for the zero temperature on the thermodynamic temperature
scale.
This scale is absolute
, and the lowest temperature is 0 regardless of the
size of the divisions on the scale (just as we write
p = 0 for zero pressure,
regardless of the size of the units we adopt, such as bar or pascal). However, we
write O°C because the Celsius
scale is not
absolute
.
To express 25.00°C as a temperature in Kelvins, we use eqn. 1.4
to write
TIK = (25.00°C)
/ ⁰ C
+ 273.15 = 25.00 +273.15 = 298.15
Note
how the units (in this case,
⁰ C
) are cancelled like numbers. This is the
procedure called 'quantity calculus' in which a physical quantity (such as
the temperature) is the product of a numerical value (25.00) and a unit (1
⁰ C
).
Multiplication of both sides by the unit K then gives
T = 298.15 K
.

18
The gas laws
2
.
1
The equation of state of a gas at low pressure was established by combining a series of
empirical laws.
a) The perfect gas law
(
We assume that the following individual gas laws are familiar:
Boyle's law:
pV = constant, at constant n, T …..(1.5 )°
Charles's law:
V = constant X T, at constant n, p ………………..(1.6 a)°
p = constant X T, at constant n, V
…………….(1.6b)°
Boyle's
and
Charles's laws
are examples of a
limiting law
, a law that is strictly true
only
Avogadro's principler
V = constant X n at constant p,T ……….(1.7 )°
•
Boyle's and Charles's laws
are examples of a
limiting law
, a law that is
strictly true only in a certain limit, in this case p 0.
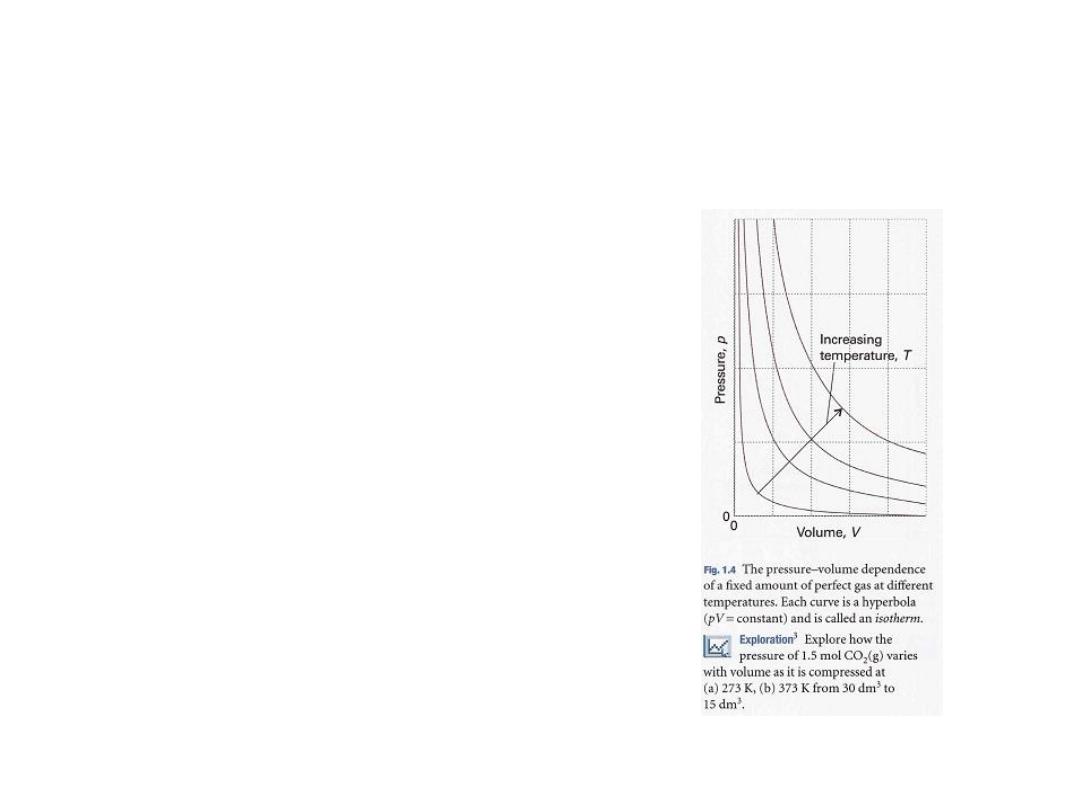
19
•
Boyle's law: pV = constant, at constant n, T
20
Charles's law: V = constant X T, at constant n, p … ……(1.6a)
p = constant X T, at constant n, V …………(1.6b)
Avogadro's principler' V = constant X n at constant p, T ….(1.7)
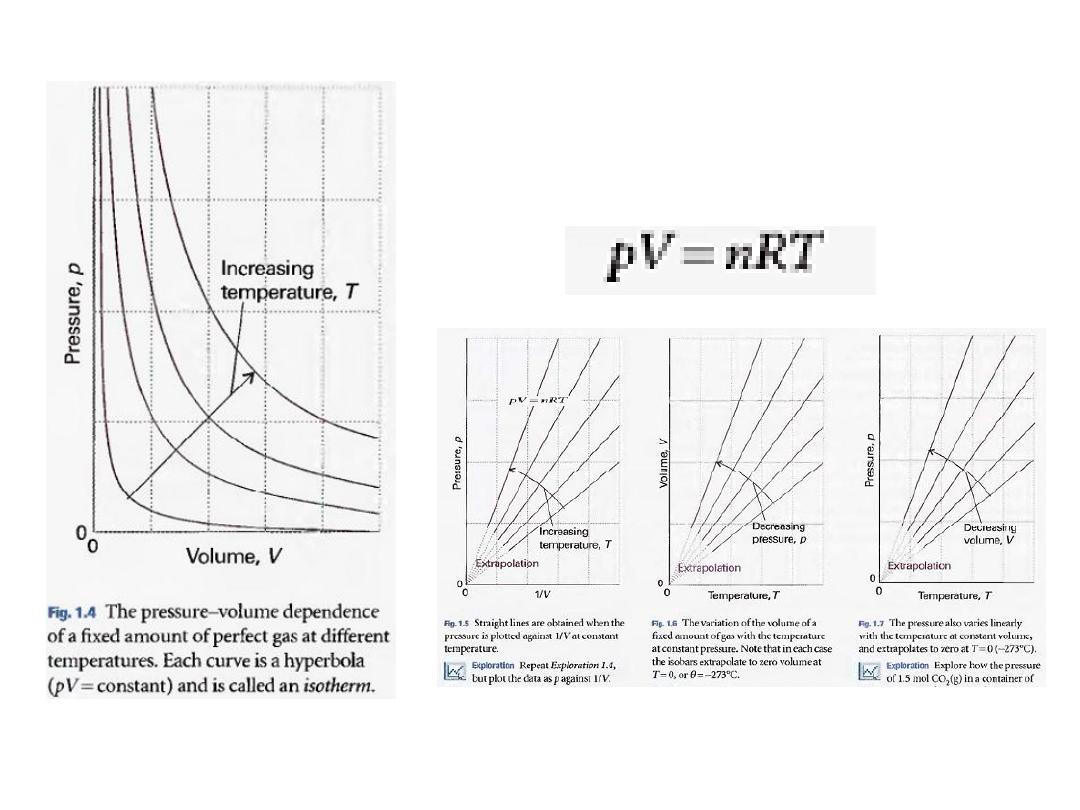
ccording to Boyle's law,
the isotherms of gases are hyperbolas
.
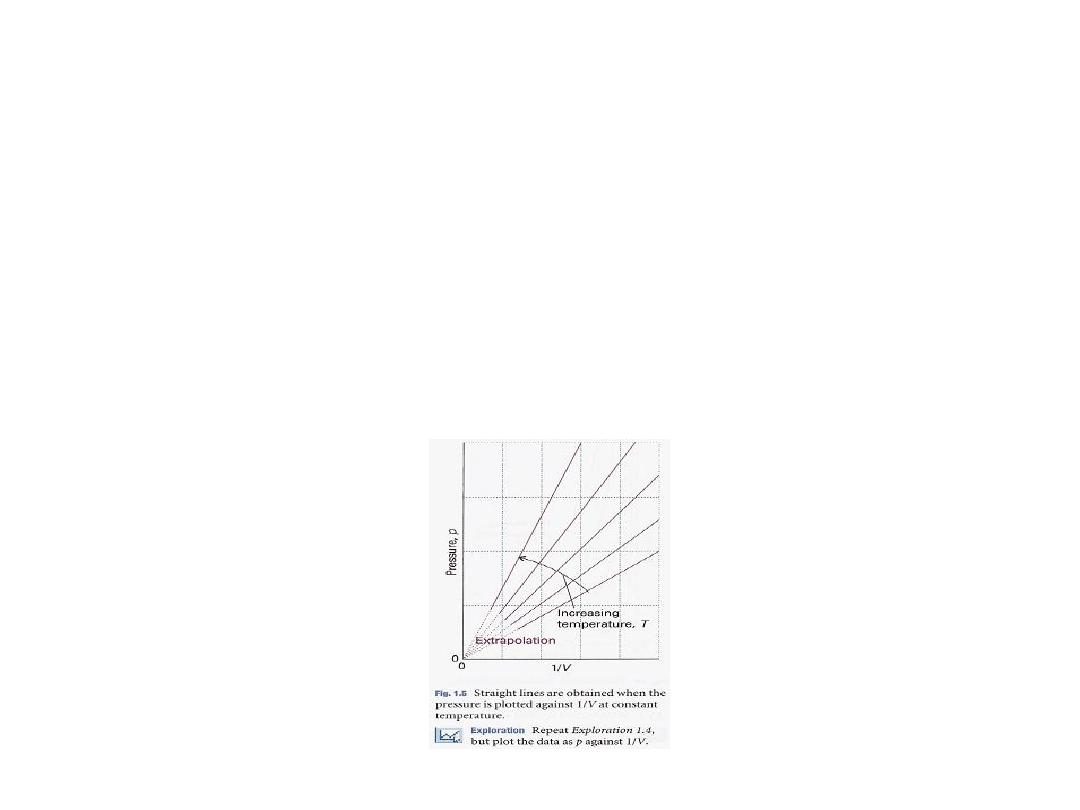
An alternative depiction, a plot of pressure against l/volume,
is shown in Fig. 1.5

21
•
An alternative depiction, a plot of pressure
against
l/volume
, is shown in Fig. 1.5.
The
linear variation of volume with temperature
summarized by
Charles's law
is illustrated in
Fig. 1.6
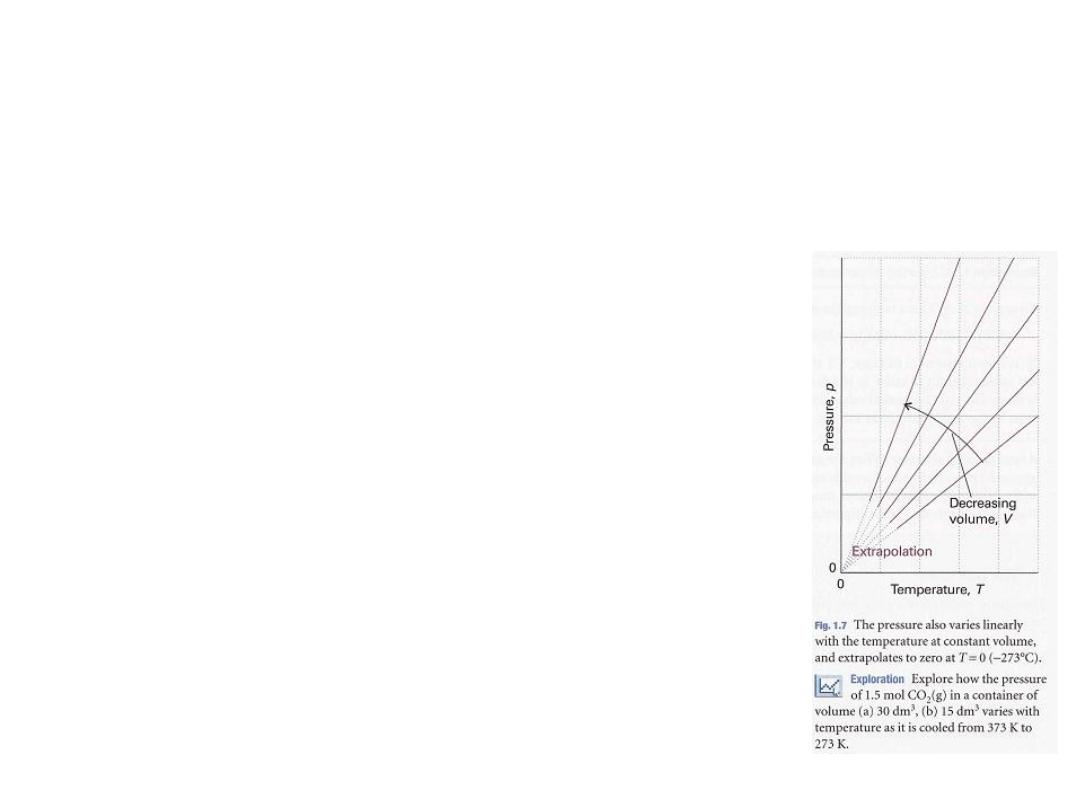
22
•
Figure 1.7:
illustrates the linear variation of
pressure with temperature.
•
The lines in this diagram are
isochores
, or lines
showing the variation of properties at
constant volume

23
•
The empirical observations
summarized by eqns 1.5-7
can be combined into a single expression:
p V = constant x nT
This expression is consistent with
Boyle's law
(p V = constant) when n and T are
of
with both forms
stant,
con
Charles's law
(
p αT
,
V α T
) when
n
and either
V
or pare
held constant, and with
Avogadro's principle (V α n)
when
p
and
T
are constant.
The constant of proportionality, which is
found
experimentally to be the same for all gases, is denoted
R and called the gas constant
. The resulting expression
pV=nRT
•
is the perfect gas equation

24
Molecular interpretation 1.1 Thekinetic model of gases

Lecture 3
Molecular interpretation 1.1
Thekinetic model of gases
ًئٌزجلا حٌضوتلا
للغازاتًكرحلا جذومنلا

2
•
ًئٌزجلا حٌضوتلا نا
لٌوب نوناقل
نة من الغازٌع تطغُض اذا وه
تصطدمًتلا تائٌزجلا ددع فعاضتٌس هناف همجح فصن ىلا
ة الضغطٌلمع ءارجا لبق ةٌنمزلا ةرتفلا للاخ نٌترمب رادجلاب
•
exerted on the walls
the average force
As a result,
is doubled.
Hence, when the volume is halved
the
pressure of the gas is doubled
,
and p x V is a
constant.
•
Boyle's law applies to all gases regardless of their
chemical identity (provided the pressure is low)
average separation
because at low pressures the
that they exert no
is so great
of molecules
influence on one another and hence travel
independently.

3
•
The molecular explanation of Charles's law
lies in
the fact that
raising the temperature of a gas
increases the average speed
of its molecules
collide with the walls more frequently and with
greater impact. Therefore they exert a greater
pressure on the walls of the container molecules.
للغازاتًكرحلا جذومنلا طورشب اٌمك تصخل ةٌعونلا صئاصخلاف
اتٌضرف ثلاث ىلع دنتسٌ يذلا و
:
are expressed
These qualitative concepts
quantitatively in terms of the kinetic model of
gases, which is described more fully in Chapter
21. Briefly, the kinetic model is based on three
assumptions:

4
1. The gas consists of molecules of mass m in
ceaseless random motion.
2. The size of the molecules is negligible, in the
sense that their diameters are much smaller
than the average distance travelled between
collisions.
3. The molecules interact only through brief,
infrequent, and elastic collisions.
An elastic collision
is a collision in which the total
translational kinetic energy of the molecules is
conserved.
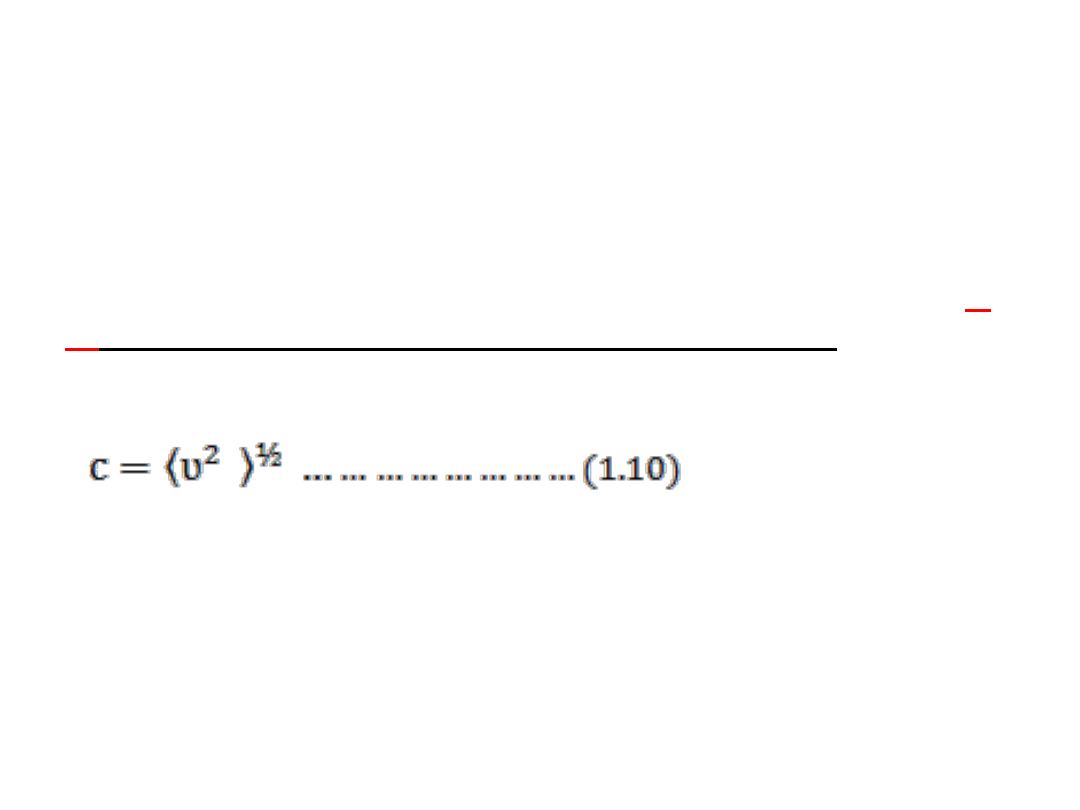
5
From the very economical assumptions of the kinetic
model
, it can be deduced
(as we shall show in detail in
Chapter 21)
that the pressure and volume of the gas
are related by
pV= ⅓ nM
C
2
………………………… (1.9)°
c
the molar mass of the molecules, and
A
N
m
where M =
, the
the root mean square speed of the molecules
is
square root of the
mean of the squares of the speeds, ʋ,
•
We see that, if the root mean square speed of the
molecules depends only on the temperature, then at
constant temperature
p V =constant
لٌوب نوناق وه اذهو
which is the content of Boyle's law

6
pV= ⅓ nM
C
2
………………………… (1.9)°
Moreover, for
eqn 1.9 to be the equation of
state of a perfect gas
, its right-hand side must be equal
to nRT. It follows that the root mean square speed of
the molecules in a gas at a temperature T must be
the root mean square speed of
that
We can conclude
the molecules of a gas is proportional to the square
root of the temperature and
inversely proportional
to the square root of the molar mass.
The root mean square speed of N
2
molecules, for instance, is
found from eqn 1.11 to be 515 m S
-1
at 298 K

7
plot of the pressure of
is a
8
.
1
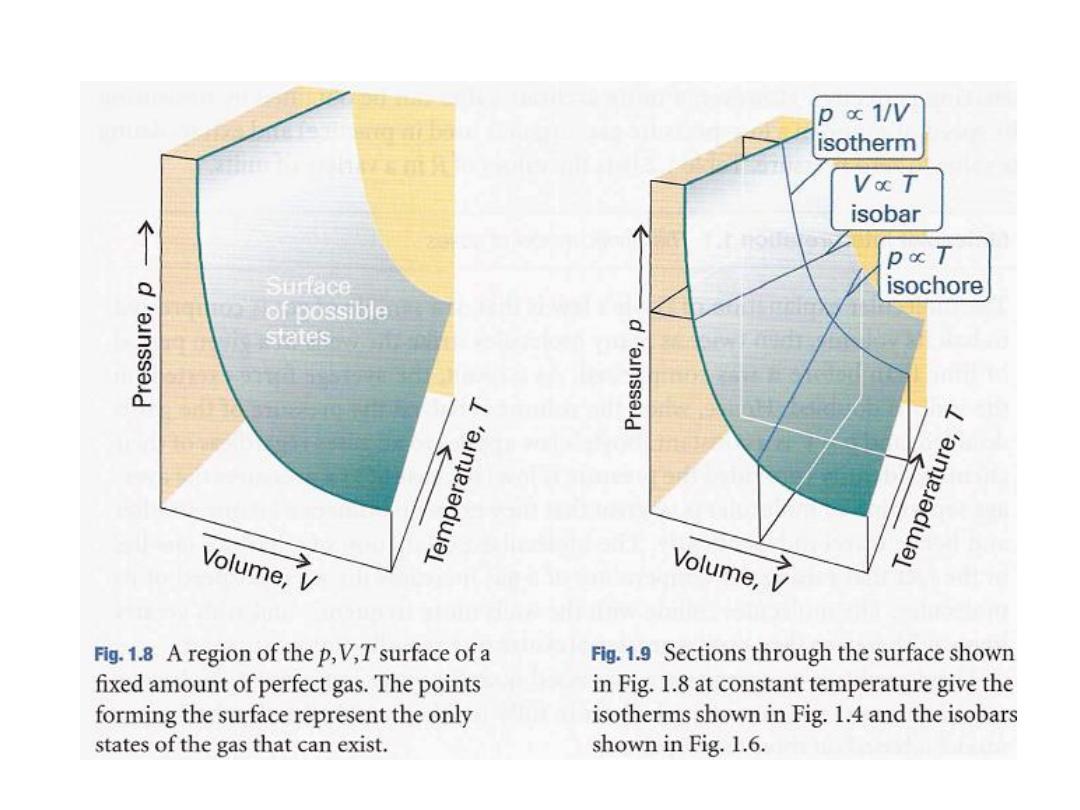
The surface in Fig.
its
against
a fixed amount of perfect gas
volume
and thermodynamic temperature as
given by eqn 1.8.
The surface depicts the only possible states of a
perfect gas: the gas cannot exist in states that
do not correspond to points on the surface.
The graphs in Figs. 1.4 and 1.6 correspond to the
sections through the surface (Fig. 1.9)
8

9
Example 1.2 Using the perfect gas equation
•
In an industrial process, nitrogen is heated to 500 K in a vessel of constant
volume. If it enters the vessel at 100 atm and 300 K, what pressure would
it exert at the working temperature if it behaved as a perfect gas?
We expect the pressure to be greater on account of the increase in
Method
temperature. The perfect gas law in the form PV/ nT = R implies that, if the
conditions are changed from one set of values to another, then because
, the two sets of values are related by
to a constant
equal
is
nT
PV/
The combined gas law
The known and unknown data are summarized in (2)

10
Answer
Cancellation of the volumes (because V
1
= V
2
) and amounts
(because n
1
=n
2
) on each side of the
combined gas law results
in
Experiment shows that the
pressure is actually 183 atm under these conditions, so the
assumption that the gas is perfect leads to a 10 per cent error
what temperature would result in the same sample exerting a pressure of300 atm? [900 K
]
11
MPACT ON ENVIRONMENTAL SCIENCE
11.1 The gas laws and the weather
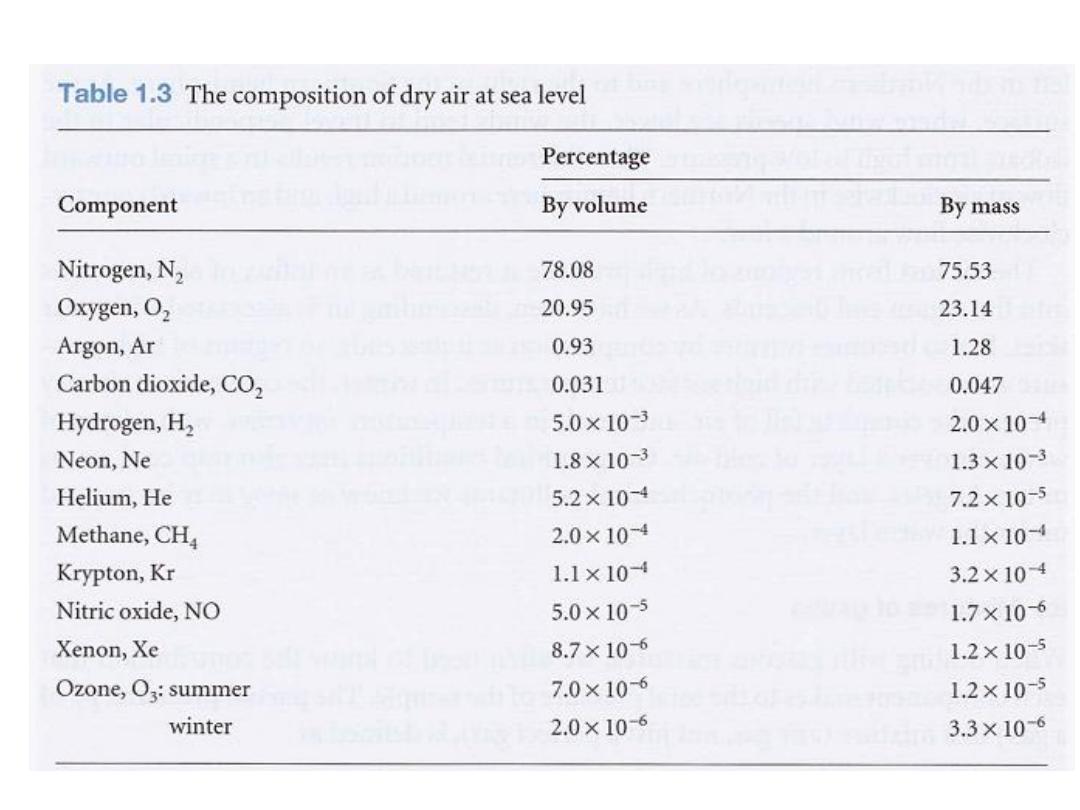
The biggest sample of gas readily accessible to us is
the atmosphere, a mixture of gases with the
composition summarized in Table 1.3. The
composition is maintained moderately constant
by diffusion and convection (winds, particularly
the local turbulence called
eddies
) but the
pressure and temperature vary with altitude and
with the local conditions, particularly in the
(the 'sphere of change'), the layer
troposphere
extending up to about
11 km
.
12

13
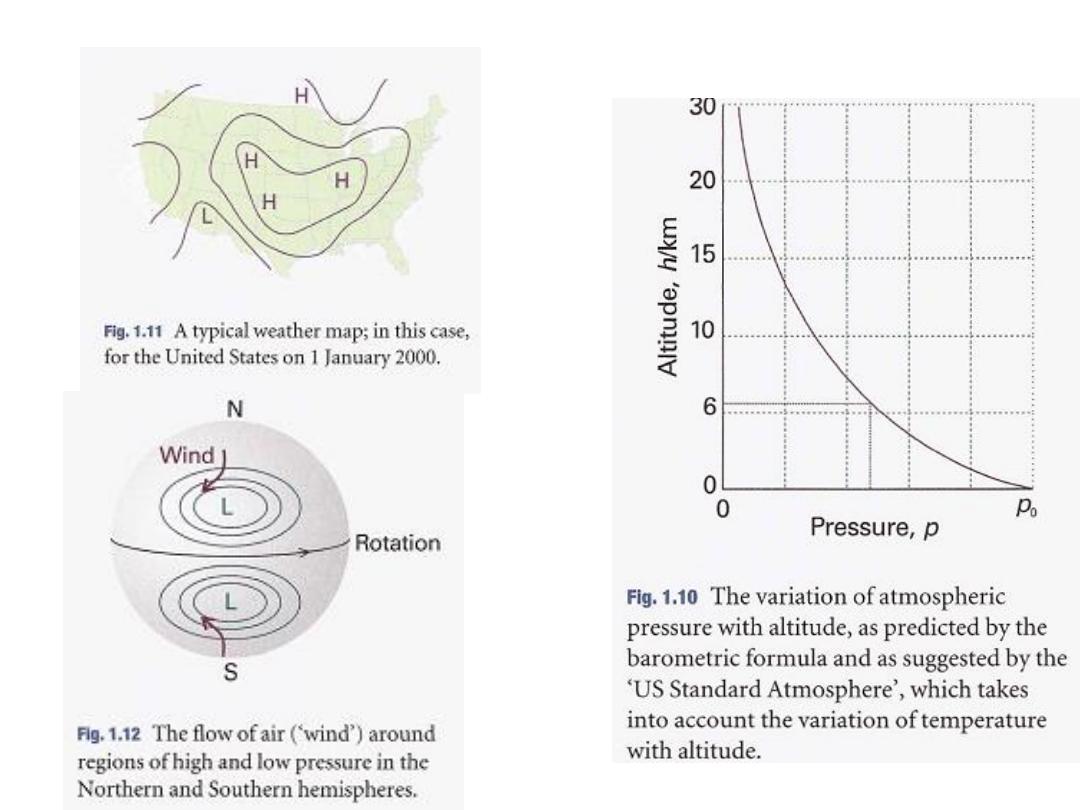
•
C at sea level,
°
15
the average temperature is
In the troposphere
falling to -57°C at the bottom of the tropopause at 11km. This
variation is much less pronounced when expressed on the Kelvin
scale, ranging from 288 K to 216 K, an average of268 K. If we
suppose that the temperature has its average value all the way up
to the tropopause, then the pressure varies with altitude, h,
according to
the barometric formula
where p
₀
is the pressure at sea level and H is a constant approximately
equal to 8 km.
More specifically,
H = RTIMg,
where M is the average molar mass of air and T is the temperature.
The barometric formula fits the observed pressure distribution quite
).
10
.
1
(see Fig.
troposphere
well even for regions well above the
14

16
(b) Mixtures of gases
When dealing with gaseous mixtures, we often need to know the
contribution that each component makes to the total pressure
of the sample. The partial pressure, P
J
of a gas
J
in a mixture (any
gas, not just a perfect gas), is defined as
of the component J, the amount of J expressed
the mole fraction
is
J
x
where
as a fraction of the total amount of molecules, n, in the sample:

16
When no J molecules are present, x
J
=0; when
only J molecules
are present, x
J
= 1. It follows from the definition of x
J
that, whatever
the composition of the mixture, x
A
+ x
B
+ ... = 1 and therefore that
the sum of the partial pressures is equal to the total pressure:
. When all
This relation is true for both real and perfect gases
the gases are perfect,
the partial pressure as defined in eqn
1.13 is also the pressure that each gas would occupy if it
occupied the same container alone at the same
temperature.
The latter is the original meaning of 'partial
pressure'. That identification was the basis of the original
formulation of
:
Dalton's law
The pressure exerted by a mixture of gases is the sum of the
pressures that each one would exist if it occupied the
container alone

17
Example 1.3 Calculating partial pressures
The mass percentage composition of dry air at sea level is approximately N
2
: 75.5; O
2
:
23.2; Ar: 1.3. What is the partial pressure of each component when the total
pressure is 1.00 atm?
Method We expect species with a high mole fraction to have a proportionally high
partial pressure. Partial pressures are defined by eqn 1.13. To use the equation, we
need the mole fractions of the components. To calculate mole fractions, which are
defined by eqn 1.14, we use the fact that the amount of molecules J of molar mass
MJ in a sample of mass m
J
is n
J
= m/ M
J
• The mole fractions are independent of
the total mass of the sample, so we can choose the latter to be 100 g (which makes
the conversion from mass percentages very easy). Thus, the mass of N, present is
75.5 per cent of 100 g, which is 75.5 g.
Answer The amounts of each type of molecule present in 100 g of air, in which the
masses of N
2
, 0
2
' and Ar are 75.5 g, 23.2 g, and 1.3 g, respectively, ar

18

19
ةٌقٌقحلا تازاغلا

Lecture 4
Realgases
ةٌقٌقحلا تازاغلا

2
Real gases
Real gases do not obey the perfect gas law exactly.
Deviations
and
high pressures
at
particularly important
are
from the law
low temperatures, especially when a gas is on the point of
condensing to liquid

3
1.3 Molecular interactions
Real gases show deviations from the perfect gas
law because molecules interact with one
another.
Repulsive forces
between molecules
assist expansion and
attractive forces
assist
compression
ان سبب حيود الغازات عن السلوك المثالي يعود لتحاث
الجزيئات مع بعضها فهناك
قوى تنافر
تعمل على تمدد الغاز
و قوى تجاذب
تعمل على تضاغط الجزيئات

4
•
are significant only when molecules are
Repulsive forces
almost in contact:
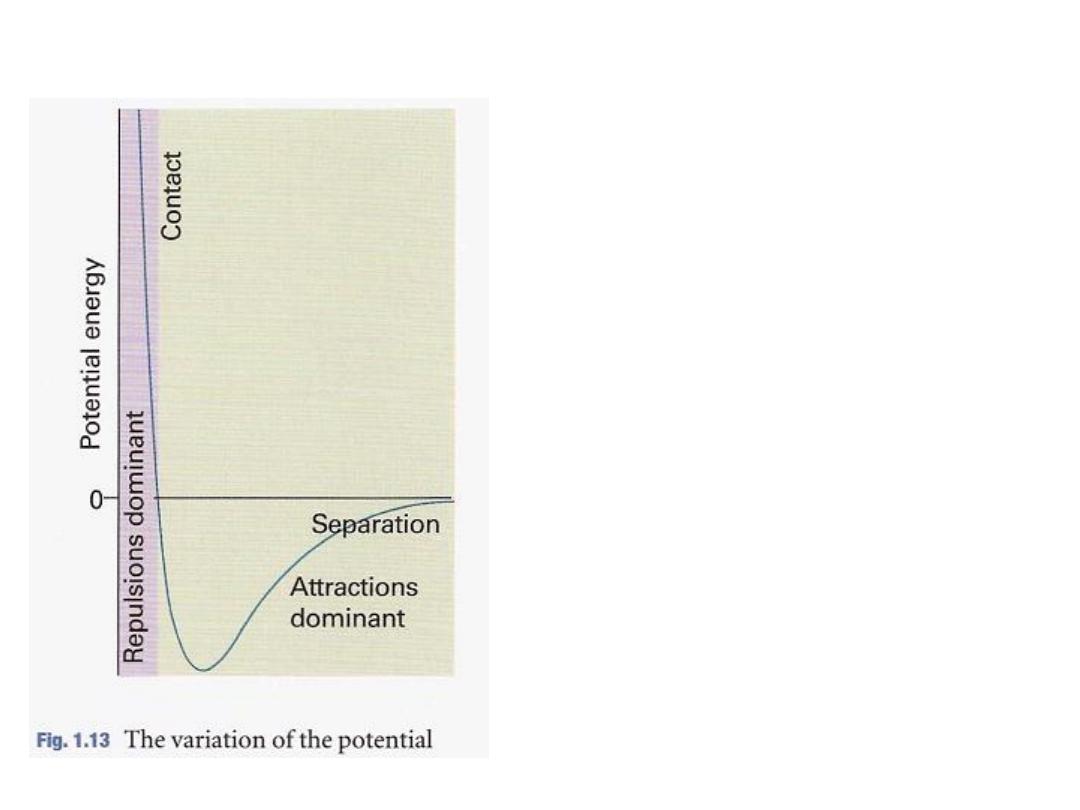
they are short -range interactions, even on
a scale measured in molecular diameters (Fig. 1.13). Because
they are short-range interactions,
•
Repulsions
can be expected
to be important
only when the
average separation of the molecules is small. This is the case
at high pressure, when many molecules occupy a small
attractive intermolecular forces
volume. On the other hand,
have a relatively long range and are effective over several
They are important when the molecules
molecular diameters.
are fairly close together but not necessarily touching (at the
intermediate
separations in Fig. 1.13).
5
•
الشكل
1.13
:
•
رٌغتب دهجلا ةقاط ًف رٌغتلا
نٌئٌزج نٌب ةلصافلا ةفاسملا
.
اذ
تنشاء طاقة
ة و موجبةٌلاع دهج
ئاتٌزجلا نٌب ةرٌصق ةفاسم دنع
نهماٌب ثاحتلا نا نٌبتل
هو تنافر
قوي
عند تلك المسافات
.
و عند
مسافات متوسطة عندما تكون
عندها
طاقة الجهد سالبة
فإن التحاث
هو تجاذب
ًو تكون هذه القوى ه
طرةٌسملا وا ةدئاسلا
.
•
رة فإن طاقةٌبك تافاسم دنع و
الجهد تساوي صفر ومن ثم فال
أتٌزجلا نٌب ثاحتل دوجو

6
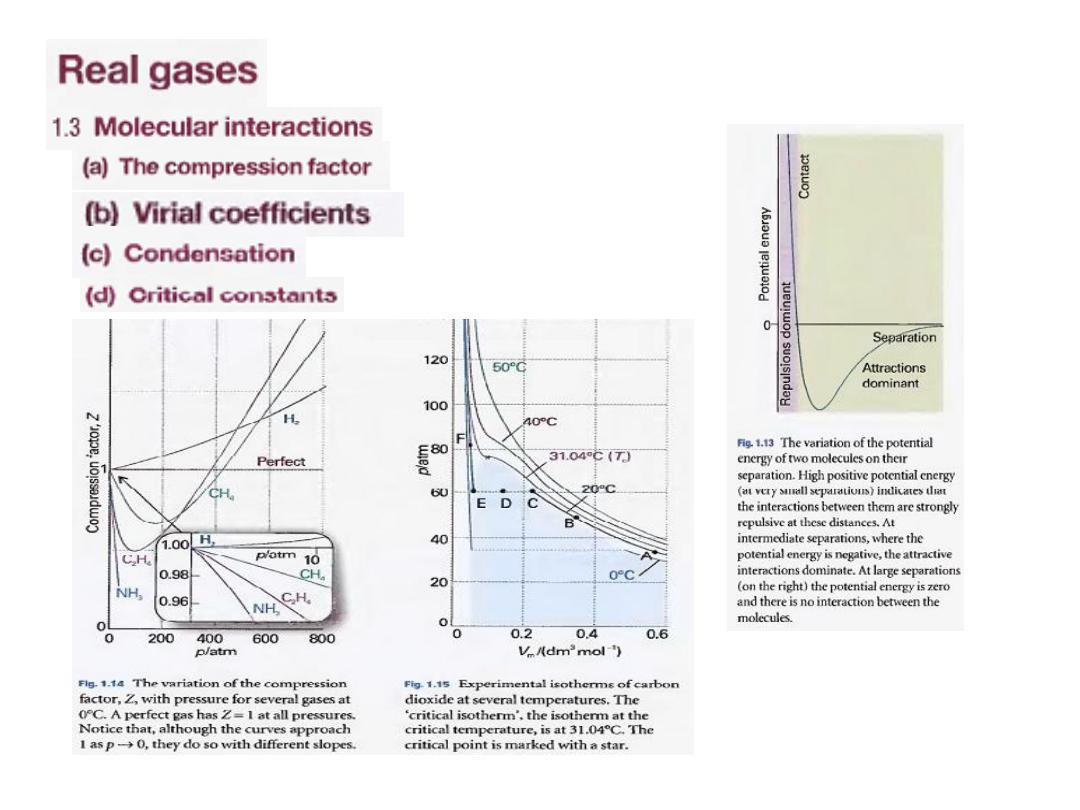
a) The compression factor
(
The compression factor, Z, of a gas is the ratio of its measured molar
volume, V
m
= V/n
to the molar volume of a perfect gas, V
⁰
m
at the same pressure and
temperature:
an
RT/p,
to
equal
the molar volume of a perfect gas is
Because
equivalent expression is:
Z=RT/p V
⁰
m
,
which we can write as:
Because for a perfect gas Z = 1 under all conditions
, deviation of Z a
measure of departure from perfect behavior.
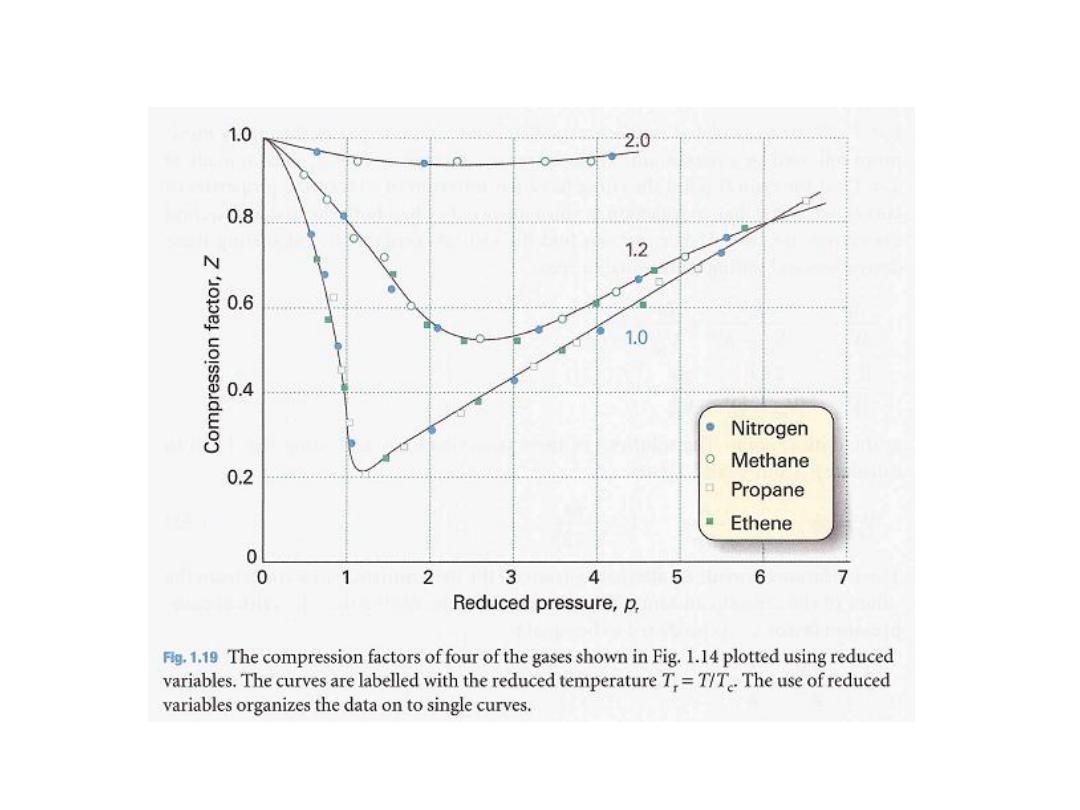
مةٌق دوٌح نا
Z
عن
1
ًود الغاز عن السلوك المثالٌح ىلع لٌلد نوكت
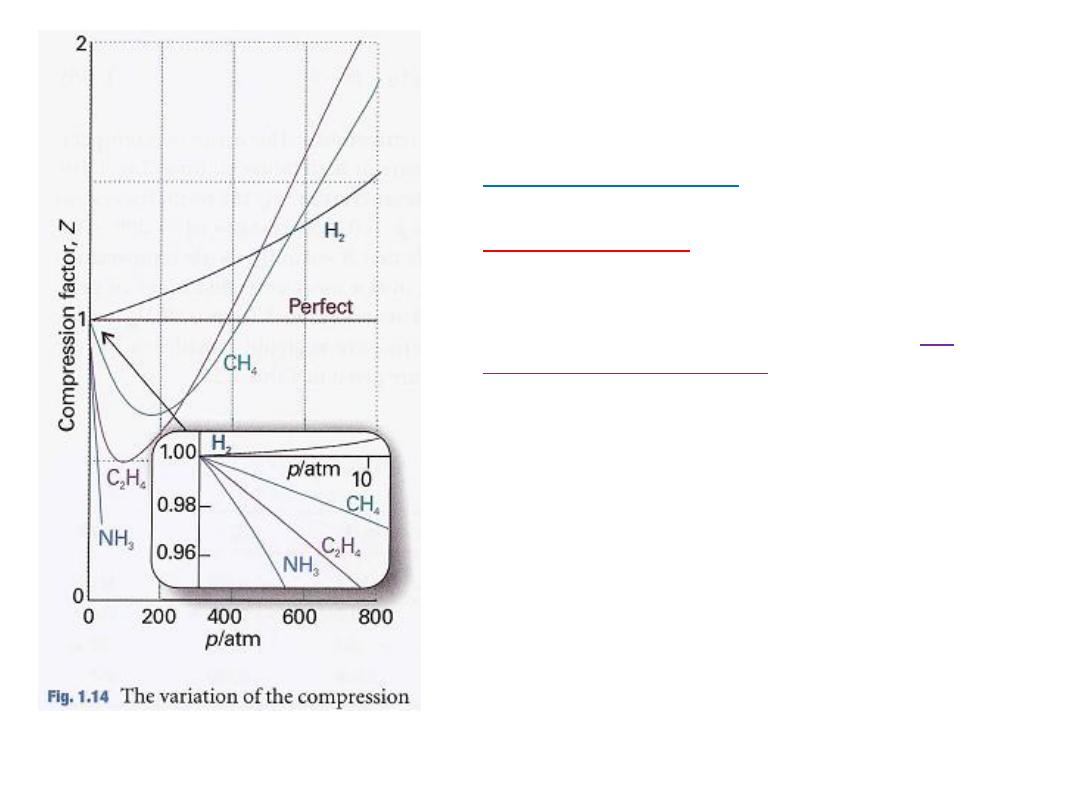
7
Some experimental values of Z are plotted
in Fig. 1.14.
the gases shown
, all
At very low pressures
have Z ≈1 and behave nearly perfectly.
,
1
, all the gases have Z>
At high pressures
signifying that they have a larger molar
volume than a perfect gas.
At
Repulsive forces are now dominant.
, most gases
intermediate pressures
have Z < 1, indicating that the attractive
forces are
reducing the molar volume
relative to that of a perfect gas.
الحظ
:
عامل التضاغطًف فلاتخلاا رواجملا لكشلا ًف
Z
مع الضغط و لغازات عدة
.
فعند درجة
0 ⁰C
ملكٌ ًلاثملا زاغلا نإف
Z=1
عٌمج دنع
اتٌنحنملا نا نم كلذ نم مغرلا ىلع نكل و طوغضلا
ـتقترب من ال
1
كلما
p
0
ل مختلفةٌم مٌق اهلف
.

8
•
معامالت فيلاير
b) Virial coefficients
Figure 1.15 shows the experimental isotherms for carbon dioxide.
At large molar volumes and high temperatures the real-gas isotherms do not
differ greatly from perfect-gas isotherms.
The small differences suggest that the perfect gas law is in fact the first term
in an expression of the form
This expression is an example of a common procedure in physical chemistry,
in which a simple law that is known to be a good first approximation (in
this case pV = nRT)
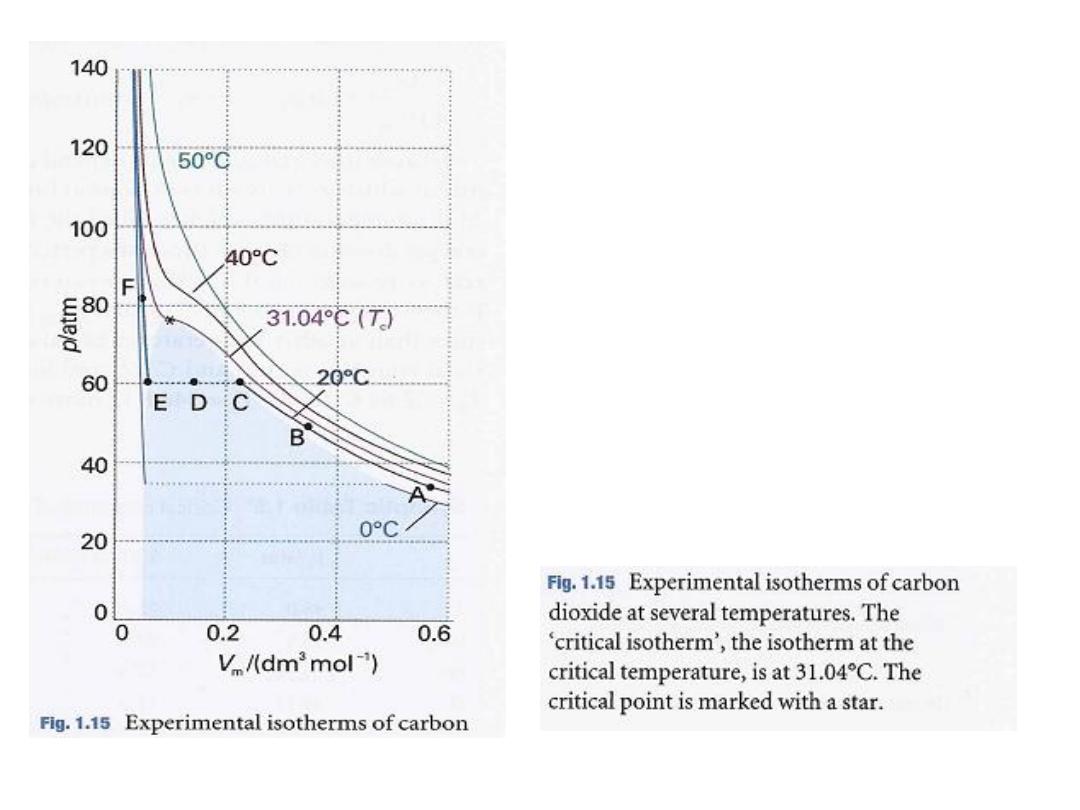
9
•
الشكل المجاورًف
:
ًانٌب لٌثمت
د الكاربونٌسكوا ًتاثل ًمرٌثوزٌا
ةٌرارحلا تاجردلا نم ددعل و
.
المخطط االيزوثيرمي الحرج هو
هٌلع عقت يذلا
•
الدرجة الحرارية الحرجة
كانت
عند
31.04⁰C
•
شرت بنجمةُأ دق ةجرحلا ةطقنلا و
على المخطط

10
reated
as the first term in a series in powers of a variable
(in this case
p). A more convenient expansion for many applications is
These two expressions are two versions of the viriaI equation of state.
By comparing the expression with eqn 1.17 we see that the term in
parentheses can be identified with the compression factor, Z.
which depend on the temperature, are the
B, C, ... ,
The coefficients
second, third, ...
viriaI coefficients
(Table lA); the first virial coefficient is 1.
The third virial coefficient, C,
is usually less important than the second
coefficient, B,
in the sense that at typical molar volumes C/V
2
m
<< B/V
m

11
We can use the virial equation
to demonstrate the
important point that, although the equation of state of a real gas may
coincide with the perfect gas law as p
0 , not all its properties necessarily
coincide with those of a perfect gas in that limit.
Consider, for example, the value of
dZ/dp, the slope of the graph of
compression factor against pressure
.
For a perfect gas dZ/dp = 0 (because Z =1 at all pressures), but for a real gas
from eqn 1.18 we obtain
However, B' is not necessarily zero,
so the slope of Z with respect to
p
does
not necessarily approach 0 (the perfect gas value), as we can see in Fig.
1.14.
Because several physical properties of gases depend on derivatives,
the properties of real gases do not always coincide with the perfect gas
values at low pressures.
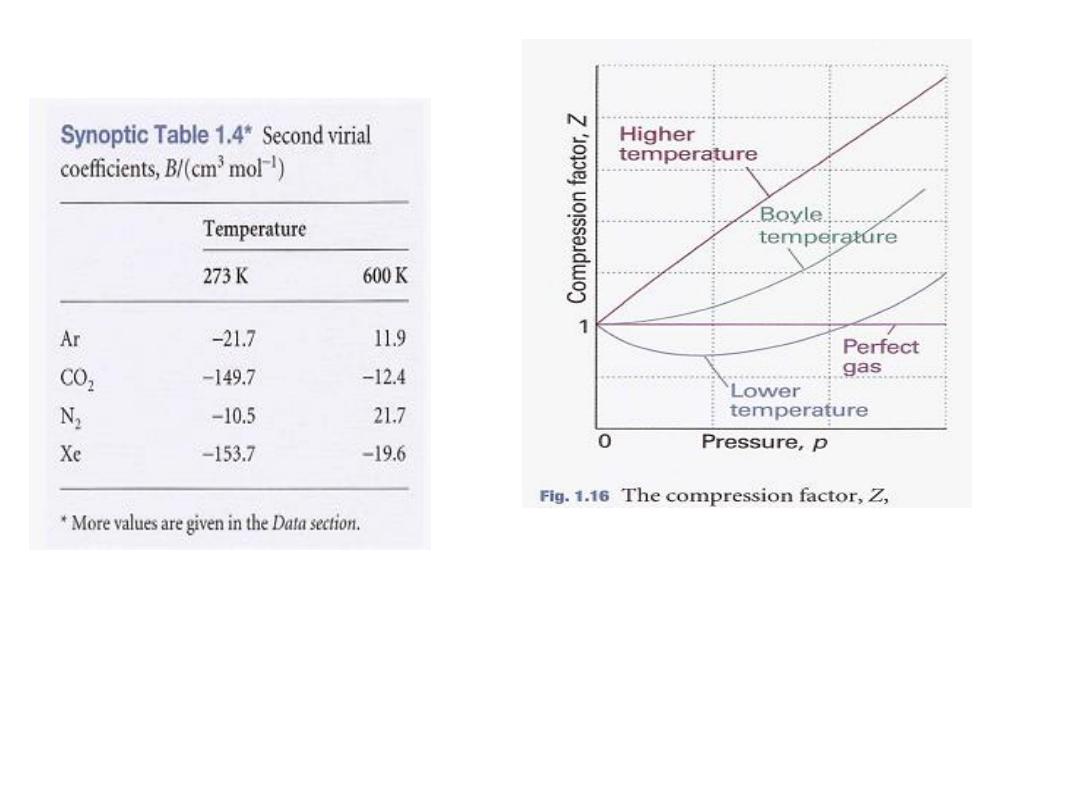
12
شكل
1.16
عامل التضاغط
Z
قترب منٌ
1
عند ضغوط
ل مختلفة و بالنسبة للغازاتٌم مٌقب اهنكل و ةئطاو
رٌغتت دق و ابلاس وا ابجوم لاٌم امهلاك انوكٌ دق ةٌقٌقحلا
ر درجات الحرارةٌغتب مٌقلا
.
كونٌ لٌوب ةجرد دنع و
ا ضمن مدىٌلاثم كلسٌس زاغلا و رفص يواسٌ لٌملا
واسع
من الشروط مقارنتا
بدرجات الحرارة االخرى
.

13
the properties of the real gas
'
B
T
,
temperature
BoyIe
do coincide with those of a perfect gas as p
0.
According to eqn 1.20b, Z has zero slope as p
0 if B = 0,
so we can conclude that B = 0 at the Boyle temperature
. It then
follows from eqn 1.19 that pV
m
≈ RT
B
over a more extended
range of pressures than at other temperatures because the
first term after 1 (that is, B/V
m
) in the
virial equation is zero and C/V
m
and higher terms are negligibly
small. For helium T
B
=22.64 K; for air T
B
=346.8 K; more values
are given
in Table 1.5
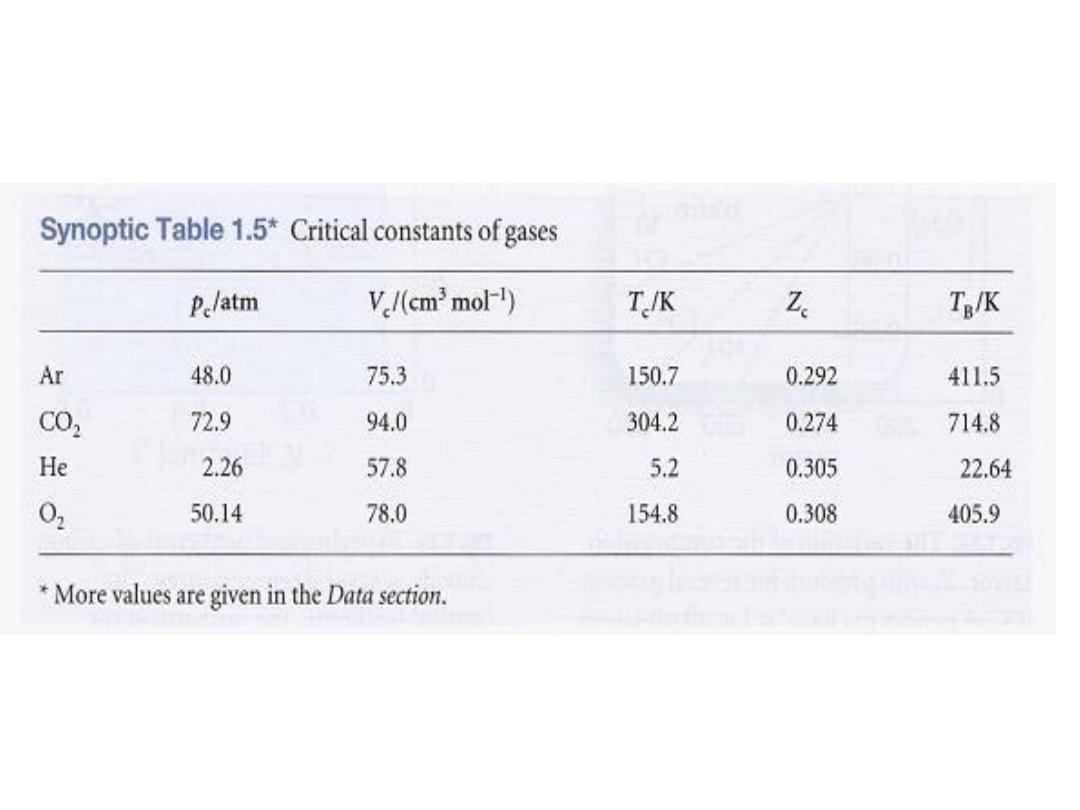
14
•
الجدول

15
(c) Condensation
Now consider what happens when we compress a sample of gas initially in
the state marked A in Fig. 1.15 at constant temperature (by pushing in a
piston). Near A, the pressure of the gas rises in approximate agreement
with Boyle's law. Serious deviations from that law begin to appear when
the volume has been reduced to B.
At C (which corresponds to about 60 atm for carbon dioxide), all similarity to
perfect behavior is lost,
for suddenly the piston slides in without
any further rise in pressure
: this
stage is represented by the horizontal line CDE. Examination of the
contents of the vessel shows that just to the left of C a liquid appears, and
there are two phases separated by a sharply defined surface.
the amount of liquid
As the volume is decreased from C through D to E,
There is no additional resistance to the piston because the gas
increases.
can respond by condensing.
The pressure corresponding to the line CDE,
is called the
,
are present in equilibrium
vapour
when both liquid and
vapour pressure of the liquid at the temperature of the experiment
.
and the piston rests on its surface. Any
the sample is entirely liquid
At E,
further reduction of volume requires the exertion of considerable
pressure, as is indicated by the sharply rising line to the left ofE. Even a
small reduction of volume from E to F requires a great increase in pressure
16
d) Critical constants
(
The isotherm at the temperature T
c
; (304.19 K, or 31.04 °C for
CO
2
) plays a special role in the theory of the states of matter.
An isotherm slightly below T
c
, behaves as we have already described: at a
certain pressure, a liquid condenses from the gas and is distinguishable from it
by the presence of a visible surface.
•
The temperature, pressure, and molar
.
The critical point of the gas
volume at the critical point
are called the critical temperature,
T
c
, critical
pressure, P
c
, and critical molar volume, V
c
, of the substance.
Collectively, P
c
, V
c
, and T
c
are the critical constants of a substance (Table
1.5).
that occupies the entire
a single phase
the sample has
c
T
At and above
a gas.
by definition,
volume of the container. Such a phase is,

17
, for instance,
The critical temperature of oxygen
signifies that it is impossible to produce liquid
oxygen by compression alone if its
temperature is greater than 155 K: to liquefy
oxygen-to obtain a fluid phase that does not
occupy the entire volume-the temperature
must first be lowered to below 155 K, and
then the gas compressed isothermally. The
single phase that fills the entire volume when
T> T
c
; may be much denser than we normally
consider typical of gases, and the name
supercritical fluid is preferred

Lecture 5
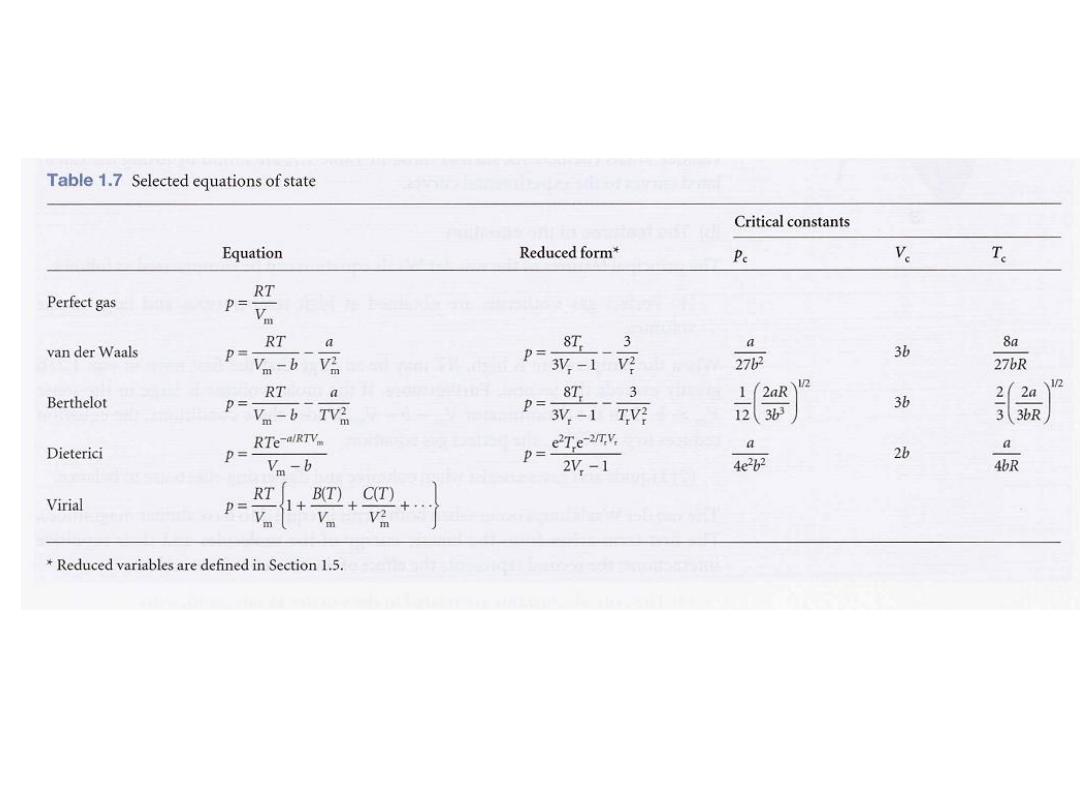
1.4 The van der Waals equation

2
1.4 The van der Waals equation:
We can draw conclusions from the virial equations of state only by inserting specific
values of the coefficients. It is often useful to have a broader, if less precise, view
of all gases. Therefore, we introduce the approximate equation of state suggested
by J.D. van der Waals in 1873. This equation is an excellent example of an
expression that can be obtained by thinking scientifically about a mathematically
complicated but physically simple problem, that is, it is a good example of 'model
building'.
The van der Waals equation is:
and a derivation is given in Justification 1.1. The equation is often written in
terms of the molar volume V
m
= V/ n as:
3
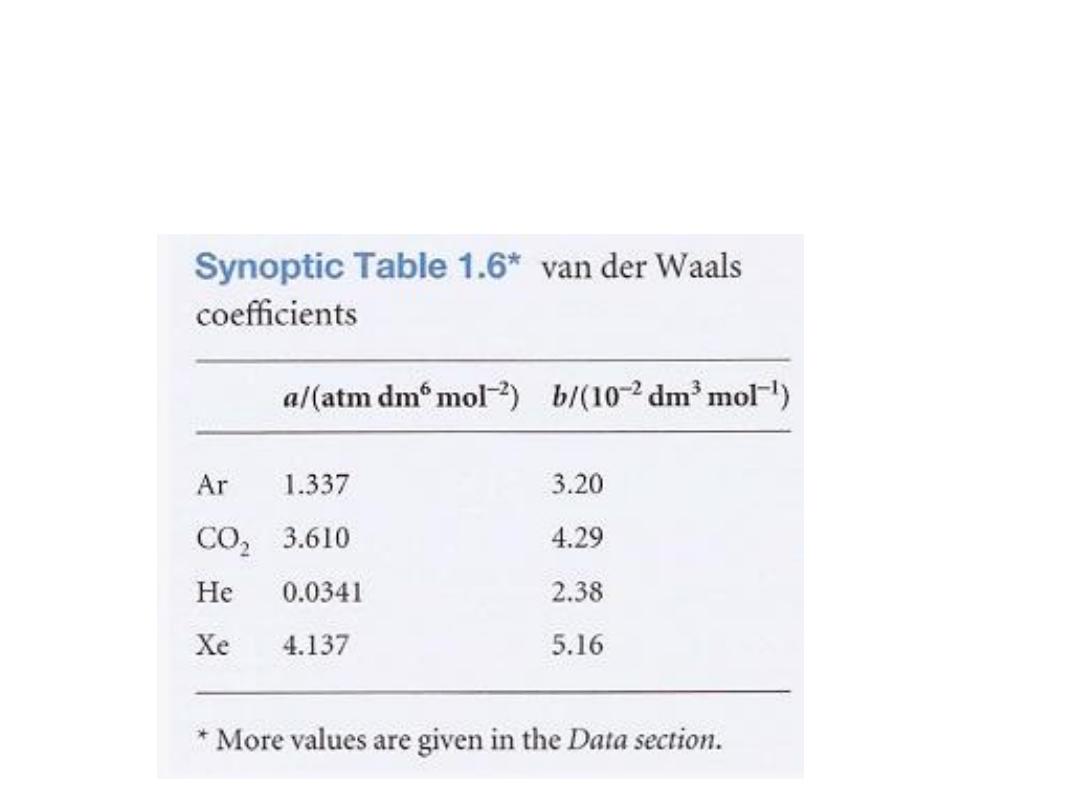
The constants a and b are called the van der Waals coefficients.
They are characteristic of each gas but independent of the temperature
(Table 1.6).
الثابتان
a
و
b
يدعيان بمعامالت فاندرفالز و هما مميزان لذلك الغاز و اليعتمدان على درجة
الحرارة
.
4
•
ايضاح
:
1
.
1
:
معادلة فاندر فالز كمعادلة حالة
:
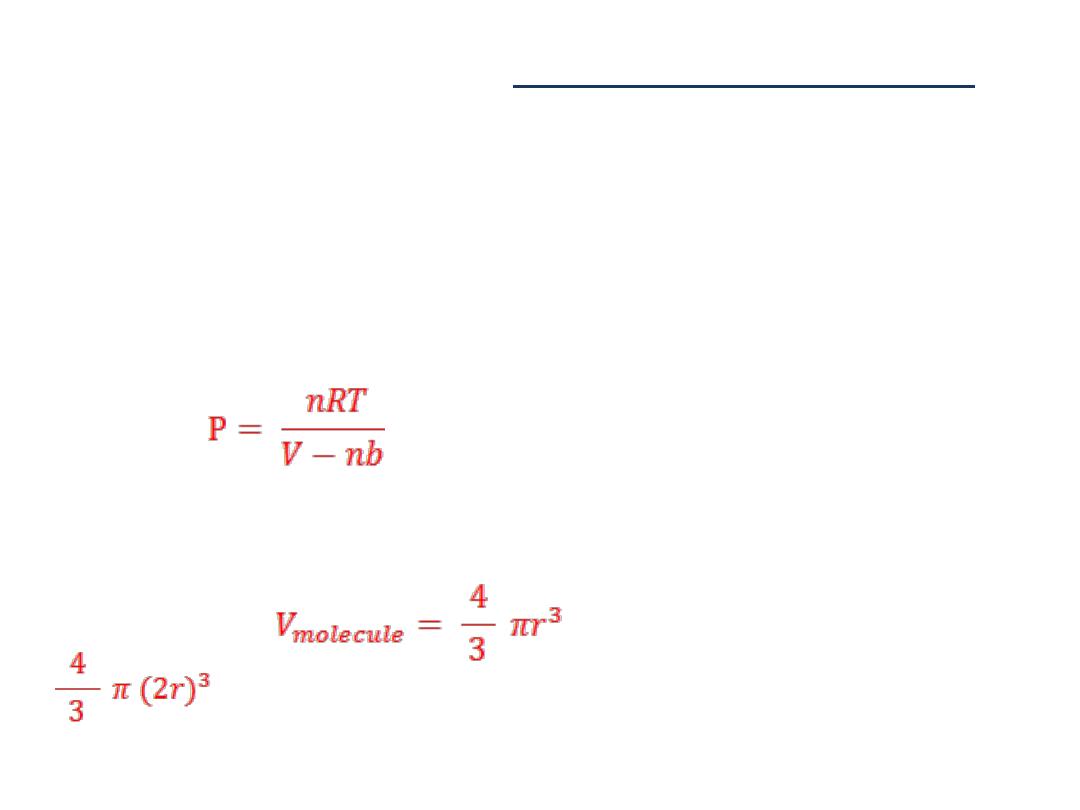
ئات تسلكٌزجلا نا نم مغرلا ىلعو نابسحلاب ذخؤٌ تائٌزجلا نٌب رفانتلا رٌثأت نا
ر قابلة لالختراق أي صلدةٌغو ةرٌغص تارك كولسك
.
كما ان الحجم الالصفري
الحجمًف كرحتت تائٌزجلا نا نم ًلادب هنا ضرتفٌ تائٌزجلل
V
انها سوف
رٌغصلا مجحلا كلذ ًف رقتست
V - nb
ث انٌح
nb
ً الحجم الكلًابٌرقت لثمٌ
ئاتٌزجلا هلغشت يذلا
.
ان االفتراضات هذه تفترض انه البد من استبدال قانون الغاز
ًالمثال
P= nRT/V
بالعالقة
:
ذلك
كون التنافر مؤثرٌ امدنع
.
ن ذات نصف قطرٌتدلص نٌتركل ةفاسم برقا نا امك
r
وحجم
ًتكون المسافة ه
2r
شغلٌُ يذلا مجحلا ناف ىذل
هو
:
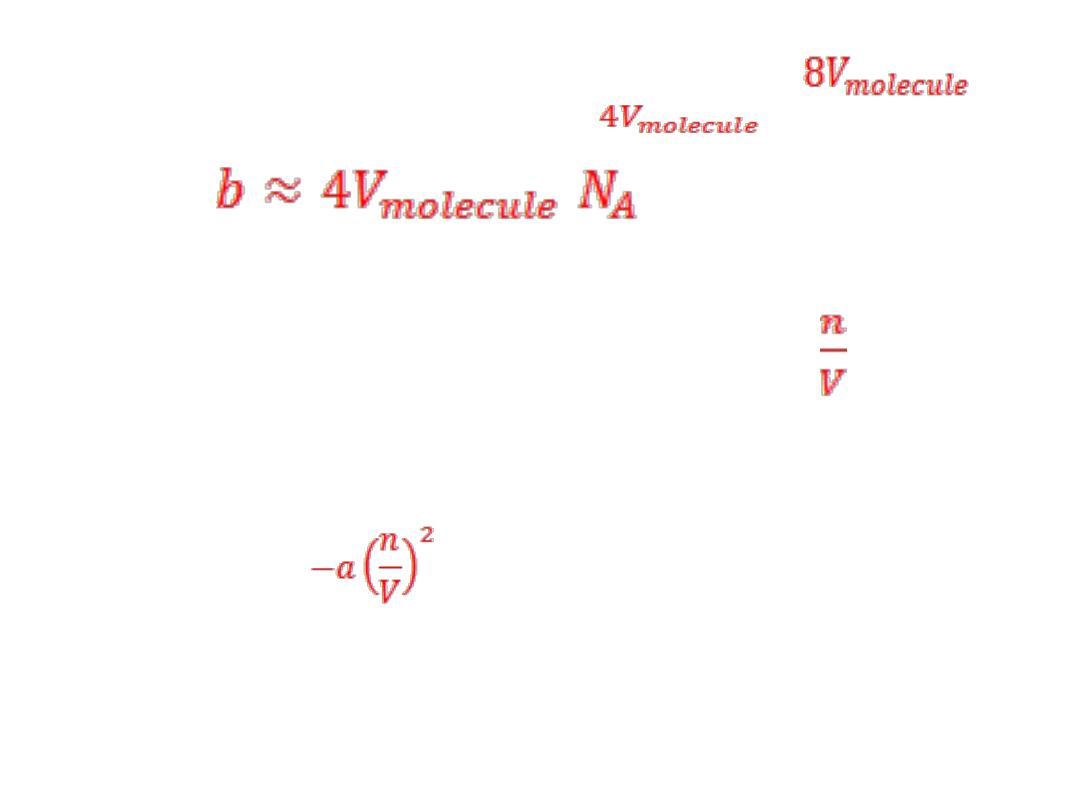
5
او
شغله الجزيء الواحد هوٌ يذلا مجحلا وا ةٌئٌزج موجح ةٌنامث يا
نصف ذلك
الحجم
هٌلعو
فان
:
من عددٍلك ىلع دمتعٌ طغضلاو
التصادمات على
تققلها اوًتلاو اهتوقو ناردجلا
اي نسبةًبسن لكشب لمعت ًتلاو بذجلا ىوق ًه اهتوق نم فعضُت
زٌكرتلا
الموالري
النموذجًف تأٌزجلا نم
.
اذن بسبب كل من التردد
(
عدد التصادمات
)
منهاًاحورطم تامداصتلا ةوقو
تبُك اذاف زٌكرتلا كلذ عبرم ىلا اٌبسن ضفخنٌس طغضلا نذا، بذاجتلا ىوق
ساويٌ طغضلا ًف ضافخنلاا رادقم
المقدار
ث انٌح
a
هو
ًر قوى التنافر والتجاذب ستعطٌثات دٌحوتبو زاغ لكل ةزٌمم ةفص وهو بجوم تباث
معادلة الحالة لفاندر فالز المعادلة
(
1.21
)

6
رٌثاتو ةٌئٌزجلا موجحلل ًاموهفم ان ّوك دق حاضٌلاا اذه ًفف
القوى
.
والمعادلة
ة لهاٌلاحلا ةقٌرطلا نكلو ىرخا قرطب اهقاقتشا نكمٌ
لهاٌوحتو ةٌضاٌرلا ةئٌهلا قاقتشا نكمٌ فٌك نٌبت ذا ةدئاف
ة من االفكارٌضاٌر ةلداعم ىلا
االزمة
.
كما وان االشتقاق له
فائدة ابقاء عدم دقة المعامالن
a , b
:
عتبرانٌ ةقٌقحلا ًفو
ئتانٌزج ناتٌصاخ امهنا نم ناٌضارتفا وا ناٌعضو نارٌغتم
قتانٌقد
.
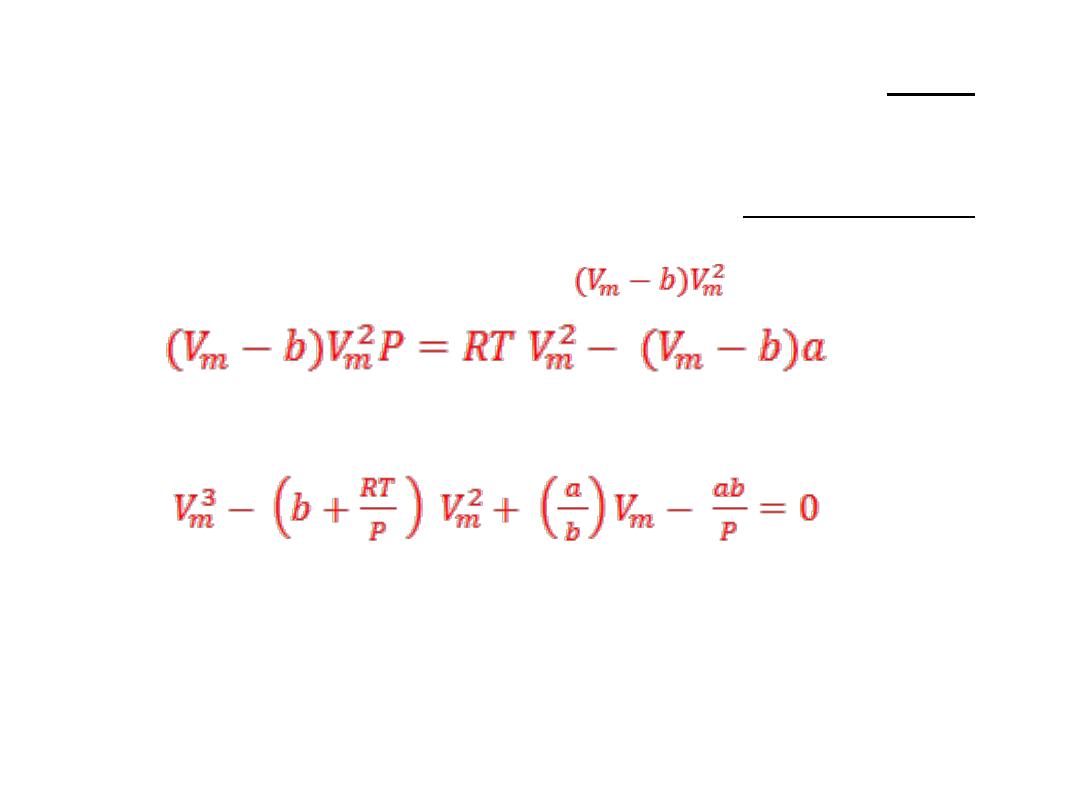
7
•
مثال
4
.
1
•
ًقدر الحجم المول
(
CO2
بدرجة
500K
وضغط
100 atm
بعد معالجة الحسابات بقوى
فاندرفالز
.
•
قة الحلٌرط
Method
•
سنستخدم العالقةًلوملا مجحلا هنم بحسن رٌبعت مادختسا ضرغل
( .
1.21b
)
وسوف نضرب
المعادلةًفرط
بالمقدار
للحصول على
:
•
وبالقسمة بالمقدار
p
وجمع االسس
ﻟ
V
m
سنحصل
على
:
•
ً انها معقدة جداّلاا ةثلاثلا ةجردلا ةلداعمل قٌقد ًضاٌر رٌبعت ىلع لوصحلا نكمٌ هنا نم مغراب
الحلًف
.
الحلًف ةٌراجتلا ةٌبوساحلا جماربلا مادختساب اهلح نكمٌ نكلو
.

8
الحل
Answer
حسب الجدول
(
1.6
)
فان
a = 3.592
و
b = 4.267 × 10
-2
dm
3
moℓ
-1
فتحت
الظروف المعطاة نجد ان
:
المعادلة بالنسبةًف نلاماعملاف
V
m
كون اذنٌ
:
فالجذر المقبول
ﻟ
X = 0.366
ًاٌلوم ًامجح ًطعٌ اذهو
V
m
=0.366 dm
3
moℓ
-1
وبالنسبة للغاز
ًكون الحجم المولٌس فورظلا هذه تحت ًلاثملا
0.410 dm
3
moℓ
-1

9
(a)
ةٌدامتعا
المعادلة
Reliability of the equation
•
ًقٌقحلا زاغلا كولس جاتنتسا عٌطتست زلاف ردناف ةلداعم نا ىدم يا ىلا ربتخنس نلااو
.
وقد تكون
مٌق ىلع لوصحلا نكمٌ هناو ةٌقٌقحلا ةداملل ةلاحلا ةلداعمل طٌسبو درفم رٌجت عقوت ًف ًادج هدحو
قها على عالقةٌبطت دعب ةقٌقد
لايرٌف
م المجدولة للمعامالن لدرجات حرارة مختلفةٌقلا مادختسابو
لٌلحت ًطت اهنا لافدناف ةلدام ةزٌم نا ًاٌددع ةمظنلاا لٌلحتو
(
رِّبُع دقو
ًاٌزمر هنع
)
سمح لناٌ
من ان
نِّوكن
ةٌقٌقحلا تازاغلا نع ةماع ةصلاخ
.
نا استخدام احدٌلع ةلداعملا لشفت امدنعو
الجدولًف تضرتفا ًتلاو ىرخلاا ةلاحلا تلاداعملا
(
1.7
)
دةٌدج ةلاح ةلداعم قاقتشاب كلذو
لايرٌف ةلداعم ىلا عوجرلا وا
.
مِّكحن نا انٌلع لوقن نا دٌرن يا
انطقة المعادلة
ة المستنتجةٌّمرٌثوزٌلاا تاططخملا عم رادقمب
الشكلًف ًاٌلمع ةجتنتسملا كلت عم اٌرظن
(
1.15
)
10
•

11
•
ًة كما فٌمرٌثوزٌلاا تاططخملا نم ةعومجم هانداو
الشكل
(1.17)
والشكل
(
1.18
. )
وبغض النظر عن التذبذب
اال انها اعطت، ةجرحلا ةرارحلا ةجرد لفسا قطانملا ًف
ة بشكل ممتازٌّمرٌثوزٌآ تاططخم
.
ان خطوط فاندر فالز
Vander Waals loops
ة بسبب انهاٌعقاو رٌغ ًه
الضغطًف ةداٌز كانه ةنٌعم طورش تحت اهنا ضرتفت
الحجم ومن ثم استبدلت برسمًف ةداٌز ىلا يدؤت هذه ثدحت
ه فان االنشوطات او المخططاتٌلعو ةٌقفا ةمٌقتسم طوطخ
ة فوق وتحت الخطوطٌواستم تاحاسم ددحت اهنا ةٌئٌزجلا
لٌو سكام بٌكرتب ىعدت ةقٌرطلا هذه
( 3 ) Maxwell
construction
ًفمعامالن فاندر فالز مثل تلك المذكورة ف
الجدول
(1.7)
قد وجدت من مطابقة المنحنات المحسوبة
ًاٌبٌرجت اهٌلع لصحملا تانحنملاو
.
12
•
•
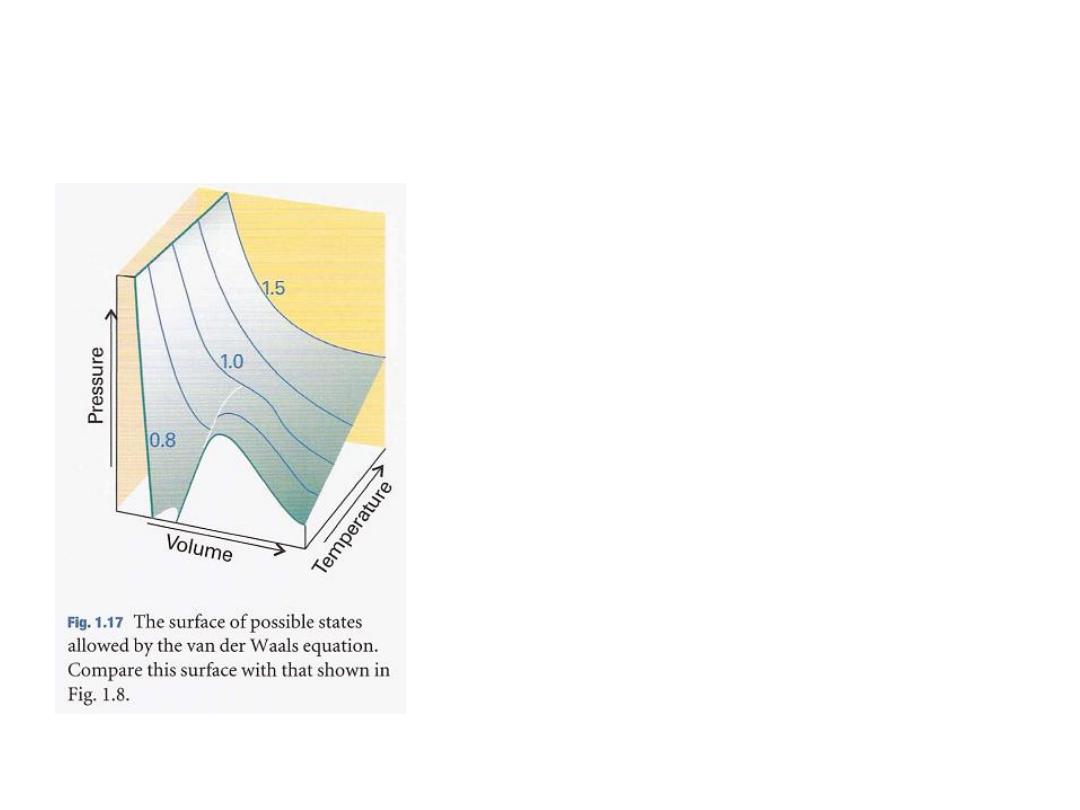
الشكل
:1.17
•
السطح المحتمل للحاالت
المسموح بمعادلة فاندرفالز
•
قارن هذا السطح مع الشكل
1.8
.
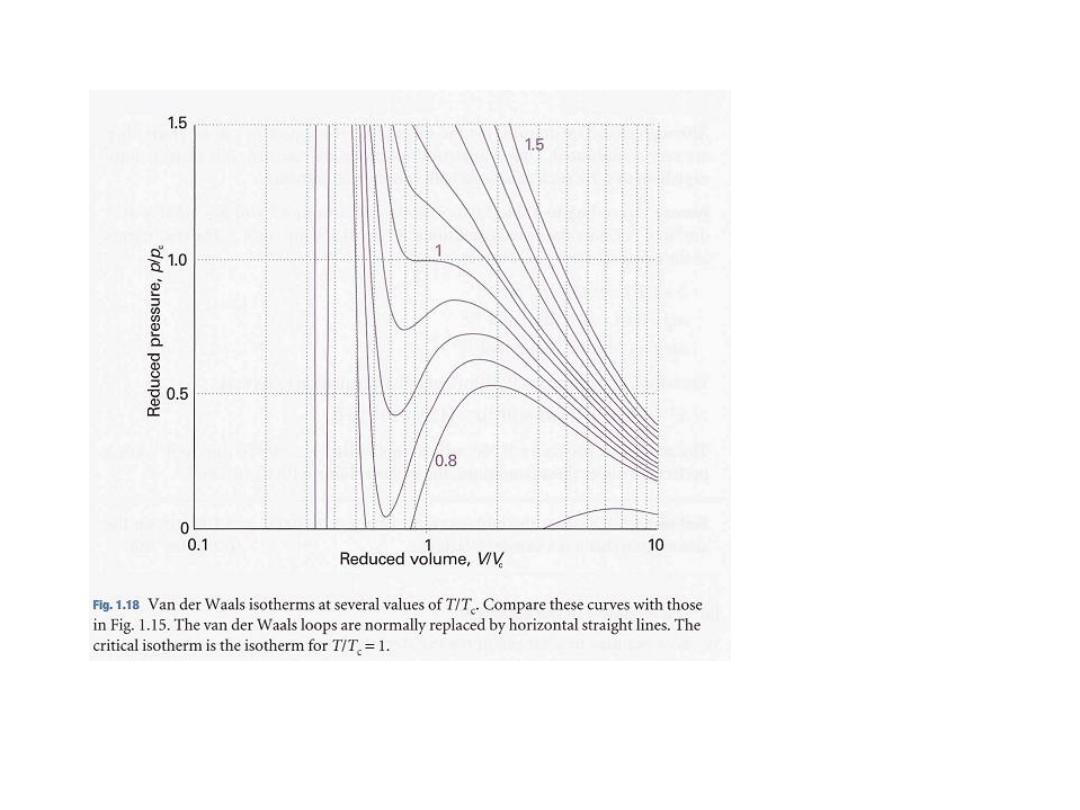
13
•
شكل
1.8
:

14
(b) The features of the equation
The principal features
of the van der Waals equation can be summarized as
follows.
(1) Perfect gas isotherms are obtained at high temperatures and large molar
volumes. When the temperature is high, RT may be so large that
the first term in eqn 1.21b greatly exceeds the second.
Furthermore, if the molar volume is large in the sense
V
m
» b, then the denominator V
m
- b ≈ V
m
. Under these conditions, the
equation reduces to p = RT/V
m
, the perfect gas equation.
(2) Liquids and gases coexist when cohesive and dispersing effects are in
balance. The van der Waals loops occur when both terms in eqn 1.21b
have similar magnitudes.
The first term arises from the kinetic energy of the molecules and their
repulsive interactions; the second represents the effect of the attractive
interactions.

15
(3) The critical constants are related to the van der Waals coefficients.
For T < T
c,
the calculated isotherms oscillate, and each one passes through a
minimum followed by a maximum. These extrema converge as T
T
c
; and
).
4
flat inflexion (
at the critical point the curve has a
;
c
T
coincide at T =
From the properties of curves, we know that an inflexion of this type occurs
when both the first and second derivatives are zero. Hence, we can find the
critical constants by calculating these derivatives and setting them equal
to zero:

16
ة الحرجٌطاغضنلاا لماع
Z
c

17
•
الحاالتًقلات ءادبم
:
ث انٌح
P
r
هو الضغط المختزل
V
r
الحجم المختزل و
T
r
درجة الحرارة المختزلة
.

19
•
للغازًقٌقحلا طغضلا داجٌا نكمٌ انناف لزتخملا طغضلا انٌطعا اذاف
•
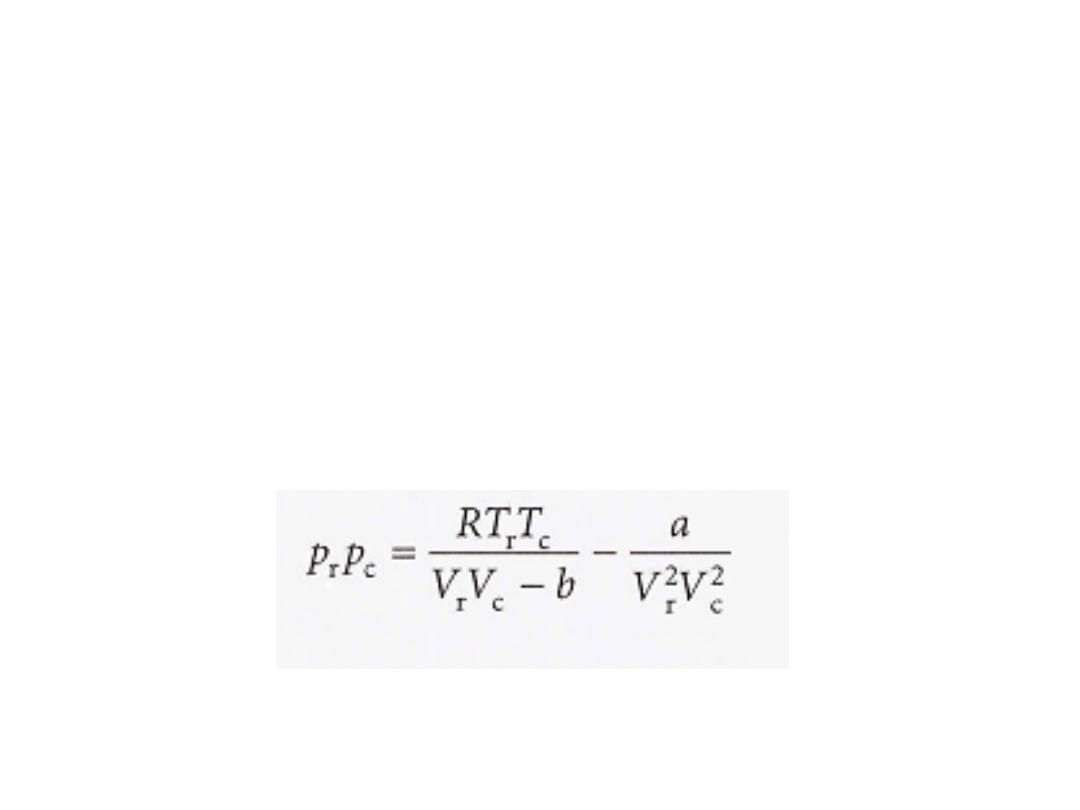
19
•
ة و لنفسٌقٌقحلا تازاغلا ناب ةٌبٌرجتلا تادهاشملا تتبثا
الحجم المختزل و درجة الحرارة المختزلة فانها سوف تسلط
الحاالتًقلات ءادبمب ىعدت ةلاحلا هذه لزتخملا طغضلا
.
و
ئاتٌزج نم ةنوكملا تازاغلا هعٌطت و ًبٌرقت وه ءادبملا اذه
ة اوٌورك تائٌزجلا نوكتلا امدنع اناٌحا لشفت و ةٌورك
مكن ان تكتب بصورةٌ زلافردناف ةلداعم و ةبطقتسم
ًلٌامك و ةلزتخملا تارٌغتملا
:
21

21
•

Lecture 6
The First Law

2
•
نمكٌادومرثلل لولاا نوناقلا
The First Law
•
الخصائص العامة للثرموداينمك
:
For the purposes of physical chemistry, the universe is divided into two parts,
.
its surroundings
and
the system
The system
is the part of the world in which we have a special interest. It may
be a reaction vessel, an engine, an electrochemical cell, a biological cell,
and so on.
comprise the region outside the system and are where we
The surroundings
make our measurements.
The type of system depends on the characteristics of the boundary that
divides it from the surroundings (Fig. 2.1).
If matter can be transferred through the boundary
between the system and
its surroundings the system is
classified as open
.
If matter cannot pass through the boundary
the system is
classified as closed
.
Both open and closed systems can exchange energy with their
surroundings.
For example, a closed system can expand and thereby raise a weight in the
surroundings; it may also transfer energy to them if they are at a lower
temperature.
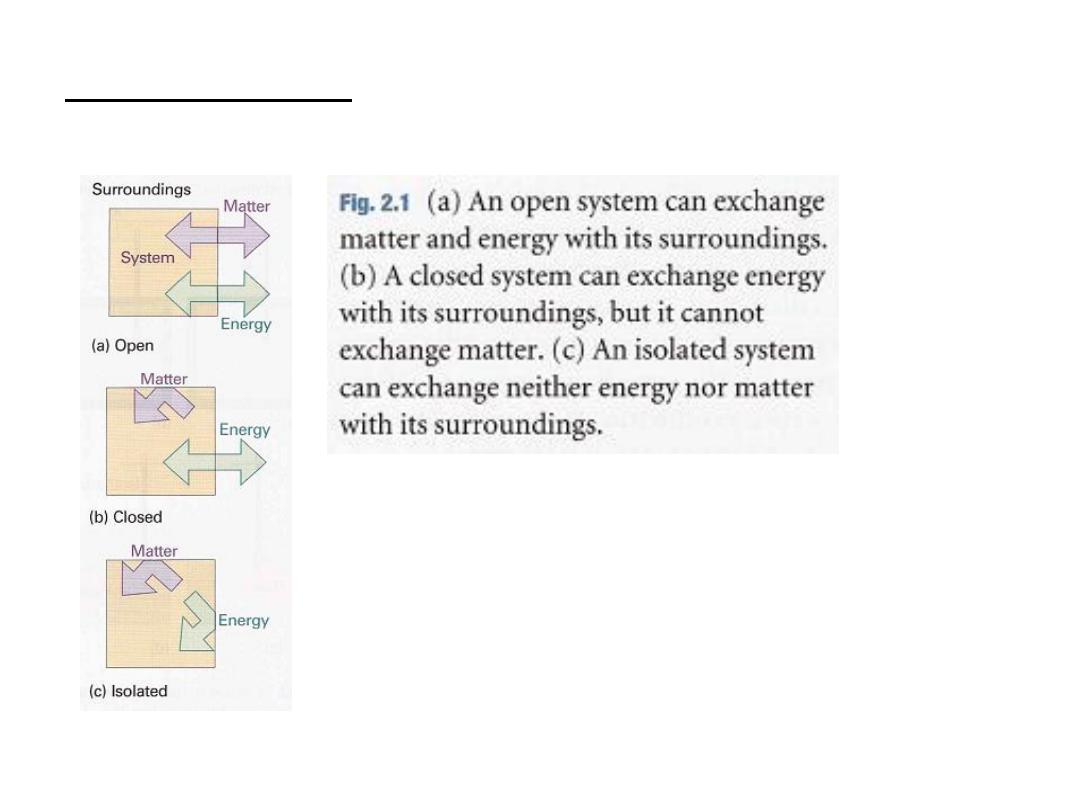
3
is a closed system that has neither
An isolated system
mechanical nor thermal contact with its surroundings
.

4
2.1. Work, heat, and energy:
The fundamental physical property in thermodynamics is work:
is motion against an opposing force.
work
An example of doing work is the expansion of a gas that pushes out a piston and
raises a weight. A chemical reaction that drives an electric current through a
resistance also does work, because the same current could be driven through a
motor and used to raise a weight.
.
is its capacity to do work
The energy of a system
ن النظام وٌب قرفلل ةجٌتنك لغشلا رٌغ ىرخا قرطب اهرٌٌغت نكمٌ ماظنللا ةقاط نا براجتلا ترهضا
مكننا القول بان الطاقة قد انتقلت كحرارةٌف طٌحملا
.
Experiments have shown
that the energy of a system may be changed by means
other than work itself. When the energy of a system changes as a result of a
temperature difference between the system and its surroundings we say that
energy has been transferred as heat. When a heater is immersed in a beaker of
water (the system), the capacity of the system to do work increases because hot
water can be used to do more work than the same amount of cold water. Not all
boundaries permit the transfer of energy even though there is a temperature
difference between the system and its surroundings

5
is a process that releases energy as heat into
An exothermic process
its surroundings. All combustion reactions are exothermic.
is a process in which energy is acquired from
An endothermic process
its surroundings as heat.
An example of an endothermic process
is the vaporization of water.
An endothermic process
energy is transferred 'as heat' from
the surroundings into the system.
Heat and work
1
.
2
Molecular interpretation
In molecular terms,
heating
is the transfer of energy that makes use of
disorderly molecular motion.
In contrast
, work is the transfer of energy that makes use of
organized motion (Fig. 2.4). When a weight is raised or lowered, its
atoms move in an organized way (up or down). The
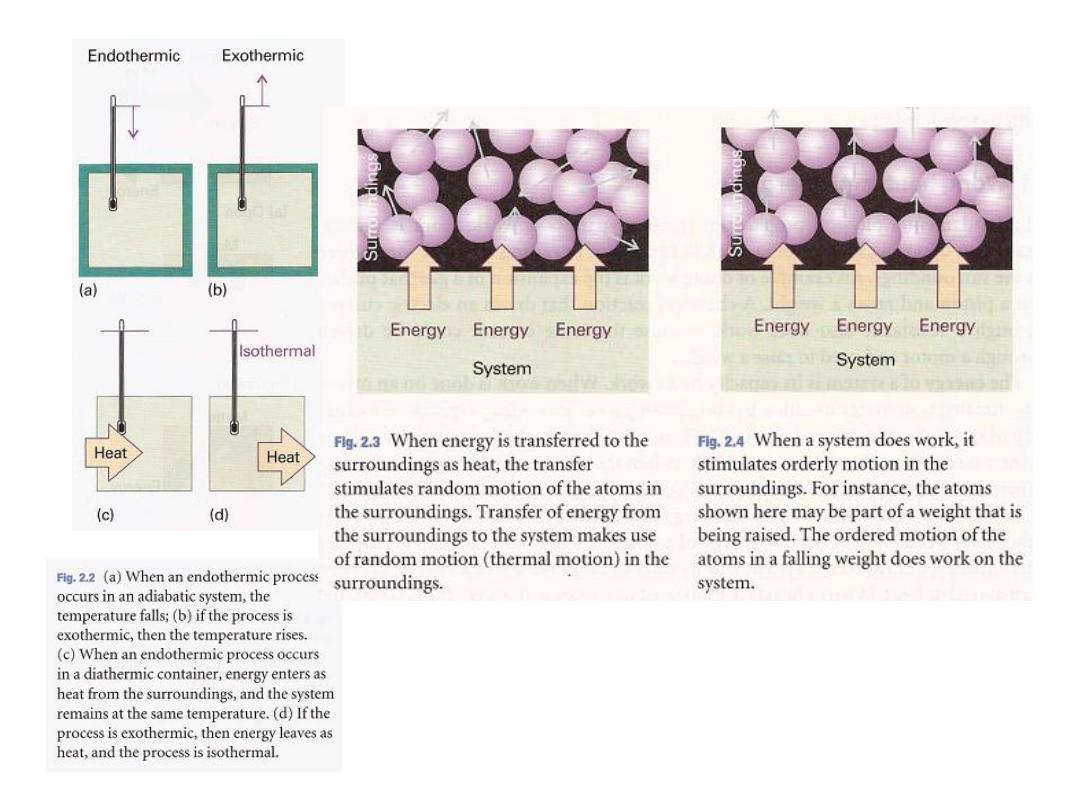
6

7
•
ن الشغل و الحرارة المسلطة على النظامٌب زٌٌمتلل
The distinction between work and heat is made in the
surroundings: The fact that a falling weight may stimulate
thermal motion in the system is irrelevant to the distinction
between heat and work:
work is identified as energy transfer making use of the
organized motion of atoms in the surroundings
, and
heat is identified
as energy transfer making use of thermal
motion in the surroundings.
I

8
2.2 The internal energy
In thermodynamics, the total energy of a system is called its internal
energy, U.
The internal energy is
the total kinetic
and
potential energy
of the
molecules in the system (see Comment 1.3 for the definitions of kinetic
and potential energy).'
We denote by
ΔU
the change in internal energy
when a system changes
of
f
to a final state
j
U
with internal energy
i
initial state
from an
internal energy U
f
:
ΔU =U
f
– U
i
……………………………….(2 .1)
in the sense that its value depends
is a state function
The internal energy
only on the current state of the system and is independent of how
that state has been prepared.
In other words, it is a function of the properties that determine the
current state of the system. Changing
ة للنظام والٌلاحلا ةلاحلا ىلع طقف دمتعت اهتمٌق نا ىنعمب يأ ةلاح ةلاد ًه ةٌلخادلا ةقاطلاف
ر تلك الحالةٌضحت ةٌفٌك ىلع دمتعت
.

9
Changing any one of the state variables,
such as the pressure
, results in a
change in internal energy.
The internal energy
is an extensive property
. That the internal energy is a
state function has consequences of the greatest importance, as we start to
unfold in Section 2.10
نٌوانعلا ًف ىرنس امك ىربك ةٌمها اهل و اظٌا ةلاح ةلاد ًه و ةلماش ةٌصاخ ًه ةٌلخادلا ةقاطلاف
الالحقة
.
heat,
Internal energy, and work
are all measured in the same units, the joule
(J). The joule, which is named after the nineteenth-century scientist J.P.
Joule, is defined as
1 J = 1 kg m² S¯²

10
A joule is quite a small unit of energy
: for instance,
each beat of the human
heart consumes about 1 J.
Changes in molar internal energy,
ΔU
m
are typically expressed in kilojoules
per mole (k] mol ¯¹). Certain other energy units are also used, but are more
common in fields other than thermodynamics.
Thus, 1 electronvolt (1 eV)
is defined as the kinetic energy acquired
when an electron is accelerated from rest through a potential difference
of 1 V; the relation between electronvolts and joules is 1 eV ≈ 0.16
aj
(where 1
aj
= 10
-18
J
).
Many processes in chemistry have an energy of
several electronvolts. Thus, the energy to remove an electron from a
sodium atom is close to 5 eV. Calories (cal) and kilocalories (kcal) are still
encountered. The current definition of the calorie in terms of joules is
1 cal = 4.184 J exactly An energy of 1 cal is enough to
raise the temperature of 1 g of water by 1°C

Lecture 7
Molecular interpretation
2.2 . The internal energy of a gas
التفسير الجزيئي للطاقة الداخلية للغاز
2
:
The internal energy of a gas
2
.
2
Molecular interpretation
A molecule has a certain
number of degrees of freedom
, such as the ability to
translate
(the motion of its centre of mass through space),
rotate
around
its centre of mass,
or vibrate
(as its bond lengths and angles change).
Many physical and chemical properties depend on the energy associated
with each of these modes of motion.
For example, a chemical bond might
break if a lot of energy becomes concentrated in it.
.
The equipartition theorem
of classical mechanics is a useful guide to the
average energy associated with each degree of freedom when the sample
is at a temperature T. First, we need to know that a
to the energy means a contribution that can be
'
'quadratic contribution
expressed as the square of a variable, such as the position or the velocity.
For example, the kinetic energy an atom of mass m as it moves through
space I
االسهام التربيعي
ر كالسرعة او الموقع مثال الطاقةٌّغتملا كلذ عبرمب هنعرَّبعٌ يذلا ماهسلااا ًنعٌ و
ة لذرة ذات كتلةٌكرحلا
m
الفضاءًف كرحتت و
I
تلكًف ةٌعٌبرت تاماهسا ةئلاث كانه نوكتسف
الطاقة
.

3
االسهام التربيعي للطاقة
There are three quadratic contributions to its
energy
.
مات بحالة توازن حراري بدرجة حرارةٌسجلا نم ددعل يواستملا ماهسلاا ةٌرظن صنتو
T
كون مساوي الىٌ و هسفن نوكٌ ةقاطلل ًعٌبرت ماهسا لك ةمٌق لدعم نا ،
1kT
ثٌح
k
مةٌقلا هلو نامزتلوب تباث لثمٌ
:
k=1.381 x 10
-23
JK
-1
then states that, for a collection of
theorem
equipartition
The
particles at thermal equilibrium at a temperature T, the average
value of each quadratic contribution to the energy is the same and
equal to 1kT, where k is Boltzrnann's constant (k = 1.381 x 10¯²³ J
K¯¹).
i
The equipartition theorem : i
s a conclusion from classical mechanics
and is applicable only when the effects of quantization can be
ignored (see Chapters 16 and 17). In practice, it can be used for
.
but not vibration
molecular translation and rotation
.
According to the equipartition theorem, the average energy of each
term in the expression above is ½kT. Therefore, the mean energy of
the atoms is
3/2
kT and the

4
where U
m
(0)
is the molar internal energy at T = 0,
when all translational motion
has ceased and
the sole contribution to the internal energy arises
from the internal structure of the atoms. This
of a
that the internal energy
equation shows
perfect gas
increases linearly with temperature.
At 25°C, (3/2)RT = 3.7 kl mol
-1
,
so translational motion contributes about 4 kJ mol
-
1
to the molar internal energy of a gaseous
sample of atoms or molecules (the remaining
contribution arises from the internal structure of
the atoms and molecules).
5
When the gas consists of polyatomic
molecules, we need to take into account
the effect of rotation and vibration.
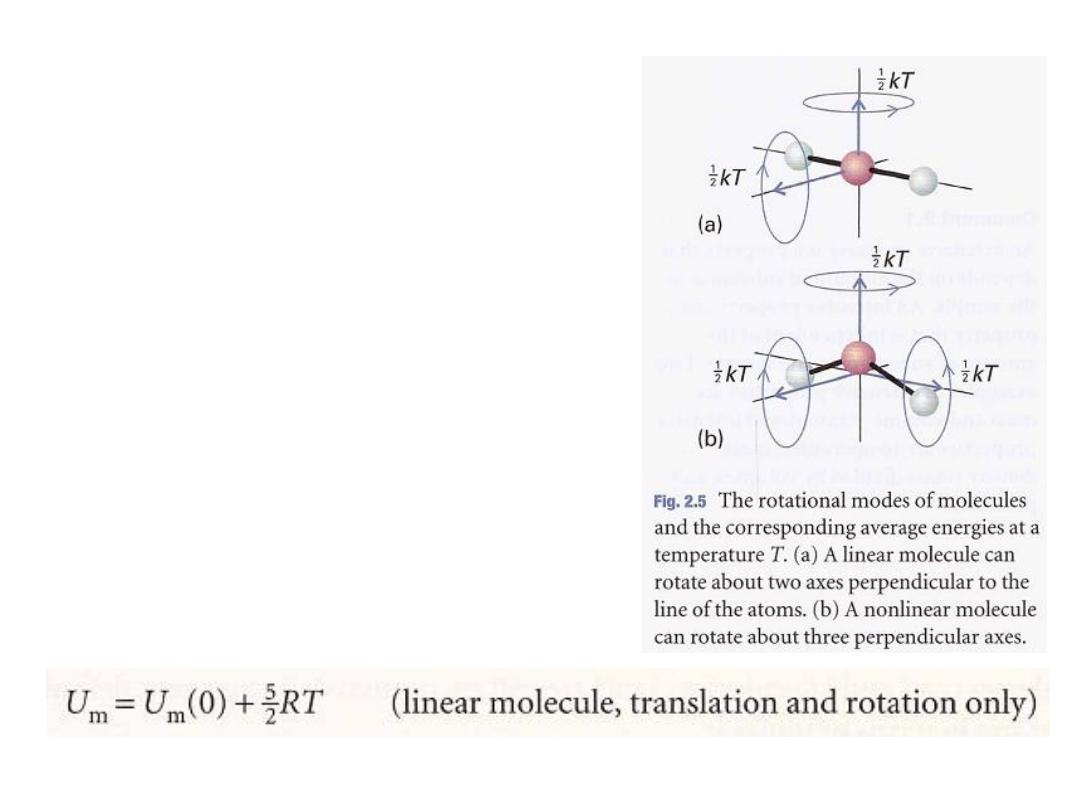
A linear molecule
, such as N
2
and CO
2
, can
rotate around two axes perpendicular to
the line of the atoms (Fig. 2.5), so it has
two rotational modes of motion, each
contributing a term tkT to the internal
energy. Therefore, the mean rotational
energy is kT and the rotational
contribution to the molar internal energy is
RT. By adding the translational and
rotational contributions, we obtain

6

7
It has been found experimentally
that
the internal energy of a system
may
be changed either by doing work on the system or by heating it
.
Whereas we may know how the energy transfer has occurred (because we
can see if a weight has been raised or lowered in the surroundings,
indicating transfer of energy by doing work, or
if ice isolated from its
surroundings, then no change in internal energy takes place.
This summary of observations is now known as the First Law of
thermodynamics and expressed as follows:
The internal energy of an isolated system is constant
.
•
We cannot use a system to do work, leave it isolated for a month, and
then come back expecting to find it restored to its original state and ready
to do the same work again. The evidence for this property is that no
'perpetual motion machine' (
a machine that does work without
consuming fuel or some other source of energy)
has ever been built.

8

9

10
•
التعبير الرياضي العام للشغل

11
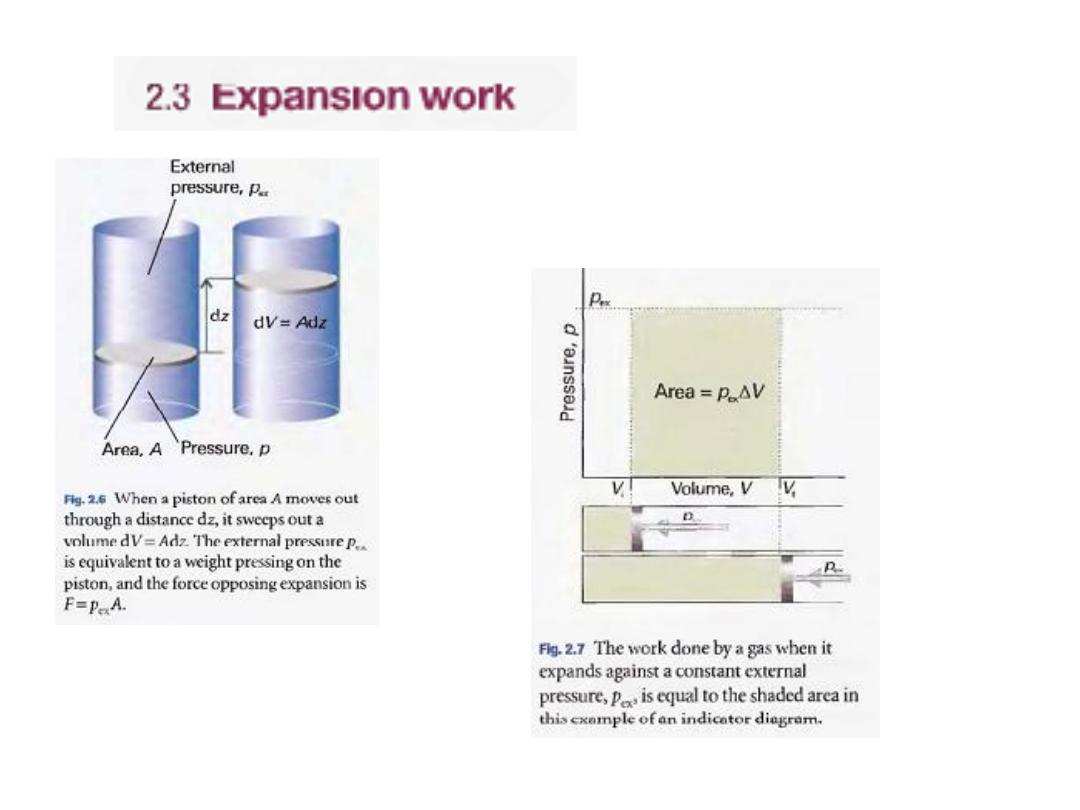
To obtain the total work done when the volume
changes from V
i
to V
f
we integrate this expression
between the initial and final volumes:
The force acting on the piston, P
ex
A, is equivalent to a
weight that is raised as the system expands.
If the system is compressed instead, then the same
weight is lowered in the sur-
(
2.6
)
00000000000

12
التوسع الحر
(b) Free expansion
By free expansion we mean expansion against zero opposing force. It occurs
when
P
ex
=O. According to eqn 2.5, dw = 0 for each stage of the expansion. Hence,
overall:

13

Lecture 8
(d) Reversible expansion

2
(
d) Reversible expansion:
A reversible change in thermodynamics is a change that can be reversed by an
infinitesimal modification of a variable.
set equal to
'is
ex
P
external pressure,
and that the
Suppose a gas is confined by a piston
Such a system is in mechanical equilibrium
the pressure, p, of the confined gas.
with its surroundings (as illustrated in Section 1.1)
because
an infinitesimal change
in the external pressure in either direction causes changes in volume in opposite
directions.
If the external pressure is reduced infinitesimally, then the gas expands
slightly. If the external pressure is increased infinitesimally, then the gas contracts
slightly. In either case
the change is reversible in the thermodynamic sense
. If, on
the other hand, the external pressure differs measurably from the internal
pressure, then changing p., infinitesimally will not decrease it below the pressure of
the gas, so will not change the direction of the process. Such a system is not in
mechanical equilibrium with its surroundings and the expansion is
thermodynamically irreversible.
To achieve reversible expansion
we set
P
ex equal
to P at each stage of the expansion.

3
To achieve reversible expansion
we set
P
ex
equal to P
at each stage of the
expansion. In practice, this equalization could be achieved by gradually
removing weights from the piston so that the downward force due to the
weights always matched the changing upward force due to the pressure of the
gas. When we set Pex = p, eqn 2.5 becomes
dW=-P
ex
dV=-pdV
……………………………………………(2.9
)·rev
(Equations valid only for reversible processes are labelled with a subscript rev.)
Although the pressure inside the system appears in this expression for the
work, it does so only because P
ex
has been set equal to P to ensure reversibility.
The total work of reversible expansion is therefore
We can evaluate the integral once we know how the pressure of the confined gas
depends on its volume. Equation 2.10 is the link with the material covered in
Chapter 1 for, if we know the equation of state of the gas, then we can express
p in terms of V and evaluate the integral.
4
•
توضيح رياضي
:

5
التوسع المعزول حراريا
(e) Isothermal reversible expansion
Consider the isothermal, reversible expansion of a perfect gas.
The expansion is made isothermal by keeping the system in
thermal contact with its surroundings (which may be a
constant-temperature bath).
Because the equation of state is
pV = nRT, we know that at each stage p = nRT/V, with V the
volume at that stage of the expansion.
The temperature T is
constant in an isothermal expansion, so (together with n and
R)
it may be taken outside the integral.
It follows that the work of
reversible isothermal expansion of a perfect gas from Vi to
V
f
at a temperature T is

6
We can express the result of the calculation
as an indicator diagram,
for the magnitude of the work done is equal to the area under the
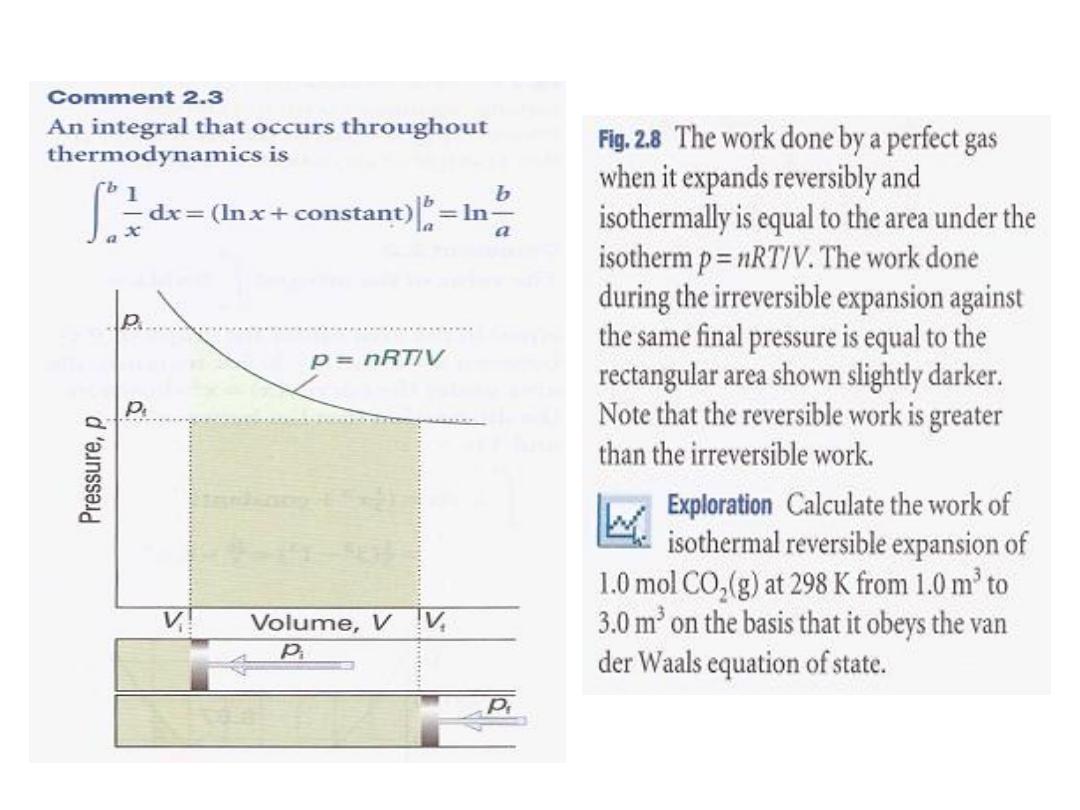
isotherm P = nRTlV (Fig. 2.8). Superimposed on the diagram is the
rectangular area obtained for irreversible expansion against
constant external pressure fixed at the same final value as that
reached in the reversible expansion. More work is obtained when
the expansion is reversible (the area is greater) because matching
the external pressure to the internal pressure at each stage of the
process ensures that none of the system's pushing power is wasted.
We cannot obtain more work than for the reversible process
because increasing the external pressure even infinitesimally at any
stage results in compression. We may infer from this discussion that,
because some pushing power is wasted when p > P
ex
' the maximum
work available from a system operating between specified initial
and final states and passing along a specified path is obtained when
the change takes place reversibly.
We have introduced the connection between reversibility and
maximum work for the special case of a perfect gas undergoing
expansion.
Later (in Section 3.5) we shall see that it applies to all
substances and to all kinds of work.
7

8
Example 2.1 Calculating the work of gas production
Calculate the work done when 50 g of iron reacts with hydrochloric acid in
(a) a closed vessel of fixed volume, (b) an open beaker at 25°C.
Method
We need to judge the magnitude of the volume change and then to decide how
the process occurs. If there is no change in volume, there is no expansion work
however the process takes place. If the system expands against a constant
external pressure, the work can be calculated from
eqn 2.8
. A general feature
of processes in which a condensed phase changes into a gas is that the volume
of the former may usually be neglected relative to that of the gas it forms.
Answer
In (a) the volume cannot change, so no expansion work is done and
w = O.
In (b) the gas drives back the atmosphere and therefore
W= - P
ex
ΔV.
We can
neglect the initial volume because the final volume (after the production of gas) is
so much larger and Δ V = V
f
- V
i
≈ V
f
= nRT/P
ex
, where n is the amount of H, pro-
duced.
Therefore,

9
Because the reaction is :
Fe(s) + 2 HCl(aq) FeCl
2
(aq) +H2(g),
we know that 1mol H
2
is generated when 1 mol F
e
is consumed, and n can be
taken as the amount of Fe atoms that react. Because the molar mass of Fe
:
is 55.85 g mol ¯¹, it follows that
The system (the reaction mixture) does 2.2 kJ of work driving back the
atmosphere.
Note that
(for this perfect gas system) the magnitude of the external pressure
does not affect the final result: the lower the pressure, the larger the
volume occupied by the gas, so the effects cancel.

10
•

11

Lecture 9
Heat Transactions
تحوالت الحرارة

2
transactions
Heat
4
.
2
In general, the change in internal energy of a system is:
dU = dq + dw
exp
+ dw
e
……………………………………….(2.12)
where
dw
e
is work in addition
(e for 'extra')
to the expansion work,
dw
exp
'
For
instance
, dw
, might be the electrical work of driving a current through a
circuit. A system kept at constant volume can do no expansion work, so
dw
exp
= 0. If the system is also incapable of doing any other kind of work (if
it is not, for instance, electrochemical cell connected to an electric
motor), then dW
e
=0 too. Under these circumstances:
dU = dq
(at constant volume, no additional work
)
--------- (2.13a)
We express this relation by writing
dU = dq
v
where the subscript implies a change at constant volume. For a
measurable change:
ΔU= qᵥ
…………………………………………………………..(2.13b)
It follows that, by measuring the energy supplied to a constant-volume system as
) when it undergoes a change of
0
as heat (q <
) or obtained from it
0
q>
(
heat
we are in fact measuring the change in its internal energy.
state,

3
(a)
Calorimetry
Calorimetry
is the study of heat transfer during physical and chemical
processes.
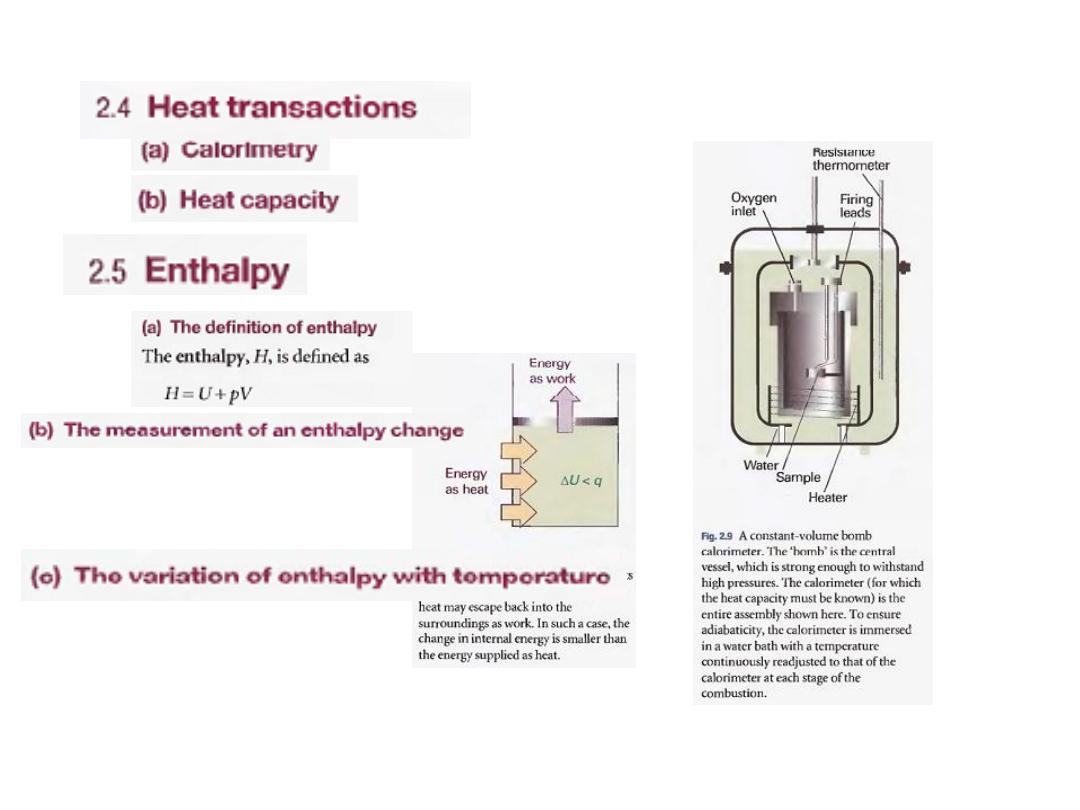
A calorimeter
is a device for measuring energy transferred as heat.
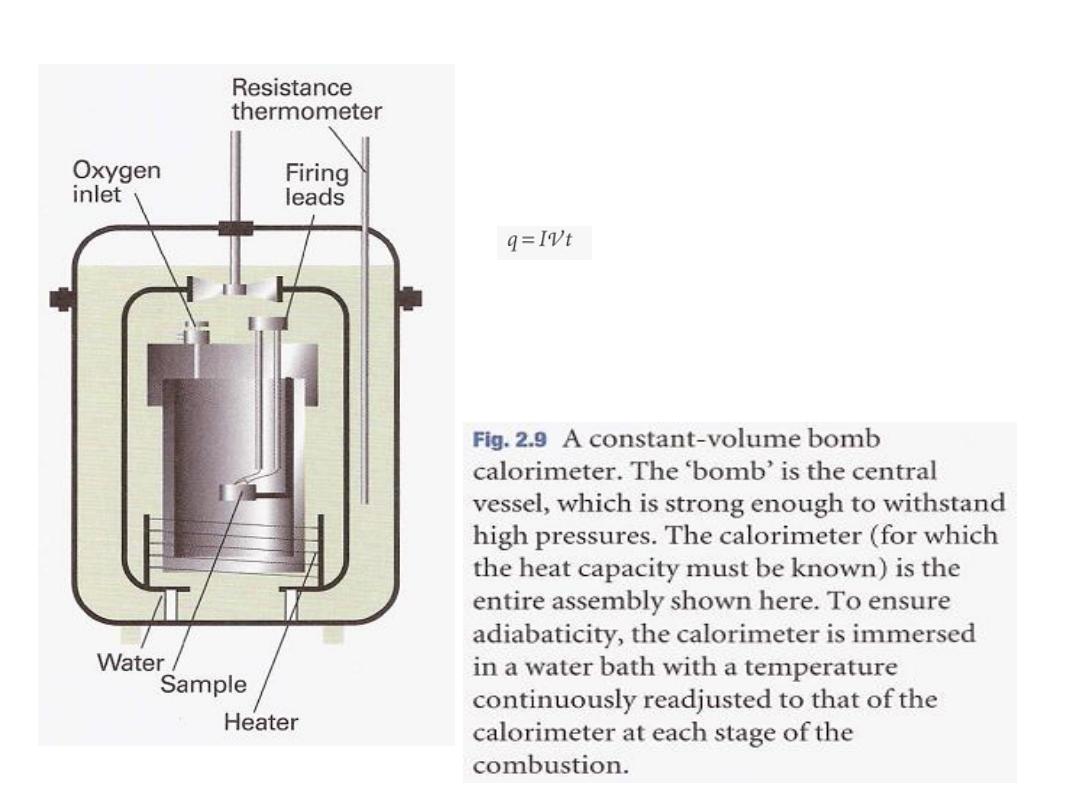
The most common device for measuring ΔU is an adiabatic bomb
calorimeter (Fig. 2.9).
The process we wish to study-which may be a chemical reaction-is
initiated inside a constant volume container, the 'bomb'. The bomb
is immersed in a stirred water bath, and the whole device is the
calorimeter. The calorimeter is also immersed in an outer water
bath. The water in the calorimeter and of the outer bath are both
monitored and adjusted to the same temperature. This
arrangement ensures that there is no net loss of heat from the
calorimeter to the surroundings (the bath) and hence that the
calorimeter is adiabatic.
4
q = CΔT …………………… (2.14a)
The calorimeter constant C
may be measured electrically
by passing a constant current, I, from a source of
known potential difference, Ѵ, through a heater for a
known period of time, t, for then
q =IѴt ……………………………. (2.14b)
Alternatively,
C may be determined by burning a known
mass of substance
(benzoic acid is often used) that
has a known heat output. With C known, it is simple to
interpret an observed temperature rise as a release of
heat.

5
2
.
2
Illustration
معايرة المسعر
The calibration of a calorimeter
6
b) Heat capacity
(
The internal energy of a substance increases when its temperature is raised.
The increase depends
on the conditions under which the heating takes
place and for the present we suppose that the sample is confined to a
For example, the sample may be a gas in a container of
.
constant volume
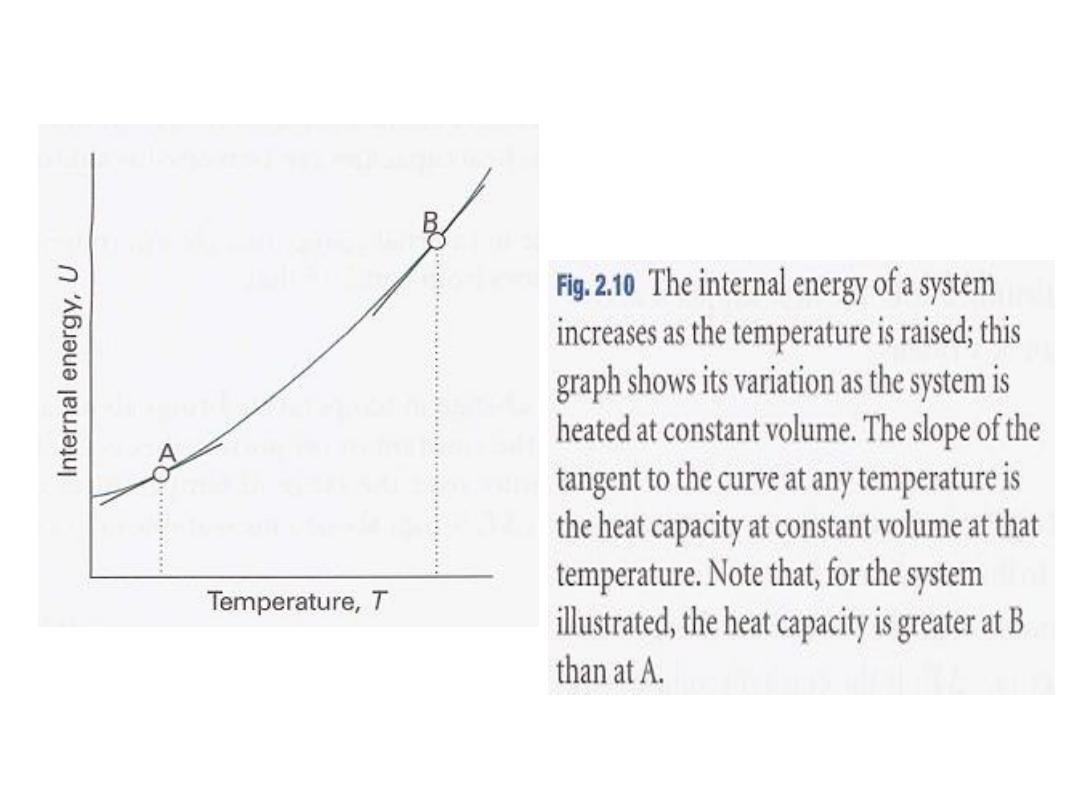
fixed volume. If the internal energy is plotted against temperature, then a
to the
The slope of the tangent
may be obtained.
10
.
2
curve like that in Fig.
called the heat capacity of the system at that
curve at any temperature is
is
and
v
C
The heat capacity at constant volume is denoted
temperature.
defined formally as
In this case, the internal energy varies with the temperature and the
volume of the sample, but we are interested only in its variation with
the temperature, the volume being held constant (Fig. 2.1l).
7
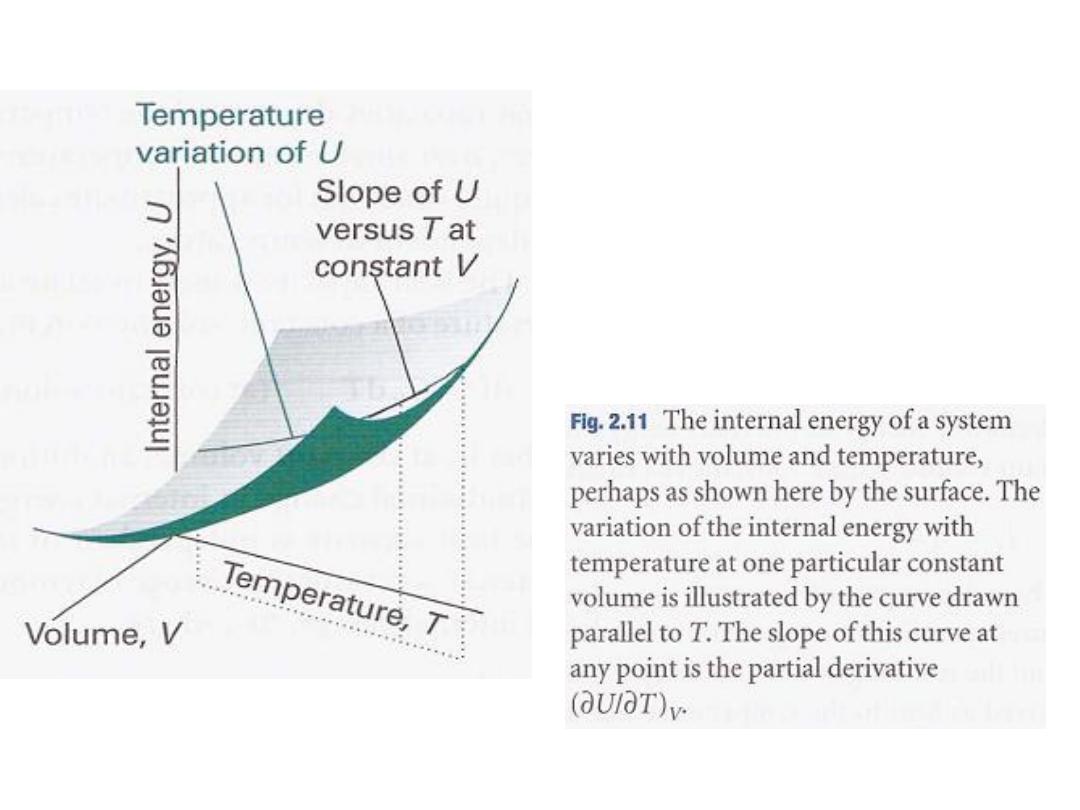
8
•
عع
•
ر الحجم و درجةٌغتب ماظنلل ةٌلخادلا ةقاطلا رٌغتت
ًانٌبلا حطسلا ًف حضوم امك و ةرارحلا
.
و قد
ة و لحجم ثابتٌلخادلا ةقاطلا ًف رٌغتلا انحضو
المرسوم بشكل موازيًنحنملا طخلاب هل رٌشٌأ دق
لمحور الحرارة
T
.
ل لهذا المنحنى عند أيٌملا و
ة للطاقةٌئزجلا ةقتشملا لثمٌس هٌلع ةطقن
ةٌلخادلا
:
(∂U/ ∂T)
v

9
•

10
•

12
Heat capacities are extensive properties
السعات الحرارية تعتبر خصائص شاملة
: 100 g of water, for instance, has 100 times the heat capacity of 1 g of water (and
therefore requires 100 times the energy as heat to bring about the same rise
in temperature).
The molar heat capacity at constant volume,
C
V
,
m
=
C
v
/
n
, is the heat capacity per
خاصية مركزة
mole of material, and is an intensive property
(
all molar quantities are intensive
). Typical values of
C
V,
m
for polyatomic gases
are close to 25 J k
-1
mol
-1
. For certain applications it is useful to know the
specific heat capacity (more informally, the 'specific heat') of a substance,
which is the heat capacity of the sample divided by the mass, usually in
grams:
C
v,s
= C
v
/ m.
The specific heat capacity of water at room temperature is close to 4 J K
-1
g
-1
.
In general, heat capacities depend on the temperature and decrease at low
temperatures. However, over small ranges of temperature at and above room
temperature, the variation is quite small and
for approximate calculations
heat capacities can be treated as almost independent of temperature.

13
**
The heat capacity is used
to relate a change in internal energy to a change
that:
15
.
2
eqn
It follows from
volume system.
-
in temperature of a constant
That is, at constant volume, an infinitesimal change in temperature brings about
an infinitesimal change in internal energy,
and the constant of proportionality
is Cv.
If the heat capacity is independent of temperature over the range of
temperatures of interest, a measurable change of temperature, ΔT, brings
about a measurable increase in internal energy,
ΔU, where

13
•
خ

Lecture 10
Enthalpy
2
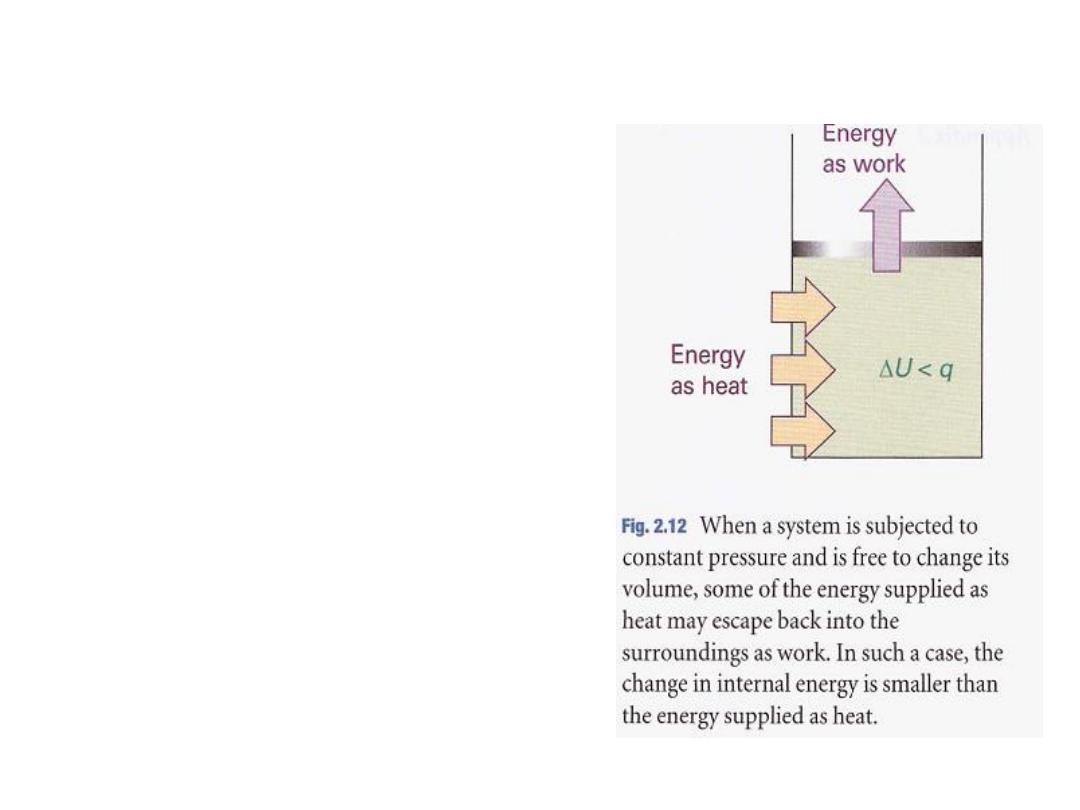
2.5 Enthalpy
The change in internal energy is not
equal to the energy transferred as
heat when the system is free to
change its volume. Under these
circumstances some of the energy
supplied as heat to the system is
returned to the surroundings as
expansion work (Fig. 2.12),
so:
dU is less than dq.
However, we shall now show that in this
case the energy supplied as heat at
constant pressure is equal to the
change in another thermodynamic
property of the system, the enthalpy.

3
(a) The definition of enthalpy
The enthalpy,
H
, is defined as:
H =U + pV …………………………………. [2.18]
where
p
is the pressure of the system and
V
is its
volume.
Because U, p, and V are all state
functions
,
the enthalpy is a state function
too
.
As is true of any state function, the change in
enthalpy, ΔH, between any pair of initial and
final states is independent of the path
between them.

4
Although the definition of enthalpy may appear arbitrary, it has
important implications for thermochemisty.
For instance, we show in the following Justification that eqn
2.18 implies that
the change in enthalpy is:
equal to the energy supplied as heat at constant pressure
(provided the system does no additional work):
dH = dq (
at constant pressure, no additional work
) --------------------- (2.19a)
For a measurable change
,

5

6
•
ضاحٌلاا تمتت
7
The result expressed in eqn 2.19 states
that,
when a system is subjected to a constant
pressure, and only expansion work can occur,
the change in enthalpy is
equal to the energy
supplied as heat.
kJ of energy
36
if we supply
For example,
through an electric heater immersed in an
open beaker of water, then the enthalpy of
the water increases by 36 kJ and we write
ΔH = +36 kJ.

8
(b) The measurement of an enthalpy change
An enthalpy change can be measured calorimetrically by monitoring the
temperature change that accompanies a physical or chemical change
occurring at constant pressure. A calorimeter for studying processes at
constant pressure is called an isobaric calorimeter. A simple example is a
thermally insulated vessel open to the atmosphere:
the heat released in the reaction is monitored by measuring the change in
temperature of the contents.
For a combustion reaction an adiabatic flame calorimeter may be used to
measure ΔT when a given amount of substance burns in a supply of oxygen
(Fig. 2.13).
Another route to ΔH is to measure the internal energy change by using a bomb
calorimeter, and then to convert ΔU to ΔH.
is so small
m
pV
for them
small molar volumes,
Because solids and liquids have
almost identical
are
internal energy
the molar enthalpy and molar
that
للمواد الصلبة و السوائل
(H
m
= U
m
+ pV
m
≈ U
m
)

9
if a process involves only solids
Consequently,
U are
Δ
H and
Δ
the values of
or liquids,
almost identical.
accompanied by
such processes are
Physically,
system
the
a very small change in volume,
does negligible work on the surroundings
when the process occurs,
so the energy
supplied
as heat stays entirely within the
system.
The most sophisticated way to measure
enthalpy changes,
however,
is to use a
differential scanning calorimeter (DSC).
Changes in enthalpy and internal energy
may also be measured by noncalorimetric
methods (see Chapter 7)0op

10
•
ةٌلخادلا ةقاطلا و ةٌبلاثنلاا نٌب ةقلاعلا لاثم
•
قة الحلٌرط

11
•
الحل

12
•
ة حسب العالقةٌلخادلا ةقاطلاب ًلاثملا زاغلل ةٌبلاثنلاا طبترت
ةٌلاتلا
:
•
ة للتفاعل الذيٌبلاثنلاا ًف رٌغتلا باسح ىلع قبطت هلاعا ةٌضاٌرلا ةقلاعلأ
ستهلك غازٌ وا زاغ ررحٌ
.

13
•
حٌضوت

14
•
مثال

15
•
الحل
