1
Reaction Rates:
Reaction Rate: The change in the concentration of a reactant or a
product with time (M/s).
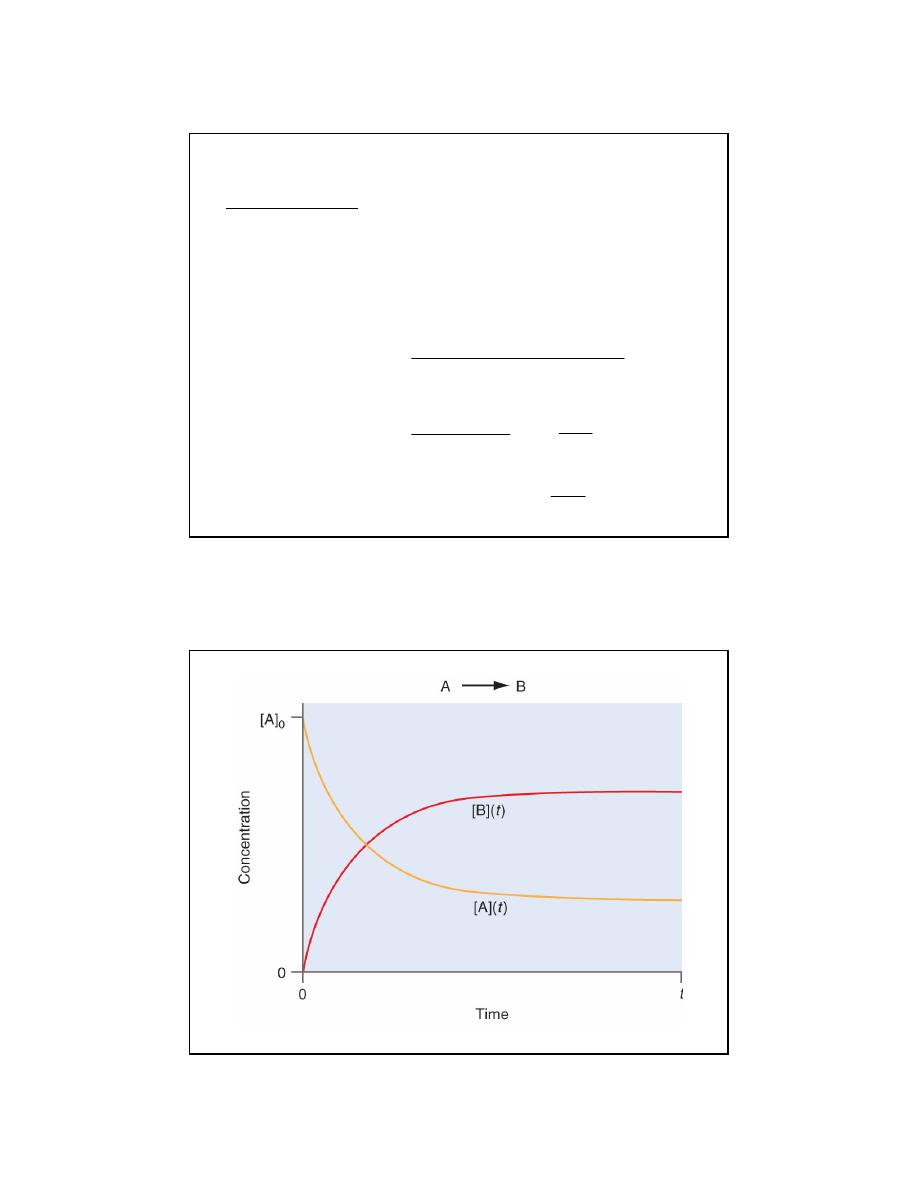
Reactant
→ Products
A
→ B
(
)
change in number of moles of B
Average rate
change in time
moles of B
t
=
∆
=
∆
∆[A]
Rate
∆t
= −
∆[B]
∆t
=
Since reactants go away with time:
Chemical Kinetics
2
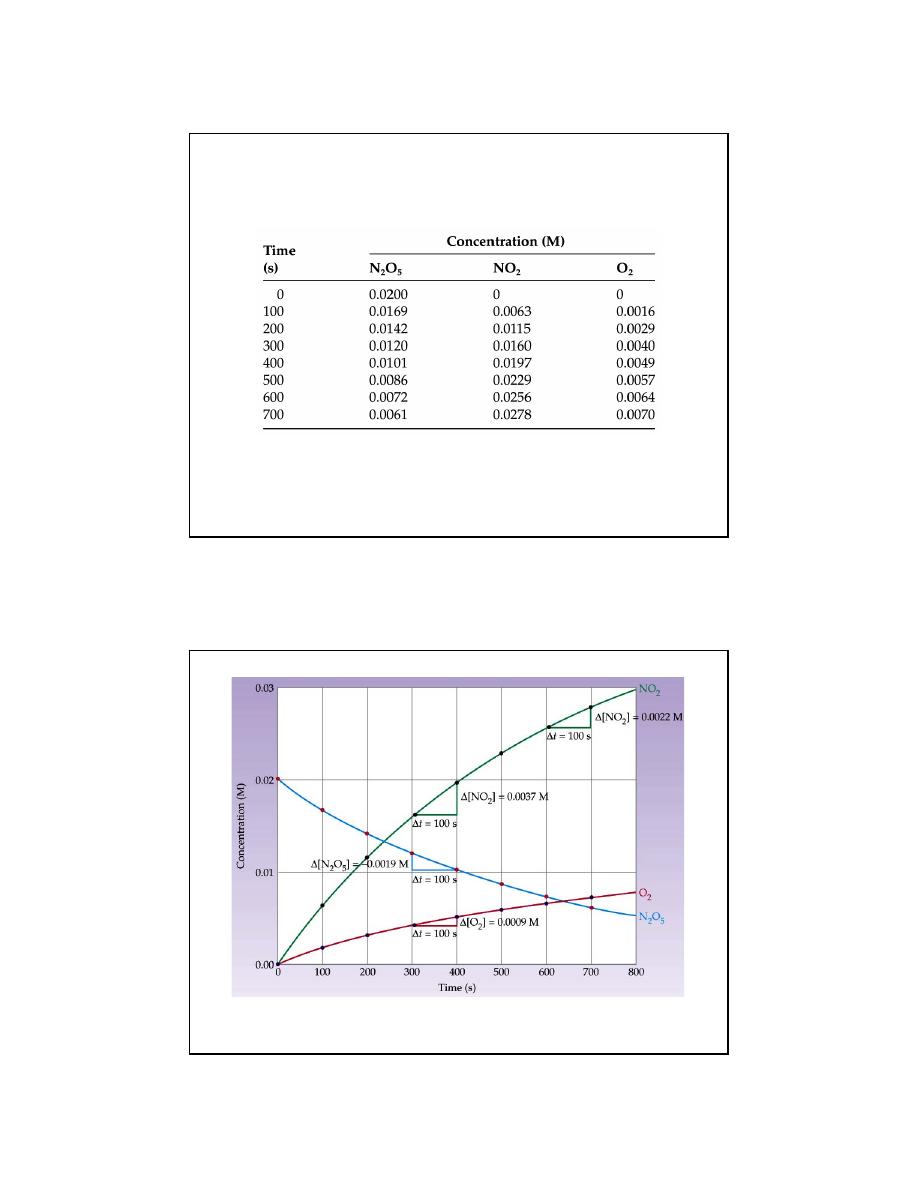
Consider the decomposition of N
2
O
5
to give NO
2
and O
2
:
2N
2
O
5
(g)
→ 4NO
2
(g) + O
2
(g)
reactants
decrease with
time
products
increase with
time

3
2N
2
O
5
(g)
→ 4NO
2
(g) + O
2
(g)
From the graph looking at t = 300 to 400 s
6
1
2
0.0009M
Rate O =
9 10 Ms
100s
−
−
= ×
5
1
2
0.0037M
Rate NO =
3.7 10 Ms
100s
−
−
=
×
5
1
2
5
0.0019M
Rate N O =
1.9 10 Ms
100s
−
−
=
×
Why do they differ?
Recall
:
To compare the rates one must account for the stoichiometry.
6
1
6
1
2
Rate O =
9 10 Ms
9 10 Ms
1
1
−
−
−
−
× ×
= ×
5
1
6
1
2
Rate NO =
3.7 10 Ms
9.2 10 M
1
4
s
−
−
−
−
×
×
=
×
5
1
6
1
2
5
Rate N O =
1.9 10 Ms
9.5 10
1
2
Ms
−
−
−
−
×
×
=
×
Now they
Now they
agree!
agree!
Reaction Rate and Stoichiometry
a
A +
b
B
→
c
C +
d
D
[ ]
[ ]
[ ]
[ ]
A
B
1
1
a
b
C
D
Rate
t
t
1
1
c
d
t
t
∆
∆
∆
∆
=
=
=
=
∆
∆
∆
−
∆
−
In general for the reaction:

4
The reaction rate law expression relates the rate of a reaction to
the concentrations of the reactants.
Each concentration is expressed with an order (exponent).
The rate constant converts the concentration expression into the
correct units of rate (Ms
−1
). (It also has deeper significance,
which will be discussed later)
For the general reaction:
For the general reaction:
Rate Law & Reaction Order
a
A +
b
B
→ c
C +
d
D
x
and
y
are the reactant orders
determined from experiment.
x
and
y
are NOT the
stoichiometric coefficients.
x
y
Rate = k [A] [B]

5
The Overall Order of a reaction is the sum of the individual
orders:
Rate (Ms
−1
) = k[A][B]
1/2
[C]
2
Overall order:
1 + ½ + 2 = 3.5 =
7/2
or
seven
−
halves order
note:
when the order of a reaction is 1 (first order) no
exponent is written.
Units for the rate constant:
The units of a rate constant will change depending upon the overall
order.
The units of rate are always M/s or Ms
–1
To find the units of a rate constant for a particular rate law, simply divide
the units of rate by the units of molarity in the concentration term of the
rate law.
Rate (Ms
–1
) = k[A] 1
st
order
1
1
Ms
k(units)
s
M
−
−
=
=
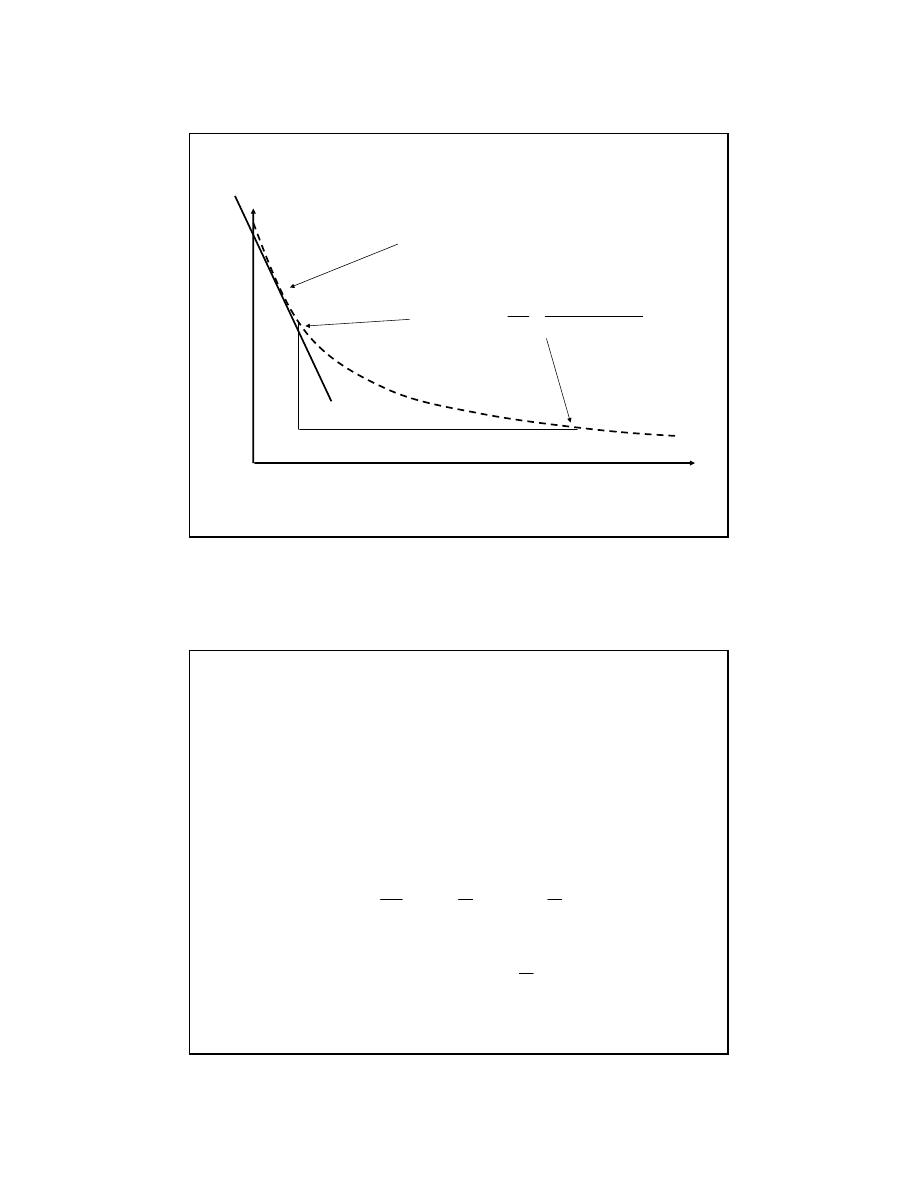
6
time (s)
Instantaneous rate (tangent line)
Y
[concentration]
Average Rate
X
time
∆
∆
=
∆
∆
Reaction Rates
concentration (M)
Rules of logarithms
log (1) = 0
log (10) = 1
log (100) = 2
Log (10
x
) = x
ln (1) = 0
ln (e) = 1
ln (e
x
) = x
log A
x
= xlog A
ln A
x
= xln A
x
x
x
A
A
A
log
log
x log
B
B
B
=
=
log(AB) = log A + log B
A
log
log A log B
B
=
−
7
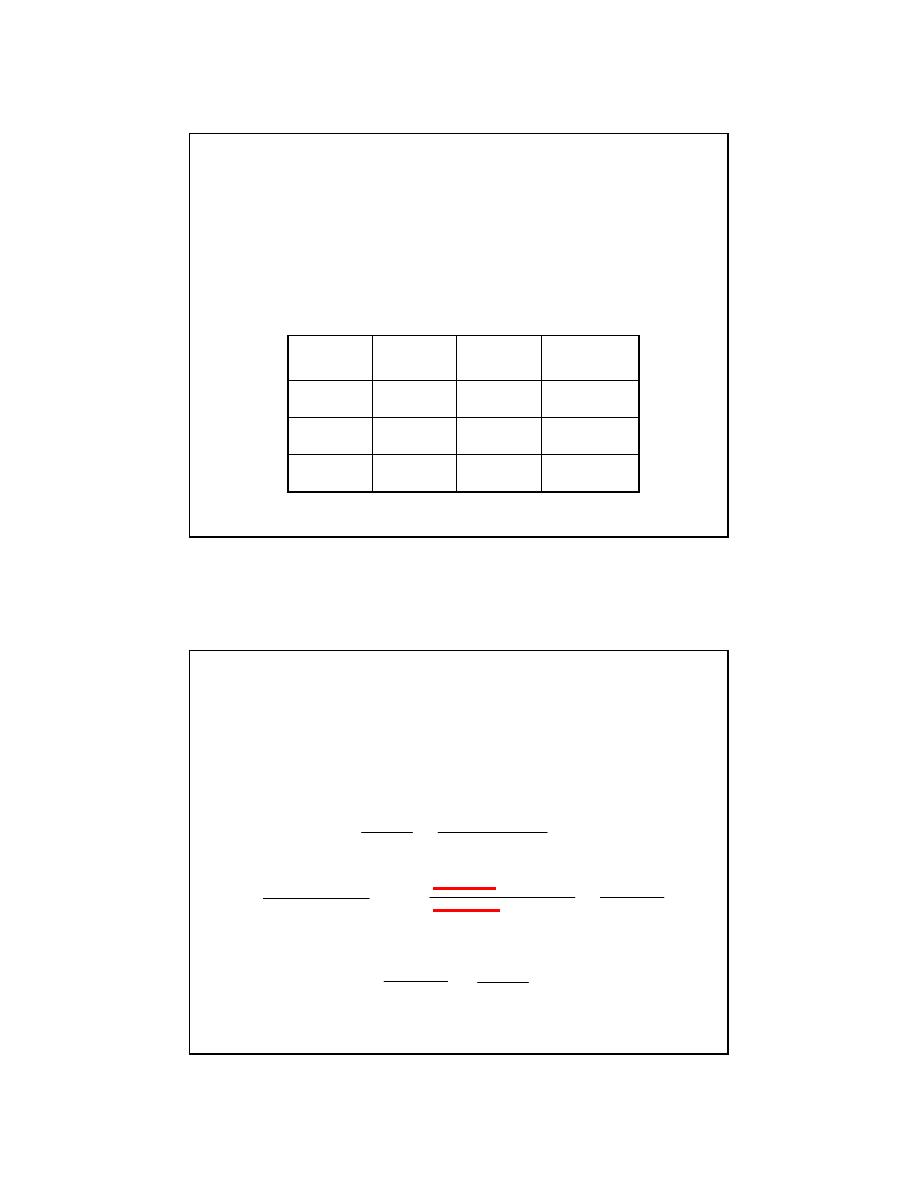
The reaction of nitric oxide with hydrogen at 1280°C is:
Determining Reaction Order: The Method of Initial Rates
2NO(g) + 2H
2
(g)
→ N
2
(g) + 2H
2
O(g)
From the following data, determine the rate law and rate constant.
0.0120
0.0200
0.0100
3
0.144
0.0300
0.0200
2
0.00600
0.0100
0.0100
1
Initial Rate
(M/min)
[H
2
]
o
(M)
[NO]
o
(M)
Run
Rate(M/min) = k [NO]
x
[H
2
]
y
The rate law for the reaction is given by:
2NO(g) + 2H
2
(g)
→ N
2
(g) + 2H
2
O(g)
Taking the ratio of the rates of runs 3 and 1 one finds:
Rate(3)
Rate(1)
=
x
y
(3)
2 (3)
x
y
(1)
2 (1)
k [NO] [H ]
k [NO] [H ]
0.0120M / min
0.00600M / min
=
x
y
x
y
k [0.0100] [0.0200]
k [0.0100] [0.0100]
y
y
[0.0200]
[0.0100]
=
2 =
y
y
[0.0200]
[0.0100]
=
y
0.0200
0.0100

8
y
0.0200
0.0100
=
2
log
y
0.0200
log
log 2
0.0100
=
( )
ylog 2
log 2
=
y = 1
Rate(1)
Rate(2)
=
x
y
(1)
2 (1)
x
y
(2)
2 (2)
k [NO] [H ]
k [NO] [H ]
0.00600
0.144
=
x
x
k [0.0100] [0.0100]
k [0.0200] [0.0300]
Now that “y” is known, we
may solve for x in a similar
manner:
1
24
=
x
1
1
2
3
×
x
1
1
2
8
=
1
1
x log
log
2
8
=
x = 3
The Rate Law is:
Rate(M/min) = k [NO]
3
[H
2
]
To find the rate constant, choose one set of data and solve:
(
) (
)
3
M
0.0120
k 0.0100M
0.0200M
min
=
(
) (
)
3
M
0.0120
min
k
0.0100M
0.0200M
=
(
) (
)
3
4
M
0.0120
min
0.0100
0.0200 M
=
3
5
M
k 6.00 10
min
−
=
×

9
Integrated Rate Laws: time dependence of concentration
For a first order process, the
rate law can be written:
A
→ products
1
[A]
Rate(Ms )
k[A]
t
−
∆
= −
=
∆
This is the “
average rate
”
If one considers the infinitesimal changes in concentration and time the rate
law equation becomes:
1
d[A]
Rate(Ms )
k[A]
dt
−
= −
=
o
[A]
t
[A]
0
d[A]
k dt
[A]
= −
∫
∫
where [A] = [A]
o
at time t = 0
and [A] = [A] at time t = t
This is the “
instantaneous rate
”
Integrating in terms of d[A] and dt:
o
[A]
t
[A]
0
d[A]
k dt
[A]
= −
∫
∫
o
[A]
ln
kt
[A]
= −
kt
o
[A]
e
[A]
−
=
Taking the exponent to each side of the equation:
or
kt
o
[A] [A] e
−
=
Conclusion:
Conclusion:
The concentration of a reactant governed by first
order kinetics falls off from an initial concentration
exponentially with time.
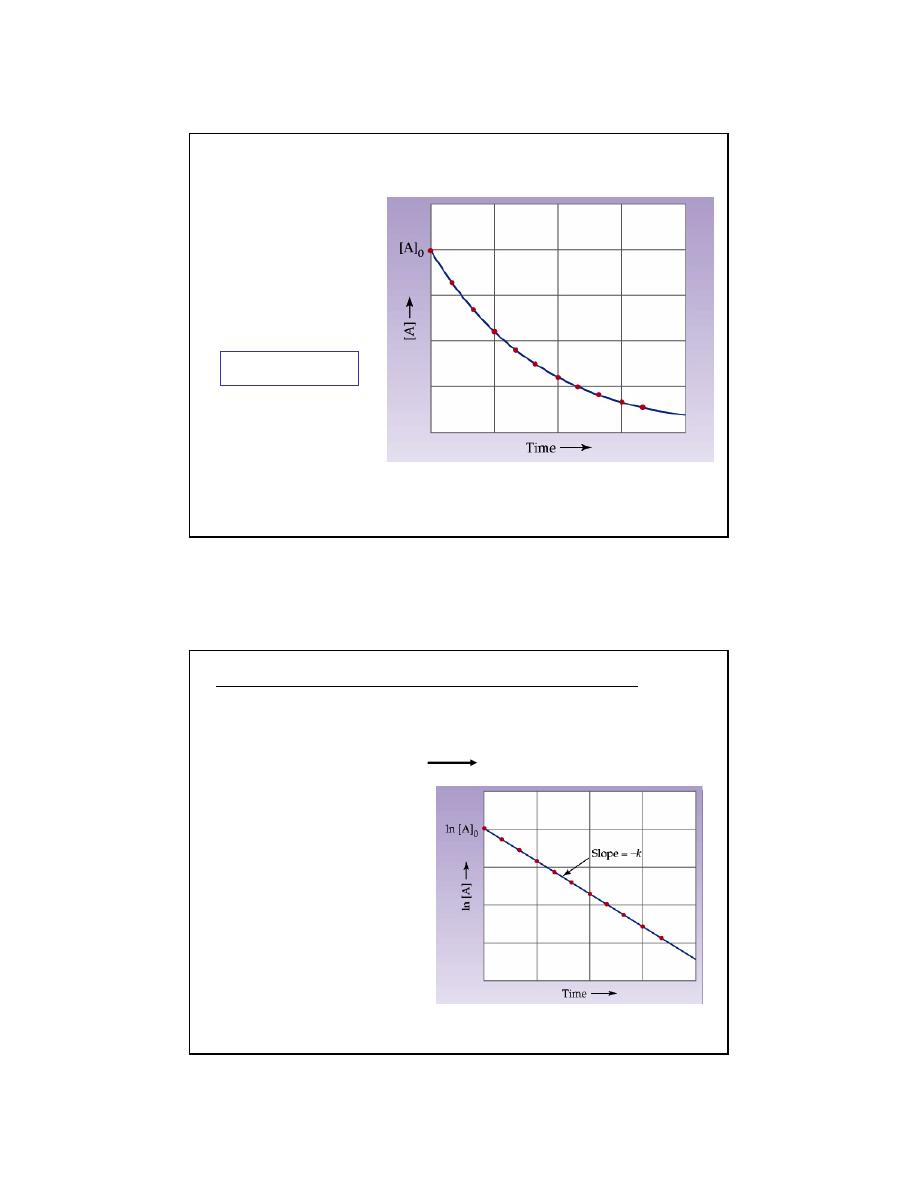
10
Recognizing a first order process:
AÆproducts
Whenever the conc. of a
reactant falls off
exponentially, the kinetics
follow first order.
kt
o
[A] [A] e
−
=
A plot of ln[A] versus time (t)
is a straight line with slope -k
and intercept ln[A]
o
(
)
kt
o
ln [A] [A] e
−
=
Determining the Rate constant for a first order process
Taking the log of the integrated rate law for a first order process we find:
o
ln[A] ln[A]
k t
=
− ×
11
Example:
The rate of decomposition of azomethane (C
2
H
6
N
2
) was
studied by monitoring the partial pressure of the reactant as a function of
time.
Determine if the data below support a first order reaction.
Calculate the rate constant for the reaction.
Time
(s)
P
(mmHg
ln (P)
0
284 5.65
100
220 5.39
150
193 5.26
200
170 5.14
250
150 5.01
Plot of lnP vs. time
y = -0.0026x + 5.6485
R
2
= 1
4.90
5.00
5.10
5.20
5.30
5.40
5.50
5.60
5.70
0
50
100
150
200
250
300
time (s)
ln
P
k = 2.6x10
-3
s
-1
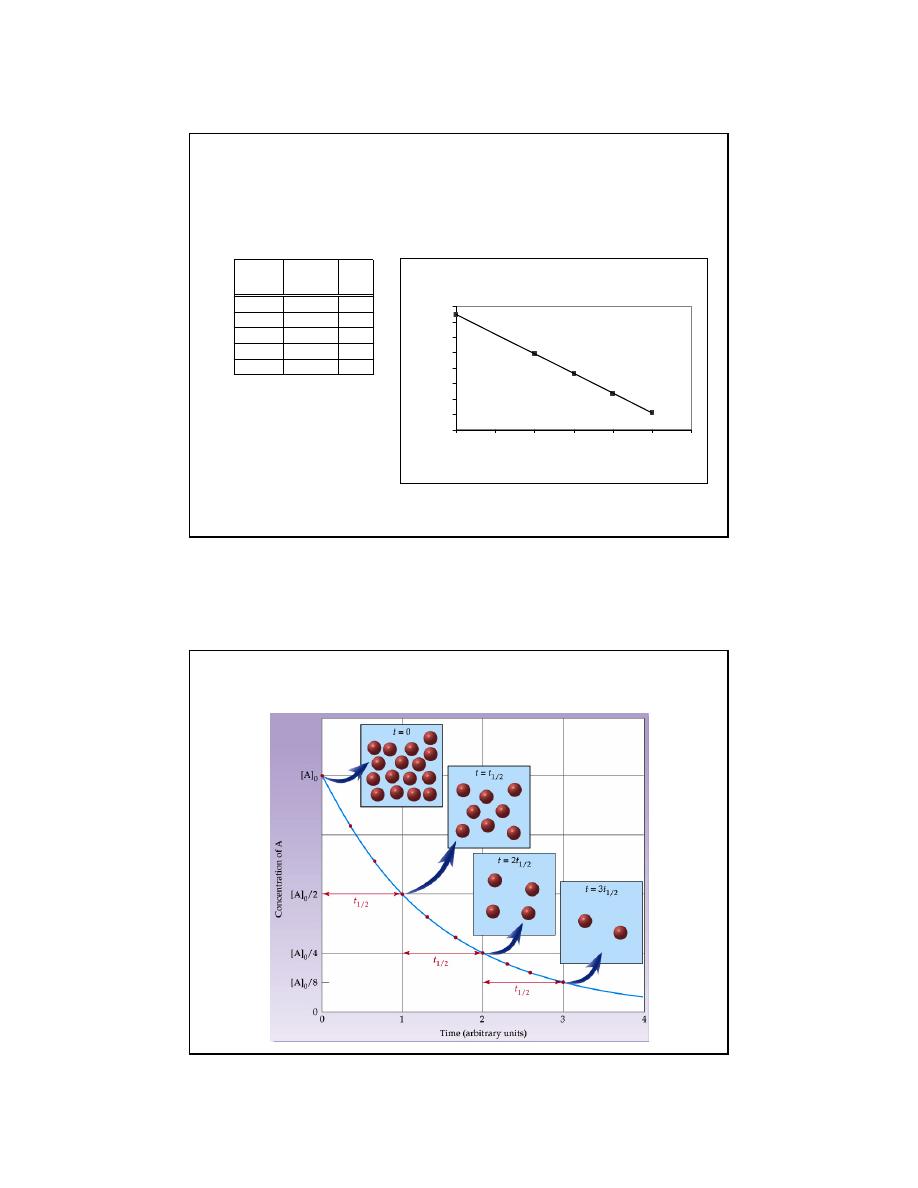
Reaction Half-Life
12
Reaction Half-life:
Half-life is the time taken for the concentration of a reactant to drop to
half its original value.
o
[A]
[A]
2
=
For a first order process the half life (
t
½
) is found mathematically from:
[ ]
[ ]
0
(1) ln A
kt ln A
= − +
[ ]
[ ]
0
(2) ln A
ln A
kt
−
= −
[ ]
0
A
(3) ln
kt
[A]
= −
[ ]
0
A
(4) ln
kt
[A]
=
[ ]
0
1
0
2
A
(5) ln
kt
[A]
2
=
1
2
ln 2
0.693
t
k
k
=
=
A certain reaction proceeds through t first order kinetics.
The half-life of the reaction is 180 s.
What percent of the initial concentration remains after 900s?
Step 1: Determine the magnitude of the rate constant, k.
1
2
ln 2
0.693
t
k
k
=
=
1
1
2
ln 2
ln 2
k
0.00385s
t
180s
−
=
=
=
kt
o
[A]
e
[A]
−
=
1
0.00385 s 900 s
o
[A]
e
[A]
−
−
×
=
= 0.0312
Using the integrated rate law, substituting in the value of k and 900s we find:
Since the ratio of [A] to [A]
0
represents the fraction of [A]
o
that remains, the
% is given by:
100
× 0.0312 = 3.12%
13
For a Second Order
Process
:
A
→ Products
Rate = k[A]
2
1
2
d[A]
Rate(Ms )
k[A]
dt
−
= −
=
Integrating as before we find:
[ ]
[ ]
0
1
1
kt
A
A
=
+
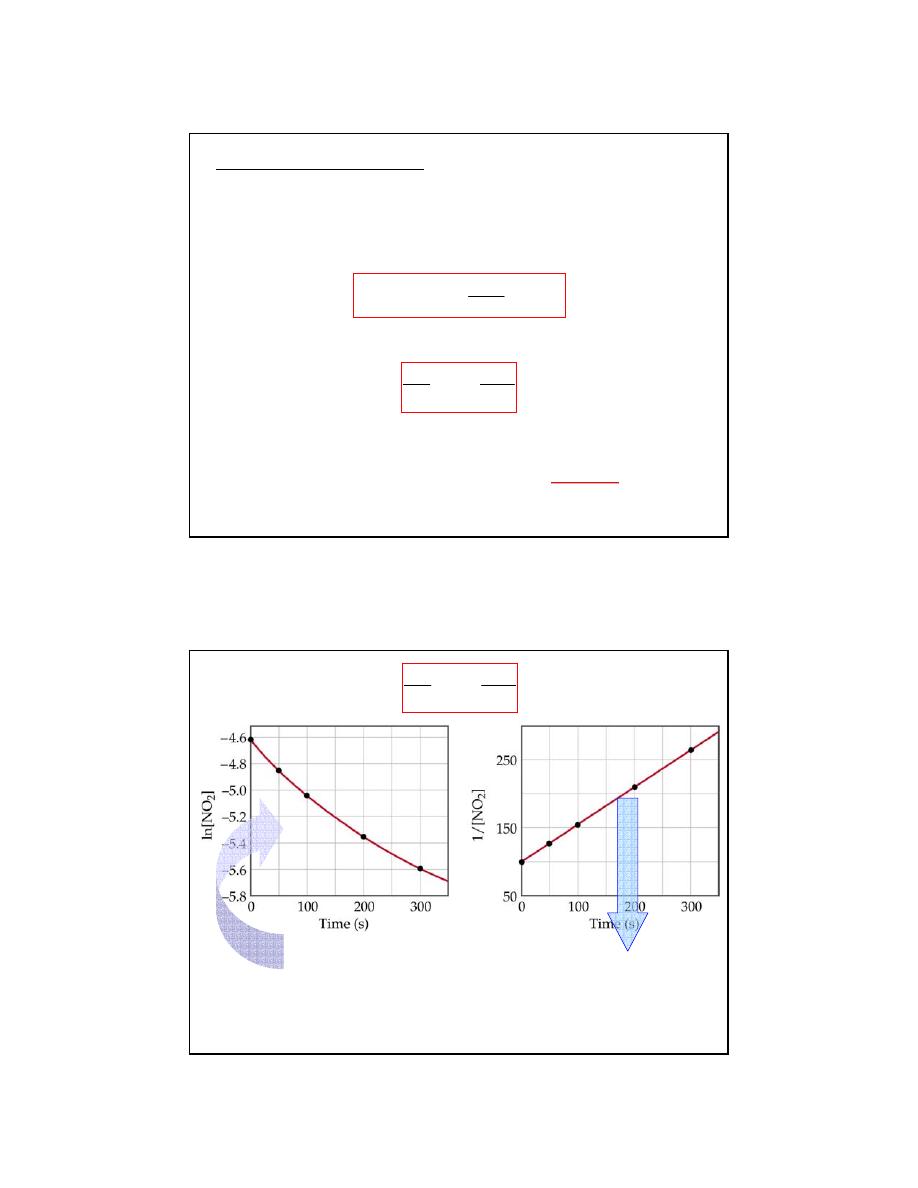
A plot of 1/[A] versus t is a straight line with slope k and intercept 1/[A]
0
For a second order reaction, a plot of ln[A] vs. t is
not linear
not linear
.
[ ]
[ ]
0
1
1
kt
A
A
=
+
Non
−
linearity indicates
that the reaction
is not first order.
Slope = k (rate constant)

14
Half-life for a second-order reaction
Unlike a first order reaction, the rate constant for a second order process
depends on and the initial concentration of a reactant.
[ ]
[ ]
t
0
1
1
kt
A
A
=
+
[ ]
[ ]
t
0
1
A
A
2
= ×
at the half–life,
Substituting and solving,
[ ]
1/ 2
0
1
t
k A
=
If [NOBr]
o
= 7.5
×
10
-3
M, how much NOBr will be left
after a reaction time of 10 minutes?
Determine the half-life of this reaction.
EXAMPLE:
The reaction
2 NOBr (g)
→ 2 NO (g) + Br
2
(g)
is a second order reaction with respect to NOBr.
k
= 0.810 M
-1
⋅
s
-1
at 10
o
C.

15
[
]
t
1
NOBr
=
[
]
[
]
t
0
1
1
kt
NOBr
NOBr
=
+
-1
-1
(0.810 M s ) (600 s)
⋅
×
3
1
7.5 10 M
−
+
×
[
]
2
-1
t
1
6.19 10 M
NOBr
=
×
[
]
3
t
NOBr
1.6 10 M
−
=
×
SOLUTION:
One can solve for the amount of NOBr after 10 minutes by
substituting the given data into the integrated rate law for a second-order
reaction.
(
Second Order
)
To determine the half-life for this reaction, we substitute the
initial concentration of NOBr and the rate constant for the
reaction into the equation for the half-life of a second-order
reaction.
1/ 2
t
=
-1
1
3
1
0.810 M s (7.5 10 M)
−
−
⋅
×
160 s
=
[ ]
1/ 2
0
1
t
k A
=
16
The
Arrhenius
Equation:
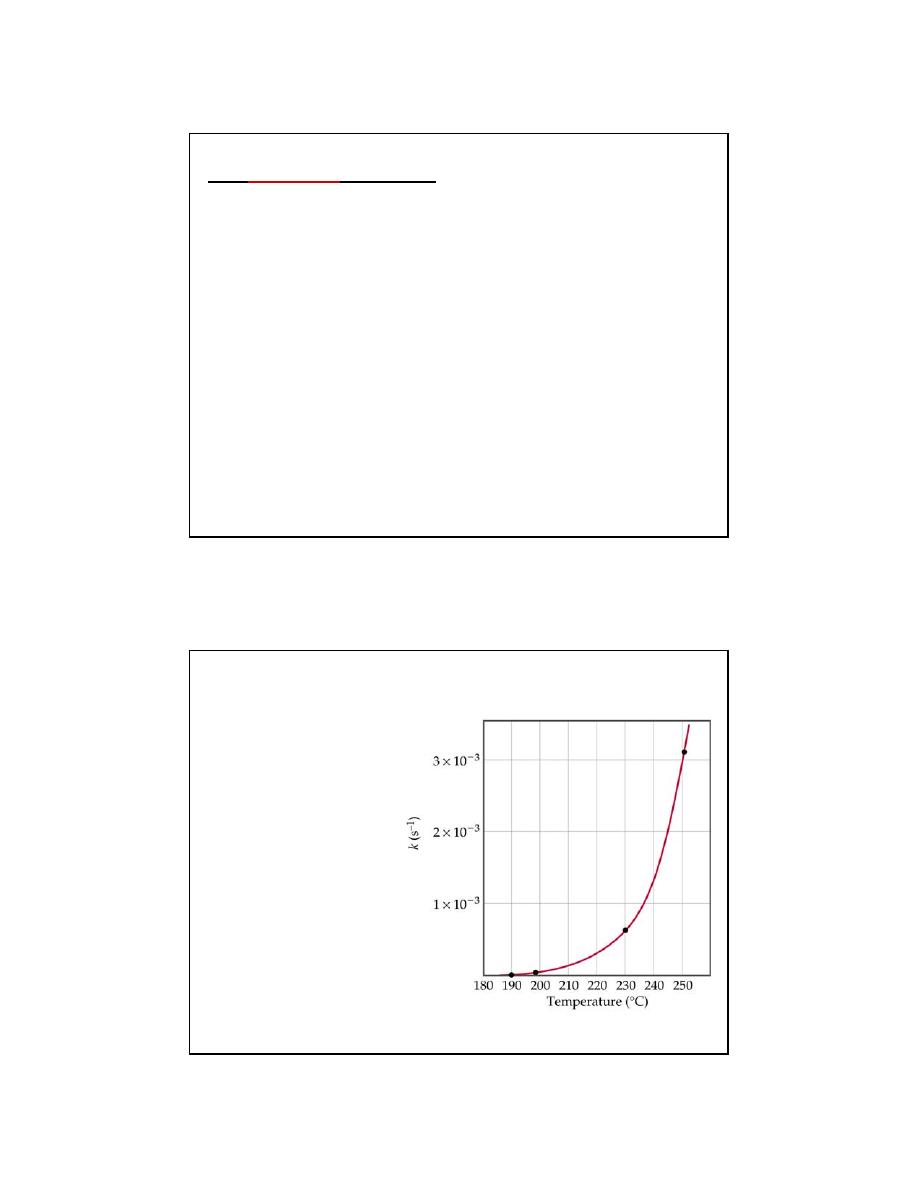
Temperature dependence of the Rate Constant
Most reactions speed up as temperature increases.
(
example:
food spoils when not refrigerated.)
k f (T)
=
Where “f” is some function.
The magnitude of a first order rate constant is seen to increase
exponentially with an increase in temperature.
f (T)
k(T)
e
∝
Therefore one can
Therefore one can
conclude that:
conclude that:

17
Why would k (along with the rate) increase with temperature?
Let’s go back to
Kinetic Molecular Theory
to understand…
The Collision Model:
Also, the more molecules present, the greater the probability of
collision and the faster the rate.
Thus reaction
rate
should
increase
with an increase in the
concentration of reactant molecules.
In order for molecules to react they must
collide.
Therefore, the greater the number of collisions the faster the rate.
As temperature increases, the molecules move faster and the
collision frequency increases.
Thus reaction
rate
should
increase
with an increase in temperature.
Activation Energy
(1) In order to form products, bonds must be broken in the
reactants.
(2) Bond breakage requires energy.
(3) Molecules moving too slowly, with too little kinetic energy,
don’t react when they collide.
The
Activation energy
,
E
a
, is the minimum energy required to
initiate a chemical reaction.
E
a
is specific to a particular reaction.
Arrhenius:
Molecules must posses a minimum amount of energy
to react. Why?
18
N
2
O(g) + O
2
(g)
→ N
2
(g) + NO
2
(g)
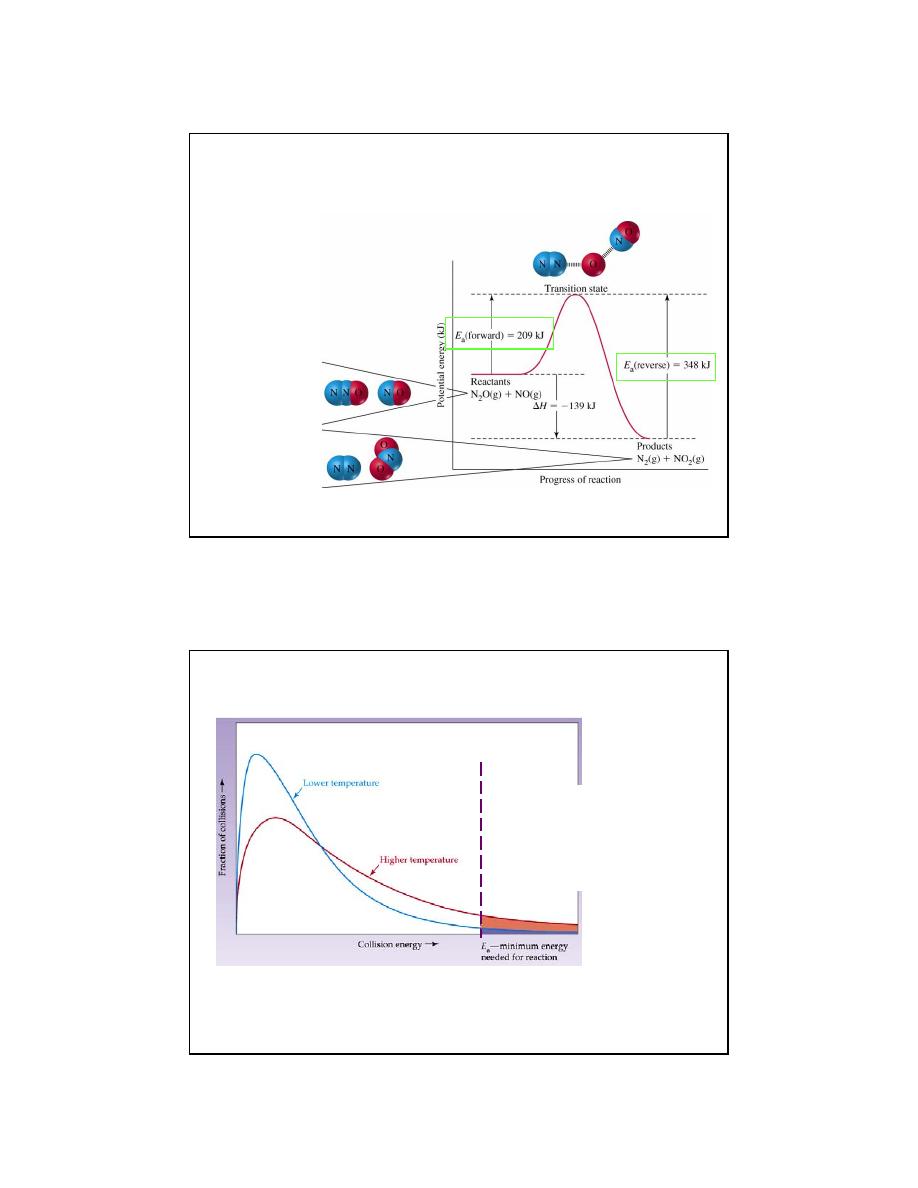
Consider the reaction:
The progress of a reaction
can be described by a
Reaction Coordinate
Reactants
Products
Recall for KMT that the temperature for a system of particles is
described by a distribution.
At higher temps, more particles have enough energy to go over the
barrier.
E > E
a
E < E
a
Since the probability of
a molecule reacting
increases, the rate
increases.

19
Orientation factors into the equation
The orientation of a molecule during collision can have a
profound effect on whether or not a reaction occurs.
Some collisions do not lead to reaction even if there is sufficient
energy.
The Arrhenius Equation
Arhenius discovered that most reaction-rate data obeyed an equation
based on three factors:
(1) The number of collisions per unit time.
(2) The fraction of collisions that occur with the correct orientation.
(3) The fraction of the colliding molecules that have an energy
greater than or equal to E
a
.
From these observations Arrhenius developed the aptly named
Arrhenius equation
Arrhenius equation
.
20
Arrhenius equation
Arrhenius equation
a
E
RT
k Ae
−
=
Both A and E
a
are specific to a given reaction.
k
is the rate constant
E
a
is the activation energy
R
is the ideal-gas
constant (8.314 J/Kmol)
T
is the temperature in K
A
A
is known the
frequency
frequency
or
pre
pre
–
–
exponential factor
exponential factor
In addition to carrying the units of the rate constant, “A” relates to
the frequency of collisions and the orientation of a favorable
collision probability
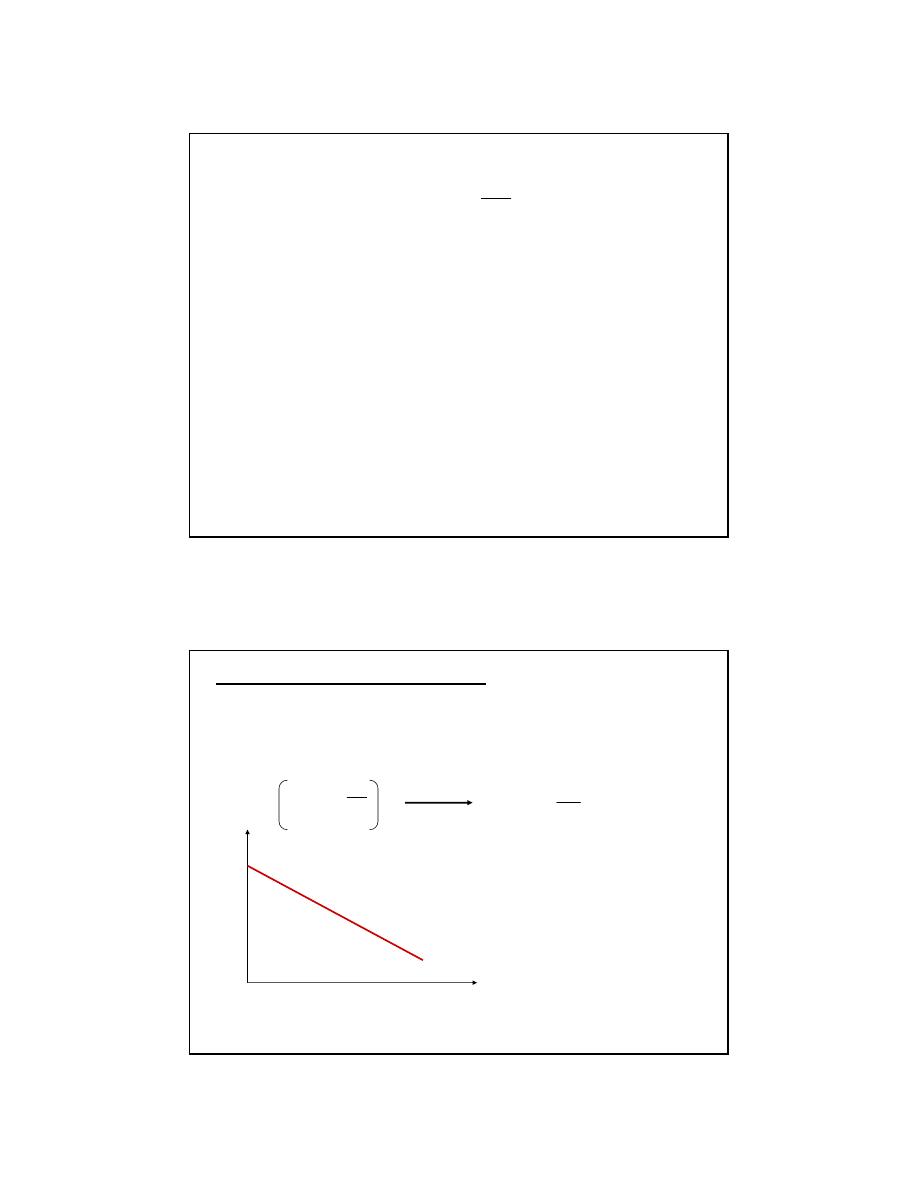
Determining the Activation Energy
E
a
may be determined experimentally.
First take natural log of both sides of the Arrhenius equation:
a
E
RT
k Ae
−
=
ln
a
E
ln k
ln A
RT
= −
+
Golly
Golly
–
–
gee, what do we
gee, what do we
have once again…
have once again…
ln k
1/T
A plot of ln k vs 1/T will
have a slope of –E
a
/R
and a y-intercept of ln A.

21
Determining the Activation Energy
a
1
1
E
ln k
ln A
RT
= −
+
a
2
2
E
ln k
ln A
RT
= −
+
2
1
ln k
ln k
−
One can determine the activation energy of a reaction by measuring
the rate constant at two temperatures:
Writing the Arrhenius equation for each temperature:
If one takes the natural log of the ratio of k
2
over k
1
we find that:
2
1
k
ln
k
=
a
2
1
1
2
E
k
1
1
ln
k
R T
T
=
−
presto!
presto!
Knowing the rate at two temps yields
the rate constant.
or
Knowing the E
a
and the rate constant
at one temp allows one to find k(T
2
)
a
1
E
ln A
RT
−
+
Substituting in the values for E
a
into the equation:
a
2
E
ln A
RT
−
+
2
1
ln k
ln k
−
=
−
Lookie
Lookie
what happens…
what happens…

22
Example:
The activation energy of a first order reaction is 50.2 kJ/mol at
25
o
C. At what temperature will the rate constant double?
2
1
k
2k
=
2
1
k
ln
k
=
1
1
2k
ln
k
ln(2)
=
a
1
2
E
1
1
R T
T
=
−
a
E
R
=
3
10 J
50.2 kJ/mol
1kJ
J
8.314
mol K
×
⋅
3
6.04 10 K
=
×
ln(2) 0.693
=
3
6.04 10 K
=
×
×
2
1
1
298K T
−
3
1
2
1
3.24 10 K
T
−
−
=
×
(1)
(1)
(2)
(2)
(3)
(3)
(4)
(4)
(5)
(5)
T
T
2
2
= 308 K
= 308 K
A 10
o
C change of
temperature doubles
the rate!!
