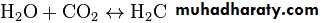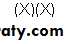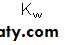Water & pH
BIOMEDICAL IMPORTANCE OF WATER:Water is the predominant chemical component of living organisms.
Its unique physical properties, which include the ability to solvate a wide range of organic and inorganic molecules, derive from water’s dipolar structure and exceptional capacity for forming hydrogen bonds.
An excellent nucleophile
Water is a reactant or product in many metabolic reactions.
Water has a slight propensity to dissociate into hydroxide ions and protons.
Regulation of water balance depends upon hypothalamic mechanisms that control thirst, on antidiuretic hormone (ADH), on retention or excretion of water by the kidneys, and on evaporative loss. Nephrogenic diabetes insipidus, which involves the inability to concentrate urine, results from the unresponsiveness of renal tubular osmoreceptors to ADH.
WATER IS AN IDEAL BIOLOGIC SOLVENT:
A water molecule is an irregular, slightly skewed tetrahedron with oxygen at its center
The two hydrogens and the unshared electrons of the remaining two sp3-hybridized orbitals occupy the corners of the tetrahedron. The 105-degree angle between the hydrogens differs slightly from the ideal tetrahedral angle, 109.5 degrees.
Water Molecules Form Hydrogen Bonds
An unshielded hydrogen nucleus covalently bound to an electron-withdrawing oxygen or nitrogen atom can interact with an unshared electron pair on another oxygen or nitrogen atom to form a hydrogen bond. Since water molecules contain both of these features, hydrogen bonding favors the self-association of water molecules into ordered arrays
Hydrogen bonding profoundly influences the physical properties of water and accounts for its exceptionally
high viscosity
high surface tension
high boiling point.
hydrogen bonds are weak and transient, with a half-life of about one microsecond. Rupture of a hydrogen bond in liquid water requires only about 4.5 kcal /mol, less than 5% of the energy required to rupture a covalent O-H bond. Hydrogen bonding enables water to dissolve many organic biomolecules that contain functional groups which can participate in hydrogen bonding. The oxygen atoms of aldehydes, ketones, and amides provide pairs of electrons that can serve as hydrogen acceptors.
Alcohols and amines can serve both as hydrogen acceptors and as donors of unshielded hydrogen atoms for formation of hydrogen bonds.
INTERACTION WITH WATER INFLUENCES THE STRUCTURE OF BIOMOLECULES
The covalent bond is the strongest force that holds molecules together.
Noncovalent forces, while of lesser magnitude, make significant contributions to the structure, stability, and functional competence of macromolecules in living cells. These forces, which can be either attractive or repulsive, involve interactions both within the biomolecule and between it and the water that forms the principal component of the surrounding environment.
Biomolecules Fold
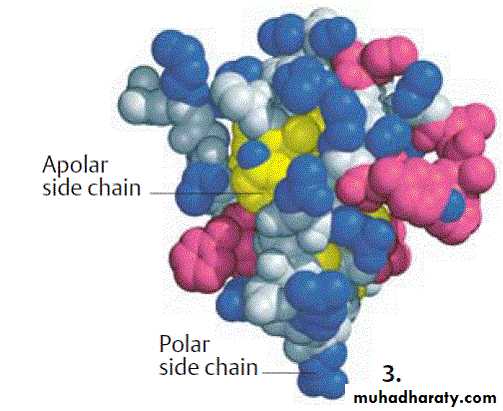
Most biomolecules are amphipathic; that is, they possess regions rich in charged or polar functional groups as well as regions with hydrophobic character. Proteins tend to fold with the R-groups of amino acids with hydrophobic side chains in the interior. Amino acids with charged or polar amino acid side chains (eg, arginine, glutamate, serine) generally are present on the surface in contact with water.
A similar pattern prevails in a phospholipid bilayer, where the charged head groups of phosphatidyl serine or phosphatidyl ethanolamine contact water while their hydrophobic fatty acyl side chains cluster together, excluding water.
Hydrophobic Interactions
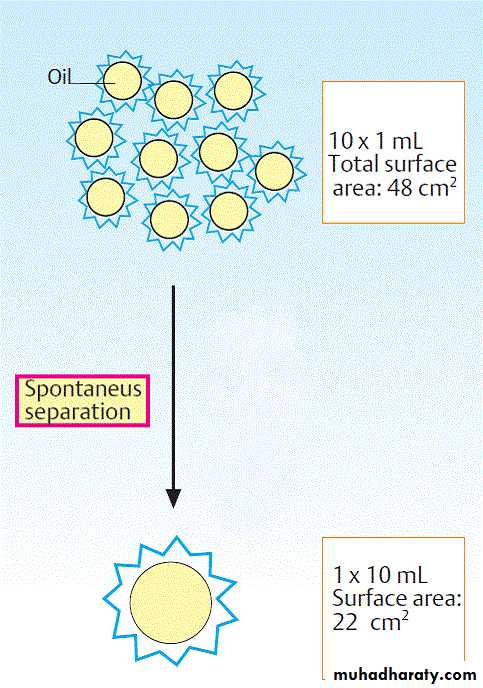
Hydrophobic interaction refers to the tendency of non-polar compounds to self-associate in an aqueous environment. This self-association is driven neither by mutual attraction nor by what are sometimes incorrectly referred to as “hydrophobic bonds.” Self association arises from the need to minimize energetically unfavorable interactions between nonpolar groups and water.While the hydrogens of nonpolar groups such as the methylene groups of hydrocarbons do not form hydrogen bonds, they do affect the structure of the water that surrounds them. Thus, nonpolar molecules tend to form droplets with minimal exposed surface area, reducing the number of water molecules affected. For the same reason, in the aqueous environment of the living cell the hydrophobic portions of biopolymers tend to be buried inside the structure of the molecule, or within a lipid bilayer, minimizing contact with water.
Electrostatic Interactions
Interactions between charged groups shape biomolecular structure. Electrostatic interactions between oppositely charged groups within or between biomolecules are termed salt bridges. Salt bridges are comparable in strength to hydrogen bonds but act over larger distances. They thus often facilitate the binding of charged molecules and ions to proteins and nucleic acids.
Van der Waals Forces
Van der Waals forces arise from attractions between transient dipoles generated by the rapid movement of electrons on all neutral atoms. Significantly weaker than hydrogen bonds but potentially extremely numerous. They act over very short distances, typically 2–4 Å.
WATER IS AN EXCELLENT NUCLEOPHILE
Metabolic reactions often involve the attack by lone pairs of electrons on electron-rich molecules termed nucleophiles on electron-poor atoms called electrophiles. Nucleophiles and electrophiles do not necessarily possess a formal negative or positive charge. Water, whose two lone pairs of sp3 electrons bear a partial negative charge, is an excellent nucleophile. Other nucleophiles of biologic importance include the oxygen atoms of phosphates, alcohols, and carboxylic acids; the sulfur of thiols. Common electrophiles include the carbonyl carbons in amides, esters, aldehydes, and ketones.
Water is a product, as shown below for the formation of a peptide bond between two amino acids.
While hydrolysis is a thermodynamically favored reaction, the amide and phosphoester bonds of polypeptides and oligonucleotides are stable in the aqueous environment of the cell. that the thermodynamics governing the equilibrium of a reaction do not determine the rate at which it will take place. In the cell, protein catalysts called enzymes are used to accelerate the rate of hydrolytic reactions when needed. Proteases catalyze the hydrolysis of proteins into their component amino acids, while nucleases catalyze the hydrolysis of the phosphoester bonds in DNA and RNA. Careful control of the activities of these enzymes is required to ensure that they act only on appropriate target molecules.
Water Molecules Exhibit a Slight but Important Tendency to Dissociate
The ability of water to ionize, while slight, is of central importance for life. Since water can act both as an acid and as a base, its ionization may be represented as an intermolecular proton transfer that forms a hydronium ion (H3O+) and a hydroxide ion (OH−):
H2O + H2O = H3O+ + OH-
The transferred proton is actually associated with a cluster of water molecules. The proton is nevertheless routinely represented as H+, even though it is in fact highly hydrated. Since hydronium and hydroxide ions continuously recombine to form water molecules, an individual hydrogen or oxygen cannot be stated to be present as an ion or as part of a water molecule. Since 1 g of water contains 3.46 X1022 molecules, the ionization of water can be described statistically. To state that the probability that a hydrogen exists as an ion is 0.01 means that a hydrogen atom has one chance in 100 of being an ion and 99 chances out of 100 of being part of a water molecule. Hydrogen ions and hydroxyl ions nevertheless contribute significantly to the properties of water. For dissociation of water,
where brackets represent molar concentrations (strictly speaking, molar activities) and K is the dissociation constant. Since one mole (mol) of water weighs 18 g, one liter (L) (1000 g) of water contains 1000 ÷18 = 55.56 mol. Pure water thus is 55.56 molar. Since the probability that a hydrogen in pure water will exist as a hydrogen ion is 1.8 X10−9, the molar concentration of H+ ions (or of OH− ions) in pure water is the product of the probability, 1.8 X10−9, times the molar concentration of water, 55.56 mol/L. The result is 1.0 X10−7 mol/L. We can now calculate K for water:
The molar concentration of water, 55.56 mol/L, is too great to be significantly affected by dissociation. It therefore is considered to be essentially constant. This constant may then be incorporated into the dissociation constant K to provide a useful new constant Kw termed the ion product for water. The relationship between Kw and K is shown below:
As its name suggests, the ion product Kw is numerically equal to the product of the molar concentrations of H+ and OH−:
At 25 °C, Kw = (10−7)2, or 10−14 (mol/L)2. At temperatures below 25 °C, Kw is somewhat less than 10−14; and at temperatures above 25 °C it is somewhat greater than 10−14. Within the stated limitations of the effect of temperature, Kw equals 10-14 (mol/L)2 for all aqueous solutions, even solutions of acids or bases. We shall use Kw to calculate the pH of acidic and basic solutions.
pH IS THE NEGATIVE LOG OF THE HYDROGEN ION CONCENTRATION
The term pH was introduced in 1909 by Sörensen, who defined pH as the negative log of the hydrogen ion concentration:
This definition suffices for many biochemical purposes. To calculate the pH of a solution:
1. Calculate hydrogen ion concentration [H+].2. Calculate the base 10 logarithm of [H+].
3. pH is the negative of the value found in step 2.
For example, for pure water at 25°C,
Low pH values correspond to high concentrations of H+ and high pH values correspond to low concentrations of H+. Acids are proton donors and bases are proton acceptors. Strong acids (eg, HCl or H2SO4) completely dissociate into anions and cations even in strongly acidic solutions (low pH). Weak acids dissociate only partially in acidic solutions. Similarly, strong bases (eg, KOH or NaOH)—but not weak bases (eg, Ca[OH]2)—are completely dissociated at high pH. Many biochemicals are weak acids.
Example 1: What is the pH of a solution whose hydrogen ion concentration is 3.2 x10−4 mol/L?
Example 2: What is the pH of a solution whose hydroxide ion concentration is 4.0x10−4 mol/L?
We first define a quantity pOH that is equal to −log [OH−] and that may be derived from the definition of Kw:
Therefore:
OrTo solve the problem by this approach:
Now:Example 3: What are the pH values of (a) 2.0 x10−2 mol/L KOH and of (b) 2.0 x10−6 mol/L KOH? The OH− arises from two sources, KOH and water. Since pH is determined by the total [H+] (and pOH by the total [OH−]), both sources must be considered. In the
first case (a), the contribution of water to the total [OH−] is negligible. The same cannot be said for the second case (b):
Once a decision has been reached about the significance of the contribution by water, pH may be calculated as above. The above examples assume that the strong base KOH is completely dissociated in solution and that the concentration of OH− ions was thus equal to that of the KOH. This assumption is valid for dilute solutions of strong bases or acids but not for weak bases or acids. Since weak electrolytes dissociate only slightly in solution, we must use the dissociation constant to calculate the concentration of [H+] (or [OH−]) produced by a given molarity of a weak acid (or base) before calculating total [H+] (or total [OH−]) and subsequently pH.
Weak Acids Have Great Physiologic Significance
Many biochemicals possess functional groups that are weak acids or bases. Carboxyl groups, amino groups, and the second phosphate dissociation of phosphate esters
are present in proteins and nucleic acids, most coenzymes, and most intermediary metabolites. Knowledge of the dissociation of weak acids and bases thus is basic to understanding the influence of intracellular pH on structure and biologic activity. Charge-based separations such as electrophoresis and ion exchange chromatography also are best understood in terms of the dissociation behavior of functional groups. We term the protonated species (eg, HA or R-NH3 +) the acid and the unprotonated species (eg, A− or R-NH2) its conjugate base. Similarly, we may refer to a base (eg, A− or R-NH2) and its conjugate acid (eg, HA or R-NH3 +). Representative weak acids (left), their conjugate bases (center), and the pKa values (right) include the following:
We express the relative strengths of weak acids and bases in terms of their dissociation constants. Shown below are the expressions for the dissociation constant (Ka ) for two representative weak acids, R-COOH and R-NH3 +.
Since the numeric values of Ka for weak acids are negative exponential numbers, we express Ka as pKa, where
Note that pKa is related to Ka as pH is to [H+]. The stronger the acid, the lower its pKa value. pKa is used to express the relative strengths of both acids and bases. For any weak acid, its conjugate is a strong base. Similarly, the conjugate of a strong base is a weak acid. The relative strengths of bases are expressed in terms of the pKa of their conjugate acids. For polyproteic compounds containing more than one dissociable proton, a numerical subscript is assigned to each in order of relative acidity. For a dissociation of
the type
the pKa is the pH at which the concentration of the acid R-NH3 + equals that of the base R-NH2. From the above equations that relate Ka to [H+] and to the concentrations of undissociated acid and its conjugate base, when
or when
ThenThus, when the associated (protonated) and dissociated (conjugate base) species are present at equal concentrations, the prevailing hydrogen ion concentration [H+] is numerically equal to the dissociation constant, Ka. If the logarithms of both sides of the above equation are taken and both sides are multiplied by −1, the expressions would be as follows:
Since −log Ka is defined as pKa, and −log [H+] defines pH, the equation may be rewritten as
ie, the pKa of an acid group is the pH at which the protonated and unprotonated species are present at equal concentrations. The pKa for an acid may be determined by adding 0.5 equivalent of alkali per equivalent of acid. The resulting pH will be the pKa of the acid.
The Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation is derived below. A weak acid, HA, ionizes as follows:Substitute pH and pKa for −log [H+] and −log Ka, respectively;
then:Inversion of the last term removes the minus sign and gives the Henderson-Hasselbalch equation:
And pOH= pKa + [ BH][B]
The Henderson-Hasselbalch equation has great predictive value in protonic equilibria. For example,(1) When an acid is exactly half-neutralized, [A−] = [HA]. Under these conditions,
Therefore, at half-neutralization, pH = pKa.
(2) When the ratio [A−]/[HA] = 100:1,(3) When the ratio [A−]/[HA] = 1:10,
Solutions of Weak Acids & Their SaltsSolutions of weak acids or bases and their conjugates exhibit buffering, the ability to resist a change in pH following addition of strong acid or base. Since many metabolic reactions are accompanied by the release or uptake of protons, most intracellular reactions are buffered. Oxidative metabolism produces CO2, the anhydride of carbonic acid, which if not buffered would produce severe acidosis. Maintenance of a constant pH
involves buffering by phosphate, bicarbonate, and proteins, which accept or release protons to resist a change in pH.
For experiments using tissue extracts or enzymes, constant pH is maintained by the addition of buffers such as MES ([2-N-morpholino]ethanesulfonic acid, pKa 6.1), inorganic orthophosphate (pKa2 7.2), HEPES (N-hydroxyethylpiperazine-N9-2-ethanesulfonic acid, pKa 6.8), or Tris (tris[hydroxymethyl] aminomethane, pKa 8.3). The value of pKa relative to the desired pH is the major determinant of which buffer is selected. Buffering can be observed by using a pH meter while titrating a weak acid or base .We can also calculate the pH shift that accompanies addition of acid or base to a buffered solution. In the example, the buffered solution (a weak acid, pKa = 5.0, and its conjugate base) is initially at one of four pH values. We will calculate the pH shift that results when 0.1 meq of KOH is added to 1 meq of each solution:
Notice that the change in pH per milliequivalent of OH− added depends on the initial pH. The solution resists changes in pH most effectively at pH values close to the pKa. A solution of a weak acid and its conjugate base buffers most effectively in the pH range pKa ± 1.0 pH unit.
Acid Strength Depends on Molecular Structure
Many acids of biologic interest possess more than one dissociating group. The presence of adjacent negative charge hinders the release of a proton from a nearby group, raising its pKa. This is apparent from the pKa values for the three dissociating groups of phosphoricacid and citric acid .
The effect of adjacent charge decreases with distance. The second pKa for succinic acid, which has two methylene groups between its carboxyl groups, is 5.6, whereas the second pKa for gultaric acid, which has one additional methylene group, is 5.4
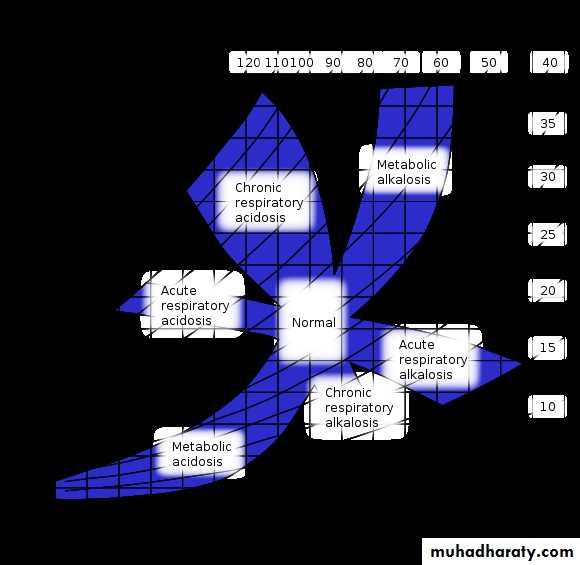
Acid–base homeostasis
Acid–base homeostasis is the part of human homeostasis concerning the proper balance between acids and bases, also called body HYPERLINK "https://en.wikipedia.org/wiki/PH" \o "PH" pH. The body is very sensitive to its pH level, so strong mechanisms exist to maintain it. Outside the acceptable range of pH,proteins are denatured and digested, enzymes lose their ability to function, and death may occur.
Mechanism
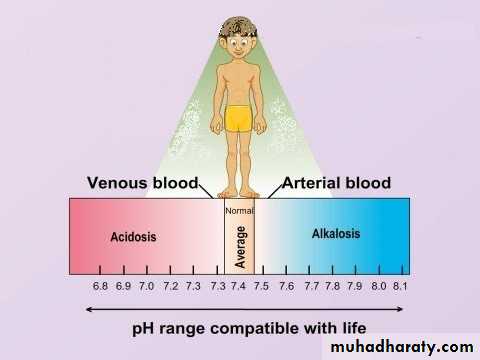
The body's acid–base balance is normally tightly regulated by buffering agents, the respiratory system, and the renal system, keeping the arterial blood pH between 7.38 and 7.42. Several buffering agents that reversibly bind hydrogen ions and impede any change in pH exist. Extracellular buffers include bicarbonate and ammonia, whereas proteins and phosphate act as intracellular buffers; The bicarbonate buffering system is especially key, as carbon dioxide (CO2) can be shifted through carbonic acid (H2CO3) to hydrogen ions and bicarbonate (HCO3-) as shown below.Metabolic acidosis is a condition that occurs when the body produces excessive quantities of acid or when the kidneys are not removing enough acid from the body. If unchecked, metabolic acidosis leads to HYPERLINK "https://en.wikipedia.org/wiki/Acidemia" \o "Acidemia" acidemia, i.e., blood pH is low (less than 7.35) due to increased production of hydrogen ions by the body or the inability of the body to form bicarbonate (HCO3−) in the kidney.
Metabolic alkalosis is a metabolic condition in which the pH of tissue is elevated beyond the normal range (7.35-7.45). This is the result of decreased hydrogen ion concentration, leading to increased bicarbonate, or alternatively a direct result of increased bicarbonate concentrations.
Respiratory acidosis is a medical emergency in which decreased ventilation (hypoventilation) increases the concentration of carbon dioxide in the blood and decreases the blood's pH (a condition generally called acidosis).
Respiratory alkalosis is a disturbance in acid and base balance due to alveolar hyperventilation. Alveolar hyperventilation leads to a decreased partial pressure of arterial carbon dioxide (PaCO2).
Acid–base imbalances that overcome the buffer system can be compensated in the short term by changing the rate of ventilation. This alters the concentration of carbon dioxide in the blood, shifting the above reaction according to Le Chatelier's principle, which in turn alters the pH. For instance, if the blood pH drops too low (acidemia), the body will compensate by increasing breathing thereby expelling CO2, and shifting the above reaction to the left such that fewer hydrogen ions are free; thus the pH will rise back to normal. For alkalemia, the opposite occurs.
The kidneys are slower to compensate, but renal physiology has several powerful mechanisms to control pH by the excretion of excess acid or base.
In response to acidosis, tubular cells reabsorb more bicarbonate from the tubular fluid, collecting duct cells secrete more hydrogen and generate more bicarbonate, and HYPERLINK "https://en.wikipedia.org/w/index.php?title=Ammoniagenesis&action=edit&redlink=1" \o "Ammoniagenesis (page does not exist)" ammoniagenesis leads to increased formation of the NH3 buffer.
In responses to alkalosis, the kidney may excrete more bicarbonate by decreasing hydrogen ion secretion from the tubular epithelial cells, and lowering rates of glutamine metabolism and ammonium excretion.
Problems
1- Physiological pH is 7.4. What is the hydrogen ion concentration of a solution at physiological pH?A.
-7.4 M
B.
0.6 M
C.
0.6 x 10 - 8 M
D.
1 x 10 - 8 M
E.
4 x 10 - 8 *
2- What is the pH of a 10 - 3 M solution of HCl?
3-Show that the pH of a solution remains 7.00 when 1.0 x 10¯11 moles of HCl is added to the solution.
Solution:
1) pH of 7.00 means this:
[H+] = 1.0 x 10¯7 M
2) Add 1.0 x 10¯11 moles of H+ to get:
1.0001 x 10¯7 M
pH = - log 1.0001 x 10¯7 = 6.9999566
3) Round the answer off to two significant figures:
pH = 7.00
By the way, no pH meter constructed is sensitive enough to determine a value like 6.9999566. Heck, it's a tricky business to get 3 or 4 sig figs on a pH meter, much less 6 or 7.
4-Assume that you prepared a solution by adding 0.05 mL (1 drop) of 0.500M HCl to 5.00 x 107 mL of "pure" water. Calculate the resultant pH. (Hint: the answer is not pH = 9.3; add up the hydronium ions from ALL sources)
Solution:
The key is to remember that "pure" water is naturally 1.00 x 10¯7 M in hydrogen ion. That's the thinking behind the "ALL sources" hint
1) Calculate total H+ in 5.00 x 107 mL of water:
(1.00 x 10¯7 mol/L) (5.00 x 104 L) = 0.005 mol
2) Calculate total H+ in HCl:
(0.500 mol/L) (0.00005 L) = 0.000025 mol
3) Add the results together:
0.005 mol + 0.000025 mol = 0.005025 mol
4) Calculate new molarity of hydrogen ion:
0.005025 mol / 5.00 x 104 L = 1.005 x 10¯7 M
5) Calculate new pH:
- log 1.005 x 10¯7 = 6.9978
Rounded off to three sig figs, the pH is 6.998. Since we had 0.05 mL, let's round off to one sig fig to arrive at a pH of 7.0.
By the way, a pH of 9.3 is arrived at like this:
H+ from HCl = 0.000025 mol total volume = 5.00 x 104 L
[H+] = 0.000025 mol / 5.00 x 104 L = 5.00 x 10¯10 M
pH = -log 5.00 x 10¯10 = 9.301
………………………………………………………………………………………………………
Sample Problem 1
a) A solution was prepared by dissolving 0.02 moles of acetic acid (HOAc; pKa = 4.8) in water to give 1 liter of solution. What is the pH?
b) To this solution was then added 0.008 moles of concentrated sodium hydroxide (NaOH). What is the new pH? (In this problem, you may ignore changes in volume due to the addition of NaOH).
c) An additional 0.012 moles of NaOH is then added. What is the pH?
Solutiona) This is a class 1 problem:
HOAc
H+
+
OAc-
pKa = 4.8
Ka = 1.6 x10-5 M
Initial Conc
0.02 M
~0
0
Change
-X+X
+X
Net
0.02-XX
Ka =
=
= 1.6 x10-5
[HOAc]initial > 100 x Ka, so... X can be ignored in the denominator.
X2/0.02 = 1.6 x10-5 ; X2 = 3.2 x10-7
X = 5.6 x10-4 M = [H+]
pH = -log(5.6 x10-4) = 3.25
b) NaOH is a strong base. It will react nearly quantitatively with HOAc to produce OAc-.
HOAc + OH-
OAc- + H2O
0.008 moles HOAc + 0.008 moles OH-
0.008 moles OAc-
Amount of HOAc remaining = 0.02 - 0.008 = 0.012 moles. Thus,[HOAc] = 0.012 M and [OAc-] = 0.008 M
Since both [HOAc] and [OAc-] are present, this is a class 3 problem.
pH = pKa + log
= 4.8 + log
= 4.8 + log(0.67)
= 4.8 - 0.17
pH = 4.63
c) After the addition of another 0.012 moles of NaOH, all of the HOAc has been converted to NaOAc. thus, [OAc-] = 0.02 M. Since only the "base form" of the HOAc is now present, this is a class 2 problem:
OAc-
+
H2O
HOAc
+OH-
Keq =
Initial Conc
0.02 M[H2O]
~0~0
Change
-X
-X
+X
+X
Net
0.02-X[H2O]
XX
So,
Kw/Ka =
=
=
Neglecting the denominator gives,
X2/0.02 = 6.25 x10-10
X2 = 12.5 x10-12
X = 3.5 x10-6 = [OH-]
[H+] = 10-14/(3.5 x10-16) = 2.9 x10-9
pH = 8.54
Note: Every problem involving titration and buffers is similar to the sample problem just given. The addition of strong base (or acid) affects the initial concentrations of HA and A-. The pH can then be determined using the appropriate class 1, 2, or 3 solutions. Given the pH, the ratio of A-/HA can be determined from the Henderson-Hasselbalch Equation. The concentrations of A- and HA can be determined if the total concentration (A- + HA) is known, or if the concentration of either species is known.