
ﺑﺴﻢ ﺍﷲ ﺍﻟﺮﺣﻤﻦ ﺍﻟﺮﺣﻴﻢ
ﻭﺍﻟﺼﻼﺓ ﻭﺍﻟﺴﻼﻡ ﻋﻠﻰ ﺃﺷﺮﻑ ﺍﻟﻤﺨﻠﻮﻗﻴﻦ ﻣﺤﻤﺪ ﺳﻴﺪ ﺍﻟﻤﺮﺳﻠﻴﻦ ﻭﻋﻠﻰ ﺁﻟﻪ ﻭﺻﺤﺒﻪ ﺃﺟﻤﻌﻴﻦ
ﺃﻣﺎ ﺑﻌﺪ ٬ ﻳﺴﺮﻧﻲ ﺃﻥ ﺃﻗﺪﻡ ﻟﻜﻢ ﻫﺬﺍ ﺍﻟﻌﻤﻞ ﺍﻟﻤﺘﻮﺍﺿﻊ ﻭﻫﻮ ﻋﺒﺎﺭﺓ ﻋﻠﻰ
ﻣﻠﺨﺼﺎﺕ ﻣﻊ ﺗﻘﻨﻴﺎﺕ
ﺍﻟﺮﻳﺎﺿﻴﺎﺕ ﻟﻤﺴﺘﻮﻯ ﺍ
ﻟﺠﺬﻉ ﺍﻟﻤﺸﺘﺮﻙ ﻋﻠ
ﻤ
ﻲ
ﻣﺠﻤﻌﺔ ﻓﻲ ﻛﺘﺎﺏ ﻭﺍﺣﺪ
ﻭﻫﻲ ﻟﻸﺳﺘﺎﺫ ﺣﻤﻴﺪ
ﺑﻮﻋﻴﻮﻥ
sefroumaths.site.voila.fr
ﺗﺠﻤﻴﻊ ﻭﺗﺮﺗﻴﺐ
ALMOHANNAD
ــــ
ا ئد
ــــ
ﺏ
ـــــــــ
ت
I
(
{
}
0,1, 2, 3, 4, 5.......
IN
=
{
}
*
1, 2, 3, 4, 5.......
IN
=
II
(
–
(1
a
2
a
k
=
k
IN
∈
.
(2
a
2
1
a
k
=
+
2
1
a
k
=
−
k
IN
∈
.
3
(
(a
! "# $ !%& $
.
(b
! "# $ !%& $
.
(c
(*
$ !%&
a
b
$) $
a b
+
.
(*
$ !%&
a
b
$) $
a b
+
.
(*
$ !%&
a
$
b
$)
a b
+
.
(d
(*
$ !%&
a
b
$) $
ab
.
(*
$ !%&
a
b
$) $
ab
.
(*
$ !%&
a
$
b
$)
ab
.
(e
$ !%&
a
b
*+! , $) $ $
.
III
(
1
(
!"
$-
a
b
$ $
.
-! $& .
a
- /0
b
$ !%&
a
a
b k
=
k
IN
∈
.
2
(
(*
0
/0
.
(*
0
, ! /0 -
0
.
(*
$ !%&
a
/0
b
b
/0
c
$)
a
- /0
b
.
3
(
# $"% !
!"
$-
a
b
$ 1 $ $
.
$ - 23! 4-! /0-!
a
b
,
/0 2
5 4 " 1
.
-
( , )
PPCM a b
a
b
∨
.
4
(
(*
-! $ !%&
a
- /0
b
$)
( , )
PPCM a b
a
=
(*
( , )
PPCM a a
a
=
IV
(
& '
1
(
!"
$-
a
b
$ $
.
-! $& .
a
6.- #
b
-! $& 7
b
".
a
$ !%&
a
/0
b
a
a
b k
=
k
IN
∈
.
/
b a
.
2
(
(*
". 6 -! !3!
0
.
(*
0
, ! ".
0
.
(*
$ !%&
b
".
a
c
".
b
$)
c
".
a
.
(*
-!
1
6 -! !3! 8 ".
.
(*
9 ".
.
(*
-
1
, ! "#
1
.
3
(
() &* +
2
,
3
,
4
,
5
,
9
,
11
,
25
a
(
"
$-
0
α
7
1
α
7
2
α
7
3
α
7
.....
7
r
α
$ #
{
}
0,1, 2, 3, 4,5, 6, 7,8, 9
6-
1
0
...
r
r
α α
α
−
%-! -! -&
! "#
0
α
! "# 7
1
α
7
............
b
(
-
-!
1
0
...
r
r
a
α α
α
−
=
-
:
(*
a
6.-! .
2
$ !%&
{
}
0
0, 2, 4, 6,8
α
∈
(*
a
6.-! .
3
$ !%&
0
1
2
3 /
r
α α α
α
+ +
+ +
(*
a
6.-! .
4
$ !%&
0
1
4 /
α α
(*
a
6.-! .
5
$ !%&
{ }
0
0,5
α
∈
(*
a
6.-! .
9
$ !%&
0
1
2
9 /
r
α α α
α
+ +
+ +
(*
a
6.-!
.
3
$
!%&
0
2
4
1
3
5
......)
(
.....)
11 / (
α α α
α α α
−
+
+
+
+
+
+
(*
a
6.-! .
25
$ !%&
{
}
1
0
00, 25, 50, 75
α α
∈
4
(
. $"% &*
!"
$-
a
b
$ 1 $ $
.
3! 4-! ".-!
$ -
a
b
"# ,
" 1
5 4
.
-
( , )
PGCD a b
a
b
∧
.
5
(
/)' 0 -
.
$-
a
b
$
*
IN
a
b
≥
.
$
( , )
PGCD a b
# ;#
6- 6
:
6.
a
b
".-! < ". "=
$ " # !%, #-!
( , )
PGCD a b
" 1 # *> ,
.
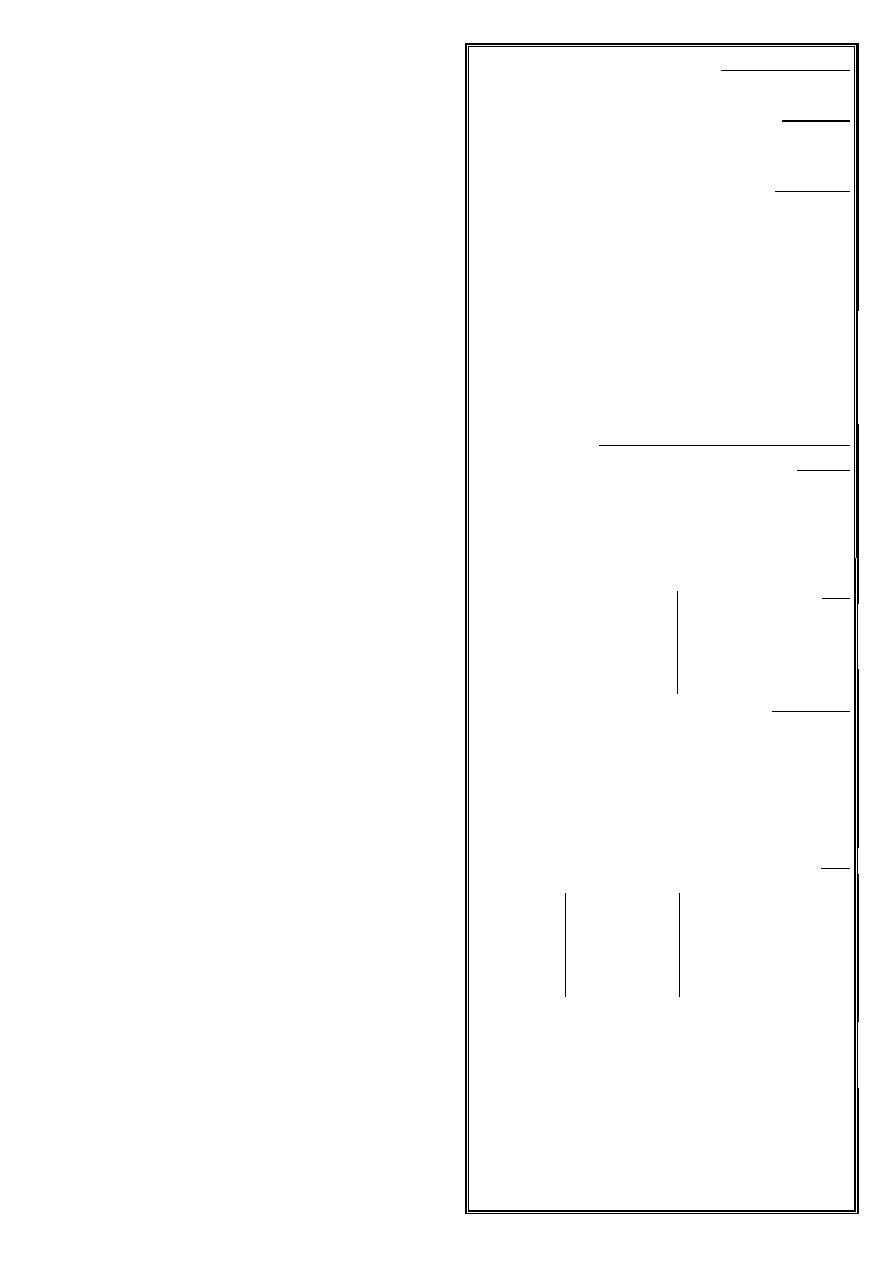
?-! @%, A* $
:
...
...
...
2
r
1
r
b
a
3
q
2
q
1
q
0
n
r
...
...
2
r
1
r
1
r
V
(
1
(
!"
- !
a
-
. $#
1
a
.
2
(
(a
-! , B. -
a
8 -
.
3! !3! 8
6-
p
B. -!
2
p
a
≤
". !3! @%, $ !%&
a
$)
a
- 1
.
". C !3! @%, 8 ; !%&
a
$)
a
-
.
(b
$ 23! 6-3! !3!
100
,
2
,
3
,
5
,
7
,
11
,
13
,
17
,
19
,
23
,
29
,
31
,
37
,
41
,
43
,
47
7
53
,
59
,
61
,
67
,
71
,
73
,
79
,
83
,
89
,
97
.
(c
-
2
p
≠
,
(d
-!
1
- E-
.
3
(
$."
2 3 (4
0
-
:
2
a
≥
< 6.
3
1
2
1
2
3
.
.
......
r
r
a
p
p
p
p
α
α
α
α
=
1
p
7
2
p
7
3
p
7
.....
7
r
p
!
6-
.
1
α
7
2
α
7
3
α
7
.....
7
r
α
6 1 6 !
.
-! 49 6-! @%,
a
6- ! F! -&
.
25
49-
-!
54
:
-
$%&
$%&
3
54
2 3
= ×
4
(
+"
.
(a
$ - 23! 4-! /0-!
a
b
F! ,
9 $ 6-! 1 6-! 6-3! ! -!
a
b
E -& 6
.
(b
$ - 3! 4-! ".-!
a
b
! -! F! ,
9 $ 6-! 6-3!
a
b
E 2 -& 6
.
25
-
:
76
632
76
632
و
∨
∧
$-
$%&
3
632
2 .79
=
2
76
2 .19
=
2
76
632
2
4
∧
=
=
3
76
632
2 .19.79
12008
∨
=
=
(c
$-
2
a
≥
3
1
2
1
2
3
.
.
......
r
r
a
p
p
p
p
α
α
α
α
=
-! 49
a
! F! -&
6-
.
-! "!#
a
,
1
2
(1
)(1
)
(1
)
r
α
α
α
+
+
+
2
54
3
27
3
9
3
3
1
2
632
2
76
2
316
2
38
2
158
19
19
79
79
1
1
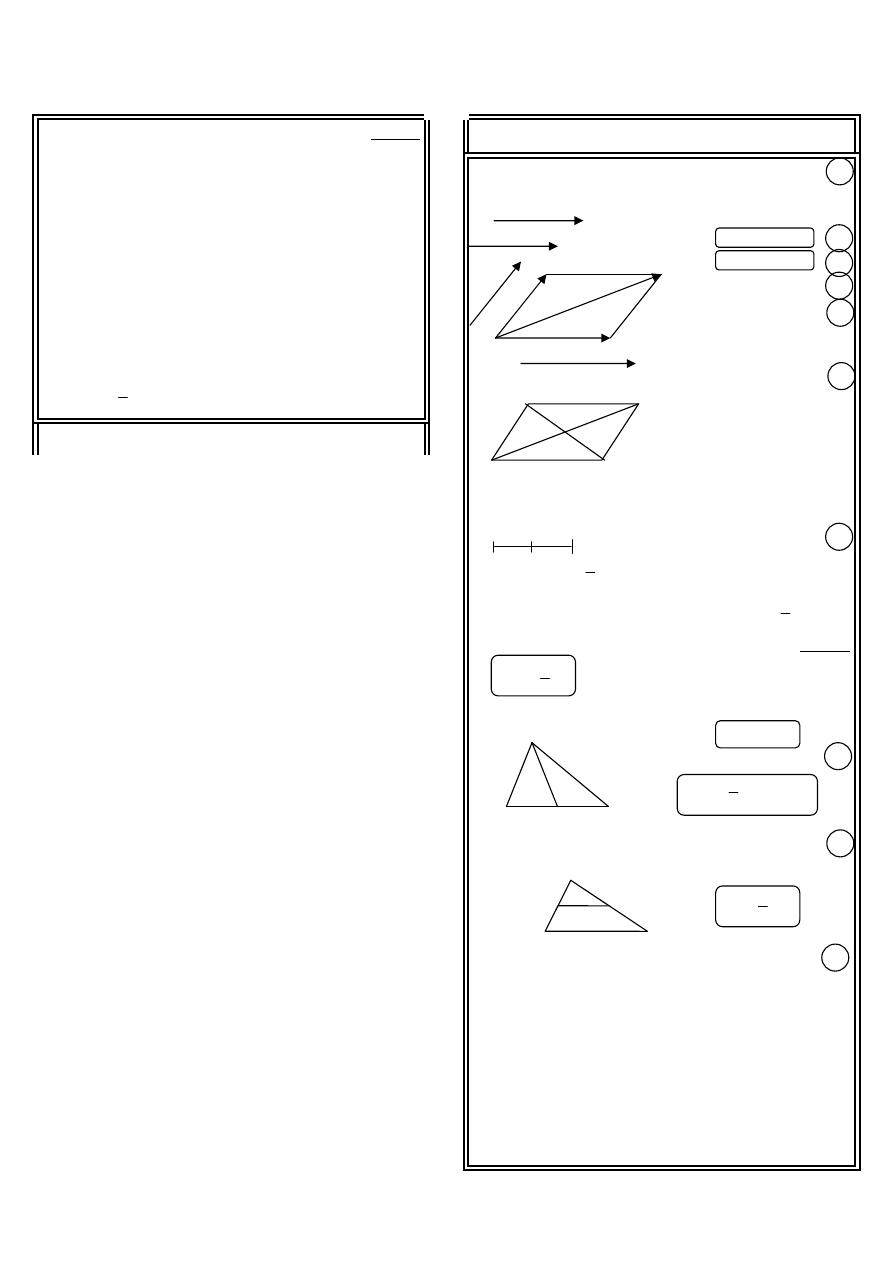
ا ب ا
(A
1
v
و
u
)
(
!"
.
2
AB
BA
= −
3
AB
BC
AC
+
=
)
$% &'(
(.
4
0
AB
=
)
A
B
=
.
5
** $+
u
v
+
,
u
v
$-.
/0+ 1
.
6
(23
(
)
ABCD
/0+ 1
4
5*
& 3%
:
(a
AB
DC
=
(b
AD
BC
=
(c
AC
AB
AD
=
+
(d
3
[ ]
AC
[ ]
BD
7-
.
7
I
& 7-
[ ]
AB
(*
AI
IB
=
(*
IA
IB
= −
(*
1
2
AI
AB
=
(*
1
2
BI
BA
=
(*
0
IA
IB
+
=
:
a
(
I
7-
[ ]
AB
$
1
2
AI
AB
=
b
(
+ 2
I
7-
[ ]
AB
+ 2 +
0
IA
IB
+
=
8
(
)
ABC
89
9
I
7-
[ ]
BC
*
(
)
1
2
AI
AB
AC
=
+
.
9
(
)
ABC
989
.
I
7-
[ ]
AB
J
7-
[ ]
AC
*
1
2
IJ
BC
=
10
(a
v
و
u
.
(b
v
و
u
v
u
α
=
+
u
v
α
=
.
(c
C
و
BوA
4 &
AC
و
AB
AB
AC
α
=
+
AC
AB
α
=
(d
( )
AB
( )
CD
4
CD
و
AB
.
:
a
(
+ 2
IK
و
IJ
&'(
)
9
IJ
IK
α
=
+
0
IJ
IK
α
β
+
=
+
.(...
:2 !
IK
و
IJ
3; &*2
&8-.
AC
و
AB
9
.
9 *
2
IJ
A B
A C
=
−
6
3
IK
A B
A C
=
−
< =
+
3
6
3
IJ
AB
DC
IK
=
−
=
3
IK
IJ
=
.
b
(
(
)
ABC
989
M
>2 &
3
MA
MB
=
73 3?
M
8 @* & 8
:
3
MA
MB
=
(
)
3
MA
MA
AB
=
+
3
3
MA
MA
AB
−
=
2
3
MA
AB
−
=
2
3
AM
AB
=
3
2
AM
AB
=
.
u
u
v
v
u
v
+
A
B
C
D
I
A
B
I
A
B
C
I
A
B
C
I
J
u
v
((((I
I
I
I
.
( )
D
( )
L
O
M
( )
P
'
M
( )
L
M
( )
D
.
'
M
M
( )
L
( )
D
.
(a
M
( )
L
!" # $ % #& '
.
(b
M
( )
D
'
O
.
(c
(
( )
L
( )
D
) '
p
( )
P
*
( )
P
.
+ ,$
'
M
'
M
-
(
)
'
p M
M
=
.
(d
,$
( )
( )
D
L
⊥
.
p
! (
( )
L
.
(II
!
.
(1
/0 1* (
:
,$
G
/0
{
}
( , ), ( , )
A
B
α
β
( )
'
p A
A
=
( )
'
p B
B
=
( )
'
p G
G
=
.
G'
/0
{
}
( ', ), ( ', )
A
B
α
β
(2
(
3" 1*
:
,$
I
3"
[ ]
AB
.
I'
/0
[
]
' '
A B
4*
( )
'
p A
A
=
( )
'
p B
B
=
(3
(
#0 1*
:
,$
AB
kCD
=
.
' '
'
'
A B
kC D
=
A'
B'
C'
'
D
" '
A
B
C
D
.
(III
(1
1
( )
L
2
(
)
L
3
(
)
L
4
(
)
L
+ 5
( )
D
(
')
D
# 6
A
B
C
D
A'
B'
C'
'
D
.
!
:
' '
'
'
AB
A B
CD
C D
=
' '
'
'
CA
C A
BD
B D
=
......
(2
1
( )
L
2
(
)
L
3
(
)
L
3
+
( )
D
(
')
D
# 6
A
B
C
A'
B'
C'
.
!
:
' '
'
'
AB
A B
AC
A C
=
' '
' '
CB
C B
AB
A B
=
......
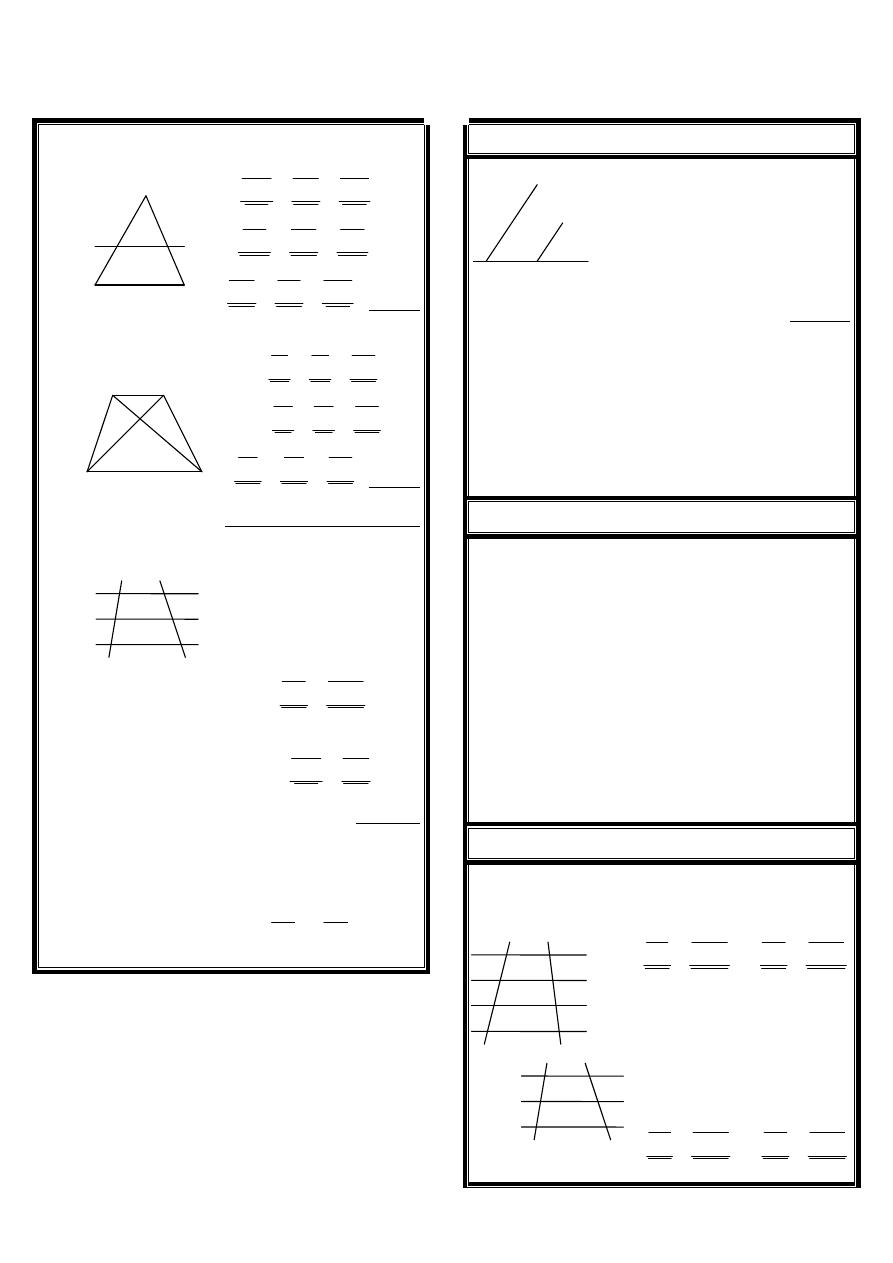
(3
(
)
ABC
77
.
( )
D
(
)
BC
(
)
AB
M
(
)
AC
N
!
:
AM
AN
MN
AB
AC
BC
=
=
AB
AC
BC
AM
AN
MN
=
=
"
MA
NA
MN
MB
NC
BC
=
≠
(4
(
)
ABCD
3* 89
I
86
.
!
:
IA
IB
AB
IC
ID
CD
=
=
IC
ID
AB
IA
IB
CD
=
=
"
BI
AI
AB
BD
AC
CD
=
≠
5
(
" # "!
:
(a
1
( )
L
2
(
)
L
3
(
)
L
3
+
( )
D
(
')
D
# 6
A
B
C
A'
B'
C'
.
,$
1
2
( ) //(
)
' '
'
'
L
L
AB
A B
AC
A C
=
.
1
2
3
( ) //(
) //(
)
L
L
L
(b
(
)
ABC
77
.
M
(
)
AB
N
(
)
AC
,$
AM
AN
AB
AC
=
.
(
) //(
)
MN
BC
"
:
(1
+":
1
;
2
;
3
;
4
< +":
0 < = 9
.
":
(5)
> !#
.
(2
+ ,$
A
B
C
D
.
AB
kCD
=
?
AB
kCD
=
A
B
C
M
N
A
B
C
D
I
A
B
C
'
A
'
B
'
C
1
(
)
L
2
(
)
L
3
(
)
L
A
B
C
'
A
'
B
'
C
1
(
)
L
2
(
)
L
3
(
)
L
'
A
'
B
'
C
'
D
A
B
C
D
( )
L
(
)
D
'
M
M
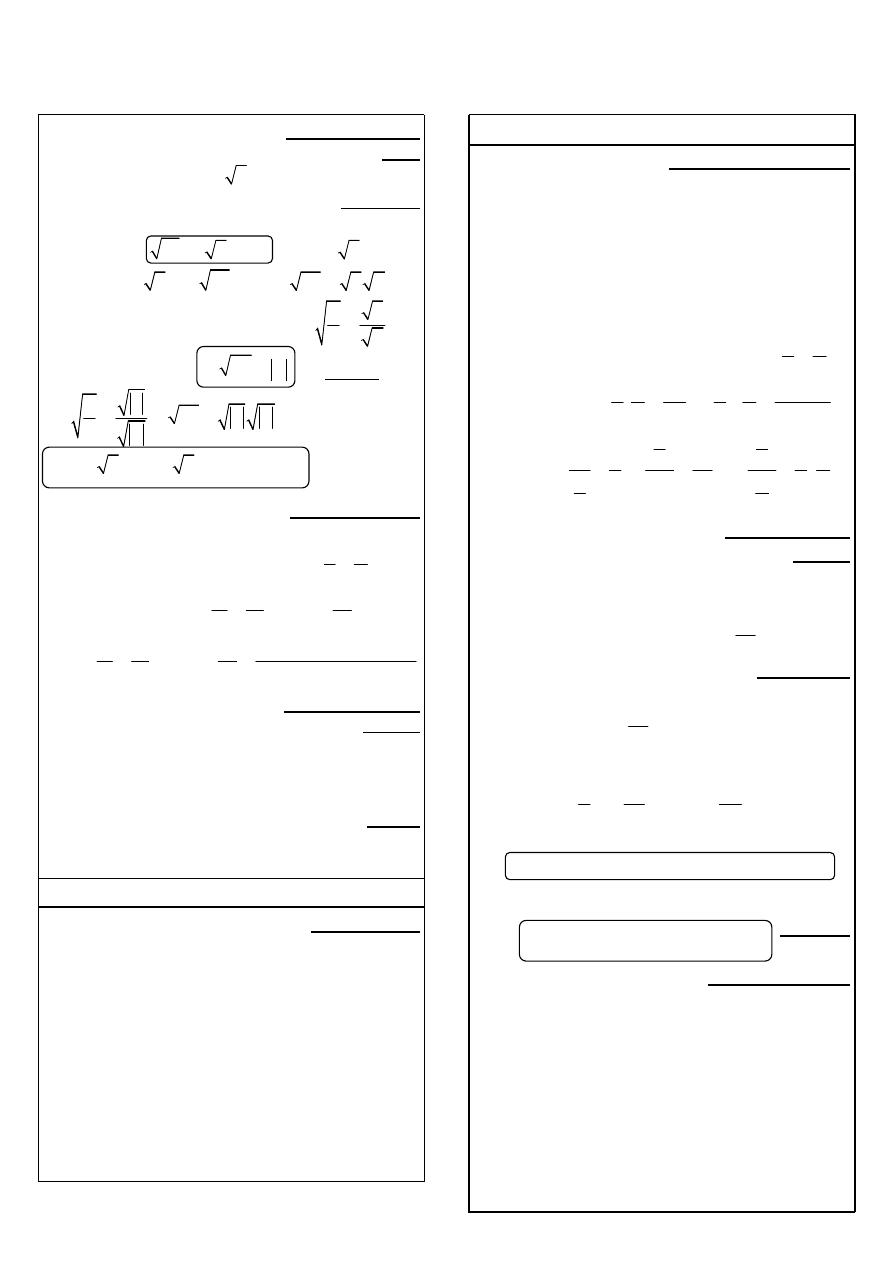
ا
ب
-
ا
IR
ب ا
IR
.
1
(
ب ا ا
IR
.
a
و
b
و
c
و
d
IR
.
(a
a
b
=
ـــــــی
a c
b
c
+ = +
(b
a
b
=
ـــــــی
.
.
a c
b c
=
(
0)
c
≠
(c
إذا آن
a
b
و
c
d
=
=
نـــــ
.
.
a c
b
d
و
a c
b d
+ = +
=
(d
.
0
a b
=
ـــــــی
0
a
=
أو
0
b
=
.
(e
.
0
a b
≠
ـــــــی
0
a
≠
و
0
b
≠
.
(g
a
c
b
d
=
ـــــــی
.
.
a d
b c
=
(
0
0)
a
وb
≠
≠
(h
a
c
ad
bc
b
d
bd
+
+ =
و
.
a c
ac
b d
bd
=
(i
a
a d
b
c
b c
d
= ⋅
و
a
a
b
c
bc
=
و
1
b
a
a
b
=
2
(
اى
IR
a
(
ی"
(
∗
0
1
a
=
(
0)
a
≠
(
∗
1
1
a
=
(
∗
. . .....
n
n fois
a
a a a
a
=
{ }
*
(
1 )
n
IN
∈
−
(
∗
1
n
n
a
a
−
=
b
(
تـــــــ%ﺥ
(a
a
و
b
*
IR
و
m
و
n
Z
.
(
∗
.
m
n
m n
a
a
a
+
=
(
∗
1
n
n
a
a
−
=
(
∗
(
)
m
n
mn
a
a
=
(
∗
(
)
.
n
n
n
ab
a b
=
(
∗
n
n m
m
a
a
a
−
=
(
∗
( )
n
n
n
a
a
b
b
=
(b
إذا آن
a
b
=
ن
2
2
a
b
=
(c
إذا آن
2
2
a
b
=
و
a
و
b
ن ةرا
a
b
=
.
(d
2
2
a
b
=
ـــــــی
a
b
=
أو
a
b
= −
.
'ـــــ(ﺡ*
أن
:
a
b
=
أن أن!" ی
2
2
a
b
=
و
a
و
b
ارة
3
(
'ت هـــــ,-
(a
2
2
2
(
)
2
a b
a
ab
b
+
=
+
+
(b
2
2
2
(
)
2
a b
a
ab
b
−
=
−
+
(c
2
2
(
)(
)
a
b
a b a b
−
= −
+
(d
3
3
2
2
3
(
)
3
3
a b
a
a b
ab
b
+
= +
+
+
(e
3
3
2
2
3
(
)
3
3
a b
a
a b
ab
b
−
= −
+
−
(f
3
3
2
2
(
)(
)
a
b
a b a
ab
b
−
= −
+
+
(g
3
3
2
2
(
)(
)
a
b
a b a
ab
b
+
= +
−
+
4
(
'",.ور ا01ا
.
ی"
a
IR
+
∈
.
د$%& 'ﺏ)ا ر*+ا
a
,د ا.ﺝ$%ا .ه
b
ي*ا
123ی
:
2
b
a
=
.
,4 و
a
b
=
.
تــــــ%ﺥ
.
(a
a
و
b
IR
+
.
(
∗
0
a
≥
(
∗
2
2
(
)
a
a
a
=
=
(
∗
ab
a b
=
(
∗
(
)
n
n
a
a
=
(
∗
a
a
b
b
=
(b
x
IR
∈
.
2
x
x
=
.
(c
إذا آن
0
ab
>
ن
:
ab
a
b
=
و
a
a
b
b
=
(d
a
IR
+
∈
2
x
a
=
ـــــــی
x
a
=
أو
x
a
= −
.
5
(
'2ﺱـــــــــ4ا
.
(a
دی$%ا نإ ل.2
a
و
b
' ' ن674
c
و
d
نآ اذإ 82 و اذإ
:
a
b
c
d
=
(b
إذا آن
:
1
2
1
2
n
n
a
a
a
b
b
b
=
=
=
ن
:
1
2
1 1
2 2
1
2
1 1
2 2
n
n
n
n
n
n
a
a
a
k a
k a
k a
b
b
b
k b
k b
k b
+
+ +
=
=
=
=
+
+ +
6
(
5 6ا ئ81ا
.
a
(
ی"
:
22د ﺡ$: ;آ
x
%ﺏ44 < ید$: ﺏ ر.=3
k
و
1
k
+
7% ی
:
1
k
x
k
≤ < +
<7د ا$%ا
k
د$%& >3=ا ئ@+ا A<ی
x
,4 و
( )
E x
k
=
أو
[ ]
x
k
=
'(ﺡ*
:
(
∗
>3=ئ ا@+ا
د$%&
x
;B )ة$ﺝ.ی ي*ا <7ا د$%ا .ه
x
.
(
∗
( )
( ) 1
E x
x
E x
≤ <
+
;
x
IR
.
(II
ــــــــ ا
ـــــــ
IR
.
1
(
تـــــــ%ﺥ
(a
(
∗
a
b
≥
ـــــــی
0
a b
− ≥
(
∗
a
b
≤
ـــــــی
0
a b
− ≤
(b
(
∗
a
b
>
ـــــــی
0
a b
− >
(
∗
a
b
<
ـــــــی
0
a b
− <
(c
(
∗
a
b
≤
7% ی
a
b
<
أو
a
b
=
.
(
∗
إذا آن
a
b
<
ن
a
b
≤
>3) ﺹD %او
.
(d
(
∗
a
b
≥
ـــــــی
a c
b
c
+ ≥ +
(
∗
a
b
>
ـــــــی
a c
b
c
+ > +
(e
(
∗
إذا آن
a
b
و
b
c
≤
≤
ن
a
c
≤
.
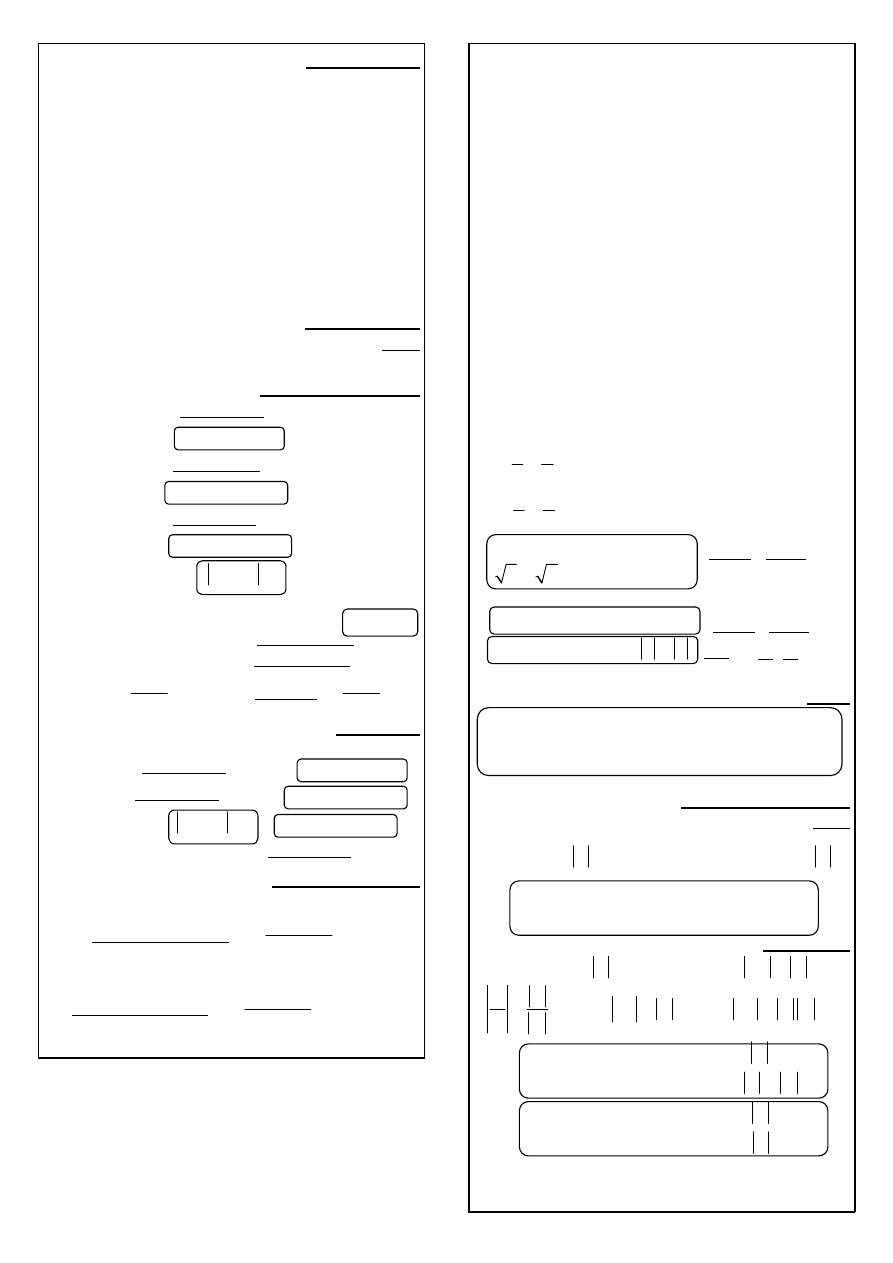
(
∗
إذا آن
a
b
و
b
c
≤
<
ن
a
c
<
.
(f
(
∗
إذا آن
a
b
و
c
d
≤
≤
ن
a c
b
d
+ ≤ +
3) ﺹD %او
>
.
(
∗
إذا آن
a
b
و
c
d
≤
<
ن
a c
b
d
+ < +
(g
(
∗
إذا آن
0
a
b
و
c
≤
≥
ن
ac
bc
≤
(
∗
إذا آن
0
a
b
و
c
≤
≤
ن
ac
bc
≥
.
(f
(
∗
إذا آن
0
0
a
b
و
c
d
≤ ≤
≤ ≤
ن
ac
bd
≤
>3) ﺹD %او
.
(
∗
إذا آن
0
0
a
b
و
c
d
≤ ≤
< <
ن
ac
bd
<
(i
0
a
>
و
0
b
>
.
(
∗
a
b
≤
ـــــــی
1
1
a
b
≥
(j
0
a
<
و
0
b
<
.
(
∗
a
b
≤
ـــــــی
1
1
a
b
≥
(k
0
a
≥
و
0
b
≥
(
∗
a
b
≤
ـــــ ی
ــ
2
2
a
b
≤
(
∗
a
b
≤
ـــــــی
a
b
≤
(l
0
a
≤
و
0
b
≤
(
∗
a
b
≤
ـــــــی
2
2
a
b
≥
(m
a
و
b
IR
a
b
≤
ـــــــی
2
2
a
b
≤
(n
ـ إذا آن
a
و
b
ارة و
0
a b
+ =
ن
0
a
=
و
0
b
=
'(ﺡ*
دی$%ا نآ اذإ
a
و
b
رن2 ، F%ﺏ)ا رو*+ا A&: نی.43ی
a
و
b
رن2 نأ !" ی
2
a
و
2
b
إرة1234و
a
و
b
G ﺙ
4ﺹIا ;%4<
(k
و
(l
.
2
(
'-. ا'.ــــــــــ ا
.
ی"
:
x
IR
.
د$%& F2&Jا F2ا
x
@) ي*ا د$%ا ه
K
ب
x
&)ف ﺏ ی%او
:
;
0
;
0
x
x
x
x
x
≥
=
−
≤
7%ی
:
(
∗
إذا آن
0
x
≥
د$%& F2&Jا F2ا ن
x
K< ه
.
(
∗
إذا آ
ن
0
x
≤
د$%& F2&Jا F2ا ن
x
K&ﺏ2 ه
.
تـــــــــــ%ﺥ
(a
(
∗
x
x
− =
(
∗
0
x
≥
(
∗
xy
x y
=
(
∗
n
n
x
x
=
(
∗
x
x
y
y
=
(b
(
∗
x
r
=
ـــــــی
x
r
=
أو
x
r
= −
.
(
∗
x
y
=
ـــــــی
x
y
=
أو
x
y
= −
.
(c
(
∗
x
r
≤
ـــــــی
r
x
r
− ≤ ≤
(
∗
x
r
≥
ـــــــی
x
r
≥
أو
x
r
≤ −
3
(
ت9ــــــــ1.ا
(a
[ ]
{
}
,
/
a b
x
IR a
x
b
=
∈
≤ ≤
(a
[ [
{
}
,
/
a b
x
IR a
x
b
=
∈
≤ <
(a
] ]
{
}
,
/
a b
x
IR a
x
b
=
∈
< ≤
(a
] [
{
}
,
/
a b
x
IR a
x
b
=
∈
< <
(a
[
[
{
}
,
/
a
x
IR x
a
+∞ =
∈
≥
(a
]
[
{
}
,
/
a
x
IR x
a
+∞ =
∈
>
(a
]
]
{
}
,
/
a
x
IR x
a
−∞
=
∈
≤
(a
]
[
{
}
,
/
a
x
IR x
a
−∞
=
∈
<
4
(
ـــــــــــ:; ا
ی"
:
وﺕت4ا Fﺕو4 ;آ
:
a
x
b
< <
و
a
x
b
≤ <
و
a
x
b
< ≤
و
a
x
b
≤ ≤
د$%& ا)PQﺕ A<ﺕ
x
K4%6
b
a
−
.
5
(
. ا'. ا
'ــــــــ,
.
(a
(i
إذا أرد أن أن
0
x
8)ی4ﺏ Fﺏ)2 FB
د$%&
x
FB$ ﺏ
r
.م2 ،
)PQ4ﺏ
0
x
x
−
$+76 و
0
0
x
x
r
≤ −
≤
(ii
إذا
أرد أن أن
0
x
طا) ﺏ Fﺏ)2 FB
د$%&
x
FB$ ﺏ
r
.م2 ،
)PQ4ﺏ
0
x
x
−
$+76 و
0
0
r
x
x
− ≤ −
≤
.
(iii
إذا أرد أن أن
0
x
د$%& Fﺏ)2 FB
x
FB$ ﺏ
r
.م2 ،
)PQ4ﺏ
0
x
x
−
$+76 و
0
r
x
x
r
− ≤ −
≤
7% ی
0
x
x
r
−
≤
.
(b
د$%& Fﺏ)2 FB د$3 نأ درأ اذإ
x
د$%ا )PQ4ﺏ م.2
x
$+76 و
a
x
b
≤ ≤
:
& أن یT474< 7ه و
:
(i
a
ه
8)ی4ﺏ Fﺏ)2ا F2ا
د$%&
x
FB$ ﺏ
r
b
a
= −
(ii
b
ه
طا) ﺏ Fﺏ)2ا F2ا
د$%&
x
FB$ ﺏ
r
b
a
= −
(iii
2
a b
+
ه
F)ﺏ2ا F2ا
د$%&
x
FB$ ﺏ
2
b
a
r
−
=
c
(
'ــــــ(ﺡ*
د$%& Fﺏ)2 FB $ی$3ﺕ ی
x
F4)ات اPQ4ا ى$ﺡإ 7ی$ Vآ اذإ ة)
:
(i
0
0
x
x
r
≤ −
≤
.ن46و
0
x
4 ﺏFﺏ)2 FB
8)ی
د$%&
x
FB$ ﺏ
r
(ii
0
0
r
x
x
− ≤ −
≤
.ن46و
0
x
طا) ﺏ Fﺏ)2 FB
د$%&
x
FB$ ﺏ
r
(iii
0
r
x
x
r
− ≤ −
≤
أو
0
x
x
r
−
≤
.ن46و
0
x
د$%& Fﺏ)2 FB
x
FB$ ﺏ
r
d
(
ي="ا یا
.
x
IR
.
(i
د$%ا
)يW%ا
(10
)
10
n
n
E
x
A< ی
8)ی4ﺏ Fﺏ)2ا F)یW%ا F2ا
د$%&
x
FB$ﺏ
10
n
−
.
(i
)يW%ا د$%ا
(10
)
1
10
n
n
E
x
+
A< ی
ﺏFﺏ)2ا Fی)W%ا F2ا
طا)
د$%&
x
FB$ ﺏ
10
n
−
.
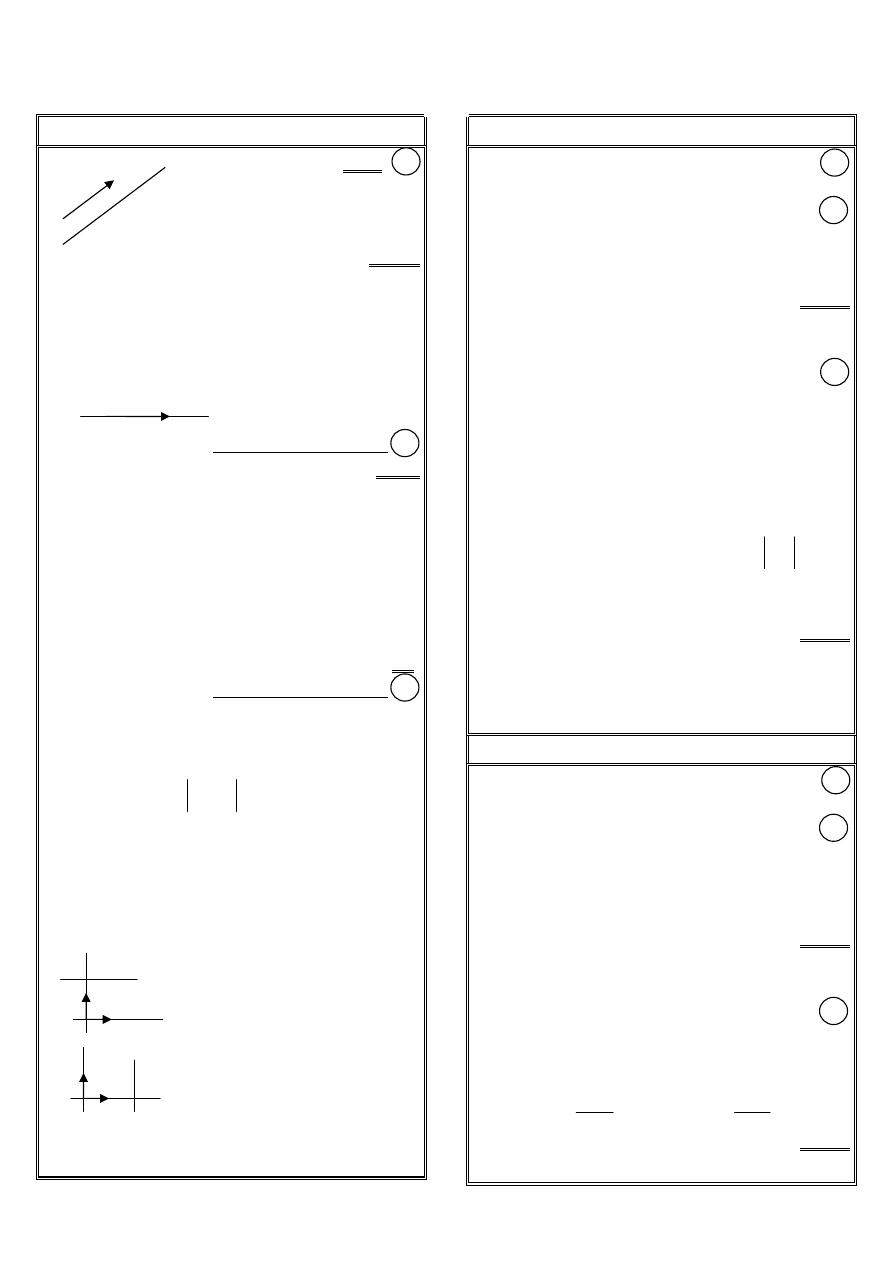
I
1
( )
,
i j
i
j
.
2
( )
,
B
i j
=
.
u
!"
u
xi
y j
= +
#
( )
,
x y
# $#%
u
&
B
( )
,
u x y
x
u
y
.
!"
:
# '$#% #(%
u
&
.
( )
,
B
i j
=
# )
u
*
i
j
.
#(%
u
xi
y j
= +
$#% +,
u
-
( )
,
x y
( )
,
u x y
.
3
( )
,
B
i j
=
.
(a
( )
1, 0
i
( )
0,1
j
b
(
# /
( )
,
u x y
(
)
,
v x y
′ ′
(
)
,
u
v x
x y
y
′
′
+
+
+
(
)
,
u
v x
x y
y
′
′
−
−
−
(
)
,
u
x
y
α α α
c
(
# /
( )
,
u x y
(
)
,
v x y
′ ′
(*
#
u
v
&
B
.
/#
1 2(#
( )
det
,
u v
! 3/#
:
( )
det
,
x
x
u v
xy
yx
y
y
′
′
′
=
=
−
′
(*
#
u
v
#(% , #(%
( )
det
,
0
u v
≠
!"
:
1
(
i
j
.
(*
#(%
0
i
j
α β
+
=
+,
0
α β
= =
(*
#(%
i
j
i
j
α β
α
β
′
′
+
=
+
+,
α α
′
=
β β
′
=
.
2
(
' #(%
A
B
C
5$
# +, 6
AB
AC
.
!
.
II
$
1
6!$ !/
( )
, ,
o i j
6
o
i
j
.
2
)!/# /
( )
, ,
R
o i j
=
M
# 7#
OM
!"
OM
xi
y j
= +
#
( )
,
x y
# $#%
M
)!/!
R
( )
,
M x y
x
M
y
!"
:
'$#% #(%
M
!/!
)
( )
, ,
o i j
)
OM
*
i
j
.
#(%
OM
xi
y j
= +
+,
( )
,
M x y
.
3
)!/# /
( )
, ,
R
o i j
=
.
# /
(
)
,
A
A
A x
y
(
)
,
B
B
B x
y
(*
(
)
,
B
A
B
A
AB x
x
y
y
−
−
.
(*
#(%
I
38
[ ]
AB
# '$#% +,
I
-
:
,
2
2
A
B
A
B
I
I
y
y
x
x
y
x
+
+
=
=
!"
:
# ' #(%
A
B
C
+,
6!$#
(
)
,
,
A AB AC
)!/
.
III
1
3/
:
A
u
/
# )#
A
1#
u
# " -
M
! #
AM
u
1
( )
,
D A u
( )
D
.
!"
:
(a
( )
,
M
D A u
∈
/
AM
u
.
(b
( )
D
)
.
#
( )
∆
( )
D
.
(c
)#
( )
AB
A
1
AB
.
2
% &'
.
($
:
( )
D
# )#
(
)
0
0
,
A x y
1#
( )
,
u a b
)! 2# $
( )
D
-
(
)
t
IR
∈
0
0
x
x
at
y
y
bt
= +
=
+
:
( )
D
/ 2## $# #(-
( )
D
# # " -
!" $##
(
)
1 3 , 2
4
t
t
+
−
6
t
IR
∈
.
9" ! /
t
IR
# !" 8
'$#
( )
D
.
"'
1
t
=
2
4
y
x
= −
=
(%
(
) ( )
4, 2
M
D
− ∈
.
3
) $
.
(a
( )
D
# )#
(
)
0
0
,
A x y
1#
( )
,
u a b
/ !" 8!
( )
D
! :
:
( ) ( )
,
M x y
D
∈
/
(
)
det
,
0
AM u
=
/
0
0
0
x
x
a
y
y
b
−
=
−
/
(
) (
)
0
0
b x
x
a y
y
−
−
−
!" / !" 8 )
0
Ax
By
C
+
+ =
:
(
) ( )
,
0, 0
A B
≠
/ -
( )
D
( )
:
0
D
Ax
By
C
+
+ =
.
(b
"# /
( )
:
0
D
a x
b y
c
+
+ =
( )
D
1 )
(
)
,
u
b a
−
.
(c
(*
#(%
( )
D
#
# +, 8,;#
( )
1, 0
i
!" 1/ 1
y
c
=
.
(*
#(%
( )
D
#
# +, #;#
( )
0,1
j
!" 1/ 1
x
c
=
.
(*
# )# - 8,;#
( )
0, 0
o
1#
( )
1, 0
i
1/
0
y
=
.
u
i
A
(
)
D
i
A
B
( )
D
O
i
j
c
(
)
D
O
i
j
c
(
)
D
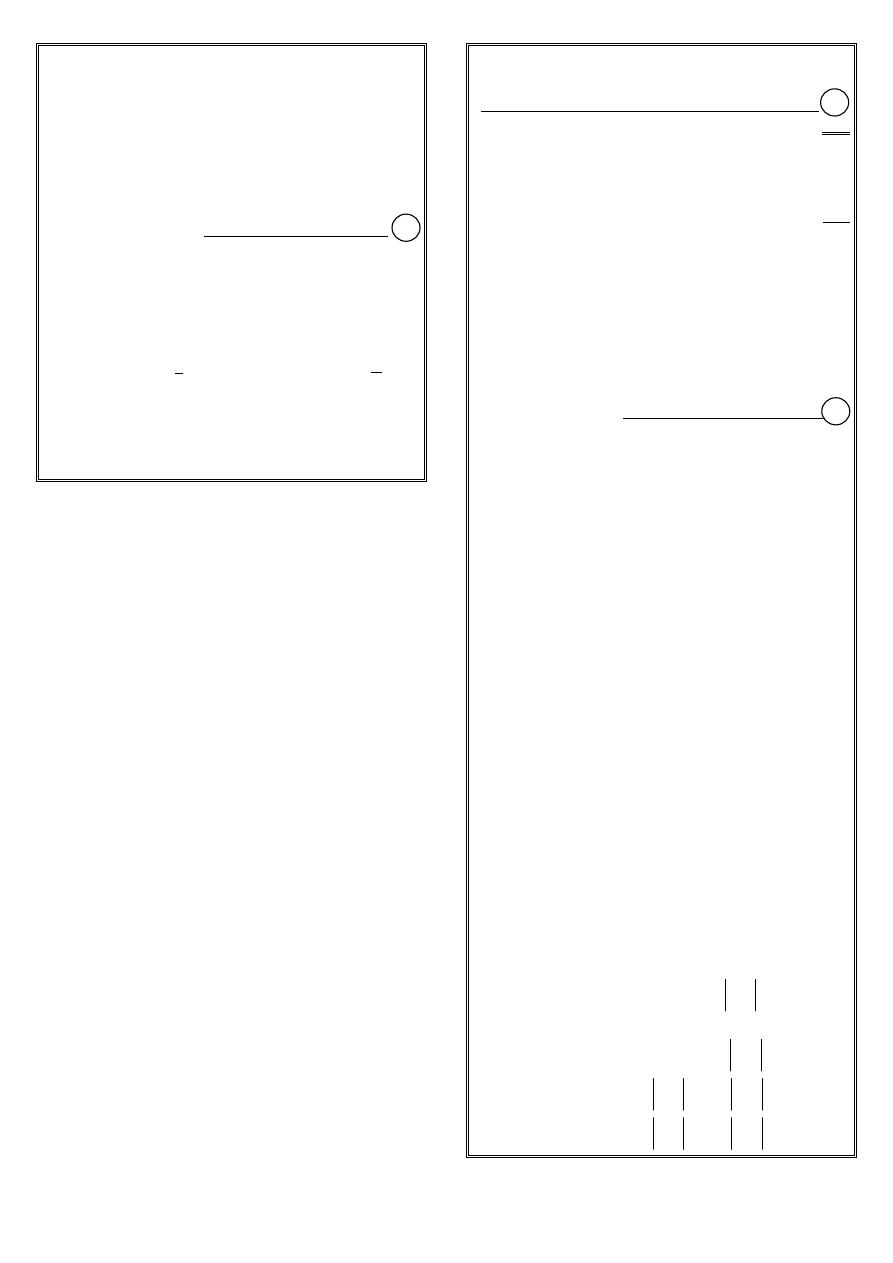
(*
# )# - #;#
( )
0, 0
o
1#
( )
0,1
j
1/
0
x
=
.
4
)$ % &' * + ) $
.
' ,
:
(a
)# /
( )
:
2
1
0
x
y
∆
+
− =
2# $ !" 8!
( )
∆
<
( )
∆
:
y
t
=
x
t
=
<=#
.
"'
:
:9
y
t
=
(%
2
1
0
x
t
+ − =
/
1 2
x
t
= −
(%
( )
1 2
x
t
y
t
= −
∆
=
.
(b
)# /
( )
( )
( )
1 2 1
:
3
2
x
t
y
t
= +
∆
= +
/ !" 8!
( )
∆
<
t
,
( )
1
( )
2
7<;# , >/
.
5$
:
( )
2
3
t
y
= − −
, >/
( )
1
1 2
6
x
y
= −
−
(%
( )
:
2
5
0
x
y
∆
+
+ =
.
5
- .
:
(a
# : #
( )
∆
( )
′
∆
?#
!
:
(i
#(%
( )
0
0
:
x
x
at
y
y
bt
= +
∆
=
+
@
( )
1
1
:
x
x
a t
y
y
b t
′ ′
= +
′
∆
′ ′
= +
A# )
( )
0
1
0
1
x
at
x
a t
S
y
bt
y
b t
′ ′
+ = +
′ ′
+ = +
(*
#(%
( )
S
# 5
.
t
=
.
t
′ =
+,
( )
∆
( )
′
∆
>/ $#% !" 8 , /
t
$ ,
( )
∆
.
(*
A! #(%
( )
S
+, !# 1 *
( ) ( )
′
∆ = ∆
.
(ii
#(%
( )
1
:
1 2
x
t
y
t
= +
∆
= − +
( )
: 2
3
1
0
x
y
′
∆
−
+ =
A# )
( )
( )
( )
( )
1
1
1 2
2
2
3
1
0 3
x
t
S
y
t
x
y
= +
= − +
−
+ =
>/
x
y
,
( )
3
# / !" 8
(*
, /# B( #(%
( )
∆
( )
′
∆
, /
.
>/
t
,
( )
1
( )
2
!" 8
.
(*
+, * /# ' #(%
( )
∆
( )
′
∆
/C
.
(*
+, !# 1 * /# ' #(%
( ) ( )
′
∆ = ∆
.
(iii
#(%
( )
:
2
1
0
x
y
∆
+
− =
( )
: 2
1
0
x
y
′
∆
− + =
A# )
( )
2
1
0
2
1
0
x
y
S
x
y
− + =
+
− =
'* D
(i
.
(b
# /
( )
( )
:
0
:
0
ax
by
c
a x
b y
c
∆
+
+ =
′
′
′
′
∆
+
+ =
(i
#(%
0
a
b
a
b
≠
′
′
+,
( )
∆
( )
′
∆
A# /
:# !" 8!
.
(ii
#(%
0
a
b
a
b
=
′
′
+,
( ) ( )
//
′
∆
∆
(*
#(%
0
a
c
a
c
≠
′
′
0
b
c
b
c
≠
′
′
+,
( ) ( )
//
′
∆
∆
C
/
.
(*
#(%
0
a
c
a
c
=
′
′
0
b
c
b
c
=
′
′
+,
( ) ( )
′
∆ = ∆
.
(c
#(%
( )
∆
( )
′
∆
#
<
u
( )
∆
v
( )
′
∆
( )
det
,
u v
(i
#(%
( )
det
,
0
u v
=
+,
( ) ( )
//
′
∆
∆
(ii
#(%
( )
det
,
0
u v
≠
+,
( )
∆
( )
′
∆
/
.
(d
#(%
( ) ( )
//
′
∆
∆
-; 2 +,
<E
.
6
/0 $
(a
#(%
( )
∆
1/ +, #=# 2#
!"
y
mx
p
=
+
/# /# B(-
8<#
.
)# 1# /# /#
( )
∆
.
(b
( )
∆
1 )
( )
,
u a b
:
0
a
≠
)
/
(
)
y y
ο′
//
( )
∆
(
1# /#
( )
∆
-
b
m
a
.
(c
# /
( )
: y
mx
p
∆
=
+
( )
: y
m x
p
′
′
′
∆
=
+
( ) ( )
//
′
∆
∆
, #(%
m
m
′
=
تدو ا
-
ات
ﻥا ر ا ﻡ تااو تدا
(I
تدو ا
1
ﺕ
x
»
ا
( )
1
1
1
0
....
n
n
n
n
P x
a x
a
x
a x
a
−
−
=
+
+ +
+
1
0
,....,
,
n
a
a a
أاد و
0
n
a
≠
(*
( )
P x
أو
P
ﺕ ودی ار
n
و
deg P
n
=
.
(*
اد!ا
1
0
,....,
,
n
a
a a
ودی"ا ت$% ﺕ
P
.
(b
& %'ﺕ$% ( )%آ اذإ -.و اذإ & یدو ن0ﺕ
.
(c
در%' ) &ا یدو"ا
.
(d
ود"ا ت$% )%آ اذإ -.و اذإ ن% یو% ن% یود ن0ﺕ
ا12
وی% ر
.
(e
ودی ار3آ
1
:
( )
P x
ax b
=
+
ﺕ ا
.
(f
ودی ار3آ
2
:
( )
2
P x
ax
bx
c
=
+ +
7$7 ﺕ
ود"ا
.
2
(a
(
)
deg
sup(deg , deg
)
P
Q
P
Q
+
≤
(b
(
)
deg
sup(deg , deg
)
P
Q
P
Q
−
≤
(c
(
)
deg
deg
deg
P Q
P
Q
⋅
=
+
3
!" #$ا
x
α
−
(a
( )
P x
ودی
.
ل إن اد0
α
ودی"9 ر:
P
2; أو
ودی"9
P
إذا آ-.و اذإ
ن%
( )
0
P
α
=
(b
( )
P x
ودی
.
( )
P x
9 ا3ﺕ
x
α
−
ن%آ اذإ -.و اذإ
( )
0
P
α
=
.
ﺡ&ﻡ
:
(a
3 ه=" نأ %درأ اذإ
( )
P x
ا3ﺕ
9
x
α
−
م0
ب%"ﺏ
( )
P
α
.
(*
ن%آ اذإ
( )
0
P
α =
نA.
( )
P x
9 ا3ﺕ
x
α
−
.
(*
ن%آ اذإ
( )
0
P
α
≠
نA.
( )
P x
9 ا3ﺕ B
x
α
−
.
(b
3 ه=" نأ %درأ اذإ
( )
P x
9 ا3ﺕ
x
α
+
م0
ب%"ﺏ
( )
P
α
−
.
II
(
ر ا ﻡ تااو تدا
II
.
1
اد*ﺡ
2
0
ax
bx
c
+
+ =
د%ا
( )
2
:
0
E
ax
bx
c
+ + =
0
a
≠
د%ا 3 3أ
( )
E
ب اد%"ﺏ م0
2
4
b
ac
∆ =
−
(*
اد
∆
د% اC ی
( )
E
.
(*
ن%آ اذإ
0
∆
〉
د%ا نA.
( )
E
% ه29 D 9 3ﺕ
.
2
1
2
2
b
b
x
x
a
a
− + ∆
− − ∆
=
=
(*
ن%آ اذإ
0
∆ =
د%ا نA.
( )
E
وا$ 3ﺕ
2
b
x
a
−
=
(*
ن%آ اذإ
0
∆
〈
د%ا نA.
( )
E
3 أي3ﺕ B
.
ﺡ&ﻡ
:
(a
د%ا
( )
2
:
2
0
E
ax
b x
c
′
+
+ =
)
G&ی
2
b
b
′
=
(
H D اC ا3
′
∆
Cض ا0
∆
.
%&وی
2
b
ac
′
′
∆ =
−
(*
ن%آ اذإ
0
′
∆
〉
د%ا نA.
( )
E
% ه29 D 9 3ﺕ
.
2
1
b
b
x
x
a
a
′
′
′
′
− + ∆
− − ∆
=
=
(*
ن%آ اذإ
0
′
∆ =
د%ا نA.
( )
E
وا$ 3ﺕ
b
x
a
′
−
=
(*
ن%آ اذإ
0
′
∆
〈
د%ا نA.
( )
E
3 أي3ﺕ B
.
(b
ن%آ اذإ
2
α
∆ =
9 3د ﺕ%ا نA.
2
1
2
2
b
b
x
x
a
a
α
α
− +
− −
=
=
2
ﺙ&ﺙ *ﺕ
دو ا
ود"ا 7$7
( )
2
P x
ax
bx
c
=
+
+
(
0
a
≠
3 ﺕ3أ
( )
P x
د%ا 3"ﺏ م0
( )
2
0
E ax
bx
c
+ + =
(*
ن%آ اذإ
0
∆
〉
د%ا نA.
E
9 3ﺕ
1
x
و
2
x
3ن ﺕ0یو
( )
P x
0 ه
( ) (
)(
)
1
2
P x
a x
x
x
x
=
−
−
(*
ن%آ اذإ
0
∆ =
د%ا نA.
( )
E
وا$ 3ﺕ
0
x
ن0یو
3ﺕ
( )
P x
0 ه
( ) (
)
2
0
P x
a x
x
=
−
(*
ن%آ اذإ
0
∆
〈
د%ا نA.
( )
E
ودی"او 3 %' 1
( )
P x
3 ﺕ%' 1
.
ﺡ&ﻡ
:
ن%آ اذإ
0
∆ =
"ن اA.
ودی
( )
P x
%ﺏ ه%J ةر%
.
3
دو ا ﺙ&ﺙ ةر-إ
.
ودة"ا
(
)
( )
2
0
a
P x
ax
bx
c
≠
=
+
+
رة%Lإ
دراﺱ
3 أ
( )
P x
3" ﺏ
م0
د%ا
( )
2
:
0
E
ax
bx
c
+ + =
(*
ن%آ اذإ
0
∆
〉
د%ا نA.
( )
E
29 D 9 3 ﺕ
2
1
x
وx
رة%Lإ ن0ﺕو
( )
P x
G ه
(*
ن%آ اذإ
0
∆ =
د%ا نA.
( )
E
وا$ 3ﺕ
0
x
و
ن0ﺕ
رة%Lإ
( )
P x
G ه
:
(*
ن%آ اذإ
0
∆
〈
د%ا نA.
( )
E
رة%Lإ ن0ﺕو 3 %' 1
( )
P x
Gه
:
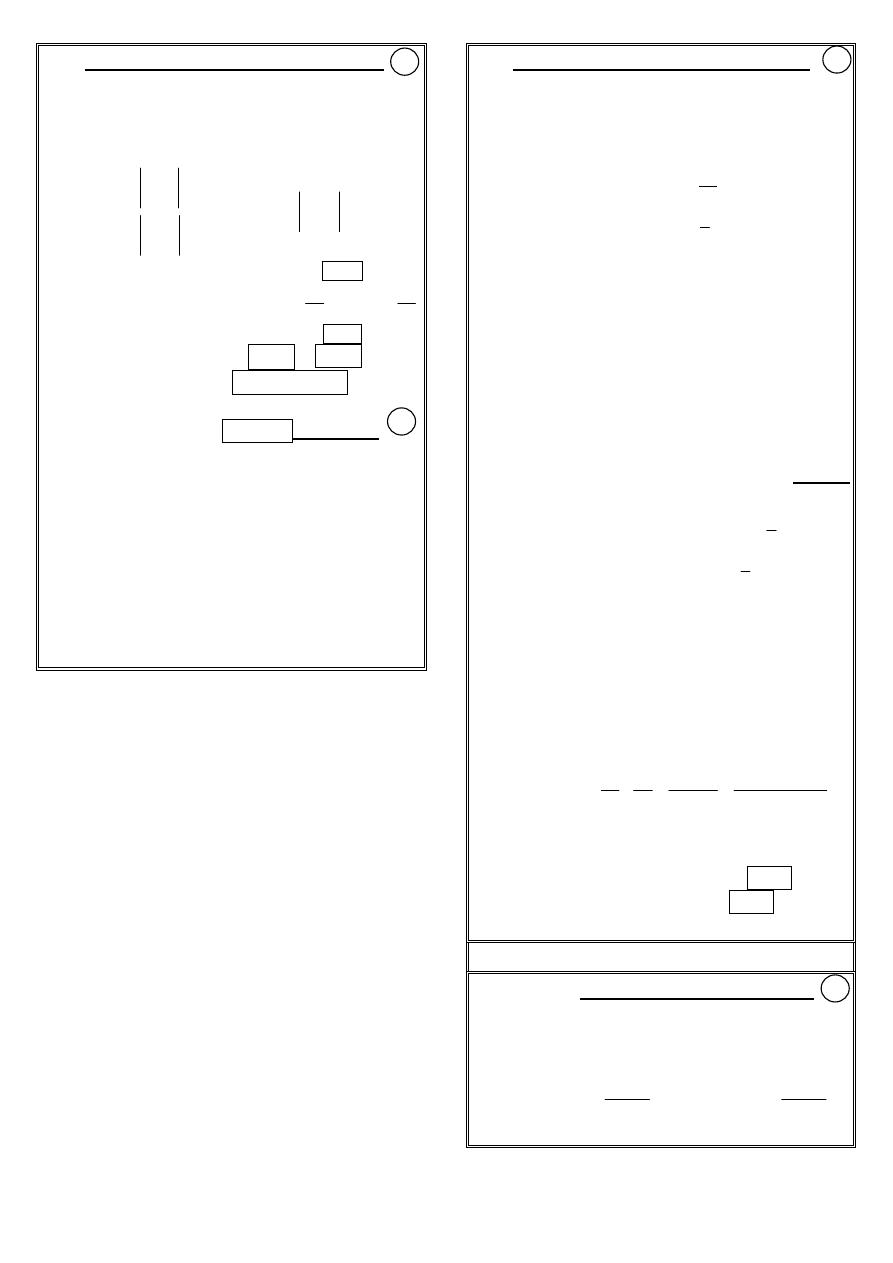
2
x
2
ax
bx
c
+
+
a
a
a
0
0
1
x
2
x
x
2
ax
bx
c
+
+
a
a
0
x
x
0
2
ax
bx
c
+
+
a
x
−∞
+∞
4
ر ا ﻡ دﻡ ير ءا و ع12ﻡ
II
.
(a
د%ا
( )
2
:
0
E
ax
bx
c
+
+ =
(*
د%ا نأ نأ %درأ اذإ
( )
E
ب%"ﺏ م0 9 3ﺕ
∆
Nو
0
∆ ≥
.
(*
د%ا 3 نوﺏ 9"ا یذ%ه ءاو ع0N ب% ی
% اQH ال% ﺱ%ﺏ
1
2
1
2
b
x
x
a
c
x x
a
−
+
=
⋅ =
(b
د ار% ی"ﺕ %درأ اذإ
II
ن0ی
و
β α
%' 9
.
ب%"ﺏ م0
α β
+
و
αβ
N
S
α β
+ =
و
P
α β
⋅ =
Gد ه%ا R:ه ن0ﺕو
2
0
x
Sx
P
−
+ =
(c
S& ا
3
% أرد
إذا
x
y
S
x y
P
+ =
⋅ =
3" ﺏ
م0
د%ا
2
0
t
St
P
− + =
ن%آ اذإ
1
x
و
2
x
نA. 9"ا %ه
1
2
x
x
y
x
≡
=
أو
2
1
x
x
y
x
=
=
(
) (
)
{
}
1
2
2
1
,
,
,
S
x x
x x
=
ﺡ&ﻡ
:
(1
و
β
α
د%ا G9
2
0
ax
bx
c
+ + =
.
أنT9
b
a
c
a
α β
αβ
+ = −
=
9 ي0 "ی ب% %درأ اذإ
و
β
α
ول%"
إ
ر%'U
α β
+
و
αβ
.
9Vأ
(* :
(
)
2
2
2
2
α
β
α β
αβ
+
=
+
−
(*
(
)
(
)
(
) (
)
(
) (
)
3
3
2
2
2
2
2
α
β
α β α
β
αβ
α β α β
αβ αβ
α β α β
αβ
+
=
+
+
+
=
+
+
−
+
=
+
+
−
(*
(
)
( )
2
2
2
2
2
2
2
2
2
1
1
α β
αβ
α
β
α
β
α β
αβ
+
−
+
+
=
=
.
2
(
1
x
و
2
x
%Vد ار ا% G9
.
دراﺱ3أ
رة%Lإ
1
x
و
2
x
ب%"ﺏ م0
1
2
x
x
+
و
1
2
x
x
⋅
.
(*
ن%آ اذإ
1 2
0
x x 〈
ن أ ادA.
1
x
و
2
x
%ﺥ ﺱXاو 0
.
(*
ن%آ اذإ
1 2
0
x x 〉
نA.
1
x
و
2
x
Gرة وه%LYا 12 %'
رة%Lإ
1
2
x
x
+
.
III
(
ا
ــــ
45ت ا
1
ر ا ﻡ تدا
I
1627
:
د%ا
( )
1
0
ax
by
c
+
+ =
أ ا
دی
a
أو
b
Z
م&
.
د%ا 3 3أ
( )
1
"
x
B ﺏ
y
ن%آ اذإ
0
a
≠
أو
"
y
ﺏ
B
x
ن%آ اذإ
0
b
≠
.
ن%آ اذإ $V
0
a
≠
N
by
c
x
a
− −
=
إذن
,
/
by
c
S
y
y
a
− −
=
∈
»
2
1627 و8ا ر ا ﻡ دﻡ ﻥ
.
S& ا
( )
ax by
c
S
a x b y
c
+
=
′
′
′
+
=
اد!ا
a
و
b
و
a
′
و
b
′
& %'9) آ
.
S& ا3 3أ
( )
S
% دات ا"ا ب%"ﺏ م0
.
a
b
ab
a b
a
b
′
′
∆ =
=
−
′
′
x
y
c
b
cb
c b
c
b
a
c
ac
a c
a
c
′
′
∆ =
=
−
′
′
′
′
∆ =
=
−
′
′
(a
ن%آ اذإ
0
∆ ≠
:
وا$ 3ﺕ S&ا نA.
.
( )
{
}
,
y
x
S
x y
y
x
∆
∆
=
=
=
∆
∆
b
(
ن%آ اذإ
0
∆ =
:
(*
ن%آ اذإ
0
x
∆ ≠
أو
0
y
∆ ≠
S&ن اA.
( )
S
3 %' 1
s
= ∅
(*
ن%آ اذإ
0
0
y
x
و
∆ =
∆ =
S&ن اA.
( )
S
إى\.%ﺕ
د%ا
.
3
- إ
ـــــــــ
رة
ax by
c
+
+
رة%Lإ
دراﺱ
3 أ
ax by
c
+
+
0
ء%]Aﺏ
م
T ا
( )
:
0
D
ax by
c
+
+ =
T ا
( )
D
ى0 ا Tی
( )
P
ى0 G2H إ
( )
( )
2
1
P
وP
.
%&^0 إذا
y
وx
J ت أي%7اAﺏ
( )
1
P
%&A.
9 3H"
ﺏ%7 ةر%Lإ
.
%&^0 وإذا
y
وx
J ت أي%7اAﺏ
( )
2
P
9 3H" %&A.
ﺏ%ا ةر%LYا 1 ةر%Lإ
.
ض0 ةر%LYا R:ه .و
y
وx
J ت%7اAﺏ
( )
1
P
أو
( )
2
P
ت%7اإ ةد% :ﺥ_
θ
Gه
0
0
y
وx
=
=
.
ا ب ا
(I
1
(
(
)
, ,
o i j
U
o
1
.
( ) ( ) (
)
1, 0 ,
0,1 ,
1, 0
A
B
C
−
a
(
M
U
.
α
!
"
AM
(*
$ !
"%
AOM
rad
α
)
α
(
(*
$ '( !
α
)* + "% ,( "%
.
b
(
:
"% +
AOB
AOC
( -
+
2
2 .1 2
R
π
π
π
=
=
+ *$
2
2
π π
=
" ! *$
AC
π
"% .
AOC
π
" !
AB
2
π
*$
"%
AOC
rad
π
" !
AB
2
π
"% *$
AOB
2
π
.
c
(
/ 0(
u
, , , ,
,
S R Q P N M
1+
:
6
AO M
π
=
3
4
AON
π
=
3
3
AOP
π
=
3
2
3
AOQ
π
=
3
4
AOR
π
=
3
5
6
AOS
π
=
.
2
(
.
%4 5 " 6( + 7
:
180
200
x
y
z
π
=
=
1+
x
"
5
.
y
"
.
z
"
.
:
8 "%
200
,180 ,
gra
rad
ο
π
.
3
(
.
( )
C
o
R
,
B A
)*
.
(*
% /8 9 6 :5
.
(*
α
"%
AOB
l
" !
AB
S
, ; +8
l
R
α
=
2
1
2
S
R
α
=
II
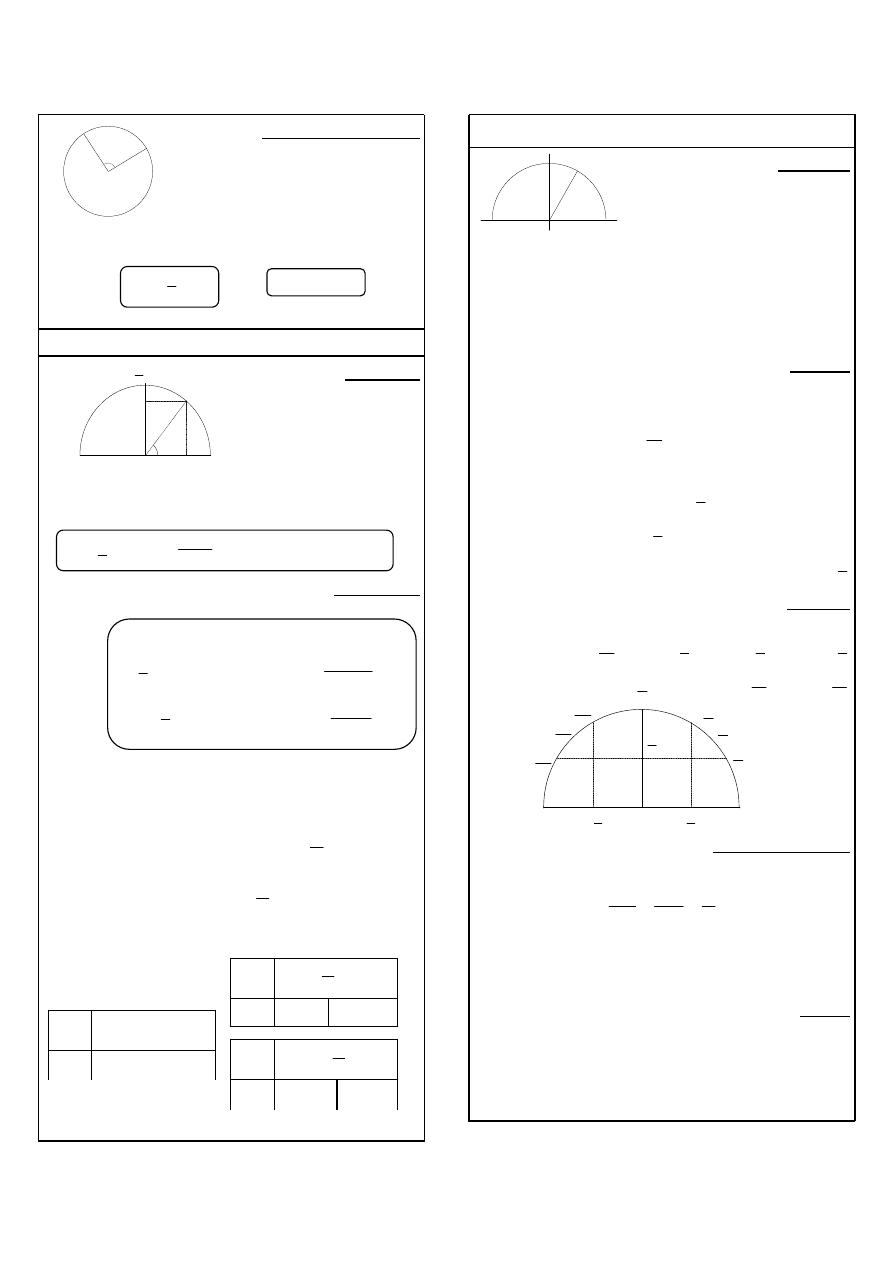
! " #$$ % & ' (
0
π
1
(
)%
:
x
1+ +
0
x
π
≤ ≤
M
U
1+
" !
AM
x
AOM
xrad
=
.
a
!<(
M
b
(
.
cos x
a
=
sin x
b
=
sin
tan
cos
x
x
x
=
2
x
π
≠
2
(
"*
:
(a
2
2
cos
sin
1
(*
x
x
+
=
2
2
1
1 tan
(*
cos
x
x
+
=
!
2
x
π
≠
sin
tan
(*
cos
x
x
x
=
!
2
x
π
≠
(b
1 cos
1
x
− ≤
≤
0
sin
1
x
≤
≤
(c
(
∗
sin
0
x
≥
!
0
x
π
≤ ≤
(
∗
*$
0
2
x
π
≤ ≤
=<
cos
0
x
≥
(
∗
*$
2
x
π
π
≤ ≤
=<
cos
0
x
≥
(
∗
tan x
cos x
(d
A
B
C
M
O
1
1
-1
A
M
1
1
-1
0
x
a
b
2
π
π
x
−
+
cosx
0
0
2
π
π
x
−
+
+
tanx
0
2
π
π
x
+
+
sinx
0
π
0
0
A
B
O
l
R
α
0
6
π
4
π
2
π
3
π
π
2
3
π
5
6
π
3
4
π
1
2
1
2
−
1
2
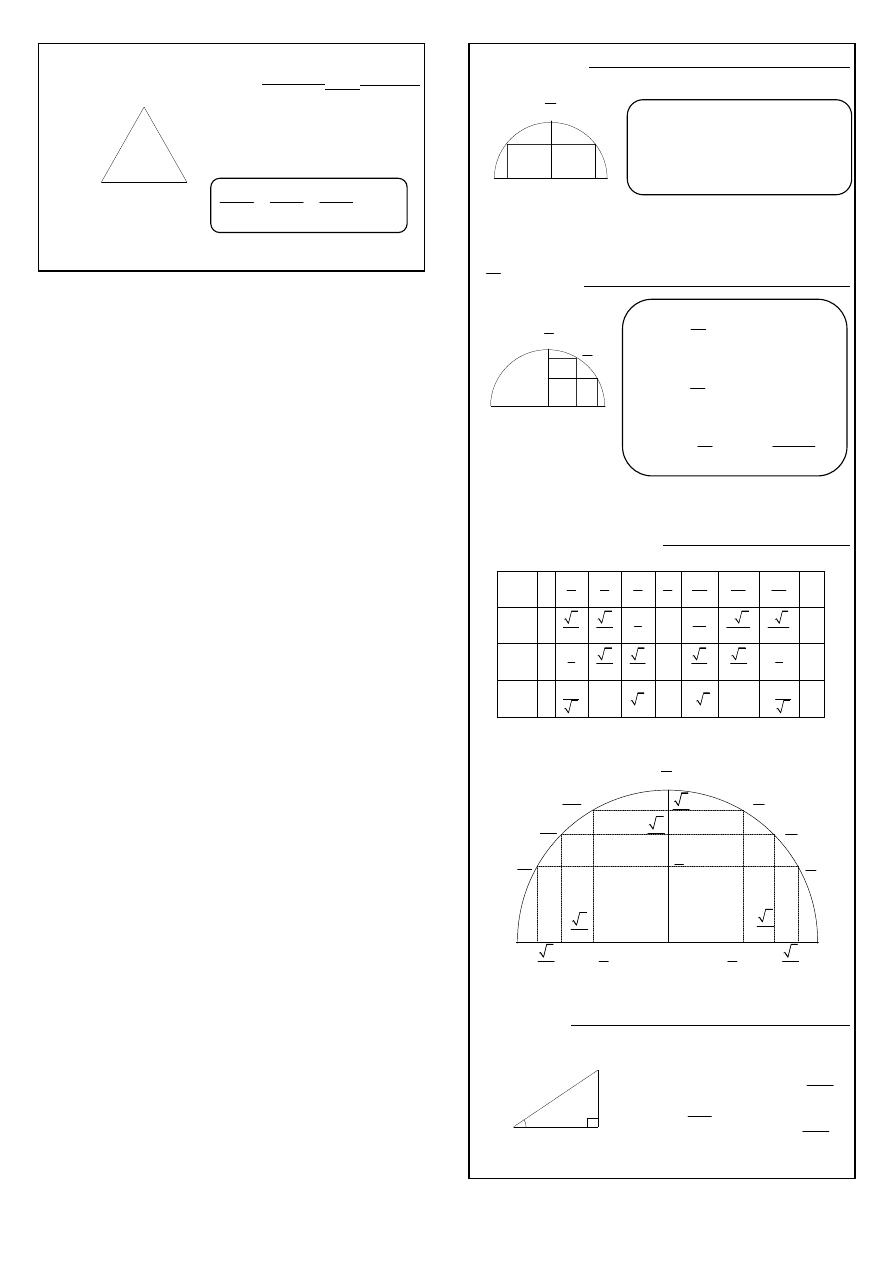
3
(
%& & ' ( ! %
x
x
π
−
(
)
cos
cos
(
x
x
a
π
−
= −
(
)
sin
sin
(
x
x
b
π
−
=
(
)
tan
tan
(
x
x
c
π
−
= −
4
(
%& & ' ( ! %
x
2
x
π
−
cos
sin
(
2
x
x
a
π
−
=
sin
cos
(
2
x
x
b
π
−
=
1
tan
(
2
tan
x
c
x
π
−
=
5
(
+, ' (
6
(
- .& #/ %
(a
(
)
ABC
< -% >>
B
AB
Cos A
AC
BC
Sin A
AC
=
=
BC
Tan A
AB
=
b
(
+
Sinus
.& #/
(
)
ABC
>>
R
. + ;
2
AB
AC
BC
R
SinC
SinB
Sin A
=
=
=
0
x
2
π
x
π
−
π
0
0
x
2
x
π
−
2
π
π
A
B
C
ˆ
A
A
B
C
1
0
-1
1
0
π
1
2
2
2
2
π
1
2
4
π
2
3
π
2
2
1
2
3
2
6
π
2
2
3
2
3
2
3
π
3
4
π
5
6
π
π
5
6
π
3
4
π
2
3
π
2
π
3
π
4
π
6
π
0
x
3
2
−
2
2
−
1
2
−
0
1
2
2
2
3
2
1
cos
x
0
1
2
2
2
3
2
1
3
2
2
2
1
2
0
sin
x
0
1
3
−
1
−
3
−
3
1
1
3
0
tan
x
1
−
×
اوال اد
(I
ا
1
(
f
f
D
2
(
:
( )
( )
( )
p x
f x
Q x
=
( )
f x
! "# $%& "# &
( )
0
Q x
≠
.
( )* +%
( )
0
Q x
=
,
}
( -./
{
f
D
= −
R
3
(
:
( )
( )
f x
P x
=
( )
f x
! "# $%& "# &
( )
0
P x
≥
0# 1 +%
( )
P x
,
)
23& 456 7
(
( )
0
P x
≥
f
D
=
(II
دا زوﺝ دا د
.
1
(
f
89 +%
f
D
) : ;%89
x
<
f
D
,
f
x
D
− ∈
=>* +% ?
(
)
f
x
−
.
(
∗
@ "#
(
)
( )
f
x
f x
− =
A&
f
3@B
.
(
∗
@ "#
(
)
( )
f
x
f x
− = −
A&
f
&
.
C/D
(a
& 5 3@B 5 5 : < E
.
(b
(
)
n
n
n
x
زوﺝn
x
x
ديn
−
=
−
x
x
− =
2
(
f
F8,( ! "# $%& "#
f
C
G H>, )I 9
J3
.
(3
f
F8,( ! "# $%& "#
f
C
) H>, )I 9
K. (
.
(III
ات دا أو رﺕ دا!ﺕ
.
1
(
!
f
- L.
I
M9
x
y
<
I
N3*
x
y
<
%
( )
f x
( )
f y
.
(
∗
@ "#
( )
( )
f x
f y
≤
A&
f
L.
I
.
(
∗
@ "#
( )
( )
f x
f y
<
A&
f
L. OP
I
.
(
∗
@ "#
( )
( )
f x
f y
≥
A&
f
L. 3QP,
I
.
(
∗
@ "#
( )
( )
f x
f y
>
A&
f
L. OP 3QP,
I
.
(
∗
@ "#
( )
( )
f x
f y
=
A&
f
L. 9I
I
.
2
(
!
f
- L.
I
M9
x
y
<
I
N3*
x
y
≠
RS9 - =>* +%
( )
( )
( , )
f x
f y
T x y
x
y
−
=
−
T 0# U
.
(
∗
@ "#
( , )
0
T x y
≥
A&
f
L.
I
.
(
∗
@ "#
( , )
0
T x y
>
A&
f
L. OP
I
.
(
∗
@ "#
( , )
0
T x y
≤
A&
f
L. 3QP,
I
.
(
∗
@ "#
( , )
0
T x y
<
A&
f
L. OP 3QP,
I
.
(
∗
@ "#
( , )
0
T x y
=
A&
f
L. 9I
I
.
3
(
" #$%
f
&
-V L.
I
L. 3QP, : W! "#
I
.
'()
(a
f
L.
I
X
f
C
Y ZQ
I
< [89 ,
\ 3 ] >3
(b
f
L. 3QP,
I
X
f
C
-V Y ^B,
I
[89 ,
\ 3 ] >3 <
(c
f
L. 9I
I
X
f
C
G ZB K3%9> < H
-V Y )3&
I
.
#!*
,
f
< )! L.
[ ]
1, 3
[ ]
5, 9
L. 3QP,
[ ]
3, 5
4RS9 -@ L > -@ Y _ `a.
.
4
(
!
( )
f x
ax b
=
+
(a
! "#
0
a
>
A&
f
L.
R
(b
! "#
0
a
>
A&
f
L.
R
(c
! "#
0
a
=
A&
f
L. 9I
R
(d
F8,
f
3%9>
.
5
(
!
(a
< 9
f
3@B
.
(
∗
W! "#
f
L.
I
A&
f
L. 3QP,
–I
.
(
∗
W! "#
f
L. 3QP,
I
A&
f
L.
–I
.
(b
< 9
f
&
.
(
∗
W! "#
f
L.
I
A&
f
L.
–I
.
(
∗
W! "#
f
L. 3QP,
I
A&
f
L. 3QP,
–I
.
(c
! "#
[ ]
,
I
a b
=
A&
[
]
,
I
b
a
− = − −
.
(IV
رف دا#
.
(1
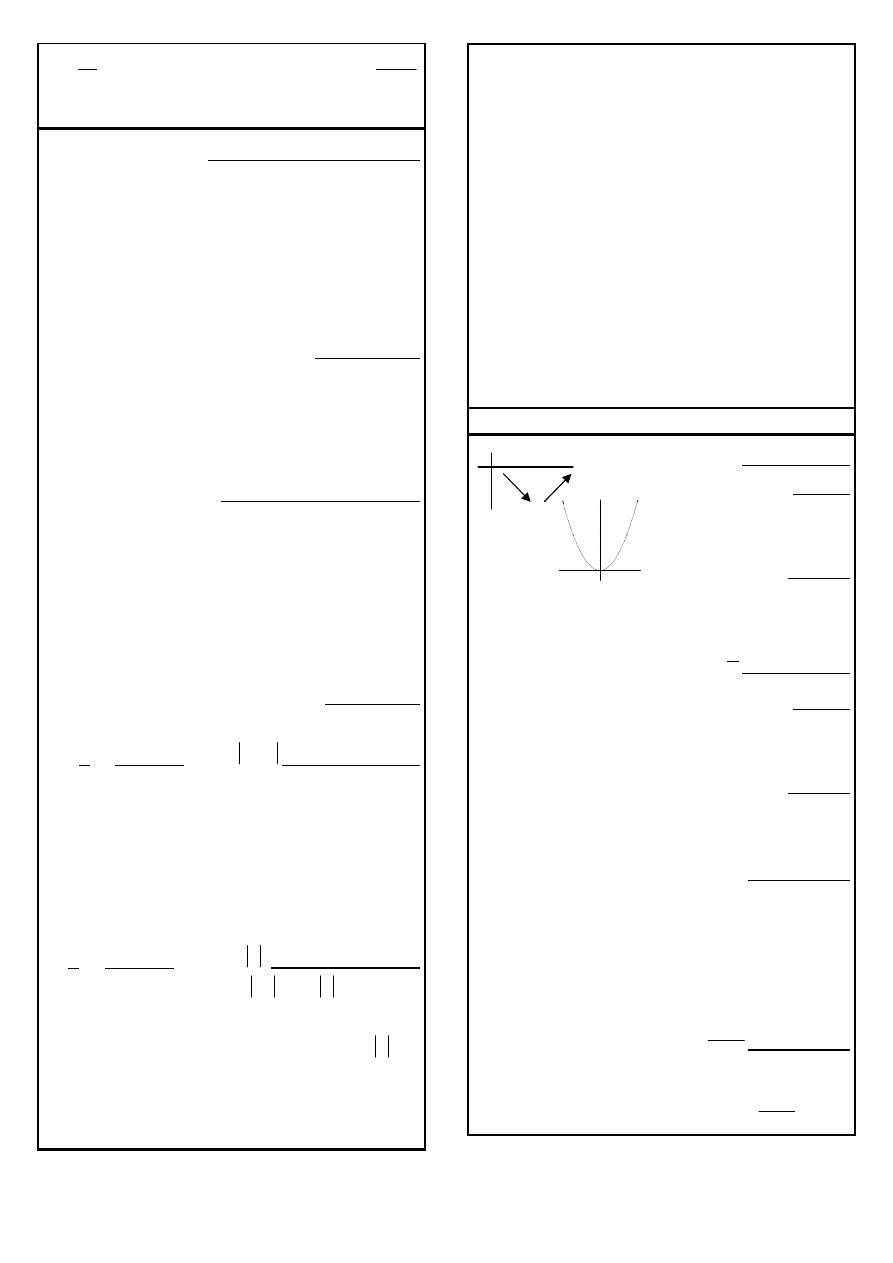
: \H : : "#
f
Y QP 3P )H%
0
x
: \H b
0
( )
(
)
f x
f x
≤
- Y
I
L. Z9c
0
x
3% d_
Q%
0
(
)
f x
.
(2
: \H : : "#
f
Y 3P )H%
0
x
: \H b
0
( )
( )
f x
f x
≥
- Y
I
L. Z9c
0
x
3% d_
0
(
)
f x
.
(3
(a
: \H
α
. QP 3P
f
: \H b
( )
f x
α
≤
Y
-
I
< N8H
0
x
<
I
N3*
0
(
)
f x
α
=
.
(b
: \H
α
. 3P
f
: \H b
( )
f x
α
≥
Y
-
I
< N8H
0
x
<
I
N3*
0
(
)
f x
α
=
.
(4
4RS -@ ! "#
f
) 0 L.
A&
α
. QP 3P
f
Y
0
x
β
3P
.
f
Y
1
x
.
(5
F8, ! "#
f
) 0 L.
A&
α
. QP 3P
f
Y
0
x
β
. 3P
f
Y
1
x
.
(V
اوال اﺝ
.
1
(
2
(
0)
( )
a
f x
ax
≠
=
a
(
! "#
0
a
>
4RS -@ A&
f
f
C
de K. ( ): T1: f.0
L. ] T@ d % J3 e
.
b
(
! "#
0
a
<
4RS -@ A&
f
f
C
0
de K. ( ): T1: f.
)g1 ] T@ d % J3 e
.
2
(
(
0)
( )
a
a
f x
x
≠
=
*
f
D
=
R
a
(
! "#
0
a
>
4RS -@ A&
f
f
C
K. ( ): d! 5_
K. ( Ze d%
.
b
(
! "#
0
a
<
4RS -@ A&
f
f
C
K. ( ): d! 5_
K. ( Ze d%
.
3
(
2
(
0)
( )
a
f x
ax
bx c
≠
=
+ +
hi# )@: <
f
C
- Q9j ]
f
C
.
J9 _
( )
f x
) 0L.
2
( )
(
)
f x
a x
α
β
=
−
+
< %.O, ?
( )
y
f x
=
X
2
(
)
y
a x
α
β
=
−
+
X
2
(
)
y
a x
β
α
− =
−
kl ?
X
x
Y
y
α
β
= −
= −
mHQ ( "#
2
Y
aX
=
K. Y
( , , )
i j
Ω
k
( , )
α β
Ω
4
(
( )
ax b
f x
cx d
+
=
+
)@: <
hi#
f
C
Q9j ]
f
C
.
J9 _
( )
f x
) 0 L.
( )
f x
x
γ
β
α
= +
−
< ;.O, ?
( )
y
f x
=
X
y
x
γ
β
α
− =
−
kl ?
X
x
Y
y
α
β
= −
= −
mHQ ( "#
Y
X
γ
=
K. Y
( , , )
i j
Ω
k
( , )
α β
Ω
.
5
(
+,- . / 0 123 04!$
.
(a
kn%
f
C
O%, J3 e k
(0, (0))
A
f
.
(b
(
∗
F8,( kn% ]
f
C
( )* +% )3& e k
( )
0
f x
=
-.o d_ W! "#
2
1
x
، x
…
kn%9 $% A&
1
( , 0)
A x
b
2
( , 0)
B x
…
.
(
∗
( -./
( )
0
f x
=
kn% $% )3&:
f
C
e k
)3&
.
6
(
5323 04!$
.
(
∗
F8,( kn% ]
f
C
g
C
( )* +%
( )
( )
f x
g x
=
-.o d_ W! "#
2
1
x
، x
…
kn%9 $% A&
1
1
( , ( ))
A x f x
b
2
2
( , (
))
B x
f x
…
.
(
∗
( -./
( )
( )
f x
g x
=
kn% $% )3&:
f
C
k
g
C
7
(
5323- 673 08
.
(a
\3,8, . p>, kq U
f
C
g
C
0# 1 +%
( )
( )
f x
g x
−
(
∗
! "#
( )
( )
0
f x
g x
−
≥
A&
f
C
r& @
g
C
.
(
∗
! "#
( )
( )
0
f x
g x
−
≤
A&
f
C
W7 @
g
C
.
(b
8@9( -./
( )
( )
f x
g x
≤
45V 7
23&
f
C
W7
g
C
8
(
!- (
( ) : ( )
E
f x
m
=
( -./
( )
E
kn% $% )3&:
f
C
K3%9>(
( ) : y
m
∆
=
9
(
123 9!:%"
( )
( )
g x
f x
=
!;)<%
f
C
.
! "#
( )
0
f x
≥
X
f
C
A& )3& e r&
( )
( )
g x
f x
=
"#
g
C
k ;HO,
f
C
.
! "#
( )
0
f x
≤
X
f
C
A& )3& e W7
( )
( )
g x
f x
= −
"#
g
C
)Is
f
C
)3& G H>
.
^9
g
C
h@ <
f
C
& e r& @(
h@ )Is )3
f
C
)3& G H>, )3& e W7 @(
.
10
(
123 9!:%"
( )
( )
g x
f x
=
!;)<%
f
C
.
,
(
)
(
)
( )
( )
g
x
f
x
f x
g x
− =
− =
=
"#
g
3@B
J3 G H>, )I 9 ,8, ^9
.
) ,
[
[
0,
x
∈ +∞
:
x
x
=
"#
( )
( )
g x
f x
=
T,
g
C
k ;HO,
f
C
.
^9
g
C
h@ <
f
C
Y @(
[
[
0,
+∞
G H>, T.Is
J3
.
0
0
f
x
ا
ـــــد ــ ا تــ
(I
ـــ ا
ـــــــ
ـــ
آ
ــــــ
A
(
!"# ﺕ
Ω
و
k
د م
.
'
M
اآ اي آ
Ω
!" و
k
#! ا$ه
ـﺏ يا
( , )
h
k
Ω
( واي یﺏ
*آ
M
( )
P
ﺏ
'
M
+ ﺏ
M
"
'
M
k
M
Ω
= Ω
.
Ω
B
(
ة&''ا ( ا
ن ا ن$ﺕ
'
M
و
'
N
رﺕ ا$0
M
و
N
ا$ا 12
ﺏآ
h
د3و اذإ ( 6و اذإ
1
k
≠
+ ﺏ
'
'
M N
k MN
=
.
C
(
ت ــــ( ﺥ
h
ﺕآ آ
Ω
!" و
k
.
(1
(
)
'
h M
M
=
76 ﺕ
'
M
k
M
Ω
= Ω
(2
إذا آن
(
)
'
h M
M
=
و
(
)
'
h N
N
=
ن86
'
'
M N
k MN
=
(3
(a
( )
h
Ω = Ω
)
نإ ل$
Ω
ة ﺏآ0
h
(
(b
(
)
h M
M
=
76 ﺕ
M
= Ω
)
ها
ی أن
Ω
ة ﺏآ>ا ة$ا ا ه
h
(
(4
إذا آن
(
)
'
h M
M
=
ن86
Ω
و
M
و
'
M
? "
.
(5
(a
ا
ی@3?ا 12 A6 یآ
:
إذا آن
G
@3
{
}
( , ), ( , )
A
B
α
β
ن86
G'
@3
{
}
( ', ), ( ', )
A
B
α
β
(b
یC>?ا 12 A6 یآا
:
إذا آن
I
C>
[ ]
A B
ن86
I'
@3
[
]
'
'
A B
(c
یDE ﺱا * 12 A6ی آا
:
إذا آن
A B
CD
α
=
ن86
'
'
'
'
A B
C D
α
=
(d
اﺱ12 A6ی آا
3
ی (
:
( ا H آ اذإ
A
و
B
و
C
6 ? "
ره$0 ن8
A'
و
B'
و
C'
? "
.
(6
ی6"?ا 12 A6ی I آا
.
إذا آن
( )
'
h A
A
=
و
( )
'
h B
B
=
ن86
'
'
A B
k AB
=
(7
ﺱ یDا یاوا سK * A6ی آا
'
'
'
BA C
B A C
∧
∧
=
(a (8
رة ا$0
[ ]
A B
ﺏآ
h
ه ا
[
]
'
'
A B
(b
L "?رة ا$0
(
)
AB
ﺏآ
h
L "? ه ا
( ' ')
A B
.
(c
L " رة$0
(
)
D
L " $ ه
(
')
D
ازي$ی
(
)
D
.
(d
ﺕی*3أ
L " رة$0
(
)
D
ـ ﺏ
h
ةر$0 یﺕ Nی
A
و
B
(
)
D
ن$ﺱو
(
)
( '
')
h D
A B
=
ةر$0 یﺕ وأ
واة
A
ن$ﺱو
(
)
h D
ر?ا L "?ا $ه
'
A
"?2 ازي$?او
L
(
)
D
) .
( )
'
h A
A
=
(
(e
إذا آن
(
)
D
را? "
Ω
ن86
(
)
(
)
h D
D
=
.
)
نإ ل$
(
)
D
?3 إ0
. (
(9
ةOاا ةر$0
( , )
C O r
ﺏآ
h
ةOاا ه
'(
',
)
C O
k r
.
P
'
( )
O
h O
=
.
(10
(a
E
و
F
ى$"?ا O3
.
(
)
( )
( )
h E
F
h E
h F
=
∩
∩
(b
H آ اذإ
M
E
F
∈
∩
ن86
(
)
( )
( )
h M
h E
h F
∈
∩
(11
ازي ی$او ا 12 A6ی آا
:
ن ان? " ?ه ی ? " ةر$0
ازین$ ن? " ?ه یزا$ ? " ةر$0 و
.
12
(
ا*+ ا
آ
.
L2 1إ ب$" ى$"?ا نأ ضN
( , , )
O i j
.
a
(
ل -
1
:
h
ﺕآ آ
(1, 2)
Ω
!" و
2
k
=
.
2 22 اT> ایﺕ *3أ
h
2ی P!
:
( , )
M x y
و
( ',
')
M x
y
+ ﺏ
(
)
'
h M
M
=
م$ و
ب"ﺏ
'
x
و
'
y
I ﺏ
x
و
y
.
ی
(
)
'
h M
M
=
ی
'
2
M
M
Ω
= Ω
وی
'( ' 1,
' 2)
M
x
y
Ω
−
−
و
2
(2
2, 2
4)
M
x
y
Ω
−
−
إذن
' 1
2
2
' 2
2
4
x
x
y
y
− =
−
− =
−
ی
'
2
1
'
2
2
x
x
y
y
=
−
=
−
ـ 22 اT> انذإ
h
ه
:
'
2
1
:
'
2
2
x
x
h
y
y
=
−
=
−
/ﺡ
:
ةر$0 یﺕ درأ اذإ
A
ـ ﺏ
h
ض$
x
و
y
تVا8ﺏ
A
إ 12 *> و
تVا
( )
h A
.
b
(
ل -
2
.
#!ا !
f
ه22ا T0 يا
:
'
3
2
:
'
3
4
x
x
f
y
y
=
+
=
−
!W ﺕی*3أ
f
?Xا *ﺏ ة>ا ( ا +!
'
'
x
x
y
y
=
=
ی
3
2
3
4
x
x
y
y
+ =
− =
ی
1
2
x
y
= −
=
إذن
f
ةو ة0 *! ﺕ
ه
( 1, 2)
Ω −
.
YZ LV
( , )
M x y
و
( ',
')
M x
y
+ ﺏ
(
)
'
h M
M
=
ی
إذن
'
3
2
'
3
4
x
x
y
y
=
+
=
−
.
وی
'(
1,
' 2)
M
x
y
Ω
+
−
ی
'(3
2 1, 3
4 2)
M
x
y
Ω
+ +
− −
ی
'(3
3, 3
6)
M
x
y
Ω
+
−
وی
3
(3
3, 3
6)
M
x
y
Ω
+
−
إذن
'
3
M
M
Ω
= Ω
وﺏ
f
ﺕآ آ
( 1, 2)
Ω −
!" و
3
k
=
.
13
(
ت 23ا 4#
.
(a
آﺕ آ د
h
.
?"
Ω
+!
A
و
B
?رﺕه$0و
A'
و
B'
.
ی
( )
'
h A
A
=
إذن
Ω
و
A
و
A'
? "
و
(
')
A A
Ω∈
.
وی
( )
'
h B
B
=
إذن
Ω
و
B
و
B'
و ? "
(
')
BB
Ω∈
وﺏ
Ω
PW ﺕ ه
(
')
AA
و
(
')
BB
(b
آﺕ " یﺕ *3أ
h
?"
k
و
ن إ كه
:
(*
آ?ا +!
Ω
و
A
Dرﺕ$0و
A'
.
ی
( )
'
h A
A
=
إذن
'
A
k
A
Ω = Ω
ب"ﺏ م$ و ،
'
A
Ω
I ﺏ
A
Ω
]^ E
'
A
A
α
Ω = Ω
نأ _" و
k
α
=
س ا 1إ ? وأ
ي!Eا
'
A
k
M
Ω = Ω
ی
'
A
k
M
Ω
=
Ω
.
(*
+!
A
و
B
?رﺕه$0و
A'
و
B'
.
ی
'
'
A B
k A B
=
ﺏ"ا یا `N P! و
.
(c
نأ ! نأ درأ اذإ
'
I
C>
[
]
'
'
A B
+!
I
و
A
و
B
+ﺏ
( )
'
h A
A
=
و
( )
'
h B
B
=
و
( )
'
h I
I
=
0aا *? " و
(5b
.
ی
I
C>
[ ]
A B
إذن
'
I
C>
[
]
'
'
A B
.
(d
نأ !
Ω
و
I
و
J
نأ ! نأ Nی ? "
( , )
( )
k
h
I
J
Ω
=
.
(e
ةر$0 د
M
Dق ﺏW ة كه
:
(*
Cی ا *? "
'
M
k
M
Ω
= Ω
(*
إذا آن
M
C>
K
[ ]
A B
*? "
(5b)
.
(*
إذا
H آ
A M
A B
α
=
*? "
(5c)
.
(*
H آ اذإ
M
*? " O3 PW ﺕ
(10)
.
)
ی
M
E
F
∈
∩
إذن
(
)
( )
( )
h M
h E
h F
∈
∩
(
(*
H آ اذإ
D2? " 22ا T>ا ی
.
(II
ي&ـــآ"'ا 6ﺙ ـــــــ'ا
A
(
!"# ﺕ
.
'
M
Ω
آي اي آ?ا *V?ا
Ω
ا#! ا$ه
ـﺏ ي
S
Ω
( واي یﺏ
Ω
*آ
M
( )
P
ﺏ
'
M
+ ﺏ
"
'
M
M
Ω
= −Ω
ی
Ω
C>
[
]
'
MM
.
M
B
(
ة&''ا ( ا
ن ا ن$ﺕ
'
M
و
'
N
ر$0
ﺕ ا
M
و
N
ا$ا 12
آي*V?ﺏ
S
Ω
( إذا6و اذإ
آن
'
'
M N
MN
= −
.
C
(
ت ــــ( ﺥ
آي?ا *V?2 !"ﺏ 0 1 !ﺕ آﺏ 2 ?ا ت0aا P?3
P
cﺏ$ ﺕ
k
ـ ﺏ
1
-
ا،
(6)
و
(9)
@!> ﺕ+
.
(6
ی6"?ا 12 A6 ی يآ?ا *V?ا
.
إذا آن
( )
'
h A
A
=
و
( )
'
h B
B
=
ن86
'
'
A B
AB
=
(9
ةOاا ةر$0
( , )
C O r
آي?ا *V?ﺏ
S
Ω
ةOاا ه
'(
', )
C O r
.
P
'
( )
O
S
O
Ω
=
.
/ﺡ
(a
(
)
'
S
M
M
Ω
=
76 ﺕ
Ω
C>
[
]
'
MM
.
(b
إذا آ
ن
(
)
'
S
M
M
Ω
=
و
(
)
'
S
N
N
Ω
=
ن86
'
'
M N
MN
= −
.
(III
ـــ ازاﺡ
ــــــــــــ
ـــ
A
(
!"# ﺕ
.
u
DE
.
DDE زا اfا
u
ه
u
ـﺏ يا #!ا
u
t
( واي یﺏ
'
M
*آ
M
( )
P
ﺏ
'
M
+ﺏ
"
'
MM
u
=
M
B
(
ة&''ا ( ا
ن ا ن$ﺕ
'
M
و
'
N
رﺕ ا$0
M
و
N
ا$ا 12
زاfﺏ
u
t
( إذا آن6و اذإ
'
'
M N
MN
=
.
C
(
ت ــــ( ﺥ
، زاg !"ﺏ 0 1 !ﺕ آﺏ 2 ?ا ت0aا P?3
ا
(1)
و
(2)
و
(3)
و
(4)
و
(6)
و
(8cde)
و
(9)
و
(12)
و
(13abd)
وی
:
(6
زا ﺕfا
6"? ا12 A6
.
(8e
إذا آ
ن
(
)
D
* ازي$ی
u
)
ی
u
ـ D3$
(
)
D
(
ن86
(
)
(
)
u
t
D
D
=
.
(9
ةOاا ةر$0
( , )
C O r
زاfﺏ
u
t
ةOاا ه
'( ', )
C O r
.
P
'
( )
u
O
t O
=
.
/ﺡ
(a
(
)
'
u
t
M
M
=
76 ﺕ
'
MM
u
=
.
(b
إذا آن
(
)
'
u
t
M
M
=
و
(
)
'
u
t
N
N
=
ن86
'
'
M N
MN
=
.
(III
'ا 6ﺙ ــــ'ا
ـــــ
ري
A
(
!"# ﺕ
.
( )
∆
ر$ يا ير$?ا *V?ا ? "
( )
∆
( )
∆
ـﺏ يا #!ا $ه
( )
S
∆
( واي یﺏ
*آ
M
( )
P
ﺏ
'
M
+ ﺏ
M
'
M
ن$ی
( )
∆
واﺱ( ا
[
]
'
MM
.
B
(
ت ــــ( ﺥ
، ري$?ا *V?2 !"ﺏ 0 1 !ﺕ آﺏ 2 ?ا ت0aا P?3
ا
(1)
و
(2)
و
(3)
و
(4)
و
(5
(6)
و
(8e)
و
(9)
و
(13abd)
وی
:
(6
6"? ا12 A6ی ير$? ا*V?ا
.
(8e
(*
إذا آن
(
)
( )
D
⊥ ∆
ن86
( )
(
)
(
)
t
D
D
∆
=
.
(*
إذا آن
(
) //( )
D
∆
ن86
( )
( ) //( )
t
D
D
∆
.
(9
ةOاا ةر$0
( , )
C O r
ري$?ا *V?ﺏ
( )
S
∆
ةOاا ه
'(
', )
C O r
.
P
( )
'
( )
O
S
O
∆
=
.
/ﺡ
(a
( )
(
)
'
S
M
M
∆
=
76 ﺕ
( )
∆
واﺱ( ا
[
]
'
MM
.
(b
إذا آن
( )
(
)
S
M
M
∆
=
76 ﺕ
( )
M
∈ ∆
L "?ا
( )
∆
ﺏ 0
.
ا
ا ءا
I
(
(1
AB
AC
.
C
H
C
(
)
AB
K
B
(
)
AC
K
! "
AB
AC
# $ %&" ' ()
.
AB AC
* +, -&
:
B
H
A
.
.
.
.
.cos(
)
AB AC
AB AH
AC AK
AB AC
BAC
∧
=
=
=
(2
/ 01 2"+3 41
AB
5
AC
678
.
0
AB AC
=
(II
(1
AB
CD
.
D
'
C
C
(
)
AB
'
D
D
(
)
AB
C
+*
.
. '
'
AB CD
AB C D
=
B
A
:
9+0 :;
.
AB CD
<1 =+ &> /&?@ / 01 "
+AB+, +C+AD5 E F " G + +AD5 E +# H+(0I JG K! L+
.
(2
(a
&"
%
.
AB AB
%&+#
2
AB
J#& *
.
(b
+*
2
2
AB
AB
=
(3
(a
6+ 2"+3 41
AB
CD
678 M N(" +O
:
.
.
AB CD
AB CD
=
(b
6+ 2"+3 41
AB
CD
678 6+3+ 6+M +O
:
.
.
AB CD
AB CD
= −
(4
(a
61 P"
AB
CD
6+ 3 6+3 41 8 41 6+Q +
(
)
AB
(
)
CD
* +
.
R"
AB
CD
⊥
(b
+*
AB
CD
⊥
S8+Q
.
0
AB CD
=
(5
2"+3 41
A
B
C
D
678 T
.
.
AB CD
AB CD
=
D
C
B
A
(6
(a
u
v
A
B
C
3
UV "
AB
u
=
AC
v
=
+*
:
.
.
u v
AB AC
=
C
v
(b
u
v
:
v
+*
.
.
cos( , )
u v
u
v
u v
∧
=
B
u
A
(c
2
2
u
u
=
u
(d
2"+3 41
u
v
678 M N(" +O
:
.
.
u v
u
v
=
(e
6+ 2"+3 41
u
v
678 6+3+ 6+M +O
:
.
.
u v
u
v
= −
(f
u
v
⊥
S8+Q
.
0
u v
=
(g
.
.
(
u v
v u
=
∗
.(
)
.
.
(
u v
w
u v
u w
+
=
+
∗
.(
)
.
.
(
u v
w
u v
u w
−
=
−
∗
(
).
.(
)
( . ) (
u v
u
v
u v
α
α
α
=
=
∗
2
2
2
(
)
2 .
(
u
v
u
v
u v
+
=
+ +
∗
2
2
2
(
)
2 .
(
u
v
u
v
u v
−
=
+ −
∗
2
2
(
).(
)
(
u
v
u
v
u
v
+
− =
−
∗
(III
!"#
1
(
$% &
.
A
(
)
ABC
+* +WW
:
2
2
2
ˆ
2
.
.cos
BC
AB
AC
AB AC
A
=
+
−
2
2
2
ˆ
2
.
.cos
AC
BA
BC
BA BC
B
=
+
−
C
B
2
2
2
ˆ
2
.
.cos
AB
CA
CB
CA CB
C
=
+
−
2
(
'()* +,-
(
)
ABC
+WW
I
T A XY
[ ]
AB
A
+*
:
2
2
2
2
2
2
BC
AB
AC
AI
+
=
+
5
2
2
2
2
1
(
)
2
2
BC
AI
AB
AC
=
+
−
C
I
B
3
(
./ 01& 23 4 )* &
.
(a
(
)
ABC
Z T*% [\+B +WW
A
'
A
XY
[ ]
BC
H
A
(
)
BC
.
+*
:
2
2
2
(
AB
AC
BC
+
=
∗
)
L^ +8 TB_
(
2
.
.
(
BA
BH BC
BH BC
=
=
∗
A
2
.
.
(
CA
CH CB
CH CB
=
=
∗
2
.
.
(
AH
HB HC
HB HC
= −
=
∗
C
I
H
B
1
'
(
2
AA
BC
=
∗
(b
(
)
ABC
*% [\+B +WW
Z T
A
.
+*
:
C
ˆ
cos
BA
B
BC
=
ˆ
cos
AC
B
BC
=
ˆ
tan
AC
B
AB
=
A
B
(c
(
)
ABC
+WW
.
+*
:
A
ˆ
ˆ
ˆ
sin
sin
sin
A
B
C
BC
AC
AB
=
=
C
B
(I
!
I
(
#
$
%
.
( )
D
( )
D
′
.
.
(*
( )
D
( )
D
′
(*
( )
D
( )
D
′
!
.
(*
( )
D
( )
D
′
"
.
(*
( )
D
( )
D
′
# ! #
$ #
% # &' " ()*
.
II
(
& %$ #
( )
D
( )
P
+
.
,-.
(*
/
( )
D
+
( )
P
(*
/
( )
D
( )
P
"
θ
(*
/
( )
D
+
( )
P
01
$
" ()*
'
( )
D
( )
P
!
.
III
(
%$ #
.
( )
P
( )
Q
.
.
,-
(*
( )
P
( )
Q
.
(*
( )
P
( )
Q
&' $ -1
!
.
(*
( )
P
( )
Q
2
/
( )
D
.
IV
(
'
1
/
( )
D
+ 3!
( )
P
( )
D
3!
( )
D
′
( )
P
.
2
+
( )
P
+ 3!
( )
Q
(*
( )
P
!
Q
(*
( )
P
!
( )
Q
.
3
& 2 45 6* !
:
a
(
%$( )*+#
)
9- : 3!
–
–
< =>
(...
b
(
,'$ %'
.
(
)
A BC
I
<1
[ ]
A B
J
<1
[ ]
A C
( ) ( )
IJ
BC
.
c
(
, %$-
*
:
(*
)'
:
( ) ( ) ( )
( ) ( )
( ) ( )
( ) ( )
P
Q
P
Q
= ∆
′
∆ ⊂
′′
∆ ⊂
′
′′
∆
∆
∩
?
( ) ( ) ( )
′
′′
∆
∆
∆
(*
)'
:
( )
( )
( )
( ')
( )
( ') //( )
P
Q
P
Q
= ∆
∆ ⊂
∆
∩
?
( ) ( )
′
∆
∆
(*
)'
:
( )
( )
( )
( ') //( )
( ') //( )
P
Q
P
Q
= ∆
∆
∆
∩
?
( ) ( )
′
∆
∆
(d
.
)'
( ) //( ')
( ') //( '')
∆
∆
∆
∆
?
( ) ( )
//
′
∆
∆
e
(
)'
( ) ( )
( ) ( ) ( )
( ) ( ) ( )
//
P
Q
H
P
H
Q
= ∆
′
= ∆
∩
∩
?
( ) ( )
//
′
∆
∆
4
( )
D
+ @
( )
P
:
(*
A
B
( )
D
A'
( )
P
.
(*
( ) ( )
//
D
P
"> " &
.
5
( )
D
+
( )
P
( )
D
( )
P
"> " &
A
( )
D
P
⊄
.
"> " 5 ,0
( )
D
( )
P
5 ,
/
( )
D
′
( )
P
( )
D
.
6
( )
P
( )
Q
( )
P
( )
Q
"> " &
( ) ( )
P
Q
≠
.
A05 $10
/
:
(*
> 5 ,
A
B
( )
P
( )
Q
( )
P
( )
Q
/ *
( )
AB
.
(*
"> " 5 ,
A
( )
′
∆
( )
′′
∆
,
( ) ( )
P
′
∆ ⊂
( )
Q
′′
∆ ⊂
( ) ( )
//
′
′′
∆
∆
.
( )
P
( )
Q
/ *
( )
∆
A
$ 3!
( )
′
∆
( )
′′
∆
.
7
,-.
I
J
K
"
0B "> &
( )
P
( )
Q
" & = & / A'
.
(D)
(D')
(D)
(D')
(D)
(D')
P
(D)
P
(D)
O
P
(D)
p
q
q
p
(D)
A
B
C
I
J
(II
.
1
(a
)'
( )
∆
+ A05 35
( )
P
( )
∆
A05 35
( )
P
.
(b
/ )'
( )
∆
+ A05 5
( )
P
?
( )
∆
/ 3 A05 5
( )
P
.
2
+
( )
P
+ A05 35
( )
Q
( )
∆
@
( )
P
A05 35
( )
Q
.
3
6*
& 2 45
:
(a
"& $>:
)
–
$
–
–
–
/% ,0.
"!
(...
(b
( )
* 4%
[ ]
AB
( )
M
∈
(
) (
)
AM
BM
⊥
(c
(
)
ABC
3 ,0.
A
I
<1
[ ]
BC
( ) ( )
AI
BC
⊥
.
(d
)'
( ) ( )
( ) ( )
′
∆ ⊥ ∆
′
′′
∆ ⊥ ∆
?
( ) ( )
′
∆ ⊥ ∆
(e
)'
( ) ( )
( ) ( )
P
P
∆ ⊥
′
∆ ⊂
?
( ) ( )
′
∆ ⊥ ∆
%/01
:
/ )'
( )
∆
/ A05 35
( )
′
∆
5 ,
+
( )
P
( )
′
∆
( )
∆
=05 35
.
4
A
B
.
5 " " "5@
A
B
+
"0 + A
[ ]
AB
+ *
<1
[ ]
AB
A05 3
[
)
AB
.
5
( )
∆
/
( )
P
( )
Q
)'
( ) ( )
( ) ( )
//
P
P
Q
∆ ⊥
?
( ) ( )
Q
∆ ⊥
6
( )
∆
( )
′
∆
( )
P
+
)'
( ) ( )
( ) ( )
//
P
′
∆
∆
∆ ⊥
?
( ) ( )
P
′
∆ ⊥
A
C
B
I
A
A
B
M
