
Chapter 2
Differential Calculus
2.1
Differentiability in one variable
Let f : R → R and a ∈ R. We say f
′
(a) ∈ R is the derivative of f at a if
lim
x
→a
f (x) − f (a)
x − a
= lim
h
→0
f (a + h) − f (a)
h
= f
′
(a).
(2.1)
Note that f
′
(a) is the slope of the tangent line to the graph of f at point
(a, f (a)).
We now look at (2.1) from another point of view. Let m = f
′
(a). From
(2.1), we have
lim
x
→a
f (x) − f (a) − m(x − a)
x − a
= lim
x
→a
E(x − a)
x − a
= 0,
where E(x − a) = f (x) − l(x) is the difference between f (x) and its linear
approximation l(x), here l(x) = m(x − a) + f (a) is the “linear” equation for
the tangent line.
Let h = x − a, we have f (a + h) = f (a) + mh + E(h), and E(h)/h → 0
as h → 0. This leads to the following definition
Definition 2.1.
f is differentiable at a if there is m ∈ R such that
f (a + h) = f (a) + mh + E(h), where lim
h
→0
E(h)
h
= 0.
(2.2)
19

20
CHAPTER 2.
DIFFERENTIAL CALCULUS
Note that m = f
′
(a) is unique when it exists.
Let S ⊂ R, then f is differentiable on S if it is differentiable at every
point of S.
Example 2.2.
If f : R → R is a constant function then f
′
(x) = 0 for all
x ∈ R.
If f (x) = cx where c is a fixed number and x ∈ R, then f
′
(x) = c for all
x.
Remark 2.3.
If f is differentiable at a then f is continuous at a.
Proposition 2.4.
Let a ∈ R and f, g : R → R be differentiable at a. Then
(i) f ± g are differentiable at a and
(f ± g)
′
(a) = f
′
(a) ± g
′
(a).
(2.3)
(ii) f g is differentiable at a and
(f g)
′
(a) = f
′
(a)g(a) + f (a)g
′
(a).
(2.4)
(iii) If g(a) 6= 0, then (f/g) is differentiable at a and
f
g
′
(a) =
f
′
(a)g(a) − g
′
(a)f (a)
g
2
(a)
.
(2.5)
In particular,
1
g
′
(a) = −
g
′
(a)
g
2
(a)
.
(2.6)
Proof. We prove, for instance (ii). Suppose
f (a + h) = f (a) + f
′
(a)h + E
1
(h), where lim
h
→0
E
1
(h)
h
= 0,
g(a + h) = g(a) + g
′
(a)h + E
2
(h), where lim
h
→0
E
2
(h)
h
= 0.
Then f (a + h)g(a + h) = f (a)g(a) + {f
′
(a)g(a) + g
′
(a)f (a)}h + E
3
(h), where
E
3
(h) = f
′
(a)g
′
(a)h
2
+ E
1
(h){g(a) + g
′
(a)h + E
2
(h)} + E
2
(h){f a) + f
′
(a)h}.

2.1.
DIFFERENTIABILITY IN ONE VARIABLE
21
Note that
E
3
(h)
h
= f
′
(a)g
′
(a)h +
E
1
(h)
h
{g(a) + g
′
(a)h + E
2
(h)} +
E
2
(h)
h
{f a) + f
′
(a)h},
which goes to zero as h → 0. Therefore (f g) is differentiable at a and its
derivative is (f g)
′
(a) is f
′
(a)g(a) + f (a)g
′
(a).
Definition 2.5.
Let S ⊂ R
n
, f : S → R, and a ∈ S.
f (a) is the maximum (largest value) of f on S if f (a) ≥ f (x) for all
x ∈ S.
f (a) is the minimum (smallest value) of f on S if f (a) ≤ f (x) for all
x ∈ S.
f has a local maximum at a if there is r > 0 such that f (x) ≤ f (a) for
all x ∈ S ∩ B(r, a).
f has a local minimum at a if there is r > 0 such that f (x) ≥ f (a) for all
x ∈ S ∩ B(r, a).
Note that if f (a) is the maximum (respectively, minimum) then it is also
a local maximum (respectively, local minimum).
Proposition 2.6.
Suppose f is defined on an open set I ⊂ R and a ∈ I. If
f has a local maximum or minimum at a and f is differentiable at a then
f
′
(a) = 0.
Proof. Suppose f (a) is a local minimum. Let δ > 0 be such that if |h| < δ,
then a + h ∈ I and f (a + h) − f (a) ≥ 0. We have
f
′
(a) = lim
h
→0
f (a + h) − f (a)
h
.
When 0 < h < δ, we have
f
(a+h)−f (a)
h
≥ 0, letting h → 0 gives f
′
(a) ≥ 0.
When −δ < h < 0, we have
f
(a+h)−f (a)
h
≤ 0, letting h → 0 gives f
′
(a) ≤ 0.
We conclude f
′
(a) = 0.
Lemma 2.7
(Rolle’s theorem). Suppose a < b and f is differentiable on
(a, b) and continuous on [a, b]. If f (a) = f (b), then there is c ∈ (a, b) such
that f
′
(c) = 0.

22
CHAPTER 2.
DIFFERENTIAL CALCULUS
Proof. Since [a, b] is compact, then there are x
1
, x
2
∈ [a, b] such that f (x
1
) =
M is the (absolute) maximum and f (x
2
) = m is the (absolute) minimum of
f on [a, b].
If M = m, then f is a constant function, hence f
′
(c) = 0 for any c ∈ (a, b).
If M 6= m, then M 6= L = f (a) = f (b) or m 6= L. Suppose M 6= L then
c = x
1
6= a, b, hence c ∈ (a, b). Since f is differentiable on the open interval
(a, b) and has a local maximum at c ∈ (a, b), then by Proposition 2.6 we have
f
′
(c) = 0.
Theorem 2.8
(Mean value theorem I). Suppose f is continuous on [a, b] and
is differentiable on (a, b). Then there is a point c ∈ (a, b) such that
f
′
(c) =
f (b) − f (a)
b − a
.
(2.7)
Note that
f
(b)−f (a)
b
−a
is the slope of the straight line going through (a, f (a))
and (b, f (b)).
Proof. Let
g(x) = f (a) +
f (b) − f (a)
b − a
(x − a) − f (x).
Then g is continuous on [a, b] and is differentiable on (a, b). Note that g(a) =
g(b) = 0 and g
′
(x) =
f
(b)−f (a)
b
−a
− f
′
(x). By Rolle’s lemma, there is c ∈ (a, b)
such that g
′
(c) = 0, hence we obtain (2.7).
Theorem 2.9.
Suppose f is differentiable on an open interval I. (a) If
|f
′
(x)| ≤ C for all x ∈ I then |f (b) − f (a)| ≤ C|b − a| for all a, b ∈ I.
(b) If f
′
(x) = 0 for all x ∈ I then f is constant in I.
(c) If |f
′
(x)| ≥ 0 (resp., > 0, ≤, < 0) for all x ∈ I then f is increasing (resp.,
strictly increasing, decreasing, strictly decreasing) on I.
Proof. Let a, b ∈ I and a < b, then f continuous on [a, b] and is differentiable
on (a, b). By the Mean Value Theorem 2.8, there is c ∈ (a, b) such that
f (b) − f (a) = f
′
(c)(b − a).

2.1.
DIFFERENTIABILITY IN ONE VARIABLE
23
We easily prove (a)–(c). For example, if f
′
(x) < 0 for all x ∈ I then f
′
(c) < 0,
therefore f (b) − f (a) < 0 for any b > a; that means f is strictly decreasing
in I.
Theorem 2.10
(Mean value theorem II). Suppose f and g are continuous
on [a, b] and is differentiable on (a, b), and g
′
(x) 6= 0 for all x ∈ (a, b). Then
there is a point c ∈ (a, b) such that
f
′
(c)
g
′
(c)
=
f (b) − f (a)
g(b) − g(a)
.
(2.8)
Proof. Apply Rolle’s lemma for the following function
h(x) = [f (x) − f (a)][g(b) − g(a)] − [g(x) − g(a)][f (b) − f (a)].
Definition 2.11.
We have the following notion of limits
• Let f : (d, a) → R
m
and L ∈ R
m
. Then lim
x
→a−
f (x) = L if
∀ε > 0, ∃δ > 0, ∀x ∈ (d, a) : a − δ < x < a =⇒ |f (x) − L| < ε. (2.9)
• Let f : (a, b) → R
m
and L ∈ R. Then lim
x
→a+
f (x) = L if
∀ε > 0, ∃δ > 0, ∀x ∈ (a, b) : a < x < a + δ =⇒ |f (x) − L| < ε. (2.10)
• Let f : (c, ∞) → R
m
and L ∈ R. Then lim
x
→∞
f (x) = L if
∀ε > 0, ∃M > 0, ∀x ∈ (c, ∞) : x > M =⇒ |f (x) − L| < ε.
(2.11)
• Let f : (−∞, c) → R
m
and L ∈ R. Then lim
x
→−∞
f (x) = L if
∀ε > 0, ∃M > 0, ∀x ∈ (−∞, c) : x < −M =⇒ |f (x) − L| < ε. (2.12)
• Let f : R
n
→ R, a ∈ R
n
. Then lim
x
→a
f (x) = ∞ if
∀M > 0, ∃δ > 0, ∀x ∈ R
n
: 0 < |x − a| < δ =⇒ f (x) > M.
(2.13)

24
CHAPTER 2.
DIFFERENTIAL CALCULUS
• Let f : R
n
→ R, a ∈ R
n
. Then lim
x
→a
f (x) = −∞ if
∀M > 0, ∃δ > 0, ∀x ∈ R
n
: 0 < |x − a| < δ =⇒ f (x) < −M. (2.14)
Note that if f : (d, a) ∪ (a, b) → R
m
and L ∈ R
m
then
lim
x
→a
f (x) = L ⇐⇒ lim
x
→a−
f (x) = lim
x
→a+
f (x) = L.
(2.15)
Theorem 2.12
(L’Hˆopital’s rule I). Suppose f and g are differentiable on
(a, b) and
lim
x
→a+
f (x) = lim
x
→a+
g(x) = 0.
(2.16)
If g
′
never vanishes on (a, b) and
lim
x
→a+
f
′
(x)
g
′
(x)
= L,
(2.17)
then
lim
x
→a+
f (x)
g(x)
= L.
(2.18)
Proof. Extend f (a) = 0, g(a) = 0. For x ∈ (a, b), we have f, g are continuous
on [a, x] and differentiable on (a, x). By Theorem 2.10, there is c ∈ (a, x)
such that
f (x)
g(x)
=
f (x) − f (a)
g(x) − g(a)
=
f
′
(c)
g
′
(c)
.
Note that c → a+ and x → a+. Letting x → a+ and using (2.17), we obtain
(2.18).
Remark 2.13.
The theorem still holds if we replace lim
x
→a+
by lim
x
→a−
,
lim
x
→a
, lim
x
→∞
, lim
x
→−∞
and the domains of f, g are appropriate.
Theorem 2.14
(L’Hˆopital’s rule II). Suppose f and g are differentiable on
(a, b) and
lim
x
→a+
|f (x)| = lim
x
→a+
|g(x)| = ∞.
(2.19)
If g
′
never vanishes on (a, b) and
lim
x
→a+
f
′
(x)
g
′
(x)
= L,
(2.20)
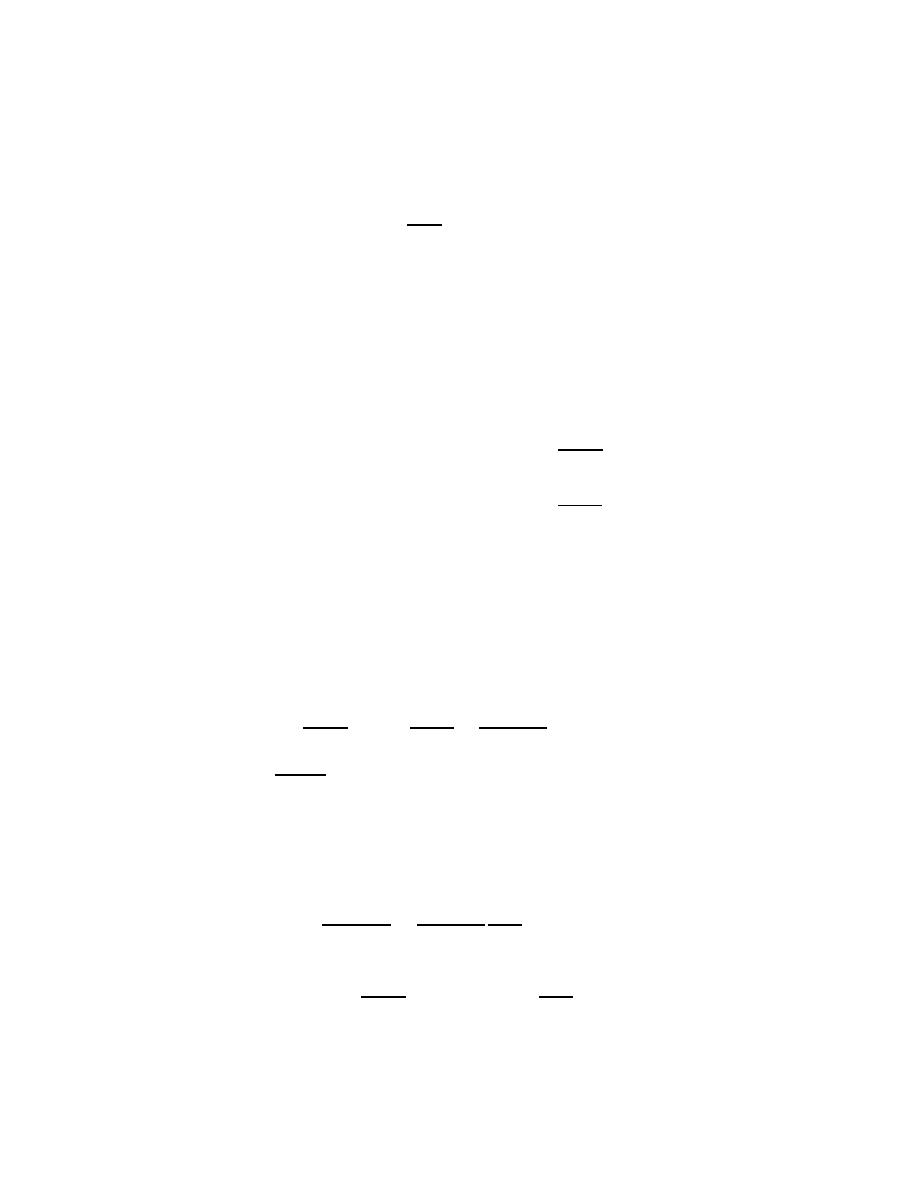
2.1.
DIFFERENTIABILITY IN ONE VARIABLE
25
then
lim
x
→a+
f (x)
g(x)
= L.
(2.21)
Theorem 2.15
(Chain rule). Let f, g : R → R and a ∈ R. Let g(a) = b and
suppose that g is differentiable at a, and f is differentiable at b. Then f ◦ g
is differentiable at a and
(f ◦ g)
′
(a) = f
′
(b)g
′
(a).
(2.22)
Proof. We have
g(a + h) = g(a) + g
′
(a)h + E
1
(h), where lim
h
→0
E
1
(h)
h
= 0,
f (b + h) = f (b) + f
′
(b)h + E
2
(k), where lim
k
→0
E
2
(k)
k
= 0.
Then (f ◦g)(a+h) = f (g(a+h)) = f (b+k) where k = k(h) = g
′
(a)h+E
1
(h).
We have
(f ◦ g)(a + h) = f (b) + f
′
(b){g
′
(a)h + E
1
(h)} + E
2
(k(h))
= (f ◦ g)(a) + f
′
(b)g
′
(a)h + E
3
(h),
(2.23)
where E
3
(h) = f
′
(b)E
1
(h) + E
2
(k(h)). Note that
E
3
(h)
h
= f
′
(b)
E
1
(h)
h
+
E
2
(k(h))
h
Claim: lim
h
→0
E
2
(k(h))
h
= 0.
Suppose the claim is true, then lim
h
→0
E
3
(h)/h = 0. Hence, according to
the Definition 2.1, we infer from (2.23) that f ◦ g is differentiable at a and
(2.22).
Proof of the claim: The idea is that
E
2
(k(h))
h
=
E
2
(k(h))
k(h)
k(h)
h
.
Since
lim
h
→0
k(h) = 0,
lim
k
→0
E
2
(k)
k
= 0,
and lim
h
→0
k(h)
h
= g
′
(a),

26
CHAPTER 2.
DIFFERENTIAL CALCULUS
we obtain lim
h
→0
E
3
(h)
h
= 0. This argument can be easily made rigorous (to
take care of the case k(h) = 0). However, the direct proof can go as follows:
Let M = |g
′
(a)| + 1. Since lim
h
→0
k
(h)
h
= g
′
(a), there is δ
1
> 0 such that
|k(h)| ≤ M|h| for 0 < |h| < δ
1
.
Let ε > 0. Since lim
k
→0
E
2
(k)
k
= 0, there is δ
2
> 0 such that |E
2
(k)| ≤
(ε/M)|k| for |k| < δ
2
(note that E
2
(0) = 0). Let δ = min{δ
1
, δ
2
/M}, then
for 0 < |h| < δ, we have |k(h)| ≤ M|h| ≤ δ
2
and hence
|E
2
(k(h))| ≤ (ε/M)|k(h)| ≤ (ε/M)M|h| = ε|h|.
Therefore lim
h
→0
E
2
(k(h))/h = 0.
Differentiability of vector-valued functions.
Let f = (f
1
, f
2
, . . . , f
m
) :
R
→ R
m
be a vector-valued function, where f
j
: R → R, for j = 1, 2, . . . m.
Let a ∈ R. Then the derivative of f at a is the vector
f
′
(a) = lim
h
→0
f (a + h) − f (a)
h
= (f
′
1
(a), f
′
2
(a), . . . , f
′
n
(a)).
(2.24)
whenever the involved quantities are defined. If f
′
(a) exists then we say f is
differentiable at a. In fact, f
′
(a) is the unique vector v ∈ R
m
such that
f (a + h) = f (a) + hv + E(h), where E(h) ∈ R
m
,
lim
h
→0
E(h)
h
= 0. (2.25)
Curves and tangent vectors.
See text, p.50.
Higher order derivatives.
Just as in lower calculus course.

2.2.
DIFFERENTIABILITY IN SEVERAL VARIABLES
27
2.2
Differentiability in several variables
2.2.1
Real-valued functions
Partial derivatives.
Let f : R
n
→ R, a = (a
1
, a
2
, . . . , a
n
) ∈ R
n
. Partial
derivative of f with respect to variable x
j
at a is
∂f
∂x
j
(a) = lim
h
→0
f (a
1
, . . . , a
j
−1
, a
j
+ h, a
j
+1
, . . . , a
n
) − f (a
1
, . . . , a
j
, . . . , a
n
)
h
(2.26)
Other notation: f
x
j
, ∂
j
f, ∂
x
j
f.
Gradient vector and Differentiability.
Let S ⊂ R
n
be open, f : S →
R
, a ∈ S. We say f is differentiable at a if there is c ∈ R
n
such that
f (a + h) = f (a) + c · h + E(h), where lim
h
→0
E(h)
|h|
= 0.
(2.27)
The vector c is the gradient of f at a and is denoted by ∇f (a).
Tangent planes.
For n = 2, f = f (x) = f (x
1
, x
2
) the graph of z = f (x)
is a surface in R
3
. Let P = (a, f (a)) be a point on the surface. The equation
for the tangent plane of the surface at P is:
z = (x − a) · ∇f (a) + f (a).
Theorem 2.16
(Chain Rule). Let g(t) = (g
1
, g
2
, . . . , g
n
) : R
m
→ R
n
, f (x) :
R
n
→ R, a ∈ R
m
, b = g(a) ∈ R
n
. If g is differentiable at a and f is
differentiable at b then f ◦ g is differentiable at a and
∂(f ◦ g)
∂t
k
(a) =
∂f
∂x
1
(b)
∂g
1
∂t
k
(a) +
∂f
∂x
2
(b)
∂g
2
∂t
k
(a) + . . . +
∂f
∂x
n
(b)
∂g
n
∂t
k
(a), (2.28)
for k = 1, 2, . . . , m. Briefly, we have
∂(f ◦ g)
∂t
k
(a) = ∇f (b) ·
∂g
∂t
k
(a),
(2.29)
for k = 1, 2, . . . , m.

28
CHAPTER 2.
DIFFERENTIAL CALCULUS
Directional derivatives.
Let u ∈ R
n
, |u| = 1, then
∂
u
f (a) = lim
h
→0
f (a + hu) − f (a)
h
.
(2.30)
We have
∂
u
f (a) = ∇f (a) · u.
(2.31)
By Cauchy-Schwarz’s inequality |∂
u
f (a)| ≤ |∇f (a)||u| = |∇f (a)|. Hence
∂
u
f (a) attains its maximum value |∇f (a)| when u = λ∇f (a) for some λ > 0.
2.2.2
Vector-valued functions
Definition 2.17.
Let f : R
n
→ R
m
, a ∈ R
n
. We say f is differentiable at a
if there is a m × n matrix L such that
f (a + h) = f (a) + Lh + E(h), where E(h) ∈ R
m
,
lim
h
→0
E(h)
|h|
= 0. (2.32)
The matrix L, denoted by Df (a) (or f
′
(a)), is called the (Fr´echet) deriva-
tive of f at a.
Proposition 2.18.
If Df (a) exists, then it is unique.
Proposition 2.19.
If f is differentiable at a then f is continuous at a.
Proposition 2.20.
Let f = (f
1
, f
2
, . . . , f
m
) : R
n
→ R
m
be differentiable
at a ∈ R
n
. Then the partial derivatives ∂
x
j
f
i
(a), for i = 1, 2, . . . , m, j =
1, 2, . . . , n, exist and the matrix Df (a) is
Df =
∂f
i
∂x
j
i=1,...,m
j
=1,...,n
=
Df
1
Df
2
..
.
Df
m
=
∂f
1
∂x
1
∂f
1
∂x
2
. . .
∂f
1
∂x
n
∂f
2
∂x
1
∂f
2
∂x
2
. . .
∂f
2
∂x
n
...
...
...
...
∂f
m
∂x
1
∂f
m
∂x
2
. . .
∂f
m
∂x
n
.
(2.33)
Theorem 2.21
(Chain Rule). Suppose g : R
k
→ R
n
is differentiable at
a ∈ R
k
and f : R
n
→ R
m
is differentiable at b = g(a) ∈ R
n
. Then their
composition H = f ◦ g : R
k
→ R
m
is differentiable at a, and
DH(a) = DF (b)Dg(a).
(2.34)

2.3.
THE MEAN VALUE THEOREM
29
Note that Df is an m × n matrix, Dg is an n × k matrix and DH is an
m × k matrix.
Theorem 2.22.
Let S ⊂ R
n
be open, f : S → R, and a ∈ S. Suppose all
partial derivatives ∂
j
f (a), for j = 1, 2, . . . , n, exist in a neighborhood of a
and are continuous at a, then f is differentiable at a.
2.3
The Mean Value Theorem
The following notation is not standard and is only used in this lecture note.
Let a, b ∈ R
n
, we denote the line segments whose endpoints are a and b
by
[a, b] = {(1 − t)a + tb : t ∈ [0, 1]},
and
(a, b) = {(1 − t)a + tb : t ∈ (0, 1)},
Note that l(t) = (1 − t)a + tb, for t ∈ [0, 1], is the equation for the closed
line segment [a, b], and l(0) = a, l(1) = b.
A subset S of R
n
is called convex if for any a, b ∈ S, we have [a, b] ⊂ S.
Note that every convex set is connected.
Theorem 2.23.
Let S be an open subset of R
n
and a, b ∈ S such that
[a, b] ⊂ S. Suppose f : S → R is continuous on [a, b] and differentiable on
(a, b), then there is a point c ∈ [a, b] such that
f (b) − f (a) = ∇f (c) · (b − a).
Corollary 2.24.
Suppose f is differentiable on an open convex set S ⊂ R
n
and |∇f (x)| ≤ M for all x ∈ S. Then |f (b) − f (a)| ≤ M|b − a| for all
a, b ∈ S.
Remark: We can use this to prove the uniform continuity of a function.
Corollary 2.25.
If S is convex, f is differentiable on S and ∇f (x) = 0 for
all x ∈ S, then f is constant on S.

30
CHAPTER 2.
DIFFERENTIAL CALCULUS
Corollary 2.25 still holds true when S is only connected.
Theorem 2.26.
Suppose f is differentiable on an open connected set S ⊂ R
n
and ∇f (x) = 0 for all x ∈ S. Then f is constant on S.
2.4
Higher-order partial derivatives
See Section 2.6 of the textbook.
Suppose f is defined on an open set S ⊂ R
n
and ∂
x
j
f , for some j ∈
{1, 2, . . . , n}, exists on S. Then whenever it makes sense, we have the second-
order derivative ∂
x
i
∂
x
j
f
.
Notation:
∂
2
f
∂x
i
∂x
j
, f
x
j
x
i
, f
ji
, ∂
x
i
∂
x
j
f, ∂
i
∂
j
f.
In particular,
∂
2
f
∂x
2
j
, f
x
j
x
j
, f
jj
, ∂
2
x
j
f, ∂
2
j
f.
Similarly, we may have third-order partial derivatives ∂
x
k
∂
x
i
∂
x
j
f where
j, i, k ∈ {1, 2, . . . , n}; or the k-order partial derivatives
∂
x
jk
. . . ∂
x
j2
∂
x
j1
f,
for k ∈ N and j
1
, j
2
, . . . , j
k
∈ {1, 2, . . . , n}.
For our convention, the zero-order derivative of f is just f itself.
Definition 2.27.
Let U ⊂ R
n
be open and f : U → R.
The function f is said to be of class C
k
on U if all the partial derivatives
of f up to order k exist and are continuous on U. Notation f ∈ C
k
(U).
If all partial derivatives of f of all orders exist and are continuous on U
then f is said of class C
∞
. Notation f ∈ C
∞
(U).
In the case of vector-valued functions, f = (f
1
, f
2
, . . . , f
m
) is said of class
C
k
, (or C
∞
,) if each f
j
, for j = 1, 2, . . . , m, is of class C
k
, (or C
∞
).

2.4.
HIGHER-ORDER PARTIAL DERIVATIVES
31
Theorem 2.28.
Let f be a function defined in an open set S ⊂ R
n
. Suppose
a ∈ S and i, j ∈ {1, 2, . . . , n}. If the derivatives ∂
i
f , ∂
j
f , ∂
i
∂
j
f and ∂
j
∂
i
f
exist in S and are continuous at a, then ∂
i
∂
j
f (a) = ∂
j
∂
i
f (a).
Corollary 2.29.
If f ∈ C
2
(S) where S ⊂ R
n
is open, then ∂
i
∂
j
f = ∂
j
∂
i
f
on S for all i, j.
For higher order derivatives, we have the following theorem
Theorem 2.30.
If f ∈ C
k
(S) where S ⊂ R
n
is open, then
∂
i
1
∂
i
2
. . . ∂
i
k
f = ∂
j
1
∂
j
2
. . . ∂
j
k
f,
whenever the sequence {j
1
, j
2
, . . . , j
k
} is a reordering of {i
1
, i
2
, . . . , i
k
}.
Multi-index Notation.
A multi-index is an n-tuple of non-negative
integers:
α = (α
1
, α
2
, . . . , α
n
),
α
j
∈ {0, 1, 2, . . .}.
Let α = (α
1
, α
2
, . . . , α
n
) be a multi-index, x = (x
1
, x
2
, . . . , x
n
) ∈ R
n
and
f : R
n
→ R. We define
|α| = α
1
+ α
2
+ . . . + α
n
,
α! = α
1
!α
2
! . . . α
n
!,
x
α
= x
α
1
1
x
α
2
2
. . . x
α
n
n
,
∂
α
f = ∂
α
1
1
∂
α
2
2
. . . ∂
α
n
n
f =
∂
|α|
f
∂x
1
α
1
∂x
2
α
2
. . . ∂x
n
α
n
.
Recall 0! = 1, 1! = 1, 2! = 2(1!) = 2, k! = k[(k − 1)!] = 1 · 2 · . . . · k.
The number |α| is called the order or degree of α. Also, |α| is the order
of the partial derivative ∂
α
f .
Theorem 2.31
(Multinomial Theorem). For any x = (x
1
, x
2
, . . . , x
n
) ∈ R
n
and k ∈ N, we have
(x
1
+ x
2
+ . . . + x
n
)
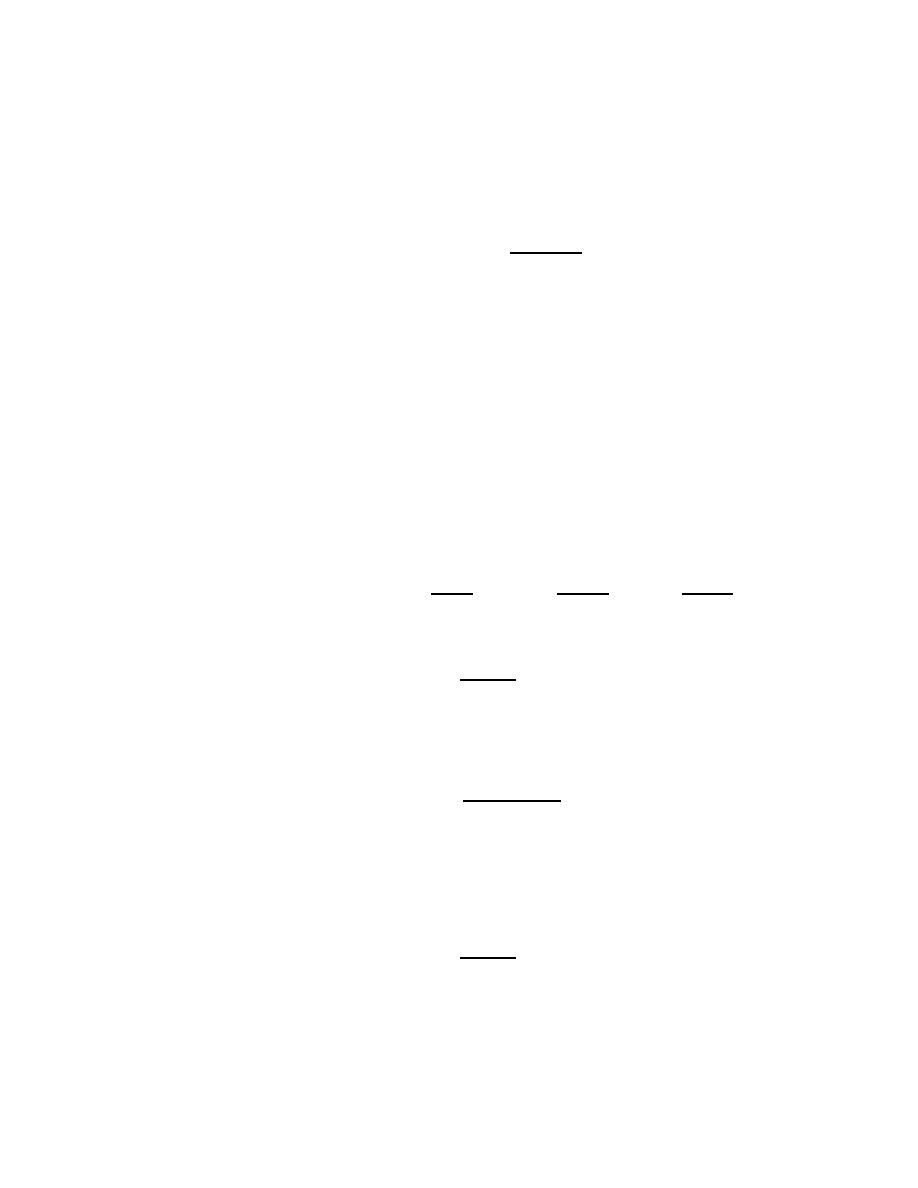
k
=
X
|α|=k
k!
α!
x
α
.
32
CHAPTER 2.
DIFFERENTIAL CALCULUS
Particularly, when n = 2,
(x
1
+ x
2
)
k
=
k
X
j
=0
k!
j!(k − j)!
x
j
.
2.5
Taylor’s Theorem
We only present Taylor’s theorem with Lagrange’s remainder.
2.5.1
In one variable
We aim to approximate the value of a function f near a using the polynomials.
The following was explained in details in class.
We write f (a + h) = P
a,k
(h) + R
a,k
(h), where P
a,k
(h) is the k-order Taylor
polynomial
P
a,k
(h) = f (a) + f
′
(a)h +
f
′′
(a)
2
h
2
+ . . . +
f
(k)
(a)
k!
h
k
=
k
X
j
=0
f
(j)
(a)
j!
h
j
.
We expect to have
lim
h
→0
R
a,k
(h)
h
k
= 0.
Theorem 2.32.
Suppose f is k + 1 times differentiable on an interval I ⊂ R
and a ∈ I. For each h ∈ R such that a + h ∈ I, there is a point c between 0
and h such that
R
a,k
(h) =
f
(k+1)
(a + c)
(k + 1)!
h
k
+1
.
The proof of the above theorem requires a generalization of Rolle’s Lemma
for higher derivatives (see Lemma 2.62 in the text).
Corollary 2.33.
If |f
(k+1)
(x)| ≤ M for all x ∈ I then
lim
h
→0
R
a,k
(h)
h
k
= 0.
See Proposition 2.65 in the text for some examples of Taylor polynomials.
2.6.
CRITICAL POINTS
33
2.5.2
In several variables
Theorem 2.34.
Suppose f : R
n
→ R is of class C
k
+1
on an open convex set
S. If a, a + h ∈ S, then f (a + h) = P
a,k
(h)R
a,k
(h)
where
P
a,k
(h) =
X
|α|≤k
∂
α
f (a)
α!
h
α
,
R
a,k
(h) =
X
|α|=k+1
∂
α
f (a + ch)
α!
h
α
,
for some c ∈ (0, 1).
Corollary 2.35.
If, in addition to Theorem 2.34, we have |∂
α
f (x)| ≤ M for
all x ∈ S and |α| = k + 1, then
|R
a,k
(h)| ≤
M
(k + 1)!
(|h
1
| + |h
2
| + . . . + |h
n
|)
k
+1
,
and consequently,
lim
h
→0
R
a,k
(h)
|h|
k
= 0.
2.6
Critical Points
Theorem 2.36.
Let S ⊂ R
n
and f : S → R. If f has a local maximum or
local minimum at a ∈ S and f is differentiable at a, then ∇f (a) = 0.
