
א מ א
א מ א
א מ א
א מ א
:
!
" # $
:
%!& '()*
.

2
................................
................................
................
3
"#$ % & '( )* + , -./ %0
................................
.........................
3
+ , -./ %0
................................
................................
..........................
3
)* + , -./
................................
................................
.........................
4
1 &
)* -./# "#$
................................
................................
.............
4
)* -./# 23 4(56
................................
................................
............
5
)* 7 8 #$ 23 9 :3#
................................
.......................
5
)* + , -./# 1 &
................................
...............................
6
"#$ % & '( -5# + , -./ %0
................................
........................
7
%23; ( -5# + , -./ < 5'
................................
...............................
7
-5# + , -./# #$ 23 =+>
................................
................
9
-5# + , -./# 1 &
................................
................................
........
10
?@ -
................................
................................
..............................
12
A>
................................
................................
..........
13

2
BC '
:
#E + , 5F GHI <; @ J G :0 K
Ω
@# %F+I :3L
.
M N OP
Q5> (& O R ST 5N@I
+ , -./ %#I -./ 5F GHI MR
)
( )* M '
(
K( W
-./ XY>R' Z [* \X 5F O ]@ + , ^$_ M`2 a bYX
.
2@ [* bYX M c(
)
-./
$( d( K X.e f('( # f(' M OP
(
$ 7 #E M`2
"( 2@ ^$ g#$ 7 #E X h#
f( %2
1
.
:3# i#' A3 \%2 W-+2 53; \X [* ^$_ O j' Z -5k@ bYX M Q5I l
^$_ g#$
)
[*
(
g g56m O no i#' #; W-j I g@H@( 8( 8A> O
$
O ( \p 5 1 :3 -./ 8
M #N MA3P MY
:* :0
.
2
-
1
م ا ة ا ا
م ا ة ا ا ا
ا زﻱ ا ة ا ا ا
ﺵوط دا ا
ة ا ا ا
ا ا ة ا ا ا$ %& ا ' ا
دا ا زﻱ ة ا ا ا
2
-
1
-
1
8(_ :0 K
_ #q + , 5F @*a
Ω = {a
1
, a
2
, a
3
, …, a
n
}
5@ r$ W
a
i
gs@
5F @t u+I (
.
M sN OP
s@# s%# \#sI + s, -./s s5F GsHI
x
i
vs@2
:
X = {x
1
, x
2
, x
3
, …, x
n
}
l5I w O(
P(x
i
)
(
p
i
8 ' -./ xI y
X
s#* G*z 8#$ :3L
x
i
)
#* J> (
x
. (
!
"
#$% & ' $( #)*
! +
1
.
, "
:
+ , -./ v x 5* fY x \#I M OP 5I v |*T 5] K
X
.
8 @# [*
X
\X
:
1
W
2
W
3
W
4
W
5
W
6
.
@X X( W%**z 8#$ GHI M OP # :
1/6
.
A3 vI(
:
,…
P(X = 1) = f(1) = 1/6, P(X = 2) = f(2) = 1/6
} ?~(
+ , -./
)*
)
0@ (
(
(
+ , -./
-5#
)
(
(
.
1
Q5@ -5# -./# @ O )* -./ y p G)@ %2 x % | < 5 YX @
- [* ( gFc GH' g#$ M #2
8
X
.

\p 5 |$ ( g#$ ST :>
–
|?
1
.
4
2
-
1
-
2
R -.>_ bYX l5I )* + , -./@ ( -5# + , -./ } ?#
. "
/" 01. 2345
1
#*" ,7 8 /9 :$ ;"
.
, "
1
:
G/ 8q :>
[2, 5]
-./
X
Y>R' 8(_ 83 K 25
4
@t [
\X
2
W
3
W
4
(
5
.
<'&
8 @# [* M
X
)
1
W
2
W
3
W
4
W
5
W
6
(
h#$ 7 #E M`2 Y( W2@ \X
f(
1
.
∑
=
=
=
6
1
1
)
(
x
x
X
P
, "
2
.
+ , -./ }I M OP }'5 *I ) |*T 5] K
X
s; y 8 a g5 :3L Z
.
K
8 @# [* a bYX
X
\X
0
W
1
W
2
.
A3 W5F 0I O A)I Q5> + , g./ }' OP xI $
Y
./ \X( W-J y 8 a g5
[* >R' -
0
W
1
W
2
-./ w W
Z
ro
:
Z = X – Y
W
...
8 @# [*
X
\X
0
W
2
W
2
.
\ #; $ OP %#* *H g#$
:
P(Z = 0) = P(X – Y = 0) = P((X = 0
∧
Y = 0)
∨
(X = 1
∧
Y = 1)
∨
(X = 2
∧
Y = 2))
=>P(Z = 0) = 0 + P(X = 1
∧
Y = 1) + 0 = 2 X 0.5² = 0.5
> 3? * "?
:
W7 K 5) ^ $ W+ K (_
...
<'&
•
# -J(5N d )* + , -./
)
#; g./
(
K vsC xs :$ fY 5 * A3 W
J ;
)
W WO$ W8 *
(...
z x@ <, fY 5 7 I W
W :
..
s I g./ \X
.
OsP
%J :% 7 I : a` #; ST @ g./ : z
.
•
K s A3 W-5# -./ XjI O# [* O .; )* -./ gY> T
2007
5+? K
.
2
-
1
-
2
-
1
\ 8#$ 1 & ' + , -./ "#$ 1 & *I
)
x#
1
(
1 & YX O jI W-./# @# [* y
* } 8( 8A> O T
+ , -./# ' -./#; 8#$ }' ( W# : 8#$( @# [
.
>
xIR "#$ 1 & l5I J
:
@ AB5 & '& C" /9 :$ . 7
.
l5o -./# ?5I
'
l5o -./ XY>R' Z [*( .;
'
./
2 W
\ #; @ # 8#$ O j@
P(X
= x)
N vI(
:
f(x)
.
y#'(
f(x)
0
9
'&
.
, "
1
.
8(_ 83# 7 "#$ 1 &
)
FI
5I v |*T
(
\ #; v
:
1
%@ #q M '
(finie)
f z dI; T ( > dI; T
n
r$ WN 5@
n
_ #E :3 + #q M ' T( Wv iH
} -J **a _ #E ( 50
$ ( 50
.
#q M ' Y;
(dénombrable)
O O( %@ .e d@; T ( %@ dI; T
W 50 _ #E A3 W" X5@ v'5'
...

:0
I
I
.
+ , -./
5
X
1
2
3
4
5
6
∑
f(x) = P(X = x)
1/6
1/6
1/6
1/6
1/6
1/6
1
, "
2
.
8 "#$ 1 &
X
*I )* }J K -J g5 W
:
X
0
1
2
∑
f(x) = P(X = x)
1/4
2/4
1/4
1
<'&
•
8#$ A3 W50 ( g#$ M C "#$ 1 & K @B6 ~ M OP
3
}sJ K J
50 X *I )*
(
8#$ Y;
10
WJ
...
•
X #* bYX 8#$2 a bYX K( W-$( @t # + , -./ M '
1
8#$( W
Q5s> # f
X
0
.
5 1 & ' "#$ 1 & YX y#
(Dyrac)
.
2
-
1
-
2
-
2
! "
\ #; @ # 8#$ O jI
P(X = x)
N vI(
:
f(x)
y#'(
f(x)
#$ 23
.
\
dI; W J OP
W
3;
M@ MC56 G*H M v #$ 2
:
∑
=
≥
x
x
f
x
f
1
)
(
)
2
0
)
(
)
1
, "
:
23 Y>RI
7 -./
X
:3L
5I 5F$ |*T FI
.
@
G* 8(_ 45,
:
f(1) = f(2) = f(3) = … f(6) = 1/6 ≥ 0
M_ N 93 45,(
:
Σf(x) = 1/6 + 1/6 + … + 1/6 = 6(1/6) = 1
2
-
1
-
2
-
3
" #$
% !
L
:3
+ , -./
J y & -# 8A> O O( H@ 8A> O )*
X
.
, "
:
8 23 8( g@H@ I :3~
X
:
( -J y 8 a g5
Z
:
( J } 50
@ g
) |*T
}'5 *I
.
\p 5 |$ ( g#$ ST :>
–
|?
1
.
6
:DE
2
F
1
.
+ 1 B
5
G
.
G
A$"
G
2
-
1
-
2
-
4
"
:3L
1 &
N y#'(
"
#F
"
#;5 (
–
8E 8#$
s # ST @t # 5/ O [*
x
W
l5'(
\ #;
:
∑
≤
=
≤
=
x
u
u
f
x
X
P
x
F
)
(
)
(
)
(
:
X
.
! "#! $ "%&
4
!
'
4
.
P(X = 4) = f(4) = 1/6 ,
P(X ≤ 4) = F(4) = P(1) + P(2) + P(3) + P(4) = 4(1/6) = 4/6
(% )*
X
+,- . /0 1 2345
F(x)
6 % /765 .89
:
:
1:$&
F(x)
$
F(z)
;!
:
X
:
1
10 <' =
>5 61 ?*
$
Z
:
=@8 1$ ' 1 >@ A7
@ /B$
.
2
1
0
X
¼
1/2
1/4
f(x)
1
3/4
1/4
F(x)
2
0
-2
Z
¼
1/2
1/4
f(x)
1
3/4
1/4
F(x)= P(X ≤ x)
f(z)
1 -
1/2 -
1/4 -
f(x)
0 1 2 x
1
1/2
1/4
z
-2 0 2
+∞
<
≤
+
+
+
⋅
⋅
⋅
<
≤
+
<
≤
<
<
−∞
=
x
x
x
f
x
f
x
f
x
x
x
x
f
x
f
x
x
x
x
f
x
x
x
F
n
n
),
(
.
.
.
)
(
)
(
,
)
(
)
(
,
)
(
,
0
)
(
2
1
3
2
2
1
2
1
1
1
C7
I
I
.
D
E F <GH
7
+&
I J 08K L%&$ M N& O 0 + 85 P I$ Q R8S 2345 D T 6
1
.
:
:&
6
(
Q '
U&
V$W XRB = 0# R3 "Y& C7Z
[ .
\]
.
\D ^6
_R`@ `*
#6
/S <1D
*$
U$ /S
aRa *$
b $1c "#! /S&
:
X
/SW
1
1.5
3
!P
0.5
0.3
0.2
W U$ /S 0 . C7Z _R <1 + 85 +& ! "#!&
B%
.
2
-
2
2
-
2
-
1
< #D E F <GHD
! " # $ %!&' ( ) *+ , - !& # $
. #
.
6& .89
5
6
O - d4@ < #D <GHD U
R
/0 ?e: O $& 1W M
.
= 1!$ +4- 2I C:& .
D <GHD f
#
+ 85 <
<
1
D + .e CB < #
-#
...
!P -B8
< #D E F <GH
6 % "85
:
x
x
x
X
x
P
x
f
x
∆
∆
+
<
<
=
→
∆
)
(
lim
)
(
0
1
Gh% 1 +% )* < # <GH % =0D 1 $& +8# 1 CB % L +& .89
$ "6 1 f'1 10 4#D [2J i Q 678 j- ]
!P =6 kh l' m #
.
+ $& I <1! (% +* $ <'$@ I - ?S . % C% O
...
)* I < #D <GHD
j08 ! /0 B%& \ -
\ -
.
0 1 2
1 -
3/4 -
1/2 -
1/4 -
x
F(x)
-1 0 1
z
F(z)
*01
2
2
2
34+5 3 "6 7 8 & 9: "
1 -
3/4 -
1/2 -
-
n6 ?!o $ =P !P V* C31
–
?ec
1
.
8
q0# U6 .
:
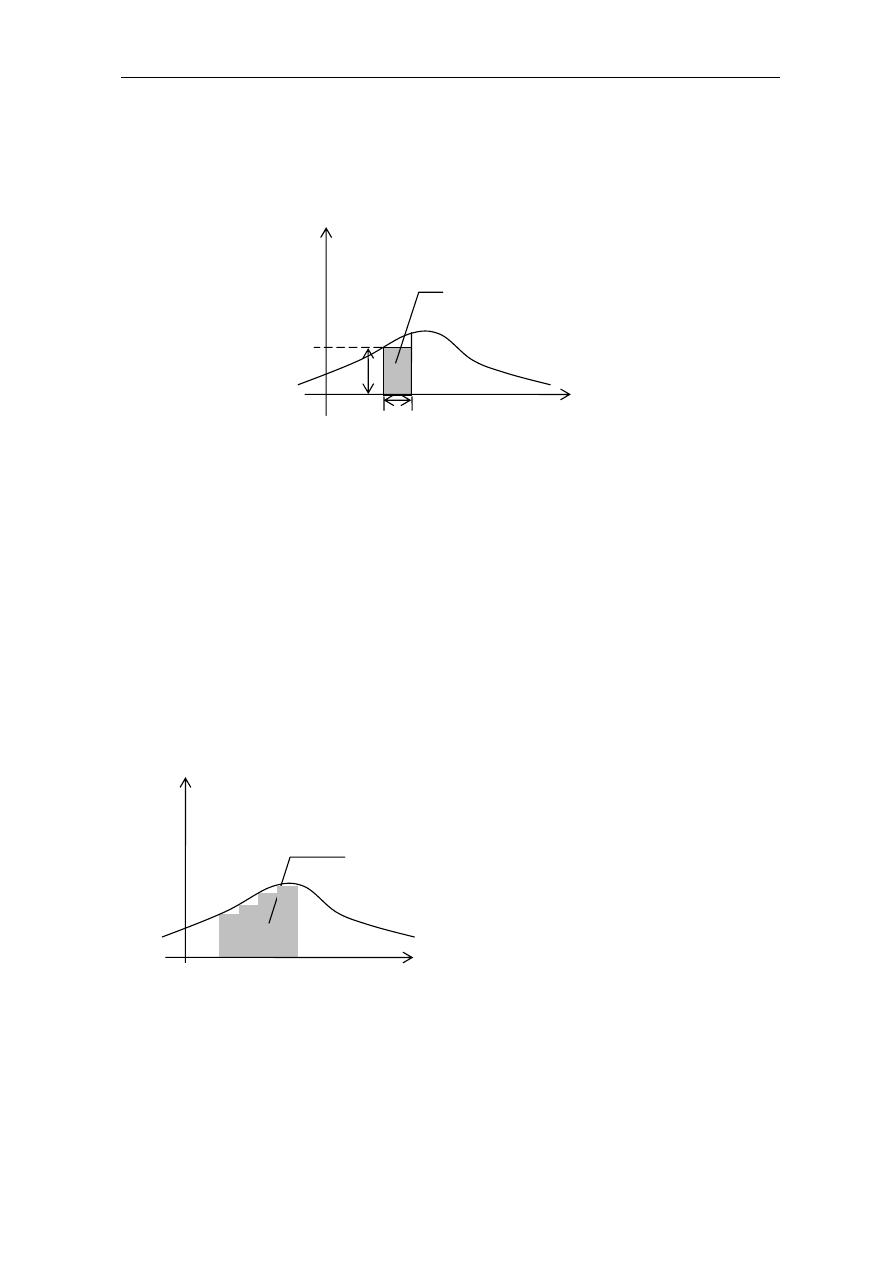
P(x < X < x + ∆x) ≈ f(x) ∆x
rs0D (t !#D T M . !# CB9 !P 2I
.
:$ ! . Gh 6Z _0Q .89 < $#D u7 . R
X
M . n
[a, b]
6 %
:
#D #0
[a, b]
<1: D
' v
X
I' 1 6$# <GHY V*
∆x
` I $1! + 85 ;w
b
:
x
1
, x
2
, . . . x
i
, . . .x
n
, x
n+1
1x
:
P(x
1
< X < x
1
+ ∆x) ≈ f(x
1
) ∆x
P(x
2
< X < x
2
+ ∆x) ≈ f(x
2
) ∆x
. . . . . . . .
P(x
n
< X < x
n
+ ∆x) ≈ f(x
n
) ∆x
j0 $
:
P(a < X < b) = P(x
1
< X < x
n
+ ∆x) ≈
∑
i
f(x
i
) ∆x
n @ $
∆x
0
1x
:
P(a < X < b) = lim
∆x
0
∑
i
f(x
i
) ∆x
6 I$
@8 V*
:
0 a x
2
x
3 ….
b x
f(x)
P(a < X < b) = P(x
1
< X < x
n
+ ∆x)
≈
∑
i
f(x
i
) ∆x
f(x)
f(x)
∆x
0 x
x x+∆x
f(x) ∆x
C7
I
I
.
D
E F <GH
9
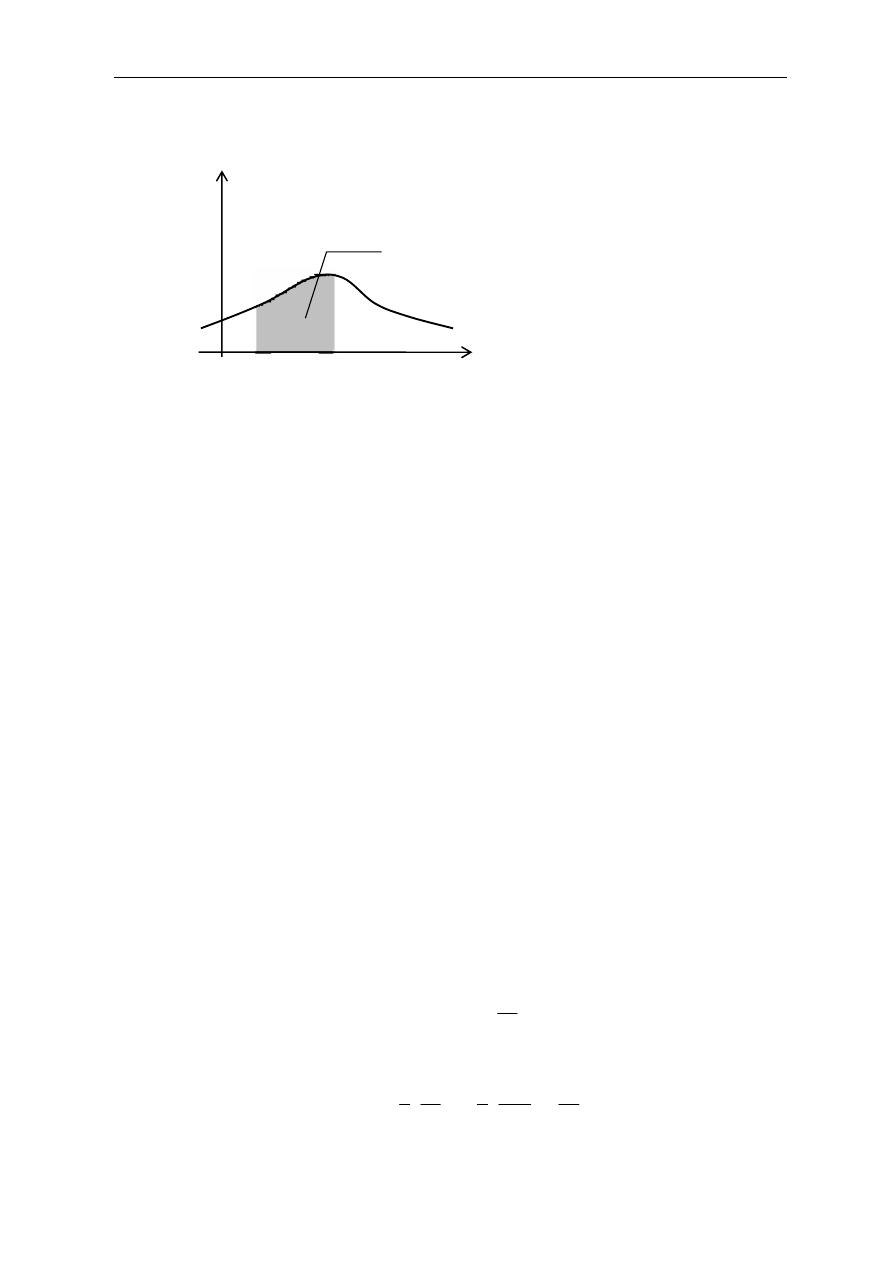
∫
=
<
<
b
a
dx
x
f
b
X
a
P
)
(
)
(
j&
/0@ ! +,- < #D <GHD ! O
x
0
N$#6
0
:
P(x
0
< X < x
0
+ ∆x) ≈ f(x
0
) ∆x => lim
∆x
0
P(x < X < x + ∆x) = 0
=> P(X = x
0
) = 0
+& RB y6 2I
:
P(X < x) = P(X ≤ x)
$
P(X > x) = P(X ≥ x)
2
-
2
-
2
6 % "85 < #D T !P -B8 z$S +& 1x T { <'S,@ C8 <'S* 1hQ@
:
∫
∞
+
∞
−
=
≥
1
)
(
)
2
0
)
(
)
1
dx
x
f
x
f
' | C7Q& }6 +& .89 P -B8 rs0 +& )* /61h .
-W ' v $ rs0D >@ ~o !#D +& % T
1! N$#5
.
3& =PM =P ! R3 . =P{ k@ =P ! #! O 175 E [2I
.
RB
:
P(X > x) = 1 – P(X ≤ x)
:
(@B 1:$&
C
-B8 1 B $ $W >ZF t
1 O !P
:
•
+ 85 +& ! "#!&
X
. 05
1
V*
2
.
•
+ 85 +& ! "#!&
X
. 05 P
1
V*
2
.
<
<
=
sinon
0
3
0
²
)
(
x
cx
x
f
9
/
1
1
9
3
1
0
²
0
1
)
(
3
0
3
0
3
0
3
=
=>
=
=
=>
=
+
+
=>
=
∫
∫
∫
∫
∞
−
∞
+
∞
+
∞
−
C
C
x
C
dx
dx
Cx
dx
dx
x
f
x
C = 1/9
.
( )
27
7
3
1
8
9
1
3
9
1
²
9
/
1
)
(
)
2
1
(
2
1
3
2
1
2
1
=
−
=
=
=
=
≤
<
∫
∫
x
dx
x
dx
x
f
x
P
0 a b x
f(x)
∫
=
<
<
b
a
dx
x
f
b
X
a
P
)
(
)
(
!"#$
–
&'
1
.
10
27
20
27
7
1
)
2
1
(
1
)
2
1
(
=
−
=
<
<
−
=
>
>
x
P
x
P
2
-
2
-
3
() *+
)
-./0 1/2
. # 3
(
/ 567 589/
:
∫
∞
−
=
≤
=
x
du
u
f
x
X
P
x
F
)
(
)
(
)
(
:
1;6 <7 = 5>?7 589/ () #@
.
< A6B () C#DE
:
P(1< x < 2)
.
0
0
)
(
)
(
:
0
*
0
=
=
=
<
∫
∫
∞
−
∞
−
du
du
u
f
x
F
x
x
27
3
9
1
²
9
1
0
)
(
)
(
:
3
0
*
3
0
3
0
0
x
u
du
u
du
du
u
f
x
F
x
x
x
x
=
=
+
=
=
<
≤
∫
∫
∫
∞
−
∞
−
0
²
9
1
0
)
(
)
(
:
3
*
3
3
0
0
+
+
=
=
≥
∫
∫
∫
∫
∞
−
∞
−
du
du
u
du
du
u
f
x
F
x
x
x
1
27
27
0
3
9
1
0
0
3
0
3
=
=
+
+
=
u
du
≥
<
≤
<
=
3
1
3
0
27
/
0
0
)
(
3
x
x
x
x
x
F
F# G$ .># AH I !; FJK$ ()
L?I MN GO FP +.Q !R S ?I
/ M> .TU
:
1
)
(
lim
1
)
(
)
(
)
(
lim
)
(
lim
=
⇒
=
=
=
∫
∫
∫
∞
∞
−
∞
→
∞
∞
−
∞
−
∞
→
∞
→
x
F
dx
x
f
du
u
f
du
u
f
x
F
x
x
x
x
V !7;
:
Lim
x
-∞
F(x) = 0
2
3
.
:
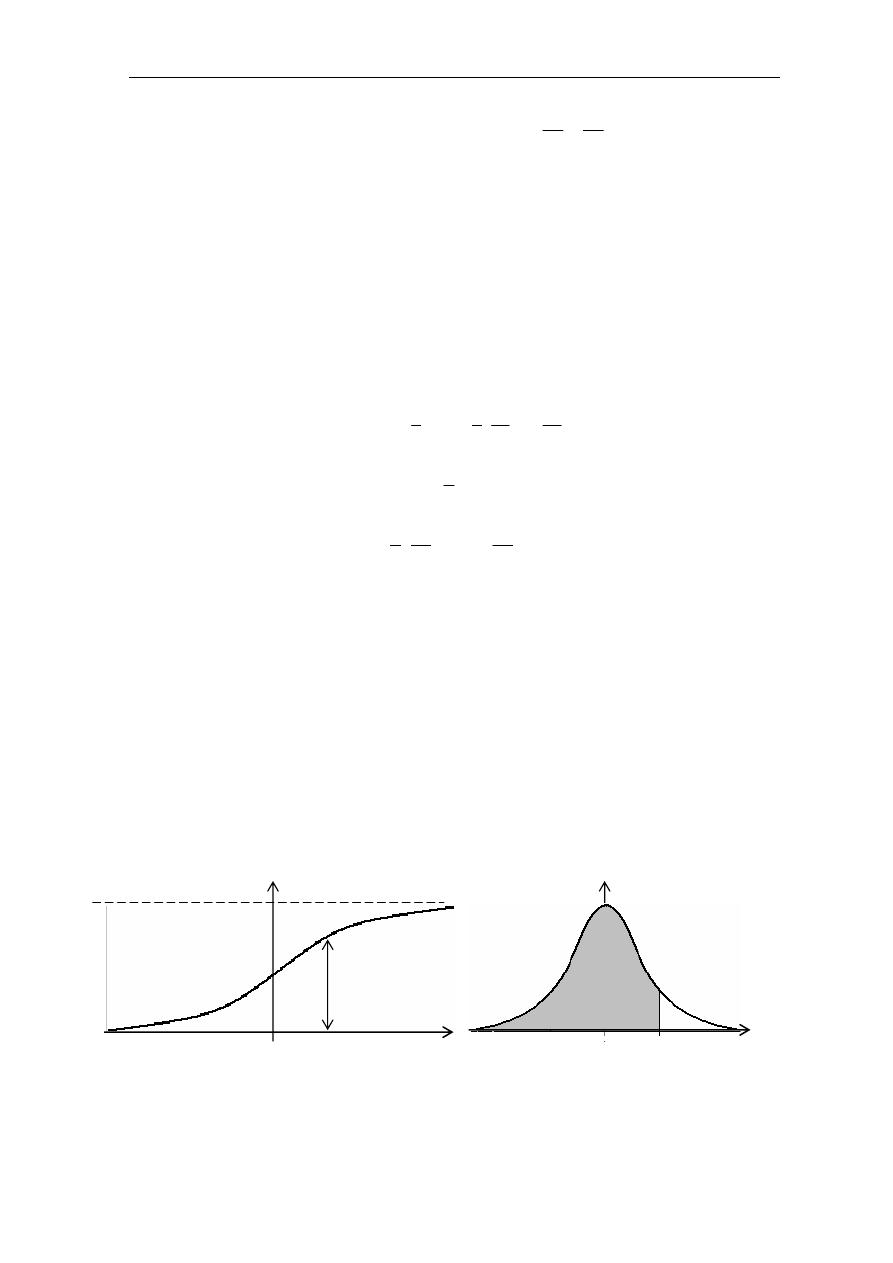
!"#
.
1 F(x)
F(x
0
)
0 x
0
x
f(x)
F(x
0
)
x
0
I
I
.
11
! "#$
% &'(
F(x)
%)*
+%,$ -. /%, 01 )
x
23
45'
f(x)
01 ) 6
& 45')
F(x)
%78
.
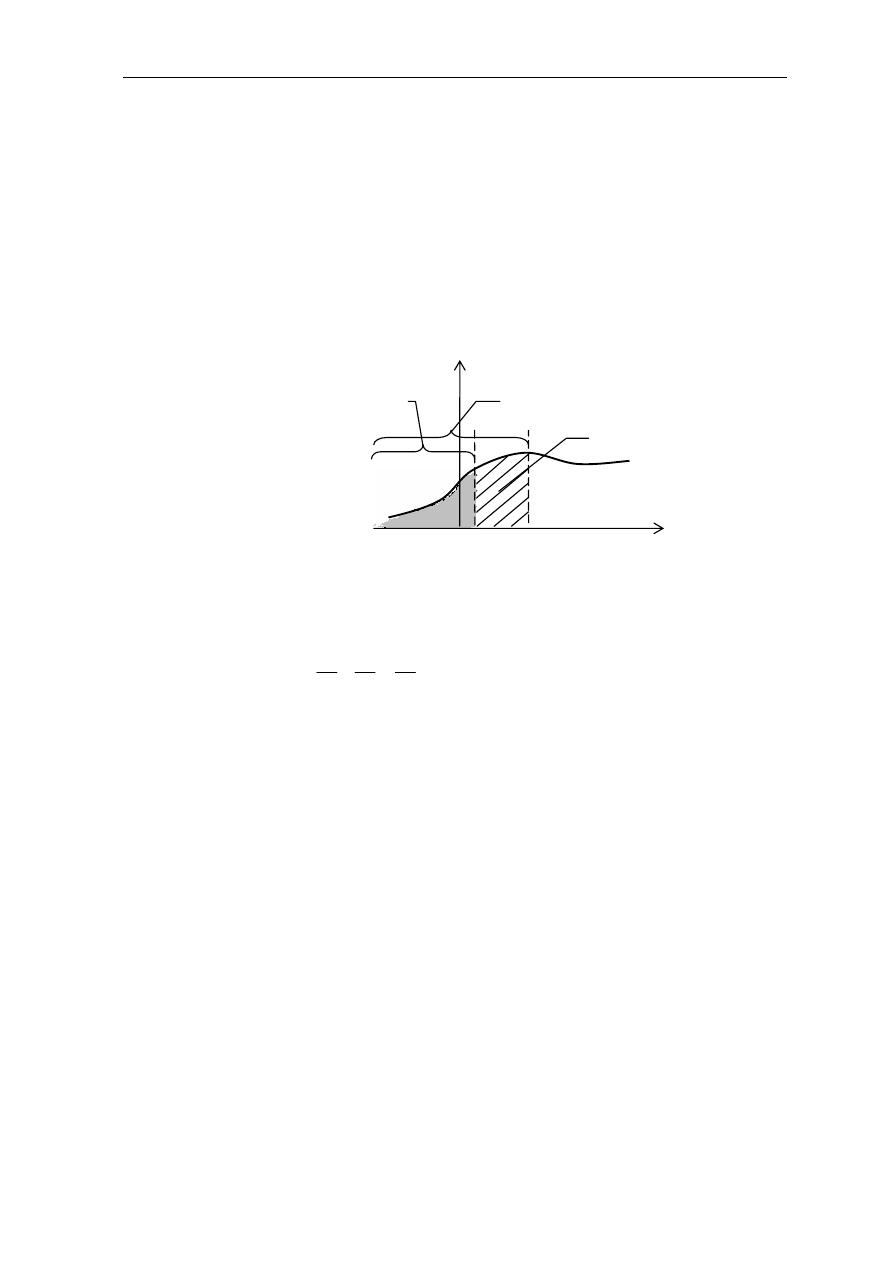
!9, %/ 9 :%9/; %<$=>6 ?<) 9@ A$= B ?<) C9,$
.
0%9/ D%,E
%) 0%F G &H>
(a, b)
&I 6 %J@% %'$+ %9 K%L B )%> ?&I
B ?
A$=
F(x)
% $!M' N86 O
:
$%
:
Q!@
a
6
b
$!> 0%F ) %RJ
X
S T O
b > a
:
P(a < x < b) = P(x < b) – P(x < a) = F(b) – F(a)
:
U1V> 0%9/ W,/ X@%, 0%L G
X
0%Y G 9 Z
(1 < x ≤ 2)
.
27
7
27
1
27
2
)
1
(
)
2
(
)
2
1
(
3
3
=
−
=
−
=
≤
<
F
F
x
P
$&
.
[', J@%, $!M' ) %ZR
:
P(X = c) = F(c + 0) – F(c)
2% 8* \ ]$ U(
F(x)
RJ' G !9,)
c
U1V> 0%9/ ^K
X
9 J
c
?6&) 0%9/ ( _#`%@
.
@%J G
2% 8*
F(x)
U1V> 0%9/ ^K RJ' U( G !9,) a
X
9 J
c
%@
0%J; +&J) b6%,$ _#`
)
d%e>+
(
0
F(x)
RJ' U( &'
.
.
45' : ! 01 )
F(x)
% g&/h i;%9/ ['
:
X = 0
O
X = 3
O
1 ≤ X < 2
O
X > 3
O
X < 0
O
X ≤ 3
"RJ' &'
0
6
3
+&Jj J'$ 45' k!
1/4
6
1/6
\')6 : -.
:
P(X = 0) = 1/4, P(X = 3) = 1/6
"@ O! +%,$ -. i;%Y G
1
6
2
" -. 6
3
&H> 0%9/ ]$ %) @%l &
X
?6&e) i;%Y U( G
\')6
:
P(X < 0) = 0, P(1 ≤ X < 2) = 0, P(X > 3) = 0, P(X ≤ 3) = 1 .
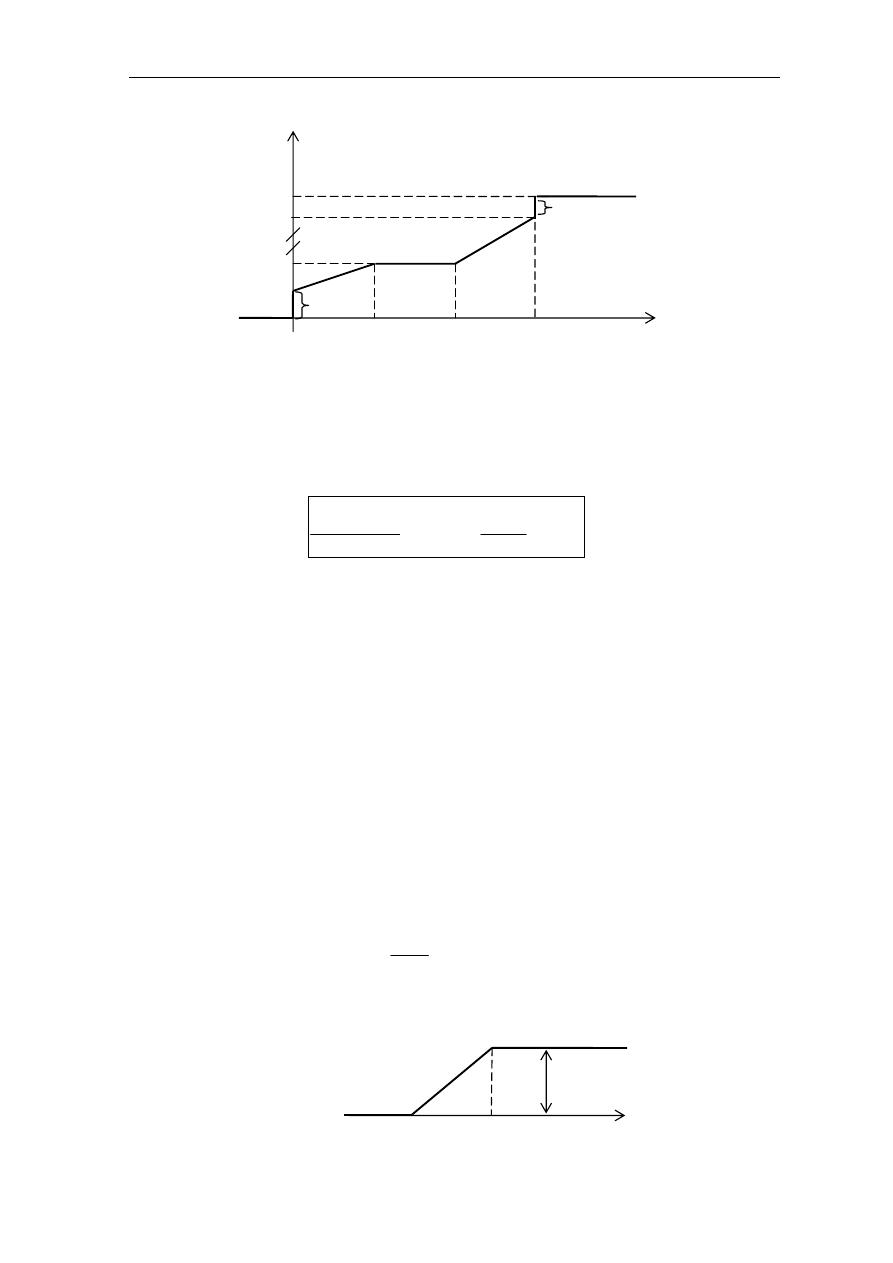
a b
x
F(a)
F(b)
f(x)
2
4
"#
X
'(
a
)
b
'( *+ ",
F(b)
)
F(a)
.
P(a < x < b)
mn%$! o%/p 6 i;%9/; q* 1&)
–
ost
1
.
12
(
)
x
x
x
e
e
x
f
e
x
F
x
x
F
x
f
x
2
2
2
2
1
)
(
1
)
(
:
0
*
0
)'
0
(
)
(
'
)
(
:
0
*
−
−
−
=
′
−
=
⇒
−
=
≥
=
=
=
<
1
2
5
.
F(x)
F(x)
.
2
-
2
-
4
& >
s '#$; &%Z
(Règle de LEIBNITZ)
K%L B m( A$= B J ) u%' G
:
)
(
)
(
)
(
)
(
x
f
dx
x
dF
x
f
dx
du
u
f
d
x
=
⇒
=
∫
∞
−
2% 8*
F(x)
J ) #J>
f(x)
0J %) 0%F G
F(x)
0%Y U( -. !9,)
.
:
9. K%L B &H6
X
m.$ %9 A$= B 2% 8*
:
≥
−
=
−
sinon
0
0
1
)
(
2
x
e
x
F
x
>
=
−
sinon
0
0
2
)
(
2
x
e
x
f
x
2
.
9. A$= B % % @ L) 6 W
X
%9.
f(x) = 1/(b - a)
0%Y G
[a, b]
6
0
N8 vw
.
>
≤
<
−
−
≤
=
b
x
b
x
a
a
b
a
x
a
x
x
F
,
1
,
,
,
0
)
(
F(x)
1
5/6
½
¼
0 1 2 3 x
F(x)
1
a b x
2
6
-. !"
(distribution uniforme)
.
P(x = 3) = 1/6
P(x = 0) = 1/4

I
I
.
13
3
.
9. K%L B W
X
% A$= B i8
≥
<
=
c
x
c
x
x
F
,
1
,
0
)
(
Dt
:
X
9 J U1V>
c
0%9/%@
1
b O
c
0 & / '9 9 J m(
X
2@%l +%# \ U( ]$ O
\ -. %)
9 J & /6 )
(singulière)
.
=
≠
=
c
x
c
x
x
f
,
1
,
0
)
(
2
-
3
!
%x .@%J i;%9/;6 9. '9 J &$&3 01 ) :%9/; A$= $!> $
.
06&H 01 ) %)* &$&5 U( $
)
:%9/; A$= 06&H
(
B -9,> O B 6
%9/; K%L
.
i;%9/; d9F $ 6 %)6B #H) > Wy %9/ K%L B %z %) B 0J m
$
b6%,
1
.
9{ &
)
A$= B 6
(
%) RJ q* 9. 9 Z !| ) 0%F 0%9/ L}
:
RJ) ? %/ G
:
∑
≤
=
≤
=
x
u
u
f
x
X
P
x
F
)
(
)
(
)
(
!9,) ? %/ G
:
∫
∞
−
=
≤
=
x
du
u
f
x
X
P
x
F
)
(
)
(
)
(
&$s) +%,) A$= B U1V> %<$! !M
)
0%Y ) osH -. %@%l 6
.(
e> %)&' !L 9{ & ~ =>
i;%F i;%9/%@ %<' / z %'h !9,)
.
A$= B %J 01 ) K%L B u%'
.
/0
:
+B 2' @
%/*
%) Q!)
)s%@ _#>!) @%|p 0%9/
)
X
:
',
(
% K%L B 01 )
:
<
<
=
sinon
0
3
0
²,
)
(
x
cx
x
f
•
@%|* > 0%9/ W,/
B!K
% +%
q6h ', G
.
