
ﻣﺪﺧﻞ ﺇﱃ
ﺍﻻﺣﺘﻤﺎﻻﺕ ﻭﺍﻹﺣﺼﺎﺀ ﺍﻟﺮﻳﺎﺿﻲ
ﻟﻄﻠﺒﺔ ﻛﻠﻴﺔ ﺍﻟﻌﻠﻮﻡ ﺍﻻﻗﺘﺼﺎﺩﻳﺔ
ﺩﺭﻭﺱ ﻣﻊ ﺃﻣﺜﻠﺔ ﻭﺗﻄﺒﻴﻘﺎﺕ ﳏﻠﻮﻟﺔ
ﺍﳉﺰﺀ ﺍﻟﺜﺎﱐ
:
ﺍﻹﺣﺼﺎﺀ
ﺍﻟﻔﺼﻞ ﺍﻟﺘﺎﺳﻊ
:
ﺍﺧﺘﺒﺎﺭﺍﺕ ﺍﻟﻔﺮﻭﺽ
ﺑﻮ ﻋﺒﺪ ﺍﷲ ﺻﺎﱀ
ﺃﺳﺘﺎﺫ
ﻣﺴﺎﻋﺪ
ﻣﻜﻠﻒ ﺑﺎﻟﺪﺭﻭﺱ
ﺑﻜﻠﻴﺔ ﺍﻟﻌﻠﻮﻡ ﺍﻻﻗﺘﺼﺎﺩﻳﺔ
–
ﺟﺎﻣﻌﺔ ﺍﳌﺴﻴﻠﺔ
.

ت س
ا
ﺍﻟﻔﺼﻞ
9
ﺎﺎﻘﻴﺒﻄﺗﻭ ﺽﻭﺮﻔﻟﺍ ﺕﺍﺭﺎﺒﺘﺧﺍ ﻢﻴﻫﺎﻔﻣ
................................
.......
3
ا ر ا
................................
................................
................................
...................
3
ار ا
!"#
.
................................
................................
................................
......
3
!"#دي ا&أ را
.
................................
................................
................................
.....
6
ام*+ا
S
ر ل*-آ
σ
ار ا
.
................................
................................
........................
8
1ام از*+ا
t
ار ا
.
................................
................................
.............................
8
345
................................
................................
................................
.............
9
6
................................
................................
................................
.............
9
ا ر او ا ر ا
................................
................................
................................
....
11
38ار ا
................................
................................
................................
...........
11
9ار ا
................................
................................
................................
...........
12
ر ا ر ا
................................
................................
................................
....
13
9;<" = وي8# را
................................
................................
................................
..
13
9;<" # وي8# را
................................
................................
................................
......
14
ا ر او ا ر ا
................................
................................
................................
.
15
AB"ار ا
................................
................................
................................
...........
15
*<ار ا
................................
................................
................................
...........
15

C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
3
ا
9
.
ارات اوض
ر ا
ا
-
ر ا
ا
-
ر ا
ا
-
تار ا
ر ا
-
ر ا
ا
وا
ﺗﻮﻃﺌﺔ
ﻏﺎﻟﺒﺎ ﻣﺎ
ﳛﺘﺎﺝ ﺍﻟ
ﺒﺎﺣﺚ
ﺘﻤﻊ ﺍﳌﺪﺭﺍ ﺹﻮﺼﲞ ﺮﺜﻛﺃ ﻭﺃ ﺔﻴﺿﺮﻓ ﺭﺎﺒﺘﺧﺍ ﱃﺇ ﻪﺜﲝ ﻦﻣ ﺎﻣ ﺔﻠﺣﺮﻣ ﰲ
ﻭﺱ
.
ﻣﻦ ﺃﻣﺜﻠﺔ ﺫﻟﻚ
:
، ﺍﺧﺘﺒﺎﺭ ﻓﺮﺿﻴﺔ ﻧﺴﺒﺔ ﺷﻔﺎﺀ ﻟﺪﻭﺍﺀ ﻣﻌﲔ،ﺔﻨﻴﻌﻣ ﺔﻘﻄﻨﻣ ﰲ ﻞﺧﺪﻟﺍ ﻝﺪﻌﻣ ﺹﻮﺼﲞ ﺔﻴﺿﺮﻓ ﺭﺎﺒﺘﺧﺍ
...
ﻳﺘﻢ ﺫﻟﻚ ﺑﺼﻴﺎﻏﺔ
ﺘﻤﻊ ﺍﳌﺪﺭﻭﺱﺍ ﻦﻋ ﺔﻴﺿﺮﻓ
)
ﺘﻤﻌﺎﺕ ﺍﳌﺪﺭﻭﺳﺔﺍ ﻭﺃ
(
ﻭﻣﻦ ﰒ ﳏﺎﻭﻟﺔ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺩﻟﻴﻞ ﺇﺣﺼﺎﺋﻲ ﻳﻨﻔﻲ ﺃﻭ ﻳﺜﺒﺖ ﻫﺬﻩ
ﺍﻟﻔﺮﺿﻴﺔ ﻭﺫﻟﻚ ﻣﻦ ﺧﻼﻝ ﺑﻴﺎﻧﺎﺕ ﻋﻴﻨﺔ
)ﺃ
ﻭ ﺃﻛﺜﺮ
(
ﻋﺸﻮﺍﺋﻴﺔ ﺑﺴﻴﻄﺔ
.
ﰲ ﻫﺬﺍ ﺍﻟﻔﺼﻞ
1
ﺳﻨﺘﻨﺎﻭﻝ ﻛﻴﻔﻴﺔ ﺍﺧﺘﺒﺎﺭ ﻓﺮﺿﻴﺎﺕ
ﻣﻮﺿﻮﻋﺔ ﺣﻮﻝ ﻣﻌﺎﱂ ﳎﺘﻤﻊ ﺃﻭ ﺃﻛﺜﺮ
.
ﺭﻳﺎﺿﻴﺎ
ﺘﻤﻊﺍ ﱂﺎﻌﻣ ﺪﺣﺃ ﺔﻴﺿﺮﻔﻟﺍ ﺺﲣ
ﺍﻹﺣﺼﺎﺋﻲ
، ﺍﻟﻨﺴﺒﺔ ﺃﻭ ﺍﻟﺘﺒﺎﻳﻦ،ﻂﺳﻮﺘﳌﺎﻛ
ﺎ ﺃﻭ ﺭﻓﻀﻬﺎ ﻋﻠﻰ ﺧﺼﺎﺋﺺ ﺇﺣﺼﺎﺋﻴﺔ ﻣﻌﺎﻳﻨﺔ ﳐﺘﺎﺭﺓﺎﺒﺛﺇ ﰲ ﺪﻤﺘﻌﻧﻭ
ﻋﺎﺩﺓ ﻣﺎ ﺗﻜﻮﻥ ﻣﻨﺎﻇﺮﺓ ﳌﻌﻠ،
ﺘﻤﻊﺍ ﺔﻤ
.
ﻣﻦ ﺃﺟﻞ ﺫﻟﻚ
ﻛﻤﺎ ﻫﻮ ﺍﳊﺎﻝ ﺑﺎﻟﻨﺴﺒﺔ،ﺱﺭﺪﻟﺍ ﺍﺬﻫ ﺪﻤﺘﻌﻳ
ﻟ
ﻋﻠﻰ ﺩﺭﺱ ﺍﳌﻌﺎﻳﻨﺔ،ﺮﻳﺪﻘﺘﻠ
.
9
-
1
-
1
.
ا ر ا
ا
ر
!"# ا
ا
ر
!"#دي ا&أ
ام*+ا
S
I ار ا1"ا 9 ر*-آ
1ز# ما*+J Iا را
t
ﺍﻟﻐﺮﺽ ﻣﻦ
ﺍﺧﺘﺒﺎﺭ ﺍﳌﺘﻮﺳﻂ ﻫﻮ ﺍ
ﺧﺘﺒﺎﺭ ﻓﺮﺿﻴﺔ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ ﻥﺃ
µ
)
ﻣﺘﻮﺳﻂ ﺍﻟﺪﺧﻞ
ﰲ ﺑﻠﺪ ﻣﺎ ﺃﻭ ﻟﻔﺌﺔ ﻣﺎ
ﻣﺘﻮﺳﻂ ﻭﺯﻥ،
،ﻣﻨﺘﺞ ﻣﻌﲔ
.
..
(
ﻳﺴﺎﻭﻱ
ﻗﻴﻤﺔ ﻣﺎ
µ
0
.
ﻟﻠﻘﻴﺎﻡ ﺑﺎﻻﺧﺘﺒﺎﺭ ﻧﺴﺘﺨﺮﺝ ﻋﻴﻨﺔ ﻋﺸﻮﺍﺋﻴﺔ
ﺑﺴﻴﻄﺔ ﻭ
ﳓﺴﺐ ﻓﻴﻬﺎ ﺍﳌﺘﻮﺳﻂ
m
2
.
ﺇﺫﺍ
ﻛﺎﻧﺖ ﺍﻟﻔﺮﺿﻴﺔ ﺻﺤﻴﺤﺔ ﻳﻔﺘﺮﺽ ﺃﻥ ﺗﻜﻮﻥ
m
ﻭ
µ
0
ﻣﺘﻘﺎﺭﺑﺘﲔ
.
ﺍﺧﺘﺒ
،ﺎﺭ ﺍﻟﻔﺮﺿﻴﺔ ﻳﻜﻮﻥ ﺑﺘﻘﻴﻴﻢ ﺍﻟﻔﺮﻕ ﺑﲔ ﻫﺎﺗﲔ ﺍﻟﻘﻴﻤﺘﲔ
ﲝﻴﺚ
ﻧﺮﻓﻀﻬﺎ ﺇﺫﺍ ﻛﺎﻥ ﺍﻟ
ﻔﺮﻕ ﻛﺒﲑﺍ
.
ﻟﺘﻘﻴﻴﻢ ﺍﻟﻔﺮﻕ ﺑﲔ ﺍﻟﻘﻴﻤﺘﲔ ﳓﺘﺎﺝ
ﺇﱃ
ﲢﺪﻳﺪ ﻃﺒﻴﻌﺔ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﻝ
M
)
ﻭ ﻫﻮ
ﻣﺎ ﻳﻌﻴﺪﻧﺎ ﺇﱃ ﻧﻈﺮﻳﺎﺕ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ
(
ﳊﺴﺎﺏ ﺍﺣﺘﻤﺎﻝ ﺍﻟﻔﺮﻕ ﺑﲔ،
m
ﻭ
µ
0
.
9
-
1
-
2
.
ا
! "ا #$ % ر
.
ﻟﻨﺘﻨﺎﻭﻝ ﻫﺬﺍ ﺍﳌﺜﺎﻝ
:
ﻧﺮﻳﺪ ﺍﺧﺘﺒﺎﺭ
،
ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
،
ﻓﺮﺿﻴﺔ
ﺃﻥ
ﻣﺘﻮﺳﻂ ﺩﺧﻞ ﺍﻟﻄﺎﻟﺐ ﰲ ﺍﻟﺴﻨﺔ ﺍﻷﻭﱃ ﻣﻦ ﲣﺮﺟﻪ
ﻳﺴﺎﻭﻱ ﺍﻟﻘﻴﻤﺔ
15000
ﺩﺝ
ﺍﻟﱵ ﻫﻲ ﻣﺘﻮﺳﻂ ﺍﻟﺪﺧﻞ ﰲ ﻋﻴﻨﺔ ﻣﻦ
100
ﺧﺮﻳﺞ ﻋﻠﻤﺎ ﺃﻥ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﻠﺪﺧﻞ ﻫﻮ
1500
ﻭﺃﻥ ﺍﻟﺪﺧﻞ ﻳﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
.
ﳓﺘﺎﺝ ﺇﱃ ﺍﳋﻄﻮﺍ
ﺕ ﺍﻟﺘﺎﻟﻴﺔ
:
−
ﺻﻴﺎﻏﺔ
،ﺍﻟﻔﺮﺿﻴﺎﺕ
1
نأ ى B Bأ ;N ؛ضو ا را ت-;=# BQاو 3;أ R;ه لوTا ،ضو ا را عC ل& 9; WB ا 9X#
3;Tا R;ه ق =ا را Z# Fإ يد[ ف 9;I"ا 9]ه 9;J ا
.
،ى أ 3^ 9
9_ لI<J 3;Tا R;ها ح a b<
BQ اc ادJ 9_ لI<J يأ #-;=#
.
R;ها ح dB فو ،ضو ا تارا ت-;=# ة a ض+B ف8 f]
g;إ 3^ا h# *_ Wر*J 3;Tا
.
2
ب I B
M
ب I B و ،3;<ا ع ة ;j
m
ة ;jا 3;-
.

.
ا
IX
.
و ا تارا
ض
.
4
−
،ﲢﺪﻳﺪ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ
−
،ﺣﺴﺎﺏ ﺍﻟﻘﻴﻤﺔ ﺍﳉﺪﻭﻟﻴﺔ ﻟﻠﻤﺘﻐﲑﺓ
−
،ﺣﺴﺎﺏ ﺍﻟﻘﻴﻤﺔ ﺍﻟﻔﻌﻠﻴﺔ ﻟﻠﻤﺘﻐﲑﺓ
−
ﺍﲣﺎﺫ ﺍﻟﻘﺮﺍﺭ
.
9
-
1
-
2
-
1
.
ﲢﺪﻳﺪ ﺍﻟﻔﺮﺿﻴﺎﺕ
)
ﺍﻟﺼﻔﺮﻳﺔ ﻭﺍﻟﺒﺪﻳﻠﺔ
:(
ﺍﳋﻄﻮﺓ ﺍﻷﻭﱃ ﰲ ﺍﻻﺧﺘﺒﺎﺭ ﻫﻮ ﲢﺪﻳﺪ ﺍﻟﻔﺮﺿﻴﺔ ﺍﳌﺮﺍﺩ ﺍﺧﺘﺒﺎﺭﻫﺎ
،
ﻭﺗﺴﻤﻰ
ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ
ﺃﻭ ﻓﺮﺿﻴﺔ
ﺍﻟﻌﺪﻡ
H
0
،
ﻭ
ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﱵ ﺳﺘﻘﺒﻞ
ﰲ ﺣﺎﻟﱵ
ﻋﺪﻡ ﻗﺒﻮﻝ
1
ﺃﻭ
ﺭﻓﺾ
ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﻭﺗﺴﻤﻰ
ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺒﺪﻳﻠﺔ
H
1
.
ﰲ ﻣﺜﺎﻟﻨﺎ ﺗﻜﺘﺐ
ﺍﻟﻔﺮﺿﻴﺘﺎﻥ ﻛﻤﺎ ﻳﻠﻲ
:
↔ H
1
: µ ≠ µ
0
H
0
: µ = µ
0
ﻳﺆﺩﻱ ﺍﻻﺧﺘﺒﺎﺭ ﺇﻣﺎ ﺇﱃ
ﺭﻓﺾ
H
o
ﻭﻧﻜﺘﺐ
RH
o
ﻭﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻧﻘﺒﻞ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺒﺪﻳﻠﺔ
H
1
: µ ≠ µ
0
،
ﺃﻭ ﺇﱃ
ﻋﺪﻡ ﺭﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﻭ
ﻧﻜﺘﺐ
R’H
0
.
µ
0
ﺍﻟﻘﻴﻤﺔ ﺍﻻﻓﺘﺮﺍﺿﻴﺔ ﻝ
µ
ﻫﻲ ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ
15000
ﻟﺬﻟﻚ ﻧﻜﺘﺐ ﺍﻟﻔﺮﺿﻴﺎﺕ ﻛﻤﺎ
ﻳﻠﻲ
:
↔ H
1
: µ ≠ 15000
H
0
: µ = 15000
ﻋﺎﺩﺓ ﻣﺎ ﺗﻜﻮﻥ
µ
0
ﳏﺪﺩﺓ ﺑﻨﺎﺀﺍ ﻋﻠﻰ ﺑﻴﺎﻧﺎﺕ ﻋﻴﻨﺔ ﻋﺸﻮﺍﺋﻴﺔ ﺑﺴﻴﻄﺔ
(µ
0
= m)
ﻭﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ،
ﳝﻜﻦ ﺍﺳﺘﺨﺪﺍﻡ ﺍﳋﺎﺻﻴﺔ
M ~ N(µ, σ
m
)
ﻹﺟﺮﺍﺀ
ﺍﺧﺘﺒﺎﺭ
ﺻﺪﻗﻴﺔ
H
0
: µ = µ
0
ﺑﺘﻘﻴﻴﻢ ﺍﻟﻔﺮﻕ ﺑﲔ
µ
0
ﻭ
m
ﺃﻱ ﺍﳌ
ﺴﺎﻓﺔ
(µ
0
– m)
،
ﺣﻴﺚ ﻧﻌﻠﻢ
ﺃﻧﻪ ﺇﺫﺍ ﻛﺎﻧﺖ
: µ = µ
0
H
0
ﺻﺤﻴﺤﺔ ﻓﺈﻥ
:
P(µ
0
– 1.64(σ
m
) ≤ m ≤ µ
0
+ 1.64(σ
m
)) = 0.90
P(µ
0
– 1.96(σ
m
) ≤ m ≤ µ
0
+ 1.96(σ
m
)) = 0.95
P(µ
0
– 2.58(σ
m
) ≤ m ≤ µ
0
+ 2.58(σ
m
)) = 0.99
ﻭﺑﺼﻔﺔ ﻋﺎﻣﺔ ﻧﻜﺘﺐ
:
P[µ
0
– z
1–α/2
(σ
m
) ≤ m ≤ µ
0
+ z
1–α/2
(σ
m
)] = 1– α
ﺃﻭ ﺣﺴﺐ ﺍﻟﻜﺘﺎﺑﺔ ﺍﻷﻛﺜﺮ ﺷﻴﻮﻋﺎ
:
α
σ
µ
α
α
−
=
≤
−
≤
−
−
−
1
)
(
2
/
1
0
2
/
1
z
m
z
P
m
ﺣﻴﺚ
:
−
z
cal
= (m – µ
0
)/σ
m
:
ﺗﺴﻤﻰ
ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
ﺃﻭ
z
ﺍﶈﺴﻮﺑﺔ
،
ﺣﻴﺚ
z
cal
~ N(0, 1)
.
−
σ
m
ﻫﻮ ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ
ﺣﻴﺚ
:
σ
m
= σ/√n
ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺎﻹﺭﺟﺎﻉ
)
ﺃﻭ
n ≤ 0.05N
(
ﻭ
1
−
−
=
N
n
N
n
m
σ
σ
ﺘﻤﻊ ﳏﺪﻭﺩ ﻭ ﺍﳌﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔﺍ ﻥﺎﻛ ﺍﺫﺇ
.
1
;J I;;ا j f] ،q ا ةرو XJ < ل-ا م*_
.
C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
5
−
1 – α/2
:
ﺍﳌﺴﺎﺣﺔ ﻋﻠﻰ ﻳﺴﺎﺭ
z
.
−
n
:
ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
.
ﺇﺫﺍ ﻛﺎﻥ
m
ﺎﻝﺍ ﺝﺭﺎﺧ
ﺍﻟﺬﻱ ﺍﺣﺘﻤﺎﻟﻪ
1 – α
ﻧﺮﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ
H
0
: µ = µ
0
ﺍﻟﱵ ﺣﺪﺩ ﻋﻠﻰ ﺃﺳﺎﺳﻬﺎ ﻫﺬﺍ
ﺎﻝ ﻭﻧﻘﺒﻞ ﺑﺎﻟﺘﺎﱄ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺒﺪﻳﻠﺔﺍ
H
1
: µ ≠ µ
0
.
ﺗﺴﻤﻰ ﻫﺬﻩ
)
ﺍﳋﻄﺔ
(
ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ
.
9
-
1
-
2
-
2
.
ﲢﺪﻳﺪ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ
ﺗﻜﺘﺐ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ ﰲ ﺍﳌﺜﺎﻝ
ﻭﻫﻲ ﻗﺎﻋﺪﺓ،ﺎﻨﻳﺪﻳﺃ ﲔﺑ ﻱﺬﻟﺍ
ﺍﺧﺘﺒﺎﺭ ﺛﻨﺎﺋﻲ
ﺍﻻﲡﺎﻩ
ﻟﻠﻤﺘﻮﺳﻂ
)
ﺃﻧﻈﺮ ﺍﻟ
ﺮﺳﻢ
ﺍﳌﻮﺍﱄ
(
ﻛﻤﺎ ﻳﻠﻲ،
:
→
−
∈
−
=
→
−
∉
−
=
−
−
−
−
0
2
1
2
1
0
0
2
1
2
1
0
;
;
H
R
z
z
m
z
RH
z
z
m
z
m
c
m
c
α
α
α
α
σ
µ
σ
µ
ﲟﻌﲎ
:
ﻧﺮﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﺇﺫﺍ ﻛﺎﻥ
z
c
∉
[–z
1–
α
/2
; z
1–
α
/2
]
ﻭﻻ ﻧ
ﺮﻓﻀﻬﺎ ﺇﺫﺍ ﻛﺎﻧﺖ
z
c
ﺎﻝﺍ ﱃﺇ ﻲﻤﺘﻨﺗ
ﺍﳌﺬﻛﻮﺭ
.
ﺗﺴﻤﻰ
z
c
ﺍﻟﻘﻴﻤﺔ ﺍﶈﺴﻮﺑﺔ
.
ﻭﳝﻜﻦ ﺃﻥ ﺗﻜﺘﺐ ﻗﺎﻋﺪ ﺍﻟﻘﺮﺍﺭ ﺑﻄﺮﻕ ﺃﺧﺮﻯ ﳍﺎ ﻧﻔﺲ ﺍﻟﺪﻻﻟﺔ ﻣﻨﻬﺎ
:
→
≤
−
→
>
−
−
−
0
2
1
0
0
2
1
0
H
R
Z
m
RH
Z
m
m
m
α
α
σ
µ
σ
µ
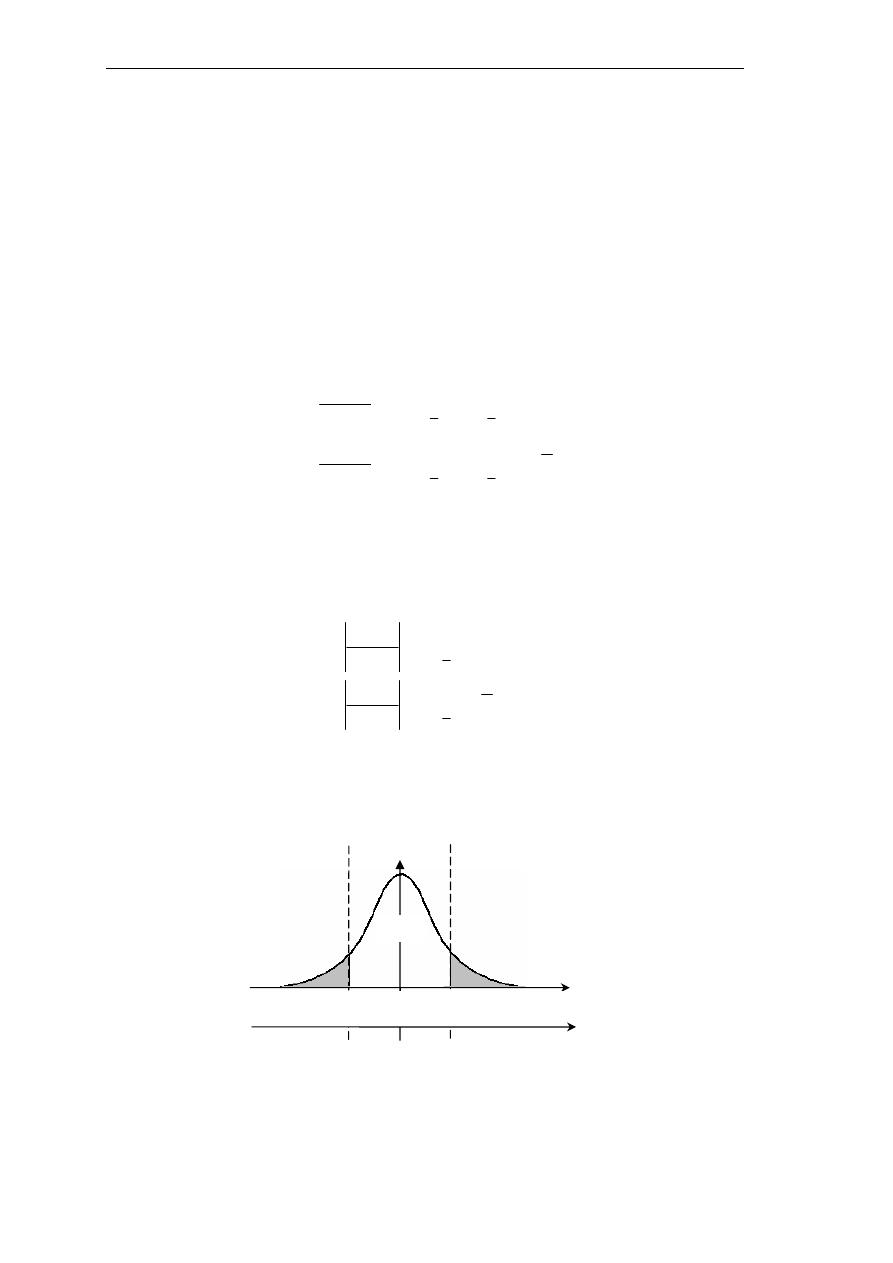
ﺍﻟﺮﺳﻢ ﺍﳌﻮﺍﱄ ﻳﺒﲔ ﰲ ﺃﻱ ﺣﺎﻟﺔ ﳝﻜﻦ ﺭﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﻭﰲ ﺃﻱ ﺣﺎﻟﺔ ﻻ ﳝﻜﻦ ﺫﻟﻚ
.
(ر
9
-
1
$ *ا را+ا , - . #/ 0/+او لا #2
RH
0
RH
0
R’H
0
-z
1
–
α/2
0 z
1
–
α/2
Z
µ
0
–
z
1
–
α/2
(σ
m
)
µ
0
µ
0
+z
1
–
α/2
(σ
m
) X
1
–
α
3-=
ا
q
3-=
ا
q
3-=
ا
ل-

.
ا
IX
.
و ا تارا
ض
.
6
ﻻﺣﻆ
:
−
ﺍﻟﻮﺻﻮﻝ ﺇﱃ ﻗﺮﺍﺭ ﺧﺎﻃ
ﻰﺀ
ﻳﻜﻮﻥ ﺇﻣﺎ ﺑﻘﺒﻮﻝ ﺍﻟﻔﺮﺿﻴﺔ
H
0
ﺑﻴﻨﻤﺎ ﻫﻲ ﺧﺎﻃﺌﺔ ﺃﻭ ﺭﻓﻀﻬﺎ ﺑﻴﻨﻤﺎ ﻫﻲ ﺻﺤﻴﺤﺔ
:
ﻓﻘﺪ
ﺗﻜﻮﻥ ﺍﻟﻔﺮﺿﻴﺔ
H
0
ﺻﺤﻴﺤﺔ ﺑﻴﻨﻤﺎ
ﻧﺘﻮﺻﻞ ﺑﺴﺒﺐ
ﻗﻴﻤﺔ
m
ﺑﻌﻴﺪﺓ ﻋﻦ
µ
0
ﺇﱃ ﺭﻓ
ﻭﻳﺴﻤﻰ ﻫﺬﺍ،ﺎﻬﻀ
ﺍﳋﻄﺄ ﻣﻦ
ﺍﻟﻨﻮﻉ ﺍﻷﻭﻝ
ﻭﻳﻜﺘﺐ،
:
P(RH
0
/ H
0
) = α
،
ﺃ
ﻭ ﻗﺪ
ﺗﻜﻮﻥ ﺍﻟﻔﺮﺿﻴﺔ
H
0
ﺧﺎﻃﺌﺔ ﺑﻴﻨﻤﺎ ﻧﺘﻮﺻﻞ ﺑﺴﺒﺐ
ﻗﻴﻤﺔ
m
ﻗﺮﻳﺒﺔ ﻣﻦ
µ
0
ﺇﱃ ﻗﺒﻮﳍ
ﺎ
ﻭﻳﺴﻤﻰ ﻫﺬﺍ،
ﺍﳋﻄﺄ ﻣﻦ ﺍﻟﻨﻮﻉ ﺍﻟﺜﺎﱐ
)
ﺃﻧﻈﺮ ﺍﳌﻠﺤﻖ
(
ﻭﻳﻜﺘﺐ
:
P(R'H
0
/ H
1
) = β
−
β
ﻏﲑ
1 –
α
ﻋﻠﻰ ﻋﻜﺲ ﻣﺎ
ﻗﺪ ﻳﺒﺪﺭ ﺇﱃ ﺍﻷﺫ
ﻓﺎﳊﺪﺛﺎﻥ،ﻥﺎﻫ
RH
0
/ H
0
ﻭ
R'H
0
/ H
1
ﻟﻴﺴﺎ
ﺣﺪﺛﺎﻥ
ﻣﺘﻌﺎﻛﺴﺎﻥ ﻭﺇﳕﺎ ﺍﳊﺪﺙ ﺍﳌﻌﺎﻛﺲ ﻝ
RH
0
/ H
0
ﻫﻮ
R'H
0
/ H
0
.
−
ﻭﻟﻜﻦ ﻻ ﳝﻜﻦ ﺗﻘﻠﻴﺺ ﺍﺣﺘﻤﺎﻝ ﻛﻼ ﺍﳋﻄﺄﻳﻦ ﻣﻌﺎ ﺇﻻ،ﱐﺎﺜﻟﺍ ﺏﺎﺴﺣ ﻰﻠﻋ ﻦﻳﺄﻄﳋﺍ ﺪﺣﺃ ﻝﺎﻤﺘﺣﺍ ﺺﻴﻠﻘﺗ ﻦﻜﳝ
ﺑﺰﻳﺎﺩﺓ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
.
9
-
1
-
2
-
3
.
ﺣﺴﺎﺏ
z
tab
ﺃﻱ
z
ﺍﳉﺪﻭﻟﻴﺔ
:
ﻭﻫﻲ
ﰲ
ﺣﺎﻟﺘﻨﺎ
)
ﺍﺧﺘﺒﺎﺭ ﺛﻨﺎﺋﻲ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
: (
z
tab
= z
1– α/2
= z
1– 0.05/2
= z
1– 0.025
= z
0.975
ﻭﻣﻦ ﺍﳉﺪﻭﻝ ﳒﺪ ﺃﻥ
z
0.975
= 1.96
.
9
-
1
-
2
-
4
.
ﺣﺴﺎﺏ
z
cal
ﺃﻱ
z
ﺍﻟﻔﻌﻠﻴﺔ
ﺃﻭ ﺍﶈﺴﻮﺑﺔ ﺃﻱ ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
:
ﻭ
ﻫﻲ ﺍﳌﺘﻐﲑ
ﺓ
ﺍﳌﻌﻴﺎﺭﻳﺔ ﻝ
M
:
33
,
5
100
/
1500
15000
15800
0
=
−
=
−
=
m
cal
m
z
σ
µ
9
-
1
-
2
-
5
.
ﺍﻟﻘﺮﺍﺭ
:
ﻧﻘﺮﺭ ﻗﺒﻮﻝ ﺃﻭ ﺭﻓﺾ
H
0
ﺣ
ﺴﺐ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ
.
ﻭﰲ ﺣﺎﻟﺘﻨﺎ ﻧﺮﻓﺾ
H
0
ﻷﻥ
z
cal
> z
tab
ﻭﻧﻘﺒﻞ
H
1
ﺃﻱ ﺃﻥ ﻣﺘﻮﺳﻂ ﺩﺧﻞ
ﺍﳋﺮﻳﺞ ﺣﺪﻳﺚ ﺍﻟﺘﻮﻇﻴﻒ ﻟﻴﺲ
15000
ﺩﺝ
.
9
-
1
-
3
.
! "ا يد .أ ر ا
.
ﻳﺘﻤﻴﺰ ﺍﻻﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ ﻋﻦ ﺍﻷﺣﺎﺩﻱ ﰲ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺒﺪﻳﻠﺔ
.
ﻫﺬﻩ ﺍﻷﺧﲑﺓ
ﻫﻲ ﻋﺪﻡ ﻣﺴﺎﻭﺍﺓ ﰲ ﺍﻻﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ ﻭﺃﻛﱪ ﲤﺎﻣﺎ
ﺃﻭ
ﺃﺻﻐﺮ ﲤﺎﻣﺎ
)
ﺣﺴﺐ
ﻛﻮﻥ ﺍﻻﺧﺘﺒﺎﺭ ﻣﻦ ﺍﻟﻴﻤﲔ ﺃﻡ ﻣﻦ ﺍﻟﻴﺴﺎﺭ
(
ﻭﻫﺬﺍ ﻳﺘﺮﺗﺐ ﻋﻠﻴﻪ ﺗﻐﻴﲑ ﰲ ﻗﺎﻋﺪﺓ،ﻱﺩﺎﺣﻷﺍ ﺭﺎﺒﺘﺧﻻﺍ ﰲ
ﺍﻟﻘﺮﺍﺭ
.
ﻳﻮﺟﺪ ﻧﻮﻋﺎﻥ ﻣﻦ ﺍﻻﺧﺘﺒﺎﺭ ﺃﺣﺎﺩﻱ ﺍﻻﲡﺎﻩ
:
9
-
1
-
3
-
1
.
ﺍﻻﺧﺘﺒﺎﺭ ﺃﺣﺎﺩﻱ ﺍﻻﲡﺎﻩ ﻣﻦ ﺍﻟﻴﻤﲔ
.
ﻟﻨﺮﺟﻊ ﺇﱃ ﺍﳌﺜﺎﻝ ﺍﻟﺴﺎﺑﻖ ﻣﻊ ﺗﻐﻴﲑ ﳏﺪﺩ ﻫﻮ ﺃﻧﻨﺎ ﻧﺮﻳﺪ ﺍﺧﺘﺒﺎﺭ ﻣﺎ ﺇﺫﺍ ﻛﺎ
ﻥ ﻣﺘﻮﺳﻂ ﺍﻟﺪﺧﻞ ﻟﻠﺨﺮﻳﺞ
15000
ﺩﺝ ﺃﻡ ﺃﻛﺜﺮ
)
ﺍﺧﺘﺒﺎﺭ ﻣﻦ ﺍﻟﻴﻤﲔ
.(
ﺃ
-
ﺍﻟﻔﺮﺿﻴﺎﺕ
:
↔ H
1
: µ > µ
0
H
0
: µ = µ
0
C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
7
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ
µ
0
= 15000
ﻟﺬﻟﻚ ﻧﻜﺘﺐ
:
↔ H
1
: µ > 15000
H
0
: µ = 15000
ﺏ
-
ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ
:
→
≤
−
=
→
>
−
=
−
−
0
1
0
0
1
0
H
R
z
m
z
RH
z
m
z
m
c
m
ca
α
α
σ
µ
σ
µ
ﺝ
-
ﺣﺴﺎﺏ
z
tab
ﺍﳉﺪﻭﻟﻴﺔ
:
)
ﺍﺧﺘﺒﺎﺭ ﻋ
ﻠﻰ ﺍﻟﻴﻤﲔ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
: (
z
tab
= z
1–α
= z
1– 0.05
= z
0.95
= 1.645
ﺩ
-
ﺣﺴﺎﺏ
z
cal
ﺃﻭ ﺍﺧﺘﺼﺎﺭﺍ
z
c
ﺍﻟﻔﻌﻠﻴﺔ
:
33
.
5
100
/
1500
1500
15800
/
0
0
=
−
=
−
=
−
=
n
m
m
z
m
cal
σ
µ
σ
µ
ﻩ
-
ﺍﻟﻘﺮﺍﺭ
:
ﻧﺮﻓﺾ
H
0
ﻷﻥ
z
cal
> z
tab
ﻭﻧﻘﺒﻞ
H
1
ﺃﻱ ﺃﻥ ﻣﺘﻮﺳﻂ ﺩﺧﻞ ﺍﳋﺮﻳﺞ ﺣﺪﻳﺚ ﺍﻟﺘﻮﻇﻴﻒ ﻟﻴﺲ
15000
ﺩﺝ
ﻭﺇﳕﺎ ﻫﻮ ﺃﻛﱪ
.
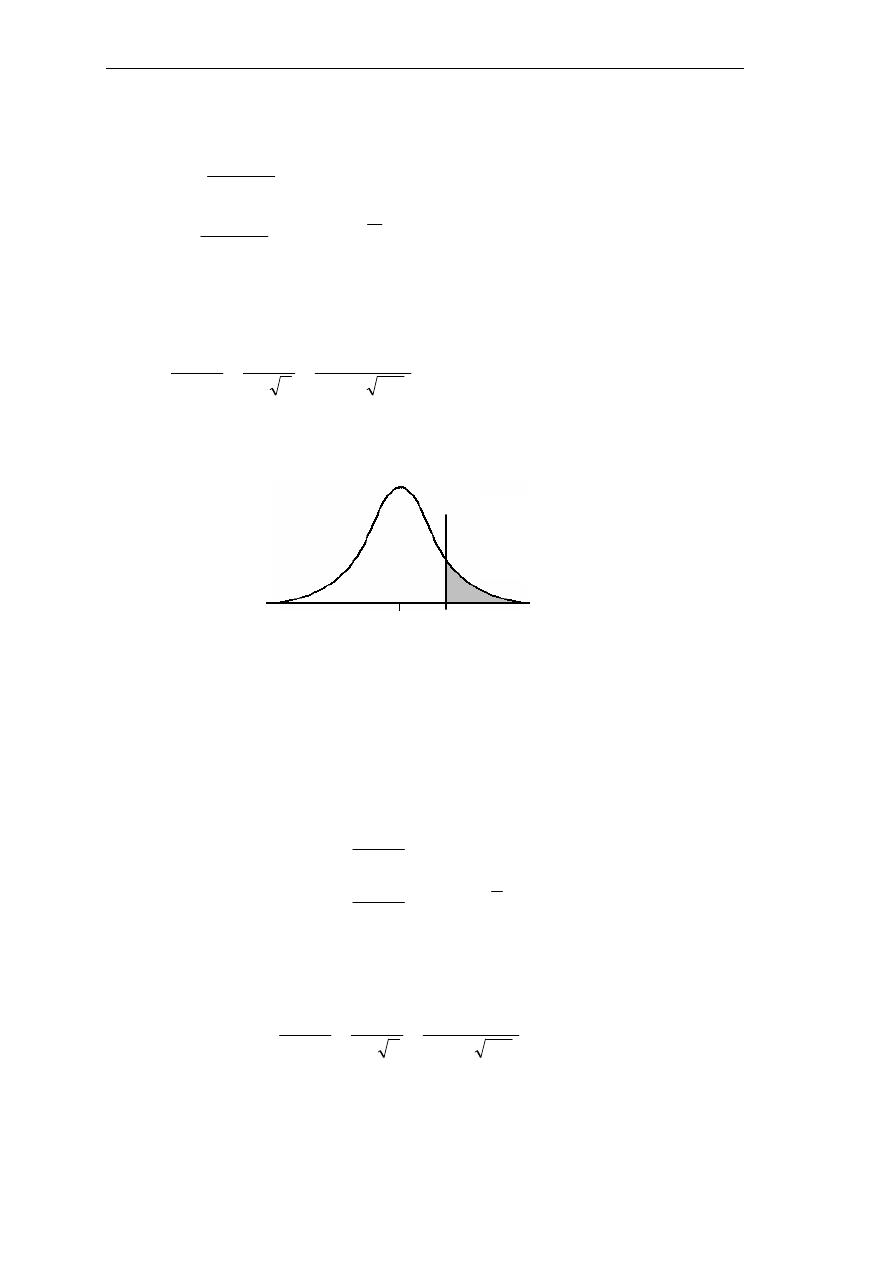
(ر
9
-
2
.
7 0/+ ا2
ا ! "ا يد .أ ر
9
-
1
-
3
-
2
.
ﺍﻻﺧﺘﺒﺎﺭ ﺃﺣﺎﺩﻱ ﺍﻻﲡﺎﻩ ﻣﻦ ﺍﻟﻴﺴﺎﺭ
ﻧﻌﻮﺩ ﺇﱃ ﻣﺜﺎﻟﻨﺎ ﻭﻧﻔﺘﺮﺽ ﺃﻥ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﻛﺎﻥ
14200
ﺩﺝ ﻭﻧﺮﻳﺪ ﺃﻥ ﳔﺘﱪ ﻣﺎ ﺇﺫﺍ ﻛﺎﻥ ﻣﺘﻮﺳﻂ ﺍﻟﺪﺧﻞ ﻣﺴﺎﻭﻳ
ﺎ
ﺃﻡ ﺃﻗﻞ
ﻣﻦ
15000
ﺩﺝ
.
ﺃ
-
ﺍﻟﻔﺮﺿﻴﺎﺕ
:
↔ H
1
: µ < 15000
H
0
: µ = 15000
ﺏ
-
ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ
:
→
−
≥
−
=
→
−
<
−
=
−
−
0
1
0
0
1
0
H
R
z
m
z
RH
z
m
z
m
cal
m
cal
α
α
σ
µ
σ
µ
ﺝ
-
ﺣﺴﺎﺏ
z
tab
) :
ﺍﺧﺘﺒﺎﺭ ﻋﻠﻰ ﺍﻟﻴﺴﺎﺭ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
: (
= –1.645
z
tab
= – z
1– α
= – z
1– 0.05
= – z
0.95
ﺩ
-
ﺣﺴﺎﺏ
z
cal
:
33
.
5
100
/
1500
1500
14200
/
0
0
−
=
−
=
−
=
−
=
n
m
m
z
m
cal
σ
µ
σ
µ
ﻩ
-
ﺍﻟﻘﺮﺍﺭ
:
ﻧﺮﻓﺾ
H
0
ﻷﻥ
z
cal
< z
tab
ﻭﻧﻘﺒﻞ
H
1
ﺃﻱ ﺃﻥ ﻣﺘﻮﺳﻂ ﺩﺧﻞ ﺍﳋ
ﺮﻳﺞ ﺣﺪﻳﺚ ﺍﻟﺘﻮﻇﻴﻒ ﺃﻗﻞ ﻣﻦ
15000
ﺩﺝ
.
α
3-=
q
ا
RH
0
0
z
1-α
.
ا
IX
.
و ا تارا
ض
.
8
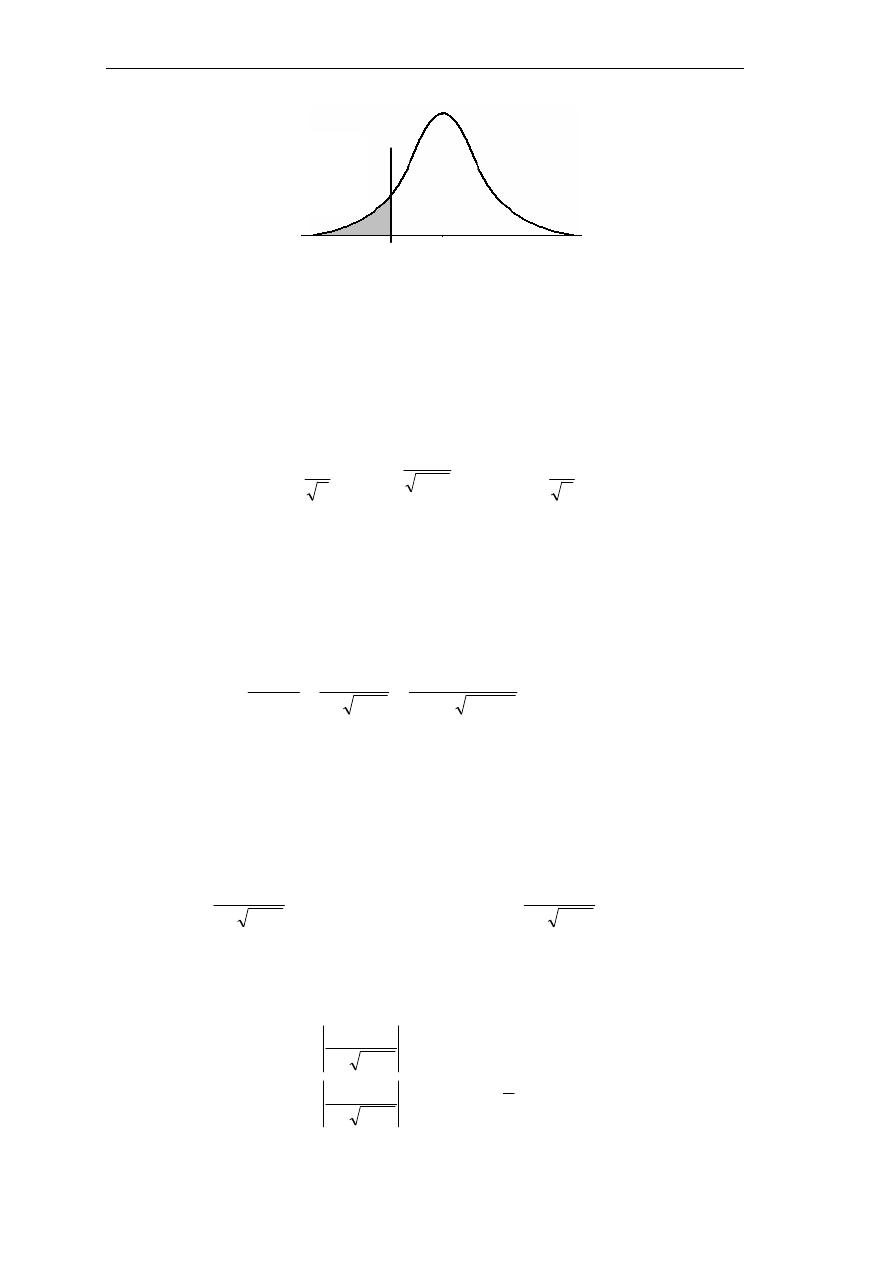
(ر
2
7 0/+ ا2
ر ا ! "ا يد .أ ر
9
-
1
-
4
.
ام:ا
S
آر ل
σ
ا ر ا #/
.
ﰲ ﺍﻟﻮﺍﻗﻊ ﻏﺎﻟﺒﺎ ﻣﺎ ﻳﻜﻮﻥ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ
ﻟﻠﻤﺠﺘﻤﻊ
ﳎﻬﻮﻻ ﻭﳓﺘﺎﺝ ﺑﺎﻟﺘﺎﱄ ﺇﱃ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﻠﻌﻴﻨﺔ
)
S
(
ﻋﻨﺪ ﺣﺴﺎﺏ
σ
m
)
ﺃﻧﻈﺮ ﺩﺭﺱ ﺍﻟﺘﻘﺪﻳﺮ
(
ﺣﻴﺚ ﻧﻌﻮﺽ ﺍﻟﻌﺒﺎﺭﺓ،
n
m
σ
σ
=
ﺏ
1
−
=
n
S
m
σ
ﺃﻭ
n
S
m
)
=
σ
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻧﺴﺘﺨﺪﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺳﺘﻴﻮﺩﻧﺖ ﺇﻻ ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻟﻌﻴﻨﺔ ﻛﺒﲑﺓ ﻓﻨﺴﺘﺨﺪﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
.
ﻣﺜﺎﻝ
:
ﰲ ﺍﳌﺜﺎﻝ ﺍﻟﺴﺎﺑﻖ ﻧﻔﺘﺮﺽ ﺃﻥ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﻠﺪﺧﻞ ﺍﻟﺸﻬﺮﻱ ﻟ
ﻟﻜﻦ ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﻠﻌﻴﻨﺔ،ﻝﻮﻬﳎ ﺐﻟﺎﻄﻠ
S = 1600
.
ﻛﻴﻒ ﳝﻜﻦ ﺍﺧﺘﺒﺎﺭ ﻣﺎ ﺇﺫﺍ ﻛﺎﻥ ﺍﻟﺪﺧﻞ ﺍﻟﺸﻬﺮﻱ ﺃﻗﻞ ﻣﻦ
15000
؟ﺩﺝ
ﺏ،ﺃ ﺕﺍﻮﻄﳋﺍ
ﻭ
ﺝ ﺗﺒﻘﻰ ﺑﺪﻭﻥ ﺗﻐﻴﲑ
.
ﺩ
-
ﺣﺴﺎﺏ
z
ﺍﻟﻔﻌﻠﻴﺔ
:
97
.
4
1
100
/
1600
1500
14200
1
/
0
0
−
=
−
−
=
−
−
=
−
=
n
S
m
m
z
m
cal
µ
σ
µ
ﻩ
-
ﺍﻟﻘﺮﺍﺭ
:
ﻧﺮﻓﺾ
H
0
ﻷﻥ
z
cal
< z
tab
ﻭﻧﻘﺒﻞ
H
1
ﺃﻱ ﺃﻥ ﻣﺘﻮﺳﻂ ﺩﺧﻞ ﺍﳋﺮﻳﺞ
ﺣﺪﻳﺚ ﺍﻟﺘﻮﻇﻴﻒ ﻟﻴﺲ
15000
ﺩﺝ
ﻭﺇﳕﺎ ﻫﻮ ﺃﻗﻞ
.
9
-
1
-
5
.
<ام از:ا
t
ا ر ا #/
.
ﰲ ﺣﺎﻟﺔ
n < 30
ﻭ
σ
ﻭﻟﻜﻦ،ﻲﻌﻴﺒﻄﻟﺍ ﻊﻳﺯﻮﺘﻟﺍ ﻡﺍﺪﺨﺘﺳﺍ ﻦﻜﳝ ﻻ ،ﻻﻮﻬﳎ
ﻟﺪﻳﻨﺎ
:
1
~
1
/
−
−
−
n
t
n
S
m
µ
ﻭ ﲢﺖ
H
0
)
µ = µ
0
: (
1
0
~
1
/
−
−
−
n
t
n
S
m
µ
ﳝﻜﻦ ﺇﺫﺍ ﺍﺳﺘﺨﺪﺍﻡ ﺗﻮﺯﻳﻊ ﺳﺘﻴﻮﺩﻧﺖ
)
ﺑﺸﺮﻁ
ﺘﻤﻊ ﻃﺒﻴﻌﻴﺎ ﺃﻭ ﻋﻠﻰ ﺍﻷﻗﻞ ﺟﺮﺳﻲ ﺍﻟﺸﻜﻞﺍ ﻊﻳﺯﻮﺗ ﻥﻮﻜﻳ ﻥﺃ
.(
ﻭ ﺗﺘﻐﲑ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ ﺗﺒﻌﺎ ﳍﺬﺍ ﺍﻟﺘﻐﻴﲑ ﻓﺘﻜﺘﺐ ﰲ ﺣﺎﻟﺔ ﺍﻻﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ ﻛﻤﺎ ﻳﻠﻲ
:
→
≤
−
−
→
>
−
−
−
−
−
−
0
2
/
1
;
1
0
0
2
/
1
;
1
0
1
/
1
/
H
R
t
n
S
m
RH
t
n
S
m
n
n
α
α
µ
µ
α
3-=
q ا
RH
0
-z
1-α 0
z
1-α

C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
9
ﰲ ﺣﺎﻟﺔ ﺍﺧﺘﺒﺎﺭ ﻣﻦ ﺍﻟﻴﻤﲔ
:
→
≤
−
−
→
>
−
−
−
−
−
−
0
1
;
1
0
0
1
;
1
0
1
/
1
/
H
R
t
n
S
m
RH
t
n
S
m
n
n
α
α
µ
µ
ﰲ ﺣﺎﻟﺔ ﺍﺧﺘﺒﺎﺭ ﻣﻦ ﺍﻟﻴﺴﺎﺭ
:
→
−
≥
−
−
→
−
<
−
−
−
−
−
−
0
1
;
1
0
0
1
;
1
0
1
/
1
/
H
R
t
n
S
m
RH
t
n
S
m
n
n
α
α
µ
µ
9
-
1
-
6
.
>7
ﻳﺘﻢ ﺍﺧﺘﺒﺎﺭ ﺍﻟﻔﺮﺿﻴﺎﺕ ﻣﻦ ﺧﻼﻝ
5
ﺧﻄﻮﺍﺕ ﻣﺘﺘﺎﻟﻴﺔ
ﻫﻲ
:
ﺻﻴﺎﻏﺔ
ﺍﻟﻔﺮﺿﻴﺎﺕ
)
ﺍﻟﺼﻔﺮﻳﺔ
ﻭﺍﻟﺒﺪﻳﻠﺔ
(
،
ﲢﺪﻳﺪ
ﻗﺎﻋﺪﺓ
ﺮﺍﺭـﻘﻟﺍ
)
ﻣﱴ
ﻧﺮﻓﺾ ﺃﻭ ﻻ ﻧﺮﻓﺾ
H
0
(
،
ﺣﺴﺎﺏ
ﺍﻟﻘﻴﻤﺔ
ﺍﳉﺪﻭﻟﻴﺔ
ﻟﻠﻤﺘﻐﲑﺓ
،
ﺣﺴﺎﺏ
ﺍﻟﻘﻴﻤﺔ ﺍﻟﻔﻌﻠﻴﺔ ﻟﻠﻤﺘﻐﲑﺓ
ﻭ،
ﺍﲣﺎﺫ
ﺍﻟﻘﺮﺍﺭ
.
ﺗﺘﺤﺪﺩ ﻛﻴﻔﻴﺔ ﺇﲤﺎﻡ ﻛﻞ ﺧﻄﻮﺓ ﺣﺴﺐ ﻃﺒﻴﻌﺔ ﺍﻻﺧﺘﺒﺎﺭ
)
ﺛﻨﺎﺋﻲ ﺃﻭ ﺃﺣﺎﺩﻱ ﺍﻻﲡﺎﻩ
(
ﻢـﺠﺣﻭ ﺔﻌﻴﺒﻃﻭ ﻊﻤﺘﺍ ﺔﻌﻴﺒﻃ ﺐﺴﺣ ،
،ﺍﻟﻌﻴﻨﺔ
...
ﻭﺗﺴﺨﺪﻡ ﰲ ﺫﻟﻚ ﻧﻈﺮﻳﺎﺕ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ
.
9
-
1
-
7
.
?@
ﺍﺣﺘﻤﺎﻝ ﺍﳋﻄﺄ ﰲ ﺍﻟﻘﺮﺍﺭ
.
ﺍﳋﻄﺄ ﺍﻷﻭﻝ ﻫﻮ ﺭﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ،ﻦﻳﺄﻄﺧ ﺪﺣﺃ ﰲ ﻊﻘﻧ ﻥﺃ ﻦﻜﳝ ﺭﺍﺮﻘﻟﺍ ﺫﺎﲣﺍ ﺪﻨﻋ ﻪﻧﺃ ﺎﻧﺮﻛﺫ
H
0
،ﺤﻴﺤﺔـﺻ ﻲـﻫ ﺎﻤﻨﻴﺑ
ﻭﺍﺣﺘﻤﺎﻟﻪ ﻫﻮ ﻣﺴﺎﺣﺔ ﻣﻨﻄﻘﺔ
ﺍﻟﺮﻓﺾ ﺃﻱ
α
ﺃﻣﺎ ﺍﳋﻄﺄ ﻣﻦ ﺍﻟﻨﻮﻉ ﺍﻟﺜﺎﱐ ﻓﻬﻮ ﻗﺒﻮﻝ ﺍﻟﻔﺮﺿﻴﺔ،
H
0
ﻭﺭﻣﺰﻧﺎ،ﺔﺌﻃﺎﺧ ﻲﻫ ﺎﻤﻨﻴﺑ
ﻻﺣﺘﻤﺎﻟﻪ ﺏ
β
ﻓ،
ﻜﻴﻒ ﳝﻜﻦ ﺣﺴﺎﺏ
β
؟
.
ﻮـﻫ ﱃﻭﻷﺍ ﻪﻠﻤﻋ ﺔﻨﺳ ﰲ ﻲﻌﻣﺎﳉﺍ ﺞﻳﺮﳋﺍ ﻞﺧﺩ ﻥﺃ ﺽﺮﺘﻔﻧﻭ ،ﺱﺭﺪﻟﺍ ﺔﻳﺍﺪﺑ ﰲ ﻰﻄﻌﳌﺍ ﻝﺎﺜﳌﺍ ﱃﺇ ﺩﻮﻌﻧ ﻚﻟﺫ ﺢﻴﺿﻮﺘﻟ
15000
ﺩﺝ ﺍﻟﺬﻱ ﳝﺜﻞ ﻣﺘﻮﺳﻂ ﺩﺧﻞ ﺍﻟﻌﻴﻨﺔ
ﺍﳌﺪﺭﻭﺳﺔ ﺍﳌﻜﻮﻧﺔ ﻣﻦ
100
ﻣﻊ ﺍﻟﻌﻠﻢ ﺃﻥ،ﺞﻳﺮﺧ
σ = 1500
.
ﺍﺣﺘﻤﺎﻝ ﺍﳋﻄﺄ ﻣﻦ ﺍﻟﻨﻮﻉ ﺍﻷﻭﻝ
:
ﺗﺮﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ
H
0
ﺇﺫﺍ ﻭﺟﺪ ﺃﻥ
m
ﻻ ﻳﻨﺘﻤﻲ ﺇﻻ ﳎﺎﻝ ﺍﻟﻘﺒﻮﻝ
:
m
∉
[15000 – 1.96(1500/100) ; 15000 + 1.96(1500/100)]
P(RH
0
/H
0
) = P(RH
0
/ X ~ N(15000, 1500))
= P(m
∉
[15000 – 1.96(1500/100) ; 15000 + 1.96(1500/100)]/X ~ N(15000, 1500))
= P(m
∉
[14706 ; 15294]/X ~ N(15000, 1500))
=> P(RH
0
/H
0
) =
α
= 0.05
ﺑﺼﻔﺔ ﻋﺎﻣﺔ ﺍﻻﺣﺘﻤﺎﻝ
)
ﻏﲑ ﺍﻟﺸﺮﻃﻲ
(
P(RH
0
)
ﻳﺘﻐﲑ ﺣﺴﺐ ﺍﻟﻘﻴﻤﺔ ﺍﳊﻘﻴﻘﺔ ﻝ
µ
ﺔـﻴﻟﺎﻌﻓﻭ ﺓﻮﻗ ﺚﲝ ﺪﻨﻋ ﻯﺮﻨﺳ ﺎﻤﻛ
ﺍﻻﺧﺘﺒﺎﺭ
.
ﺍﺣﺘﻤﺎﻝ ﺍﳋﻄﺄ ﻣﻦ ﺍﻟﻨ
ﻮﻉ ﺍﻟﺜﺎﱐ
)
ﻗﺒﻮﻝ ﻓﺮﺿﻴﺔ ﺧﺎﻃﺌﺔ
(
:
ﺗﻘﺒﻞ ﺍﻟﻔﺮﺿﻴﺔ
H
0
ﺇﺫﺍ ﻭﺟﺪ ﺃﻥ
m
، ﺗﻨﺘﻤﻲ ﺇﱃ ﳎﺎﻝ ﺍﻟﻘﺒﻮﻝ
m
∈
[15000 – 1.96(1500/100) ; 15000 + 1.96(1500/100)]
m
∈
[14706 ; 15294]
.
ا
IX
.
و ا تارا
ض
.
10
ﻭﻳﻜﻮﻥ ﻫﺬﺍ ﺍﻟﻘﺒﻮﻝ ﺧﻄﺄ ﺇﺫﺍ ﻛﺎﻥ ﺍﳌﺘﻮﺳﻂ ﺍﳊﻘﻴﻘﻲ ﻟﻠﻤﺠﺘﻤﻊ
µ
ﳐﺘﻠﻔﺎ ﻋﻦ
m = 15000
.
ﺔـﻟﺎﺣ ﻲﻔﻓ
µ
= 14500
ﻣﺜﻼ ﻳ
ﻜﺘﺐ ﺍﺣﺘﻤﺎﻝ ﺍﳋﻄﺄ ﻣﻦ ﺍﻟﻨﻮﻉ ﺍﻟﺜﺎﱐ ﻭﳛﺴﺐ ﻛﻤﺎ ﻳﻠﻲ
:
P(R'H
0
/H
1
) =
β
= P(m
∈
[14706 ; 15294]/X ~ N(14500, 1500))
)
29
.
5
37
.
1
(
100
/
1500
14500
15294
100
/
1500
14500
14706
≤
≤
=
−
≤
≤
−
=
z
P
z
P
β
= F(5.29) – F(1.37) = 0.9999 – 0.9152 =>
β
= 0.0848
ﰲ ﺣﺎﻟﺔ
µ
= 14000
ﻳﻜﻮﻥ ﺍﺣﺘﻤﺎﻝ ﺍﳋﻄﺄ ﻣﻦ ﺍﻟﻨﻮﻉ ﺍﻟﺜﺎﱐ ﺃﻗﻞ،
:
P(R'H
0
/H
1
) =
β
= P(m
∈
[14706 ; 15294]/X ~ N(14000, 1500))
)
63
.
8
71
.
4
(
100
/
1500
14000
15294
100
/
1500
14000
14706
≤
≤
=
−
≤
≤
−
=
z
P
z
P
β
= F(8.63) – F(4.71) = 0.00000126 < 0.0848
14000 15000
14706 15294
14500 15000
14706 15294
R'H
0
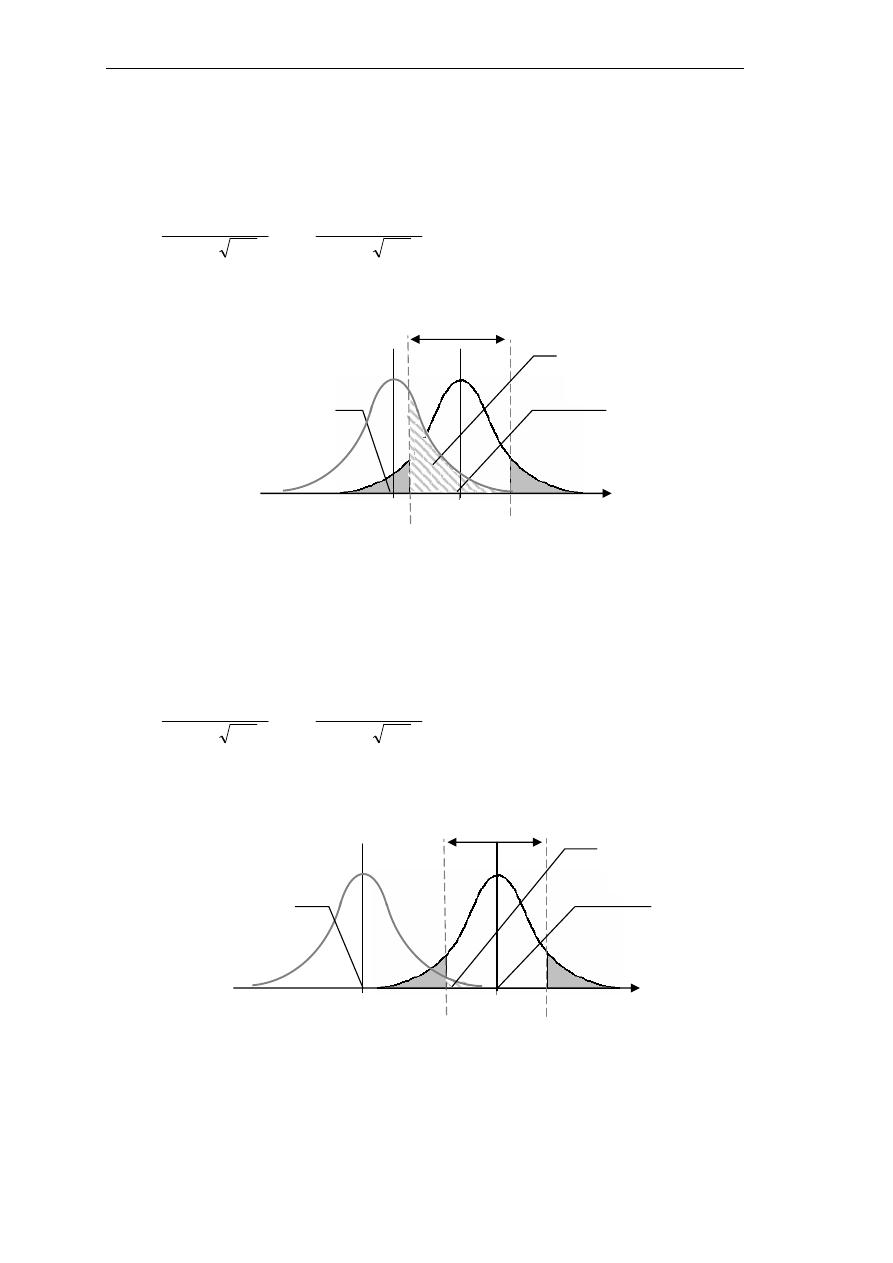
(ر
9
-
2
# *ا عا B2:ا ل .ا
:
DE F+/ ل-
.
ا
ا
-;-
ا
Cا ا
ββββ
ل- ل .ا
DE F+/
R'H
0
ββββ
- ل .ا
ل
DE F+/
- أ
ا
-;-ا
ا
Cا ا
C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
11
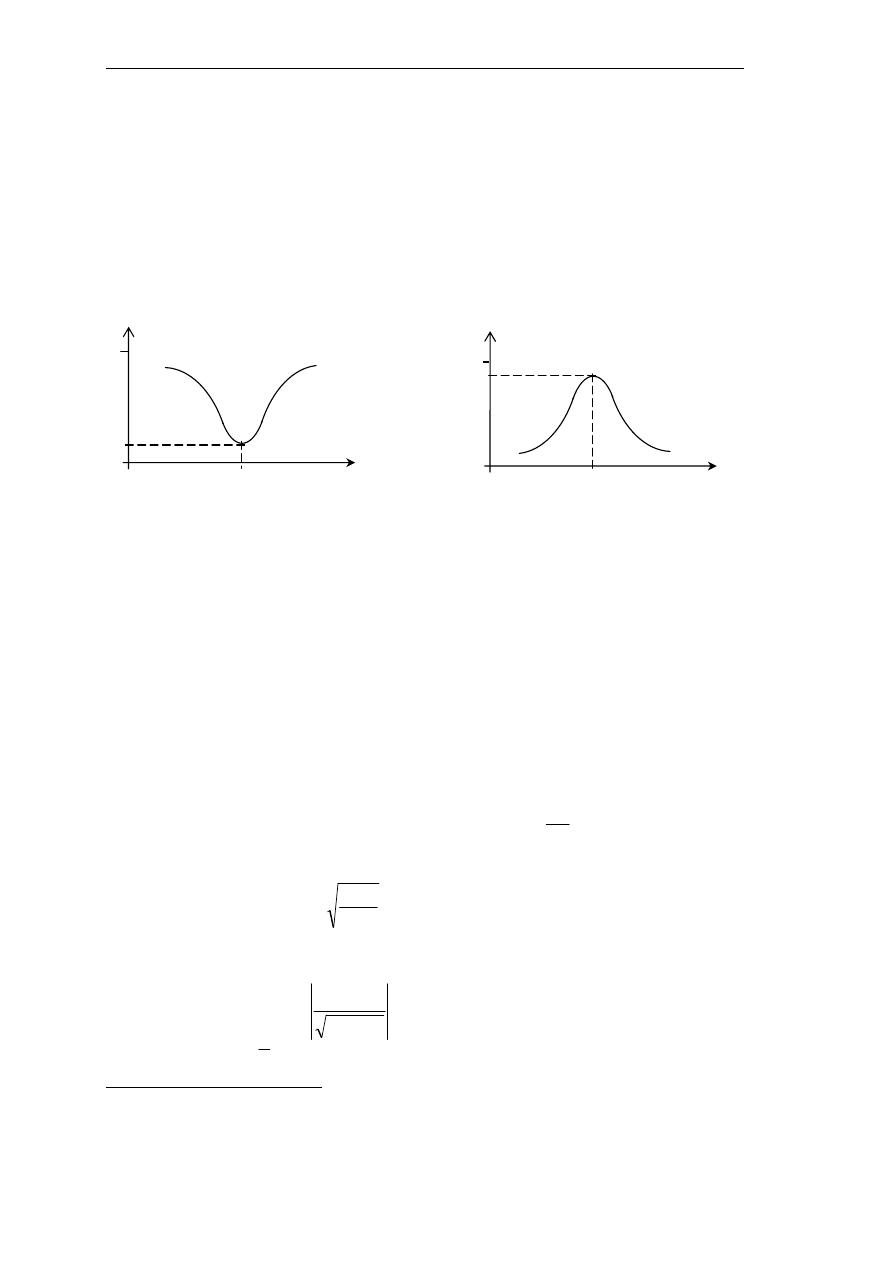
ﻗﻮﺓ ﺍﻻﺧﺘﺒﺎﺭ ﻭﻓﻌﺎﻟﻴﺘﻪ
.
ﻳﻘﻴﺲ
ﺍﺣﺘﻤﺎﻝ ﺭﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ
P(RH
0
)
ﻗﻮﺓ ﺍﻻﺧﺘﺒﺎﺭ
،ﺃﻱ ﺍﻟﻘﺪﺭﺓ ﻋﻠﻰ ﺭﻓﺾ ﺍﻟﻔﺮﺿﻴﺔ
ﻓﻴﻤﺎ ﻳﻘﻴﺲ ﺍﺣﺘﻤﺎﻝ
ﻗﺒﻮﳍﺎ
P(R'H
0
)
ﻓﻌﺎﻟﻴﺔ ﺍﻻﺧﺘﺒﺎﺭ
)
ﺃﻧﻈﺮ
ﺍﻟﺮﺳﻢ ﺃﺩﻧﺎﻩ
.(
ﻭﺗﺘﻔﺎﻭﺕ ﺍﻻﺧﺘﺒﺎﺭﺍﺕ ﻣﻦ ﺣﻴﺚ ﺍﻟﻘﻮﺓ ﻭﺍﻟﻔﻌﺎﻟﻴﺔ ﲝﺴﺐ ﺗﺼﻤﻴﻢ
ﺍﻻﺧﺘﺒﺎﺭ ﻭﲝﺴﺐ ﻧﻮﻋﻪ
1
.
ﻭﻳﺘﻮﻗﻒ
ﺍﺣﺘﻤﺎﻝ ﻗﺒﻮﻝ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﻭﺍﺣ
ﺘﻤﺎﻝ ﺭﻓﻀﻬﺎ
ﻋﻠﻰ ﺍﻟﻘﻴﻤﺔ
ﺍﳊﻘﻴﻘﻴﺔ ﻝ
µ
ﻟﻜﻦ ﻟﻴﺲ
ﻭﻫﻮ ﻣﺎ ﻳﺒﻴﻨﻪ ﺍﻟﺮﺳﻢ ﺍﻟﺘﺎﱄ؛ﺔﻘﻳﺮﻄﻟﺍ ﺲﻔﻨﺑ
ﺘﻤﻊ ﺍﻟﻄﺒﻴﻌﻲﺍ ﺔﻟﺎﺣ ﰲ ﻂﺳﻮﺘﳌﺍ ﺭﺎﺒﺘﺧﺎﺑ ﺹﺎﳋﺍ
.
9
-
2
.
ا ر ا
ا ر او
38ار ا
9ار ا
9
-
2
-
1
.
ا ر ا
ﻳﺘﻌﻠﻖ ﻫﺬﺍ ﺍﻻ
ﺘﻤﻊ ﺍﻟﱵ ﺗﺘﺼﻒ ﲞﺎﺻﻴﺔ ﻣﺎﺍ ﺕﺍﺩﺮﻔﻣ ﺔﺒﺴﻨﺑ ﺭﺎﺒﺘﺧ
)
p
(
ﺣﻴﺚ ﻳﺆﻛﺪ ﺍﻻﺧﺘﺒﺎﺭ ﺃﻭ ﻳﻨﻔﻲ ﺻﺤﺔ ﻓﺮﺿﻴﺔ ﻣﻌﻴﻨﺔ،
ﲞﺼﻮﺹ ﻗﻴﻤﺔ
p
.
ﻳﺮﻣﺰ ﻟﻠﻘﻴﻤﺔ ﺍﻻﻓﺘﺮﺍﺿﻴﺔ ﺏ
p
0
ﻭﺗﻜﺘﺐ ﺍﻟﻔﺮﺿﻴﺔ ﻛﻤﺎ ﻳﻠﻲ
:
H
0
: p = p
0
ﻟﻠﻘﻴﺎﻡ ﺑﺎﻻﺧﺘﺒﺎﺭ ﻧﺴﺘﺨﺪﻡ ﺧﺼﺎﺋﺺ
p’
ﺍﻟﻨﺴﺒﺔ ﰲ ﺍﻟﻌﻴﻨﺔ
)
ﺃﻧﻈﺮ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻨﺴﺒﺔ
:
ﻧ
ﻈﺮﻳﺔ
6
.(
n
pq
p
p
E
p
p
=
=
=
'
'
²
;
)
'
(
σ
µ
ﻋﻨﺪ
n ≥ 30
:
(p, σ
p'
)
p’ ≈ N
)
ﻗﺎﻧﻮﻥ
ﻣﻮﺍﻓﺮ
-
ﻻﺑﻼﺱ
(
ﺍﺳﺘﻨﺎﺩﺍ ﺇﱃ ﻫﺬﻩ ﺍﳋﺼﺎﺋﺺ ﻭﲢﺖ
H
0
:
≈
n
q
p
p
N
p
0
0
0
;
'
ﻭ ﻣﻦ ﰒ ﳝﻜﻦ ﲢﺪﻳﺪ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ ﲝﺴﺐ ﻃﺒﻴﻌﺔ ﺍﻻﺧﺘﺒﺎﺭ
ﻛﻤﺎ ﻳﻠﻲ
:
ﰲ ﺣﺎﻟﺔ ﺍﻻﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ
:
>
−
−
.
sinon
.
/
'
0
2
/
1
0
0
0
0
H
R
z
n
q
p
p
p
si
RH
α
1
ارات
( نو
(Les tests non paramétriques)
ه
تارا 9 ةv Qآأ ةد_
(
(tests paramétriques)
،
ا أ g<ز# 3<;w وأ 1"ا ص+J 3;C 9X# ا ه R<J تارا
ر
ات
1XB اR< نو*J
;
1"ا R< ص+J ت;C
.
5Q g<= 9Z ;Tا ا]ه ،BQا نود تارا 9 لوTا عا F _ ارد -B ف
:
ت8;; *Bور
1976
(Ronald Céhéssat)
ص
253
.
µ
0
µµµµ
P(RH
0
)
α
1
µ
0
µ
P(R'H
0
)
1-α
1
(ر
9
-
3
(1)
@
/ H
ر ا
ة- H@
ر ا
(2)

.
ا
IX
.
و ا تارا
ض
.
12
ﰲ ﺣﺎﻟﺔ ﺍﺧﺘﺒﺎﺭ ﻣﻦ ﺍﻟﻴﻤﲔ
:
>
−
−
.
sinon
/
'
0
1
0
0
0
0
H
R
z
n
q
p
p
p
si
RH
α
ﰲ ﺣﺎﻟﺔ ﺍﺧﺘﺒﺎﺭ ﻣﻦ ﺍﻟﻴﺴﺎﺭ
:
−
<
−
−
.
sinon
/
'
0
1
0
0
0
0
H
R
z
n
q
p
p
p
si
RH
α
ﻣﺜﺎ
ﻝ
:
ﺗﻘﺪﺭ ﺍﻟﺪﻭﺍﺋﺮ ﺍﻟﺮﲰﻴﺔ ﻧﺴﺒﺔ ﺍﳌﺘﺨﺮﺟﲔ ﺍﳉﺎﻣﻌﻴﲔ ﺍﻟﺬﻳﻦ ﳛﺼﻠﻮﻥ ﻋﻠﻰ ﻋﻤﻞ ﰲ ﺍﻟﺴﻨﺔ ﺍﻷﻭﱃ ﺍﻟﱵ ﺗﻠﻲ ﲣﺮﺟﻬﻢ ﺏ
70
%
ﻭﺟﺪﺕ ﺩﺭﺍﺳﺔ ﺃﺟﺮﻳﺖ ﻋﻠﻰ ﻋﻴﻨﺔ ﻣﻦ
900
ﻃﺎﻟﺐ ﺃﻥ ﻧﺴﺒﺔ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﻋﻤﻞ
67
%
.
ﻛﻴﻒ ﳝﻜﻦ ﺍﺧﺘﺒﺎﺭ
ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
ﻣﺎ ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻟﻨ
ﺴﺒﺔ ﺍﻟﺮﲰﻴﺔ ﺻﺤﻴﺤﺔ ﺃﻡ ﻣﺒﺎﻟﻎ ﻓﻴﻬﺎ
؟
H
0
: p = 0.70 ↔ H
1
: p < 0.70
=> RH
0
64
.
1
34
.
196
900
/
)
3
.
0
(
7
.
0
7
.
0
67
.
0
/
'
05
.
0
1
0
0
0
−
=
−
<
−
≅
−
=
−
−
z
n
q
p
p
p
9
-
2
-
2
.
ا ر ا
،ﻻﺧﺘﺒﺎﺭ ﺻﺪﻗﻴﺔ ﻓﺮﺿﻴﺔ ﲞﺼﻮﺹ ﻗﻴﻤﺔ ﺗﺒﺎﻳﻦ ﳎﺘﻤﻊ ﻣﺎ
H
0
: σ² = σ
0
² ↔ H
1
: σ² = σ
0
²
ﻧﺴﺘﻌﻤﻞ ﺍﳌﻘﺪﺭ ﻏﲑ ﺍﳌﻨﺤﺎﺯ
1
)²
(
²
ˆ
−
−
=
∑
n
m
X
S
i
i
ﺣﻴﺚ ﰲ ﺣﺎﻟﺔ ﺍﻟﻌﻴﻨﺔ ﺍﻟﻜﺒﲑﺓ
)
n ≥ 50
ﰲ ﺃﺣﺴﻦ ﺍﻷﺣﻮﺍﻝ
(
،
ﻭﲢﺖ
H
0
ﻓﺈﻥ
:
4
4
4
0
4
2
0
)
(
).
1
.
0
(
/
)
(
²
ˆ
µ
µ
σ
µ
σ
−
=
≈
−
−
=
X
E
N
n
S
T
ﺣﻴﺚ
µ
4
ﻫﻮ ﺍﻟﻌﺰﻡ ﺍﳌﺮﻛﺰﻱ ﻣﻦ ﺍﻟﺪﺭﺟﺔ ﺍﻟﺮﺍﺑﻌﺔ
.
ﺬﺍ ﺍﻟﺸﻜﻞ ﺗﻜﺘﺐ ﻗﺎﻋﺪﺓ ﺍﻟﻘﺮﺍﺭ ﻟﻼﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ ﻛﻤﺎ ﻳﻠﻲﻭ
:
>
−
−
−
.
sinon
/
)
(
²
ˆ
0
2
/
1
4
0
4
2
0
0
H
R
z
n
S
si
RH
α
σ
µ
σ
ﻭﰲ ﺣﺎﻟﺔ
µ
4
ﳎﻬﻮﻝ ﳝﻜﻦ ﺍﺳﺘﺨﺪﺍﻡ ﻛﻤﻘﺪﺭ
:
m
4
= E(x
i
– m)
4
.
ﺣﻴﺚ،ﺎﻴﻌﻴﺒﻃ ﻊﻤﺘﺍ ﻥﺎﻛ ﺍﺫﺇﻭ
µ
4
= 3σ
4
ﻓﺈﻥ،
ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
ﳝﻜﻦ ﺃﻥ ﺗﻜﺘﺐ ﻛﻤﺎ ﻳﻠﻲ
:
).
1
.
0
(
/
2
²
ˆ
2
0
2
0
N
n
S
T
≈
−
=
σ
σ

C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
13
9
-
3
.
ا ر ا
ر
9;<" = وي8# را
9;<" # وي8# را
ﻳﺘﻨﺎﻭﻝ ﻫﺬﺍ ﺍﻻﺧﺘﺒﺎﺭ ﻣﻘﺎﺭﻧﺔ ﺑﲔ ﳎﺘﻤﻌﲔ ﻣﻦ ﺧﻼﻝ
ﺍﳌ
ﺘﻮﺳﻂ
ﺃﻭ ﺍﻟﺘﺒﺎﻳﻦ ﻟﻜﻞ ﻣﻨﻬﻤﺎ
...
،ﻭﺳﻨﺮﻛﺰ ﻫﻨﺎ ﻋﻠﻰ ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
ﺇﺫ ﻣﻦ ﺍﻟﺴﻬﻞ ﻋﻠﻰ ﺍﻟﻄﺎﻟﺐ ﺍﺳﺘﻨﺘﺎﺝ ﻛﻴﻔﻴﺔ ﺇﲤﺎﻡ ﺍﳋﻄﻮﺍﺕ ﺍﻷﺧﺮﻯ ﻋﻠﻰ ﺿﻮﺀ ﻣﺎ ﺳﺒ
ﻖ
.
9
-
3
-
1
.
#2 يو " ر ا
ﺍﻟﻐﺮﺽ ﻣﻦ ﺍﻻﺧﺘﺒﺎﺭ ﻫﻮ ﺗﺄﻛﻴﺪ ﺃﻭ ﻧﻔﻲ ﺗﺴﺎﻭﻱ ﻣﺘﻮﺳﻄﻲ ﳎﺘﻤﻌﲔ ﻣﻦ ﺧﻼﻝ ﻋﻴﻨﺘﲔ ﻋﺸﻮﺍﺋﻴﺘﲔ ﺑﺴﻴﻄﺘﲔ ﻣﺴﺘﻘﻠﺘﲔ
.
ﺗﻜﺘﺐ ﺍﻟﻔﺮﺿﻴﺎﺕ
)
ﰲ ﺣﺎﻟﺔ ﺍﻻﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ
(
ﻛﻤﺎ ﻳﻠﻲ
:
H
0
: µ
1
= µ
2
↔ H
1
: µ
1
≠
µ
2
ﻟﺘﺤﺪﻳﺪ ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
ﳕﻴﺰ ﺑﲔ ﺣﺎﻟﺔ ﻛﻮﻥ ﺗﺒﺎﻳﻨ
ﺘﻤﻌﲔ ﳎﻬﻮﻟﲔﺍ ﺎﻨﻳﺎﺒﺗ ﻥﻮﻛ ﺔﻟﺎﺣﻭ ﲔﻣﻮﻠﻌﻣ ﲔﻌﻤﺘﺍ ﺎ
ﻓ،
ﻨﻌﺘﻤﺪ ﻋﻠﻰ
ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
T
ﺃﻭ
T’
ﲝﺴﺐ ﺍﳊﺎﻟﺔ
.
9
-
3
-
1
-
1
.
ﺘﻤﻌﲔ ﻣﻌﻠﻮﻣﲔﺍ ﺎﻨﻳﺎﺒﺗ
1
-
ﺘﻤﻌﲔ ﻃﺒﻴﻌﻴﲔﺍ
:
)
1
,
0
(
~
²
²
2
2
1
1
2
1
N
n
n
m
m
T
σ
σ
+
−
=
2
-
ﳎﺘﻤﻌﲔ ﻣﺎ
)
n
1
, n
2
≥ 30
:(
)
1
,
0
(
²
²
2
2
1
1
2
1
N
n
n
m
m
T
≈
+
−
=
σ
σ
9
-
3
-
1
-
2
.
ﺘﻤﻌﲔ ﳎﻬﻮﻟﲔﺍ ﺎﻨﻳﺎﺒﺗ
1
-
ﺍ
ﺘﻤﻌ
ﺎﻥ
ﻃﺒﻴﻌﻴ
ﺎ
ﻥ
:
ﺘﻤﻌﲔ ﻣﺘﺴﺎﻭﻳﲔﺍ ﺎﻨﻳﺎﺒﺗ ﻥﺎﻛ ﺍﺫﺇ
2
2
1
2
1
2
2
1
1
2
1
2
1
~
1
1
2
²
²
'
−
+
+
−
+
+
−
=
n
n
t
n
n
n
n
S
n
S
n
m
m
T
2
-
ﳎﺘﻤﻌﲔ ﻣﺎ
)
n
1
, n
2
≥ 30
:(
)
1
,
0
(
1
²
1
²
2
2
1
1
2
1
N
n
S
n
S
m
m
T
≈
−
+
−
−
=
ﻣﺜﺎﻝ
:
ﻧﺴﺤﺐ ﻣﻦ ﳎﺘﻤﻌﲔ ﻃﺒﻴﻌﻴﲔ ﻣﺘﺴﺎﻭﻳﻲ ﺍﻟﺘﺒﺎﻳﻦ ﻋﻴﻨﺘﲔ ﺣﺠﻢ ﺍﻷﻭﱃ
18
ﻭﺣﺠﻢ ﺍﻟﺜﺎﻧﻴﺔ
21
.
ﻭﺟﺪﻧﺎ
ﺍﻟﻨﺘﺎﺋﺞ ﺍﻟﺘﺎﻟﻴﺔ
:
m
1
= 81, m
2
= 76, S²
1
= 9, S²
2
= 8.
ﻛﻴﻒ ﳝﻜﻦ
ﺇﺟﺮﺍﺀ
ﺘﻤﻌﲔ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔﺍ ﻲﻄﺳﻮﺘﻣ ﻱﻭﺎﺴﺗ ﺭﺎﺒﺘﺧﺍ
5
%
؟

.
ا
IX
.
و ا تارا
ض
.
14
H
0
: µ
1
= µ
2
↔ H
1
: µ
1
≠
µ
2
43
.
5
21
1
18
1
2
21
18
)
8
(
21
)
9
(
18
76
81
1
1
2
'
2
1
2
1
2
2
2
2
1
1
2
1
≅
+
−
+
+
−
=
+
−
+
+
−
=
n
n
n
n
S
n
S
n
m
m
T
0
37
;
975
.
0
43
.
5
336
.
2
RH
t
⇒
<
≅
9
-
3
-
2
.
" يو " ر ا
#
ﺍﻟﻐﺮﺽ ﻣﻦ ﺍﻻﺧﺘﺒﺎﺭ ﻫﻮ ﺗﺄﻛﻴﺪ ﺃﻭ ﻧﻔﻲ ﺗﺴﺎﻭﻱ ﺗﺒﺎﻳﻨﺎ ﳎﺘﻤﻌﲔ ﻣﻦ ﺧﻼﻝ ﻋﻴﻨﺘﲔ ﻋﺸﻮﺍﺋﻴﺘﲔ ﺑﺴﻴ
ﻄﺘﲔ ﻣﺴﺘﻘﻠﺘﲔ
.
ﺗﻜﺘﺐ ﺍﻟﻔﺮﺿﻴﺎﺕ
)
ﰲ ﺣﺎﻟﺔ ﺍﻻﺧﺘﺒﺎﺭ ﺍﻟﺜﻨﺎﺋﻲ
(
ﻛﻤﺎ ﻳﻠﻲ
:
H
0
: σ²
1
= σ²
2
↔ H
1
: σ²
1
≠ σ²
2
ﻧﻌﺘﻤﺪ ﰲ ﺍﻻﺧﺘﺒﺎﺭ ﻋﻠﻰ ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
)
T
ﺃﻭ
T’
(
ﺘﻤﻌﲔﺍ ﻥﻮﻛ ﺐﺴﲝ
ﻃﺒﻴﻌﻴﲔ ﺃﻡ ﻏﲑ ﺫﻟﻚ
.
9
-
3
-
2
-
1
.
ﳎﺘﻤﻌﲔ ﻃﺒﻴﻌﻴﲔ
1
-
ﺍﳊﺎﻟﺔ ﺍﻟﻌﺎﻣﺔ
:
1
;
1
2
2
2
1
2
1
~
ˆ
ˆ
'
−
−
=
n
n
F
S
S
T
2
-
ﰲ ﺣﺎﻟﺔ
n
1
, n
2
≥ 30
)
1
;
0
(
1
1
1
1
2
1
/
ˆ
ˆ
ln
2
1
2
1
2
2
2
1
N
n
n
S
S
T
≈
−
+
−
=
9
-
3
-
2
-
2
.
ﳎﺘﻤﻌﲔ ﻣﺎ
(n
1
, n
2
≥ 50)
1
-
µ
4
(1)
;
µ
4
(2)
ﻣﻌﺮﻭﻓﲔ
:
)
1
;
0
(
ˆ
ˆ
/
)
ˆ
ˆ
(
2
4
2
)
2
(
4
1
4
1
)
1
(
4
2
2
2
1
N
n
S
n
S
S
S
T
≈
−
−
−
−
=
µ
µ
2
-
ﰲ ﺣﺎﻟﺔ
µ
4
(1)
;
µ
4
(2)
ﻏﲑ ﻣﻌﺮﻭﻓﲔ
:
ﻧﻌﻮﺽ
µ
4
ﺏ
m
4
.
ﻣﺜﺎﻝ
:
ﻧﺴﺤﺐ ﻣﻦ ﳎﺘﻤﻌﲔ ﻃﺒﻴﻌﻴﲔ ﻋﻴﻨﺘﲔ ﺣﺠﻢ ﺍﻷﻭﱃ
18
ﻭﺣﺠﻢ ﺍﻟﺜﺎﻧﻴﺔ
21
.
ﻭﺟﺪﻧﺎ ﺍﻟﻨﺘﺎﺋﺞ ﺍﻟﺘﺎﻟﻴﺔ
:
m
1
= 81, m
2
= 76, S²
1
= 9, S²
2
= 8.
ﺘﻤﻌﲔ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔﺍ ﻲﻄﺳﻮﺘﻣ ﻱﻭﺎﺴﺗ ﺭﺎﺒﺘﺧﺍ ﺀﺍﺮﺟﺍ ﻦﻜﳝ ﻒﻴﻛ
5
%
؟
H
0
: σ²
1
= σ²
2
↔ H
1
: σ²
1
≠
σ²
2
Ŝ²
1
= S²
1
. n
1
/ (n
1
–1) = 9 (18)/17 ≈ 9.53 ;
Ŝ²
2
= S²
2
. n
2
/ (n
2
–1) = 8 (21)/20 = 8.4
Ŝ²
1
/ Ŝ²
2
≈ 1.135 ; F
0.05 ; 17 ; 20
≈ 2.17
0
1
;
1
;
2
1
H
R
F
T
n
n
⇒
<
−
−
α

C ا ء&Eا و ت&ا Fإ *
–
ءI"ا
2
15
9
-
4
.
ك ر ا
2
ا ر ا و ا ر ا وأ
.
9
-
4
-
1
.
ا ر ا
ﻭﻧﻔﺘﺮﺽ ﺃﻥ ﻟﺪﻳﻨﺎ ﻋﺪﺩﺍ،ﺔﺒﺴﻨﻟﺍ ﺭﺎﺒﺘﺧﺍ ﱃﺇ ﺪﻌﻨﻟ
k
ﻣﻦ ﺍﳋﺼﺎﺋﺺ ﺍﳌﺘﻨﺎﻓﻴﺔ
،
ﺘﻤﻊﺍ ﰲ ﺎﻬﻨﻣ ﻞﻛ ﻖﻘﲢ ﺔﺒﺴﻧ
ﻫﻲ
p
i
ﺣﻴﺚ
∑p
i
= 1
.
ﻧﺮﻳﺪ ﺍﺧﺘﺒﺎﺭ ﻓﺮﺿﻴﺔ
ﺣﻮﻝ ﻗﻴﻢ
ﻫﺬﻩ ﺍﻟﻨﺴﺐ
:
p
i
≠ p
i0
H
0
: p
i
= p
i0
(i = 1, 2, . . . k ) ↔ H
1
:
)
ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺒﺪﻳﻠﺔ ﻫﻲ ﺃﻥ
ﺇﺣﺪﻯ ﺍﻟﻨﺴﺐ ﺍﻻ
ﻓﺘﺮﺍﺿﻴﺔ
p
i0
ﻋﻠﻰ ﺍﻷﻗﻞ ﻏﲑ ﻣﺴﺎﻭﻳﺔ ﻟﻠﻘﻴﻤﺔ ﺍﳊﻘﻴﻘﻴﺔ
(.
ﻣﺘﻐﲑﺓ ﺍﻟﻘﺮﺍﺭ
:
ﻹﳒﺎﺯ ﺍﻻﺧﺘﺒﺎﺭ ﻧﺴﺘﺨﺮﺝ ﻋﻴﻨﺔ
)
ﻧﺮﻣﺰ ﳊﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺏ
n
(
ﻭ
ﳓﺴﺐ ﻓﻴﻬﺎ
ni
ﻋﺪﺩ ﻣﺮﺍﺕ ﲢﻘﻖ
ﻛﻞ
ﺧﺎﺻﻴﺔ
.
ﺇﺫﺍ ﲢﻘﻘﺖ ﺍﻟﺸﺮﻭﻁ
ﺍﻟﺜﻼ
ﺛﺔ ﺍﻟﺘﺎﻟﻴﺔ
:
n ≥ 30
،
np
i0
≥ 1
ﻭ
ﻋﻠﻰ ﺍﻷﻗﻞ ﰲ
80
%
ﻣﻦ ﺍﳊﺎﻻﺕ
np
i0
≥ 5
ﻧﱪﻫﻦ ﺃﻥ
:
2
1
0
0
)²
(
−
≈
−
=
∑
k
i
i
i
i
np
np
n
T
χ
ﻣﺜﺎﻝ
:
ﻳﺘﻘﺪﻡ ﺇﱃ ﺍﻧﺘﺨﺎﺑﺎﺕ ﻣﻌﻴﻨﺔ
3
ﻣﺮﺷﺤﲔ
:
ﺏ ﻭﺝ،ﺃ
.
ﻧﺮﻳﺪ ﺍﺧﺘﺒﺎﺭ ﻓﺮﺿﻴﺔ ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
5
%
ﺣﻮﻝ ﺷﻌﺒﻴﺘﻬﻢ ﻛﻤﺎ
ﻳﻠﻲ
:
H
0
: p
1
= 0.4, p
2
= 0.35, p
3
= 25
ﺃﺟﺮﻱ ﺍﺳﺘﺠﻮﺍﺏ ﻝ
n = 400
ﻧﺎﺧﺐ ﻓﻜﺎﻥ ﺗﻮﺯﻋ
ﻲ
ﻓﺌﺎﺕ ﺍﳌﺴﺎﻧﺪﻳﻦ ﻋﻠﻰ ﺍﻟﺘﻮﺍﱄ
:
n
i
= 170, 135, 95
ﻟﺪﻳﻨﺎ
n = 400 ≥ 30
،
ﻭ
ﺍﻷﻋﺪﺍﺩ ﺍﻻﻓﺘﺮﺍﺿﻴﺔ
:
np
i0
= 400(0.4) = 160, 400(0.35) = 140, 400(0.25) = 100 ≥ 1
ﻭ ﺍﻟﺸﺮﻁ
np
i0
≥ 5
ﰲ
ﺃﻛﺜﺮ ﻣﻦ
80
%
ﻣﻦ
ﺍﳊﺎﻻﺕ
ﳏﻘﻖ
.
05
.
1
100
)²
100
95
(
140
)²
140
135
(
160
)²
160
170
(
)²
(
0
0
=
−
+
−
+
−
=
−
=
∑
i
i
i
i
np
np
n
T
Χ²
2 ; 0.95
= 5.99 > 1.05 => H
0
.
ﲟﺎ ﺃﻥ
T
ﺃﻗﻞ ﺑﻜﺜﲑ ﻣﻦ
X²
ﳝﻜﻦ ﻗﺒﻮﻝ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ
.
9
-
4
-
2
.
ا
ا ر
ﻭﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻧﻘﺎﺭﻥ ﺑﲔ ﺗﻜﺮﺍﺭﺍﺕ ﺍﻟﻌﻴﻨﺔ،ﺮﺧﺁ ﻊﻳﺯﻮﺘﺑ ﲔﻌﻣ ﻊﻳﺯﻮﺗ ﻞﻳﺪﻌﺗ ﺭﺎﺒﺘﺧﻻ ﺎﻀﻳﺃ ﺔﻘﻳﺮﻄﻟﺍ ﻩﺬﻫ ﻡﺪﺨﺘﺴﺗ
)
ﺍﻟﺘﻜﺮﺍﺭﺍﺕ ﺍﳊﻘﻴﻘﻴﺔ
(
n
i
ﻭﺗﻜﺮﺍﺭﺍﺕ ﺍﻓﺘﺮﺍﺿﻴﺔ
n
i0
ﺣﻴﺚ ﺗﺼﺎﻍ ﺍﻟﻔﺮﺿﻴﺎﺕ ﻛﻤﺎ ﻳﻠﻲ،
:
ﻋﻠﻰ ﺍﻷﻗ
ﻞ ﺇﺣﺪﻯ ﺍﻟ
ﺘﻜﺮﺍﺭﺍﺕ
ﺍﻟﻨﻈﺮﻳﺔ
n
i0
ﻏﲑ ﻣﺴﺎﻭﻳﺔ ﻟﻠ
ﺘﻜﺮﺍﺭ
ﺍﳊﻘﻴﻘﻲ
n
i
H
0
: n
i
= n
i0
(i = 1, 2, … k) ↔ H
1
:
ﻹﺟﺮﺍﺀ ﺍﻻﺧﺘﺒﺎﺭ ﻧﺴﺘﺨﺪﻡ ﺍﻟﻘﺎﻧﻮﻥ ﺍﻟﺘﺎﱄ
:
2
1
0
0
)²
(
−
−
≈
−
=
∑
m
k
i
i
i
i
n
n
n
T
χ
ﺣﻴﺚ
m
ﻋﺪﺩ ﻣﻌﺎﱂ
ﺍ
ﺘﻤﻊ
ﺍﳌ
ﻘﺪﺭﺓ ﺍﻧﻄﻼﻗﺎ ﻣﻦ ﺑﻴﺎﻧﺎﺕ ﺍﻟﻌﻴﻨﺔ ﻟﺘﺤﺪﻳﺪ ﺍﻟﺘﻜﺮﺍﺭﺍﺕ ﺍﻟﻨﻈﺮﻳﺔ
.
ﻣﺜﺎﻝ
.
ﻃﻠﺒﻨﺎ ﻣﻦ
10
ﺃﻓﺮﺍﺩ ﺃﻥ ﻳﻌﻄﻮﻧ
ﺎ ﻛﻞ ﻣﻨﻬﻢ
ﺑﻄﺮﻳﻘﺔ ﻋﺸﻮﺍﺋﻴﺔ
10
ﺃﺭﻗﺎﻡ ﺗﺘﺮﺍﻭﺡ ﺑﲔ
0
ﻭ
9
.
ﻧﺮﻳﺪ ﺃﻥ ﳔﺘﱪ
،
ﲟﺴﺘﻮﻯ
ﻣﻌﻨﻮﻳﺔ
5
%
،
ﻣﺎ ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻟﻌﻴﻨ
ﺎﺕ
ﺍﶈﺼﻠﺔ ﻓﻌﻼ ﻋﺸﻮﺍﺋﻴﺔ
ﻋﻠﻤﺎ ﺃﻥ
ﺍﳌﺸﺎﻫﺪﺍﺕ ﺍﻟﻔﻌﻠﻴﺔ
n
i
ﻣﻦ ﻛﻞ ﺭﻗﻢ
ﻛﺎﻧﺖ ﻛﺎﻟﺘﺎﱄ
:

.
ا
IX
.
و ا تارا
ض
.
16
x
i
0
1
2
3
4
5
6
7
8
9
n
i
10
8
9
14
8
9
11
9
12
10
ﺍﳊﻞ
.
ﺃﻥ
ﺗﻜﻮﻥ
ﺍﻟﻌﻴﻨﺎﺕ
ﻋﺸﻮﺍﺋﻴﺔ ﻳﻌﲏ ﺃﻥ ﻳﻜﻮﻥ ﻟﻜﻞ ﺭﻗﻢ ﻣﻦ ﺍﻷﺭﻗﺎﻡ
0
ﺇﱃ
9
ﻧﻔﺲ ﺍﻻﺣﺘﻤﺎﻝ ﰲ ﺃﻥ ﻳﺘﻢ ﺍﺧﺘﻴﺎﺭﻩ ﰲ ﻛﻞ ﻣﺮﺓ
.
ﻣﻌﲎ ﻫﺬﺍ ﺃﻧﻪ ﺇﺫﺍ ﺍﻋﺘﱪﻧﺎ ﺍﻟﺮﻗﻢ ﺍﳌﺨﺘﺎﺭ ﻣﻦ ﻗﺒﻞ ﺍﻟﻔﺮﺩ ﰲ ﻛﻞ ﻣﺮﺓ ﻛﻤﺘﻐﲑﺓ ﻋﺸﻮﺍﺋﻴﺔ
X
ﻓﺈﻥ
X
ﺗﺘﺒﻊ ﺗﻮﺯﻳﻊ ﺍﺣﺘﻤﺎﱄ ﻣﺘﻌﺎﺩﻝ
(uniforme)
ﺃﻱ ﺃﻥ ﻟﻜﻞ ﺍﻟﻘﻴﻢ ﻧﻔﺲ ﺍﻻﺣﺘﻤﺎﻝ
0.1
.
ﻟﺪﻳﻨﺎ ﺇﺫ
ﺍ ﺗﻮﺯﻳﻌﺎﻥ ﻓﻌﻠﻲ ﻭﻧﻈﺮﻱ ﻧﺮﻳﺪ ﺍﺧﺘﺒﺎﺭ ﺍﳌﻄﺎﺑﻘﺔ ﺃﻭ ﺍﻟﺘﻘﺎﺭﺏ
ﻭ ﻫﻮ ﻣﺎ ﻳﺴﻤﻰ ﺑﺎﺧﺘﺒﺎﺭ ﺍﻟﺘﻌﺪﻳﻞ،ﺎﻤﻬﻨﻴﺑ
(Teste d’ajustement)
.
x
i
0
1
2
3
4
5
6
7
8
9
n
i
10
8
9
14
8
9
11
9
12
10
n
io
10
10
10
10
10
10
10
10
10
10
(
)
(
)
2
.
3
9
.
16
2
.
3
0
²
2
²
1
²
1
²
1
²
2
²
4
²
1
²
2
0
10
1
2
95
.
0
,
1
10
1
2
0
0
>
=
=
+
+
+
+
+
+
+
+
+
=
−
=
−
=
∑
χ
k
i
i
i
i
n
n
n
T
ﲟﺎ ﺃﻥ
T
ﺃﻗﻞ ﺑﻜﺜﲑ ﻣﻦ
X²
ﳝﻜﻦ
ﻗﺒﻮﻝ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﺑﺄﻥ
X
ﺗﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﳌﺘﻌﺎﺩﻝ
ﻣﺎ ﻳﻌﲏ
ﺃﻥ
ﺍﻷﺭﻗﺎﻡ ﺍﺧﺘﲑﺕ
ﺑﻄﺮﻳﻘﺔ ﻋﺸﻮﺍﺋﻴﺔ
.
ﻣﺜﺎﻝ
2
.
ﳌﺪﺓ ﺳﺎﻋﺘﲔ ﰎ ﻋﺪ
X
:
ﻋﺪﺩ
ﺍﻟﺰﺑﺎﺋﻦ ﺍﻟﺬﻳﻦ ﻳﺼﻠﻮﻥ ﰲ ﺍﻟﺪﻗﻴﻘﺔ ﺇﱃ ﺷﺒﺎﻙ ﻣﻌﲔ
.
ﻧﺮﻳﺪ ﺍﺧﺘﺒﺎﺭ
ﲟﺴﺘﻮﻯ ﻣﻌﻨﻮﻳﺔ
0.05
ﻓﺮﺿﻴﺔ ﺃﻥ
X
ﺗﺘﺒﻊ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ
.
ﺍﳌﺸﺎﻫﺪﺍﺕ ﻛﺎﻧﺖ ﻛﺎﻟﺘﺎﱄ
:
xi
0
1
2
3
4
5
6
7
8
9
10
11
ni
4
9
24
25
22
18
6
5
3
2
1
1
ﺍﳊﻞ
.
ﻟﺘﺤﺪﻳﺪ ﺍﻟﻘﻴﻢ ﺍﻟﻨﻈﺮﻳﺔ ﺣﺴﺐ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻨﻈﺮﻱ ﺑﻮﺍﺳﻮﻥ ﳓﺘﺎﺝ ﺇﱃ ﲢﺪﻳﺪ ﻣﻌﻠﻤﺔ ﻫﺬﺍ ﺍﻷﺧﲑ
.
ﻧﻌﻠﻢ ﺃﻥ ﻣﻌﻠﻤ
ﺔ
ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ
ﺗﺴﺎﻭﻱ ﺍﻟﺘﻮﻗﻊ ﻭﺗﺴﺎﻭﻱ ﰲ ﺍﻟﻮﻗﺖ ﺫﺍﺗﻪ ﺍﻟﺘﺒﺎﻳﻦ
.
ﲝﺴﺎﺏ ﻫﺬﻳﻦ ﺍﳌﺆﺷﺮﻳﻦ ﻟﻠﻤﺘﻐﲑﺓ
X
ﳒﺪ
ﳘﺎ ﻋﻠﻰ ﺍﻟﺘﻮﺍﱄ
3.7
ﻭ
4.41
ﻟﺬﻟﻚ
ﻧﺄﺧﺬ ﻛﻘﻴﻤﺔ ﺗﻘﺪﻳﺮﻳﺔ
ﻝ
λ
ﺍﻟﻘﻴﻤﺔ
4
.
ﳓﺴﺐ ﺇﺫﺍ ﺑﺎﺳﺘﺨﺪﺍﻡ ﺗﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ ﲟﻌﻠﻤﺔ
4
ﺍﺣﺘﻤﺎﻻﺕ ﺍﻟﻘﻴﻢ ﻣﻦ
0
ﺇﱃ
11
ﰒ ﻧﻀﺮﺏ ﻫﺬﻩ ﺍﻻﺣﺘﻤﺎﻻﺕ ﰲ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
n = 120
ﻟﻠﺤﺼﻮﻝ ﻋﻠﻰ ﺍﻟﻘﻴﻢ
n
i0
ﻣﻊ ﺍﻟﺘﻘﺮﻳﺐ ﳊﺬﻑ ﺍﻷﺭﻗﺎﻡ ﺑﻌﺪ
ﺍﻟﻔﺎﺻﻠﺔ ﻭ ﺍﳊﺮﺹ ﻋﻠﻰ ﺃﻥ ﻳﺒﻘﻰ ﺍ
ﻤﻮﻉ
120
.
xi
0
1
2
3
4
5
6
7
8
9
10
11
∑
ni
4
9
24
25
22
18
6
5
3
2
1
1
120
nio
2
9
18
23
23
19
13
7
3
2
1
0
120
ﻧﻌﻴﺪ ﲡﻤﻴﻊ ﺍﻟﻘﻴﻤﺘﲔ ﺍﻷﻭﻟﻴﲔ ﻭﺍﻷﺭﺑﻊ ﺍﻷﺧﲑﺓ ﻟﺘﻠﺒﻴﺔ ﺍﻟﺸﺮﻁ
np
i0
≥ 5
ﻣﺎ ﳚﻌﻞ ﻋﺪﺩ ﺍﻟﻘﻴﻢ
k = 8
ﺑﺪﻻ ﻣﻦ
12
.
ﺬﺍ
ﺗﻜﻮﻥ ﻋﺪﺩ ﺩﺭﺟﺎ ﺕ ﺍﳊﺮﻳﺔ
8-1-1 = 6
ﲟﺎ ﺃﻥ ﻫﻨﺎ ﻣﻌﻠﻢ ﻭﺍﺣﺪ ﻟﻠﺘﻮﺯﻳﻊ ﺍﻟﻨﻈﺮﻱ ﰎ ﺗﻘﺪﻳﺮﻩ ﺍﻧﻄﻼﻗﺎ ﻣﻦ ﺍﻟﻌﻴﻨﺔ
.
(
)
14
.
7
6
.
12
14
.
7
2
95
.
0
,
6
1
2
0
0
>
=
=
−
=
∑
=
χ
k
i
i
i
i
n
n
n
T
ﲟﺎ ﺃﻥ
T
ﺃﻗﻞ ﺑﻜﺜﲑ ﻣﻦ
X²
ﳝﻜﻦ ﻗﺒﻮﻝ ﺍﻟﻔﺮﺿﻴﺔ ﺍﻟﺼﻔﺮﻳﺔ ﺑﺄﻥ ﻋﺪﺩ ﺍﻟﺰﺑﺎﺋﻦ
X
ﺍﻟﺬﻳﻦ ﻳﺼﻠﻮﻥ
ﺇﱃ ﺍﻟﺸﺒﺎﻙ ﰲ ﺍﻟﺪﻗﻴﻘﺔ ﻳﺘﺒﻊ
ﺍﻟﺘﻮﺯﻳﻊ ﺑﻮﺍﺳﻮﻥ
.

C ا ء&Eا و ت&ا Fإ *
17
ﺍﳌﺮﺍﺟﻊ
ﳏﺎﺿﺮﺍﺕ ﰲ ﺍﻹﺣﺼ،ﺪﻤﳏ ﺱﻼﻛ
، ﺩﻳﻮﺍﻥ ﺍﳌﻄﺒﻮﻋﺎﺕ ﺍﳉﺎﻣﻌﻴﺔ،ﻲﻘﻴﺒﻄﺘﻟﺍ ﺀﺎ
1993
.
ﻣﻔﺎﻫﻴﻢ ﻣﻦ ﺣﺴﺎﺏ ﺍﻻﺣﺘﻤﺎﻻﺕ،ﺪﲪﺃ ﺕﺎﺒﻴﺷ
-
ﺳﻠﺴﻠﺔ ﺍﻟﺮﻳﺎﺿﻴﺎﺕ ﰲ ﺍﳉﺎﻣﻌﺔ،ﺔﻟﻮﻠﳏ ﻦﻳﺭﺎﲤﻭ ﺱﻭﺭﺩ
.
،ﺭﺟﺎﻝ ﺳﻌﺪﻱ
، ﺩﻳﻮﺍﻥ ﺍﳌﻄﺒﻮﻋﺎﺕ ﺍﳉﺎﻣﻌﻴﺔ،ﺀﺎﺼﺣﻻﺍﻭ ﺕﻻﺎﻤﺘﺣﻻﺍ ﰲ ﺕﺍﺮﺿﺎﳏ
2005
.
Aîvazian S., Enukov I., Mekhaline L., Eléments de modélisation et
traitement primaire de données, Editions Mir, Moscou, 1983, traduit du
russe par Djilali Embarek, 1986.
Boyer Luc et Equilbey Noël, Histoire du management, Les éditions
d'organisation, Paris, 1990.
Céhéssat Ronald, Exercices commentés de statistique et informatique
appliquées, Dunod, 1976, Paris.
Droesbeke Jean-Jacques, Eléments de statistique, Série SMA, Edition de
l'Université de Bruxelles et Edition Ellipses, 1997, Belgique.
Gnédenko, B. Béliaev,Y. Soloviev, A. Méthodes mathématiques en
théorie de la fiabilité, Ed. Mir, 1972, Moscou.
Kazmier Léonard J., Statistique de la gestion, théorie et problèmes, Série
Schaum, McGraw Hill, 1982, N. Y.
Lavoie Réginald, Statistique appliquée, Auto-apprentissage par objectifs,
Presses de l'Université du Québec, 1981, Canada.
McGee Victor E., Principes de statistiques, 1975.
Salvator Dominick, Econométrie et statistique appliquée, cours et
problèmes, Série Schaum, McGrow Hill, 1985, N. Y.
Spiegel Murray R., probabilités et statistique, cours et problèmes, Série
Schaum, McGraw Hill, 1985, N. Y.
