
ﻣﺪﺧﻞ ﺇﱃ
ﺍﻻﺣﺘﻤﺎﻻﺕ ﻭ ﺍﻹﺣﺼﺎﺀ ﺍﻟﺮﻳﺎﺿﻲ
ﻟﻄﻠﺒﺔ ﻛﻠﻴﺔ ﺍﻟﻌﻠﻮﻡ ﺍﻻﻗﺘﺼﺎﺩﻳﺔ
ﺩﺭﻭﺱ ﻣﻊ ﺃﻣﺜﻠﺔ ﻭﺗﻄﺒﻴﻘﺎﺕ ﳏﻠﻮﻟﺔ
ﺍﳉﺰﺀ ﺍﻟﺜﺎﱐ
:
ﺍﻹﺣﺼﺎﺀ
ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺑﻊ
:
ﻧﻈﺮﻳﺔ ﺍﳌﻌﺎﻳﻨﺔ
ﺑﻮ ﻋﺒﺪ ﺍﷲ ﺻﺎﱀ
ﺃ
ﺳﺘﺎﺫ ﻣﺴﺎﻋﺪ
ﻣﻜﻠﻒ ﺑﺎﻟﺪﺭﻭﺱ
ﺑﻜﻠﻴﺔ ﺍﻟﻌﻠﻮﻡ ﺍﻻﻗﺘﺼﺎﺩﻳﺔ
–
ﺟﺎﻣﻌﺔ ﺍﳌﺴﻴﻠﺔ
.

ت س
ا
ﺍﻟﻔﺼﻞ
7
ﻧﻈﺮﻳﺔ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ
................................
.......................
3
ه إ
................................
................................
................................
..............................
3
ا وا
................................
................................
................................
...........................
3
ا"ا ا
–
$%&ا ا"ا ا
–
ا اد
................................
................................
..................
4
ا
................................
................................
................................
...........................
5
إ ا
................................
................................
................................
...........................
5
ت$*+ ا ز-
................................
................................
................................
..............
5
ت$*+ ا ز- .*
................................
................................
................................
................
5
/ ا$0 وأ ت$*+ ا ز- 2&-
................................
................................
...............................
6
4ز ا- &5
M
................................
................................
................................
.........................
8
780
................................
................................
................................
...........................
9
&%+ ز ا-
................................
................................
................................
...................
10
او قو + ا ز-
................................
................................
................................
....
12
2&. وا*ا
................................
................................
................................
.........................
12
2$* 2= ق + ا ز- &5
................................
................................
................................
.....
12
2> ?&- &% و2&+ ا ز-
................................
................................
........................
13
2&+ ز ا-
................................
................................
................................
.........................
13
2&- &% ز ا-
................................
................................
................................
.......................
15
780
................................
................................
................................
.........................
16
@+
................................
................................
................................
.........................
17

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
3
ا
7
ا ز
إ ه
-
زت ا
ت!
-
"#! ا$ز
-
$ %(وق وا! ا $ز
-
)" ! ا$ز
-
) " "# ا$ز
ﰲ ﳎﺘﻤﻌ
ﺎﺗﻨﺎ ﺍﳌﻌﺎﺻﺮﺓ ﻻ ﳝﺮ ﻳﻮﻡ ﺩﻭﻥ ﺃﻥ ﻳﻌﻠﻦ ﻋﻦ ﻧﺘﺎﺋﺞ ﺍﺳﺘﻘﺼﺎﺀ ﺃﺟﺮﺗﻪ ﳎﻠﺔ
ﺃﻭ
ﺟﺎﻣﻌﺔ
ﺣ
ﻮﻝ
ﻴﺔ ﺃﻭـﺳﺎﻴﺳ ﻊﻴـﺿﺍﻮﻣ
ﻣﻨﻬﺎ ﺍﻻﺳﺘﻘﺼﺎﺀﺍﺕ ﺍﳌﺜﲑﺓ ﻟﻠﺠﺪﻝ ﺣﻮﻝ ﺍﻵﺭﺍﺀ ﺍﻟﺴﻴﺎﺳﻴﺔ ﻟﻠﻤﻮﺍﻃﻨﲔ ﺃﺛﻨﺎﺀ ﺍ،ﺓﺩﺪﻌﺘﻣ ﺔﻴﻋﺎﻤﺘﺟﺍ
ﺔـﻴﺑﺎﺨﺘﻧﻻﺍ ﺕﻼﻤﳊ
.
ﰲ
ﻋﺎﱂ ﺍﻷﻋﻤﺎﻝ ﺗﻘﻮﻡ ﺍﳌﺆﺳﺴﺎﺕ ﻋﻦ ﻃﺮﻳﻖ ﻣﺼﺎﱀ ﺍﻟﺘﺴﻮﻳﻖ ﻭﻣﺼﺎﱀ
ﻼﻉـﻃﻺﻟ ﺕﺍﺀﺎﺼﻘﺘﺳﺍ ﺀﺍﺮﺟﺈﺑ ﺮﻳﻮﻄﺘﻟﺍﻭ ﺙﻮﺤﺒﻟﺍ
ﻋﻠﻰ ﺗﻮﺟﻬﺎﺕ ﺍﳌﺴﺘﻬﻠﻜﲔ
،
...
ﺃﻭ ﻛﻴﻒ؟ ﺔﻔﻠﺘﺨﳌﺍ ﺕﺍﺀﺎﺼﻘﺘﺳﻻﺍ ﺎﻬﻴﻠﻋ ﺪﻨﺘﺴﺗ ﱵﻟﺍ ﺔﻴﺿﺎﻳﺮﻟﺍ ﺔﻳﺮﻈﻨﻟﺍ ﺲﺳﻷﺍ ﻲﻫ ﺎﻤﻓ
؟ﺘﻤﻊ ﺍﻟﺬﻱ ﺃﺧﺬﺕ ﻣﻨﻪﺍ ﺺﺋﺎﺼﺧ ﻰﻠﻋ ﺔﻨﻴﻋ ﺕﺎﻧﺎﻴﺑ ﻝﻼﺧ ﻦﻣ ﻝﻻﺪﺘﺳﻻﺍ ﻦﻜﳝ
ﺎـﻫﲑﻏﻭ ﺔﻠﺌﺳﻷﺍ ﻩﺬﻫ ﻰﻠﻋ ﺔﺑﺎﺟﻹﺍ
ﺗﺘﻄﻠﺐ ﻓﻬﻢ
ﺍﻟﻌﻼﻗﺎﺕ ﺍﻟﺮﻳﺎﺿﻴﺔ ﺑﲔ ﺍﳋﺼﺎﺋﺺ ﺍﳌﺨﺘﻠﻔﺔ ﻟﻠﻤﺠﺘﻤﻊ
، ﺍﻟﺘﺒﺎﻳﻦ ﻭﻏﲑﻫﺎ،ﻂﺳﻮﺘﳌﺍ ﻞﺜﻣ
ﻭ
ﺍﳋﺼﺎﺋﺺ ﺍﳌﻨﺎﻇﺮﺓ ﳍﺎ
ﰲ ﺍﻟﻌﻴﻨﺔ ﻭﻫﻮ
ﻣﺎ ﺳﻨﺘﻨﺎﻭﻟﻪ ﰲ ﻫﺬﺍ ﺍﻟﻔﺼﻞ
.
ﰲ ﺍﻟﻔﺼﻮﻝ ﺍﳌﻘﺒﻠﺔ ﺳﻨﺪﺭﺱ ﻋﺪﺩﺍ ﻣﻦ ﺍﻟﺘﻄﺒﻴﻘﺎﺕ ﳍﺬﻩ ﺍﻟﻌﻼﻗﺎﺕ ﺍﻟﺮﻳﺎﺿﻴﺔ
.
7
-
1
ه إ
ا وا
ا اد وا
دا H
ا"ا ا
إ ا
7
-
1
-
1
وا$ %ا
ﻧﺸﺮﺡ ﻣﺼﻄﻠﺤﻲ
ﺘﻤﻊ ﻭﺍﻟﻌﻴﻨﺔﺍ
(Population et échantillon)
ﻭ ﻧﻌﺮﻓﻬﻤﺎ
ﻣﻦ ﺧﻼﻝ
ﺍﻷﻣﺜﻠﺔ ﺍﻟﺘﺎﻟﻴﺔ
:
-
ﻳﺮﻏﺐ ﺑﺎﺣﺚ ﺯﺭﺍﻋﻲ ﰲ ﺗﻘﺪﻳﺮ
ﻣﺘﻮﺳﻂ ﻋﺪﺩ ﺣﺒﺎﺕ ﺍﻟﻘﻤﺢ ﻟﺴﻨﺒﻠﺔ ﺍﻟﻘﻤﺢ ﺍﶈﻠﻲ
ﺍﳉﺰﺍﺋﺮﻱ
"
ﳏﻤﺪ ﺍﻟﺒﺸ
ﲑ
."
ﻳﻜﻮﻥ ﺍﻟﺒﺎﺣﺚ ﻋﻴﻨﺔ ﻣﻦ
100
ﺳﻨﺒﻠﺔ
.
ﻳ
ﻌﺪ ﺍﳊﺒﺎﺕ ﰲ ﺍﻟﺴﻨﺎﺑﻞ ﻓﻴﺤﺼﻞ ﻋﻠﻰ ﳎﻤﻮﻋﺔ ﻣﻦ
100
، ﻋﺪﺩ
ﻳﻘﺴﻢ
ﻤﻮﻉﺍ
ﻋﻠﻰ
100
ﻓﻴ
ﺤﺼﻞ ﻋﻠﻰ ﺍﻟ
ﻌﺪﺩ
ﺍﳌ
ﺘﻮﺳﻂ
ﳊﺒﺎﺕ ﺍﻟﻘﻤﺢ ﰲ ﺍﻟﺴﻨﺒﻠﺔ
ﰲ ﺍﻟﻌﻴﻨﺔ
.
ﺍﻟﻨﺘﻴﺠﺔ
ﺗﺴﺘﺨﺪﻡ ﻟﺘﻘﺪﻳﺮ
ﻣﺘﻮﺳﻂ
ﻋﺪﺩ
ﺣﺒ
ﺎﺕ
ﺍﻟﻘﻤﺢ ﻣﻦ ﺍﻟﻨﻮﻉ
ﺍﶈﻠﻲ
.
ﺘﻤﻊﺍ ﻦﻋ ﱪﻌﻧ ﻥﺃ ﻦﻜﳝ
ﺍﳌﺪﺭ
ﻭﺱ
)
ﻫﻮ ﻫﻨﺎ
ﻋﺪﺩ ﺣﺒﺎﺕ ﺳﻨﺒﻠﺔ ﳏﻤﺪ ﺍﻟﺒﺸﲑ
(
ﲟﺘﻐﲑﺓ ﻋﺸﻮﺍﺋﻴﺔ
X
ﳍﺎ ﻣﺘﻮﺳﻂ
)
ﺗﻮﻗﻊ
ﺭﻳﺎﺿﻲ
(
µ
ﻭﺗﺒﺎﻳﻦ
σ²
ﻭﻏﲑﳘﺎ ﻣﻦ،
ﺘﻤﻊﺍ ﱂﺎﻌﻣ
.
ﰲ ﺍﳌﻘﺎﺑﻞ ﻛﻞ ﻗﻴﻤﺔ ﳏﺼﻞ ﻋﻠﻴﻬﺎ ﰲ ﺍﻟﻌﻴﻨﺔ
x
i
ﻫﻲ ﲢﻘﻖ
)
réalisation
(
ﳌ
ﺘﻐﲑﺓ
ﻉ ﻧﺮﻣﺰ ﳍﺎ ﺏ
X
i
.
ﻧﺴﺘﻨﺘﺞ ﺃﻥ
ﺍﻟﻌﻴﻨﺔ
ﳝ
ﻜﻦ
ﺗﻌﺮﻳﻔﻬﺎ ﺭﻳﺎﺿﻴﺎ ﺑ
ﺘﻮﻟﻴﻔﺔ ﻣ
ﻦ ﺍﳌﺘﻐﲑﺍﺕ ﺃﻭ ﲟ
ﺘﻐﲑﺓ ﻣﺘﻌﺪﺩﺓ ﺍﻷﺑﻌﺎﺩ
1
:
{X
1
, . . . , X
n
}
.
ﻛﻞ ﻗﻴﻤﺔ ﳏﺼﻞ ﻋﻠﻴﻬﺎ ﰲ ﺍﻟﻌﻴﻨﺔ ﻫﻲ،ﻯﺮﺧﺃ ﺔﻬﺟ ﻦﻣ
ﺃﻳﻀﺎ
ﲢﻘﻖ
ﺘﻤﻊﺍ ﺓﲑﻐﺘﳌ
X
ﻟﺬﻟﻚ ﻓﺈﻥ،
ﺍﻟﺘﻮﻗﻊ ﺍﻟﺮﻳﺎﺿﻲ ﻟﻜﻞ
ﻣﺘﻐﲑﺓ
X
i
ﺘﻤﻊﺍ ﺓﲑﻐﺘﳌ ﻲﺿﺎﻳﺮﻟﺍ ﻊﻗﻮﺘﻟﺍ ﻪﺴﻔﻧ ﻮﻫ
X
ﺘﻤﻊﺍ ﻦﻳﺎﺒﺗ ﻮﻫ ﺎﻬﻨﻳﺎﺒﺗﻭ ،
:
1
ة L Mأ D% وأ N= N- 2-د 2 ا نآ ?
2E= ذات
)
E&ا S ة Lا TUأ
.(

ا
VII
.
ا TU
4
E(X
i
) = µ
،
V(X
i
) = σ²
ﺧﺼﺎﺋﺺ ﻛﻞ ﻣﺘﻐﲑﺓ ﻣﻦ ﻣﺘﻐﲑﺍﺕ ﺍﻟﻌﻴﻨﺔ ﻭﺧﺼﺎﺋﺺ،ﻊﻤﺘﺍ ﺺﺋﺎﺼﺧ ﲔﺑ ﺰﻴﻴﻤﺘﻟﺍ ﺐﳚ
ﺍﻟﻌﻴﻨﺔ
)
ﻧﺮﻣﺰ ﳋ
ﺼﺎﺋﺺ ﺍﻟﻌﻴﻨﺔ
ﺑﺄﺣﺮﻑ ﻻﺗﻴﻨﻴﺔ
-
M
، ﻟﻠﻤﺘﻮﺳﻂ ﺍﳌﺮﺟﺢ
S
ﻟﻼﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻭ
S²
ﻟﻠﺘﺒﺎﻳﻦ
-
ﺘﻤﻊﺍ ﺺﺋﺎﺼﺧ ﻦﻋ ﺎﻫﺰﻴﻴﻤﺘﻟ
µ
،
σ
ﻭ
σ²
(
ﻭﺗ
ﻜﺘﺐ
ﻛﻤﺎ ﻳﻠﻲ
:
2
)
(
1
²
,
1
∑
∑
−
=
=
µ
i
i
X
n
S
X
n
M
ﻻﺣﻆ
.
ﺧﺼﺎﺋﺺ ﺍﻟﻌﻴﻨ
ﺔ
ﻫﻲ ﺩﻭﺍﻝ ﰲ ﻣﺘﻐﲑﺍﺕ ﺍﻟﻌﻴﻨﺔ
.
ﻣﺜﺎﻝ
2
.
ﺗﺮﻏﺐ ﻫﻴﺄﺓ ﻣﻌﻴﻨﺔ ﺑﺎﻟﺒﺤﻮﺙ ﺍﻟﺴﻴﺎﺳﻴﺔ ﰲ ﺗﻘﺪﻳﺮ ﻧﺴﺒﺔ ﺍﻟﻨﺎﺧﺒﲔ ﺍﳌﺴﺎﻧﺪﻳﻦ ﳌﺮﺷﺢ ﻣﻌﲔ ﰲ
10
ﻓﺘﻘﻮﻡ،ﺕﺎﻳﻻﻮﻟﺍ
ﺑﺎﺳﺘﺠﻮﺍﺏ
100
ﻧﺎﺧﺐ ﻣﻦ ﻛﻞ ﻭﻻﻳﺔ
.
ﺘﻤﻊ ﺑﻴﻨﻤﺎ ﺍﻝﺍ ﻥﻮﻠﺜﳝ ﺮﺸﻌﻟﺍ ﺕﺎﻳﻻﻮﻟﺍ ﰲ ﻥﻮﺒﺧﺎﻨﻟﺍ
1000
ﻧﺎﺧﺐ ﺍﳌﺴﺘﺠﻮﺑﻮﻥ
ﳝﺜﻠ
ﻮﻥ ﺍﻟﻌﻴﻨﺔ
.
ﻣﺜﺎﻝ
3
.
ﻣﻦ ﺃﺟﻞ ﻣﻌﺮﻓﺔ ﻣﺪﻯ ﺩﻗﺔ ﺻﻨﻊ ﻗﻄﻌﺔ ﻧﻘﺪﻳﺔ ﺗﺮﻣﻰ ﺍﻟﻘﻄﻌﺔ
100
ﻣﺮﺓ ﻭﳓﺴﺐ ﻋﺪﺩ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺍﻟﺼﻮﺭﺓ
ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﻫﻨﺎ ﻫﻮ،ﺔﺑﺎﺘﻜﻟﺍﻭ
100
.
ﻣﺜﺎﻝ
4
.
ﺎ ﰒﻮﻟ ﻞﺠﺴﻧ ﺓﺮﻛ ﺐﺤﺴﺑ ﺕﺍﺮﳌﺍ ﻦﻣ ﺩﺪﻋ ﻡﻮﻘﻧ ،ﲔﻌﻣ ﻥﻮﻟ ﻦﻣ ﱵﻟﺍ ،ﻕﻭﺪﻨﺻ ﻞﺧﺍﺩ ﺕﺍﺮﻜﻟﺍ ﺔﺒﺴﻧ ﺮﻳﺪﻘﺘﻟ
ﻧﻌﻴﺪﻫﺎ
.
ﻋﺪﺩ ﺍﻟﻜﺮﺍﺕ
ﺍﳌﺴﺤﻮﺑﺔ ﳝﺜﻞ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
.
ﻻﺣﻆ
:
−
ﺘﻤﻊ ﻳﻘﺼﺪ ﺑﻪ ﺍﻟﻘﻴﺎﺳﺎﺕ ﺃﻭ ﺍﻟﻘﻴﻢ ﻭﻟﻴﺲ ﺍﻷﻓﺮﺍﺩ ﺃﻭ ﺍﻷﺷﻴﺎﺀ ﺍﻟﱵ ﰎ ﻗﻴﺎﺳﻬﺎﺍ ﺢﻠﻄﺼﻣ
)
،ﳎﺘﻤﻊ ﺍﻷﻭﺯﺍﻥ
ﳎﺘﻤﻊ ﺁﺭﺍﺀ ﺍﻟﻨﺎﺧﺒﲔ
(..
.
−
ﺘﻤﻊ ﻗﺪﺍ
ﻻ
ﻳﻜﻮﻥ ﳏﺪﻭﺩﺍ
)
ﻧﺘﺎﺋﺞ ﺭﻣﻴﺎﺕ ﻗﻄﻌﺔ ﺍﻟﻨﻘﺪ
(.
ﺘﻤﻊ ﺏﺍ ﻢﺠﳊ ﺰﻣﺮﻧ
N
ﻭﳊﺠﻢ ﺍﻟﻌﻴﻨﺔ ﺏ،
n
.
7
-
1
-
2
*ا ا
ا
–
#"ا ا*ا ا
–
ا اد
ﻋﻨﺪ ﺍﻟﻘﻴﺎﻡ ﺑﺎﳌﻌﺎﻳﻨﺔ ﻧﺒﺤﺚ ﻋﺎﺩﺓ ﻋﻦ ﻋﻴﻨﺔ ﳑﺜﻠﻪ ﻟﻠﻤﺠﺘﻤﻊ ﺣﱴ ﺗﻌﻜﺲ ﺧﺼﺎﺋﺼﻪ ﰲ ﺣﺪﻭﺩ ﺍﻹﻣﻜﺎﻧﻴﺎﺕ ﺍﳌﺎﻟﻴﺔ ﻭﺍﻟﻮﻗﺖ
ﺍﳌﺘ
ﺎﺡ
.
ﺍﻟﻌﻴﻨﺔ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ
(Echantillon aléatoire)
-
ﻭﺗﺴﻤﻰ ﺃﻳﻀﺎ ﺍﻟﻌﻴﻨﺔ ﺍﻻﺣﺘﻤﺎﻟﻴﺔ
-
ﻫﻲ
ﺃﺣﺪ ﺍﻟﻄﺮﻕ ﻟﺘﻜﻮ
ﻳﻦ ﻋﻴﻨﺔ
ﻭ ﻫﻲ
ﺘﻤﻊ ﺍﺣﺘﻤﺎﻻ ﻣﻌﻠﻮﻣﺎ ﻭﺃﻛﱪ ﻣﻦ ﺍﻟﺼﻔﺮ ﻟﻜﻲ ﺗﻈﻬﺮ ﰲ ﺍﻟﻌﻴﻨﺔﺍ ﰲ ﺓﺩﺮﻔﻣ ﻞﻜﻟ ﻥﻮﻜﻳ ﱵﻟﺍ
.
ﺳﻨﺘﻄﺮﻕ ﰲ ﺩﺭﺍﺳﺘﻨﺎ
ﻟﻨﻮﻉ ﳏﺪﺩ
ﻣﻦ ﺍﻟﻌﻴﻨﺎﺕ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ
ﻫﻮ
ﺍﻟﻌﻴﻨﺔ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ ﺍﻟﺒﺴﻴﻄﺔ ﻭ
ﻫﻲ
ﺍﻟﱵ ﺗﻜﻮﻥ ﺍﺣﺘﻤﺎﻻﺕ ﲨﻴﻊ ﺍﳌﻔﺮﺩﺍﺕ ﻟﻠﻈﻬﻮﺭ ﰲ
ﺍﻟﻌﻴﻨﺔ
ﻣﺘﺴﺎﻭﻳﺔ
ﻭﺃﻛﱪ ﻣﻦ ﺍﻟﺼﻔﺮ
1
.
ﻣﻦ ﻃﺮﻕ
ﺗﻜﻮﻳﻦ
ﻋﻴﻨﺔ ﻋﺸﻮﺍﺋﻴﺔ ﺑﺴﻴﻄﺔ
ﻃﺮﻳﻘﺔ ﺍﻟﻘﺮﻋﺔ
)
ﻻﺧﺘﻴﺎﺭ ﻋﺪﺩ ﻣﻦ ﺍﻟﻄﻠﺒﺔ
ﰒ ﻧﺴﺤﺐ ﻣﻨﻬﺎ ﺑﺎﻟﺼﺪﻓﺔ ﻋﺪﺩ ﻣﻦ ﺍﻟﻘﺼﺎﺻﺎﺕ ﲟﻘﺪﺍﺭ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ،ﺕﺎﺻﺎﺼﻗ ﰲ ﺔﺒﻠﻄﻟﺍ ﺀﺎﲰﺃ ﻞﻛ ﺐﺘﻜﻧ ﺎﻴﺋﺍﻮﺸﻋ
(
ﻭﻃﺮﻳﻘﺔ ﺍﻷﻋﺪﺍﺩ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ
)
ﺘﻤﻊ ﰒ ﳓﺪﺩ ﺍﻟﻌﻴﻨﺔ ﻣﻦ ﺧﻼﻝ ﳎﻤﻮﻋﺔ ﻣﻦ ﺍﻷﻋﺪﺍﺩ ﺗﺆﺧﺬ ﻣﻦ ﺍﳉﺍ ﺕﺍﺩﺮﻔﻣ ﻢﻗﺮﻧ
ﺪﺍﻭﻝ
ﺍﻹﺣﺼﺎﺋﻴﺔ ﻟﻸﻋﺪﺍﺩ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ
2
ﺃﻭ ﻋﻦ ﻃﺮﻳﻖ ﺑﺮﻧﺎﻣﺞ ﺑﺎﳊﺎﺳﻮﺏ
(
.
ﰲ ﻫﺬﺍ ﺍﻟﻔﺼﻞ ﺳﻨﻤﻴﺰ ﺑﲔ ﺣﺎﻟﺘﲔ
:
ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻨﻔﺎﺩﻳﺔ
(Echantillonnage exhaustif)
ﻭﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﻏﲑ
ﺍﻟﻨﻔﺎﺩﻳﺔ
.
ﻧﻘﺼﺪ ﺑﺎﻟﻌﻴﻨﺔ ﻏﲑ ﺍﻟﻨﻔﺎﺩﻳﺔ
(
non exhaustif
)
ﺍﻟﻌﻴﻨﺔ ﺍﻟﱵ
ﻳﻜﻮﻥ
ﻓﻴﻬﺎ
ﺍﻟﺴﺤﺐ
ﺘﻤﻊﺍ ﻦﻣ
ﺑﺎﻹﺭﺟﺎﻉ
،
ﺎ ﻻﻷ
ﺘﻤﻊﺍ ﺕﺍﺩﺮﻔﻣ ﺩﺎﻔﻧ ﱃﺇ ﻱﺩﺆﺗ
ﻣﻊ ﺗﻜﺮﺍﺭ ﺍﻟﺴﺤﺐ
ﻷﻧﻪ
ﳝﻜﻦ
ﺃﻥ ﺗﻈﻬﺮ
ﻣﻔﺮﺩﺓ
ﺘﻤﻊﺍ ﻦﻣ
ﺃﻛﺜﺮ ﻣﻦ ﻣﺮﺓ ﰲ ﺍﻟﻌﻴﻨﺔ
3
1
تا 2 +W عاUY ض U @+ا ?
.
2
ا"ا داE>Yا لوE\ TUأ
.
3
نأ A ه ،^C ها * ?ا A ا ت_8ا 2 دE> ? نار a- نA كه
تا L
ا
Xi
وا+^%
?UC
،
c @^
و ،دU H ا dUآ اذإ ل8^*Cا ط
اfgه ?
ر ا&>ا 2a
?UC
.
?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
5
ﻭ
ﻴﻓ
ﻬﺎ
ﺗﻜﻮﻥ ﻣﺘﻐﲑﺍﺕ ﺍﻟﻌﻴﻴﻨﺔ
X
i
ﻣﺴﺘﻘﻠﺔ ﻭﳍﺎ ﻧﻔﺲ ﺍﻟﺘﻮﺯﻳﻊ
.
ﻋﻠﻰ
ﺍﻟﻌﻜﺲ ﻧﺴﻤﻲ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ ﻣﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔ
ﺣﻴﺚ ﻻ ﳝﻜﻦ ﺃﻥ ﺗﻈﻬﺮ ﻣﻔﺮﺩﺓ ﰲ ﻋ
ﻴﻨﺔ ﺃﻛﺜﺮ ﻣﻦ ﻣﺮﺓ
ﻭ ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻻ ﺗﻜﻮﻥ ﻧﺘﺎﺋﺞ ﺍﻟﺴﺤﺐ
)
ﻣﺘﻐﲑﺍﺕ ﺍﻟﻌﻴﻨﺔ
(
ﻣﺴﺘﻘﻠﺔ
1
ﻣﺒﺪﺋﻴﺎ
.
7
-
1
-
3
$ % ا
ﺘﻤﻊﺍ ﱂﺎﻌﻣ
(Paramètres d’une population)
ﻫﻲ
ﺧﺼﺎﺋﺼﻪ ﻣﺜﻞ ﺍﳌﺘﻮﺳﻂ
µ
ﺍﻟﺘﺒﺎﻳﻦ،
σ²
،
ﻧﺴﺒﺔ ﺧﺎﺻﻴﺔ ﻣﺎ ﻓﻴﻪ
p
،
...
ﻛﻤﺎ ﻧﻌﺪ ﻣﻦ
ﺘﻤﻊ ﺃﻳﻀﺎ ﻃﺒﻴﻌﺔ ﺗﻮﺯﻳﻌﻪ ﺍﻻﺣﺘﻤﺍ ﺺﺋﺎﺼﺧ
ﺎﱄ
f(x)
ﻛﺄﻥ ﻳﻜﻮﻥ ﻃﺒﻴﻌﻴﺎ ﺃﻭ ﻏﲑﻩ
.
7
-
1
-
4
ا إ
ﺘﻤﻊﺍ ﱂﺎﻌﻣ ﺮﻳﺪﻘﺘﻟ
)
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ
µ
ﺘﻤﻊﺍ ﻦﻳﺎﺒﺗ ،
²
σ
ﺍﻟﻨﺴﺒﺔ
p
(...
ﺎﺝ ﺇﱃـﺘﳓ ﺚﻴﺣ ،ﺔﻨﻴﻌﻟﺍ ﺕﺎﻧﺎﻴﺑ ﻦﻣ ﻖﻠﻄﻨﻧ
ﺣﺴﺎﺏ ﻣﻌﺎﱂ ﻣﺜﻞ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ
m
ﺗﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ،
S²
ﺍﻟﻨﺴﺒﺔ ﰲ ﺍﻟﻌﻴﻨﺔ،
2
p’
.
ﻧﺴﻤﻲ ﻛﻞ ﻗﻴ،ﺔﻣﺎﻋ ﺔﻔﺼﺑ
ﺐـﺴﲢ ﺔـﻤ
ﺘﻤﻊ ﺇﺣﺼﺎﺋﻴﺔ ﺍﳌﻌﺎﻳﻨﺔﺍ ﱂﺎﻌﻣ ﺔﻤﻴﻗ ﺮﻳﺪﻘﺗ ﻞﺟﺃ ﻦﻣ ﺔﻨﻴﻌﻟﺍ ﺕﺎﻧﺎﻴﺑ ﻦﻣ ﺎﻗﻼﻄﻧﺍ
.
ﺭﻳﺎﺿﻴﺎ
،
ﺇﺣﺼﺎﺋﻴﺔ ﺍﳌﻌﺎﻳﻨﺔ
(Statistique
de l’échantillonnage)
ﻫﻲ ﻛﻞ ﺩﺍﻟﺔ ﰲ ﺍﳌﺘﻐﲑﺍﺕ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ ﺍﻟﱵ ﲤﺜﻞ ﺍﻟﻘﻴﻢ ﺍﶈﺼﻞ ﻋﻠﻴﻬﺎ ﰲ ﺍﻟﻌﻴﻨﺔ
.
7
-
2
ز
ت ا
ز ا- .*
ت$*+
ت$*+ ا ز- 2&-
ت$*+ ا ز- &5
7
-
2
-
1
ت! ا $ز -
ﻣﺴﺄﻟﺔ
:
ﺘﻤﻊﺍ ﻦﻜﻴﻟ
1
،
3
،
5
،
6
،
8
.
ﻣﺎ ﻫﻲ ﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔ ﳌﺘﻮﺳﻂ ﻋﻴﻨﺔ
)
ﻧﺮﻣﺰ ﳌﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﺏ
M
ﺃﻭ
X
ﻭ
ﻧﺮﻣﺰ
ﻟﻠﻘﻴﻤﺔ ﺍﻟﱵ ﺗﺄﺧﺬﻫﺎ
ﻫﺬﻩ ﺍﳌﺘﻐﲑﺓ ﲝﺮﻑ ﺻﻐﲑ
(
ﻣﺴﺤﻮﺑﺔ
ﺑﺎﻹﺭﺟﺎﻉ
ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ،
؟ﻣﻜﻮﻧﺔ ﻣﻦ ﻣﻔﺮﺩﺗﲔ
1
-
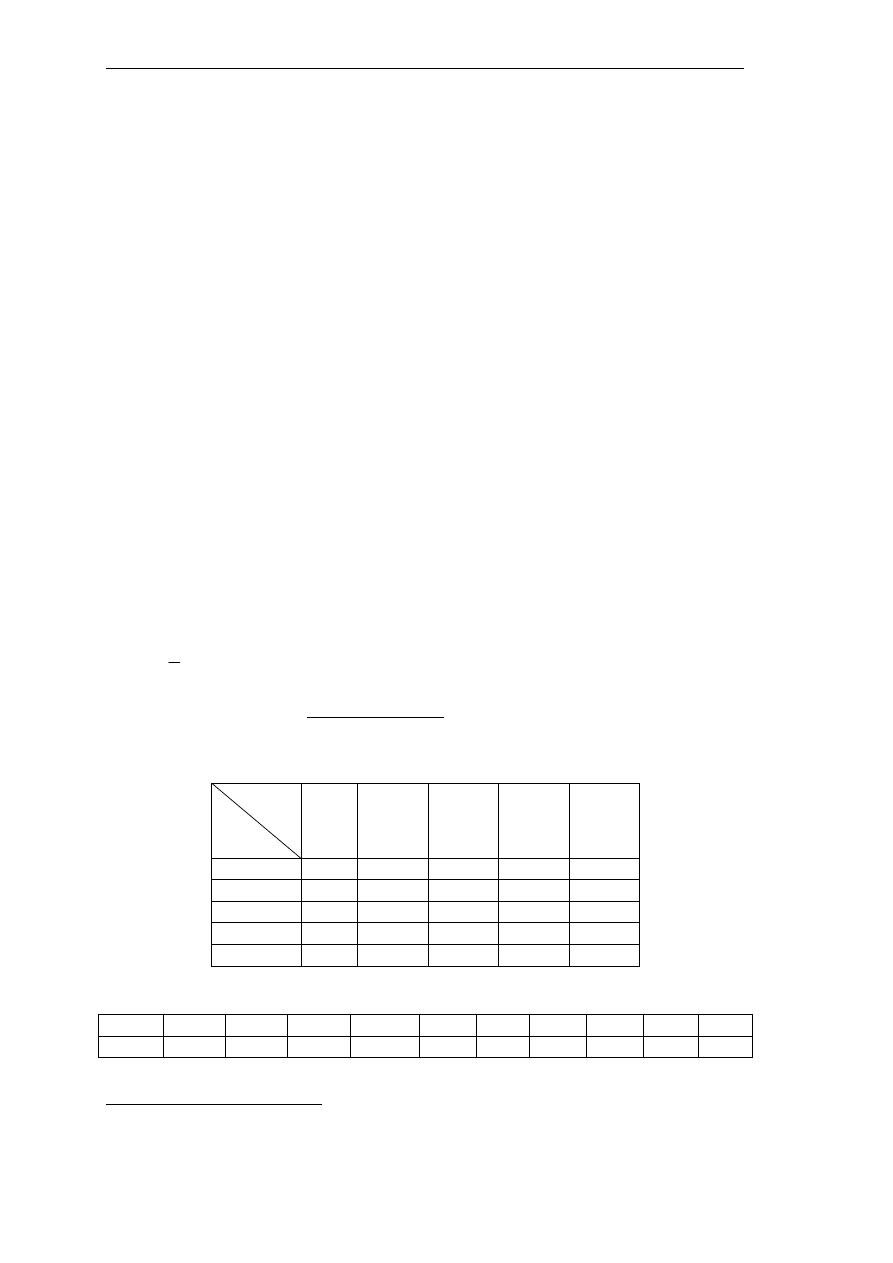
ﰲ ﺣﺎﻟﺔ ﺍﻟﺴﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ
:
ﳓﺘﺎﺝ ﺇﱃ
ﲢﺪﻳﺪ ﲨﻴﻊ ﺍﳊﺎﻻﺕ ﺍﳌﻤﻜﻨﺔ ﻟﻠﻤﺘﻮﺳﻂ
m
i
ﺔـﻨﻴﻋ ﻞـﻛ ﺐﺴﺣ
ﱵـﻟﺍﻭ
ﻋﺪﺩﻫﺎ
:
5
²
=
25
ﺍﳌﺸﺎﻫﺪﺓ
2
ﺍﳌﺸﺎﻫﺪﺓ
1
1
3
5
6
8
1
1
2
3
3.5
4.5
3
2
3
4
4.5
5.5
5
3
4
4.5
5.5
6.5
6
3.5
4.5
5.5
6.5
7
8
4.5
5.5
6.5
7
8
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﻝ
M
:
m
i
1
2
3
3.5
4
4.5
5.5
6.5
7
8
p
i
1/25
2/25
3/25
2/25
2/25
5/25
4/25
3/25
2/25
1/25
1
اا ت=%ا hU D+> i* U S/- لءM &آ 2 ة L7 &%U N- ا نa- E> jUY _Yا D+> E&
+^% ا تا L ر&>ا 2a S 2و
.
2
-C ف /= ا lW F Uو ،&%ا اE> ،UU ف /= ا lW F U
.
ا
VII
.
ا TU
6
E(M) = ∑m
i
(p
i
) = 4.6
ﻧﻼﺣﻆ ﺃﻥ ﺍﻟﺘﻮﻗﻊ ﺍﻟﺮﻳﺎﺿﻲ ﻝ
M
ﻣﺴﺎﻭﻱ ﻝ
µ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ
:
µ = (1 + 3 + 5 + 6 + 8)/5 = 4.6
2
-
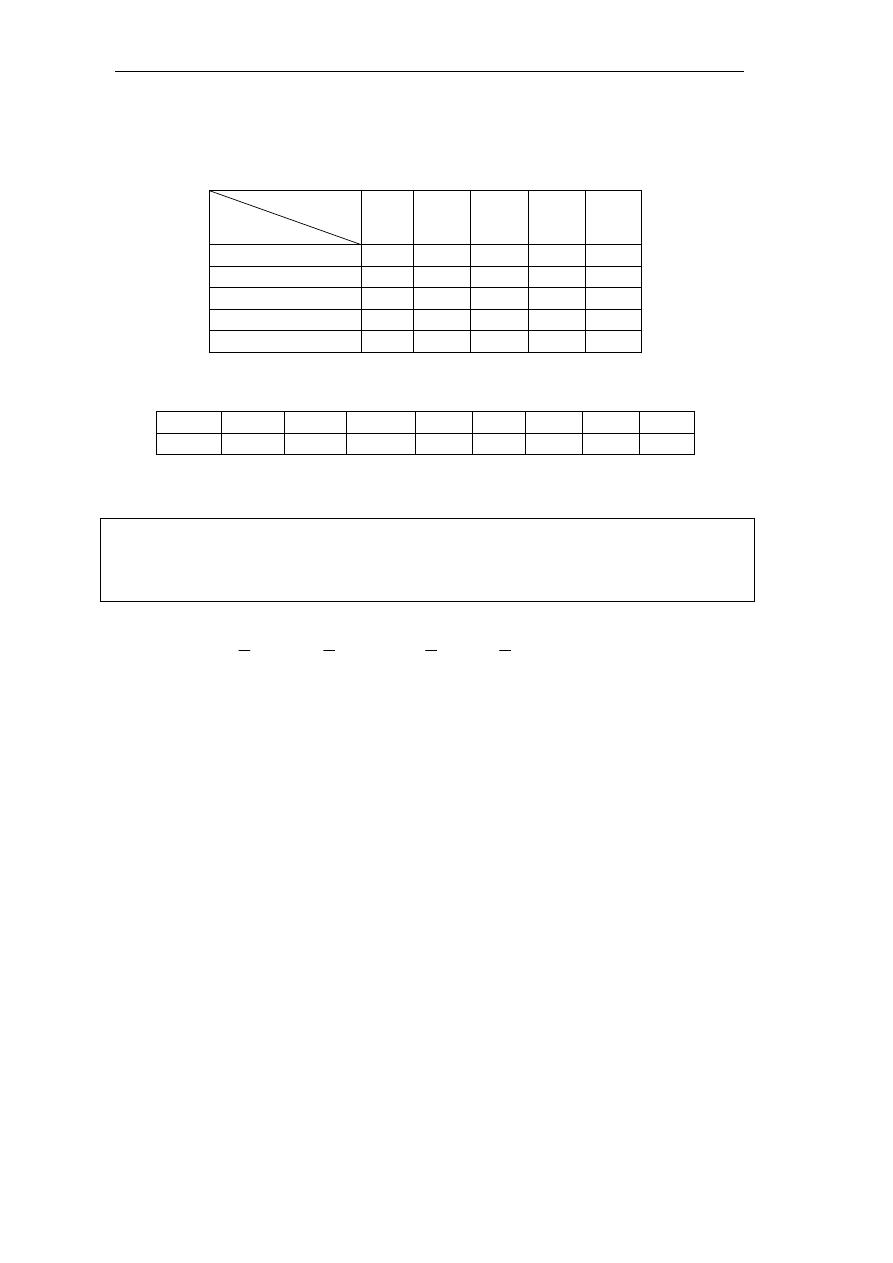
ﰲ ﺣﺎﻟﺔ ﺍﻟﺴﺤﺐ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
.
ﺍﳌﺸﺎﻫﺪﺓ
2
ﺍﳌﺸﺎﻫﺪﺓ
1
1
3
5
6
8
1
–
2
3
3.5
4.5
3
2
–
4
4.5
5.5
5
3
4
–
5.5
6.5
6
3.5
4.5
5.5
–
7
8
4.5
5.5
6.5
7
–
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻻﺣﺘﻤﺎﱄ ﻝ
M
m
i
2
3
3.5
4
4.5
5.5
6.5
7
p
i
2/20
2/20
2/20
2/20
4/20
4/20
2/20
2/20
E(M) = ∑m
i
. p
i
= 4.6
ﻧﻼﺣﻆ ﻣﺮﺓ ﺃﺧﺮﻯ ﺃﻥ ﺍﻟﺘﻮﻗﻊ ﺍﻟﺮﻳﺎﺿﻲ ﳌﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﻣﺴﺎﻭﻱ ﳌ
ﺘﻤﻊﺍ ﻂﺳﻮﺘ
:
µ = 4.6
(./
1
.
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎﺘﻤﻊ ﻣﺎ ﻭ
M
ﺘﻤﻊﺍ ﺕﺍﺫ ﻦﻣ ﺔﺑﻮﺤﺴﻣ ﺔﻨﻴﻋ ﻂﺳﻮﺘﻣ ﻞﺜﲤ ﻉ ﺓﲑﻐﺘﻣ
)
ﺑﺎﻹ
ﺭﺟﺎﻉ ﺃﻭ
ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
(
ﻓﺈﻥ،
E(M) = µ
m
= µ
ﺍﻟﱪﻫﺎﻥ
:
X
i
)
ﻣﺘﻐﲑﺍﺕ ﺍﻟﻌﻴﻨﺔ
(
.
1
1
)
(
1
1
)
µ
µ
µ
=
=
=
=
=
∑
∑
∑
n
n
n
Xi
E
n
Xi
n
E
i
i
i
E(M)
ﻻﺣﻆ
.
ﻭﺗﻌﲏ ﺃﻧﻨﺎ ﻧﺘﻮﻗﻊ ﺇﺫﺍ ﺳﺤﺒﻨﺎ ﻋﻴﻨﺔ ﻣﻦ ﳎﺘﻤﻊ ﺃﻥ،ﻪﻧﻭﺪﺑ ﻭﺃ ﻉﺎﺟﺭﻹﺎﺑ ﺐﺤﺴﻟﺍ ﱵﻟﺎﺣ ﻰﻠﻋ ﺔﺠﻴﺘﻨﻟﺍ ﻩﺬﻫ ﻖﺒﻄﻨﺗ
ﻟﺬﻟﻚ ﻳﺴﺘﺨﺪﻡ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﻟﺘﻘﺪﻳﺮ،ﻊﻤﺘﺍ ﻂﺳﻮﺘﳌ ﺎﻳﻭﺎﺴﻣ ﺔﻨﻴﻌﻟﺍ ﻂﺳﻮﺘﻣ ﻥﻮﻜﻳ
ﺘﻤﻊ ﺇﺫﺍ ﻛﺎﻥ ﻫﺬﺍ ﺍﻷﺧﲑﺍ ﻂﺳﻮﺘﻣ
ﻓﻨﻜﺘﺐ،ﻻﻮﻬﳎ
:
M
=
µ
)
ﻭ ﻧﻘﻮﻝ ﺇﻥ ﺍﻹﺣﺼﺎﺋﻴﺔ
M
ﺘﻤﻊﺍ ﺔﻤﻠﻌﳌ ﺓﺭﺪﻘﻣ ﻲﻫ
µ
.
ﺘﻤﻊ ﻭﺍﻟﻘﻴﻤﺔ ﺍﻟﺍ ﺔﻤﻠﻌﳌ ﺔﻴﻘﻴﻘﳊﺍ ﺔﻤﻴﻘﻟﺍ ﲔﺑ ﻕﺮﻔﻟﺍ
ﺘﻘﺪﻳﺮﻳﺔ
ﻳﺴﻤﻰ
ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ
ﻭ
ﻳﺘﻢ ﻗﻴﺎﺳﻪ
ﺑﺘﺒﺎﻳﻦ
ﺍﳌﻘﺪﺭ
،
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ
σ²
m
.
7
-
2
-
2
)"
ت! ا $ز
ا01 وأ
7
-
2
-
2
-
1
ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺎﻹﺭﺟﺎﻉ
ﻣﺜﺎﻝ
.
ﺘﻤﻊ ﰲ ﺍﳌﺴﺄﻟﺔﺍ ﻦﻳﺎﺒﺗ ﺐﺴﺣﺃ
1
ﺃﺣﺴﺐ ﺍﻟﺘﺒﺎﻳﻦ،
)
ﻭﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ
(
ﻟﺘﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ
σ
²
m
ﻋﻠﻤﺎ
ﺘﻤﻊ ﻭﺗﺒﺎﻳﻦ ﻣﺘﻮﺳﻄﺎﺕ ﺍﻟﻌﻴﻨﺎﺕ ﺍﳌﻤﻜﻨﺔﺍ ﻦﻳﺎﺒﺗ ﲔﺑ ﻥﺭﺎﻗ ،ﻉﺎﺟﺭﻹﺎﺑ ﺔﺑﻮﺤﺴﻣ ﺔﻨﻴﻌﻟﺍ ﻥﺃ
)
ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ
.(
ﻣﻦ ﺍﳉﺪﻭﻝ
1
ﳓﺴﺐ ﺗﺒﺎﻳﻦ ﻫﺬﻩ ﺍﳌﺘﻮﺳﻄﺎﺕ،ﺎﺎﻄﺳﻮﺘﻣﻭ ﺔﻨﻜﻤﳌﺍ ﺕﺎﻨﻴﻌﻟﺍ ﲔﺒﻳ ﻱﺬﻟﺍ ،
.
σ²
m
= ∑
i
(m
i
– µ
m
)²p
i
= 2.92;
σ² = [∑
i
(x
i
– µ)² ]/5 = 5.84

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
7
ﻧﻼﺣﻆ ﺃﻥ ﺗﺒﺎﻳﻦ
M
ﺘﻤﻊﺍ ﻦﻳﺎﺒﺗ ﻦﻣ ﻞﻗﺃ
.
ﻫﺬﺍ ﺍﳌﺜﺎﻝ ﳝﻬﺪ ﻟﻠﻨﻈﺮﻳﺔ ﺍﻟﺘﺎﻟﻴﺔ
ﻋﻦ ﺧﻄﺄ ﺍﳌﻌ
ﺎﻳﻨﺔ ﰲ ﺣﺎﻟﺔ ﺍﻟﺴﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ
:
(./
2
.
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎﺘﻤﻊ ﻣﺎ ﻭ
M
،ﺘﻤﻊ ﺑﺎﻹﺭﺟﺎﻉﺍ ﺕﺍﺫ ﻦﻣ ﺔﺑﻮﺤﺴﻣ ﺔﻨﻴﻋ ﻂﺳﻮﺘﻣ ﻞﺜﲤ ﻉ ﺓﲑﻐﺘﻣ
ﻓﺈﻥ ﺗﺒﺎﻳﻦ
M
)
ﺗﺒﺎﻳﻦ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ
(
ﻳﻜﺘﺐ ﻛﻤﺎ ﻳﻠﻲ
:
n
m
²
2
σ
σ
=
ﺣﻴﺚ
n
ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
.
ﺍﻟﱪﻫﺎﻥ
:
(
)
∑
∑
=
=
=
i
i
i
i
m
X
V
n
X
n
V
M
V
²
1
1
)
(
²
σ
ﲟﺎ ﺃﻥ
ﺍﻟﺴﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ ﻓﺈﻥ
X
i
ﻣﺴﺘﻘﻠﺔ ﻭﳍﺎ ﻧﻔﺲ ﺍﻟﺘﻮﺯﻳﻊ ﺇﺫﺍ ﳍﺎ ﻧﻔﺲ ﺍﻟﺘﺒﺎﻳﻦ ﻭﻣﻨﻪ
:
∑
=
⇒
=
=
i
m
i
i
m
n
X
nV
n
X
V
n
²
²
)
(
²
1
)
(
²
1
²
σ
σ
σ
ﻻﺣﻆ
ﻭﻫﻮ ﺃﻣﺮ ﻣﺘﻮﻗﻊ،ﺔﻨﻴﻌﻟﺍ ﻢﺠﲝ ﺎﻴﺴﻜﻋﻭ ﻊﻤﺘﺍ ﻦﻳﺎﺒﺘﺑ ﺎﻳﺩﺮﻃ ﺮﺛﺄﺘﻳ ﺔﻨﻳﺎﻌﳌﺍ ﺄﻄﺧ ﻥﺃ
:
ﻛﻠﻤﺎ ﻛﺎﻧﺖ ﺍﻟﻌﻴﻨﺔ ﺃﻛﱪ
ﺘﻤﻊ ﺃﻛﺜﺮ ﲡﺎﻧﺴﺎﺍﻭ
)
ﺃﻗﻞ ﺗﺸﺘﺘﺎ
(
ﻛﺎﻥ ﺍﻟﺘﻘﺪﻳﺮ ﺃﺩﻕ ﻣﺎ ﻳﻌ
ﲏ ﺧﻄﺄ ﻣﻌﺎﻳﻨﺔ ﺃﻗﻞ
)
ﺃﻧﻈﺮ ﺍﻟﺮﺳﻢ ﺃﺩﻧﺎﻩ
.(
ر
7
–
1
ا% ةد67 89 ا01
7
-
2
-
2
-
2
ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
.
ﰲ ﺍﳌﺴﺄﻟﺔ
1
ﺃﺣﺴﺐ ﺗﺒﺎﻳﻦ ﺍﳌﺘﻮﺳﻄﺎﺕ ﺍﳌﻤﻜﻨﺔ ﻟﻠﻌﻴﻨﺔ
σ²
m
ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ
ﺘﻤﻊ ﻭﺗﺒﺎﻳﻦﺍ ﻦﻳﺎﺒﺗ ﲔﺑ ﻥﺭﺎﻗ ،ﻉﺎﺟﺭﺇ
ﺍﳌﺘﻮﺳﻄﺎﺕ ﺍﳌﻤﻜﻨﺔ ﻟﻠﻌﻴﻨﺔ
.
ﺎﺎﻄﺳﻮﺘﻣﻭ ﺔﻨﻜﻤﳌﺍ ﺕﺎﻨﻴﻌﻟﺍ ﱃﺇ ﺍﺩﺎﻨﺘﺳﺍ
)
ﺍﳉﺪﻭﻝ
2
(
ﳓﺴﺐ ﺗﺒﺎﻳﻦ
M
:
σ²
m
= ∑
i
(m
i
– µ
m
)² p
i
= 2.19
ﺘﻤﻊﺍ ﻦﻳﺎﺒﺗ
:
σ² = [∑
i
(x
i
– µ)² ]/N = E(X²) – E(X)² = (1 + 9 + 25 + 36 + 64) / 5 – 4.6² = 4.85
ﻻﺣﻆ
ﻣﺮﺓ ﺃﺧﺮﻯ ﺃﻥ
ﺗﺒﺎﻳﻦ
M
ﺘﻤﻊﺍ ﺓﲑﻐﺘﻣ ﻦﻳﺎﺒﺗ ﻦﻣ ﻞﻗﺃ
X
.
ﻻﺣﻆ ﺃﻳﻀﺎ ﺃﻥ ﺗﺒﺎﻳﻦ
M
ﺤﺐـﺴﻟﺍ ﺔﻟﺎﺣ ﰲ ﻪﻨﻣ ﻞﻗﺃ
ﺑﺎﻹﺭﺟﺎﻉ
2.19 < 2.92
ﳑﺎ ﻳﻌﲏ ﺃﻥ ﺍﻟﺴﺤﺐ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ ﻳﻌﻄﻲ ﺧﻄﺄ ﻣﻌﺎﻳﻨﺔ ﺃﻗﻞ؛
.
ﻫﺬﺍ ﳝﻬﺪ ﻟﻠﻨﻈﺮﻳﺔ ﺍﻟﺘﺎﻟﻴﺔ
ﻋﻦ ﺧﻄﺄ
ﺍﳌﻌﺎﻳﻨﺔ ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
:
µ
m
σ
m
= σ/√n
n
3
> n
2
n
2
> n
1
n
1

ا
VII
.
ا TU
8
(./
3
.
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎ
ﺘﻤﻊ ﻣﺎ ﺣﺠﻤﻪ
N
ﻭ
M
ﻣﺘﻐﲑﺓ ﻉ ﲤﺜﻞ ﻣﺘﻮﺳﻂ ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ
n
ﻣﺴﺤﻮﺑﺔ ﻣﻦ ﺫﺍﺕ
ﻓﺈﻥ ﺗﺒﺎﻳﻦ،ﻉﺎﺟﺭﺇ ﻥﻭﺪﺑ ﻊﻤﺘﺍ
M
)
ﺗﺒﺎﻳﻦ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ
(
ﻳﻜﺘﺐ ﻛﻤﺎ ﻳﻠﻲ
:
−
−
=
1
²
2
N
n
N
n
m
σ
σ
ﺍﻟﱪﻫﺎﻥ
:
(
)
+
=
=
=
∑
∑
∑
∑
=
≠
=
n
j
i
j
i
i
n
i
i
i
i
i
m
x
x
x
v
n
X
V
n
X
n
V
1
1
)
,
cov(
)
(
²
1
²
1
1
²
σ
ﻟﻜﻦ
ﺍﻟﺘﺒﺎﻳﻦ ﺍﳌﺸﺘﺮﻙ ﰲ ﺣﺎﻟﺔ ﻣﺘﻐﲑﺍﺕ ﻋﻴﻨﺔ ﻋﺸﻮﺍﺋﻴﺔ
ﻧﻔﺎﺩﻳﺔ
ﻳﺴﺎﻭﻱ
–σ²/(N-1)
ﻭﺗ
ﻮﺟﺪ
A²
n
ﺬﻩـﳍ ﺔـﻨﻜﳑ ﺔـﺒﻴﺗﺮﺗ
ﺍﳌﺘﻐﲑﺍﺕ ﻣﺜﻨﺎ ﻣﺜﻨﺎ
.
ﺇﺫﻥ
:
−
Ν
−
−
+
=
−
Ν
−
+
=
1
)
)(
1
(
1
1
A
1
²
2
2
2
2
2
n
2
2
σ
σ
σ
σ
σ
n
n
n
n
n
n
m
−
Ν
−
Ν
=
−
Ν
+
−
−
=
−
Ν
−
−
+
=
1
1
1
1
1
)
1
(
1
²
2
2
2
n
n
n
N
n
n
n
n
σ
σ
σ
ﻻﺣﻆ
:
-
ﻳﺘﻀﺎﺀﻝ ﺗﺄﺛﲑ
ﺍﻟﻨﺴﺒﺔ
1
−
−
N
n
N
)
ﻭﺗﺴﻤﻰ ﻣﻌﺎﻣﻞ ﺍﻹﺭ
ﺟﺎﻉ
(
ﻭﻣﻦ ﰒ ﳝﻜﻦ ﺇﳘﺎﻟﻪ ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻟﻌﻴﻨﺔ ﺻﻐﲑﺓ ﺟﺪﺍ
ﺘﻤﻊﺍ ﻢﺠﺣ ﻊﻣ ﺔﻧﺭﺎﻘﳌﺎﺑ
1
(
n/N <
0.05
)
ﻷﻧﻪ ﻳﻘﺘﺮﺏ ﻣﻦ
1
.
-
ﻗﻴﻤﺔ
ﻣﻌﺎﻣﻞ
ﺍﻹﺭﺟﺎﻉ
ﺃﻗﻞ ﻣﻦ
1
ﻛﻠﻤﺎ ﻛﺎﻥ
n>1
ﻫﺬﺍ ﻳﻌﲏ ﺃﻥ ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ ﺃﻗﻞ ﻣﻨﻪ،
ﺘﻤﻊﺍ ﺔﻤﻠﻌﳌ ﺔﻗﺩ ﺮﺜﻛﺃ ﺍﺮﻳﺪﻘﺗ ﻲﻄﻌﺗ ﻉﺎﺟﺭﺇ ﻥﻭﺪﺑ ﺔﻨﻳﺎﻌﳌﺍ ﻥﺃ ﲏﻌﻳ ﺎﻣ ﻉﺎﺟﺭﻹﺎﺑ ﺔﻨﻳﺎﻌﳌﺍ ﺔﻟﺎﺣ ﰲ
µ
.
ﻳﺰﻳﺪ ﻫﺬﺍ ﺍﻟﻔﺮﻕ
ﺑﲔ ﺩﻗﺔ ﺍﻟﺘﻘﺪﻳﺮ ﰲ ﺍﳊﺎﻟﺘﲔ ﻛﻠﻤﺎ ﺯﺍﺩ ﺣﺠﻢ
ﺍﻟﻌﻴﻨﺔ
n
.
7
-
2
-
3
$ ز":
;ا
M
ﺑﻌﺪ ﺩﺭﺍﺳﺔ ﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔ ﻝ
M
ﻣﻦ ﺍﳌﻬﻢ ﺩﺭﺍﺳﺔ ﻃﺒﻴﻌﺔ ﺗﻮﺯﻳﻊ ﻫﺬﻩ ﺍﻹﺣﺼﺎﺋﻴﺔ ﻻﺳﺘﺨﺪﺍﻡ ﺫﻟﻚ ﰲ ﺗﻘﺪﻳﺮ،ﺔﻨﻳﺎﻌﳌﺍ ﺄﻄﺧﻭ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ
µ
ﲟﺠﺎﻝ ﺣﻴﺚ ﳓﺘﺎﺝ ﺇﱃ ﲢﺪﻳﺪ ﺍﺣﺘﻤﺎﻝ ﺍﻟﺼﻮﺍﺏ ﻭﺍﳋﻄﺄ ﰲ ﻫﺬﺍ ﺍﻟﺘﻘﺪﻳﺮ ﳑﺎ ﻳﻘﺘﻀﻲ ﲢﺪﻳﺪﻱ ﻃﺒﻴﻌﺔ
ﺗﻮﺯﻳﻊ ﺍﻹﺣﺼﺎ
ﺋﻴﺔ
.
ﻧﺪﺭﺱ ﻃﺒﻴﻌﺔ ﺗﻮﺯﻳﻊ ﻣﺘﻮﺳﻂ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ ﻣﻦ ﺧﻼﻝ ﺍﻟﻨﻈﺮﻳ
ﺘﲔ ﺍﻟﺘﺎﻟﻴﺘﲔ
:
(./
4
.
ﺘﻤﻊ ﻣﻮﺯﻉ ﻃﺒﻴﻌﻴﺎ ﲟﺘﻮﺳﻂﺍ ﻥﺎﻛ ﺍﺫﺇ
µ
ﻭﺗﺒﺎﻳﻦ
σ
²
ﻓﺈﻥ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﺍﳌﺴﺤﻮﺑﺔ ﻣﻨﻪ
ﻋﺸﻮﺍﺋﻴﺎ
ﻳﺘﺒﻊ ﺃﻳﻀﺎ
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﲟﺘﻮﺳﻂ
µ
ﻭﺗﺒﺎﻳﻦ
σ²/n
ﻭﻧﻜﺘﺐ،
M ~ N(µ, σ/√n)
ﺃﻭ
~ N( 0, 1)
n
m
z
/
σ
µ
−
=
ﻻﺣﻆ
-
ﺘﻤﻊ ﳏﺪﻭﺩ ﻭﺍﳌﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔ ﻧﺴﺘﺒﺪﻝ ﺍﻟﻌﺒﺎﺭﺓﺍ ﺔﻟﺎﺣ ﰲ
σ/√n
ﺏ
1
−
−
=
N
n
N
n
m
σ
σ
-
ﻭﺃﻳﺎ ﻛﺎﻥ ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ،ﻪﻧﻭﺪﺑﻭ ﻉﺎﺟﺭﻹﺎﺑ ﺔﻨﻳﺎﻌﳌﺍ ﲔﺘﻟﺎﳊﺍ ﰲ ﺔﻘﻘﳏ ﺔﻳﺮﻈﻨﻟﺍ ﻩﺬﻫ
.
1
&% ا?%-
n/N
ب F و ،ء^*Cا لE
f
.

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
9
ﺘﻤﻊ ﻟﻴﺲ ﺑﺎﻟﻀﺮﻭﺭﺓ ﻃﺒﻴﻌﻴﺎﺍ ﻥﺎﻛ ﺍﺫﺇ ﱴﺣ ﻲﻌﻴﺒﻄﻟﺍ ﻊﻳﺯﻮﺘﻟﺍ ﻡﺍﺪﺨﺘﺳﺍ ﻦﻜﳝ ﺔﻘﻴﻘﳊﺍ ﰲ
)
ﳎﻬﻮﻝ ﺍﻟﺘﻮﺯﻳﻊ
(
ﺑﺸﺮﻁ
ﺃﻥ ﻻ
ﺗﻜﻮﻥ ﺍﻟﻌﻴﻨﺔ ﺻﻐﲑﺓ ﻭﺫﻟﻚ ﺍﺳﺘﻨﺎﺩﺍ ﺇﱃ ﻧﻈﺮﻳﺔ ﺍﻟﻨﻬﺎﻳﺔ ﺍﳌﺮﻛﺰﻳﺔ
1
:
(./
5
.
ﺘﻤﻊ ﺫﺍ ﻥﺎﻛ ﺍﺫﺇ
ﺍ
ﻣﺘﻮﺳﻂ
µ
ﻭﺗﺒﺎﻳﻦ
σ
²
ﻟﻜﻦ
ﻟﻴﺲ ﺑﺎﻟﻀﺮﻭﺭﺓ ﻃﺒﻴﻌﻴﺎ ﻓﺈﻥ ﻣﺘﻮﺳﻂ ﺍﻟﻌﻴﻨﺔ ﺍﳌﺴﺤﻮﺑﺔ ﻣﻨﻪ
M
ﻳﺆﻭﻝ
ﺇﱃ
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻟﻌﻴﻨﺔ ﻛﺒﲑﺓ
(
n ≥ 30
)
،
ﻭﻧﻜﺘﺐ
M ≈ N(µ, σ
m
)
.
ﺗﻄﺒﻴﻖ
:
ﳎ
ﺘﻤﻊ ﺣﺠﻤﻪ
900
ﲟﺘﻮﺳﻂ
20
=
µ
ﻭ
σ =12
.
ﻧﺴﺘﺨﺮﺝ ﻛﻞ ﺍﻟﻌﻴﻨﺎﺕ ﺍﳌﻤﻜﻨﺔ
ﺫﺍﺕ ﺣﺠﻢ
n
.
ﺃﺣﺴﺐ ﺍﳌﺘﻮﺳﻂ ﻭﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﺘﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ ﰲ ﺣﺎﻟﺔ
) :
1
(
ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ
n = 36
،
)
2
(
n = 64
ﰲ ﺣﺎﻟﺔ
(
n = 36
)
ﺃﺣﺴﺐ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﻳﻜﻮﻥ
M
ﳏﺼﻮﺭﺍ
ﺑﲔ
18
ﻭ
22
،
ﺃﺣﺴﺐ ﻧﻔﺲ ﺍﻻﺣﺘﻤﺎﻝ ﰲ
ﺣﺎﻟﺔ
n = 64
.
E(M) = µ = 20
(1) n = 36 : n/N = 36/900 = 0.04 < 0.05 => σ
m
= σ/√n = 12/√36 = 2
92
.
1
1
900
64
900
64
12
05
.
0
071
.
0
900
64
900
:
64
)
2
(
=
−
−
=
⇒
>
=
=
⇒
=
=
m
N
n
N
n
σ
0.6827
)
Z
Z
P(Z
22)
m
P(18
1
Z
,
1
-
36
12/
20
-
18
n
/
µ
-
m
Z
2
1
2
1
1
=
<
<
=
<
<
=>
=
=
=
=
σ
1.04
Z
,
1.04
-
1.92
20
-
18
1
n
/
µ
-
m
Z
2
1
1
=>
=
=
=
−
−
=
N
n
N
σ
0.70
)
04
.
1
Z
P(-1.04
22)
m
P(18
=
<
<
=
<
<
=>
7
-
2
-
4
=>1
ﺍﳉﺪﻭﻝ ﺍﻟﺘﺎﱄ ﻳﺒﲔ ﺃﻫﻢ ﺧﺼﺎﺋﺺ ﺗﻮﺯﻳﻊ ﺍﳌﻌﻴﻨﺔ ﻟﻠﻤﺘﻮﺳﻄﺎﺕ
.
ول@A
7
-
1
.
ت! ا $ز )B @BاCا هأ
ﺍﳋﺎﺻﻴﺔ
ﺍ
ﳌﻌﺎﻳﻨﺔ
ﺘﻤﻊﺍ
µ
m
= µ,
n
m
²
2
σ
σ
=
ﺳﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ
ﳎﺘﻤﻊ ﻣﺎ
ﲟﺘﻮﺳﻂ
µ
ﻭﺗﺒﺎﻳﻦ
σ
²
µ
m
= µ,
−
−
=
1
²
2
N
n
N
n
m
σ
σ
ﺳﺤﺐ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
ﳎﺘﻤﻊ
ﺣﺠﻤﻪ
N
ﲟﺘﻮﺳﻂ
µ
ﻭﺗﺒﺎﻳﻦ
σ
²
M ~ N(µ, σ
m
)
ﺳﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ ﺃﻭ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
ﳎﺘﻤﻊ ﻣﻮﺯﻉ ﻃﺒﻴﻌﻴﺎ
ﲟﺘﻮﺳﻂ
µ
ﻭﺗﺒﺎﻳﻦ
σ
²
M ≈ N(µ, σ
m
)
ﻋﻨﺪﻣﺎ ﻳﻜﻮﻥ
n
ﻛﺒﲑﺍ
(
n ≥ 30
)
ﳎﺘﻤﻊ
ﲟﺘﻮﺳﻂ
µ
ﻭﺗﺒﺎﻳﻦ
σ
²
ﻟﻜﻦ ﻟﻴﺲ ﺑﺎﻟﻀﺮﻭﺭﺓ ﻃﺒﻴﻌﻴﺎ
1
@=%ا ا ? Fآ ا ا TU TUأ
.
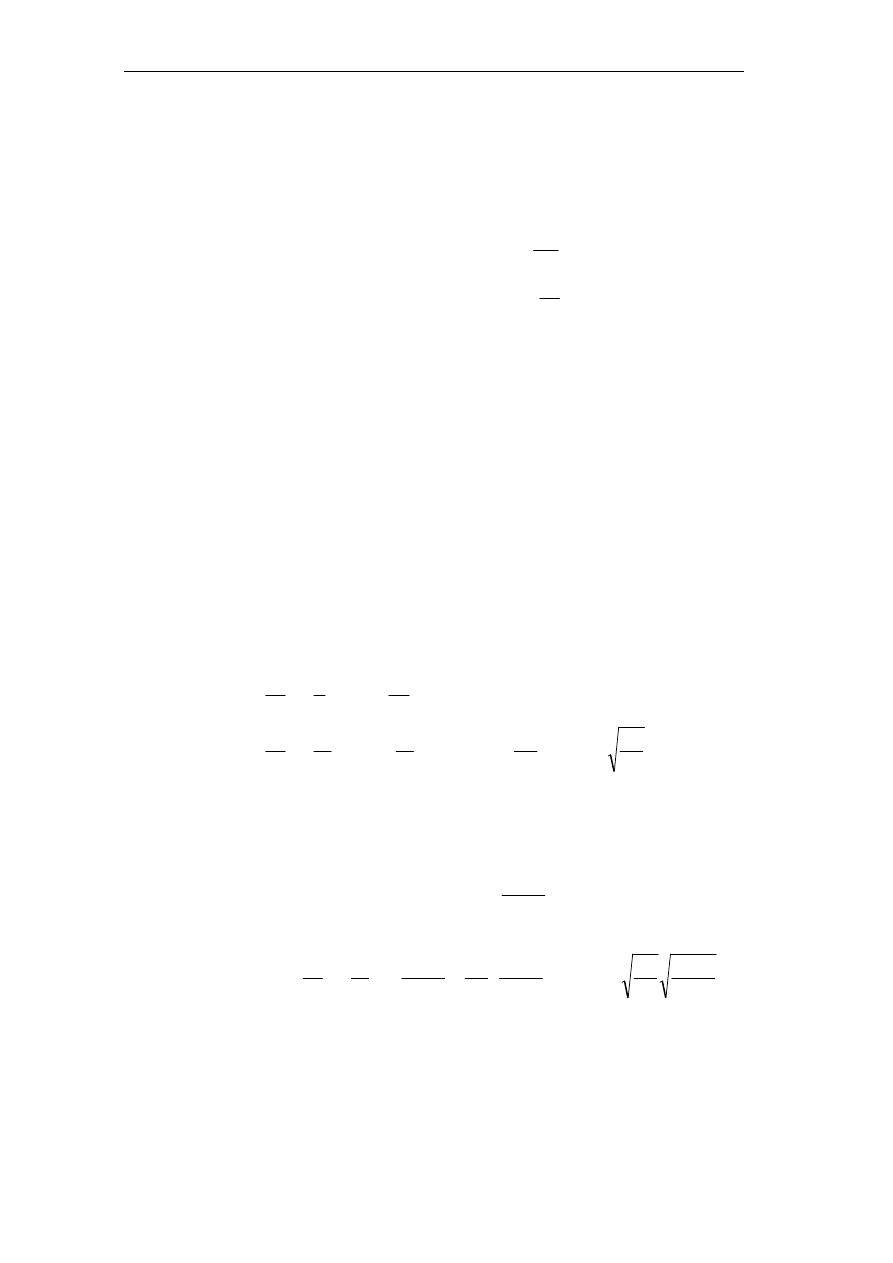
ا
VII
.
ا TU
10
7
-
3
"# ا ز
ا
?A ا _
+ ز ا- 2&-و
&%
+ ز ا- &5
&%
ﺘﻤﻊ ﺍﻟﻜﺴﺮﺍ ﰲ ﺔﺒﺴﻨﻟﺎﺑ ﺪﺼﻘﻧ
:
N
N
p
a
=
،
ﺣﻴﺚ
N
ﺘﻤﻊ ﻭﺍ ﻢﺠﺣ
N
a
ﻋﺪﺩ
ﺍﳌ
ﻔﺮﺩﺍﺕ ﺍﻟﱵ ﺗﺘﺤﻘﻖ ﻓﻴﻬﺎ ﺻﻔﺔ ﻣﺎ
.
ﻭﻧﻘ
ﺼ
ﺪ ﺑﺎﻟﻨﺴﺒﺔ ﰲ ﺍﻟﻌﻴﻨﺔ ﺍﻟﻜﺴﺮ
:
n
n
p
a
=
′
ﺣﻴﺚ
n
ﺣﺠﻢ ﺍﻟﻌﻴﻨﺔ ﻭ
n
a
ﻋﺪﺩ ﻣﻔﺮﺩﺍﺕ
ﺍﻟ
ﻌﻴﻨﺔ ﺍﻟﱵ ﲢﻘﻖ ﻧﻔﺲ ﺍﻟﺼﻔﺔ
.
ﻧﺪﺭﺱ ﺧﺼﺎﺋﺺ ﺍﻹﺣﺼﺎﺋﻴﺔ
p’
ﺘﻤﻊﺍ ﰲ ﺔﺒﺴﻨﻟﺍ ﺮﻳﺪﻘﺘﻟ ﻡﺪﺨﺘﺴﺗ ﺔﻴﺋﺎﺼﺣﺇ ﺎﻷ ﱄﺎﻤﺘﺣﻻﺍ ﺎﻬﻌﻳﺯﻮﺗ ﻭ
p
.
ﻣﺜﺎﻝ
.
ﺳﺤﺒﻨﺎ ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ
31
ﻣﻦ ﻧﻘﺎﻁ ﺍﻟﻄﻠﺒﺔ ﰲ ﺍ
ﻣﺘﺤﺎﻥ ﺍﻹﺣﺼﺎﺀ ﺍﻟﺮﻳﺎﺿﻲ ﻓﻜﺎﻧﺖ ﻛﺎﻟﺘﺎﱄ
:
3
،
18.5
،
10.5
،
19.5
،
11.5
،
14
،
11
،
16.5
،
18
،
7.5
،
3.5
،
2.5
،
2.5
،
8.5
،
10.5
،
8.5
،
2
،
5
،
12
،
1.5
،
5.5
،
8.5
،
6
،
15
،
6
،
6
،
10
،
2.5
،
1
،
2.5
،
3
.
ﺃﺣﺴﺐ
p’
:
ﻧﺴﺒﺔ ﺍﻟﻄﻠﺒﺔ ﺍﳊﺎﺻﻠﲔ ﻋﻠﻰ ﺍﳌﻌﺪﻝ
ﰲ ﺍﻟﻌﻴﻨﺔ
.
ﻟﺪﻳﻨﺎ
12
ﻧﻘﻄﺔ ﺃﻛﱪ ﺃﻭ ﺗﺴﺎﻭﻱ ﺍﻟﻌﺸﺮﺓ
(n
a
= 12
)
ﺇﺫﻥ
p’ = 12/31 = 0.387
7
-
3
-
1
D )" او EF(ا $9 ا
p’
ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﻏﲑ ﺍﻟﻨﻔﺎﺩﻳﺔ
)
ﺳﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ
(
ﻓﺈ
ﻥ
ﺍﺣﺘﻤﺎﻝ ﲢﻘﻴﻖ ﺍﻟﺼﻔﺔ ﺛﺎﺑﺖ
ﺑﺎﻟﻨﺴﺒﺔ ﳌ
ﻔﺮﺩﺍﺕ
ﺍﻟﻌﻴﻨﺔ
ﻭﻫﻮ ﺫﺍﺗﻪ ﺍﻟﻨﺴﺒﺔ
ﺘﻤﻊﺍ ﰲ
p
ﻫﺬﺍ،
ﻳ
ﻌﲏ ﺃﻥ ﻋﺪﺩ ﻣﻔﺮﺩﺍﺕ ﺍﻟﻌﻴﻨﺔ
ﺍﻟﱵ ﲢﻘﻖ ﺍﻟﺼﻔﺔ ﻳﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ
.
npq
n
V
np
n
E
p
n
B
n
a
a
a
=
=
)
(
;
)
(
);
,
(
~
ﳝﻜﻦ ﺇﺫﻥ ﺍﺳﺘﻨﺘﺎﺝ ﺍﳋﺼﺎﺋﺺ ﺍﻟﻌﺪﺩﻳﺔ ﻟﻺﺣﺼﺎﺋﻴﺔ
p’
ﻣﻦ ﺧﺼﺎﺋﺺ
n
a
:
( )
n
pq
n
pq
npq
n
n
V
n
n
n
V
p
n
np
n
E
n
n
n
E
p
p
a
a
p
p
a
a
p
=
⇒
=
⇒
=
=
=
=
⇒
=
=
=
′
′
′
σ
σ
σ
µ
µ
2
2
'
'
²
1
)
(
²
1
1
ﻟﺬﻟﻚ ﻳﺼﻠﺢ ﺃﻥ ﻧﺴﺘﺨﺪﻡ
p’
ﻟﺘﻘﺪﻳﺮ
p
ﻭ ﻧﻜﺘﺐ
:
p
p
′
=
)
ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﺔ
ﺘﻤﻊ ﳏﺪﻭﺩﺍﻭ
ﻓﺈﻥ
n
a
ﺗﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﺍﳍﻨﺪﺳﻲ ﺍﻟﺰﺍﺋﺪ ﻭﻧﻜﺘﺐ
n, p)
n
a
~ H(N,
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻓﺈﻥ
:
1
)
(
;
)
(
−
−
=
=
N
n
N
npq
n
V
np
n
E
a
a
ﻭﻣﻨﻪ ﻓﺈﻥ ﺍﻟﺘﻮﻗﻊ ﺍﻟﺮﻳﺎﺿﻲ ﻝ
p’
ﻭﺍﻟﺘﺒﺎﻳﻦ ﻳﻜﻮﻧﺎﻥ
:
1
1
1
²
1
;
2
'
−
−
=
⇒
−
−
=
−
−
=
=
=
′
′
N
n
N
n
pq
N
n
N
n
pq
N
n
N
npq
n
n
n
V
p
p
a
p
p
σ
σ
µ
ﳝﻜﻦ ﺇﳘﺎﻝ ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ ﺇﺫﺍ ﻛﺎﻧﺖ
n < 0.05N
ﻷﻥ ﻗﻴﻤﺔ ﺍﳌﻌﺎﻣﻞ ﺗﺆﻭﻝ ﺇﱃ
1
.
ﻣﺜﺎﻝ
.
ﺍﻧﻄﻼﻗﺎ
ﻗﺪﺭ ﻧﺴﺒﺔ ﺍﻟﻄﻠﺒﺔ ﺍﳊﺎﺻﻠﲔ ﻋﻠﻰ ﺍﻟﻌﻼﻣﺔ ﻋﺸﺮﺓ ﺃﻭ ﺃﻛﺜﺮ،ﻖﺑﺎﺴﻟﺍ ﻝﺎﺜﳌﺍ ﺔﻨﻴﻋ ﺕﺎﻧﺎﻴﺑ ﻦﻣ
ﻣﻦ ﳎﻤﻮﻉ ﺍﻟﻄﻠﺒﺔ
ﻭﻋﺪﺩﻫﻢ
300
.
ﺃﺣﺴﺐ ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﻤﻘﺪﺭ ﺍﳌﺴﺘﺨﺪﻡ
.
ﻟﺪﻳﻨﺎ
E(p’) = p
ﺎ ﺭﺪﻘﻧ ﱵﻟﺍ ﺔﻤﻴﻘﻟﺍ ﻥﺫﺇ
p
:
ﻧﺴﺒﺔ ﺍﳊﺎﺻﻠﲔ ﻋﻠﻰ ﺍﻟﻌﺸﺮﺓ ﰲ ﳎﻤﻮﻉ ﺍﻟﻄﻠﺒﺔ ﻫﻲ ﺍﻟﻨﺴﺒﺔ ﰲ ﺍﻟﻌﻴﻨﺔ ﺃﻱ
0.387
.
ﻭﻧﻜﺘﺐ
:
387
.
0
=
′
=
p
p
)

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
11
ﳊﺴﺎﺏ ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ ﳓﺘﺎﺝ ﻋﻠﻰ ﺍﺳﺘﺒﺪﺍﻝ
p’
ﺏ
p
ﻷﻥ ﻫﺬﻩ ﺍﻷﺧﲑﺓ ﺗﺒﻘﻰ ﳎﻬﻮﻟﺔ
.
0069
.
0
1
300
31
300
31
)
387
.
0
1
(
387
.
0
1
1
2
=
−
−
−
=
−
−
′
′
≅
−
−
=
′
N
n
N
n
q
p
N
n
N
n
pq
p
σ
7
-
3
-
2
ا$ز
ل
p’
ﻧﻌﻠﻢ ﻣﻦ ﻧﻈﺮﻳﺔ ﻣﻮﺍﻓﺮ
)
ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺑﻖ
(
ﺃﻧﻪ
ﰲ ﺣﺎﻟﺔ
n
ﻛﺒﲑﺓ ﲟﺎ ﻓ
ﻴﻪ ﺍﻟﻜﻔﺎﻳﺔ ﻓﺈﻥ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻳ
ﻌﻄﻲ ﻧﺘﺎﺋﺞ
ﻣﻘﺎﺭﺑﺔ
ﻟﻠﺘﻮﺯﻳﻊ ﺍﻟﺜﻨﺎﺋﻲ
ﻝ
n
a
ﻭ ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻓﺈﻥ
ﺎ ﺧﻄﻴﺎ ﺔﻄﺒﺗﺮﳌﺍ ﺓﲑﻐﺘﳌﺍ
p’
ﺗﺆﻭﻝ ﻫﻲ ﺍﻷﺧﺮﻯ ﺇﱃ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
.
(./
6
:
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎﺘﻤﻌ
ﺎ
ﻣﺎ
ﺃﻳﻦ
p
ﻭ،ﺔﻨﻴﻌﻣ ﺔﻔﺻ ﺕﺍﺫ ﺕﺍﺩﺮﻔﳌﺍ ﺔﺒﺴﻧ
p’
ﻣ
ﺘﻐﲑﺓ
ﻉ ﲤﺜﻞ ﻧﺴﺒﺔ
ﺍﳌﻔﺮﺩﺍﺕ ﺫﺍﺕ
ﻧﻔﺲ
ﺍﻟﺼﻔﺔ ﰲ ﻋﻴﻨﺔ
ﻋﺸﻮﺍﺋﻴﺔ
ﻣﺴﺤﻮﺑ
،ﺘﻤﻊﺍ ﺕﺍﺫ ﻦﻣ ﺔ
ﻓﺈﻥ
:
ﻋﻨﺪ
ﻣﺎ
n ≥ 30
:
(p, σ
p'
)
p’ ≈ N
ﻣﻼﺣﻈ
ﺎﺕ
:
-
ﺍﺳﺘﺨﺪﺍﻡ ﺗﻮﺯﻳﻊ ﻣﺴﺘﻤﺮ
)
ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
(
ﳊﺴﺎﺏ ﺍﺣﺘﻤﺎﻝ ﻣﺘﻌﻠﻖ ﲟﺘﻐﲑﺓ ﻣﺘﻘﻄﻌﺔ ﻳﻘﺘﻀﻲ ﺍﻟﻘﻴﺎﻡ ﺑﺘﺼﺤﻴﺢ
ﻣﻌﲔ
.
ﺑﺎﻟﻨﺴﺒﺔ ﻝ
X
ﺍﻟﺘﺼﺤﻴﺢ ﻳﻜﻮﻥ ﺑﺰﻳﺎﺩﺓ ﺃﻭ ﻃﺮﺡ
0.5
ﻷﻥ ﻛﻞ ﻗﻴﻤﺔ
n
a
ﺗ
ﻌﺘﱪ
ﳎﺎﻻ
ﺣﺪﻭﺩﻩ
n
a
- 0.5
ﻭ
n
a
+ 0.5
.
ﺑﺎﻟﻨﺴﺒﺔ ﻝ
p’
–
ﺎ ﳎﺮﺩ ﺗﺎﺑﻊ ﳌﺘﻐﲑﺓ ﻣﺘﻘﻄﻌﺔﻷ ﺔﻌﻄﻘﺘﻣ ﺓﲑﻐﺘﻣ
n
a
-
ﺍﻟﺘﺼﺤﻴﺢ ﻳﻜﻮﻥ ﺑﺈﺿﺎﻓﺔ
ﺃﻭ ﻃﺮﺡ
1/(2n)
ﻭﻳﺴﻤﻰ ﻫﺬﺍ
ﻣﻌﺎﻣﻞ ﺍﻟﺘﺼﺤﻴﺢ
.
-
ﺇﺿﺎﻓﺔ ﻣﻌﺎﻣﻞ ﺍﻟﺘﺼﺤﻴﺢ ﺗﻜﻮﻥ ﰲ ﺣﺎﻟﱵ
ﺣﺴﺎﺏ
P(p’ >…)
ﺃﻭ
P(p’ ≤ …)
ﻭ ﺍﻟﻄﺮﺡ ﻳﻜﻮﻥ ﰲ ﺣﺎﻟﱵ
ﺣﺴﺎﺏ
:
P(p’<…)
ﺃﻭ
P(p’ ≥…)
.
-
ﻳﺆﻭﻝ ﻣ
ﻌﺎﻣﻞ ﺍﻟﺘﺼﺤﻴﺢ ﺇﱃ ﺍﻟﺼﻔﺮ
-
ﻭﻣﻦ ﰒ ﳝﻜﻦ ﺇﳘﺎﻟﻪ
–
ﰲ ﺣﺎﻟﺔ
n
ﻛﺒﲑﺓ
.
ﻣﺜﺎﻝ
.
ﻧﻠﻘﻲ ﻗﻄﻌﺔ ﻧﻘﺪﻳﺔ
20
ﻣﺮﺓ
.
ﻟﻴﻜﻦ
X
ﻋﺪﺩ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺻﻮﺭﺓ
.
-
ﺃﺣﺴﺐ
P(X = 8)
ﰒ ﺃﺩﺭﺱ ﺇﻣﻜﺎﻧﻴﺔ ﺍﺳﺘﺨﺪﺍﻡ
ﻗﺎﻧﻮﻥ
ﻣﻮﺍﻓﺮ
-
ﻻﺑﻼﺱ ﳊﺴﺎﺏ ﻧﻔﺲ ﺍﻻﺣﺘﻤﺎﻝ
.
,
X ~ B(20, 0.5) => P(X = 8) = C
8
20
(0.5)
8
(0.5)
12
= 0.1201
ﻟﺪﻳﻨﺎ
np = 10 > 5
ﻭﻛﺬﻟﻚ
nq = 10 > 5
ﻭﺇﺫﺍ ﺷﺌﻨﺎ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﻘﺎﻋﺪﺓ ﺍﻟﺜﺎﻧﻴﺔ ﻓﺈﻧﻨﺎ ﳒﺪ ﺃﻳﻀﺎ ﺃﻥ،
:
n =20
،
np = 10
،
nq = 10
ﳝﻜﻦ ﺇﺫﺍ ﺍﻋﺘﺒﺎﺭ،
)
1
,
0
(
)
5
.
0
)(
5
.
0
(
20
10
N
x
npq
np
x
x
x
≈
−
=
−
=
−
σ
µ
ﻭﻣﻦ ﰒ ﺍﺳﺘﺨﺪﺍﻡ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﺍﳌﻌﻴﺎﺭﻱ
ﺎﻝ ﺍﳌﻌﱪ ﻋﻦ ﺍﻟﻘﻴﻤﺔﺍ ﻝﺎﻤﺘﺣﺍ ﺏﺎﺴﳊ
8
ﻭﻫﻮ
[7.5, 8.5]
12
.
0
)
67
.
6
12
.
1
(
24
.
2
10
5
.
8
24
.
2
10
5
.
7
)
5
.
8
*
5
.
7
(
=
−
≤
≤
−
=
−
≤
≤
−
=
≤
≤
Z
P
Z
P
X
P
ﻧﺴﻤﻲ ﻋﻤﻠﻴﺔ ﺍﺳﺘﺒﺪﺍﻝ ﺍﻟﻘﻴﻤﺘﲔ
7.5
ﻭ
8.5
ﺏ ﺍﻟﻘﻴﻤﺔ
8
ﻋﻤﻠﻴﺔ ﺗﺼﺤﻴﺢ
.
ﻣﺜﺎﻝ
2
.
ﺃﺣﺴﺐ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﺗﻜﻮﻥ ﻧﺴﺒﺔ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺍﻟﺼﻮﺭﺓ
ﻋﻨﺪ ﺇﻟﻘﺎﺀ ﻗﻄﻌﺔ ﻧﻘﺪﻳﺔ
ﺃﻗﻞ ﲤﺎﻣﺎ ﻣﻦ
50
%
ﰲ
30
ﺭﻣﻴﺔ
.
P(p' < 0.5) = P(X/30 < 0.5). X ≈ N(
µ
, σ) => p' = X/30 ≈ (p, σ
p'
)
σ
p'
= √(pq/n) = 0.091 => p' ≈ (0.5, 0.091)
)
0.48
≤
p'
(
P
) =
)
n
2
/(
1
–
.5
0
≤
p'
(
P
) =
.5
0
p' <
(
P
ﻻﺣﻆ
:
ﻧﺴ
ﺘﺨﺪﻡ
ﻣﻌﺎﻣﻞ ﺍﻟﺘﺼﺤﻴﺢ
ﻷﻥ
P(p' < 0.5)
ﻫﻲ ﰲ ﺍﻷﺻﻞ
:
P(X < 15)
ﻭ ﻷﻥ
X
ﻣﺘﻐﲑﺓ ﻣﺘﻘﻄﻌﺔ
)
ﻋﺪﺩ
ﺍﻟﺼﻮﺭ
(
ﻭﺟﺐ ﺍﺳﺘﺒﺪﺍﻝ ﺑﺎﻻﺣﺘﻤﺎﻝ ﺍﻟﺴﺎﺑﻖ ﺍﻻﺣﺘﻤﺎﻝ
:
P(X ≤14.5)
ﻣﺎ ﻳﻘﺎﺑﻞ
:
P(p' ≤ 0.5 – 1/(2n))
.
P(p' ≤ 0.48) = P(Z ≤ (0.48 – 0.5)/0.091) = P(Z ≤ 0.18) = 0.571

ا
VII
.
ا TU
12
ﺃﺣﺴﺐ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﺗﻜﻮﻥ ﻧﺴﺒﺔ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺍﻟﺼﻮﺭﺓ ﺃﻗﻞ ﺃﻭ ﺗﺴﺎﻭﻱ
50
%
ﰲ
30
ﺭﻣﻴﺔ
.
P(p' ≤ 0.5) = P(p' ≤ 0.5 +
1/(2n)) = P(p' ≤ 0.517)
ﺃﺣﺴﺐ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﺗﻜﻮﻥ ﻧﺴﺒﺔ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺍﻟﺼﻮﺭﺓ ﺃﻛﱪ ﺃﻭ ﺗ
ﺴﺎﻭﻱ
50
%
ﰲ
30
ﺭﻣﻴﺔ
.
)
0.48
≤
p'
(
P
–
1
≅
)
.48
0
≥
p'
(
P
) =
)
n
2
/(
1
–
.5
0
≥
p'
(
P
) =
.5
0
≥
p'
(
P
ﺃﺣﺴﺐ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﺗﻜﻮﻥ ﻧﺴﺒﺔ ﻣﺮﺍﺕ ﺍﳊﺼﻮﻝ ﻋﻠﻰ ﺍﻟﺼﻮﺭﺓ ﺃﻛﱪ ﲤﺎﻣﺎ ﻣﻦ
50
%
ﰲ
30
ﺭﻣﻴﺔ
.
P(p' > 0.5) = P(p' > 0.5 +
1/(2n)) = P(p' > 0.517)
≅
1 – P(p' ≤ 0.517)
7
-
4
ا ز
$ وق وا
او قو + ا ز- 2&-و .*
او قو + ا ز- &5
7
-
4
-
1
)" وا- ا
(./
7
.
ﻟﻴﻜﻦ ﻟﺪﻳﻨﺎ ﳎﺘﻤﻌ
ﺎﻥ
ﻧﺴﺤﺐ ﻣﻦ ﻛﻞ
ﳎﺘﻤﻊ
ﳓﺴﺐ ﰲ،ﺔﻴﺋﺍﻮﺸﻋ ﺔﻨﻴﻋ
ﺘﻤﻊ ﺍﻷﻭﱃﺍ ﻦﻣ ﺔﺑﻮﺤﺴﳌﺍ ﺔﻨﻴﻌﻟﺍ
ﺇﺣﺼﺎﺋﻴﺔ
ﻣﺎ
S
1
)
ﺍﻟﺘﺒﺎ،ﺔﻨﻴﻌﻟﺍ ﻂﺳﻮﺘﻣ
،ﻳﻦ
(...
ﻭﳓﺴﺐ ﻧﻔﺲ ﺍﻹ
ﺣﺼﺎﺋﻴﺔ ﰲ
ﻋﻴﻨﺔ
ﺘﻤﻊ ﺍﻟﺜﺎﱐ ﻭﻧﺴﻤﻴﻬﺎﺍ
S
2
.
µ
S1
±
S2
= µ
S1
±
µ
S2 ;
σ²
S1
±
S2
= σ²
S1
+ σ²
S2
ﻣﺜﺎﻝ
1
.
ﺇﺫﺍ ﻛﺎﻧﺖ ﺍﻹ
ﺣﺼﺎﺋﻴﺔ ﻫﻲ
ﺍﳌﺘﻮﺳﻂ
ﻓﺈﻥ
:
µ
m1 – m2
= µ
m1
– µ
m2
= µ
1
– µ
2
σ²
m1 – m2
= σ²
m1
+ σ²
m2
= σ²/n
1
+ σ²/n
2
ﻣﺜﺎﻝ
2
.
ﺇﺫﺍ ﻛﺎﻧ
ﺖ ﺍﻻﺣﺼﺎﺋﻴﺔ ﻫﻲ
ﺍﻟﻨﺴﺒﺔ
ﻓﺈﻥ
:
µ
p1 – p2
= µ
p1
– µ
p2
= p
1
– p
2
σ²
p1 – p2
= σ²
p1
+ σ²
p2
= p
1
q
1
/n
1
+ p
2
q
2
/ n
2
ﻣﺜﺎﻝ
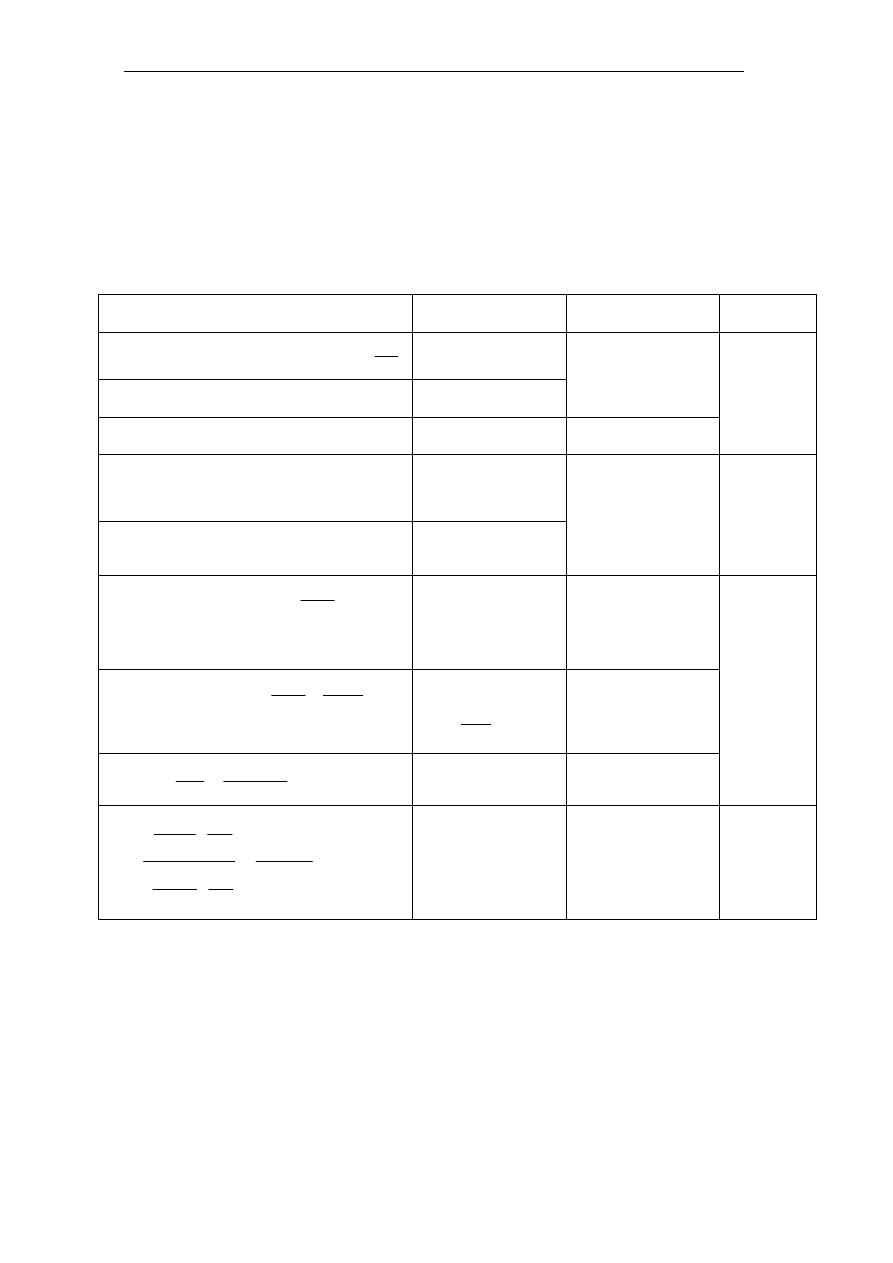
:
ﺘﻤﻊﺍ ﻦﻜﻴﻟ
U
1
:
3
،
7
،
8
.
ﺘﻤﻊﺍﻭ
U
2
:
2
،
4
.
ﲢﻘﻖ ﻣﻦ ﺃﻥ
:
µ
U1 – U2
= µ
U1
– µ
U2
; σ²
U1 – U2
= σ²
U1
+ σ²
U2
.
µ
U1
= (3 + 7 + 8)/3 = 6 ; µ
U2
= (2 + 4)/2 = 3 =>
µ
U1
– µ
U2
= 6 – 3 = 3
µ
U1 – U2
= (1 + 5 + 6 – 1 + 3 + 4)/6 = 3
σ²
U1
= (3² + 7² + 8²)/3 – 6² = 14/3 ;
σ²
U2
= (2² + 4²)/2 – 3² =1 => σ²
U1
+ σ²
U2
= 17/3
σ²
U1 – U2
= (1² + 5² + 6² + 1² + 3² + 4²) / 6 – 3²
= (1 + 25 + 36 + 1 + 9 + 16) / 6 – 9 = 17/3
7
-
4
-
2
) ) 7 (ق! ا $ز ":
TU
8
.
ﰲ ﺣﺎﻟﺔ
≥ 30
n
1
ﻭ
n
2
ﻳﻘﺘﺮﺏ ﺗﻮﺯﻳﻊ ﺍﳌﺘﻐﲑﺓ ﺍﳌﻌﻴﺎﺭﻳﺔ ﻟﻠﻔﺮﻕ ﺑﲔ ﻣﺘﻮﺳﻄﲔ ﻣﻦ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ،
ﺍﳌﻌﻴﺎﺭﻱ
،
ﻭ
ﻧﻜﺘﺐ
:
µ
m1 – m2
≈ N(0, 1 )
U
1
U
1
–
U
2
3
7
8
U
2
2
1
5
6
4
-1
3
4

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
13
ﻣﺴﺄﻟﺔ
:
ﺃﺣﺴﺐ ﰲ ﺍﳌﺴﺄﻟﺔ
1
ﺃﺣﺴﺐ ﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔ ﻟﺘﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ ﺍﳌﺴﺤﻮﺑﺔ ﺑﺎﻹﺭﺟﺎﻉ ﻣﻦ ﺧﻼﻝ ﻣﺘﻮﺳﻂ،ﻊﻤﺘﺍ ﻦﻳﺎﺒﺗ
ﺘﻤﻊ ﻭﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔﺍ ﻦﻳﺎﺒﺗ ﲔﺑ ﻥﺭﺎﻗ ،ﺔﻨﻜﻤﳌﺍ ﺕﺎﻨﻴﻌﻟﺍ ﺕﺎﻨﻳﺎﺒﺗ
ﻟﺘﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ
.
7
-
5
' " ا ز
' ( ) " "# و
&+ ز ا-
2
2&- &% ز ا-
7
-
5
-
1
$ز
ا
)" !
7
-
5
-
1
-
1
ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺑﺎﻹﺭﺟﺎﻉ
ﻟﺪﻳﻨﺎ
:
(
)
(
)
(
)
²)
(
²)
(
1
²)
(
²
1
²
²
1
²
²
2
²
1
²
2
²
1
²
2
²
1
²
1
²)
(
m
E
x
E
n
m
E
x
E
n
m
x
n
E
m
m
x
n
E
n
nm
x
n
m
x
n
E
m
mx
x
n
E
m
x
n
E
S
E
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
−
=
−
=
−
=
+
−
=
+
−
=
+
−
=
−
=
∑
∑
∑
∑
∑
∑
∑
∑
ﺘﻤﻊﺍ ﺓﲑﻐﺘﻤﻠﻟ ﻲﺿﺎﻳﺮﻟﺍ ﻊﻗﻮﺘﻟﺍﻭ ﻦﻳﺎﺒﺘﻟﺍ ﺲﻔﻧ ﺎﳍ ﺔﻨﻴﻌﻟﺍ ﺕﺍﲑﻐﺘﻣ ﻥﺃ ﺎﲟﻭ ﻦﻳﺎﺒﺘﻟﺍ ﺺﺋﺎﺼﺧ ﻡﺍﺪﺨﺘﺳﺎﺑﻭ
:
[
]
[
]
(
)
²
²
²
1
)
(
²
)
(
1
²)
(
)²
(
)
(
²)
(
)²
(
²)
(
)
(
2
2
µ
σ
µ
σ
µ
µ
−
−
+
=
+
−
+
=
+
=
=>
−
=
∑
m
m
i
i
i
i
i
i
i
i
n
n
n
m
V
x
V
n
S
E
x
E
x
V
x
E
x
E
x
E
x
V
−
=
−
=
−
−
+
=
n
n
n
n
1
²
)
1
1
²(
²
²
²
²
)²]
σ
σ
µ
σ
µ
σ
(./
9
.
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎﺘﻤﻊ ﻣﺎ ﻭ
S
²
ﻣﺘﻐﲑﺓ ﻉ ﲤﺜﻞ ﺗﺒﺎﻳﻦ ﻋﻴﻨﺔ
ﺣﺠﻤﻬﺎ
n
ﻣﺴﺤﻮﺑﺔ
ﻣﻨﻪ
ﺑﺎﻹﺭﺟﺎﻉ
)
ﺃﻭ ﺑﺪﻭﻥ
ﺇﺭﺟﺎﻉ ﻣﻦ ﳎﺘﻤﻊ ﻏﲑ ﳏﺪﻭﺩ
(
ﻓﺈﻥ،
:
−
=
=
n
n
S
E
S
1
²
²)
(
²
σ
µ
)
ﻋﻨﺪ
n ≥ 30
:
E(S²) ≈
σ²
(
ﻻﺣﻆ
:
-
ﻣﻦ ﺍﻟﻨﻈﺮﻳﺔ ﻧ
ﺴﺘﻨﺘﺞ
ﺃﻥ
:
²
1
²
σ
=
−
n
n
S
E
ﻭ
ﺑﺎﻟﺘﺎﱄ
ﻧﻘﻮﻝ ﻋﻦ
1
²
−
n
n
S
ﺃﻧﻪ ﻣﻘﺪﺭ
"
ﻏﲑ ﻣ
ﻨﺤﺎﺯ
"
ﻝ
σ²
ﻭ
ﻳﺮﻣﺰ ﻟﻪ
1
ﺏ
²
S
)
ﺣﻴﺚ
:
1
²
)
(
1
²
²
−
−
=
−
=
∑
n
m
X
n
n
S
S
i
i
)
-
²
S
)
ﻫﻮ
ﺃﻳﻀﺎ
ﻣﻘﺪﺭ
ﻳﺘﻀﺎﺀﻝ ﺗﺒﺎﻳﻨﻪ
)
ﻣﺘﻘﺎﺭﺏ
2
(
ﻷﻥ ﺗﺒﺎﻳﻨﻪ ﻛﻤﺎ ﻳﻠﻲ
:
]
)
[(
,
)
1
(
3
²)
(
4
4
4
4
µ
µ
σ
µ
−
=
−
−
+
=
x
E
n
n
n
n
S
V
)
1
$ E> 24 ا2-ه 2= F ا? Uأ =7 i$ اE
N hا = ماEW*ا E> وأ ءCا \ا
SPSS
أو
STATISTIQUA
،ه H وأ
+ ا&* اتCu اv= ل* اE> D وأ
.
2&ا نأ Dإ ةرc4ا رE - 2Lا 2= @ +
F = Uأ j F لEا
σ²
n-1
D+> @+$ ، ا2&- j+> @+$ E_و ،
S²
2&-
.
2
E^ا ? Fا H رE^ا و بر^ا رE^ا م TUأ
.

ا
VII
.
ا TU
14
ﻣﺴﺄﻟﺔ
:
ﺃﺣﺴﺐ ﰲ ﺍﳌﺴﺄﻟﺔ
1
ﺃﺣﺴﺐ ﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔ ﻟﺘﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ ﺍﳌﺴﺤﻮﺑﺔ ﺑﺎﻹﺭﺟﺎﻉ ﻣﻦ ﺧﻼﻝ، ﻊﻤﺘﺍ ﻦﻳﺎﺒﺗ
ﻣﺘﻮﺳﻂ
ﺘﻤﻊ ﻭﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔﺍ ﻦﻳﺎﺒﺗ ﲔﺑ ﻥﺭﺎﻗ ،ﺔﻨﻜﻤﳌﺍ ﺕﺎﻨﻴﻌﻟﺍ ﺕﺎﻨﻳﺎﺒﺗ
ﻟﺘﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ
.
S² = (1/n)∑ (Xi – m)²
(∑
i
S²
i
)/25 = 73/25 = 2.92 => E(S²) = 2.92
σ² = E(X²) – E(X)² = [(1 + 9 + 25 + 36 +
64)/5] – 4.6² = (135/5) – 21 = 5.84
E(S²) = 2.92 = 5.84/2 = σ² (1/n)
ﰲ ﺣﺎﻟﺔ
ﻛﻮﻥ
ﺘﻤﻊ ﻃﺒﻴﻌﻴﺍ
ﺎ
ﻓﺈﻥ
ﻣﺘﻐﲑﺍﺕ ﺍﻟﻌﻴﻨﺔ ﻫﻲ ﺍﻷﺧﺮﻯ ﺳﺘﻜﻮﻥ ﻃﺒﻴﻌﻴﺔ
ﺎ ﺍﳌﻌﻴﺎﺭﻳﺔ ﺍﳌﺮﻛﺰﻳﺔ ﺳﺘﻜﻮﻥﺍﲑﻐﺘﻣﻭ
ﻣﺘﻐﲑﺍﺕ ﻃﺒﻴﻌﻴﺔ ﻣﻌﻴﺎﺭﻳﺔ
ﻭﻣﻨ
ﻪ ﻓﺈﻥ ﳎﻤﻮﻉ ﻣﺮﺑﻌﺎﺕ
،ﻫﺬﻩ ﺍﻷﺧﲑﺓ
ﺃﻱ
σ
]²
/
∑[(X
i
– m)
،
ﺳﺘﺘﺒﻊ ﺍﻟﺘﻮﺯﻳﻊ ﻙ
2
ﺏ
n –1
ﺩﺭﺟﺔ ﺣﺮﻳﺔ
)
ﺍﻹﺣﺼﺎﺋﻴﺔ ﲢﺘﻮﻱ ﻋﻠﻰ
n –1
ﻣﺘﻐﲑﺓ ﻣﺴﺘﻘﻠﺔ
(
.
ﻟﻜﻦ
:
= nS²/σ
²
σ
]²
/
∑[(X
i
– m)
ﺇﺫﻥ
:
(./
10
.
ﺇﺫﺍ
ﻛﺎﻥ
S²
ﺗﺒﺎﻳﻦ
ﻋﻴﻨﺔ
ﻋﺸﻮﺍﺋﻴﺔ ﺣﺠﻤﻬﺎ
n
ﻣﺄﺧﻮﺫﺓ
ﻓﺈﻥ،ﻲﻌﻴﺒﻃ ﻊﻤﺘﳎ ﻦﻣ
:
2
1
~
²
²
ˆ
)
1
(
²
²
−
−
=
n
S
n
nS
χ
σ
σ
ﻣﺜﺎﻝ
:
ﻟﻴﻜﻦ ﳎ
ﺘﻤﻊ ﻃﺒﻴﻌﻲ ﺣﺠﻤﻪ
100
ﻧﺴﺤﺐ ﻣﻨﻪ ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ
n = 16
.
ﻣﺎ ﻫﻮ ﺍﺣﺘﻤﺎﻝ ﺃﻥ ﻳﻜﻮﻥ ﺗﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ
S²
ﺃﻗﻞ ﻣﻦ ﺃﻭ ﻳﺴﺎﻭﻱ
10
ﺘﻤﻊﺍ ﻦﻳﺎﺒﺗ ﻥﺃ ﺎﻤﻠﻋ
80
.
)
2
(
80
)
16
(
10
80
16
²
)
10
²
(
.
~
80
16
²
~
²
²
)
,
(
~
2
15
2
1
16
2
1
≤
=
≤
=
≤
⇒
⇒
−
−
χ
χ
χ
σ
σ
µ
P
S
P
S
P
S
n
S
N
X
n
ﻣﻦ ﺍﳉﺪﺍﻭﻝ ﺍﻹﺣﺼﺎﺋﻴﺔ ﳒﺪ
P(X²
15
≤ 2) < 0.005
7
-
5
-
1
-
2
ﺣﺎﻟﺔ
ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ
(./
11
:
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ
ﲤﺜﻞ ﳎﺘﻤﻌ
ﺎ
ﻣﺎ
ﳏﺪﻭﺩ
ﻭ
S
²
ﻣﺘﻐﲑﺓ ﻉ ﲤﺜﻞ ﺗﺒﺎﻳﻦ ﻋﻴﻨﺔ
ﻧﻔﺎﺩﻳﺔ
،ﺘﻤﻊﺍ ﺕﺍﺫ ﻦﻣ ﺔﺑﻮﺤﺴﻣ
ﻓﺈﻥ ﺍﻟﻘﻴﻤﺔ ﺍﳌﺘﻮﻗﻌﺔ ﻟﺘﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ ﺗﻜﺘﺐ
:
−
−
=
=
1
1
²
²)
(
²
N
N
n
n
S
E
S
σ
µ
)
ﻋﻨﺪﻣﺎ ﻳﻜﻮﻥ
N
ﻛﺒﲑ
ﺍ
ﺟﺪﺍ
ﻓﺄﻥ
N/ (N–1)
ﺗﺆﻭﻝ ﺇﱃ
1
(
ﺗﺴﻤﻰ
S²
ﺗﺒﺎﻳﻦ ﺍﻟﻌﻴﻨﺔ
.
ﻣﺴﺄﻟﺔ
:
ﰲ ﺍﳌﺴﺄﻟﺔ
1
ﺃﺣﺴﺐ ﺗﺒﺎﻳﻦ ﺍﳌﺘﻮﺳﻄﺎﺕ ﺍﳌﻤﻜﻨﺔ ﻟﻠﻌﻴﻨﺔ
σ
²
m
ﰲ ﺣﺎﻟﺔ
ﺍﳌﻌﺎﻳﻨﺔ ﺑﺪﻭﻥ
ﺘﻤﻊ ﻭﺗﺒﺎﻳﻦ ﺍﳌﺘﻮﺳﻄﺎﺕ ﺍﳌﻤﻜﻨﺔﺍ ﻦﻳﺎﺒﺗ ﲔﺑ ﻥﺭﺎﻗ ،ﻉﺎﺟﺭﺇ
ﻟﻠﻌﻴﻨﺔ
.
ﺍﻟﺘﺒﺎﻳﻨﺎﺕ ﺍﳌﻤﻜﻨﺔ
S²
i
0
1
4
6,25
12,3
1
0
1
2,25
6,25
4
1
0
0,25
2,25
6,25
2,25
0,25
0
1
12,3
6,25
2,25
1
0
ﺍﻟﺘﺒﺎﻳﻨﺎﺕ ﺍﳌﻤﻜﻨﺔ
S
²
i
1
4
1
6,25
2,25
0,25
12,3
6,25
2,25
1

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
15
(∑
i
S²
i
) = 36.5 ; (∑
i
S²
i
)/10 = 3.65 => E(S²) = 3.65
σ² = E(X²) – E(X)²
= [(1 + 9 + 25 + 36 + 64)/5] – 4.6² = 5.84
E(S²) = 3.65 = 5.84 .(5/4) (1/2) = σ²[(n –1)/ n] [N/ (N–1)]
7
-
6
' " "# ا ز
ﺭﺃﻳﻨﺎ ﰲ ﺍﻟﻔﺼﻞ ﺍﻟﺴﺎﺑﻖ ﺃﻥ
:
~ F
ν1,ν2
2
2
1
1
/
/
ν
ν
X
X
X
=
ﰲ ﺣﺎﻟﺔ ﺍﳌﺘﻐﲑﺗﺎﻥ ﺍﻟﻌﺸﻮﺍﺋﻴﺘﺎﻥ ﻣﺴﺘﻘﻠﺘﺎﻥ
ﻭ
X
1
~ χ
ν
1
²
ﻭ
χ
ν
2
²
X
2
~
ﻭ
ﻣﻦ ﺍﻟﻨﻈﺮﻳﺔ
10
ﻧﻌﻠﻢ ﺃﻥ
2
1
~
²
²
ˆ
)
1
(
²
²
−
−
=
n
S
n
nS
χ
σ
σ
ﺇﺫﺍ ﻛﺎﻥ
ﺘﻤﻊ ﻃﺒﻴﻌﻲ ﻭﻣﻨﻪﺍ
:
(./
12
:
ﻟﻴﻜﻦ ﻟﺪﻳﻨﺎ ﳎﺘﻤﻌﺎﻥ ﻃﺒﻴﻌﻴﺎﻥ ﺗﺒﺎﻳﻨﺎﳘﺎ
σ²
1
, σ²
2
.
ﺘﻤﻌﲔ ﻋﻴﻨﺘﲔ ﻋﺸﻮﺍﺋﻴﺘﲔﺍ ﻦﻣ ﺐﺤﺴﻧ
ﺣﺠﻤﻴﻬﻤ
ﺎ
ﻋﻠﻰ ﺍﻟﺘﻮﺍﱄ
n
1
, n
2
:
1
;
1
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
1
2
1
/
ˆ
/
ˆ
1
1
1
1
−
−
→
=
−
−
=
n
n
F
S
S
n
n
S
n
n
S
F
σ
σ
σ
σ
ﻣﺜﺎﻝ
.
ﻟﺘﻜﻦ ﻟﺪﻳﻨﺎ
ﻋﻴﻨﺘ
ﺎ
ﻥ
ﺣﺠﻤﻴﻬﻤ
ﺎ
8
ﻭ
10
ﻣﺴﺤﻮﺑﺘﲔ ﻣﻦ ﳎﺘﻤﻌﲔ ﻃﺒﻴﻌﻴﲔ ﺗﺒﺎﻳﻨﺎﳘﺎ ﻋﻠﻰ ﺍﻟﺘﻮﺍﱄ
20
ﻭ
36
.
ﻣﺎ ﺍﺣﺘﻤﺎﻝ
ﺃﻥ
؟ ﻳﻜﻮﻥ ﺗﺒﺎﻳﻦ ﺍﻷﻭﱃ ﺃﻛﱪ ﻣﻦ ﺿﻌﻒ ﺗﺒﺎﻳﻦ ﺍﻟﺜﺎﻧﻴﺔ
)
2
(
)
2
(
2
2
2
1
2
2
2
1
>
=
>
S
S
P
S
S
P
36
1
9
10
20
1
7
8
2
1
1
1
1
1
1
1
1
2
1
1
1
1
2
2
2
2
2
2
2
1
1
1
2
1
2
2
2
2
2
1
1
1
2
2
2
2
2
2
2
1
1
1
2
1
>
−
−
=
−
−
>
−
−
=
n
n
S
n
n
S
P
n
n
n
n
n
n
S
n
n
S
P
σ
σ
σ
σ
σ
σ
= P(F
7, 9
> 3.7)
ﻣﻦ ﺍﳉﺪﻭﻝ ﳒﺪ
0.05 > P(F
7, 9
> 3.7) > 0.01
و
ﺑﺎﻟﺘﺤﺪﻳﺪ
P(F
7, 9
> 3.7) = 0.036
ا
VII
.
ا TU
16
7
-
7
*+,
ﺍﳉﺪﻭﻝ ﺍﻟﺘﺎﱄ ﻳﻠﺨﺺ ﻣﺎ ﻭﺭﺩ ﰲ ﺍﻟﻨﻈﺮﻳﺎﺕ ﺍﻟﺴﺎﺑﻘﺔ ﻋﻦ ﺗﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟ
ﺬﺍـﻛﻭ ﲔﺘﻴﺋﺎﺼﺣﺇ ﲔﺑ ﻕﺮﻔﻟﺍﻭ ﻉﻮﻤﺍ ،ﺔﺒﺴﻨﻠ
ﺍﻟﺘﺒﺎﻳﻦ
.
ول@A
7
-
2
)" ! و$ %ا وقو(! ،"#! ا $ز )B 8L!
ﺍﳋﺎﺻﻴﺔ
ﺍﳌﻌﺎﻳﻨﺔ
ﺘﻤﻊﺍ
ﺇﺣﺼﺎﺋﻴﺔ ﺍﻟﻌﻴﻨﺔ
n
pq
p
p
E
p
p
=
=
=
'
'
²
;
)
'
(
σ
µ
ﺃﻳﺎ ﻛﺎﻧﺖ
n
(p, σ
p'
)
p’ ≈ N
n ≥ 30
ﳎﺘﻤﻊ
ﻏﲑ ﳏﺪﻭﺩ
ﳊﺴﺎﺏ
σ²
p'
ﻧﻀﺮﺏ ﰲ ﻣﻌﺎﻣﻞ ﺍﻹﺭﺟﺎﻉ
.
ﺍﳌﻌﺎﻳﻨﺔ ﻧﻔﺎﺩﻳﻪ
ﳎﺘﻤﻊ
ﳏﺪﻭﺩ
ﺍﻟﻨﺴﺒﺔ
p'
µ
S1
±
S2
= µ
S1
±
µ
S2
σ²
S1
±
S2
= σ²
S1
+ σ²
S2
ﺳﺤﺐ ﺑﺎﻹﺭﺟﺎﻉ
µ
m1 – m2
≈ N(0, 1 )
≥ 30
n
1
ﻭ
n
2
ﳎﺘﻤﻊ ﻣﺎ
ﺍﻟﻔﺮﻕ ﺑﲔ
ﺇﺣﺼﺎﺋﻴﺘﲔ
ﻭ ﳎﻤﻮﻋﻬﻤﺎ
s
1
±
s
2
−
=
=
n
n
S
E
S
1
²
²)
(
²
σ
µ
ﰲ ﺣﺎﻟﺔ
E(S²) ≈
σ² : n ≥ 30
ﺳﺤﺐ
ﻋﻴﻨﺔ ﺑﺎﻹﺭﺟﺎﻉ
)
ﺃﻭ ﺑﺪﻭﻥ ﺇﺭﺟﺎﻉ ﻣﻦ
ﳎﺘﻤﻊ ﻏﲑ ﳏﺪﻭﺩ
(
ﳎﺘﻤﻊ ﻣﺎ
−
−
=
=
1
1
²
²)
(
²
N
N
n
n
S
E
S
σ
µ
N/ (N–1)
ﺗﺆﻭﻝ ﺇﱃ
1
ﰲ ﺣﺎﻟﺔ
N
ﻛﺒﲑ ﺟﺪﺍ
ﻋﻴﻨﺔ
ﻧﻔﺎﺩﻳﺔ
ﳎﺘﻤﻊ ﳏﺪﻭﺩ
2
1
~
²
²
ˆ
)
1
(
²
²
−
−
=
n
S
n
nS
χ
σ
σ
ﻋﻴﻨﺔ ﺣﺠﻤﻬﺎ
n
ﳎﺘﻤﻊ ﻃﺒﻴﻌﻲ
ﺍﻟﺘﺒﺎﻳﻦ
S²
1
;
1
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
1
2
1
/
ˆ
/
ˆ
1
1
1
1
−
−
→
=
−
−
=
n
n
F
S
S
n
n
S
n
n
S
F
σ
σ
σ
σ
ﻋﻴﻨﺘﲔ ﻋﺸﻮﺍﺋﻴﺘﲔ
ﺣﺠﻤﻴﻬﻤ
ﺎ
ﻋﻠﻰ ﺍﻟﺘﻮﺍﱄ
n
1
, n
2
ﳎﺘﻤﻌﺎﻥ ﻃﺒﻴﻌﻴﺎﻥ ﺗﺒﺎﻳﻨﺎﳘﺎ
σ²
1
,
σ²
2
F

?A ا ء4ا و تCCا Dإ 0E
.
ءF ا
2
.
17
7
-
7
-
1
MN!
7
-
7
-
1
-
1
ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﺘﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻠﺘﺒﺎﻳﻦ
ﺇﺫﺍ ﻛﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎﺘﻤﻊ ﻣﺎ ﻭ
S
²
ﻓﺈﻥ،ﻊﻤﺘﺍ ﺕﺍﺫ ﻦﻣ ﺔﺑﻮﺤﺴﻣ ﺔﻨﻴﻋ ﻦﻳﺎﺒﺗ ﻞﺜﲤ ﻉ ﺓﲑﻐﺘﻣ
:
−
=
sinon
~
si
/
2
²
4
4
²
n
N
X
n
S
σ
µ
σ
σ
ﻣﻦ ﺃﺟﻞ
n ≥ 100
ﺗﻮﺯﻳﻊ،
S
²
ﻳﻘﺘﺮﺏ ﻛﺜﲑﺍ ﻣﻦ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ
.
7
-
7
-
1
-
2
ﺍﻻﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ ﻟﺘﻮﺯﻳﻊ ﺍﳌﻌﺎﻳﻨﺔ ﻟﻼﳓﺮﺍﻑ ﺍﳌﻌﻴﺎﺭﻱ
ﺇﺫﺍ ﻛ
ﺎﻧﺖ
X
ﻡ ﻉ ﲤﺜﻞ ﳎﺘﻤﻊ ﻣﺎ ﻭ
S
ﻓﺈﻥ،ﻊﻤﺘﺍ ﺕﺍﺫ ﻦﻣ ﺔﺑﻮﺤﺴﻣ ﺔﻨﻴﻋ ﻦﻳﺎﺒﺗ ﻞﺜﲤ ﻉ ﺓﲑﻐﺘﻣ
:
−
≈
=
sinon
²
4
ou
~
si
/
2
4
4
σ
σ
µ
σ
σ
n
N
X
N
X
n
S
ﻣﻦ ﺃﺟﻞ
n ≥ 100
ﺗﻮﺯﻳﻊ،
S
ﻳﻘﺘﺮﺏ ﻛﺜﲑﺍ ﻣﻦ ﺍﻟﺘﻮﺯﻳﻊ ﺍﻟﻄﺒﻴﻌﻲ ﻭ
µ
s
≈ S
ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ
:
ﳓ
ﺘﺎﺝ
ﺃﺣﻴﺎﻧﺎ
ﺘﻤﻊ ﺇﱃﺍ ﻢﻴﺴﻘﺗ ﱃﺇ ﺔﻨﻴﻌﻟﺍ ﺭﺎﻴﺘﺧﺍ ﻞﺒﻗ
ﳎﺘﻤﻌﺎﺕ ﺟﺰﺋﻴﺔ
(sous populations)
،
ﲝﻴﺚ
ﻳﻜﻮﻥ ﻛﻞ ﻣﻨﻬﺎ
ﳑﺜﻼ ﰲ ﺍﻟﻌﻴﻨﺔ
.
ﻓﺈﺫﺍ ﺃﺭﺩ
ﻧﺎ
ﺩﺭﺍﺳﺔ ﺍﻟﻄﻠﺒﺔ ﻓﻘﺪ
ﳓ
ﺘﺎﺝ ﺃﻥ
ﻧ
ﻮﺯ
ﻳ
ﻋﺪﺩ،ﺲﻨﳉﺍ ﺭﺎﻴﻌﻣ ﺐﺴﺣ ﺔﺒﻠﻄﻟﺍ ﺕﺎﺌﻓ ﻰﻠﻋ ﺔﺳﺍﺭﺪﻟﺍ ﺔﻨﻴﻋ ﻊ
، ﺍﻟﺘﺨﺼﺺ،ﺔﻴﺳﺍﺭﺪﻟﺍ ﺕﺍﻮﻨﺳ
...
ﺗﺴﻤﻰ،ﺔﻠﻘﺘﺴﻣﻭ ﺔﻄﻴﺴﺑ ﺔﻴﺋﺍﻮﺸﻋ ﺔﻴﺋﺰﺟ ﺕﺎﻨﻴﻋ ﻦﻣ ﺔﻧﻮﻜﻣ ﺔﻴﻠﻜﻟﺍ ﺔﻨﻴﻌﻟﺍ ﺢﺒﺼﺗ ﺚﻴﲝ
ﺬﻩ ﺍﻟﻄﺮﻳﻘﺔ ﺍﻟﻌﻴ ﺔﻧﻮﻜﳌﺍ ﺔﻨﻴﻌﻟﺍ
ﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ
(
Echantillons stratifiés)
.
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ ﻛﻴﻒ ﳝﻜﻦ ﺗﻘﺪﻳﺮ ﻣﺘﻮﺳﻂ
؟ﺘﻤﻊ ﻣﻦ ﺧﻼﻝ ﻣﺘﻮﺳﻄﺎﺕ ﺍﻟﻌﻴﻨﺎﺕ ﺍﳉﺰﺋﻴﺔﺍ
ﻧﺮﻣﺰ ﻟ
ﻠﻤﺠﺘﻤﻊ
ﺏ
U
ﻭ
ﻧﺮﻣﺰ ﻟﻠﻤﺠﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔ
)
ﻟﻴﻜﻦ ﻋﺪﺩﻫﺎ
H
(
ﺏ
U
1
, U
2
, ..., U
h
،
ﺣﺠﻢ ﻛﻞ ﻣﻨﻬﺎ
N
h
ﺣﻴﺚ
N = ∑N
h
ﻛﻞ،
ﳎﺘﻤﻊ ﺟﺰﺋﻲ ﻟﻪ
ﻣﺘﻮﺳﻂ
µ
h
و
ﺗﺒﺎﻳﻦ
σ²
h
.
ﰲ ﻫﺬﻩ ﺍﳊﺎﻟﺔ
ﺘﻤﻊ ﺇﱃ ﺗﺒﺎﻳﻦ ﺩﺍﺧﻠﺍ ﻦﻳﺎﺒﺗ ﻞﻴﻠﲢ ﻢﻬﳌﺍ ﻦﻣ
ﻲ
)
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔﺍ ﻞﺧﺍﺩ
(
ﻭ
ﺗﺒﺎﻳﻦ ﺑﻴﲏ
)
ﺑﲔ
ﺍ
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔ
.(
(
)
∑
∑
∑∑
∑∑
+
=
−
+
=
=
−
+
−
=
−
=
=
=
=
=
h
entre
dans
h
h
h
h
h
H
h
Nh
i
h
h
ih
H
h
Nh
i
ih
N
N
N
N
X
N
X
N
2
2
2
1
1
1
1
²
²
...
)²
(
1
)²
(
1
²
σ
σ
µ
µ
σ
σ
µ
µ
µ
µ
σ
ﺗﺴﻤﻰ ﻫﺬﻩ ﺍﳌﻌﺎﺩﻟﺔ ﻣﻌﺎﺩﻟﺔ ﲢﻠﻴﻞ ﺍﻟﺘﺒﺎﻳﻦ
1
.
ﻧﺮﻣﺰ ﻟﻠﻌﻴﻨﺎﺕ ﺍﳉﺰﺋﻴﺔ ﺏ
s
h
ﻟﻜﻞ ﻣﻨﻬﺎ ﺣﺠﻢ،
n
h
(
n = ∑n
h
)
ﻭﻣﺘﻮﺳﻂ،
M
h
.
1
TUأ ا 2 EF
:
،y=ج ج دروز
1997
ص،
284
.
ا
VII
.
ا TU
18
ﳝ
ﺘﻤﻊﺍ ﻂﺳﻮﺘﻣ ﺮﻳﺪﻘﺗ ﻦﻜ
µ
ﻣﻦ ﺧﻼﻝ ﺍﳌﺘﻮﺳﻂ ﺍﳊﺴﺎﰊ ﳌﺘﻮﺳﻄﺎﺕ ﺍﻟﻌﻴﻨﺎﺕ ﺍﳌﺮﺟﺢ ﺑﺄﺣﺠﺎﻣﻬﺎ ﻭﻧﻜﺘﺐ
:
∑
=
h
h
h
N
M
N
1
µ
)
ﺣﻴﺚ
:
µ
=
∑
h
h
h
N
M
N
E
1
ﺃﻣﺎ ﺍﳋﻄﺄ ﺍﳌﻌﻴﺎﺭﻱ ﻓﻴﻌﻄﻰ ﺑﺎﳌﻌﺎﺩﻟﺔ
:
∑
∑
−
−
=
h
h
h
h
h
h
h
h
h
h
n
N
n
N
N
N
N
M
N
V
2
2
1
²
1
σ
ﻻﺣﻆ ﺃﻥ ﺍﳋﻄﺄ ﺍﳌﻌﻴﺎﺭﻱ ﻳﺘﺄﺛﺮ ﻃﺮﺩﻳﺎ ﺑﺎﻟﺘﺒﺎﻳﻦ ﺍﻟﺪﺍﺧﻠﻲ ﻟﻠ
ﻤﺠﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔ
σ²
h
.
ﺘﻤﻊ ﰲﺍ ﻂﺳﻮﺘﻣ ﺮﻳﺪﻘﺗ ﻥﺃ ﻝﺪﻳ ﺍﺬﻫ
ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ
)
ﻣﻦ ﺧﻼﻝ ﺍﳌﺘﻮﺳﻂ ﺍﳌﺮﺟﺢ ﳌﺘﻮﺳﻄﺎﺕ ﺍﻟﻌﻴﻨﺎﺕ
(
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔﺍ ﻥﻮﻜﺗ ﺎﻣ ﺭﺪﻘﺑ ﺔﻗﺩ ﺮﺜﻛﺃ ﻥﻮﻜﻳ
ﺘﻤﻊ ﻣﺘﺠﺎﻧﺴﺔ ﺩﺍﺧﻠﻴﺎﺍ ﺎﻬﻴﻟﺇ ﻢﺴﻗ ﱵﻟﺍ
.
ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ ﺍﻟﻨﺴﺒﻴﺔ
.
ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ ﺍﻟﻨﺴﺒﻴﺔ
(échantillonnage stratifié proportionnel)
ﺘﻤﻊﺍ ﱃﺇ ﺔﻴﺋﺰﳉﺍ ﺔﻨﻴﻌﻟﺍ ﺔﺒﺴﻧ ﻞﻌﲜ ﻢﺘﺗ
ﺘﻤﻊﺍ ﱃﺇ ﺔﻴﻠﻜﻟﺍ ﺔﻨﻴﻌﻟﺍ ﺔﺒﺴﻨﻟ ﺔﻳﻭﺎﺴﻣﻭ ﺕﺎﻨﻴﻌﻟﺍ ﻞﻜﻟ ﺔﺒﺴﻨﻟﺎﺑ ﺔﻳﻭﺎﺴﺘﻣ ﻲﺋﺰﳉﺍ
:
n
1
/N
1
= n
2
/N
2
= . . . = n
h
/N
h
= n/N
ﺘﻤﻊ ﳝﻜﻦ ﺗﻘﺪﻳﺮﻩ ﻣﺒﺎﺷﺮﺓﺍ ﻂﺳﻮﺘﻣ ﻥﺈﻓ ﺔﻟﺎﳊﺍ ﻩﺬﻫ ﰲ
ﲟﺘﻮﺳﻂ
ﺍ
ﻟﻌﻴﻨﺔ ﺍﻟﻜﻠﻴﺔ
)
ﻛﻤﺎ ﰲ ﺍﻟﻌﻴﻨﺔ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ ﺍﻟﺒﺴﻴﻄﺔ
:(
M
M
T
n
T
n
N
N
T
n
N
N
M
N
N
h
h
h
h
h
h
h
h
h
h
h
=
=
=
=
=
=
∑
∑
∑
∑
µ
µ
)
)
1
1
1
1
ﻭﰲ ﺣﺎﻟﺔ ﳎﺘﻤﻌﺎﺕ ﺟﺰﺋﻴﺔ ﻛﺒﲑﺓ،ﺎﻨﻫ ﻲﻄﻌﺗ ﺔﻴﻘﺒﻄﻟﺍ ﺔﻨﻳﺎﻌﳌﺍ ﺔﻟﺎﺣ ﰲ ﺔﻨﻳﺎﻌﳌﺍ ﺄﻄﳋ ﺔﻘﺑﺎﺴﻟﺍ ﺔﻐﻴﺼﻟﺍ
:
n
N
n
n
N
N
N
n
N
M
N
V
dans
h
h
h
h
h
h
2
2
1
1
1
1
σ
σ
−
=
−
≅
∑
∑
ﺑﺎﳌﻘﺎﺭﻧﺔ ﻣﻊ ﺧﻄﺄ ﺍﳌﻌﻴﻨﺔ ﰲ ﺣﺎﻟﺔ ﺍﻟﻌﻴﻨﺔ ﺍﻟﻌﺸﻮﺍﺋﻴﺔ ﺍﻟﺒﺴﻴﻄﺔ
)
ﺑﺎﻹﺭﺟ
ﺎﻉ ﻭﺑﺪﻭﻧﻪ
(
ﳒﺪ ﺃﻥ ﺍﳌﻌﺎﻳﻨﺔ ﰲ ﺣﺎﻟﺔ ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔ ﺃﻛﺜﺮ ﺍﻧﺴﺠﺎﻣﺎﺍ ﺖﻧﺎﻛ ﺖﻤﻠﻛ ﺩﺍﺩﺰﻳ ﲔﺴﺤﺘﻟﺍ ﺍﺬﻫﻭ ،ﻕﺩﺃ ﺍﺮﻳﺪﻘﺗ ﺓﺩﺎﻋ ﻲﻄﻌﺗ ﺔﻴﺒﺴﻨﻟﺍ
.
ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ ﺍﳌﺜﺎﻟ
ﺔﻴ
.
ﺍﻟﻐﺮﺽ ﻣﻦ ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ ﺍﳌﺜﺎﻟﻴﺔ ﻫﻮ ﲢﺴﲔ ﺍﻟﺘﻘﺪﻳﺮ ﺃﻛﺜﺮ
)
ﲣﻔﻴﺾ ﺧﻄﺄ ﺍﳌﻌﺎﻳﻨﺔ
(
ﺑﺘﻮﺯﻳﻊ ﺍ
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔﺍ ﻰﻠﻋ ﺔﻨﻴﻌﻟ
ﻛﻤﺎ ﰲ ﺍﳌﻌﺎﻳﻨﺔ ﺍﻟﻄﺒﻘﻴﺔ ﺍﻟﻨﺴﺒﻴﺔ،ﻲﺋﺰﳉﺍ ﻊﻤﺘﺠﻤﻠﻟ ﱯﺴﻨﻟﺍ ﻢﺠﳊﺍ ﺐﺴﺣ ﺎﻬﻌﻳﺯﻮﺗ ﻦﻣ ﻻﺪﺑ ﺎﻬﻣﺎﺠﺴﻧﺍ ﺔﺟﺭﺩ ﺐﺴﺣ
.
ﻳﻌﲏ
ﺮﺜﻛﻷﺍ ﺔﻴﺋﺰﳉﺍ ﺕﺎﻌﻤﺘﺠﻤﻠﻟ ﺎﻤﺠﺣ ﻞﻗﺃ ﺕﺎﻨﻴﻋﻭ ،ﺎﻣﺎﺠﺴﻧﺍ ﻞﻗﻷﺍ ﺔﻴﺋﺰﳉﺍ ﺕﺎﻌﻤﺘﺠﻤﻠﻟ ﺎﻤﺠﺣ ﱪﻛﺃ ﺕﺎﻨﻴﻋ ﲔﻴﻌﺗ ﻚﻟﺫ
ﲝﻴﺚ ﺗﻜﻮﻥ ﺃﺣﺠ،ﺎﻣﺎﺠﺴﻧﺍ
ﺎﻡ ﺍﻟﻌﻴﻨﺎﺕ ﺍﳉﺰﺋﻴﺔ ﻣﺘﻨﺎﺳﺒﺔ
)
ﻃﺮﺩﻳﺎ
(
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔ ﺍﻟﱵ ﺗﺴﺤﺐ ﻣﻨﻬﺎﺍ ﺕﺎﻨﻳﺎﺒﺗ ﻊﻣ
.
ﻋﻨﺪﻣﺎ
ﺘﻤﻌﺎﺕ ﺍﳉﺰﺋﻴﺔ ﻛﺒﲑﺓ ﲟﺎ ﻓﻴﻪ ﺍﻟﻜﻔﺎﻳﺔ ﳓﺪﺩ ﻫﺬﻩ ﺍﻷﺣﺠﺎﻡ ﻛﻤﺎ ﻳﻠﻲﺍ ﻥﻮﻜﺗ
:
h
h
j
j
j
h
N
N
n
n
σ
σ
∑
≅
