
حماضرات اإلحصاء الرياضي
لطلبة كلية العلوم االقتصادية
بوعبد اهلل صاحل
5002
-
5002


- 1 -
فهرس
المحتويات
................................
................................
................................
................................
................................
نبذة تاريخية عن تطور علم االحصاء
................................
................................
................................
................................
................................
تذكري باملفاهيم األساسية لالحتماالت
................................
................................
................................
Epreuve, événement, probabilité
................................
................................
األركان الخمسة في حساب االحتماالت
................................
القاعدة السادسة أو حساب االحتمال حسب تعريف باسكال لالحتمال
................................
................................
..............................
ترميز أو التعبير الرياضي عن االحتماالت
................................
استخدام نظرية المجموعات للتعبير عن األحداث العشوائية
................................
................................
نظرية االحتمال السببي أو نظرية بايز
................................
................................
..............................
................................
................................
...............................
................................
ئية المتقطعة وتوزيعها االحتمالي
................................
................................
................................
................................
................................
التوزيع االحتمالي للمتغيرة المتقطعة
................................
شروط دالة الكثافة للمتغيرة المتقطعة
................................
التمثيل البياني لدالة الكثافة االحتمالية ل م ع المتقطعة
................................
................................
مفهوم المتغيرة العشوائية المستمرة وتوزيعها االحتمالي
................................
تعريف المتغيرة العشوائية المستمرة
................................
................................
................................
خصائص دالة الكثافة االحتمالية للمتغيرة العشوائية المستمرة
..............................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
..............................
................................
................................

- 2 -
................................
................................
La fonction génératrice des moments M
................................
................................
..............................
نظرية شيبيشيف ونظرية األعداد الكبيرة
................................
Inégalité de Bienaymé CHEBYCHEV
................................
................................
التوزيعات االحتمالية األكثر استخداما
................................
التوزيعات الحتمالية المتقطعة األكثر استخداما
................................
Distribution hyper géométrique
:التوزيع الهندسي الزائد المتعدد
Distribution Multi-hypergéométrique
................................
................................
)التوزيع الثنائي السالب (باسكال
Distribution binomiale négative
................................
................................
................................
................................
................................
التوزيعات االحتمالية الشائعة المستمرة
................................
التوزيع الطبيعي أو توزيع البالس قوس
................................
................................
................................
..............................
................................
................................
املتغريات العشوائية متعددة األبع
................................
................................
................................
)التوزيعات المشتركة المتقطعة والدالة الهامشية (الحدية
................................
................................
................................
................................
................................
..............................
................................
................................
................................
................................
توقع وتباين المتغيرة العشوائية متعددة األبعاد
................................
................................
................................
................................
................................
................................
................................
..............................
دوال املتغريات العشوائية والتقارب
................................
................................
Distribution en Khi-carré (ou Khi-deux)
................................
................................
................................
..............................
السلوك التقاربي لبعض التوزيعات االحتمالية
................................
التقارب بين التوزيع الثنائي والتوزيع الطبيعي
................................
.االنتقال من متغيرة متقطعة إلى متغيرة متصلة
................................
التقارب بين التوزيع الثنائي وتوزيع بواسون
................................

- 3 -
................................
................................
................................
................................
................................
................................
................................
................................
العينة النفادية والعينة غير النفادية
Echantillon exhaustif et non exhaustif
................................
................................
Statistique de l’échantillonnage
................................
................................
................................
متوسط توزيع المعاينة للمتوسطات
................................
تباين توزيع المعاينة للمتوسطات
................................
................................
................................
................................
................................
................................
..............................
................................
................................
توزيع المعاينة للفروق والمجاميع
................................
................................
................................
................................
توزيع المعاينة للفرق بين متوسطين
................................
توزيع المعاينة للتباين وتوزيع المعاينة لنسبة تبايني عينتين
................................
................................
................................
................................
................................
................................
................................
...............................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
................................
..............................
................................
................................
................................
................................
................................
)طريقة المعقولية العظمى (طريقة االحتمال األكبر
................................
مفاهيم اختبارات الفروض وتطبيقاهتا
................................
................................
................................
................................
................................
.االختبار أحادي االتجاه للمتوسط
................................
................................
................................
................................
................................
................................
..............................
................................
................................
................................
................................
................................
................................
................................
................................

- 4 -
................................
...............................
................................
................................
................................
................................
................................
................................
................................
................................

محاضرات اإلحصاء الرياضي
ب. ص
-
1
-
م
قدمة
هذه المطبوعة
هذه املطبوعة هي عبارة عن حماضرات اإلحصاء
حسب الربنامج الوزاري ملقياس
"
إحصاء
5
"
للسنة الثانية علوم
ال
تسيري
.
لكي يستفيد الطلبة من القاعدة اليت اكتسبوها عند دراسة اإلحصاء الوصفي يف السنة،ةيناثلا ةنسلا ةبلطل سايقلما اذه جمرب
. لكن هدفه األساسي هو التمهيد لدراسة اإلحصاء التطبيقي يف السنة الثالثة،لىولأا
هدف هذا املقياس هو ت
قدمي علم
اإل
حصاء الرياضي
،
.أي األساس الرياضي لإلحصاء التطبيقي
لكن تقدمي هذه املادة لطلبة العلوم،ةسدنلها و مولعلا تايلك في سايقلما اذه ةدام سردت ،تايضايرلا نم اعرف اهرابتعاب
.اإلنسانية يتضمن صعوبة خاصة
هذه
املطبوعة
هي مثرة
جتربة سنوات عدي
ة يف
تدري
اإلحصاء
بكلية
الع
لوم االقتصادية
جلامعة املسيلة
ولقد،
حاولنا أن
نستفيد من هذه التجربة لصياغة
حمتوى
املقياس
بطريقة تالئم مستوى طل
بة
هذه الكلية و
.طبيعة التخصص
لتحقيق هذا الغرض
حرصنا على ربط املفاهيم والقواعد النظرية باستخداماهتا التطبيقية
؛
فعملنا
على إعطاء
أمثلة حملولة عن كل
مفهوم جديد. و
ألن فهم القواعد الرياضية يكون أسهل إذا كان للمتلقي خلفية عن املشكلة اليت حيتاج
،حلها إىل استخدام هذه القواعد
عملنا يف كثري من األحيان إىل
التقدمي
لبعض الدروس
أو النظري
ات
مبسأ
لة
تكون مبثابة
وأحيانا مبثابة مشكلة،ديهمتلا
ننطلق منها
لن
توصل إىل
النظرية
.
هذا و
ننبه
طلب
تنا األعزاء
إىل أنه
ي
فرتض
هبم عند دراسة
اإلحصاء الرياضي أن يكونوا قادرين
على
استيعاب املفاهيم الرياضية بعموميتها و ال يبقوا خياهلم حبي األمثلة واملسائ
ل
فاإلحصاء الرياضي غري اإلحصاء التطبيقي الذي يعىن بتطبيقات هذه املفاهيم في،ةاطعلما
.ما بعد
أطوهلا الفصل الثاين،لوصف ةيناثم ىلع ررقلما جمانبرلا نمضتي
"املتغريات العشوائية" نونعلما
.
من
أ
جل املوازنة بني الفصول
رأينا أن
نعيد جتزئة حمتويات الربنامج. فأعدنا ت
قس
ي
م
حمتويات الفصل الثاين إىل
3
ومجعنا حمتويات،همجلح ارظن لوصف
الفصل السابع و الثام
.ن يف فصل واحد لتعلقهما مبوضوع واحد
ولقد قسمنا الفصول إىل
مباحث
حبيث،
يوافق
املبحث
حماضرة
واحدة يف أغلب األحيان
و،
التزمنا
يف الغالب األعم
لكن سوف جيد القارئ أننا توسعنا يف بع،ررقلما جهنلماب
ض
فله أن يلم هبذه االستطرادات إن رأى أن،تاقحللما للاخ نم بناولجا
و إال،ةررقلما ةيسيئرلا طاقنلا مهف نم نكتم دق ه
.فإننا ننصحه بأن مير عليها مرور الكرام
و
غين عن الذكر أن حمتوى هذه املطبوعة من نظريات وقواعد لي من إبداع
و إمنا هي قواعد مبسوطة يف املراجع مجعناها وعرضناها بأسلوب،اهفلؤم
رأينا أنه األنسب مل
ستوى طالب كلي
ة ال
علوم
.االقتصادية
و
هنيب هبم أن ال يبخلوا علينا مبالحظاهتم وتعليقاهتم،عضاوتلما لمعلا اذه انئلامز و انتبلطل مدقن ذإ
ح
ىت
.نستفيد منها لطبعات مقبلة حبول اهلل
متطلبات المقياس
فيما يتعلق مبا
حتتاج
ه
متابعة
وفهم
هذا املقياس
من املهم التمييز بني الفصل األول،
وبقية
الفص
ول األخرى. فالفصل األول
الذي
يتضمن
املفاهيم األساسية لعلم ا
،الحتماالت ال حيتاج استيعابه إىل مستوى عايل يف الرياضيات
أ
ما
باقي الفصول
في
تطلب فهمها أن يقوم الطالب مبراجعة عدد من املفاهيم الرياضية أغلبها متضمنة يف برنامج الرياضيات للسنة األوىل. تتمثل
هذه
التكامل (خاصة التكامل بالتجزئة) والدوال األسية. كما حيتاج الطالب إىل قاعدة،قاقتشلاا ،لاودلا في اساسأ ميهافلما
. التكامل الثنائي والسالسل الشهرية،متيراغوللا ميهافم في ةطيسب
كلمة إلى الطلبة
كثريا ما نالحظ أن الطلبة يستخدمون التمارين املقدمة يف السالسل كنما
ذج أو شبه قوانني يف حد ذاهتا حياولون ح
فظها
بينما هي يف احلقيقة جمرد وسيلة لفهم الدرس. هذا التشبث بالشكل دون املضمون
يف
حماولة يائسة ملواج
هة االمتحان
دون

- 2 -
فهم حقيق ملضمون املادة هو نتيجة حتمية بالنسبة ملن ال يتابع احملاضرات والتطبيقات باملراجعة املستمرة و ال
ف
ورية
. وحسب
ىلع دمتعي امم رثكأ مهفلا ىلع اساسأ دمتعي سايقم هنأ اهببس سايقلما اذه في ةبلطلا اههجاوي تيلا ةبوعصلا نإف انيأر
لىإ جاتيح انمإو ،هتراهم تناك امهمو يرخلأا اذه لذب امهم ،ذاتسلأا نم يقلتلا قيرط نع ىتأتي لا مهفلا اذهو .ركذتلا
جهد مستقل يبذله الطالب مب
فرده
مع قدر
.من الرتكيز و املثابرة
"الوصفة السحرية"
لفهم هذه املادة
،
ه
ي
املراجعة جبرعات
منتظمة و فورية (بعد كل حماضرة قبل النوم
1
!
.) مع شيء من الرتكيز على القواعد واملفاهيم حىت يتم فهمها فهما جيدا
وليع
مل الطالب على تعميق فهمه
من خالل متارين السالسل و لكن ال
جامدة"جذانم" اهذختي
أو قواعد إضافية
.
إن
هدف األستاذ واجلامعة ككل هو إعداد الطالب ملواجهة املشكالت املعقدة للتسيري
،
وهذا
اهلدف ال يتحقق
إال
بتنمية
الذكاء
الو
تزو
د
بعدد من التقنيات املساعدة
. إن اجلائزة احلقيقية اليت جيب أن يتوقعها الطالب من دراسة باجلامعة
ه
ي تكوين
قدرة على التعلم الذايت أكثر من جتميع كم من املعارف اليت قد ال حيتاجها أبدا
، و هي من جهة أخرى،
تك
وين
ذهنية
للاخ نم اله لولح عادبإ ثم نمو قيقدو حضاو لكش في اهتغايصو ةدقعلما تايعضولاو تلاكشلما ليلتح ىلع ةرداق ةلقتسم
.تفكريه اخلاص
هذه القدرة ال تتأتى
إذا عود الطالب نفسه على إعمال فكره
مطوال
يف املسائل اليت تطرحه
ا التمارين
مما
يعطي الطالب
القدرة على
التحليل والرتكيب واالستنباط واالستدالل كأس التفكري املنتج واملبدع. إن الوصول إىل هذه
القدرة على مواجهة مشكالت وحلها هي غاية أساسية للتعليم اجلامعي وهي أحسن
رأمسال جيمعه الطالب ليستثمر
ه حياته
.العامة واخلاصة معا
نبذة تاريخية عن تطور علم االحصاء
5
. اإلثارة و احلمى،بصعتلا ،سدلحا نم ةرمتسم و ةلصفنم لحارم برع مدقتي ثحبلا نإف اذكهو"
و
ذات
يوم
تتحقق
أخريا الفرحة
و ي
تذوق طعمها من
.عاش تلك اللحظات الفريدة
[…]
أ
لربت
أينشتاين
3
قبل
الشروع يف دراسة
الطرائق املختلفة
لإلحصاء الرياضي
يستحسن أن حييط الطالب
بنظرة
عن
التط
ور التارخيي ل
إلحصاء
كممارسة وكعلم
وأن،
ي
طلع على جمموعة من
أبرز
من كتبوا يف هذا العلم
.
الفترة
ما قبل الميالد إلى غاية القرن
81
تدل احلفريات اليت وجدت يف:
أماكن متعددة على استخدام اإلحصاء من قبل
عدد من
احلضارات القدمية عرب املعمورة. منذ القدم استخدم احلكام
واألمراء
اإلحصاء كوسيلة للرقابة
،
و
أداة
إلد
ارة اململكة
أو املدينة أو املقاطعة
واستخدموا يف ذلك،
.تعداد السكان وجرد السلع واملوارد املختلفة
يف
احلضارة السو
م
رية
،
اليت سادت
يف بالد ما بني ال
نهرين
2
آالف إىل ألفي سنة
ق
بل امليالد
،
واليت ازدهرت فيها التجارة
بشكل كبري
كانت قوائ،
م من السلع
واألشخاص تدون على ألواح من الصلصال
وقد،
وجدت حفريات مشاهبة تثبت استخدام اجلرد
يف عهد
احلض
ارة املصرية
اليت سادت
3
آالف سنة قبل ا
مليالد. احلضارة
املصرية
اليت قامت على التسيري والتقسيم الدقيق ملياه النيل اتسمت إ
دارهتا
باملركزية الشديدة وهذا الذي أعطى األمهية
للتدوين
كوسيلة للمراقبة
،
فقد كان للمصريني القدامى مدارس يتعلم
فيها املوظفون
القراءة والكتابة
وا
وكان مما يت،ابه لومعلما ينناوقل
علمه املوظف أن ال اعتبار ألمر أو عقد ما مل يكن مكتوبا. واستخدم اجل
رد
لدى مجيع احلضارات القدمية تقريبا كاحلضارة الصينية
و
اهلندية
و
اليابانية
و
وكذا حضار،ةينامورلاو ةينانويلا
ة اإلنكا
يف
الساحل
1
يعلمنا علم نف الرتبية أن أكثر من
20
باملئة من املعلومات اليت نتعلم
ها ننساها يف التسع ساعات األوىل
. فأنقذ معلوماتك يف الساعات األوىل قبل أن تتبخر
!
2
سلسلة،ءاصحلإا في تايساسأ ،كيبزورد كاج نوج :نع ةييخراتلا تامولعلما مظعم تذخأ
(SMA)
دار،
(Ellips)
،
1992
ص،
5
.
3
من كتاب
ه:
كيف أرى العامل. ترمجه إىل الفرنسية
، فالماريون، يراب ،ويرنوه ييجر
1999
.
:عن
Microsoft ® Encarta ®
5002. © 1993-5002 Microsoft Corporation.

محاضرات اإلحصاء الرياضي
ب. ص
-
3
-
الغريب أل
مريكا اجلنوبية
(ابتداءا من القرن
15
إىل غاية
1295
)
. يف ه
ذا العهد
كان
اإلحصاء عبارة عن جرد
ا
ملواد واألفراد
.وأحيانا جند نظاما لتصنيف املعلومات لكن مل يوجد دليل على عمليات معاجلة هلذه املعطيات
أما يف أوربا،لالما تيب اياطع نم نيديفتسلما ءاصحلإ نيودتلاب رمأ نم لوأ )ر( نامثع ةفيللخا ناك يملاسلإا دهعلا في
فنجد أن أ
ول اآلثار عن عمليات التعداد ترجع إىل
1002
فقط وبالتحديد يف بريطانيا. أما يف فرنسا فإن عمليات التعداد
ترجع إىل القرن
11
الذي شهد ميالد أول تسجيالت عقود احلالة املدنية وإجبارية تسجيل عقود االزدياد يف عهد فرنسوا
األول. يف فرنسا دائما جتدر اإلشارة إىل أنه يف ا
لقرن
19
حني أراد
″
كولبريت
″
-
أب اإلدارة الفرنسية
–
أن يدفع ببالده
هترازو تدهش نأ هتازجنم نم ناكو ...ةيوق ةيزكرم ةرادإ سأ ،تقولا كلذ في ايناطيرب هتغلب يذلا يعانصلا ىوتسلما لىإ
(
1230
-
1220
) عددا من عمليات التحقيق الكربى. وشهدت أملانيا وبريطانيا تطورا مشاهبا
باإلضافة إىل د
.ول أخرى
وقد كان
"قرانت"
(
1250
-
1291
GRANT :
) أول من استعمل
يف
1225
مصطلحات علم السكان مثل اخلصوبة
كما قارن بني معدالت والدة اإلناث والذكور. وقد طور هذا العامل مع عامل آخر هو بييت؛ةايلحا ةدم لوطو
(PETTY)
طريقة لتعداد السكان من خالل املعطيات
"طريقة املضاعف" ىعدت )...تايفولا ددع ،نكاسلما ددع نع( ةيوناثلا
(Multiplicateur)
عرفت بعد ذلك حتسينات متتالية على أيدي علماء آخرين منهم خاصة
"البالس"
(LAPLACE)
يف
1902
.
ظهور نظرية االحتماالت في قرن
81
و
81
:
تارخييا ارتبط ظهور نظرية االحتماالت بألعاب احلظ ا
ليت كانت سائد
ة
ةدئاسلا ةينيدلا ءاوجلأاو بتكلا ةعابط راشتنا ةلق نكل .صاخ لكشب كونبلا اهمظنتو رشع عباسلا نرقلا في ابروأ في ةرثكب
اليت ال تبارك هذه األلعاب منعت انتشار
الكتابات يف هذا الشأن
. وي
نسب
البعض أول الكتابات يف علم االحت
ماالت إىل
( "باسكال" لماعلا
1253
-
1225
(PASCAL
"هندسة احلظ" كاذنآ هاسمأ امع بتك يذلا
(La géométrie du
hasard)
. وكان ذلك من خالل
رسائل له مع زميله املعروف هو اآلخر
"فرمات"
(
1201
–
1222
FERMAT :
. )
كم ينبغي من رمية" باعللأا ةاوه دحأ لاكساب ىلع اهحرط تيلا ةلأسلما صاخ لكشب ددصلا اذه في ركذتو
مل
كع ي نرد
حىت ميكن املراهنة بتفاؤل على احلصول على جمموع
15
؟
. مث جاء علماء آخرون كانت هلم إضافات بارزة يف هذه الفرتة"
مثل هاجيان
(HUYGEN :
1259
–
1292
)
جاك برنويل،
(JACQUES BERNOULLI)
،
موافر
(MOIVRE)
وكذا
اليبنيتز
(
1212
–
1912
LEIBNIZ :
). كما ساهم يف ه
ذه الفرتة اليت سبقت القرن
19
علماء كبار أمثال
(
LAPLACE
(GAUSSE, BAYES,
.عرفت نظرية االحتماالت على أيديهم إجنازات كبرية
القرن
81
وذلك لقياس نسبة اخلطأ يف"يعيبطلا عيزوتلا" يهو تلاامتحلاا ةيرظن رصانع مهأ ىدحإ تزرب نرقلا اذه في :
جمال احلسابات الفلكية. كان
هذا من مثرة عمل العاملني البالس وقوس
GAUSSE)
و
(LAPLACE
. يف هذا القرن أيضا
ظهرت حسابات االرتباط لقالتو
(GALTOU)
كما برزت أمساء مثل كتلت
(QUETLET)
وآخرون
.
القرن العشر
و
:ن
أي بصياغة رياضية ناضجة يف شكل قوانني،نلآا اهارن امك تلاامتحلاا ةيرظن
م
ربهن عليه
ا رياضي
إمنا،ا
.تبلورت يف القرن العشرين وبالضبط يف بدايته
و
( من األمساء اليت برزت يف الفرتة األوىل
1900
–
1950
) من هذا القرن
جند من بريطانيا بريسون
(KARLE PEARSON)
و
من روسيا ماركوف
(MARKOV)
و
من فرنسا بوريل
(BOREL)
.
( يف الفرتة الثانية
1951
–
1935
) درست مسائل التوقع
حيث كان لفيشر،
(FISHER)
.دورا بارزا
يف الفرتة املمتدة من
1933
إىل هناية احلرب العاملية الثانية برزت اختبارات الفروض على يد ناميان
(NEYMAN)
وإيقون
بريسون
(EGON PEARSON)
وبداية النظرية احلديثة للمعاينة لناميان
(NEYMAN)
باإلضافة إىل خطط التجارب

- 4 -
لفيشر. بداية
من اخلمسينات تكاثرت الكتابات يف جمال اإلحصاء حيث عرفت نظرية التقدير وحتليل البيانات. وبالتدريج
.انتشر استخدام اإلحصاء يف امليادين املختلفة والعلوم التجريبية واإلنسانية
م
:لخص
تارخييا إذا كانت أوىل استعماالت اإلحصاء ارتبطت حباجة الدولة لتنظيم اجلباية والتجني
د
و
در
اسة السكان فإن
لاجمك ظلحاو ةفدصلا باعلأ لئاسبم رملأا لوأ تطبترا )يضايرلا ءاصحلإا لصأ( تلاامتحلاا باسح في تاساردلا لىوأ
جديد أثار فضول عدد من العلماء الذين أسسوا هذا العلم يف القرن
19
. التطور السريع لعلم االحتماالت كفرع من
الرياضيات كان يف بدابة القرن
50
لكن أهم عناصر اإلحصاء الرياضي كما هو معروف اآلن تبلورت يف النصف األخري
.منه
تعريف
علم ا
إلحصاء
تعريف
مصطفى الخواجة
1
: وهي تلك الطريقة اليت متكن من،ةيئاصحلإا ةقيرطلا ،ءاصحلإا ملعب دصقي" :
،مجع احلقائق عن الظواهر املختلفة يف شكل قياسي
تسجيل بيانات تلك احل
،قائق يف جداول تلخيصية
.عرض بيانات تلك اجلداول بيانيا وحتليلها هبدف معرفة اجتاهات هذه الظواهر والعالقات فيما بينها
أي أن علم اإلحصاء خيتص بالطريقة العملية جلمع وتنظيم وتلخيص وعرض وحتليل البيانات هبدف الوصول إىل نتائج
مقبولة وقرارات على ضوء هذا التحليل. أي
علم استنباط احلقائق من األرقام بأسلوب علمي"هنأ ديدش زايجإب لوقلا نكيم
".وبطريقة علمية
وفرع اإلحصاء الذي يهدف,يليلحتلا ءاصحلإاو يفصولا ءاصحلإا اهمو ينمسق لىإ ءاصحلإا ملع ميسقت نكيمو" ...
فقط إىل وصف وحتليل جمموعة معينة دون الوصول إىل نتائج أو استدالل خاص
باجملموعات األكرب أو األخرى فإن
ه يسمى
باإلحصاء الوصفي
،
أما اإلحصاء التحليلي فيهتم بعمليات التنبؤ والتقدير عن طريق استخدام جزء من اجملموعة للوصول
". ولذلك يعتمد يف جزء كبري منه على نظرية االحتماالت،اهلك ةعوملمجا ىلع هقيبطت نكيم ماع مكح وأ رارق لىإ
تعريف
جال
وطو جياللي
5
اإلحصاء هو علم مجع وترتيب معلومات خاصة بظاهرة معينة وقياس الوقائع كأساس لالستقراء" :
."
تعريف
جون جاك دراوزبيك
3
جمموعة الطرق اليت هتدف إىل" لمشي يذلا ملعلا كلذ هنأب ءاصحلإا لماعلا اذه فرعي :
يت" :ءاصحلإا ملع عوضوم نع لوقيو "... تايطعلما ةلجاعم
رفـعم ،تانايبلا كلت ىلع لوصلحا ةيفيك ةرفعبم رملأا قلع
ة من
".أين يتم جتميعها وبأي شكل يكون ذلك التجميع
تعريف
دومنيك سلفاتور
1
واستخدام املعطيات،ليلتحو ،ضرعو ،عمبج ةقلعتلما ةيضايرلا قرطلا عوممج وه ءاصحلإا " :
الرقمية. هذه العمليات متكن من استخالص استنتاجات و
اختاذ قرارات إزاء حالة عدم التأكد اليت نواجهها يف جمال االقتص
اد
وجمال األعمال أو يف علوم اجتماعية
و
".فيزيائية أخرى
1
، اإلسكندرية،ةيعمالجا رادلا ،ءاصحلإا في ةمدقم :ةجاولخا ىفطصم
5005
ص،
5
.
5
، اإلحصاء مع متارين ومسائل حملولة،ليلايج وطلاج
5005
ديوان املطبوعات اجلامعية،
،
ص
3
.
3
،دروزبيك
.مرجع سابق
1
، دار ماك قراو هيل،موش ةلسلس ،يقيبطتلا ءاصحلإاو يسايقلا داصتقلاا ،روتافلاس كينيمود
1902
ص،
1
.

محاضرات اإلحصاء الرياضي
ب. ص
-
5
-
ويواصل الكاتب
«
منيز بني اإلحصاء الوصفي واإلحصاء االستداليل
(Statistique Inductive)
حيوصل،صخلي لولأا
وحيلل
كما من
أما الثاين في،تايطعلما نم
الكل يسمى يف هذه احلالة اجملتمع (أو،ءزلجا ةسارد للاخ نم لكلا ىلع طقس
العامل
Univers
) واجلزء يسمى العينة. صحة اإلسقاط تتطلب إذا أن تكون العينة ممثلة وأن تكون احتمال اخلطأ حمسوبا
."
فيما خيصنا
ي،
هتم هذا املقياس بدراسة الفرع الثاين من اإلحصاء
املتمثل يف
اإلحص
اء االستداليل
،
وهن
كا
من يسمي هذا
" الفرع من اإلحصاء
اإل
حصاء
ال
."تطبيقي
من املهم ذكر هذه التسميات حىت يعلم الطالب أن بإمكامنه البحث عن مادة
،املقياس يف مراجع حتت هذه العناوين وغريها مثل االقتصاد القياسي
االحتماالت، االحتماالت،يداصتقلاا ءاصحلإا
واملتغريات ال
عشوائية أو ببساطة اإلحصاء
.
االحصاء
التطبيقي
"رجيينالد الفوا" فيرعت
1
:
املسألة األساسية لإلحصاء التطبيقي تتمثل نظريا كما"
نريد دراسة عدد من اخلصائ:يلي
ص
لكن ألسباب خمتلفة ال ميكن أن نشمل بالدراسة كل أفراد اجمل،ام عمتلمج )...يسايسلا هجوتلا ،نزولا ،رمعلاك(
تمع. هلذا
لكك عمتلمجا ىلع ميمعت ىلع لمعن ةنيعلا ةسارد ماتمإ دنعو ،صئاصلخا هذه ةساردل )ةنيع( عمتلمجا نم ءزج ةسارد لىإ أجلن
." لفرض عدم اخلطأ يف هذا التعميم،مييقتلا عم ةدهاشلما قئاقلحا
حوصلة
:
بصفة عامة ومن خالل مجيع التعريفات السابقة ميكن القول أن علم اإل
حصاء يهتم بكيفية مجع
و
ترتيب
و
عرض
البيانات
و
.كذا كيفية حتليلها للخروج خبالصة مفهومة
1
الكيبيك،يقيبطتلا ءاصحلإا ،اوفلا دلانييجر
،
1901
ص،
1,1

محاضرات اإلحصاء الرياضي
ص
.ب
I
-
1
-
الفصل
I
.
تذكير
بال
مفاهيم
األساسية ل
الحتماالت
مفاهيم أساسية
الترميز
األكثر علوا" و اديقعت رثكلأا انهأ ىلع تلاامتحلاا ضعبلا برتعي ايلعلا تاـيـــــــــــــــضاـيرلا مولع ينب نم
"
!!
واحلقيقة،
غري
ذلك. إهنا ال تعدو أن
ت
كون
بة ملن يريدــــــسنلاب
حقا
فهم
ا
عةــــــضب في صخلتت ةيلــــــسم ةبعل
قواعد
بديه
ية
.
اهيــــــضي لاو
بعــــشلا عيجم ىلع اهتــــسارد ةيمتح رــــسفي ام ،نيدايلما عيجم في اهدجاوتو اتهامادختــــسا ددعت لاإ تلاامتحلاا ةطاــــسب
اـــسح مهف نإف يريـــستلاو داـــصتقلاا لماعل ةبـــسنلاب .ابيرقت
ب االحتماالت هو أداة
يومية
اكل اـــشلما ةلجاعلم
ملطروحة واختاذ
تبىن يف،تيبلا بر تىحو لب ،يرسلما تارارقف .رارقلا
99
%
من احلاالت على
معلومات
.غري مؤكدة
المبحث
1
.
مفاهيم أساسية
الحدث واالحتمال،ةبرجتلا موـهفم
خصائص االحتمال
القواعد األساسية في حساب االحتمال
تعريف باسكال
لالحتمال
8
مفهوم التج
الحدث واالحتمال،ةبر
Epreuve, événement, probabilité
(أ
)
االحتمال
و الحدث
Evénement et probabilité
كثريا ما خيلط الطلبة بني هذين املفهومني
الرتباطهما ببعض
.
فاحلدث العشوائي هو
واقعة أو نتيجة م
ا
أما،
االحتمال
ف
هو
عدد
فر والواحدـصلا ينب
يعرب
( عن حظوظ وقوع احلدث
لي شرطا أن يكون زمن
وقوع احلدث
ف،لبقتسلما وه
قد يكون
رــضالحا وأ يــضالما
.)
ابقـــسلا يقارعلا يئرلا لئــس
-
قبل حرب اخلليج األوىل
-
ما هو احتمال اهنزامكم يف هذه احل
؟ رب
ةــيناــكمإ ىدــم ىلع قيقد لــكـــــــــــــــشب يربعتلا في بــغرن اــمدــنع ."نويلم لىإ دــحاو" :باــجأــف
ادةــع اــننإــف ينعم ثدــح عوقو
:لـثم تاراـبع لـمعتـــــــــــــــسن
100
%
د أوـكؤلما ثدـحلل
20
%
للحدث احملتمل و
1
‰
إذن،دعبتـــــــــــــــسلما ثدحلل لاثم
حنن
نستخدم الكسور يف سلم تصاعدي من
0
إىل
1
حبيث يرمز،
0
لالستحالة و
1
.للتأكد
مثال
ورة عند رمي قطعة نقدية هوــــص ىلع لوــــصلحا لامتحا .
1
/
5
و احتمال احل،
" ول على الوجهـــــص
2
عند رمي"
حجر
نرد هو
1
/
2
.
.. فهي عمليات على،داتحلاا و عطاقتلا تايلمع امأ ةمــسقلا و ءادجلل عــضتخ نأ نكيم و اهحرط وأ دادعلأا عجم نكيم
.ح أن نكتب احتمال تقاطع (أو احتاد) احتمالـــــــــــــــصي لا كلذ لجأ نم .دادـعلأا ىلع تـــــــــــــــسيل و تاـعوملمجا
متثل هذه
القاعدة ا
.لذهبية األوىل يف االحتماالت ويف هذا املقياس ككل
ال واإلمكانيةـمتحلاا ينب زييمتلا بـيجو
)(اإلمكانية هي حدث
. فاالحتمال
يف مفهوم العلم
هو عدد يقي حظ
وظ وقوع
ميه نتيجة أو حدثـــــــــــسن ام ءيـــــــــــش
أو إمكانية
.. أما اإلمكانية فهي حدث أو نتيجة ما من بني أحداث أو نتائج أخرى
خي
تلف عن هذا املفهوم العلمي تعريف الناس لالحتمال. ف
كثريا ما تطلق كلمة االحتمال و يقصد هبا إمكانية
،
فيقال
مثال

الفصل األول
المفاهيم األساسية لالحتمال
- 2 -
" أو يقال"ةدراو ةيناكمإ هذه نإ حيحصلا و "نكمم لامتحا اذه نإ"
إذا رمينا حجر نرد هناك
2
و الصحيح"تلاامتحإ
"
هناك
2
إمكانيات أو
2
نتائج حمتملة
"
... ،
(
ب
)
التجربة
Epreuve
رح املفهوم اجملرد للتجربة و متييزها عن احلدثـــــــشل
ميكن القول أن
التجربة هي أم احلدث
أو
أم
.النتيجة
أل
ن التجربة تتفرع
.رورة إىل أحداثـــــــضلاب
ففي
ابقةـــــــسلا ةلوقلما
التجربة هي احلرب،
بينما
اهلزمية هي نتيجة
ممكنة
للحرب
.و
التجربة
قد
تقبل
نتيجتني أو أكث
.ر
ومفهوم التجربة يف علم االحتماالت مفهوم عام و مرن
،
فإذا كنا ندرس احتمال احلصول على الوجه
2
عند رمي قطعة نرد
دات التالفة آللة ما ميكن اعتبار كل وحدة منتجةـحولا نم ينعم ددـع لاـمتحا سردـن اـنك اذإ و ،يمرلا يه ةـبرجتلا نوكت
وإذا كنا ندرس احتمال عدد معني م،ةبرجتك
...بني يف مقياس ما نعترب كل طالب كتجربةـــــــــــــسارلا ةبلطلا ن
ن
قول احتمال
.حدث أو احتمال نتيجة وال نقول إحتمال جتربة
2
خصائص اإلحتمال
:عادة ما نعرب عن هذه اخلصائص بالطريقة التالية
االحتمال هو عدد موجب متاما أو معدوم
)(ال يكون سالبا
.
جمموع احتماالت أحداث جتربة ما ي
.ساوي الواحد
وميكن إضافة خاصية ثالثة تستنتج بديهيا من اخلاصيتني السالفتني
و
هي أن االحتمال يك
ون حمصورا بني
0
و
1
. أي أنه ال ميكن أن يكون سالبا
و
.ال أن يكون أكرب من الواحد
3
األركان الخمسة
في
حساب
االحتماالت
هناك
مخ
قواعد أساسية يف حساب االحتمال نذكرها اآلن با
قتضاب إلبراز أمهيتها ونعود لشرحها ف
ما بعد
وسنحتاج
إىل استخدام هذه القواعد يف مجيع فصول املقياس
.
1
.
احتمال وقوع حدث يساوي
1
مطروحا منه احتمال احلدث املعاك . جمموع احتمال احلدث واحتمال احلدث
املعاك يساوي
1
.
5
.
يساوي احتمال وقوع األول م"ب" و "أ" ناثدح عوقو لامتحا
ضروبا يف احتمال وقوع الثاين ملا يكون األول قد
.وقع فعال
3
.
احتمال
وقوع حدثان مستقالن يساوي جداء االحتمالني أي احتمال احلدث األول مضروبا يف احتمال احلدث
.الثاين
1
.
. ونقول أن احلدثان متنافيان،رفصلا يواسي هسكعو ثدلحا عوقو لامتحا
2
.
يساوي مج"ب" وأ "ا" ثدح عوقو لامتحا
.ع احتمايل احلدثني مطروحا منه احتمال حتققهما معا
4
القاعدة ال
سادسة
أو
حساب االحتمال حسب
تعريف باسكال لالحتمال
عرف
بليز باسكال
(Blaise Pascal :
1253
)
االحتمال
:بالشكل التايل

محاضرات اإلحصاء الرياضي
ص
.ب
I
-
3
-
إذ،ةنكملما تلاالحا ددع ىلع اموسقم ثدلحا عوقول ةمئلالما تلاالحا ددع وه ثدح لامتحا"
ا
".اقرتضنا أن كل احلاالت هلا نف االحتمال يف الوقوع
1
:مثال
ما
؟ هو احتمال احلصول على عدد زوجي عند رمي قطعة نرد
. احلدث واالحتمال يف هذا املثال،ةبرجتلا نم لك ينب
( هناك ثالث حاالت مالئمة للحصول على عدد زوجي:باولجا
5
،
1
و
2
). أما العدد الكلي للحاالت املمكنة
فهو
2
:
(
1
،
5
،
3
،
1
،
2
،
2
.)
وبافتراض أن كل الحاالت الممكنة لها نفس االحتمال
فإن احتمال احلصول على عدد زوجي
هو
=
.
.، ال ميكن استخدام هذه العالقة إذا مل تكن احتماالت احلاالت متساوية:هيبنت
مثال
2
. صندوق به
9
كريات منها
2
محراء. نسحب
3
كريات معا. ما هو احتما
ل أن تكون كلها محراء
بني كل من؟
التجربة
و
.احلدث يف هذا املثال
عدد احلاالت املالئمة
:وعدد احلاالت املمكنة
. إذا االحتمال هو
.
التجربة هي السحب من
... احلدث أو النتيجة هي احلصول على،قودنصلا
مثال
3
. فوج مكون من
10
طلبة. نسحب بالقرعة
اسم
من العشرة. ما هو
؟احتمال أن يكون الطالب أمحد
بني كل من
التجربة
و
.احلدث
نسحب (بدون إعادة) عينة من
3
؟أمساء من العشرة. ما هو احتمال أن يكون منهم الطالب أمحد
:اجلواب
1
)ا
حتمال
احلدث األول أو النتيجة األوىل هي
،
5
:) عدد الطرق املمكنة للعينة
عدد احلاالت املالئمة لكي يكون،
:أمحد يف العينة
:االحتمال هو إذا
... ، النتيجة أو احلدث هي أن يكون الطالب أمحد،بحسلا يه ةبرجتلا
مثال
4
. يتناف أمحد مع
3
زمالئه على أعلى نقطة يف كل من االمتحانات الستة للسداسي. إذا كانت حظوظ الطلبة
أن يفوز أمحد بأعلى نقطة:لامتحا وه ام ،ةيواستم ةعبرلأا
) أن يفوز أحد الطلبة (أيا كان؟ةتسلا تاناحتملاا نم لك في
؟بأعلى نقطة يف االمتحانات الستة
:اجلواب
1
) هناك
1092
=
1
2
إذا االحتمال هو؛ يياقلما عيمبج دحمأ زوف ةلاح اهنم ،ةسفانلما جئاتنل ةنكمم ةلاح
1/1092
.
5
)
هناك
1
طلبة إذا هناك
1
حاالت لفوز أحد الطلبة جبمي
إذا االحتمال هو، يياقلما ع
1/1092
.
5
خالصة
االحتمال هو عدد ال يزيد عن
1
و ال يقل عن
0
.
1
رجيينالد الفوا
1901
ص،
5
و
3
.
6
3
2
1
3
5
C
3
7
C
35
10
3
7
3
5
C
C
10
1
3
10
C
36
!
)!
(
!
2
9
2
9
1
3
1
10
C
x
x
n
n
C
C
C
x
n
20
3
240
36
3
/
)
8
)(
9
(
10
36
3
10
2
9
C
C

الفصل األول
المفاهيم األساسية لالحتمال
- 4 -
التجربة واحلدث واالحتمال هي مفاهيم ال جيب اخللط بينها. التجربة يتولد عنها أحداث (نتائج أو حاالت) خمتلفة. التجربة
مفهوم مرن يتطلب أحيانا نظرة
ذكية
وخيال
. من املهم اكتساب
هذه املهارة يف حتديد ما هي التجربة أو التجارب يف م
سألة
ما ألن ذلك هو املفتاح لفهم و حل املسألة
.
هناك مخ قواعد يف حساب االحتمال
هي األركان األساسية لعلم االحتماالت. هذه القواعد متعلقة
:ب
ا
حتمال ا
حلدث
املعاك
،
،باحتمال حتقق حدثني معا
باحتمال حتقق حدثني م
،عا إذا كانا مستقالن
،باحتمال حتقق أحد حدثني
.و متعلقة باحتمال حتقق احلدث و عكسه معا
المبحث
2
.
الترميز أو التعبير الرياضي عن االحتماالت
الطبيعة هي كتاب"
لغته
جاليلي"تايضايرلا
(
1221
-
1215
)
استخدام نضرية المجموعات
التعبير الرياضي عن قواعد
جمع
و
ضرب االحتماالت
نظري
ة بايز
نستخدم الرتميز من أجل التوصل إىل تعبري دقيق و واضح لقواعد احلساب االحتمايل وهي ذاهتا القواعد األربعة املذكورة يف
.اجلزء األول
نعرب عن احتمال حدث ما بطريقة رياضية فنكتب
P(A)
ونعرب عن احتمال وقوع احلدث
:
X = x
:كما يلي
P(X = x)
أو
P(x)
.
اح:لاثم
احلصول على الوجه" :ثدلحا لامت
2
: عند إلقاء حجر نرد يكتب"
1/2
=
P(X =
2
)
: أو باختصار،
1/2
( =
P(
2
:و أحيانا خنتصر أكثر فنكتب
1/2
=
P
.
8
استخدام ن
ظ
رية المجموعات للتعبير عن األحداث العشوائية
من خالل البنود التالية تستخدم نظرية اجملموعات للتعبري عن األحداث ال
:عشوائية
1
.
نعرب عن النتائج املمكنة لتجربة ما ب
Ω
،
و
.تسمى اجملموعة الكلية أو فضاء العينة
5
.
نعرب عن احلدث مبجوعة جزئية
A
حيث،ةنيعلا ءاضف نم
A
.هي جمموعة من النتائج املمكنة للتجربة
3
.
إذا انتهت التجربة بنتيجة متثل عنصرا من
A
نقول أن احلدث
A
.قد حتقق
1
.
احلدث الذي حيت
وي على نقطة أو عنصر واحد من
Ω
.يسمى عادة حدث بسيط
مثال
.
:لتكن جلينا جتربة هي إلقاء مكعب نرد. أكتب جمموعة فضاء العينة مث عرب عمليا عن األحداث التالية
احلدث
A
احلصول على العدد:
2
)(حدث بسيط
{
2
}
, A=
{
1
,
5
,
3
,
1
,
2
,
2
= }
Ω
محاضرات اإلحصاء الرياضي
ص
.ب
I
-
5
-
احلدث
B
احلصول ع:
{ لى عدد زوجي
5
,
1
,
2
}
=
B
احلدث
C
احلصول على عدد أويل:
{
5
,
3
,
2
}
=
C
احلدث
D
احلصول على عدد فردي:
{
1
,
3
,
2
}
=
D
مثال
2
أكتب جمم:لياوتلا ىلع ينتيدقن ينتعطق يمر يه ةبرتج انيدل نكتل :
وعة فضاء العينة مث عرب عن
:
احلدث
A
) احلصول على مرتني كتابة (حدث بسيط:
{
PP
}
, A =
{
PP, PF, FP, FF
=}
Ω
احلدث
B
{ احلصول على كتابة مرة واحدة:
FP, PF
}
B =
احلدث
C
احلصول على كتابة يف الرمية األوىل:
{
PF, PP
}
=
C
2
.
احلدث،تناك ايأ ام ةبرتج في ةنكملما ثادحلأا ينب نم
Φ
ميثل احلدث املستحيل ألنه ال ميكن أن يتحقق
.عنصر منها
P(Φ) =
0
.
2
.
حدث اجملموعة األساسية،تناك ايأ ام ةبرتج في ةنكملما ثادحلأا ينب نم
Ω
وهو احلدث األكيد ألنه،اهسفن
.البد أن يتحقق أحد عناصرها على األقل
P(Ω) =
1
9
.
اجلمع،حرطلا ،عطاقتلاو داتحلإا لثم تايلمع قيبطتب
.... على اجملموعات حنصل على جمموعات جديدة جزئية
من
Ω
ومن مث أحداث جديدة يف
Ω
: . من ذلك
AUB
إما:ثدلحا وه
A
أو
B
.أو كالمها
A∩B
:هو احلدث
A
و
B
.يف وقت معا
A
C
هو احلدث املعاك ل
A
.
B
–
A
هو احلد
:ث
A
لكن لي
B
.
0
.
إذا كان
Φ
=
A∩B
نقول أن
A
و
B
متنافيان (أو غري متالئمان) أي ال ميكن وقوعهما معا
(
mutuellement exclusifs
.)
إذ كان:ينترم ةيدقن ةعطق يمرن :لاثم
A
"مرتني كتابة" ثدلحا وه
و
B
"صورة على األقل"
.
A = {PP}. B = {PF, FP, FF}
A∩B
=
Φ
2
التعبير الرياضي عن
قواعد
حساب
االحتماالت
(أ
)
الحدث المعاكس
أو التعبير الرياضي عن القاعدة رقم
8
.
Evénement contraire
نعرب عن احلدث املعاك ل
A
ب
Ā
أو
A'
و
احتماله هو احتمال عدم حتقق احلدث
A
،
: ونكتب
P(Ā) + P(A) =
8
<=> P(Ā) =
8
– P(A)
نرمي ق:لاثم
طعة نقدية
و
نرمز ب
P
للكتابة
و
F
:للصورة (الوجه). نالحظ أن
P(P) = P(F') =
1
– P(F) <=> P(P) + P(F) =
1
A
Ā
Ω

الفصل األول
المفاهيم األساسية لالحتمال
- 6 -
مثال
5
عند رمي حجر نرد فإن احتمال احلصول على العدد:
2
:هو
P(
2
) =
1/2
فما هو احلدث املعاك يف هذه،
؟احلالة وما احتماله
احلدث املعاك هو احلصول على عدد غري
2
،
و
:احتماله هو
P(
2
') =
1
– P(
2
) =
1
– (
1/2
) =
2/2
.
مثال
3
ماهو احلدث املعاك،يجوز ددع ىلع لوصلحا لامتحا وه ام ،درن رجح يمرن :
و
؟ما هو احتماله
P(nombre pair) = P(
5
ou
1
ou
2
) =
3/2
،احلدث املعاك هو احلصول على عدد غري زوجي
و
:احتماله
P(impair) =
1
– P(pair) =
1
– (
3/2
) =
3/2
.
(
ب
)
" احتمال وقوع الحدث
A
" و"
B
"
أيا كانت
(
قاعدة
رقم
2
.)
P(A∩B) = P(A)* P(B/A)
P(A∩B∩C) = P(A)* P(B/A)* P(C/(A∩B))
A, B, C
أحداث ما
) متنافية أو ال،لا وأ ةلقتسم(
،
(
A
/
B
)
P
ي
سمى االحتمال الشرطي ل
B
علما أن
A
حم
قق
.
:ومن املعادلة األوىل حنصل على
لما
0
<
(
A
)
P
(
A
)
P
( /
A∩B
)
P
( =
A
/
B
)
P
حيث
A
تصبح فضاء املعاينة مبا أن
A
.حمقق
:مثال
1
) أحسب عند إلقاء حجر نرد احتمال احلصول على قيم أقل من
1
(حدث
B
.)
5
) أحسب ا
حتمال احلصول على نتيجة أقل من
1
إذا علمت أن الوجه احملصل ملكعب النرد عدد فردي
)
حدث
(A
.
3
) أحسب احتمال احلصول على قيمة أكرب أو يساوي
1
.إذا علمت أن النتيجة عدد فردي
P(B) = P(
1
ou
5
ou
3
) = P(
1
) + P(
5
) + P(
3
) =
3/2
P(B/A) = P(B∩A)/P(A)
P(B∩A) = P (impaire et ≤
1) = P(
1
ou
3
) = P(
1
) + P(
3
) =
1/2
+
1/2
=
5/2
P(B/A) = P(B∩A)/P(A) =
5/2
/
3/2
=
5/3
(
ج
)
" احتمال وقوع الحدث
A
" و"
B
" لما"
A
" و"
B
( مستقالن"
قاعدة
رقم
3
.)
P(A∩B) = P(A) * P(B) (P(B/A) = P(B))
وهو تعريف استقالل حدثني
،
أي أن وقوع
B
ال
يتأثر بوقوع
A
أو عدم وقوعه نقول أن
A
و
B
،مستقالن
P(A∩B∩C) = P(A) * P(B) * P(C) P(C/(A∩B)) = P(C)
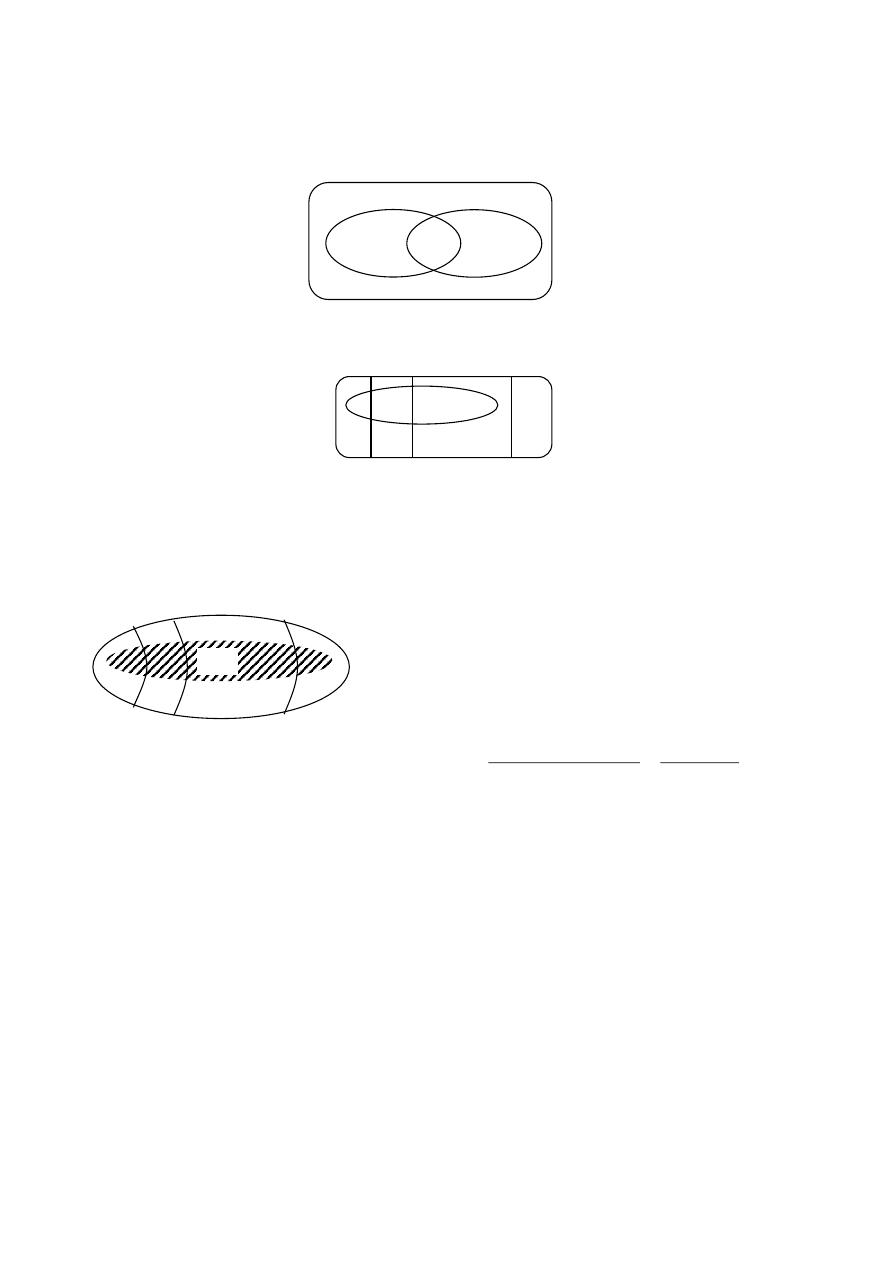
A\B A
∩
B B\A
A
B
Ω
رسم
8
الحدث
B/A
غير الحدث
B\A
محاضرات اإلحصاء الرياضي
ص
.ب
I
-
7
-
:مثال
نرمي حجر نرد وقطعة نقدية معا. ما هو احتمال احلصول على الصورة
و
العدد
2
(نتيجة مكعب النرد مستقلة؟
.)عن نتيجة القطعة النقدية
P(A∩B) = P(A).P(B) =
0,2
*
1/2
=
1/15
.
مثال
2
. نلقي قطعة نقدية مرتني. أحسب احتمال احلصول على صورة يف الرمية األوىل
و
.يف الرمية الثانية
P(FF) = P(A∩B) = P(A) P(B) =
0,2
*
0,2
=
0,52
مثال
3
. صندوق به
2
كريات
5
محراء
و
3
بيضاء. نسحب كرية نسجل لوهنا مث نعيدها للصن
دوق
و
نكرر العملية
3
.مرات
o
أحسب احتمال احلصول على
5
،كريات محراء
3
.)كريات محراء (أحداث مستقلة
o
؟)كيف يكون االحتمال يف حالة كون السحب بدون إرجاع الكرية (أحداث غري مستقلة
0/52
=
5/2
*
5/2
) =
5
) P(R
1
) = P(R
5
R
∩
1
P(RR) = P(R
0/152
=
5/2
*
5/2
*
5/2
) =
3
) P(R
5
) P(R
1
) = P(R
3
R
∩
5
R
∩
1
P(RRR) = P(R
5/50
=
1/1
*
5/2
) =
1
/R
5
) P(R
1
) = P(R
5
R
∩
1
P(RR) = P(R
0
=
0
*
1/1
*
5/2
)) =
5
∩R
1
/(R
3
) P(R
1
/R
5
) P(R
1
) = P(R
3
R
∩
5
R
∩
1
P(RRR) = P(R
(د
)
" احتمال وقوع حدث
A
" أو"
B
(القاعدة رقم"
4
.)
P(AUB) = P(A) + P(B) – P(A∩B)
(
ه
)
احتمال وقو
"ب" وأ "أ" ثدح ع
( متنافيان"ب" و "أ" امل
القاعدة رقم
5
.)
لتكن األحداث امل
تنافية
A, B
P(AUB) = P(A) + P(B) (P(A∩B) =
0
)
P(AUBUC) = P(A) + P(B) + P(C) (P(A∩B∩C) =
0
)
(و
)
قواعد إضافية مهمة
من أجل
5
A
⊂
1
A
:فإن
)
5
P(A
≤
)
1
P(A
و
–
)
5
) = P(A
1
A
–
5
P(A
)
1
P(A
A
∩B
A
B
Ω
A
Ā
Ω
A
1
A
2
Ω
الفصل األول
المفاهيم األساسية لالحتمال
- 8 -
من أجل
A
و
B
:أحداث أيا كانت
P(A∩B) + P(A∩B’) = P(A)
إذا كان
A
:هو نتيجة أحد أو بعض األحداث املتنافية
n
A
……
,
1
, A
3
, A
5
, A
1
A
)
n
A
+ P(A∩
…….
+
)
3
) + P(A∩A
5
) + P(A∩A
1
P(A) = P(A∩ A
3
نظرية اال
حتمال السببي أو نظرية بايز
Théorème ou règle de BAYES
لتكن
1
A
،
5
A
،
3
A
،
.
.
.
k
A
،
.
.
.،
n
A
أحداث متنافية فيما بينها حيث احتادها يشكل اجملموعة الكلية
)(األساسية
Ω
و،
A
حدث ما يتحقق عن طريق واحد أو أكثر من األحداث
k
A
إذا علمنا أن،
A
حنسب،ققتح
احتمال حتققه عن طريق احلدث
k
A
:كما يلي
تسمى هذه النظرية نظرية االحتمال السب ي ألهنا متكن من حساب احتمال أن يكون حدث ما
)
k
(A
هو املسبب لوقوع
( حدث آخر
A
.)
مثال
و:
ظ
فت أمينة
مكتب
(
1
A
) مبكتب للمحاسبة حيث تولت
طبع
50
%
من ال
فواتري. يشغل
( املكتب عاملتني أخريني إحدامها
5
A
) تطبع
30
%
من الفواتري
و
( األخرى
3
A
)
20
%
. ترتكب املوظفة اجلديدة أخطاء
يف
2
%
( بينما نسبة اخلطأ لدى الثانية،يرتاوفلا نم
5
A
)
5
%
و
( لدى الثالثة
3
A
)
1
%
.
أخذت فاتورة بشكل عشوائي فتبني أن هبا أخطاء. استبعدت األوىل أن
تكون هي من أجنزت الفاتورة حبجة أهنا ال
تنجز
إال
50
%
،من الفواتري
و
(ردت عليها العامالت األخريات بأن نسبة األخطاء لديها هي األكرب
2
%
.)
1
( . أحسب احتمال أن تكون املوظفة اجلديدة
1
A
) هي اليت حررت الفاتورة
و
قارن مع احتمال أن يكون
مصدر اخلطأ هو
5
A
أو
3
A
.
5
. أحسب
.جمموع االحتماالت الثالث
)
(
)
(
)
/
(
)
(
)
/
(
)
(
)
/
(
1
A
P
A
A
P
A
A
P
A
P
A
A
P
A
P
A
A
P
k
n
k
k
k
k
k
k
A
1
A
2
A
k
. . . A
n
A
Ω
رسم
2
رسم يوضح نظرية بايز
A
1
A
2
A
k
. . . A
n
A
Ω
A∩B’ A
∩B
B
∩B
’
A
B
Ω

محاضرات اإلحصاء الرياضي
ص
.ب
I
-
9
-
3
. أن تكون هبا أخطاء،تلاسارلما عوممج نم ابئاوشع ةراتمخ ةروتاف نوكت نأ لامتحا بسحأ .
يظهر من احلساب أن االحتمال األكرب هو أن تكون
3
A
.هي اليت حررت الفاتورة
5
.
جمموع االحتماالت
1
/A) =
3
/A) + P(A
5
/A) + P(A
1
P(A
ألهنا متثل احتماالت األ
حداث املتنافية
.الثالث
3
:. احتمال وجود خطأ يف مراسلة ما
4
خالصة
باستخدام نظرية اجملموعات كأساس للرتميز يف جمال االحتماالت ميكن احلصول على صياغة أكثر دقة للمفاهيم
:املختلفة. هبذه الطريقة نستخدم
رمز التقاطع
∩
( "و" ةرابع نع لادب
et
الوجه" لامتحا :لاثم )
5
و
2
: يف رمييت نرد"
P(
5
) * P(
2
)
=
(
"
2
"
∩
P("
5
"
رمز اإلحتاد
U
" " أو"ةرابع نع لادب
ou
احتمال الوجه:لاثم "
5
أو
2
يف رمية نرد
P("
2
"U"
5
") = P(
2
) +
P(
5
)
رمز املتمم
A
C
أو
Ā
عك" ةرابع نع لادب
A
؛"
A)
P(
–
1
Ā) =
P(
من خالل هذا الرتميز ميكن أن نعرب بسهولة ع
.ن القواعد اخلمسة األساسية حلساب االحتماالت
- P(A∩B) = P(A)* P(B/A)
)
بشرط
0
( <
A
)
P
(
(
A
)
P
( /
A∩B
)
P
( =
A
/
B
)
=> P
عندما يكون احلدثان مستقالن
- P(A∩B) = P(A)* P(B)
- P(AUB) = P(A) + P(B) – P(A∩B)
عن
: دما يكون احلدثان متنافيان أي
- P(AUB) = P(A) + P(B) (P(A∩B) = 1)
.مسألة
نسمي،ينترم ةيدقن ةعطق يمرن
A
"
"مرتني كتابة
و
B
: عرب عن احلدث،"لىولأا ةرلما في ةباتك"
A
،
B
،
Ā
،
A∩B
،
AUB
،
B
–
A
،
B – A
A = {PP}, B = {PP, FP}, Ā = {PF, FP, FF},
A∩B = {PP}, AUB = {PP, FP}, A – B = Φ, B – A= {FP}
476
.
0
01
.
0
*
5
.
0
02
.
0
*
3
.
0
05
.
0
*
2
.
0
01
.
0
*
5
.
0
)
/
(
)
(
)
/
(
)
(
)
/
(
2857
.
0
01
.
0
*
5
.
0
02
.
0
*
3
.
0
05
.
0
*
2
.
0
02
.
0
*
3
.
0
)
/
(
)
(
)
/
(
)
(
)
/
(
238
.
0
01
.
0
*
5
.
0
02
.
0
*
3
.
0
05
.
0
*
2
.
0
05
.
0
*
2
.
0
)
/
(
)
(
)
/
(
)
(
)
/
(
3
1
3
3
3
3
1
2
2
2
3
1
1
1
1
k
k
k
k
k
k
k
k
k
A
A
P
A
P
A
A
P
A
P
A
A
P
A
A
P
A
P
A
A
P
A
P
A
A
P
A
A
P
A
P
A
A
P
A
P
A
A
P
012
.
0
01
.
0
*
5
.
0
02
.
0
*
3
.
0
005
.
0
*
2
.
0
)
/
(
)
(
)
(
k
k
A
A
P
A
P
A
P
الفصل األول
المفاهيم األساسية لالحتمال
- 11 -
5
ملحق
(أ
)
التعبير الهندسي عن االحتماالت
قبل
الشروع يف
حل
م
سألة مركبة لالحتماالت يستحسن حتليلها ب
استعمال أشكال هندسية
توضح عناصر ا
)ملسألة (األحداث
والعالقات بينها. يستخدم هلذا الغرض شجرة
.االحتمال (أنظر امللحق) وخمطط فني
ت
بني شجرة االحتمال األحد
اث املتنافية
ثادحلأا ليثمتل مدختسيف ينف ططمخ امأ ،لصأ نم عرفتت ناصغأ للاخ نم كلذو ةرركلما وأ ةدحاولا ةبرجتلا نع جتنت تيلا
.الفرعية دوائر داخل مستطيل ميثل التجربة
يراعى يف رسم الشجرة أن يكون جم
موع احتماالت كل تفريعة يساوي الواحد. التفريعة هي مبثابة شجرة فرعية حتتوي أحداث
. لكوهنا متثل النتائج احملتملة لتجربة جزئية،ةيفانتم
.مثال. نرمي قطعة نقدية مرتني
.أحسب احتمال احلصول على مرتني صورة
P(face ∩ face) = P(face) * P(face/face) =
0,2
*
0,2
=
0,52
.
A
رسم
1
مخطط فين
صورة
P(face/face) = 5.0
صورة
P(face) = 5.0
كتابة
P(pile) = 5.0
كتابة
P(pile/face) = 5.0
صورة
P(face/pile) = 5.0
كتابة
P(pile/pile) = 5.0
P(FF) = P(F) P(F/F)
P(FP) = P(F) P(P/F)
P(PF) = P(P) P(F/p)
P(PP) = P(P) P(P/P)

محاضرات اإلحصاء الرياضي
ص
.ب
I
-
11
-
(
ب
)
في
مفهوم الحدث العشوائي
جيب املالحظة أن كلمة
حدث
بل املقصود أننا نتحدث عن حدث،نوناق يلأ عضيخ لا ثدلحا نأ نيعت لا يئاوشع
ال
نعلم مسبقا ما إذا كان سيقع أو ال
يقع. اهلزمية اليت وقعت يف احلرب وأي هزمية كانت هلا أسباهبا وليست حم
ض مصادفة

الفصل األول
المفاهيم األساسية لالحتمال
- 12 -
عمياء. واحلقيقة أن ال شيء يف الطبيعة يقع باملصادفة. فال معىن لكلمة مصادفة إال أننا مل نقصد وقوع الشيء. فعندما
نينأ اهنم ةاقلالما هذه لىإ تدأ بابسأ كانه نكل .هتلباقلم ططخأ لمو دصقأ لم نينأ نيعي اذهف ،ةفدص نلافب تيقتلا لوقأ
... سلكت طريقا معينا
كذل
ك
إذا رمينا مكعب نرد
2
مرات
فإننا ال نعلم إذا كنا س
( نحصل على مرة واحدة الوجه
2
.)
لذلك قيمة
P(X)
(مثال
1/2
=
(
2
)
P
) هي قيمة نظرية
لكن،
( إذا رمينا مكعب عدد كبري جدا من املرات
1000
مرة
( مثال) فنتوقع أن عدد مرات احلصول على الوجه
2
) سيكون قريبا جدا من العدد
1000
/
2
.
موضوع علم االحتماالت
."هندسة احلظ" مسا هيلع قلطأ كلذلو ،ةيئاوشعلا ثادحلأا ينناوق في ثحبلا وه
(
ج
)
في
حساب عدد الحاالت الممكنة أو المالئمة
باإلضافة إىل التوفيقات والرتتيبات واألس
،
حنتاج أحيانا حلساب عدد الطرق املمكنة أو املالئمة إىل مفهوم
surjection
.
surj (n, k) = k [surj (n-
1
, k) + surj (n-
1
, k-
1
)] , (n, k >
0
),
Surj (n,
1
) =
1
, Surj (
1
,
1
) =
1
, surj (
1
, k >
1
) =
0
:مثال
( يف املثال
1
) أحسب
:احتمال أن يفوز كل طالب على األقل مبقياس واحد
: عدد احلاالت املالئمة هو
Surj (
2
,
1
) =
1
[surj (
2
,
1
) + surj (
2
,
3
)]
:حلساب ذلك حنتاج إىل حساب سلسلة من القيم
Surj (
2
,
3
) =
3
[surj (
1
,
1
) + surj (
1
,
5
)], mais: Surj (
1
,
5
) =
5
[surj (
3
,
5
) + surj (
3
,
1
)] ,
mais: Surj (
3
,
5
) =
5
[surj (
5
,
5
) + surj (
5
,
1
)],
mais : Surj (
5
,
5
) =
5
[surj (
1
,
5
) + surj (
1
,
1
)] =
5
(
0+1
) =
5
=> Surj (
3
,
5
) =
5
(
5+1
) =
2
, …
2
2
1
3
5
n
k
0
0
0
0
5
5
0
0
0
2
2
3
0
0
51
32
11
1
0
150
510
120
30
2
950
1000
8550
210
25
2
االحتمال هو إذا
1220/1092
.

محاضرات اإلحصاء الرياضي
ص
.ب
- 1 - II
الفصل
II
.
المتغير
ة
العشوائية
مفهوم المتغيرة العشوائية
المتقطعة
مفهوم المتغيرة العشوائية
المست
مرة و توزيعها االحتمالي
املبحث
1
.
مفهوم المتغيرة العشوائية المتقطعة
و
توزيعها االحتمالي
1
مفهوم المتغيرة العشوائية
مفهوم المتغيرة العشوائية المتقطعة
التوزيع االحتمالي للم
تغيرة العشوائية المتقطعة
شروط دالة الكثافة للم
تغيرة العشوائية المتقطعة
التمثيل البياني لدالة الك
ثافة للم
تغيرة العشوائية المتقطعة
دالة التوزيع للم
تغيرة العشوائية المتقطعة
:مسألة
أجري
ت
ة علىــسارد
1000
نوات الثالث األوىلــسلا للاخ بيــصأ لفط
من عمره
مبرض
ما
.
( بينت الدراسة أن احتمال اإلصابة مرتبط بالزمن
X
السنة:
:) من خالل دالة الكثافة التالية
أحسب احتمال
أن تكون إصابة طفل خمتار عشوائيا من العينة املدروسة
يف
السنة األوىل
.
شهر، شهرةدلم ضرلما لجاعي
و
أو،فصن
3
:أشهر حسب اجلدول التايل
X
األشهر
1
1,2
3
االحتمال
0,2
0,3
0,5
أحسب احتمال أن تكون مدة عالج طفل من العينة شهر
و
.نصف على األكثر
8
مفهوم المتغيرة العشوائ
ية
هي
قيمة
متغرية يلحق بقيمها احتماالت حتقق
.كل قيمة
يرمز للمتغرية ع حبرف التيين كبري. ومنيز بني م ع
املتقطعة
و
م
.العشوائبة املتصلة أو املستمرة
: مثال
يف جتربة إلقاء مكعب نرد ميكن أن نسمي الوجه الذي يستقر عليه الكعب متغرية عشوائية
X
. القيم املمكنة
ل
X
:هي
1
،
5
،
3
،
1
،
2
،
2
.
وهو هنا،اهققتح لامتحا قحلن نأ نكيم ةميق لكب
1/2
: . ونكتب مثال
,…
P(X =
1
) = f(
1
) =
1/2
, P(X =
5
) = f(
5
) =
1/2
الحظ أن القيم املمكنة ل
X
(
1
،
5
،
3
،
1
،
2
،
2
،) هي متنافية
و
لذلك فإن جمموع احتماالهتا
يساوي
1
.
مثال
2
.
يف جتربة إلقاء قطعة ن
قدية مرتني ميكن أن نعني املتغرية العشوائية
X
.اليت متثل عدد مرات احلصول على كتابة
يف هذه احلالة القيم املمكنة ل
X
هي
0
،
1
،
5
. ال حظ أنه ميكن تعيني متغريات عشوائية أخرى انطالقا منن نف
1
:يف الربنامج األصلي
1
-
.مفهوم املتغرية العشوائية. اخرتنا هذا التقسيم لكي يتناسب كل جزء مع الزمن املخصص للمحاضرة
sinon
0
3
0
²,
)
(
x
cx
x
f
6
1
1
)
(
x
x
X
P

الفصل الثاني
المتغيرة العشوائية
- 2 -II
مثال،ةبرجتلا
Y
وهي متغرية تأخد القيم،ةروص ىلع لوصلحا تارم ددع
0
،
1
،
5
،
مث املتغرية
Z
حبث
Z = X - Y
...
القيم املمكنة ل
X
هي
0
،
5
،
-
5
:. االحتماالت امللحقة بقيمها ميكن حساهبا كما يلي
P(Z =
0
) = P(X – Y =
0
) = P(X =
0
et Y =
0
ou X =
1
et Y =
1
ou X =
5
et Y =
5
) =>
P(Z =
0
) =
0
+ P(X =
1
et Y =
1
) +
0
=
5
*
0,2²
=
0.5
2
المتغي
رة العشوائية المتقطعة
. وهي اليت تأخذ عددا منتهيا من القيم املمكنة يف جمال مغلق،ةلصفنم ع م اضيأ ىمست و
مثال
داخل اجملال املغلق:
[
5
,
2
]
املتغرية
X
املعرفة يف املثال األول تأخذ
1
.قيم ممكنة
3
التوزيع االحتمالي للمتغيرة المتقطعة
هي جمموعة القيم املمكنة مع ا
الحتماالت املرتبطة بقيم املتغرية. نرمز للمتغرية حبرف كبري
و
للقيم ا
ليت تأخذها املتغرية حبرف
صغري. نعرب عن احتمال قيمة معينة كما يلي
P(X = x)
و
: نكتب أيضا
f(x)
. وتسمى الدالة
f(x)
دالة الكثافة
.االحتمالية
:مثال
التوزيع االحتمايل مل ع للمثال األول (إلقاء مكع
:ب نرد) يكتب كما يلي
X
1
5
3
1
2
2
P(X = x)
1/2
1/2
1/2
1/2
1/2
1/2
1
مثال
2
.
التوزيع االحتمايل ل
X
: عدد مرات الصورة يف رميتني لقطعة نقدية،
X
0
1
5
P(X = x)
1/1
5/1
1/1
1
4
شروط دالة الكثافة للمتغيرة المتقطعة
نعرب عن احتمال قيمة معينة كما يلي
P(X = x)
و
: نكتب أيضا
f(x)
وتسمى الدالة
f(x)
.دالة الكثافة االحتمالية
لكي ميكن اعتبار دالة ما
،
أيا كانت
،
:دالة كثافة احتمالية جيب أن يتحقق شرطان اثنان
مثال
نأخذ دالة الكثافة ل:
X
:نتيجة إللقاء حجر نرد
f(
1
) = f(
5
) = f(
3
) = … f(
2
) =
1/2
≥
0
,
الشرط األول حمقق
،
و
:الشرط الثاين أيضا ألن
Σf(x) =
1/2
+
1/2
+ … +
1/2
=
2
(
1/2
) =
1
5
التمثيل البياني لدالة الكثافة االحتمالية ل م ع المتقطعة
مت
ثل
املتغرية العشوائية
املتقطعة لي من خالل منحىن ولكن من خالل أعمدة متوازية على حمور
X
.
منثل بيانيا منحنيات دوال الكثافة:لاثم
ل
X
و
Z
.املعرفة على إلقاء قطعة نقدية مرتني
x
x
f
x
f
1
)
(
)
2
0
)
(
)
1
محاضرات اإلحصاء الرياضي
ص
.ب
- 3 - II
رسم
3
التمثيل البياين لدالة الكثافة للمتغرية العشوائية املتقطعة
5
دالة التوزيع
F(x)
للمتغيرة العشوائية المتقطعة
تعرف دالة التوزيع
-
و
الدالة التجمي" اضيأ ىمست
"عية
–
:كما يلي
F(x) = P(X ≤ x)
وميكن استنتاج دالة التوزيع من دالة الكثافة االحتمالية
f(x)
:كما يلي
إذا كانت
X
تأخذ عددا منتهيا من القيم فإن
F(x)
:ميكن تعريفها كما يلي
مثااااااال
د قيمــــــــجوأ :
F(x)
و
F(z)
ةــــــــلثملأل
السابقة
و
.مثلهما بيانيا
5
1
0
X
1/1
1/5
1/1
f(x)
1
3/1
1/1
F(x)=P(X≤x)
5
0
-
5
Z
1/1
1/5
1/1
f(x)
1
3/1
1/1
F(x)=P(X≤x)
.مالحظة
وأكرب قيمة ممكنة هلا هي،لامج يأ في ةصقانتم نوكت لا يهو ،ايملس لاكش ةعطقتلما ع ملل عيزوتلا ةلاد ذخأت
1
.
x
u
u
f
x
X
P
x
F
)
(
)
(
)
(
-2 1 2
z
f(z)
1
1/2
1/4
f(x)
1 1
2
x
1
1/2
1/4
رسم
4
التمثيل البياني لدالة التوزيع للمتغيرة ال
عشوائية المتقطعة
x
x
x
f
x
f
x
f
x
x
x
x
f
x
f
x
x
x
x
f
x
x
x
F
n
n
),
(
.
.
.
)
(
)
(
,
)
(
)
(
,
)
(
,
0
)
(
2
1
3
2
2
1
2
1
1
1
1 1
2
1
3/4
1/2
1/4
x
F(x)
-2 1 2
z
1
3/4
1/2
1/4
F(z)

الفصل الثاني
المتغيرة العشوائية
- 4 -II
محاضرات اإلحصاء الرياضي
ص
.ب
- 5 - II
المبحث
2
.
مفهوم المتغيرة العشوائية
المستمرة
و
توزيعها االحتمالي
تعريف المتغيرة العشوائية المستمرة
التوزيع االحتمالي للم
تغيرة العشوائية المستمرة
خصائص دالة الكثافة االحتمالية للم
تغيرة العشوائية المستمرة
دالة التوزيع
للم
تغيرة العشوائية المستمرة
قاعدة اليبنيتز
8
تعريف المتغيرة العشوائية المستمر
ة
أو هي تأخذ أي قيمة داخل هذا اجملال. من أجل هذا فأن،دودمح لامج في ميقلا نم ايهانتم لا اددع ذخأت ع ةيرغتم يه
... ، احلجم،ةفاسلما ،نزولا ،نمزلا لثم ةرمتسم نوكت ةرمتيلما ةيرغتلما سايق تادحو
2
التوزيع االحتمالي المستمر
هو جمموعة القيم اليت ميكن أن تأخذها املت
غرية ع املستمرة
و
االحتماالت امللحقة هبا. نسمي توزيعا كهذا دالة الكثاف
ة
. وهي ممثلة مبنحىن متصل،لامتحلاا ةلاد وأ ةيلامتحلاا
الحظ أنه مبا أن
X
فإن احتمال قيمة بعينها هو احتمال يؤول إىل،لامج يأ لخاد ميقلا نم ايهانتم لا اددع ذخأت
.الصفر
P(X=x)
0
لذلك فإن دا
لة الكثافة تستعمل حلساب
احتمال جمال. ويكون ذلك حبساب املساحة حتت منحىن
f(x)
.بني حدود اجملال
الحظ أن إشارة التكامل هنا تقابل إشارة اجملموع يف
.حالة املتغرية ع املتقطعة
3
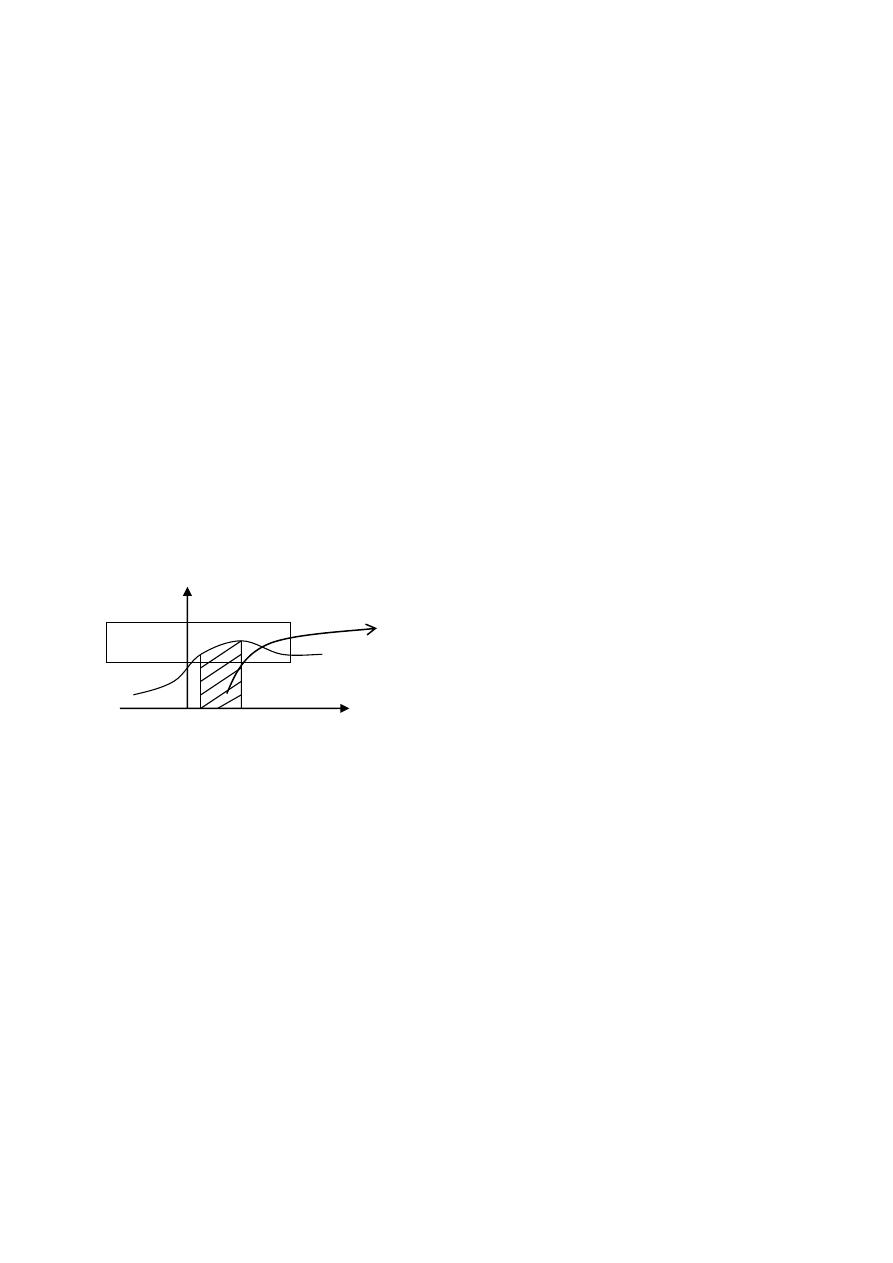
خصائص دالة الكثافة االحتمالية للمتغيرة العشوائية المستمرة
باستبدال إشارة التكامل
بإشارة اجملموع جند أن شروط دالة
: الكثافة االحتمالية للم ع املستمرة تكتب كما يلي
كما أن املساحة اإلمجالية بني املنحىن،ع لما رومح لفسأ لزني نأ نكيم لا ةفاثكلا ةلاد نىحنم نأ اذإ يهيدبلا نم
و
احملور
.األفقي تساوي الواحد
هذه اخلصائص تفيدنا يف حساب احتماالت
.بعض اجملاالت من خالل احتماالت جماالت أخرى
:مثال
أوجد قيمة الثابت
C
اليت حتقق الشرطني األول
و
:الثاين لدالة الكثافة االحتمالية يف الدالة التالية
أحسب احتمال أن تكون
X
تنتمي للمجال من
1
إىل
5
.
أحسب احتمال أن تكون
X
ال تنتمي للمجال من
1
إىل
5
.
1
a b
x
f(x)
1
)
(
)
2
0
)
(
)
1
dx
x
f
x
f
b
a
dx
x
f
b
x
a
P
)
(
)
(
رسم
0
التمثيل البياني لدالة الكثافة للمتغيرة
العشوائية المستمرة
الفصل الثاني
المتغيرة العشوائية
- 6 -II
لكي تكون
x
دالة كثافة جيب أن يكون
C =
1/9
.
4
دالة التوزيع
F(x)
للمتغيرة العشوائية المستمرة
:تعرف دالة التوزيع للمتغرية املستمرة كما يلي
لدالة التوزيع أمهية أكرب بالنسبة للمتغرية املستمرة. السبب يف ذلك
أننا هنتم
،
يف حالة املتغرية املستمرة
،
باحتمال جمال
و
لي
وحلساب احتمال جمال من األيسر التعويض،ةطقن لامتحاب
يف
بفرض:ةيلاتلا ةدعاقلا نم كلذ حضتي .ةرم لك في لماكتلا باسح نم لادب عيزوتلا ةلاد
a, b
نقطتان من جمال تعريف
X
حبيث،
b > a
. حلساب احتمال أن تكون
X
تنتمي إىل اجملال
]a, b]
:
مثال
:
أوجد دالة التوزيع
.للمتغرية املذكورة يف املثال السابق
:استخدم دالة التوزيع حلساب االحتمال
P(
1
< x <
5
)
.
sinon
0
3
0
²
)
(
x
cx
x
f
9
/
1
1
9
3
1
0
²
0
1
)
(
3
0
3
0
3
0
3
C
C
x
C
dx
dx
Cx
dx
dx
x
f
27
7
3
1
8
9
1
3
9
1
²
9
/
1
)
(
)
2
1
(
2
1
3
2
1
2
1
x
dx
x
dx
x
f
x
P
27
20
27
7
1
)
2
1
(
1
)
2
1
(
x
P
x
P
0
0
)
(
)
(
:
0
*
0
du
du
u
f
x
F
x
x
27
3
9
1
²
9
1
0
)
(
)
(
:
3
0
*
3
0
3
0
0
x
u
du
u
du
du
u
f
x
F
x
x
x
x
1
27
27
0
3
9
1
0
0
²
9
1
0
)
(
)
(
:
3
*
3
0
3
3
3
0
0
u
du
du
u
du
du
u
f
x
F
x
x
x
3
1
3
0
27
/
0
0
)
(
3
x
x
x
x
x
F
x
du
u
f
x
X
P
x
F
)
(
)
(
)
(
1
a b
x
f(x)
)
(
)
(
)
(
)
(
)
(
a
F
b
F
a
X
P
b
X
P
b
x
a
P
27
7
27
1
27
2
)
1
(
)
2
(
)
2
1
(
3
3
F
F
x
P
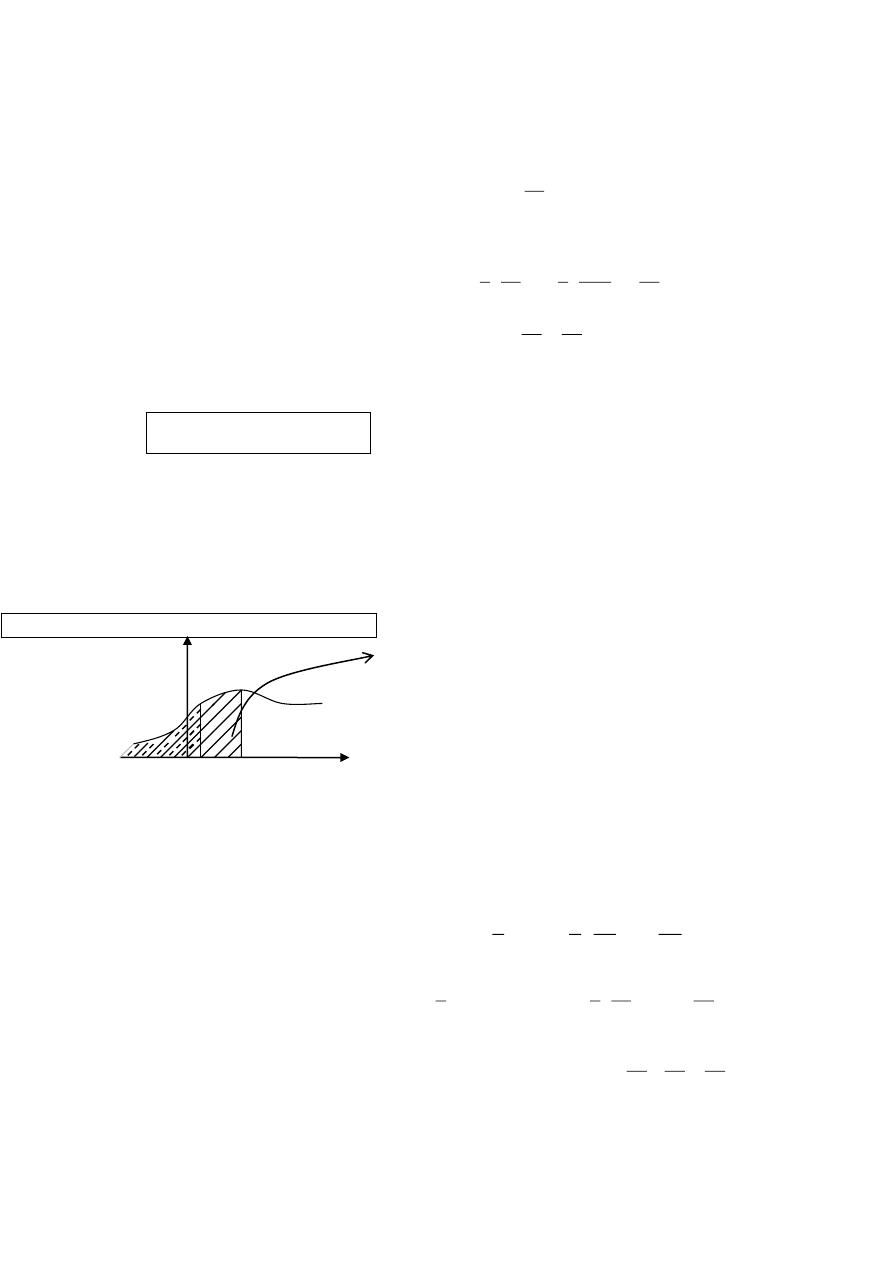
رسم
6
حساب االحتمال من خالل دالة التوزيع

محاضرات اإلحصاء الرياضي
ص
.ب
- 7 - II
5
قاعدة اليبنيز
Règle de LEIBNITZ
:تفيد هذه القاعدة الرياضية العامة يف استنتاج أن مشتقة دالة التوزيع هي دالة الكثافة
مثال
أوجد دالة الكثافة للمتغرية:
X
إذا
:كانت دالة التوزيع كما يلي
5
خالصة
المبحث
األول و الثاني
يتم
تعريف
التوزيع االحتمايل (أو القانون االحتمايل) ملتغرية
عشوائية من خالل
حتديد القيم املمكنة للمت
غرية و االحتماالت
.املقابلة هلا
يتم هذا التحديد إما من خالل جدول
)
)جدول التوزيع االحتمايل
. تسمى دالة كثافة االحتمالية،ةلاد وأ
اــيواـــــــــــــــسم تلااــمتحلاا عوممج نوكي نأ و اــمود ةــبجوم نوكت نأ بــيج ةــيلاــمتحا ةــفاــثك ةــلاد اــنهأ اــم ةــلاد نع لوقن يكل
.للواحد
الدالة التجميعية (أو دالة التوزيع) متثل احتمال جمال من أصغر قيمة للمتغرية إىل نقطة ما
:
ــة م متقطعــلاــح في
ة و
ة مــلاــح في
.مستمرة
نظرا لتعريفها تأخذ دالة التوزيع مسارا متزايدا (أو ثابتا على أجزاء من اجملال). تربز أمهية الدالة التجميعية أكثر عندما تكون
.املتغرية مستمرة ألننا هنتم حينها باحتماالت جماالت. ميكن استنتاج دالة الكثافة من خالل اشتقاق دالة التوزيع
)
(
)
(
)
(
)
(
x
f
dx
x
dF
x
f
dx
du
u
f
d
x
sinon
0
0
1
)
(
2
x
e
x
F
x
sinon
0
0
2
)
(
2
x
e
x
f
x
x
u
u
f
x
X
P
x
F
)
(
)
(
)
(
x
du
u
f
x
X
P
x
F
)
(
)
(
)
(
x
x
x
e
e
x
f
e
x
F
x
x
F
x
f
x
2
2
2
2
1
)
(
1
)
(
:
0
*
0
)'
0
(
)
(
'
)
(
:
0
*


محاضرات اإلحصاء الرياضي
ص
.ب
- 1 -III
الفصل
III
.
التوقع الرياضي
و
التباين
التوقع الرياضي
التباين
و
االنحراف المعياري
العزوم
الدالة المتجددة للعزوم
نظرية األعداد الكبيرة،فيشيبيش ةيرظن
:مسألة
أرسلت مؤسسة عروضا إىل
1
عمالء. احتمال تلقي طلبية من العميل األول هي
0,5
من،
العميل الثاين
0,3
من العميل الثالث،
0,32
و
0,1
من العميل الرابع. يف انتظار ردود العمالء ما هو
؟العدد املتوقع من الطلبيات
اب احتمال حتقق حدث أو أحداث معينة بل حنتاج للخروج بتوقع معني يلخصـــــــــــــــسح يفكي لا تلاالحا نم دـيدـعلا في
لة بني خيارات متاحة مقيمةــــضافلما بعــــصي دق ىرخأ ةهج نم .انمامأ ةحورطلما ةيعــــضولا
بب ارــــسب ةنيعم غلاببم
تباط كل
ذخأ نكيم فيكف ،ةرطامخ بركأ نمـضتت تيلا كلت يه ةيدودرم رثكلأا تارامثتـسلاا نأ فورعلما نم ؛ةفلتمخ ةرطاخبم غلبم
بان املخاطرةـــــسلحا في
و
املبلغ املتوقع وبطريقة دقيقة
و
إن طريقة التوقع وبقية املفاهيم األخرى الواردة؛ةيعوـــــضوم
أعاله ميكن
أن ت
.ساعدنا يف ذلك
المبحث
1
.
التوقع الرياضي
Espérance mathématique
تعريف التوقع
توقع دالة
8
تعريف التوقع
:يعرف التوقع الرياضي ملتغرية عشوائية متقطعة كما يلي
و
:يعرف التوقع الرياضي ملتغرية عشوائية مستمرة كما يلي
نرمز للتوقع أحيانا ب
μ
أو
x
μ
.
:مثال
نلقي قطعة نقدية
1
م
.رات. أحسب العدد املتوقع من املرات اليت حنصل فيها على وجه
اجملموع
1
3
5
1
0
X
عدد مرات وجه
12/12
=
1
1
)
1/5
(
1
)
1/5
(
1
1
)
1/5
(
2
1
)
1/5
(
1
1
)
1/5
(
P(X)
35/12
=
5
1
)
1/5
(
1
1
)
1/5
(
15
1
)
1/5
(
15
1
)
1/5
(
1
0
XP(X)
n
i
i
i
n
i
i
i
x
f
x
x
X
P
x
X
E
1
1
)
(
)
(
)
(
dx
x
xf
X
E
)
(
)
(
2
16
/
32
)
(
)
(
1
n
i
i
i
x
X
P
x
X
E

الفصل الثالث
التوقع الرياضي
و التباين
- 2 -III
العدد املتوقع هو مرتني من بني
1
.رميات
مثال
2
.
نلقي قطعة نقدية مرة واحدة. يربح الالعب
50
ل على الرقمـــــــــصح اذإ جد
5
ويربح،
10
ل علىـــــــــصح اذإ جد
الرقم
1
،
و
20
ل على الرقمــــصح اذإ جد
2
رــــسيخو ،
10
ل على الرقمــــصح اذإ جد
1
،
30
ل على الرقمــــصح اذإ جد
3
،
و
20
دج إذا حصل على الرقم
2
. حتقق مما إذا كانت العبة متوازنة (هل توقع
.)الربح يساوي توقع اخلسارة
اجلواب هو أن اللعبة غري متوازنة ألن توقع الربح أكرب من توقع اخلسارة
E(x) =
30/2
=
2
>
0
اجملموع
2
2
1
3
5
1
نتيجة الرمي
-
20
-
20
10
-
30
50
-
10
نتيجة المراهنة
X
2/2
1/2
1/2
1/2
1/2
1/2
1/2
P(X=x)
(
150
-
90
)/
2
>
0
20/2
-
20/2
10
/
2
-
30/2
50/2
-
10/2
X*P(X=x)
مثال
3
:. أوجد التوقع الرياضي للمتغرية ذات دالة الكثافة التالية
2
توقع دالة
العزوم املركزية،نيابتلا لثم يياقلما نم ددع باسح دنع ةلاد عقوت مدختسي
و
.العزوم املرتبطة باألصل
لتكن
X
م ع هلا دالة كثافة
f(x)
،
و
y = g(x)
م ع تابعة هل
.ا
يف حالة
X
:م متصلة
مثال
8
. نلقي قطعة نقدية مرتني. نسمي
X
،عدد مرات احلصول على صورة
و
Y=X
²
. أحسب
E(X)
و
E(Y)
.
المجموع
2
1
0
X
1
1/1
1/2
1/1
P(X = x)
E(X) =
1
1/2
1/2
0
X*P(X)
1
1
0
X
²
E(X
²) = 2/2
1
1/2
0
X
²
*P(X)
مثال
2
لتكن:
X
م ع ذات دال
،ة الكثافة التالية
و
Y = g(x) =
3
x
²
-
5
x
. أحسب
E(Y)
.
0
2
0
2
.
0
.
)
2
1
(
.
0
.
)
(
)
(
dx
x
dx
x
x
dx
x
dx
x
xf
x
E
3
4
0
3
2
1
0
)
(
2
0
3
x
x
E
x
x
f
x
g
x
g
E
Y
E
)
(
)
(
))
(
(
)
(
dx
x
f
x
g
x
g
E
Y
E
)
(
)
(
))
(
(
)
(
sinon
0
2
0
2
1
)
(
x
x
x
f
sinon
0
2
0
2
1
)
(
x
x
x
f
محاضرات اإلحصاء الرياضي
ص
.ب
- 3 -III
3
خصائص التوقع الرياضي
E (C) = C
E(CX) = CE(X)
E(X+Y) = E(X) + E(Y)
إذا كانت
.املتغريتان مستقلتان
E(XY) = E(X)E(Y)
:مثال
تتوقع مؤسسة أن تتلقى كل شهر
3
طلبيات من العميل
A
و
1
من
B
.
أحسب العدد املتوقع
من الطلبيات املتلقاة من
A
.يف السنة
.أحسب العدد اإلمجايل املتوقع من الطلبيات املتلقاة يف شهر
يعني كل عميل من طرفه مندوبا عن كل طلبية ملتابعة إمتامها. كم تتوقع أن يلزم من مقابلة لتعريف مندويب العميل
A
مبندويب
B
.
E(
15
A) =
15
E(A) =
15
(
3
) =
32
E(A*B) = E(A)*E(B) =
1
*
3
=
15
.
E(A + B) = E(A) + E(B) =
3
+
1
=
9
المبحث
2
.
التباين
و
االنحراف المعياري
Variance et écart type
تعريف التباين
خصائص التباين
المتغيرة المعيارية
8
تعريف التباين
يعرف التباين ملتغرية عشوائية كما يلي
:
و
.االحنراف املعياري هو جذر التباين
σ = √V(X) = √σ
²
.
: يف حالة املتغرية العشوائية املتقطعة
: يف حالة املتغرية العشوائية مستمرة
.مثال
نلقي قطعة نقدية مرتني. نسمي
X
أحسب،ةروص ىلع لوصلحا تارم ددع
V(X)
.
المجموع
2
1
0
X
1
1/1
1/2
1/1
P(X = x)
E(X) = μ =
1
1/2
1/2
0
X*P(X)
1
0
1
(X-μ)
²
dx
x
x
dx
x
x
x
dx
x
x
dx
x
f
x
g
x
g
E
Y
E
)
0
)(
2
²
3
(
)
2
/
)(
2
²
3
(
)
0
)(
2
²
3
(
)
(
)
(
))
(
(
)
(
3
10
6
20
3
16
12
2
1
3
2
4
3
2
1
0
)
2
/
)(
2
²
3
(
0
)
(
2
0
3
4
2
0
x
x
dx
x
x
x
Y
E
²
)
(
²
X
E
X
Var
X
)
(
²
)
(
x
f
x
X
V
x
dx
x
f
x
X
V
)
(
²
)
(

الفصل الثالث
التوقع الرياضي
و التباين
- 4 -III
V(X) =
1/2
1/1
0
1/1
(X-μ)
²
*
P(X)
مثال
2
.
لتكن
X
أحسب تباين؛ةيلاتلا ةفاثكلا ةلاد تاذ ع م
X
.
2
خصائص التباين
V(X) = E(X
²
) - E(X)
²
V(CX) = C
²
V(X) , V (C) =
0
يف حالة استقالل املتغريتان عن بعضهما
V(X + Y) = V(X) + V(Y)
,
V(X - Y) = V(X) + V(Y)
:مثال
ن
لقي قطعة نقدية مرتني. نسمي
X
أحسب،ةروص ىلع لوصلحا تارم ددع
V(X)
باستخدام الصيغة
V(X) = E(X
²
) - E(X)
²
.
لتكن املتغرية
Y =
5
X
. أحسب
V(Y)
نلقي حجر نرد،
و
نسمي
Z
النتيجة احملصل عيها. أحسب تباين املتغرية
W
:حيث
W = Z - Y
المجموع
2
1
0
X
1
1/1
1/2
1/1
P(X = x)
E(X) = μ
=
1
1/2
1/2
0
X P(X)
1
1
0
(X)
²
E(X)
²
=
2/2
1
1/2
0
(X)
²
* P(X)
V(X) = E(X
²
) - E(X)
²
= (
2/2
) -
1
=
1/2
V(Y) = V(
2
X) =
2²
V(X) =
1
(
1/2
) =
2
.
V(W) = V(Z-
2
X) = V(Z) +V(
2
X) = V(Z) +
2²
V(X).
V(Z) = E(Z
²
) – E(Z)
²
= (
1/1
)[
1²²2²²2²²1²²5²²1²
]-(
1/1
)[
1²2²2²1²5²1
] =
60/1
V(W) = (
60/1
) +
1
(
1/2
) =
62/1
=
12.16
3
/
4
.
)
(
²
²
dx
x
f
x
0
9
16
3
8
2
1
0
0
3
4
2
3
4
0
*
3
4
²
2
0
2
2
0
2
2
2
0
2
x
x
x
dx
x
dx
x
x
dx
x
9
4
9
32
3
32
8
2
1
9
16
3
²
8
2
1
²
2
0
3
x
x
x
sinon
0
2
0
2
1
)
(
x
x
x
f

محاضرات اإلحصاء الرياضي
ص
.ب
- 5 -III
3
المتغيرة المعيارية
Variable centrée réduite
ميكن أن نلحق بأي متغرية عشوائية
X
)متغرية معيارية (تسمى أيضا املتغرية املركزية
و
يرمز هلا
X*
. تلحق املتغرية املعيارية
باملتغرية احلقيقية من أجل امل
قارنة ألن املتغرية املعيارية لي هلا وحدة كاملرت أو الساعة ... وإمنا هي تعرب عن كل قيمة
x
ل
X
من خالل املسافة بني
x
و
التوقع
μ
حمسوبة ل بالوحدة األصلية
و
.إمنا باالحنرافات املعيارية
من خالل خصائص التوقع
و
التباين نستخرج التوقع
و
.التباين للمتغرية املعيارية
مثال
أحسب:
X*
من أجل متوسط
90
احنراف معياري،
2
،
و
X
:يساوي
22
،
20
،
20
،
92
،
00
،
90
.
: القيم هي:باولجا
-
3
،
-
5
،
-
1
،
1
،
5
،
0
.
مثال
2
. يتدرب عامالن أمحد وعلي من أجل املشاركة يف ماراتون عيد العمال
1
ماي. يشرتط يوم املسابقة أن يكون وزن
املرتشح ال يتجاوز اجمل
ال
μ ±
1,2
σ
.
إذا كان الوزن املتوسط بالكغ هو
μ =
90
و
االحنراف املعياري هو
2
كغ. هل سيقبل العامالن أمحد
و
:علي إذا كان وزهنما
99
،كغ
و
00
؟كغ
جمال القبول هو من:باولجا
25,2
كغ إىل
99,2
لذلك فسريفض علي،غك
و
.يقبل أمحد
4
خالصة
ي و التباين هي أهم املــضايرلا عقوتلا
بان كما يليــسيح و ةيرغتلما صئاــصخ نع ةبرعلما تارــشؤ
ب كونــسح ،
املتغرية متقطعة
أو مستمرة
:
لكل من ا
لتوقع و التباين
1
خصائص أساسية
:تتمثل فيما يلي
V(C) =
0
توقع عدد ثابت
E (C) = C
V(CX) = C
²
V(X)
E(CX) = CE(X)
يف حالة استقالل املتغريتان
عن بعض
هما
V(X + Y) = V(X) + V(Y)
,
V(X - Y) = V(X) + V(Y)
E(X+Y) = E(X) + E(Y)
V(X) = E(X
²
) - E(X)
²
.يف حالة استقالل املتغريتان عن بعضهما
E(XY) = E(X)E(Y)
من أجل املقارنة بني املتغريات تستخدم املتغرية املعيارية اليت تسمح بالتعبري عن قيمة
x
لي من
خالل وحداهتا األصلية
...) وإمنا بعدد االحنرافات املعيارية اليت تفصل بني القيمة،نمز ،ترم ،غك(
x
.والتوقع الرياضي
X
X *
0
)
(
)
(
1
)
(
1
*)
(
E
X
E
X
E
X
E
X
E
1
²
²
²
²
1
²
²
²)
*
(
²
0
*
²
*)
(
*
*)
(
X
E
X
E
X
E
X
E
X
E
X
E
X
V
n
i
i
i
n
i
i
i
x
f
x
x
X
P
x
X
E
1
1
)
(
)
(
)
(
dx
x
xf
X
E
)
(
)
(

الفصل الثالث
التوقع الرياضي
و التباين
- 6 -III
التوقع الرياضي والتباين للمتغرية املعيارية
مها على التوايل
0
و
1
.
حلساب التوقع الرياضي لدالة ما يف
X
أو،نيابتلا لاثم(
X
²
) نضرب قيم الدالة
يف االحتماالت املقابلة ل
X
:
X
X *
x
x
f
x
g
x
g
E
Y
E
)
(
)
(
))
(
(
)
(
dx
x
f
x
g
x
g
E
Y
E
)
(
)
(
))
(
(
)
(

محاضرات اإلحصاء الرياضي
ص
.ب
- 7 -III
المبحث
3
.
العز
و
م
و
الدالة المتجددة للعزوم
العزوم
ا
لدالة المتجددة للعزوم
8
العزوم
Les moments
ك
العزم املركزي:موزعلا نم ينعون ينب زينم .ةلاد عقوت تاقيبطت نم مزعلا برتعي نيابتلا ام
و
العزم امل
رتبط باألصل. تستخدم
العزوم يف حساب عدد م
ن املقايي مثل معامل التماثل
(coefficient d'asymétrie) α
3
ومعامل التفلطح
(Kurtosis ou coefficient d'aplatissement) α
1
.
(أ
)
العزم المركزي
r
μ
Le moment central
.
يعرف العزم املركزي من الدرجة
r
للم ع
X
:كما يلي
.
.
.
,
2
,
1
,
0
,
r
X
E
r
r
حيسب العزم املركزي حسب طبي
:عة املتغرية متقطعة أو مستمرة كما يلي
. مثال
أحسب العزوم املركزية من الدرجة
0
،
1
،
5
و
3
:للمتغرية ع ذات دالة الكثافة
:مثال
ب العزوم املركزية من الدرجةــــسحأ
0
،
1
،
5
و
3
ورــــص ىلع لوــــصلحا تارم ددع لثتم تيلا ةعطقتلما ع ةيرغتملل
ة
يف
.رميتني لقطعة نقدية
(
ب
)
العزم المرتبط باألصل
r
μ'
Moment autour de la moyenne
:يعرف العزم املرتبط باألصل كما يلي
²
)
(
0
0
)
(
)
(
1
1
)
1
(
2
2
2
1
1
1
0
0
0
X
V
X
E
E
X
E
X
E
E
X
E
dx
x
f
x
r
r
)
(
)
(x
f
x
r
i
i
r
sinon
0
2
0
,
2
/
)
(
x
x
x
f
1
)
(
1
)
(
0
0
dx
x
f
dx
x
f
x
0
)
1
(
)
(
)
(
)
(
1
dx
x
f
dx
x
xf
dx
x
f
x
9
4
²
)
(
2
2
dx
x
f
x
0
2
0
2
3
3
3
3
3
)
5
(
27
)
67
(
16
)
0
(
3
4
2
3
4
)
0
(
3
4
)
(
dx
x
dx
x
x
dx
x
dx
x
f
x
.
.
.
,
2
,
1
,
0
),
(
'
r
X
E
r
r

الفصل الثالث
التوقع الرياضي
و التباين
- 8 -III
مثال
:
أحسب العزوم املرتبطة باألصل من الدرجة
0
،
1
،
5
،
3
و
1
:للمتغرية ع املتصلة ذات دالة الكثافة
مثال
2
.
لـــصلأاب ةطبترلما موزعلا بـــسحأ
من الدرجة
0
،
1
،
5
،
3
و
1
ولـــصلحا تارم ددع لثتم تيلا ةعطقتلما ع ةيرغتملل
.على صورة يف رميتني لقطعة نقدية
(
ج
)
العالقة بين العزم المركزي
و
العزم المرتبط باألصل
ميكن أيضا احلصول على العزوم املرتبطة باألصل من الدرجة
r
من خالل اشتقاق الدالة املتجددة للعزوم
r
.مرة
2
ال
دالة المتجددة للعزوم
(t)
x
M
La fonction génératrice des moments
)الدالة املتجددة للعزوم هي دالة مرتبطة مبتغرية (معلمة
t
باإلضافة إىل ارتباطها ب
X
،
و
:د م ع كما يلي
:يف حالة م ع متقطعة
:و يف حالة م ع مستمرة
dx
x
f
e
t
M
tx
x
)
(
)
(
:مثال
أكتب الدالة املتج
ددة للعزرم من أجل
t ≠
0
:للم ع املعرفة يف كما يلي
تستخدم الدالة املتجددة للعزوم حلساب العزم املركزي من درجة
r
:
2
'
2
2
'
2
'
1
1
'
1
'
0
0
'
0
²
²
²
²
)
(
)
(
1
1
)
1
(
)
(
X
E
X
E
E
X
E
3
16
6
2
1
)
2
(
'
,
5
16
5
2
1
)
2
(
'
,
9
12
9
4
3
4
²
'
,
3
/
4
'
,
1
'
2
0
6
2
0
4
4
2
0
5
2
0
3
3
2
2
2
1
0
x
dx
x
x
x
dx
x
x
r
r
i
i
r
i
r
i
r
r
r
r
C
C
0
1
1
1
'
)
1
(
.
.
.
'
)
1
(
.
.
.
'
'
)
(
)
(
tx
x
e
E
t
M
x
tx
x
x
f
e
t
M
)
(
)
(
sinon
0
2
0
2
1
)
(
x
x
x
f
0
2
1
0
)
0
(
)
(
)
0
(
)
(
2
0
2
2
0
0
dx
xe
dx
e
dx
x
f
e
dx
e
t
M
tx
tx
tx
tx
x
t
e
V
dx
e
dV
dx
dU
x
U
VdU
UV
UdV
t
M
tx
tx
x
,
.
]
[
2
1
2
1
)
(
2
0
2
0
2
0
²
2
1
2
2
1
2
1
)
(
2
2
2
2
2
0
2
0
t
e
t
e
t
e
t
t
e
dx
t
e
t
e
x
t
M
t
t
t
t
tx
tx
x
sinon
0
2
0
2
1
)
(
x
x
x
f

محاضرات اإلحصاء الرياضي
ص
.ب
- 9 -III
،روط معينةــش ققتح دنع لاثم ،ينيلامتحا ينعيزوت يواــست تابثلإ ع م دلا مدختــست امك
و
ــحنتاج ذلك خاص
ةــسارد دنع ة
التقارب بني التوزيعات االحتمال
:ية. النظرية اليت نستعملها يف ذلك هي كاآليت
لتكن م ع
X
و
Y
هلما الد م ع
(t)
x
M
و
(t)
y
M
نقول أن م ع؛
X
و
Y
:هلما نف التوزيع االحتمايل إذاا
(t)
y
(t) = M
x
M
:كما تستخدم الد م ع إلثبات إستقالل توزيعني احتماليني. النظرية اليت نستعملها يف ذلك هي كاآليت
إذا
X
و
Y
هلما الد م ع،ناتلقتسم ع م
(t)
x
M
و
(t)
y
M
: فإن؛
(t)
y
M
.
(t)
x
(t) = M
x+y
M
3
خالصة
العزم
و الدالة املتجدد للعزوم هي ع
بارة عن توقع
ات دوال
(أنظر
املبحث
السابق). يدخل العزم يف حساب بعض املؤش
رات
. معامل التفلطح و معامل التماثل،يضايرلا عقوتلا و نيابتلا لثم
يعرف العزم املركزي من الدرجة
r
للم ع
X
:كما يلي
.
.
.
,
2
,
1
,
0
,
r
X
E
r
r
:يعرف العزم املرتبط باألصل كما يلي
.
.
.
,
2
,
1
,
0
),
(
r
X
E
r
r
:تعرف الدالة املتجددة للعزوم كما يلي
تستخدم الدالة املتجددة للعزوم إلثبات التقارب بني توزيعات احتمالية و
ذلك من خالل نظريتني أساسيتني
.
نقول أن م ع
X
و
Y
:هلما نف التوزيع االحتمايل إذاا
(t)
y
(t) = M
x
M
إذا
X
و
Y
:م ع مستقلتان فإن
(t)
y
(t) . M
x
(t) = M
x + y
M
المبحث
4
.
نظرية شيبيشيف ونظرية األعداد الكبيرة
متراجحة شيبيشيف
نظرية األعداد الكبيرة
8
متراجحة شيبيشيف
Inégalité de Bienaymé CHEBYCHEV
هي نظرية ختص م ع املتقطعة
و
اليت يكون هلا متوسط،ءاوسلا ىلع ةرمتسلما
و
تباين حمدود. تستخدم هذه الن
ظرية يف قياس
تت حول التوقعـــشتلا
μ
،
و
افة (الفرق) بينهاـــسلما تيلا تادرفلما )ةبـــسن وأ( لامتحا قيرط نع كلذ
و
بني
μ
تزيد عن مقدار
:ما
P(-ε ≥ (x - μ) ≥ ε)
:اراــصتخا رثكأ ةرابعب وأ
P(|x - μ| ≥ ε)
بة الــسنلا هذه نإف فيــشيبيــش ةيرظن بــسح .
تزيد عن
σ
²
/ε
²
،
:وذلك مهما كانت طبيعة التوزيع. ونعرب عن هذه النظرية كما يلي
إذا كانت
X
هلا متوسط،ةعطقتم وأ ةلصتم ع م
μ
وتباين حمدود
σ
²
فإنه مهما يكن،
ε
عدد موجب
:متاما
0
)
(
t
avec
dt
t
M
d
r
x
r
r
)
(
)
(
tx
x
e
E
t
M

الفصل الثالث
التوقع الرياضي
و التباين
- 11 -III
: نضع،ةللاد رثكأ ةغايص لجأ نم و
σ
= k
ε
: فنجد
: لدينا أيضا،ةجيتنلا فن نم اقلاطنا ،هنأ ظحلا
:ساالال
إذا كان أقل من:ةحيحـــص ةرابعلا هذه له
10
%
لون على تقديرـــصيح ايرولاكابلا ناحتما في نيزئافلا نم
فهذا يعين أن أكثر من،نــــــــــسح نم رثكأ
90
%
.نــــــــــسح نم لقأ ريدقت ىلع نولــــــــــصيح ايرولاكابلا في نيزئافلا نم
.اجلواب نعم
:مثال
لتكن
X
هلا متوسط؛ناك ايأ اعيزوت عبتت ع م
μ
وتباين حمدود
σ
²
،
و
ε
؛عدد موجب متاما
1
.
أحسب احلد األقصى لالحتمال
P(-ε ≥ (x - μ) ≥ ε)
من أجل
ε =
5
σ
،
ε =
3
σ
،
ε =
1
σ
.
5
.
أحسب احلد األدىن لالح
تمال
P(-ε < (x - μ) < ε)
من أجل
ε =
5
σ
،
ε =
3
σ
،
ε =
1
σ
.
مثال
2
.
يتم أخذ أوزان عمال مركب احلجار من أجل ترشيحهم للمشاركة يف ماراتون عيد العمال
1
.ماي
1
.
يح على األقلـــــشرت متي ثيبح لوبقلا لامج ديدتح نكيم فيك
92
%
يح أقل منـــــشرت ضفر ،لامعلا نم
52
%
؟من العمال
5
.
حد
د قيم اجملال إذا كان الوزن املتوسط االفرتاضي هو
90
،كغ
و
االحنراف املعياري
2
.كغ
²
²
)
(
x
P
²
1
)
(
k
k
x
P
²
²
1
)
(
x
P
x
P
,
16
1
4
)
(
4
,
9
1
3
3
,
4
1
2
)
(
2
²
²
)
(
x
P
x
P
x
P
x
P
x
P
x
P
x
P
,
16
/
15
16
1
1
4
)
(
4
,
9
/
8
9
1
1
3
3
,
4
/
3
4
1
1
2
)
(
2
²
²
1
)
(
x
P
x
P
x
P
x
P
x
P
x
P
x
P
%
75
4
1
1
2
)
(
.
2
²
²
1
)
(
x
P
x
queP
déjà
savons
nous
Lorsque
x
P
x
P
%
25
4
1
2
.
2
²
²
)
(
x
P
que
déjà
savons
nous
Lorsque
x
P
x
P

محاضرات اإلحصاء الرياضي
ص
.ب
- 11 -III
1
.
إن أكثر من
92
%
العمال هلم أوزان ال تبتعد بأكثر من
σ
5
وهذا ميكن التعبري عنه بطريقة،طـــــــــــــــسوتلما نع
اوي منــــسي وأ لقأ نإ :لوقلاب ىرخأ
52
باملئة من العمال هلم أوزان أبعد من الوزن
ط بأكثر منــــسوتلما
σ
5
.
إذا ميكن اختاذ جمال قبول
μ
25
σ
.لتحقيق اهلدف املسطر
2
.
اجملال الذي حيقق اهلدف حسب القيم املعطاة للمتوسط
و
االحنراف املعياري هو من
20
إىل
00
.كغ
مثال
3
.
متوسط مدة التمدرس يف جمتمع معني هي
0
واالحنراف املعياري،تاونس
σ =
1
.
1
.
أحسب أدىن احتمال
ملدة متدرس بني
2
و
10
.سنوات لفرد خمتار عشوائيا من هذا اجملتمع
5
.
أحسب أقصى احتمال ملدة متدرس ال تزيد عن
2
سنوات أو ال تقل عن
10
.سنوات
أدىن احتمال ملدة متدرس بني
2
و
10
سنوات لفرد خمتار عشوائيا من هذا اجملتمع
هي
0,92
.
أدىن احتمال ملدة متدرس ال تزيد عن
2
س
نوات أو ال تقل عن
10
هو
0,52
.
2
نظرية األعداد الكبيرة
Théorème des grands nombres
تعترب نظرية األعداد الكبرية من نتائج نظرية شيبيشيف ويستفاد منها بشكل خاص يف نظرية املعاينة. تصاغ هذه النظرية
:بالشكل اآليت
لتكن املتغريات
1
X
،
5
X
. . . . متغريات عشوائية مستقل،
ة هلا نف التوزيع االحتمايل
ولكل منها
نف
املتوسط
μ
و
التباين
σ
²
إذا كانت
, . . .),
5
,
1
(n =
n
+ . . . +X
2
+ X
8
= X
n
S
مبا أن
/n) = µ
n
E(S
فإن مضمون هذه النظرية هو أن احتمال أن تبتعد املتغرية
/n
n
S
عن قيمتها املتوقعة بأكث
ر من
ε
هو
0
عندما
n →∞
.
تسمى هذه الصياغة أيضا بقانون األعداد الكبرية الضعيف. حيث أن قانون األعداد الكبرية القوي
:هو
1
/n = µ] =
n
S
n→∞
P[lim
3
خالصة
نظرية شيبيشاف ونظرية األعداد الكبرية
من النظريات اليت تقي تشتت املتغرية و هي
من تطبيقات
توقع دالة
:
إذا كان
ت
X
طــــــــــــسوتم اله ،ةعطقتم وأ ةلــــــــــــصتم ع م
μ
وتباين حمدود
σ
²
فإنه مهما يكن،
ε
عدد
:موجب متاما
4
/
3
²
2
1
1
)
2
(
)
6
10
(
:
2
.
2
6
,
2
10
1
,
8
.
²
1
1
)
(
x
P
x
P
k
Pour
k
k
x
P
4
/
1
²
2
1
)
2
(
:
2
.
2
6
.
²
1
)
(
x
P
k
soit
k
k
x
P
0
lim
n
S
P
n
n

الفصل الثالث
التوقع الرياضي
و التباين
- 12 -III
لتكن املتغريات
1
X
،
5
X
تقلة هلا نف التوزيع االحتمايلــسم ةيئاوــشع تايرغتم . . . . ،
ولك
ل منها
نف املتوسط
μ
والتباين
σ
²
إذا كانت
, . . .),
5
,
1
(n =
n
+ . . . +X
2
+ X
8
= X
n
S
²
²
)
(
x
P
0
lim
n
S
P
n
n
محاضرات اإلحصاء الرياضي
ص
.ب
- 1 -IV
الفصل
IV
.
التوزيعات
االحتمالية
األكثر استخداما
التوزيعات االحتمالية المتقطعة
التوزيعات االحتمالية المستمرة
المبحث
1
.
التوزيعات الحتمالية المتقطعة األكثر استخداما
التوزيع الثنا،يلونرب عيزوت ،ددعتملا دئازلا يسدنهلا عيزوتلا ،دئازلا يسدنهلا عيزوتلا
التوزيع،يئ
الثنائي السالب
. توزيع بواسون،ددعتملا عيزوتلا ،يسدنهلا عيزوتلا ،)لاكساب(
وائيةــــــــــشعلا ةيرغتلما موهفم انفرع نأ دعب
و
.هريةــــــــــشلا ةيلامتحلاا تاعيزوتلا نم ددع سردن نأ نلآا اننكيم ليامتحلاا عيزوتلا
ائل يف جمال التــــــــسلما نم ديدعلا لح في تاعيزوتلا هذه مدختــــــــست
ناعيــــــــصلا يريــــــــس
و
التجاري
و
يف اإلدارة. ومن
أكثر هذه
ينناوقلا راكذتـــسا ىلع ارداق بلاطلا نوكي نأ ضترفي ةرـــضالمحا ةيانه في .نوـــساوب عيزوتو يئانثلا عيزوتلا :اعويـــش تاعيزوتلا
ومن خالل التطبيقات يفرتض أن يتمكن من معرفة مىت وكيف ميكن استخدام ك،ةيساسلأا اهصئاصخو ةسوردلما
ل
.قانون
8
:التوزيع الهندسي الزائد
Distribution hyper géométrique
(أ
)
:استنتاج صيغة قانون التوزيع الهندسي الزائد
مثال
8
.
ندوق بهـص
2
كريات منها
1
اءـضيب
و
5
حب بدون إرجاعـسن .ءارحم
3
كريات. احسب احتمال احلصول على
،كرتني بيضاوين
3
و،ءاضيب ةدحا وةيرك ،ءاضيب تايرك
.ال كرية بيضاء
ندوق كرياتـــص نم بحـــسن اننأ ضترفن
بدون إرجاع
عددها
n
ندوق حيتوي علىـــصلا ناك اذإ ،
N
كرية منها
b
اءـــضيب
وr
محراء
(N = b + r)
فإن احتمال احلصول على عدد معني
x ≤ b
من الكريات البيضاء ميكن أن حنصل عليه من
خالل القانون الكالسيكي لالحتماالت (ع احلاالت ا
)ملالئمة /ع احلاالت املمكنة
و
:ذلك باستخدام التوفيقات
قانون التوزيع اهلندسي الزائد:ةغيصلا هذه ىمست
و
نكتب
b, p)
X ~ H(N,
حيث
:
p = b/N
و
=
1-p
q = r/N
:ميكن اآلن اإلجابة على أسئلة املثال كما يلي
P(X=
5) = C
15
. C
53
/ C
12
=
15/50 , P(x = 3) = C
13
. C
50
/ C
23
=
1/2 , …
(
ب
)
خصائص التوزيع الهندسي الزائد
. للتوزيع اهلندسي الزائد عالقة بالتوزيع الثنائي سنذكرها عندما نتطرق هلذا األخري:ةظحلام
n
N
x
n
r
x
b
C
C
C
x
X
P
)
(
1
²
,
N
n
N
npq
np
الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 2 -IV
2
:التوزيع الهندسي الزائد المتعدد
Distribution Multi-hypergéométrique
(أ
)
استنتاج صيغة قانون التوزيع الهندسي الزائد المت
عدد
( ميكن بسهولة تعميم القانون السابق على حالة وجود أكثر من صنفني
k
حيث من كل صنف لدينا،)فنص
Ni
،كرية
(
Ni = N
Σ
مثال؛ةنيعم ةجيتن لامتحا باسلحو ، )
5
( كريات بيضاء
5
=
1
X
، )
2
،محراء
1
. . . ميكن،ءاقرز
حساب عدد احلاالت املالئمة واملمكنة من خالل التوفيقات ك
:ما يلي
(
ب
)
خصائص التوزيع الهندسي الزائد المتعدد
: مالحظة
.للتوزيع اهلندسي الزائد عالقة بالتوزيع الثنائي سنذكرها عندما نتطرق هلذا األخري
3
توزيع برنولي
8
Distribution de Bernoulli
(أ
)
استنتاج صيغة قانون برنولي
إذا كانت حتتمل نتيجت"ةيلونرب" انهأ ةبرتج نع لوقن
ني (حدثني) متنافيتني
A
و
A’
.
نسمي
A
جناح
و
A’
.فشل
نعترب املتغرية ع
X
اليت متثل
عدد مرات النجاح
تأخذ،
X
القيمة
1
عند حتقق احلدث
A
و
0
.يف احلالة املعاكسة
نرمز عادة ب
p
الحتمال حتقق احلدث"حاجنلا لامتحا"
A
و
q =
1
- p
ل). يعنيــــــــــــــشفلا( كاعلما ثدلحا لامتحا
توزيع بر
: نويل كما يلي
ونكتب
X ~ B(
8, p)
(
ب
)
خصائص توزيع برنولي
.q = p => E(X) = p.
1
.p +
1
=
i
p
i
x
Σ
E(X) =
V(X) = E(X
²) – E(X)² = (1².p + 0².q) – p² = p – p² = p(1- p) = pq => V(X) = qp.
الدالة المت
جددة للعزوم
.
t
M(t) = q + pe
=>
p
t
1
q + e
t
0
) = e
xt
M(t) = E(e
معامل التماثل
1
بإسم
Jacques Bernoulli
الذي درس هذا التوزيع يف أواخر القرن
19
.
n
x
N
N
C
C
C
C
x
X
x
X
x
X
P
k
i
k
i
n
N
k
x
k
N
x
N
x
N
k
k
1
1
2
2
1
1
2
2
1
1
,
.
.
.
)
.
.
,.
,
(
i
i
i
np
N
N
n
X
E
)
(
.
1
,
0
,
)
0
(
,
)
1
(
X
q
X
P
p
X
P
qp
p
q
qp
qp
p
q
qp
²
²
²)
²
(
3
3
3
²)
²
(
)
1
(
)
0
(
)
(
3
3
3
3
3
3
p
q
qp
qp
pq
p
p
q
p
x
p
x

محاضرات اإلحصاء الرياضي
ص
.ب
- 3 -IV
4
التوزيع الثنائي
Distribution binomiale
(أ
)
:استنتاج صيغة قانون التوزيع الثنائي
إذا كررنا جتربة برنويل
n
مرة فإن
X
:(عدد مرات النجاح) تأخذ القيم
X =
0, 1, 5, 3, . . . n
لنفرتض التجربة الربنولية رمي قطعة نقدية
مكررة
عدد
n
،من املرات
و
X
( عدد مرات احلصول على صورة
F
:)
: حالة
n =
5
X =
0, 1, 5.
8
q
8
p
2
) = P(FP) + P(PF) = p*q + q*p =
1
, P(X=
²
) = q*q = q
0
=
P(X
: حالة
n =
3
X =
0, 1, 5, 3.
8
q
2
p
3
) = P(FFP ou PFF ou FPF) =
5
, P(X=
3
) = P(FFF) = p*p*p = p
3
P(X=
: حالة
1
n =
X =
0, 1, 5, 3, 1.
8
q
3
p
4
) = P(FFFP ou PFFF ou FPFF ou FFPF) =
3
P(X=
يف النتيجة األخرية نالحظ العدد
3
هو
x
العدد،
1
هو
n-x
،
و
العدد
1
هو عدد الطرق املالئمة للحصول على
ثال
ث
جناحات
من بني
(
n=
1
)
: وميكن حسابه كما يلي،براتج
وبالتايل فاحتمال عدد ما
x
من النجاحات من بني
n
جتربة برنولية حيسب كما يلي
:
حيث
x
،عدد مرات النجاح
p
احتمال النجاح
يف التجربة الواحدة
،)(يبقى ثابت عند تكرار التجربة
q =
1-p
احتمال
الفشل
و
n
عدد التجا
.رب
" قانون التوزيع الثنائي" فيرعت وه و
:ويكتب قانون التوزيع االحتمايل أيضا كما يلي
x
n
x
x
n
p
p
C
x
X
P
)
1
(
)
(
وأ
X ~ B(n, p)
.
(
ب
)
شروط استخدام التوزيع الثنائي
o
جتربة برنولية مكررة عدد حمدد من املرات
o
احتمال النجاح يف التجربة ثابت
)(التجارب مستقلة
مثال
أحسب عند:
رمي قطعة نقدية
متوازنة
1
مرات احتمال احلصول على
:
، مرتني،ةدحاو ةرم ،ةروص ةرم لاو
3
،مرات
1
.مرات
12
/
1
=
1
0,2
0
0,2
1
0
) = C
0
=
=> P(X
x
-
n
q
x
p
n
x
x) = C
=
P(X
5
0,2
5
0,2
1
5
) = C
5
=
P(X
3
0,2
1
0,2
1
1
) = C
1
=
P(X
مثال
2
نسحب:
باإلرجاع
3
كر
يات من
صندوق
حيتوي
2
كريات منها
3
.محراء
أحسب احتمال احلصول على
كري
تني
محراء
.
1
)
5/2
(
5
)
3/2
(
3
5
) = C
5
P(X=
)!
(
!
!
x
n
x
n
C
x
n
.
.
..
,
3
,
2
,
1
,
,
.
.
..
,
3
,
2
,
1
,
0
,
)
(
n
n
x
q
p
C
x
X
P
x
n
x
x
n

الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 4 -IV
(
ج
)
خصائص التوزيع الثنائي
التوقع
و
التباين
:
ميكن اعتبار
X
تقلة برنوليةــسم تايرغتم عوممج
n
X
+
…
+
i
X
…
+
5
X
+
1
X = X
هلا نف املعلم
p
وبالتايل نف الت
وقع
(E(Xi) = p)
أيضا. إذا باستخدام خصائص التوقع
و
:التباين جند
E(X) = np
pi = n p =>
Σ
E(Xi) =
Σ
) =
n
X
+
…
+
i
X
…
+
5
X
+
1
E(X) = E(X
),
n
X
+
…
+
i
X
…
+
5
X
+
1
V(X) = V(X
Xi
مستقلة إذن
V(X) = ΣV(Xi) = Σpq =>V(X) = npq
مثال
أحسب التوقع:
و
التباين للمثال ال
: سابق
باعتبار:موزعلل ةددجتلما ةلادلا
X
تقلةــــــــسم ةيلونرب تايرغتم عوممج
n
X
+
…
+
i
…X
+
5
X
+
1
X
=
X
هلا نف
املعلم
p
و
:نف الدالة املتجددة للعزوم
]
t
[q + pe
(t) =
X
M
:وباستخدام النظرية السابقة خبصوص الدالة م للعزوم
من أجل"
1
X
و
5
X
تقلة هلاـــسم ع م
ال
دالة م
للعزوم
(t)
1
x
M
و
(t)
5
x
M
:فإن
(t)
5
x
(t). M
1
x
= M
(t)
5
x
+
1
x
M
؛ "
:نستنتج
(t)
xn
… M
(t)
5
x
. M
(t)
1
x
(t) = M
+…xn
5
+x
1
x=x
(t) = M
X
M
n
]
t
[q + pe
(t) =
X
M
>
) =
xnt
E(e
…
)
t
5
x
E(e
.
)
t
1
x
(t)= E(e
X
M
معامل التماثل
يكون منحىن التوزيع الثنائي متما
ثال عندما
= ½
=> p
1
=
p
5
=>
0
=
3
α
معامل التفلطح
يكون منحىن التوزيع معتدال عندما
1/2
=> qp =
3
=
1
α
(د
)
العالقة بين التوزيع الهندسي الزائد:براقت ةدعاق
و
التوزيع الثنائي
الةـح في
N
كبري جدا (يؤول إىل
∞
) فإن
)
1
-
n) / (N
-
(N
تؤول إىل
1
(
n
.)حمدود
و
م
ن جهة أخرى يعطي التوزيع
.الثنائي نتائج قريبة من التوزيع اهلندسي الزائد ويصبح السحب بدون إرجاع مطابقا تقريبا للسحب باإلرجاع
5
)التوزيع الثنائي السالب (باسكال
Distribution binomiale négative
(أ
)
:استنتاج صيغة قانون التوزيع الثنائي السالب
:مثال
نرمي قطعة نقود إىل
ول علىـصلحا ةياغ
3
ل على ذلك بعدــصنح نأ لامتحا بـسحأ .)لا وأ ةيلاتتم( ةروــص تارم
2
،رميات
1
،رميات
3
توقع عدد الرميات الالزمة،تايمر
و
.أحسب التباين
)
(
.
.
.
)
(
)
(
.
3
3
3
3
3
3
p
q
npq
x
p
np
x
x
p
x
p
npq
npq
p
p
npq
2
1
)
1
(
3
npq
p
q
encore
ou
3
:
npq
pq
6
1
3
4

محاضرات اإلحصاء الرياضي
ص
.ب
- 5 -IV
لكن هذه املرة،ةرركم )لشفو حانج ينتجيتن( ةيلونرب ةبرتج انيدل نكيل ديدج نم
إلى غاية الحصول على ع
( دد معين
r
)
من ا
لنجاحات
.
X
يف هذه احلالة هي
عدد مرات تكرار التجربة
إىل غاية احلصول على
r
.جناح
نعلم أن حتقق النجاح؟ لامتحلاا بسيح فيك
r
مرة احتماله
r
p
واحتمال الفشل
r
-
x
مرة يساوي
r
-
x
q
. إذا االحتمال
من جداء هذين االحتمالنيـــضتي بولطلما
r
-
x
q
r
p
. لكن هناك عددا من الطرق امل
ال
ئم
ة لتحقيق
r
جناح من بني
X
جتربة
مع العلم أن آخر جتربة هي جناح. هذا العدد يساوي إذا عدد الطرق املالئمة الختيار
1
-
r
جناح من بني
1
-
x
جتربة
-
x
1
-
r
C
1
.)(التجربة األخرية معلومة النتيجة
يسمى هذا التوزيع توزيع باسكال أو الثنائي السالب ونكتب
:
r, p)
,
N
(
X~B
مي
:كن إذا اإلجابة على أسئلة املثال السابق مبا يلي
1/32
) =
1/1
) (
1/0
(
2
=
5
(½)
3
(½)
1
5
= C
3
-
2
q
3
p
1
-
2
1
-
3
) = C
2
=
P (X
5
=
15/5
=
²)
1/5
) / (
1/5
(
3
=
²
= rq/p
²
σ
,
5
) =
1/5
/(
3
µ = r/p =
(
ب
)
خصائص التوزيع الثنائي السالب
5
التوزيع الهندسي
Distribution géométrique
(أ
)
استنتاج صيغة قانون التوزيع الهندسي
نرمي قطعة نقدية إىل أن حنصل على صورة. احتمال أن يتطلب ذلك
1
:رميات هو
) = P(PPPF)
1
P(X=
ول على النتيجة أو احلدث املطلوب (جناح مرةــــصلحا ةياغ لىإ ةبرجتلا رركن ةرلما هذهو ةيلونبرلا ةبرجتلا لىإ ديدج نم دوعن
.)واحدة
وائيةـــــــــــــــشعلا ةيرغتلما
X
ل فيها النجاح) تتبع التوزيعـــــــــــــــصح تيلا ةرلما اهيف ابم( ةبرجتلا راركت تارم ددع لثتم تيلا
.اهلندسي
إذا رمزنا الحتمال النجاح ب
p
والحتمال الفشل ب
q
:فإن االحتمال ميكن كتابته كما يلي
p
3
) = q
1
P(X=
وبصفة عامة فإن احتمال أي قيمة ل
X
يعرب عنه
: كما يلي
(
ب
)
خصائص التوزيع الهندسي
:مالحظة
التوزيع اهلندسي ما هو إال حالة خاصة من توزيع باسكال حيث
1
r =
,
.
.
.
,
3
,
2
,
1
,
...
,
2
,
1
,
,
)
(
1
1
r
r
r
r
X
q
p
C
x
X
P
r
x
r
r
x
r
t
t
qe
e
p
t
M
p
rq
p
r
1
)
(
,
²
²
,
nq
nq
q
q
q
)
1
(
3
)²
2
(
3
,
1
4
3
.
.
.
,
3
,
2
,
1
,
)
(
1
X
p
q
x
X
P
x
t
t
qe
e
p
t
M
p
q
p
1
)
(
,
²
²
,
1
q
p
q
q
²
12
,
1
4
3

الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 6 -IV
1
التوزيع المتعدد
Distribution multinomiale
(أ
)
استنتاج صيغة قانون التوزيع الثنائي المتعدد
مثال
. نرمي قطعة نرد
1
مرات. أوجد احتمال احلصول على مرتني
الرقم
2
و
مرتني الرقم
1
.
تعمل التوزيع املـــــسي ،طقف ينتجيتن لبقت ةبرتج ةلاح في لمعتـــــسي لولأا امنيبف ،يئانثلا عيزوتلل ميمعت وه ددعتلما عيزوتلا
تعدد
للحالة العامة حيث يكون للتجربة عدد
k
ها. نرمز هلذه النتائج بـــــــضعب نع براجتلا ةيللاقتـــــــسا عم .ةنكملما جئاتنلا نم
k
, . . . A
5
, A
1
A
و
الحتماالهتا ب
k
, . . . p
3
, p
5
, p
1
p
). مبا إن األحداث (النتائج
Ai
متنافية فإن
:
1
=
k
+ . . . + p
3
+ p
5
+ p
1
p
إذا كررنا هذه التجربة
متعددة
النتائج عدد
n
من املرات فسيكون لدينا لكل حدث (نتيجة) متغرية عشوائية متثل عدد مرات
.وقوعه
نرمز هلذه املتغري
ات ب
k
, . . . X
5
, X
1
X
حيث
= n
k
X
+ . . . +
5
+ X
1
X
.
:حيسب احتمال احلدث املركب
k
= x
k
, . . ., X
5
x
=
5
, X
1
x
=
1
X
: كما يلي
(
ب
)
خصائص التوزيع المتعدد
k
) = np
k
E(X
, . . . ,
5
) = np
5
, E(X
1
) = np
1
E(X
k
q
k
) = np
k
V(X
. . .
,
5
q
5
) = np
5
, V(X
1
q
1
) = np
1
V(X
(
ج
)
العالقة مع التوزيع الهندسي الزائد المتعدد
عندما،ددعتلما دئازلا يسدنلها عيزوتلا في
N∞, Ni∞, Ni/N pi
يستخدم التوزيع املتعدد حلساب؛
.االحتماالت
:مثال
إذا رمينا قطعة نرد
15
ب احتمال أن يظهر كل رقم عدد من املرات يتناــــــــــسحأ ،ةرم
ب مع الرقم ذاته (الرقمــــــــــس
1
الرقم،ينترم رهظي
5
يظهر
1
الرقم،تارم
3
يظهر
2
مرات
و
.)هكذا
مثال
3
ندوق بهــــــــــــص نم بحــــــــــــسن .
2
كريات مرقمة من
1
إىل
2
بع مرات على التوايل كرية مث نرجعها إىلــــــــــــس
:الصندوق. أوجد احتمال
3
كريات ذات رقم
1
كريتني ذات رقم،
5
و
كريتني ذات رقم
1
.
k
x
k
x
x
k
k
k
p
p
p
x
x
x
n
x
X
x
X
x
X
P
.
.
.
!
.
.
.
!
!
!
)
,
.
.
.
,
,
(
2
1
2
1
2
1
2
2
1
1
12
4
6
2
1
)
6
/
1
(
.
.
.
)
6
/
1
²(
6
/
1
!
12
.
.
.
!
6
!
4
!
2
!
42
)
12
.
.
.
,
4
,
2
(
X
X
X
P

محاضرات اإلحصاء الرياضي
ص
.ب
- 7 -IV
1
توزيع بواسون
8
Distribution de Poisson
(أ
)
استنتاج صيغة قانون
تو
زيع بواسن
لتكن لدينا جتربة برنولية مكررة عدد كبري جدا أو الهنائي من املرات. مبدئيا املتغرية
X
اليت متثل عدد النجاحات تتبع
لكن قد يصعب حساب االحتمال باستعمال صيغة هذا التوزيع عند،يئانثلا عيزوتلا
ما تكون
n
كبرية. مثال إحتمال
50
جناح إذا كانت
100
n =
هو
:
.
، يصبح عدد مرات تكرار التجربة مقاسا بالزمن؛رارمتساب ةبرجتلا رركتت امدنع
و
يكون احتمال حتقق احلدث يف
حلظة زمن
صغريا جدا. حنتاج يف هذه احلالة إىل إجياد صيغة عامة تعادل صيغة التوزيع الثنائي عندما
n
ي
ؤول إىل
∞
.
نضع
λ
ثابت حبيث
n
λ/
p =
:
: لكن
ومبا أن
:فإن
و هو احتمال
x
جناح يف وحدة زمن واحدة حسب توزيع بواسون حيث
λ >
0
. ونكتب
X~P(λ)
:مالحظة
(
ب
)
خصائص توزيع بواسون
1
باسم سيميون دونيز بواس
ون
)
1010
-
1901
Denis Poisson (
-
Siméon
الفيزيائي و الرياضي الفرنسي الذي استخدم هذا لقانون سنة
1039
يف كتابه حبث
يف احتمال األحكام يف جمال اجلرمية و يف اجملال املدين
(Recherche sur la probabilité des jugements en matière criminelle et en
matière civile)
حيث أ
دخل كنهاية لقانون باسكال والقانون الثنائي. إال أن أول استعمال له للقانون الذي حيمل امسه يعود إىل
1030
. جتدر اإلشارة إىل أن
بواسون صاحب الفضل يف نظرية مهمة أخرى هي نظرية األعداد الكبرية اليت تنسب لشيبيشيف. أنظر ج ج دراوزبيك
[
1999]
.
80
20
20
100
999
.
0
001
.
0
)
20
(
C
P
x
n
x
x
n
x
x
n
n
n
x
x
n
n
q
p
C
x
p
1
!
!
!
)
(
x
n
x
n
n
x
x
n
n
n
n
x
p
)
1
(
)
(
!
)
1
).....(
2
)(
1
(
)
(
x
n
n
x
n
x
n
n
n
n
n
n
n
x
p
x
)
1
(
!
)
1
(
.....
)
2
(
)
1
(
)
(
x
n
x
n
x
n
x
n
n
)
1
(
!
)
1
1
).....(
2
1
)(
1
1
(
1
n
0
1
n
,
.
.
.
,
0
2
n
=>
!
)
1
(
)
(
x
n
x
p
x
n
x
x
n
x
n
n
n
n
)
1
(
)
1
(
)
1
(
: نأخذ
e
n
n
n
)
1
1
(
lim
=>
e
n
n
n
)
1
(
lim
=>
.
)
1
(
lim
e
n
x
n
x
n
x
x
n
x
n
n
x
n
x
x
p
n
n
n
)
1
(
)
1
(
!
)
1
(
!
1
)
(
0
.
.
.
2
1
e
n
n
n
1
lim
1
0
1
1
lim
x
x
n
n
.
.
.
,
2
,
1
,
0
!
)
(
x
x
e
x
p
x
...
71828
.
2
1
1
lim
e
n
n
n
1
3
,
1
,
)
1
(
exp
)
(
,
)
(
)
(
4
3
t
e
t
M
X
V
X
E
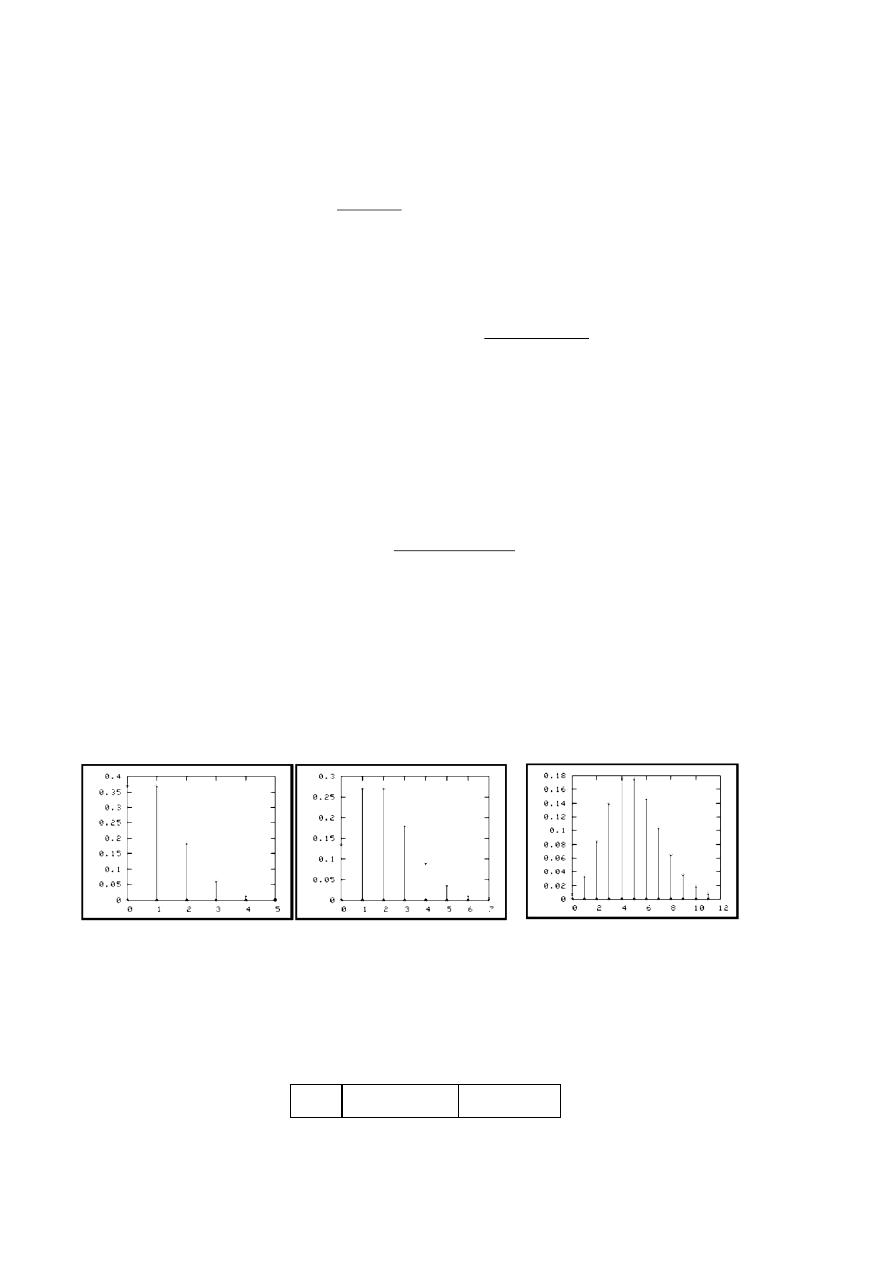
الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 8 -IV
(
ج
)
حساب احتمال عدد من األحداث
في
t
.وحدة زمن
من أجل عدد أو مقدار
t
من وحدات الزمن نعوض
λ
ب
t
λ
:فنجد
.
.
.
,
3
,
2
,
1
,
0
,
!
)
(
X
x
e
t
x
X
P
t
x
t
.مثال
بفرض أن عدد املكاملات اهلاتفية اليت تصل إىل مركز هاتفي معني تتبع توزيع بواسون مبعدل
2
λ=
.يف الثانية
أحسب
احتمال وصول
9
مكاملات يف ثانية
و
نصف
.
(د
)
حساب اح
تمال عدد
من األحداث من فئة معينة
.
إذا كان
X
يتبع توزيع بواسون مبعدل
λ
فإن،
aX
Y=
هو اآلخر يتبع توزيع بواسون مبعدل
λ
a
.
مثال
ون مبعدلـــــساوب عيزوت عبتت ينعم يفتاه زكرم لىإ لـــــصت تيلا ةيفتالها تالماكلما ددع نأ ضرفب .
2
λ=
،يف ثانية
وأن
2
%
من هذه املكاملات هي مكامل
.ات دولية
أحسب احتمال أن تصل
9
.مكاملات دولية يف ثانية
(
ه
)
التمثيل البياني لتوزيع بواسون
دالة توزيع بواسون هي دالة متناقصة لكون قوة
e
سالبة (وهي أقوى من قوة
λ
،)
يرسم توزيع،اعطقتم اعيزوت هنوكل
بواسون من خالل مدرج أعمدة
(Diagramme en bâtons)
. هذا قد يصعب مال
حظة سلوك التوزيع إال باستخدام
حيث يظهر أن التوزيع يقرتب شيئا فشيئا من التوزيع الطبيعي،جيردتلاب ةدعاصتم لماعبم ةلثمأ ةدع
مل
ا
λ
كبري مبا فيه
.الكفاية
الرسوم البيانية
.التالية تبني ذلك
رسم
7
سلوك ت
وزيع بواسون عند زيادة املعلمة من
1
إىل
5
إىل
2
)(من اليسار إىل اليمني
(و
)
.استخدام توزيع بواسون بدال من التوزيع الثنائي
عندما
∞
n
و
املتوسط ثابت يؤول التوزيع الثنائي إىل التوزيع بواسون. عمليا يعطي توزيع بواسون نتائج قريبة من التوزيع
:الثنائي ملا
30
≥
n
و
5
<
np
أو
5
<
nq
!
7
)
5
(
5
.
1
)
7
(
)
5
(
5
.
1
)
7
(
5
.
1
7
e
X
P
t
!
9
))
5
(
05
.
0
(
)
9
(
)
5
(
05
.
0
9
e
X
P

محاضرات اإلحصاء الرياضي
ص
.ب
- 9 -IV
و
يستخدم بعض من اإلحصائيني أيضا كشرط الستعمال قانون بواسون بدال من القانون الثنائي القاعدة التالية
1
:
25
≥
n
و
0،8
≤
p
مثال
نأخذ عشوائيا:
10
وحدات من انتاج آلة نسبة إنتاجها التالف
10
%
. أحسب احتمال أن يكون هناك وحدتان
.تالفتان
0.8131
) =
0
0,9
) (
²
0،1
(
10
5
) = C
5
=
P(X
ط
5
:. باستعمال توزيع بواسون
حنسب أوال قيمة املعلمة
λ
:)(معلمة قانون بواسون
1
=
0،1
*
10
= µ = np =
λ
8،8131
=
e)
5
/(
1
=
!
5
) /
1
-
* e
5
1
(
/x! =
λ
-
* e
x
λ
) =
5
P(
(ز
)
االستخدام العملي لتوزيع بواسون
ظ
تعمل يف جماالت متعددة. فمنـــــــــــسي مويلا هنكل ،ةردانلا ثادحلأا ليثمتل طقف لمعتـــــــــــسي ةليوط ةترفل نوــــــــــساوب عيزوت ل
هرية لــشلا ةــساردلا
(Ladislaus Bortkiewics)
بح اليومــصأ شويلجا في دايلجا تاكــصب دونلجا تاباــصإ ثداوح نع
منها مراقبة اجلودة؛تلاالمجا تىش في لمعتسي نوـساوب عيزوت
االتصاالت (عدد ا،راظتنلاا رهاوظ يريست ،ايئاصحإ
ملكاملات
،)يف وحدة زمن
تخدمـــــــــسي امك
يف الفيزياء
عة ويف البيولوجياـــــــــشم ةدام نم ةثعبنلما تائيزلجا ددع ةـــــــــساردل ةيوونلا
ا
لدقيقة
(microbiologie)
ملراقبة تكاثر البكترييا يف حقل جتارب
،
كما يستخدم
يف البيولوجيا وحىت يف علم األح
.وال اجلوي
ففي هذا النوع من؛"راظتنلاا رهاوظب" ةقلعتم لئاسم ةسارد دنع صاخ لكشب نوساوب عيزوت مدختسي ،يريستلا لامج في
،املسائل
عدد الطائرات اليت:كلذ ةلثمأ نم .نوساوب عيزوت عبتي ةمدلخا ناكم لىإ نئابزلا لوصو نأ ضترفي ام ايرثك
ت
صل
في يديرب بتكم لىإ نوصلي نيذلا نئابزلا ددع ،نمز ةدحو في ءانيم لىإ صلت تيلا رخاوبلا ددع ،نمز ةدحو في راطلما لىإ
... ،ىفـــشتـــسم لىإ لـــصت تيلا ةيلاجعتـــسلاا تلاالحا ددع ،يفتاه زكرم لىإ لـــصت تيلا ةيفتالها تالماكلما ددع ،نمز ةدحو
تسمى هذه الظواهر يف نظرية صفوف االن
."بظواهر الوصول" راظت
مثال
8
.. بينت دراسة أن عدد حوادث العمل يف معمل معني يتبع توزيع بواسون مبعدل حادثتني يوميا
:أوجد احتمال أن ال يسجل أي حادث يف يوم معني. أوجد احتمال حادث على األقل يف يوم
5
-
= e
λ
-
e
) =
0
=
P(X
! =>
0
/
λ
-
* e
0
λ
/x! =
λ
-
* e
x
λ
) =
0
=
P(X
5
-
e
–
1
=
λ
-
e
-
8
=
)
8
P(X ≥
!] =>
0
/
λ
-
* e
0
λ
[
–
1
) =
0
P(
-
1
) =
1
≥
P(X
مثال
2
اعةــسلا ينب ةنيعم نيزنب ةطمح لىإ لـصت تيلا تارايــسلا ددع نأ ةقباـس ةيئاــصحإ ةـسارد تنيب .
15:00
و
15:02
طـسوتلما في وه
3
ل إىلـصت تيلا تارايـسلا ددع نأ ةـساردلا تنيب امك ،تارايـس
احملطة يتبع توزيع بواسون. أوجد احت
مال
أن تصل
1
سيارات بني
15:00
و
15:02
.
= متوسط عدد السيارات يف الساعة
5
*
3
=
2
:ومنه
2
-
e
*
21
=
51
/
2
-
* e
1592
=
!
1
/
2
-
* e
1
2
) =
1
P(X=
1
أنظر دروزبيك
1999
ص،
525
.

الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 11 -IV
ا للتوزيع الثنائيـضيأو نوـساوب عيزوتل نأ لىإ ةراـشلإا يغبني ،يرخلأا في
ائص مهمة ال يتسع املقام لذكرـصخ
ها يف إطار هذا
دجوت امك ؛ةــــــــصــــــــصختلما عجارلما في اهتعلاطم لىإ بلاطلا لينح كلذل ،تاقيبطتلا في اهــــــــضعبل ضرعتنــــــــس نكلو ،سردلا
تخداماهتا مثل التوزيع املتماثلــــــسا ددعتل ارظن ةمهم ىرخأ تاعيزوت
(distribution uniforme)
مل نتطرق هلا يف هذا،
الد
. ندعو الطالب الستكماهلا من خالل حبثه اخلاص،سر
1
خالصة
اجلدول امللحق يلخص أهم الن
.قاط حول التوزيعات املتقطعة الشهرية
محاضرات اإلحصاء الرياضي
ص
.ب
- 11 -IV
التوزيع
متى يستخدم
القيم الممكنة للمتغيرة
االحتمال
التوقع
و
التباين
الهندسي الزائد
b,p)
X~ H(N,
.سحب بدون إرجاع
.كريات من صنفني
X ={
0،1,5,…,b}
,
b ≤ b + r = N
p = b/N
و
q = r/N
n
حوبةــــــسلما تايركلا ددع
N
ال
عدد
الكلي ل
لكريات
b
عدد الكريات البيضاء
r
ع الكريات احلمراء
الهنادساااااااااااي الزائد
المتعدد
روط تـــــــــــــــــــــش ـــــــفـــــــن
عم دــــــئازلا يـــــــــــــــسدـــــنلها
ينفنــــــص نم رثكأ دوجو
.من الكريات
Xi
={
0،1،5,…,Ni} ,
Σxi = n, ΣNi =
N
)=
k
=x
k
,…X
5
=x
5
,X
1
=x
1
P(X
/N)
i
] = n (N
i
E[X
i
= np
باااااااااااااارنااااااااااااااولااااااااااااااي
X~B(
8, p)
ريـــــــغ( ةدــــــــحاو ةــــــــبرــــــتج
.مكررة) تقبل نتيجتني
X = {
0, 1}
P(X =
1) = p,
P(X =
0) = 1 - p = q
μ = p, σ
²= pq
الثنائي
X~B(n, p)
،ةـــجيتنلا ةـــيئاـــنث براـــتج
مكررة
و
( تقلةــــــــــــــسم
p
.)ثابت
X = {
0،1،5…,n}
x
-
n
q
x
p
n
x
x) = C
=
P(X
μ= np, σ
² = npq
باسااااااااكال (الثنائي
)السالب
X
اربـــجتلا ددـــع يه
ىلع لوــــــــــصحلل ةمزلالا
ددــع
r
اتــحاــجنلا نم
ةــــــــيــــــلوــــــنرــــــب براــــــــتج في
.مكررة
X = {r, r +
1, r
+
5, …, +∞}
r
-
x
q
r
p
1
-
x
1
-
r
x) = C
=
P(X
μ = r/p ,
σ
² = rq/p²
الهندسي
X
اربـــجتلا ددـــع يه
الالزمة
ول علىــــــــــصحلل
براتج في لولأا حاجنلا
.برنولية مكررة
X =
{
1،5,…,+∞}
p
1
-
x
x) = q
=
P(X
μ =
1/p,
σ
² = q/p²
التوزيع المتعدد
عـــيزوـــتـــلـــل مـــيـــمـــعـــت وـــه
الثنائي على جتربة مكرر
ة
.متعددة النتائج
k
) = np
k
E(X
k
q
k
) = np
k
V(X
بااااااااااااااااواسااااااااااااااااااااااااااون
X~P(λ)
λ >
0
X
اتــحاــجنلا ددــع
دد كــــع في
دا منــــج يرب
ددع( ةيلونبرلا براـجتلا
في ةــــــفلاــــــتلا تادــــــحولا
ددع اــــضيأ وأ .)ةنحــــش
ةترف في ثادـــــــحلأا نم
.زمن
X =
{
0،1،5,…,+∞}
λ
-
e
) =
0
=
X
(
P
λ
-
e
-
1
) =
1
≥
P(X
E(x) = V(x) = λ
n
N
x
n
r
x
b
C
C
C
x
X
P
)
(
1
²
,
N
n
N
npq
np
1
²
,
N
n
N
npq
np
n
N
xk
Nk
x
N
x
N
x
N
xk
x
x
Nk
N
N
xk
Nk
x
N
x
N
x
N
C
C
C
C
C
C
C
C
C
C
3
3
2
2
1
1
...
2
1
...
2
1
3
3
2
2
1
1
N
Ni
n
xi
Ni
xi
i
k
i
k
i
1
1
,
,
0
,
)
,
.
.
.
,
,
(
2
2
1
1
k
k
x
X
x
X
x
X
P
k
x
k
x
x
k
p
p
p
x
x
x
n
.
.
.
!
.
.
.
!
!
!
2
1
2
1
2
1
!
)
(
x
e
x
X
P
x
)!
(
!
!
x
n
x
n
C
x
n
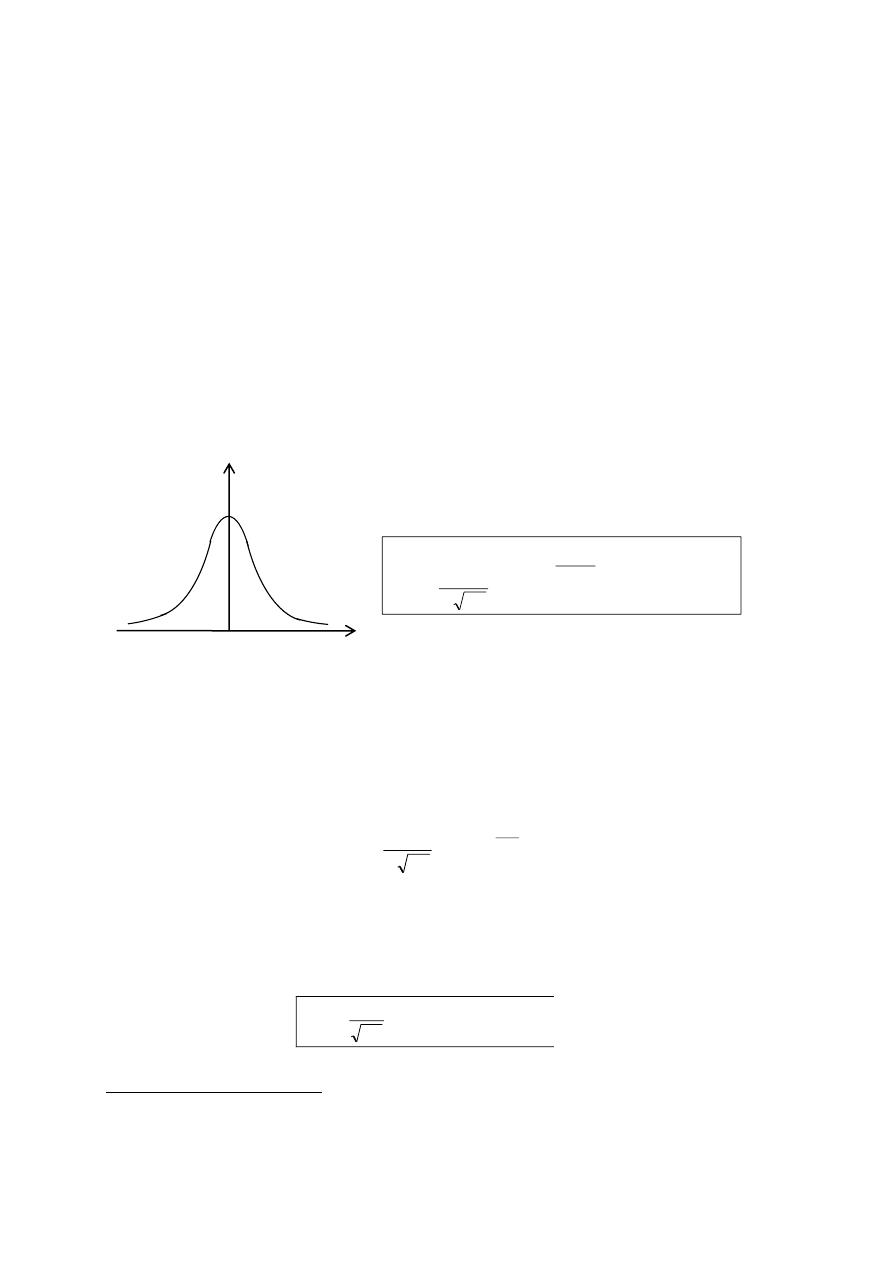
الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 12 -IV
المبحث
2
.
التوزيعات االحتمالية الشائعة المستمرة
التوزيع الطبيعي
التوزيع األسي
توزيع قاما
توز
يع بيت
ا
8
التوزيع الطبيعي أو توزيع البالس قوس
1
Gausse
-
de Laplace
D.
Normale ou
.
D
يعد
التوزيع الطبيعي من أهم التوزيعات االحتمالية شائعة االستخدام ملا له من خصائص تنطبق على نسبة كبرية من
الظواهر الطبيعية واالجتماعية واالقتصادية. فلو اخرتنا بالصدفة مئة أو أل
فا من املارين يف شار ع ما وقسنا أط
واهلم لوجدنا
ونسبة قليلة من طوال القامة،ام طسوتم نم ةبيرق اهنم ةيربك ةبسن
و
نسبة مقاربة هلا من قصار القامة. ومثل هذا بال
نسبة
أو ما ميكن أ،ةبسنلا لثيم يذلا نىحنلما ناكل ناجتم دماعتم ملعم في تانايبلا هذه انلثم ولو .نازولأل
ن
نسميه
،االحتمال
ذا شكل جرسي متماثل حول املتوسط وهي صفات التوزيع الطبيعي
(الشكل
9
)
:
(أ
)
صيغة القانون
تكتب دالة الكثافة
ملنحىن
:للتوزيع الطبيعي كما يلي
حيث
µ
و
σ
مها على التوايل التوقع
و
.االحنراف املعياري
ونكتب
X ~ N(µ, σ)
دالة التوزيع (الدالة التجميعي
ة) للتوزيع الطبيعي
:تكتب كما يلي
المتغيرة المركزية أو المعيارية
:
تستخدم املتغرية املعيارية
Z = (X-µ)/σ
لتكوين اجلداول اإلحصائية لالحتماالت
:
P(
0
≤ Z ≤ z)
أو
F(z) = P(Z ≤ z)
،
حيث تسمح بكتابة الدالة
f
و
F
بداللة جم
هول واحد
Z
بدال من
3
جم
اهيل
x
و
µ
و
σ
وذلك
:كما يلي
1
باسم
العاملان الرياضيان الفيزيائيان و الفلكيان الفرنسي
Pière Simon de Laplace
)
1059
-
1919
(
و
األملاين
Carl Freidrich Gauss
-
الصورة هلذا األخري
-
،
(
1999-1022)
الذين كانا من أوائل من اكتشف هذا القانون. أما من أعطاه تسمية التوزيع الطبيعي فهو
Pearson
يف
1093
. أنظر
(
1999) J. J. Droesbeke
ص،
359
.
x
x
e
x
f
2
2
/
1
2
1
)
(
x
v
dv
e
x
X
P
x
F
2
2
/
1
2
1
)
(
)
(
z
z
f
e
z
2
/
²
2
1
)
(
f(x)
x
μ
رسم
8
الشكل العام للتوزيع الطبيعي
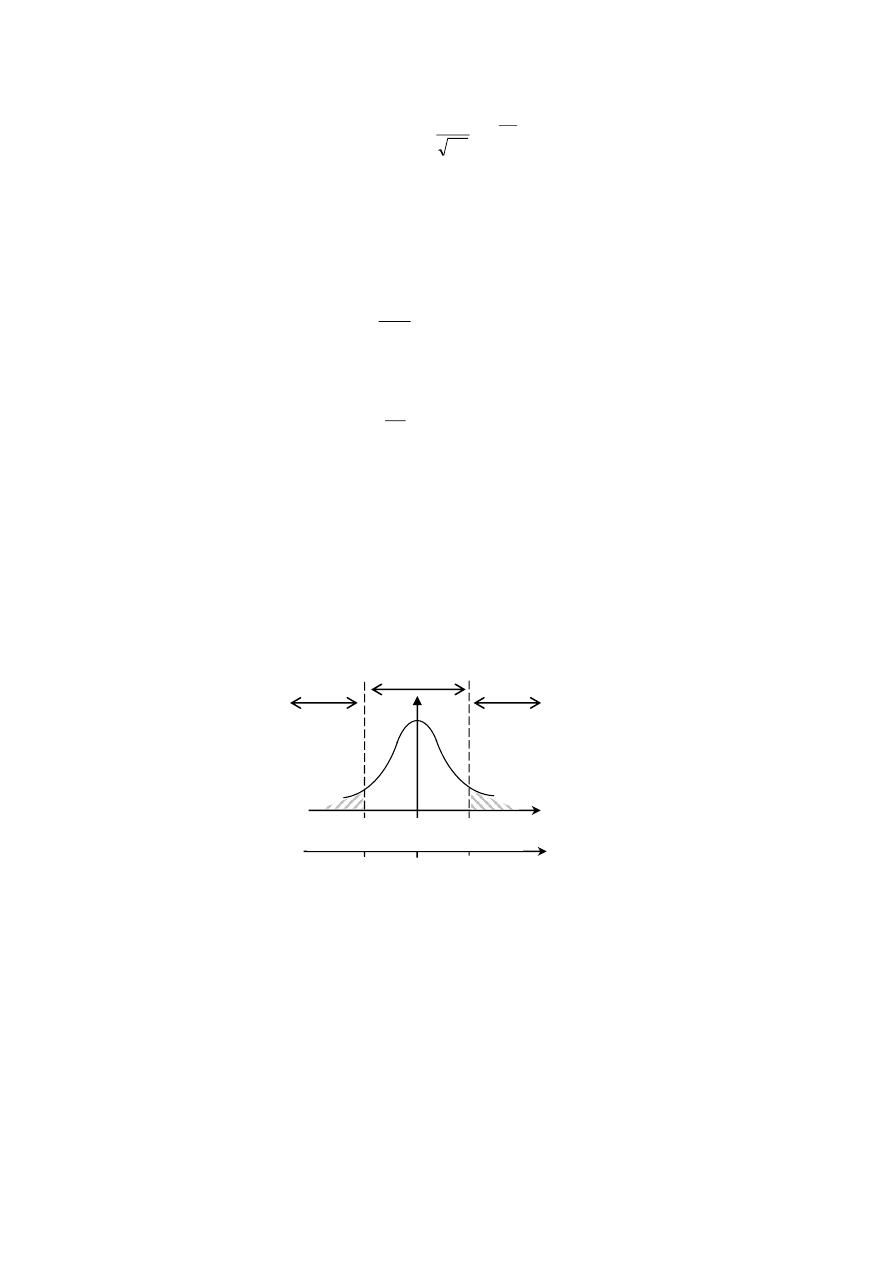
محاضرات اإلحصاء الرياضي
ص
.ب
- 13 -IV
بالنظر إىل العالقة
اخلطية
بني املتغريتني
X
و
Z
،
فإن
Z
تتبع نف توزيع
X
.أي التوزيع الطبيعي
و
ن
:علم أن
0
) =
Z
(
E
8
) =
Z
(
V
(
ب
)
خصائص التوزيع الطبيعي
الدالة المتجددة للعزوم
:
من خصائص التوزيع الطبيعي أنه يعترب
معتدال ال
مدبب
ا
وال مفلطح
حيث،ا
يعترب
معامل التفلطح
3
=
1
α
للتوزيع الطبيعي
معيارا العتدال املنحن
يات
.
املتوقعة
من خصائص التوزيع الطبيعي
أيضا
أنه
متماثل ح
ول القيمة
تماثل منحنى
X
حول املتوسط (أنظر الشكل
3
)
يعين متاثل ملنحىن
Z
حول
0
مما يعين أنه من أجل أي قيمة للمتغرية،
املعيارية
z >
0
:
P(
0
≤ Z ≤ z) = P(-z ≤ Z ≤
0
) = P(-z ≤ Z ≤ z) /
2
P(Z ≤ -z) =
1
- P(Z ≤ z) = P(Z ≥ z)
و لقد مت باستخدام املتغرية املعيارية
Z
:حساب االحتماالت (املساحات) حتت املنحىن ومنها خاصة
P(-σ ≤ X ≤ σ) = P(-σ ≤ Z ≤ σ) = 1.6837,
P(-
5 σ ≤ X ≤ 2 σ) = P(-5 ≤ Z ≤ 2) = 149544,
P(-
3 σ ≤ X ≤ 3 σ) = P(-3 ≤ Z ≤ 3) = 149973.
هذه القيم وغريها متوفرة يف اجلداول اإلحصائية اليت جندها يف الكثري من املراجع
،
كما ميكن حساهب
ب ا
سا
.تخدام احلاسوب
z
u
du
e
z
Z
P
z
F
2
²
2
1
)
(
)
(
رسم
1
استخدام تماثل الوزيع
الطبيعي في حساب االحتماالت
0
3
3
3
2
²
²
exp
)
(
t
t
t
M
x
Z
P(Z ≥ z)
P(Z ≤ -z)
P(-z ≤ Z ≤ z)
-z
1 z
µ
X
الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 14 -IV
مثال
باستعم:
ال اجلداول االحصائية
1
: ) أحسب
P(
0
≤ Z ≤ z)
حيث
z =
1
,
5
,
3
5
)
أحسب
P(-z ≤ Z ≤ z)
من أجل نف القيم ل
z
.
1
)
0,3113
،
0,19952
،
0,19022
5
)
0,2059
،
0,9212
،
0,9993
(
ج
)
العالقة بين التوزيع الطبيعي
و
التوزيع الثنائي
يف حالة
n
كبرية
و
p
غري قريب من
0
مي
.كن اعتبار التوزيع الثنائي كتقريب جيد للتوزيع الطبيعي
و
يعطي
التوزيعان نتائج أكثر
تقاربا كلما كانت
n
:كبرية أكثر. ونكتب
ويسرع تقارب التوزيع الثنائي من التوزيع الطبيعي كون
p
قريب من
0,2
.
قاعدة التقريب
:
عموما نعتبر التقريب إلى التوزيع الثنائي مالئما عندم
ا
np
و
nq
كالهما أكبر من
5
.
عدد من االحصائيني
1
:يعتمد قاعدة أخرى هي أن يكون أحد الشرطني التاليني متوفرين
1
أنظر
دراوزبيك
1999
. ص
525
.
npq
np
x
z
dz
e
b
z
a
P
b
a
z
n
,
2
1
)
(
lim
2
/
²
10
,
10
,
20
9
nq
np
n
ou
npq
رسم
15
المساحات األساسية تحت
منحنى التوزيع الطبيعي
μ - 6σ
μ - 5σ
μ - 4σ
μ - 3σ
μ - 2σ
μ -1σ
μ
μ +1σ
μ + 2σ
μ + 3σ
μ + 4σ
μ + 5σ
μ + 6σ
2σ = 68.26%
4σ = 95.44%
6σ = 99.73%
8σ = 99.9937%
10σ = 99.999943%
12σ = 99.9999998%

محاضرات اإلحصاء الرياضي
ص
.ب
- 15 -IV
(د
)
العالقة بين التوزيع الطبيعي
و
توزيع بواسون
عندما
λ→ ∞
فإن التوزيعني الطبيعي
و
:بواسون يعطيان نتائج متطابقة . ونكتب
رس
م
11
سلوك توزيع بواسون عند زيادة املعلمة من
1
إىل
5
إىل
2
)(من اليسار إىل اليمني
:قاعدة التقريب
o
عموما نعتبر أن التقريب مالئم
من التوزيع بواسون إلى التوزيع الطبيعي
عند
ما
λ ≥
80
o
فيما يعتمد عدد من اإلحصائيين
1
كشرط للتقريب
85
≥
λ
وميكن أن تتقارب نتائج التوزيعات الثالث
معا
:
بواسون،يئانثلا
و
الطبيعي حسب الشروط املذكورة
)
أنظر حل التطبيق
أدناه
).
2
التوزيع األسي
Distribution exponentielle
مدة مكامل،ديبرلا كابش ةمدخ ةدم كلذ نم .نمزلا سايقب ةقلعتم لئاسم في يسلأا عيزوتلا مدختسي ام ةداع
ة
مدة،ةيفتاه
مدة،ةلآ حيلصت مدة،نحش ةرخاب غيرفت
انتظار زبون قبل احلصول على اخلدمة...يف العلوم الدقيقة يستخدم
ا
لتوزيع األسي
لتمثيل مدة حياة الذرات املشعة
(atomes radioactives)
حيث يعرب الوسيط عن اللحظة اليت يبقى،ككفتت نأ لبق
فيها نصف اجملتمع األصلي
5
.
من
كقاعدة عامة يستخدم التوزيع األسي لتمثيل مدة حياة ظاهرة ما إذا كان:تيلآا مهف يرورضلا
هلا
متوسط
ث
ابت
1
/λ
وكانت هذه الظاهرة ال ختضع للتقادم
(vieillissement)
أي أن مدة حياة الظاهرة بعد حلظة ما
T
ال تتبع اللحظة
T
؛
أي ال تتأثر باملدة اليت دامتها الظاهرة من قب
.ل
مثال
قد ن
ستبعد استخدام التوزيع األسي لتمثيل مدة حياة آلة عامل
ة قبل
ةايح ةدلم ةبسنلاب رملأا كلذك ،لبق نم ةللآا اهتلمع تيلا ةدلما نع لاقتسم يل ةظلح في اهلطعت لامتحا نلأ اهلطعت
اإلنسان
.
لظاهرة ما م_رخآ عيزوت يأ وأ_ يسلأا عيزوتلا ليثتم ةقد نم ققحتن ،ايلمع
ن خالل
تقنيات
اختبارات الف
روض
وبالتحديد،
.اختبار التجان و التعديل
فإن املدة بني وقوع،عيزوتلا اذه عبتي ام ثادحأ عوقو ناك اذإف ،نوساوب عيزوتلاب ةقلاع يسلأا عيزوتلل نأ لىإ ايرخأ يرشن
حدثني تتبع التوزيع األسي
إذا كان وصول الزبائن إىل مركز خدم،كلذ ىلع لاثمك ؛
ة ما يتبع التوزيع بواسو
ن فإن املدة الزمنية
والزبون املوايل تتبع التوزيع األسي. تتبني هذه العالقة عند"أ" نوبز لوصو ينب
استنتاج صيغة القان
.ون األسي
1
.املرجع نفسه
5
راجع موقع موسوعة
Wikipédia
.
b
a
z
dz
e
b
x
a
P
2
²
2
1
lim

الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 16 -IV
(أ
)
صيغة القانون
األسي
أو دالة الكثافة و الدالة التجميعية للتوزيع
.
بينت دراسة أن عدد حوادث العمل يف معمل معني
تت
بع توزيع بواسون مبعدل
λ
حادث يوميا
.
أوجد احتمال أن يسجل حادث على األقل (حادث أو أكثر) يف
مدة
t
.يوم
t
λ
-
e
-
8
=
)
8
≥
P(X
-
* e
t
0
λ
[
-
1
) =
0
P(
-
1
=
)
1
≥
P(X
=>
!]
0
/
t
λ
لنرمز ب
T
للزمن (باليوم) بني حادثني
إذن سيكون لدينا
f(t)
،دالة الكثافة للزمن بني حادثني
و
F(t) = P(T ≤ t)
دالة
التوزيع ل
T
.
لنحسب
احتمال
P
أن
يكون الزمن بني حادثني
يوم
أو أقل
:
لدينا
P = P(T ≤ t =
1
)
إذن
:
(
1
............ )
P = F(t =
1
)
الحظ
من ناحية أخرى
أ
ن
P
هو معادل الحتمال أن يسجل على األقل حادث يف يوم معني
:
(
5
..........)
t
λ
-
e
-
1
=
)
1
≥
P(X
=
P
( من
1
)
(و
5
) نستنتج أن
)
3
............(
t
λ
-
e
-
8
=
)
t
F(
و منه
)’
t
λ
-
e
-
1
)’ = (
t
) = F(
t
f(
إذن
t
λ
-
e
λ
) =
t
f(
:قاعدة
إذا كان حدث عشوائي ما يتكرر يف الزمن وفق توزيع بواسون
:
فإن الزمن
T
:بني حادثني يتبع التوزيع التايل
حيث
λ
.عدد حقيقي موجب
.و يسمى هذا التوزيع التوزيع األسي ويسمى أيضا التوزيع األسي السالب لعالقته بتوزيع بواسون
(
ب
)
التمثيل البياني للتوزيع األسي
!
)
(
x
x
p
e
x
0
,
0
0
,
)
(
e
f
رسم
12
دالة الكثافة للتوزيع األسي

محاضرات اإلحصاء الرياضي
ص
.ب
- 17 -IV
(
ج
)
خصائص التوزيع األسي
3
توزيع قاما
amma
g
Distribution
توزيعي قاما و بيتا ميثالن جمموعة واسعة من التوزيعات ذات معلمتني تتميز مبرونة وقدرة على توليد توزيعات متعددة
حسب قيم املعلمتني. ندرس هذين التوزيعني أيضا لعالقتهما بالتوزيعات
F
،
t
و،
ك
5
. يستخدم توزيع قاما لتمثيل بعض
الظواهر مثل توزيع الدخل واالدخار حتت شروط معينة
8
.
(أ
)
صيغة القانون
.
:نقول عن متغرية عشوائية أهنا تتبع توزيع قاما إذا كانت دالة كثافتها كما يلي
حيث
α)
Γ(
هي الدالة قاما
:
ونكتب
β)
Γ(α,
X ~
(
ب
)
خ
صائص توزيع قام
ا
α
-
)
t
β
-
8
) = (
t
(
M
,
²
= α β
²
σ
α β ,
µ =
Pour α>
1
: Γ(α) = (α-
1
)Γ(α-
1
) et si α
N : Γ(α) = (α-
1
) ! , Γ(
1/5
) = √π
من خصائص توزيع قاما عالقته بالتوزيع األسي
كما سنرى يف السلسلة
.
.مثال
:أحسب ما يلي
مثال
5
.
أحسب املتوسط و
التباين للمتغريات
العشوائي
ة
X
و
Y
و
Z
:املعرفة كما يلي
1
: سلسلة،تانايبلل ةيلولأا ةلجاعلما و ةجذمنلا ئدابم ،نورخآ و نايزافيآ :رظنأ
Mathématiques
،
Editions Mir
، موسكو،
1903
ترمجه من،
الروسية
،إىل الفرنسية جياليل مبارك
1902
. ص
120
.
t
t
M
Med
x
)
(
,
)
2
ln(
,
²
/
1
²
,
/
1
0
,
0
,
0
,
0
0
,
)
(
)
(
/
1
x
x
e
x
x
f
x
.
5
.
2
,
5
.
4
,
7
,
,
,
0
2
/
1
0
6
0
4
dx
x
e
dx
e
x
dt
e
t
x
x
t
2
/
1
,
720
!
6
7
,
24
!
4
)
5
(
0
2
/
1
0
2
/
1
0
6
0
4
dx
e
x
dx
x
e
dx
e
x
dt
e
t
x
x
x
t
5
.
1
)
5
.
0
(
5
.
1
)
5
.
2
(
,
720
!
6
7
)
5
.
0
)(
5
.
1
)(
5
.
2
(
5
.
3
5
.
0
)
5
.
0
)(
5
.
1
)(
5
.
2
(
5
.
3
5
.
2
)
5
.
2
(
5
.
3
5
.
3
5
.
3
1
5
.
3
5
.
4
0
0
1
dt
e
t
t
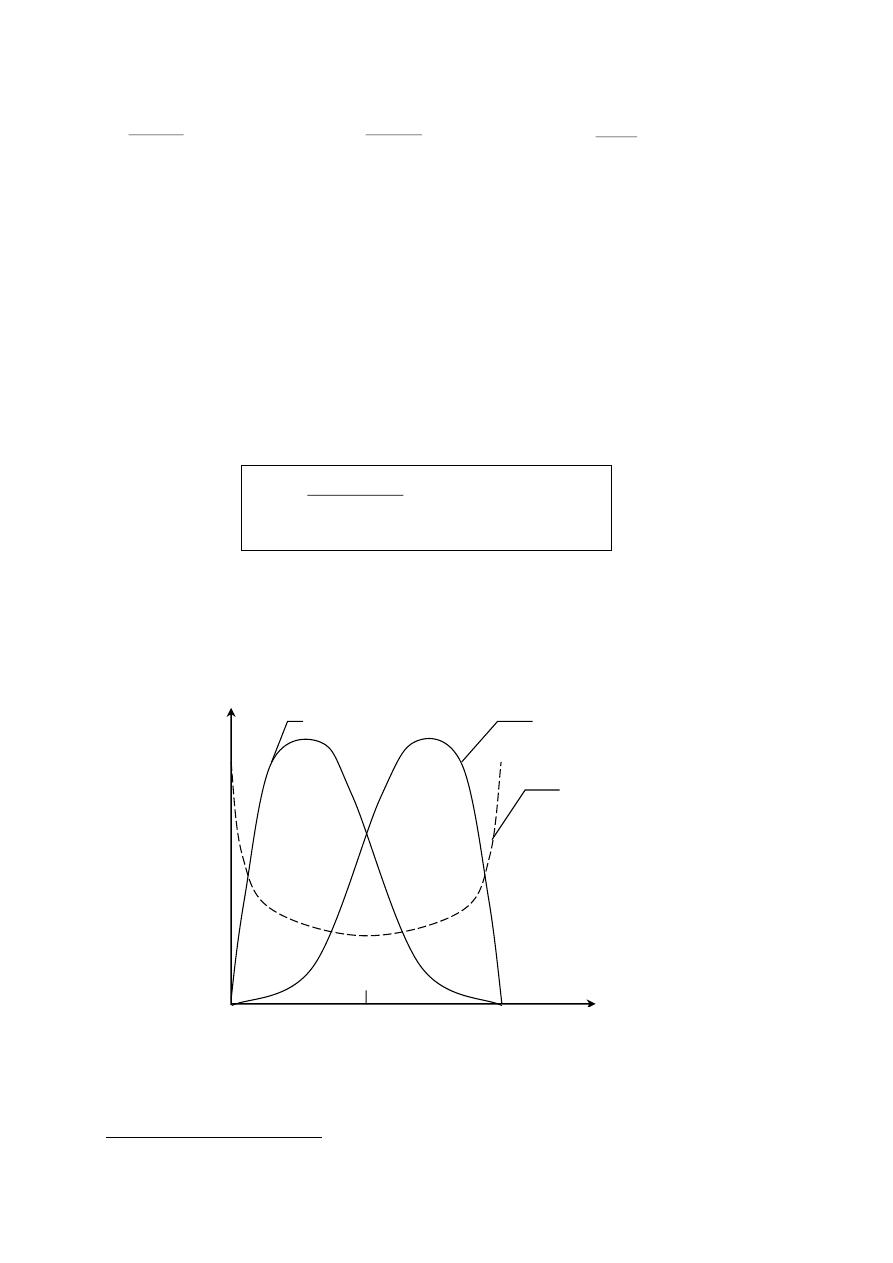
الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 18 -IV
4
توزيع بيتا
Distribution bêta
يتميز توزيع بيتا مبرونته الكبرية
تبعا لقيم معلمتيه (أنظر الرسم
11
)
حيث
يستخدم حلساب توزيع
t
²
،
F
، التوزيع الثنائي،
الثنائي السالب وغريها
8
،
وتستخدم لتمثيل بعض املتغريات اليت ترتاوح بني
0
و
1
مثل نسب،
ة ما كنسبة التالف أو
. إخل،تاعيبلما
(أ
)
صيغة القانون
.
:نقول عن متغرية عشوائية أهنا تتبع توزيع بيتا إذا كانت دالة كثافتها كما يلي
حيث
α, β)
B(
:هي الدالة بيتا
و نكتب
B(α, β)
X ~
= 4,
= 2
رسم
13
التمثيل البياين لدالة الكثافة للتوزيع بيتا من أجل قيم خمتلفة للمعامل
1
.املرجع السابق
0
,
0
0
,
6
)
(
,
0
,
0
0
,
)
6
(
4
)
(
,
0
,
0
0
,
5
2
)
(
2
4
4
/
3
5
2
/
4
z
z
e
z
z
f
y
y
e
y
y
f
x
x
e
x
x
f
z
y
x
3
²
,
3
)
1
(
3
,
64
²)
4
(
4
²
,
16
)
4
(
4
,
20
²)
2
(
5
²
²
,
10
)
2
(
5
z
z
y
y
x
x
)
0
,
(
0
1
0
,
1
)
(
1
1
ailleurs
x
x
x
x
f
0
,
,
)
1
(
)
,
(
1
0
1
1
du
u
u
B
1
1,5 1،1 x
f(x)
= 2,
= 4
= 4,
= 2
= 1/2,
= 1/2

محاضرات اإلحصاء الرياضي
ص
.ب
- 19 -IV
(
ب
)
خصائص توزيع بيتا
(
ج
)
العالقة بين الدالتين قاما
و
بيتا
:
:مثال. أحسب ما يلي
مثال
5
:. أحسب ما يلي
وباستعمال العالقة
جند
:أن دالة الكثافة للتوزيع بيتا تكتب أيضا
للتوز
يعني قاما وبيتا عالقة بعدد من التوزيعات املهمة كالتوزيع األسي وتوزيع كاي تربيع
من ذلك،
م
ثال
أن
التوزيع األسي هو
حالة خاصة من توزيع قاما عندما
α =
8
, β =
8
/λ
.
مثال
3
. أحسب النسبة املتوقعة
لإلنتاج ال
تالف
و
ال
تباين
إذا كانت نسبة اإلنتاج التالف تتبع التوزيع،
ا
:لتايل
:من املثال السابق لدينا
بوضع
و
يساويان
1
و
2
على التوايل
جند أن،
B(
1
,
2
)
X ~
:ومنه
مثال
1
واحتمال أن تبلغ النسبة،ةعقوتلما ةبسنلا بسحأ .لياتلا عيزوتلا عبتت ةسسؤم في عابلما جاتنلإا ةبسن .
أ
كثر من
32
%
.
1
²
²
,
)
(
)
(
)
(
)
,
(
B
)
(
)
1
,
(
),
,
1
(
),
2
,
(
),
2
/
1
,
2
/
1
(
),
4
,
3
(
N
n
n
B
n
B
n
B
B
B
n
n
n
n
B
n
n
n
n
B
n
n
n
n
n
B
B
B
1
!
)!
1
(
)
1
,
(
,
1
!
)!
1
(
)
,
1
(
),
1
(
)!
1
(
!
1
)!
1
(
)
2
,
(
,
)
2
/
1
(
)
2
/
1
(
)
2
/
1
,
2
/
1
(
,
60
1
120
2
)!
1
7
(
)!
1
4
(
)!
1
3
(
)
4
,
3
(
n
n
n
n
B
n
n
n
n
n
n
n
B
n
n
n
n
B
1
!
1
)!
1
(
)
1
,
(
,
1
)!
1
(
)!
1
(
!
)!
1
(
1
)
,
1
(
,
)!
1
(
1
)!
1
2
(
!
1
)!
1
(
)
2
,
(
1
0
1
0
3
4
)
1
(
,
)
1
(
dx
x
x
dx
x
x
,
)
2
,
3
(
B
12
/
1
)]
4
(
3
/[
1
)]
1
(
/[
1
)
2
,
3
(
n
n
B
6
/
1
!
3
!
1
!
1
)
2
,
2
(
)
1
(
,
280
1
!
8
!
3
!
4
)
4
5
(
)
4
(
5
)
4
,
5
(
)
1
(
1
0
1
0
3
4
B
dx
x
x
B
dx
x
x
)
(
)
(
)
(
)
,
(
B
ailleurs
x
x
x
x
f
,
0
1
0
,
1
)
(
)
(
)
(
1
1
sinon
,
0
1
0
,
)
1
(
6
)
(
5
x
x
x
f
).
6
,
1
(
/
1
6
/
1
)
,
1
(
B
n
n
B
.
20
/
1
)
5
(
16
4
)
1
²(
²
,
2
/
1
الفصل الرابع
التوزيعات االحتمالية األكثر استخداما
- 21 -IV
5
خالصة
اجلدول التايل يلخص خ
.صائص التوزيعات االحتمالية املستمرة األكثر استخداما
التوزيع
دالة الكثافة
،
التوقع
و
التباين
خصائص التوزيع
الاتوزيع الطبيعي
المعياري
,
0
X~N(
)
1
E(Z) =
0
, V(Z) =
1
P(Z ≤ -z) =
1
- P(Z ≤ z) =
P(Z ≥ z)
P(-σ ≤ X ≤ σ) =
P(-1 ≤ Z ≤ 1) = 146837,
P(-
5 σ ≤ X ≤ 2 σ) =
P(-
5 ≤ Z ≤ 2) = 149544,
P(-
3 σ ≤ X ≤ 3 σ) =
P(-3 ≤ Z ≤ 3) = 149973.
التوزيع األسي
=
1/λ,
σ² = 1/ λ²
-
1
F(x) =
x
λ
-
e
P(X ≤
) =
0,23
توزيع قاما
X
~Γ(α,β)
µ = α β,
σ
²
= α β
²
توزيع بيتا
B(α, β)
X~
3125
.
0
²
3
)
1
(
12
)
35
.
0
(
1
²
:
.
)
1
²(
12
)
35
.
0
(
%
60
5
/
3
2
3
3
)
2
,
3
(
~
)
2
,
3
(
/
1
12
4
*
3
12
sinon
,
0
1
0
),
1
²(
12
)
(
1
35
,
0
1
35
,
0
3
1
35
,
0
dx
x
x
x
X
P
x
u
et
dx
x
v
soit
dx
x
x
X
P
B
X
B
x
x
x
x
f
z
z
f
e
z
2
/
²
2
1
)
(
0
,
0
0
,
)
(
e
f
0
,
0
,
0
,
0
0
,
)
(
)
(
/
1
x
x
e
x
x
f
x
)
0
,
(
0
1
0
,
1
)
(
1
1
ailleurs
x
x
x
x
f
1
²
²
,
0
,
,
)
1
(
)
,
(
1
0
1
1
du
u
u
B
)
(
)
(
)
(
)
,
(
B
0
0
1
dt
e
t
t
محاضرات اإلحصاء الرياضي
ص
.ب
- 1 -V
الفصل
V
.
ا
لمتغيرات العشوائية متعدد
ة
األبعاد
المتغيرة
ال
ثنائية
االستقالل التباين
و
االرتباط
درسنا
يف الفصل األول املفاهيم
و
القواعد األساسية يف نظرية االحتماالت كاالحتمال البسيط
و
االحتمال امل
تعدد
و
قاعدة
مجع وضرب االحتماالت
.
تساعد
هذه املفاهيم
املسري على التقدير وعلى اختاذ القرار املناسب جتاه مسائل متشعبة وغري
.مؤكدة النتائج
يف الفصل الثاين
درسنا مفهوم املتغرية العشوائية والتوزيع االحتمايل (أو القانون االحتمايل) وتطرقنا إىل
عدد
من التوزيعات اال
.حتمالية الشهرية
تستخدم املتغرية العشوائية
ل
تمثيل الظواهر املختلفة من أجل دراستها والت
.وقع بشأهنا
يف
هذا الفصل سنتناول نوعا من املتغريات العشوائية وتوزيعاهتا وهي املتغري
ات
العشوائية
ذات أكثر من ب
عد
باإلضافة إىل مفاهيم،
أخرى
مهمة
متعلقة باالرتباط بني املتغ
.ريات
ذلك أن العديد من الظواهر وا
ملسائل اليت تطرح أمام املسري تتض
من أكثر من
ةيمك لثم ةدع تايرغتبم رثأتي يعارز مسوم لوصمحو ،فيلاكتلاو دئاعلا ةلصمح يه ةسسؤم طاشن ةجيتنف ،ةدحاو ةيرغتم
األمطار واألمسدة واملساحة املزروعة
. سوف نقتصر يف دراستنا على املتغرية ذات ب
عدين اثنني وهو ما يطلق عل
يه املتغرية
الثنائية
.
المبحث
1
.
المتغيرة الثنائية
التوزيعات المشتركة المتقطعة
و
)الدوال الحدية (الهامشية
التوزيعات المشتركة المتصلة
التوزيع الشرطي
8
التوزيعات المشتركة المتقطعة
و
الدالة الهامشية
)(الحدية
Fonction marginale
(أ
)
تعريف
املتغري
ةــميق يه ةدــحاو ةــميق ىلع يل فقوتت ةيرغتم يه ةــيئاــنثلا ة
X
ة متغريتني اثنتني. مــميق ىلع فقوتت اــنمإ و لاثم
ــث
ال
ذلك
،
.تمرة و نقطة التطبيق أو نقطة السداسي األول ونقطة السداسي الثاينـسلما ةباقرلا ةطقن ىلع فقوتي بلاطلا لدعم
ة تتوقف على متغرييتـيلاـلما ةـنـــــــــــــــسلا ةـجيتن كـلذـك
.ذاـكهو ،تاداريلإا و فيلاـكتلا
دقيق للمتغريـلا فيرعتلا
ة يتأتىـيئاـنثلا ة
:باستخدام الرتميز كما يلي
لتكن
لدينا
متغريتان عشوائيتان متقطعتان
X
و
Y
،
:لنرمز لالحتمال
P(X = x,Y = y)
ب
f(x,y)
:
f(x,y) = P(X = x,Y = y)
f(x,y) ≥
0
1
f(x,y) =
y
∑
x
∑
تسمى الثنائية
(X,Y)
مت
غرية ذات بعدين
و
f(x,y)
دالة
ال
كثاف
ة االحتمالية هلا ونقول أيضا دالة الكثافة املشرتكة للمتغريتني
X
و
Y
و
ميكن التعبري عن
ها
.)عن طريق جدول لالحتماالت املشرتكة (جدول التوزيع املشرتك
الفصل الخامس
المتغيرة العشوائية ثنائية
البعد
- 2 -VI
(x)
1
f
m
y
. . .
5
y
1
y
Y
X
)
1
(x
1
f
)
m
,y
1
f(x
. . .
)
5
,y
1
f(x
)
1
y
,
1
f(x
1
x
)
5
(x
1
f
)
m
,y
5
f(x
. . .
)
5
,y
5
f(x
)
1
,y
5
f(x
5
x
. . .
. . .
. . .
. . .
. . .
. . .
)
n
(x
1
f
)
m
,y
n
f(x
. . .
)
5
,y
n
f(x
)
1
,y
n
f(x
n
x
1
)
n
(y
5
f
. . .
)
5
(y
5
f
)
1
(y
5
f
(y)
5
f
احتمال
x
=
X
حيسب
و
يكتب كما يلي
)
k
f(x,y
m
1
k=
(x) = ∑
1
x) = f
=
P (X
احتمال
y
=
Y
حيسب
و
يكتب كما يلي
,y)
i
f(x
n
1
i=
(y) = ∑
5
y) = f
=
P (Y
الدالتني
(x)
1
f
و
(y)
5
f
تسميان الدالت
ا
ن اهلامشيت
ا
ن (احلديت
ا
: ن) حيث
1
=
(x)
1
∑ f
و
1
=
(y)
5
∑ f
(
ب
)
الدالة التجميعية
الدالة التجميعية
للمتغرية
الثنائية
(X,Y)
تكتب
ك
:ما يلي
f (u, v)
y
≤
v
∑
x
≤
u
∑
y) =
≤
Y
x,
≤
F (x, y) = P (X
مثال
:
نرمز،درن رجحو ةيدقن ةعطق يمرن
ب
X
،لعدد مرات ظهور الصورة
و
Y
.للرقم الذي يظهر من مكعب النرد
o
أكتب التوزيع االحتمايل املشرتك للمتغريتني
،
o
:أحسب احتماالت األحداث التالية
احلصول
على صورة مع الرقم
2
احلصول على الرقم،ةروصلا ىلع لوصلحا ،
2
.
o
أحسب االحتمال
P(X ≤
1
, Y ≤
3
)
،
P(X ≤
5
, Y ≤
2
)
.
(x)
1
f
2
2
1
3
5
1
X\Y
/
5
1/15
1/15
1/15
1/15
1/15
1/15
0
8/2
8/82
1/15
1/15
1/15
1/15
1/15
1
1
1/2
1/2
1/2
1/2
1/2
1/2
(y)
5
f
احتمال احلصول ع
لى صورة مع الرقم
2
:
P (X =
1
et Y =
2
) = f(
1
,
2
) =
1/15
احتمال احلصول على الصورة
1/5
+ . . . =
1/15
+
1/15
=
)
k
y
,
1
f(
n
1
k=
) = ∑
1
(
1
) = f
1
=
P (X
احتمال احلصول على الرقم
2
1/2
=
1/15
+
1/15
=
)
2
,
i
f(x
m
1
i=
) = ∑
2
(
5
) = f
2
=
P (Y
1
) =
2
≤
, Y
5
≤
, P(X
1/5
=
)
1/15
(
2
=
f(u,v)
3
≤
v
∑
1
≤
u
∑
=
)
3
,
8
F(
) =
3
≤
, Y
1
≤
P(X

محاضرات اإلحصاء الرياضي
ص
.ب
- 3 -V
.سلال
؟من بني التوزيعات االحتمالية الشهرية اليت رأينا يف الفصل الثاين أيها يعترب توزيعا مشرتكا
(
التوزيع:باولجا
املتعدد
.)
2
التوزيعات المشتركة المتصلة
(أ
)
تعريف
لتكن لدينا
X
و
Y
متغريتان ع
نعرف دالة الكثافة االحتمالية املشرتكة هلم،ناتلصتم
ا
1
كما يلي
:
P(X = x, Y = y) = f(x, y)
f(x, y) ≥
0
1
=
dy
dx
y)
f(x,
+∞
∞
-
∫
+∞
∞
-
∫
(
ب
)
الدالة التجميعية
ن
:كتب دالة التوزيع (الدالة التجميعية) كما يلي
dv
du
v)
f(u,
y
∞
-
v=
∫
x
∞
-
u=
∫
=
)
y
≤
Y
x,
≤
P(X
=
y)
F(x,
و مي
:كن استنتاج دالة الكثافة املشرتكة من الدالة الرتاكمية باالشتقاق كما يلي
f(x, y) = ∂
²
F / (∂x ∂y)
من جهة أخر
ى
dv
du
v)
f(u,
∞
∞
-
v=
∫
x
∞
-
u=
∫
x) =
≤
P(X
(x) =
1
F
dv
du
v)
f(u,
y
∞
-
v=
∫
∞
∞
-
u=
∫
y) =
≤
P(Y
(y) =
5
F
ونسمي الدالت
ا
ن
(x)
1
F
و
(y)
5
F
الدالت
ا
ن الرتاكميت
ا
ن (التجميعيت
ا
ن) اهلامشيت
ا
ن (احلديت
ا
.)ن
ولتحديد احتمال
X
و
Y
حمصورت
ا
:ن يف جمالني ما نكتب
dy
dx
y)
f(x,
d
y=c
∫
b
x=a
d) = ∫
≤
y
≤
b, c
≤
x
≤
P(a
(
ج
)
الدوال الهامشية
الدالتان اهلامشيتان (احلديتان) للكثافة االحتمالية للثنائية
(X, Y)
:فيعرب عنها كما يلي
du
y)
f(u,
+∞
∞
-
u=
= ∫
(y)
5
v) dv , f
f(x,
+∞
∞
-
v=
(x) = ∫
1
f
مثال
:
لدينا دالة الكثافة االحتمالية املشرتكة للمتغريتني
X
و
Y
:املعرفة كما يلي
1
ونقول أيضا دالة الكثافة االحتمالية للثنائية
(X,Y)
.

الفصل الخامس
المتغيرة العشوائية ثنائية
البعد
- 4 -VI
أكتب دالة التوزيع اهلامشية لكل من املتغريتني
أحسب احتمال
0
< x <
5
أحسب احتمال،
1
< y <
3
.
dv
du
v)
f(u,
∞
∞
-
v=
∫
x
∞
-
u=
= ∫
x)
≤
P(X
(x) =
1
F
,
0
(x) =
1
: F
0
<
x
*
*
0
≤ x <
1
:
dv
du
92
uv/
2
1
v=
∫
x
0
u=
∫
+
0
=
dv
du
92
uv/
∞
∞
-
v=
∫
x
∞
-
u=
∫
(x) =
1
F
.
12
²/
x
) =
15/92
(
5
²/
u] du = x
15
[
x
0
u=
∫
1/92
=
uv dv] du
2
1
v=
∫
[
x
0
u=
∫
1/92
=
1
(x) =
1
F
:
1
≥
x
*
dv
du
v)
f(u,
y
∞
-
v=
∫
∞
∞
-
u=
= ∫
y)
≤
P(Y
y) =
(
5
F
,
0
(y) =
5
: F
1
<
y
our
P
*
1
≤ y <
2
:
]
5
/
)
1
-
²
[u (y
1
0
u=
∫
1/92
=
uv dv] du
y
1
v=
∫
[
1
0
u=
∫
1/92
=
dudv
92
uv/
y
1
v=
∫
1
0
u=
+ ∫
0
(y) =
5
F
du
24
/
)
8
-
²
(y
=
)
12/5
(
)
1
-
²
(y
))
92
*
5
/(
1
= (
1
0
)
5
²/
(u
)
1
-
²
) (y
92
/
1
*
1/5
(
=
1
=
(y)
5
: F
2
≥
y
*
,
¼
=
1/12
=
)
0
(
1
F
–
)
5
(
1
= F
)
5
<
x
<
0
P(
P(
1
< y <
3
) =
0
/
51
=
8/3
sinon
0
5
1
,
4
0
,
96
)
,
(
y
x
xy
y
x
f
4
1
4
0
16
/
²
0
0
)
(
1
x
x
x
x
x
F
5
1
5
1
24
/
)
1
²
(
1
0
)
(
2
y
y
y
y
y
F
محاضرات اإلحصاء الرياضي
ص
.ب
- 5 -V
3
التوزيع الشروطي
Distribution conditionnelle
يف حالة
X
،
Y
فإن دالة الكثافة االحتمالية الشرطية ل،ناتعطقتم ناتيئاوشع ناتيرغتم
(X|Y = y)
تكتب ك
ام
يلي
f(x/y)
:وحتسب كما يلي
)
(
)
,
(
)
(
)
,
(
)
/
(
1
x
X
P
y
Y
x
X
P
x
f
y
x
f
y
x
f
و هذا استنادا إىل القانون التقليدي لال
:حتماالت الشرطية
)
(
)
(
)
/
(
A
P
B
A
P
A
B
P
ا
لتوزيع االحتمايل ل
X
حيث
= y
Y
هو جمموعة قيم املتغرية
X
عند تثبيت
Y
و
االحتماالت
f(x/y)
.املقابلة هلا
مثال
.
لتكن
X
عدد مرات احلصول على ص
ورة عند رمي قطعة نقدية مرتني
و
Y
الفرق بالقيمة املطلقة بني عدد مرات
.الصورة وعدد مرات الكتابة
أكتب التوزيع االحتمايل ل
Y|X =
1
،
أكتب التوزيع
ا
ن االحتمالي
ا
ن ل
X|Y =
0
و
X|Y =
5
.
يف
حالة
X
و
Y
:متغريتان ع متصلتان نكتب
dy
f(y/x)
d
c
dx) = ∫
+
x
≤
X
≤
d / x
≤
Y
≤
P(c
4
خالصة
احتمال ثنائية
:عشوائية و حيسب كما يلي
f(x,y) = P(X = x,Y = y)
ل
:لتعبري عن احتمال قيمة ما إلحدى املتغريتني نكتب
(x)
1
P (X = x) = f
.و تسمى دالة الكثافة اهلامشية
االحتمال التجمي
:عي ملتغريتني فيعرب عنه من خالل دالة التوزيع املشرتكة
F (x, y) = P (X ≤ x, Y ≤ y)
.تنطبق هذه التعاريف على كل من املتغريات املتقطعة و املستمرة
( للتعبري عن التوزيع االحتمايل إلحدى املتغريتني بشرط أن تأخذ املتغرية الثانية قيمة ما
0
: مثال) فنكتب،
P(X/Y =
0
)
حلساب االحتماالت الشرطية ل
X
:تستخدم القاعدة
)
(
)
,
(
)
(
)
,
(
)
/
(
1
x
X
P
y
Y
x
X
P
x
f
y
x
f
y
Y
X
P
المبحث
2
.
االستقالل التباين
و
االرتباط
تعريف استقالل متغيرتين
توقع
و
تباين المتغيرة العشوائية متعددة األبعاد
التباين المشترك
معامل االرتباط
X
0
1
5
Y
1
0
P(X/Y=
0
)
0
1
0
P(y/x=
1
)
0
1
P(X/Y=
5
)
1/5
0
1/5

الفصل الخامس
المتغيرة العشوائية ثنائية
البعد
- 6 -VI
8
تعريف استقالل متغيرتين
رأينا يف الفصل األول
أن حدثني عشوائيني
A
و
B
:يكونان مستقالن إذا كان
P(A et B) = P(A) P(B)
انطالقا من
هذه
تكون املتغريتان العشوائيتان املتق،ةدعاقلا
طعتان
X
و
Y
مستقلتان
إذا
و
:فقط إذا كان
P(X = x, Y = y) = P(X = x) P(Y = y)
(y)
5
f
(x)
1
f
=
y)
f(x,
يف حالة كون املتغريتني
متصلتني نكتب
:
P(X ≤ x, Y ≤ y) = P(X ≤ x) P(Y ≤ y)
)
(y
5
F
(x)
1
F
=
y)
F(x,
أي أن املتغريتان املستقلتان مه
ا ا
ل
لتان ميكن كتابة دالة التوزيع املشرتكة هلما (أو دالة الكثافة املشرتكة) يف شكل جداء
دالتني
.)هامشيتني تراكميتني (أو دالتني هامشيتني للكثافة
.مثال
ل
يكن
X
و
Y
م
ع مستمرين
:حيث دالة الكثافة املشرتكة هلما معرفة كما يلي
بني أن املتغريتني
X
و
Y
.مستقلتني
(y) cqfd
5
(x) * f
1
y => f(x, y) = f
5
x * c
1
xy = c
5
c
1
=> f(x, y) = c
5
*c
1
Soit c = c
مثال
2
.
ليكن
X
و
Y
و
Z
م
ع متقطعة. متثل
X
عدد مرات احلصول على صو
رة يف رمية لقطعة نقدية و
Y
عدد مرات
احلصول على صورة يف رمية موالية. و
Z
الفرق بالقيمة املطلقة بني
X’
و
Y’
اللذان ميثالن على التوايل عدد مرات احلصول
على الصورة/الكتابة يف جمموع رميتني لقطعة نقدية
.
من الواضح أن
X
و
Y
مستقلتان
ألن
P(X = x,Y = y) = P(X = x) P(Y = y)
عند كل قيم
X
و
Y
.
،على العك من ذلك
جند أن
Z
ليست مستقلة عن
X’
فمثال
:
P(X’=
0
, Z =
5
) =
1/5
≠
P(X’ =
0
) P(Z =
5
) = (
1/1
.
1/5
) =
1/0
2
توق
ع
و
تباين المتغيرة العشوائية متعددة األبعاد
.ينطبق كل من تعريف التوقع الرياضي والتباين الذين تناولنامها فيما سبق على املتغرية العشوائية متعددة األبعاد
لتكن
X
و
Y
متغريتان عشوائيتان مت
قطعتان
،
و
f(x, y)
.دالة كثافة مشرتكة هلما
y) ,
f(x,
x
y
∑
x
∑
=
E(X)
=
x
µ
y)
f(x,
y
y
∑
x
∑
=
E(Y)
=
y
µ
y)
f(x,
²
)
y
µ
–
(y
y
∑
x
= ∑
]
²
)
y
µ
–
E[(y
=
y
²
σ
y) ,
f(x,
²
)
x
µ
–
(x
y
∑
x
= ∑
]
²
)
x
µ
–
E[(x
=
x
²
σ
sinon
0
5
1
,
4
0
,
)
,
(
y
x
cxy
y
x
f
X
Y
0
1
Z
X’
0
1
5
X’
0
1
5
Z
0
5
0
¼
¼
1
1
1
1
x
p
¼
½
¼
z
p
½
½
1
½
½
5
½
0
½

محاضرات اإلحصاء الرياضي
ص
.ب
- 7 -V
يف
حالة
X
و
Y
متغريتان م
ستمرتان
:
.
dy
dx
f(x,y)
y
+∞
∞
-
∫
+∞
∞
-
∫
=
y
dy , µ
dx
y)
f(x,
x
+∞
∞
-
∫
+∞
∞
-
∫
=
E(X)
=
x
µ
dy ,
dx
y)
f(x,
²
)
x
µ
–
(x
+∞
∞
-
∫
+∞
∞
-
∫
=
]
²
)
x
µ
–
E[(x
=
x
²
σ
dy
dx
y)
f(x,
²
)
y
µ
–
(y
+∞
∞
-
∫
+∞
∞
-
∫
=
]
²
)
y
µ
–
E[(y
=
y
²
σ
مثال
.
ليكن لدينا
التوزيع املشرتك
:املعرف كما يلي
:املطلوب حساب
E(y), E(x)
،
y
²
, σ
x
²
σ
5
-
=
1/5
-
=
2/5
–
1/5
) =
1/0
+
1/0
+
1/1
(
2
–
)
1/0
+ ¼ +
0
/
1
(
1
y) =
f(x,
x
y
∑
x
∑
=
E(x)
1/5
-
) =
1/0
+
1/0
(
9
+
)
1/0
+
1/1
(
5
–
+ ¼)
1/0
(
1
-
=
y)
f(x,
y
y
∑
x
∑
=
E(Y)
y)
f(x,
²
)
x
µ
-
(x
y
∑
x
= ∑
]
²
)
x
µ
–
E[(x
=
x
²
σ
= (
1
+
5
)
²
(
1/0
+ ¼ +
1/0
) + (-
2
+
5
)
²
(
1/1
+
1/0
+
1/0
) =
9
(
1/5
) +
9
(
1/5
) =
9
y)
(x,
f
²
)
y
µ
-
(y
y
∑
x
= ∑
]
²
)
y
µ
–
E[(y
=
y
²
σ
= (-
1
+
1/5
)
²
(
1/0
+
1/1
) + (-
5
+
1/5
)
²
(
1/1
+
1/0
) + (
9
+
1/5
)
²
(
1/0
+
1/0
)
=
19/1
(
3/0
) +
9/5
(
3/0
) + (
12/5
)
²
(
5/0
) =
221
/
35
=
50،31
كما ميكن حساب كل من القيم السابقة باستخدام ال
دوال اهلاشية
(x)
1
f
و
(y)
5
f
.
5
-
) =
1/0
(
2
–
)
1/0
(
1
(x) =
1
f
x
x
∑
E(x) =
V(x) = E(x
²
) – E
²
(x)
= [
1²
(
1/0
) + (–
2
)
²
(
1/0
)] – (–
5
)
²
=
9
3
التباين المشترك
Covariance
يعرف
:التباين املشرتك كمايلي
)]
y
µ
–
)(Y
x
µ
–
E[(X
=
xy
σ
=
Y)
(X,
Cov
يف حالة
X
و
Y
:متغريتان متقطعتان
y)
)f(x,
y
µ
–
)(y
x
µ
–
(x
y
∑
x
∑
=
xy
σ
يف حالة
X
و
Y
متغريتان
مستمرتان
:
9
-
5
-
1
y
X
1/0
1/1
1/0
1
1/0
1/0
1/1
-
2
(x)
8
f
9
-
5
-
1
Y
X
4/1
1/0
1/1
1/0
8
4/1
1/0
1/0
1/1
-
5
1
2/1
3/1
3/1
(y)
2
f

الفصل الخامس
المتغيرة العشوائية ثنائية
البعد
- 8 -VI
dy
dx
y)
f(x,
)
y
µ
–
(y
)
x
µ
–
(x
+∞
∞
-
∫
+∞
∞
-
∫
=
xy
σ
(أ
)
خصائص
التباين المشترك
1
.
من تعريف التباين
مي
كن أن
:نستنتج
)]
y
µ
–
)(Y
x
µ
–
E[(X
Cov(X, Y) =
]
y
µ
x
µ
+
Y
x
µ
–
y
µ
X
–
= E[XY
y
µ
x
µ
+
E(X)E(Y)
–
E(X)E(Y)
–
(XY)
= E
= E(XY) – E(X) E(Y)
Cov(X, Y) = E(XY) – E(X) E(Y)
5
.
يف حالة
X
و
Y
متغريتان مستقلتان
1
نعلم من خصائص التوقع
الرياضي أن
E(XY) = E(X)
E(Y)
و
منه
:
Cov(X, Y) = E(XY) – E(X) E(Y) = E(XY) – E(XY)
Cov (X, Y) =
0
3
.
يف حالة
X
و
Y
:متغريتان مستقلتان أو غري مستقلتني
5
Cov (X, Y)
2
Var (X ± Y) = V(X) + V(Y)
1
.
القيمة املطلقة للتباين املشرك ال تكون أكرب من جداء االحنرافني ا
:ملعياريني
y
σ
x
σ
≤
|
xy
σ
|
2
.
يف حالة
X
و
Y
متغريتان مرتبطتان متاما مثال
X
=
Y
:فإن
= V(X) V(Y)
Y)
Cov(X,
4
معامل االرتباط
من اخلاصي
( ة
5
)
نستنتج أن الكسر
يساوي
0
يف حالة
X
و
Y
مستقلتان
و
( من اخلاصية
2
) نستنتج أنه
يف حالة
X
و
Y
متغريتان مرتبطتان متاما
فإن الكسر يساوي
1
.
يةــــــصالخا نم ىرخأ ةهج نم
1
تنتج أن الــــــسن
بةــــــسن
( ترتاوح قيمته بني
-
1
)
(و
1
):
. من أجل هذا
تستعمل النسبة
:
. وتسمى معامل االرتباط،ينتيرغتلما ينب طابترلاا سايقل
يف حالة
r
معدوم
نقول أن
المتغيرت
ان
غير مرتبطت
ني
من غري أن جنزم أهنما مستقلت،
ا
.ن
.مثال. أوجد التباين املشرتك واالرتباط للتوزيع املشرتك املذكور يف املثال السابق
Cov(X, Y) = E(XY) – E(X) E(Y)
1
فقد يكون التباين املشرتك مساويا للصفر من غري أن يكون املتغريتان مستقلتان فعال. املعادلة هي يف ا،حيحص امود ةرورضلاب يل كعلا
حل
قيقة
متثل شرطا ولكنه لي
بني،ادوجوم ناك اذإ ،طابترلاا فعض ىلع ةللادلل كترشلما نيابتلا ةيمودعم ةجيتن لامعتسا نكيم لباقلماب .ايفاك اطرش
املتغريتني. الشرط االزم وال
كايف الستقالل متغريتني
.هو املذكور سابقا يف تعريف االستقالل
y
x
xy
1
1
y
x
xy
y
x
xy
r

محاضرات اإلحصاء الرياضي
ص
.ب
- 9 -V
E(XY) =
1
(-
1
)(
1/0
) + (
1
)(-
5
)(
5/0
) + (
1
)(
9
)(
1/0
) + (-
2
)(-
1
)(
5/0
) + (-
2
)(-
5
)(
1/0
) + (-
2
)(
9
)(
1/0
) =
1,92
E(X) =
1
(
1/0
) + (-
2
)(
1/0
) = -
5
, E(Y) = -
1
(
3/0
) –
5
(
3/0
) +
9
(
5/0
) = -
1/5
.
Cov(X, Y) =
1,92
– (-
5
)(-
1/5
) =
0,91
,
3
=
x
σ
=>
9
=
²
)
5
-
(
–
)
1/0
(
²
)
2
-
) + (
1/0
(
1
(X) =
²
E
–
)
²
E(X
=
V(X)
=
y
σ
=>
50,31
(Y) =
²
E
–
)
²
V(Y) = E(Y
1,2
.
5
خالصة
نقول عن متغريتان أهنما مستقلتان إذا أمكن
كتابة دالة التوزيع املشرتكة هلما (أو دالة الكثافة املشرتكة) يف شكل جداء
:)دالتني هامشيتني تراكميتني (أو دالتني هامشيتني للكثافة
)
(y
5
(x) f
1
f(x, y) = f
:أي أن
P(X = x, Y = y) = P(X = x) P(Y = y)
من جهة أخرى نقي االرتباط بني متغريتني من خالل معامل االرتباط
،
ويف هذه احلالة يكون التباين املشرتك
Cov(X, Y) = E(XY) – E(X) E(Y)
معدوما ألنه تبعا خلصائص التوقع الرياضي يف حالة االستقالل فإن
E(XY)
=
E(X) E(Y)
.لكن العك لي بالضرورة صحيح
تخدم معامل االرتباطــــسي
ائي جيـــــصحلإا نكل ،ينتيرغتلما ينب طابترلاا ىلع رــــشؤمك
ب أن يكون متنبه
ا إىل
.حمدودية هذا املؤشر
05
.
0
)
5
.
4
(
3
75
.
0
y
x
xy
r
y
x
xy
r

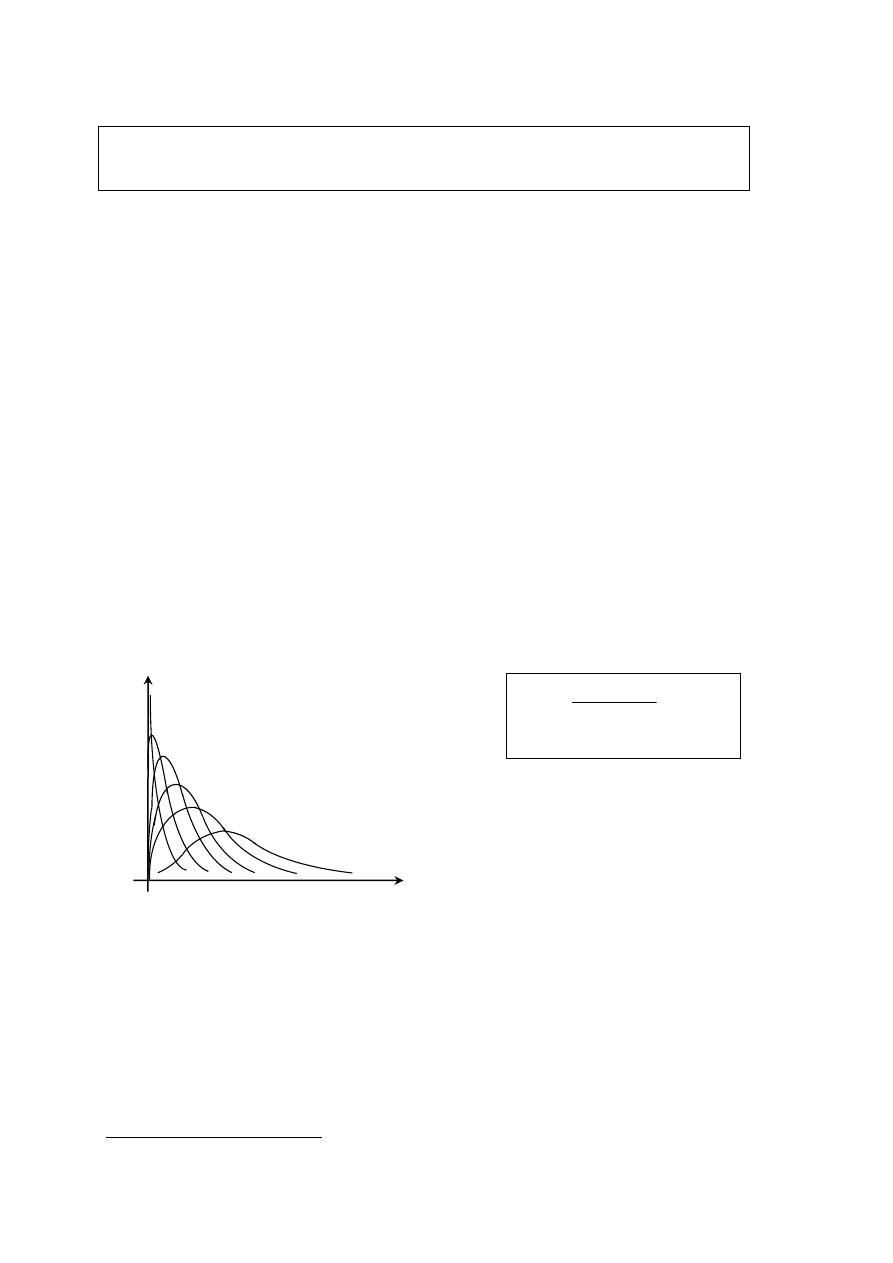
محاضرات اإلحصاء الرياضي
ص
.ب
- 1 -VI
الفصل
VI
.
دوال المتغيرات العشوائية والتقارب
ك: ةيطخلا ريغ لاودلا
2
فيشر وستيودنت،
التقارب
و
السلوك
نظرية النهاية المركزية،يبراقتلا
نتناول يف
املبحث
األول من
هذا الفصل عدد من التوزيعات ذات االست
خدام
الواسع يف
اإلحصاء
اال
ستداليل
و
التطبيقي
" خاصة يف جمايل
التقدير
"
و"
اختبار الفروض
"
،
حيث
يستخدم
اإلحصائي
هذه التوزيعات يف عمله من أجل الوصو
ل إىل
بشأن"رارق"
"
اجملتمع
"
املدروس
انطالقا من بيانات يتحصل عليها من عينة
.
يف
املبحث
الثاين سنتطرق لل
تقارب بني التوزيعات
االحتمالية املختلفة
ا
ليت درسناها من قبل
.
المبحث
1
.
ك:ةيطخلا ريغ لاودلا
2
فيشر وستيودنت،
توزيع ك
2
توزيع ستيودنت
توزيع فيشر
8
توزيع ك
2
8
deux)
-
carré (ou Khi
-
Distribution en Khi
توزيع ك
5
: وميكن تعريفه كما يلي،اهعاونأب ضورفلا رابتخا لامج في امادختسا تاعيزوتلا رثكأ نم وه
لتكن
ν
X
, . . .
2
X
,
8
X
( متغريات عشوائية مستقلة كل منها تتبع التوزيع الطبيعي املعياري،
1
=
σ
,
0
=
µ
). املتغرية
²
ν
X
+ . . . +
²
2
+ X
²
8
X = X
:هلا دالة الكثافة التالية
حيث
α)
Γ(
:هي الدالة قاما
1
يرجع الفضل يف اكتشاف هذا التوزيع إىل
ف هلمرت
)
1092
(F. Helmert,
و كارل بريسون
)
1900
(Karl Pearson,
.
0
0
0
2
/
2
)
(
2
/
2
/
1
2
/
x
x
e
x
x
f
x
0
0
1
dt
e
t
t
x
ν = 15
ν = 11
ν = 6
ν = 3
ν = 1
ν = 2
1
6
12
18
24
1425
f(x)
رسم
14
تدرج منحنى ك
2
حسب درجة الحرية
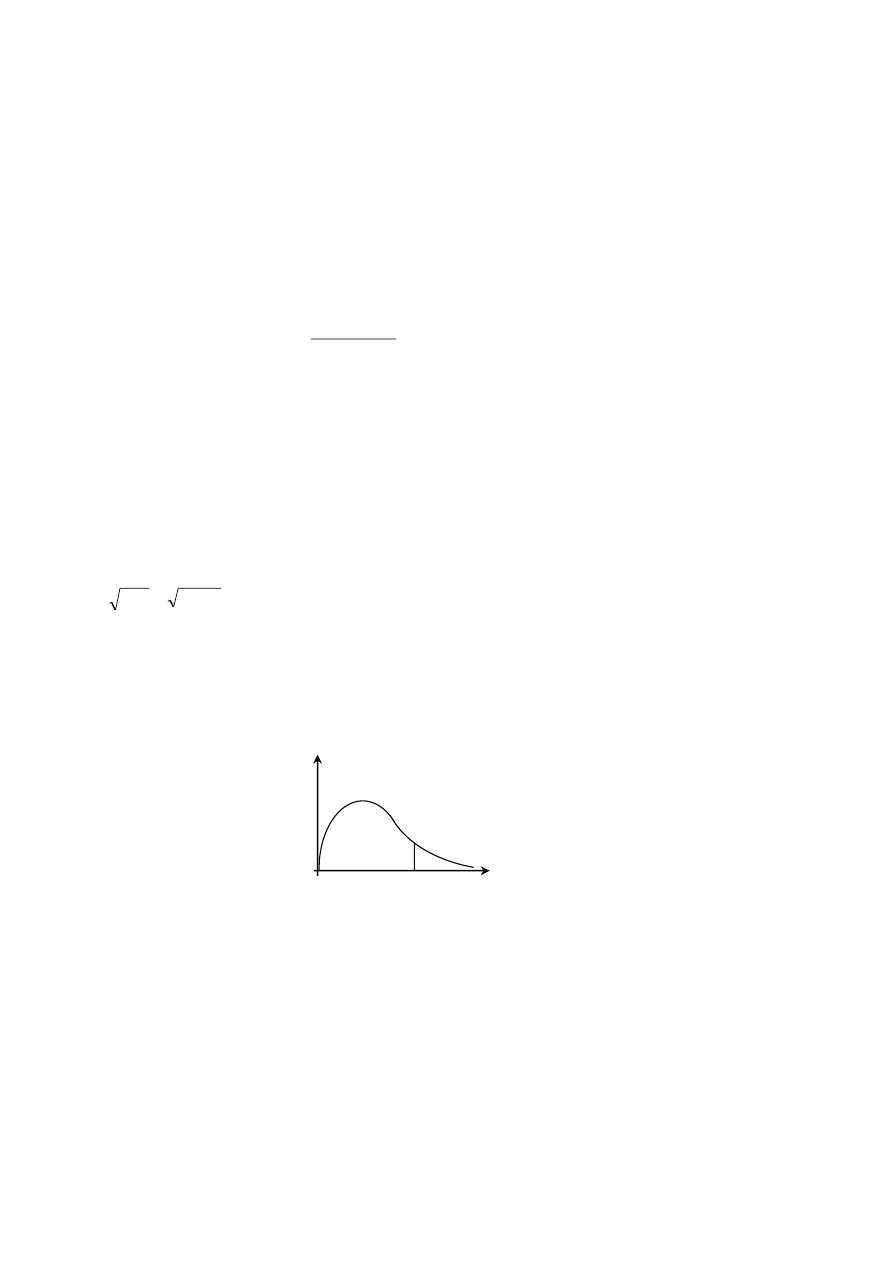
الفصل السادس
دوال المتغيرة العشوائية و التقارب
- 2 -VI
و نقول أن
X
تتبع التوزيع ك
5
ب
ν
درجة حرية ونكتب
ν
²
χ
X ~
.
الدالة التجميعية
)
²
χ
F(
تكتب كما يلي
:
(أ
)
خصائص توزيع ك
2
5
ν/
-
)
t
5
-
1
) = (
t
(
M
,
ν
2
=
)
X
(
V
ν,
) =
X
(
E
دالة التوزيع ك
5
هي
هي حالة خاصة من توزيع قاما بوضع
α = ν/
5
, β =
5
.
ويأخذ منحىن
f(x)
شكله حسب قيمة الثابت
ν
ونالحظ من الرسم أن املن
حىن يبتعد شيئا فشيئا عن احملو
ر
العمودي ويأخذ شكال جرسيا كلما زادت قيمة
ν
. ونربهن أنه عند
ν
كبري
)
30
≥
ν
(
فإن
.تتبع التوزيع الطبيعي املعياري
،يف اجلداول االحصائية
تعني نقطة (قيمة املتغرية) ك
5
على احملور األفقي (أنظر الرسم املقابل) من خالل
ν
باإلضافة إىل
ا
ملساحة
p
على يسار ك
5
حتت املنحىن
)
p
ν;
²
χ
≤
P(X
=
(p
. وأحيانا حتدد النقطة ك
5
بداللة املساحة
( على ميينها
p
-
1
=
α
)
لذلك
:جند يف كتب االحصاء كل من الكتابتني
ν
p,
²
χ
و
ν
,
α
²
χ
رسم
10
تعيني نقطة ك
5
على احمل
ور من خالل قيمة
p
:نظرية
لتكن
م ع مستقلة عددها
n
حيث
n
ν
²
~ χ
n
, X
, . . .
8
ν
²
χ
~
8
X
هذه
جمموع
املتغريات
T
ν
²
χ
~
i
ν
= ∑
T
ν
0
0
0
)
2
/
(
2
1
)
²
(
0
2
/
1
)
2
/
(
2
/
x
x
du
e
u
x
P
x
u
1
2
²
2
n
i
i
T
X
X
1
x
1
f(x)
p=1- α
α
χ
²
p,ν
محاضرات اإلحصاء الرياضي
ص
.ب
- 3 -VI
2
توزيع ستيودنت
1
Distribution de Student
لتكن املتغريتان العشوائيتان املستقلتان
Y
و
Z
حيث
)
8
,
0
N(
Y~
و
²
ν
χ
Z ~
؛
املتغرية
تتبع توز
يع
هلا دالة الكثافة التالية
و نقول أن املتغرية
X
تتبع توزيع
ستيودنت ب
ν
درجة حرية
و
:نكتب
ν
T ~ t
(أ
)
خصائص توزيع ستيودنت
E(T) =
0
, V(T) = ν/(ν-
5
) si (ν >
2
)
رسم
16
تدر
ج
منحىن
ستيودنت حس
ب درجة احلرية
نالحظ أن منحىن
t
متماثل حول املتوسط
0
مما يعين أن لكل نقطة موجبة
t
نقطة مناظرة هلا سالبة حيث
املساحة حتت املنحىن على ميني
t
تساوي املساحة حتت املنحىن علي يسار
t)
–
(
،
و
نكتب
p
t
-
=
p
-
1
t
.
باإلضافة إىل ذلك فإن منحىن
f(t)
يقرتب من املنحىن الطبيع
ي املعياري كلما زادت قيمة
ν
يعترب،امومعو .
اإلحصائيون أن املنحنيان يتطابقان تقريبا عند
0
3
≥
ν
.
،يف اجلداول االحصائية
)تعني نقطة (قيمة املتغرية
t
من خالل
ν
واملساحة
p
على يسار
t
حتت املنحىن
)
)
p
ν;
t
≤
P(T
=
(p
. وأحيانا حتدد النقطة
t
بداللة املساحة على ميين
( ها
p
-
1
=
α
)
: ونكتب
ν
p,
t
أو
ν
,
α
t
.
1
يرجع الفضل يف إجياد هذا القانون إىل ويليام سيلي قوسي
)
1939
-
1092
(William Sealy Gosset) (
ونشر،تندويتس مساب اهلك هتلااقم رشن يذلا
مقالته حول هذا القانون عام
1900
بعنوان
« The probable error of a mean »
دراوزبيك: رظنأ
1999
ص،
525
.
/
Z
Y
T
t
t
t
f
2
1
²
1
2
2
1
)
(
0
0
1
dt
e
t
t
طبيعي
ν = 4
ν = 1
144
f(t)
-4 -3 -2 -1 1 1 2 3 4
t
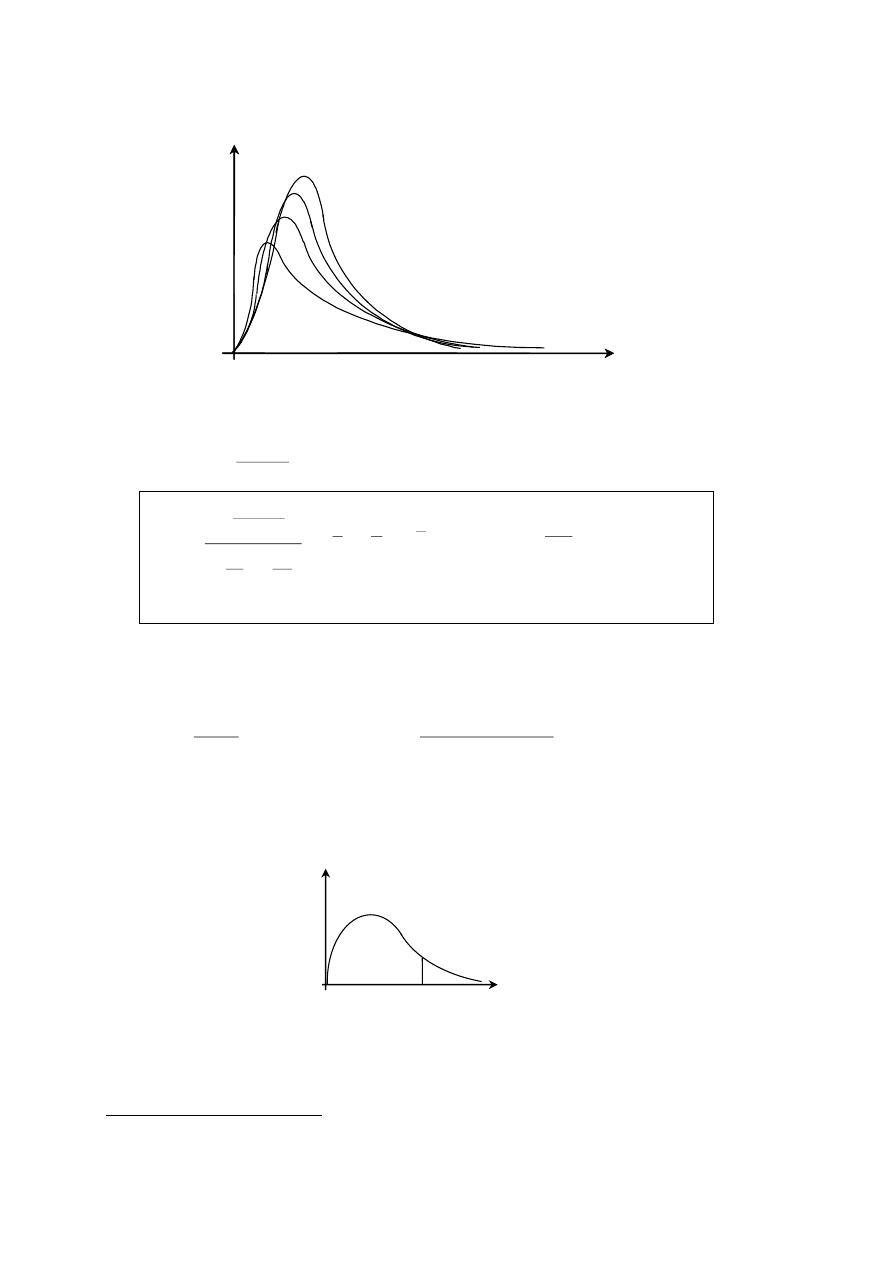
الفصل السادس
دوال المتغيرة العشوائية و التقارب
- 4 -VI
3
( توزيع فيشر
F
)
8
Snédecor
-
Distribution F de Fisher
رسم
11
تدرج منحىن فيشر حسب درجة احلرية
ليكن لدينا املتغريتان العشوائيتان املستقلتان
²
1
ν
χ
~
1
X
و
²
5
ν
χ
~
5
X
: . املتغرية
هلا دالة ا
:لكثافة
و نقول أن املتغرية
X
تتبع توزيع فيشر ب
1
ν
و
5
ν
درجة حرية
و
:نكتب
5
ν
,
1
ν
F
~
X
(أ
)
:خصائص توزيع فيشر
ويظهر من املعادلة تبعية منحىن
f(x)
باإلضافة ل
x
إىل كل من
1
ν
و
5
ν
و
لذلك حتدد أي نقطة
F
من خالل ثالثة
:معامل
1
ν
و
5
ν
و
p
(املساحة حتت املنحىن على
يسار النقطة
F
ونكتب، )
5
ν
,
1
ν
p,
F
و
يف الغالب تعطي اجلداول اإلحصائية قيم
F
عند
0,92
p =
و
0,99
p =
.
رسم
18
تعيين قيمة
F
يتم في الجدول يتم من خالل
2
ν
, ,
1
ν
و
P
نظرية
8
.
1
رونالد آيلمر فيشر
)
1925
-
1090
(Ronald Aylmer Fisher) (
(إجنلرتا) يعترب مؤس نظرية التقدير و جورج وادل سنيديكور
(George
Waddel Snédecor) (
1001-1991)
ص،قباسلا عجرلما رظنأ )يكيرمأ(
520
.
x
(10, 50)
(10, ? )
(10, 10)
1.0
(10, 4)
f(x)
0,5
0
1
2
3
4
2
2
1
1
/
/
X
X
X
0
0
0
2
2
2
)
(
2
1
2
1
)
2
(
2
2
2
1
2
1
2
1
2
1
1
2
1
x
x
x
x
x
f
)
4
(
2
4
)
2
(
2
²
,
)
2
(
2
2
2
2
2
1
2
1
2
2
2
2
2
x
1
f(x)
p=1- α
α
F
p,ν
1
, ,ν
2
محاضرات اإلحصاء الرياضي
ص
.ب
- 5 -VI
نظرية
2
.
نظرية
3
.
4
خالصة
ميكن تلخيص أهم ما تضمنه هذا
املبحث
:يف اجلدول التايل
التوزيع
المتغيرة العشوائية
أهم ما يجب معرفته عن دالة الكثافة
توزيع ك
2
ν
²
χ
X ~
إذا كانت
Xi
متغريات عشوائية مستقلة كل
و،يرايعلما يعيبطلا عيزوتلا عبتت اهنم
²
ν
+ . . . + X
²
2
+ X
²
8
X = X
:إذن
ν
²
χ
X ~
f(x) =
0 si x ≤ 1
E(X) = ν, V(X) =
2ν
توزيع ستيودنت
ν
T ~ t
لتكن املتغريتان العشوائيتان املستقلتان
Y
و
Z
حيث
)
8
,
0
Y~ N(
و
²
ν
χ
Z ~
؛
:إذن
ν
~ t
E(T) =
0,
V(T) = ν/(ν-
5) si (ν > 2)
توزيع فيشر
5
ν
,
1
ν
X ~ F
واــشع ناتيرغتم انيدل تناك اذإ
تــسم ناتيئ
قلتان
:حيث
²
1
ν
χ
~
1
X
و
²
5
ν
χ
~
5
X
،
فإن
5
ν
,
1
ν
~ F
f(x) =
0 si x ≤ 1
,
;
المبحث
2
.
السلوك التقاربي لبعض التوزيعات االحتمالية
التقارب بين التوزيع الثنائي
و
التوزيع الطبيعي
االنتقال من متغيرة متقطعة إلى متغيرة مستمرة
التقارب بين التوزيع الثنا
ئي وتوزيع بواسون
نظرية النهاية المركزية
نتناول يف هذا
املبحث
د بالتقاربــصقنو .ةيرهــشلا ةيلامتحلاا تاعيزوتلا نم ددع ينب لــصيح يذلا براقتلا تلااح ضعب
تخدامـــسا ةيناكمإ نيعي امم ،ينعم لامتحا صوـــصبخ ةبراقتم جئاتن ناعيزوتلا يطعي نأ )لاثم نوـــساوبو يئانثلا( ينعيزوت ينب
1
2
2
1
,
,
,
,
1
/
1
p
p
F
F
2
),
2
/
(
1
,
1
,
1
p
p
t
F
2
,
,
,
p
p
F
/
Z
Y
T
2
2
1
1
/
/
X
X
X
2
,
,
,
p
p
F
2
),
2
/
(
1
,
1
,
1
p
p
t
F
1
2
2
1
,
,
,
,
1
/
1
p
p
F
F
الفصل السادس
دوال المتغيرة العشوائية و التقارب
- 6 -VI
تناــسارد دنع موهفلما اذه لىإ زايجإب لبق نم انقرطت دق اننأ املع .ينعم لامتحا باــسلح )رثكأ انايحأو( ينيلامتحا ينعيزوت
.هلذه التوزيعات
8
التقارب بين التوزيع الثنائي
و
التوزيع الطبيعي
لندرس السلوك التقاريب ملتغرية التوزيع الثنائي
X~B(n,p)
عندما تؤول
n
إلىأعداد كبري
.ة جدا
ليكن
X
، مرتني: ةيدقن ةعطق يمر دنع ةروص ىلع لوصلحا تارم ددع لثيم
1
،مرات
0
،مرات
12
.مرات
برسم
منحنيات
Pi
للحاالت
n =
5
،
n =
1
،
n =
0
،
n =
12
يظهر
السلوك التقاريب للمتغرية
X
.
رسم
11
السلوك التقاريب للتوزيع الثنائي ملا
p =
0,2
يظهر من مقارنة املنحنيات األربعة أن زيادة قيمة
n
تؤدي إىل احلصول على منحىن
ذا شكل جرسي
و
متماثل حول التوقع
µ
.
هذه املالحظة تصدق أيضا يف حالة
p ≠
0,2
.لكن التحول يكون أكثر بطأ
n = 2
0
0 ,1
0 ,2
0 ,3
0 ,4
0 ,5
0 ,6
0
1
2
3
4
X
p
(x
)
n = 4
0
0,1
0,2
0,3
0,4
0
2
4
6
X
P
(x
)
n = 8
0,00
0,05
0,10
0,15
0,20
0,25
0,30
0
2
4
6
8
10
X
P
(x
)
n = 16
0,00
0,05
0,10
0,15
0,20
0,25
0
5
10
15
20
X
P
(x
)
5
1
0
Xi
¼
1/5
1/1
i
P
1
3
5
1
0
Xi
1/12
1/12
2/1
1/12
1/12
i
P
8
7
6
5
4
3
2
1
1
X
i
1،11
4
1،13
1
1،11
9
1،21
9
1،27
3
1،21
9
1،11
9
1،13
1
1،11
4
i
P
محاضرات اإلحصاء الرياضي
ص
.ب
- 7 -VI
من أجل التعميم نعترب املتغرية املعيارية
z = (x - µ)/σ
امللحقة بذات املتغرية ذات التوزيع الثنائي
X
. إن السلوك التقاريب
ل
Z
املالجظ يف الشكل أسفله هو ما تثبت
:ه النظرية التالية
ونكتب
N(
0،1
)
Y ≈
.
رسم
20
السلوك التقاريب للتوزيع الثنائي
من خالل املتغرية املعيارية
املعيارية
:قاعدة
يف حالة
n
كبرية
و
p
غري قريب من
0
.ميكن اعتبار التوزيع الثنائي كتقريب جيد للتوزيع الطبيعي
و
يعط
ي التوزيعان نتائج
أكثر تقاربا كلما كانت
n
:كبرية أكثر. ونكتب
و مما يسرع تقارب التوزيع الثنائي من التوزيع الطبيعي كون
p
قريب من
0,2
: وكقاعدة
عموما نعتبر أن التقريب مالئم عندما
np
و
nq
كالهما أكبر من
5
.
عدد من االحصائيني
1
يعتمد قاعدة أخرى هي أن يكون أ
:حد الشرطني التاليني متوفرين
o
npq ≥
1
o
n ≥
20
, np ≥
80
, nq ≥
80
يف حالة
p =
0,2
( الشرط،
1
) يتحقق عند
n =
32
و
الثاين عند
n =
50
.
1
ص،قباسلا عجرلما
525
.
).
1
,
0
(
:
)
,
(
~
N
npq
np
X
Y
p
n
X
soit
n
B
b
a
u
n
du
e
b
npq
np
x
a
P
2
²
2
1
)
(
lim
Pi
Pi
Pi
Pi

الفصل السادس
دوال المتغيرة العشوائية و التقارب
- 8 -VI
يف حالة
p =
0,10
الشرطني يتحققان عند،
n =
100
.
2
.االنتقال من متغيرة متقطعة إلى متغيرة متصلة
ال
ستخدام التوزيع الطبيعي بد
ال
من
التوزيع الثنائي
يعين حساب االحتمال عن طريق توزيع مستمر بينما املتغري
ة متقطعة. من
أجل ذلك
.يتم اعتبار كل قيمة يف املتغرية األصلية جماال
مثا
.ل
احتمال
1
جناحات خالل
n
:جتربة يصاغ كما يلي
P(
3,2
≤ X ≤
1,2
)
.
مثال
2
نرمي قطعة نقدية:
50
مرة. ليكن
X
عدد مرا
ت احلصول على صورة. أحسب
P(X =
0
)
مث أدرس إمكانية
استخدام نظرية موافر
-
.البالس حلساب نف االحتمال
X ~ B(
20
,
0.5
)
,
P(X =
1
) = F(
1
) – F(
1
) =
0.2581
–
0.8385
=
0,1501
.
لدينا
np =
10
>
2
وكذلك
nq =
10
>
2
،
و
: إذا شئنا استخدام القاعدة الثانية فإننا جند أيضا أن
n =
80
،
np
=
80
،
nq=
80
ميكن إذا اعتبار،
Y = (X-
10
)/√
2
~ N(
0
,
1
)
. نستخدم املتغرية املستمرة
X*
بدال من
X
حلساب
احتمال اجملال املعرب عن القيمة
0
و
هو
[
1.5
,
1.5
]
3
التقارب بين التوزيع الثنائي
و
توزيع بواسون
يعطي توزيع بواسون نتائج قريبة من التوزيع الثنائي ملا
n ≥
30
و
np <
2
أو
nq <
2
و يستخدم بعض اإلحصائيني كشرط الستعمال قانون بواسون بدال من القانون الثنائي القاعدة التالية
1
:
n ≥
52
و
p ≤
0،1
: مثال
10
%
نأخذ،افلات دعي ام ةلآ جاتنإ نم
30
وحد
ة
.من انتاج هذه اآللة عشوائيا
أحسب احتمال أن يك
.ون هناك وحدتان تالفتان
55
.
0
=
)
21
0.1
) (
²
0،8
(
30
2
) = C
2
=
P(X
لدينا
n ≥
52
،
p ≤
0,1
:
)الستعمال توزيع بواسون حنسب أوال قيمة املعلمة (معلمة قانون بواسون
λ = µ = np =
30
*
0،8
=
3
P(
2
) = λ
x
* e
-
λ
/x! = (
3
2
* e
-
3
) /
2
! =
0,55
4
نظرية النهاية ال
مركزية
لتكن املتغريات
1
X
،
5
X
. . . . متغريات عشوائية مستقلة هلا نف التوزيع االحتمايل بتباين ومتوسط حمددين. إذا كانت،
, . . .),
5
,
1
(n =
n
X
+ . . . +
2
+ X
8
= X
n
S
فإن
n
S
تتبع التوزيع الطبيعي عندما
n →∞
.
و
مبا أن
) = nµ
n
E(S
و
n
√
σ
=
Sn
σ
: فإننا تكتب
1
املرجع السابق
12
.
0
)
67
.
6
12
.
1
(
24
.
2
10
5
.
8
24
.
2
10
5
.
7
)
5
.
8
*
5
.
7
(
Z
P
Z
P
X
P

محاضرات اإلحصاء الرياضي
ص
.ب
- 9 -VI
يف احلقيقة فإن النظرية حمققة عندما تكون املتغريات املستقلة
Xi
هلا نف املتوسط والتباين حىت ولو مل يكن هلا بالضرورة
لاو ليامتحلاا عيزوتلا فن تايرغتملل نوكي نأ طترشي لا ثيح ةيرظنلا هذله ىرخأ غيص دجوت هنأ ملعلا عم ،عيزوتلا فن
حىت أن تكون مست
.قلة
جتدر اإلشارة إىل أن نظرية موافر
-
ذلك أن متغرية،ةيزكرلما ةياهنلا ةيرظن نم ةصاخ ةلاح يه اقباس اهيلإ انقرطت تيلا سلابلا
تتبع القانون
B(n, p)
ميكن اعتبارها جمموعا لعدد من املتغريات املستقلة ذات التوزيع الربنويل
B(
1
, p)
.
b
a
z
n
n
dz
e
b
n
n
S
a
P
2
²
2
1
lim
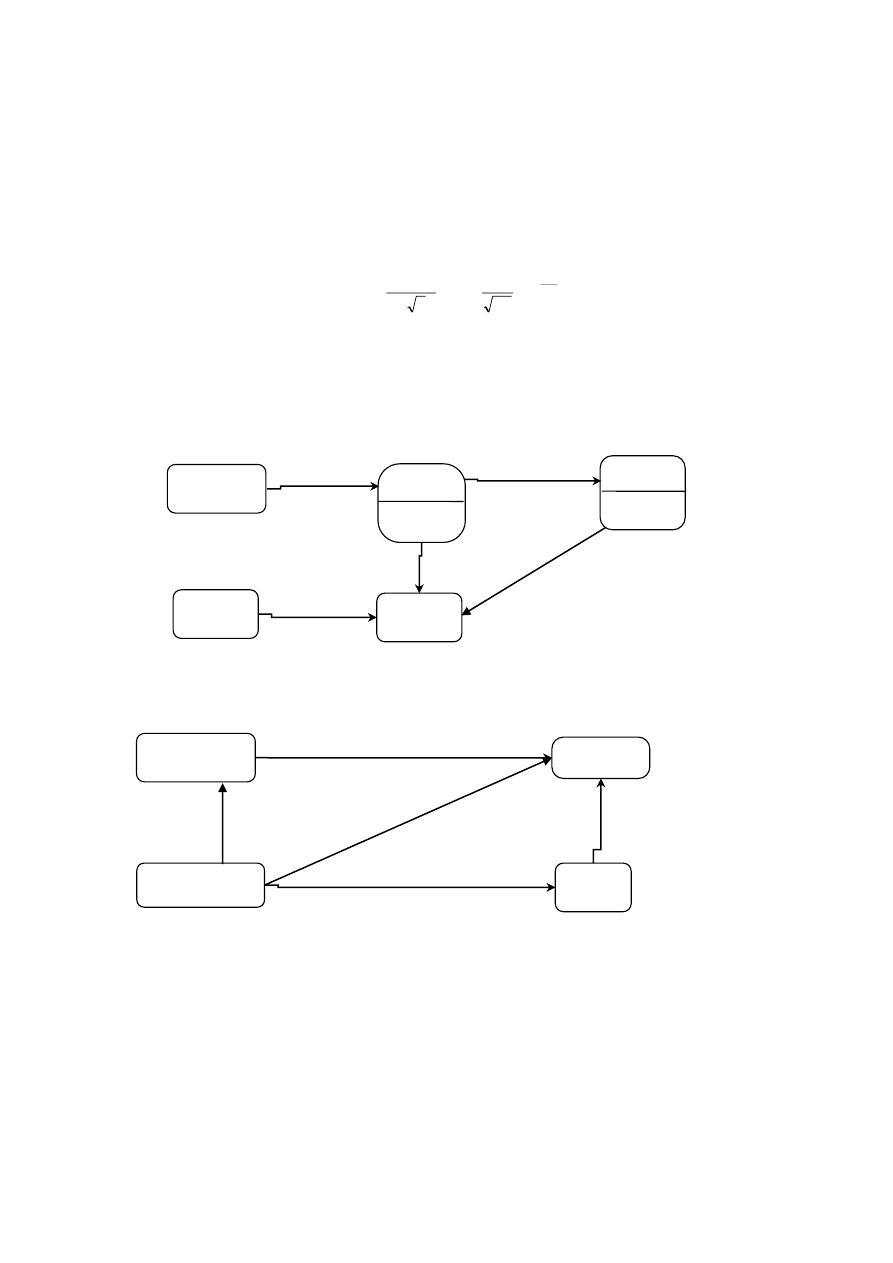
الفصل السادس
دوال المتغيرة العشوائية و التقارب
- 11 -VI
5
خالصة
ال
ستخدام التوزيع الطبيع
ي بد
ال من
التوزيع الثنائي
يعين حساب االحتمال عن طريق توزيع مستمر بينما املتغري
ة متقطعة. من
أجل ذلك
.يتم اعتبار كل قيمة يف املتغرية األصلية جماال
نظرية النهاية املركزية
تنص على أن
n
S
(
متغريات عشوائية مستقلة هلا نف التوزيع االحتمايل بتباين ومتوسط حمددين
) ت
تبع
التوزيع الطبيعي عندما
n →∞
مبتوسط
) = nµ
n
E(S
و
n
√
σ
=
Sn
σ
:ونكتب
الرسم البياين التايل يبني
ال
قواعد املستخدمة كشروط للتقريب بني التوزيعات االحتمالية
املذكورة آ
نفا
يف املبحث باإلضافة
إىل
التوزيعات األخرى
اليت درست يف الفصول السابقة
(الرمز
cr
يعين متغري
.)ة معيارية
b
a
z
n
n
dz
e
b
n
n
S
a
P
2
²
2
1
lim
[N(1, 1)]²
t
ν
²
Χ
ν
2
/ ν
F
ν1, ν2
ν→ ∞
ν = 1
ν
1
= 1
ν
2
= ν
ν
1
= 1
ν
2
→ ∞
ν
1
= ν
ν
2
→ ∞
رسم يبين قواعد التقريب بين القوانين االحتمالية األكثر
استخدامااالحتمالية
B (n, p)
B
cr
(n, p)
H(N, n, p)
P (λ)
P
cr
(λ)
N(1, 1)
t
ν
n < N/11
n ≥ 25 ; p ≤ 0,10
np = λ
n ≥ 20
np ≥10
nq ≥10
λ≥15
ν→ ∞
محاضرات اإلحصاء الرياض
ي
ص
.ب
- 1 -VII
الفصل
VII
.
نظرية توزيع المعاينة
مفاهيم
إحصائية
توزيع
ات
المعاينة
للمتوسطات
توزيع المعينة للنسبة
توزيع المعاينة للفروق و المجاميع
توزيع المعاينة للتباين
و
توزيع المعاينة لنسبة تباينين
تنتشر
يف جم
ففي عامل األعمال تقوم املؤسسات عن طريق مصاحل التسويق ومصاحل،ءاصقتسلاا تايلمع ةرصاعلما انتاعمت
اءات لإلطالع على توجهات املستهلكنيـصقتـسا ءارجإب ريوطتلاو ثوحبلا
،
ويف وسائل اإلعالم ال مير يوم دون أ
ن يعلن
تقصاء أجرته جملةـسا جئاتن نع
أو
جامعة
ح
ول
مواضيع سياسية
منها االستقصاءات املثرية للج،ةددعتم ةيعامتجا وأ
دل
ية للمواطنني أثناء اـــــــــــسايـــــــــــسلا ءارلأا لوح
تند عليهاـــــــــــست تيلا ةيـــــــــــضايرلا ةيرظنلا ـــــــــــسلأا يه امف .ةيباختنلاا تلاملح
؟هنم تذخأ يذلا عمتلمجا صئاــــصخ ىلع ةنيع تانايب للاخ نم للادتــــسلاا نكيم فيك وأ ؟ ةفلتخلما تاءاــــصقتــــسلاا
اإلج
ابة
على هذه األسئلة و غريها
تتطلب فهم
العالقات الرياضية بني اخلصائص املختلفة للمجتمع
م
التباين،طسوتلما لث
،وغريها
و
اخلصائص املنا
ظ
رة هلا يف العينة
وهو
ما سنتناوله يف هذا الفصل. يف الفصول املقبلة سندرس عددا من التط
بيقات
.هلذه العالقات الرياضية
المبحث
1
.
مفاهيم إحصائية
المجتمع والعينة
العينة النفادية
و
العينة غير النفادية
العينة العشوائية
معالم مجتمع
إحصائية المعاينة
8
المجتمع
و
العينة
Population et échantillon
:نشرح هذين املصطلحني من خالل األمثلة التالية
فتقوم أخذ أو،يدنجلل طسوتلما نزولا ريدقت في ةيركسعلا ةرادلإا بغرت دق
زان عينة من
100
جندي من بني
.)جمموع اجلنود (اجملتمع
ترغب هيأة معينة بالبحوث السياسية يف تقدير نسبة الناخبني املساندين ملرشح معني يف
10
فتقوم،تايلاولا
باستجواب
100
ناخب من كل والية. الناخبون يف الواليات العشر ميثلون اجملتمع بينما ال
1000
ناخب
املستجوبون مي
.ثلون العينة
من أجل معرفة مدى دقة صنع قطعة نقدية ترمى القطعة
100
مرة
و
حنسب عدد مرات احلصول على الصورة
و
حجم العينة هنا هو،ةباتكلا
100
.
لتقدير نسبة الكرات داخل صندوق
،
اليت من لون معني
،
نقوم عدد من املرات بسحب كرة نسجل لوهنا مث
نعيدها. عدد الكرات املسحوبة مي
.ثل حجم العينة

الفصل السابع
نظرية توزيع المعاينة
- 2 -VII
نالحظ أن مصطلح اجملتمع يقصد به القياسات أو القيم
و
،لي األفراد أو األشياء اليت مت قياسها (جمتمع األوزان
جمتمع
نوكت ةداع يهف ةنيعلا امأ ،)دقنلا ةعطق تايمر جئاتن( دودمح يرغ وأ ادودمح نوكي دق عمتلمجا نأ امك ،)..ينبخانلا ءارآ
ونرمز عادة،ةدودمح
حلجم اجملتمع ب
N
وحلجم العينة ب،
n
.
2
العينة النفادية والعينة غير النفادية
Echantillon exhaustif et non exhaustif
نسمي هذه املعاينة غري نفادية ألن تكرار العملية ال ي،ةنيعلا في ةرم نم رثكأ ةدرفلما رهظت نأ نكيم ثيح عاجرلإاب بحسلا نوكي امدنع
ؤ
دي
إىل تقليص عدد
،املفردات يف اجملتمع
و
العك نسمي املعاينة بدون إرجاع معاينة نفادية. هناك فرضيتان تتكرران يف عدد من العالقات
الرياضية اليت سنراها الحقا
،
مها فرضية أن قيم مفردات العينة مستقلة
و
اجملتمع الهنائي. يتحقق شرط االستقالل إذا كانت املعاينة غ
،ري نفادية
وإذا كانت كذل
. ميكن اعتبار اجملتمع جمتمعا غري حمدود،ك
3
العينة العشوائية
Echantillon aléatoire
من أجل أن تكون
العينة ممثلة للمجتمع
نقول عن،)عقاولا في كلذ قيقتح بعصي دق( ايرظن .ةيئاوشعلا ةنيعلا يه ةمدختسلما قرطلا دحأ ،
عينة أهنا عشوائية إذا كان
لكل مفردة يف اجملتمع نف
االحتمال ألن تكون يف العينة
. تسمى هذه العينة بالع
ينة العشوائ
ية البسيطة. إلجناز
ذلك إما أن نسحب املفردات بطريقة عشوائية أو نرقم مفردات اجملتمع مث حندد العينة من خالل جمموعة من األعداد تؤخذ من اجلداول
اإلحصائية لألعداد العشوائية
1
.
4
معالم المجتمع
Paramètre d’une population
... من خصائص اجملتمع أيضا طبيعة توزيعه االحتمايل،لثامتلا لماعم ،نيابتلا ،طسوتلما لثم هصئاصخ نم ةعوممج عمتلمجا لماعبم دصقن
f(x)
.كأن يكون طبيعيا أو غريه
5
إحصائية المعاينة
Statistique de l’échantillonnage
لتقدير معامل اجملتمع (متوسط اجملت
مع
µ
تباين اجملتمع،
σ
²
النسبة
p
حيث حنتاج إىل حساب معامل مثل،ةنيعلا تانايب نم قلطنن )...
متوسط العينة
m
تباين العينة،
S
²
النسبة يف العينة،
p’
نسمي كل قيمة حتسب انطالقا من بيانات العينة من أجل تقدير،ةماع ةفصب .
قيمة معامل اجملتمع إحصائية املعاينة. نظريا
(رياضيا) إحصائية املعاينة هي كل دالة يف املتغريات العشوائية اليت متثل القيم احملصل علي
.ها يف العينة
المبحث
2
.
توزيع
المعابنة
للمتوسطات
متوسط
توزيع المعاينة للمتوسطات
تباين
توزيع المعاينة للمتوسطات
طبيعة
توزيع المعاينة للمتوسطات
8
متوسط توزيع المعاينة للمتوسطات
مسأل
ة
ليكن اجملتمع:
1
،
3
،
2
،
2
،
0
. ما هي القيمة املتوقعة ملتوسط عينة مسحوبة
باإلرجاع
( مكونة من مفردتني
m
؟)
أحسب متوسط اجملتمع
µ
. قارن بني
m
و
µ
. من أجل حتديد ذلك أحسب مجيع احلاالت املمكنة للمتوسط
i
m
.حسب كل عينة
العينات املمكنة العينات املمكنة ذات احلجم
n =
5
من جمتمع حجمه
2
:عددها
2
*
2
=
52
1
.أنظر جدول األعدلد العشوائية

محاضرات اإلحصاء الرياض
ي
ص
.ب
- 3 -VII
العينات املمكنة
املتوسطات املمكنة للعينة (معاينة
غ نفادية
)
i
m
(
1
,
1
)
(
3
,
1
)
(
5
,
1
)
(
6
,
1
)
(
8
,
1
)
1
5
3
3،2
1،2
(
1
,
3
)
(
3
,
3
)
(
5
,
3
)
(
6
,
3
)
(
8
,
3
)
5
3
1
1،2
2،2
(
1
,
5
)
(
3
,
5
)
(
5
,
5
)
(
6
,
5
)
(
8
,
5
)
3
1
2
2،2
2،2
(
1
,
6
)
(
3
,
6
)
(
5
,
6
)
(
6
,
6
)
(
8
,
6
)
3،2
1،2
2،2
2
9
(
1
,
8
)
(
3
,
8
)
(
5
,
8
)
(
6
,
8
)
(
8
,
8
)
1،2
2،2
2،2
9
0
القيمة املتوقعة
m
ل
i
m
هي متوسط قيمها وهي
4،6
=
25
) /
i
m
i
m = (∑
.
:حساب متوسط اجملتمع
µ = (
1
+
3
+
5
+
6
+
8
)/
5
=
4.6
مث
ال
5
. أوجد نف مطالب املثال
1
. يف حالة السحب
بدون إرجاع
.
العينات املمكنة عددها
:
10
=
2
5
C
القيمة املتوقعة
m
ل
i
m
هي متوسط قيمها وهي
:
4،6
=
11
) /
i
m
i
= (∑
m
E(m) = µ
: متوسط اجملتمع
µ = (
1
+
3
+
5
+
6
+
8
)/
5
=
4.6
نظرية
8
.
إذا كانت م ع متثل جمتمع ما
و
m
متغرية ع مت
فإن القيمة املتوقعة،عمتلمجا تاذ نم ةبوحسم ةنيع طسوتم لث
ملتوسط العينة
E(M)
:تكتب كما يلي
= µ
m
E(M) = µ
لنرمز ب: ناهبرلا
Xi
لقيم املتغرية األصلية
X
.
2
تباين توزيع المعاينة للمتوسطات
(أ
)
حالة المعاينة باإلرجاع
مثال
.
أحسب تباين اجملتمع يف املسألة
1
أح،
سب التباين (واالحنراف املعياري) لتوزيع املعاينة للمتوسطات
m
²
σ
علما أن
.)تاطسوتملل ةنياعلما عيزوت( ةنكملما تانيعلا تاطسوتم نيابتو عمتلمجا نيابت ينب نراق ،)ةيدافن غ( عاجرلإاب ةبوحسم ةنيعلا
.
1
1
)
(
1
1
)
(
n
n
n
Xi
E
n
Xi
n
E
X
E
i
i
i
العينات املمكنة بدون إرجاع
املتوسطات املمكنة للعينة أو
توزيع المعاينة للمتوسطات (معاينة نفادية
)
m
i
(
1, 3)
5
(
1, 2)
(
3, 2)
3
1
(
1, 2)
(
3, 2)
(
2, 2)
3،2
1،2
2،2
(
1, 0)
(
3, 2)
(
2, 0)
(
2, 0)
1،2
2،2
2،2
9
mi
الفصل السابع
نظرية توزيع المعاينة
- 4 -VII
;
2492
=
25
]/
²
)
m
–
i
m
(
i
= [∑
m
²
σ
5484
=
5
]/
²
µ)
–
i
x
(
i
[∑
=
²
σ
2492
=
5484
/
2
:هذا املثال ميهد للنظرية التالية
نظرية
5
.
إذا كانت م ع متثل جمتمع ما
و
i
m
فإن تباين،عاجرلإاب عمتلمجا تاذ نم ةبوحسم ةنيع طسوتم لثتم ع ةيرغتم
i
m
(تباين توزيع
:املعاينة للمتوسطات) يكتب كما يلي
حيث
n
.حجم العينة
لنرمز ب:ناهبرلا
Xi
لقيم املتغرية األصلية
X
.
(
ب
)
.حالة المعاينة بدون إرجاع
:مسألة
يف املسألة
1
أحسب تباين املتوسطات املمكنة للعينة
m
²
σ
يف حالة املعاينة بدون
قارن بني تباين اجملتمع،عاجرإ
وتباي
.ن املتوسطات املمكنة للعينة
:تباين املتوسطات املمكنة للعينة
2419
=
11
]/
²
)
m
–
i
m
(
i
= [∑
m
²
σ
:تباين اجملتمع
5484
=
5
]/
²
µ)
–
i
x
(
i
= [∑
²
σ
( أو
ب
ط
:ريقة ثانية
σ
²
= E(X
²
) – E(X)
²
= (
1
+
9
+
25
+
36
+
64
) /
5
-
446²
=
5484
)
:املقارنة بني تباين متوسط العينة و تباين اجملتمع
:هذا ميهد للنظرية التالية
نظرية
3
.
إذا كانت
X
م ع متثل جمتمع ما حجمه
N
و
i
m
متغرية ع متثل متو
سط عينة حجمها
n
مسحوبة من ذات
فإن تباين،عاجرإ نودب عمتلمجا
i
m
:(تباين توزيع املعاينة للمتوسطات) يكتب كما يلي
وتسمى النسبة
معامل
.اإلرجاع
n
m
²
2
.
²
²
²
1
²
²
1
)
(
²
1
1
)
(
n
n
n
n
Xi
V
n
Xi
n
V
X
V
i
i
i
1
5
2
5
2
84
.
5
19
.
2
1
²
2
N
n
N
n
m
1
N
n
N
1
5
3
3،2
1،2
5
3
1
1،2
2،2
3
1
2
2،2
2،2
3،2
1،2
2،2
2
9
1,2
2،2
2،2
9
0
املتوسطات املمكنة للعينة أو
)توزيع املعاينة للمتوسطات (معاينة نفادية
mi
2
3
4
3،0
4،0
0،0
4،0
0،0
6،0
1
محاضرات اإلحصاء الرياض
ي
ص
.ب
- 5 -VII
3
وطبيعة توزيع
m
:ندرس طبيعة توزيع متوسط توزيع املعاينة للمتوسطات من خالل النظريات التالية
نظرية
1
.
إذا كان اجمل
تمع موزع طبيعيا مبتوسط
µ
و
تباين
σ
²
فإن متوسط العينة املسحوبة منه يتبع أيضا التوزيع الطبيعي
مبتوسط
µ
و
تباين
σ
²
/n
ونكتب،
m ≈ N(µ, σ
²
/n)
نظرية
2
.
:)(نظرية النهاية المركزية
إذا كان اجملتمع الذي تسحب منه العينة ذو متوسط
µ
و
تباين
σ
²
لكن
لي بالضرورة
طبيعيا فإن
املتغرية املعيارية ل
m
أي
تؤول إىل التوزيع الطبيعي املعياري عندما يكون
n
كبريا
)
35
≥
n
(
ونكتب
:
z ≈ N(
5
,
1
)
.
يف حالة اجملتمع حمدود واملعاينة نفادية نستبدل العبارة
σ/√n
ب
عمليا يستخدم اإلحصائيني هذه الصيغة املعدلة مبعامل اإلرجاع لالحنراف
املعياري عندما
n/N ≥
5.50
:مثال
جمتمع حجمه
155
مبتوسط
21
=
µ
و
σ =
12
. نستخرج كل العينات املمكنة. أحسب املتوسط واالحنراف
املعياري لتوزيع املعاينة للمتوسطات يف حالة
( :
1
)
حجم العينة
n =
36
،
(
5
)
n =
64
.
2
=
36
/√
12
n =
/√
σ
=
m
σ
=>
5.50
<
5.54
=
36/911
: n/N =
36
) n =
1
(
E(m) = µ =
21
مثال
5
.
باستخدام معطيات املثال السابق
(n =
36
)
أحسب احتمال أن يكون
m
حمصورا
بني
10
و
55
.
أحسب نف االحتمال يف حالة
n =
64
.
4
خالصة
.اجلدول التايل يبني أهم خصائص توزيع املعينة للمتوسطات
n
m
z
/
1
N
n
N
n
m
92
.
1
1
900
64
900
64
12
05
.
0
071
.
0
900
64
900
:
64
)
2
(
m
N
n
N
n
0.6827
)
Z
Z
P(Z
22)
m
P(18
1
Z
,
1
-
36
12/
20
-
18
n
/
µ
-
m
Z
2
1
2
1
1
0.70
)
04
.
1
Z
P(-1.04
22)
m
P(18
1.04
Z
,
1.04
-
1.92
20
-
18
1
n
/
µ
-
m
Z
2
1
1
N
n
N

الفصل السابع
نظرية توزيع المعاينة
- 6 -VII
الخاصية
المعاينة
المجتمع
µ
=
m
E(M) = µ
سحب باإلرجاع أو بدون إرجاع
جمتمع ما
سحب باإلرجاع
جمتمع ما
سحب بدون إرجاع
جمتمع ما
حجمه
N
)
/n
²
σ
m ≈ N(µ,
سحب باإلرجاع أو بدون إرجاع
جمتمع موزع طبيعيا مبتوسط
µ
وتباين
σ
²
)
1
,
5
≈ N(
عندما يكون
n
كبريا
(n ≥
35
)
جمتمع مبتوسط
µ
وتباين
σ
²
لكن
لي بالضر
ورة طبيعيا
المبحث
3
.
توزيع المعاينة للنسبة
و طبيعة التوزيع،نيابتلا ،طسوتلما ينبت ةيلاتلا ةيرظنلا
اإلحصائية
p'
. نسبة خاصية ما يف العينة:
نظرية
2
:
لتكن
X
م ع متثل جمتمع ما غري حمدود وموزع طبيعيا حيث
p
نسبة املفردات يف اجملتمع ذات صفة معين
ة،
ولتكن
’
p
م ع متثل ن
حنصل على توزيع لإلحصائية،عمتلمجا تاذ نم ةبوحسلما ةنيعلا في ةروكذلما ةفصلا تاذ تادرفلما ةبس
’
p
حيث معامله
E(p')
و
'
p
σ
،
هذه املعامل تساوي
:
عند
35
n ≥
:
)
p'
σ
(p,
N
≈
p’
عندما يكون اجملتمع حمدودا واملعاينة نفاديه نضرب يف معامل
اإلرجاع
عند حساب اال
.حنراف املعياري
مثال
1
.
الحظت إدارة اجلامعة أنه يف عينة من
100
،طالب
10
حصلوا أخريا على شهادة. تريد اإلدارة تقدير نسبة
الطلبة الذين حيصلون على الشهادة داخل جمال يكون احتماله
90
.باملائة
,
31
; n ≥
149
) =
2
p
p’<
<
1
P(p
نفرتض أن
N
: كبري حبيث
n/N <
5.50
1
م سبياجال
1902
ص
05
.
n
m
²
2
1
²
2
N
n
N
n
m
n
m
z
/
n
pq
p
p
E
p
p
'
'
²
;
)
'
(
p
P
p
z
z
z
z
P
p
p
p
P
n
p
p
p
(
(
z
p'
p
p)
-
'
0.05
100
)
6
.
0
(
4
.
0
)
1
(
(p,
N
~
p'
p'
'
2
2
1
p'
p'
محاضرات اإلحصاء الرياض
ي
ص
.ب
- 7 -VII
المبحث
4
.
توزيع المعاينة للفروق
و
المجاميع
متوسط و تباين توزيع المعاينة للفروق و المجاميع
طبيعة توزيع المعاينة للفروق و المجاميع
8
المتوسط
و
التباين
حنسب يف كل عينة حمسوبة من اجملتمع األول اإلحصائية،ةيئاوشع ةنيع امهنم لك نم بحسن ينعمتمج انيدل نكيل
1
S
و
حنسب نف االحصا
ئية (املتوسط مثال أو التباين ...) يف كل عينة من اجملتمع الثاين ونسميها
5
S
. إن الفرق
5
S
–
1
S
:يشكل بدوره متغرية عشوائية هلا املتوسط والتباين التاليني
2
S
µ
–
1
S
= µ
2
S
–
S
µ
2
S
²
+ σ
1
S
²
= σ
2
S
–
1
S
²
σ
مثال
1
. إذا كانت االحصائية هي
المتوسط
:فإن
2
µ
–
1
= µ
2
m
µ
–
1
m
= µ
2
m
–
1
m
µ
2
n
/
²
+ σ
1
n
/
²
= σ
2
m
²
+ σ
1
m
²
= σ
2
m
–
1
m
²
σ
مثال
5
. إذا كانت االحصائية هي
النسبة
:فإن
2
p
–
1
= p
2
p
µ
–
1
p
= µ
2
p
–
1
p
µ
/
2
q
2
p
+
1
/n
1
q
1
= p
2
p
²
+ σ
1
p
²
= σ
2
p
–
1
p
²
σ
2
n
:إذا كان االهتمام هو على جمموع االحصائيتني بدال من الفرق بينهما فإن
2
S
+ µ
1
S
= µ
2
S
+
1
S
µ
2
S
²
+ σ
1
S
²
= σ
2
S
+
1
S
²
σ
2
وطبيعة توزيع المعاينة للفرق بين متوسطين
نظرية
9
:
يف حالة
35
≥
1
n
و
5
n
يقرتب توزيع املتغرية املعيارية للفرق بني متوسطني من التوزيع الطبيعي،
.املعياري
و
:نكتب
)
1
,
5
≈ N(
2
m
-
1
m
µ
مثال
8
:
ليكن اجملتمع
1
U
:
3
،
9
،
0
.
و
اجملتمع
5
U
:
5
،
1
.
: حتقق من أن
.
2
U
²
+ σ
1
U
²
= σ
2
U
–
1
U
²
σ
;
2
U
µ
–
1
U
= µ
2
U
–
1
U
µ
=>
3
=
2
)/
4
+
2
= (
2
U
; µ
6
=
3
)/
8
+
1
+
3
= (
1
U
µ
3
=
3
–
6
=
2
U
µ
–
1
U
µ
3
=
6
)/
4
+
3
+
1
–
6
+
0
+
1
= (
2
U
–
1
U
µ
;
1443
=
²
6
-
3
)/
²
8
+
²
1
+
²
3
= (
1
U
²
σ
1
م سبياجال
1902
ص
100
1
U
2
U
–
1
U
3
1
8
2
U
2
1
5
6

الفصل السابع
نظرية توزيع المعاينة
- 8 -VII
=
2
U
²
σ
+
1
U
²
σ
=>
1
=
²
3
-
2
)/
²
4
+
²
2
= (
2
U
²
σ
1143
=
²
3
-
6
/
)
²
4
+
²
3
+
²
1
+
²
6
+
²
0
+
²
1
(
=
2
U
–
1
U
²
σ
(
1
+
20
+
36
+
1
+
1
+
16
) /
6
-
1
=
1143
المبحث
5
.
توزيع المعاينة للتباين
وتوزيع المعاينة لنسبة تبايني عينتين
توزيع المعاينة للتباين
توزيع المعاينة لنسبة تباينين
8
توزيع
المعاينة
للتباين
(أ
)
حالة المعاينة باإلرجاع
أحسب تباين اجملتمع يف املسألة:ةلأسم
1
أحسب القيمة املتوقعة لتباين العينة املسحوبة باإلرجاع من خالل متوسط،
قارن بني تباين اجملتمع وال،ةنكملما تانيعلا تانيابت
ق
يمة املتوقعة
.لتباين العينة
2.12
) =
²
=>E(S
2492
=
73/25
=
25
)/
i
²
S
i
(∑
σ² = E(X²) – E(X)²
= [(1 + 9 + 25 + 36 + 64)/5] - 446² = (135/5) - 21 = 0.84
E(S²) = 2492 = 5484/2
=
σ² (1/n)
نظرية
0
:
إذا كانت م ع متثل جمتمع ما
و
S
²
متغرية ع متثل تباين عينة مسحوبة باإلرجاع (أو بدون إرجاع من جمتمع
)غري حمدود
حجمها
n
: فإن،
(عند
n ≥
35
:
E(S
²
) ≈ σ
²
)
:الربهان
: من النظرية جند أن:ةظحلام
و
نقول عن
ل"فرحنم يرغ" ردقم هنأ
²
σ
و
يرمز له
ب
‘
S
²
:حيث
n
n
S
E
S
1
²
²)
(
²
n
n
n
n
x
E
x
V
X
V
n
x
E
x
E
n
x
x
n
E
x
x
n
E
S
E
i
i
i
i
i
i
i
1
²
)
1
1
²(
²
²
²
²
)²]
(
)
(
[
²
)
(
1
²)
(
²)
(
1
²
²
1
²
1
²)
(
²
1
²
n
n
S
E
1
²
n
n
S
4
-1
3
4
التباينات املمكنة
i
²
S
1
1
4
6،25
12،3
1
1
1
2،25
6،25
4
1
1
1،25
2،25
6،25
2،25
1،25
1
1
12،3
6،25
2،25
1
1

محاضرات اإلحصاء الرياض
ي
ص
.ب
- 9 -VII
نظرية
1
:
إذا أخذنا عينات عشوائية حجمها
n
: فإن،يعيبط عمتمج نم
مثاال
هـمجح يعيبط عمتمج نكيل :
100
ه عينة حجمهاـنم بـحـــــــــــــــسن
n =
12
. ما هو احتمال أن يكون تباين العينة
S
²
أقل من أو
يساوي
10
علما أ
ن تباين اجملتمع
00
.
من اجلدول
0,002
<
)
5
≤
12
²
P(X
(
ب
)
حالة
المعاينة بدون إرجاع
يف املسألة:ةلأسم
1
أحسب تباين املتوسطات املمكنة للعينة
m
²
σ
يف حالة املعاينة بدون
قارن بني تبا،عاجرإ
ين اجملت
مع
.وتباين املتوسطات املمكنة للعينة
(∑
i
S²
i
) = 3645 ; (∑
i
S²
i
)/11 = 3465 => E(S²) =
3.60
σ² = E(X²) – E(X)²
= [(1 + 9 + 25 + 36 + 64)/5] - 446² = 0.84
E(S²) = 3465 = 5484*(5/4) (1/2)
= σ² * [(n-1)/ n] [N/ (N-1)]
نظرية
11
:
إذا كانت م ع متثل جمتمع ما
حمدود
و
²
S
متغرية ع متثل تباين عينة
نفادية
،مسحوبة من ذات اجملتمع
فإن القيمة املتوقعة لتباين العينة تكتب
:
(عندما يكون
N
كبري جدا
N/ (N-
1
)
تؤول إىل
1
)
2
توزيع المعاينة لنسبة تباينين
:رأينا يف الفصل السابق أن
5
ν
,
1
ν
~F
يف حا
لة املتغريتان العشوائيتان مستقلتان
و
²
1
ν
χ
~
1
X
و
²
5
ν
χ
~
5
X
.
من النظرية
9
:نستنتج ما يلي
1
²
²
ˆ
n
n
S
S
2
1
~
²
²
ˆ
)
1
(
²
²
n
S
n
nS
1
15
²
~
²
²
))
,
(
~
80
16
²
(
)
2
²
(
)
10
²
(
n
nS
N
X
S
P
P
S
P
1
1
²
²)
(
²
N
N
n
n
S
E
S
2
2
1
1
/
/
X
X
X
التباينات املمكنة
i
²
S
1
4
1
6،25
2،25
1،25
12،3
6،25
2،25
1

الفصل السابع
نظرية توزيع المعاينة
- 11 -VII
نظرية
12
:
ليكن لدينا جمتمعان طبيعيان تباينامها
5
²
, σ
1
²
σ
.
نسحب من اجملتمعني عينتني عشوائيتني حجمهما
على التوايل
5
, n
1
n
:
مثال
8
.
عينتني حجمهما
0
و
10
مسحوبتني
من جمتمعني طبيعيني تباينامها على التوايل
50
و
32
. ما احتمال أن يكون تباين
؟األوىل أكرب من ضعف تباين الثانية
)
347
>
9
,
7
= P(F
من اجلدول جند
1411
) >
347
>
9
,
7
> P(F
1415
و يف احلقيقة
14136
) =
347
>
9
,
7
P(F
3
ملحق
(أ
)
االنح
راف المعياري لتوزيع المعاينة للتباين
نظرية
11
:
إذا كانت
X
م ع متثل جمتمع ما و
²
S
: فإن،عمتلمجا تاذ نم ةبوحسم ةنيع نيابت لثتم ع ةيرغتم
من أجل
n ≥
111
توزيع،
S
²
.يقرتب كثريا من التوزيع الطبيعي
(
ب
)
االنحراف المعياري لتوزيع المعاينة لالنحراف المعياري
من أ
جل
111
n ≥
توزيع،
S
يقرتب كثريا من التوزيع الطبيعي
و
S
≈
s
µ
1
م سبيجال
1902
ص
102
.
1
;
1
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
1
2
1
/
ˆ
/
ˆ
1
1
1
1
n
n
F
S
S
n
n
S
n
n
S
F
0.036
3.7)
P(F7,9,
:
Exactement
0.01.
3.7)
P(F7,9,
05
.
0
:
.
703
.
3
36
1
9
10
20
1
7
8
2
1
1
1
1
1
1
1
1
2
1
1
1
1
)
2
(
)
2
(
9
;
7
2
2
2
2
2
2
2
1
1
1
2
1
2
2
2
2
2
1
1
1
2
2
2
2
2
2
2
1
1
1
2
1
2
2
2
1
2
2
2
1
table
la
De
F
P
n
n
S
n
n
S
P
n
n
n
n
n
n
S
n
n
S
P
S
S
P
S
S
P
sinon
~
si
/
2
²
4
4
²
n
N
X
n
S
sinon
²
4
ou
~
si
/
2
4
4
n
N
X
N
X
n
S
محاضرات اإلحصاء الرياض
ي
ص
.ب
- 11 -VII
4
خالصة
اجلدول التايل يلخص ما ورد يف النظريات
السابقة
من
2
إىل
10
.
الخاصية
المعاينة
المجتمع
إحصائية العينة
جمتمع موزع طبيعيا
غري حمدود
النسبة
)
p'
σ
(p,
N
≈
p’
n ≥
35
حلساب
p'
σ
نضرب يف معامل
اإلرجاع
.
املعاينة نفاديه
جمتمع طبيعي
حمدود
2
S
µ
–
1
S
= µ
2
S
–
S
µ
2
S
+ µ
1
S
= µ
2
+ S
1
S
µ
2
S
²
+ σ
1
S
²
= σ
2
S
–
1
S
²
σ
2
S
²
+ σ
1
S
²
= σ
2
+ S
1
S
²
σ
سحب باإلرجاع
جمتمع ما
الفرق بني
.إحصائيتني ما
)
1
,
5
≈ N(
2
m
-
1
m
µ
35
≥
1
n
و
5
n
سحب باإلرجا
ع (أو
بدون إرجاع من جمتمع
)غري حمدود
حجمها
n
جمتمع ما وتباين عينة
S
²
ال
تباين
E(S
²
) ≈ σ
²
n ≥
35
حجمها
n
جمتمع طبيعي
عينة
نفادية
جمتمع ما حمدود و
S
²
متثل
تباين العينة
N/ (N-
1
)
تؤول إىل
1
N
كبري جدا
عينتني عشوائيتني
حجمهما على التوايل
5
n
,
1
n
جمتمعان طبيعيان تباينامها
σ
²1 , σ²5
نسبة تباينني
n
pq
p
p
E
p
p
'
'
²
;
)
'
(
n
n
S
E
S
1
²
²)
(
²
2
1
~
²
²
ˆ
)
1
(
²
²
n
S
n
nS
1
1
²
²)
(
²
N
N
n
n
S
E
S
1
;
1
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
1
2
1
/
ˆ
/
ˆ
1
1
1
1
n
n
F
S
S
n
n
S
n
n
S
F

محاضرات اإلحصاء الرياضي
ب. ص
- 1 -VIII
الفصل
VIII
.
نظرية التقدير
مفاهيم أساسية
طرق التقدير بمجال
طرق تأسيس المقدر
يف الفصل السابق درسنا
من خالل
جمموعة من النظريات العالقة الرياضية بني
معامل
العينة واملعامل املناظرة هل
ا يف اجملتمع مثل
ا،طسوتلما
النسبة...كما درسنا العالقة بني شكل توزيع اجملتمع وشكل التوزيع االحتمايل ملعامل العينة. تظهر هذه،نيابتل
ام اذهو ،ةساردلا لمح عمتلمجا لماعمو صئاصخ ريدقتل رثكأ مدختست اهنكلو اهلماعمو ةنيعلا صئاصلخ فيصوتك تاقلاعلا
.سنتعرف عليه يف هذا الفصل
المبحث
1
.
مفاهيم أساسية
بع
ض خصائص المقدر
التقدير بمجال،يطقنلا ريدقتلا
8
بعض خصائص المقدر
1
لتقدير معلمة من معامل جمتمع حمل دراسة
،
حنتاج إىل اختيار اإلحصائية املناسبة يف العينة لتقدير هذه املعلمة. غالبا ما
تكون
كأن نقدر متوسط اجملتمع،ردقم نسحأ يه ةنيعلا في ةرظانلما ةملعلما
µ
من خالل
متوسط العينة
m
µ
. تسمى اإلحصائية
.املستخدمة يف التقدير املقدر
(أ
)
المقدر غير المتحيز
ائية ما بأهنا مقدر غري متحيزــــصحإ نع لوقن
sans biais
اويـــــسم يــــضايرلا اهعقوت وأ اهطــــسوتم ناك اذإ عمتلمجا ةملعلم
ا
.ملعلمة اجملتمع
مثال
نقول عن متوسط العينة:
m
أنه
مقدر غري متحيز ملت
وسط اجملتمع
µ
ألن
E(m) = µ
.
يف املقابل نسمي اإلحصائية
S
²
يف معاينة باإلرجاع أهنا
مقدر متحيز ل
σ
²
ألن
E(S
²
) = σ
²
(n-
8
)/n ≠ σ
²
بينما تعترب االحصائية،
= S
²
n/(n-
8
)
S’
²
.مقدرا غري متحيز يف معاينة باإلرجاع
(
ب
)
الكفاءة
تتعلق كفاءة
(efficacité)
مقدر ما مبقدار التب
فإذا كان ملقدرين (إحصائيتني) نف،ةيئاصحلإل ةنياعلما عيزوتل نيا
.املتوسط نقول عن املقدر ذو توزيع املعاينة األقل تباينا أنه األكثر كفاءة
مثال
لكل من توزيعي املعاينة للمتوسط والوسيط نف املتوسط هو متوسط اجملتمع:
µ
،
لكن يعترب
املتوسط
m
مقدرا أكثر
كفاءة ملتو
سط اجملتمع
µ
من الوسيط ألن تباين توزيع املعاينة للمتوسطات
V(m) = σ
²
/n
أقل من تباين توزيع املعاينة
: للوسيط
V(méd) = σ
²
π/
2
n = (σ
²
/n) (
3.84851/2
) > σ
²
/n
.
من البديهي
أن
إال أنه قد يلجأ ملقدرات أخرى لسهولة،لضفلأا وه ةزيحتم يرغو ةلاعف تاردقم مادختسا
احل
.صول عليها
1
سبياجال
1902
ص،
501
.
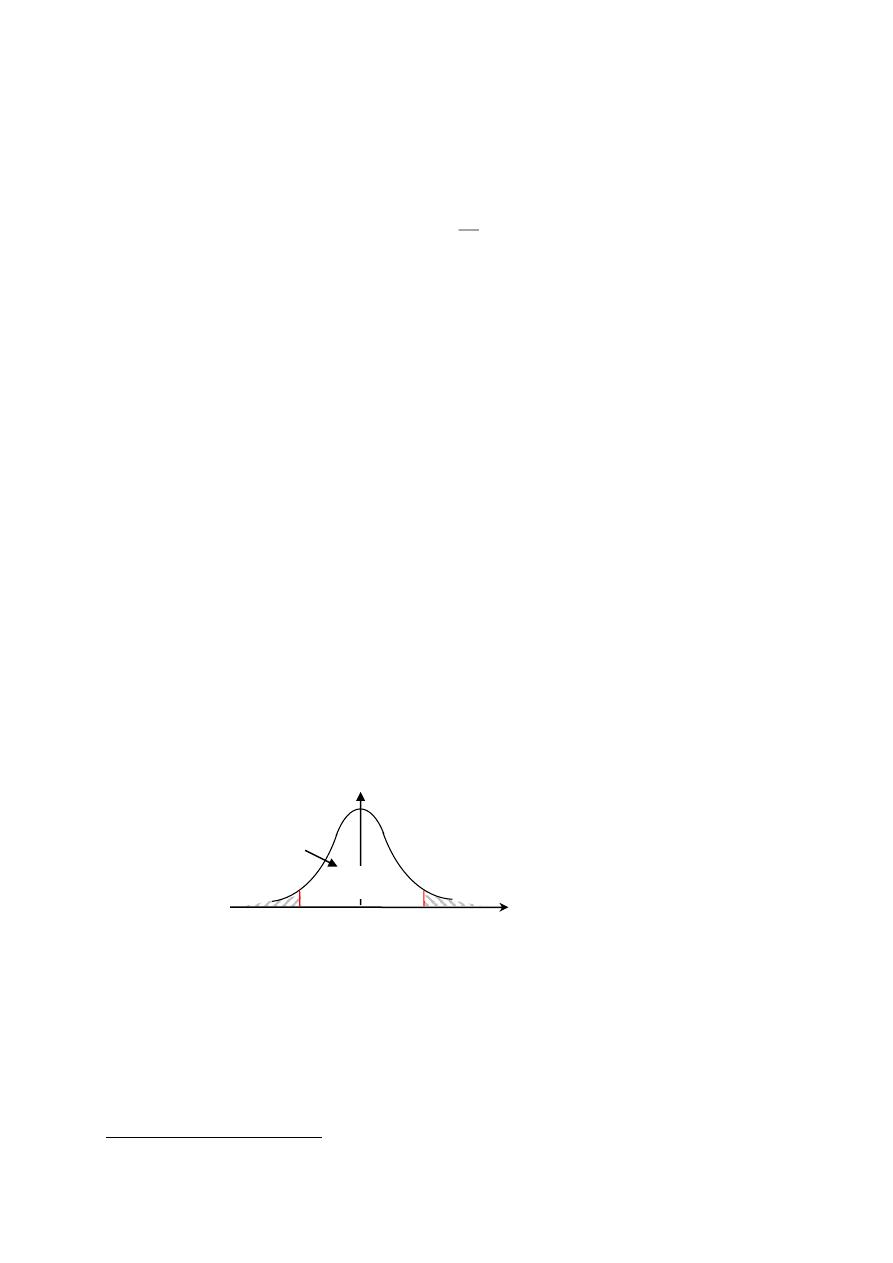
الفصل الثامن
نظرية التقدير
- 2 -VIII
(
ج
)
التقارب
convergeance
نقول عن مقدر أنه متقارب
.إذا كان يؤول إىل قيمة املعلمة املقدرة عندما يؤول حجم العينة إىل ما ال هناية
مثال
: يعترب متوسط العينة مقدرا متقاربا ملتوسط اجملتمع ألن:
2
التقدير النقطي
والتقدير بمجال
1
.
قد حنتاج إىل تقدير
ملعلمة جمتمع بقيمة واحدة ونقول عن هذا التقدير أنه
تقدير نقطي
و أحيانا أخرى،
حن
تاج
إىل تقدير
معلمة اجملتمع بنقطتني حيددان جمال لقيمة املعلمة ونقول عن هذا النوع من التقدير أنه
تقدير بمجال
.
مثال
إذا قدرنا دخل األسرة يف منطقة ما ب:
10000
نكون قد قدرنا دخ،جد
ل األسرة تقديرا نقطيا. يكون تقديرنا مبجال
إذا قلنا مثال أن الدخل يساوي
10000
2
5000
أي أنه يرتاوح بني
12000
و
50000
.دج
(أ
)
درجة التأكد
ــمى بدرجة أو مســسي ام لالمجاب قحلن كلذل ،ددلمحا لالمجا لىإ لاعف يمتنت ةملعلما نوكت نأ لامتحا مييقت يغبني ايملع ريدقتلا نوكي يكل
ت
وى
،الثقة
ويرمز له ب
p
. االحتمال املعاك يسمى احتمال اخلطأ ويرمز له ب
α
."مستوى املعنوية"" اضيأ ىمسيو ،
:مثال
[ دخل األسرة يف املنطقة (أ) ينتمي إىل اجملال
12000
،
50000
]
مبستوى معنوية
2
%
أي مبستوى ثقة
92
%
.
وتسمي احلدود
12000
و
50000
حدود الثقة
.
(
ب
)
تعيين حدود
مجال الثقة
توى الثقة). ففي حالةـــــــــــــــسم( ةيونعلما ىوتـــــــــــــــسم للاخ نم ددتح اهرودب تيلا ةقثلا تلاماعم للاخ نم ةقثلا دودح ددـتح
تخدام التوزيع الطبيعي للتقدير تكون القيمتنيــــــــسا
2
1,92
توى ثقةــــــــسم لجأ نم ةقثلا تلاماعم
92
%
بينما القيمتني
25,20
متثالن معامالت الثقة من أجل مستو
ى ثقة
99
%
.
:مثال
ليكن
s
µ
و
s
σ
ائية ماــــصحلإ ةنياعلما عيزوت يرايعم فارنحاو طــــسوتم
s
حيث
µ
=
s
µ
. إذا كان توزيع املعاينة ل
s
توزيعا طبيعيا (كما هو احلال بالنسبة ألغلب اإلحصائيات عندما
(n ≥
30
)
) فإننا نقدر مثال وبالنظر إىل توزيع
s
:أن
القيمتني
s
σ
8.15
±
s
µ
متثالن
حدود الثقة
ب
92
%
،
و
s
σ
2.51
±
s
µ
حدود الثقة ب
99
%
.
1
املرجع السابق
.
0
²
)
(
,
)
(
n
n
m
V
m
E
f(z)
-z
1-α/2
1
z
1-α/2
z
1-α
جمال الثقة
رسم
21
مجال الثقة للتوزيع الطبيعي
محاضرات اإلحصاء الرياضي
ب. ص
- 3 -VIII
يف حالة التوزيع الطبيعي يرمز حلدود الثقة ب
c
Z
أو
2
α/
-
8
Z
)(أنظر الرسم
.
المبحث
2
.
التقدير بمجال
كيفية تعيين
مجال الثقة للمتوسط
كيفية تعيين
مجال الثقة للنسبة
كيفية تعيين
مجال الثقة للتباين
كيفية ت
عيين
مجال الثقة
لنسبة تباينين
8
مجال الثقة للمتوسط
يقدر متوسط اجملتمع
µ
من خالل اإلحصائية
m
.
(أ
)
تقدير
µ
باستخدام التوزيع الطبيعي
.نستخدم التوزيع الطبيعي لتحديد جمال الثقة إذا علمنا أن اجملتمع الذي سحبت منه العينة يتبع التوزيع الطبيعي
ويف حالة العينة املمتدة
)
30
≥
n
(
ميكن كذلك االستفادة من
نظرية النهاية املركزية
1
أن
m
تتبع التوزيع الطبيعي
.
:تكتب حدود جمال الثقة كما يلي
أو
و
يف حالة
σ
:جمهول
و نستخدم هذه الصيغة إال إذا كان اجملتمع حمدود (ذا حجم
N
) واملعاينة نفادية
:حيث تصبح الصيغة كاآليت
إال أنه غالبا ما يكون االحنراف املعياري للمجتمع
σ
ولذلك نعوض،لاوهمج
σ
يف الصيغ السابقة باملقدر
S’
أو
S
.
اجلدول اآليت يبني قيم
c
z
: اليت متثل حدود جمال الثقة حبسب مستوى الثقة
مستوى الثقة
1
-α
0,99
0,90
0.15
0,90
0,0
0,2
α
مستوى املعنوية
0,01
0,05
0,02
0,10
0,5
0,2
1
- α/
5
0,992
0,99
0,992
0,92
0,9
0,92
5
α/
-
1
Z
05,2
5,352
8.15
1,212
1,505
0,291
مثال
نقدر أن:
µ
يوجد
داخل اجملال
m
σ
15
.
8
±
m
مبستوى ثقة
159
(
0,92
) أي مبستوى معنوية
2
%
(
0,02
،)
وداخل اجملال
m
σ
51
.
2
±
m
مبستوى ثقة
119
أي مبستوى معنوية
,01
0
...
(
ب
)
تقدير
µ
باستخدام التوزيع
t
:
يف حالة العينة الصغرية
)
30
<
(n
و
σ
جمهول نستخدم توزيع ستيودنت لتحديد جماالت الثقة ل
µ
. مثال القيم
-
0,992
t
؛
0,992
t
حتد
92
%
من املساحة حتت املنحىن ونقول أن
0,992
; t
0,992
t
-
متثل القيم احلرجة أو معامالت
الثقة عند مستوى
ثقة
92
%
:ونكتب
1
اليت ختص يف احلقيقة توزيع جمموع قيم العينة
-
يف حالة كون العينة كبرية مبا فيه الكفاية
-
ولي
. املتوسط
n
S
z
m
c
'
1
n
S
z
m
c
n
z
m
c
1
N
n
N
n
z
m
c
الفصل الثامن
نظرية التقدير
- 4 -VIII
ومنه نستخلص جمال الثقة ل
µ
:كما يلي
2
مجال الثقة للنسبة
(أ
)
حالة
المجتمع غير محدود أو المعاينة غير نفادية
و
العينة الممتدة
(n ≥ 35)
:
لتكن
s
يف عينة ذات حجم"تاحانج" ةبسن لثتم ةيئاصحإ
n ≥
30
مستخرجة من جمتمع ثنائي حيث
p
هي نسبة
النجا
.حات
ت
ستعمل التوزيع الطبيعي لتقدير
p
فنعني
حدود الثقة ل
p
:كما يلي
p
σ
c
p’ ± z
أين
p’
نسبة النجاحات
،يف العينة
نعلم من الفصل السابق أن
ومنه حيدد جمال الثقة ل
p
:كما يلي
n
p
p
z
p
c
)
1
(
'
(
ب
)
في حالة كون المجتمع محدود ذا حجم
N
:والمعاينة نفادية
1
)
1
(
'
N
n
N
n
p
p
z
p
c
3
مجال الثقة للتباين
: لتقدير التباين واالحنراف املعياري جملتمع مبجال ثقة نستعمل اخلاصية
.
:مثال
جمال الثقة ب
92
%
:حيدد كما يلي
ومنه نستنتج جمال الثقة ل
σ
:كما يلي
نظرا ألن توزيع ك
5
إذ توجد طريقة لتضييق جم،لثملأا يل هلاعأ لالمجا نإف لثامتم يرغ
ال الثقة أكثر إذا مل نش
أ أن تكون
. وهذا خبالف التوزيعات املتماثلة كالطبيعي وستيودنت،ةيواستم نىحنلما فارطأ
975
.
0
975
.
0
/
ˆ
t
n
S
m
t
n
S
t
m
n
S
t
m
ˆ
ˆ
975
.
0
975
.
0
n
pq
p
1
²
~
²
²
ˆ
)
1
(
²
²
n
S
n
nS
975
.
0
025
.
0
²
²
²
ˆ
)
1
(
²
²
²
S
n
nS
025
.
0
975
.
0
025
.
0
975
.
0
ˆ
1
ˆ
1
S
n
S
n
ou
S
n
S
n

محاضرات اإلحصاء الرياضي
ب. ص
- 5 -VIII
4
مجاالت الثقة لنسبة تباينين
رأينا سابقا (نظرية
11
من الفصل
2
) أنه إذا كان لدينا جمتمعان
طبيعيان
تباينامها
5
²
, σ
1
²
σ
وسحبنا منهما عينتني
عشوائيتني حجم
هما على التوايل
5
, n
1
n
: فإن
إذا ميكن تكوين تقدير
مب
جال ل
F
عند مستوى ثقة
0,90
:كما يلي
:و من مث ميكن تقدير النسبة بني تبايين اجملتمعني كما يلي
1
;
1
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
1
2
1
/
ˆ
/
ˆ
1
1
1
1
n
n
F
S
S
n
n
S
n
n
S
F
99
.
0
2
2
2
2
2
1
2
1
01
.
0
/
ˆ
/
ˆ
F
S
S
F
2
2
2
1
01
.
0
2
2
2
1
2
2
2
1
99
.
0
ˆ
ˆ
1
ˆ
ˆ
1
S
S
F
S
S
F

الفصل الثامن
نظرية التقدير
- 6 -VIII
5
خالصة
لتقدير إحصائية جمتمع نستخدم نظريات توزيع املعاينة. هذه النظريات
تتناول خصائص
إحصائيات الع
ينة
م
ن مت
وسط
،العينة
النسبة
يف العينة
... ،
.و عالقتها باإلحصائيات املناظرة هلا يف اجملتمع
جدول
1
توزيع املعاينة للمتوسطات حسب
طبيعة
توزيع
. معلومية التباين و حجم العينة،عمتلمجا
قانون
n
تباين
المجتمع
(
σ
²
)
قانون
المجتمع
N(µ ; σ/√n)
σ/√n
n <
30
أو
n ≥
30
معلوم
طبيعي
N(µ ; S’/√n)
S’/√n
n ≥
30
غري معلوم
1
-
n
α;
t
S’/√n
n <
30
N(µ ; σ/√n)
σ/√n
n ≥
30
معلوم
غري معلوم
N(µ ; S’/√n)
S’/√n
n ≥
100
غري معلوم
جدول
2
حتديد جمال الثقة
للنسبة
للتباين وللنسبة،
بني تباينني
المجتمع
ال
توزيع االحتمالي
ل
إلحصائية
مجال الثقة
جمتمع غري حمدود أو
معاينة غري نفادية و عينة
ممتدة
(n ≥ 31)
التوزيع الطبيعي
n
p
p
z
p
c
)
1
(
'
جمتمع حمدود ذا حجم
N
واملعاينة نفادية
التوزيع الطبيعي
1
)
1
(
'
N
n
N
n
p
p
z
p
c
غري معلوم
أو
أ،ينيعيبط ينعمتمج
و
عينتني مسحوبتني من
.جمتمع طبيعي واحد
مثال
عند مستوى ثقة
0,90
:
x
x
1
²
~
²
²
ˆ
)
1
(
²
²
n
S
n
nS
025
.
0
975
.
0
025
.
0
975
.
0
ˆ
1
ˆ
1
S
n
S
n
ou
S
n
S
n
025
.
0
975
.
0
025
.
0
975
.
0
ˆ
1
ˆ
1
S
n
S
n
ou
S
n
S
n
1
;
1
2
2
2
2
2
1
2
1
2
2
2
2
2
2
2
1
1
1
2
1
2
1
/
ˆ
/
ˆ
1
1
1
1
n
n
F
S
S
n
n
S
n
n
S
F
975
.
0
025
.
0
²
²
²
ˆ
)
1
(
²
²
²
S
n
nS
2
2
2
1
01
.
0
2
2
2
1
2
2
2
1
99
.
0
ˆ
ˆ
1
ˆ
ˆ
1
S
S
F
S
S
F

محاضرات اإلحصاء الرياضي
ب. ص
- 7 -VIII
5
ملحق. مجاالت الثقة للفروق والمجاميع
إذا كانت
1
s
و
5
s
تكتب حدود الثقة للفروق بني،ناتلقتسم ناتنيعلاو ،يعيبطلا عيزوتلا نم بترقي عيزوت اله ةنياعم اتيئاصحإ
املعامل اليت متثلها اإلحصائيتني ك
:ما يلي
: يف حالة اجملموع
مثال
حندد جمال الثقة للفرق،نيدودمح يرغ ينعمتمج نم ينتبوحسم ،ينتلقتسم ينتنيع اطسوتم اهم ناتيئاصحلإا تناك اذإ :
(و للمجموع) بني متوسطي اجملتمعني
5
µ
-
1
µ
: كما يلي
مثال
2
مس،ينتلقت مسينتنيع في ناتبسن اهم ناتيئاصحلإا تناك اذإ :
: حوبتان من جمتمعني غري حمدودين
املبحث
3
.
طرق تأسيس المقدر
1
طريقة العزوم
)طريقة المعقولية العظمى (االحتمال األكبر
وإذا كان هذا املقدر ال يتصف باخلصائص،ةنيعلا في اتهيرظن ةرشابم ذخأن نأ عمتجملل ام ةملعم ردقم رايتخلا قرطلا دحأ
املطلوبة جنري عليه تعديال (استخدا
م
S’
²
بدال من
S
²
لتقدير
σ
²
). توجد طرق أخرى لتحديد املقدر األنسب منها طريقة
.املعقولية العظمى واليت تدعى أيضا طريقة االحتمال األكرب واليت تنسب إىل العامل فيشر وكذا طريقة العزوم
8
وط
ريقة العزوم
ليكن املطلوب تقدير عدد
K
: من معامل اجملتمع
k
, . . , θ
5
, θ
1
θ
. نكون
مجلة معادالت عددها
K
. تتضمن كل
معادلة مساواة العزم املرتبط باألصل من الدرجة
k
ملتغرية اجملتمع
X
:
)
k
= E(X
k
µ’
بنظريه ملتغرية املعاينة،
x
:
, , K
5
,
1
k =
k
i
x
i
/n)∑
1
= (
k
m’
:مثال
ليكن
X ~ B(
50
; p)
. تقدير
p
بطريقة العزوم انطالقا من عينة يتم كما ي
:لي
لدينا عدد املعامل املراد تقديرها
K =
1
: إذا حنتاج إىل معادلة واحدة
µ =
50
p
.
و
منه
p =
50
/µ
نأخذ إذا،
كمقدر ل
p
:القيمة
p’
و
: حنسبها كما يلي
p’ = m/
50
.
:يف حالة تقدير معلمتني للمجتمع حنتاج أن نستعمل مجلة املعادلتني
5
= m’
5
µ = m , µ’
1
دراوزبيك
1999
ص
.
300
.
2
1
2
1
²
²
2
1
2
1
S
S
c
S
S
c
z
S
S
z
S
S
2
1
2
1
²
²
2
1
2
1
S
S
c
S
S
c
z
S
S
z
S
S
2
2
2
1
2
1
2
1
2
1
2
1
n
n
z
m
m
z
m
m
c
m
m
c
2
2
1
1
2
1
'
'
2
1
'
'
'
'
2
1
n
pq
n
pq
z
p
p
z
p
p
c
p
p
c
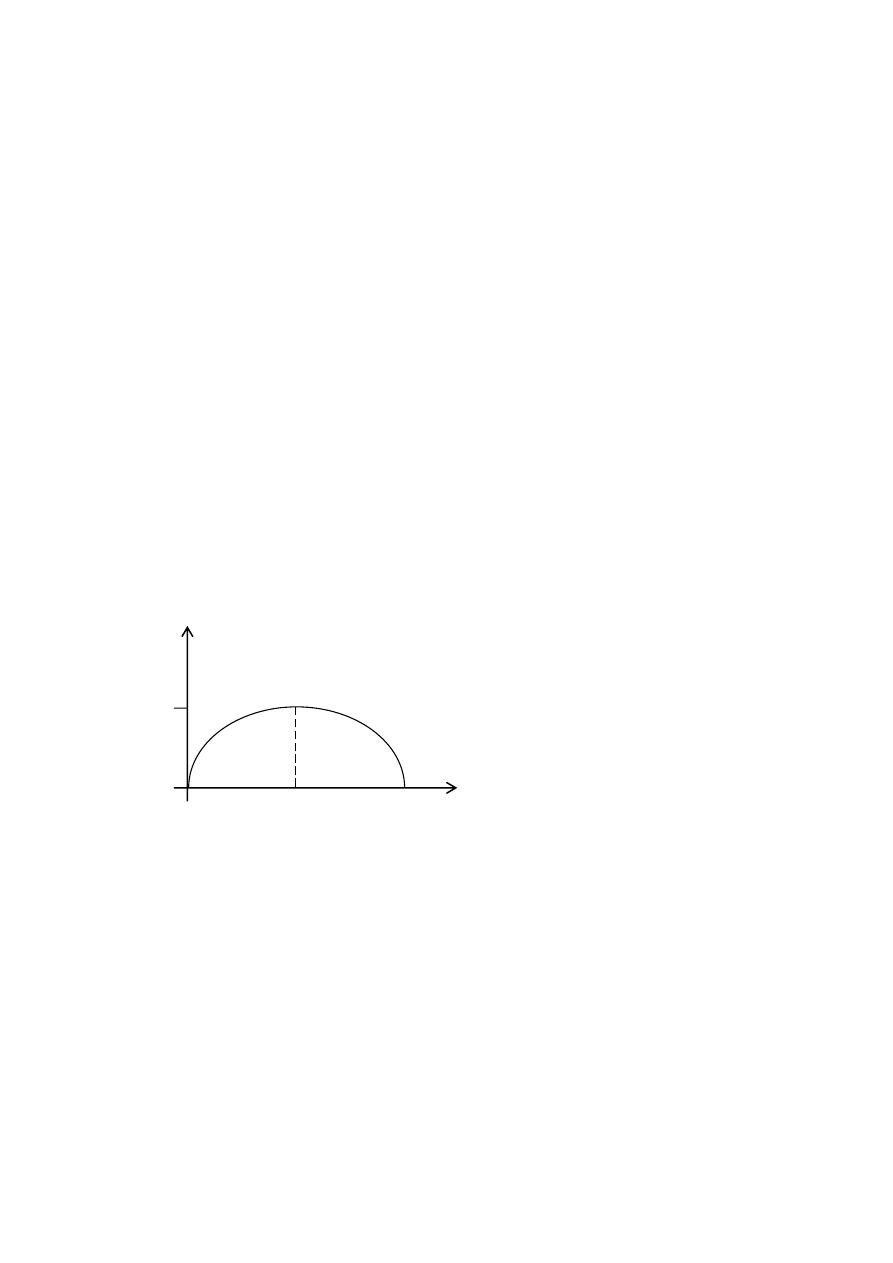
الفصل الثامن
نظرية التقدير
- 8 -VIII
مثا
ل
2
:
لتكن
X ~ N(µ; σ
²
)
. نسحب عينة ذات متوسط
m
،
و
تباين
S
²
. لتقدير
µ
و
σ
²
حنتاج إىل حل مجلة
:املعادلتني
.هذه الطريقة قد تعطي مقدرات متحيزة كما يف هذه احلالة
2
)وطريقة المعقولية العظمى (وطريقة االحتمال األكبر
نريد تقدير معلمة: ةعطقتم عمتلمجا ةيرغتم نوك ةلاح
θ
و
ولدينا عينة غري نفادية (املتغريا ت اليت متثل قيم،عمتجملل ةدحا
ةميق ب طبترم اتهاذب ةنيع ققتح لامتحا نأ يهيدبلا نم .عمتجملل عيزوتلا فن اله )ةلقتـــــــــسم ةنيعلا في اهيلع لـــــــــصلمحا
: املعلمة اجملهولة
θ)
= L(
)
n
, …,x
5
, x
1
P(x
. هناك قيمة ل
θ
ول على العينةـــــــــصلحا لامتحا مظعت
،ل عليهاـــــــــصلمحا
هذه نع ثحبلا في ىمظعلا ةيلوقعلما ةقيرط لثمتت .لعفلاب تلصح ةنيعلا نأ ابم ةحيحصلا يه ةميقلا كلت نأ ضترفنو
القيمة. أي البحث عن
θ
اليت تعظم
L(θ)
: حيث،
)
n
f(x
. . .
)
5
f(x
.
)
1
f(x
; θ) =
n
x
, . . . ,
1
f(x
θ) =
L(
.
تعتمد طريقة املعقولية العظمى عل
ى تعظيم دالة االحتمال املشرتكة
L(θ)
.
مثال
ليكن:
X ~ B(p)
وائيا من اجملتمع. نرد تقديرــــشع بوحــــسم درف ىدل " أ " ةيــــصالخا دوجو وه حاجنلا ثيح ،
p
اــهمجح ةــنيع للاخ نم
5
ةــميقلا يه اــم .
p’
ل
p
ةــجيتنلا لــعتج تيلا
1
،
0
ا هيــم يأ ؟لااــمتحا رثكلأا يه
p’
اليت
جتعل
p(
0,1
) = pq
؟أكرب ما ميكن
ح أن أكرب قيمة لـــــــــــضاولا نم
p(
0,1
)
هي
¼
و
ا هيــــهققتح تيلا ةــــميقلا
p’ =
1/5
ذاــــبهو ،
.جنيب على التساؤل
²
²
ˆ
ˆ
est
solution
la
²
²
'
²
²
'
or
'
'
2
2
2
2
S
m
S
m
m
m
m
p
1
1/2
P(141
)
1/4
رسم
22
أقصى قيمة ل
P(5،1)
مح
اضرات اإلحصاء الرياضي
ب. ص
- 1 -IX
الفصل
IX
.
مفاهيم اختبارات الفروض
و
تطبيقاتها
اختبار المتوسط
اختبار النسبة
و
اختبار التباين
اختبارات المقارنة بين مجتمعين
اختبار ال
تجانس و
اختبار
التعديل
يف الفصل السابق تناولنا كيفية تقدير معامل اجملتمع من خالل بيانات العينة
و
بعض خصائص املقدر اجل
يد. يف هذا الفصل
8
سنتناول كيفية اختبار فرضيات موضوعة حول معامل جمتمع أو أكثر. حيتاج الدارس أحيانا يف مرحلة ما من حبثه إىل اختبار
فرضية أو أكثر خبصو
اختبار،ةنيعم ةقطنم في لخدلا لدعم صوصبخ ةيضرف اختبار:كلذ ةلثمأ نم .سوردلما عمتلمجا ص
) ... يتم ذلك بصياغة فرضية عن اجملتمع املدروس (أو اجملتمعات املدروسة،ينعم ءاودل ءافش ةبسن ةيضرف
و
من مث حماولة
احلصول على دليل إحصائي ينفي أو يثبت هذه الفرضية
و
ذلك من خالل
بيانات عينة (أو أكثر) عشوائية بسيط
ة. ختص
، النسبة أو التباين،طسوتلماك عمتلمجا لماعم دحأ ةيضرفلا
و
نعتمد يف إثباهتا أو رفضها على خصائص إحصائية
.معاينة خمتارة
. على درس املعاينة،ريدقتلا سردل ةبسنلاب لالحا وه امك ،سردلا اذه دمتعي كلذ لجأ نم
المبحث
1
.
اختبار المتوسط
اال
ختبار
ثنائي االتجاه ل
لمتوسط
اال
ختبار
أحادي االتجاه ل
لمتوسط
استخدام
S
كمقدر لتباين المجتمع في اختبار المتزسط
اختبار المتزسط باستخدام توزيع
t
( يتناول هذا االختبار متوسط اجملتمع
µ
.. ، متوسط وزن منتج معني،لخدلا طسوتم لثم ،)
و
يؤكد اختبار املتوسط
فرضية مساوات
ه لقيمة ما
0
µ
.
و
للقيام باالختبار نستخرج عينة عشوائية حنسب فيها املتوسط
m
مث نستخدم التوزيع
االحتمايل ل
m
لقياس قرب أو بعد هذه القيمة من
0
µ
.
8
.اختبار ثنائي االتجاه للمتوسط
نريد اختبار فرضية حول متوسط دخل الطالب يف السنة األوىل من ختر:لاثلما اذه لوانتنل
ولتكن القي،هج
مة االفرتاضية هي
12000
:دج كمتوسط للدخل الشهري. حنتاج إىل اخلطوات التالية
حساب القي،رارقلا ةدعاق ديدتح ،تايضرفلا ديدتح
مة
. اختاذ القرار،ةيرغتملل ةيلعفلا ةميقلا باسح ،ةيرغتملل ةيلودلجا
(أ
)
تحديد الفرضيات
(الصفرية
و
:)البديلة
0
: µ ≠ µ
1
↔ H
0
: µ = µ
0
H
1
غري أننا نرى أن الفصل بني هذي؛ضورفلا رابتخا تاقيبطت نياثلاو ةيساسأ ميهافم لولأا ،ضورفلا رابتخا عوضوم لوح ينلصف جمانبرلا نمضت
ن
اجلزئني سوف يؤدي
يصعب شرح املفاهيم األساسي،ىرخأ ةهج نم .ةيساسلأا ميهافملل قرطتلا راركت لىإ
ة مبعزل عن التطبيقات أي مبعزل عن بنود
املبحث
الثاين. ل
ذلك فسوف خنوض
مباشرة يف
املبحث
ويف أثنائه سنتطرق إىل املفاهيم املذكورة يف،تاقيبطتلا ءزج يأ ،نياثلا
املبحث
.األول

الفصل التاسع
مفاهيم اختبارات الفروض و تطبيقاتها
- 2 -IX
تسمى الفرضية
0
H
الفرضية الصفرية
،أو فرضية العدم
و
يؤدي االختبار إما إىل رفضها
و
نكتب
o
RH
و
يف هذه احلالة نقبل
الفرضية البديلة
أو املعاكسة أو عدم رفضها
و
نكتب
0
R’H
.
0
µ
هي القيمة االفرتاضية ل
µ
و
هي يف هذه احلالة
12000
لذلك نكتب الفرضيات كما
:يلي
12000
µ ≠
:
1
↔ H
12000
: µ =
0
H
عادة ما تكون
0
µ
حمددة بناءا على بيانات عينة عشوائية بسيطة
m)
=
0
(µ
ويف هذه احلالة،
ميكن استخدام اخلاصية
/n)
²
σ
N(µ,
~
m
حيث أنه حتت،رابتخلاا ءارجلا
0
H
: فإن
/n)
²
σ
,
0
N(µ
~
m
مما يعين معلومية احتمال أن يكون
m
قريب إىل درجة م
ا من
0
µ
: فمثال
0,90
)) =
m
σ
(
1,21
+
0
µ
≤
m
≤
)
m
σ
(
1,21
–
0
P(µ
2
0,9
)) =
m
σ
(
1,92
+
0
µ
≤
m
≤
)
m
σ
(
1,92
–
0
P(µ
99
.
0
)) =
m
σ
(
5,20
+
0
µ
≤
m
≤
)
m
σ
(
5,20
–
0
P(µ
:وبصفة عامة نكتب
α
-
1
=
]
)
m
σ
(
5
α/
-
1
z
+
0
µ
≤
m
≤
)
m
σ
(
5
α/
-
1
z
–
0
µ
[
P
أو حسب الكتابة األكثر شيوعا
:
:حيث
m
σ
)/
0
µ
-
(m
( :
متغيرة القرار
) هي املتغرية املعيارية ل
m
و
نرمز هلا ب
c
z
حيث،
)
1
,
0
~ N(
z
.
m
σ
:حتدد كما يلي
√n
σ/
=
m
σ
يف حالة املعاينة باإلرجاع
(أو
N
0,02
≤
n
)
و
.يف احلالة املعاكسة
1
- α/
5
املساحة على يسار:
z
.
n
. حجم العينة:
ميكن إذا كان
m
خارج اجمل
ال
1
-α
أن نرفض الفرضية الصفرية اليت حدد على أساسها هذا اجملال،
و
نقبل بالتايل
الفرضية
.البديلة
.تسمى هذه (اخلطة) قاعدة القرار
(
ب
)
تحديد قاعدة القرار
تكتب قاعدة القرار يف املثال
وهي قاعدة،انيديأ ينب يذلا
اختبار ثنائي
االتجاه
(أنظر الشك
ل
1
)
: كما يلي،
1
)
(
2
/
1
0
2
/
1
z
m
z
P
m
1
N
n
N
n
m
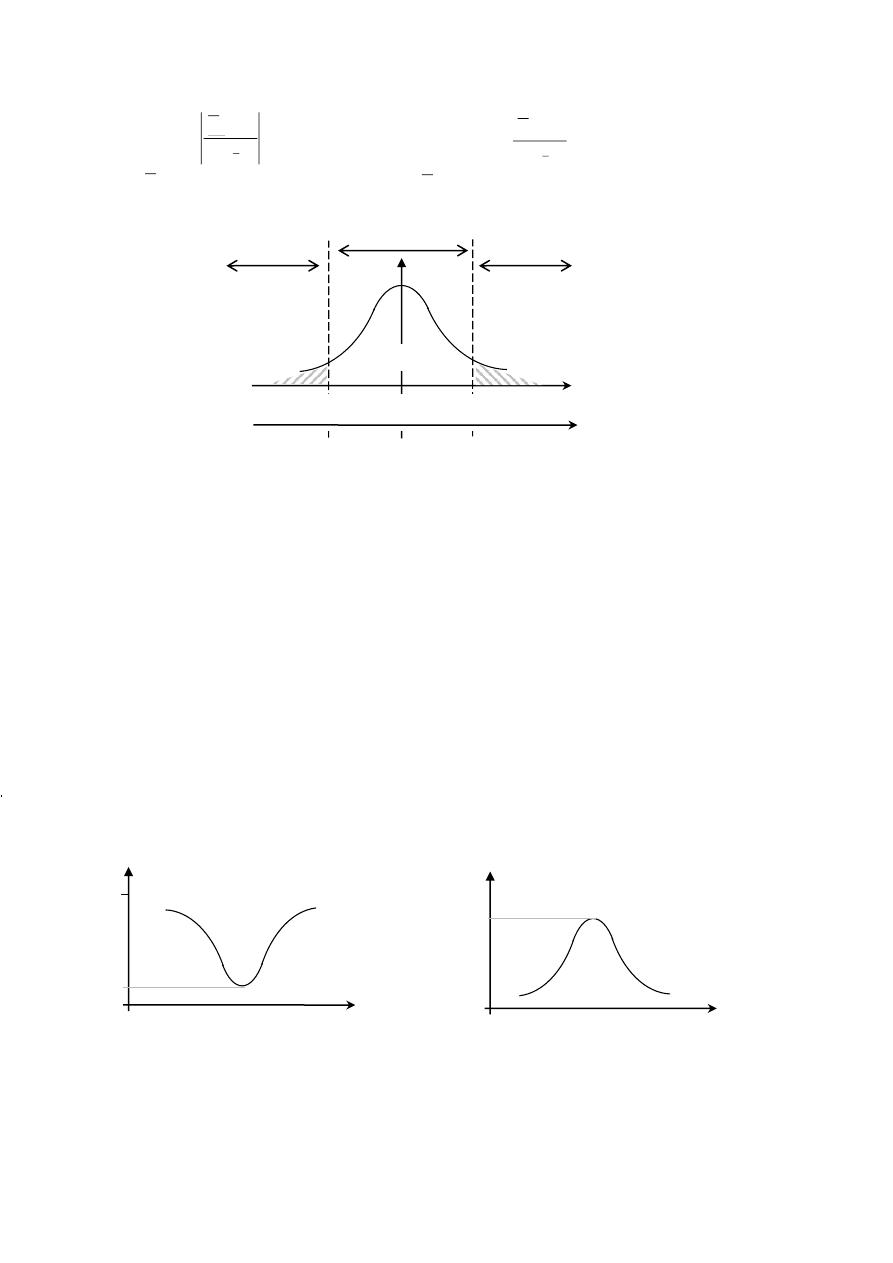
مح
اضرات اإلحصاء الرياضي
ب. ص
- 3 -IX
أ
و
رسم
23
منطقيت القبول و الرفض يف حالة قاعد القرار الثنائية
:ول إىل قرار خاطىءـــــصولا في لثمتت ةرطامخ ةطلخا هذه نمـــــضتت
يةـــــضرفلا نوكت دقف
0
H
حيحة بينما تقودنا قيمةـــــص
m
ويسمى هذا،اهضفر لىإ ةلصلمحا
الخطأ
من النوع األول
،
و
احتماله
α
: ويكتب،
α
) =
0
/ H
0
P(RH
،
و قد تقودنا قيمة
m
إىل قبول
0
H
ويسمى هذا،ةئطاخ يه اميف
الخطأ من النوع الثاني
و
احتماله
α
-
1
و
يكتب
:
α
-
1
) =
1
/ H
0
P(R’H
ولكن ال ميكن تقليص احتمال كال،نياثلا باسح ىلع نيأطلخا دحأ لامتحا صيلقت نكيم و
اخلطأين معا إال ب
زيادة حجم
.العينة
و يقي احتمال رفض الفرضية الصفرية
)
0
P(RH
قوة االختبار
(أنظر الشكل
5
)
فيما يقي احتمال قبوهلا
)
0
P(R’H
فعالية االختبار
(أنظر الشكل
5
).
و
يتوقف كال االحتمالني على القيمة
احلقيقية ل
µ
.
.
sinon
.
;
0
2
/
1
2
/
1
0
0
H
R
z
z
X
z
si
RH
X
c
.
sinon
.
0
2
/
1
0
0
H
R
z
X
si
RH
X
z
RH
1
RH
1
R’H
1
-z
1-α/2
1 z
1-α/2
µ
1
-z
1-α/2
(σ
m
)
µ
1
µ
1
+z
1-α/2
(σ
m
)
1-α
µ
1
µ
P(RH
1
)
α
1
µ
1
µ
P)R’H
1
)
1-α
1
رسم
20
(1)
منحنى الفعالية
Figure 24
منحنى القوة
(2) منحنى القوة

الفصل التاسع
مفاهيم اختبارات الفروض و تطبيقاتها
- 4 -IX
(
ج
)
حساب
z
الجدولية
:
و
يرمز هلا ب
t
z
،) وهي املشار إليها يف قاعدة القرار (الشكل الثاين،ثيح
و
يف حالتنا (اختبار ثنائي مبستوى معنوي
ة
2
%
)
:
0,992
= z
052
.
0
-
1
= z
0,02/5
-
1
= z
5
α/
-
1
= z
t
z
ومن اجلدول جند أن
1,92
=
0,992
z
.
(د
)
حساب
z
الفعلية
:
و
يرمز هلا ب
c
z
و
هي املتغري املع
يارية ل
m
: )(أنظر قاعدة القرار الشكل األول
(
ه
)
القرار
:
نقرر قبول أو رفض
0
H
.حسب قاعدة القرار
و
يف حالتنا نرفض
0
H
ألن
t
> z
c
z
ونقبل
1
H
أي أن متوسط دخل اخلريج
حديث التوظيف لي
12000
.دج
2
.االختبار أحادي االتجاه للمتوسط
يتميز االختبار الثنائي عن األحادي يف الف
رضية البديلة اليت هي عدم مساواة يف االختبار الثنائي
و
أكرب متاما أو أصغر متاما
. وهذا يرتتب عليه تغيري يف قاعدة القرار،يداحلأا رابتخلاا في )ةلالحا بسح(
(أ
)
.االختبار أحادي االتجاه من اليمين
لنرجع إىل املثال السابق مع تغيري حمدد هو أننا نريد اختبار ما إذا كان م
توسط الدخل للخريج
12000
دج أم أكثر
.)(اختبار من اليمني
أ-
: الفرضيات
0
: µ > µ
1
↔ H
0
: µ = µ
0
H
يف هذه احلالة
12000
=
0
µ
لذلك نكتب
:
12000
: µ >
1
↔ H
12000
: µ =
0
H
ب
-
قاعدة القرار
:
ج
-
حساب
z
:الجدولية
(اختبار على اليمني مبستوى معنوية
2
%
)
:
0,92
= z
0,02
-
1
= z
α
-
1
= z
t
z
ومن اجلدول جند أن
1,212
=
0,92
z
د
-
حساب
z
الفعلية
:
33
.
5
100
/
1500
1500
15800
0
X
c
X
z
.
sinon
.
0
1
0
0
H
R
z
X
si
RH
X
33
.
5
100
/
1500
1500
15800
/
0
0
n
X
X
z
X
c

مح
اضرات اإلحصاء الرياضي
ب. ص
- 5 -IX
ه
-
القرار
نرفض:
0
H
ألن
t
> z
c
z
ونقبل
1
H
أي أن متوسط دخل اخلريج حديث التوظيف لي
12000
دج
و
إمنا هو
.أكرب
(
ب
)
االختبار أحادي االتجاه من اليسار
نعود إىل م
ثالنا
و
نفرتض أن متوسط العينة كان
11500
دج
و
نريد أن خنترب ما إذا كان متوسط الدخل مساوي أم أقل من
12000
.دج
أ-
: الفرضيات
12000
: µ <
1
↔ H
12000
: µ =
0
H
ب
-
:قاعدة القرار
ج
-
حساب
z
الجدولية
(اختبار على اليسار مبستوى معنوية:
2
%
: )
1,212
-
=
0,92
z
-
=
0,02
-
1
z
-
=
α
-
1
z
-
=
t
z
د
-
حساب
z
:الفعلية
ه
-
القرار
نرفض:
0
H
ألن
t
< z
c
z
ونقبل
1
H
أي أن متوسط دخل اخلريج حديث التوظيف أقل من
12000
. دج
3
استخدام
S
كمقدر ل
σ
.في اختبار المتوسط
يف األمثلة السابقة افرتضنا أن
σ
يف الواقع غالبا ما يكون االحنر،مولعم
اف املعياري جمهوال
و
حنتاج بالتايل إىل است
خدام
( االحنراف املعياري للعينة
S
) عند حساب
m
σ
حيث نعوض العبارة،)ريدقتلا سرد رظنأ(
√n
σ/
m =
σ
ب
أو
مثال
لكن االحنراف املعياري لل،لوهمج بلاطلل يرهشلا لخدلل يرايعلما فارنحلاا نأ ضترفن قباسلا لاثلما في :
ع
ينة
S =
1200
. كيف ميكن اختبار ما إذا كان الدخل الشهري أقل من
12000
؟دج
. ج تبقى بدون تغيري، ب ،أ تاوطلخا
د
-
حساب
z
الفعلية
:
ه
-
القرار
نرفض:
0
H
ألن
t
< z
c
z
ونقبل
1
H
أي أن متوسط دخل اخلريج حديث التوظيف لي
12000
دج
و
إمنا هو
.أقل
4
استخدام التوزيع
t
في اخت
.بار المتوسط
يف حالة
n<
30
و
σ
ولكن،يعيبطلا عيزوتلا مادختسا نكيم لا ،لاوهمج )عمتجملل يرايعلما فارنحلاا(
: لدينا
.
sinon
.
0
1
0
0
H
R
z
X
si
RH
X
33
.
5
100
/
1500
1500
14200
/
0
0
n
X
X
z
X
c
1
n
S
m
n
S
m
'
97
.
4
99
/
1600
1500
14200
1
/
0
0
n
S
X
X
z
X
c

الفصل التاسع
مفاهيم اختبارات الفروض و تطبيقاتها
- 6 -IX
و حتت
0
H
(
0
µ = µ
: )
. )ميكن إذا استخدام التوزيع ستيودنت (بشرط أن يكون توزيع اجملتمع طبيعيا أو على األقل جرسي الشكل
و تتغري قاعدة القرار
:تبعا هلذا التغيري فتكتب يف حالة االختبار الثنائي كما يلي
:يف حالة اختبار من اليمني
:يف حالة اختبار من اليسار
5
خالصة
يتم اختبار الفرضيات من خالل
2
خطوات متتالية وهي
:
حتديد
)الفرضيات (الصفرية والبديلة
حتديد قاعدة القرار
حساب
القيمة
اجلدولية
للمتغرية
حساب
القيمة الفعلية للمتغرية
اختاذ
القرار
.
ب طبيعة اجملتمع و طبيعة و حجمــــــسح ،)هاتجلاا يداحأ وأ يئانث( رابتخلاا ةعيبط بــــــسح ةوطخ لك ماتمإ ةيفيك ددحتت
. ... و تسخدم يف ذلك نظريات توزيع املعاينة،ةنيعلا
المبحث
2
.
اختبار النسبة
واختبار التباين
اختبار النسبة
اختبار التباي
ن
8
اختبار النسبة
( يتعلق هذا االختبار بنسبة مفردات اجملتمع اليت تتصف خباصية ما
p
حيث يؤكد االختبار أو ينفي صحة فرضية معينة،)
خبصوص قيمة
p
. يرمز للقيمة االفرتاضية ب
0
p
وتكتب الفرضية كما يلي
:
0
: p = p
0
H
للقيام باالختبار نستخدم خصائص
p’
النسبة يف العينة
نظرية: ةبسنلل ةنياعلما عيزوت رظنأ(
2
.)
1
~
1
/
n
t
n
S
X
1
0
~
1
/
n
t
n
S
X
.
sinon
.
1
/
0
2
/
1
;
1
0
0
H
R
t
n
S
X
si
RH
n
.
sinon
1
/
0
1
,
1
0
0
H
R
t
n
S
X
si
RH
n
.
sinon
1
/
0
1
;
1
0
0
H
R
t
n
S
X
si
RH
n

مح
اضرات اإلحصاء الرياضي
ب. ص
- 7 -IX
عند
30
n ≥
:
)
p'
σ
(p,
p’ ≈ N
(نظرية موافر
-
)البالس
استنادا إىل هذه اخلصائص
و
حتت
0
H
:
:و من مث ميكن حتديد قاعدة القرار حبسب طبيعة االختباركما يلي
:يف حالة االختبار الثنائي
:يف حالة اختبار من اليمني
يف
: حالة اختبار من اليسار
:مثال
تقدر الدوائر الرمسية نسبة املتخرجني اجلامعيني الذين حيصلون على عمل يف السنة األوىل اليت تلي خترجهم ب
90
%
. وجدت دراسة أجريت على عينة من
900
طالب أن نسبة احلصول على عمل
29
%
. كيف ميكن اختبار ما
إذا كانت النسبة الرمسية صحي
مبستوى معنوية،اهيف غلابم مأ ةح
2
%
.
0,90
: p <
1
↔ H
0,90
: p =
0
H
ومنه نرفض الفرضية
0
H
.
2
اختبار التباين
،الختبار صدقية فرضية خبصوص قيمة تباين جمتمع ما
²
0
= σ
²
: σ
1
H
↔
²
0
=σ
²
: σ
0
H
نستعمل املقدر غري املنحاز
( . حيث يف حالة العينة الكبرية
20
≥
n
يف أحس
، )ن األحوال
وحتت
0
H
فإن
حيث
1
µ
:هو العزم املركزي من الدرجة الرابعة. وهبذا الشكل تكتب قاعدة القرار لالختبار الثنائي كما يلي
n
pq
p
p
E
p
p
'
'
²
;
)
'
(
n
q
p
p
N
p
0
0
0
;
'
.
sinon
.
/
'
0
2
/
1
0
0
0
0
H
R
z
n
q
p
p
p
si
RH
.
sinon
/
'
0
1
0
0
0
0
H
R
z
n
q
p
p
p
si
RH
.
sinon
/
'
0
1
0
0
0
0
H
R
z
n
q
p
p
p
si
RH
64
.
1
34
.
196
900
/
)
3
.
0
(
7
.
0
7
.
0
67
.
0
/
'
05
.
0
1
0
0
0
z
n
q
p
p
p
1
)²
(
²
ˆ
n
X
X
S
i
i
4
4
4
0
4
2
0
)
(
).
1
.
0
(
/
)
(
²
ˆ
X
E
N
n
S
T

الفصل التاسع
مفاهيم اختبارات الفروض و تطبيقاتها
- 8 -IX
و
يف حالة
1
µ
: جمهول ميكن استخدام كمقدر
1
m)
–
= E(xi
1
m
.
حيث،ايعيبط عمتلمجا ناك اذإو
1
σ
3
=
1
µ
فإن،
متغيرة القرار
ميكن أن ت
:كتب كما يلي
.
sinon
/
)
(
²
ˆ
0
2
/
1
4
0
4
2
0
0
H
R
z
n
S
si
RH
).
1
.
0
(
/
2
²
ˆ
2
0
2
0
N
n
S
T

مح
اضرات اإلحصاء الرياضي
ب. ص
- 9 -IX
المبحث
3
.
اختبار المق
ا
رنة بين مجتمعين
اختبار تساوي متوسطي مجتمعين
اختبار تساوي تبايني مجتمعين
يتناول هذا االختبار مقارنة بني جمتمعني من خالل
امل
توسط
أو التباين لكل منهما
...
و
سنركز هنا على متغري
إذ،رارقلا ة
من السهل على الطالب استنتاج كيفية إمتام
.اخلطوات األخرى على ضوء ما سبق
8
اختبار تساوي متوسطي مجتمعين
الغرض من االختبار هو تأكيد أو نفي تساوي متوسطي جمتمعني من خالل عينتني عشوائيتني بسيطتني مستقلتني. تكتب
:الفرضيات (يف حالة االختبار الثنائي)كما يلي
5
µ
≠
1
: µ
1
H
↔
5
µ
=
1
: µ
0
H
لتحديد متغرية ال
قرار
نعتمد يف االختبار على متغرية القرار
T
أو
T’
حبسب احلالة (ن
رتك
،)للطالب استنتاج قاعدة القرار
.حيث منيز بني حالة كون تباينا اجملتمعني معلومني وحالة كون تباينا اجملتمعني جمهولني
(أ
)
تباينا المجتمعين معلومين
1
-
:اجملتمعني طبيعيني
5
-
( جمتمعني ما
30
≥
5
, n
1
n
:)
(
ب
)
تباينا المجتمعين مجهولين
1
-
اجملتمع
ان
طبيعي
ا
:ن
إذا كان تباينا اجملتمعني متساويني
5
-
( جمتمعني ما
30
≥
5
, n
1
n
:)
مثال
نسحب من جمتمعني طبيعيني متساويي التباين عينتني حجم األوىل:
10
و
حجم الثانية
51
:. وجدنا النتائج التالية
)
1
.
0
(
~
2
2
2
1
2
1
2
1
N
n
n
X
X
T
)
1
,
0
(
2
2
2
1
2
1
2
1
N
n
n
X
X
T
2
2
1
2
1
2
2
2
2
1
1
2
1
2
1
~
1
1
2
'
n
n
t
n
n
n
n
S
n
S
n
X
X
T
)
1
,
0
(
1
1
2
2
2
1
2
1
2
1
N
n
S
n
S
X
X
T

الفصل التاسع
مفاهيم اختبارات الفروض و تطبيقاتها
- 11 -IX
.
0
=
5
²
S
,
9
=
1
²
, S
92
=
5
, m
01
=
1
m
كيف ميكن اجراء اختبار تساوي متوسطي اجملتمعني مبستوى معنوية
2
%
.
5
µ
≠
1
: µ
1
↔ H
5
= µ
1
: µ
0
H
2
اختبار تساوي تباين
ي
مجتمعين
.الغرض من االختبار هو تأكيد أو نفي تساوي تباينا جمتمعني من خالل عينتني عشوائيتني بسيطتني مستقلتني
تكتب الفرضيات (يف حا
:لة االختبار الثنائي)كما يلي
5
²
σ
≠
1
²
σ
:
1
↔ H
5
²
σ
=
1
²
σ
:
0
H
نعتمد يف االختبار على متغرية القرار
T
أو
T’
حيث منيز بني حالة كون اجملتمعني،ةلالحا بسبح
طبيعيني أم غري ذ
.لك
(أ
)
مجتمعين
وطبيعيين
1
-
:احلالة العامة
5
-
يف حالة
30
≥
5
, n
1
n
(
ب
)
مجتم
عين ما
)
20
≥
5
, n
1
(n
8
-
)
5
(
1
µ
;
)
1
(
1
µ
: معروفني
5
-
يف حالة
)
5
(
1
µ
;
)
1
(
1
µ
نعوض: ينفورعم يرغ
1
µ
ب
1
m
.
مثال
:
نسحب من جمتمعني طبيعيني عينتني حجم األوىل
10
و
حجم الثانية
51
:. وجدنا النتائج التالية
.
0
=
5
²
, S
9
=
1
²
, S
92
=
5
, m
01
=
1
m
كيف
ميكن اجراء اختبار تساوي متوسطي اجملتمعني مبستوى معنوية
2
%
؟
5
²
σ
≠
1
²
σ
:
1
H
↔
5
²
σ
=
1
²
σ
:
0
H
0,1
=
50
)/
51
(
0
) =
1
-
5
n
/ (
5
n
*
5
²
S
=
5
²
’
S
;
9,23
≈
19
)/
10
(
9
) =
1
-
1
n
/ (
1
n
*
1
²
S
=
1
²
’
S
0
37
;
975
.
0
2
1
2
1
2
2
2
2
1
1
2
1
43
.
5
336
.
2
43
.
5
21
1
18
1
2
21
18
)
8
(
21
)
9
(
18
76
81
1
1
2
'
RH
t
n
n
n
n
S
n
S
n
X
X
T
1
;
1
2
2
2
1
2
1
~
ˆ
ˆ
'
n
n
F
S
S
T
)
1
;
0
(
1
1
1
1
2
1
/
ˆ
ˆ
ln
2
1
2
1
2
2
2
1
N
n
n
S
S
T
)
1
;
0
(
ˆ
ˆ
/
)
ˆ
ˆ
(
2
4
2
)
2
(
4
1
4
1
)
1
(
4
2
2
2
1
N
n
S
n
S
S
S
T

مح
اضرات اإلحصاء الرياضي
ب. ص
- 11 -IX
5,19
≈
50
;
19
;
0,02
; F
1,132
≈
5
²
/ S’
1
²
S’
0
> R’H
=
1
-
5
;n
1
-
1
; n
α
T < F
المبحث
4
.
اختبار االستقالل
و
التجانس
اختبار التجانس
اختبار التعديل
8
اختبار التجانس
،لنعد إىل اختبار النسبة
و
نفرتض أن لدينا عددا
k
من اخلصائص املتنافية
،
نسبة حتقق كل منها يف اجملتمع
i
p
حيث
i
∑p
=
1
:. نريد اختبار فرضية تساوي هذه النسب
0
i
p
≠
i
p
:
1
, . . . k ) ↔ H
5
,
1
(i =
0
i
p
=
i
: p
0
H
(الفرضية البديلة هي أن
إحدى النسب النظرية
0
i
p
على األقل غري مساوية للقيمة احلقيقية
).
متغيرة القرار
( إلجناز االختبار نستخرج عينة حنسب فيها عدد مرات حتقق اخلصائص:
i
n
) . إذا حتققت الشروط
30
n ≥
،
1
≥
0
i
p
و
على األقل يف
00
%
من احلاالت
2
≥
0
i
np
: نربهن أن
2
اخت
ب
ار التعديل
ويف هذه احلالة نقارن بني تكرارات العينة (التكرارات،رخآ عيزوتب ينعم عيزوت ليدعت رابتخلا اضيأ ةقيرطلا هذه مدختست
)احلقيقية
i
n
وتكرارات افرتاضية
0
i
n
: حيث تصاغ الفرضيات كما يلي،
على األقل إحدى ال
ت
كرارات
النظرية
0
i
n
غري مساوية لل
تكرار
احلقيقي
i
n
:
1
k) ↔ H
…
,
5
,
1
(i =
0
i
= n
i
: n
0
H
m
.عدد من معامل من اجملتمع املقدرة انطالقا من بيانات العينة لتحديد التكرارات النظرية
مثال
:
يتقدم إىل انتخابات معينة
3
ب،أ :ينحشرم
و
ج. نريد اختبار فرضية مبستوى معنو
ية
2
%
:حول شعبيتهم كما يلي
52
=
3
, p
0,32
=
5
, p
0,1
=
1
: p
0
H
أجري استجواب ل
100
: ناخب فكان توزع فئات املساندين على التوايل
190
،
132
،
92
.
لدينا
30
≥
100
n =
األعداد االفرتاضية،
1
≥
100
,
110
,
120
=
0
i
np
،
و
أكثر من
00
%
من
2
≥
0
i
np
.
.
0
=> R’H
1,02
>
99
.
2
=
0,92
;
5
²
Χ
2
1
0
0
)²
(
k
i
i
i
i
np
np
n
T
2
1
0
0
)²
(
m
k
i
i
i
i
n
n
n
T
05
.
1
100
)²
100
95
(
140
)²
140
135
(
160
)²
160
170
(
)²
(
0
0
i
i
i
i
np
np
n
T
