١
Chapter two
Functions
2-1- Exponential and Logarithm functions :
Exponential functions : If a is a positive number and x is any number ,
we define the exponential function as :
y = a
x
with domain : -∞ < x < ∞
Range : y > 0
The properties of the exponential functions are :
1. If a > 0 ↔ a
x
> 0 .
2. a
x
. a
y
= a
x + y
.
3. a
x
/ a
y
= a
x - y
.
4. ( a
x
)
y
= a
x.y
.
5. ( a . b )
x
= a
x
. b
x
.
6.
x
y
y
x
y
x
)
a
(
a
a
.
7. a
-x
= 1 / a
x
and a
x
= 1 / a
-x
.
8. a
x
= a
y
↔ x = y .
9. a
0
= 1 ,
a
∞
= ∞ , a
-∞
= 0 , where a > 1 .
a
∞
= 0 , a
-∞
= ∞ , where a < 1 .
The graph of the exponential function y = a
x
is :
Logarithm function : If a is any positive number other than 1 , then
the logarithm of x to the base a denoted by :
y = log
a
x where x > 0
At a = e = 2.7182828… , we get the natural logarithm and denoted by :
y = ln x
Let x , y > 0 then the properties of logarithm functions are :
1. y = a
x
↔ x = log
a
y and y = e
x
↔ x = ln y .
2. log
e
x = ln x .
3. log
a
x = ln x / ln a .
٢
4. ln (x.y) = ln x + ln y .
5. ln ( x / y ) = ln x – ln y .
6. ln x
n
= n. ln x .
7. ln e = log
a
a = 1 and ln 1 = log
a
1 = 0 .
8. a
x
= e
x. ln a
.
9. e
ln x
= x .
The graph of the function y = ln x is :
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0
1
2
3
4
5
X
y
e
Application of exponential and logarithm functions :
We take Newton's law of cooling :
T – T
S
= ( T
0
– T
S
) e
t k
where T is the temperature of the object at time t .
T
S
is the surrounding temperature .
T
0
is the initial temperature of the object .
k is a constant .
EX-1-
The temperature of an ingot of metal is 80
o
C and the room
temperature is 20
o
C . After twenty minutes, it was 70
o
C .
a) What is the temperature will the metal be after 30 minutes?
b) What is the temperature will the metal be after two hours?
c) When will the metal be 30
o
C?
Sol. :
0091
.
0
20
6
ln
5
ln
k
e
60
50
e
)
T
T
(
T
T
k
20
S
0
S
tk
C
6
.
65
T
C
6
.
45
761
.
0
*
60
e
60
20
T
)
a
o
o
)
0091
.
0
(
30
C
1
.
40
T
C
1
.
20
335
.
0
*
60
e
60
T
T
)
b
o
o
)
0091
.
0
(
120
S
.
hrs
3
.
3
t
6
ln
t
0091
.
0
e
60
10
)
c
t
0091
.
0
٣
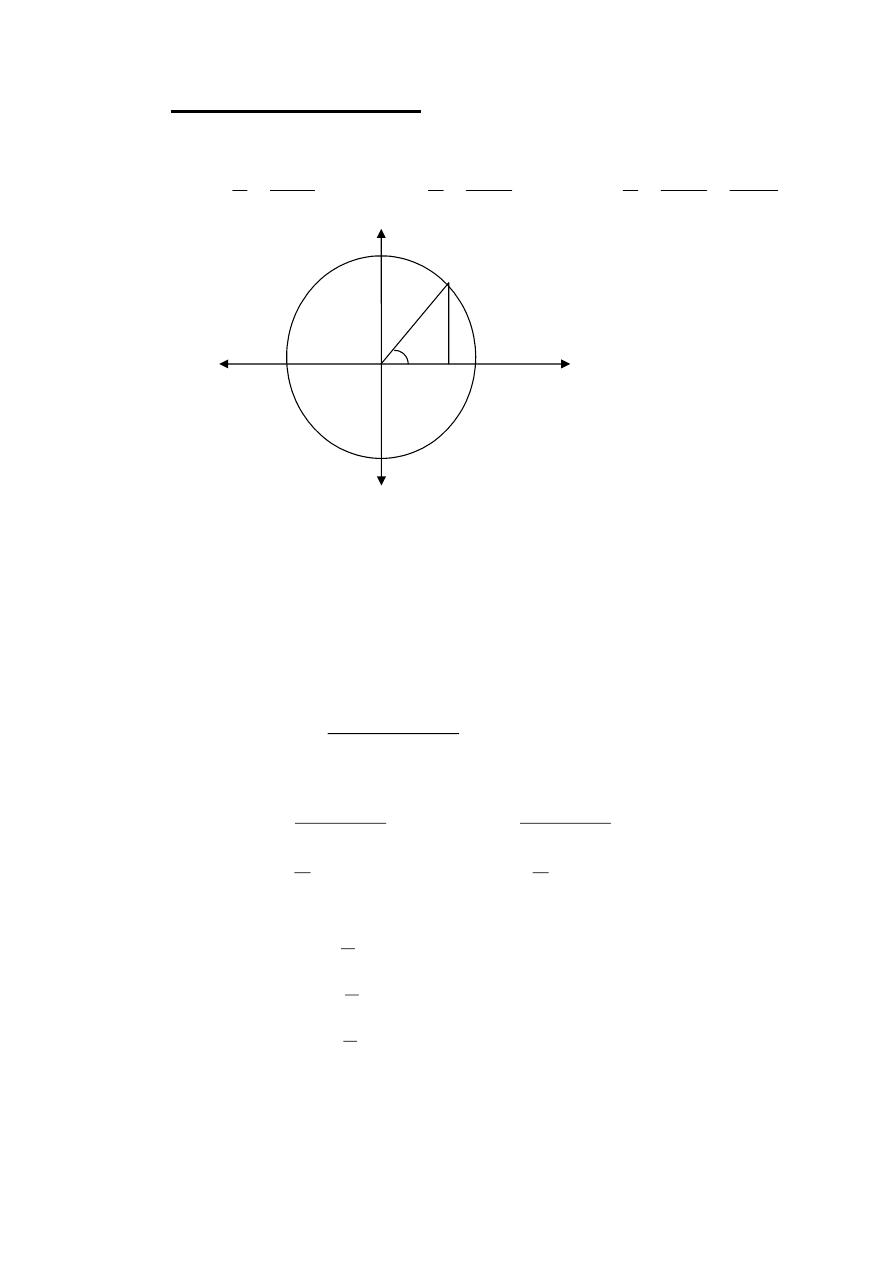
2-2- Trigonometric functions :
When an angle of measure θ is placed in
standard position at the center of a circle of radius r , the trigonometric
functions of θ are defined by the equations :
Cos
Sin
Cot
1
x
y
tan
,
sec
1
r
x
Cos
,
csc
1
r
y
Sin
The following are some properties of these functions :
tan
.
tan
1
tan
tan
)
tan(
)
5
Sin
.
Sin
Cos
.
Cos
)
(
Cos
)
4
Sin
.
Cos
Cos
.
Sin
)
(
Sin
)
3
csc
Cot
1
and
sec
tan
1
)
2
1
Cos
Sin
)
1
2
2
2
2
2
2
)]
(
Sin
)
(
Sin
[
2
1
Cos
.
Sin
)]
(
Cos
)
(
Cos
[
2
1
Cos
.
Cos
)]
(
Cos
)
(
Cos
[
2
1
Sin
.
Sin
)
10
tan
)
tan(
and
Cos
)
(
Cos
and
Sin
)
(
Sin
)
9
Sin
)
2
(
Cos
and
Cos
)
2
(
Sin
)
8
2
2
Cos
1
Sin
and
2
2
Cos
1
Cos
)
7
Sin
Cos
2
Cos
and
Cos
.
Sin
2
2
Sin
)
6
2
2
2
2
x
y
o
r
θ
٤
2
Sin
.
2
Sin
2
Cos
Cos
2
Cos
.
2
Cos
2
Cos
Cos
)
12
2
Sin
.
2
Cos
2
Sin
Sin
2
Cos
.
2
Sin
2
Sin
Sin
)
11
θ
0 Π / 6 Π / 4 Π / 3 Π / 2 Π
Sinθ 0 1/2
1/√2 √3/2
1
0
Cosθ 1 √3/2 1/√2 1/2
0
-1
tanθ 0 1/√2
1
√3
∞ 0
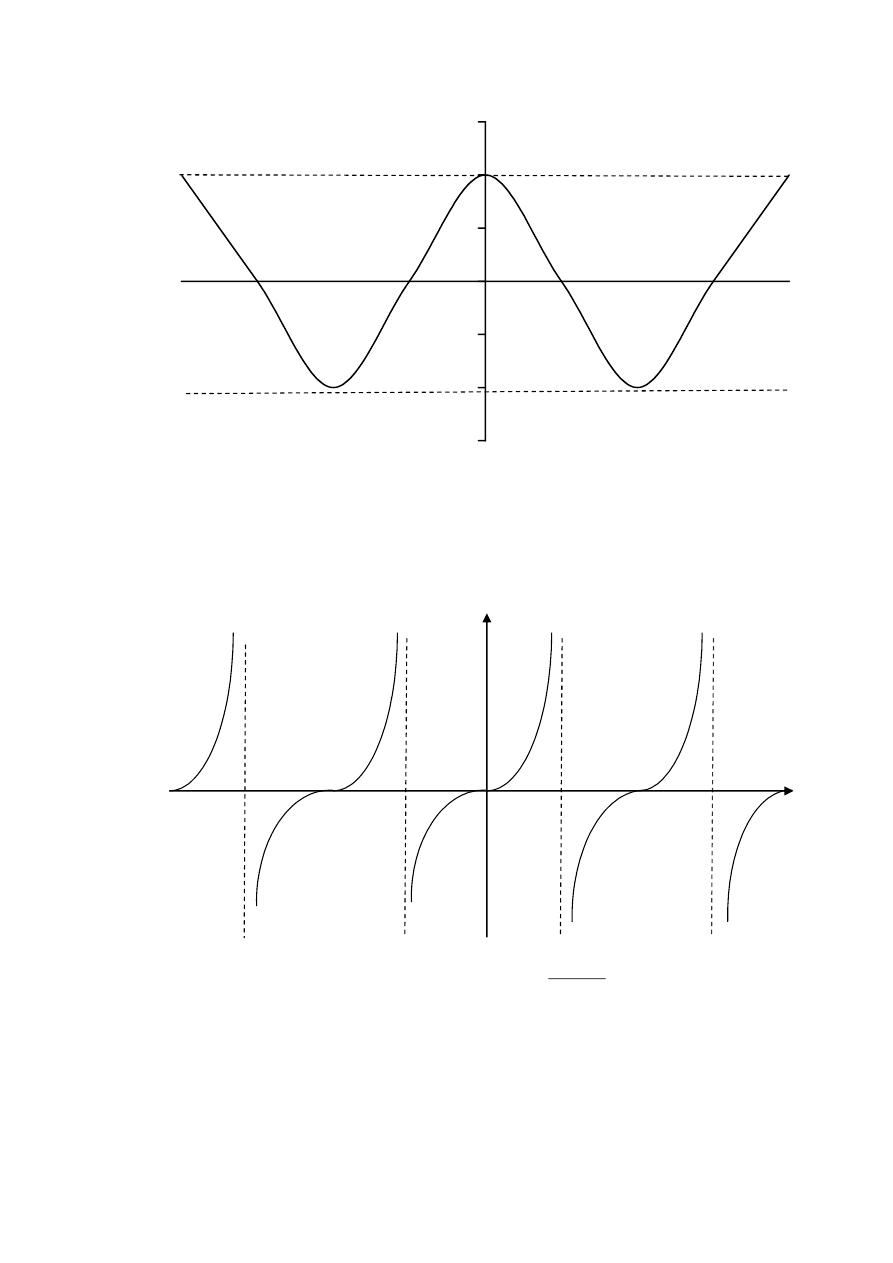
Graphs of the trigonometric functions are :
-1.5
-1
-0.5
0
0.5
1
1.5
1
y
1
:
R
x
:
D
Sinx
y
y
x
-2Л -Л Л 2Л
٥
-1.5
-1
-0.5
0
0.5
1
1.5
1
y
1
:
R
x
:
D
Cosx
y
y
x
-2π -π 0 π 2π
y
:
R
2
1
n
2
x
:
D
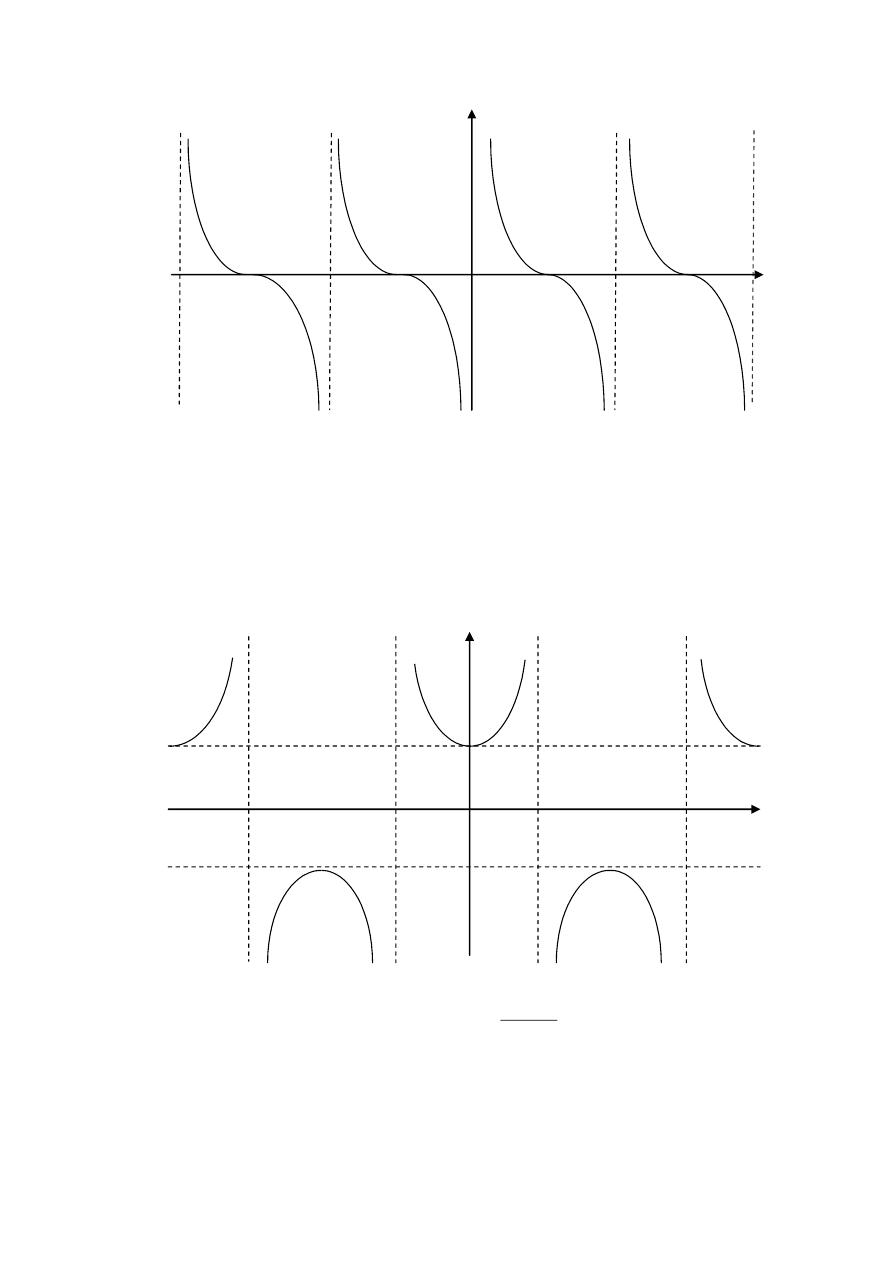
x
tan
y
y
x
-2Л -Л Л 2Л
٦
-2π -π 0 π 2π
y
:
R
n
x
:
D
Cotx
y
y
x
-2π -π 0 π 2π
1
-1
1
y
or
1
y
:
R
2
1
n
2
x
:
D
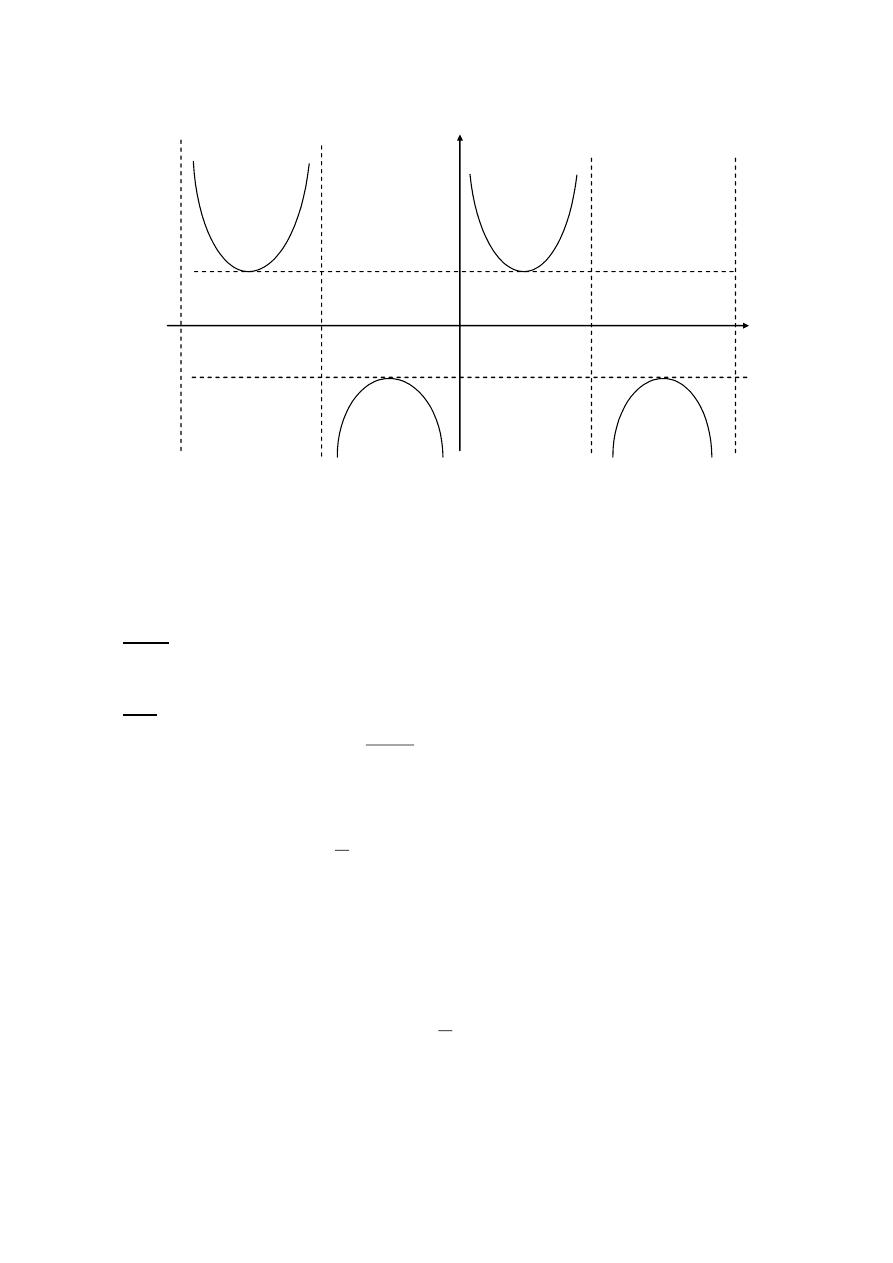
Secx
y
y
x
٧
-2π -π 0 π 2π
1
-1
1
y
or
1
y
:
R
n
x
:
D
x
csc
y
y
x
EX-2 -
Solve the following equations , for values of θ from 0
o
to 360
o
inclusive .
a) tan θ = 2 Sin θ b) 1 + Cos θ = 2 Sin
2
θ
Sol.
-
o
o
o
o
o
300
,
60
2
1
Cos
or
360
,
180
,
0
0
Sin
either
0
)
Cos
2
1
(
Sin
Sin
2
Cos
Sin
Sin
2
tan
)
a
Therefore the required values of θ are 0
o
,60
o
,180
o
,300
o
,360
o
.
o
o
o
2
2
180
1
Cos
or
300
,
60
2
1
Cos
either
0
)
1
Cos
)(
1
Cos
2
(
)
Cos
1
(
2
Cos
1
Sin
.
2
Cos
1
)
b
There the roots of the equation between 0
o
and 360
o
are 60
o
,180
o
and 300
o
.
,......
3
,
2
,
1
,
0
n
Where

٨
EX-3- If tan θ = 7/24, find without using tables the values of Secθ and Sinθ.
Sol.-
25
7
r
y
Sin
and
24
25
x
r
Sec
25
24
7
r
24
7
x
y
tan
2
2
EX-4- Prove the following identities :
Csc
Sec
Cot
tan
Cot
tan
Csc
Sec
)
c
Sin
Cos
Sin
Cos
)
b
Sec
.
Csc
Sec
.
tan
Csc
)
a
2
2
4
4
2
Sol.-
.
S
.
H
.
R
Csc
Sec
Cot
tan
Cos
.
Sin
1
Cos
.
Sin
1
.
Cos
Sin
Cos
Sin
Cos
Sin
1
Sin
Cos
Cos
Sin
Sin
1
Cos
1
Cot
tan
Csc
Sec
.
S
.
H
.
L
)
c
.
S
.
H
.
R
Sin
Cos
)
Sin
Cos
).(
Sin
Cos
(
Sin
Cos
.
S
.
H
.
L
)
b
.
S
.
H
.
R
Sec
.
Csc
Cos
1
.
Sin
1
Cos
.
Sin
Sin
Cos
Cos
1
.
Cos
Sin
Sin
1
Sec
.
tan
Csc
.
S
.
H
.
L
)
a
2
2
2
2
2
2
2
2
4
4
2
2
2
2
2
EX-5- Simplify
Csc
.
a
x
when
a
x
1
2
2
.
Sol.-
tan
a
1
Cot
a
1
a
Csc
a
1
a
x
1
2
2
2
2
2
2
.
EX-6- Eliminate θ from the equations :
i) x = a Sinθ and y = b tanθ
ii) x = 2 Secθ and y = Cos2θ
Sol.-
٧
٤٢
٩
1
y
b
x
a
1
Cot
Csc
Since
y
b
Cot
b
y
tan
tan
b
y
x
a
Csc
a
x
Sin
Sin
.
a
x
)
i
2
2
2
2
2
2
2
2
2
2
2
2
2
x
8
y
x
x
4
x
x
4
y
Sin
Cos
y
2
Cos
y
x
2
Cos
Sec
2
x
)
ii
EX-7- If tan
2
θ – 2 tan
2
β = 1 , show that 2 Cos
2
θ – Cos
2
β = 0 .
Sol. –
.
D
.
E
.
Q
0
Cos
Cos
2
0
Cos
2
Cos
1
0
Sec
2
Sec
1
)
1
Sec
(
2
1
Sec
1
tan
2
tan
2
2
2
2
2
2
2
2
2
2
EX-8- If a Sinθ = p – b Cosθ and b Sinθ = q + a Cosθ .Show that :
a
2
+b
2
= p
2
+q
2
Sol.-
2
2
2
2
2
2
2
2
2
2
2
2
b
a
)
Sin
Cos
(
b
)
Cos
Sin
(
a
)
aCos
bSin
(
)
bCos
aSin
(
q
p
Cos
.
a
Sin
.
b
q
and
Cos
.
b
Sin
.
a
p
EX-9- If Sin A = 4 / 5 and Cos B = 12 / 13 ,where A is obtuse and B is
acute . Find , without tables , the values of :
a) Sin ( A – B ) , b) tan ( A – B ) , c) tan ( A + B ) .
Sol. -
4
x
2
x
2
-3
5
4
A
B
13
12
5

٠١
56
33
12
5
.
3
4
1
12
5
3
4
B
tan
.
A
tan
1
B
tan
A
tan
)
B
A
tan(
)
c
16
63
12
5
.
3
4
1
12
5
3
4
B
tan
.
A
tan
1
B
tan
A
tan
)
B
A
tan(
)
b
65
63
13
5
.
5
3
13
12
.
5
4
SinB
.
CosA
CosB
.
SinA
)
B
A
(
Sin
)
a
EX-10 – Prove the following identities:
Cot
1
2
Cos
2
Sin
1
2
Cos
2
Sin
)
d
SecB
.
SecA
CscB
.
CscA
CscB
.
CscA
.
SecB
.
SecA
)
B
A
(
Sec
)
c
CosB
.
CosA
)
B
A
(
Sin
B
tan
A
tan
)
b
CosB
.
SinA
.
2
)
B
A
(
Sin
)
B
A
(
Sin
)
a
١١
Sol.-
.
S
.
H
.
R
Cot
Sin
Cos
Sin
2
Cos
.
Sin
2
Cos
2
Cos
.
Sin
2
1
)
Sin
Cos
(
Cos
.
Sin
2
1
)
Sin
Cos
(
Cos
.
Sin
2
1
2
Cos
2
Sin
1
2
Cos
2
Sin
.
S
.
H
.
L
)
d
.
S
.
H
.
L
)
B
A
(
Sec
)
B
A
(
Cos
1
SinB
.
SinA
CosB
.
CosA
1
CosB
1
.
CosA
1
SinB
1
.
SinA
1
SinB
1
.
SinA
1
.
CosB
1
.
CosA
1
SecB
.
SecA
CscB
.
CscA
CscB
.
CscA
.
SecB
.
SecA
S
.
H
.
R
)
c
.
S
.
H
.
L
B
tan
A
tan
CosB
.
CosA
SinB
.
CosA
CosB
.
SinA
CosB
.
CosA
)
B
A
(
Sin
.
S
.
H
.
R
)
b
.
S
.
H
.
R
CosB
.
SinA
.
2
SinB
.
CosA
CosB
.
SinA
SinB
.
CosA
CosB
.
SinA
)
B
A
(
Sin
)
B
A
(
Sin
.
S
.
H
.
L
)
a
2
2
2
2
2
2
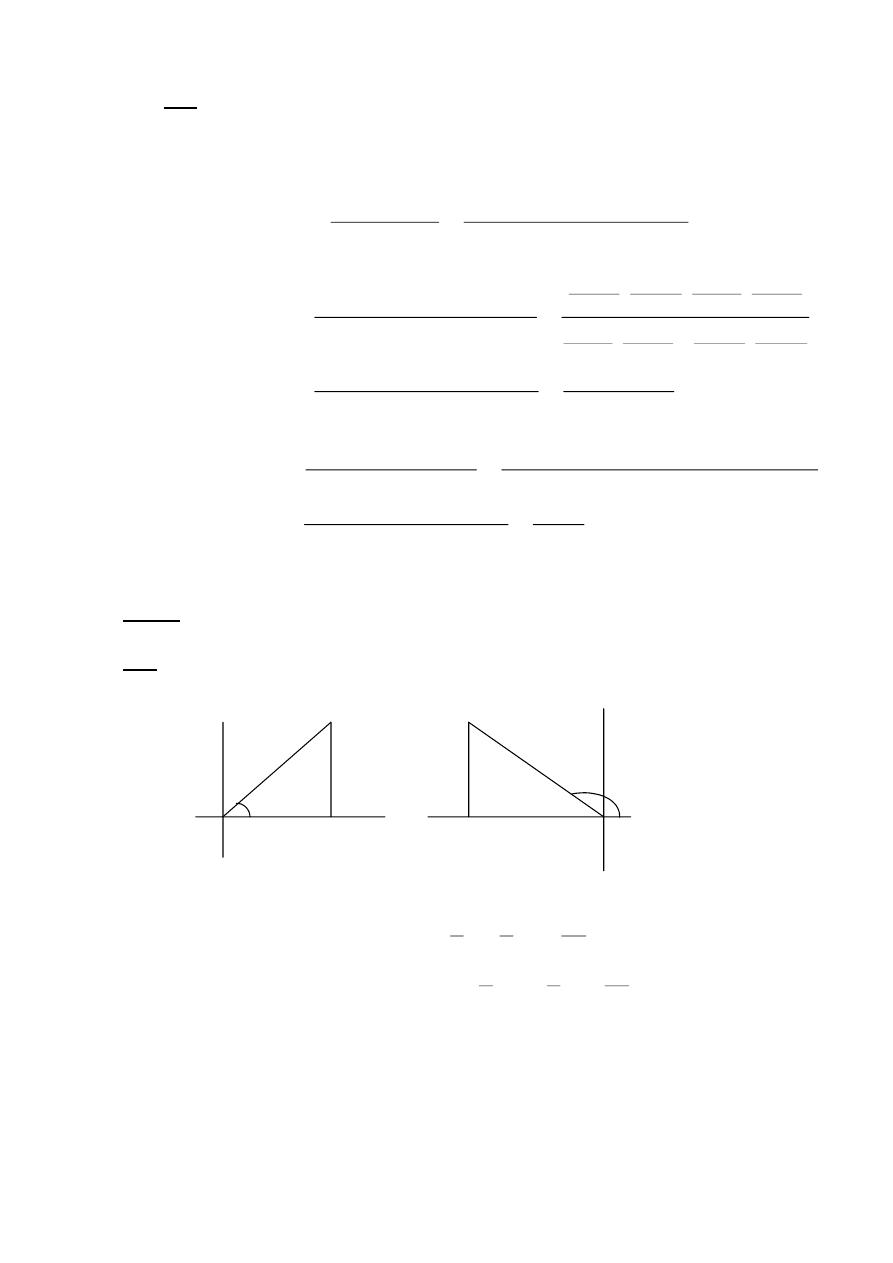
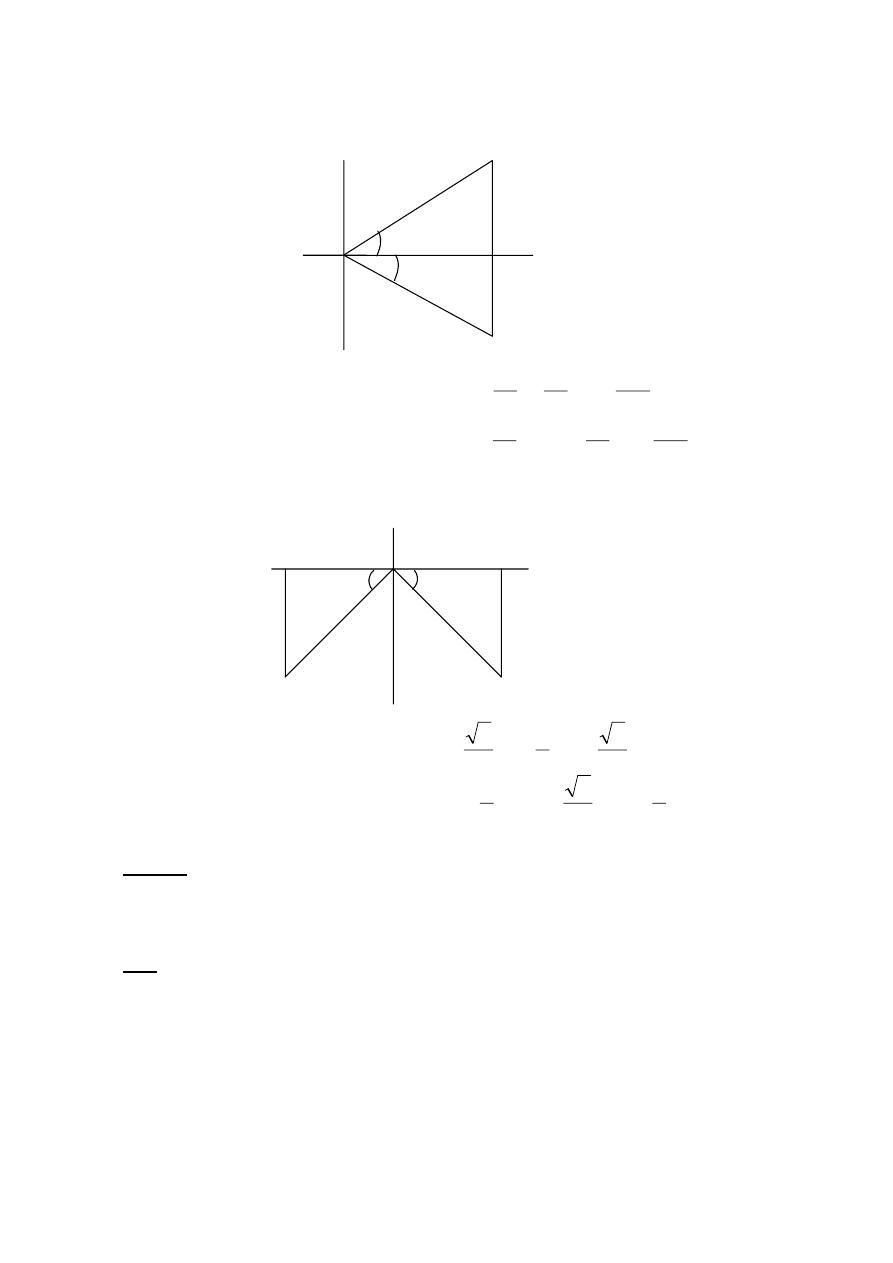
EX-11 – Find , without using tables , the values of Sin 2θ and Cos 2θ, when:
a) Sinθ = 3 / 5 , b) Cos θ = 12/13 , c) Sin θ = -√3 / 2 .
Sol. –
a)
25
7
)
5
3
(
)
5
4
(
Sin
Cos
2
Cos
25
24
)
5
4
.(
5
3
.
2
Cos
.
Sin
.
2
2
Sin
2
2
2
2
-4
5
3
θ
3
٥
θ
٤
٢١
b)
169
119
)
13
5
(
)
13
12
(
Sin
Cos
2
Cos
169
120
)
13
12
).(
13
5
(
2
Cos
.
Sin
.
2
2
Sin
2
2
2
2
c)
2
1
)
2
3
(
)
2
1
(
Sin
Cos
2
Cos
2
3
)
2
1
).(
2
3
(
2
Cos
.
Sin
2
2
Sin
2
2
2
2
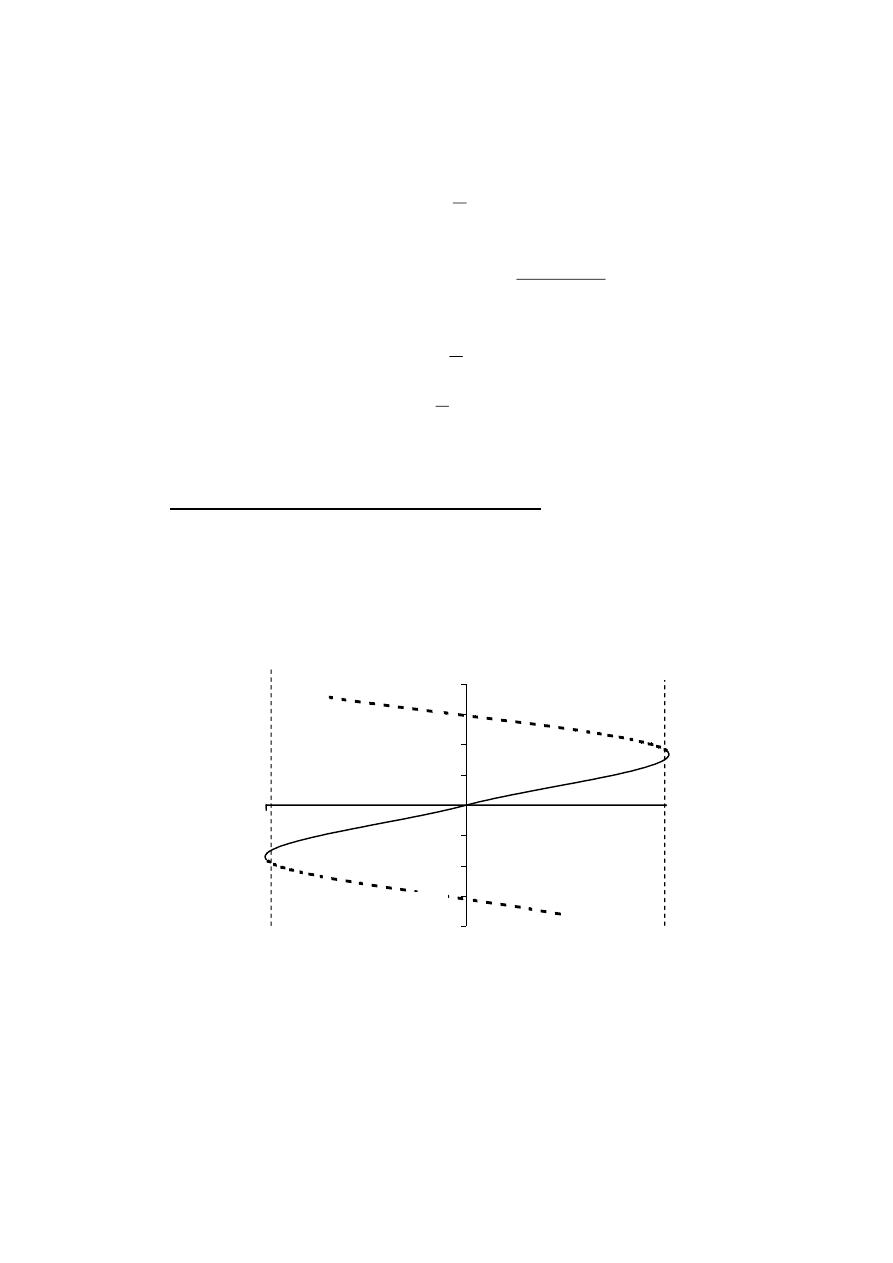
EX-12- Solve the following equations for values of θ from 0
o
to 360
o
inclusive:
a) Cos 2θ + Cos θ + 1 = 0 , b) 4 tan θ . tan 2θ = 1
Sol.-
5
٣١
-5
θ
θ
٢١
٣١
1
θ
θ
١
-
-√3
2
-√3
2
٣١
o
o
o
o
o
o
o
o
2
2
o
o
o
o
o
o
o
o
2
6
.
341
,
4
.
198
,
6
.
161
,
4
.
18
6
.
341
,
6
.
161
3
1
tan
or
4
.
198
,
4
.
18
3
1
tan
either
1
tan
9
1
tan
1
tan
2
.
tan
.
4
1
2
tan
.
tan
.
4
)
b
270
,
240
,
120
,
90
240
,
120
2
1
Cos
or
270
,
90
0
Cos
either
0
)
1
Cos
.
2
(
Cos
0
1
Cos
1
Cos
2
0
1
Cos
2
Cos
)
a
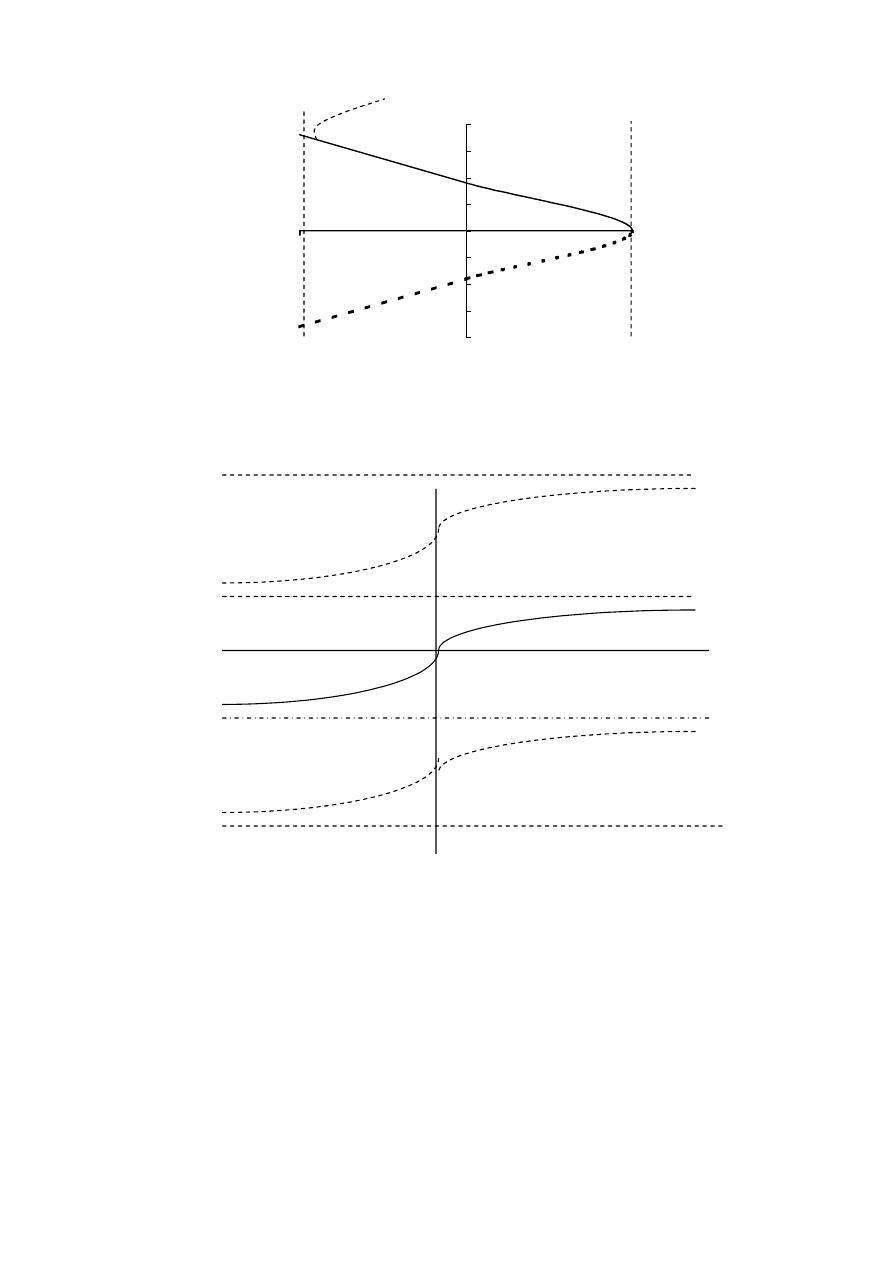
2-3- The inverse trigonometric functions :
The inverse trigonometric
functions arise in problems that require finding angles from side
measurements in triangles :
y
Sin
x
Sinx
y
1
-200
-150
-100
-50
0
50
100
150
200
-1
1
90
y
90
:
R
1
x
1
:
D
x
Sin
y
y
x
1
-
٤١
-1
1
180
y
0
:
R
1
x
1
:
D
x
Cos
y
y
x
1
90
y
90
:
R
x
:
D
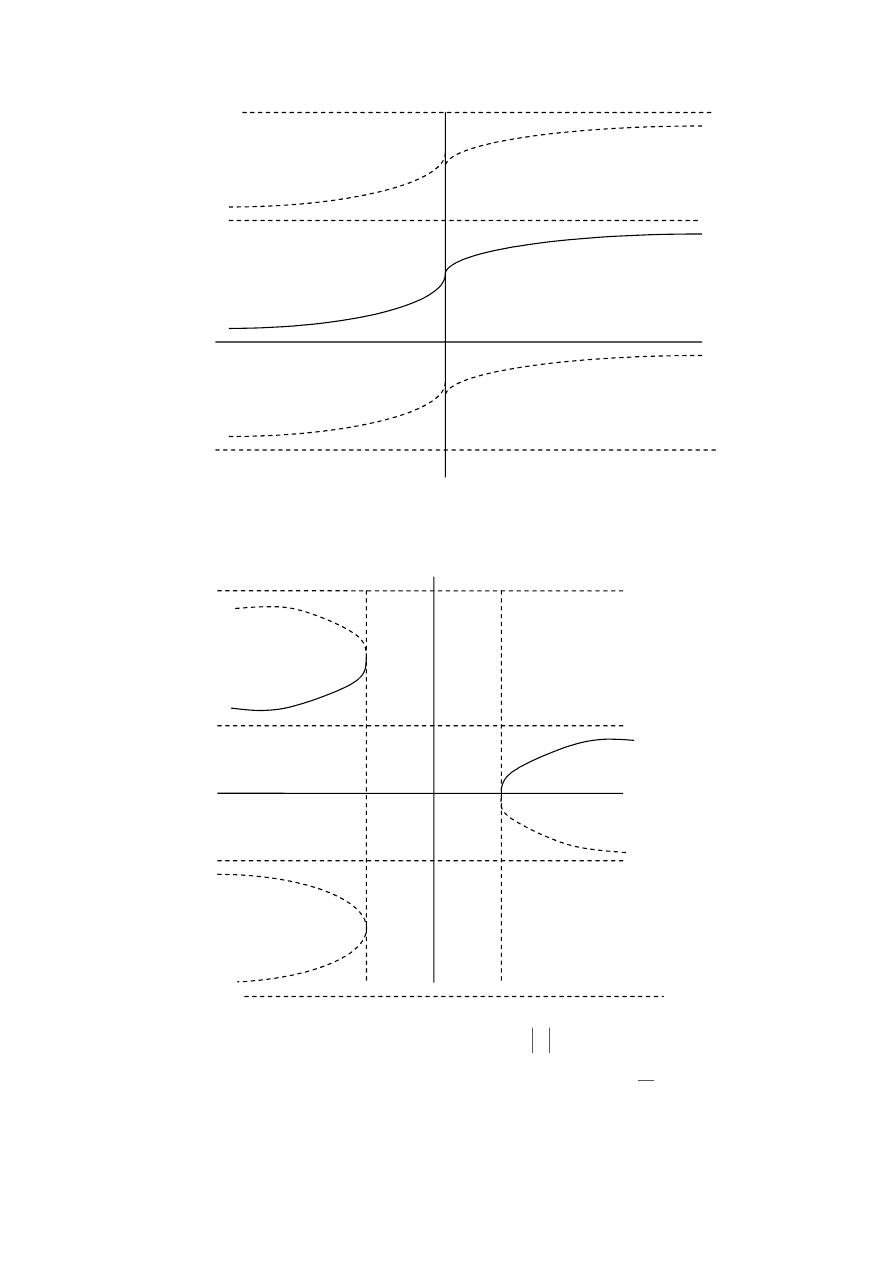
x
tan
y
y
x
1
π
-
π
0
-
٥١
y
0
:
R
x
:
D
x
Cot
y
y
x
1
2
y
,
y
0
:
R
1
x
:
D
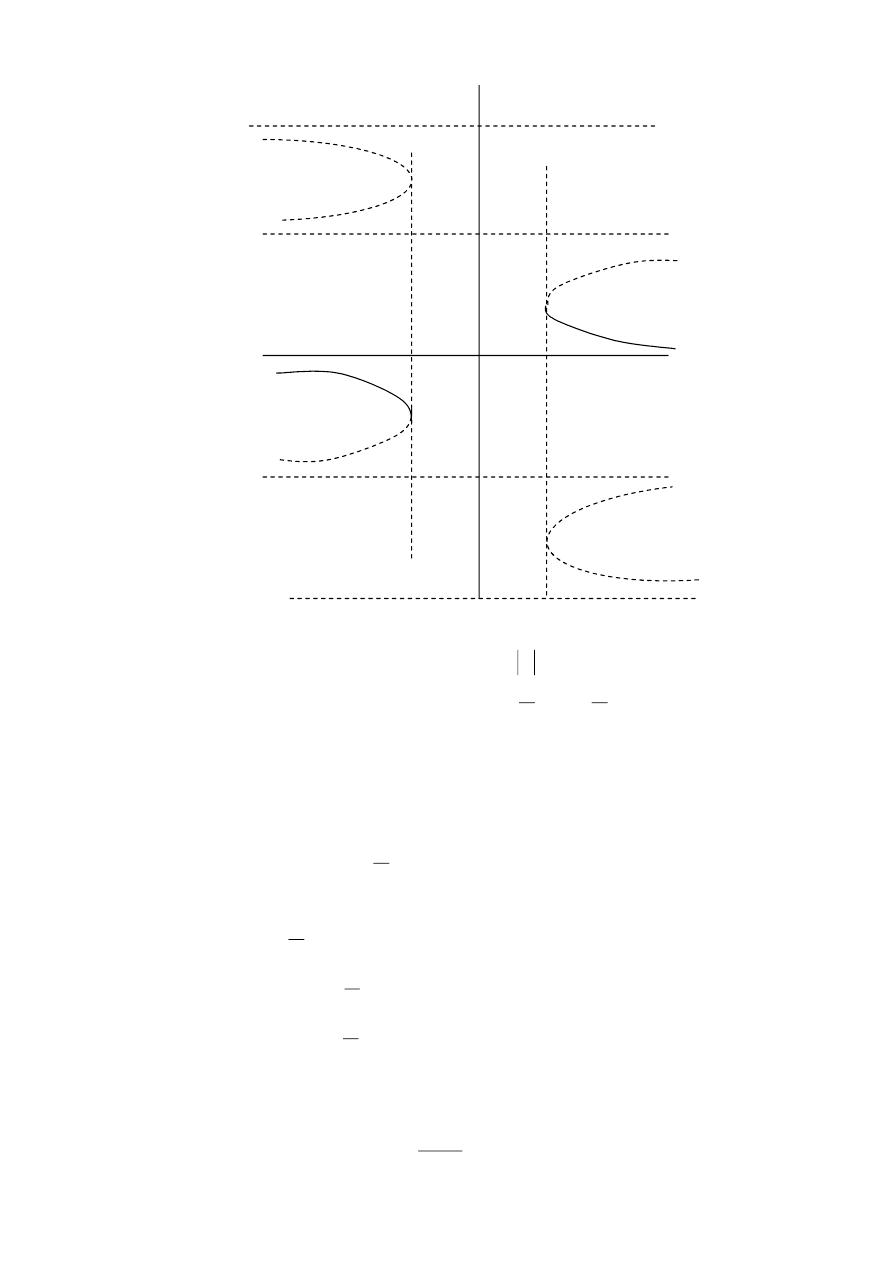
x
Sec
y
y
x
1
π
-
π
0
π
2
1
-1
-
٦١
0
y
,
2
y
2
:
R
1
x
:
D
x
Csc
y
y
x
1
The following are some properties of the inverse trigonometric
functions :
x
Sec
)
x
(
Sec
.
8
x
1
Sin
x
Csc
.
7
x
1
Cos
x
Sec
.
6
x
tan
2
x
Cot
.
5
x
tan
)
x
(
tan
.
4
2
x
Cos
x
Sin
.
3
x
Cos
)
x
(
Cos
.
2
x
Sin
)
x
(
Sin
.
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
x
Sin
Cscx
Sinx
1
)
Sinx
(
that
noted
and
1
1
1
-1
π
-π
0
2π
-2π
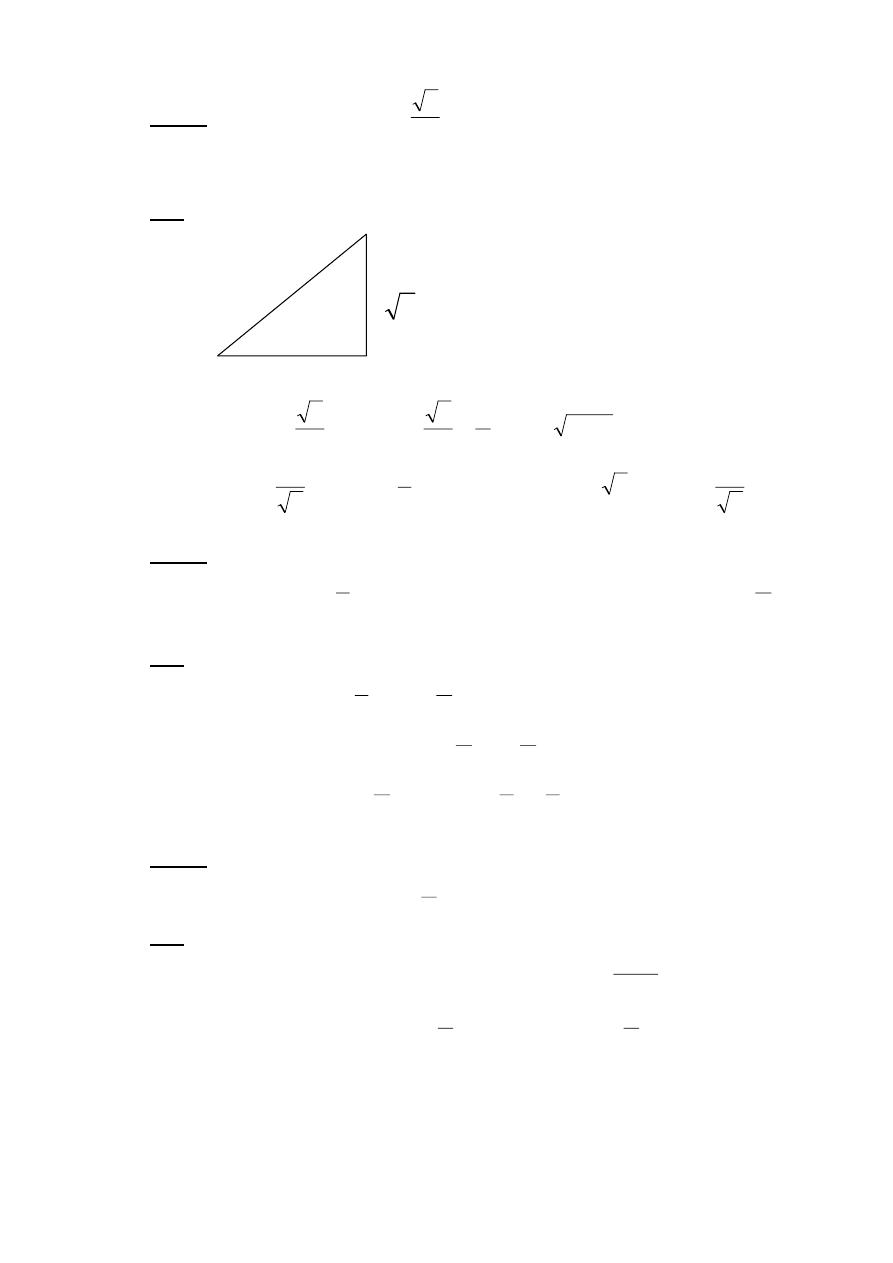
٧١
EX-13- Given that
2
3
Sin
1
, find :
Cot
,
and
,
tan
,
Sec
,
Cos
,
Csc
Sol.-
3
1
Cot
,
3
tan
,
2
Sec
,
2
1
Cos
,
3
2
Csc
1
3
4
r
y
x
2
3
Sin
2
3
Sin
1
EX-14 – Evaluate the following expressions :
)
6
Sin
(
Cos
)
c
)
1
(
Sin
1
Sin
)
b
)
2
1
Cos
(
Sec
)
a
1
1
1
1
Sol.-
3
2
)
2
1
(
Cos
)
6
Sin
(
Cos
)
c
)
2
(
2
)
1
(
Sin
1
Sin
)
b
2
3
Sec
)
2
1
Cos
(
Sec
)
a
1
1
1
1
1
EX-15- Prove that :
x
Sin
)
x
(
Sin
)
b
x
1
Cos
x
Sec
)
a
1
1
1
1
Sol.
x
Sin
)
x
(
Sin
)
x
(
Sin
y
Siny
x
)
y
(
Sin
x
x
Sin
y
Let
)
b
x
1
Cos
x
Sec
x
1
Cos
y
Cosy
1
x
Secy
x
x
Sec
y
Let
)
a
1
1
1
1
1
1
1
1
٢
١
3
٨١
2-4- Hyperbolic functions :
Hyperbolic functions are used to describe
the motions of waves in elastic solids ; the shapes of electric power lines
; temperature distributions in metal fins that cool pipes …etc.
The hyperbolic sine (Sinh) and hyperbolic cosine (Cosh) are defined
by the following equations :
1
u
Csch
u
Coth
and
1
u
Sech
u
tanh
.
5
1
u
Sinh
u
Cosh
.
4
e
e
2
Sinhu
1
Cschu
and
e
e
2
Coshu
1
Sechu
.
3
e
e
e
e
Sinhu
Coshu
Cothu
and
e
e
e
e
Coshu
Sinhu
u
tanh
.
2
)
e
e
(
2
1
Coshu
and
)
e
e
(
2
1
Sinhu
.
1
2
2
2
2
2
2
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
Sinhy
.
Sinhx
Coshy
.
Coshx
)
y
x
(
Cosh
.
10
Sinhy
.
Coshx
Coshy
.
Sinhx
)
y
x
(
Sinh
.
9
0
0
Sinh
and
1
0
Cosh
.
8
Sinhu
)
u
(
Sinh
and
Coshu
)
u
(
Cosh
.
7
e
Sinhu
Coshu
and
e
Sinhu
Coshu
.
6
u
u
2
1
x
2
Cosh
x
Sinh
and
2
1
x
2
Cosh
x
Cosh
.
13
x
Sinh
x
Cosh
x
2
Cosh
.
12
Coshx
.
Sinhx
.
2
x
2
Sinh
.
11
2
2
2
2
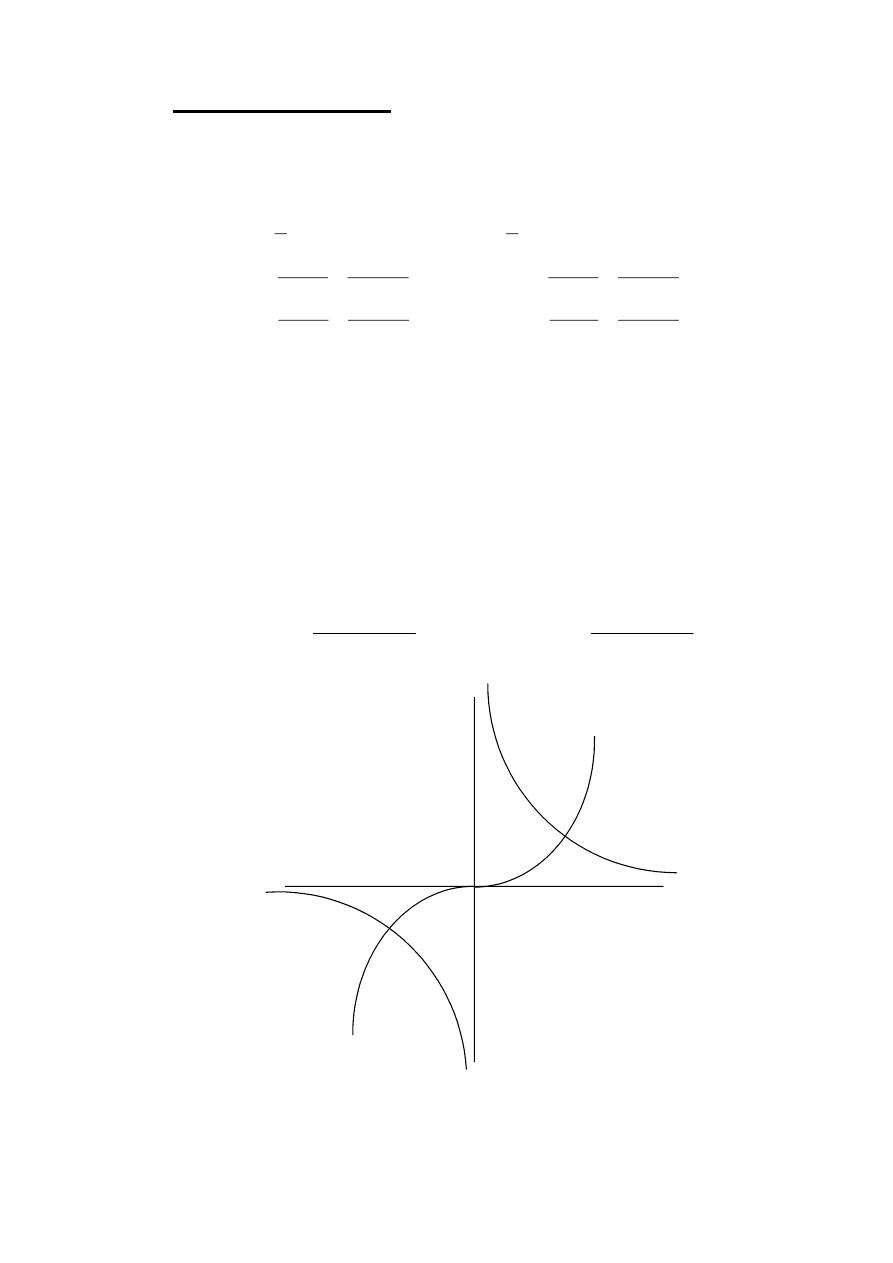
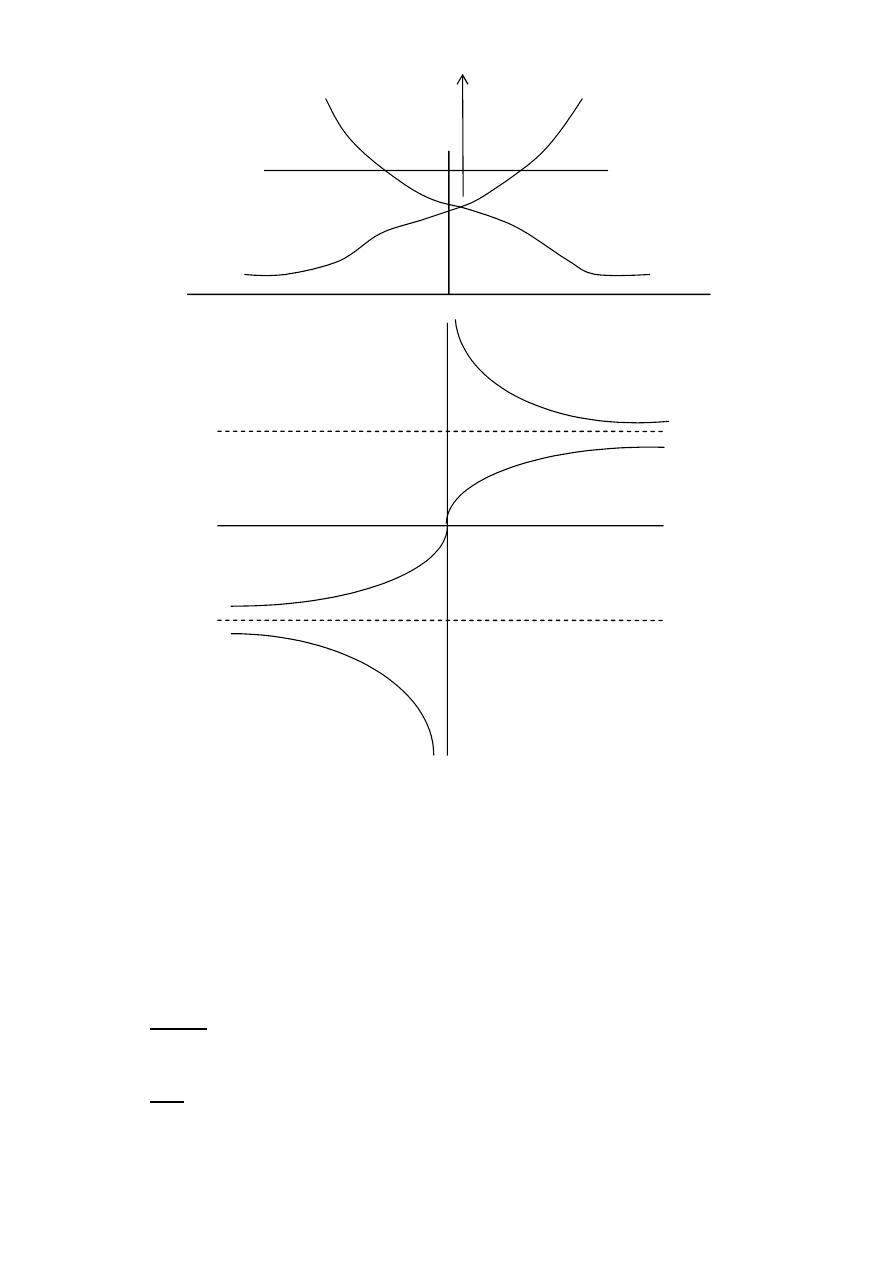
y=Sinhx
y=Cschx
y=Cschx
0
٩١
0
0
0
1
1
1
1
0
y
:
R
and
0
x
:
D
Cschx
y
1
y
0
:
R
and
x
:
D
Sechx
y
1
y
or
1
y
:
R
and
0
x
:
D
Cothx
y
1
y
1
:
R
and
x
:
D
x
tanh
y
1
y
:
R
and
x
:
D
Coshx
y
y
:
R
and
x
:
D
Sinhx
y
y
x
y
x
y
x
y
x
y
x
y
x
EX-16- Let tanh u = - 7 / 25 , determine the values of the remaining five
hyperbolic functions .
Sol.-
1
-1
y=tanhx
y=Cothx
0
y=Cothx
1
y=Coshx
0
y=Sechx
y
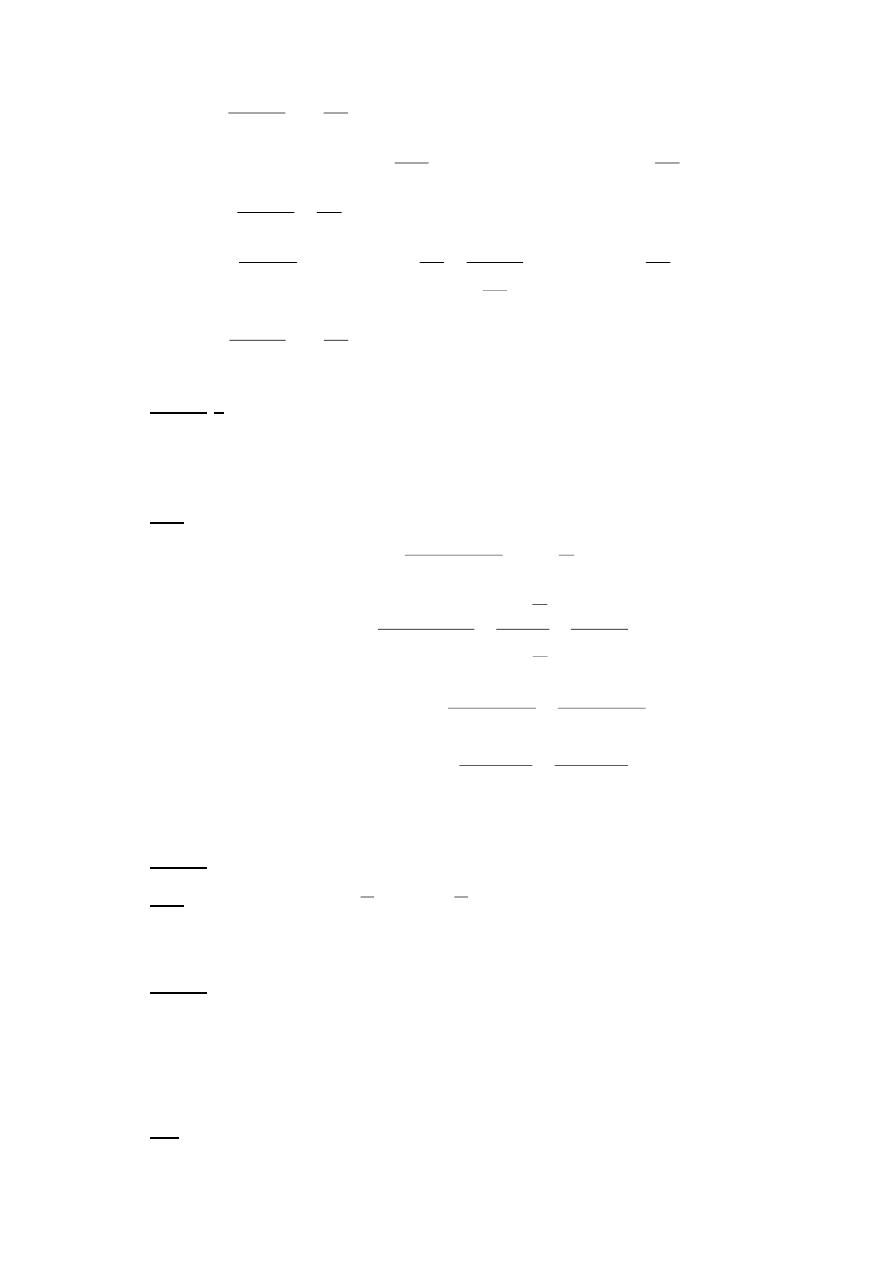
٠٢
7
24
Sinhu
1
Cschu
24
7
Sinhu
24
25
Sinhu
25
7
Coshu
Sinhu
u
tanh
24
25
Sechu
1
Coshu
25
24
Sechu
1
u
Sech
625
49
1
u
Sech
u
tanh
7
25
u
tanh
1
Cothu
2
2
2
EX-17-
Rewrite the following expressions in terms of exponentials .
Write the final result as simply as you can :
4
)
Coshx
Sinhx
(
)
d
x
5
Sinh
x
5
Cosh
)
c
)
x
tanh(ln
)
b
)
x
(ln
Cosh
2
)
a
Sol.-
x
4
4
x
x
x
x
4
x
5
x
5
x
5
x
5
x
5
2
2
x
ln
x
ln
x
ln
x
ln
x
ln
x
ln
e
2
e
e
2
e
e
)
Coshx
Sinhx
(
)
d
e
2
e
e
2
e
e
x
5
Sinh
x
5
Cosh
)
c
1
x
1
x
x
1
x
x
1
x
e
e
e
e
)
x
tanh(ln
)
b
x
1
x
2
e
e
.
2
)
x
(ln
Cosh
2
)
a
EX-18- Solve the equation for x : Cosh x = Sinh x + 1 / 2 .
Sol. -
2
ln
x
2
ln
1
ln
x
2
1
e
2
1
Sinhx
Coshx
x
EX-19 – Verify the following identity :
a) Sinh(u+v)=Sinh u. Cosh v + Cosh u.Sinh v
b) then verify Sinh(u-v)=Sinh u. Cosh v - Cosh u.Sinh v
Sol.-

١٢
.
S
.
H
.
R
Sinhv
.
Coshu
Coshv
.
Sinhu
)
v
(
Sinh
.
Coshu
)
v
(
Cosh
.
Sinhu
))
v
(
u
(
Sinh
.
S
.
H
.
L
)
b
.
S
.
H
.
L
)
v
u
(
Sinh
2
e
e
2
e
e
2
e
e
2
e
e
.
2
e
e
Sinhv
.
Coshu
Coshv
.
Sinhu
.
S
.
H
.
R
)
a
)
v
u
(
v
u
v
v
u
u
v
v
u
u
EX-20 – Verify the following identities :
v
Cosh
u
Cosh
v
Sinh
u
Sinh
)
d
u
Sinh
4
Sinhu
3
Sinhu
.
u
Cosh
3
u
Sinh
u
3
Sinh
)
c
)
v
u
(
Cosh
)
v
u
(
Cosh
2
1
Coshv
.
Coshu
)
b
)
v
u
(
Sinh
)
v
u
(
Sinh
2
1
Coshv
.
Sinhu
)
a
2
2
2
2
3
2
3
Sol. –
.
S
.
H
.
R
v
Cosh
u
Cosh
)
1
v
Cosh
(
1
u
Cosh
v
Sinh
u
Sinh
.
S
.
H
.
L
)
d
)
II
.(
S
.
H
.
R
u
Sinh
4
Sinhu
3
u
Sinh
)
u
Sinh
1
.(
Sinhu
3
)
I
.(
S
.
H
.
R
u
Sinh
u
Cosh
.
Sinhu
3
Sinhu
).
u
Sinh
u
Cosh
(
Coshu
.
Coshu
.
Sinhu
2
Sinhu
.
u
2
Cosh
Coshu
.
u
2
Sinh
)
u
u
2
(
Sinh
.
S
.
H
.
L
)
c
.
S
.
H
.
L
Coshv
.
Coshu
Sinhv
.
Sinhu
Coshv
.
Coshu
Sinhv
.
Sinhu
Coshv
.
Coshu
2
1
)
v
u
(
Cosh
)
v
u
(
Cosh
2
1
.
S
.
H
.
R
)
b
.
S
.
H
.
L
Coshv
.
Sinhu
Sinhv
.
Coshu
Coshv
.
Sinhu
Sinhv
.
Coshu
Coshv
.
Sinhu
2
1
)
v
u
(
Sinh
)
v
u
(
Sinh
2
1
.
S
.
H
.
R
)
a
2
2
2
2
2
2
3
3
2
3
2
2
2
2-5- Inverse hyperbolic functions :
All hyperbolic functions have
inverses that are useful in integration and interesting as differentiable
functions in their own right .
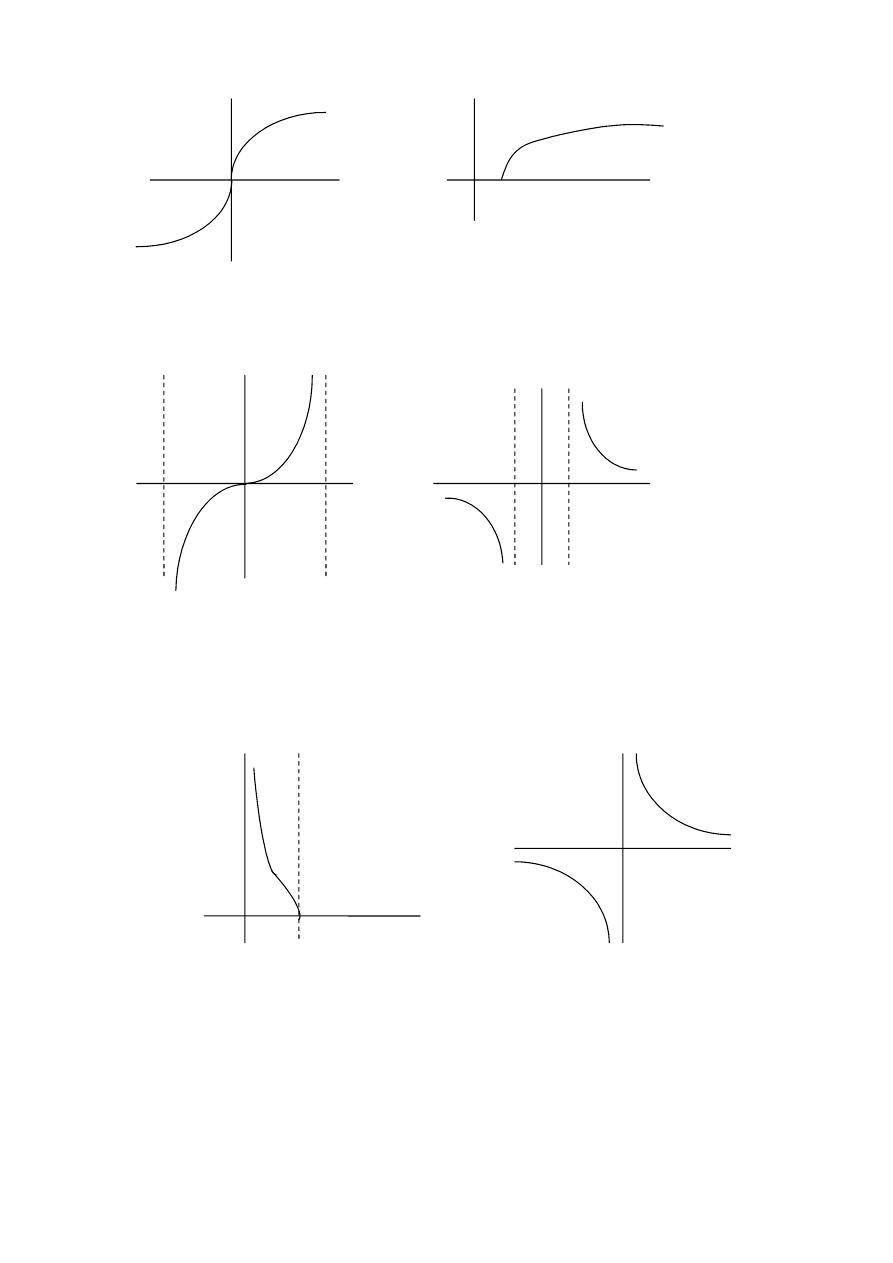
٢٢
y
:
R
x
:
D
x
Sinh
y
y
x
1
0
y
:
R
1
x
:
D
x
Cosh
y
y
x
1
1
0
١
-
١
-1
١
0
y
:
R
1
x
or
1
x
:
D
x
Coth
y
y
x
1
y
:
y
R
1
x
1
:
x
D
x
1
tanh
y
١
0
y
:
R
1
x
0
:
D
x
Sech
y
y
x
1
0
y
:
R
0
x
:
D
x
Csch
y
y
x
1

٣٢
Some useful identities :
x
1
Sinh
x
1
x
x
1
ln
x
Csch
.
6
x
1
Cosh
x
x
1
1
ln
x
Sech
.
5
x
1
tanh
1
x
1
x
ln
.
2
1
x
Coth
.
4
x
1
x
1
ln
.
2
1
x
tanh
.
3
)
1
x
x
ln(
x
Cosh
.
2
)
1
x
x
ln(
x
Sinh
.
1
1
2
1
1
2
1
1
1
1
2
1
2
1
EX-21 - Derive the formula :
)
1
x
x
ln(
x
Sinh
2
1
Sol.-
)
1
x
x
ln(
y
or
0
1
x
x
ce
sin
neglected
)
1
x
x
ln(
y
either
1
x
x
e
2
4
x
4
x
2
e
0
1
e
.
x
2
e
e
2
1
e
x
2
e
e
Sinhy
x
x
Sinh
y
Let
2
2
2
2
y
2
y
y
y
2
y
y
2
y
y
1

٤٢
Problems – 2
1. A body of unknown temperature was placed in a room that was held at
30
o
F . After 10 minutes , the body's temperature was 0
o
F , and 20
minutes after the body was placed in the room the body's temperature
15
o
F . Use Newton's law of cooling to estimate the body's initial
temperature . (ans.:-30
o
F)
2. A pan of warm water 46
o
C was put in a refrigerator . Ten minutes later ,
the water's temperature was 39
o
C , 10 minutes after that , it was 33
o
C .
Use Newton's law of cooling to estimate how cold the refrigerator was ?
(ans.:-3
o
C)
3. Solve the following equations for values of θ from -180
o
to 180
o
inclusive:
i) tan
2
θ + tan θ = 0 ii) Cot θ= 5 Cos θ
iii) 3 Cos θ + 2 Sec θ + 7 = 0 iv) Cos
2
θ + Sin θ + 1 = 0
(ans.:i)-180,-45,0,135,180; ii)-90,11.5,90,168.5; iii)-109.5,109.5; iv)-90)
4. Solve the following equations for values of θ from 0
o
to 360
o
inclusive:
i) 3 Cos 2θ – Sin θ + 2 = 0 ii) 3 tan θ = tan 2θ
iii) Sin 2θ. Cos θ + Sin
2
θ = 1 iv) 3 Cot 2θ + Cot θ = 1
(ans.:i)56.4,123.6,270;
ii)0,30,150,180,210,330,360;
iii)30,90,150,270;
iv)45,121,225,301)
5. If Sin θ = 3/ 5 , find without using tables the values of :
i) Cos θ ii) tan θ (ans.: i) 4/5 ; ii) 3/4 )
6. Find, without using tables, the values of Cos x and Sin x , when Cos 2x is :
a) 1/8 , b) 7/25 , c) -119/169
)
13
12
,
13
5
)
c
;
5
3
,
5
4
)
b
;
4
7
,
4
3
)
a
:
.
ans
(
7. If Sin A = 3/5 and Sin B = 5/13 , where A and B are acute angles , find
without using tables , the values of :
a) Sin(A+B) , b) Cos(A+B) , c) Cot(A+B) (ans.: 56/65; 33/65; 33/56)
8. If tan A = -1/7 and tan B = 3/4 , where A is obtuse and B is acute , find
without using tables the value of A – B . (ans.: 135 )
9.Prove the following identities :

٥٢
B
tan
)
B
A
(
Sin
)
B
A
(
Sin
)
B
A
(
Cos
)
B
A
(
Cos
)
v
Sin
Sec
Cos
tan
Sin
Sec
)
iv
)
tan
Sec
(
Sin
1
Sin
1
)
iii
Cos
Sec
)
Sec
1
(
Sin
)
ii
Csc
.
Sec
Csc
Sec
)
i
2
2
2
2
2
2
2
2
2
2
2
h
Sin
x
Cos
h
Sin
.
x
tan
x
tan
)
h
x
tan(
)
h
x
tan(
2
1
)
viii
C
tan
.
B
tan
.
A
tan
C
tan
B
tan
A
tan
:
that
show
,
triangle
a
of
angles
are
C
,
B
,
A
If
B
tan
.
A
tan
A
tan
.
C
tan
C
tan
.
B
tan
1
C
tan
.
B
tan
.
A
tan
C
tan
B
tan
A
tan
)
C
B
A
tan(
)
vii
)
B
A
(
Sin
.
SinA
)
B
A
(
Cos
.
CosA
CosB
)
vi
2
2
2
A
tan
3
1
A
tan
A
tan
3
A
3
tan
)
xiii
A
4
Sin
3
A
3
Sin
.
A
Cos
4
A
3
Cos
.
A
Sin
4
)
xii
)
3
4
Cos
(
4
1
Cos
Sin
)
xi
A
2
tan
1
A
2
Cos
A
4
Cos
A
2
Sin
A
4
Sin
)
x
x
2
Cos
1
x
2
Cos
1
x
tan
)
ix
2
3
3
3
4
4
Sinhv
.
Sinhu
Coshv
.
Coshu
)
v
u
(
Cosh
verify
then
and
Sinhv
.
Sinhu
Coshv
.
Coshu
)
v
u
(
Cosh
)
xvi
x
tan
2
x
Cot
)
xv
x
Cos
)
x
(
Cos
)
xiv
1
1
1
1
Sinhnx
Coshnx
)
Sinhx
Coshx
(
)
xx
Coshu
3
u
Cosh
4
Coshu
.
u
Sinh
4
Coshu
u
3
Cosh
)
xix
)
v
u
(
Cosh
)
v
u
(
Cosh
2
1
Sinhv
.
Sinhu
)
xviii
)
v
u
(
Sinh
)
v
u
(
Sinh
2
1
Sinhv
.
Coshu
)
xvii
n
3
2
10. If
Cos
Sin
1
u
, prove that
Cos
Sin
1
u
1
and deduce formula for Sinθ ,
Cosθ , tanθ in terms of u. (ans.:(u
2
-1)/(u
2
+1); 2u/(u
2
+1);(u
2
-1)/(u
2
+1))

٦٢
11. If
)
x
(
Cos
2
)
x
(
Sin
; prove that :
tan
2
1
tan
2
x
tan
.
12. If
)
x
(
Cos
)
x
(
Sin
; prove that :
1
x
tan
.
13. If
2
Sin
Sin
y
and
2
Cos
Cos
x
. Show that :
4
Sin
3
Sin
2
2
Sin
xy
2
)
ii
4
Cos
3
Cos
2
2
Cos
y
x
)
i
2
2
14. If
2
Cos
B
2
Cos
.
A
2
Cos
, prove that :
2
2
2
2
2
Sin
B
Sin
.
A
Cos
B
Cos
.
A
Sin
15. If S = Sin θ and C = Cos θ , simplify :
C
S
S
C
)
iii
,
C
1
.
C
S
1
.
S
)
ii
,
S
1
C
.
S
)
i
2
2
2
(ans.:i) Sinθ; ii)1; iii) Secθ.Cscθ)
16. Eliminate θ from the following equations :
2
tan
y
and
tan
x
)
iv
tan
Sin
y
and
tan
Sin
x
)
iii
Cos
Sin
y
and
Cos
Sin
x
)
ii
Sec
.
b
y
and
Csc
.
a
x
)
i
)
x
1
x
2
y
)
iv
;
1
)
y
x
(
4
)
y
x
(
4
)
iii
;
2
y
x
)
ii
;
1
y
b
x
a
)
i
:
.
ans
(
2
2
2
2
2
2
2
2
2
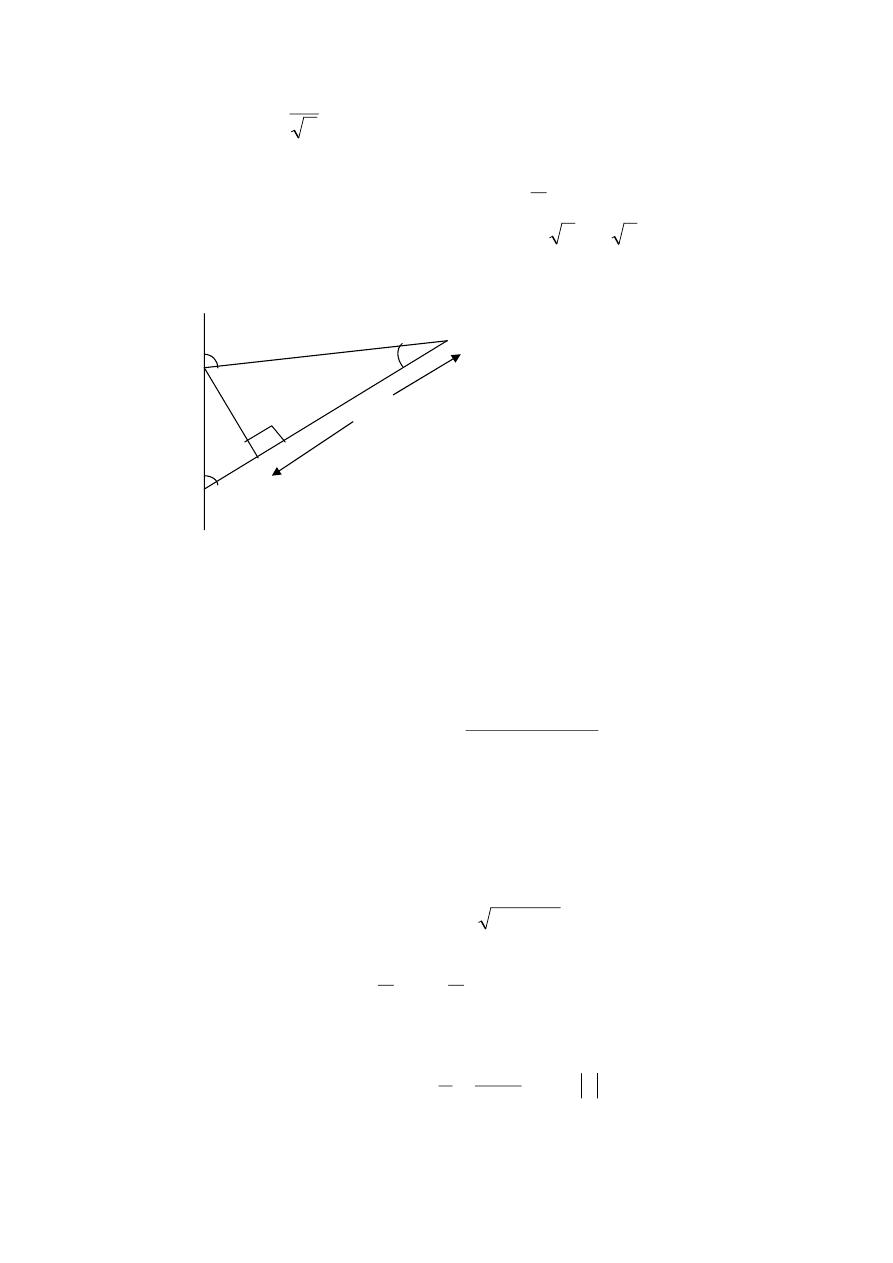
17. In the acute – angled triangle OPQ , the altitude OR makes angles A and
B with OP and OQ . Show by means of areas that if OP=q , OQ=p ,
OR=r : p.q.Sin(A+B) = q.r.SinA + p.r. SinB.
18. Given that
2
1
Sin
1
, find Cosα , tanα , Secα , and Cscα.
)
2
;
3
2
;
3
1
;
2
3
:
.
ans
(
19. Evaluate the following expressions :
٧٢
)
6
Sin
(
Cos
)
f
)
8
.
0
Sin
(
Cos
)
e
)
1
(
Sin
1
Sin
)
d
)
0
Cos
(
Cot
)
c
)
2
Sec
(
Csc
)
b
)
2
1
Cos
(
Sin
)
a
1
1
1
1
1
1
1
)
3
/
2
;
6
.
0
;
;
0
;
3
/
2
;
2
/
1
:
.
ans
(
20. Find the angle α in the below graph ( Hint : α+β = 65
o
) :
(ans.: 42.2)
21. Let Sech u = 3/5 , determine the values of the remaining five hyperbolic
functions .
)
4
/
3
Cschu
;
4
/
5
Cothu
;
5
/
4
u
tanh
;
3
/
4
Sinhu
;
3
/
5
Coshu
:
.
ans
(
22. Rewrite the following expressions in terms of exponentials , write the
final result as simply as you can :
)
Sinhx
Coshx
ln(
)
Sinhx
Coshx
ln(
)
d
x
3
Sinh
x
3
Cosh
)
c
Sinhx
Coshx
1
)
b
)
x
ln
.
2
(
Sinh
)
a
(ans.:(x
4
-1)/(2x
2
); e
x
; e
--3x
; 0 )
23. Solve the equation for x ; tanh x = 3/5 . (ans.: ln 2 )
24. Show that the distance r from the origin O to the point P(Coshu,Sinhu)
on the hyperbola x
2
– y
2
= 1 is
u
2
Cosh
r
.
25. If θ lies in the interval
2
2
and Sinh x = tan θ . Show that :
Cosh x = Sec θ , tanh x =Sin θ , Coth x = Csc θ , Csch x = Cot θ , and
Sech x = Cos θ .
26. Derive the formula :
1
x
;
x
1
x
1
ln
2
1
x
tanh
1
27. Find :
x
ln
x
Cosh
lim
1
x
. (ans.: ln 2 )
α
65
o
٠٥
١٢
β
