
Lecture no.2-7 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
1
DIFFRENTIA TION AND INTEGRATION OF POWER SERIES
Consider the power series
∑ a
k
(x − x
0
)
k
= a
k
+ a
k
(x − x
0
) + a
k
(x − x
0
)
2
+ ⋯
∞
k=0
(1)
With a given interval of convergence I. For each x in I we may define a new function f by
f(x) = ∑ a
k
(x − x
0
)
k
∞
k=0
(2)
EXAMPLE 1:We know that
∑ x
k
∞
k=0
= 1 + x + x
k
+ ⋯ =
1
1 − x
if |x| < 1 (3)
Thus the function
1
1−x
for |x| < 1 can be defined by
f(x) =
1
1 − x
= ∑ x
k
∞
k=0
if |x| < 1
EXAMPLE 2: Substituting
x
4
for x in (3) leads to the equality
f(x) =
1
1 − x
4
= ∑ x
4k
= 1 + x
4
+ x
8
+ x
12
+ ⋯ if |x| < 1
∞
k=0
EXAMPLE 3 Substituting
−x for x in (3) leads to the equality
f(x) =
1
1 − (−x)
=
1
1 + x
∑(−1)
k
x
k
∞
k=0
= 1 − x + x
2
− x
3
+ x
4
− ⋯ if |x| < 1
Once we see that certain function can be written as power series, the next question that naturally
arises is whether such function can be differentiated and integrated The remarkable theorem
given next ensures that every function represented as a power series can be differentiated and
integrated at any x such that|
x| < R . the radius of convergence Moreover, we see how the
derivative and integral can be calculated .
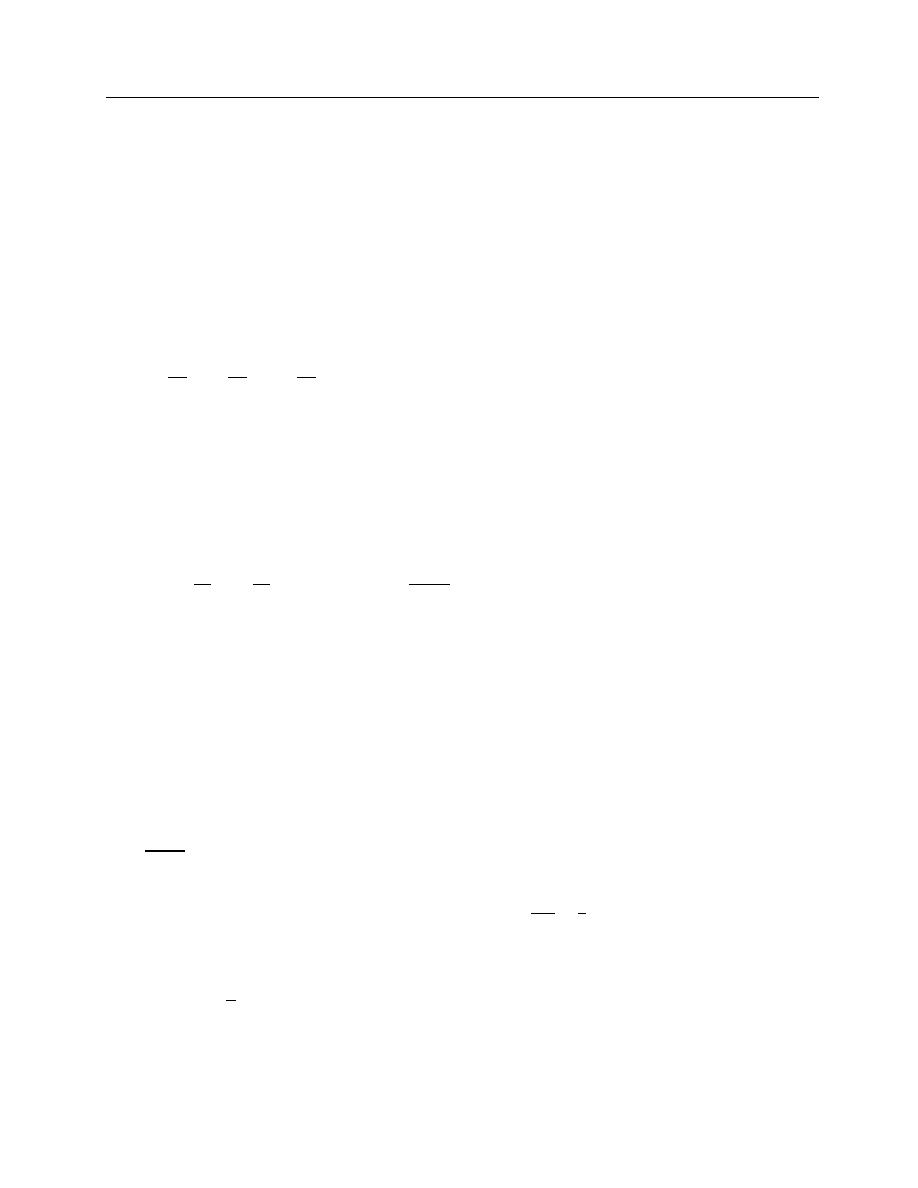
Lecture no.2-7 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
2
Theorem 1: Let the power series
∑
a
k
x
k
∞
k=0
have the radius of convergence
R > 0 Let
f(x) = ∑ a
k
x
k
∞
k=0
= a
0
+ a
1
x + a
2
x
2
+ ⋯ for |x| < R
Then for
|x| < R we have the following:
(i) f (x) is continuous
(ii)The derivative f
′
(x)exists . and
f
′
(x) =
d
dx
a
0
+
d
dx
a
1
x +
d
dx
a
2
x
2
+ ⋯
= a
1
+ 2a
2
x + 3a
3
x
2
+ ⋯ ∑
ka
k
x
k−1
∞
k=1
(iii) The antiderivative ∫ f(x) dx exists and
∫ f(x) dx = ∫ a
0
dx + ∫ a
1
x dx + ∫ a
2
x
2
dx + ⋯
= a
0
x + a
1
x
2
2
+ a
2
x
3
3
+ ⋯ + C = ∑ a
k
x
k+1
k + 1
∞
k=0
+ C
Moreover, the two series ∑
ka
k
x
k−1
∞
k=1
and ∑
ka
k
x
k+1
/(k + 1)
∞
k=0
both have the radius of
convergence R
Simply put, this theorem says that the derivative of a converging power series is the series of
derivatives of its terms and that the integral of a converging power series is the series of integrals
of its terms
EXAMPLE 4 From Example 3 we have
1
1 + x
= 1 − x + x
2
− x
3
+ ⋯ = ∑(−1)
k
x
k
∞
k=0
(4)
for
|x| < 1 Substitutingu = x + 1 . we havex = u − 1 and
1
1+x
=
1
u
. if − 1 < x < 1. then 0 <
u < 2 . and we obtain
1
u
= 1 − (u − 1) + (u − 1)
2
− (u − 1)
3
+ ⋯ ∑(−1)
k
(u − 1)
k
∞
k=0

Lecture no.2-7 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
3
For
0 < u < 2 Integration then yields
In
u = ∫
du
u
= u −
(u−1)
2
2
+
(u−1)
3
3
− ⋯ + C
Since In
1 = 0 . we immediately find that C = −1 . so that
In = ∑(−1)
k
(u − 1)
k
k + 1
∞
k=0
(5)
For
0 < u < 2 Here we have expressed the logarithmic function defined on the interval as a
power series
EXAMPLE 5: The series
f(x) = 1 + x +
x
2
2!
+
x
3
3!
+ ⋯ = ∑
x
k
k!
∞
k=0
(6)
Converges for every real number x
(i ∙ e ∙. R = ∞; But
f
′
(x) =
d
dx
1 +
d
dx
x +
d
dx
x
2
2!
+ ⋯ = 1 +
x
2
2!
+ ⋯ = f(x)
Thus f satisfies the differential equation
f
′
= f.
f(x) = ce
x
(7)
For some constant c Then substituting into equations (6) and (7) yields
f(0) = 1 = ce
0
= c .
So that
f(x) = e
x
We have obtained the important expansion that is valid for any real number x:
e
x
= 1 + x +
x
2
2!
+
x
3
3!
+ ⋯ = ∑
x
k
k!
∞
k=0
(8)
For example, if we substitute the value
x = 1 into (8), we obtain partial sum approximations
for
e = 1 + 1 +
1
2!
+ ⋯ (see Table 1) The last value ∑
x
k
k!
∞
k=0
is correct to five decimal places
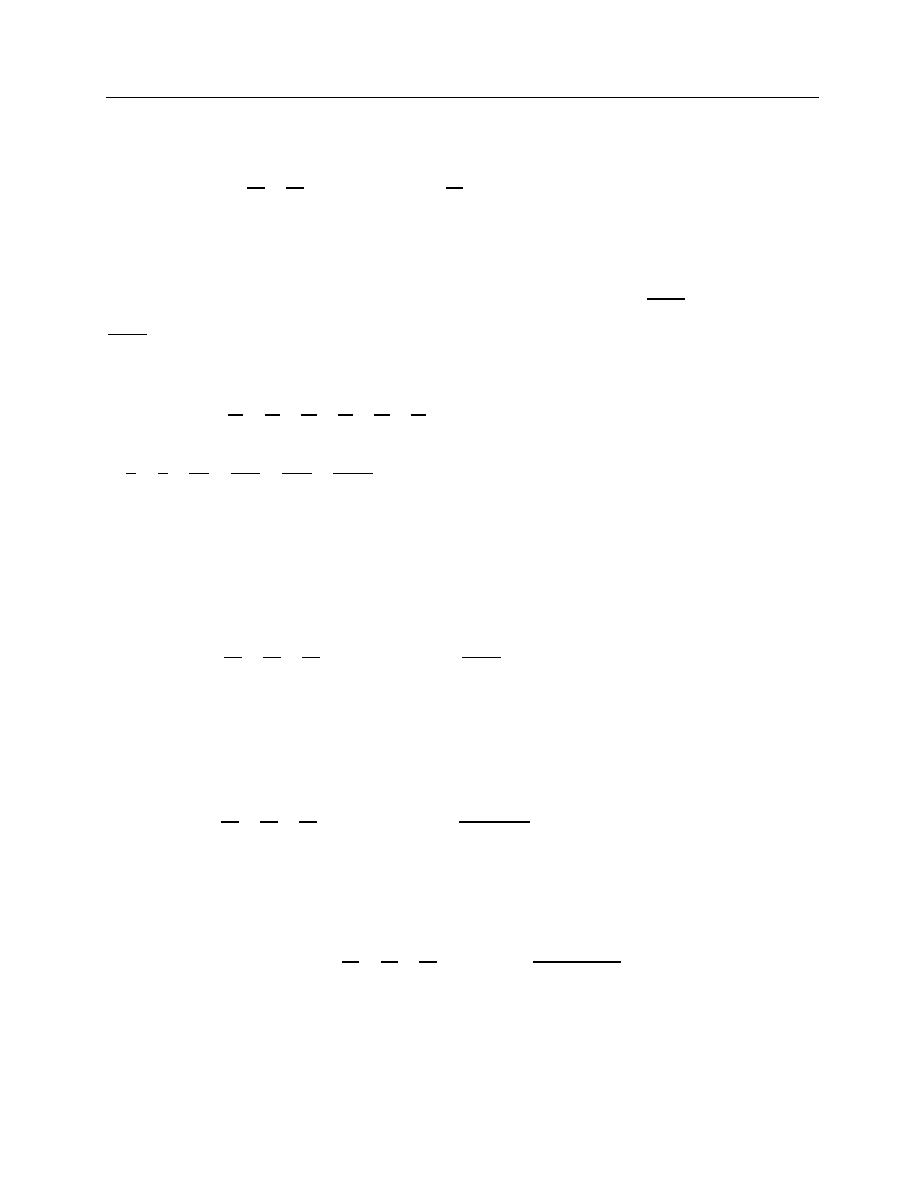
Lecture no.2-7 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
4
EXAMPLE 6: Substituting
x = −x in (8) we obtain
e
−x
= 1 + x +
x
2
2!
+
x
3
3!
+ ⋯ = ∑(−1)
k
x
k
k!
∞
k=0
(9)
Since this is an alternating series if
x > 0 . tells us that the error |S − S
n
| . In
approximating
e
−x
for x > 0 is bounded by|a
n+1
| = x
n+1
/(n + 1)! ∙† for example, to
calculate
e
−1
with an error of less than
10 ∙ 000. we must have |S − S
n
| ≤
1
(n+1)!
< 0 ∙ 0001 =
1
10.000
. or(n + 1)! > 10 ∙ 000 If n = 7. (n + 1)! = 8! = 40.320. so that∑
(−1)
k
7
k=0
/k! will
approximate
e
−1
correct to four decimal places We obtain
e
−1
≈ 1 − 1 +
1
2!
−
1
3!
+
1
4!
−
1
5!
+
1
6!
−
1
7!
=
1
2
−
1
6
+
1
24
−
1
120
+
1
720
−
1
5040
= 0 ∙ 5 − 0 ∙ 16667 + 0 ∙ 04167 − 0 ∙ 00833 + 0 ∙ 00139 − 0 ∙ 0002 ≈ 0 ∙ 36786
Note that
e
−1
≈ 0 ∙ 36788 correct to five decimal places
EXAMPLE 7 Consider the series
f(x) = 1 −
x
2
2!
+
x
4
4!
−
x
6
6!
+ ⋯ = ∑(−1)
k
x
2k
(2k)!
∞
k=0
(10)
It is easy to see that
R = ∞ since the series is absolutely convergent for every x by comparison
with the series (8) for
e
x
[ The series (8) is larger than the series (10) since it contains the
terms
x
n
/n! for n both even and odd, not just for n even , as in (10)]Differentiating we obtain
f
′(x)
= −x +
x
3
3!
+
x
5
5!
−
x
7
7!
+ ⋯ = ∑(−1)
k
x
2k+1
(2k + 1)!
∞
k=0
(11)
Since this series has a radius of convergences
R = ∞ . we can differentiate once more to
obtain
f
′′(x)
= −1 +
x
2
2!
+
x
4
4!
−
x
6
6!
+ ⋯ = ∑
(−1)
k+1
x
2k
(2k)!
∞
k=0
= −f(x)
Thus we see that f satisfies the differential equation
f
′′
+ f = 0 (12)

Lecture no.2-7 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
5
Moreover, from equations (10) and (11) we see that
f (0) = 1 and f
′
(0) = 0 (13)
It is easily seen that the function
f(x) = cos x satisfies equation (12) together with the conditions
(13) In fact, although .We do not prove here; it is the only function that does so Thus we have
cos x = 1 −
x
2
2!
+
x
4
4!
−
x
6
6!
+ ⋯ = ∑ (−1)
k
x
2k
(2k)!
∞
k=0
(14)
Since
d
dx
cos x = − sin x .
We obtain, from (14), the series (after multiplying both sides by -1)
sin x = x −
x
3
3!
+
x
5
5!
−
x
7
7!
+ ⋯ = ∑(−1)
k
x
2k+1
(2k + 1)!
∞
k=0
(15)
Power series expansions can be very useful for approximate integration
EXAMPLE8 : Calculate
∫ e
−t2
1
0
with an error
< 0 ∙ 0001
Solution Substituting
t
2
for x in (9) , we find that
e
−t
2
= 1 − t
2
+
t
4
2!
+
t
6
3!
+ ⋯ = ∑(−1)
k
t
2k
k!
∞
k=0
(16)
Then we integrate to find that
∫ e
−t2
x
0
dt = x −
x
3
3!
+
x
5
5 ∙ 2!
−
x
7
7 ∙ 3!
+ ⋯ = ∑
(−1)
k
x
2k+1
(2k + 1)!
∞
k=0
(17)
The error
|S − S
n
| is bounded by |a
n−1
| = |
x
2(n+1)−1
[2(n+1)+1](n+1)!
|
In our example
x = 1 . so we need to choose n so that
1
(2n + 3)(n + 1)!
< 0 ∙ 0001. or (2n + 3)(n + 1)! > 10.000
If
n = 6 . then (2n + 3 )(n + 1)! = (15)(7)! = 75.600 With this choice of n(n = 5 is too
small ), we obtain

Lecture no.2-7 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
6
∫ e
−t2
1
0
dt = x −
1
3
+
1
5 ∙ 2!
−
1
7 ∙ 3!
+
1
9 ∙ 4!
−
1
11 ∙ 5!
+
1
13 ∙ 6!
≈ 1 − 0 ∙ 33333 + 0 ∙ 1 − 0 ∙ 02381 + 0 ∙ 00463 − 0 ∙ 00076 + 0 ∙ 00011 = 0 ∙ 74684.
And to four decimal places,
∫ e
−t2
1
0
dt = 0 ∙ 7468
PROBLEMS :
1 ∙ By substituting x
2
for x in (4) , find a series expansion for
1
1+x
2
that is valid for |
x| < 1
2. Integrate the series obtained in Problem 1 to obtain a series expansion for
tan
−1
x
3.Use the result of Problem 2 to obtain an estimate of π that is correct to two decimal places
4. Use the series expansion for In x to calculate the following to two decimal places of accuracy:
(a) In 0.5
In Problems 5-13 estimate the given integral to within the given accuracy
5 ∙ ∫ e
−t2
1
0
dt ; error 0 ∙ 01 6 ∙ ∫ e
−t3
1
0
dt; error < 0 ∙ 001
7 ∙ ∫ cos t
2
dt ; error 0 ∙ 001
1
2
0
8 ∙ ∫ sin t
2
dt ; error 0 ∙ 0001
1
2
0
9 ∙ ∫ t
2
e
−t2
1
0
dt ; error 0 ∙ 01
[ Hint: The series explanation of
t
2
e
−12
is obtained by multiplying each term of the series
expansion of
e
−12
by t
2
]
10 ∙ ∫ t
5
e
−t5
1
0
dt; error < 0 ∙ 0001 11 ∙ ∫ cos √t
1
0
dt; error < 0 ∙ 001
12 ∙ ∫ t sin √t dt; error < 0 ∙ 001
1
0
13 ∙ ∫
dt
1 + t
8
; error < 0 ∙ 0001
1
2
0
14. Find a series expansion for
xe
x
that is valid for all values of x
15. Use the result of Problem 14 to find a series expansion for
∫ te
x
dt
x
0
