
Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
1
TAYLOR AND MACLAURIN SERIES
In the last two sections we used the fact that within its interval of convergence, the function
f (x) = ∑ a
k
(x − x
0
)
k
∞
k=0
Is differentiable and integrable In this section we look more closely at the coefficients and show that
they can be represented in terms of derivatives of the function f .We begin with the case and assume
that so that theorem on power series differentiation applies We have
f (x) = ∑ a
k
x
k
∞
k=0
= a
0
+ a
1
x + a
2
x
2
+ a
n
x
n
+ ⋯. (1)
And clearly,
f(0) = a
0
+ 0 + 0 + ⋯ + 0 + ⋯ = a
0
(2)
If we differentiate (1), we obtain
f
′
(x) = ∑ a
k
x
k−1
∞
k−1
= a
1
+ 2a
2
x + a
3
x
2
+ ⋯ + na
n
x
n−2
+ ⋯ (3)
And
f
′
(0) = a
1
(4)
Continuing to differentiate, we obtain
f
′′
(x) = ∑ k(k − 1) a
k
x
k−2
∞
k=1
= 2a
2
+ 3 ∙ 2a
3
x + 4 ∙ 3a
4
x
2
+ ⋯ + n(n − 1)na
n
x
n−2
+ ⋯
And
f
′
′(0) = 2a
2
Or
a
2
=
f
′
′(0)
2
=
f
′
′(0)
2!
(5)
Similarly,
f
′′′
(x) = ∑
k(k − 1)(k − 2) a
k
x
k−3
∞
k=3
= 3 ∙ 2a
3
x + 4 ∙ 3a
4
x + 5 ∙ 4 ∙ 3a
5
x
2
+ ⋯ + n(n − 1)(n − 2)a
n
x
n−3
+ ⋯
And
f
′′′
(0) = 3 ∙ 2a
3
, Or
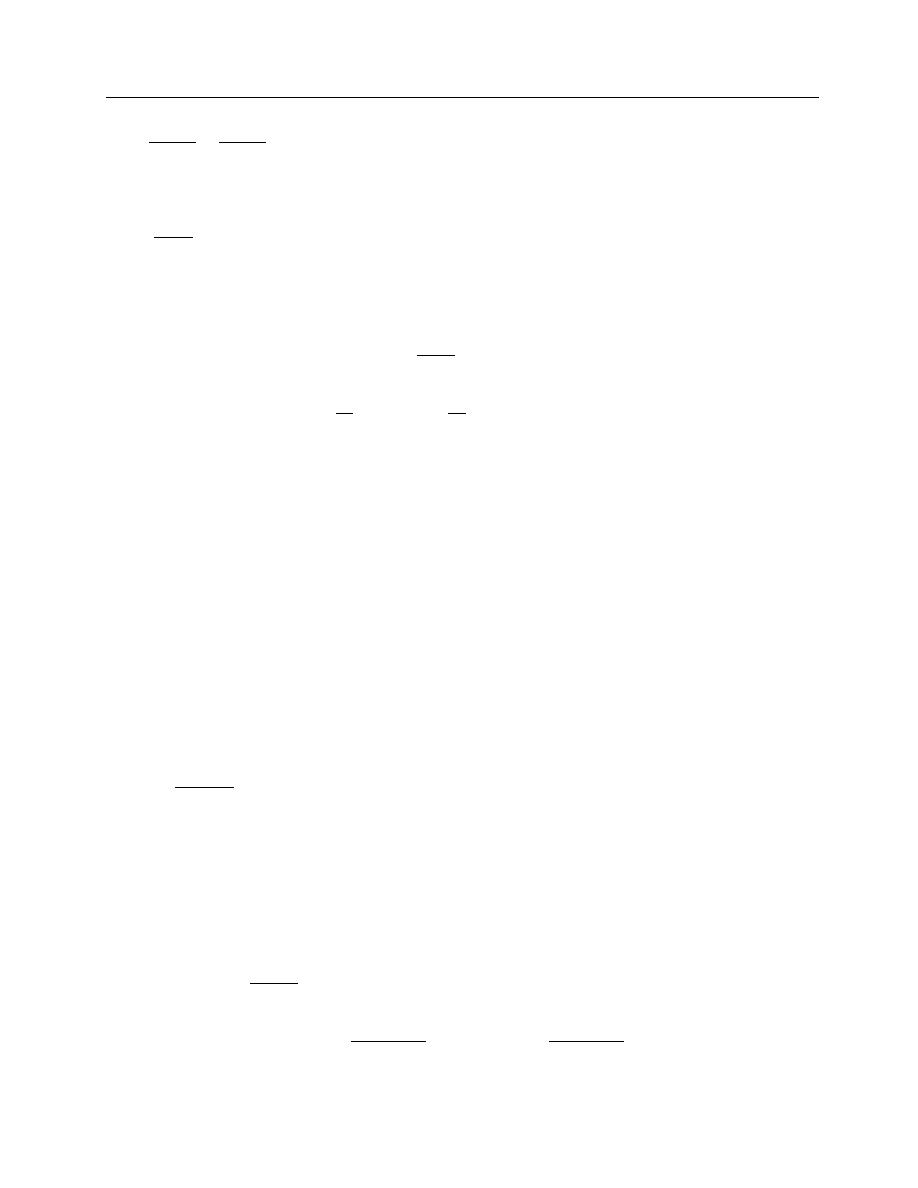
Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
2
a
3
=
f
′′′
(0)
3 ∙ 2
=
f
′′′
(0)
3!
(6)
It is not difficult to see that this pattern continues and that for every positive integer n
a
n
=
f
(n)
(0)
n!
(7)
For
n = 0 we use the convention 0! = 1 and f
(0)
(x) = f(x) Then formula (7) holds for
every n , and we have the following:
If
f (x) = ∑
a
k
x
k
∞
k=0
then f(x) = ∑
f
(k)
(0)
k!
∞
k=0
x
k
= f(0) + f
′
(0)x + f
′′
(0)
x
2
2!
+ ⋯ f
(n)
(0)
x
n
n!
+ ⋯ (8)
for every x in the interval of convergence
In the general case, if
f (x) = ∑ a
k
( x − x
0
)
k
∞
k=0
=
a
0
+ a
1
(x − x
0
) + a
2
(x − x
0
)
2
+ ⋯ + a
n
(x − x
0
)
n
+ ⋯. (9)
Then
f(x
0
) = a
0
.
And differentiating as before, we find that
a
n
=
f
(n)
(x
0
)
n!
(10)
Thus we have the following If
f (x) = ∑ a
k
( x − x
0
)
k
∞
k=0
Then
f (x) = ∑
f
(k)
(x
0
)
k!
( x − x
0
)
k
∞
k=0
= f(x
0
) + f
′(x
0
)
(x − x
0
) + f
′′(x
0
)
( x − x
0
)
2
2!
+ ⋯ + f
(n)
(x
0
)
( x − x
0
)
n
n!
+ ⋯ (11)

Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
3
for every x in the in terval of convergence
Definition 1 TAYLOR AND MACLAURIN SERIES The series in (11) is called the Taylor
series of the function f at
x
0
The special case x
0
= 0 in (8) is called a Maclaurin series ‡ We
see that the first n terms of the Taylor series of a function are simply the Taylor polynomial
described in Section 13 .1.
WARNING: We have shown here that if
f (x) = ∑
a
k
( x − x
0
)
k
∞
k=0
. then f is infinitely
differentiable
(i ∙ e ∙. f has derivatives of all orders) and that the series for f is the Taylor
series or Maclaurin series if
x
0
= 0) of f What we have not shown is that if f is infinitely
differentiable at
x
0
. then f has Taylor series expansion at x
0
In general , this last
statement is false, as we will see in Example 3 on page 749
EXAMPLE 1 Find the Maclaurin series for
e
x
Solution If
f (x) = e
x
. then f (0) = f
′
(0) = ⋯ = f
(k)
(0) = 1. and
́
e
x
= ∑
x
k
k!
∞
k=0
= 1 + x +
x
2
2!
+
x
3
3!
+ ⋯ +
x
n
n!
+ ⋯ (12)
What this example shows is that if has a Maclaurin series expansion, then the series must be the
series (12) It does not show that actually does have such a series expansion To prove that the
series in (12) is really equal to we differentiate, as in Example 14.9.5, and use the fact that the
only continuous function that satisfies
f
′
(x) = f (x). f (0) = 1
Is the function
e
x
EXAMPLE 2 Assuming that the function can be written as a Maclaurin series, find that series
Solution If
f (x) = cos x . then f (0) = 1. f
′
(0) = 0. f
′′
(0) = −1 f
′′′
(0) = 0.
f
(4)
(0) = 1. and so on . so that if cos x = ∑
a
k
x
k
∞
k=0
.
Then
cos x = f(0) + f
′
(0) +
f
′′
(0)x
2
2!
+
f
′′′
(0)x
3
3!
+
f
(4)
(0)x
4
4!
+ ⋯.
Or
cos x = 1 −
x
2
2!
+
x
4
4!
−
x
6
6!
+ ⋯ = ∑
(−1)
k
x
2k
(2k)!
∞
k=0
(13)
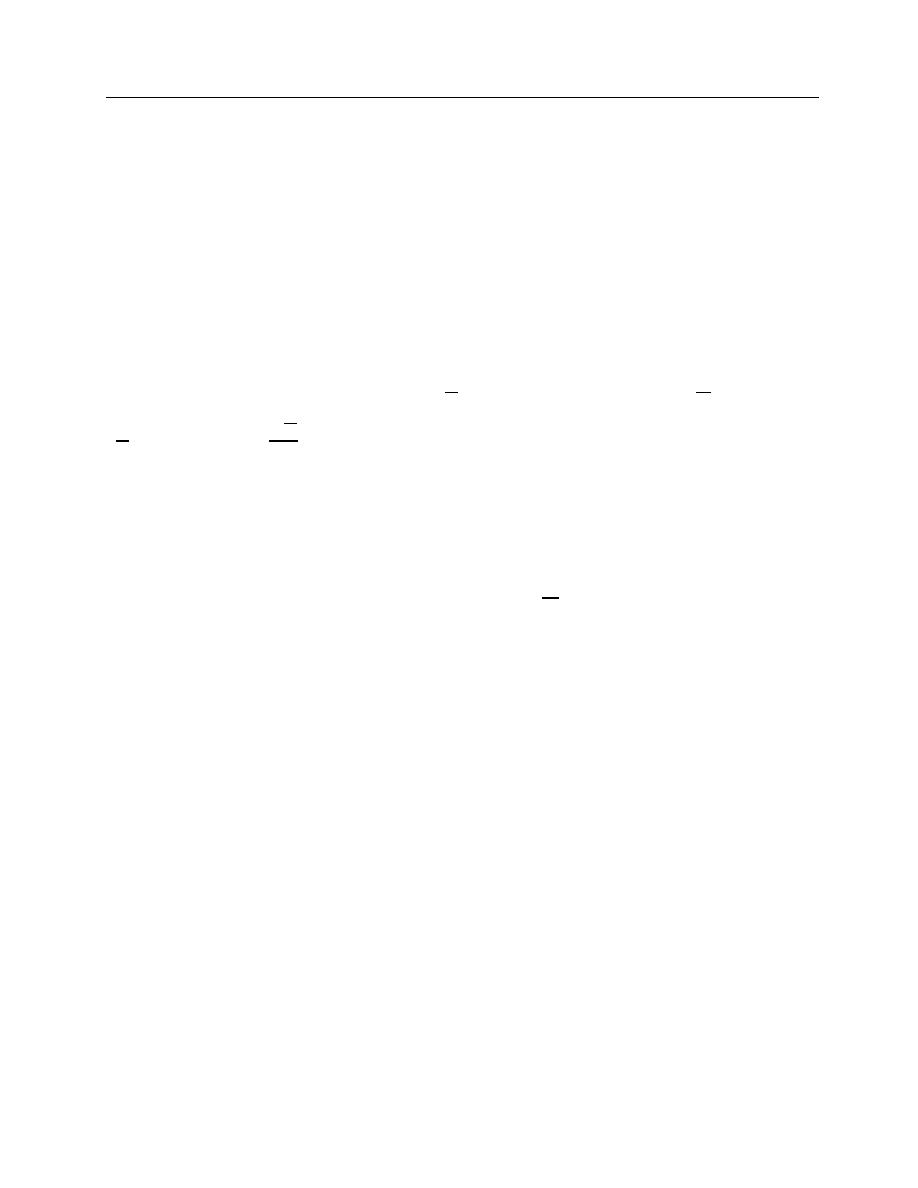
Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
4
NOTE Again, this does not prove that the equality in (13) is correct It only shows that if has a
McLaurin expansion, then the expansion must be given by (13) We will show that has a
McLaurin series in Example 5
EXAMPLE 3 Let
f (x) = {e
−1/x
2
. if x ≠ 0
0. if x = 0
Find a Maclaurin expansion for f if one exists
Solution. First, we note that since
lim
x→∞
e
−1/x
2
= 0. fis continuous Now recall from Example
12.3.5, that
lim
x→∞
x
a
e
−bx
= 0. if b > 0 Let y =
1
x
2
Y Then as x → 0. y → ∞ Also
1
x
n
=
(
1
x
2
)
n/2
so that lim
x→0
(
e
−
1
x2
x
n
) = lim
y→∞
y
n/2
e
−y
= 0 by Example 12.3.5.
Now for as so that is continuous at 0 Similarly, which also approaches 0 as by the limit result
above In fact, every derivative of f is continuous and for every n , Thus f is infinitely
differentiable, and if it had a Maclaurin series that represented the function, then we would have
f (x) = f(0) + f
′
(0) + f
′′
(0)
x
2
2!
+ ⋯
But
f(0) + f
′
(0) + f
′′
(0) = ⋯ = 0 . so that the Maclaurin series would be the zero series But
since f is obviously not the zero function, we can only conclude that there is no Maclaurin series
that represents f at any point other than 0
Example 3 illustrates that infinite differentiability is not sufficient to guarantee that a given
function can be represented by its Taylor series Something more is needed
Definition 2 ANALYTIC FUNCTION We say that a function f is analytic at
x
0
if f can be
represented by a Taylor series in some neighborhood of
x
0
We see that the function and are analytic at 0, while the function
f (x) = {e
−1/x
2
. if x ≠ 0
0. if x = 0
Is not, A condition that guarantees analytic of an infinitely differentiable function is given below
Theorem 1. Suppose that the function f has continuous derivatives of all orders in a neighborhood
N
(x
0
) of the number x
0
.Then f is analytic at
x
0
if and only if

Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
5
lim
n→∞
R
n
(x) = lim
n→∞
f
(n+1)
(C
n
)
(n + 1)!
(x − x
0
)
n+1
= 0 (14)
For every x in N
(x
0
) whereC
n
is between
x
0
and x
REMARK The expression between the equal sings in (14) is simply the remainder term given
by Taylor 's theorem
Proof :The hypotheses of Taylor 's theorem apply, so that can write, for any n,
f(x) = P
n
(x) + f(x) = R
n
(x). (15)
Where
P
n
(x) is the nth degree Taylor Polynomial for f To show that f is analytic , we
must show that
lim
n→∞
P
n
(x) = f (x) (16)
For every
x in N(x
0
) But if x is in N(x
0
) we obtain , from (14)and (15) ,
lim
n→∞
P
n
(x) = lim
n→∞
[f (x) − R
n
(x)] = f (x) − lim
n→∞
R
n
(x) = f (x) − 0 = f (x)
Conversely , if is analytic, then
f (x) = lim
n→∞
P
n
(x)so R
n
(x) → 0 as n → ∞
EXAMPLE 4 If
f (x) = e
x
thenf
(n)
(x) = e
x
. and
0 < C
n
< |x|
lim
n→∞
|
f
(n+1)
(C
n
)
(n + 1)!
(x − x
0
)
n+1
| = lim
n→∞
e
C
n
|x|
(n+1)
(n + 1)!
≤ e
|x|
lim
n→∞
|x|
(n+1)
(n + 1)!
→ 0 .
Since
|x|
(n+1)
(n+1)!
is the
(n + 2) and term in the converging power series ∑
|x|
k
∞
k=0
/k! and the terms in
a converging power series
→ 0 , Since this result is true for any x ∈ ℝ we may take N =
(−∞. ∞) to conclude that the series (12) is valid for every real number x
EXAMPLE 5 Let Since all derivatives of cos x are equal to
± sin x or ± cos x . we see
that
|f
(n+1)
(C
n
)| ≤ 1 Then forx
0
= 0. |R
n
(x)| ≤ |x|
(n+1)
/(n + 1)! which→ 0 as n → ∞. so that
the series(13) is also valid for every real number x
EXAMPLE 6 it is evident that for the function in Example 3,
R
n
(x) ↛ 0 if x ≠ 0 This follows
from the fact that
R
n
(x) = f (x) − P
n
(x) = e
−
1
x2
− 0 = e
−
1
x2
≠ 0 if x ≠ 0
EXAMPLE 7 Find the Taylor expansion for
f (x) = In x at x = 1

Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
6
Solution Since
f
′
(x) =
1
x
. f
′′
(x) = −
1
x
2
. f
′′
(x) =
2
x
3
. f
(4)
(x) = −
6
x
4
. ⋯.
f
(n)
(x) =
(−1)
n+1
(n − 1)!
x
n
. we find that f(1) = 0. f
′
(1) = 1. f
′′
(1) = −1. f
′′′
(1) = 2 .
f
(4)
(1) = −6. ⋯. f
(n)
(1) = (−1)
n+1
(n + 1)! Then wherever valid .
In x = ∑ f
(k)
(1)
(k − 1)
k
k!
∞
k=0
(17)
we showed that
In (1 + x) = ∑
(−1)
k+1
x
k
k
+ R
n+1
(x).
n+1
k=1
(18)
Where
R
n+1
(x) → 0 as n → ∞ whenever −1 < x ≤ 1 From (18) we see that
In u = In [ 1 + (u − 1)] ∑
(−1)
k+1
(u − 1)
k
k
+ R
n+1
(u − 1).
n+1
k=1
(19)
Where
R
n+1
(u − 1) → 0 as n → ∞ whenever −1 < x ≤ u − 1 ≤ 1. or 0 < u ≤ 2 But this
implies that the series (17) converges to In (x) for
0 < x ≤ 2 Whenx = 2 . we obtain from (17),
In 2 = 1 −
1
2
+
1
3
−
1
4
+
1
5
− ⋯ = ∑
(−1)
k+1
k
∞
k=1
. (20)
EXAMPLE 8 Find a Taylor series for
f (x) = sin x at x =
π
3
Solution Here
f (
π
3
) =
√3
2
. f
′
(
π
3
) =
1
2
. f
′′
(
π
3
) = −
√3
2
. f
′′′
(
π
3
) = −
1
2
.
and so on, so that
sin x =
√3
2
+
1
2
(x −
π
3
) −
√3
2
[x − (
π
3)]
2
2!
−
1
2
[x − (
π
3)]
3
3!
+
√3
2
[x − (
π
3)]
4
4!
+ ⋯
The proof that this series is valid for every real number x is similar to the proof in Example 5 and
is therefore omitted

Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
7
We provide here a list of useful Maclaurin series:
e
x
= ∑
x
k
k!
∞
k=0
= 1 + x +
x
2
2!
+
x
3
3!
+ ⋯ (21)
cos x = ∑
(−1)
k
x
2k
(2k)!
∞
k=0
= 1 −
x
2
2!
+
x
4
4!
−
x
6
6!
+ ⋯ (22)
sin x = ∑
(−1)
k
x
2k+1
(2k + 1)!
= x −
x
3
3!
+
x
5
5!
−
x
7
7!
∞
k=0
+ ⋯ (23)
cosh x = ∑
x
2k
(2k)!
∞
k=0
= 1 +
x
2
2!
+
x
4
4!
−
x
6
6!
+ ⋯ (24)
sinh x = ∑
x
2k+1
(2k + 1)!
= x −
x
3
3!
+
x
5
5!
−
x
7
7!
∞
k=0
+ ⋯ (25)
BINOMIAL SERIES
We close this section by deriving another series that is quite useful. Let
f (x) = (1 + x)
r
. where r
is a real number not equal to an integer. We have
f
′
(x) = (1 + x)
r−1
.
f
′′
(x) = r(r − 1)(1 + x)
r−2
.
f
′′′
(x) = r(r − 1)(r − 2)(1 + x)
r−3
.
⋮
f
(n)
(x) = r(r − 1)(r − 2) ⋯ (r − n + 1)(1 + x)
r−n
Not that since r is not an integer ,
r − n is never equal to 0 , all derivatives exist and are
nonzero as long as
x ≠ −1 Then
f(0) = 1 .
f′(0) = r .

Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
8
f
′′(0)
= r(r − 1).
⋮
f
(n)
(0) = r(r − 1) ⋯ (r − n + 1) .
And we can write
(1 + x)
r
= 1 + rx +
r(r − 1)
2!
x
2
+
r(r − 1)(r − 2)
3!
x
3
+ ⋯
+
r(r − 1) ⋯ (r − n + 1)
n!
x
n
+ ⋯ (26)
= 1 + ∑
r(r − 1) ⋯ (r − k + 1)
k!
x
k
∞
k=0
The series (26) is called the binomial series
PROBLMS
1 ∙ Find the Maclaurin series sin x for all real x
2. Find the Taylor series for
e
x
at 1
3. Find the Maclaurin series for
e
−x
4. Find the Taylor series for
cos x at
π
4
5.Find the Taylor series for
sinh x at In 2
6. Find the Maclaurin series for
e
ax
. a is real
7. Find the Maclaurin series for
x e
x
8. Find the Maclaurin series for
x
2
e
−x
2
9. Find the Maclaurin series for
(sin x)/x
10. Find the Taylor series for
e
x
at x = −1
11. Find the Maclaurin series for
sin
2
x[Hint ∶ sin
2
x = (1 − cos 2x)/2]
12. Find the Taylor series of
√x at x = 4. What is its radius of convergence?
13. Find the Maclaurin series of
sin
−1
xWhat is its radius of convergence?
Hint: Expand
1
√1−x
2
and in

Lecture no.2-8 by Hussein J. AbdulHussein
Advanced Calculus II Al Muthanna University, College of Science
9
14. Use the Maclaurin series for
sin x to obtain the Maclaurin series for sin x
2
15. Find the Maclaurin series for
cos x
2
16. Use Equation (26) to find a power series representation for
√1 + x
4
17. Use the result of problem 26 to find a power series representation for
√1 + x
3
4
