Binary Adder
A binary adder is a digital circuit that produces the arithmetic sum of two binary
numbers. It can be constructed with full adders connected in cascade
(بشكك
)متعاقكwith the output carry from each full adder connected to the input carry of the
next full adder in the chain.
Addition of n-bit numbers requires a chain of (n) full adders or a chain of one-half
adder and (n-1) full adders.
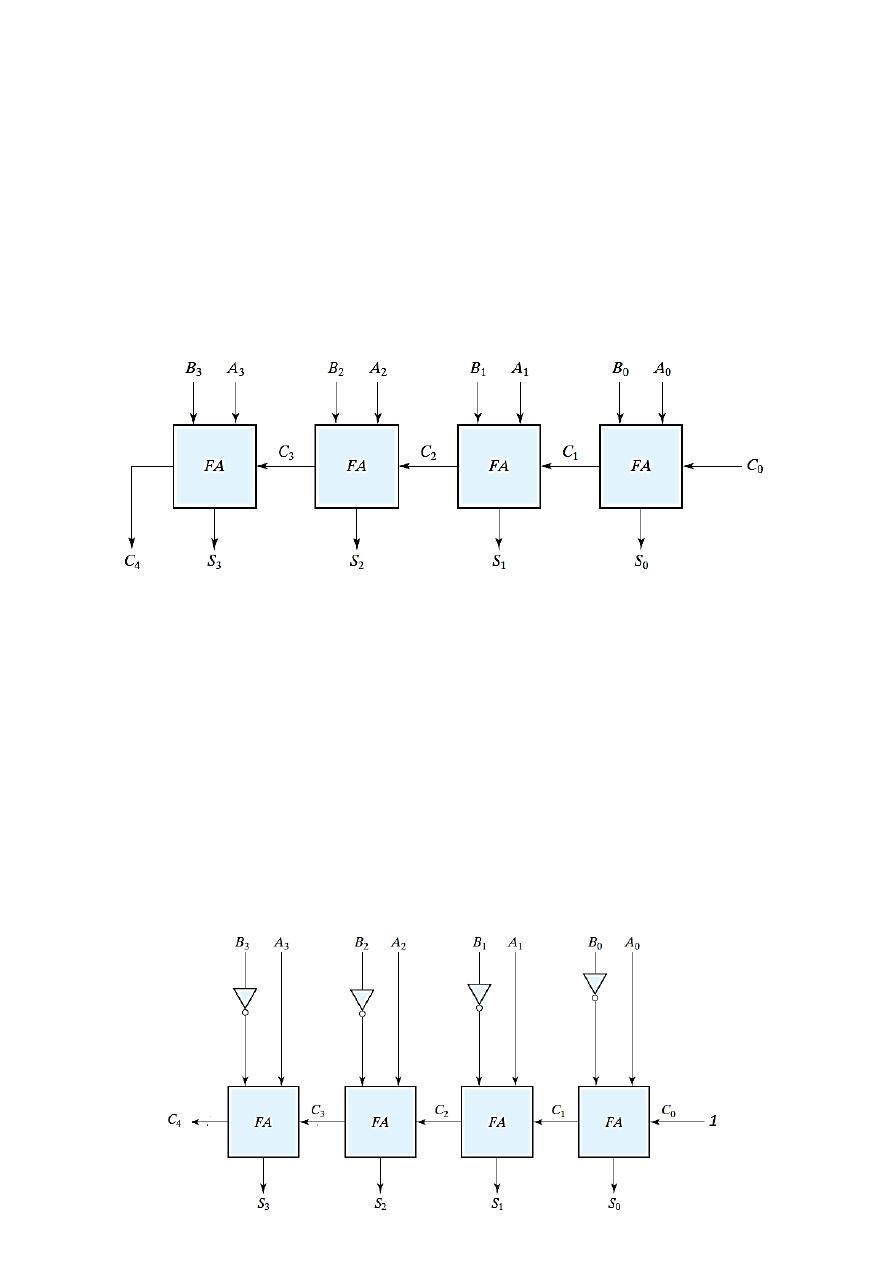
Ex) Draw the diagram of a four-bit binary adder constructed from using full adders
only.
The input carry Co is set to zero.
It is important to note all the inputs should be available at the adder in order to get
the right output. However, input carry C3 does not settle to its final value until C2 is
available from the previous stage. Similarly, C2 has to wait for C1 and so on down to
C0. The carry propagation time is an important attribute of the adder because it limits
the speed with which two numbers are added.
Binary Adder
– Subtractor
The subtraction A
– B can be done by taking the 2’s complement of B and adding it
to A. The
2’s complement can be obtained by taking the 1’s complement and adding
1. The 1’s complement can be implemented with inverters.
Thus, the circuit for subtracting A
– B consists of an adder with inverters placed
between each data input B.
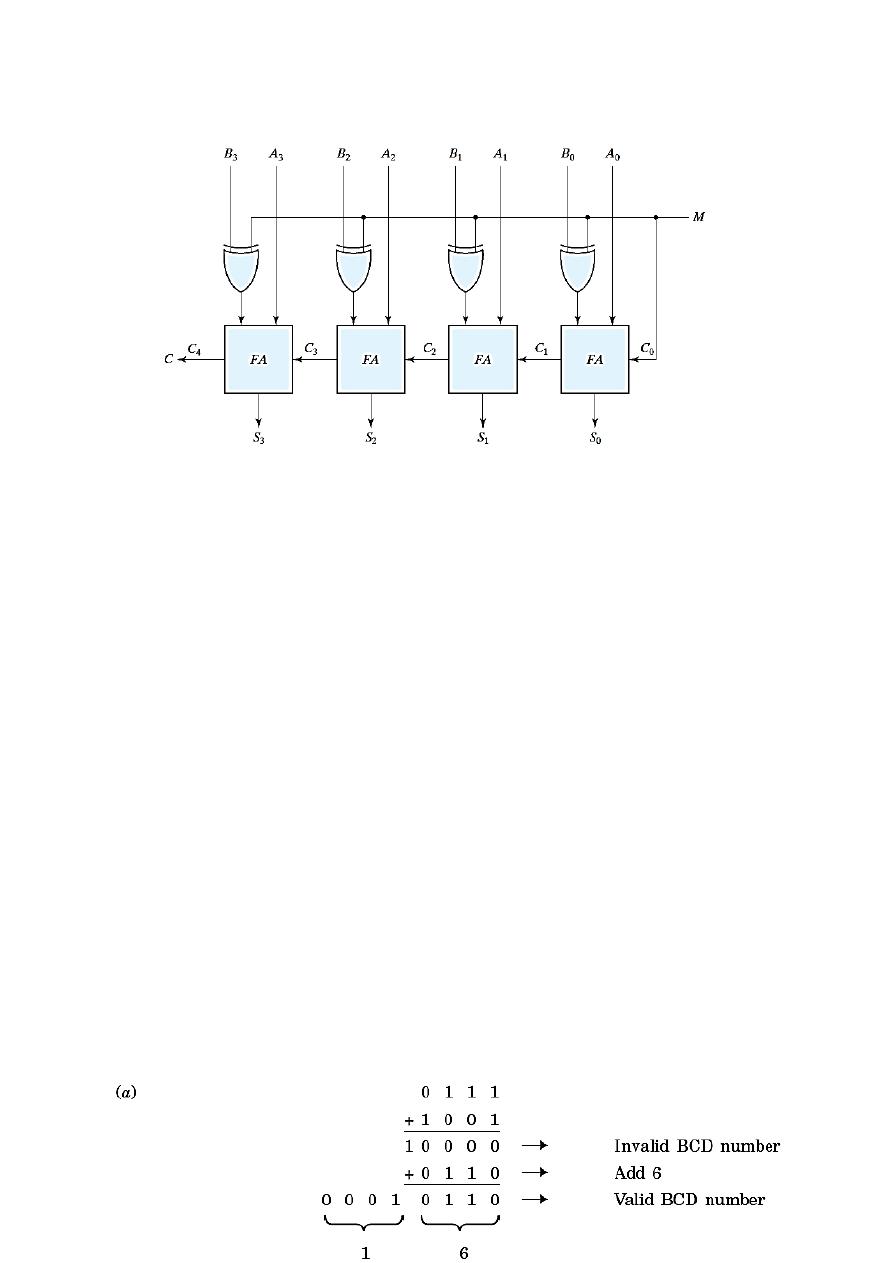
The addition and subtraction operations can be combined into one circuit with one
common binary adder by including an exclusive-OR gate with each full adder.
The mode input M controls the operation. When M = 0, X-OR acts as buffer and the
circuit is an Adder. When M = 1, X-OR acts as inverter and the circuit becomes a
Subtractor.
BCD Adder
The same binary adder can be used as BCD adder. In BCD code, each decimal digit
from 1 to 9 is coded in 4-bit binary numbers. But with 4-bit binary sixteen different
groups (0-15) can be obtained, whereas we require only ten groups (0-9) to write
BCD code. The other six groups are called forbidden codes in BCD and they are
invalid.
BCD Addition Rules
I. First add the two numbers using normal rules for binary addition.
II. If the 4-bit sum is equal to or less than 9, it becomes a valid BCD number.
III. If the 4-bit sum is greater than 9 or if a carry-out of the group is generated, it is an
invalid result. In such a case,
since there is a difference of 6 between the binary
and BCD, add (0110)
2
to the 4-bit sum in order to skip the six invalid states and
return the code to BCD format.
Ex) Add the following BCD numbers:
(a) 0111 and 1001
(b) 10010010 and 01011000.
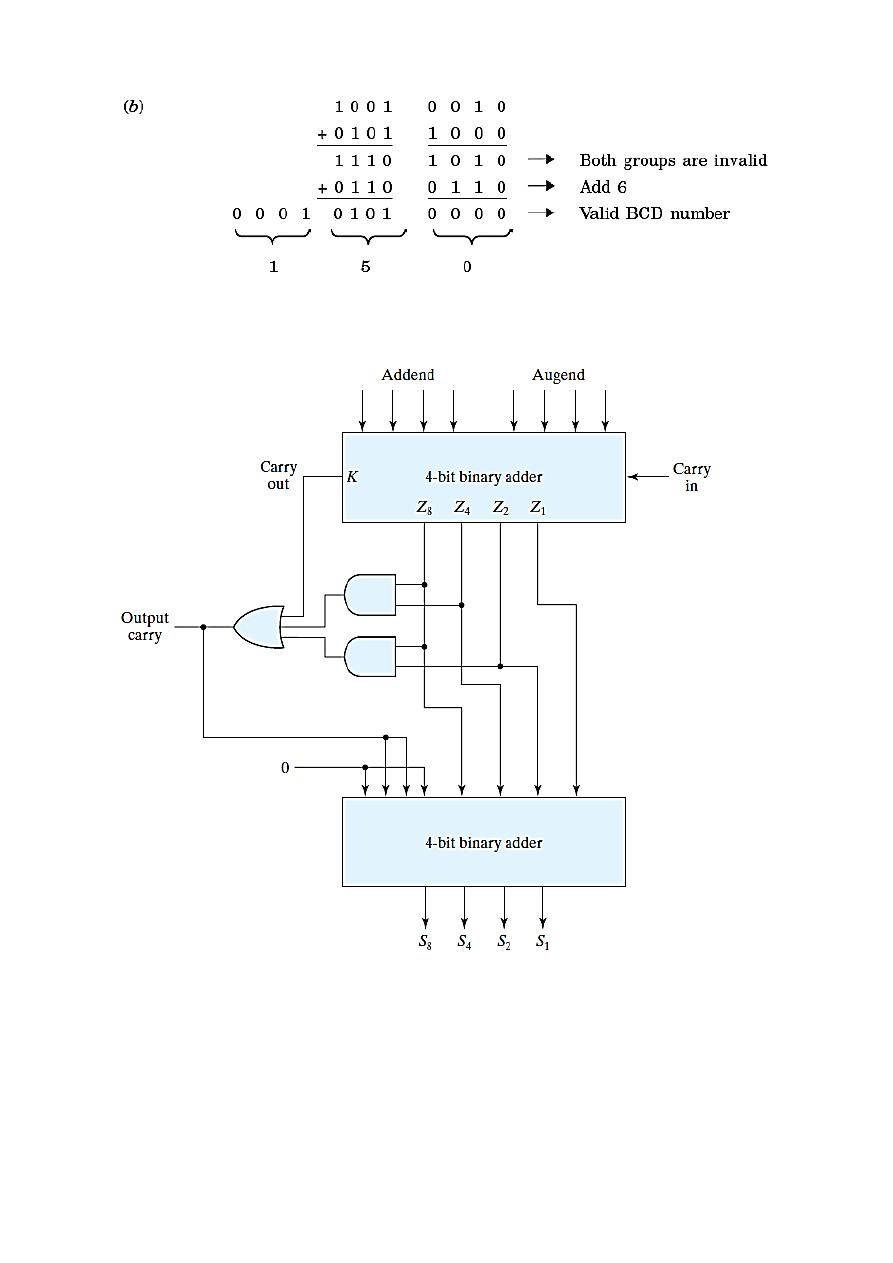
Two 4-bit binary adders can be used to perform BCD addition. The adders will form
the sum in binary and produce a result that ranges from 0 through 19 as follow
The first adder performs normal binary addition. Then, the results are checked to see
if there the result is greater than 9 or if a carry-out of the group is generated.
It is obvious that a correction is needed when the first binary adder has an output
carry of 1. The other six combinations from 1010 through 1111 also need a
correction. The result is greater than 9 if Z
8
and Z
4
equal to 1 or Z
8
and Z
2
equal to 1.
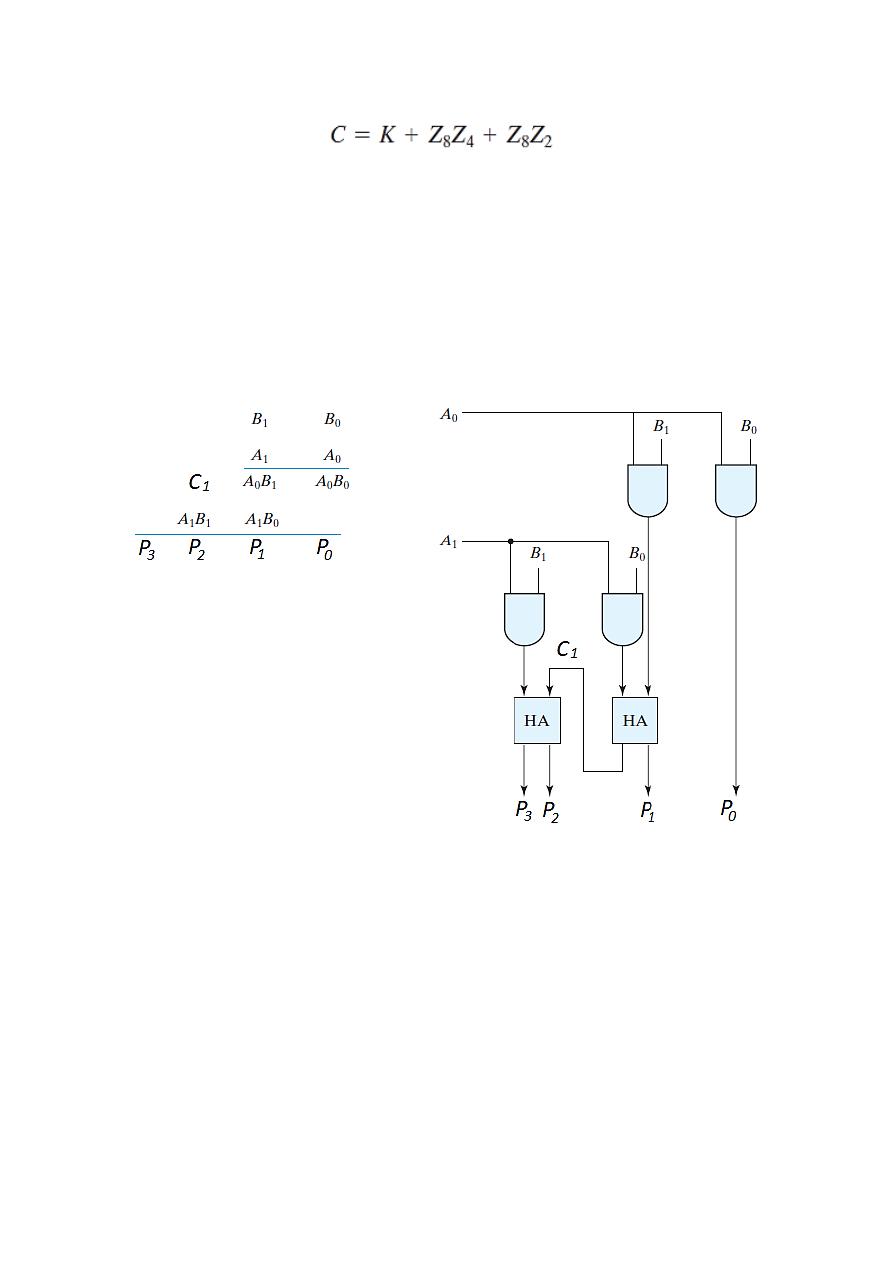
The final Boolean function for the correction is
Or you can use the truth table and K-map to find this function {Homework}
Binary Multiplier
Multiplication of binary numbers is performed in the same way as multiplication of
decimal numbers. The multiplication of two bits produces a 1 if both bits are 1
otherwise, it produces a 0.
