
6
College of Medicine/Babylon University
Medical Physics Module
Session 1
Lecture 1:
Forces On and In the Body
Objectives
: after the end of this lecture, the student must know:
1- The application of gravitational forces on Various body parts
2- The application of Newtons laws of dynamics in medicine
Gravitational force : Newton’s law: this law state that there is a force of attraction
between any two objects, our weight is due to attraction between the earth and
our body .
One important medical effect of gravitational force is the formation of varicose
veins in the legs, as the venous blood travels against force of gravity on its way to
the heart.
Another medical effect of gravity is on the bones. Gravitational force on the
skeleton in some way contributes to healthy bones, if person becomes weight less
such as in orbiting satellite, he may lose bone mineral and may be serious problem
on very long journey.
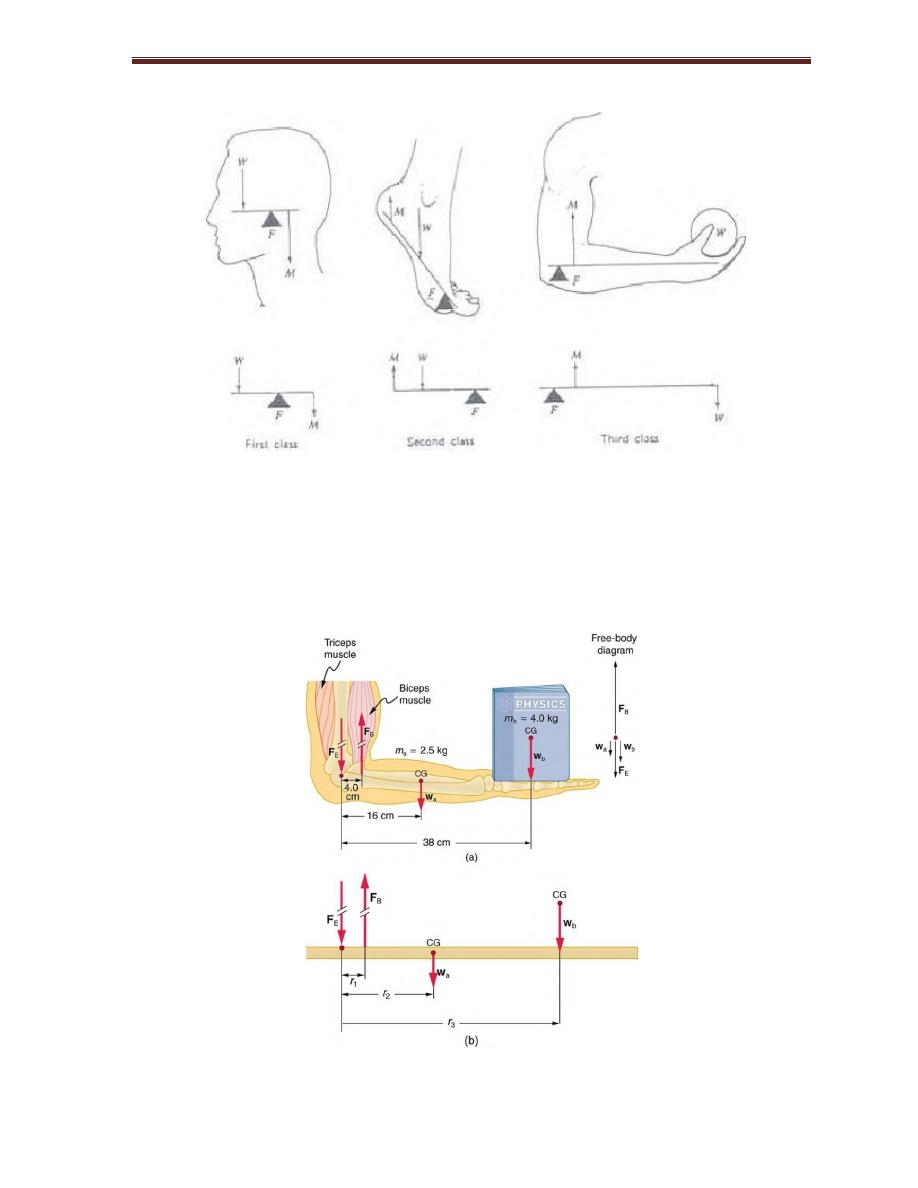
Statics
Many of muscle and bone systems of the body acts as levers, levers are classified as,
first, second, and third. The last are most common in the body, second are next
common.
College of Medicine/Babylon University
Medical Physics Module
Figure 1
: lever system in the body
We can find the force supplied by the biceps, if we sum the torques about pivot
point at the joint
Figure 2:
lever system in the body, forearm

College of Medicine/Babylon University
Medical Physics Module
4 M – 30 W = 0
M = 7.5 W
we neglect the weight of forearm
M = 3.5 H + 7.5 W include forearm
The arm can be raised and held out horizontally from shoulder by deltoid muscle,
by taking sum of torques about shoulder joint
T = 2 W1 + 4 W2 / sin α
Figure 3:
the forearm at an angle
W1= weight of the arm = 68 N
W2 = weight in the hand = 45 N
T = 1145 N
The force needed to hold up the arm is large.

9
College of Medicine/Babylon University
Medical Physics Module
Frictional Forces
When person walking as the hell of the foot touch the ground a force is
transmitted from the foot to the ground.
Can resolve this force into horizontal and vertical components.
Maximum force of friction f is:
F= μ N
Where N is the normal force, μ is the coefficient of friction, horizontal force = 0.15
w where is W is the person weight (this is large frictional force must be in order to
prevent heel from slipping).
The coefficient of friction in the joints is lower than in engineering materials. The
lungs move inside the chest, the intestine have slow rhythmic motion (peristalsis) as
they move the food toward its final destination. All of these organs are lubricated
by slippery mucus covering to minimize friction.
Dynamics
Newtons second law is:
F = m a a = acceleration= dv/dt
F = ∆( mv) / ∆t
Example of dynamic force in the body is the apparent increase in weight when the
heart beats (systole). About 60 gm of blood is given velocity about 1m/ sec
upward in about 0.1 sec.
The momentum P = m v = 0.6 Kg x 1 m/sec = 0.06 Kg m /sec
The downward reaction force ( Newtons third law ) produced is:
0.06 Kg/sec /0.1 sec = 0.6 N (this is enough to produce noticeable jiggle)

10
College of Medicine/Babylon University
Medical Physics Module
Stokes has shown that for spherical object of radius ( a ), retarding force ( Fd ) and
terminal velocity ( v ) are related by
Fd = 6Π a ƞ v ƞ = viscosity
When the particle is moving at constant speed the retarding force is equilibrium
with the difference between gravitational force and upward buoyant force (the
weight of the liquid the particle displaces) thus we have
Force of gravity Fg = 4/3 Π a
3
ρ g
Buoyant force Fb = 4/3 Π a
3
ρ˳ g
Retarding force Fd = 6Π a ƞ v
Fg - Fb = Fd
V = 2 a
2
/ 9 ƞ [ g ( ρ - ρ˳ ) ] sedimentation velocity
This equation is valid for spherical objects.
In some forms of diseases such as rheumatic fever, rheumatic heart disease, and
gout RBC clumps together ,and the effective radius increase thus increased
sedimentation velocity occur.
In other diseases such as hemolytic jaundice and sickle cell anemia RBC change
shape or break, the radius decreases, thus the rate of sedimentation velocity
decreases.
