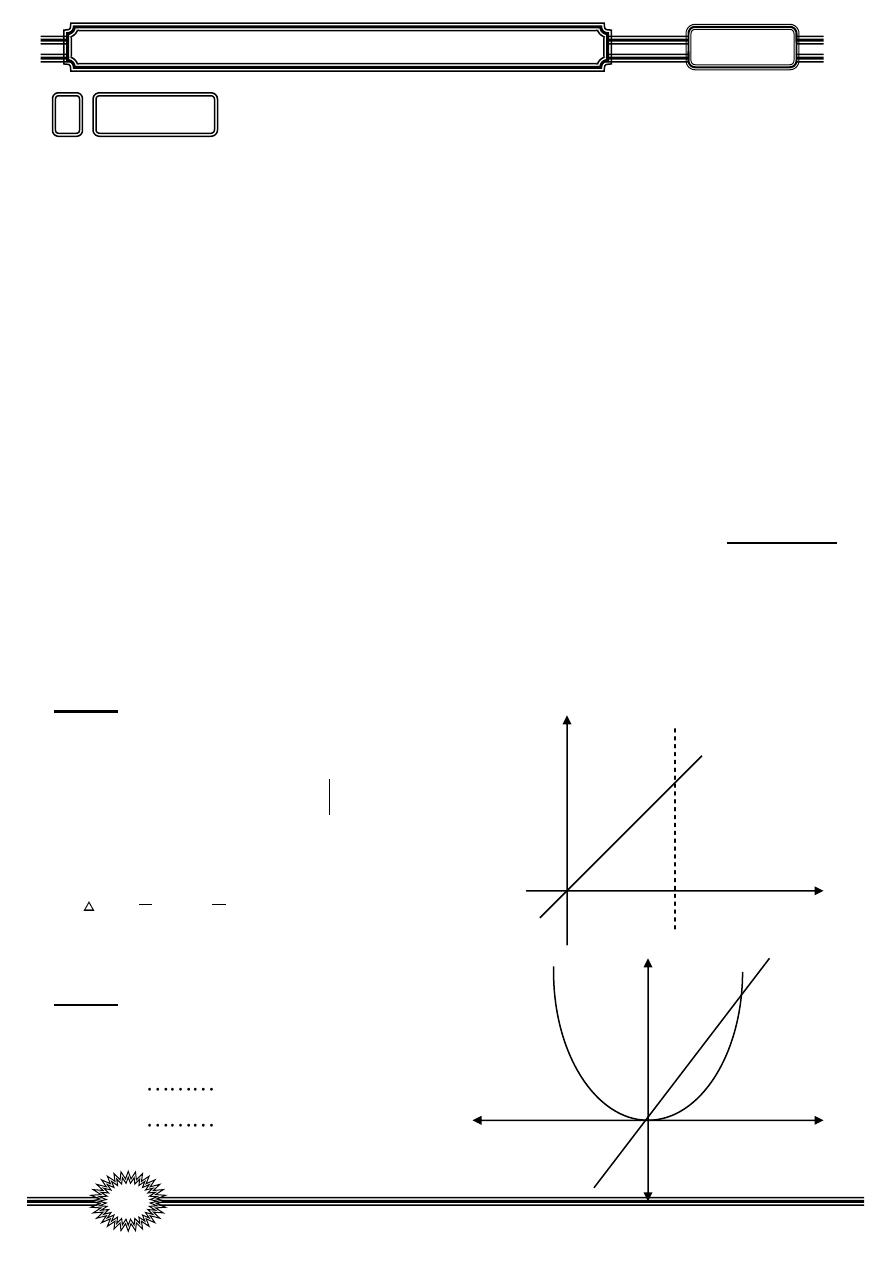
DEFINITE INTEGRAL APPLICATIONS
LEC : 3
61
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
a) Area between f(x) and the axis
( )
,
( )
,
b
b
a
a
d
b
c
a
A
f x dx
y dx
area respected to x
axis
A
g y dy
x dy
area respected to y
axis
b) Area between two curves
y
1
=f(x
1
), y
2
=f(x
2
), x
1
=g(y
1
), x
2
=g(y
2
)
1
2
1
2
1
2
1
2
(
)
,
,
(
)
,
,
b
a
d
c
A
y
y
dx
x
axis
y
y
A
x
x
dy
y
axis
x
x
: مالحظاث هامت
(1
. اذا اعطاوا دالت وحدود تكامل فالحل يكون مباشر
(2
اذا اعط
. اوا دالتيه بدون حدود تكامل فىقاطع الدالتيه
(3
فاذا اعطى المساحت بالىسبت للمحور, روحملا ىلع دامتعلااب نوكي لحلاف , لماكت دودح نودب طقف تلاد اواطعا اذا
x
وضيف معادلت
y=0
واذا اعطى المساحت بالىسبت للمحور
y
وضيف معادلت
x=0
. ثم وقاطع الدالتيه,
(4
اذا طل
ب المساحت بالىسبت للمحور
x
وحدود التكامل معطاة بالىسبت للمحور
y
فيجب تحويل حدود التكامل
بداللت
x
. والعكس صحيح
axis from x=0 , x=2 and
-
by the line y=2x and the x
Find the area bounded
-
:
EXAM
check the result by geometrically.
Find the area between the curves :
-
:
EXAM
2
3
y
x
and the line
y
x
Solution :
2
2
2
(1)
3
(2)
3
3
0
y
x
y
x
x
x
x
x
Area
1
y=2x
x=2
(2,4)
y=3x
2
y
x
(3,9)
2
2
2
2
0
0
2
4
1
1
.
(2)(4)
4
2
2
b
a
A
y dx
x dx
x
unit
In Geometry
A
b h
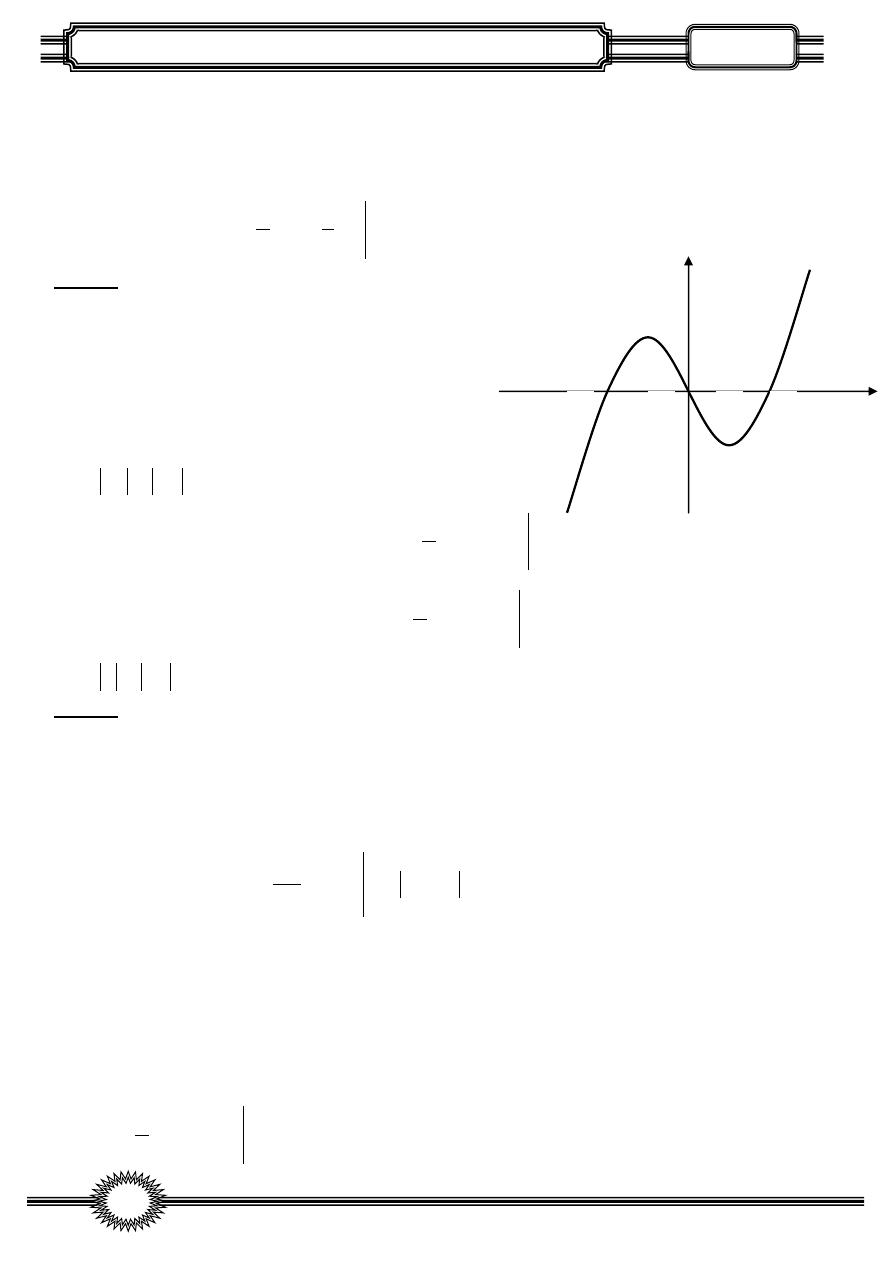
DEFINITE INTEGRAL APPLICATIONS
LEC : 3
61
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
1
2
1
2
3
3
2
2
3
2
0
0
(
3)
0
0 ,
3
(
)
,
3
1
(3
)
4.5
2
3
b
a
x x
x
x
A
y
y dx
y
y
x
x
dx
x
x
unit
Find the area between the curves :
-
:
EXAM
2
(
4)
y
x x
and the x-axis
Solution :
2
2
1
2
0
0
0
2
3
4
2
1
2
2
2
2
2
2
2
3
4
2
2
0
0
0
(
4)
0
(
4)
0
0,
2,
2
1
(
4)
(
4 )
2
4
4
1
(
4)
(
4 )
2
4
4
4
4
8
y
x x
y
x x
x
x
x
A
A
A
A
x x
dx
x
x dx
x
x
A
x x
dx
x
x dx
x
x
A
y=10 and the
-
Find the area between the line x
-
:
EXAM
a) x-axis b)y-axis
from x=0 , x=5
5
5
2
0
0
5
10
)
,
10
10
(
10)
10
37.5
37.5
2
)
,
10
10
(
10)
0
10
&
5
5
b
a
d
c
a
A
y dx
x
y
y
x
x
x
dx
x
b
A
x dy
x
y
x
y
A
y
dy
x
y
x
y
5
2
10
1
10
?
2
y
y
A
1
A
2
-2
2
0
DEFINITE INTEGRAL APPLICATIONS
LEC : 3
61
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
DEF: if f(x) ≥ 0 cont. on [a,b] if the area bounded by f(x) and the x-axis from x=a to
x=b rotated about the x-axis then :
2
2
[ ( )]
b
b
x
a
a
V
f x
dx
y dx
DEF: if g(y) ≥ 0 cont. on [c,d] if the area bounded by g(y) and the y-axis fromy=c to
y=d rotated about the y-axis then :
2
2
[ ( )]
d
d
y
c
c
V
g y
dy
x dy
DEF : if the area bounded between two curves is rotated about x-axis
2
2
1
2
1
2
(
)
,
b
x
a
V
y
y
dx
y
y
DEF : if the area bounded between two curves is rotated about y-axis
2
2
1
2
1
2
(
)
,
d
y
c
V
x
x
dy
x
x
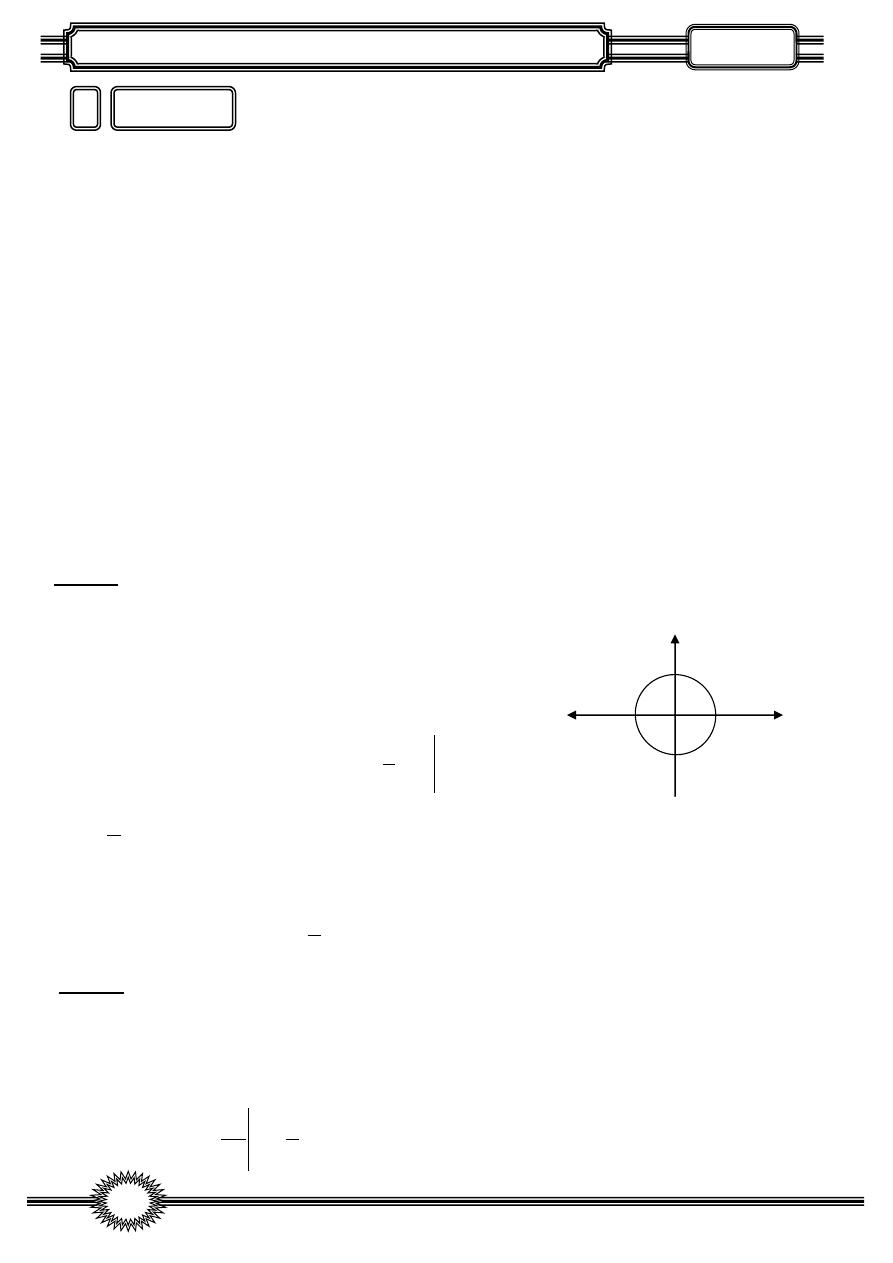
The area bounded by the circle with radius r and center is the origin is
-
:
EXAM
rotated about the x-axis , find the volume generated and check the result by geom.
2
2
2
2
2
2
2
2
2
2
2
2
3
0
0
3
3
3
3
(
)
1
2
(
)
2 (
)
3
4
3
4
3
b
r
x
a
r
r
r
x
y
r
y
r
x
V
y dx
r
x
dx
r
x
dx
r x
x
r unit
In Geometry
thevolume of sphare is
r unit
axis,
-
y
is rotated about the
2
2
1
x y
The area bounded by the function
-
:
EXAM
find the volume generated from y=1 , y=2 .
2
2
2
2
2
2
2
3
1
,
1
1
1
2
d
y
c
d
c
V
x dy
x y
x
y
y dy
unit
y
Volumes
2
r
r
r
r

DEFINITE INTEGRAL APPLICATIONS
LEC : 3
61
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
1
-
The area bounded by the line y=x
-
:
EXAM
a) is rotated about the x-axis b) is rotated about the y-axis
find the volume generated from those rotation from x=0,1
2
2
2
1
1
2
3
3
0
0
2
2
2
0
0
2
3
3
1
1
)
,
1
(
1)
(
1)
(
1)
3
3
)
,
1
1
(
1)
0
1 &
1
0
(
1)
(
1)
3
3
b
x
a
d
y
c
a V
y dx
y
x
y
x
x
dx
x
unit
b V
x dy
y
x
x
y
x
y
x
y
x
y
y
dx
y
unit
If y=f(x) is continous with continous derivative at each point of the curve from (a,f(a))
to (b,f(b)) then :
2
2
1 (
)
,
.
1 (
)
,
.
b
a
d
c
dy
dy
S
dx
if
is cont
dx
dx
dx
dy
S
dy
if
is not cont
dy
dx
3
2
2
1
(
2)
,
0,3
3
y
x
from x
Find the length of the segment of curve
-
:
EXAM
1
1
2
2
1
2
2
2
3
2
2
2
0
3
3
2
2
4
2
0
0
3
3
2
2
2
0
0
3
3
0
1 3
(
2) (2 )
(
2)
.
[0,3]
3 2
1 (
)
1 ( (
2) )
1
(
2)
2
1
(
1)
(
1)
?
3
b
a
dy
x
x
x x
cont on
dx
dy
S
dx
x x
dx
dx
x
x
dx
x
x
dx
x
dx
x
dx
x
x
Arc Length
3

DEFINITE INTEGRAL APPLICATIONS
LEC : 3
02
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
2
3
,
1,8
y
x
from x
Find the length of the segment of curve
-
:
EXAM
1
3
1
3
1
3
1
2
3
3
3
2
3
3
2
2
4
4
2
1
1
4
4
1
1
2
2
.
[ 1,8]
3
3
3
1
1&
8
4
2
3
9
1 (
)
1
2
4
9
4 2
9
1
(1
)
4
9 3
4
8
13
[(10)
(
) ]
?
27
4
dy
x
not cont on
dx
x
dx
x
x
y
x
y
dy
S
x
dy
x
dy
S
y dy
y

DEFINITE INTEGRAL APPLICATIONS
LEC : 3
06
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
1- Find the area bounded by the line 2x-5y=10 from x=0 , 10 about the x&y – axis.
2- Find the area bounded by the curves :
2
2
2
3
2
2
,
,
1, 2
,
sec
,
,
45, 45 ,
,
2
,
2
,
2
3
,
y
x
y
x
x
x
axis
y
x
y
x
x
x
axis
y
x
y
x
y
x
axis
y
x
x
y
x
x
x
axis
3- Find the volume generated from rotation between curves :
2
2
2
sec
,
0 ,
45,60
,
25
,
3
,
sc
,
2 ,
45,60
,
1
,
2
,
1,1 ,
sin
,
cos
,
0, 45 ,
tan
,
1 ,
45,60
,
y
x
y
x
x
axis
y
x
y
x
axis
y
c
x
y
x
x
axis
x
y
x
y
y
y
axis
y
x
y
x
x
x
axis
y
x
y
x
x
axis
2
&
9
y
x
y
4- Find the horizontal line y=k that divides the area between
into two equal parts .
&
2
x
y
x
5- Find the vertical line x=k that divides the area between
into two equal parts .
6- Find the volume of the solid that result when the reigon above the x-axis and below
2
2
2
2
1
, ,
0
x
y
a b
a
b
to the ellipse
7- Let V be the volume of the solid that result when the reigon enclosed by
1
,
0 ,
2 ,
(0
2)
y
y
x
x
b
b
x
is revolved about the x-axis , find the value of " b " for which V=3.
8- Find the exact arc length of the curve over the stated interval : -
3
2
4
4
2
3
1
0,1
24
48
,
2, 4
1
1
1, 4
8
4
y
x
x
xy
y
y
x
y
y
y
MOHAMED SABAH AL TAEE
M.SC / MATHEMATICS
E-MAIL : msmt_80@yahoo.com
2013 -2014
