THE EXPONETIAL FUNCTIONS
LEC : 5
62
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
Properties of exp. fun.
0
1
,
1
,
2.718...
.
(
)
(
)
.
0
a b
a
b
ax
a x
x
a
x
Lne
e
e
e
e e
e
e
e
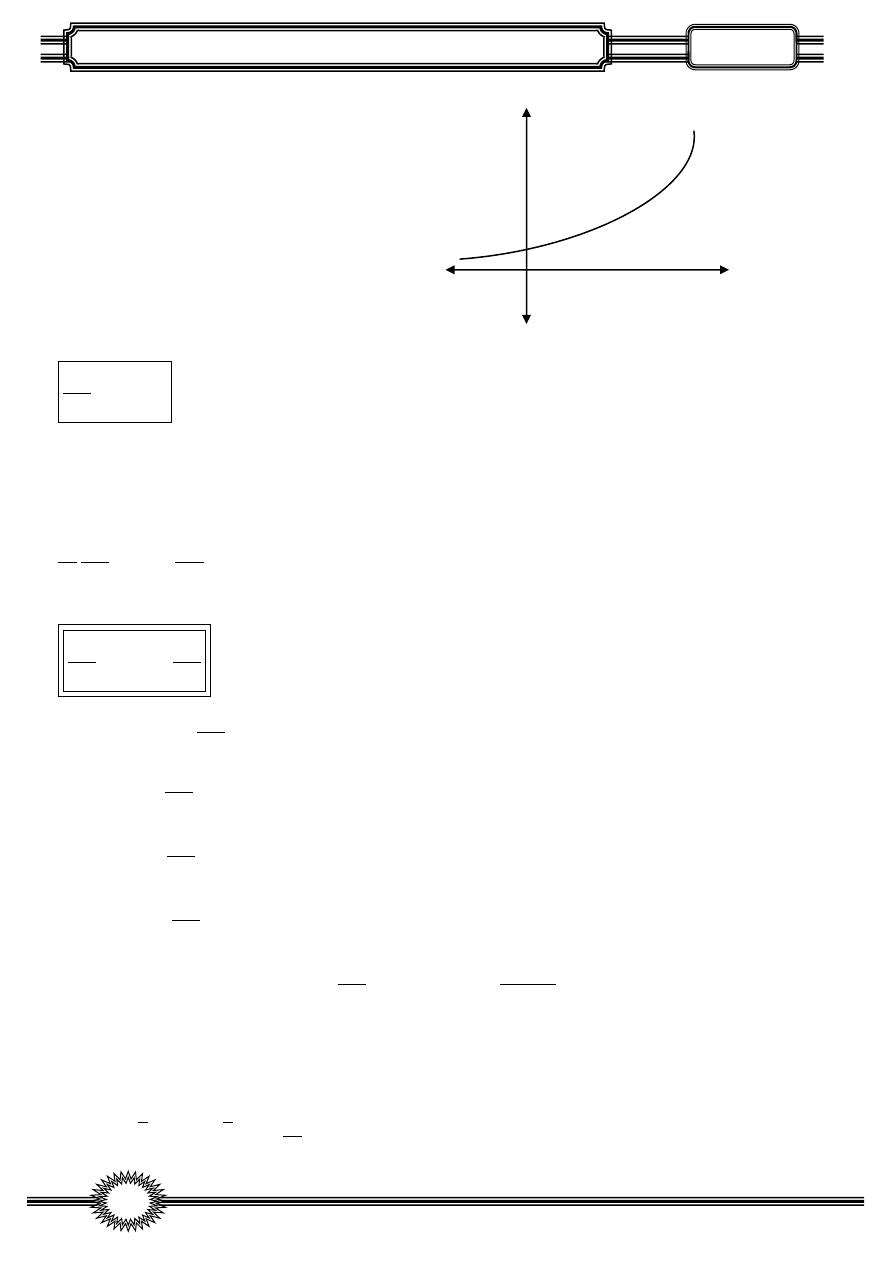
its domain is all real no
its range are y
the graph of y
e is
: أشتقاق اندوال االسية
x
x
d
e
e
dx
Proof:
1
1
x
x
x
let y
e
Lny
Lne
xLne
x
dy
dy
y
e
y dx
dx
and in general form
u
u
d
du
e
e
dx
dx
EXAM: Find
dy
dx
to :
3
3
3
3
3
3
2
2
(3)
3
( 1)
(1)
1
(3
)
3
0
x
x
x
x
x
x
x
x
x
x
x
x
x
dy
y
e
e
e
dx
dy
y
e
e
e
dx
dy
y
xe
xe
e
xe
e
dx
dy
y
e
LnLnx
x
e
e
x
x
dx
xLnx
EXAM : Simplify
2
2
2
2
2
( )
2
( )
x
x
y
y
Lnx
Lnx
Ln
Ln
y
e
e
x
x
y
e
e
y
x
e

THE EXPONETIAL FUNCTIONS
LEC : 5
62
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
: تكامالت اندوال االسية
x
x
e dx = e
C
and in general form :
u
u
e du = e
C
EXAM : Find
2
3
3
3
4
4
4
2
2
2
3
2
2
2
2
2
2
2
1
1
4
4
4
1
1
2
2
2
3
1
1
6
6
6
x
x
x
x
x
x
Lnx
Lnx
x
x
x
x
x
x
x
x
x
e dx
e dx
e
C
e
dx
e
dx
e
C
x
e
dx
e
dx
x dx
C
x e
dx
x e
dx
e
C
e
e
dx
Ln e
e
C
e
e
,
x
u
a
a
Exponetial fun. of type
x
x
xLna
Lna
x
a
e
e
a
اشتقاق اندانة االسية
من نوع
x
a
x
x
d
a
a Lna
dx
and in general form :
u
u
d
du
a
a Lna
dx
dx
EXAM: Find
dy
dx
to :
4
4
2
2
3
3
3 .
3.(4
)
7
7 .
7.(2 )
1
10
10
.
10.( )
x
x
x
x
Lnx
Lnx
dy
y
Ln
x
dx
dy
y
Ln
x
dx
dy
y
Ln
dx
x

THE EXPONETIAL FUNCTIONS
LEC : 5
62
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
تكامم اندانة االسية من نوع
x
a
,
0 ,
1
u
u
a
a du
C
a
a
Lna
EXAM : Find
2
2
2
3
3
3
1
1 7
7
7 2
2
2
7
x
x
x
x
x
dx
C
Ln
x dx
x dx
C
Ln
EXAM : a) Find the area bounded by the curve
4x
y
e
and the x-axis from x=-1 , 1
b) The area in (a) rotated about the x-axis , find the volume generated ?
1
1
4
4
1
1
4
4
2
1
1
2
4
2
8
1
1
1
8
3
1
1
( )
4
1
4
( )
(
)
?
8
b
x
x
a
b
x
x
x
a
x
a A
ydx
e
dx
e
e
e
unit
b V
y dx
e
dx
e
dx
e
unit
1) Show that
2
2
2
( )
.
(1
)
( )
.
(1
)
x
x
a
y
xe
satisfies the eq
xy
x y
b
y
xe
satisfies the eq
xy
x
y
2) Find
dy
dx
to :
3
(1
)
,
,
x
x
x
e
y
Ln
xe
y
y
x e
Lnx
3) Find
1
2
,
1
x
x
e
dx
e
dx
x
MOHAMED SABAH AL TAEE
M.SC / MATHEMATICS
E-MAIL : msmt_80@yahoo.com
2013 -2014
