TRIGONOMETRIC FUNCTIONS
LEC : 6
92
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
الدوال المثلثية
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Opposite
sin
Hypotenuse
cos
Hypotenuse
:
sin
sin
, cos
cos
sin
cos
1
sin
cos
1
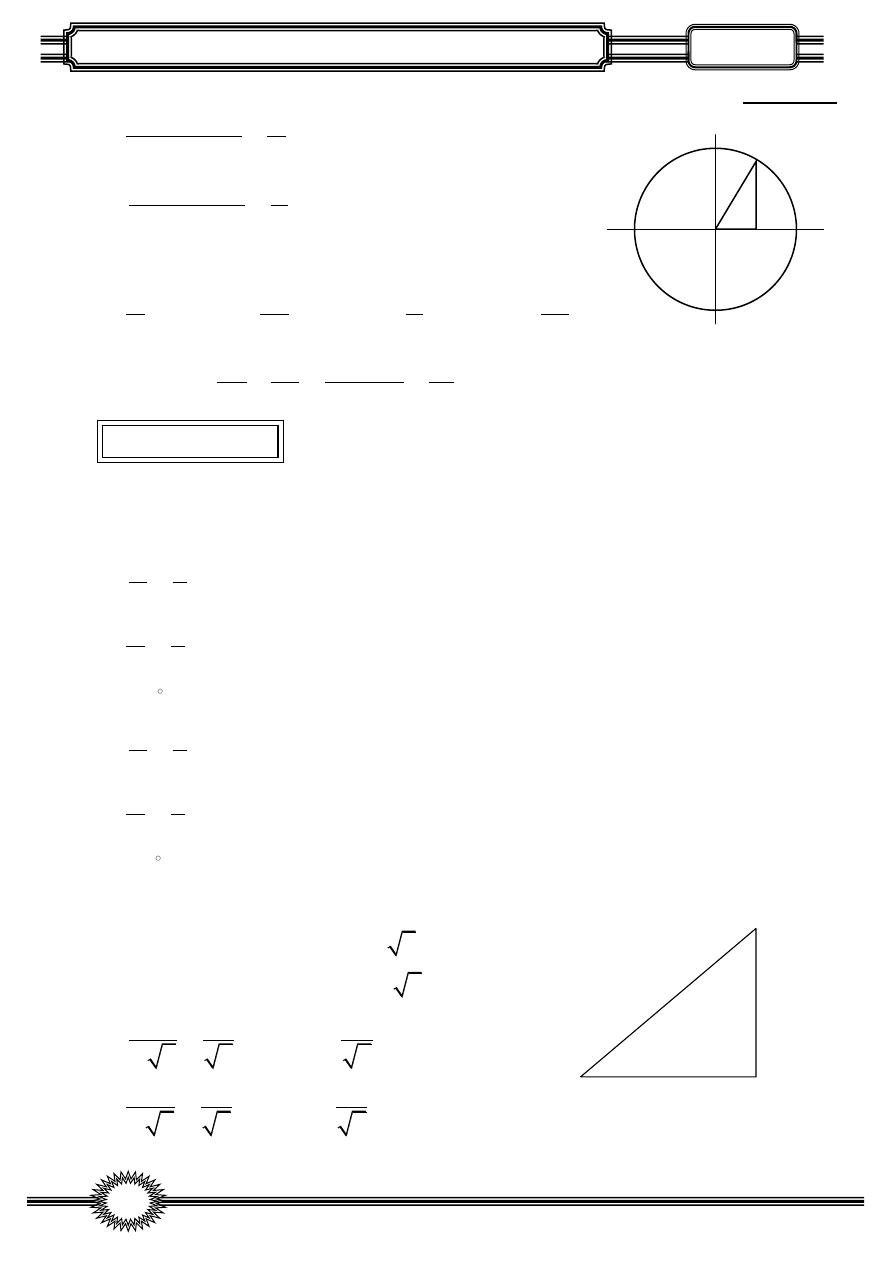
y
r
A djance
x
r
By phythaghore theorem we get
y
y
x
x
r
r
r
r
y
x
x
y
r
r
r
r
r
2
2
2
2
2
2
2
2
2
2
2
2
2
1)
0
cos
1
cos
1
0
sin
0
sin
0
2)
90
0
cos
0
cos
0
sin
1
sin
1
3)
45
,
2
2
2
2
1
1
cos
cos
2
2
2
1
1
sin
sin
2
2
2
x
r
r
r
y
r
r
x
r
r
y
r
r
r
x
y
r
y
x
x
x
r
x
r
r
x
y
y
r
y
r
r
y
x
x
y
y
x
r
y
x
y
r
45
TRIGONOMETRIC FUNCTIONS
LEC : 6
03
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
2
2
2
2
2
2
2
2
4)
30
4
3
3
:
3
3
3
cos
cos
2
2
1
sin
sin
2
2
5)
60
1
cos
cos
2
2
3
3
sin
sin
2
2
x
y
r
L
y
L
y
L
y
L
by same we get
x
L
x
L
r
L
y
L
r
L
x
L
r
L
y
L
r
L
2
3
2
90
60
30
45
0
0
-1
0
1
3
2
1
2
1
2
0
Sin
1
0
-1
0
1
2
3
2
1
2
1
Cos
0
∞
0
∞
3
1
3
1
0
Tan
Some Rules of Trig. Fun. :-
2
2
2
2
2
2
sin
cos
1
sec
1 tan
sc
1
t
sin(
)
sin
cos
cos
sin
cos(
)
cos
cos
sin
sin
c
co
A
B
A
B
A
B
A
B
A
B
A
B
2L
L
L
2L
2L
60
60
60
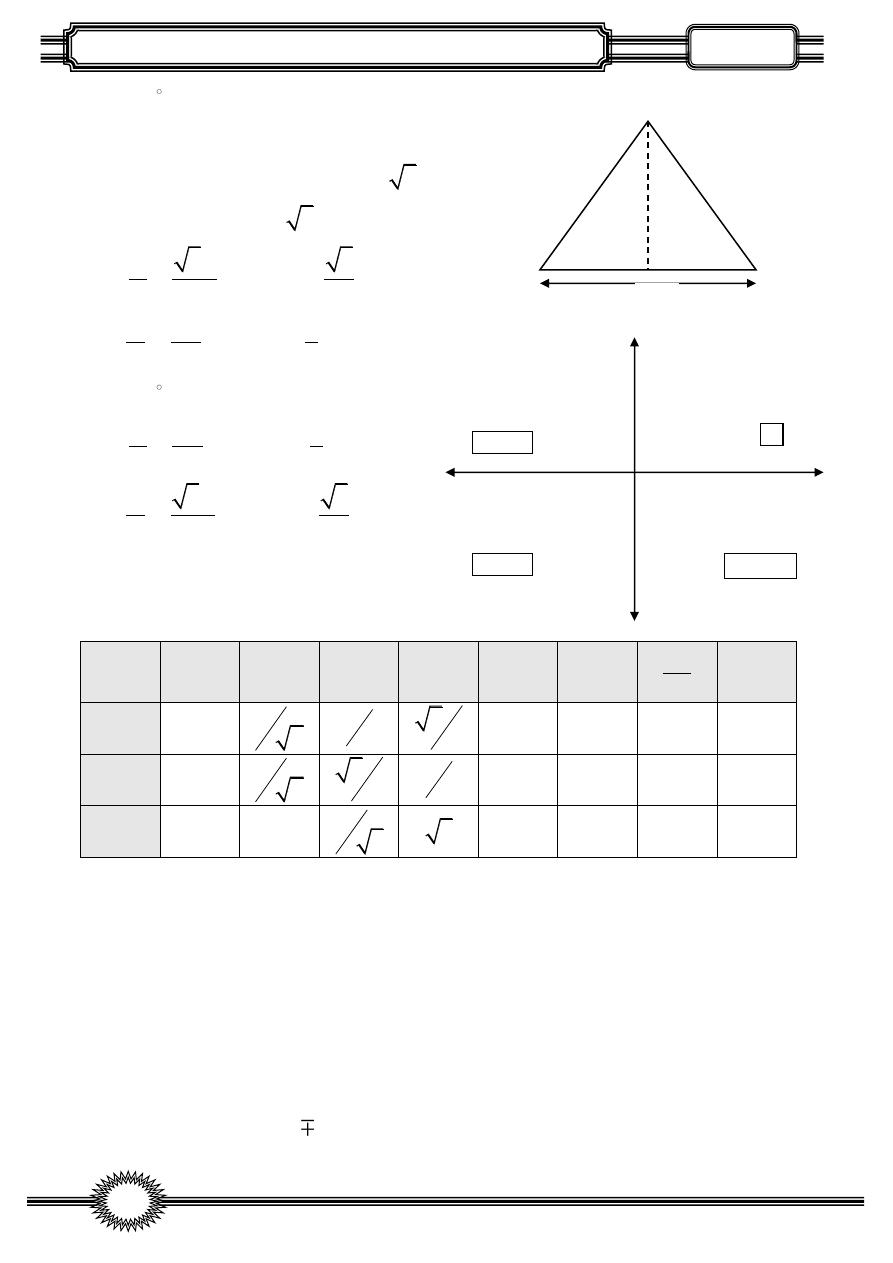
Sin +
Cos +
Tan +
Sin +
Cos
-
Tan -
Sin -
Cos -
Tan +
Sin -
Cos +
Tan -
x
x
x
2
x
TRIGONOMETRIC FUNCTIONS
LEC : 6
03
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
2
2
2
2
2
2
2
tan
tan
tan(
)
1 tan
tan
2 tan
tan(2 )
1 tan
sin 2
2sin
cos
cos 2
cos
sin
cos 2
1 2sin
cos 2
2cos
1
1
sin
(1 cos 2 )
2
1
cos
(1 cos 2 )
2
sin
sin
2sin
cos
2
2
sin(
) sin(
)
2cos
sin
A
B
A
B
A
B
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
B
A
B
A
B
A
B
A
B
A
B
EXAM :
3
sin(120)
sin(
60)
sin 60
2
3
sin(240)
sin(
60)
sin 60
2
3
sin(300)
sin(2
60)
sin 60
2
1
sin(330)
sin(2
30)
sin 30
2
sin(
)
sin
cos
cos
sin
cos
2
2
2
cos(
)
cos
cos
sin
sin
sin
2
2
2

TRIGONOMETRIC FUNCTIONS
LEC : 6
09
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
مشتقات الدوال المثلثية
Derivative of Trig. Fun.
2
2
2
2
1
sin
cos
.
sin
cos
2
cos
sin
.
cos
sin
3
tan
sec
.
tan
sec
4
t
sc
.
t
sc
5
sec
sec
tan
.
sec
sec tan
d
d
du
x
x
in Gen
u
u
dx
dx
dx
d
d
du
x
x
in Gen
u
u
dx
dx
dx
d
d
du
x
x
in Gen
u
u
dx
dx
dx
d
d
du
co x
c
x
in Gen
co u
c
u
dx
dx
dx
d
d
du
x
x
x
in Gen
u
u
u
dx
dx
d
6
sc
sc
t
.
sc
sc
t
x
d
d
du
c
x
c
x co x
in Gen
c
u
c
u co u
dx
dx
dx
Proof :
0
0
0
0
0
0
0
sin(
) sin
sin cos
sin
cos
sin
1
sin
lim
lim
sin [1 cos
] sin
cos
lim
sin [1 cos
]
sin
cos
lim
lim
[1 cos
]
sin
sin
lim
cos
lim
sin (0)
cos
x
x
x
x
x
x
x
d
x
x
x
x
x
x
x
x
x
dx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
(1)
cos x
0
0
0
0
0
0
0
cos(
) cos
cos cos
sin sin
cos
2
cos
lim
lim
cos [1 cos
] sin sin
lim
cos [1 cos
]
sin
sin
lim
lim
[1 cos
]
sin
cos
lim
sin
lim
cos (0)
sin
x
x
x
x
x
x
x
d
x
x
x
x
x
x
x
x
x
dx
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
(1)
sin
x
x

TRIGONOMETRIC FUNCTIONS
LEC : 6
00
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
EXAM :
tan
tan
2
2
sin
2
sin
2
2
2
2
2
cos 4
sin 4 (4)
4sin 4
(sec
)
5cos5
sin 5
5cot 5
sin 5
(
1)
(
1)
sin
(
1)
1
2
sin
(
1).cos
1
2
sin
(
1).cos
1
x
x
x
x
dy
y
x
x
x
dx
dy
y
e
e
x
dx
dy
x
y
Ln
x
x
dx
x
y
x
Lny
Ln x
x Ln x
dy
x
x
Ln x
x
y dx
x
dy
x
y
x
Ln x
x
dx
x
dy
dx
2
sin
2
2
2
2
2
2
2
2
(
1)
sin
(
1).cos
1
sin
(1 cos ) cos
sin ( sin )
1 cos
(1 cos )
cos
cos
sin
1 cos
1
1 cos
(1 cos )
(1 cos )
x
x
x
x
Ln x
x
x
x
dy
x
x
x
x
y
x
dx
x
dy
x
x
x
x
dx
x
x
x
:
EXAM
2
sin 3 ,
3sin 6
2sin 3 cos3 (3)
2sin 3 cos3
sin 6
sin 6
(3)
3sin 6
dy
if y
x
prove that
x
dx
dy
x
x
dx
x
x
x
dy
x
x
dx
0
y
y
Show that y=cosx & y=sinx are solution of the eq.
:
EXAM
1)
cos
sin
cos
cos
cos
0
. .
2)
sin
cos
sin
sin
sin
0
. .
y
x
y
x
y
x
y
y
x
x
L H S
y
x
y
x
y
x
y
y
x
x
L H S

TRIGONOMETRIC FUNCTIONS
LEC : 6
03
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
0
y
y
Show that y =A sinx+ B cosx is solution of the eq.
:
EXAM
sin
cos
cos
sin
sin
cos
sin
cos
sin
cos
0
. .
y
A
x
B
x
y
A
x
B
x
y
A
x
B
x
y
y
A
x
B
x
A
x
B
x
L H S
تكامالت الدوال المثلثية
Trig. Fun. Integration
2
2
1
cos
sin
2
sin
cos
3
sec
tan
4
csc
t
5
sec tan
sec
6
sc
t
sc
u du
u
C
u du
u
C
u du
u
C
u du
co u
C
u
u du
u
C
c
u co u du
c
u
C
:
EXAM
2
cos
cos
2
2
2
2
2
4
1
cos5
sin 5
5
1
sec 3
tan 3
3
sin
sec 2
1 2sec 2
1
1 tan 2
1 tan 2
2 1 tan 2
2
sin
tan
cos
sec
cos
1
tan 3
(sec 3
1)
sec 3
1
tan 3
3
sin
x
x
x dx
x
C
x dx
x
C
e
x dx
e
C
x
x
dx
dx
Ln
x
C
x
x
u
u du
du
Ln
u
Ln
u
C
u
x dx
x
dx
xdx
dx
x
x
C
5
4
5
2
1
cos
sin
5
1
cos
sin
cos
5
cos
1
cos
csc cot
csc
sin
sin
sin
x
x dx
x
C
x
x dx
x
C
x
x
dx
dx
x
xdx
x
C
x
x
x

TRIGONOMETRIC FUNCTIONS
LEC : 6
03
MOHAMED SABAH AL TAEE \ MOSUL UNIVERSITY \ MATHEMATICS SCIENCES
2
( 1)
2
2
2
2
2
2
2
( 1)
cos
cos sin
sin
csc
sin
1
1
1 sin
1 sin
1 sin
1 sin
1 sin
1 sin
1 sin
1
sin
(
)
(sec
sin
cos
)
cos
cos
cos
cos
tan
tan
sec
1
x
dx
x
x dx
x
x
C
x
x
x
dx
dx
dx
x
x
x
x
x
x
dx
dx
x
x
x dx
x
x
x
x
x
x
x
C
2
4
(4)
1
(1)
2cos
2cos
,
sin 4
8
(2)
sin
2cos
&
2cos
(3)
csc
1
sin sec
cot
,
,
,
tan
cot
1
tan
1 csc
(4)
sec (sec
tan )
sec (tan
cos
dy
if y
x
x
show that
x
dx
show that y
x
x is solution to
y
y
x
y
y
x
dy
Find
to
dx
x
x
x
x
y
y
y
y
x
x
x
x
x
Find
x
x
x dx
x
x
x
2
)
sec
cos
sin 2
cos
1
1 cos 2
(1 sin
csc )
dx
x
dx
x
x
dx
x
dx
x
x
x dx
MOHAMED SABAH AL TAEE
M.SC / MATHEMATICS
E-MAIL : msmt_80@yahoo.com
2013 -2014
