
١١

Principles of Geophysics (250G)
(G
it P
ti
)
(Gravity Prospecting)
Compiled by
Compiled by
Prof. Dr. Abudeif A. Bakheit
Prof. Dr. Abudeif A. Bakheit
Email :
Email :
abakheit
abakheit57
57@yahoo.com
@yahoo.com
٢

Gravity Prospecting
•Gravitational methods are based on the measurement at
the surface of small variations in gravitational field
the surface of small variations in gravitational field.
•These variations are caused by lateral changes in the
distribution of mass in the earth's crust.
•Gravity method of prospecting is considered as a direct
method for the search of metallic minerals and in
method for the search of metallic minerals and in
studying the structure of a given region.
•It may be used as indirect method for the search of oil
and gas. In this case, structure favorable for the oil and
٣
gas accumulations are detected.

Principals of the Gravitational Field
The low of universal gravitation:
g
•According to Newton this law states that all
•According to Newton, this law states that all
bodies are attracted to each other with a force
th t i
ti
l t
th i
d
that is proportional to their masses and
inversely proportional to the square of the
distance between them.
•The law may be written as follows:
F = -f m
m / r
2
(1)
٤
F = -f . m
1
. m
2
/ r
………(1)

•Where “m
1
&m
2
” are the interacting point masses.
1
2
g p
“r” is the distance between them.
“f” is the universal gravitational constant.
•The constant “f” equals to the force of attraction
of two unit masses (m
1
= m
2
=1 gr.) separated by one
centimeter apart.
٥

I th CGS
t
f
it (
ti
t
In the CGS system of units (centimeter-gram-
second), “f” is equal to 6.67x10
-8.
•The dimensions of
“f”
can be obtained , when
,
the force is expressed in dynes
( cm.gr/sec
2
)
,
mass in grams
(gr )
and distance in centimeters
mass in grams
(gr.)
and distance in centimeters
(cm)
.
Then:
2
2
2
f = F . r
2
/m
1
.m
2
= cm. gr. cm
2
/ sec
2
. gr. gr
f = cm
3
. gr
-1
. sec
-2
٦
g

The Attraction acceleration
•The attraction force of the earth acting on a
The attraction force of the earth acting on a
unit mass laying on its surface can be obtained
from formula (1)
from formula (1).
•Considering that m
1
= 1 gr., m
2
= M ( the
Considering that m
1
1 gr., m
2
M ( the
mass of the earth) and “r” = R ( the radius of
the earth) Then the equation (1) leads to :
the earth). Then the equation (1) leads to :
F
1
= - f . M / R
2 ………………..
(2)
F
1
f . M / R
(2)
F
1
is known as the attraction acceleration
٧
1

The centrifugal acceleration
g
•The centrifugal force acts on the mass of the
earth as a consequence of its rotation around
earth as a consequence of its rotation around
its axis (Fig. 1).
•This force is proportional to the radius of
rotation “l” and the square of the angular
rotation l and the square of the angular
velocity “ω”
٨

•It can be written as:
P = l . ω
2
. m
When
m = 1 gr.
We obtain the centrifugal acceleration.
P = l . ω
2
•The component of “P” along “F ” will have the form:
•The component of “P” along “F
1
” will have the form:
P = l . ω
2
. cos φ …… (3)
φ
( )
Where “φ” is the latitude of the area at which gravity
is measured
is measured
٩

Pole P
1
= Zero ( cos 90 = 0)
P
1
= l . ω
2
. cos φ
Equator P
1
=l .
ω
2
( cos 0=1)
Fig.(1):Variation of centrifugal and attraction forces.
٠١

The Gravitational acceleration
e G a tat o a acce e at o
•The Gravitational acceleration “ g “ is the sum
of attraction acceleration F
1
and centrifugal
of attraction acceleration F
1
and centrifugal
acceleration P
1
.
g = F
1
+ P
1
g = -f . M /R
2
+ l . ω
2
. cos φ…..….…(4)
١١

•In the “CGS” units system , the acceleration
developed by a mass of one gram through the
ti
f
f
f
d
i t k
th
action of a force of one dyne is taken as the
unit of gravitational acceleration and is called
unit of gravitational acceleration and is called
“gal” ( in the honors of Galileo , who first
measured the force of gravity)
gal = dyne/gr = gr . cm/sec
2
. gr = cm/sec
2
٢١

I
it
ti
ll
it “
l”
•In gravity prospecting smaller units “mgal”
which is equal to 0.001 gal is always used.
which is equal to 0.001 gal is always used.
•The gravitational acceleration on the earth's
The gravitational acceleration on the earth s
surface varies between about 978 gals at the
equator and 983 gals at the poles.
٣١

Th
f t
d i
th
it ti
l
•The
factors
reducing
the
gravitational
acceleration at equator are:
•Centrifugal force varies from zero at the poles
g
p
to about 3.4 gals at the
equator. This
variation is the main cause of the normal
variation is the main cause of the normal
variation of the gravitational acceleration from
the equator to the poles
the equator to the poles.
•The flattening in the polar regions of the earth
•The flattening in the polar regions of the earth
also contribute to this variation.
٤١

Gravitational potential and equipotential surfaces
•Gravitational potential is a continuous function, the
derivatives of this function along the directions X, Y, and
Z are the projections of gravity in these directions
Z are the projections of gravity in these directions.
•The gravitational potential “W” is the sum of the
g
p
potentials of attraction “V” and centrifugal force “U”.
V
f
/
U
½
2
l
2
V = f . m / r
U = ½ . ω
2
. l
2
So
W = f m / r + ½ ω
2
l
2
(5)
So,
W = f . m / r + ½ . ω
2
. l
2
………..….(5)
٥١

Potential field properties
•
It can be easily shown that the function “W” satisfies
the following:
the following:
1. Its derivatives along certain directions are the
t
f
it ti
l
l
ti
l
th
components of gravitational acceleration along these
directions.
2. The change of potential (dW) when a mass is moved
from point to another (ds) is equal to the work
p
( )
q
expended in the movement.
3
F
i t l
t d
t id
tt
ti
th
3. For a point located outside attracting masses , the sum
of the second vertical derivatives of the attraction
t ti l l
th
f
th
l
di t
i
٦١
potential along the axes of orthogonal coordinates is
zero.

1- Its derivatives along certain directions are the
t
f
it ti
l
l
ti
l
th
components of gravitational acceleration along these
directions.
δW/δx = F1.cos (F1,x) + P1.cos (P1,x) = F1x+P1x
δW/δy = F1.cos (F1,y) + P1.cos (P1,y) = F1y+P1y
δW/δz = F1.cos (F1,z) + P1.Zero = F1z
Where F1x, F1y, F1z, P1x and P1y are projections of
the strength of the attraction and centrifugal forces
respectively
٧١
respectively.

2- The change of potential (dW) when a mass is moved
from point to another (ds) is equal to the work expended
from point to another (ds) is equal to the work expended
in the moment.
dW = F dS
dW = F
1
. dS
Where
“F
1
” is the field strength and
“dS” is the elementary movement of mass
“dS” is the elementary movement of mass
If th
i t i
d i
di
ti
di l
t th
•If the point is moved in a direction perpendicular to the
direction of the force “F” dW = 0. Such a surface is called
equipotential surface because of the constancy of
potential on it.
potential on it.
•In the case of displacement of a point mass along the line
٨١
of action of the force “F” , then
dW = F . ds

3- For a point located outside attracting masses , the sum
of the second
derivatives of the attraction potential
along the axes of orthogonal coordinates is zero
along the axes of orthogonal coordinates is zero
(Laplace`s theorem)
δ
2
v/δx
2
+ δ
2
v/δy
2
+ δ
2
v/δz
2
= zero
•When the point being attracted lies inside the attracting
masses, the Laplace equation leads to the equation
,
p
q
q
Poisson`s equation
δ
2
/δ
2
δ
2
/δ
2
δ
2
/δ
2
4 f
δ
2
v/δx
2
+ δ
2
v/δy
2
+ δ
2
v/δz
2
= - 4 π f σ
Where “σ” is the mass density
٩١
Where σ is the mass density

•If we are concerned with the gravitational potential,
W = f m / r + ½ l
2
. ω
2
•The Laplace`s equation will be :
2
2
2
2
2
2
2
δ
2
W/δx
2
+ δ
2
W/δy
2
+ δ
2
W/δz
2
= 2ω
2
And Poisson`s equation will be:
And Poisson s equation will be:
δ
2
W/δx
2
+δ
2
W/δy
2
+δ
2
W/δz
2
=-4 π f σ +2ω
2
٠٢

Normal Gravitational Field
o
a G a tat o a
e d
•The values of gravity depend on the latitudes.
When the earth is considered as an ideal
When the earth is considered as an ideal
ellipsoid , then the gravitational field is known
as the normal field .
١٢

•Clairaut`s theorem gave firstly the essential
correlation between the figure of the earth
correlation between the figure of the earth
and the distribution of gravity on it, given in
the form:
g = g
e
( 1 + β sin
2
φ – β` sin
2
2 φ )
β = 5/2 q- α , β` = 1/8 α
2
+1/4 α β
٢٢

Where:
g
is the equatorial gravity
g
e
is the equatorial gravity
φ
is the latitude of the locality.
α = a-b/a
is the flattening of the earth, a and b
are semimajor and semi minor axes of the earth.
q = ω
2
l / g
is the ratio of centrifugal force to
q
ω l / g
e
is the ratio of centrifugal force to
gravity at the equator.
٣٢

•If the earth is taken as triaxial ellipsoid a term
d
di
l
it d i
dd d t th l t
ti
depending on longitudes is added to the last equation
g = g
e
[1+ β sin
2
φ – β`sin
2
2φ + β``cos
2
φ cos
2
(λ- λ
o
)]
•The Clairaut theorem is employed to determine the
flattening of the earth from known values of gravity and
to calculate theoretical gravity values for points at known
to calculate theoretical gravity values for points at known
latitudes.
٤٢

•The formula with numerical coefficients describing the
gravitational field, is called the standard gravity
formula
formula.
•Only two formulae have found practical application,
Helmert`s and Cassins formulae.
٥٢

Th H l
` f
l f
bi i l lli
id i
•The Helmert`s formula for biaxial ellipsoid is;
g = 978.03 (1+0.005302 sin
2
φ – 0.000007 sin
2
2φ )
g 978.03 (1 0.005302 sin φ 0.000007 sin 2φ )
•The Helmert`s formula for triaxial ellipsoid is:
978 052 [ 1+0 005285 i
2
0 0000007 i
2
2 +
g =978.052 [ 1+0.005285 sin
2
φ– 0.0000007 sin
2
2φ +
0.000018 cos
2
φ cos2(λ- 17°)]
0 0000 8 cos φ cos (
7 )]
•The Cassins formula for biaxial ellipsoid is:
978 049 (1+0 0052884 i
2
0 0000059 i
2
2 )
٦٢
g =978.049 (1+0.0052884 sin
2
φ– 0.0000059 sin
2
2 φ)

Geoid
•It is an equipotential surface that coincide with the level
of oceans and seas.
•The direction of the force of gravity at any point on the
Geoid is normal to this surface
Geoid is normal to this surface.
٧٢
Fig.(3):The Geoid

•The geoid appears as a convenient surface for
l i
ll
d
l
f
i Fi (3)
relating all measured values of gravity Fig.(3).
I f t it i diffi lt t
th
l
f
•In fact it is difficult to compare the values of
gravity measured at different elevations; but
g
y
;
when they are reduced to the geoid surface,
they appear to be at one level which enable us
to compare them
to compare them
٨٢

Measurements of gravity acceleration
•There are three methods for determining gravity:
g
y
•There are three methods for determining gravity:
-The pendulum method.
p
-The measurement of velocity of a freely falling body.
- The weighing method (by means of a spring balance).
٩٢

1-The Pendulum method:
Th
d l
th d i th fi t
d
th d
•The pendulum method is the first used method
for the measurement of gravity (Fig.4).
Fig.(4): The pendulum
٠٣

The methods of gravity determination by using
The methods of gravity determination by using
the pendulum can be classified into:
•The absolute method, in which determinations
f
i
i
f
of gravity at any point from measured
oscillation periods and pendulum length is
done
(irrespective
of
the
place
of
measurement).
measurement).
•The used equation is (T =π √ l / g
)
١٣

•The relative method, in which the increment
f
i
f
i i i
i
of gravity from the initial point to the
observation point is determined from the
obse vat o
po t s dete
ed
o
t e
increment of the oscillation period of the
pendulum
•The used equation is (Δg/g
o
= 2ΔT/T
o
)
٢٣

2- Determination of gravity by measuring the
velocity of freely falling bodies:
•This method enables gravity “g” to be determined by
the formula:
the formula:
S = g . T
2
/ 2
g
Where
“S” is the path traversed by the freely falling body
“T” i h i
k
b h f lli
b d
“T” is the time taken by the falling body
٣٣

3- Gravity determination by weighing:
•This method is based on compensating the force F1= mg
by a mass raised in the field of force by the elastic
by a mass raised in the field of force by the elastic
strength of a wire string or pressure of an elastic gas.
•Consider a mass “m” is suspended from an elastic
spring having an initial length “l ” and loaded length
spring having an initial length l
o
and loaded length
“l”. Then , according to Hooke`s law,
mg = τ ( l l )
mg = τ ( l – l
o
)
Where “ τ “ is the stretching of the spring
٤٣
Where τ is the stretching of the spring.

•From the last relation we find that the increment of
•From the last relation we find that the increment of
length is proportional to the change of gravity, then:
m Δg = τ Δ l
Δg = τ / m Δ l
g
Δg = K Δ l
Where “K” is the spring constant
•This method is always relative, i.e. all instruments
for measuring gravity by weighing (gravimeters)
enable the variations of gravity to be measured with
enable the variations of gravity to be measured with
respect to some initial value.
٥٣

Reduction of Gravity Data
•The gravity values cannot be compared in the form in
which they are obtained.
y
•The corrections of obtained gravity data enable it to be
reduced to a certain standard surface (sea level) for
reduced to a certain standard surface (sea level) for
comparison.
-The observed values of gravity depend on:
•The location of the station on the earth's surface,
i.e. its coordinates and elevation.
•The density distribution within the earth.
•The topography of the surrounding localities
٦٣
•The topography of the surrounding localities

•To obtain the part of the observed gravity
p
g
y
values relating to the density variations that
interest us we divide its values into;
interest us, we divide its values into;
- A part that varies regularly reflecting the
p
g
y
g
figure of the ideal earth,
- And into anomalies that reflect the internal
structure of the upper part of the earth.
pp
p
٧٣

•The actual value of gravity is observed on the surface
of the earth at point (A), the standard value is given for
point (B) on the surface of the Geoid (Fig. 5).
point (B) on the surface of the Geoid (Fig. 5).
٨٣
Fig.(5):Diagram of surfaces in gravity reductions

•In order to obtain the gravity it is necessary
to reduce the observed value to the surface of
the geoid.
g
•The
gravity anomaly is obtained by
subtracting the standard value for the ideal
earth from the actual gravity value observed
g
y
at the station
Δg = g
ob
– g
th
٩٣

1- Drift correction:
•All gravity instruments have certain amount
f d ift
ti
i ti
d
t th t th
i
of drift or time variation due to that the spring
and the associated mountings are not perfectly
stable.
Th
h
i
t
di
•These may cause changes in meter reading
which are larger than those due to the small
gravity differences being measured.
The field
ork m st be cond cted in a
a
•The field work must be conducted in a way
that this drift can be determined and
٠٤
corresponding corrections made.
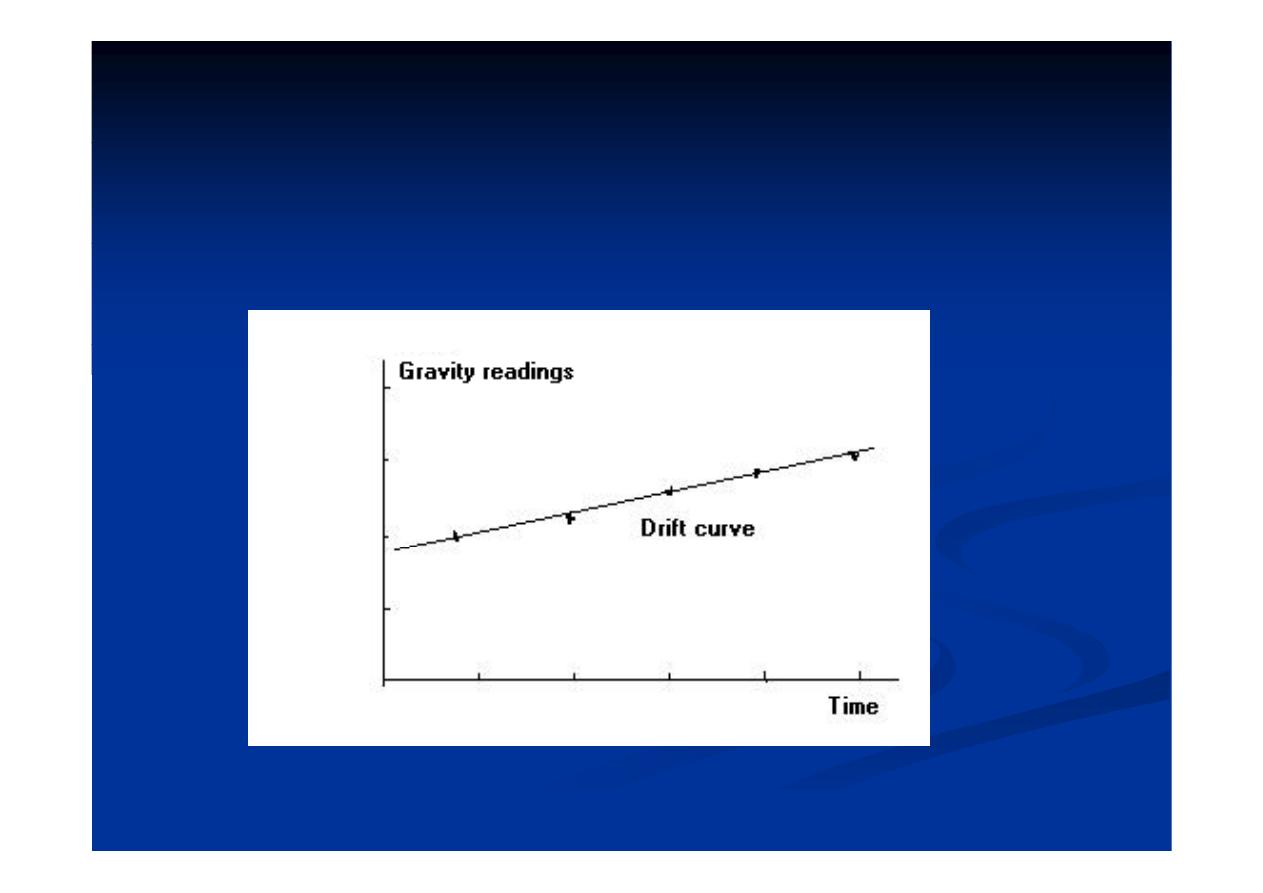
•Drift
curves
are
obtained
by
repeated
y
p
occupation of a single field station at intervals
during the day (see Fig. 6).
during the day (see Fig. 6).
١٤
Fig.( 6 ):Gravimeter drift curve

2 Earth Tidal Correction:
2- Earth Tidal Correction:
•The changes in gravity caused by movement of
g
g
y
y
the sun and moon have amplitudes as large as
0 3 mgal They depend on latitude and time
0.3 mgal. They depend on latitude and time.
•The changes in gravity can be calculated
g
g
y
theoretically for any time and place.
•It is not practice to obtain the correction
directly , this is because the variation is smooth
y ,
and relatively slow., So it is easily taken out in
the instrument drift correction
٢٤
the instrument drift correction.

3 El
ti
C
ti
3- Elevation Correction:
•Correction to gravity values which must
Correction to gravity values which must
be made due to the differences in elevations
t k
f t
ff t
take care of two effects:
A- The free air effect
A- The free air effect
B- The Bouguer effect
g
٣٤
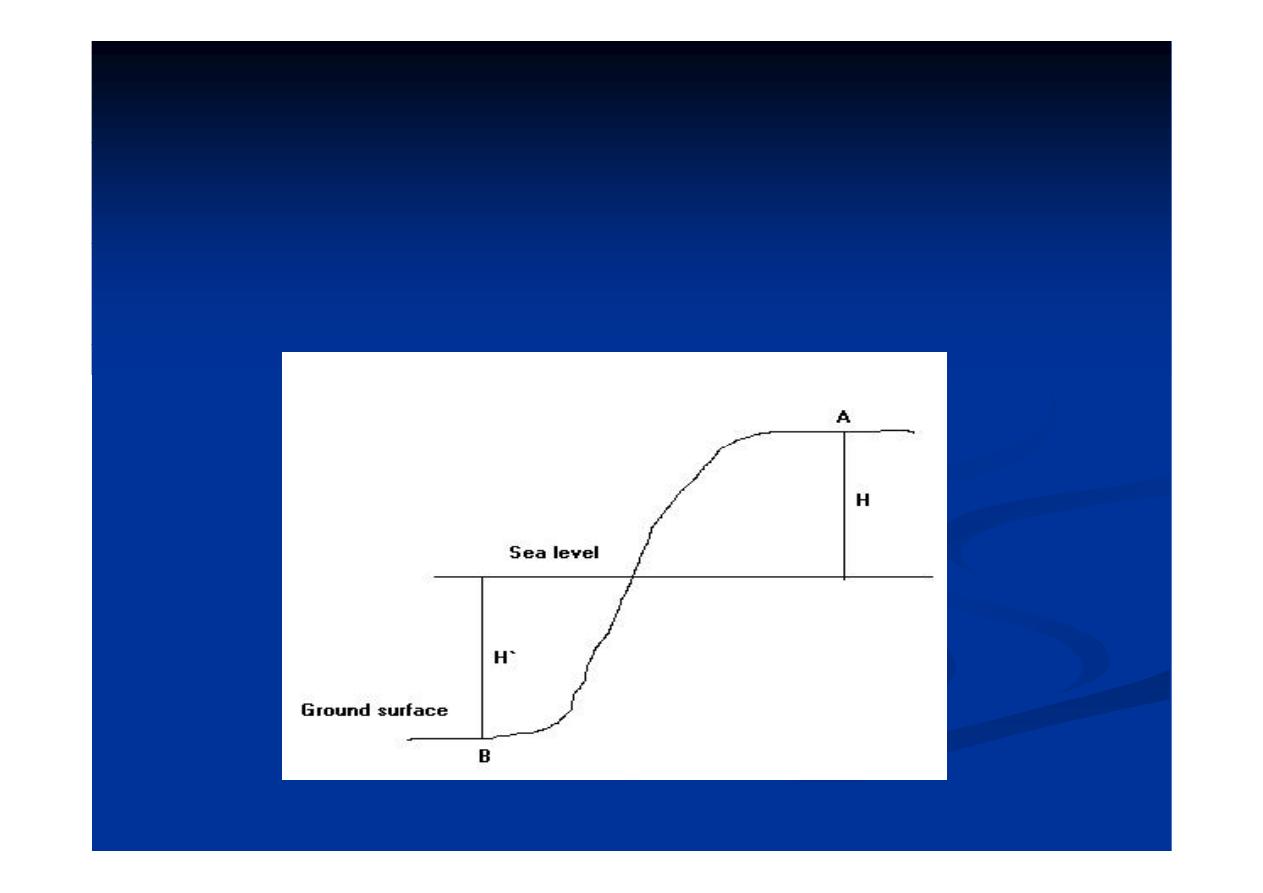
A- Free air correction:
Th
ti l d
f
it
ith i
f
•The vertical decrease of gravity with increase of
elevation is taken care of by the free-air correction. The
l
f f
i
ti
“d f”
b
l l t d
value of free-air correction “dgf” can be calculated
(Fig. 7) :
dg
F
= - 2 g / R H ……….(42)
٤٤
Fig. (7 ):Free-air effect

•If we take;
-The mean radius of the earth “R”=6.367 x
10
8
cm, gravity at sea level and at latitude 45
10 cm, gravity at sea level and at latitude 45
g = 980.629 gals, and the elevation H = 1 cm ,
dg
F
= - 2 x 980.629/6.367x10
8
=
0 3086 10
5
l/
-0.3086x10
-5
gal/cm =
- 0.3086 mgal / m = - 0.09406 mgal / ft
٥٤

i
i
•The corrections can be made to any arbitrary
reference or datum level, or it may be made to
sea level.
Si
i
l i l hi h
l
i
•Since a station at a relatively higher elevation
has a lower gravity (because it is farther from
the center of the earth), the correction must be
added to it.
added to it.
• While the corrections must be subtracted
from stations at lower elevations than the
reference level (Fig. 7).
٦٤
reference level (Fig. 7).

B- Bouguer Correction:
•The Bouguer correction take care to the attraction of
the material between a reference elevation and that of
the material between a reference elevation and that of
the individual station.
•Considering the material as an infinite horizontal
slab, the gravity attraction for a point on the surface
slab, the gravity attraction for a point on the surface
of a slab of thickness “h” and density “σ “(Fig. 8) is:
d
2
f
h
dg
B
= 2 π f σ h
Which for f = 6.6732 x 10
-8
gives:
Which for f 6.6732 x 10
gives:
dg
B
= 0.04193 x σ mgal/ m
٧٤
= 0.01278 x σ
mgal/ ft
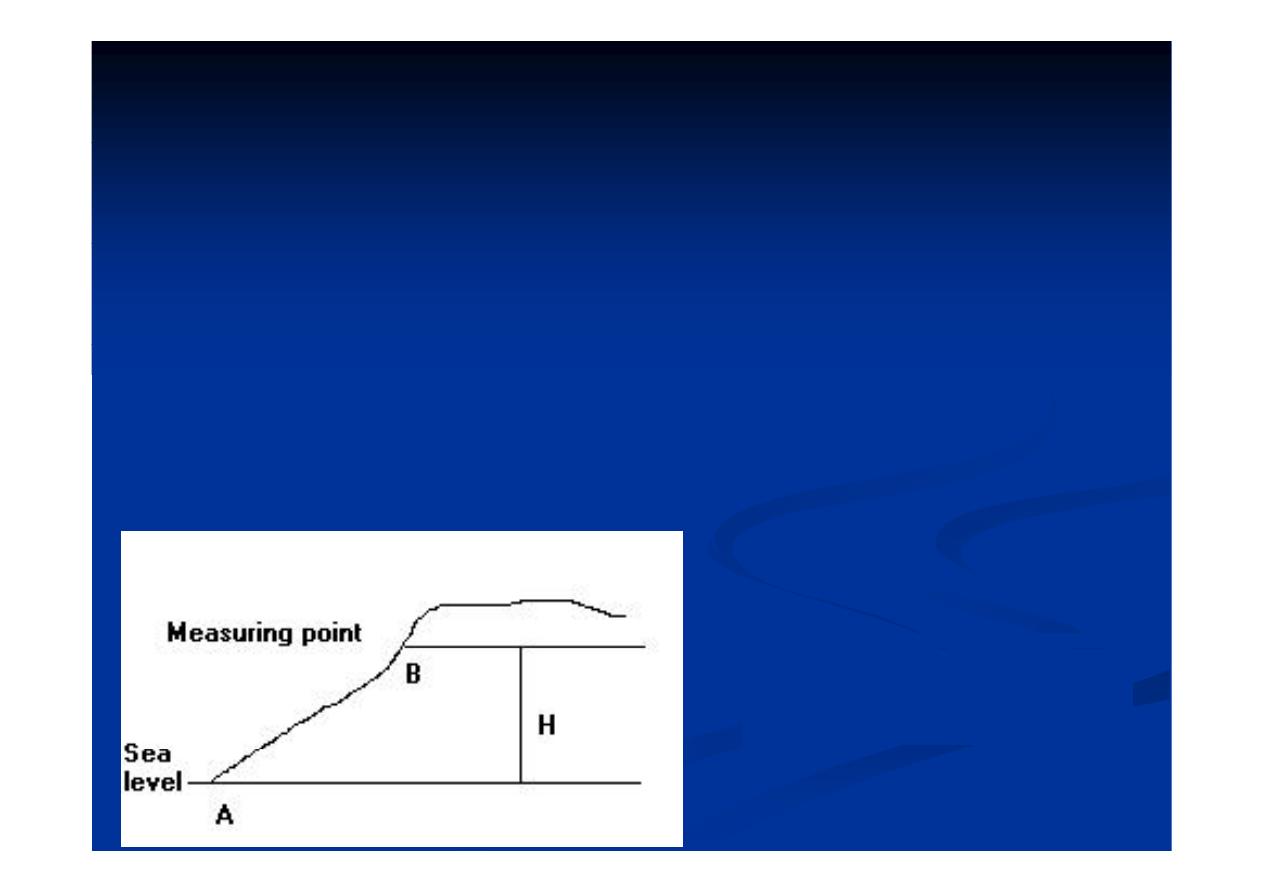
•In a station “B” higher than the reference elevation “A”
its gravity value is increased because of the attraction
, its gravity value is increased because of the attraction
of the slab of material between it and the reference level
and the correction is subtracted (Fig 8)
and the correction is subtracted (Fig. 8).
•If the station is lower than the reference elevation , its
gravity value is decreased because of the lake of
attraction of the absent material between it and the
reference level and the correction is added.
Fig.(8):The Bouguer
gravity effect
٨٤
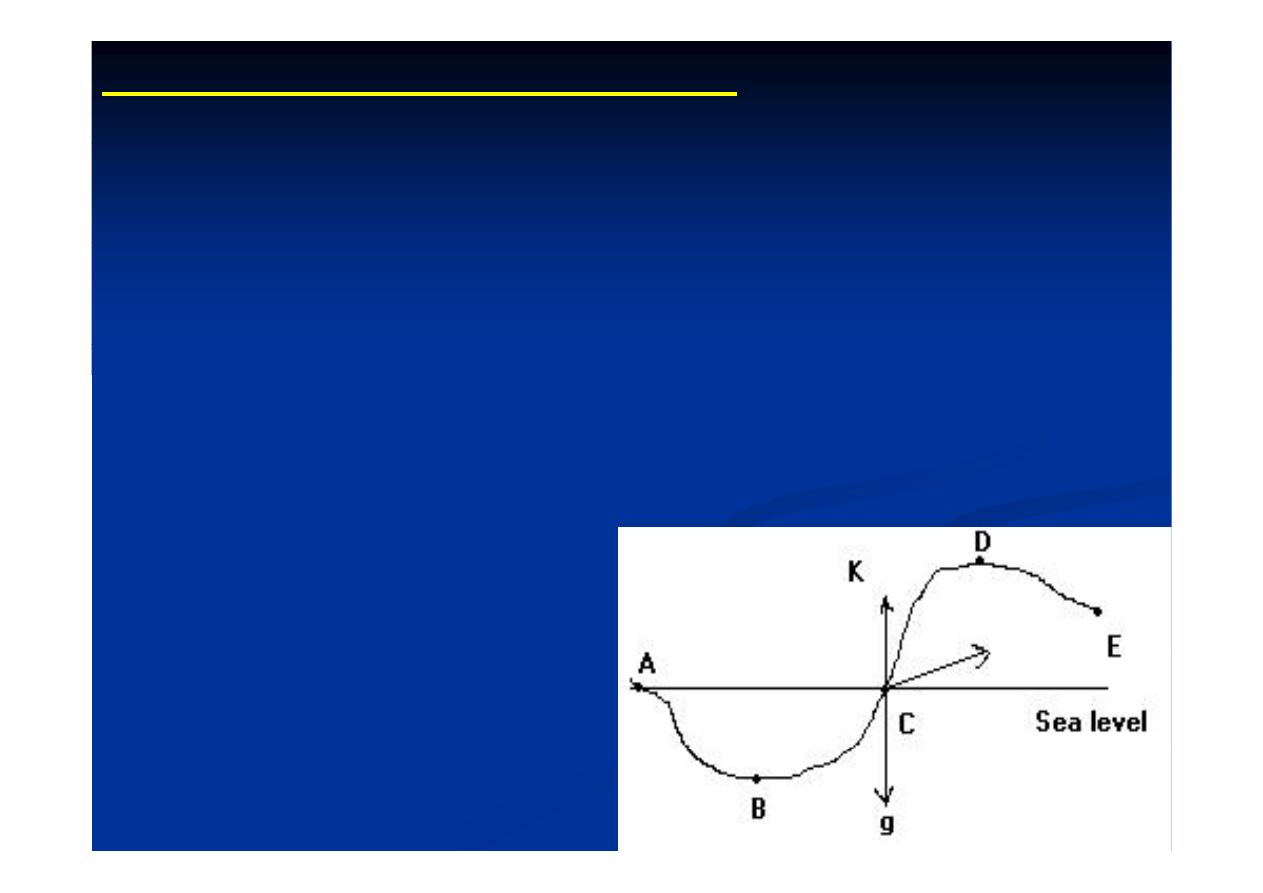
4-Topographic (terrain) correction:
T
hi
ti
l
d
th
b
d
•Topographic correction always reduce the observed
gravity value irrespective of whether there is a rise or a
d
i
th
it
t ti
depression near the gravity station.
•
The presence of extra mass “CDE” lying higher than the
p
y g
g
observation point will give rise to an additional force
directed towards the mass. The vertical component “CK”
p
of this force will reduce the value of “g” (Fig. 9).
Fig.(9): Gravity effect
of relief
٩٤
of relief

•The lake of mass in the region “ABC” will also bring
down the value of “g” with respect to the value that
would be obtained if the entire region below the point
of observation were filled
•In practice topographic corrections are calculated
•In practice topographic corrections are calculated
from zone charts, nomograms and terrain correction
tables that enable us to fined the correction from
tables, that enable us to fined the correction from
topographic maps for any point at which gravity is
measured
measured.
٠٥

Interpretation of Gravity Data
•The interpretation of gravity data involves qualitative
d
tit ti
i t
t ti
and quantitative interpretation.
1-Qualitative Interpretation of Gravity Data:
•The result of gravity surveys (after the corrections) is
the Bouguer gravity anomaly map.
the Bouguer gravity anomaly map.
•The objective of gravity interpretation is to translate
j
g
y
p
gravity data to geological terms, to give the features of the
subsurface structures
subsurface structures.
•From the various characteristics of the map, the
١٥
amplitude, shape and the sharpness of the anomalies.

•The location and form of the structure which
•The location and form of the structure which
produce the gravity disturbance can be deduced.
•The
magnitude of a gravity anomaly is
important because the size of an anomaly is
important because the size of an anomaly is
proportional to the size of the structure and the
d
it
t
t
density contrast.
•The direction of elongation of iso anomaly
•The direction of elongation of iso anomaly
contours of gravity suggests the direction of the
l
th
f
th
t
t
i
th
length
of
the
structure
causing
them.
Concentrated masses produce approximately
٢٥
circular anomaly patterns.

2-Quantitative Interpretation of Gravity Data
I i
h i
i
f
i
d
i ld
It is the interpretation of gravity data to yield
the numerical characteristics of the body being
studied (depth and dimensions).
Th
i
i
i
i
f
i
d
•The quantitative interpretation of gravity data
involves:
A - Anomaly separation and filtration.
B- Calculation of gravity effects of different
causative bodies
٣٥
causative bodies.

REFERENCES
REFERENCES
-Nettleton, L.L., (1976):
Gravity and Magnetic in oil
prospecting. McGraw Hill Book Co., New York: 464P
Sazhina N and Grushinsky N (1971):
Gravity
-Sazhina, N. and Grushinsky, N. (1971):
Gravity
Prospecting. Mir Publishers, Moscow, 491 P.
-Dobrin and Savit (1986):
Introduction to geophysical
prospecting 4th Ed. ,Mc Graw Hill book company,
New York, 867p.
Telford W M Gildart L P Sheriff R E and Keys
-Telford, W. M., Gildart, L. P., Sheriff, R. E., and Keys,
D. A. (1990):
Applied Geophysics , Cambridge
University Press 770 P
٤٥
University Press, 770 P.

٥٥
