
1
First stage
physics
Lec-2
9/12/2015
.د
تيماء
Forces on and in the Body
Forces in the body
1. Muscular forces that cause the blood to circulate and the lungs to take in air .
2. Molecular forces (bone , calcium atom ) .
3. Electric forces .
4. Gravitational forces .
Gravitational forces
Newton laws state that : there is a force of attraction between any two objects ( our weigh
is due to the attraction between the earth
and our bodies )
Gravitation force
F = mg
Where F is the force of gravity
m is the mass
g is the acceleration due to the gravity
Medical effects of gravitation forces
Medical effects of gravitation forces is the formation of varicose veins in the legs as the
venous blood travels against the force of gravity on its way to the heart , and the second
effects is on the bone .If a person becomes weightless such as in orbiting satellite , he
may lose bone mineral .Long term bed rest removes much of the force of the body weight
from bones .
Forces on the Body
1. Static force : where the body is in equilibrium.
2. Dynamic force : where the body is accelerated .
1.Static Force
When objects stationary ( static ) they are in state of equilibrium .
The sum of the forces in any direction is equal to zero .
The force is a vector quantity
2
Torque
Torque = force x length
The sum of the torque's about any axis is equals to zero .
For example :
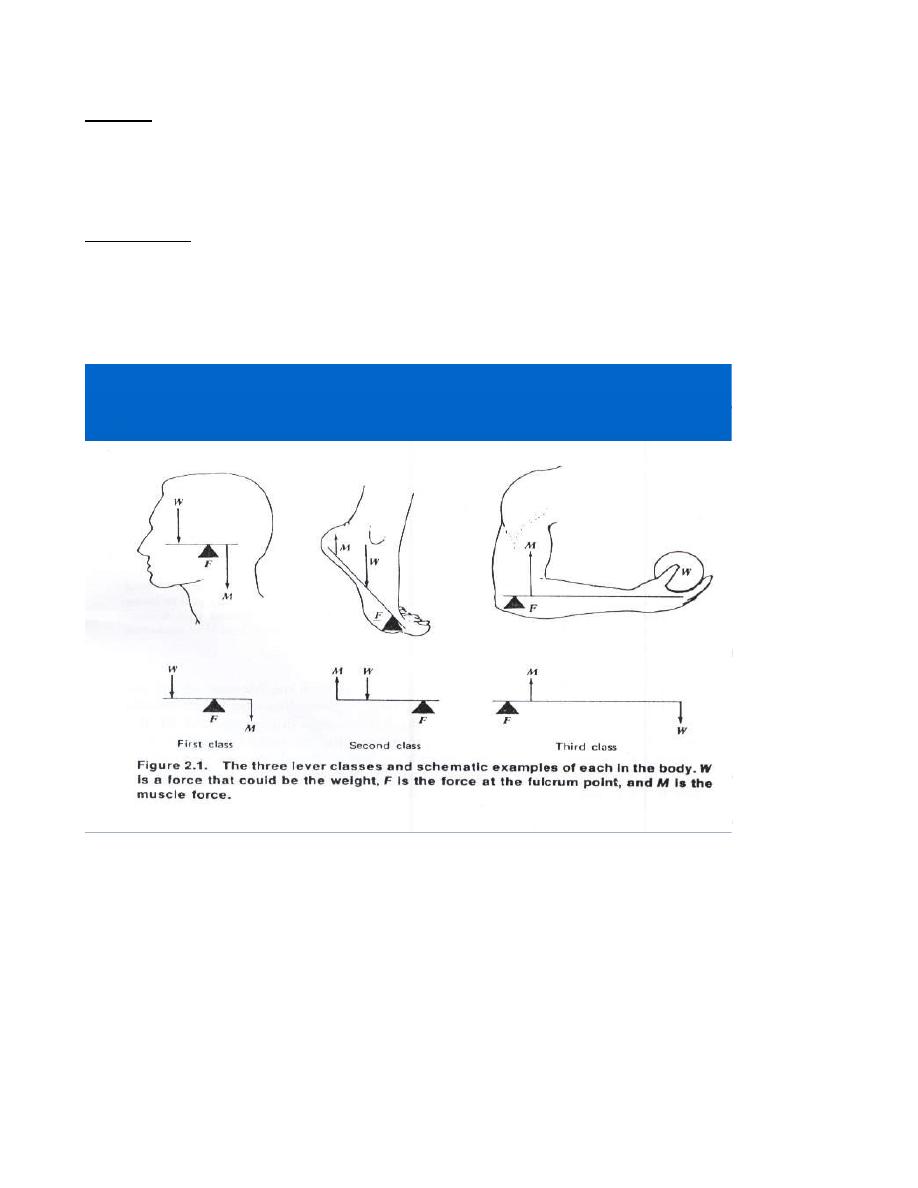
In the body , many of the muscles and bones systems acts as levers .
Levers are classified as first , second, and third - class systems as shown in figure 1.
Figure 1
Figure 1
3
Example of a levers system in the body
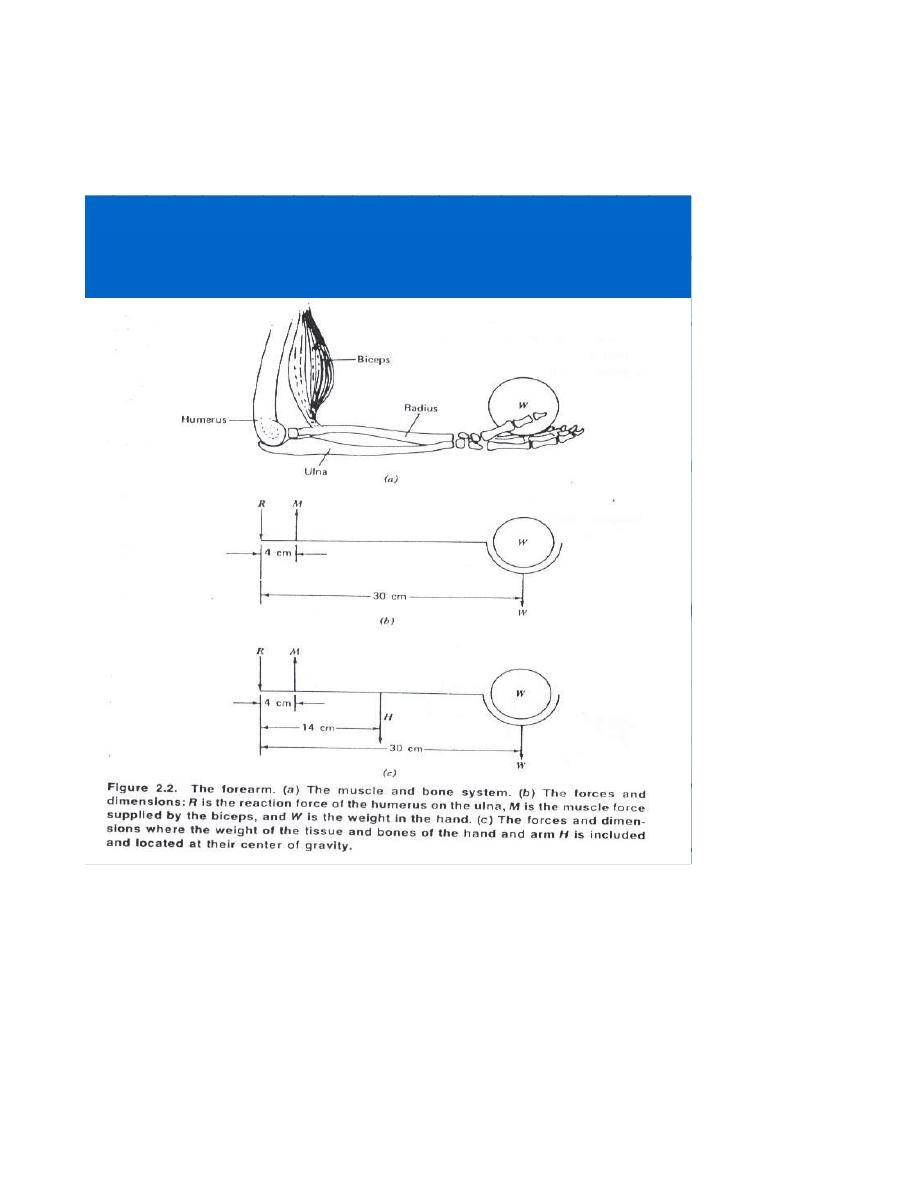
A simple class of a levers in the body is the case of the biceps muscle and the radius bone
acting to support a weight W in the hand , as shown in figure 2.
Figure 2
Figure 2

4
For example , we can find the force supplied by the biceps, if we sum the torque's about
the pivot point at the joint (figure 2b ).
There are only two torque's ;
1.due the weight W acting clock wise ,
for example: torque =Lenght(L) x force(W)
Let L =30 cm
Torque = 30W
2. produced by the muscle force M,
which is counterclockwise,
for example: torque = L x M
Let L=4 cm
Torque = 4 M
;
when the arm is in equilibrium , we find that
4M = 30W
where M is the muscular force ,
W is weight of the body
M = 7.5 W
If W = 20 Newton
M=7.5 x 20
M = 15 Newton
In case of finding the center of gravity for the weight of the forearm and hand H , we consider
all the weight at point as shown in figure2c.
For example
a typical value of hand is H = 15 N
By assuming torque's about the joint we obtain
4 M = 30 W + 14 H
4 M/100 =( 30 W + 14 H )/100
M =7.5 W + 3.5 H
W = weight = 20 N
H = hand weight = 15 N
M =7.5 W + 3.5 H
M =7.5 x 20 + 3.5 x 15
M = 15 + 52.5
M = 67.5 Newton

5
Frictional Force
Friction and energy loss due to friction appear every day in our life .
The maximum force of friction F is
F = µ N
Where N is a Normal force .
µ Is the coefficient between
the two surfaces
The value of µ depends upon the two materials in contact , and it is essentially
independent of the surface area , as shown in Table 1.
Table 1
Table 1
When a person is walking , as the heel of the foot touches the ground a force is
transmitted from the foot to the ground (figure 3).

6
Figure 3
Figure 3
we can resolve this force into horizontal and vertical components . the vertical reaction
force is applied by the surface and is labeled
N (normal force ) . the horizontal reaction component must be applied by frictional
forces, as shown in figure 3
Measurements have been made of the horizontal force component of the heel as it strikes
the ground when a person is walking , and it has been to be = 0.15 W ,
Where W is the person ´s weight .
The frictional force is large enough both when the heel touches down and when the toe
leaves the surface to prevent a person from slipping .this how large the frictional force
must be in order to prevent the heel from slipping .The coefficient of friction in bone
joints is very small (Table 1) .
If a disease of the joint exists, the friction may become large .
The synovial fluid in the joint is involved in the lubrication .
The saliva we add when we chew food acts as a lubricant (to reduce the friction force ).
For example , if you swallow a piece of dry toast you become painfully aware of this lack
of lubricant .

7
Dynamics force
According to second law of Newton , the force is equal
F = ma
momentum = mv
The change in momentum Δ(mv) over a short interval of time is
F = Δ(mv )
Δt
For dynamic force
Example :1
A 60 Kg person walking at 1 m/sec bumps into a wall and stops in a distance of 2.5
cm in about 0.05 sec . what is the force developed on impact ?
Δ(mv) = (60 Kg ) (1m/sec) – (60 Kg ) ( 0 m/sec)
= 60 Kg m/sec
the force developed on impact is
F = Δ(mv )
Δt
F = 60Kg m/sec
0.05
F = 1200 Kg m/sec²
F = 1200 Newton
Example::2
Q.2 a. A person walking at 1 m/sec hits his head on a steel beam . Assume his head
stops in 0.5 cm in about 0.01 sec. If the mass of his head is 4Kg ,What is the force
developed ?
Δ(mv) = (4Kg)(1m/sec)-(4Kg)(0m/sec)
= 4 Kg m/sec
F = Δ(mv )
Δt
F = 4 kg m/sec
0.01
F = 400 Newton

8
Q.2 b if the steel beam has 2 cm of padding and Δt is increased to 0.04 sec , what
is the force developed ?
F = Δ(mv)
Δt
F = ( 4 Kg m/sec)
0.o4 sec
F = 100 Newton

9
Solutions
Force in and on the body
Q.5 A muscle is capable of supplying a maximum force per unit area
7
of 3.1 x 10 N/m² . If the cross sectional area muscle is 20 cm²,
what is the maximum force that can be supplied at the muscles normal
length ?
7
force = 3.1 x 10 N/m²
area -
4
cross sectional area = 20 x 10 m²
-
4
7
force = (20 x 10 m²)(3.1 x 10 N/m²)
4
maximum force = 6.2 x 10 N
Q.6 The action of chewing involves a third –class lever system . figure A
shows the jaw and chewing muscle ;figure B is the lever diagram.
M is the force supplied by the chewing muscles that close the jaw
about the fulcrum F . W is the force exerted by the front teeth .
a . If l2 = 3l1 and W = 100 N find M.
b. If the front teeth have a surface area of 0.5cm² in contact with an
apple , find the force per unit area for part A.
Answer Q6
Q6.a. The sum of the torques about F = 0 .
Ml
1
–W(1
1
+l
2
) =0
Where l
2
= 3l
1
Ml
1
= W(l
1
+3l
1
)
M = 4 W
M = 400 N
6
b. 100 N = 2 x 10 N / m²
-
4
0.5 x 10 m²
Figure 1
10
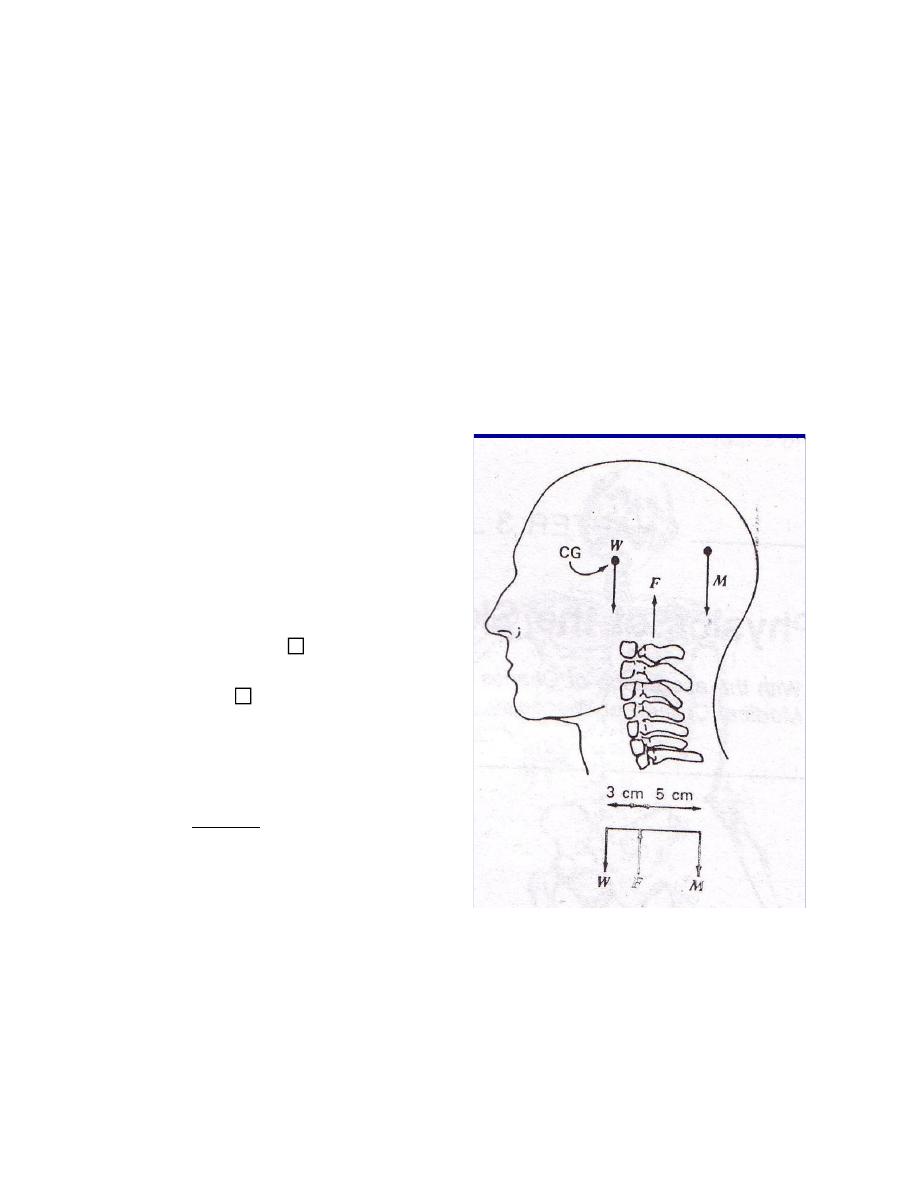
Q. 7 One first class lever system involves the extensor muscle ,
which exerts a force M to hold the head erect (figure2) : the
force W of the weight of the head , located at its center of
gravity , lies forward of the force F exerted by the first
cervical vertebra . the head has a mass of about 4 kg or is
about 40N.
a. Find F and M .
b. If the area of the first cervical vertebra, which the head rests
on ,is 5 cm² , find the stress on it .
c . What is this stress for a 70 Kg person standing on his head ?
how does this stress compare with the maximum compression
8
strength for bones ( 1.7 x10 N/m²) .
The distance between F and W =3 cm
The distance between F and M =5 cm
3W = 5M
M = 0.6 W
W= 4 kg
Or W= 40 N
M= o.6 x 40 = 24 N
F = W + M
F= 64 N
The stress is 64/5 x 10ˉ
stress = 1.28 x 10
N/m²
The mass of body is 70 kg
The mass of head is 4 kg
In standing position = 70 – 4 = 66 kg
The stress = 66 x 9.8
-4
5x 10
6
The stress = 1.3 x 10 N/m²
Which is less 1 % of the maximum compression strength .
Figure 2

11
Q.8 A 50kg person jumping from a height of 1 m is travelling at 4.5 m/sec just
prior to landing . Suppose she lands on a pad and stops in 0.2 sec .
What maximum force will she experience ?
• F = Δ (mv )
• Δt
• F = 50x 4.5
• 0.2
• F =1125 N
Q. 9 Estimate the force on the forehead in
figure 2 if the mass of the head is
4 kg , its velocity is 15 m/sec ,
and the padded dash stops it in
0.002 sec .
F = Δ (mv )
Δt
F = 4 x 15
0.002
4
F = 3 x 10 N
