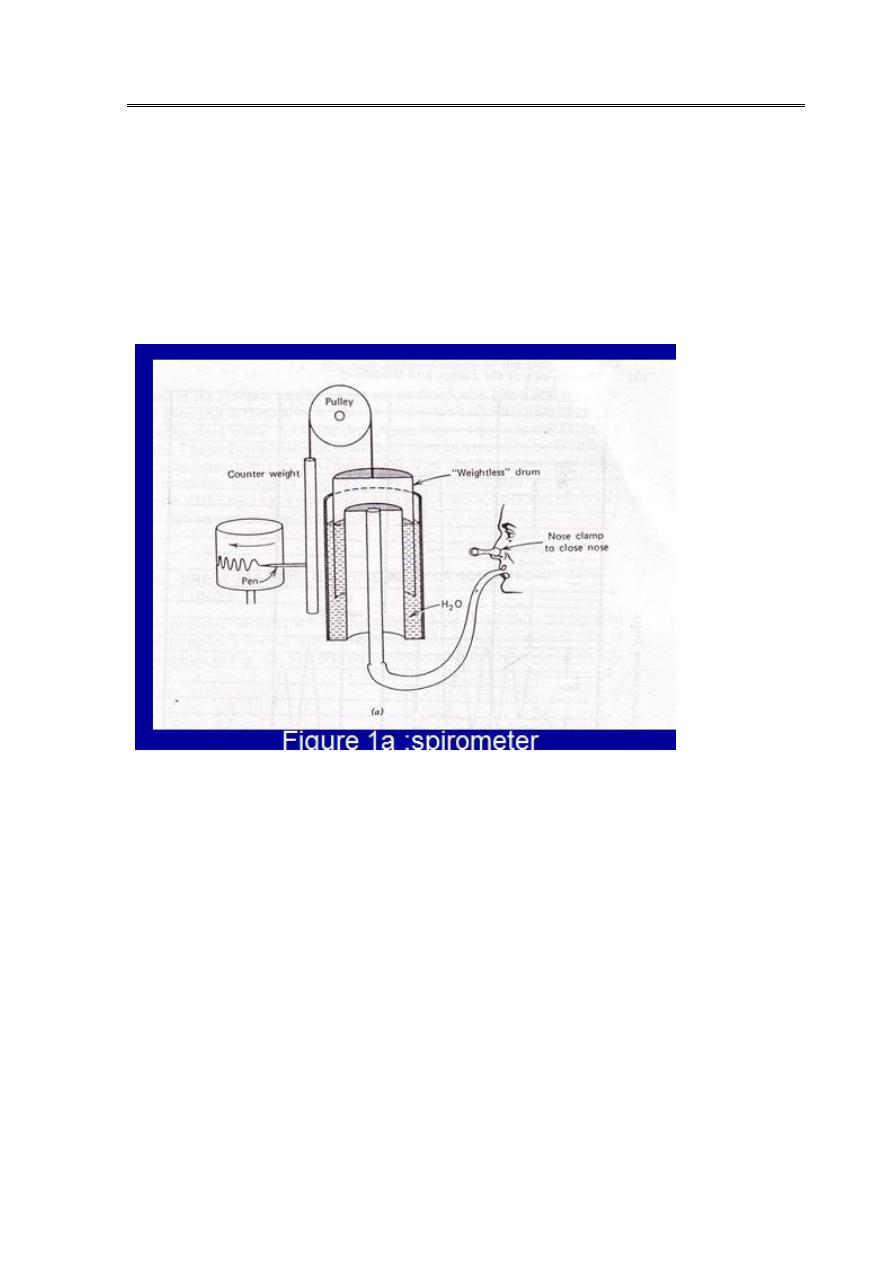
first stage
Medical Physics
Lec-7
4/1/2016
د.تيماء
M
M
e
e
a
a
s
s
u
u
r
r
e
e
m
m
e
e
n
n
t
t
o
o
f
f
L
L
u
u
n
n
g
g
s
s
V
V
o
o
l
l
u
u
m
m
e
e
T
T
h
h
e
e
s
s
p
p
i
i
r
r
o
o
m
m
e
e
t
t
e
e
r
r
i
i
s
s
a
a
n
n
i
i
n
n
s
s
t
t
r
r
u
u
m
m
e
e
n
n
t
t
u
u
s
s
e
e
d
d
t
t
o
o
m
m
e
e
a
a
s
s
u
u
r
r
e
e
a
a
i
i
r
r
f
f
l
l
o
o
w
w
i
i
n
n
t
t
o
o
a
a
n
n
d
d
o
o
u
u
t
t
t
t
h
h
e
e
l
l
u
u
n
n
g
g
s
s
a
a
n
n
d
d
r
r
e
e
c
c
o
o
r
r
d
d
i
i
t
t
o
o
n
n
a
a
g
g
r
r
a
a
p
p
h
h
o
o
f
f
v
v
o
o
l
l
u
u
m
m
e
e
v
v
e
e
r
r
s
s
u
u
s
s
t
t
i
i
m
m
e
e
.
.
T
T
h
h
i
i
s
s
i
i
n
n
s
s
t
t
r
r
u
u
m
m
e
e
n
n
t
t
c
c
o
o
n
n
s
s
i
i
s
s
t
t
s
s
o
o
f
f
a
a
c
c
o
o
u
u
n
n
t
t
e
e
r
r
b
b
a
a
l
l
a
a
n
n
c
c
e
e
d
d
b
b
e
e
l
l
l
l
f
f
r
r
e
e
e
e
t
t
o
o
m
m
o
o
v
v
e
e
i
i
n
n
t
t
h
h
e
e
v
v
e
e
r
r
t
t
i
i
c
c
a
a
l
l
p
p
l
l
a
a
n
n
e
e
,
,
a
a
s
s
s
s
h
h
o
o
w
w
n
n
i
i
n
n
f
f
i
i
g
g
u
u
r
r
e
e
(
(
1
1
)
)
.
.
I
I
t
t
h
h
a
a
s
s
a
a
w
w
a
a
t
t
e
e
r
r
–
–
s
s
e
e
a
a
l
l
s
s
o
o
t
t
h
h
a
a
t
t
i
i
t
t
f
f
o
o
r
r
m
m
s
s
a
a
n
n
a
a
i
i
r
r
t
t
i
i
g
g
h
h
t
t
c
c
h
h
a
a
m
m
b
b
e
e
r
r
o
o
f
f
v
v
a
a
r
r
i
i
a
a
b
b
l
l
e
e
v
v
o
o
l
l
u
u
m
m
e
e
.
.
T
T
h
h
e
e
c
c
h
h
a
a
n
n
g
g
e
e
s
s
i
i
n
n
v
v
o
o
l
l
u
u
m
m
e
e
o
o
f
f
t
t
h
h
i
i
s
s
c
c
h
h
a
a
m
m
b
b
e
e
r
r
a
a
r
r
e
e
r
r
e
e
c
c
o
o
r
r
d
d
e
e
d
d
o
o
n
n
a
a
c
c
h
h
a
a
r
r
t
t
.
.

W
W
h
h
e
e
n
n
b
b
r
r
e
e
a
a
t
t
h
h
i
i
n
n
g
g
t
t
h
h
r
r
o
o
u
u
g
g
h
h
t
t
h
h
e
e
m
m
o
o
u
u
t
t
h
h
p
p
i
i
e
e
c
c
e
e
i
i
n
n
t
t
o
o
t
t
h
h
e
e
s
s
p
p
i
i
r
r
o
o
m
m
e
e
t
t
e
e
r
r
w
w
i
i
t
t
h
h
a
a
n
n
o
o
s
s
e
e
c
c
l
l
i
i
p
p
a
a
p
p
p
p
l
l
i
i
e
e
d
d
,
,
t
t
h
h
e
e
a
a
i
i
r
r
i
i
n
n
t
t
h
h
e
e
l
l
u
u
n
n
g
g
s
s
,
,
a
a
i
i
r
r
p
p
a
a
s
s
s
s
a
a
g
g
e
e
a
a
n
n
d
d
t
t
h
h
e
e
s
s
p
p
i
i
r
r
o
o
m
m
e
e
t
t
e
e
r
r
i
i
s
s
a
a
c
c
l
l
o
o
s
s
e
e
d
d
s
s
y
y
s
s
t
t
e
e
m
m
s
s
.
.
T
T
h
h
u
u
s
s
,
,
w
w
h
h
e
e
n
n
t
t
h
h
e
e
l
l
u
u
n
n
g
g
s
s
v
v
o
o
l
l
u
u
m
m
e
e
i
i
n
n
c
c
r
r
e
e
a
a
s
s
e
e
s
s
i
i
n
n
t
t
h
h
e
e
i
i
n
n
s
s
p
p
i
i
r
r
a
a
t
t
i
i
o
o
n
n
t
t
h
h
e
e
v
v
o
o
l
l
u
u
m
m
e
e
o
o
f
f
g
g
a
a
s
s
i
i
n
n
t
t
h
h
e
e
s
s
p
p
i
i
r
r
o
o
m
m
e
e
t
t
e
e
r
r
i
i
s
s
r
r
e
e
d
d
u
u
c
c
e
e
d
d
,
,
a
a
n
n
d
d
w
w
h
h
e
e
n
n
t
t
h
h
e
e
l
l
u
u
n
n
g
g
v
v
o
o
l
l
u
u
m
m
e
e
d
d
e
e
c
c
r
r
e
e
a
a
s
s
e
e
s
s
i
i
n
n
e
e
x
x
p
p
i
i
r
r
a
a
t
t
i
i
o
o
n
n
,
,
t
t
h
h
e
e
s
s
p
p
i
i
r
r
o
o
m
m
e
e
t
t
e
e
r
r
v
v
o
o
l
l
u
u
m
m
e
e
i
i
n
n
c
c
r
r
e
e
a
a
s
s
e
e
s
s
.
.
T
T
i
i
d
d
a
a
l
l
v
v
o
o
l
l
u
u
m
m
e
e
:
:
i
i
s
s
d
d
e
e
f
f
i
i
n
n
e
e
d
d
a
a
s
s
t
t
h
h
e
e
a
a
m
m
o
o
u
u
n
n
t
t
o
o
f
f
a
a
i
i
r
r
i
i
n
n
o
o
r
r
o
o
u
u
t
t
p
p
e
e
r
r
b
b
r
r
e
e
a
a
t
t
h
h
.
.
I
I
n
n
s
s
p
p
i
i
r
r
a
a
t
t
o
o
r
r
y
y
r
r
e
e
s
s
e
e
r
r
v
v
e
e
v
v
o
o
l
l
u
u
m
m
e
e
.
.
:
:
i
i
s
s
t
t
h
h
e
e
a
a
d
d
d
d
i
i
t
t
i
i
o
o
n
n
a
a
l
l
a
a
m
m
o
o
u
u
n
n
t
t
o
o
f
f
a
a
i
i
r
r
w
w
h
h
i
i
c
c
h
h
c
c
a
a
n
n
b
b
e
e
i
i
n
n
s
s
p
p
i
i
r
r
e
e
d
d
a
a
t
t
t
t
h
h
e
e
e
e
n
n
d
d
o
o
f
f
a
a
n
n
o
o
r
r
m
m
a
a
l
l
i
i
n
n
s
s
p
p
i
i
r
r
a
a
t
t
i
i
o
o
n
n
.
.
E
E
x
x
p
p
i
i
r
r
a
a
t
t
o
o
r
r
y
y
R
R
e
e
s
s
e
e
r
r
v
v
e
e
v
v
o
o
l
l
u
u
m
m
e
e
:
:
i
i
s
s
t
t
h
h
e
e
a
a
d
d
d
d
i
i
t
t
i
i
o
o
n
n
a
a
l
l
a
a
m
m
o
o
u
u
n
n
t
t
o
o
f
f
a
a
i
i
r
r
w
w
h
h
i
i
c
c
h
h
c
c
a
a
n
n
b
b
e
e
e
e
x
x
p
p
i
i
r
r
e
e
d
d
a
a
t
t
t
t
h
h
e
e
e
e
n
n
d
d
o
o
f
f
a
a
n
n
o
o
r
r
m
m
a
a
l
l
e
e
x
x
p
p
i
i
r
r
a
a
t
t
i
i
o
o
n
n
.
.
R
R
e
e
s
s
i
i
d
d
u
u
a
a
l
l
v
v
o
o
l
l
u
u
m
m
e
e
:
:
i
i
s
s
t
t
h
h
e
e
a
a
m
m
o
o
u
u
n
n
t
t
o
o
f
f
a
a
i
i
r
r
r
r
e
e
m
m
a
a
i
i
n
n
i
i
n
n
g
g
i
i
n
n
t
t
h
h
e
e
l
l
u
u
n
n
g
g
s
s
a
a
t
t
t
t
h
h
e
e
e
e
n
n
d
d
o
o
f
f
a
a
f
f
o
o
r
r
c
c
e
e
d
d
e
e
x
x
p
p
i
i
r
r
a
a
t
t
i
i
o
o
n
n
.
.

C
C
a
a
p
p
a
a
c
c
i
i
t
t
y
y
B
B
y
y
a
a
d
d
d
d
i
i
n
n
g
g
a
a
l
l
l
l
f
f
o
o
u
u
r
r
t
t
y
y
p
p
e
e
s
s
o
o
f
f
v
v
o
o
l
l
u
u
m
m
e
e
t
t
o
o
g
g
e
e
t
t
h
h
e
e
r
r
,
,
w
w
e
e
g
g
e
e
t
t
t
t
h
h
e
e
t
t
o
o
t
t
a
a
l
l
l
l
u
u
n
n
g
g
c
c
a
a
p
p
a
a
c
c
i
i
t
t
y
y
.
.
I
I
f
f
w
w
e
e
a
a
d
d
d
d
o
o
n
n
l
l
y
y
i
i
n
n
s
s
p
p
i
i
r
r
a
a
t
t
o
o
r
r
y
y
r
r
e
e
s
s
e
e
r
r
v
v
e
e
v
v
o
o
l
l
u
u
m
m
e
e
,
,
t
t
i
i
d
d
a
a
l
l
v
v
o
o
l
l
u
u
m
m
e
e
,
,
a
a
n
n
d
d
e
e
x
x
p
p
i
i
r
r
a
a
t
t
o
o
r
r
y
y
r
r
e
e
s
s
e
e
r
r
v
v
e
e
v
v
o
o
l
l
u
u
m
m
e
e
w
w
e
e
g
g
e
e
t
t
t
t
h
h
e
e
v
v
i
i
t
t
a
a
l
l
c
c
a
a
p
p
a
a
c
c
i
i
t
t
y
y
.
.
I
I
f
f
w
w
e
e
a
a
d
d
d
d
o
o
n
n
l
l
y
y
t
t
h
h
e
e
e
e
x
x
p
p
i
i
r
r
a
a
t
t
o
o
r
r
y
y
r
r
e
e
s
s
e
e
r
r
v
v
e
e
v
v
o
o
l
l
u
u
m
m
e
e
a
a
n
n
d
d
r
r
e
e
s
s
i
i
d
d
u
u
a
a
l
l
v
v
o
o
l
l
u
u
m
m
e
e
,
,
w
w
e
e
g
g
e
e
t
t
f
f
u
u
n
n
c
c
t
t
i
i
o
o
n
n
a
a
l
l
r
r
e
e
s
s
i
i
d
d
u
u
a
a
l
l
c
c
a
a
p
p
a
a
c
c
i
i
t
t
y
y
(
(
F
F
R
R
C
C
)
)
.
.
V
V
e
e
n
n
t
t
i
i
l
l
a
a
t
t
i
i
o
o
n
n
V
V
e
e
n
n
t
t
i
i
l
l
a
a
t
t
i
i
o
o
n
n
i
i
s
s
t
t
h
h
e
e
c
c
o
o
n
n
t
t
i
i
n
n
u
u
o
o
u
u
s
s
p
p
r
r
o
o
c
c
e
e
s
s
s
s
o
o
f
f
m
m
o
o
v
v
i
i
n
n
g
g
a
a
i
i
r
r
i
i
n
n
a
a
n
n
d
d
o
o
u
u
t
t
o
o
f
f
t
t
h
h
e
e
l
l
u
u
n
n
g
g
s
s
.
.
V
V
e
e
n
n
t
t
i
i
l
l
a
a
t
t
i
i
o
o
n
n
i
i
s
s
u
u
s
s
u
u
a
a
l
l
l
l
y
y
e
e
x
x
p
p
r
r
e
e
s
s
s
s
e
e
d
d
i
i
n
n
v
v
o
o
l
l
u
u
m
m
e
e
p
p
e
e
r
r
u
u
n
n
i
i
t
t
m
m
i
i
n
n
u
u
t
t
e
e
,
,
o
o
r
r
l
l
i
i
t
t
e
e
r
r
s
s
p
p
e
e
r
r
m
m
i
i
n
n
u
u
t
t
e
e
s
s
.
.
any
is define as the force per unit length acting across
:
Surface tension
line drawn in the surface and tending to pull the surface apart across the
line .
Newton
F
S =
L m
Surface tension of a liquid can be regarded as the potential energy per
unit area of the surface .
E
E
x
x
c
c
e
e
s
s
s
s
p
p
r
r
e
e
s
s
s
s
u
u
r
r
e
e
i
i
n
n
s
s
i
i
d
d
e
e
a
a
s
s
p
p
h
h
e
e
r
r
i
i
c
c
a
a
l
l
a
a
i
i
r
r
b
b
u
u
b
b
b
b
l
l
e
e
C
C
o
o
n
n
s
s
i
i
d
d
e
e
r
r
a
a
s
s
p
p
h
h
e
e
r
r
i
i
c
c
a
a
l
l
a
a
i
i
r
r
b
b
u
u
b
b
b
b
l
l
e
e
o
o
f
f
r
r
a
a
d
d
i
i
u
u
s
s
R
R
,
,
i
i
n
n
s
s
i
i
d
d
e
e
a
a
l
l
i
i
q
q
u
u
i
i
d
d
o
o
f
f
s
s
u
u
r
r
f
f
a
a
c
c
e
e
t
t
e
e
n
n
s
s
i
i
o
o
n
n
S
S
.
.

P
P
1
1
i
i
s
s
t
t
h
h
e
e
p
p
r
r
e
e
s
s
s
s
u
u
r
r
e
e
i
i
n
n
s
s
i
i
d
d
e
e
t
t
h
h
e
e
b
b
u
u
b
b
b
b
l
l
e
e
P
P
2
2
i
i
s
s
t
t
h
h
e
e
p
p
r
r
e
e
s
s
s
s
u
u
r
r
e
e
o
o
u
u
t
t
s
s
i
i
d
d
e
e
t
t
h
h
e
e
b
b
u
u
b
b
b
b
l
l
e
e
P
P
1
1
>
>
P
P
2
2
T
T
h
h
e
e
b
b
u
u
b
b
b
b
l
l
e
e
d
d
i
i
v
v
i
i
d
d
e
e
d
d
i
i
n
n
t
t
o
o
t
t
w
w
o
o
h
h
e
e
m
m
i
i
s
s
p
p
h
h
e
e
r
r
e
e
T
T
h
h
e
e
c
c
i
i
r
r
c
c
u
u
m
m
f
f
e
e
r
r
e
e
n
n
c
c
e
e
o
o
f
f
t
t
h
h
e
e
c
c
i
i
r
r
c
c
l
l
e
e
=
=
2
2
п
п
R
R
S
S
u
u
r
r
f
f
a
a
c
c
e
e
t
t
e
e
n
n
s
s
i
i
o
o
n
n
w
w
i
i
l
l
l
l
e
e
x
x
e
e
r
r
t
t
a
a
d
d
o
o
w
w
n
n
w
w
a
a
r
r
d
d
f
f
o
o
r
r
c
c
e
e
F
F
=
=
2
2
п
п
R
R
S
S
o
o
n
n
t
t
h
h
e
e
u
u
p
p
p
p
e
e
r
r
h
h
e
e
m
m
i
i
s
s
p
p
h
h
e
e
r
r
e
e
,
,
a
a
n
n
d
d
e
e
q
q
u
u
a
a
l
l
u
u
p
p
w
w
a
a
r
r
d
d
f
f
o
o
r
r
c
c
e
e
o
o
n
n
l
l
o
o
w
w
e
e
r
r
h
h
e
e
m
m
i
i
s
s
p
p
h
h
e
e
r
r
e
e
.
.
(
(
P
P
1
1
–
–
P
P
2
2
)
)
п
п
R
R
²
²
i
i
s
s
t
t
h
h
e
e
d
d
o
o
w
w
n
n
w
w
a
a
r
r
d
d
f
f
o
o
r
r
c
c
e
e
o
o
n
n
t
t
h
h
e
e
u
u
p
p
p
p
e
e
r
r
h
h
e
e
m
m
i
i
s
s
p
p
h
h
e
e
r
r
e
e
i
i
s
s
b
b
a
a
l
l
a
a
n
n
c
c
e
e
b
b
y
y
a
a
t
t
h
h
r
r
u
u
s
s
t
t
d
d
u
u
e
e
t
t
o
o
t
t
h
h
e
e
e
e
x
x
c
c
e
e
s
s
s
s
p
p
r
r
e
e
s
s
s
s
u
u
r
r
e
e
(
(
P
P
1
1
–
–
P
P
2
2
)
)
.
.
A
A
t
t
e
e
q
q
u
u
i
i
l
l
i
i
b
b
r
r
i
i
u
u
m
m
(
(
P
P
1
1
-
-
P
P
2
2
)
)
п
п
R
R
²
²
=
=
2
2
п
п
R
R
S
S
P
P
1
1
-
-
P
P
2
2
=
=
2
2
S
S
R
R
F
F
o
o
r
r
s
s
p
p
h
h
e
e
r
r
i
i
c
c
a
a
l
l
d
d
r
r
o
o
p
p
o
o
f
f
w
w
a
a
t
t
e
e
r
r
,
,
t
t
h
h
e
e
e
e
x
x
c
c
e
e
s
s
s
s
p
p
r
r
e
e
s
s
s
s
u
u
r
r
e
e
i
i
s
s
P
P
1
1
–
–
P
P
2
2
=
=
4
4
S
S
R
R
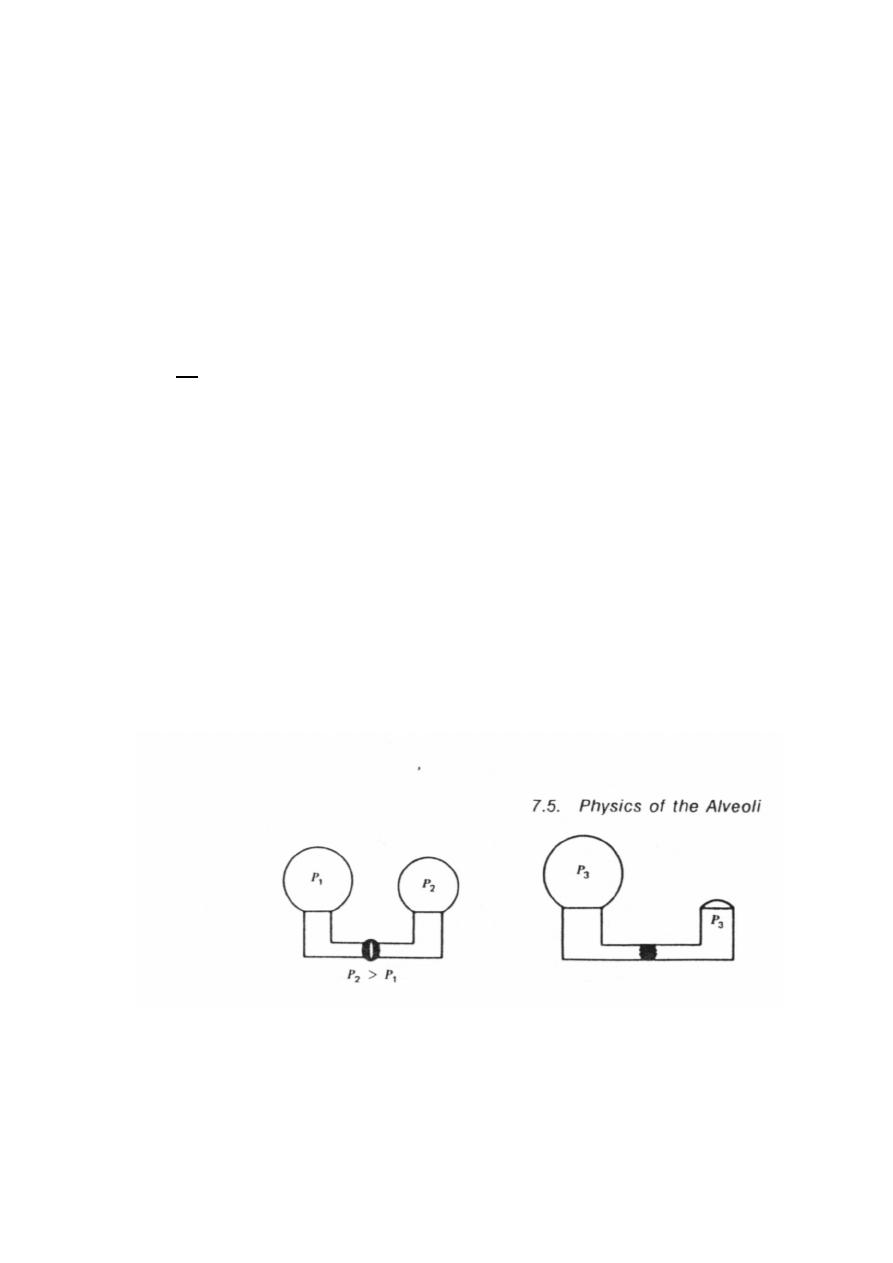
Physics of the Alveoli
The alveoli are physically like millions of small interconnected bubbles .
They have a natural tendency to get smaller due the surface tension of a
unique fluid lining .This lining called surfactant , it is necessary for the lung to
function properly .
To understand the physics of alveoli we have to understand the physics of
bubbles. According to Laplace ̉s law , the pressure inside a bubble is inversely
proportional to the radius and directly proportional to the surface tension .
Laplace ̉s law
4S
P=
R
surfactant :
The compliance of the lungs is made greater by the presence of surfactant in
the alveoli . This substance acts like a detergent and reduce the surface tension
of the water in the alveoli .
Example
The pressure inside a soap bubble depends on its radius (figure 3).
(a) when the valve between two bubbles is closed , the pressure is greater in
small bubble .
(b) when the valve is opened , the smaller bubble empties into the larger ,
leaving a spherical cap with the same radius as the new large bubble .
figure3
The surface tension of a fluid can be found by measuring how much force is
necessary to pull a loop of a wire from a clean liquid surface (figure4).

The surface tension of water –air interface is 72 dynes/cm
.
Figure4
Figure (3)
Figure5;
The surface tension of the surfactant that lines the alveoli of healthy
individuals plays a major role in lung function .The surface tension of the

surfactant is not constant , as shown in figure (5) .The surfactant acts like a
detergent and reduces the surface tension of the water in the alveoli .
Figure (5) Graph of surface tension of a lung extract containing surfactant .
Note the large decrease in surface tension as the area decreases and the
different curve obtained as the area increases . The vertical line at 70 dynes/
cm shows that the surface tension of water is constant with changes in area .
This graph(figure5) .shows that the surface tension of the alveoli is a function
of area .
Elasticity of lungs
The lungs and chest wall are elastic structures. The combined elasticity may
be measured by relaxing the respiratory muscles, and then by how much the
volume increases , when the pressure in the lungs increased.
∆P
Elasticity =
∆v
∆P = is the change in pressure
∆V = is the change in volume
In respiratory mechanics it is usually to consider elasticity , but its
reciprocal .
a small change in
: is the change in the volume produced by
Compliance
pressure .
Liters/cm of water
∆v
Compliance =
∆p
Compliance in normal range is
0.18- 0.26 Liter/cm H2O
T
T
h
h
e
e
B
B
r
r
e
e
a
a
t
t
h
h
i
i
n
n
g
g
M
M
e
e
c
c
h
h
a
a
n
n
i
i
s
s
m
m
Breathing is normally under unconscious control . The physiological
control of breathing depends on many factors , but the respiratory center of the
brain exerts primary control .
If a lung were removed from the chest all the air would be squeezed from
it and it would collapse to about one third of its size much as a balloon
collapses when air is let out of it .
The lungs can be thought of as millions of small balloons , all trying to
collapse . The lungs do not normally collapse because they are in an airtight
container – the chest . As the diaphragm and rib cage move the lungs stay in
contact with them .
Two forces keep the lungs from collapsing:
1. Surface tension between the lungs and the
chest wall .
2. Air pressure inside the lungs .
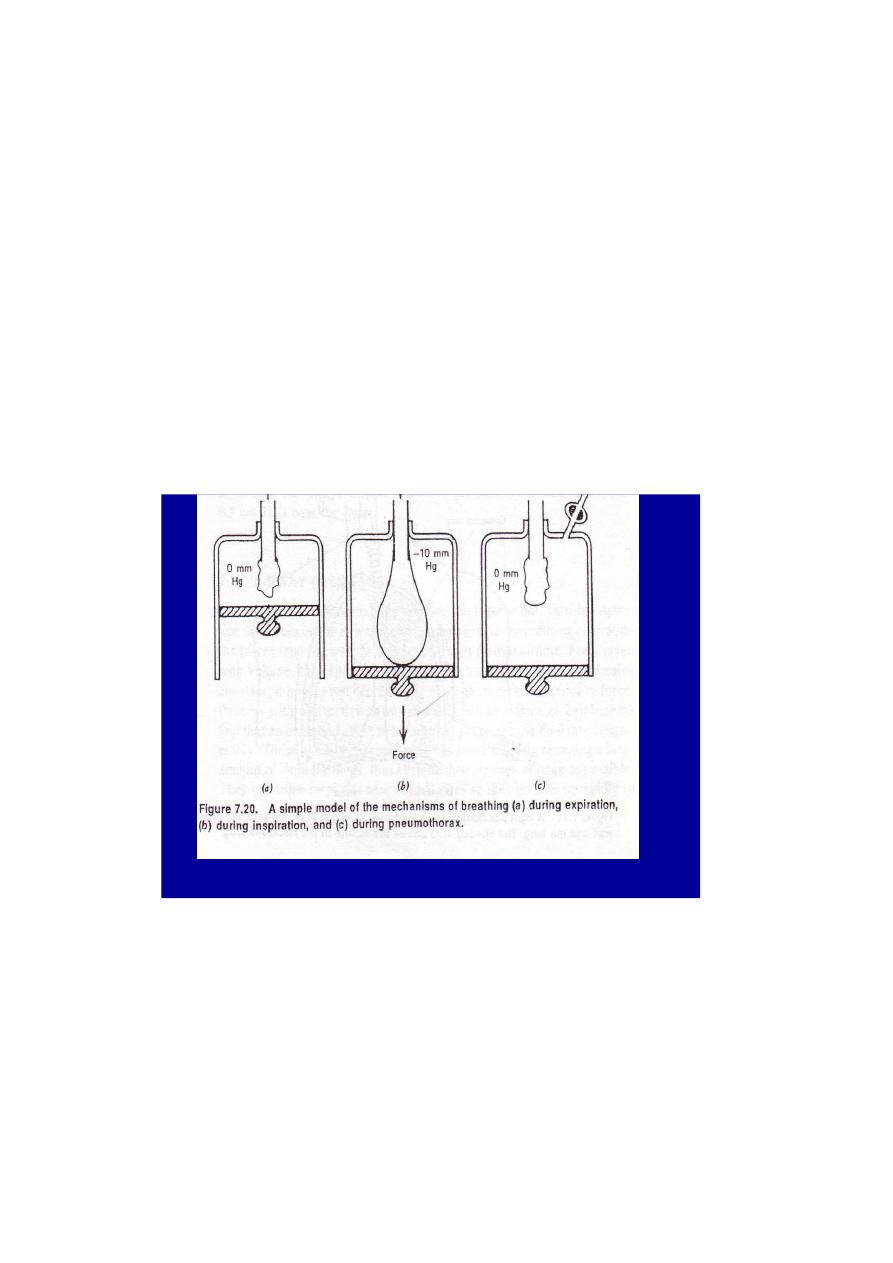
Figure 6
If the lungs overcame the surface tension forces and pulled away from
the chest wall a vacuum would be created since air can not reach the
intrathoraic space .Since the air inside
5
the lungs is at atmospheric pressure (10 N/m²) ,it would push the lungs
back in contact with the chest wall . There is normally a negative pressure
of 5 to 10 mm Hg in the intrapleural space . Various muscles are involved
in breathing . Normally most breathing is done by contracting the
diaphragm muscles . These pull the diaphragm down expanding the lungs
.When we inspire ,we pull the diaphragm down as shown in figure (6) .

This produces a slight negative pressure in the lungs and air flows in ,
when we expire ,we relax the diaphragm muscles , the elastic forces in the
lungs cause the diaphragm to return to its neutral position , and air flows
out of the lungs without any active muscular effort .
Since both the lungs and chest wall are elastic ,we can represent them
with springs ,figure(7) .Under normal conditions they are coupled together
“the lung” springs are stretched and “chest” springs are compressed .
During a pneumothorax , the lungs and chest are independent and the
springs representing them go to their relaxed positions as indicated in
figure (7b) . the lungs collapses ,and the chest wall enlarges .
The intrathoracic space is not always at negative pressure . If you
close your wind pipe and forcefully try to expire , the intrathoracic
pressure can become quite high . This is called a Valsalva manenver .
Airways Resistance
We can breath in more rapidly than we can breath out . During inspiration
the forces on the airways tend to open them further; during expiration the
forces tend to close the airways and thus restrict air flow .
The flow of air in the lungs is analogous to the flow of current in an
electrical circuit . “Ohm s law” for air flow looks like ohms law for
electrical circuit , with voltage replaced by pressure difference ∆P and
current replaced by the rate of airflow ∆v/∆t or V .
Airway resistance R
g
is the ratio of ∆ P to V.
cm H2O
∆P
=
g
R
V Liter/sec
The flow rate of air flow is
∆v
V =
∆t
R
g
depends on the dimensions of the tube and the viscosity of the gas η.
The time constant of lungs is related to the airway resistance R
g
and the
compliance C .
Time constant for the lung =R
g
C
This is analogous to the time constant RC or capacitor C to discharge
through a resistance R in an electrical circuit .
The time constant of the lung is complicated since many parts of the
lung are interconnected . If one part of the lung has a larger time constant
than other parts , it will not get its share of the air and that part of the lung
will be poorly ventilated .
Osmosis
If we have two salts solutions of different concentrations separated by a
membrane permeable to water not to salt , it is found that in time the solution
on the two side will have the same strength . These due to the passage of
water from the weak salt solution to the stronger . Such phenomena is known
Osmotic Pressure
as osmosis .
Is the force under which a solvent moves from a solution of a lower solute
concentration to a solution of higher solute concentration .When these
solution are separated by a selectively permeable membrane .
PV =nRT
•
Where P is the osmotic pressure
•
V is the volume
•
n is the number of mole
R is the universal gas constant = 8.3 J/mole
T is the absolute temperature
The osmotic pressure is proportional to the concentration of the solute ,
Which means inversely proportional to the volume of the solution .
It is also proportional to the absolute temperature .
