
Probability
Dr. Nadia Aziz
C.A.B.C.M
Department of community medicine

Objectives
1- Define the probability.
2- Explain the applications of probability in
medical sciences.
3- Describe types of probability.

Introduction
Science is
uncertain
. Scientists are sometimes wrong.
Many studies are inconclusive.
Why is that?
Nature is complex and full of unexplained biological
variability.
Almost all methods of observation and experiment
are
imperfect
.

Introduction
Science and scientists cope with uncertainty by
calculating probabilities, they are able to
describe what has happened and predict what
should happen in future under similar
conditions.
Probability
The theory of probability provides the foundation
of
statistical inference
.
The understanding probability is essential for
understanding
p value
and
confidence interval
.

Probability
Definition
It is the likelihood of occurrence of a certain
event compared to the total events.
no. of times
E
occur
P (
E
)=
no. of times
E
can occur
P(
E
) probability of occurrence of event
E

Probability
The value of probability = 0 – 1
No negative
value in probability.
Probability (E) = 0 means event is
impossible
Probability (E) = 1 means event is
sure

Probability& relative frequency
Probability ≃ percentage (%)
If we keep taking random selections (repeated
sampling), the accumulated long – term relative
frequency with which the event occurs
(characteristic observed) is
equal
the proportion
of the subpopulation with that characteristic.

Probability& relative frequency
So sometimes proportion and probability are used
interchangeably.
Example: the probability of serum cholesterol level
between 180 and 210(mg/100 ml) is the
proportion of people in a certain target population
having their cholesterol levels falling between 180
and 210 (mg/100 ml).

Probability& relative frequency
The sum of the probabilities (or relative
frequencies) of all event that can occur in the
sample must be 1 (or 100%)

Example
In a sample of 50 people, 21 had blood group O, 22
had blood group A, 5 had type B, and 2 had blood
group AB
p(O)= 0.42 p(A)= 0.44
p(B)= 0.1 p(AB)= 0.04
p(neither A nor O)= 0.14
p(not AB)= 1 - 0.04= 0.96
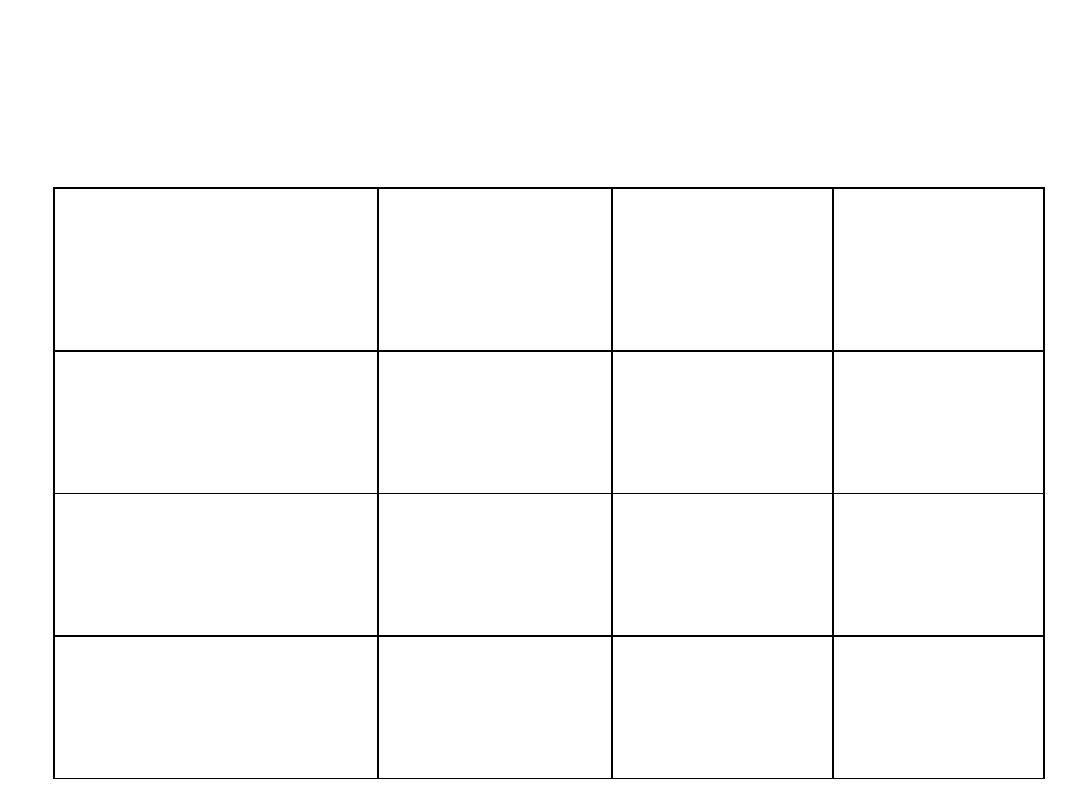
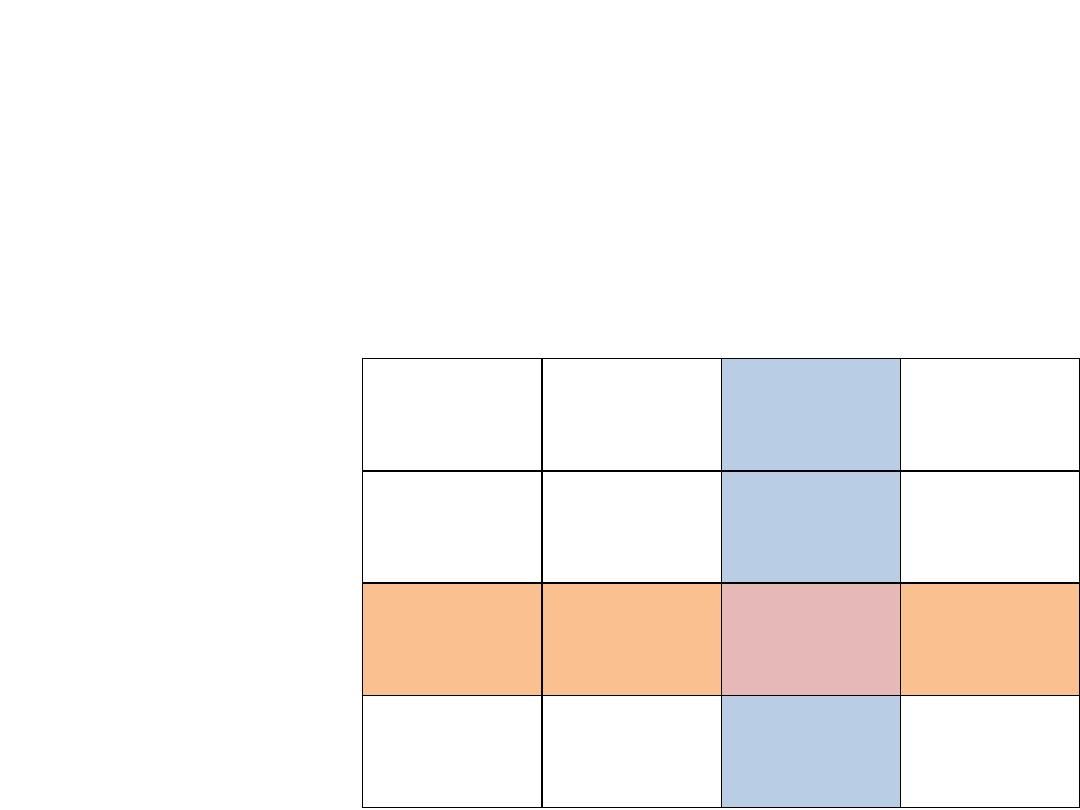
The data from cancer screening test:
Disease
+ve
Disease
-ve
Total
Test +ve
9
5
14
Test -ve
6
80
86
Total
15
85
100
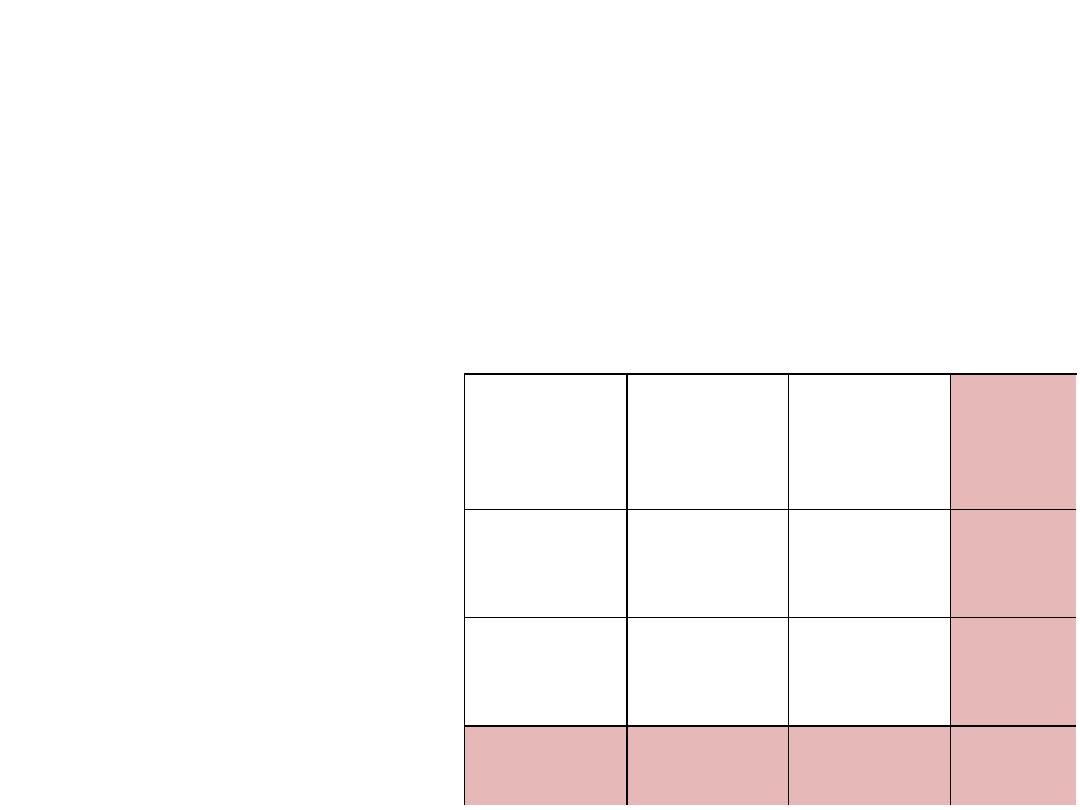
Marginal probabilities
P( Disease +ve) =15 / 100
P( Disease -ve)=85/100
P (Test +ve)=14/100
P (Test -ve)=86/100
Disease
+ve
Disease
-ve
Total
Test +ve
9
5
14
Test -ve
6
80
86
Total
15
85
100

Joint probability
These are the probabilities for two events or
more (such as having the disease
and
having a
positive test result ) occurring
simultaneously
.
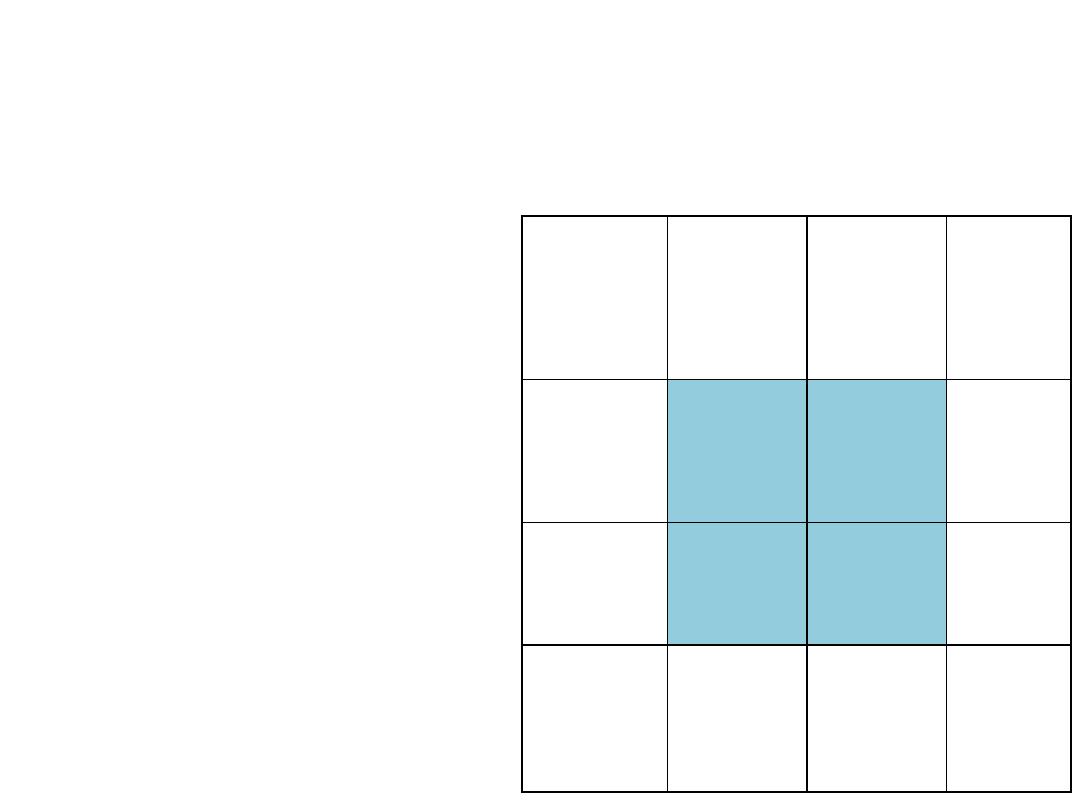
Joint probability
P (Dis +ve, test +ve)= 9/100
P (Dis +ve, test –ve)= 6 /100
P (Dis –ve, test +ve)= 5 / 100
P (Dis –ve, test –ve)= 80/
1
00
Disease
+ve
Disease
-ve
Total
Test +ve
9
5
14
Test -ve
6
80
86
Total
15
85
100
Conditional probabilities
The probability of occurrence of an event
given that
another event had already occurred
Example 1:
P (disease +ve / test +ve =
(9/100)/(14/100) =
= 9/14
Disease
+ve
Disease
-ve
Total
Test +ve
9
5
14
Test -ve
6
80
86
Total
15
85
100
Conditional probabilities
Example 2:
P(disease –ve/test –ve)=
P (dis –ve & test –ve)/test –ve=
(80/100)/(86/100)=
80/86= 0.93
Disease
+ve
Disease
-ve
Total
Test +ve
9
5
14
Test -ve
6
80
86
Total
15
85
100
Probability
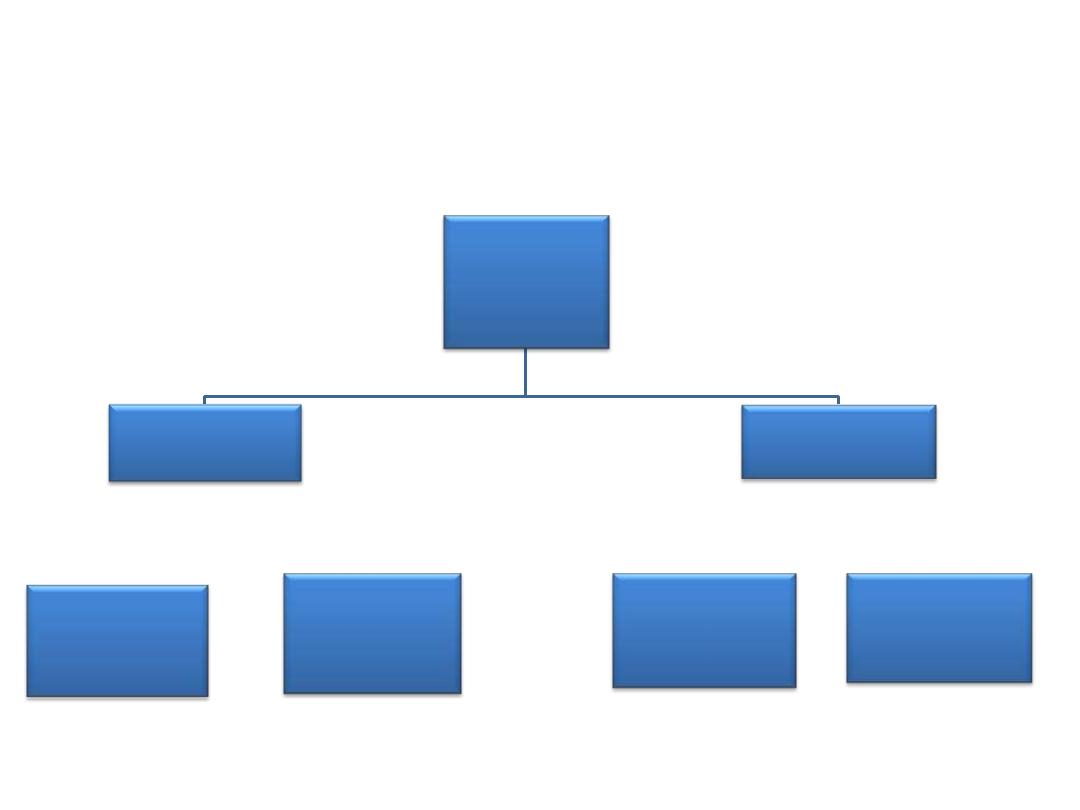
Rules
Multiplication rule
(And, ∩, both)
Additional rule
(or, U, either)
Independent
Non
independent
Mutually
exclusive
Non - mutually
exclusive

Rules of probability
1- Multiplication rule (and, ∩ ,both)
A- Independent
B- Non independent
2- Additional rule (or, ∪ , either)
A- Mutually exclusive
B- Non mutually exclusive

Rules of probability
1- Multiplication rule
A-
Independent event
P (E
1
∩ E
2
) = P (E
1
) x P (E
2
)
Ex: the probability that an individual belonging to
blood
group A
is 0.42, and the individual being a
football player
is 0.50. what is the probability of the individual both
belonging to blood group A
and
being football player?

Multiplication rule
Since the events are
independent
P (E
1
∩ E
2
) = P E
1
x P E
2
= 0.42 x 0.50 = 0.21

Multiplication rule
B- Non independent
If the two events are not independent, they
have a statistical relationship or we say that
they are
statistically associated
Example:
What is the probability of selecting an individual who is
disease +ve
and
test –ve
P( dis +ve & test –ve ) =
P(dis +ve/test –ve).p test –ve =
6/86 x 86/100=
6/100 = 6%
Diseas
e
+ve
Diseas
e
-ve
Total
Test
+ve
9
5
14
Test
-ve
6
80
86
Total
15
85
100

Addition rule
A-
Mutually exclusive
This means the events can
not occur together
Ex: the probability that an individual has a blood
group A is 0.4 and the probability that another
individual has a blood group B is 0.3.
What is the probability of the individual belonging
to blood group A
or
B ?

Addition rule
P (bl. Group A
or
bl. Group B)=
0.4
+
0.3 = 0.7
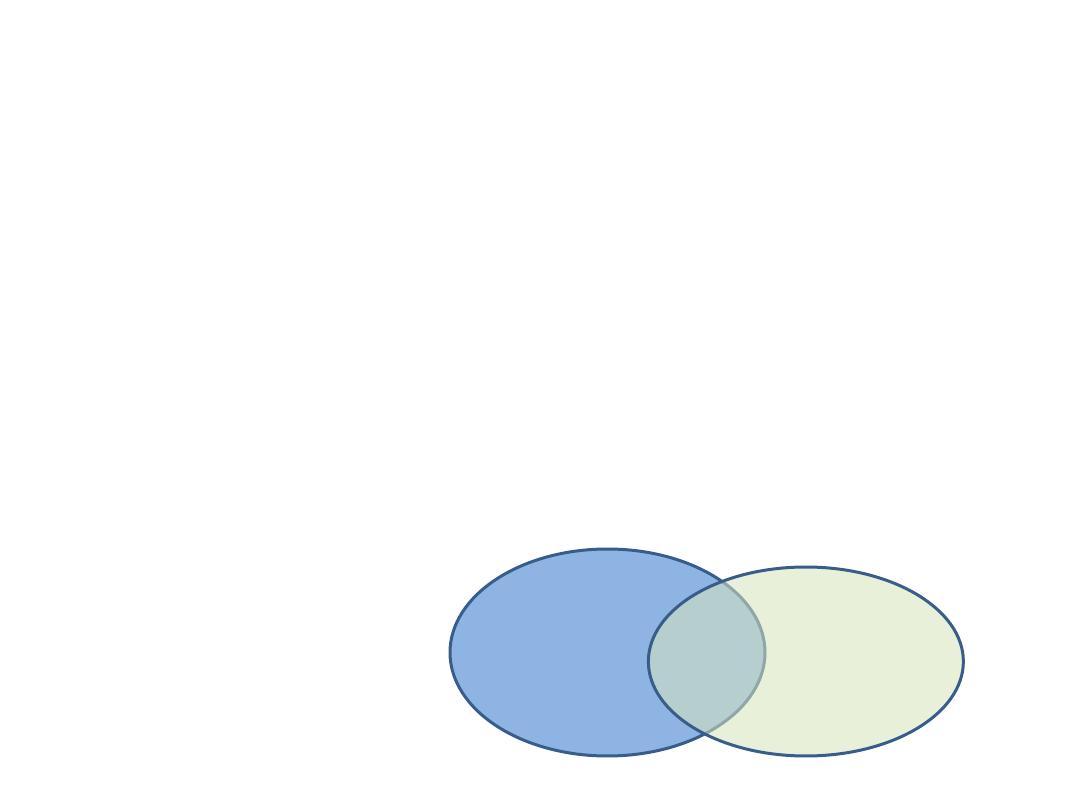
Addition rule
B-
Non mutually exclusive
:
Given two events A &B, the probability that event A, or
event B, or both occur is equal to the probability that
event A occurs, plus the probability that event B occurs,
minus
the probability that the events occur
simultaneously.
A
A&B B

Example:
What is the probability of having disease –ve or
test –ve ?
P(dis –ve or test –ve)=
P(dis –ve)+p(test –ve) –p(dis –ve &test –ve)=
85/100 + 86/100- 80/100= 91/100 =0.91
Disease
+ve
Disease
-ve
Total
Test +ve
9
5
14
Test -ve
6
80
86
Total
15
85
100
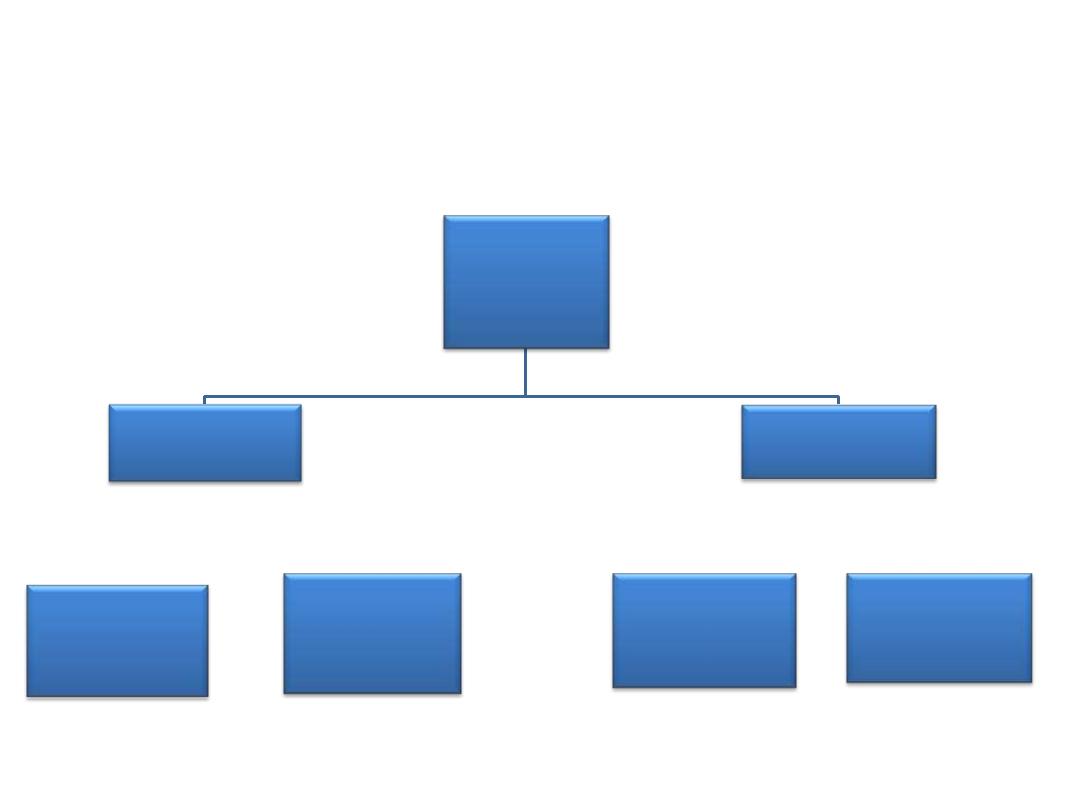
Summery
Probability
Rules
Multiplication rule
(And, ∩, both)
Additional rule
(or, U, either)
Independent
Non
independent
Mutually
exclusive
Non - mutually
exclusive

Thank you
&
Good luck
