Mechanics
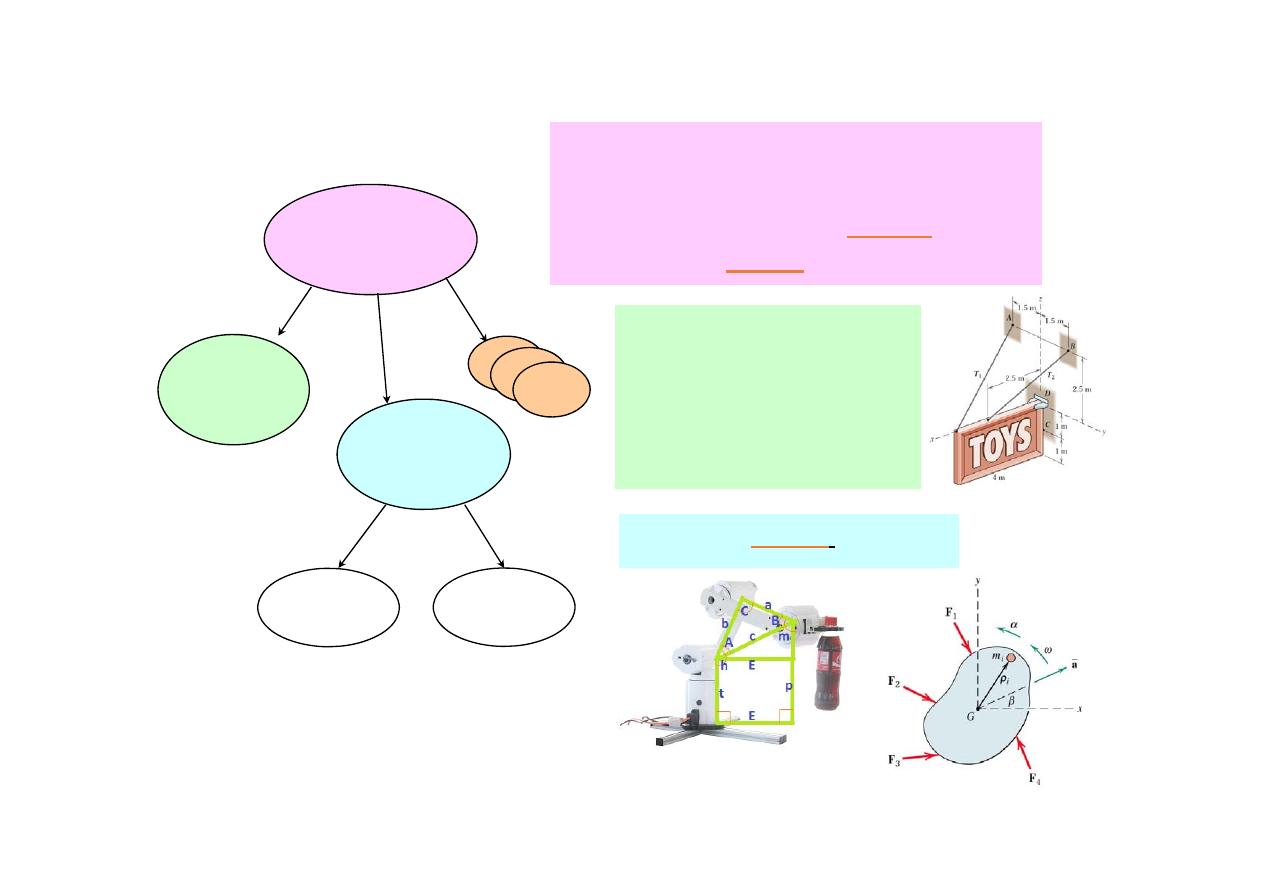
Mechanics
Statics
Dynamics
‐Equilibrium
‐Selected Topics
Kinematics
Kinetics
‐Particles
‐Rigid Bodies
‐Particles
‐ Rigid Bodies
A branch of physical science
which deals with ( the states of
rest or motion of )
bodies under
action of forces
Dynamics:
Motion
of bodies
Statics:
Equilibrium
of bodies
(no accelerated motion)
under action of Forces
Mechanics
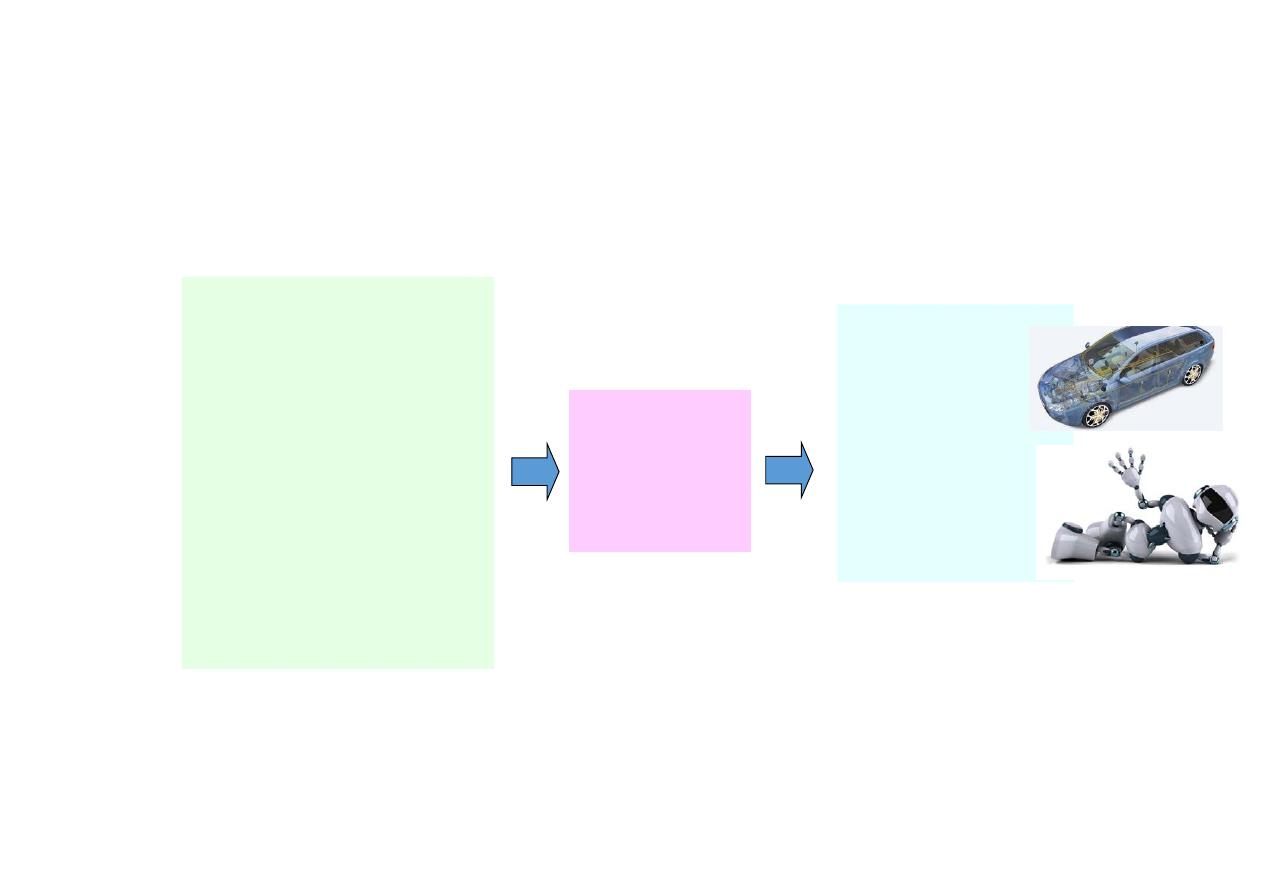
Mechanics
Statics
Dynamics
Mech. of Materials
Fluid Mechanics
Vibration
Fracture Mechanics
Etc.
Structures
Automotive
Robotics
Spacecraft
Etc.
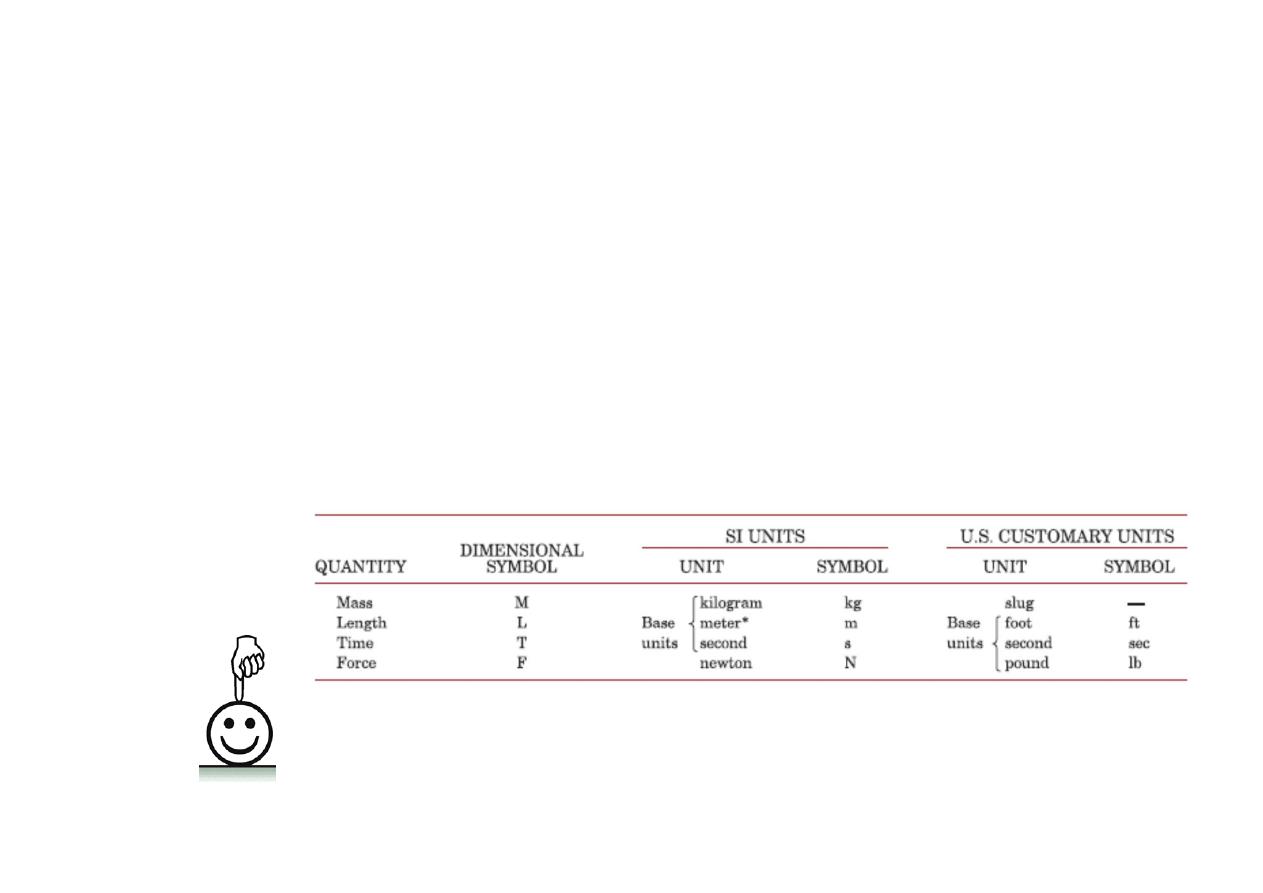
Basic Concepts
Basic Concept ‐ Definition
Space
: Collection of points whose relative positions can be described
using “a coordinate system”
Time
is a measure of the succession of events and is considered an
absolute quantity.
Mass
: is the quantitative measure of the inertia or resistance to
change in motion of a body [Dynamics]. Mass may also be considered as the
quantity of matter in a body.
position,
velocity,
acceleration
r

Kinematics:
is the branch of classical mechanics which describes the motion
of points, bodies (objects) and systems of bodies (groups of objects)
without consideration of the causes of motion. So you only have velocities
and accelerations without the forces/torques which creates the motion.
Kinetics:
is a term for the branch of classical mechanics that is concerned
with the relationship between the motion of bodies and its causes, namely
forces and torques. So here you have both velocities, accelerations and the
forces which creates the motion.
Force:
is the vector action of one body on another

A particle:
is a body of negligible dimensions. When the dimensions of a
body are irrelevant to the description of its motion or the action of forces
on it, the body may be treated as a particle. An airplane, for example, may
be treated as a particle for the description of its flight path.
A rigid body:
is a body whose changes in shape are negligible compared
with the overall dimensions of the body or with the changes in position of
the body as a whole.
• In dynamics, force is an action that tends to cause acceleration of
an object.
• The SI unit of force magnitude is the
newton
(
N
). One newton is
equivalent to one kilogram‐meter per second squared (
kg∙m/s
2
or
kg∙m ∙ s
– 2
)
SCALARS AND VECTORS
Scalars
: associated with “
Magnitude
” alone
Vectors
: associated with “
Magnitude
” and “
Direction
”
‐
mass
,
density
,
volume
,
time
,
energy
, …
‐
force, displacement
,
velocity
,
acceleration, …
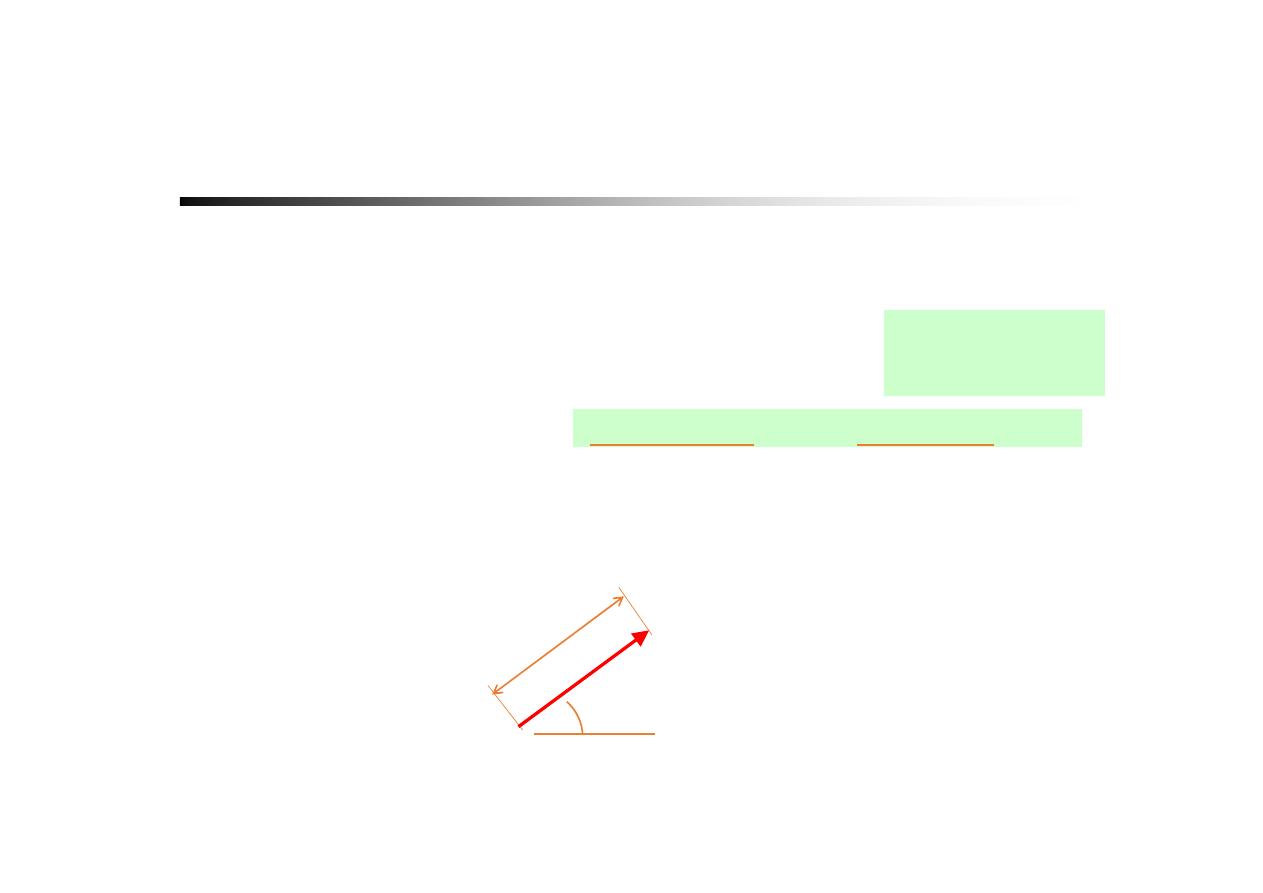
: Direction
or V
| |
V
Magnitude:
V
or
V
Vector :
free vector
(“math” vector)
8
Vector: magnitude & direction, components
•
Scalar multiplication
•
Addition, subtraction
•
Dot product
•
Cross product
•
Mixed triple product
Manipulation
Scalar & Vector
,
(
)
aA
A
B A
B
A B
A B
A B C
Mathematical Meanings
vs
Physical Meanings

Physical Quantity of Vector
Vectors representing physical quantities can be classified
• Fixed Vector
•
Its action is associated with a
unique point of application
•
Described by magnitude, direction & pt of application
• Sliding Vector
•
Has a
unique line of action
in space but not a unique point of
application
•
Described by magnitude, direction & line of action
• Free Vector
•
Its action is
not confined or associated with a unique line in
space
.
•
Described by magnitude & direction
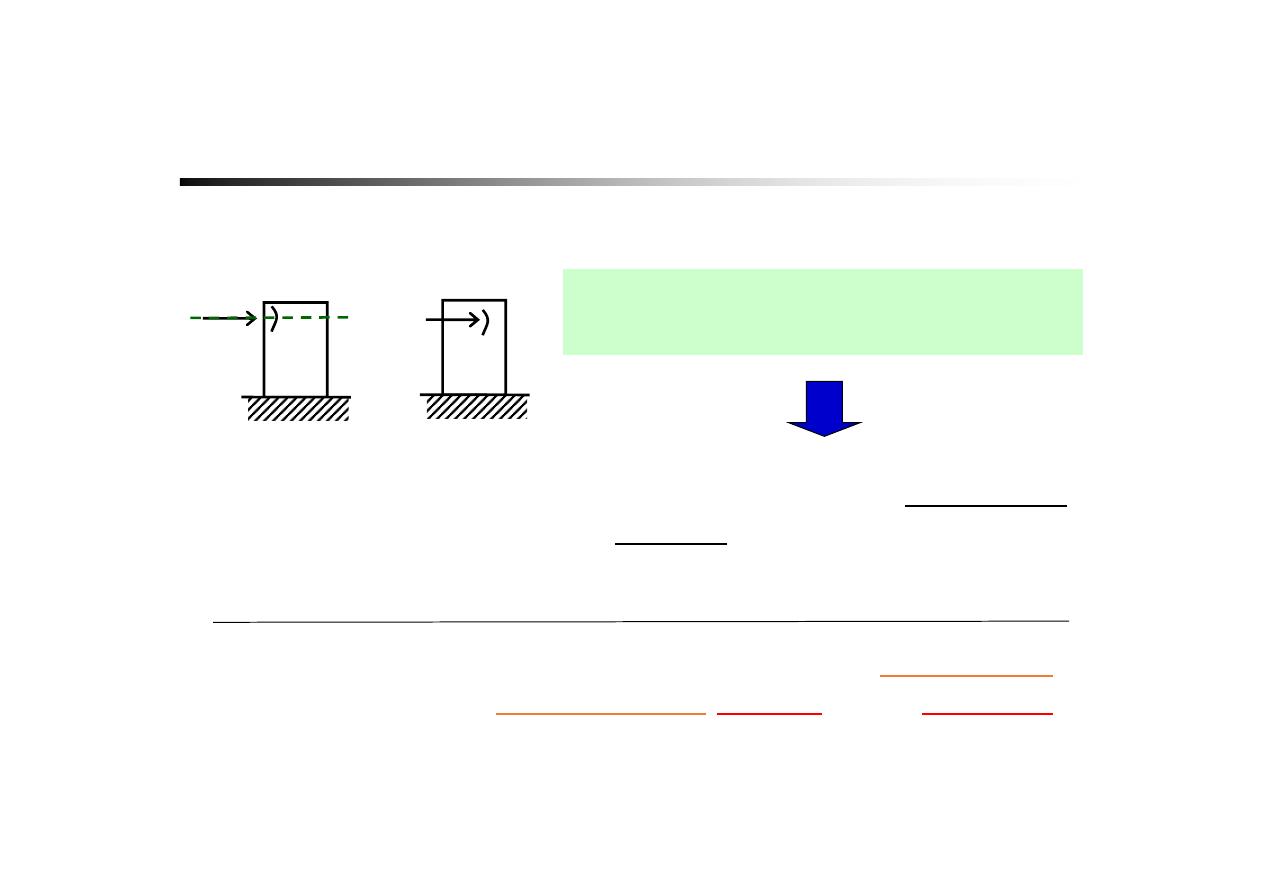
The Principle of
Transmissibility
“A force may be applied at any point on its given
line of action
without altering the
resultant effects
external
to the
rigid body
on which it acts.”
We can slide the force along its line
of action.
(force can be considered as sliding vector)
F
F
=
?
The two force can be
considered equivalent if
……
If we concerns only about the
external resultant effects
on
rigid body.
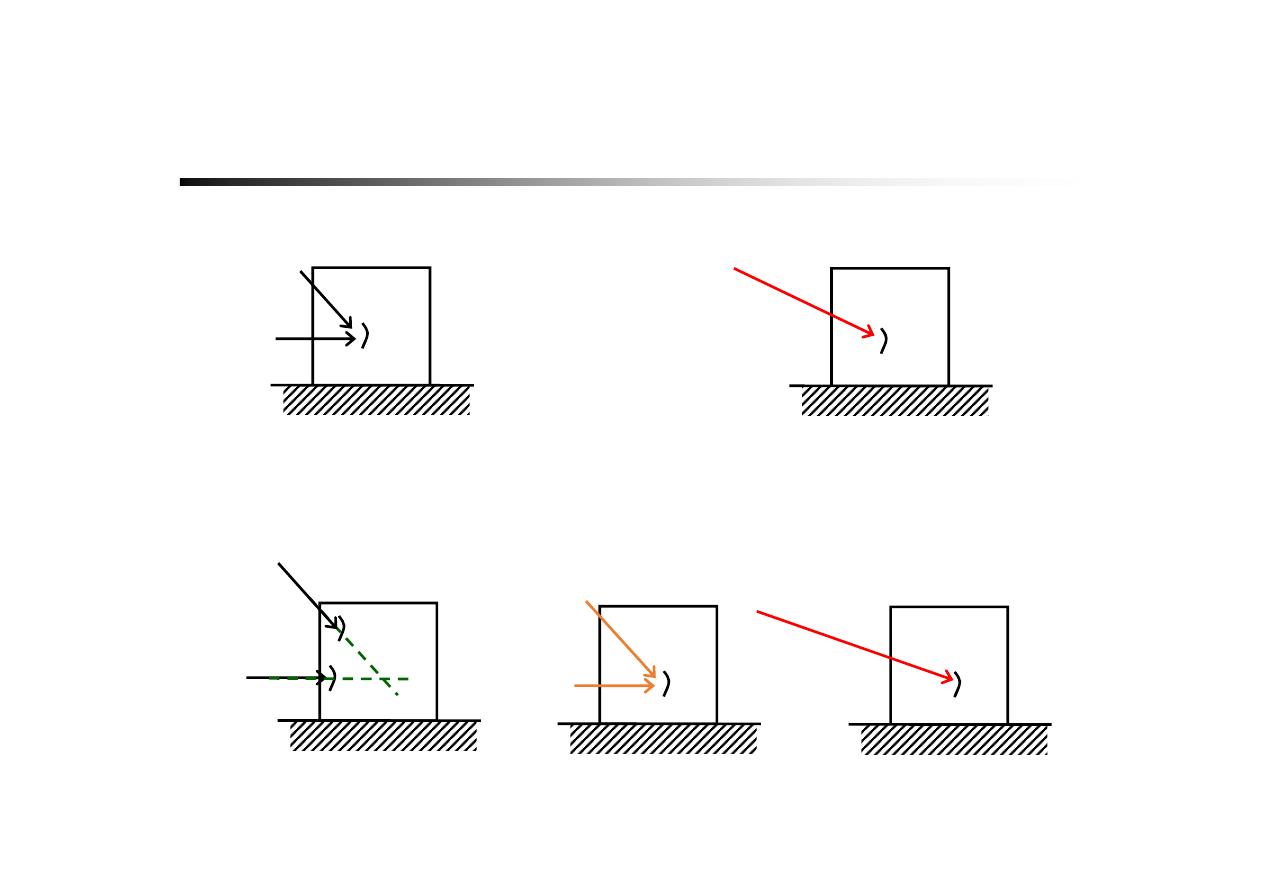
Summation of Force
1
F
2
F
1
2
F
F
1
F
2
F
1
F
2
F
1
2
F
F
if there are sliding vectors
concurrent forces
non‐concurrent
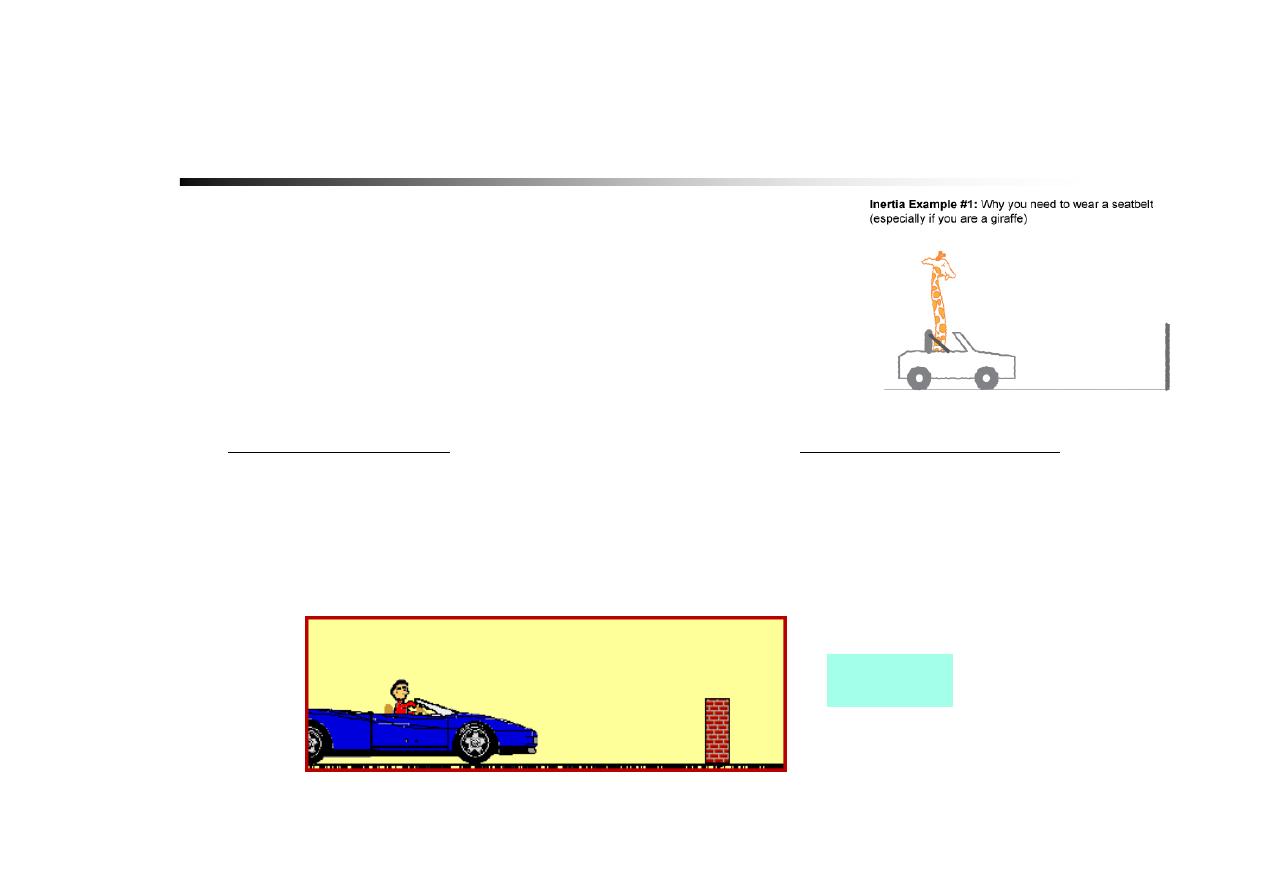
NEWTON’S LAWS OF MOTION (1
st
Law)
The study of rigid body mechanics is
formulated on the basis of Newton’s laws of
motion.
0
F
First Law:
An object at rest
tends to stay at rest
and an object in motion
tends to stay in motion
with the
same speed
and in the
same
direction,
unless acted upon by an unbalanced force
.
A particle remains at rest or continues to move with uniform
velocity (in a straight line with a constant speed) if there is no unbalanced
force acting on it

NEWTON’S LAWS OF MOTION (2
nd
Law)
Second Law:
The acceleration of a particle is
proportional to the vector sum
of
forces acting on it, and is in the
direction of this vector sum
.
m
F
a
a
m
F
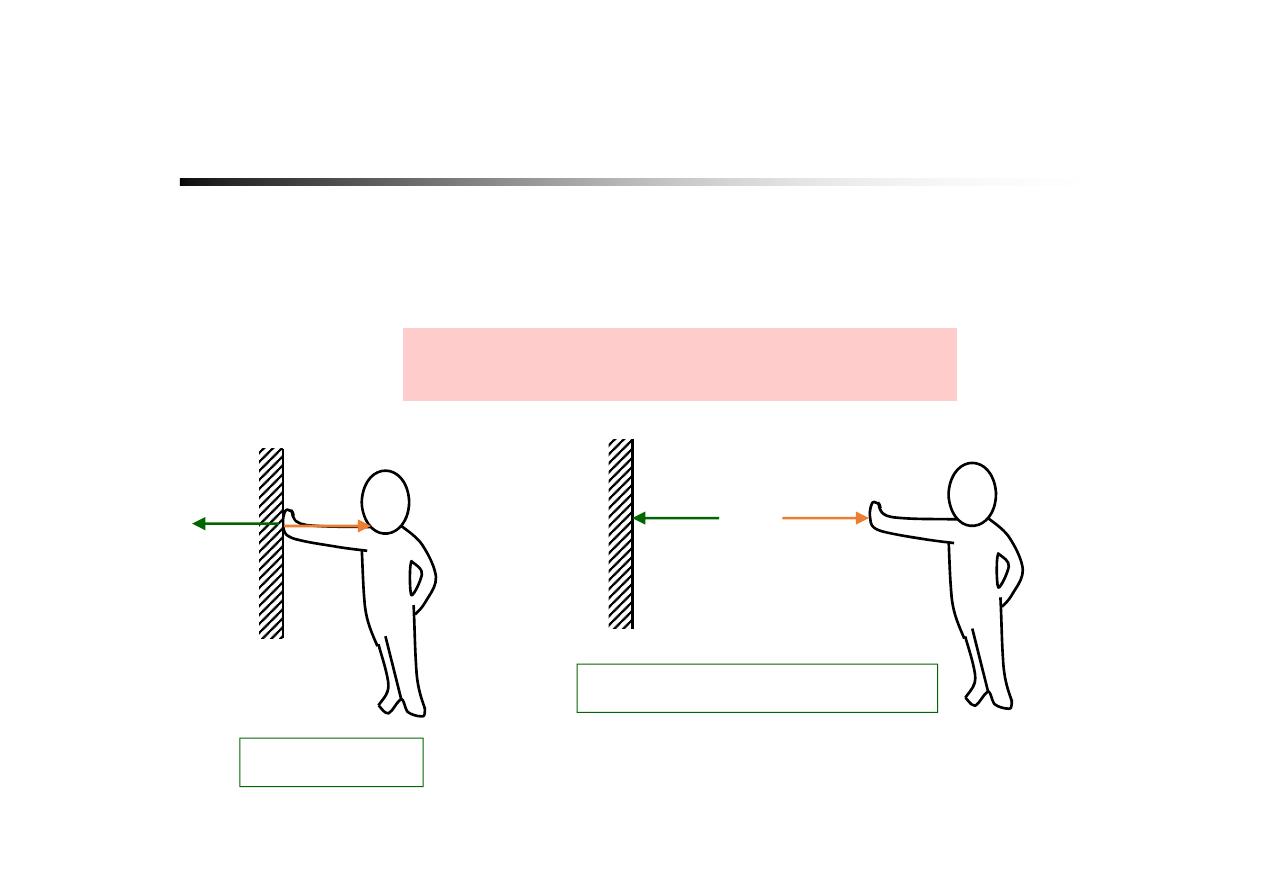
NEWTON’S LAWS OF MOTION
Third Law:
The mutual forces of
action and reaction
between two
particles are
equal in magnitude
,
opposite in direction
,
and
collinear
.
F
F
F
F
Confusing?
Concept of
FBD
(
Free Body Diagram
)
Point: Isolate the body
Forces always occur in pairs – equal and
opposite action-reaction force pairs.

Newton’s Law of Gravitation
2
r
GMm
F
‐ M & m are particle masses
‐ G is the universal constant of gravitation,
6.673 x 10
‐11
m
3
/kg‐s
2
‐ r is the distance between the particles.
For Gravity on earth
(at sea level)
where
‐ m is the mass of the body in question
‐ g = GM/R
2
= 9.81 m/s
2
(32.2 ft/s
2)
W
mg
M
m
r
F
m
M
W=mg
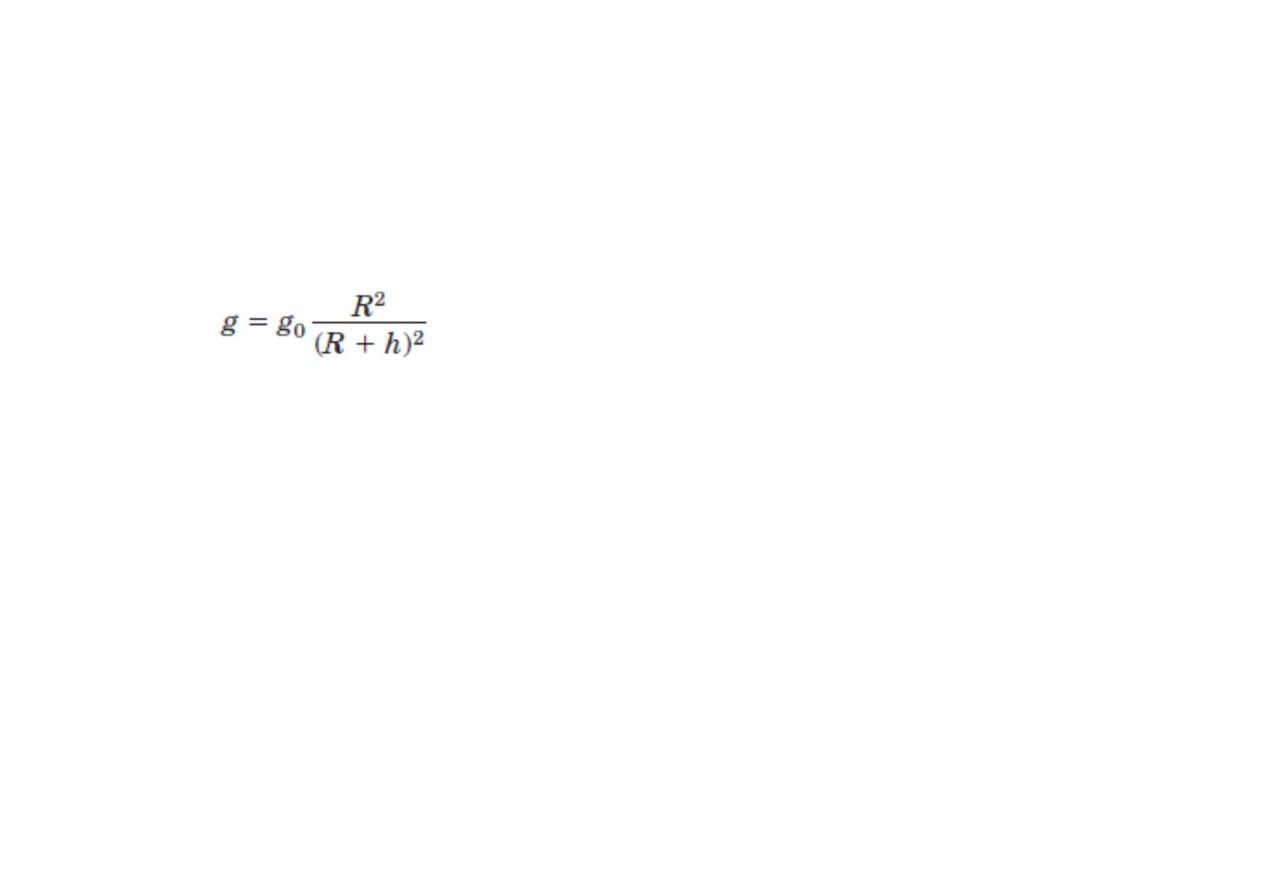
Effect of Altitude
g
0
: represents the absolute acceleration due to gravity at sea level
h :the absolute value at an altitude
R: is the radius of the earth
Problems pp18
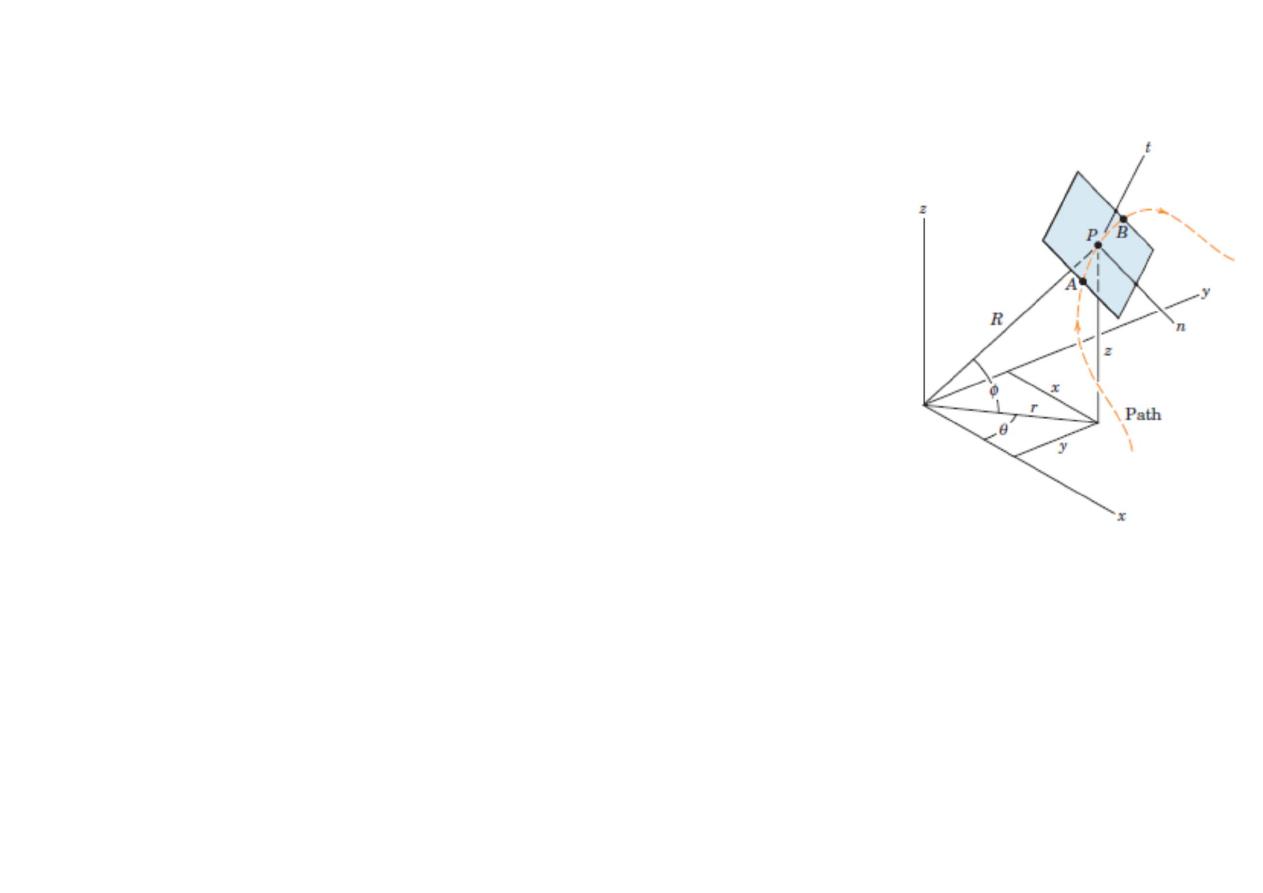
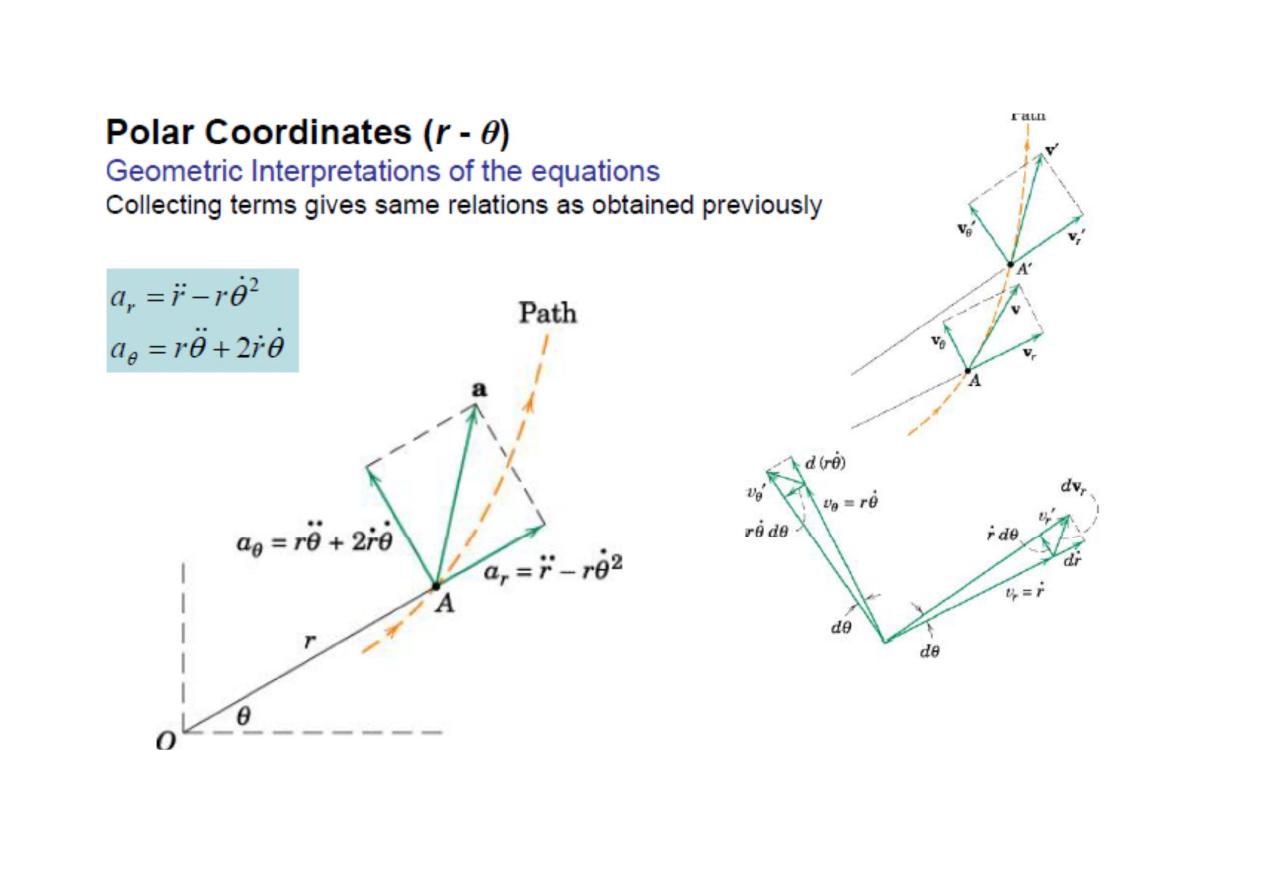
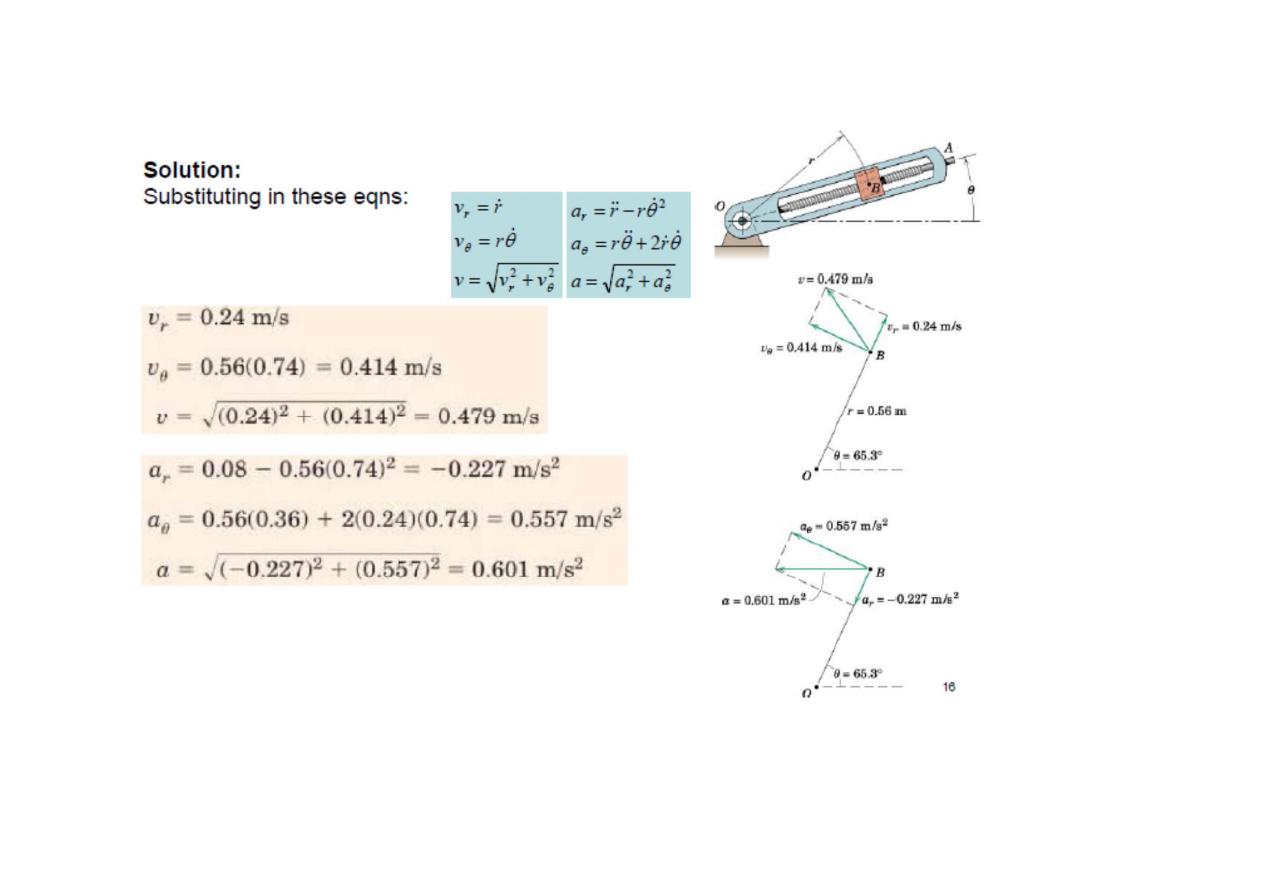
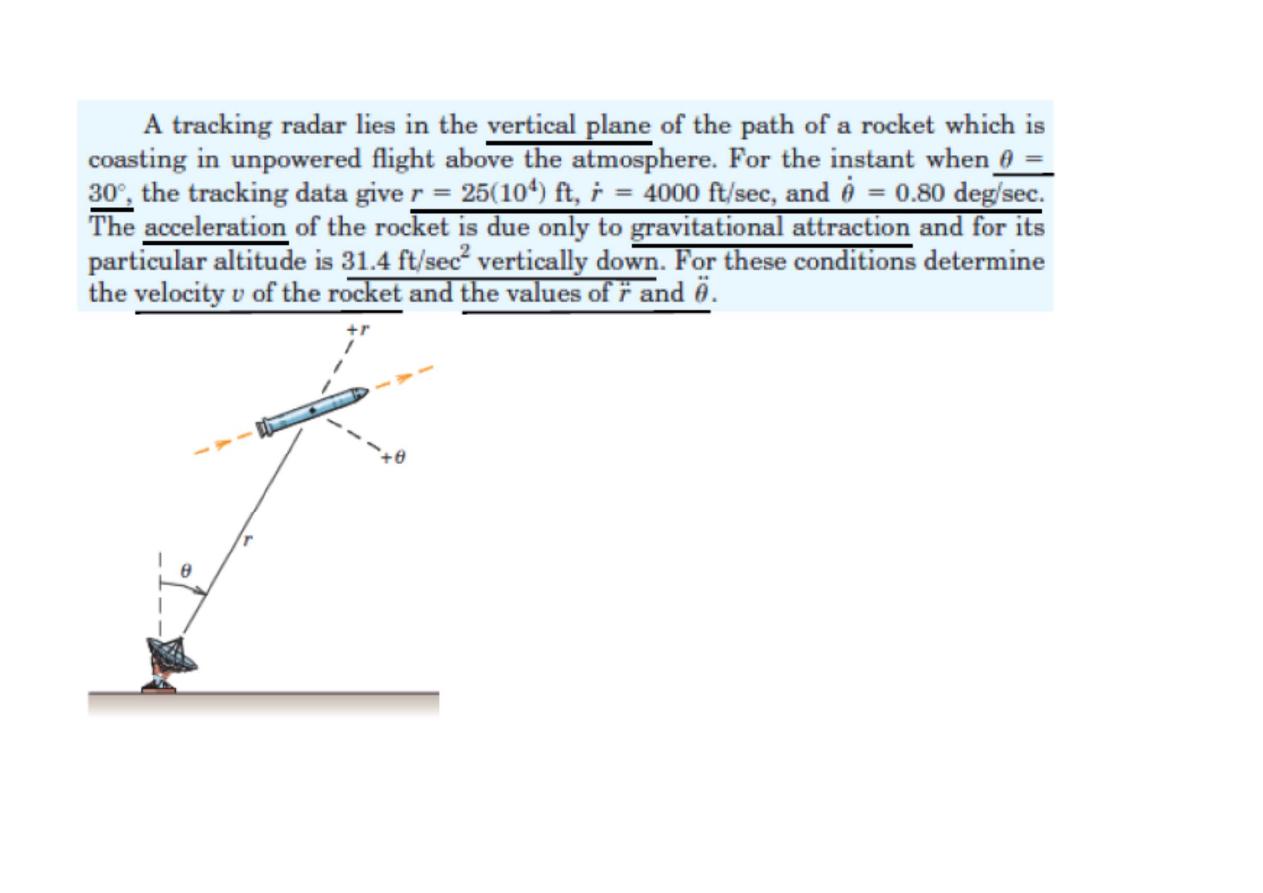
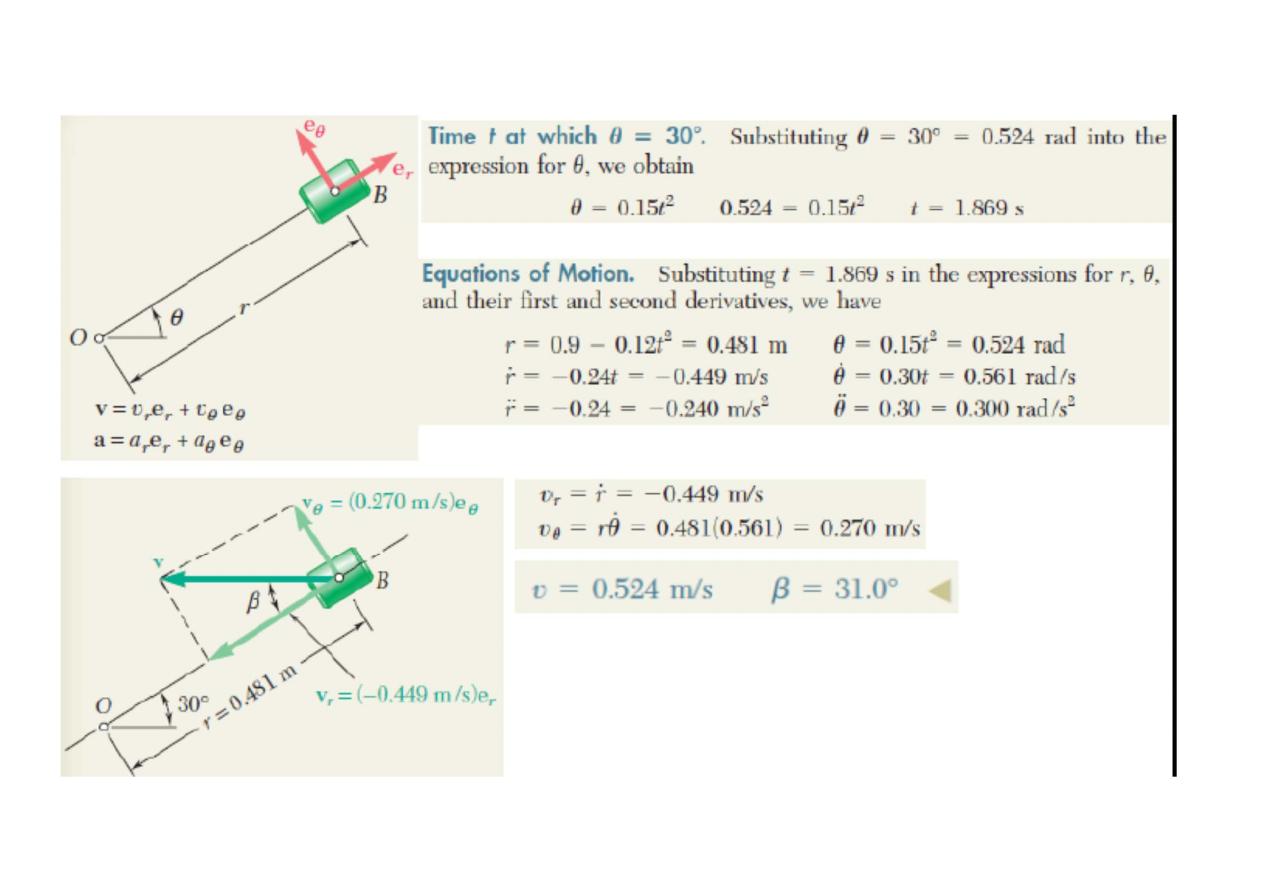
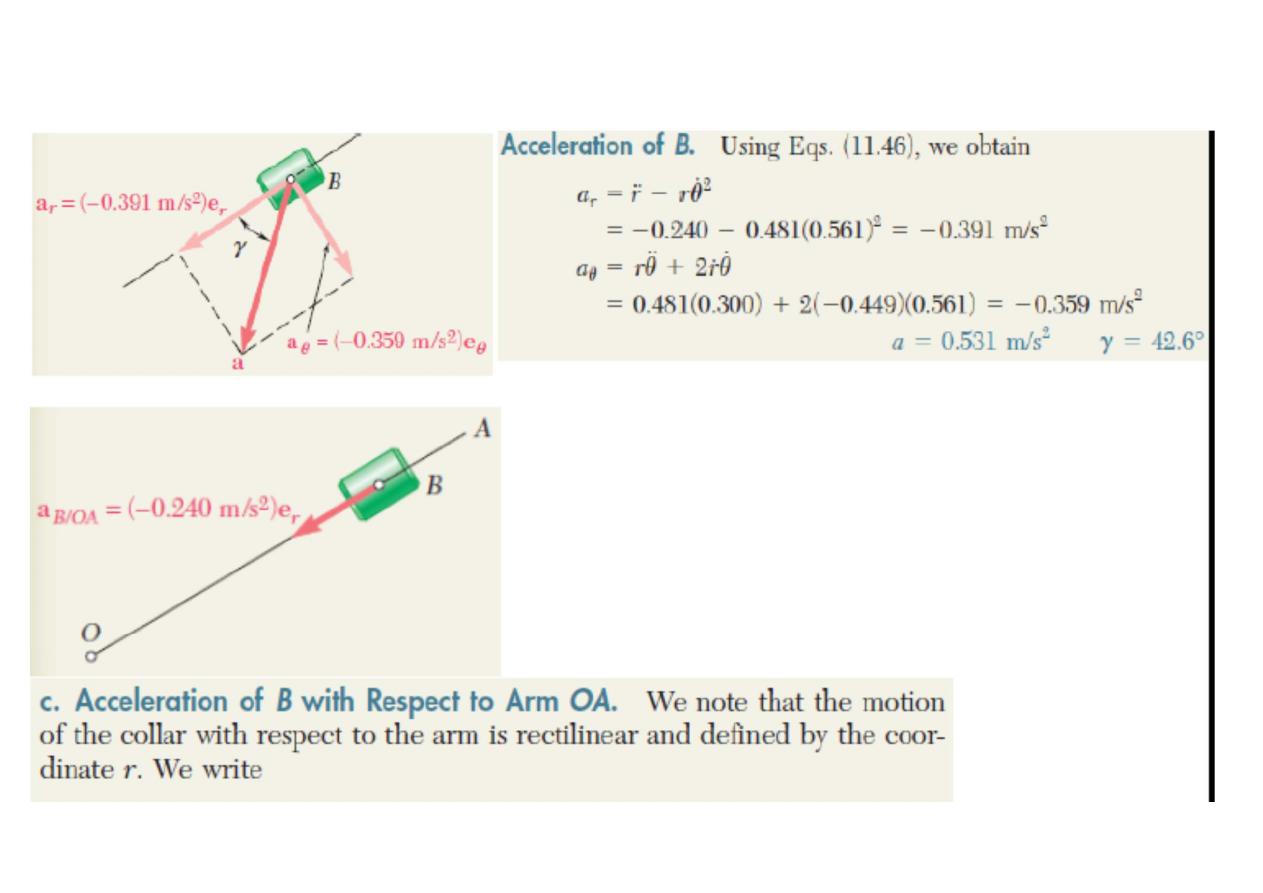
Kinematics of Particles
Particle motion and Choice of Coordinates
Constrained motion: the particle is confined to a
specified path
Unconstrained motion: there are no physical
guides
position of particle P at any time t can be described by specifying its rectangular
coordinates* x, y, z, its cylindrical coordinates r, , z,θ or its spherical coordinates
R,θ , φ .
Absolute-motion
analysis
:
coordinates measured from fixed reference axes
Relative motion
analysis
:
coordinates measured from moving reference axes

Rectilinear Motion

Velocity and Acceleration
then
then

Acceleration and velocity are vector quantities and can be positive or negative
• Differntial equation relating displcement, velocity and acceleration
• For
constant acceleration
we can integrate these equations as follows

SAMPLE PROBLEM 2/1-4 P 27-30




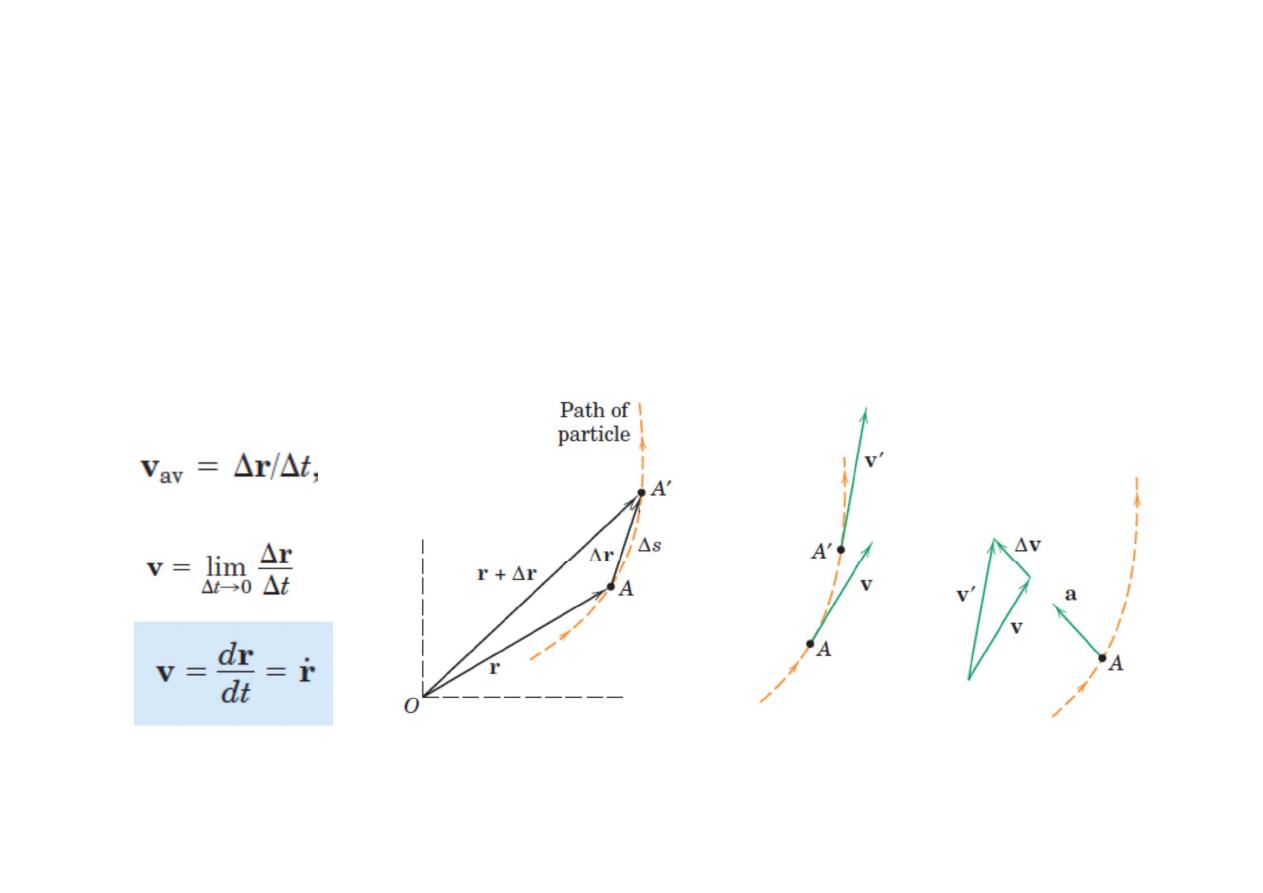
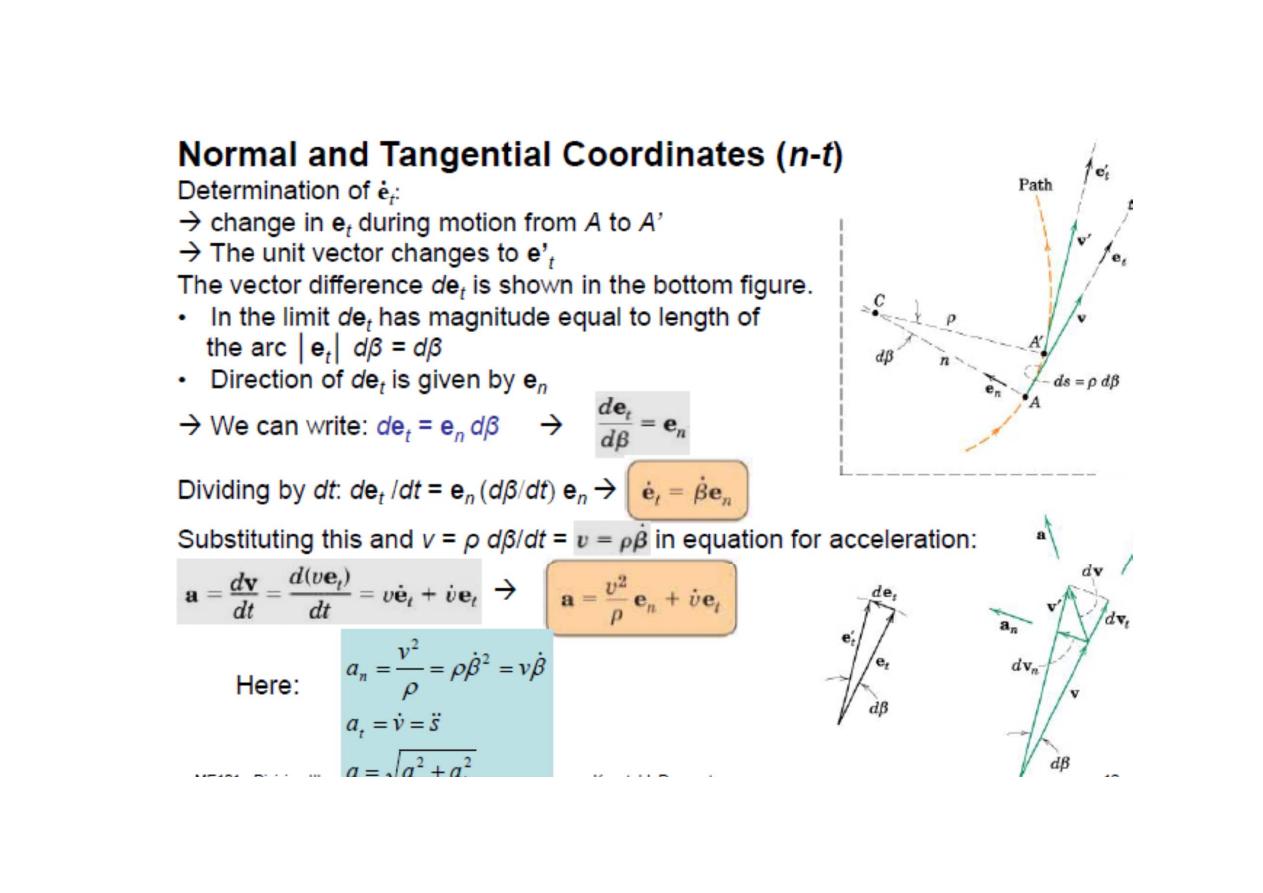
Plane Curvilinear Motion
vector analysis to describe
the motion, since the results will be independent of any particular coordinate
system.
Velocity
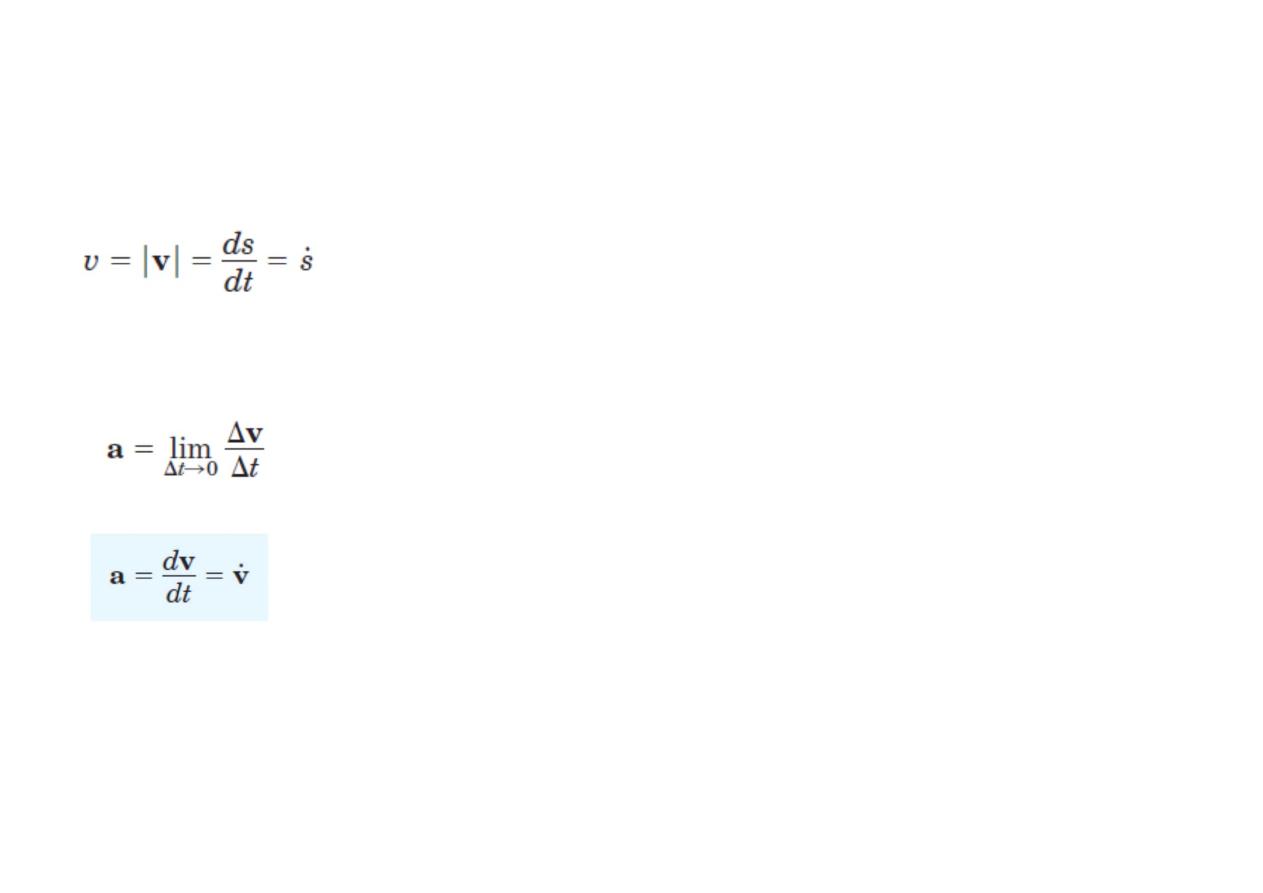
The magnitude of v is called the
speed
and is the scalar
Acceleration
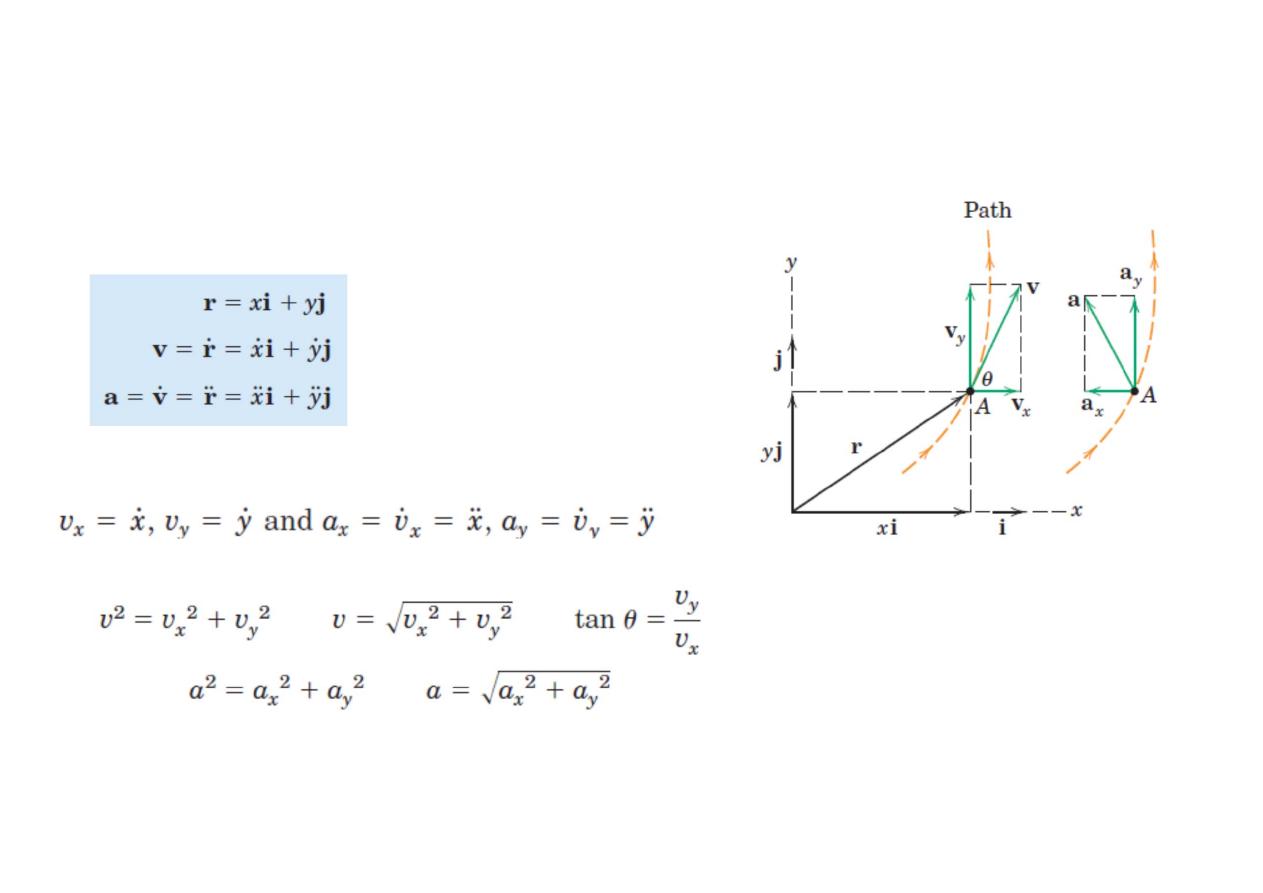
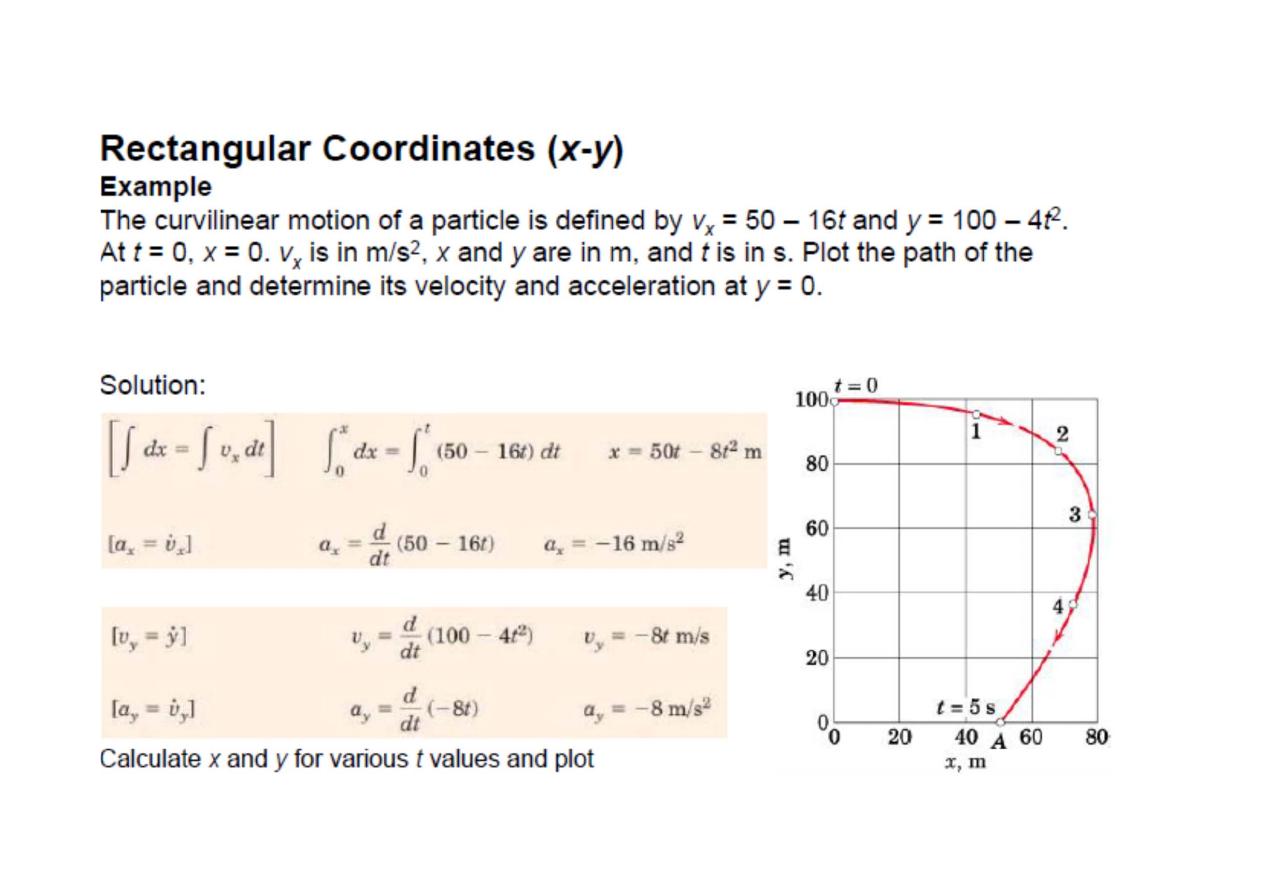
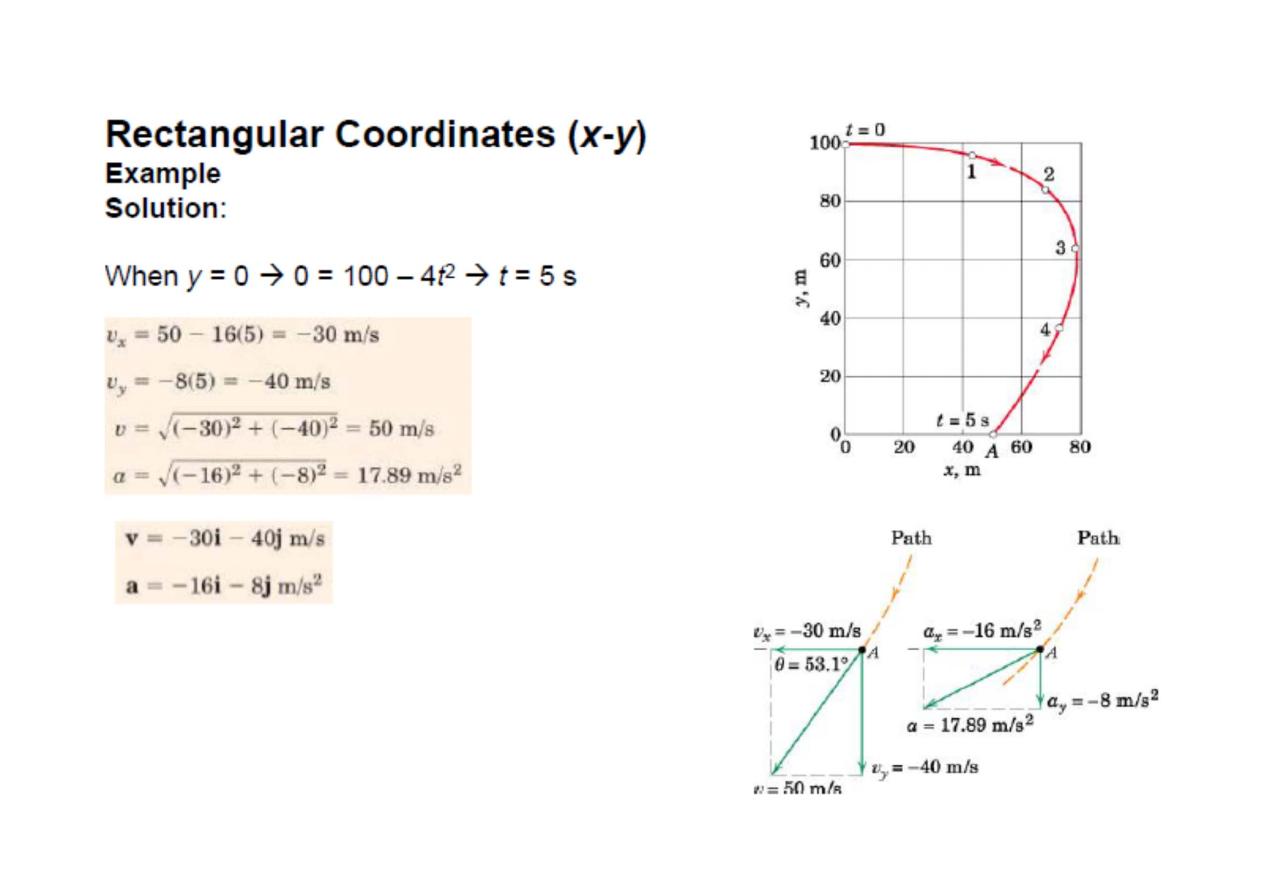
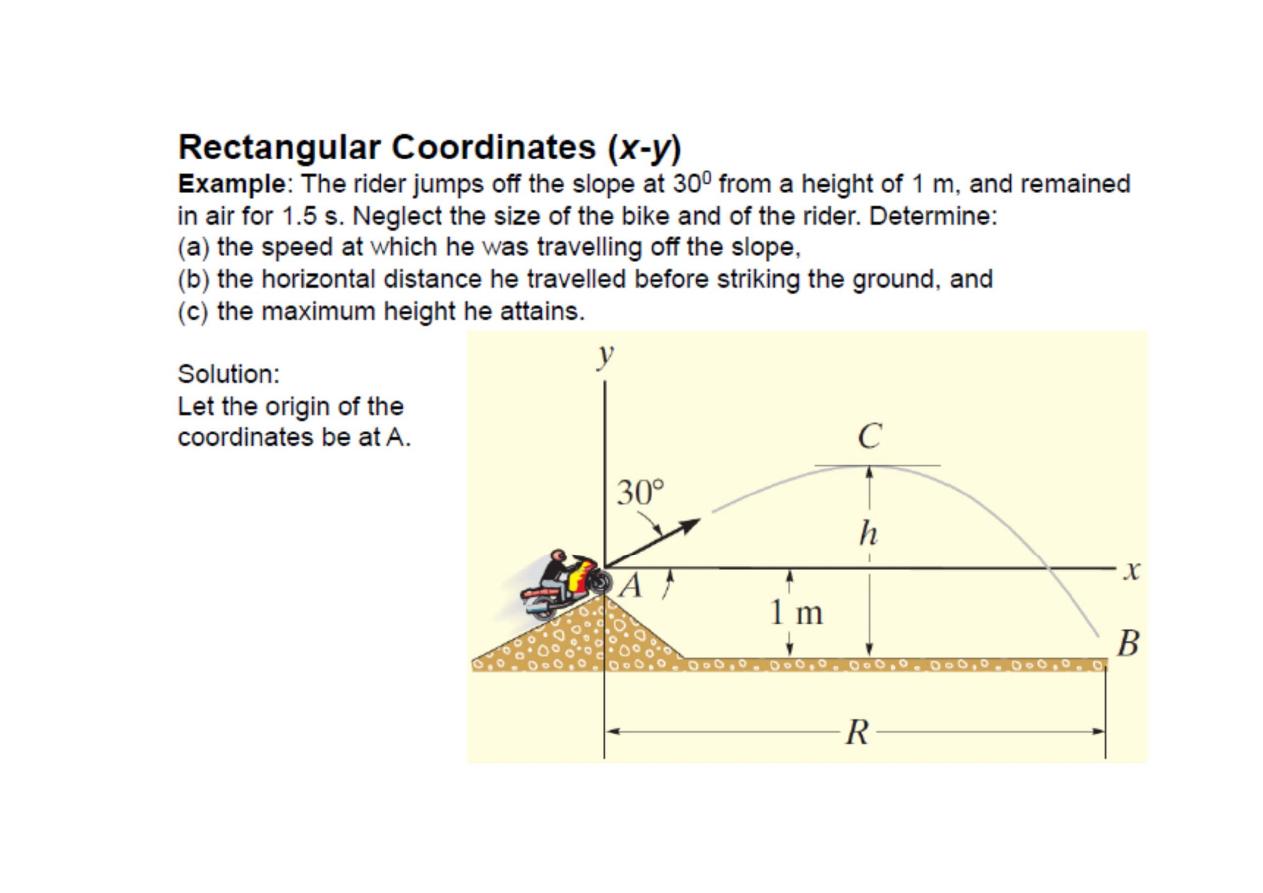
Rectangular Coordinates (x-y)
Vector Representation
The scalar values of the components of v and a
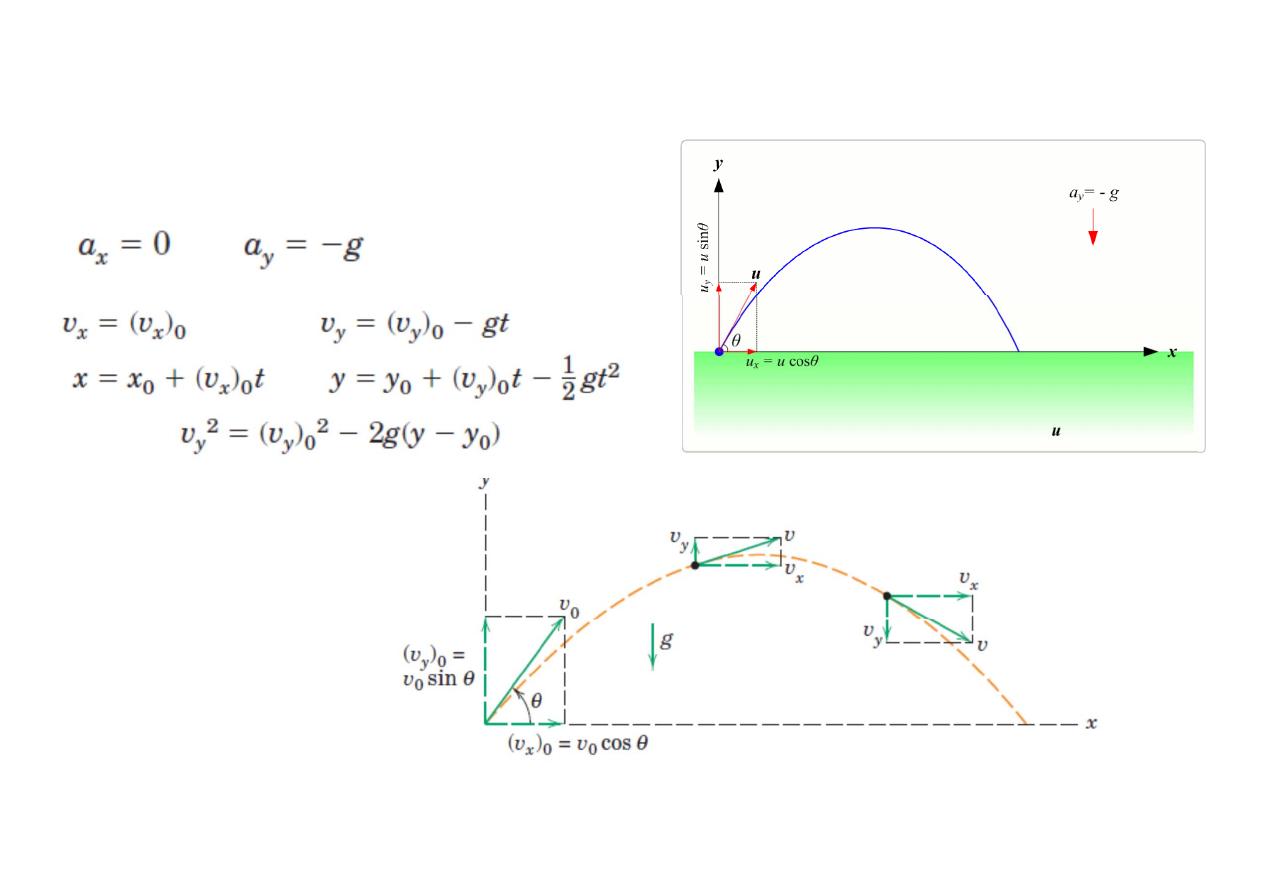
Projectile Motion
1. neglect aerodynamic drag
2.acceleration due to gravity is
constant
acceleration components
the
x
- and
y
-motions are
independent


0.348


2/65
2/67
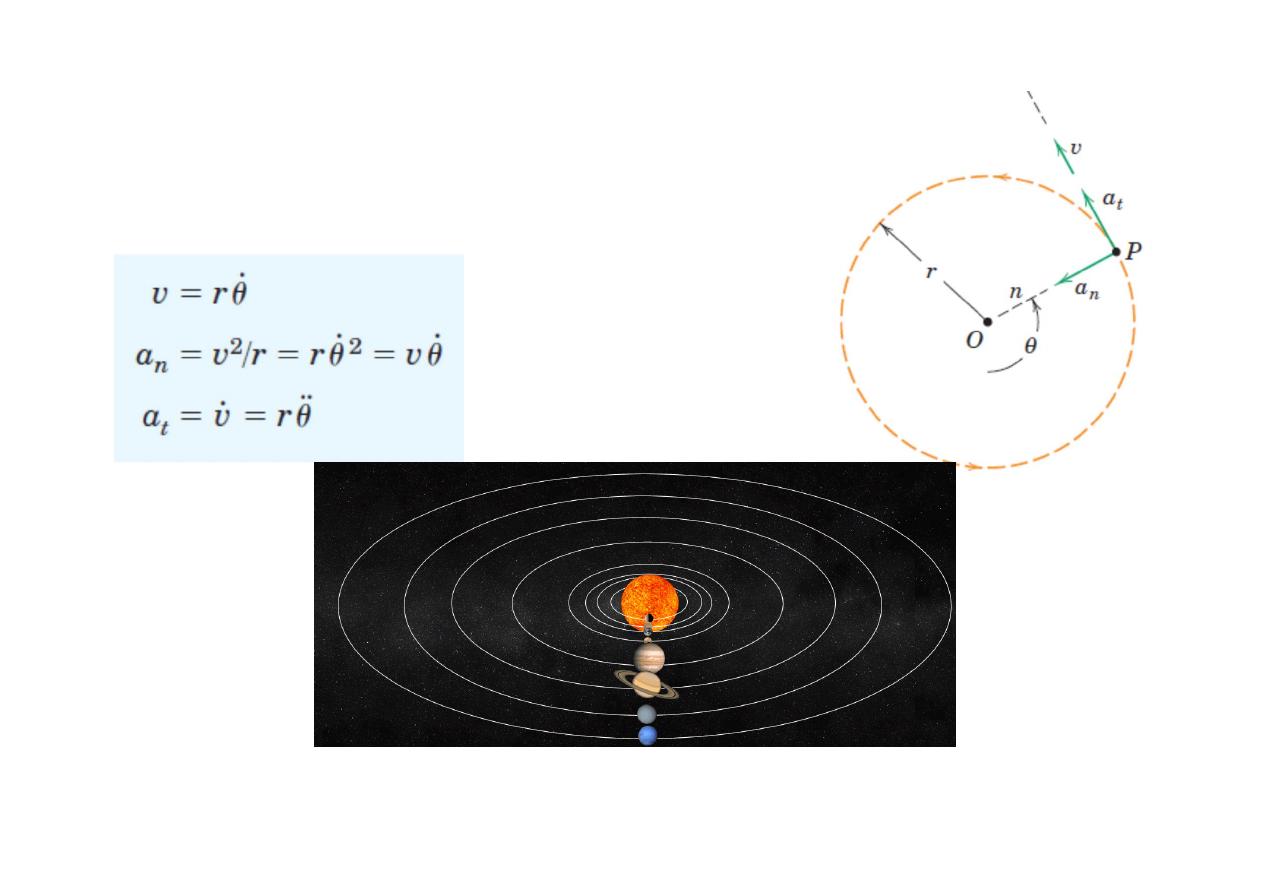
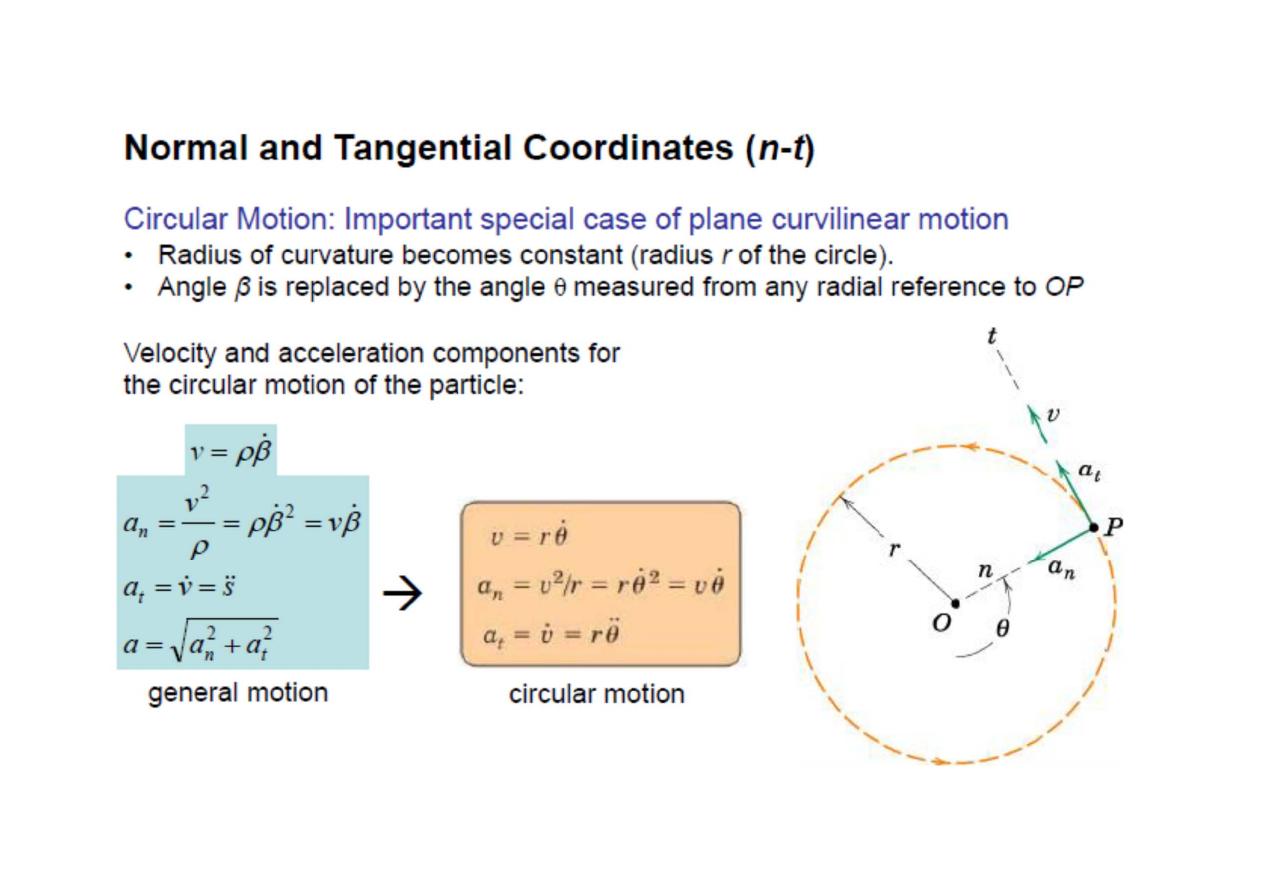
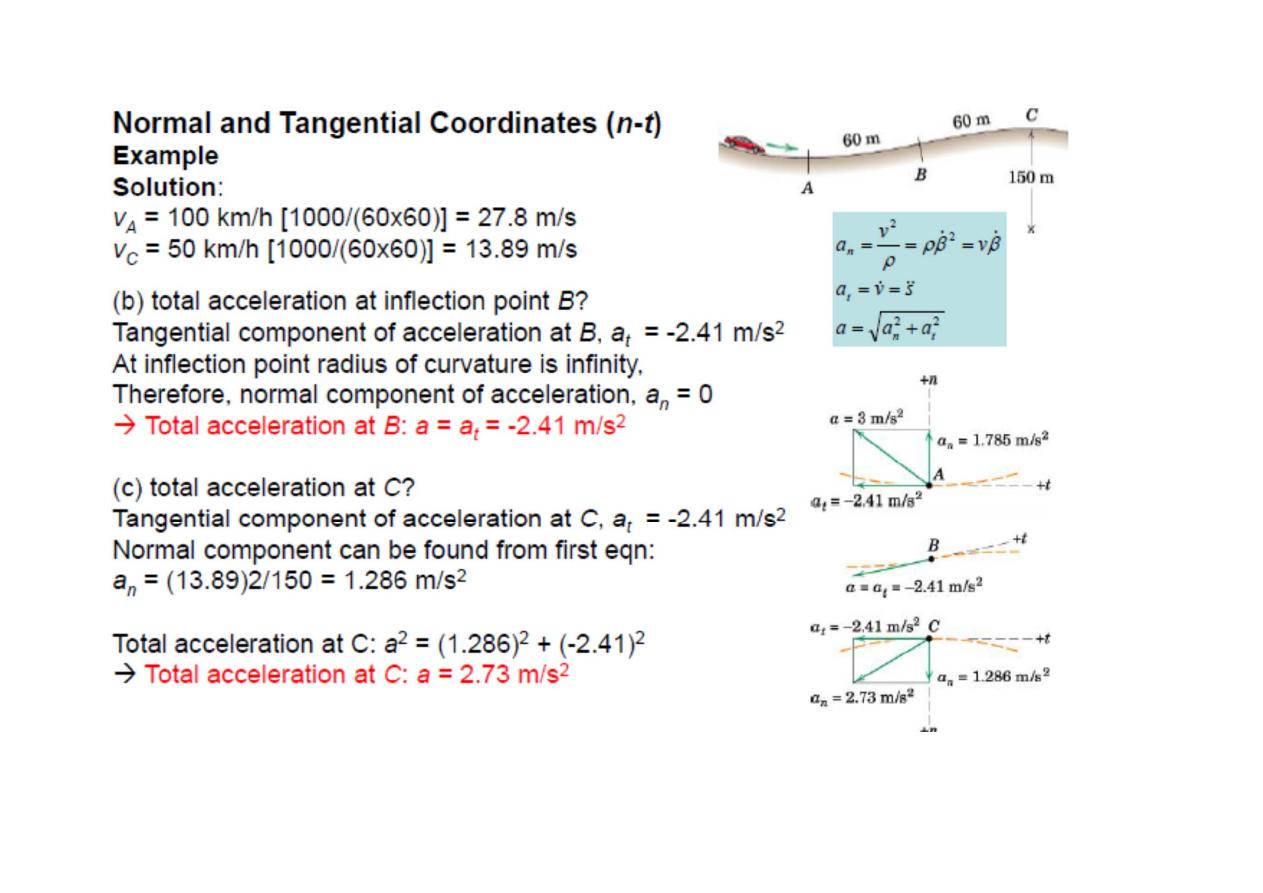
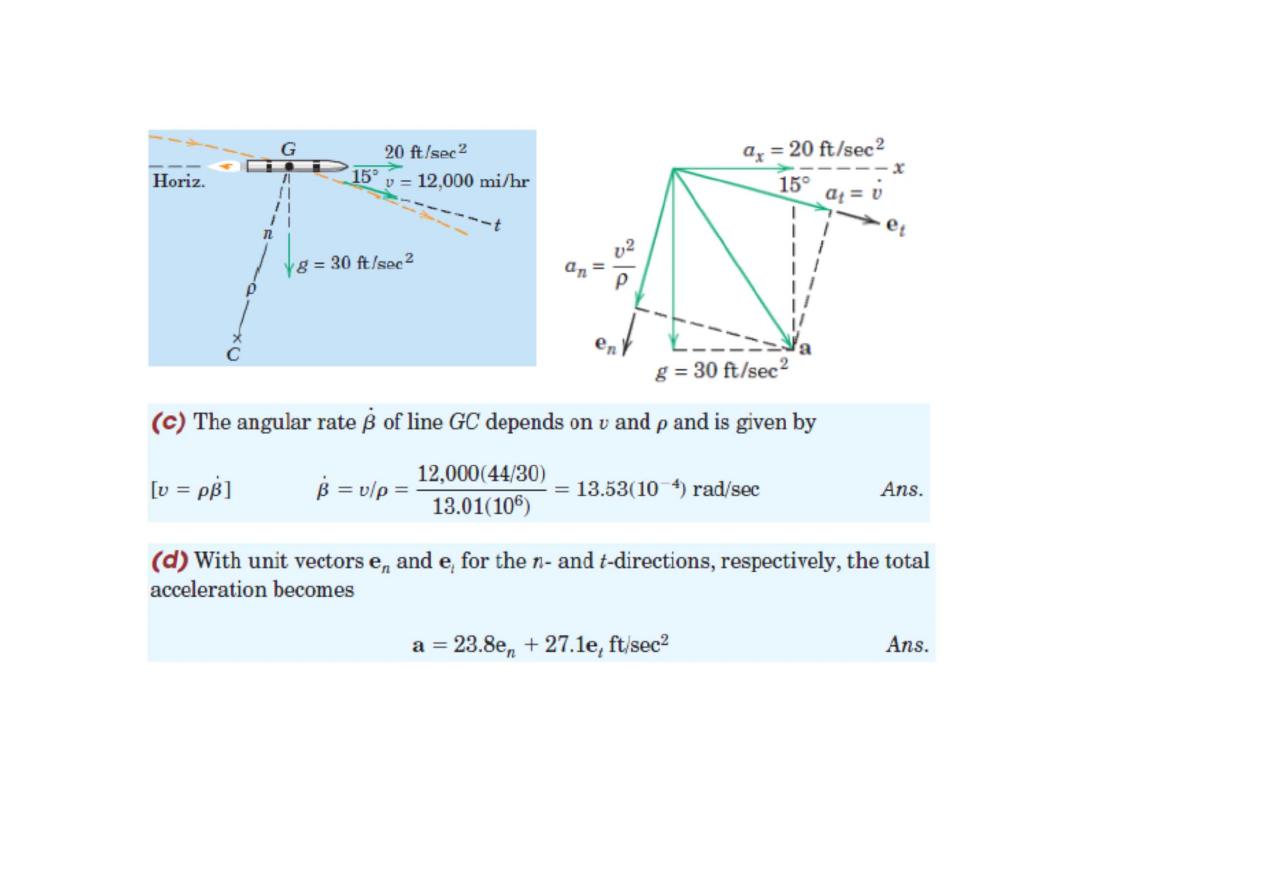
Circular Motion

Plane Curvilinear Motion:
Plan curvilinear motion